Evolution of market shares with repeated purchases and heterogeneous network externalities

Abstract

We investigate how market shares change when a new, superior technology exhibiting network externalities is introduced in a market initially dominated by an old technology. This is done under the assumption that consumers are heterogeneous in their valuation of technology quality and network externalities and that goods are not (perfectly) durable and thus have to be bought repeatedly. When both technologies are unsponsored, the old technology dominates when the quality difference is small, and it disappears when the quality difference is large. When the new technology is sponsored, the relationship between the quality difference and the long-run market share of the new technology is non-monotonic and the old technology always continues to exist.

1 Introduction

The value individuals attach to consuming many technological products (such as telephones, software and hardware) or products that require maintenance depends on how many others are using these goods. This phenomenon is known as network externality. In the literature, it is well-known that network externalities may create barriers to entry, preventing adoption of new goods, possibly of a higher quality. This can lead to the society being “locked-in” with an inefficient technology. A classical—although, according to some (e.g. Liebowitz and Margolis 1990), mistaken—example is the QWERTY standard commonly used in typewriters and computer keyboards (see David 1986). Nuclear power reactors in Europe are another example—the dominant technology is light water, although many scientists consider it to be inferior to heavy water or gas graphite technology (Cowan 1990).

In many situations, the importance of network externalities for the individual adoption decision will differ between different consumers. An important reason for this differentiation is that people use the same technology in a variety of ways, and some require more coordination than others. In the QWERTY example, a large company with many typists and a high rotation of personnel will care more about the network externality than a free-lance journalist, who uses her keyboard herself and for whom typing speed is important. Similarly, a scientist who frequently writes papers together with his colleagues will care more about the possibility of exchanging files than someone who works primarily alone. In the existing literature on technology adoption, however, consumer heterogeneity with respect to their valuation is usually not modeled. Typically, in models with horizontally non-differentiated goods, consumers are either homogenous (as, e.g., in Farrell and Saloner 1986; Katz and Shapiro 1986a, 1992), or they have identical preferences with respect to network externalities (as, e.g., in Farrell and Saloner 1985; Cabral 1990; Agliardi 1994). Another typical feature of existing models is the assumption that users are “stuck” forever (or at least for a long time) with the technology they choose (e.g. Farrell and Saloner 1985, 1986; Katz and Shapiro 1986a, b, 1992).

In this paper, we study the classical question concerning the possibility of “lock-in” in markets where consumers value network externalities. We do this under two novel assumptions. First, we assume that the consumers’ valuation of network externalities and quality is heterogeneous across the population.¹ Second, we assume that users adopt (buy) a technology in every period, and thus they cannot be stuck with their past purchases and do not incur any switching costs. The motivation for this assumption is twofold. First, it extends the analysis of technology adoption to markets of goods which are not durable. One can think here of goods, such as software, which depreciate fast, e.g. due to technological progress, like software. Another group of products to which our analysis may apply are goods of immediate consumption, such as entertainment goods, where network externalities arise due to social considerations. Second, it shows that inefficiencies in technology adoption can arise even if users can switch between technologies costlessly.

Specific questions that we ask here are: is it possible that the new technology is not adopted by anyone, despite its higher quality? If it attracts some users, under what conditions will the new technology take over the market? Does there exist an equilibrium with both technologies present? We also investigate the market shares when the new technology is sponsored by a provider that chooses prices to maximize long-run profits.

To answer these questions, we study a model with two products, an old, inferior good and a new, superior good. We assume that quality can be objectively measured and that consumers differ in their valuation of quality. This means that if product A is of a higher quality than product B, then everyone regards A to be better than B, but for some people, the quality difference is relatively more important than for others. Users differ also in their valuation of network externalities. One could think here for instance of software: some users care mostly about speed, reliability or user-friendliness, whereas for others the ability to exchange files with colleagues or to move them between computers is more important. The valuation for quality is independent of the valuation for network externalities. Consumers decide in every period which good to buy solely on the basis of the present (net) expected utility.

We study the questions outlined above in two different environments. First, in Section 3, we address the pure demand side effect by considering technology adoption in a world where technology is competitively provided and firms are passive. Second, in Section 4, we study the situation in which the new technology is introduced by a profit-maximizing firm, while maintaining the assumption of competitively provided old technology. This assumption, also made by, e.g., Katz and Shapiro (1986a) and Farrell and Saloner (1986), can be justified on the grounds that the new technology is protected by a patent, while the patent on the old technology has already expired so that it is provided competitively, with all firms taking prices as given.²

In every period, market shares adjust to their equilibrium values given the price of the new technology in that period and the market share at the beginning of the period. Our basic results are as follows. When both technologies are not sponsored, two equilibrium market shares may emerge: if the difference in qualities is larger than a certain threshold value, the new technology will be the unique technology in the market. If the quality advantage is lower than this threshold value, the two technologies co-exist and the entrant will have the smallest market share. It is easy to see why the new technology has to have the whole market if it has a market share larger than half: if both quality and market share of one technology are higher, all consumers derive more utility from this product than from the other and, hence, will switch to this new technology. The possible emergence of two equilibrium market shares and the discontinuous jump of market shares at the threshold value are the main results of this section.

Section 4 examines whether these results continue to hold when the new technology is protected by a patent and provided by a price-setting firm. Unlike in the basic model, the market share of the new technology is now non-monotonic in the quality advantage. When the quality difference is small, the long-run market share of the new technology remains small. When the quality difference takes intermediate values, the sponsor of the new technology is able to get a large market share and keep it in the long run. When the quality difference becomes large, the firm can earn a higher profit by raising price to a level at which fewer people with a low valuation of quality adopt the new technology, which allows it to extract more surplus from the quality-loving consumers. Therefore, the fact that the new technology is sponsored results in its having a lower market share.

We also analyze welfare properties of the different equilibrium configurations. Social welfare is maximized when the new technology takes over the whole market. This only happens when the technologies are unsponsored and when the quality difference is high enough. In both the unsponsored and sponsored case, the introduction of a new technology decreases welfare if its quality advantage is small, and it increases welfare when its quality advantage is large.

Since the literature on technology adoption in the presence of network externalities is extensive, we devote a separate section to a brief overview. This is done in Section 2. The rest of the paper is organized as follows. Section 3 on unsponsored technologies considers the pure demand effects due to heterogeneous network externalities. This section allows us to illustrate the main concepts in a relatively simple setting. Section 4 introduces the sponsor of the new technology. Section 5 concludes. Most proofs are given in the Appendix.

2 Related literature

The seminal papers on the adoption of a new, incompatible technology are those by Farrell and Saloner (1985, 1986) and Katz and Shapiro (1986a, b), followed by Katz and Shapiro (1992) and many others. Just as in this paper, two situations are typically studied: in one, technologies are provided by a competitive industry at marginal cost, while in the other, technologies are sponsored. Another way to classify the literature is to distinguish the models where the total number of users remains constant and the network of the new technology arises due to consumers switching from old to new technology (e.g. Farrell and Saloner 1985, 1986; Agliardi 1994; Michihiro 1998), from those where a technology is adopted only once and the new network can arise due to the arrival of new generations (Farrell and Saloner 1986; Katz and Shapiro 1986a, b, 1992; Choi 1994, 1997; De Bijl and Goyal 1995; Regibeau and Rockett 1996). In some of the switching models, the decision to remain in the old network may be changed later, whereas the choice of the new technology is irreversible (Farrell and Saloner 1985).

The literature shows that both too much adoption (excess momentum) and too little (excess inertia) can take place. Consider the case of unsponsored technologies. Excess inertia may arise because users are not sure whether they will be followed if they switch (Farrell and Saloner 1985), because they expect others not to switch (Katz and Shapiro 1992) or because they are not willing to bear a temporary loss of network benefits (Farrell and Saloner 1986). In general, excess inertia follows from the fact that individuals do not take into account the positive effect that their adoption of the new technology would have on others. In models with several generations excess inertia can also take place because the users who arrive first do not wait for the new technology to appear (Choi 1994, 1997; Choi and Thum 1998), or choose the technology that is cheaper now, instead of one that is expected to be cheaper in the future (Katz and Shapiro 1986b). This decreases the welfare of younger users, who must either lose the network of the old users, or use the less efficient technology.

Excess momentum, on the other hand, often arises because, as some users adopt the new technology, those who continue to use the old technology are left with a smaller network (Farrell and Saloner 1986; De Bijl and Goyal 1995; Choi 1994). It can also arise if users have heterogeneous preferences and if it is only possible to commit to the new technology (Farrell and Saloner 1985). In that case, those with a preference for the new technology will switch and the other users may be forced to switch to their less preferred technology. In general, excess momentum arises because users who adopt a new technology do not take into account the negative effect that they have on old users, or on those who will switch later.

New technology sponsorship does not systematically increase or decrease efficiency. Sponsorship can give the new technology an advantage if both technologies are always present, but the old one has a cost (or quality) advantage now, and the new one later (Katz and Shapiro 1986a). In that case, the new producer can price below cost first to build an installed base and raise prices later. On the other hand, if only the new technology is sponsored and is not available in the first period, early users may be unwilling to adopt it because they will expect to be exploited by its sponsor in the future (Choi and Thum 1998). When the timing of the introduction of the new technology is a decision variable, the new technology will tend to be introduced too early, because its sponsor does not take into account the lost network benefits of consumers of the old technology, and the profits of the incumbent (Katz and Shapiro 1992; Regibeau and Rockett 1996).

In the model presented in this paper, the new network arises due to switching, and the cases of both unsponsored technologies and sponsored new technology are studied. Unlike in some models described above, excess momentum is not possible in our model, since the optimal outcome has all users switching to the new technology. That is because, for a given network size, the new technology is preferred by everyone, and because switching is costless. On the other hand, excess inertia can arise when users expect that it will be the case. Sponsorship exacerbates the inertia because a profit-maximizing firm may prefer to extract more surplus from consumers with a high valuation of quality rather than gain as large a market share as possible.

3 Unsponsored technologies

In this section, we describe the demand side in detail and show whether and if so to what extent a new technology will be adopted in markets where the valuations of network size and quality are heterogeneous. We assume here that both technologies are competitively provided, that is, their presence is not connected to any particular seller and their prices are equal to marginal cost (which we assume to be zero). In this section we also define the concept of a stable equilibrium given the initial market share, which we will use in the rest of the paper. We explicitly show how stable equilibrium market shares depend on the quality difference between both technologies.

The technology that consumers buy lasts one period. In each period, therefore, consumers decide whether or not to adopt one of the available technologies. Each consumer chooses the technology that maximizes expected utility in that period.

As explained in the Introduction, all consumers care about quality and about network externalities, but the importance of these factors varies across consumers. The utility from consuming nothing is zero, while the actual utility from consuming each technology depends on its quality, market share (which represents network externalities), and the consumer’s type, given by a pair of coefficients (α,β). More precisely,

$$ \begin{array}{*{20}c} {{u^{1}_{\theta } {\left( {x_{t} } \right)} = v + \alpha q_{1} + \beta x_{t} }} & {{{\text{for}}\;{\text{the}}\;{\text{new}}\;{\text{technology}}\;{\text{,}}\;{\text{and}}}} & {{u^{0}_{\theta } {\left( {x_{t} } \right)} = v + \alpha q_{0} + \beta {\left( {1 - x_{t} } \right)}}} & {{{\text{for}}\;{\text{the}}\;{\text{old}}\;{\text{technology,}}}} \\ \end{array} $$

where ν > 0 is the basic valuation for any technology, q ₁ > q ₀ > 0 are qualities of the new and old technology and x _t ∈(0, 1) is the market share of the new technology in period t. Since adopting a technology gives always non-negative utility, the market is covered, and we take 1 − x _t to be the market share of the old technology. The coefficient α determines the consumer’s valuation of quality, while β is the valuation of popularity. We assume that α and β are independently and uniformly distributed on the interval (0,1). As the market shares in period t are unknown at the beginning of the period when consumers decide which technology to adopt, we denote by $E{\left[ {u_{{\alpha ,\beta }} {\left( t \right)}} \right]}$ the expected utility of consumer (α,β) in period t and it follows that

$$ E{\left[ {u_{{\alpha ,\beta }} {\left( t \right)}} \right]} = \left\{ {\begin{array}{*{20}l} {{\begin{array}{*{20}c} {{E{\left[ {u^{1}_{{\alpha ,\beta }} {\left( t \right)}} \right]} = u^{1}_{{\alpha ,\beta }} {\left( t \right)}}} \\ {{E{\left[ {u^{0}_{{\alpha ,\beta }} {\left( t \right)}} \right]} = u^{0}_{{\alpha ,\beta }} {\left( t \right)}}} \\ {0} \\ \end{array} } \hfill} & {{\begin{array}{*{20}l} {{{\text{if}}\;{\left( {\alpha {\text{,}}\beta } \right)}\;{\text{consumes}}\;{\text{the}}\;{\text{new}}\;{\text{technology,}}} \hfill} \\ {{{\text{if}}\;{\left( {\alpha {\text{,}}\beta } \right)}\;{\text{consumes}}\;{\text{the}}\;{\text{old}}\;{\text{technology,}}} \hfill} \\ {{{\text{if}}\;{\left( {\alpha {\text{,}}\beta } \right)}\;{\text{consumes}}\;{\text{no}}\;{\text{technology}}{\text{.}}} \hfill} \\ \end{array} } \hfill} \\ \end{array} {\text{ }}} \right. $$

The sequencing of actions is as follows. Initially, only the old technology is available in the market, and everyone is consuming it. At the beginning of the game the new, better technology becomes available to consumers, who then make a choice based on comparison of expected utilities. A consumer of type (α,β) chooses the new technology, if and only if,

$$ v + \alpha q_{1} + \beta Ex_{t} \geqslant v + \alpha q_{0} + \beta {\left( {1 - Ex_{t} } \right)} $$

where Ex _t is the expected market share of the new technology in period t. We define an equilibrium of this model as a situation in which (1) every consumer maximizes his (expected) utility given his expectations about market share and (2) the expectations are fulfilled. More formally,

Definition 1

An equilibrium is a pair (Ex,x) such that

• 1. Each consumer (α,β) maximizes $E{\left[ {u_{{\alpha ,\beta }} {\left( t \right)}} \right]}$ given Ex _t  = Ex,

• 2. Ex = x.

In the case of unsponsored technologies, equilibria can be easily characterized. Let $q = q_{1} - q_{0}$. If there exists a set of indifferent consumers (α ^*, β ^*), then it must be true that there exist pairs (α ^*, β ^*), 0 < α ^* < 1 and 0 < β ^* < 1, such that

$$\alpha ^{ * } q = \beta ^{ * } {\left( {1 - 2Ex_{t} } \right)}$$

(1)

and all consumers with $\alpha ^{ * } \geqslant {\beta ^{ * } {\left( {1 - 2Ex_{t} } \right)}} \mathord{\left/ {\vphantom {{\beta ^{ * } {\left( {1 - 2Ex_{t} } \right)}} q}} \right. \kern-\nulldelimiterspace} q$ (and only those) choose the new technology. Note that, in equilibrium, either x = 1, or x < 1/2. If 1/2 < x < 1, then all consumers prefer the new technology, which is a contradiction. The distribution of consumers among both technologies for x _t  < 1/2 is shown in Fig. 1.

Fig. 1

Distribution of two technologies

Since α and β are uniformly distributed, the market share of the new technology is equal to the area of the shaded triangle. Observe that 0 < x _t  < 1/2 implies ${1 > q} \mathord{\left/ {\vphantom {{1 > q} {{\left( {1 - 2Ex_{t} } \right)} > 0}}} \right. \kern-\nulldelimiterspace} {{\left( {1 - 2Ex_{t} } \right)} > 0}$. Thus, in equilibrium

$$ x = {0.5q} \mathord{\left/ {\vphantom {{0.5q} {{\left( {1 - 2x} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {1 - 2x} \right)}}, $$

which after transformation gives a quadratic equation that can be solved for x.

$$ - 2x^{2} + x - 0.5q = 0 $$

(2)

Basically, two possibilities emerge:

• a. If q ≥ 0.25, then Eq. 2 has no solution with x < 1. In this case, the only equilibrium is x = 1.

• b. If q < 0.25, then Eq. 2 has two solutions: $x_{1} = \frac{{1 - {\sqrt {1 - 4q} }}} {4}$ and $x_{2} = \frac{{1 + {\sqrt {1 - 4q} }}} {4}$.

If the expectations of consumers are rational, the game is essentially static: consumers correctly predict the equilibrium market shares. If multiple equilibria are possible, the outcome will depend on which equilibrium is expected to arise. We consider a dynamic adjustment process where boundedly rational consumers have adaptive expectations, with $Ex_{t} = x_{{t - 1}}$. In that case the equilibrium that is eventually reached depends on the initial conditions. Figure 2 illustrates the dynamic process when the quality advantage of the new technology is q < 0.25.

Fig. 2

The dynamic process when the quality advantage of the new technology is q < 0.25 

From the Figure it is clear that x ₁ is the stable equilibrium for x ₀ < x ₂, and x = 1 is the stable equilibrium if x ₀ > x ₂. x ₂ is also an equilibrium, but it is not stable: a very small change in market share in either direction would make the system converge to either x ₁, or x = 1. Using this dynamic analysis, we may define a stable equilibrium given an initial market share of x ₀ as follows:

Definition 2

A stable equilibrium given an initial market share of x ₀ is a pair (Ex,x) which (1) satisfies Definition 1 and (2) emerges as the stable outcome of the dynamic model in which consumers’ expectations are given by $Ex_{t} = x_{{t - 1}}$ and the initial market share of the new technology is x ₀.

The above analysis can then be summarized as follows.

Proposition 1

The stable equilibrium market share given x ₀  = 0 is

$$ \begin{array}{*{20}l} {{x = 1} \hfill} & {{if} \hfill} & {{q \geqslant 0.25} \hfill} \\ {{x = \frac{{1 - {\sqrt {1 - 4q} }}} {4}} \hfill} & {{if} \hfill} & {{q < 0.25.} \hfill} \\ \end{array} $$

Figure 3 shows the equilibrium market share of the new technology as a function of its quality advantage. The equilibrium market share of the new technology will be either 1, or less than 0.25. Which of them arises depends on the quality difference. A larger quality advantage leads to a larger market share, which is quite intuitive. However, the market share does not increase continuously with the quality difference: there is a critical value, $\overline{q} = 0.25$, such that, if $q < \overline{q}$, the equilibrium market share is less than 0.25, and if $q > \overline{q}$, the new technology gains the whole market. This is caused by the critical mass effect: once the new technology has a sufficiently large market, it will be preferred by all types of consumers, not only those with a taste for quality. Moreover, we see that, if q > 0, the better technology always has some market share. This follows from the idea that there are some consumers who care almost only about quality.

Fig. 3

The equilibrium market share of the new technology

We now compare social welfare before and after the introduction of the new technology. In the case of unsponsored technology, the welfare is equal to the sum of individual consumer surpluses. Note that, since the market is always covered, the surplus must always be at least v, the sum of consumers’ basic valuations. When everyone consumes only one technology, the total surplus is

$$ SW = v + {\int\limits_0^1 {{\int\limits_0^1 {{\left( {\alpha q_{0} + \beta } \right)}d\alpha d\beta } } = v + {{\left( {q_{0} + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {q_{0} + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2,} } $$

before the introduction of the new technology, and

$$ SW = v + {\int\limits_0^1 {{\int\limits_0^1 {{\left( {\alpha q_{0} + \beta } \right)}d\alpha d\beta } } = v + {{\left( {q_{1} + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {q_{1} + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2,} } $$

if everyone uses the new technology. Thus, the surplus change in case everyone switches to the new technology is $\Delta SW = q \mathord{\left/ {\vphantom {q 2}} \right. \kern-\nulldelimiterspace} 2 > 0$. This is the situation in which social welfare is maximized: everyone uses the technology of the highest quality and enjoys maximum network benefits.

If the new technology has only a small market share in equilibrium, the welfare effect is not obvious: the consumers who use the new technology in the equilibrium derive more utility from its quality, but they lose a large part of the network externality. The remaining consumers do not gain anything in terms of quality and they lose a part of the network benefits.

The net effect on total surplus is calculated by the surplus change for the users of the new technology

$$ \Delta CS_{1} = {\int\limits_0^{\frac{q} {{1 - 2x}}} {{\int\limits_{\frac{{1 - 2x}} {q}\beta }^1 {{\left( {\alpha q_{1} + \beta x - {\left( {\alpha q_{0} + \beta } \right)}} \right)}d\alpha d\beta } }} } = \frac{{{\left( {1 - 3x} \right)}q^{2} }} {{6{\left( {1 - 2x} \right)}^{2} }} = \frac{{{\left( {3{\sqrt {1 - 4q} } + 1} \right)}q^{2} }} {{6{\left( {{\sqrt {1 - 4q} } + 1} \right)}^{2} }} > 0, $$

and for the users of the old technology

$$ \begin{array}{*{20}c} {\Delta CS_{0} = {\int\limits_0^{\frac{q} {{1 - 2x}}} {{\int\limits_0^{\frac{{1 - 2x}} {q}\beta } {{\left( { - \beta x} \right)}d\alpha d\beta } } + } }{\int\limits_{\frac{q} {{1 - 2x}}}^1 {{\int\limits_0^1 {{\left( { - \beta x} \right)}d\alpha d\beta } }} } = \frac{{{\left( {q^{2} - 3{\left( {1 - 2x} \right)}^{2} } \right)}x}} {{6{\left( {1 - 2x} \right)}^{2} }} = } \\ { = \frac{{{\left( {4q^{2} + 12q - 6 - 6{\sqrt {1 - 4q} }} \right)}{\left( {1 - {\sqrt {1 - 4q} }} \right)}}} {{24{\left( {1 + {\sqrt {1 - 4q} }} \right)}^{2} }} < 0.} \\ \end{array} $$

Thus, the total welfare change equals

$$ \Delta SW = - \frac{{q{\left( {3 - 2q} \right)}{\left( {1 + {\sqrt {1 - 4q} }} \right)}}} {{12{\left( {1 - 2q + {\sqrt {1 - 4q} }} \right)}}} < 0. $$

Thus, if the equilibrium market share of the new technology is small, the loss of network benefits dominates the gain from higher quality and social welfare decreases. The larger the equilibrium market share of the new technology, the larger the loss.

The bold line in Fig. 4 shows how social welfare in equilibrium depends on the quality difference, given that the quality of the old technology, q ₀, is fixed. The welfare before the introduction of the new technology is represented by the horizontal line, and the diagonal dashed line shows welfare in the optimum, which, for higher q, coincides with the equilibrium outcome. As q increases, equilibrium social welfare changes nonmonotonically. Initially it decreases and moves away from the social optimum, because the market share of the new technology grows, and network benefits for users of the old technology fall. When q reaches its critical value, the social optimum is achieved where the new technology gets the whole market.

Fig. 4

Social welfare change

4 Sponsored new technology

In this section, we analyze the case where the new technology is put on the market by a firm that sets prices to maximize profits. The old technology is still unsponsored and available at price zero. To study the changing incentives of the firm as its market share changes, we consider an infinite price-setting process, in which, in every period T, first the firm chooses the price, and then the equilibrium market share given initial x ₀ is determined by the dynamic adjustment process described in Section 3, where consumers make their decisions by comparing net utilities.

After the firm has chosen its price, consumers make their choices, comparing the net expected period T utilities from choosing each technology:

$$ \begin{array}{*{20}l} {{E{\left[ {u^{1}_{\theta } {\left( T \right)}} \right]} - p_{T} = v + \alpha q_{1} + \beta Ex_{T} - p_{T} } \hfill} \\ {{E{\left[ {u^{0}_{\theta } {\left( T \right)}} \right]} = v + \alpha q_{0} + \beta {\left( {1 - Ex_{T} } \right)}.} \hfill} \\ \end{array} $$

(3)

Since the price is set in every period T, new stable equilibria and new market shares may arise in every period. As a stable equilibrium market share depends on the initial market share, the market share in period T influences the market share in period T + 1.

At the beginning of every period T, the firm sets the price in order to maximize its total discounted profits. Thus, the firm maximizes

$$ \Pi = {\sum\limits_{T = 1}^\infty {\delta ^{{T - 1}} \Pi _{T} } }, $$

where δ∈[0,1) is a discount factor and Π _T is the firm’s profit in period T. Since production costs are zero, per-period profits are

$$ \Pi _{T} = p_{T} x_{T} . $$

The outcome of the maximalization will be a sequence of prices and market shares, ${\left[ {p_{T} ,x_{T} } \right]}^{\infty }_{{T = 1}}$. We first derive the per-period demand function for the new technology, i.e. the stable equilibrium market share which arises in each period given the price of the new technology and initial market shares. Next, we describe the optimal pricing strategy of the firm.

To calculate demand, we use the same definitions of stable equilibrium market shares as in Section 3. From Eq. 3 it follows that a consumer (α,β) chooses the new technology, if

$$ aq + \beta {\left( {2Ex_{T} - 1} \right)} - p_{T} \geqslant 0. $$

Note first that everyone prefers the new technology if and only if Ex _T  > 1/2 and p _T  = 0, whereas everyone prefers the old technology if and only if Ex _T  < 1/2 and p _T  > q. It follows that, if p _T  = 0, there exists an equilibrium with x _T  = 1, while if p _T  > q, there exists an equilibrium with x _T  = 0. In both cases, there might also exist other equilibria, in which 0 < x _T  < 1. When 0 < p _T  < q, only such equilibria are possible. Depending on the values of p _T and q, five types of situations (and potential equilibria) with 0 < x _T  < 1 exist. These types are illustrated in Figs. 5 and 6. The shaded area shows the consumers who prefer the new technology given the expected market share Ex _t (and thus its resulting market share in subperiod t, x _t ), while the remaining consumers have a preference for the old technology. In equilibrium, Ex _t  = x _t .

Fig. 5

a p _T  < q and $Ex_{t} < {{\left( {p_{T} - q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} - q + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$. b p _T  < q and ${{\left( {p_{T} - q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} - q + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2 < Ex_{t} < {{\left( {p_{T} + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$. c p _T  < q and $Ex_{t} > {{\left( {p_{T} + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$

Fig. 6

a p _T  > q and $Ex_{t} > {{\left( {p_{T} + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$. b p _T  > q and ${{\left( {p_{T} - q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} - q + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2 < Ex_{t} < {{\left( {p_{T} + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$

Note that the situation represented in Fig. 6a cannot be an equilibrium: it is clear from the figure that x _T  < 1/2, which contradicts $x_{T} = Ex_{T} > {{\left( {p_{T} - q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} - q + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$. That leaves four possible equilibria to be considered. The eventual outcomes depend on the value of q, the quality difference between technologies. Lemmas 1–3 characterize the demand function of the firm for different values of the quality difference q. The proof of Lemma 2, the most difficult one, can be found in the Appendix; other proofs are available upon request.

Lemma 1

Suppose that q > 1. The demand function of the firm in period T is

$$ \begin{array}{*{20}l} {{ - \quad x_{T} = 0} \hfill} & {{if\;p_{T} > q,} \hfill} \\ {{ - \quad x_{T} = \frac{{q - {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }}} {{4q}}} \hfill} & {{{if\;q^{2} } \mathord{\left/ {\vphantom {{if\;q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}} < p_{T} \leqslant q,} \hfill} \\ {{ - \quad x_{T} = \frac{{2q - 2p_{T} - 1}} {{2{\left( {q - 1} \right)}}}} \hfill} & {{if\;q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}} < {p_{T} \leqslant q^{2} } \mathord{\left/ {\vphantom {{p_{T} \leqslant q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}},} \hfill} \\ {{ - \quad x_{T} = \frac{{3q + {\sqrt {q{\left( {q - 4p^{2}_{T} } \right)}} }}} {{4q}}} \hfill} & {{if\;p_{T} \leqslant q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}.} \hfill} \\ \end{array} $$

Lemma 2

Suppose that 0.25 ≤ q ≤ 1. The demand function of the firm in period T is

• $\begin{array}{*{20}c} {{x_{T} = 0}} & {{if\;p_{T} > q,}} \\ \end{array}$

• $x_{T} = \frac{{q - {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }}} {{4q}}$ $if\;p_{T} > {{\sqrt q }} \mathord{\left/ {\vphantom {{{\sqrt q }} 2}} \right. \kern-\nulldelimiterspace} 2$ , or $\begin{array}{*{20}l} {{if\;q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}} < p_{T} < {{\sqrt q }} \mathord{\left/ {\vphantom {{{\sqrt q }} 2}} \right. \kern-\nulldelimiterspace} 2} \hfill} & {{and} \hfill} & {{x_{{T - 1}} < {{\left( {3q - {\sqrt {q{\left( {q - 4p^{2}_{T} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {3q - {\sqrt {q{\left( {q - 4p^{2}_{T} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q},\,\quad or} \hfill} \\ {{if\;{q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}} < p_{T} < q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}} \hfill} & {{and} \hfill} & {{x_{{T - 1}} < {{\left( {1 - 2q + 2p_{T} } \right)}} \mathord{\left/ {\vphantom {{{\left( {1 - 2q + 2p_{T} } \right)}} {{\left[ {2{\left( {1 - q} \right)}} \right]}}}} \right. \kern-\nulldelimiterspace} {{\left[ {2{\left( {1 - q} \right)}} \right]}},\quad or} \hfill} \\ {{if\;{{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2 < p_{T} < {q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}} \hfill} & {{and} \hfill} & {{x_{{T - 1}} < {{\left( {q + {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {q + {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q},} \hfill} \\ \end{array}$

• $x_{T} = \frac{{3q + {\sqrt {q{\left( {q - 4p^{2}_{{T - 1}} } \right)}} }}} {{4q}}$ otherwise.

Lemma 3

Suppose that q < 0.25. The demand function of the firm in period T is

• 1. If p _T  > q

  • $\begin{array}{*{20}l} {{x_{T} = 0,} \hfill} & {{if\;p_{T} \geqslant {{\left( {4q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {4q + 1} \right)}} 8}} \right. \kern-\nulldelimiterspace} 8,\quad or} \hfill} \\ {{} \hfill} & {{if\;q \leqslant p_{T} < {{\left( {4q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {4q + 1} \right)}} 8}} \right. \kern-\nulldelimiterspace} 8\quad and\quad x_{{T - 1}} < {{\left( {3 - {\sqrt {4q - 8p_{T} + 1} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {3 - {\sqrt {4q - 8p_{T} + 1} }} \right)}} 4}} \right. \kern-\nulldelimiterspace} 4.} \hfill} \\ \end{array}$

  • $x_{T} = \frac{{3 + {\sqrt {4q - 8p_{T} + 1} }}} {4}$ otherwise.

• 2. If p _T  < q

  • $x_{T} = \frac{{q - {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }}} {{4q}}$, $\begin{array}{*{20}l} {{if\;p_{T} > q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}} \hfill} & {{and} \hfill} & {{x_{{T - 1}} < {{\left( {3q - {\sqrt {q{\left( {q - 4p^{2}_{{T - 1}} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {3q - {\sqrt {q{\left( {q - 4p^{2}_{{T - 1}} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q},\quad or} \hfill} \\ {{if\;{q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}} < p_{T} < q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}} \hfill} & {{and} \hfill} & {{x_{{T - 1}} < {{\left( {1 - 2q + 2p_{T} } \right)}} \mathord{\left/ {\vphantom {{{\left( {1 - 2q + 2p_{T} } \right)}} {{\left[ {2{\left( {1 - q} \right)}} \right]}}}} \right. \kern-\nulldelimiterspace} {{\left[ {2{\left( {1 - q} \right)}} \right]}},\quad or} \hfill} \\ {{if\;p_{T} < {q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}} \hfill} & {{and} \hfill} & {{x_{{T - 1}} < {{\left( {q - {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {q - {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q},} \hfill} \\ \end{array}$

  • $x_{T} = \frac{{3q + {\sqrt {q{\left( {q - 4p^{2}_{T} } \right)}} }}} {{4q}}$ otherwise.

Figures 7a–c illustrate Lemmas 1–3, showing the market share of the firm as a function of its price. In comparison to the case of unsponsored new technology, two additional equilibrium market shares are possible: no entry of the new superior good, x _T  = 0, and a market share of the new technology that is larger than half, but smaller than 1. When the price of the new technology is larger than zero, some potential customers will not find it worthwhile to buy it even if they have a preference for high quality and a large network.

Fig. 7

a q > 1. b 0.25 < q<1. c q < 0.25

The shape of the demand function depends on the value of the quality difference between technologies. Most striking is the difference between the cases q > 1 and 0.25 < q < 1. For large q, the demand function is continuous and each price can only lead to one value of demand, which is not the case if q < 1. The reason is that, for large q, network externalities, which are the cause of the discontinuity, are relatively less important. The total value of network externalities, βx or β(1 − x _T ), cannot be larger than one, while the total value of increased quality, αq, is larger than one for at least some consumers. Therefore, the demand function for the case q > 1 resembles the demand function for the case where no network externalities are present (thus β = 0 for all consumers). For a comparison, we depict this demand function, described by the expression $x_{T} = 1 - p \mathord{\left/ {\vphantom {p q}} \right. \kern-\nulldelimiterspace} q$, in Fig. 7a as a dashed line. Compared to the case with β = 0, the presence of network externalities increases the elasticity of demand, except for the case when p is very low or very high. In these cases, the consumers of the new technology benefit from large network externalities and therefore are more reluctant to switch away from it when its price goes up.

When q < 1, network externalities are relatively more important in determining the consumers’ choice, leading to a multiplicity of equilibrium market shares for a given price. Whenever two equilibria are possible, the upper curve of the demand correspondence represents the case where high quality has a high initial market share. For a certain critical price, $\widetilde{p}$, the demand function will jump from the upper segment of the demand function to the lower one. The discontinuity point depends positively on the initial market share.

We now proceed to describing the optimal price path for the sponsor of the new technology. As the firm sets its prices to maximize total profits, $\Pi = {\sum\nolimits_{T = 1}^\infty {\delta ^{{T - 1}} \Pi _{T} } }$, and as profits in period T are equal to $\Pi _{T} = p_{T} x_{T} {\left( {p_{T} ,x_{{T - 1}} } \right)}$, past prices influence the current profits through the impact on today’s market share. Clearly, a large initial market share is an advantage: at given prices in the two-equilibrium range, a larger initial market share results in a larger demand.

Proposition 2 characterizes the optimum prices of the sponsor of the new technology for different values of q.

Proposition 2

There ³ are parameters q″′ < q″ < q′ and θ, such that the optimal pricing path for the sponsor of new technology is as follows.

• 1. $\begin{array}{*{20}c} {{If\;q \geqslant q\prime ,\;\;then}} & {{p^{ * }_{T} = p^{m} }} & {{for\;T = 1,2 \ldots }} \\ \end{array}$

• 2. $\begin{array}{*{20}c} {{If\;q \leqslant q < q\prime ,\;\;then}} & {{p^{ * }_{T} = p^{l} }} & {{for\;T = 1,2 \ldots }} \\ \end{array}$

• 3. $\begin{array}{*{20}c} {If\;q\prime < q < q,\;\;then}{p^{ * }_{T} = p^{u} }{for\;T = 1} \\ {and}{p^{ * }_{T} = p^{l} }{for\;T = 2,3, \ldots } \\ \end{array}$

• 4. $\begin{array}{*{20}c} {If\;\;1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-\nulldelimiterspace} 4 < q < q\prime \prime \prime ,\;\;then}{p^{ * }_{1} = p^{u} }{for\;T = 1} \\ {and}{p^{ * }_{1} = p^{l} }{for\;T = 2,3, \ldots if\;\delta > \delta ^{ * } ,^{4} } \\ {}{p^{ * }_{1} = p^{s} }{for\;all\;T = 1,2,3, \ldots if\;\delta < \delta ^{ * } .} \\ \end{array}$ ⁴

• 5. $\begin{array}{*{20}c} {{q < 0.25,\;\;then}} & {{p^{ * }_{1} = p^{s} }} & {{for\;all\;T = 1,2,3, \ldots }} \\ \end{array}$

where $p^{m} = {{\left( {2q - 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - 1} \right)}} 4}} \right. \kern-\nulldelimiterspace} 4$, $p^{l} = {{\left( {{\sqrt {2q} }{\sqrt {3{\sqrt {17} } - 5} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {{\sqrt {2q} }{\sqrt {3{\sqrt {17} } - 5} }} \right)}} 8}} \right. \kern-\nulldelimiterspace} 8$, $p^{u} = {{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$ and $p^{s} = {2q} \mathord{\left/ {\vphantom {{2q} 3}} \right. \kern-\nulldelimiterspace} 3 - {\left( {{{\sqrt {q{\left( {4q + 9} \right)}} }} \mathord{\left/ {\vphantom {{{\sqrt {q{\left( {4q + 9} \right)}} }} 6}} \right. \kern-\nulldelimiterspace} 6} \right)}\cos {\left( {{{\left( {\pi + \theta } \right)}} \mathord{\left/ {\vphantom {{{\left( {\pi + \theta } \right)}} 3}} \right. \kern-\nulldelimiterspace} 3} \right)}$.

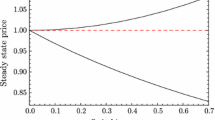
The next two Figures illustrate Proposition 2. Figure 8 shows the optimal price, and Fig. 9 the resulting market share of the new technology as a function of q. In both figures, the dotted line represents the optimal price and the resulting market share, respectively, when network externalities are absent.

Fig. 8

Optimal price as a function of q

Fig. 9

Market share as a function of q

Figure 8 shows the intuitive notion that the larger the quality difference, the larger the price the provider of the superior technology charges. It is interesting to note that, apart from an intermediate range of quality difference [0.25, q″], the optimal price is constant over time and varies only with the exogenous quality difference. When the quality difference is very small, this price is very small and equal to p ^s, represented in the Figure by the bold curvature. When the quality difference is somewhat larger, the optimal pricing structure depends on the discount factor. If the future is valued enough, i.e., if δ is large enough, the optimal pricing path is such that, in the first period, a low undercutting price p ^u is asked, represented in the Figure by the dashed line, to gain a substantial market share and a large price p ^l, represented in the Figure by the thin curvature, ever after. If the discount factor is relatively low, it is better for the provider of the new technology to set one constant, somewhat moderate, price p ^s. When the quality difference is larger, i.e., q > q″′, it is optimal, for all discount factors, to start with a low price in period 1 and continue with a large price from period 2 onwards. When the quality difference grows, the undercutting price p ^u and the large price p ^l converge towards one another when the quality difference increases, and from q″ they coincide.

An interesting outcome, illustrated in Fig. 9, is that the market share is non-monotonic in q. The long-run market share (all segments drawn in continuous line) first increases, then stays constant, and then decreases in q. A higher q has a two-fold effect on the firm’s market share. The direct effect is positive: a higher q leads to a higher x for a given price. The indirect effect is negative: a higher q leads to a higher optimal price, which impacts market share negatively. When there are no network externalities (see the dotted line), the two effects exactly cancel each other so that the market share stays constant. The firm chooses its price so that it serves only people with a relatively high valuation of quality.

With network externalities, the relationship between the two effects becomes more complicated. For small q and a small market share, the direct positive effect dominates. For intermediate q, both effects cancel out, but at a much higher market share than without network externalities. The firm keeps a large market share in order to attract not only consumers with a high valuation of quality, but also those with a low valuation of quality but high willingness to pay for network externalities. When the quality difference becomes very large, it becomes more profitable to give up this last group of consumers in order to be able to extract more surplus from quality-loving consumers.

Consider now the long-run welfare change when the new technology is sponsored. The welfare change is equal to the change in gross consumers surplus of consumers who choose the new technology, ΔGCS ₁, and in the consumer surplus of consumers of old technology ΔCS ₀. Just as in the case of unsponsored technologies, the social welfare is maximized when everyone adopts the new technology. However, unlike in that case, this never happens when the new technology is sponsored. Proposition 3 describes the welfare change as a consequence of the introduction of the new technology.

Proposition 3

The introduction of the new technology increases (decreases) social welfare in the long run if $q > q\prime {\left( {q < 0.25} \right)}$. If 0.25 < q < q″′, social welfare increases if, and only if the new technology has a dominant market share.

Proposition 3 is illustrated in Fig. 10. In all three distinguished cases, gross surplus of consumers of the new technology increases, indicating that the increase in surplus due to higher quality is larger than the decrease due to the loss of network externalities. The surplus of the consumers of the old technology decreases, because they only experience the loss of network externalities. The net change in social welfare depends on whether or not the new technology gains a large market share.

Fig. 10

Social welfare when the new technology is sponsored

5 Conclusions

We have examined the adoption of technology in a market where consumers have to make a purchasing decision in every period and have different valuations of both network size and quality. In Section 3, we considered the case of unsponsored technologies, and in Section 4, we analyzed the implication of the new technology being supplied by a profit-maximizing seller. We showed that, even though consumers are not stuck with past purchases, the better technology may not gain the whole market in equilibrium, due to lagging expectations. We also found that market outcomes depend on the quality advantage of the new technology. In the case of unsponsored new technology, the higher the quality difference, the higher the market share of the new technology. There is a critical value such that, for larger quality differences, the new superior technology will be used in the whole market, and for lower quality differences, the old technology remains dominant in the market.

When the new technology is sponsored, the relationship between the quality difference and the long-run market share becomes non-monotonic. The market share initially increases, but then decreases as the quality difference increases. The reason is that, for intermediate q, the firm finds it profitable to serve not only the consumers with a high valuation for quality, but also those with a low valuation of quality and high valuation of network externalities. When the quality difference is large, the firm prefers to give up the consumers who care mostly about network externalities in order to extract more surplus from those who care much about quality.

The introduction of the new technology does not necessarily increase social welfare. When the quality difference is small and the equilibrium market share of the new technology small, the gain of consumers who switch to the new technology does not outweigh the loss in network externalities for consumers who do not switch. When the new technology has a much higher quality, its introduction increases social welfare. However, the social optimum, in which everyone uses the new technology, can only be achieved when the new technology is unsponsored.

Appendix

Proof of Lemma 2

For this case, we have to consider potential equilibria represented in Figs. 5 and 6. We have already shown in the text that a situation as in Fig. 6a cannot be an equilibrium. Below, in (1) we show that the other situation with p _T  > q- shown in Fig. 6a—cannot be an equilibrium. This implies that the only equilibrium for p _T  > q is x _T  = 0. In (2) we analyze the potential equilibria where p _T  > q.

• (1) Suppose that p _T  > q. Then, it follows from Fig. 6b that x _T  > 0 only if $Ex_{T} > {{\left( {p_{T} + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$. In this case, $x_{T} = 1 - \frac{{p_{T} }} {{2x_{T} - 1}} + \frac{1} {2}{\left( {\frac{{p_{T} }} {{2Ex_{T} - 1}} - \frac{{p_{T} - q}} {{2Ex_{T} - 1}}} \right)}$. Substituting Ex _T  = x _T and transforming gives the following quadratic equation:

  $$ 4x^{2}_{T} - 6x_{T} + 2 + 2p_{T} - q = 0. $$

  (4)

  Equation 4 has no solution if $4{\left( {1 - 8p_{T} + 4q} \right)} < 0$; thus if $p_{T} > {{\left( {4q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {4q + 1} \right)}} 8}} \right. \kern-\nulldelimiterspace} 8$. If $q > 1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-\nulldelimiterspace} 4$, then p _T  > q implies $p_{T} > {{\left( {4q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {4q + 1} \right)}} 8}} \right. \kern-\nulldelimiterspace} 8$. It follows that, when p _T  > q, then there is no equilibrium with x _T  > 0.

• (2) Let $x\prime _{1} ,x\prime _{2} ,x,x\prime _{1} ,x\prime _{2}$ be defined as in the proof of Lemma 1. Note first in situations (a) and (c) the dynamic process and equilibrium conditions are just as in Lemma 1, with the difference that now the condition $x_{T} < {{\left( {p_{T} - q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} - q + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$ for equilibrium (a) and $x_{T} > {{\left( {p_{T} + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$ for equilibrium c is always satisfied. It follows $x_{T} = x\prime _{1}$ is an equilibrium when $p_{T} > {{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$, and $x_{T} = x_{2} \prime$ is an equilibrium when $p_{T} < {{\sqrt q }} \mathord{\left/ {\vphantom {{{\sqrt q }} 2}} \right. \kern-\nulldelimiterspace} 2$.

Consider now equilibrium (b). When q < 1, then x″ satisfies the condition ${{\left( {p_{T} - q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} - q + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2 < x_{T} < {{\left( {p_{T} + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$ if ${q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}} < p_{T} < q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}$. Observe, however, that x″ is not stable now: analyzing the dynamic process reveals that x _t  > x _t−1 if x _t−1 > x″, and x _t  < x _t−1 otherwise. It follows that equilibrium of type (b) does not exist for q < 1. If q = 1, then for $p_{t} = 1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2$ every $1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-\nulldelimiterspace} 4 < x_{T} < 3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-\nulldelimiterspace} 4$ satisfies the equilibrium condition and can be a stable equilibrium.

Note that, when q < 1, ${{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2 < {{\sqrt q }} \mathord{\left/ {\vphantom {{{\sqrt q }} 2}} \right. \kern-\nulldelimiterspace} 2$, and thus there is a range of p _T where both equilibria (a) and (b) are possible. There, the eventual stable equilibrium depends on the initial x ₀ . For each p _T there exists a critical $\overline{x}$ such that, if $x_{{T - 1}} < \overline{x}$, then the ‘low’ equilibrium (type a) arises, whereas $x_{{T - 1}} > \overline{x}$ will lead to the ‘high’ equilibrium (type c). To find this critical $\overline{x}$ we need to analyze the dynamic process in situations (a), (b) and (c). From the proof Lemma 1 and the discussion of type (b) equilibrium above, we know that the dynamic process is the following:

• (a) If $x_{{t - 1}} < {{\left( {p_{T} - q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} - q + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$, then x _t  > x _{t   − 1} if $x_{{t - 1}} < x\prime _{1}$ or $x_{{t - 1}} > x\prime _{2}$ and x _t  < x _{t   − 1} otherwise.

• (b) If ${{\left( {p_{T} - q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} - q + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2 < x_{{t - 1}} < {{\left( {p_{T} + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$, then x _t  < x _{t   − 1} if x _{t   − 1} < x″ and x _t  < x _{t   − 1} otherwise.

• (c) If $x_{{t - 1}} > {{\left( {p_{T} + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$, then x _t  > x _{t   − 1} if $x\prime _{1} < x_{{t - 1}} < x\prime _{2}$ and x _{t   − 1} < x _t otherwise.

The critical $\overline{x}$ depends on the relationship between $x\prime _{2} ,x$ and $x\prime _{1}$, on the one hand, and ${{\left( {p_{T} - q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} - q + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$ and ${{\left( {p_{T} + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$ on the other. Three subcases can arise here:

• (2.1) $q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}} < p_{T} < {{\sqrt q }} \mathord{\left/ {\vphantom {{{\sqrt q }} 2}} \right. \kern-\nulldelimiterspace} 2$.

  In this case, $x\prime _{2} > {{\left( {p_{T} - q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} - q + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$, $x > {{\left( {p_{T} + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$ and $x\prime _{1} > {{\left( {p_{T} + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$. Figure 11 shows that the low equilibrium x ₁′ arises if $x_{{T - 1}} < x\prime _{1}$, and the high equilibrium $x\prime _{2}$ arises if $x_{{T - 1}} > x\prime _{1}$. Hence, $\overline{x} = x\prime _{1}$.

• (2.2) ${q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}} < p_{T} < q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}$.

  In this case, $x\prime _{2} > {{\left( {p_{T} - q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} - q + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$, ${{\left( {p_{T} - q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} - q + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2 < x < {{\left( {p_{T} + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$ and $x\prime _{1} < {{\left( {p_{T} + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$. Figure 12 shows that the low equilibrium x ₁′ arises if x _T−1 < x″, and the high equilibrium $x\prime _{2}$ arises if x _T−1 > x″. Thus, $\overline{x} = x$.

• (2.3) ${{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2 < p_{T} < {q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}$.

  In this case, $x\prime _{2} < {{\left( {p_{T} - q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} - q + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$, $x < {{\left( {p_{T} - q + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} - q + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$ and $x\prime _{1} < {{\left( {p_{T} + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p_{T} + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$. Figure 13 shows that the low equilibrium x ₁′ arises if $x_{{T - 1}} < x\prime _{2}$, and the high equilibrium $x\prime _{2}$ arises if $x_{{T - 1}} > x\prime _{2}$. Thus, $\overline{x} = x\prime _{2}$.

Fig. 11

$q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}} < p_{T} < {{\sqrt q }} \mathord{\left/ {\vphantom {{{\sqrt q }} 2}} \right. \kern-\nulldelimiterspace} 2$

Fig. 12

${q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}} < p_{T} < q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}$

Fig. 13

${{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2 < p_{T} < {q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}$

Proof of Proposition 2

We calculate the optimal price path of the firm for the three ranges of q described in Lemmas 1–3: q > 1, 0.25 ≤ q ≤ 1 and q < 0.25. We consider these three ranges of q in turn.

Case 1

q > 1. In this case, the demand function of the firm is given by Lemma 1. Note that the market share in a given period does not depend on the market share in the previous period, and therefore the optimal price does not depend on the initial market share either and it will be the same in all periods. Therefore, in the proof we drop the index T. The optimal p can take values from one of three ranges: (a)${q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}} < p \leqslant q$, (b) $q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}} < p \leqslant {q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}$ and (c) $p \leqslant q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}$. We consider these three ranges in turn.

• (a) ${q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}} < p \leqslant q$. The profits are $\pi = p{{\left( {q - {\sqrt {q{\left( { - 4p^{2} + 8pq + q - 4q^{2} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {q - {\sqrt {q{\left( { - 4p^{2} + 8pq + q - 4q^{2} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q}$. The first and second derivatives of this function with respect to p are

  $$ {\partial \pi } \mathord{\left/ {\vphantom {{\partial \pi } {\partial p}}} \right. \kern-\nulldelimiterspace} {\partial p} = \frac{{q - {\sqrt {q{\left( { - 4p^{2} + 8pq + q - 4q^{2} } \right)}} }}} {{4q}} - p\frac{{q - p}} {{{\sqrt {q{\left( { - 4p^{2} + 8pq + q - 4q^{2} } \right)}} }}}, $$

  and

  $$ \begin{array}{*{20}l} {{{\partial ^{2} \pi } \mathord{\left/ {\vphantom {{\partial ^{2} \pi } {\partial p^{2} }}} \right. \kern-\nulldelimiterspace} {\partial p^{2} } = - \frac{{q - p}} {{{\sqrt {q{\left( { - 4p^{2} + 8pq + q - 4q^{2} } \right)}} }}} - \frac{{q - p}} {{{\sqrt {q{\left( { - 4p^{2} + 8pq + q - 4q^{2} } \right)}} }}} - } \hfill} \\ {{ - p\frac{{ - q}} {{{\left( { - 4p^{2} + 8pq + q - 4q^{2} } \right)}{\sqrt {q{\left( { - 4p^{2} + 8pq + q - 4q^{2} } \right)}} }}} = } \hfill} \\ {{ = \frac{{3pq - 2q^{2} - 8{\left( {p - q} \right)}^{2} }} {{{\left( { - 4p^{2} + 8pq + q - 4q^{2} } \right)}{\sqrt {q{\left( { - 4p^{2} + 8pq + q - 4q^{2} } \right)}} }}}.} \hfill} \\ \end{array} $$

  (5)

  The denominator of the second derivative is positive. The minimum value of the numerator is ${q{\left( {2q - {\sqrt {2q} }} \right)}} \mathord{\left/ {\vphantom {{q{\left( {2q - {\sqrt {2q} }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$, which is positive if q > 0.5. Thus, for q > 0.5, this segment of the profit function is convex, which implies that there cannot be an interior maximum. Since the profit function is continuous and differentiable at $p = {q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}$, this implies that optimal $p < {q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}$.

• (b) $q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}} < p \leqslant {q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}$. Here, the profit function is $\pi = {p{\left( {2q - 2p - 1} \right)}} \mathord{\left/ {\vphantom {{p{\left( {2q - 2p - 1} \right)}} {{\left( {2{\left( {q - 1} \right)}} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {2{\left( {q - 1} \right)}} \right)}}$. It is easy to show that the maximal profit is obtained at $p = {{\left( {2q - 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - 1} \right)}} 4}} \right. \kern-\nulldelimiterspace} 4$, which satisfies $p < {q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}$ for all relevant q and which satisfies $p > q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}$ if $q > {{\left( {{\sqrt {17} } + 3} \right)}} \mathord{\left/ {\vphantom {{{\left( {{\sqrt {17} } + 3} \right)}} 4}} \right. \kern-\nulldelimiterspace} 4$. Thus, there exists a maximum in this range if $q > {{\left( {{\sqrt {17} } + 3} \right)}} \mathord{\left/ {\vphantom {{{\left( {{\sqrt {17} } + 3} \right)}} 4}} \right. \kern-\nulldelimiterspace} 4$. Otherwise, the fact that the profit function is continuous and differentiable at $p = q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}$ implies that in the optimum $p < q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}$.

• (c) $p \leqslant q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}$. Here, profits are $\pi = p{{\left( {3q + {\sqrt {q{\left( {q - 4p^{2} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {3q + {\sqrt {q{\left( {q - 4p^{2} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q}$. The first order condition for a maximum is

  $$ {\partial \pi } \mathord{\left/ {\vphantom {{\partial \pi } {\partial p}}} \right. \kern-\nulldelimiterspace} {\partial p} = \frac{{3q + {\sqrt {q{\left( {q - 4p^{2} } \right)}} }}} {{4q}} - \frac{{p^{2} }} {{{\sqrt {q{\left( {q - 4p^{2} } \right)}} }}} = 0. $$

  After some transformations, this condition simplifies to $16p^{4} + 5p^{2} q - 2q^{2} = 0$, which has a unique real and nonnegative solution, $p = {{\left( {{\sqrt {2q} }{\sqrt {3{\sqrt {17} } - 5} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {{\sqrt {2q} }{\sqrt {3{\sqrt {17} } - 5} }} \right)}} 8}} \right. \kern-\nulldelimiterspace} 8$. This satisfies $p \leqslant q \mathord{\left/ {\vphantom {q {{\left( {q + 1} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {q + 1} \right)}}$ if $q \leqslant {{\left( {{\sqrt {17} } + 3} \right)}} \mathord{\left/ {\vphantom {{{\left( {{\sqrt {17} } + 3} \right)}} 4}} \right. \kern-\nulldelimiterspace} 4$. It is easy to show that the profit function is concave at the optimal p.

  It follows from (a), (b) and (c) that the optimal $p = p^{m} = {{\left( {2q - 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - 1} \right)}} 4}} \right. \kern-\nulldelimiterspace} 4$ if $q > {{\left( {{\sqrt {17} } + 3} \right)}} \mathord{\left/ {\vphantom {{{\left( {{\sqrt {17} } + 3} \right)}} 4}} \right. \kern-\nulldelimiterspace} 4$ and $p = p^{l} = {{\left( {{\sqrt {2q} }{\sqrt {3{\sqrt {17} } - 5} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {{\sqrt {2q} }{\sqrt {3{\sqrt {17} } - 5} }} \right)}} 8}} \right. \kern-\nulldelimiterspace} 8$ if $1 < q \leqslant {{\left( {{\sqrt {17} } + 3} \right)}} \mathord{\left/ {\vphantom {{{\left( {{\sqrt {17} } + 3} \right)}} 4}} \right. \kern-\nulldelimiterspace} 4$.

Case 2

0.25 ≤ q ≤ 1. Here, the demand function in period T is given by Lemma 2. Unlike in Case 1, it now also depends on x _{T   − 1}. The optimal price in period T will thus also depend on x _{T   − 1}. (Note that since the time horizon of the firm is infinite, it will not depend on T). However, we do not need to consider each initial market share separately. Note the following:

• For a given p _T , all initial market shares $x_{{T - 1}} > {{\left( {3q - {\sqrt {q{\left( {q - 4p^{2}_{T} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {3q - {\sqrt {q{\left( {q - 4p^{2}_{T} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q}$ result in the same x _T and the same holds for all $x_{{T - 1}} < {{\left( {q + {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {q + {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q}$. Moroever, ${{\left( {q + {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {q + {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} {4q > 0.25}}} \right. \kern-\nulldelimiterspace} {4q > 0.25}$ and ${{\left( {3q - {\sqrt {q{\left( {q - 4p^{2}_{T} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {3q - {\sqrt {q{\left( {q - 4p^{2}_{T} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q} < 0.75$ for all p _T .

• In period 0, x ₀ = 0 and in all subsequent periods, either $x_{T} = {{\left( {3q + {\sqrt {q{\left( {q - 4p^{2}_{T} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {3q + {\sqrt {q{\left( {q - 4p^{2}_{T} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q} > 0.75$ or $x_{T} = {{\left( {q - {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {q - {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q} < 0.25$.

It follows that, to characterize fully the optimal pricing path of the firm, it is enough to find the optimal price for x _T−1 < 0.25 and x _T−1 > 0.75.

Suppose first that the discount factor δ = 0, and so only current profits count. Below, in (1) we calculate the optimum price for x _T−1 > 0.75, and in then in (2) we do the same for x _T−1 < 0.25.

• (1) x _T−1 > 0.75. The profit function is

  $$ \begin{array}{*{20}l} {{\Pi _{T} = 0} \hfill} & {{{\text{if}}\;p_{T} \geqslant q,} \hfill} \\ {{\Pi _{T} = {p_{T} {\left( {q - {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{p_{T} {\left( {q - {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q}} \hfill} & {{{\text{if}}\;{{\sqrt q }} \mathord{\left/ {\vphantom {{{\sqrt q }} 2}} \right. \kern-\nulldelimiterspace} 2 < p_{T} < q,} \hfill} \\ {{\Pi _{T} = {p_{T} {\left( {3q + {\sqrt {q(q - 4p^{2}_{T} )} }} \right)}} \mathord{\left/ {\vphantom {{p_{T} {\left( {3q + {\sqrt {q(q - 4p^{2}_{T} )} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q}} \hfill} & {{{\text{if}}\;p_{T} \leqslant {{\sqrt q }} \mathord{\left/ {\vphantom {{{\sqrt q }} 2}} \right. \kern-\nulldelimiterspace} 2.} \hfill} \\ \end{array} $$

  (6)

  Note that the price that maximizes current profits must either satisfy ${{\sqrt q }} \mathord{\left/ {\vphantom {{{\sqrt q }} 2}} \right. \kern-\nulldelimiterspace} 2 < p_{T} < q$, or $p_{T} \leqslant {{\sqrt q }} \mathord{\left/ {\vphantom {{{\sqrt q }} 2}} \right. \kern-\nulldelimiterspace} 2$. In the former case, the period T−profits will be less than q/4. If, on the other hand, $p_{T} \leqslant {{\sqrt q }} \mathord{\left/ {\vphantom {{{\sqrt q }} 2}} \right. \kern-\nulldelimiterspace} 2$, then $\Pi _{T} = p_{T} {{\left( {3q + {\sqrt {q{\left( {q - 4p^{2}_{T} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {3q + {\sqrt {q{\left( {q - 4p^{2}_{T} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q}$. We have shown in subcase (c) of Case 1 that this is maximized for $p_{T} = {{\left( {{\sqrt {2q} }{\sqrt {3{\sqrt {17} } - 5} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {{\sqrt {2q} }{\sqrt {3{\sqrt {17} } - 5} }} \right)}} 8}} \right. \kern-\nulldelimiterspace} 8$, which always satisfies $p_{T} \leqslant {{\sqrt q }} \mathord{\left/ {\vphantom {{{\sqrt q }} 2}} \right. \kern-\nulldelimiterspace} 2$. In this case, $x_{T} \approx 0.82 > 0.75$ and $\Pi _{T} \approx 0.39{\sqrt q } > q \mathord{\left/ {\vphantom {q 4}} \right. \kern-\nulldelimiterspace} 4$. This implies that optimal $p_{T} = p^{l} = {{\left( {{\sqrt {2q} }{\sqrt {3{\sqrt {17} } - 5} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {{\sqrt {2q} }{\sqrt {3{\sqrt {17} } - 5} }} \right)}} 8}} \right. \kern-\nulldelimiterspace} 8$.

• (2) x _T−1 < 0.25. Here the profit function in period T is:

  $$ \begin{array}{*{20}l} {{\Pi _{T} = 0} \hfill} & {{{\text{if}}\;p_{T} \geqslant q,} \hfill} \\ {{\Pi _{T} = p_{T} {{\left( {q - {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {q - {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q}} \hfill} & {{{\text{if}}\;{{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2 < p_{T} < q,} \hfill} \\ {{\Pi _{T} = p_{T} {{\left( {3q + {\sqrt {q{\left( {q - 4p^{2}_{T} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {3q + {\sqrt {q{\left( {q - 4p^{2}_{T} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q}} \hfill} & {{{\text{if}}\;p_{T} \leqslant {{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2.} \hfill} \\ \end{array} $$

  (7)

Here, either (a) ${{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2 < p_{T} < q$ or (b) $p_{T} \leqslant {{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$ is optimal. We consider these two price ranges in turn.

• (a) ${{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2 < p_{T} < q$. Then, x _T  < 0.25, and profits in period T are $\Pi _{T} = p_{T} {{\left( {q - {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {q - {\sqrt {q{\left( { - 4p^{2}_{T} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q}$, which corresponds to subcase (a) of Case 1 above. We have shown that this profit function is convex if q ≥ 0.5. This implies that, in this price range, the optimal price is $p_{T} = {{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2 + \varepsilon$, which gives $\Pi _{T} = {q{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{q{\left( {2q - {\sqrt q }} \right)}} 4}} \right. \kern-\nulldelimiterspace} 4$. However, setting a price just outside this range, $p_{T} = {{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$ gives a market share x _T  > 0.75 and higher profits. Thus, if q ≥ 0.5, then the optimal price lies in range (b).

  Suppose now that q < 0.5. Then, the profit function is concave for some p _T and thus there might be a local maximum in this range. To find this maximum, we need to take a derivative of the profit function with respect to p _T , which gives

  $$ \frac{{d\pi _{T} }} {{dp_{T} }} = \frac{{8p_{T} ^{2} - 12p_{T} q - q + 4q^{2} }} {{4{\sqrt {q{\left( {q - 4q^{2} + 8p_{T} q - 4p^{2}_{T} } \right)}} }}} + \frac{1} {4}. $$

  Comparing this to zero we obtain two solutions:

  $$ \begin{array}{*{20}c} {p\prime = \frac{{2q}} {3} + \sqrt[3]{{\frac{{q^{2} }} {{32}} + \frac{{q^{3} }} {{216}} + {\sqrt {\frac{{q^{5} }} {{6912}} + \frac{{q^{4} }} {{1536}} - \frac{{q^{3} }} {{4096}}} }}} + \frac{{q \mathord{\left/ {\vphantom {q {16}}} \right. \kern-\nulldelimiterspace} {16} + {q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {36}}} \right. \kern-\nulldelimiterspace} {36}}} {{\sqrt[3]{{\frac{{q^{2} }} {{32}} + \frac{{q^{3} }} {{216}} + {\sqrt {\frac{{q^{5} }} {{6912}} + \frac{{q^{4} }} {{1536}} - \frac{{q^{3} }} {{4096}}} }}}}},} \\ {p = \frac{{2q}} {3} + {\left( {\frac{{i{\sqrt 3 }}} {2} - \frac{1} {2}} \right)}\sqrt[3]{{\frac{{q^{2} }} {{32}} + \frac{{q^{3} }} {{216}} + {\sqrt {\frac{{q^{5} }} {{6912}} + \frac{{q^{4} }} {{1536}} - \frac{{q^{3} }} {{4096}}} }}} - {\left( {\frac{{i{\sqrt 3 }}} {2} + \frac{1} {2}} \right)}\frac{{q \mathord{\left/ {\vphantom {q {16}}} \right. \kern-\nulldelimiterspace} {16} + {q^{2} } \mathord{\left/ {\vphantom {{q^{2} } {36}}} \right. \kern-\nulldelimiterspace} {36}}} {{\sqrt[3]{{\frac{{q^{2} }} {{32}} + \frac{{q^{3} }} {{216}} + {\sqrt {\frac{{q^{5} }} {{6912}} + \frac{{q^{4} }} {{1536}} - \frac{{q^{3} }} {{4096}}} }}}}}.} \\ \end{array} $$

  Two cases can arise here. If $q > q\prime = {3{\sqrt 3 }} \mathord{\left/ {\vphantom {{3{\sqrt 3 }} 2}} \right. \kern-\nulldelimiterspace} 2 - 9 \mathord{\left/ {\vphantom {9 4}} \right. \kern-\nulldelimiterspace} 4 \approx 0.35$, then ${q^{5} } \mathord{\left/ {\vphantom {{q^{5} } {6912}}} \right. \kern-\nulldelimiterspace} {6912} + {q^{4} } \mathord{\left/ {\vphantom {{q^{4} } {1536}}} \right. \kern-\nulldelimiterspace} {1536} - {q^{3} } \mathord{\left/ {\vphantom {{q^{3} } {4096}}} \right. \kern-\nulldelimiterspace} {4096} > 0$, and thus p′ is the only real solution. In that case, p′ is the only potential maximum in this range. However, since the second derivative of the profit function, given by Eq. 5, is positive for $p_{T} > {2q} \mathord{\left/ {\vphantom {{2q} 3}} \right. \kern-\nulldelimiterspace} 3$, p′ must be a minimum. Thus, when $q > {3{\sqrt 3 }} \mathord{\left/ {\vphantom {{3{\sqrt 3 }} 2}} \right. \kern-\nulldelimiterspace} 2 - 9 \mathord{\left/ {\vphantom {9 4}} \right. \kern-\nulldelimiterspace} 4$, then the optimum price lies in range (b).

  The second case is $q < {3{\sqrt 3 }} \mathord{\left/ {\vphantom {{3{\sqrt 3 }} 2}} \right. \kern-\nulldelimiterspace} 2 - 9 \mathord{\left/ {\vphantom {9 4}} \right. \kern-\nulldelimiterspace} 4$. In that case, p′ is no longer a real number.⁵ However, it can be shown⁶ that, in that case, p″ is real and can take three values:

  $$ \begin{array}{*{20}c} {p^{{{\left( 1 \right)}}} = \frac{{2q}} {3} - \frac{{{\sqrt {q{\left( {4q + 9} \right)}} }}} {6}\cos {\left( {\frac{{\pi - \theta }} {3}} \right)},} \\ {p^{{{\left( 2 \right)}}} = \frac{{2q}} {3} - \frac{{{\sqrt {q{\left( {4q + 9} \right)}} }}} {6}\cos {\left( {\frac{{\pi + \theta }} {3}} \right)},} \\ {p^{{{\left( 3 \right)}}} = \frac{{2q}} {3} - \frac{{{\sqrt {q{\left( {4q + 9} \right)}} }}} {6}\cos {\left( {\frac{{\theta + 3\pi }} {3}} \right)} = \frac{{2q}} {3} + \frac{{{\sqrt {q{\left( {4q + 9} \right)}} }}} {6}\cos {\left( {\frac{\theta } {3}} \right)},} \\ \end{array} $$

  where $\cos \theta = \frac{{2q{\left( {4q + 27} \right)}}} {{{\left( {4q + 9} \right)}{\sqrt {q{\left( {4q + 9} \right)}} }}}$ and $\sin \theta = \frac{{3{\sqrt {3{\left( {27 - 72q - 16q^{2} } \right)}} }}} {{{\left( {4q + 9} \right)}{\sqrt {q{\left( {4q + 9} \right)}} }}}$.

  We need to determine whether one of them could be the optimum price satisfying the condition ${{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2 < p_{T} < q$ and if so, which one. Note that, if q ≤ 1, then 0 ≤ cosθ ≤ 1 and 0 ≤ sinθ ≤ 1, which implies that 0 ≤ θ ≤ π/2. This in turn means that $\cos {\left( {{{\left( {\theta - \pi } \right)}} \mathord{\left/ {\vphantom {{{\left( {\theta - \pi } \right)}} 3}} \right. \kern-\nulldelimiterspace} 3} \right)} > \cos {\left( {\theta \mathord{\left/ {\vphantom {\theta 3}} \right. \kern-\nulldelimiterspace} 3} \right)} > \cos {\left( {{{\left( {\theta + \pi } \right)}} \mathord{\left/ {\vphantom {{{\left( {\theta + \pi } \right)}} 3}} \right. \kern-\nulldelimiterspace} 3} \right)} > 0$, and thus $p^{{{\left( 3 \right)}}} > p^{{{\left( 2 \right)}}} > p^{{{\left( 1 \right)}}}$. It can be checked that ${\partial \pi _{T} } \mathord{\left/ {\vphantom {{\partial \pi _{T} } {\partial p_{T} }}} \right. \kern-\nulldelimiterspace} {\partial p_{T} } < 0$ if $p_{T} < p^{{{\left( 1 \right)}}}$ or $p^{{{\left( 2 \right)}}} < p_{T} < p^{{{\left( 3 \right)}}}$ and ${\partial \pi _{T} } \mathord{\left/ {\vphantom {{\partial \pi _{T} } {\partial p_{T} }}} \right. \kern-\nulldelimiterspace} {\partial p_{T} } > 0$ otherwise, which implies that $p^{{{\left( 2 \right)}}}$ is the unique maximum of the profit function. We still need to check that ${{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2 < p^{{{\left( 2 \right)}}} < q$. It can immediately be seen that $p^{{{\left( 2 \right)}}} < q$ and from 0 ≤ θ ≤ π/2 it follows that

  $$ p^{{{\left( 2 \right)}}} = \frac{{2q}} {3} - \frac{{{\sqrt {q{\left( {4q + 9} \right)}} }}} {6}\cos {\left( {\frac{{\pi + \theta }} {3}} \right)} > \frac{{2q}} {3} - \frac{{{\sqrt {q{\left( {4q + 9} \right)}} }}} {{12}} > \frac{{2q - {\sqrt q }}} {2}. $$

  It follows that, for q < q″′, there exists a local optimum $p_{T} = p^{s} = \frac{{2q}} {3} - \frac{{{\sqrt {q{\left( {4q + 9} \right)}} }}} {6}\cos {\left( {\frac{{\pi + \theta }} {3}} \right)}$, in which x _T  < 0.25.

• (b) $p_{T} \leqslant {{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$. Here, x _T  > 0.75 and $\Pi _{T} = {p_{T} {\left( {3q + {\sqrt {q{\left( {q - 4p^{2}_{T} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{p_{T} {\left( {3q + {\sqrt {q{\left( {q - 4p^{2}_{T} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q}$, which corresponds to subcase (c) of Case 1. We have shown that the profit function is maximized for $p_{T} = {{\left( {{\sqrt {2q} }{\sqrt {3{\sqrt {17} } - 5} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {{\sqrt {2q} }{\sqrt {3{\sqrt {17} } - 5} }} \right)}} 8}} \right. \kern-\nulldelimiterspace} 8$. This satisfies $p_{T} \leqslant {{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$ if $q > q \equiv {{\left( {3{\sqrt {17} } + 3 + 4{\sqrt 2 }{\sqrt {3{\sqrt {17} } - 5} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {3{\sqrt {17} } + 3 + 4{\sqrt 2 }{\sqrt {3{\sqrt {17} } - 5} }} \right)}} {32}}} \right. \kern-\nulldelimiterspace} {32} \approx 0.96$. Otherwise, optimal $p_{T} = {{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$.

Combining (a) and (b), we can distinguish three ranges of q. If q″ < q < 1, then optimal p _T  = p ^l, which leads to x _T  > 0.75. If q″′ < q < q″, then optimal p _T  = p ^u which results in x _T  > 0.75. Finally, if 0.25 < q < q″′, two local maxima exist: p ^u and p ^s. If $\Pi _{T} {\left( {x^{s} ,p^{u} } \right)} > \Pi _{T} {\left( {x^{s} ,p^{s} } \right)}$, (recall that x ^s denotes any market share lower than 0.25), then p ^u will be chosen, otherwise p ^s is optimal. For example, when q = 0.25, then $p_{T} = {2q} \mathord{\left/ {\vphantom {{2q} 3}} \right. \kern-\nulldelimiterspace} 3 - {{\sqrt {q{\left( {4q + 9} \right)}} }} \mathord{\left/ {\vphantom {{{\sqrt {q{\left( {4q + 9} \right)}} }} {6\cos }}} \right. \kern-\nulldelimiterspace} {6\cos }{\left( {{{\left( {\pi + \theta } \right)}} \mathord{\left/ {\vphantom {{{\left( {\pi + \theta } \right)}} 3}} \right. \kern-\nulldelimiterspace} 3} \right)}$ is the global optimum, when $q = {3{\sqrt 3 }} \mathord{\left/ {\vphantom {{3{\sqrt 3 }} 2}} \right. \kern-\nulldelimiterspace} 2 - 9 \mathord{\left/ {\vphantom {9 4}} \right. \kern-\nulldelimiterspace} 4$, then $p_{T} = {{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$ is.

Suppose now that δ > 0, which means that the firm cares about future profits. Note that, since a higher market share in period T increases profits in period T+1, higher δ increases incentives to gain a x _T  > 0.75 in period T. We have shown in (1) that, if x _T−1 > 0.75, then the price that maximizes current profits, p ^l, leads to x _T  > 0.75, and thus p ^l will also be optimal when δ > 0. Suppose now that x _T−1 > 0.25. In that case, we have shown in (2) that, when q > q″′, the price that maximizes current profits, p _T  = p ^l for q > q″ and p _T  = p ^u for q″′ < q < q″, leads to x _T  > 0.75, and thus it is also optimal when δ > 0. If, on the other hand, q < q″′, we have shown that, for δ = 0, two local maxima exist, p ^u leading to a large, and p ^s to a small market share. If δ > 0 then p ^u will be chosen if it leads to higher total discounted profits. Thus

$$ \Pi ^{u} + \delta \mathord{\left/ {\vphantom {\delta {{\left( {1 - \delta } \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {1 - \delta } \right)}}\Pi ^{l} > 1 \mathord{\left/ {\vphantom {1 {{\left( {1 - \delta } \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {1 - \delta } \right)}}\Pi ^{s} , $$

with Π^u, Π^l and Π^s are defined as in footnote 4. Otherwise, p ^s will be chosen.

Case 3

q < 0.25. Here, the demand function is given by Lemma 3. Here again the demand in period T depends on the initial market share in a similar way as when 0.25 ≤ q ≤ 1. However, note that, if x ₀ < 0.25, then x _T  > 0.75 will never arise. That is because in this situation attaining a large market share requires $p_{1} \leqslant {{\left( {2q - {\sqrt q }} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - {\sqrt q }} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$, which for q < 0.25 contradicts p ₁ ≥ 0. It follows, then, that for every T, x _T−1 < 0.25. Thus, the profit function in each period is

$$ \begin{array}{*{20}l} {{\Pi _{T} = 0} \hfill} & {{{\text{if}}\;p_{T} \geqslant q,} \hfill} \\ {{\Pi _{T} = {{\left( {q - {\sqrt {q{\left( { - 4p_{T} ^{2} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {q - {\sqrt {q{\left( { - 4p_{T} ^{2} + 8p_{T} q + q - 4q^{2} } \right)}} }} \right)}} {4q}}} \right. \kern-\nulldelimiterspace} {4q}} \hfill} & {{{\text{if}}\;p_{T} < q.} \hfill} \\ \end{array} $$

In Case 2.(2) subcase (a) we have shown that for this demand function there exists an interior profit-maximizing price if q > q″′. This price is given by

$$ p_{T} = p^{s} = \frac{{2q}} {3} - \frac{{{\sqrt {q{\left( {4q + 9} \right)}} }}} {6}\cos {\left( {\frac{{\pi + \theta }} {3}} \right)} < q. $$

This completes the proof.

Proof of Proposition 3

We analyze the social welfare in the long run for different values of q in turn.

• (1) If q ≥ q′, then the long run solution is $p = {{\left( {2q - 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - 1} \right)}} 4}} \right. \kern-\nulldelimiterspace} 4$ and $x = {{\left( {2q - 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {2q - 1} \right)}} {{\left( {4q - 4} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {4q - 4} \right)}} > 0.5$. Since p < q and ${{\left( {p + q - 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p + q - 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2 < x < {{\left( {p + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$, the equilibrium situation is as in Fig. 5b and ΔGCS ₁, ΔCS ₀ and ΔSW are given by

  $$ \begin{array}{*{20}l} {{\Delta GCS_{1} = {\int_0^1 {{\int_{\frac{p} {q} + \frac{{1 - 2x}} {q}\beta }^1 {{\left( {\alpha q - \beta \left( {1 - x} \right.} \right)}d\alpha d\beta } }} } = \frac{{36q^{3} - 36q^{2} + 9q - 2}} {{96q{\left( {q - 1} \right)}}},} \hfill} \\ {{\Delta CS_{0} = {\int_0^1 {{\int_0^{\frac{p} {q} + \frac{{1 - 2x}} {q}\beta } {{\left( { - \beta x} \right)}d\alpha d = - \frac{{{\left( {2q - 1} \right)}{\left( {6q^{2} - 9q - 1} \right)}}} {{96q{\left( {q - 1} \right)}^{2} }},} }} }} \hfill} \\ {{\Delta SW = \Delta GCS_{1} + \Delta CS_{0} = \frac{{{\left( {3q - 1} \right)}{\left( {12q^{3} - 24q^{2} + 15q - 1} \right)}}} {{96q{\left( {q - 1} \right)}}}.} \hfill} \\ \end{array} $$

  Analyzing these expressions we see that if q ≥ q′, then ΔGCS ₁ > 0, ΔCS ₀ < 0 and ΔSW > 0.

• (2) If $0.25 \leqslant q < q\prime$, then the long run solution with $p = {{\left( {{\sqrt {2q} }{\sqrt {3{\sqrt {17} } - 5} }} \right)}} \mathord{\left/ {\vphantom {{{\left( {{\sqrt {2q} }{\sqrt {3{\sqrt {17} } - 5} }} \right)}} 8}} \right. \kern-\nulldelimiterspace} 8$ and $x = {{\left( {{\sqrt {17} } + 9} \right)}} \mathord{\left/ {\vphantom {{{\left( {{\sqrt {17} } + 9} \right)}} {16}}} \right. \kern-\nulldelimiterspace} {16} > 0.5$ is possible. Since p < q and $x > {{\left( {p + 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p + 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$, the equilibrium situation is as in Fig. 5c and ΔGCS ₁, ΔCS ₀ and ΔSW are given by

  $$ \begin{array}{*{20}c} {\Delta GCS_{1} = {\int_0^{\frac{p} {{2x - 1}}} {{\int_{\frac{p} {q} - \frac{{2x - 1}} {q}\beta }^1 {{\left( {\alpha q - \beta (1 - x} \right)}d\alpha d\beta } } + } }{\int_{\frac{p} {{2x - 1}}}^1 {{\int_0^1 {{\left( {\alpha q - \beta (1 - x} \right)}d\alpha d\beta } }} } = } \\ { = - \frac{{3q - 15qx - 2p^{3} - 3q^{2} + 24qx^{2} + 3p^{3} x + 12q^{2} x - 12qx^{2} - 12q^{2} x^{2} }} {{6q{\left( {2x - 1} \right)}^{2} }} = } \\ { = 0.5q - {\left( {7{\sqrt {17} } - 33} \right)}{\sqrt {6{\sqrt {17} } - 10} }{\sqrt q } + {{\left( {{\sqrt {17} } - 7} \right)}} \mathord{\left/ {\vphantom {{{\left( {{\sqrt {17} } - 7} \right)}} {32}}} \right. \kern-\nulldelimiterspace} {32},} \\ {\Delta CS_{0} = {\int_0^{\frac{p} {{2x - 1}}} {{\int_0^{\frac{p} {q} - \frac{{2x - 1}} {q}\beta } {{\left( { - \beta x} \right)}d\alpha d\beta } }} } = - \frac{{xp^{3} }} {{6q{\left( {2x - 1} \right)}^{2} }} = - \frac{{{\left( {3{\sqrt {17} } - 5} \right)}{\sqrt {3{\sqrt {17} } - 5} }{\sqrt 2 }}} {{768}}{\sqrt q },} \\ {\Delta SW = 0.5q - \frac{{{\left( {5{\sqrt {17} } - 19} \right)}{\left( {6{\sqrt {17} } - 10} \right)}{\sqrt q }}} {{384}} + \frac{{{\sqrt {17} } - 7}} {{32}}.} \\ \end{array} $$

  Analyzing these expressions we see that if q > 0.25, then ΔGSC ₁ > 0, ΔCS ₀ < 0 and ΔSW > 0.

• (3) If q < q′″, then the long run solution with p = p ^s and x < 0.25 is possible. Since p < q and $x < {{\left( {p + q - 1} \right)}} \mathord{\left/ {\vphantom {{{\left( {p + q - 1} \right)}} 2}} \right. \kern-\nulldelimiterspace} 2$, the equilibrium is as in Fig. 5a and ΔGCS ₁, ΔCS ₀ and ΔSW are given by

  $$ \begin{array}{*{20}l} {{\Delta GCS_{1} = {\int_0^{\frac{{q - p}} {{1 - 2x}}} {{\int_{\frac{p} {q} + \frac{{1 - 2x}} {{q - p}}\beta }^1 {{\left( {\alpha q - \beta \left( {1 - x} \right.} \right)}d\alpha d\beta } }} } = \frac{{{\left( {q - p} \right)}^{2} {\left( {5pq + q^{2} + 3{\left( {p + q} \right)}{\sqrt {q^{2} - 4q^{3} + 8pq^{2} - 4p^{2} q} }} \right)}}} {{6{\left( {q + {\sqrt {q^{2} - 4q^{3} + 8pq^{2} - 4p^{2} q} }} \right)}^{2} }},} \hfill} \\ {{\Delta CS_{0} = {\int_0^{\frac{{q - p}} {{1 - 2x}}} {{\int_0^{\frac{p} {q} + \frac{{1 - 2x}} {q}\beta } {{\left( { - \beta x} \right)}d\alpha d\beta + } }} }{\int_{\frac{{q - p}} {{1 - 2x}}}^1 {{\int_0^1 {{\left( { - \beta x} \right)}d\alpha d\beta } }} } = = - \frac{{{\left( {3q - 2{\left( {q - p} \right)}^{3} - 6{\left( {q - p} \right)}^{2} + 3{\sqrt {q^{2} - 4q^{3} + 8pq^{2} - 4p^{2} q} }} \right)}{\left( {q - {\sqrt {q{\left( {q + 8pq - 4p^{2} - 4q^{2} } \right)}} }} \right)}}} {{12{\left( {q + {\sqrt {q\left( {q + 8pq - 4p^{2} - 4q^{2} } \right.} }} \right)}}},} \hfill} \\ {{\Delta SW = \Delta GCS_{1} + \Delta CS_{0} = - \frac{{{\left( {q + {\sqrt {q^{2} - 4q^{3} + 8pq^{2} - 4p^{2} q} }} \right)}{\left( {q - p} \right)}^{2} {\left( {3 - 4p - 2q} \right)}}} {{12q{\left( {q - 2{\left( {q - p} \right)}^{2} + {\sqrt {q{\left( {q - 4{\left( {q - p} \right)}^{2} } \right)}} }} \right)}}}.} \hfill} \\ \end{array} $$

  Analyzing these expressions we see that if q < q″′, then ΔGCS ₁ > 0, ΔCS ₀ < 0 and ΔSW < 0.