Measuring 1-mm-accurate local survey ties over kilometer baselines at McDonald Geodetic Observatory

Abstract

The goal for the next generation of terrestrial reference frames (TRF) is to achieve a 1-mm- and 0.1-mm/yr-accurate frame realization through the combination of reference station solutions by multi-technique geodetic observatories. A potentially significant source of error in TRF realizations is the inter-system ties between the instruments at multi-technique stations, usually independently determined through ground-based local surveying. The quality of local tie surveys is varied and inconsistent, largely due to differences in measurement techniques, surveying instruments, site conditions/geometries, and processing methods. The Global Geodetic Observing System (GGOS) has tried to address these problems by issuing guidelines for the construction and layout of future multi-technique observatories, promoting uniformity and quality while minimizing existing problems with local surveying that are exacerbated over longer baseline distances. However, not every observatory is going to be able to completely satisfy these guidelines, and in this work, a successful endeavor to satisfy the accuracy goals while exceeding the GGOS baseline guideline is detailed for the McDonald Geodetic Observatory (MGO) in the Davis Mountains of Texas, USA. MGO consists of a VLBI Geodetic Observing System (VGOS), infrastructure in place for a Space Geodesy Satellite Laser Ranging (SGSLR) telescope, and several Global Navigation Satellite Systems (GNSS) stations spanning a 900 m baseline and a 120 m elevation change. The results of the local ties between the GNSS stations across the near-kilometer baseline, as measured from their antenna reference points, show sub-mm precision and 1 mm accuracy validated through repeatability across several surveys conducted in 2021as well as 1 mm consistency with the monthly averaged daily solutions of the GNSS-based positioning. In this paper, we report these results as well as the framework of the surveys with sufficient detail and rigor in order to give confidence to the quality claims and to present the novel design and techniques employed in the procedure, processing, and error-budget analysis, which were determined through iterative research methods across repeated survey campaigns.

1 Motivation and approach

1.1 Terrestrial reference frames

The goal for the next generation of terrestrial reference frames (TRF) is to achieve a 1-mm- and 0.1-mm/yr-accurate frame realization through the combination of positions of fiducial geodetic observatories, motivated by the user needs from commercial and scientific disciplines that rely on high precision positioning and spatial referencing (National Academies Report, 2020). The following list presents geodetic definitions of terms describing the quality of positioning in a reference frame. While these terms were applied in this paper to distance measurements and position determination, the basic definitions remained consistent as used to evaluate the results in the paper.

From Precise Geodetic Infrastructure: National Requirements for a Shared Resource, 2010. Terms to Describe the Quality of Positioning Within a Reference Frame

• Precision: the ability to repeat the determination of position within a reference frame. Precision is necessary to resolve changes in position over time, and it is measured using statistical methods on samples of estimated positions.

• Accuracy how close a station position within a reference frame is to the truth. Precision contributes to accuracy but takes into account systematic biases arising from calibration errors or imperfect observation models.

• Stability the predictability of the reference frame and the positions of the stations used to define the frame. In a stable reference frame, the defining parameters behave in a consistent manner, with no discontinuities over the time span of the geodetic observations. Furthermore, the ITRF should remain internally consistent, even as it is updated from time to time. Local site stability typically implies that all stations at that site do not move relative to each other, and that the site does not have nonlinear motions relative to the ITRF.

• Drift the relative rotation, translation, and scale between different reference frames, which results in different velocities between stations given in each frame. Drift results from instability in one or both of the frames being compared, which in turn may result from the systematic error in the measurement techniques, lack of precision in the measurements, or differences in station motion models.

The network solutions for positions and velocities of reference stations with multiple geodetic techniques are combined into one terrestrial reference frame via Helmert transformation (Altamimi et al. 2016). The Helmert transformation, long used in geodesy (Watson et al. 2006), is an affine similarity transformation which maintains parallelism and co-linearity, but disallows skew, scaling of different dimensions, and reflection. The result is a 7-parameter definition in 3-D Cartesian Space: three translation parameters, three rotations parameters, and one scale parameter for all dimensions. In frames that include velocity information, an additional seven parameters for rates are included for a 14-parameter transformation. In order to combine multiple geodetic technique network solutions to a single TRF via a Helmert transformation, connections are needed between each technique network. These connections (local ties) are independent measurements of the relative position between the reference points of each instrument at a subset of fiducial stations that host multiple techniques. Local ties are measured typically through ground-based surveying of physical points on these instrument systems, of which the inverse solution of these point measurements provides the 3-D geometric relative positions between the co-located instrument reference points. There is a distinction to be made between intra-technique local ties, which are ties measured between a pair of instrument systems of the same technique, and inter-technique local ties, which are ties measured between a pair of instrument systems of different techniques. Inter-technique local ties are the type that allow for the connection and redundancy necessary to combine multiple geodetic technique frames into a single TRF. For a strong combination and TRF realization, many such ties between different systems at multi-technique sites must exist and be precisely and accurately known (Pearlman et al. 2015).

The International Terrestrial Reference Frame 2014 (ITRF2014) realization has a reported accuracy of its origin of 3 mm at reference epoch 2010.0 and a stability of 0.2 mm/yr with reference to the previous ITRF2008 (Altamimi et al. 2016). Additionally, the implicit scale and scale rates estimated for the individual SLR and VLBI solutions differ by 1.37 ppb and 0.02 ppb/yr (an equivalent 8.8 mm difference in position on the Earth’s surface) (Altamimi et al. 2016). The arithmetic average of the values derived by the two techniques determines the scale and scale rates for the ITRF (Altamimi et al. 2016). According to the International Earth Rotation and Reference Systems Service (IERS), this choice is “justified by the fact that [they] do not have any means to discriminate between the two technique solutions and therefore their simple average is a fair choice that minimizes the scale impact for these two techniques when using the ITRF2014 products” (Altamimi et al. 2016). ITRF2020 is consistent in its origin with ITRF2014 to within 2 mm with a stability of 0.2 mm/yr (IERS 2023). The scale of ITRF2020 is 0.42 ppb larger than the scale of ITRF2014. However, the scale discrepancy between VLBI and SLR has decreased to 0.22 ppb (equivalent to 1.4 mm) (Pavlis et al. 2023).The scale discrepancy has decreased from ITRF2014 to ITRF2020 largely due to the estimation and correction of systematic biases in the SLR technique (Pavlis et al. 2023). While sources of discrepancy may also be at the measurement and geodetic technique level, the errors in local ties between geodetic instruments at multi-technique stations, particularly discrepancies between the measured ties and the relative position derived by space geodetic techniques, remain one of the most relevant limitations in the quality of the TRF (Boucher et al. 2015). Local ties require a level of scrutiny equivalent to the primary geodetic techniques because (1) they have direct impact to the combination parameters defining the TRF (Abbondanza et al. 2017); (2) they are effectively ingested into the TRF combination as a fifth technique (IERS 2004); and (3) they have the ability, given sufficient accuracy, to shed light on technique-level/site-specific errors and biases through cross-validation with other techniques (IERS 2004). In this mindset, this work presents meticulously surveyed and analyzed local ties at McDonald Geodetic Observatory (MGO) from three field campaigns in 2021 and new/innovative methods that produced them.

It is important to make the distinction that the surveys in this work measured intra-technique local ties between only GNSS stations and not inter-technique local ties such as those ingested into multi-technique TRF combinations. Due to the limitations in the scope of this work, which was to demonstrate a method for measuring ties across kilometer baselines with significant elevation change prior to all geodetic instruments being implemented, ties to instrument systems other than GNSS were not measured. They are the goals of continuations of this project, and as of the time this paper was written, plans for conducting additional surveys including all the available geodetic stations at MGO are already underway. What can be said about the unique value of the measurement and analysis of the intra-technique ties in this work, however, is that the internal repeatability of the surveyed local ties and the external cross-validation the local tie-derived positions with the GNSS positions give more support to the claims that:

• 1. The devised GNSS reference point measurement method is effective,

• 2. The braced quadrilateral surveying framework is capable of achieving 1 mm accuracy independent of geodetic reference point measurement and geodetic technique positioning differences.

The analyses just mentioned are discussed in detail in Sect. 4. Clearly, if no intra-technique ties were measured and only inter-technique ties were measured, it would be more difficult to externally validate the precision and accuracy of the local tie surveying framework, especially in measuring each different type of reference point, amidst different errors in the multiple geodetic techniques involved. With the future addition of inter-technique local ties, should those new ties produce larger errors and worse repeatability than the GNSS intra-technique ties, it would more clearly indicate problems in the measurement of the reference points of the added geodetic systems or further demonstrate the need for local ties to constrain the global positions produced by the different geodetic techniques at the observatory.

The characteristics of errors in local ties significantly affect TRF-defining parameters, where inappropriate values can cause distortions, such as incorrectly reported standard deviations and biases to certain components of the tie (Glaser et al. 2018). Earlier calculations asserted that local ties needed accuracy of 1-2 mm in order not to limit the mm-accuracy potential needed of TRF realizations (Sarti et al. 2004). VLBI was most sensitive to incorrect local tie standard deviations due to poor geometry and needing information on the origin to be transferred from other techniques. The TRF appears more sensitive to biases in certain components of ties in sites that we relocated in poorly covered regions of the globe. The uneven distribution and sparseness of all networks other than the GNSS is well understood (IERS 2023). Simulation of technique-level biases indicates that GNSS, whose ties to other geodetic instruments dominate the existing local ties, result in the largest distortions if there were a technique-level bias to all their stations, likely due to their importance in transferring origin, scale and orientation between the other techniques (Glaser et al. 2018).

Thus, accurate TRF definition requires proper characterization and representation of local tie errors; elimination of biases and errors in local ties; and increased density of multi-technique core sites in poorly covered regions of the globe with accurate local ties. McDonald Observatory was identified in (Glaser et al. 2018) as an important core site where simulated errors in local ties would produce large distortions to TRF parameters, indicating McDonald Observatory was an anchor for the SLR and GPS in the North American region. With the addition of new geodetic instruments and additional techniques at the expanded McDonald Geodetic Observatory (MGO), local ties and possible errors at MGO will further impact future TRF realizations.

1.2 Local ties in the ITRF

Station coordinates and their uncertainties from the different geodetic techniques are ingested into the ITRF using data in the SINEX (Solution INdependent EXchange) format (IERS 2023). Similarly, local ties are ingested as3-D globally referenced coordinates and variance–covariance matrix (VCM) connecting instrument reference points in SINEX format (Altamimi et al. 2017). In ITRF2005, only 45% of local ties were reported with fully populated VCM (Altamimi et al. 2007). ITRF2008 saw 63% full VCM reported (Altamimi et al. 2011). ITRF2014 saw 80% full VCM reported (Altamimi et al. 2016). This number continues to trend upward in future TRF realizations as new local ties and new observatories are incorporated and older ties lacking in a full VCM are re-measured. The procedure for the ITRF combination is to use the local ties as independent measurements of the relative position of the instrument reference points weighted by an appropriate VCM.

For each survey of local ties at a geodetic observatory, there should be a local tie SINEX file and a survey report. The report guidelines and templates ask for basic summaries as described in Long et al. (2000) and the IERS Template for Local Tie Report Layout (IERS). Given these guidelines and the diversity of surveying techniques, most local tie surveys are reported with varying levels of procedural and mathematical detail. Consciously acknowledging the purpose of the reports, they assume knowledge of “basic concepts of geodetic surveying” and do not attempt to “detail or justify the approach taken, but merely report the results of each major computation step” (Woods et al. 2007). Re-measurement is recommended to provide validation, long-term robustness, and monitoring of site motions to the requisite sub-mm per year (Pearlman et al. 2015).

Local tie surveys submitted to the IERS were evaluated for their fit to the space geodetic data in preliminary TRF combinations. Those for which the post-fit residuals exceeded a certain threshold were down-weighted by assigning variances larger than those reported in the SINEX (Altamimi et al. 2016). IERS performs calculations of Weighted Root Mean Scatter of all tie residuals in their East, North, Up, reference frames to find that the overall tie quality to be at the level of 3 mm (Altamimi et al. 2016). Any local tie that is reported more precisely than 3 mm in their variance is adjusted to the 3 mm minimum in the processing (Altamimi et al. 2016). The residuals for the local ties used in the latest ITRF2020 are available on the ITRF website. While this ensures that problematic data are kept in check, it does not emphasize the issue that many local ties need better documentation, re-evaluation, re-measurement, and monitoring.

The Global Geodetic Observing System (GGOS) has tried to address the problem of disparate survey quality by issuing guidelines for the construction and layout of future multi-technique geodetic observatories as core sites (Pearlman et al. 2022), promoting uniformity and quality of core sites while minimizing existing challenges with local surveying that are exacerbated over longer baseline distances. At the current level of surveying, the GGOS Requirements for Core Sites (Pearlman et al. 2022) recommends that co-located instrumentation be no more than 200 m apart, at similar elevations, and in mutually clear view in order to achieve the 1 mm accuracy demands of the TRF. The GGOS recommendations are infeasible for many observatories that are already or have plans for becoming multi-technique observatories to be considered core sites. However, geodetic observatories with baselines longer than 200 m by necessity could be safely allowed to join the multi-technique TRF realization as core sites by addressing issues with survey quality at longer baselines.

Other attempts at improving local ties involve technological advancements in surveying instruments and apparatuses, as well as new techniques such as the usage of space-based local ties such as GPS-derived local ties (Abbondanza et al. 2009). In this work, GPS-derived local ties were used as cross-validation of the terrestrial surveyed intra-technique local ties and for global orientation of the local reference frame of the survey, of which TRF combinations are particularly sensitive. Local tie surveys that also include GPS-derived local ties and intra-technique local ties may strengthen the global orientation of local ties and scale estimates in TRF combinations.

The goal of this work is to establish and demonstrate a new framework for achieving millimeter-accurate survey ties in a geodetic site that does not satisfy the geometric requirements recommended by GGOS: McDonald Geodetic Observatory which has a greater than 800 m baseline between VLBI, GNSS, and, in the near future, an SLR system; and is located in the Davis Mountains of Texas. This research effort is meant to motivate the improvement of accuracy and availability of local ties by pushing the limit of preferred geodetic station layouts and by providing a survey framework described in sufficient detail that the design and analysis principles can be applied to other sites.

1.3 Local tie surveying

In this section, a basic overview of local tie surveying, methods, and instruments with their pros and cons is given as motivating the chosen methods and instruments.

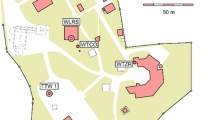
The core need for local ties at multi-technique observatories is the definition and monitoring of unique polygons of measured geometric reference points for all geodetic instruments. An example of such a polygon is illustrated in Fig. 1. Note the specific configuration and labels shown are for MGO. This is a time variable polygon that is subject to different dynamic effects, and in its measurement, is subject to different errors, instrument limitations, and procedural/processing choices. Local surveys measuring this polygon vary in quality inevitably due to the global separation of geodetic observatories: different groups will survey different observatories each under unique conditions requiring different procedures (Fig. 2).

Fig. 1

An example polygon representing the network of geodetic instruments and local ties for McDonald Geodetic Observatory

Fig. 2

McDonald Geodetic Observatory

The basic geodetic surveying concepts and methods needed to obtain the best results are variable in each scenario. In addition to the methods, choice of equipment such as surveying instrumentation and the peripherals including retro-reflectors, mounts, rods, and level bubbles are a significant factor. The best results are usually judged by precision and accuracy, but under different constraints, these may be traded for cost and time efficiency. When measuring local ties, precision and accuracy is valued highest with best available methods and equipment chosen for each scenario. A total station, which can measure both distances and horizontal/vertical angles by emitting a laser at a reflective target and measuring the reflection back, is typically used for long distance surveys (greater than 100 m). Total stations directly measure slant distances but must indirectly obtain horizontal and vertical distances through combination with the angle measurements. Modern total stations have measurement accuracies at the sub-mm level (e.g., ± 0.6 mm + 1 ppm) for distances and at the half arc second level (± 0.5″) for angles (Leica 2023). However, total stations may not achieve that level of accuracy and precision in practice due to several sources of error such as collimation, atmospheric effects, calibration, instrument heights, prism offsets, prism limitations, curvature, stability, temperature fluctuation, and user error.

When long distance surveys involve great changes in elevation between instrument and target, it is recommended to measure the vertical distances directly through differential geodetic leveling (NOAA 2017). This splits a survey into two components: the horizontal 2-D positioning and the geodetic leveling. There are three techniques of geodetic leveling: differential, trigonometric, and barometric (NOAA 2017).Trigonometric leveling is the process of calculating vertical heights using measured vertical angles and known/measured distances (NOAA 2017), also known as indirect leveling and employed by total stations. While relatively economical due to simultaneous measurement of slant distance and horizontal angle, it is less accurate due to limitations in measuring vertical angles over long distances due to atmospheric effects and Earth’s curvature (NOAA 2017). The distance measurement is affected by delays in the laser time-of-flight and phase change; and angle measurements are affected by refraction of the light path (Rüeger 1990). These effects are difficult to measure, model, and correct (Rüeger 1990). The refraction of the vertical angle is the most problematic, with changes of thousandths of a degree over a kilometer resulting in decimeter-level errors in height (Ferhat et al. 2020).

Differential leveling is a direct and more accurate method of leveling that takes readings from two height staves that are held at target locations directly in front of and behind the surveying instrument (NOAA 2017). By measuring to both, the difference in height between the two locations is determined. The distance between the two locations is typically less than 100 m. In order to calculate vertical heights over longer distances, digital leveling is applied repeatedly over traversals of shorter segments of the baseline and the cumulative height difference is calculated. Precise digital levels are rated for accuracies of ± 0.3 mm/km for heights in a 1 km “double run” survey with operating ranges up to 120 m (Leica 2023). There are limitations to differential leveling: compounding instrumental errors during numerous traversals and requiring suitable areas for traversal. In other words, for difficult terrain such as mountains with problematic sight lines, traversal may be impractical and trigonometric leveling may be more suitable (NOAA 2017).

Therefore, this work makes use of 3-D positioning and indirect leveling with a total station at the McDonald Geodetic Observatory. The compounding errors due to repeated setups of precise digital leveling was determined to be greater than the errors in trigonometric leveling due to atmospheric effects and Earth curvature when mitigated through survey design, procedural modifications, and error correction using modeling. These strategies are discussed in Sect. 2.

1.4 McDonald Geodetic Observatory

The site of this research was the McDonald Geodetic Observatory (MGO), located at the McDonald Observatory in the Davis Mountains, Texas. McDonald Observatory has a history as the site of a fiducial reference for positioning via the NASA McDonald Laser Ranging System (MLRS), the MDO1 GPS station, and several established geodetic markers. Hosted at the astronomical observatory of the University of Texas at Austin, MGO is a joint effort between NASA and UT Austin designed to extend the three-decade long record of precise positions at the observatory by deploying the next generation geodetic instrumentation. The geodetic instruments at this site include a new VLBI Global Observing System (VGOS)which is the modern standard and state-of-the-art for VLBI developed by the International VLBI Service for Geodesy and Astrometry (IVS), several new GNSS stations, and a superconducting gravimeter. The infrastructure is in place for a Space Geodesy Satellite Laser Ranging(SGSLR) system, which is the modern standard and state-of-the-art for SLR developed by the Space Geodesy Program at NASA. MGO is awaiting delivery of the main telescope and laser. Extrapolating from the observatory’s past importance for GPS and SLR local ties, it is expected that the GNSS-VGOS, GNSS-SGSLR, and VGOS-SGSLR inter-technique local ties will also be very important to the accurate realization of future TRFs. An important characteristic of MGO is that it falls outside of the Global Geodetic Observing System’s requirements for a core site, dimensionally speaking. The instruments at McDonald are split among two key locations: the VGOS site which is in a low elevation valley in the west and the SGSLR site which is atop the Mt. Fowlkes peak to the east. The baseline between the two sites is over 800 m and the elevation change is over 120 m. The measurement of a 1-mm-accurate co-location tie for a site in this layout through conventional survey practice faces many challenges due to atmospheric effects, instrument errors and noise, and procedural errors that are all magnified by the long baseline and elevation change.

The McDonald Observatory consists of two mountain peaks: Mt. Locke and Mt. Fowlkes. Between the two mountains is a saddle point and at the base is a valley. The SGLSR is being constructed at the peak of Mt. Fowlkes near the location of the retired MLRS, alongside GNSS stations and several already operating astronomical telescopes. The mountain peak space is limited and is occupied by other observatories. The VGOS site is located in the valley, approximately 800 m away from the SGSLR with an elevation drop of 120 m. McDonald Observatory is situated at an altitude of 2000 m above sea level and latitude of 30.7 degrees in the arid region of west Texas. It has an annual average high of 30 degrees Celsius in June, annual average low of 0 degrees Celsius in January, a rainy season in May to November with 2-10 cm of rain monthly, and a dry season in December to April.

A motivator for the closer study of the geodetic instruments at McDonald Observatory was the apparent drift seen in the position time series between the MLRS station and the nearby MDO1 GNSS station as seen in Fig. 3. Located at the same site less than 100 m apart, MLRS exhibited a downward drift of about 1 mm/yr for 20 years while MDO1 remained relatively stable. The pursuit of sub-mm precision and accuracy in this work was motivated by attempts to directly measure site motion through regular surveys. In order to understand the cause of this apparent sinking, whether related to a problem with equipment, monumentation, or analysis technique, one of the long-term goals at MGO is the continuous monitoring of the stability and drift of a local ground control network (LGCN) and geodetic instrument reference points with precise and accurate local ties. This motivating problem has yet to be resolved as it is outside the scope of this particular work, however, it remains a goal of ongoing and future work.

Fig. 3

Time series for McDonald Observatory’s GPS station, MDO1, and the SLR station as represented by its geodetic marker, 7080

The precision and accuracy of the local ties were evaluated based on metrics of quality for local ties presented in Table 1. These metrics were analogous and consistent with the metrics of quality for the global geodetic infrastructure defined in Sect. 1.1. The framework was a result of iterations at the procedural and analysis levels until a record of three successful campaigns were completed satisfying the metrics of quality through repetition, consistency, and validation. The site-specific methods for conducting the millimeter-accurate survey at MGO were described and strategies to mitigate budgeted error sources were discussed. Results were shown for a series of surveys of the kilometer local ties between the GNSS stations at MGO.

Table 1 Metrics of quality for local tie surveying

2 Experiment design and procedure

The pre-analysis conducted in this work estimated that the accumulation of errors through the traversal over MGO distances would render 2-D surveying with differential leveling less accurate than 3-D surveying with indirect leveling because of the winding path that would be traversed. Therefore, the survey framework described in this paper employed 3-D surveying using a total station to measure directly measure range and angles to survey targets across the kilometer local tie baseline. The following sections outline the layout of the survey network, the instrumentation used, the campaign structure, and the procedure.

2.1 Surveying network layout

The layout of a LGCN consisting of target monuments (TMs) and the so-called braced quadrilateral of instrument positions (IP) is now described. The foundation for achieving millimeter accuracy was to establish a control network with strong geometry and well-known positions. The layout consists of two LGCN, one each surrounding the VGOS and the SGSLR sites, formed of ideally around six TMs at each site with mounting points for precision survey and precision metrology reflectors. Precision metrology in this usage refers to the field of “measuring and evaluating the accuracy and reliability of industrial components and systems.” Precision metrology uses laser-based equipment and procedures that produce measurements at orders of magnitude higher precision than typical precision surveying, though these are typically applied at shorter distances and in indoor, controlled environments. The fusion of elements of the two fields was a unique aspect that set this framework apart from previous local tie surveys. The TMs were the local reference points that realize the coordinate systems for the surveys between the SGSLR, VGOS, GNSS and other geodetic systems. The permanent coordinates stored in the LGCN allow for repeated surveys to re-acquire the local coordinate system of each site so that stability and drift of the geodetic instruments can be relatively measured. By storing the coordinate system in the target monuments, the total station measurement instrument need not be repeatedly set up over a specific location in the network. The position of the instrument in the coordinate system can be acquired by measuring to the LGCN. Thus, the errors due to the repeatability of instrument set-ups were eliminated.

Bridging the two LGCN was a separate network of four Instrument Positions (IPs), from where observations were collected using the total station instrument at one IP while all the IP and target monuments (TMs) were observed as targets. This network of IPs, which was dubbed the braced quadrilateral (BQ), provides observation redundancy. Each TM and each geodetic system reference point were at least surveyed from two IP, and each IP was surveyed from the other three IP. This is not typical in surveying, where commonly from a single instrument position, each point in the network is measured once with no redundancy, or an instrument is moved through many instrument positions, compounding procedural and systematic errors with each additional setup (NOAA 2017). The procedure developed in this work instead measured all baselines in one LGCN from the two nearby IPs and the baselines forming the braced quadrilateral measured from every IP. The baselines from the LGCN were bridged by the braced quadrilateral baselines.

The observations of the braced quadrilateral made a complete set of near-simultaneous, reciprocal observations of the kilometer baseline. The method of simultaneous reciprocal measurement applying to characterize and mitigate refraction is well-known in the surveying field. It is typically applied to direct vertical leveling for meeting high precision heights (Ceylan et al. 2008; Hirt et al. 2010; Yang et al. 2021). In this work the method of reciprocal measurements was applied to our method of indirect leveling using a total station. Simultaneous reciprocal measurement requires the use of two instruments of equal precision. This work showed that within the braced quadrilateral, the average of reciprocal measurements taken over the span of a couple of hours using a single instrument arrived at a notably accurate vertical angle, within the total 3 mm level accuracy of current local ties. By observing all the IPs in the braced quadrilateral from each IP, every baseline had paired sets of reciprocal observations. Thus, any path-dependent effects such as refraction were effectively cancelled. Only four instrument setups were required, yielding redundant, geometrically constrained measurements.

At the time of this work, construction of the MGO was underway, and the SGSLR and permanent target monuments were not emplaced. This work utilized semi-permanent monuments placed at opportunistic locations in the available geodetic infrastructure with unimpeded lines of sight in order to facilitate the ongoing experimentation and development of the surveying framework. However, this work demonstrated that even with the provisional LGCN, the precision and repeatability of the network positions including GNSS stations was at the 1-2 mm level. Figure 4 shows the current network layout at MGO. The LGCN at the VGOS site had four target monuments spread out in approximately within 60 m of at least one instrument position. TM11, TM12, and TM13 were in a geometrically strong formation. TM14 was known to be a point of weakness; however, it was also the closest control point to MGO4. For this work, TM11 was chosen as the “site marker” for MGO, the origin of the local reference frame to which relative changes in local ties were calculated over time in repeated surveys. While TM11 is not a permanent marker attached to the lithosphere, the stability of the monument was sufficient for the time scale of the experiments in this work. Selection and installation of a permanent site marker for MGO requires more consideration that is outside the scope of this paper, however, is important to the future work completing the inter-technique local tie surveys of MGO. The SGSLR site posed significant challenges to finding and maintaining lines of sight between the geodetic instruments, any instrument positions, and viable target monument locations with the current monument design. Thus, only one target monument (TM21) remained visible to both IP and only one IP could observe either GNSS station (MDO1 and MGO2). A layout updated for the SGSLR will require tall monuments for both the LGCN and the IPs in order to achieve proper visibility. These are site-specific challenges, which can be unavoidable. In the future, these challenges can be mitigated with appropriate investment (Fig. 5).

Fig. 4

Current local network layout

Fig. 5

(Left) Target monument design, (right) target monument mounted with the BMR

2.2 Instrumentation

This work made use of solely commercially available survey and precision metrology equipment. A Leica TS30 total station was used to collect the survey measurements of the MGO network. Two of these instruments were employed: one owned and contributed to this effort by John Griffin Surveyors, and the other loaned by NGA as part of their collaboration with this project. The TS30 is specified to have 0.6 mm accuracy ± 1 ppm in its distance measurement and 0.5as accuracy in its angle measurements to precise reflectors.

The type of reflector used with the TS30 depended on the target measured. The TMs were equipped with PLX Ball-Mounted Hollow Retroreflectors, specified at 0.002 mm accuracy during calibration at 20 ± 0.1 ℃ (Hubbs 2023). These prisms are recommended for use at distances within 60 m and under climate-controlled conditions. At temperatures departing from 20 ℃, thermal expansion of the sphere was not negligible at the micrometer level but within sub-mm precision needed for this work. The ball mounted retroreflectors were mounted in magnetic pin nests that slotted into the target monuments, centering over the same points on the monuments each survey. At the distances from the TS30 to the TMs, by design less than 60 m, the accuracy of the measurement to the ball-mounted retroreflectors was demonstrated to be greater than measurements to standard survey reflectors despite the lack of climate-control. At longer distances, the accuracy of the measurement to the BMRs was greatly reduced. The instrument positions in the braced quadrilateral, when not occupied with the TS30, were equipped with Leica GPH1P Single-Prism Precision Reflectors. These reflectors are rated for 0.3 mm centering accuracy and usable at distances up to 3500 m (Leica 2023). To achieve the kilometer-baseline local tie at 1 mm accuracy, target reflectors with sub-millimeter centering accuracies were used at each measured point in the local tie network polyhedron. Actual measurement accuracies were expected to be lower than the specifications.

A MET3 Meteorological Sensor was used to record atmospheric parameters at the VGOS site during the surveys so that corrections for atmospheric delay and refraction could be later applied to the observations during the data processing. The MET3 was provided by Clark Wilson from the Jackson School of Geosciences at The University of Texas at Austin. The MET3 recorded pressure to 0.08 hPa, temperature to 0.5 degrees C, and relative humidity to 2% accuracy (Paroscientific 2023). The SGSLR site at Mount Fowlkes is equipped with a continuously operating weather station used with the astronomical telescopes. The atmospheric data were accessed from the McDonald Observatory online weather archive (Hobby-Eberly Telescope Engineering 2003) and also used to apply corrections for atmospheric delay and refraction. Details on the application of the corrections are given in Sect. 3.2.The specifications for the instrumentation just described are summarized in Appendix A.

2.3 Monumentation

The target monuments used in this work were constructed out of readily available materials and intended as semi-permanent structures for the purpose of demonstrating the surveying framework. 2 m-long threaded steel rods of 2.54 cm diameter were placed about 1 m into the ground and secured with epoxy. A 15 cm deep and 30 cm diameter cylinder was cut from the surface surrounding the monument. A 15.24 cm diameter PVC pipe was placed around the steel rod down into the shallow cutout. The cutout was then filled with cement. When not in use, the PVC pipe surrounding the rod was capped. This system protected the steel rod from external conditions and simultaneously worked to decouple it from the near-surface soil dynamics. At the top of the rod was a precisely machined sleeve in which the pin nests for the Ball Mounted Hollow Retro-reflectors (BMRs) were accurately placed and removed with ease.

2.4 Campaign structure

The local tie survey campaigns presented in this work occurred on May 16-20, 2021; September 15–17, 2021; and November 29–December 2, 2021. Each campaign allowed for at least 2 full local tie surveys of the LGCN and the instrument positions in the braced quadrilateral. This allowed for comparisons of surveys over daily and seasonal periods. The September campaign and November/December campaign also surveyed the reference point of the MGO GNSS monuments.

In this work, the following terminology is used: a set is the collection of one pair of forward and reverse observations to each of the targets visible to the TS30 at its current instrument position, i.e. the nearby LGCN, the braced quadrilateral, and the nearby geodetic instruments; a session is one occupation of an IP by the TS30 completing multiple sets of observations of its targets; a survey is a one-day complete observation of the survey network from each of the four IP locations; and a campaign is a multi-day collection of surveys. Figure 6 shows the hierarchical organization of these terms.

Fig. 6

Hierarchical organization of local tie surveys

Each survey took about an hour of set-up and about 4–6 h to complete in a single day. The best conditions to begin surveying occurred in the late morning to early afternoon, as measurements taken at this time across the kilometer baseline had smaller biases due to atmospheric refraction (sub-millimeter versus several millimeters biases as seen in the post-fit residuals). This was likely due to the convective turbulence uniformly mixing the lower atmosphere along with reaching the plateau of daytime temperatures, stabilizing the refractivity of the line of sight across the kilometer baseline over the duration of the surveys. Before starting a survey, the instruments were allowed to acclimate to the outdoor conditions for at least twenty minutes. Wind and rain conditions for the day were also judged. Before beginning the observation sessions, tripods were placed at the four TS30 instrument positions. Each tripod was leveled with an adjustable mount and internal leveling system, and automatic compensator of the TS30 before beginning any observation session. These components set and automatically maintained the vertical orientation relative to the local gravity (Leica 2023). This ensured that the instrument tripods would not need to be re-leveled at any point during the survey, keeping the physical positions of the points consistent throughout the entire survey.

A session began with the set-up phase at a particular IP. Leica precision reflectors were placed at the three unoccupied instrument position tripods facing the instrument position that will be occupied by the TS30. BMRs were placed on the target monuments in the nearby LGCN also facing the TS30. The MET3 atmospheric data collection was initialized at the VGOS site. The atmospheric data at the SGSLR site were recorded by the Mt. Fowlkes permanent weather station. Before beginning the observation phase, the TS30 was programmed to its current location. The vertical angle reference was set to the local vertical defined during the previous leveling step. The horizontal angle reference was defined by the baseline between IP1 and IP3 along the diagonal of the braced quadrilateral. This was done by observing IP3 with the TS30 when occupying IP1 and setting the horizontal angle of the instrument in that orientation to 0 degrees. Subsequent setups recapture the horizontal orientation by measuring to the IP across the diagonal of the braced quadrilateral (i.e. IP2 to IP4, IP3 to IP1, and IP4 to IP2) and using the LGCN positions as measured at IP1. Errors in the orientation between these setups are corrected for in the analysis step as described in Sect. 3.3.

During the surveying phase, at least four sets of observations were collected from each instrument position to all the nearby defined targets: the LGCN, the braced quadrilateral, and the nearby geodetic instruments. In this work, only the GNSS stations were measured to. The observations collected were raw range in meters, vertical angle in degrees, and horizontal angle in degrees. Each measurement was an average of a Direct and Reverse observation by the total station, a technique wherein the instrument observed a target in one orientation, rotated itself horizontally by 180 $^\circ$ and then vertically by 180 $^\circ$, and observed the same target again while upside-down. The averaging of the direct and reverse observations eliminated systematic biases in the instrument such as collimation error and gravity loading. The total station was operated with Automatic Target Recognition (ATR), a mode in which the total station observed pre-defined targets for a specific number of sets without user input/interaction. This system significantly reduced individual measurement time and allowed for more sets of observations to be collected in a single survey and allowed for reciprocal measurements to be taken within reasonable time gaps. In general, ATR points to targets at lower accuracy than a trained human operator could. However, for the total station used in this work, corrections were automatically applied to the pointing via location of maximum return pixels on the instrument’s CCD (charge-coupled device) with the resulting accuracy comparable to manual pointing.

2.5 Survey structure and methods

First the LGCN and braced quadrilateral were measured in one ATR program. Then in the same job, the GNSS stations visible to that IP were measured. Figure 7 shows a diagram of the unique method for measuring the reference point on the GNSS antenna. The BMRs were used to collect a semi-circle of about 6 to 10 observations around the circumference of the base of the choke ring, pressed by hand directly below the ground plane. The center of this circle would be the observed reference point position. The description of the algorithm is presented in Sect. 3.4.

Fig. 7

Method of measuring the antenna reference point of choke ring GNSS antennas

After completing the observations to the targets, the TS30 moved to the next IP and the previous IP was replaced with a precision reflector. The reflectors on the other IP and the nearby TMs were pointed toward the new location of the TS30. The TS30 set-up and surveying phases repeated through the next three IP locations. Since the braced quadrilateral was fully observed during the first observation session, the horizontal orientation was reacquired by observing the furthest IP in the braced quadrilateral from the current location. IP2 referenced IP4, IP3 referenced IP1, and IP4 referenced IP2.

Three analyses and results from campaigns following this framework are presented in the next section. The campaign in May 2021 did not measure the GNSS stations, however, the campaigns in September 2021 and November/December 2021 did.

3 Data processing

This section describes the observations obtained in the surveying, pre-processing steps, and the nonlinear least squares problem for solving the network.

3.1 Observations and assigned uncertainties

The TS30 is capable of applying certain corrections, such as atmospheric delay in the form of a ppm correction to distance, and other pre-processing actions, such as averaging forward and reverse observations, before outputting data to a job file in a Leica proprietary format. In order to understand all the effects on the measurements at the lowest level of data collection, all internal corrections were turned off in the instrument and the data were output in a custom format text file containing fields for instrument position name, target name, raw range, raw zenith angle, raw azimuth angle, time of observation, and reflector offset. These raw observations were the un-averaged individual forward and reverse observations for all repeated sets. Additionally included were all set-up observations and all observation blunders. Though the data in this raw form required significantly more pre-processing and screening to become usable, the effects and possible origins of errors were more readily seen and identified.

Observation blunders typically constituted measurement outliers (on the order of greater than few millimeters) caused by, for example, weak back-sighting to the reference azimuth at an instrument position; poor leveling or re-leveling of the reference zenith of the instrument; inputting incorrect prism offsets; obstructed lines of sight by leaves, branches, fences, or animals; and displacement of points (either instrument, tripod, or prism) during survey due to things like user error or strong winds. Outliers caused by blunders were identifiable as individual observations that were statistically outside the cluster of similar observations to the same point from the same instrument position (greater than sub-millimeter and few arcseconds), a set of observations that was overall much noisier than the instrument precision or other sets of observations (greater than sub-millimeter and few arcseconds), or a set of observations that was significantly biased to the rest of the survey (greater than 1 cm and 1arcminute).

Accounting for instrument specifications, environmental effects, and tuning to the data collected from surveys at MGO, the 1-sigma uncertainties for each observable were set to: range + / − 0.1 mm, vertical angle + / − 13arcseconds, and horizontal angle + / − 1arcseconds. The uncertainties used in the subsequent estimation process were tuned by performing a statistical hypothesis test, determining the probability of obtaining observations at least as extreme as those collected at MGO, given the resultant estimated network positions calculated using the process described in Sects. 3.2 and 3.3. In these tests, the positions of the points in the MGO network were estimated using some nominal observation uncertainties (the instrument specifications) and the null hypothesis $H_{0}$ is that observation post-fit residuals for range, vertical angle, and horizontal angle do in fact come from a measurement distribution with these nominal uncertainties and from the resultant estimated positions of points in the network. The significance value was chosen as $\alpha = 0.05$, meaning that a less than or equal to 5% chance that the null hypothesis was not true would be acceptable. The sets of observation post-fit residuals belonging to each of the $i = 1:3$ observation types were tested for their fit to the expected uncertainty values. The number of observation post-fit residuals in each observation type is denoted as $M_{i}$. Since there are three observation types being tested, the degrees of freedom, $df$, was equal to 2. Therefore, the Chi-square for this problem was denoted as $\chi_{0.05,2}^{2}$ with a Chi-square value of 5.99. The test statistic was denoted as $\overline{x}$ and was calculated by Eq. 1.$O_{i}$ represented the number of observation residuals within the 2-sigma uncertainty level (95%) of the i^th observation type. $E_{i}$ represented the expected number of observations to fall within the 2-sigma (95%) of the i^th observation type which is equal to 95% of the total number of observation residuals of the i^th type.

$$ x = \mathop \sum \limits_{i = 1}^{3} \frac{{\left( {O_{i} - E_{i} } \right)^{2} }}{{E_{i} }} = \mathop \sum \limits_{i = 1}^{3} \frac{{\left( {O_{i} - (0.95*M_{i} } \right)^{2} }}{{\left( {0.95*M_{i} } \right)}} $$

(1)

Using the data from the September 16th survey, then the following values are calculated:

• $M_{i} = 102$ observations

• $E_{i} = 0.95*M_{i} = 96.9$ observations

• $O_{1} = 81$ range observations

• $O_{2} = 85$ vertical angle observations

• $O_{3} = 84$ horizontal angle observations

The calculated value of the test statistic using Eq. 1 is 5.79. The test statistic is less than the Chi-square value, and the observation residuals failed to produce an extreme enough result to reject the null hypothesis. Therefore, the null hypothesis, that the observation residuals were produced from a measurement distribution with the proposed uncertainties and calculated estimated state, was not rejected. Thus, the proposed uncertainties were deemed reasonable within the definition of the test. An approximate p-value for this test, the probability that a more extreme measurement sample could be produced than the tested sample under the null hypothesis was tuned to be about 5%.

3.2 Pre-processing observations

In the pre-processing stage, range observations were corrected for atmospheric delay of the total station laser using the first and second velocity corrections for electronic distance measurement (Rüeger 1990). Atmospheric data were collected at both endpoints of the kilometer baseline at the two LGCN: the VGOS site and the SGSLR site. For each survey observation, the atmospheric observations nearest in time were used, and interpolation of the data in time was found unnecessary. For observations from IPs to the nearby LGCN, the respective endpoint atmospheric dataset was used. For observations across the kilometer baseline, the average of the two endpoint atmospheric datasets was used. The average of the two endpoints was a rough approximation of the atmosphere along the entire laser path when using the first and second velocity corrections, models designed for observations across relatively flat terrain.

The first velocity correction is a 10-100 ppm correction. Over a kilometer baseline, a delay of the several centimeter-level was expected. The second velocity correction is smaller, resulting in a sub-mm correction over a kilometer. The equations for both velocity corrections are given in Appendix B. After correction, the remaining error was dependent on the accuracy of the atmospheric measurements and the model representation of the atmosphere along the laser path. Due to the elevation changes across the MGO kilometer baseline, the approximation of the atmosphere along the laser path with only end-point meteorological data collected at the VGOS and SGSLR sites, errors in velocity correction were measured to be as large as 2 mm across the kilometer baseline. This error was quantified via an estimated a scale difference when comparing the repeatability of surveys conducted under similar conditions on consecutive days. This manifested as a scale difference because the velocity corrections alter the value of the range measurements and so errors in those corrections essentially change the observed size of the observatory. This is further discussed in the analysis in Sect. 4. Errors in the velocity correction fall within the total 1-3 mm error budget.

The measured ranges were then corrected for “reduction to the wave chord” (Rüeger 1990). Light traveling through the atmosphere with a horizontal component relative to a local gravity reference frame, will follow a slight curved wave path. Reducing the curved wave path between two points to the straight chord between them takes into account the coefficient of refraction of the local atmosphere, and the curvature of the Earth at that latitude. The equations for the reduction to wave chord correction are provided in Appendix B. This correction is small, at the sub-millimeter-level at a kilometer baseline.

There was consideration made to the measurement and correction of the deflection of the vertical between the VGOS and SGSLR sites. Modeling using the full EGM2008 revealed a difference of about 47mas. In consideration of the kilometer size of the network, a deflection to the measured vertical angles of 47mas would produce a change in vertical height of about 0.2 mm. While this effect was below the observed effect of the refraction on vertical angle and the measurement uncertainty in the vertical angle, a correction of 47mas was applied to the observations across the kilometer baseline of one end of the braced quadrilateral.

To simplify the estimation observation-state relation equations, the three real observations were reparameterized into three pseudo-observations. These pseudo-observations were the three Cartesian components of the distance between instrument and target in a local gravity-aligned reference frame, $\left( {{\Delta }x, {\Delta }y, {\Delta }z} \right)$. Equation 2.1–2.3 reparameterized the observations into observations of distance in the x, y, and z directions where $r$ was the observed range, $V$ was the observed vertical angle, and $H$ was the observed horizontal angle. The uncertainty in range is $\sigma_{r}$, in vertical angle is $\sigma_{V}$, and in horizontal angle is $\sigma_{H}$. Then the uncertainty of the reparameterized distances was calculated using linearized propagation of uncertainty in Eq. 3.1–3.3 where $P_{{{\text{obs}}}}$ is the variance–covariance matrix of the observations, $J$ is the Jacobian of Eqs. 2.1–2.3, and $P_{{{\text{pseudo}}}}$ is the propagated variance–covariance matrix of the pseudo-observations. The three observations of range, vertical, and horizontal angle were uncorrelated measurements collected by three independent systems in the total station: the phase-based distance laser and the two independent rotary encoders for each axis of rotation. The pseudo-observations were correlated due to the reparameterization and the variance–covariance matrix produced by the propagation of uncertainty contained off-diagonal covariance terms. The effect of these terms in the weighting matrix in the estimation process was negligible compared to a weighting matrix based off the diagonal variance terms only.

The reparameterization allowed for the observation-state relation equations to take the form of position coordinate differences as seen in Eq. 4 in Sect. 3.3, with no numerically significant effect on the estimated solutions, formal errors, or post-fit statistics. When calculating post-fit residuals, the conversion was inverted to reproduce the forms of the original measurements of range and angles for analysis.

$$ {\Delta }x = r*\cos \left( V \right)*{\text{cos}}\left( H \right) $$

(2)

$$ {\Delta }y = r*\cos \left( V \right)*{\text{sin}}\left( H \right) $$

(3)

$$ {\Delta }z = r*\sin \left( V \right) $$

(4)

$$ P_{obs} = \left[ {\begin{array}{*{20}c} {\sigma_{r}^{2} } & 0 & 0 \\ 0 & {\sigma_{V}^{2} } & 0 \\ 0 & 0 & {\sigma_{H}^{2} } \\ \end{array} } \right] $$

(5)

$$ J = \left[ {\begin{array}{*{20}c} {\frac{\partial }{\partial r}{\Delta }x} & {\frac{\partial }{\partial V}{\Delta }x} & {\frac{\partial }{\partial H}{\Delta }x} \\ {\frac{\partial }{\partial r}{\Delta }y} & {\frac{\partial }{\partial V}{\Delta }y} & {\frac{\partial }{\partial H}{\Delta }y} \\ {\frac{\partial }{\partial r}{\Delta }z} & {\frac{\partial }{\partial V}{\Delta }z} & {\frac{\partial }{\partial H}{\Delta }z} \\ \end{array} } \right] $$

(6)

$$ P_{{{\text{pseudo}}}} = JP_{{{\text{obs}}}} J^{{\prime }} $$

(7)

3.3 Nonlinear least squares problem

The estimated vector of unknowns contained the three position coordinates for all the points in the network: 4–6 TMs, 4 IPs, and 6–10 GNSS antenna points per station. Figure 8 shows how the four IP sessions were rotated to combine into a single local reference frame by estimating orientation biases via inclusion of three 3-axis rotations in the estimated vector of unknowns to rotate three IP frames to the frame of one IP. Assuming observations collected at IP1 were in the desired final LGCN frame, the observations from IPs 2–4 were rotated to the local frame of IP1 by fitting common points (i.e., the braced quadrilateral). While corrections to the deflection of the vertical were applied in the pre-processing of observations, this additional Helmert transformation would theoretically correct for any remaining deflection of the vertical in addition to horizontal misalignments during TS30 measurement collection.

Fig. 8

The local reference frame at each IP, oriented to each location’s gravity vector. A rotational transformation of the orientation of each of the local reference frames aligns the observations from each of the four IPs into the same local frame for combination and processing

There needed not be an accurate a priori error variance constraint for the estimated state in this nonlinear least squares estimation problem. The network positions were given loose a priori within 100 m of their general location in the LGCN. One point, however, was fixed to define the origin of the LGCN through a very small a priori. For simplicity, it was assigned the coordinates (0, 0, 0). The rotations were each assigned an a priori of 0, nominally assuming no rotation a priori. By fixing the origin to a specific point in the LGCN, the survey errors distributed outward where points further from this fixed point had greater uncertainty in position.

The observation-state relation equations model the relative difference in coordinate positions contained in the vector of unknowns. The equation for some i^th number pseudo-observation of distance in the $x$ direction ${\Delta }x_{i}$, where $i$ was an index going from $i = 1:N$ total pseudo-observations of IP to target pairs, is given by Eq. 4.

$$ \Delta x_{i} = x_{{{\text{target}}}}^{{{\text{IP}}}} - x_{{{\text{IP1}}}}^{{{\text{IP}}}} = \left[ {\begin{array}{*{20}c} 1 & { - R_{z} } & {R_{y} } \\ \end{array} } \right]*\left( {\left[ {\begin{array}{*{20}c} {x_{{{\text{target}}}}^{{{\text{LGCN}}}} } \\ {y_{{{\text{target}}}}^{{{\text{LGCN}}}} } \\ {z_{{{\text{target}}}}^{{{\text{LGCN}}}} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {x_{{{\text{IP}}}}^{{{\text{LGCN}}}} } \\ {y_{{{\text{IP}}}}^{{{\text{LGCN}}}} } \\ {z_{{{\text{IP}}}}^{{{\text{LGCN}}}} } \\ \end{array} } \right]} \right) $$

(8)

$$ R_{{{\text{IP}}}} = \left[ {\begin{array}{*{20}c} 1 & { - R_{z} } & {R_{y} } \\ {R_{z} } & 1 & { - R_{x} } \\ { - R_{y} } & {R_{x} } & 1 \\ \end{array} } \right] $$

(9)

Equation 4 additionally includes a rotation the unknown positions of the target $\left( {x_{{{\text{target}}}} ,y_{{{\text{target}}}} ,z_{{{\text{target}}}} } \right)$, and of the IP $\left( {x_{{{\text{IP}}}} ,y_{{{\text{IP}}}} ,z_{{{\text{IP}}}} } \right)$ in the desired LGCN frame into the IP frame in which the observation was taken. For calculating difference in position between two points in the $x$ coordinate, the positions were rotated about the $z$ axis and the $y$ axis through small angle rotations $R_{z}$ and $R_{y}$, respectively. The superscript LGCN denotes positions that were in the LGCN frame. The superscript IP denotes positions that were in the original IP reference frame of the observation. The rotations were obtained from the rows of the full 3-axis small angle rotation matrix $R_{{{\text{IP}}}}$ in Eq. 5. Each IP required a unique rotation transformation except for IP1 whose local reference frame was used as the LGCN frame. The rotation was applied for all pseudo-observations of $\left( {x,y,z} \right)$ position differences from IP2, IP3, and IP4. Nonlinearity was introduced with the estimation of these rotations between IPs. The stacked equations for all observations formed a nonlinear system y = h (x). The unknown vector $x$ contained both the unknown positions of points in the network and the unknown IP rotations. The function h was no longer a matrix but a nonlinear relationship model between the knowns and unknowns.

If there were $N$ number of IP to target pairs; at least four repeated sets of observations to each pair, and three pseudo-observations of differences in position for each IP to target pair in $\left( {x,y,z} \right)$, then the system had $3*4N = 12N$ observations. There were $3N$ unknown coordinates and $9$ unknown rotations (three per IP2, IP3, and IP4).

This work employed the Gauss–Newton nonlinear batch least squares filter, which linearized the problem by estimating a small linear change ${\Delta }\hat{X}$ to the estimate $\hat{X}$. This small linear change was solved for via a Taylor series expansion of Eqs. 4–5. Equation 8 was modified to include weights on the observations $W$ and a priori for the estimate $X_{0}$ with covariance matrix $P_{x}$. The difference between the prior $X_{0}$ and the estimate $\hat{X}$ was ${\Delta }\overline{x}$. The covariance of $\hat{X}$ is given by Eq. 9.

$$ \hat{X}_{new} = \hat{X}_{old} + {{\Delta \hat{X}}} $$

(10)

$$ {\Delta y} = y - h\left( {\hat{X}_{old} } \right) $$

(11)

$$ {\Delta }\hat{X} = \left( {H^{T} WH + P_{x}^{ - 1} } \right)^{ - 1} \left( {{\text{H}}^{{\text{T}}} {\Delta }y + P_{x}^{ - 1} {\Delta }\overline{x}} \right) $$

(12)

$$ Pxx|y = \left( {H^{T} WH + P_{x}^{ - 1} } \right)^{ - 1} $$

(13)

Inputs to the program implementing this estimation problem were the survey observation file and the two weather data files. The post-fit residuals were calculated as the “Observed – Calculated” or O-C. The network adjustment was made with respect to the pseudo-observations, but the post-fit residuals were calculated from the original observations through inversion of the synthesis equations. By inspection of the resultant residuals in the form of the original observations of range and angles, the character of errors in the observations and their influence on the estimated network solution are recoverable with no loss of information content from the pseudo-observation processing. All of the data collection, pre-processing, least squares implementation/estimation, and analyses were completed in a suite of scripts written in Matlab.

4 Reference point measurement method

The laser survey observations collected at the GNSS antennas were processed simultaneously with the other survey observations of the LGCN and the braced quadrilateral. The positions of each point measured about the reference point were estimated within the survey local reference frame. The vectors between the points were equivalent to chords within the circle containing the points. The cross-product of pairs of these chords calculates the normal vector to the plane of the assumed circle. The average of these cross-products gave a good measure of the normal vector to the ground plane of the antenna relative to the local vertical of the TS30. The standard deviation of the Up coordinates of each point in the semi-circle was also calculated. By inspection of the normal vector and the standard deviation of Up coordinates, it was determined that each of the antennas had horizontal ground planes to within 0.2 mm and the semi-circle of points could be treated as part of a 2-D circle.

The normal vector to the ground plane of the antenna was also necessary for applying the correction for the offset of the ground plane to the center of the ball-mounted retroreflectors. The true ground plane was measured by correcting the positions of the semi-circle of points by half the radius of the ball-mounted retroreflector applied in the normal direction of the ground plane.

After the correction for the prism offset was applied, the points can be fitted with a 2-D circle via Eq. 10. The known coordinates for the points were represented as $\left( {x_{i} ,y_{i} } \right)$ where $i = 1, 2, \ldots n$. The coefficients $a,b,c$ were the unknowns.

$$ ax_{i} + by_{i} + c = x_{i}^{2} + y_{i}^{2} $$

(14)

This was a linear system that can be written in the form of $Ax = B$ as in Eq. 12. The solution of the linear system for $x$ is given by Eq. 12.

$$ Ax = B \to \left[ {\begin{array}{*{20}c} {x_{1} } & {y_{1} } & 1 \\ {x_{2} } & {y_{2} } & 1 \\ {\begin{array}{*{20}c} \ldots \\ {x_{n} } \\ \end{array} } & {\begin{array}{*{20}c} \ldots \\ {y_{n} } \\ \end{array} } & {\begin{array}{*{20}c} \ldots \\ 1 \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} a \\ b \\ c \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {x_{1}^{2} + y_{1}^{2} } \\ {x_{2}^{2} + y_{2}^{2} } \\ {\begin{array}{*{20}c} \ldots \\ {x_{n}^{2} } \\ \end{array} + y_{2}^{2} } \\ \end{array} } \right] $$

(15)

$$ x = \left( {A^{T} A} \right)^{ - 1} A^{T} B $$

(16)

Once the coefficients were estimated, they were used to calculate the center $\left( {x_{c} ,y_{c} } \right)$ and radius $r$ of the 2-D circle with Eq. 13.

$$ \begin{aligned} & a = 2x_{c} \\ & b = 2y_{c} \\ & c = r^{2} - x_{c}^{2} - y_{c}^{2} \\ \end{aligned} $$

(17)

5 Results

The analysis of the results from the nonlinear least squares estimation and the reference point solution followed the metrics of quality described in Table 1. The solutions, post-fit residuals, and formal statistics were evaluated.

5.1 Estimation results

After operational blunders were identified and corrected, remaining features in the post-fit residuals were analyzed. Figure 9 shows an example of the post-fit residuals from the survey on September 16, 2021. The X-axis denotes the $i^{th}$ observation in the set of observations, which are organized by IP-to-target pairs. The Y-axis shows the residual in either millimeters for range or degrees for angles. The first few observations were from IP1 to each measured target, followed by observations from IP2, and so on up to IP4. Range residuals were consistently sub-millimeter. The horizontal angle post-fit residuals typically show no further biases or errors after correcting for orientation/setup biases and estimating rotations between IPs. The vertical angle post-fit residuals showed biases between clusters of different IP-to-target observations. Within the clusters of observations to the same IP-to-target pairs, the precision seen is much higher with variation less than 0.001 degree. The short range observations of the LGCN typically showed up to 0.005 degree biases in the residuals and the kilometer-baseline observations of braced quadrilateral IPs showed 0.005–0.020 degree biases in the residuals. This was expected, given that the reciprocal observations along the braced quadrilateral were designed to average out the atmospheric refraction effect. If one side of the reciprocal measurements across the kilometer baseline were removed from the least squares adjustment, the biases in the vertical post-fit residuals disappear and their character becomes similar to the horizontal post-fit residuals. However, the entire network becomes biased on the decimeter-level with no indication in the data without outside validation. The removal of one side of the reciprocal observations produces an inaccurate solution but does confirm that the biases seen in the vertical angle post-fit residuals were a product of the reciprocal observations, reinforcing that there was a path-dependent refraction effect present. It can therefore be said that for any long-distance survey where there is significant elevation change, one-way solutions without reciprocal observations can be deceptively precise while greatly inaccurate.

Fig. 9

Post-fit residuals for range, vertical angle, and horizontal angle observations from the survey of the survey network during the second day of the Sept 2021 Campaign at McDonald Geodetic Observatory. Blue dots depict the post-fit residuals of individual observations collected. Overlaying the post-fit residuals is a box-whisker plot describing the distribution. The middle line through the orange box indicates the median. The vertical width of the orange box denotes the first and third quartiles of the distribution. The black whisker lines are drawn at the maximum and minimum post-fit residuals not considered outliers. The orange circles show the post-fit residuals considered possible outliers

The estimated sigmas show 1-2 mm uncertainty in the East and North directions for points across the kilometer baseline, furthest from the assigned origin of the local reference frame. The formal sigmas in the Up direction were at the few millimeter level. The Up uncertainty was once again misleading in the assessment of the quality of the survey in this work due to the reliance on reciprocal measurements to counteract the effects of refraction. While the solution split the difference between the biases to arrive at a more accurate estimate, statistically, including the large biases in the estimation led to high formal uncertainty. Therefore, the formal sigmas do not account for systematic errors or their cancellation by procedure.

5.2 Repeatability

Post-fit residual analysis evaluates the quality and precision of the individual survey and the network solution but does not provide any insight into the accuracy, i.e., how closely the network solution reflects the truth. Unlike a simulation, there is no known truth for real measurement data. If the assumptions about the system being measured were correct, and all physical influences acting upon the system were modeled and understood correctly, then the measurement data should be able to establish some confidence in a truth through repeatability of results using measurements from different experiments. In contrast, a system that is poorly observed and poorly modeled should produce inconsistent results in different experiment setups over time. This concept was applied to the surveying at MGO. The goal was to achieve systematically repeatable and consistent results over multiple survey campaigns.

The local tie accuracy through repeatability was quantified through the solutions of the LGCN positions from the surveying. These solutions were all created within unique local reference frames tied to the orientation and leveling setups of the TS30 total station when the data were collected. In order to compare the positions of one network solution to another, these local reference frames must be transformed to one another via estimation of a full seven parameter Helmert transformation with three translations, three rotations, and one scale. Note that the scale in the local reference frame is not a measurement of or related to the global scale of terrestrial reference frames determined by space geodetic observations. In this transformation, the target monuments in the LGCN were considered the same points across each different network solution. Therefore, these points should transform from one network solution in its local reference frame to best fit into another network solution in its local reference frame.

In the estimation of the individual network solutions, one point was held fixed to an a priori to define the origin of its local frame. In the estimation of the Helmert transformation parameters, all of the points in both network solutions were fixed and considered without error. The transformation parameters were estimated to best fit the exact coordinates. After the network solutions were transformed into the same frame, they were differenced to compare the consistency of the surveying positioning. Pre-transformation and post-transformation position differences were compared and the values of the estimated Helmert transformation parameters were examined. Daily solutions from data collected in the same campaign were tested first for the short-term and then compared to solutions from previous campaigns for the long-term. The effect of scale in the transformation was studied by choosing to estimate or neglect that parameter in each repeatability comparison.

In Fig. 10, the results of the LGCN solution comparisons between surveys conducted one day apart are shown. The first set of plots is comparisons without a scale difference estimated and the second set of plots is comparisons with a scale difference estimated. The final plot shows the differences in scale between these daily surveys. The columns in the first two sets of plots denote the survey campaigns and the rows are comparisons of the maximum differences in positions shown in the approximate East-North and East-Up planes, respectively. The points shown are pairings of surveys compared to one another within the same survey campaign (May 2021, Sept 2021, and Dec 2021) conducted only days apart. Each color dot corresponds to a target monument in the LGCN. The axes label “deviation” refers to a change in position in a particular direction of a target monument from one day of surveying to the next, i.e., “deviation from initial position”. When scale was estimated, the daily differences in surveying positions in East-North were within 0.5 mm and the daily differences in East-Up were within 1 mm except for Dec 2021 where the daily difference was within 1.5 mm in the Z direction (Up). It is evident that a scale correction in the local reference frames mainly influences the East position of TM21, which is the sole point available at the SGSLR site and the furthest point from the fixed origin of the local reference frame (TM11).

Fig. 10

(Top) Daily repeatability of LGCN network solutions at MGO without estimating scale difference, (middle) daily repeatability of LGCN network solutions at MGO with estimating scale difference, (bottom) the estimated daily scale difference for all three campaigns

In Fig. 11, the results of comparisons LGCN positions in East-North-Up (ENU) between surveys conducted over a seven-month period are shown. The X-axis denotes the Modified Julian Date of each survey, and the Y-axis denotes the deviation in each of the directions in millimeters from the May 19, 2021, network solution with TM11 as the site marker representing the consistent origin of the local reference frame. Each color dot is one monument in the LGCN tracked through six surveys in 2021. The long-term repeatability between the survey campaigns was within 2 mm in all three directions. The left column of plots shows the monthly repeatability without estimating scale and the right column of plots shows monthly repeatability with estimating scale. The bottom plot shows the scale difference of all surveys compared to the May 19, 2021, survey. By inspection, the effect of scale was mostly seen in the East direction along the longest baselines in the network. These results gave confidence in the accuracy of the current methods but did not offer a dense enough and long enough time series to draw definitive conclusions about the causes for these monthly changes in position in the MGO network nor cause of the variation in the scale from survey to survey. A comprehensive program should include continuous monitoring of the site.

Fig. 11

The long-term/seasonal repeatability of LGCN survey at MGO as compared to the May 19, 2021, survey for all surveys in the May 2021, Sept 2021, and Dec 2021 campaigns

5.3 External validation with GNSS technique

To externally validate the accuracy of the local ties and the surveying procedure, direct comparisons were made to the GNSS-derived positions of the stations. These positions were calculated using the double-difference method of processing with phase ambiguity resolution (DD-A) expressed in ITRF2014. The GNSS positions were produced using the Multi-Satellite Orbit Determination Program (MSODP) by solving for satellite orbits, clock errors, and station positions while applying constraints to align the solution with ITRF2014. Daily solutions were processed and were averaged over a month. In this work, the monthly mean solutions for September 2021 and December 2021 were used for comparison to the surveys conducted on September 16th, September 17th, November 30th, and December 2nd.

To characterize site motions observed by the GNSS technique, the relative change in positions of the GNSS stations from September 2021 to December 2021 was calculated using the monthly mean solutions from the respective months. The difference in position was calculated with and without including a Helmert transformation between the two solutions, as shown in Table 2. Relative position as used here was defined as relative to the position of one station at the starting epoch, in this case shifting the ITRF2014 frame to a frame with origin at MGO5 in September 2021. Since this was a small-scale network of stations, using relative positions allowed for the examination of the station motions and application of transformations at the observatory scale rather than the global scale. The relative positions in December 2021 deviated by about 1-2 cm in all three directions consistently between the three GNSS stations when comparing the two solutions alone. When comparing the two solutions with an estimated Helmert transformation, the positions fit to the sub-mm level given a 1-2 cm translation, 10″ rotation about the X-axis, 4″ rotation about the Y-axis, and a 0.4 mm/km scale correction. The scale correction was negligible but the rotations were necessary to reduce deviations from a few millimeters to sub-mm. The consistent centimeter-level deviations which were corrected with the 1-2 cm estimated translation vector were attributed to the plate velocities that were not included in the DD-A solution.

Table 2 Difference in double-difference (DD-A) monthly mean positions for GNSS stations at MGO from September 2021 to December 2021 with and without Helmert transformation estimated

The global ITRF2014 position coordinates of GNSS stations MGO2, MGO4, and MGO5 as measured by the survey on September 16, 2021, are presented in Table 3. These positions were referenced to the GNSS-derived monthly mean solution of the GNSS stations in ITRF2014 for September 2021. The positions in the local reference frame at MGO were transformed to the global frame. This transformation was estimated using a similar iterative Gauss–Newton nonlinear least squares algorithm as presented in Eq. 9–13, fitting the survey-derived local frame positions to the GNSS-derived DD-A monthly mean global positions of the GNSS stations. To reiterate, the transformation was applied to a local network with coordinates no larger than one kilometer, therefore, the estimated scale is a local scale and not related to the global scale. The transformed survey positions were consistent with the GNSS-derived positions to the sub-mm. The scale difference between the local ties and the GNSS-derived positions was only 1 mm at the kilometer level. The translation and rotation parameters were necessary to bring the local network into the terrestrial reference frame.

Table 3 GPS station local tie from surveys in 2021and comparison to GNSS-derived ties from DD-a monthly mean solutions

This process was repeated for the other three surveys of the GNSS station reference point: September 17, November 30, and December 2. All the local tie surveys fall within sub-mm of the GNSS DD-A positions when fitted with a Helmert transformation except for the September 17th survey. The LGCN positions in this survey were consistent with the Sept 16th survey LGCN positions to sub-mm, suggesting there was a blunder in the survey observations of at least one of the antennae in the Sept 17th survey. This was supported by the fact that the estimated scale difference between the survey-derived positions and the GNSS-derived positions was smaller than the other three surveys despite having larger deviations: the error in the positions was not something that can be accounted for via a scale, meaning that it was not likely to be related to errors in the kilometer baseline but likely in the measurement of the relative baseline between MGO4 and MGO5. The solution to these blunders could not be eliminated in the data processing phase and required re-measurement of both MGO4 and MGO5. Weakness in the measurement of MGO4 and MGO5 is possibly due to the sub-optimal layout of the provisional LGCN used in this work. The distance between the IPs and TMs to the GNSS antennas is further than is recommended for using the BMR targets.

6 Conclusions

This work demonstrated the ability to measure local ties to sub-mm daily repeatability and 1-2 mm seasonal repeatability for a geodetic observatory with kilometer baselines that do not meet the GGOS core site layout recommendations. The kilometer baseline was predominantly in the East direction and the network geometry was proportionally much smaller in the North and Up directions. Errors in the measurement of the baseline manifested as a scale difference between surveys that scales the East dimension of the network with lesser effects on the other two dimensions. An estimated scale difference between each local tie survey improved repeatability results. The effect, however, was only of about 1-2 mm and mainly seen in the May 2021 and December 2021 Campaigns. The scale difference between campaigns was larger than between daily surveys. However, estimating a scale correction did not reduce the absolute deviations between the campaigns to the level of the daily survey comparisons. It was concluded that given the 1-2 mm repeatability and precision of the local tie surveying at the daily and monthly timescales, any larger errors or trends seen in follow-up surveys would either be systematic errors in a particular campaign or local site movement signals observed through the surveying.

Though certain un-modeled effects may influence the local ties over longer periods of time, local ties over short periods (days) should be very close and over moderately long periods (months) should remain within a tolerance of reasonable assessment of site motion. Even with monument designs specifically engineered for stability and longevity, some amount of movement in physical location is almost always assured whether from thermal expansion, settling due to its own weight, or from variability of local uplift and subsidence, hydrological load, or lateral soil/ground movements. The daily conditions at MGO do not cause day-to-day variability in monuments greater than 1-2 mm based on the sub-mm repeatability demonstrated in the surveys. Site deformation over longer periods at the few millimeters level is possible. Un-modeled tropospheric variability could be the largest error source in the observed local ties on the day-to-day timescale, manifesting as biases to the vertical component of positions and differences in scale for repeated surveys. The effect both in range and angle observations is exacerbated over the kilometer baseline. As the seasonal climate changes, any long-term trends in un-modeled tropospheric variability should be measurable signals. Continuous monitoring at MGO should be able to observe and resolve site deformations and un-modeled seasonal tropospheric variability with some confidence.

For the early experiments with the surveying procedure, especially during the early stages of construction of MGO, semi-permanent monuments were sufficient to establish single survey precision and daily repeatability between surveys. The LGCN monuments were not in ideal locations for establishing ground control of the finalized MGO observatory layout. Due to observability issues at the SGSLR site, there was only one available TM for surveying and the ties to the GNSS station MDO1 could not be made. Additionally, the monuments were not emplaced in rock but in the compacted clay soil dominating the area especially at the VGOS site. It was difficult to determine the degree these monuments move on the monthly and seasonal time spans between survey campaigns from the sparse data and short time series of surveying. Characterizing site motions and geodetic system stability are long-term goals of this work and one of the motivations for achieving sub-mm precision and accuracy in each survey. Therefore, weakness in the geometry and stability of the LGCN monuments and restricted lines of sight present challenges to refining the accuracy and precision of the surveying procedure. Replacement monuments in a new LGCN at both the Godsend SGSLR sites to facilitate future surveying and research should be based on the short-drilled braced monument design by [UNAVCO].

With continuous data measured at LGCNs well placed at geodetic sites, and with the resolution of long-term trends and/or seasonal signals, a case builds for the consideration of time-variable local ties. In the current state of TRF realization, local ties are treated as static distances applicable for a specific epoch. It is not considered how ties might change over time or when in an observatory environment’s loading cycle a tie is measured. Given a sufficiently long continuous time series for a particular local tie or set of local ties at an observatory, the time variability can be removed with models for the long-term trends and cyclical signals. This will reduce the local tie time series to a cluster of points about some time-invariable mean local tie that can be confidently used with other geodetic station data at the epoch of any TRF combination. The observed time variability of local ties will also help contextualize observed drifting of stations in the space geodetic data by isolating local monument motion.

Even without fully characterizing time variability at the site, the local ties between the GNSS monuments at MGO produced in this work are at the level of accuracy and precision that they are comparable to local ties currently used in the ITRF and are therefore ingestible into realizations of TRF. Confidence in this claim stems from the rigorous analysis of error residuals and repeatability across multiple surveys and the external validation with GNSS-derived positions of stations. The Helmert transformation parameters that facilitate the comparisons of derived positions between surveys and global positions are closely examined, especially differences in observed scales. This study led to the identification of procedural and model errors that reduced the scale discrepancies. The remaining scale differences are at the level of atmospheric effects and measurement precision.

Appendices

Appendix

Appendix A

Instrumentation Specs.

• Leica TS-30 Total Station

  • Two Instruments: one owned by John Griffin Surveyors, one loaned by NGA

  • ½” Angles, 0.6 mm + 1 ppm

  • Certified: 0.13 mm distance, 0.2 mgon Hz, 0.26 mgon V

• Leica GPH1P Single-Prism Precision Reflectors

  • 0.3 mm accuracy

• PLX Ball Mounted Hollow Retroreflectors (BMRs)

  • 0.002 mm accuracy

• MET3 Meteorological Sensor

  • From Clark Wilson, JSG

  •  ± 0.08 hPa accuracy

  • 0.5 deg C accuracy

  • 2% Rel. Humidity Accuracy

https://het.as.utexas.edu/HET/weather.htm

Appendix B

First velocity correction

The first velocity correction is applied to all distance measurements to correct the speed of light through the tropospheric medium (Rüeger 1990). The first velocity correction is a part per million. Therefore, at kilometer scales, the effect is significant at the millimeter level of precision. In set of Eqs. 18, $d^{\prime}$ is the measured distance before correction and $d$ is the distance after first velocity correction. The correction is based off a ratio between the reference refractive index $n_{ref}$ for the particular instrument and the group refractive index $n_{L}$ of the environment. $n_{ref}$ is a function of the speed of light in a vacuum divided by constants of the instrument: the unit length $U$ or half the modulation wavelength, and the frequency of modulation $f_{mod}$.

$$ \begin{aligned} & d = \frac{{n_{ref} }}{{n_{L} }}d^{\prime} \\ & n_{ref} = \frac{c}{{2Uf_{mod} }} \\ & U = \frac{1}{2}\lambda_{mod} \\ \end{aligned} $$

(18)

In set of Eqs. 19, the group refractive index $n_{L}$ is a function of the vacuum wave number $\sigma$ of the laser, the density factor of dry air $D_{s}$, and the density factor of water vapor $D_{w}$ (Rüeger 1990). The density factor of dry air is a function of the dry air partial pressure $P_{s}$ and the measured temperature $T$ in Kelvin. Pressure is measured in millibars. The dry air partial pressure $P_{s}$ is a calculated from the difference between the measured pressure $P$ and the actual partial water vapor pressure $P_{w}$. $P_{w}$ is calculated from the environment relative humidity $H_{rel}$ in percent and the saturation water vapor pressure $P_{ws}$. $P_{ws}$ is calculated from the measured pressure and measured temperature converted to Celsius $T_{C}$. The density factor of water vapor $D_{s}$ is a function of the partial pressure of water vapor $P_{w}$ and the measured temperature $T$.

$$ n_{L} = \left( {\sigma ,D_{s} ,D_{w} } \right) $$

(19)

$$ \begin{aligned} n_{L} = & \left( {1466389.0*\frac{{238.0185 + \sigma^{2} }}{{\left( {238.0185 - \sigma^{2} } \right)^{2} }} + 47729.9*\frac{{57.362 + \sigma^{2} }}{{\left( {57.362 - \sigma^{2} } \right)^{2} }}} \right)*D_{s} \\ & \quad + \left( {6487.31 + 174.174*\sigma^{2} - 3.55750*\sigma^{4} + 0.61957*\sigma^{6} } \right)*D_{w} \\ \end{aligned} $$

$$ \sigma = \frac{1}{\lambda } $$

$$ D_{s} = \frac{{P_{s} }}{T}*\left( {1 + P_{s} *\left( {57.90*10^{ - 8} - \frac{{9.3250*10^{ - 4} }}{T} + \frac{0.25844}{{T^{2} }}} \right)} \right) $$

$$\begin{aligned} D_{w} &= \frac{{P_{w} }}{T}*\Bigg( 1 + P_{w} *\left( {1 + 3.7*10^{ - 4} *P_{w} } \right)\\& \quad *\left( { - 2.37321*10^{ - 3} + \frac{2.23366}{T} - \frac{710.792}{{T^{2} }} + \frac{{7.75141*10^{4} }}{{T^{3} }}} \right) \Bigg)\end{aligned} $$

$$ where P_{s} = P - P_{w} $$

$$ P_{w} = H_{rel} *\frac{{P_{ws} }}{100} $$

$$ P_{ws} = \left( {1.007 + \left( {3.46*10^{ - 6} } \right)*P} \right)*6.1121*e^{{\frac{{17.502*T_{C} }}{{240.97 + T_{C} }}}} $$

Second velocity correction

The second velocity correction further corrects the distance measurement for the change in the refractive index due to the curvature of Earth’s atmosphere (Rüeger 1990). $d^{\prime}$ is the uncorrected measured distance, $d$ is the distance corrected using Eqs. B.1, and $d_{{{\text{final}}}}$ is the distance after the two corrections. The change in the refractive index ${\Delta }n$ is proportional to square of the measured distance and calculated using the curvature of the Earth $R_{E}$ at the given latitude and the coefficient of refraction $k$. The coefficient of refraction $k$ is dependent on the time of day and height above the ground. It is difficult to measure and is usually approximated with models. The needed precision of $k$ is not high. The second velocity correction is a part per billion correction meaning sub-millimeter at kilometer scales.

$$ \begin{aligned} & d_{{{\text{final}}}} = d + \left( { - d^{\prime}*\Delta n} \right) \\ & {\Delta }n = \left( {k - k^{2} } \right)*\frac{{d^{^{\prime}2} }}{{12*R^{2} }} \\ \end{aligned} $$

(20)

The TS-30 has built-in functionality to correct for atmospheric delay given input atmospheric parameters; however, the atmospheric parameters cannot be adjusted over time while the instrument is operating, nor can variability along the light path be considered. Therefore, we do not use the built-in atmospheric correction and instead apply the corrections post-data collection. This also allows greater flexibility to input time-varying atmospheric parameters to each observation as well as to account for the spatially varying conditions across the light path. This is a key capability, as the atmospheric variability from the VGOS site to the SGSLR site varies significantly over 120 m elevation change.

Reduction to wave chord

The reduction-to-wave-chord correction is a final correction to the distance that accounts for the curvature of the path taken by the light due to the curvature of the atmosphere, rather than a correction to the speed of light itself (Rüeger 1990). This correction reduces the path of the measurement laser to a straight-line distance. The reduced distance $d$ is calculated with Eq. B.4 using the unreduced distance $d^{\prime}$, the curvature of the Earth $R_{E}$, and the coefficient of refraction $k.$

$$ d = 2*\frac{{R_{E} }}{k}*\sin \left( {d^{\prime}*\frac{k}{{2R_{E} }}} \right) $$

(21)