A new spherical harmonic approach to residual terrain modeling: a case study in the central European Alps

Abstract

For decades, the residual terrain model (RTM) concept (Forsberg and Tscherning in J Geophys Res Solid Earth 86(B9):7843–7854, https://doi.org/10.1029/JB086iB09p07843, 1981) has been widely used in regional quasigeoid modeling. In the commonly used remove-compute-restore (RCR) framework, RTM provides a topographic reduction commensurate with the spectral resolution of global geopotential models. This is usually achieved by utilizing a long-wavelength (smooth) topography model known as reference topography. For computation points in valleys this neccessitates a harmonic correction (HC) which has been treated in several publications, but mainly with focus on gravity. The HC for the height anomaly only recently attracted more attention, and so far its relevance has yet to be shown also empirically in a regional case study. In this paper, the residual spherical-harmonic topographic potential (RSHTP) approach is introduced as a new technique and compared with the classic RTM. Both techniques are applied to a test region in the central European Alps including validation of the quasigeoid solutions against ground-truthing data. Hence, the practical feasibility and benefits for quasigeoid computations with the RCR technique are demonstrated. Most notably, the RSHTP avoids explicit HC in the first place, and spectral consistency of the residual topographic potential with global geopotential models is inherently achieved. Although one could conclude that thereby the problem of the HC is finally solved, there remain practical reasons for the classic RTM reduction with HC. In this regard, both intra-method comparison and ground-truthing with GNSS/leveling data confirms that the classic RTM (Forsberg and Tscherning 1981; Forsberg in A study of terrain reductions, density anomalies and geophysical inversion methods in gravity field modeling. Report 355, Department of Geodetic Sciences and Surveying, Ohio State University, Columbus, Ohio, USA, https://earthsciences.osu.edu/sites/earthsciences.osu.edu/files/report-355.pdf, 1984) provides reasonable results also for a high-resolution (degree 2160) RTM, yet neglecting the HC for the height anomaly leads to a systematic bias in deep valleys of up to 10–20 cm.

1 Introduction

The shortest wavelengths of the Earth’s gravity field are highly correlated with the topography. The purpose of any topographic reduction in gravity modeling is smoothing the observations (gravity, deflections of the vertical, etc.) in order to improve interpolation and prediction of the data. By this, the required data density in context of the sampling theorem and, consequently, aliasing errors are significantly reduced. In the context of geoid or quasigeoid modeling, reducing the bandwidth of the residual data also facilitates to find a suitable parameterization in least-squares techniques.

In the framework of the remove-compute-restore (RCR) technique to compute geoid or quasigeoid models, residual terrain modeling (RTM) is a most widely used strategy to process together data given in different representations and containing different information about the topography on different frequency bands, i.e., terrestrial observations of gravity field functionals in discrete points, global geopotential models (GGM) given as spherical harmonic (SH) coefficients, and digital elevation models (DEM) usually represented by regular grids. In context of a regional computation, the discrete terrestrial gravity data contain information for the whole spectrum of the gravity field, but due to the sampling theorem (size of the area, point spacing) they are not capable of resolving the lowest and highest frequencies. In this regard, the GGM provides information of the low-frequency component and thereby also accounts for large part of the far-zone effect. In the sense of band-limited data, the RTM then delivers the high-frequency spectrum of the topographic signal.

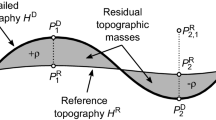
The basic idea of the RTM reduction has been first described already 40 years ago (Forsberg and Tscherning 1981; Forsberg 1984). The topographic effect is computed with respect to a smoothed topographic surface, frequently referred to as “reference topography” or “RTM surface.” For negative RTM heights, where the actual topography is below the RTM surface, a negative density is used, so that mountains are virtually removed and valleys are filled up through the RTM reduction. This approach assumes an approximate relation between the RTM surface and the long-wavelength signal due to the topography in the GGM. Thus, in the practical implementation in context of the RCR technique, the spectral resolution of the RTM surface in the space domain (not to be confused with the grid spacing here) is typically chosen in accordance with the maximum SH degree of the GGM applied. However, shorter wavelengths may be used with advantage as long as the desired smoothing of the discrete terrestrial data is achieved and the latter are available with sufficient spatial extent and density according to the sampling theorem.

The RTM surface can be constructed by, e.g., simple averaging or more sophisticated filter operations in the space domain. Another option is the truncation of the spectrum of the topographic heights to the desired resolution by spherical harmonic (SH) analysis and subsequent synthesis (see e.g. Hirt et al. 2019). Since the contributions of “negative” and “positive masses” cancel out at larger distances, computation of the RTM reductions in the space domain is possible and usually done with a constant integration radius around the computation point (Forsberg and Tscherning 1981; Schwabe et al. 2014).

As a result, the reduced field is supposed to be residual yet smooth. This means that the short wavelengths are decorrelated from topography and contain deviations between the assumed and real (albeit unknown) mass densities only, so that in case of a standard density the reduced field merely resembles a high-pass filtered Bouguer anomaly. On the other end of the spectrum, the long-wavelength components of the signal are mostly removed, making the field practically stationary when considered as a stochastic process.

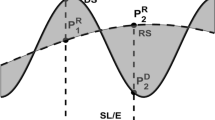
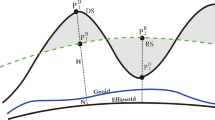
The well-known problem from the theoretical viewpoint is that after the RTM reduction computation points in valleys are buried inside the topography, making the reduced potential field non-harmonic. Numerically, this shows in large biases in these points, so that the initial aim of the RTM reduction, i. e., achieving residual yet smooth values for the compute step, fails. In the original RTM approach, this is solved by a so-called harmonic correction (HC) to the gravity (Forsberg and Tscherning 1981; Forsberg 1984)

$$\begin{aligned} \delta g_{\text {hc}} = 4 \pi G \rho \cdot \text {MIN}\left( H_P - H_{\bar{P} }, 0\right) , \end{aligned}$$

(1)

with G the gravitational constant and $\rho$ the assumed standard density. $\bar{P}$ is the projection of the topographic point P along the vertical onto the RTM surface. To be on the safe side, we remind the important note already made by many authors (e.g., Forsberg 1984; Klees et al. 2022) that, following this sign convention, the HC $\delta g_{\text {hc}}$ must be added to the RTM reduction, which is then subtracted from the gravity observations in the remove step or added in the restore step.

Recently, the HC in the context of the RTM technique was revisited and refined by various authors (e.g., Omang et al. 2012; Yang et al. 2022; Klees et al. 2023). Some studies also describe approaches to avoid the HC. For example, in the “baseline RTM technique” (Rexer et al. 2018; Hirt et al. 2019) SH coefficients of the topographic potential are derived from SH coefficients of the height function, whereas (Bucha et al. 2019) propose a cap modification to realize the spectral filtering in the RTM approach. Finally, already Vermeer and Forsberg (1992) pursued a completely different approach in the frequency domain, yet in planar approximation.

In this study, we present another approach to account for the residual topography which has similarities with the “RTM baseline approach” by Hirt et al. (2019). Based on regional gravity and GNSS/leveling data from the D-A-CH geoid project (Schwabe et al. 2021) we show that the quasigeoids computed by this method and by the classic RTM method are consistent, i.e., agree at the centimeter level. This is the first main result of this paper.

It has been a long-accepted assumption since Forsberg and Tscherning (1981) that the HC for the height anomaly can be neglected. Until shortly, most studies dealing with the HC or refined RTM approaches thus only considered gravity, or mainly focused on analyzing the results of various approaches regarding their magnitude and differences. Recently, closed-form expressions for the HC were derived by Klees et al. (2023), indicating that the HC in fact can contribute up to 20 cm in terms of the height anomaly in mountainous regions. Still, authors of recent case studies seem widely unaware of its significance (e.g. Lin et al. 2023). Moreover, effective empirical verification of the HC for the height anomaly was impeded by the lack of sufficiently accurate ground-truthing data (GNSS/leveling) to actually trace the impact of the HC in the relevant regions (e.g. Omang et al. 2012; Yang et al. 2022). With the growing role of the (quasi)geoid in GNSS-based height determination, this is now changing. But even based on the new GSVS17 dataset for the “Colorado geoid computation experiment” (Wang et al. 2021), Yang et al. (2023, Section 5.2) only observe a very small reduction in terms of standard deviation. Thus, we consider the significance of HC for the height anomaly as an ongoing topic. To finally demonstrate by our comparisons that it is indeed indispensable in regional quasigeoid modeling is therefore the second main result of this paper.

The manuscript is structured as follows. In Sect. 2, recent findings regarding the HC in context of the classic RTM (Forsberg and Tscherning 1981) are summarized. Our new approach based on the residual spherical harmonic topographic potential (RSHTP) is introduced in Sect. 3. Data and implementation of the techniques in the case study are described in Sect. 4. Results are presented in Sect. 5 and discussed in context in Sect. 6. Finally, conclusions are drawn in Sect. 7.

2 Recent findings regarding the HC in the classic RTM

The classic approach to derive the HC according to Eq. (1) considers the effect of a condensed Bouguer plate between the points $\bar{P}$ and P and the effect of harmonic downward continuation of the exterior gravitational potential of the plate in $\bar{P}$ to the interior point P (Forsberg and Tscherning 1981). In recent years, various authors have published formulas for the HC based on refined approximation schemes, e.g., applying the condensation to a spherical shell (e.g., Klees et al. 2022, Eqs. (1), (2)). As far as the HC in terms of the gravity disturbance is concerned, this provides the same result like Eq. (1) except for negligible higher-order terms (see Eq. (6)).

However, while Forsberg and Tscherning (1981) claim the effect of the condensation is nearly zero for height anomalies, Yang et al. (2022) showed that in case of the Bouguer plate approximation it is in fact $\zeta _{\text {hc}} = - \pi G \rho \left( H_{\bar{P}} - H_P \right) ^2 / \gamma$ (to be added to the RTM reduction according to our sign convention introduced in Sect. 1). Omang et al. (2012) reported $\zeta _{\text {hc}} = - 4\pi G \rho \left( H_{\bar{P}} - H_P \right) ^2 / \gamma$, but without detailed derivation.

Recently, based on a cylinder configuration Klees et al. (2023) published the closed-form expressions (in the following the “HC case” $H_{\bar{P}}-H_P > 0$ is implicitly assumed)

$$\begin{aligned} \delta g_{\text {hc}}&= -4 \pi G \rho \left( H_{\bar{P}} - H_P \right) \end{aligned}$$

(2)

$$\begin{aligned} \Delta g_{\text {hc}}&= -4 \pi G \rho \left( H_{\bar{P}} - H_P \right) \left( 1 - u \right) \end{aligned}$$

(3)

$$\begin{aligned} \zeta _{\text {hc}}&= -\frac{2 \pi G \rho \left( H_{\bar{P}} - H_P \right) ^2}{\gamma _P} \end{aligned}$$

(4)

for the gravity disturbance, the gravity anomaly and the height anomaly, respectively (modified after Klees et al. 2023, Eqs. (36)–(40)). Therein, $u = \left( H_{\bar{P}} - H_P\right) / r_P$. The last term in $\Delta g_{\text {hc}}$ does not exceed 0.14 mGal even in extreme cases. Typically, it keeps below 10 µGal and can therefore be neglected (Klees et al. 2023). A formula similar to Eq. (4) has been derived by Ågren (2004, Eq. 29), but in context of the analytical continuation bias inside the topography when computing geoid heights from a GGM. A simplified approach leading to the same closed-form expressions except for higher-order terms of u and $u^2$ can be summarized as follows:

Imagine a spherical shell bounded by concentric spheres in P and $\bar{P}$. The formulas for the internal and external attraction and potential of the spherical shell are derived, e.g., in MacMillan (1958, pp. 35–40) and Wichiencharoen (1982, Table 1). However, the latter seems to contain errors and should be used with caution (see “Appendix A”). Consider the HC as the difference between the internal potential of the shell in P and the external potential of the shell in P after condensing it onto a sphere passing through P. Due to symmetry, the condensed shell can be treated as a pointmass located in the geocenter, and the HC can be easily computed from the total mass. We obtain

$$\begin{aligned} \delta g_{\text {hc}}&= \delta g_P^{\text {shell}} - \delta g_P^{\text {shell,condensed}} \end{aligned}$$

(5)

$$\begin{aligned}&= -4\pi G\rho \left( H_{\bar{P}}-H_P \right) \left( 1+u+\frac{u^2}{3}\right) \end{aligned}$$

(6)

for the HC in terms of gravity disturbance, and

$$\begin{aligned} \delta V_{\text {hc}}&= \delta V_P^{\text {shell}} - \delta V_P^{\text {shell,condensed}} \end{aligned}$$

(7)

$$\begin{aligned}&= -2\pi G\rho \left( H_{\bar{P}}-H_P \right) ^2 \left( 1+\frac{2u}{3}\right) . \end{aligned}$$

(8)

in terms of the potential. For typical RTM configurations, the magnitude of the negative RTM height keeps below 2000 m. For example, in the Mont Blanc area, the negative RTM height even for a RTM corresponding to degree 300 (relates to 133 km Boxcar filter) is 1462 m. Accordingly, the terms of order u remain below 0.14 mGal (as already noticed above) or 0.1 mm, respectively, and thus can be safely neglected in practice. Since the magnitude of the effect is small (ca. 20 cm for a RTM wavelength corresponding to SH degree 2160, see Table 2 in Sect. 5.2), we can safely take the normal gravity at the computation point instead of the corresponding telluroid point. Thus, the HC in terms of the height anomaly according to Bruns’ theorem (Hofmann-Wellenhof and Moritz 2005) is obtained as in Eq. (4) and the resemblance with the closed-form expressions according to Klees et al. (2023) is shown.

Carrying out elaborate analytical derivations of the downward continuation, Klees et al. (2023) show that these formulas are in fact exact. The discussion of all the other published HC has therefore become obsolete. Thus, in our regional quasigeoid study using the RCR technique (Sect. 5), we will focus on the impact of Eq. (4) on the restored height anomalies when comparing with an alternative approach to model the topography (Sect. 3) as well as independent validation data from GNSS/leveling.

3 The residual spherical harmonic topographic potential approach (RSHTP)

In the following, a reduction similar to the RTM approach is defined as the difference between the full-scale topographic potential in the space domain (i. e., complete topographic reduction) and a truncated expansion of the topographic potential into spherical harmonics up to a suitable maximum degree $n_\text {max}$.

A similar approach has been described as “baseline RTM technique” by Rexer et al. (2018) and Hirt et al. (2019). However, there the SH coefficients of the potential are computed from a SH expansion of the topographic height function H, which implies a convolution in the SH domain. For an acceptable error, height coefficients are thus needed until, e.g., degree 10,800 or even 21,600 for potential coefficients up to degree 2160. Furthermore, only the gravitational effect is considered in that study, but not the potential.

Instead, we will compute the SH coefficients of the potential directly from the DEM heights. For this reason, and also because in fact there is no smoothed reference topography (RTM surface) involved at all, we find it appropriate to refer to this method as the “residual spherical harmonic topographic potential” (RSHTP) approach.

In spherical approximation, the computation of the Newtonian gravitational field from a grid of topographic heights involves numerical integration of spherical tesseroids, i. e., fragments of spherical shells bounded by inner and outer radii $r_1$ and $r_2$ as well as parallels (spherical co-latitudes) $\theta _1$, $\theta _2$ and meridians $\lambda _1$ and $\lambda _2$. Let $l'$ be the running distance in the integration between the computation point and the positions within the tesseroid, given as

$$\begin{aligned} l' = \sqrt{r^2 + r'^2 - 2r r' \cos \psi '} \end{aligned}$$

(9)

with

$$\begin{aligned} \cos \psi ' = \left( \cos \theta \cos \theta ' + \sin \theta \sin \theta ' \cos \left( \lambda ' - \lambda \right) \right) . \end{aligned}$$

(10)

Let us also assume a constant density $\rho$ within the cell. Then the contribution V of this grid cell in terms of the potential is

$$\begin{aligned} V = G \rho \int \limits _{r_1}^{r_2} \int \limits _{\theta _1}^{\theta _2} \int \limits _{\lambda _1}^{\lambda _2} \frac{1}{l'} \left. r'\right. ^2 \sin \theta ' \textrm{d}\lambda ' \textrm{d}\theta ' \textrm{d}r'. \end{aligned}$$

(11)

Note that here we used the term “spherical approximation” related only to one aspect, i.e., associating a DEM grid cell with the shape of a spherical tesseroid. The other aspect, replacing the geoid with a sphere as far as the base and the position in space of the tesseroids is concerned, is just a matter of practical implementation and therefore not discussed here.

As it is well known, there is no analytical solution to Eq. (11) in the space domain, and numerical methods have to deal with a singularity in the computation point if the latter is located on the surface of the DEM (Grombein et al. 2013). However, for a finite SH expansion of the inverse distance up to a certain cut-off degree $n_\text {max}$, the integral can be solved analytically.

Combining (rewritten from Hofmann-Wellenhof and Moritz 2005, Eq. (1–108))

$$\begin{aligned} \frac{1}{l'}&= \sum _{n=0}^{n_\text {max}}\sum _{m=0}^{n} \frac{1}{2n+1} \frac{\bar{P}_{nm}\left( \sin \theta \right) }{r^{n+1}} \left. r '\right. ^n \bar{P}_{nm} \left( \sin \theta '\right) \nonumber \\&\qquad \times \left[ \cos m\lambda \cdot \cos m\lambda ' + \sin m\lambda \cdot \sin m\lambda ' \right] \end{aligned}$$

(12)

and (modified from Hofmann-Wellenhof and Moritz 2005, Eq. (2–78)),

$$\begin{aligned} V&= \frac{GM}{r} \sum _{n=0}^{n_\text {max}}\sum _{m=0}^{n} \left( \frac{a}{r}\right) ^n \bar{P}_{nm}\left( \sin \theta \right) \left[ \bar{C}_{nm}\cos m\lambda \right. \nonumber \\&\quad \left. \mathrel + \bar{S}_{nm}\cos m\lambda \right] \end{aligned}$$

(13)

we arrive at

$$\begin{aligned} \begin{Bmatrix} \left. \bar{C}_{nm}^{T} \right. \\ \left. \bar{S}_{nm}^{T}\right. \end{Bmatrix}&= \frac{G \rho }{GM\, (2n+1)} \int \limits _{r_1}^{r_2} \int \limits _{\theta _1}^{\theta _2} \int \limits _{\lambda _1}^{\lambda _2} \frac{\left. r'\right. ^{n+2}}{a^n} \nonumber \\&\quad \mathrel \times \bar{P}_{nm}\left( \sin \theta '\right) \begin{Bmatrix} \cos m\lambda ' \\ \sin m\lambda ' \end{Bmatrix} \sin \theta ' \textrm{d}\lambda ' \textrm{d}\theta ' \textrm{d}r' \end{aligned}$$

(14)

for the contribution of each DEM element to the fully normalized SH coefficients $\left. \bar{C}_{nm}^{T}\right.$, $\left. \bar{S}_{nm}^{T}\right.$ of the topographic potential. To this end, replace the left-hand side of Eq. (11) with Eq. (13), use Eq. (12) in the integral on the right-hand side of Eq. (11), and solve for $\bar{C}_{nm}^{T}$ and $\bar{S}_{nm}^{T}$ to obtain Eq. (14). $\bar{P}_{nm}(\cdot )$ is the fully normalized associated Legendre function. The scaling coefficients for the normal field GM (geocentric gravitational constant) and a (major axis of the reference ellipsoid) have to be chosen by convention. In this study, we assume the GRS80 (Moritz 2000) normal potential to be used as the standard in context of the disturbing potential.

The series in Eq. (12) is subject to the divergence problem. Theoretically, it is only valid for $n_\text {max} \rightarrow \infty$, and also the condition $r > r'$ must be satisfied for the series to converge. It has been shown that SH series diverge on the topography once that the topographic density models are realistic enough or $n_\text {max}$ is large enough. Thus, methods like the RSHTP or the RTM will likely fail for irregularly shaped asteroids, or even the Moon (Hirt and Kuhn 2017). However, the scope of this study is the comparably regularly shaped Earth. Here, reasonable results can be obtained by truncating the infinite potential series to a suitable $n_\text {max}$ as a means of regularization. To demonstrate this for a typical resolution of a combined GGM (degree 2160 resp. 2190) was one of the goals in Sect. 5.

The kernel can be factorized into three items, each dependent only on a single integration variable. Thus, we can rewrite Eq. (14) in the form

$$\begin{aligned} \begin{Bmatrix} \left. \bar{C}_{nm}^{T}\right. \\ \left. \bar{S}_{nm}^{T}\right. \end{Bmatrix}&= \frac{G \rho }{GM\, (2n+1)} \int \limits _{r_1}^{r_2} \frac{\left. r'\right. ^{n+2}}{a^n} \textrm{d}r' \nonumber \\ {}&\quad \mathrel \times \int \limits _{\theta _1}^{\theta _2} \bar{P}_{nm}\left( \sin \theta '\right) \sin \theta ' \textrm{d}\theta ' \mathrel \times \int \limits _{\lambda _1}^{\lambda _2} \begin{Bmatrix} \cos m\lambda ' \\ \sin m\lambda ' \end{Bmatrix} \textrm{d}\lambda '. \end{aligned}$$

(15)

The definite integral of the associated Legendre functions by recursion is elaborated in detail in Fukushima (2012). An alternative recursion formula is derived in Wei (2016). However, for a small enough cells the integration with respect to $\theta '$ and $\lambda '$ can be replaced by finite differences. Thus, Eq. (15) can be approximated in the form of a massline integral

$$\begin{aligned} \begin{Bmatrix} \left. \bar{C}_{nm}^{T}\right. \\ \left. \bar{S}_{nm}^{T}\right. \end{Bmatrix}&= \frac{G \rho }{GM\, (2n+1)} \int \limits _{r_1}^{r_2} \frac{\left. r'\right. ^{n+2}}{a^n} \textrm{d}r' \nonumber \\&\quad \mathrel \times \bar{P}_{nm}\left( \sin \bar{\theta }\right) \sin \bar{\theta } \begin{Bmatrix} \cos m\bar{\lambda } \\ \sin m\bar{\lambda } \end{Bmatrix} \Delta \lambda \Delta \theta , \end{aligned}$$

(16)

with $\bar{\theta }$ and $\bar{\lambda }$ denoting the spherical coordinates of the cell centers. Moreover, in practical computations the cell size can be safely replaced by the nominal grid resolution in terms of the geodetic latitude ($\Delta \theta \approx -\Delta \varphi$). After evaluating the partial integral with respect to $\textrm{d}r'$, the final formula is obtained as

$$\begin{aligned} \begin{Bmatrix} \bar{C}_{nm}^{T} \\ \bar{S}_{nm}^{T} \end{Bmatrix}&= \frac{G \rho }{GM (2n+1)(n+3)} \left( \frac{r'}{a} \right) ^n r'^3 \Bigg |_{r_1}^{r_2} \nonumber \\&\quad \mathrel \times \bar{P}_{nm}\left( \sin \bar{\theta }\right) \sin \bar{\theta } \times \begin{Bmatrix} \cos m\bar{\lambda } \\ \sin m\bar{\lambda } \end{Bmatrix} \Delta \lambda \Delta \bar{\theta }. \end{aligned}$$

(17)

Numerical tests showed that the magnitude of the effect of the massline approximation is correlated with the height of the column $r_2 - r_1$. At 1 arc-minute grid resolution, it is limited to ±8 mm in the most mountainous parts of the study area.

Equivalent expressions were already considered by Forsberg and Tscherning (1981, Eqs. 27–30), yet we have no knowledge whether they were ever actually tried in practice in context of the RCR technique. Considering the computational implementation, Eq. (17) is similar to the usual SH analysis except that it additionally includes the massline kernel (the $r^3$ term) to multiply with.

Once the SH coefficients $\bar{C}_{nm}^{T}$, $\bar{S}_{nm}^{T}$ of the topography have been determined by summation over all tesseroids, the reduction containing the high-pass filtered effect of topography can be computed as

$$\begin{aligned} \delta g_\text {RSHTP}&= \delta g_\text {FST} - \delta g_\text {SHT} \end{aligned}$$

(18)

$$\begin{aligned} \Delta g_\text {RSHTP}&= \Delta g_\text {FST} - \Delta g_\text {SHT} \end{aligned}$$

(19)

$$\begin{aligned} \delta V_\text {RSHTP}&= \delta V_\text {FST} - \delta V_\text {SHT} , \end{aligned}$$

(20)

where $(\cdot )_\text {FST}$ denotes the full-scale topographic signal computed in the space domain, i. e., the usual topographic reduction by evaluating Newton’s volume integral between the topography and the geoid (exemplified by Eq. (11) in terms of the potential), and $(\cdot )_\text {SHT}$ denotes the spectrally truncated topographic signal computed in the space domain by SH synthesis (exemplified by Eq. (13) in terms of the potential) from the topographic coefficients (Eq. 17). Basic formulas for the SH synthesis of other functionals can be found in standard textbooks on physical geodesy or, e.g., Gruber et al. (2014).

The residual quantities are then obtained as

$$\begin{aligned} \delta g_\text {res,RSHTP}&= \delta g_\text {obs} - \delta g_\text {GGM} - \delta g_\text {RSHTP} \end{aligned}$$

(21)

$$\begin{aligned} \Delta g_\text {res,RSHTP}&= \Delta g_\text {obs} - \Delta g_\text {GGM} - \Delta g_\text {RSHTP} \end{aligned}$$

(22)

$$\begin{aligned} T_\text {res,RSHTP}&= T_\text {obs} - T_\text {GGM} - \delta V_\text {RSHTP} , \end{aligned}$$

(23)

where T is the disturbing potential, $\delta g$ are gravity disturbances and $\Delta g$ are gravity anomalies. Of course, the approach can also be applied to other observable functionals of the gravity field, e.g., deflections of the vertical.

$(\cdot )_\text {GGM} - (\cdot )_\text {SHT}$ can be efficiently computed in one SH synthesis if the GGM is accordingly reduced at coefficient level using $\bar{C}_{nm}^{T}$, $\bar{S}_{nm}^{T}$ (provided that the underlying GM and a of the SH coefficients are scaled to match those of the GGM). Rearranging the terms as written below, this can be interpreted as if first the observation $(\cdot )_\text {obs}$ (here gravity) is reduced for the full-scale topographic effect in the space domain, which gives a no-topography quantity $(\cdot )_\text {NT} = (\cdot )_\text {obs} - (\cdot )_\text {FST}$, and then the corresponding band-limited quantity for the GGM $(\cdot )_\text {GGM-SHT} = (\cdot )_\text {GGM} - (\cdot )_\text {SHT}$ is subtracted. Thus, the terms $\delta g_\text {NT}$ and $\Delta g_\text {NT}$ resemble the no-topography gravity disturbance and the Bouguer anomaly, respectively.

$$\begin{aligned} \delta g_\text {res,RSHTP}&= \left( \delta g_\text {obs} - \delta g_\text {FST} \right) - \left( \delta g_\text {GGM} - \delta g_\text {SHT} \right) \nonumber \\ {}&= \delta g_\text {NT} - \delta g_\text {GGM-SHT} \end{aligned}$$

(24)

$$\begin{aligned} \Delta g_\text {res,RSHTP}&= \left( \Delta g_\text {obs} - \Delta g_\text {FST} \right) - \left( \Delta g_\text {GGM} - \Delta g_\text {SHT} \right) \nonumber \\&= \Delta g_\text {NT} - \Delta g_\text {GGM-SHT} \end{aligned}$$

(25)

$$\begin{aligned} T_\text {res,RSHTP}&= \left( T_\text {obs} - \delta V_\text {FST} \right) - \left( \delta T_\text {GGM} - \delta V_\text {SHT} \right) \nonumber \\&= T_\text {NT} - \delta T_\text {GGM-SHT} , \end{aligned}$$

(26)

The SH topographic coefficients of the potential according to Eq. (17) only need to be evaluated and reduced from the GGM coefficients once. However, whereas the RTM technique allows for integration over a fixed radius (see Sect. 1), this approach requires a fixed-area computation. In the following, we will use the term fixed-area computation in two different contexts depending on the method. Related to the RSHTP approach, it means the summation of the DEM cells over a fixed regional domain instead of a global summation, i.e., using a truncated topography over a regional domain and assuming zero outside. Related to the classic RTM approach, we will use it also to differentiate from the abovementioned integration over a fixed radius, i.e., the same portion of topography is modeled for each computation point.

The expansion of the topographic heights into SH coefficients of the potential according to Eq. (17) relies on the orthogonality of the spherical harmonics on the sphere. Fixed-area computation will cause spectral leakage in addition to the usual effects of truncating the SH expansion to $n_\text {max}$ or introducing jumps at the boundaries of the grid (“edge effects”). This means that when expanding regional data into SH, the power in the data is distributed differently across the SH degrees compared to expanding global data (Slobbe et al. 2012). The impact of this on the computations in the space domain, particularly in context of RCR computations for the regional quasigeoid, are considered in Sect. 5.1.

Fig. 1

Datasets (blue dots: gravity stations, black triangles: GNSS/leveling points) and data domains (plot area: gravity domain, orange inlay: geoid domain)

4 Setup of the case study

The modeling approaches including the new method described in Sect. 3 were investigated using the data from the D-A-CH (Germany-Austria-Switzerland) geoid project. This initiative was formed in 2017 between the Federal Agency of Cartography and Geodesy (BKG) of Germany, the State Agency for Spatial Information and Rural Development (LGL, Federal State of Baden-Württemberg, Germany), the Agency for Digitisation, High-Speed Internet and Surveying (LDBV, Free State of Bavaria, Germany), the Federal Office of Metrology and Surveying (BEV) of Austria and the Topographic Office (swisstopo) of Switzerland. It aimed to promote a cooperation in the field of regional gravity field modeling, to exchange and improve the underlying data and models, and to facilitate cross-border height determination for users of geodetic coordinates in the border region of the three countries (Schwabe et al. 2021). It was recently extended to the whole Alpine region under the name European Alps Geoid (BKG 2022; Bauer and Schwabe 2023).

The inner region to compute the quasigeoid was chosen to be centered around the Lake Constance and also to roughly cover equal areas of Switzerland, Austria and the German federal states of Baden-Württemberg and Bavaria. Within the D-A-CH cooperation, available point gravity data and GNSS/leveling data were exchanged in an area extending about 100 km further (Fig. 1). Data of France were also contributed from swisstopo’s archives after consultation with the data owners. Newest gravity data from ongoing fieldworks in the autonomous Italian province of South Tyrol were provided by the Cadastre of South Tyrol. Unfortunately, no point data were available for the other Italian territories in the test area.

Fig. 2

Differences between gravity station heights and MERIT DEM. The orange inlay marks geoid domain of the test area

For the most part, the data density and quality is comparably good (average point density 0.7 per km² in the inner geoid domain, agreement of gravity station heights with DEM heights typically better than 10 m, only a few apparent outliers in the visual inspection of the residual gravity data after the remove step). Coarser data prevail in the high mountain areas of Switzerland and Austria, mostly outside geoid area, as well as data gaps in parts of Italy and France. Also, the georeference of the gravity points in France is not always clear, which becomes apparent through larger differences between point heights and DEM (Fig. 2). The errors in the gravity data and the lack of data in the area to the south of the geoid area make the study of the impact of different approaches to handle topography more difficult. However, since we use the same data and an identical RCR processing scheme except for the topographic reduction, the main conclusions to be drawn from the comparison are not substantially affected.

Both gravity and GNSS/leveling data were homogenized to ETRS89 coordinates and EVRS normal heights. This included application of national a priori geoid models and height transformation grids, as far as applicable, and also conversion to the zero-tide system for both ellipsiodal and normal heights in the GNSS/leveling data.

As for the GGM, the GECO model (Gilardoni et al. 2016) up to degree 2190 and order 2159 was used. The SH coefficients beyond degree 2160 in this model originate from a prior conversion of ellipsoidal harmonics to spherical harmonics. In this context, we used the model coefficients “as is” in the SH synthesis, i.e., up to degree 2190. However, as far as the cut-off wavelength in the classic RTM approach is concerned, the model is considered as “degree 2160.”

On the other hand, the $n_\text {max}$ for the SH expansion of the topographic potential ($(\cdot )_\text {SHT}$ term) in the RSHTP approach was chosen at degree 2160. Testing different combinations of $n_\text {max}$ for both $(\cdot )_\text {GGM}$ and $(\cdot )_\text {SHT}$, as well as for the regional vs. global case (see Sect. 5.1), it was found that this provided the best results for the area, based on the empirical standard deviation of the residual gravity data (Table 1) as the criterion.

All functionals of the disturbing potential in this study are defined in accordance with the normal potential of the Geodetic Reference System 1980 (Moritz 2000). In this regard, the coefficients of the GECO model were rescaled accordingly following (Gruber et al. 2014, Eq. (4.21)). Also, all quantities from the GGM are computed according to the zero-tide convention.

Regarding the DEM, it was decided to use the global 3 arc-second MERIT DEM (Yamazaki et al. 2017) for this study since a spectrally filtered RTM surface to be used in context of the classic RTM approach was readily available by means of the MERIT2160 dataset (Hirt et al. 2019). Also, MERIT was one of the best available DEM from global satellite radar data at that time (Zahorec et al. 2021, Appendix C). MERIT2160 is a set of SH coefficients of the height function up to degree 2160 which was derived from the global MERIT grid. The corresponding RTM reference surface computed from SH synthesis of the MERIT2160 coefficients, also to SH degree 2160, was provided by Christian Hirt (personal communication).

The respective domains in which the data are given were defined like this:

• Geoid domain: 46.75° N – 48.35° N (ca. 180 km) / 7.5° E – 11.5° E (ca. 300 km)

• Gravity domain: 45.85° N – 49.25° N (ca. 380 km) / 6.1° E – 12.9° E (ca. 510 km)

• DEM domain (regional case): 44.95° N – 50.15° N (ca. 580 km) / 4.7° E – 14.3° E (ca. 720 km)

The locations of the gravity and of the geoid domain are visualized in Fig. 1 alongside with the point data.

The processing scheme is as follows:

• 1. Remove step

  • (a) Computation of residual gravity disturbance at station height. Here, we directly evaluate the norm of the full gravity vector $\left| \textbf{g}\right|$ from the GGM, i. e., $\delta g_\text {res,RTM} = g_\text {obs} - \left| \textbf{g} \right| _\text {GGM} - \delta g_\text {RTM}$ or $\delta g_\text {res,RSHTP} = g_\text {obs} - \left| \textbf{g} \right| _\text {GGM-SHT} - \delta g_\text {FST}$, respectively. The quantities $\left| \textbf{g} \right| _\text {GGM}$ and $\left| \textbf{g} \right| _\text {GGM-SHT}$ were computed according to Eqs. (4.49) and (4.52) in Gruber et al. (2014) using the unreduced GGM coefficients $\left. \bar{C}_{nm}\right.$ (after rescaling to GM and a of GRS80), $\left. \bar{S}_{nm}\right.$ and the reduced GGM coefficients $\left. \bar{C}_{nm}\right. - \left. \bar{C}_{nm}^{T}\right.$, $\left. \bar{S}_{nm}\right. - \left. \bar{S}_{nm}^{T}\right.$ (see Eq. (17)), respectively. Note that this approach resembles the computation of residual gravity disturbances with respect to the normal potential of the GRS80 system but without explicitly evaluating the normal gravity.

• 2. Compute step

Note that the following approach for the compute step in this study was chosen out of convenience over, e.g., least-squares techniques such as collocation or estimation of radial base functions. It is not specific or a requirement to the RTM or the RSHTP method in the remove and restore steps. The aim was to transform residual gravity to residual height anomalies in mostly the same way for each of the compared methods RTM and RSHTP in order to study the isolated impact of the different topographic reduction schemes.

Table 1 Standard deviations (SD) of residual gravity (mGal) after the remove step for different $n_{\text {max}}$ regarding the global geopotential model (GGM) GECO and the SH expansion of the topography according to Eq. (17)

The parameters quoted in the following substeps were determined empirically during previous computations in the same area within the D-A-CH project (using the RTM approach with the same terrestrial gravity data and the GECO GGM to model the gravimetric quasigeoid of the area, and using the same GNSS/leveling data for validation). While this setup does not necessarily provide the optimal GNSS/leveling fit also for the RSHTP approach in each subregion (see results in Sect. 5.4), in particular in view of the Wong-Gore kernel modification, it still proved as a reasonable reference for the method comparisons with no impact on the general characteristics and conclusions.

• (a) Data preselection 1: All gravity points where the station height differs from the DEM height by more than 10 m were rejected. This relates to a total of ca. 5 percent for the whole dataset. The choice of this global threshold value might be too pessimistic in some mountain areas with new and accurately measured gravity stations, e.g., South Tyrol. However, it was done after extensive empirical tests in order to reliably circumvent gross errors in some problematic data sources, e.g., in France. Anyway, the data selection applies equally in the method comparison, so again the main characteristics and findings do not seem affected.

• (b) Data preselection 2: For each cell of the grid (see next step) the median of the residual gravity values was computed, and only the corresponding data point of that median value was used together with its original location in the gridding. This has proven useful as another robust means to filter outliers.

• (c) Gridding: Using the simple collocation mode of the GRAVSOFT program GEOGRID (Forsberg and Tscherning 2014), the residual gravity data were interpolated onto a geographical grid with 0.01° spacing (target grid). Relevant interpolation parameters with this method: Correlation length of the model covariance function (second-order Markov model) 15 km, a priori standard deviation (assumed white noise of the data, somewhat optimistic for the parts of the data in Austria and Switzerland) 0.1 mGal, number of nearest points per quadrant (subselection of data around each computation point) 5.

• (d) Conversion of residual gravity $\delta g_{\text {res,}(\cdot )}$ to residual height anomalies $\zeta _{\text {res,}(\cdot )}$ was realized in the frequency domain by means of Fast Fourier Transform, as implemented in the GRAVSOFT program SPFOUR (Forsberg and Tscherning 2014). Wong-Gore modification of the Stokes kernel was applied up to degree 160. Note in this context that, since we operate with smoothed residual gravity values (decorrelated with height), the impact of applying the Stokes function (Hofmann-Wellenhof and Moritz 2005, Eq. (2–305)) in terms of gravity anomalies instead of the Hotine-Koch function (ibid., Eq. (2–369)) in terms of gravity disturbances is numerically negligible in this configuration.

• 3. Restore step

  • (a) Station heights for the target grid (0.01° grid spacing) were resampled from the original MERIT DEM grid.

  • (b) Computation of restored height anomalies $\zeta _\text {RTM} = \zeta _\text {res,RTM} + \zeta _\text {RTM} + \zeta _\text {GGM}$ or $\zeta _\text {RSHTP} = \zeta _\text {res,RSHTP} + \delta \zeta _\text {FST} + \zeta _\text {GGM-SHT}$, respectively, for computation points in the target grid and for the GNSS/leveling points. The grids are mainly used for visualization and grid-based comparisons in Sect. 5. For the comparison with GNSS/leveling data in Sect. 5.4. Only the residual height anomaly $\zeta _{\text {res,}(\cdot )}$ was interpolated from the grid coming out of the compute step, whereas the terms for the RTM and RSHTP reductions were directly evaluated for the location and height of the GNSS/leveling points.

For the classic RTM reductions $(\cdot )_\text {RTM}$ the reference topography (RTM surface) was derived from the model MERIT2160 (Hirt et al. 2019), as outlined above. In the following, we will refer to this as the “SH-filtered RTM surface,” or short “RTM-SH.” Additionally, a running average filter with 15 km diameter was also tested, hereafter referred to as “15 km boxcar filter,” or short “RTM-Boxcar.” However, in our comparison of RTM and RSHTP in Sect. 5 we will focus on the RTM-SH approach. For detailed material including also the results and comparisons for the RTM-Boxcar approach the reader is refered to the Electronic Supplementary Material (ESM1). Here, we only summarize our observation that the RTM-Boxcar solution produced significantly larger residual gravity values. This confirms again that the RTM-SH surface is more consistent with the GGM counterpart than the RTM-Boxcar surface, a conclusion already drawn in Hirt (2010).

Computation of the topographic effects in the space domain was done as follows. In the innermost zone of 150 m around a computation point, the formulas for the rectangular prism (MacMillan 1958; Forsberg 1984; Nagy et al. 2000) were used. Beyond, the optimized formulas for the tesseroid according to Grombein et al. (2013) were applied. Between 150 m and 5400 m distance from the computation point the tesseroids are vertically subdivided so that their height does not exceed the horizontal resolution (i. e., max. 90 m). Unlike the horizontal subdivision, this reduces the near-zone approximation error of the tesseroids considerably (Schwabe et al. 2015). In the computation of the SH topographic coefficients for the RSHTP approach unaltered tesseroids were used. However, in order to save computation time, the original MERIT DEM grid was downsampled to 1 arc-minute resolution. In both cases, the fixed-area computation extended over the whole DEM area as specified above, and the 3-D geometry of the topography was treated in ellipsoidal approximation neglecting the (quasi)geoidal variation, i. e., assuming $r \approx r_0(\varphi ) + H_{\text {DEM}}$. In all computations involving topography (RTM and RSHTP), the standard density $\rho = 2670\,\text {kg}\,\text {m}^{-3}$ was applied.

In general, station heights were introduced in terms of ellipsoidal coordinates (i.e., including ellipsoidal height) and mapped to geocentric co-latitude and radius when computing terms from SH coefficients ($(\cdot )_\text {GGM}$, $(\cdot )_\text {SHT}$, $(\cdot )_\text {GGM-SHT}$) by SH synthesis, whereas for the computations to evaluate the topographic effect in the space domain ($(\cdot )_\text {RTM}$, $(\cdot )_\text {FST}$) the physical height was used both related to the DEM and the height of the computation point. This means that for the latter the geoid was neglected in the inner geometry of the topography, and the prisms or tesseroids are placed on the ellipsoid. This also applies for the SH expansion of the topography (computation of the coefficients according to Eq. (17)) in the RSHTP approach.

Where necessary, physical heights and ellipsoidal heights were converted using EGG08 (Denker et al. 2009) as an a priori height transformation grid. In context of the station heights of the gravity data this implicitly means the conversion between gravity anomalies and gravity disturbances. It is safe to assume that the conversion does not impose any additional noise or bias larger than 0.1 mGal to the gravity data. Thus, the impact on the practical RCR quasigeoid results is negligible.

Finally, while the HC to gravity (Eq. 1) was routinely applied in the computations of the RTM reductions in the remove step, the HC in terms of the height anomaly according to Eq. (4) was evaluated separately and its impact on the results was analyzed in detail in Sects. 5.3 and 5.4.

Fig. 3

Difference between global and regional computation of the RSHTP reduction. Left panel: gravity disturbances, right panel: height anomalies

5 Results

5.1 Comparison of global versus regional SH expansion of the topographic potential in the RSHTP approach

This section is dedicated to the study of the leakage effect that the SH expansion of the topography from regional DEM data has on the RSHTP reduction. To this end, we will first consider a simulation experiment without using any regional terrestrial gravity data. This includes forward modeling of the terms in Eqs. (21)–(26), here displayed for $n_\text {max} = 2190$ regarding the $(\cdot )_\text {GGM}$ terms and $n_\text {max} = 2160$ related to the $(\cdot )_\text {SHT}$ terms.

As described in Sect. 4, over the regional domain of the study area the MERIT DEM (Yamazaki et al. 2017) was used at original 3 arc-sec resolution for the full-scale topographic reduction ($(\cdot )_\text {FST}$) and downsampled to 1 arc-min in the SH expansion of the topography ($(\cdot )_\text {SHT}$). In the global case, the downsampled 1 arc-min version of the MERIT DEM was used outside the study area both for the $(\cdot )_\text {SHT}$ and the $(\cdot )_\text {FST}$ terms.

However, it should be noted that the MERIT DEM is technically not a global DEM. The southern boundary of the grid domain is located in the Southern Ocean at 60° southern latitude with zero heights all along the boundary. Thus, the Antarctic continent is missing in the MERIT DEM. In view of the orthogonality problem the simulations for the global SH expansion presented here are therefore formally only valid for a hypothetical Earth in which Antarctica does not exist. However, considering the outcome of our comparison with the regional computation as presented below, we have no indication that this “quasi-global” computation significantly changes the numerical results of the restored height anomalies for the study area, as compared to a “true global” computation.

Detailed viewgraphs for the various quantities, including forward modeled fields for gravity disturbance and height anomaly are compiled in the electronic supplementary material (ESM2). Here we only consider the differences of the RSHTP reduction ($(\cdot )_\text {FST}$ minus $(\cdot )_\text {SHT}$) for the global minus the regional case. These are shown in Fig. 3. The same distinct high-frequency striping pattern appears for both functionals with magnitudes up to 12 mGal or 4 cm, respectively. This pattern does not seem to correspond with the local terrain height.

In order to simulate the remaining effect like in a RCR computation of the quasigeoid, we first propagated the gravity differences (Fig. 3, left panel) to height anomalies using the same method as in the actual regional quasigeoid modeling (Sects. 5.2–5.4) based on the Stokes integral in the frequency domain (program SPFOUR, see Sect. 4). For consistent comparison with the actual RCR results (see next paragraph) we again applied the Wong-Gore kernel modification up to degree 160. From that, we evaluated the simulated closure difference with respect to the directly computed height anomaly differences. The result is shown in the left panel of Fig. 4. In the electronic supplementary material the propagation is computed without Wong-Gore modification, resulting in a only slightly different picture.

Fig. 4

Simulated (left panel) and actual (right panel) closure differences in the remove-compute-restore computation of the height anomaly due to the SH expansion of the topographic potential from global vs. regional topography data

Fig. 5

RTM height (left panel) and HC for the height anomalies according to Eq. (4) (right panel) for the classic RTM with SH-filtered RTM surface. Areas where the HC is zero ($H_P > H_{\bar{P}}$) are shown in gray to demonstrate the characteristic truncation pattern of the RTM-SH surface

Table 2 Descriptive statistics of residual fields, RTM topography and HC for height anomalies

Furthermore, we also compared the complete RCR quasigeoid computation using the actual gravity data as in Sects. 5.2–5.4 for the global and the regional SH expansion of the topography. The actual closure difference according to that is shown in the right panel of Fig. 4. Simulated and actual closure differences largely correspond except for the areas void of terrestrial gravity stations. The magnitude in the inner part of the study area (“geoid domain” as defined in Sect. 4) remains in both cases below ±9 mm. The respective standard deviations are 1.8 mm (simulated) versus 2.3 mm (actual). This includes a long-wavelength component but also high-frequency features that seem to be correlated with the terrain height. Zahorec et al. (2021, Fig. 10) demonstrates that the distant relief effect in the complete topographic reduction depends on the height of the computation point. Thus, we presume that the two different topographic potentials in the global and in the regional case might produce a residual distant relief effect which is not fully absorbed through the RCR technique.

The important observation is that the residual oscillations due to the spectral leakage are diminished down to the millimeter level in the closure differences. This confirms that the total error due to the fixed-area implementation of the RSHTP approach is acceptable in RCR computations. Also, it should not affect the comparison between the RSHTP and the RTM-SH approach in the following subsections.

5.2 HC for the height anomaly in the study area and comparison of residual fields

Starting with our regional RCR study, let us first analyze and compare the residual gravity data after reduction of GGM and RTM according to the setup described in Sect. 4.

Firstly, Fig. 5 visualizes the situation for the RTM surface derived from SH expansion up to degree 2160 (RTM-SH surface). The left panels shows the respective negative RTM heights $H_P - H_{\bar{P}}$ according to Eq. (1), and the right panels display the corresponding HC in terms of the height anomaly. The typical truncation effect of the SH expansion in the space domain becomes apparent in the RTM-SH surface. In some valleys, the HC for the height anomaly attains values of up to 10–20 cm (Table 2).

Considering the residual gravity disturbances after the restore step, both RTM-SH and RSHTP approach provide an equally effective reduction of the observations, as displayed in the left panels of Fig. 6 and confirmed by the statistics in Table 2. Application of the compute step as described in Sect. 4 provides the corresponding grids of residual height anomalies (right panels of Fig. 6). In both methods they are reduced to 4 cm (standard deviation) or ca. 20 cm (maximum), respectively. In that context, it should be considered that the study area features the highest mountains (Dufourspitze, altitude 4634 m) and steepest valleys in the region where even latest high-resolution combined GGM are not entirely underpinned by terrestrial gravity data. Compared to the magnitude of the residual fields, the differences between the methods (Fig. 6, bottom panels) are smaller by about the factor 2 (gravity disturbances) to 4 (height anomalies).

On the other hand, if the gridding residuals of the residual gravity data are considered, the RSHTP approach performs about 10 % better than the RTM-SH approach. From this we suppose that the RSHTP approach provides a slightly better smoothing of the observations at the very short scales. This is in line with the observations made by Hirt et al. (2019, Figs. 8a and 10b).

Fig. 6

Residual gravity (left panels) and height anomalies (right panels) for the classic RTM with SH-filtered RTM surface (top panels) and the RSHTP approach (middle panels). The differences of these quantities for the two methods (RTM-SH minus RSHTP) are displayed in the bottom panels

Fig. 7

Impact of the HC on the restored height anomalies in the classic RTM approach. Differences between RSHTP results and classic RTM with SH-filtered RTM surface before (left panel) and after (right panel) application of the HC in the restore step

Table 3 Comparative statistics of restored height anomaly grids

5.3 Comparison of quasigeoid results

Next, we compare the results of the height anomaly grids that are obtained after restoring the contributions of the GGM and of the topography. Figure 7 displays the respective differences (RTM-SH minus RSHTP) before (left panel) and after (right panel) the HC according to Eq. (4) is applied in the RTM-SH approach. The related numerical statistics are compiled in Table 3. From that, a number of observations can be made.

First, the HC shows up in the figures nearly one-to-one as a systematic difference if not applied in the classic RTM. This is also reflected in the numerical statistics in Table 3. Here, the significantly larger standard deviation of about 20–30 % in the restore step is only one aspect when neglecting the HC to the height anomaly in the restore step. More importantly, a pronounced asymmetry in the minima and maxima (span maximum minus mean being much larger than the span mean minus minimum) is observed as well. Our conclusion is that these results are manifestation of the systematic behavior of the HC, taking on only negative values.

Fig. 8

Zoom-in of residual differences (mean offset of $-$ 1.1 cm in the area removed) between restored height anomalies (RSHTP minus RTM-SH as in Fig. 7, right panel) in the Swiss-Austrian border zone close to Bludenz

Apart from that, the results of the two approaches appear very consistent. In the deep valleys some correlation with topography is still noticeable, but at a much smaller magnitude. Instead, as in the lowlands, the typical correlated long-wavelength residuals known from RCR computations prevail. As an example for the agreement on the very local scale, Fig. 8 provides a zoom-in for the Swiss-Austrian border zone close to Bludenz (47.03° N, 9.80 ° E, mean altitude ca. 1700 m, max. altitude ca. 2940 m) for which the restore step was done at the original 3 arc-second resolution of the MERIT DEM. Apart from a mean difference of 11 mm in that region that was removed for the plot, the residual differences between the classic RTM with SH-filtered reference topography and the RSHTP approach have a standard deviation of 2.3 mm and do not exceed 8 mm. Considering the roughness of the quasigeoid in mountainous regions (the restored height anomalies in this area differ up to ±7 cm or ±3.5 cm from the moving average over distances of 2 km or 1 km, respectively, not shown here), this is remarkable.

5.4 Validation against GNSS/leveling data

Section 5.3 provides a first indication of the consistency between the two methods and also of the importance of the HC for the restored height anomalies in the classic RTM approach. An independent validation is feasible by comparison of the quasigeoid models with GNSS/leveling data.

To this end, the residual height anomalies after the compute step were interpolated at the locations of the GNSS/leveling points, and the contributions of the GGM and the topography was restored in these sites by direct point-wise computation. Combined figures with geographical plots and histograms per country are presented in Figs. 9, 10 and 11. Moreover, the descriptive statistics for each subarea and country are summarized in Table 4.

Let us now study the impact of the HC for the RTM method in detail. Figure 9 shows the results in the inner region (geoid domain) before (top panel) and after (bottom panel) application of the HC, whereas Figs. 10 covers the outer region (gravity domain). Firstly, from the colored dots in the mountainous regions of Austria and Switzerland it becomes clear that, apart from areas with edge effects along the borders to France and Italy, the residuals are much smaller and homogenenous if the HC in terms of the height anomaly is applied in the restore step. Secondly, the histograms confirm the observation from Sect. 5.3 related to the symmetry of the residuals, in particular for the areas of Austria and Switzerland.

Since no explicit HC is needed in the RSHTP approach, Fig. 11 directly shows the results for the inner (geoid domain, top panel) and outer (gravity domain, bottom panel) regions, respectively. In general, the distribution of the residuals resembles the classic RTM with HC for the height anomalies (bottom panels of Figs. 9 and 10), respectively.

The improvement in the GNSS/leveling comparisons is also reflected in Table 4. Here we focus on Switzerland, where several high mountain peaks are present and a large number of GNSS/leveling points is available. As can be seen from the highlighted fields in the table, application of the HC in terms of the height anomaly lowers the standard deviations by around 30 %, and the residuals appear centered. Finally, with a fit of less than 2 cm (standard deviation) in the inner region, both approaches seem to provide consistent results. Thus, it is confirmed empirically that the classic RTM approach is severely biased in mountainous regions if the HC is neglected for the height anomalies in the restore step.

Regarding the significance of the results in view of the accuracy of the GNSS/leveling data we will limit ourselves again to the dataset which is the most relevant for the main focus area of the interpretation (see, e.g., Table 4, Figs. 9, 10 and 11), i.e., Switzerland. From Urs Marti (swisstopo), we received by personal communication the information that the points can be assigned to two categories. The first category has an assumed accuracy of ca. 1 cm and includes leveled GNSS permanent stations as well as field points observed in multiple GNSS campaigns and/or sessions of at least 24 h. These make up around 75 percent of the points. The second category has an assumed accuracy of ca. 3 cm and includes field points that were observed only once in sessions between 4 and 20 h. These make up around 25 percent of the points. Considering the HC values in Switzerland of up to 20 cm and the reduction of the residuals of 30 to 40 percent in terms of standard deviation and more than 50 percent in terms of maximum residual for the inner region (Table 4), this should still be sufficient to consider the comparisons between the tested methods based on these data significant. Moreover, this level of accuracy is also in line with the figures reported for, e.g., the Colorado experiment (Wang et al. 2021, Table 6).

Fig. 9

GNSS/leveling residuals $h_\text {GNSS}-H_\text {lev}-\zeta _\text {grav}$ in the inner region (geoid domain) for the classic RTM approach with SH-filtered RTM surface, before (top panel) and after (bottom panel) application of the HC for the height anomaly. A mean offset per country was subtracted to account for remaining datum differences in the national reference frame realizations

Fig. 10

GNSS/leveling residuals $h_\text {GNSS}-H_\text {lev}-\zeta _\text {grav}$ in the outer region (gravity domain) for the classic RTM approach with SH-filtered RTM surface, before (top panel) and after (bottom panel) application of the HC for the height anomaly. A mean offset per country was subtracted to account for remaining datum differences in the national reference frame realizations

Fig. 11

GNSS/leveling residuals $h_\text {GNSS}-H_\text {lev}-\zeta _\text {grav}$ in the inner region (geoid domain) (top panel) and in the outer region (gravity domain) (bottom panel) for the RSHTP approach. A mean offset per country was subtracted to account for remaining datum differences in the national reference frame realizations

Table 4 Descriptive statistics of GNSS/leveling residuals

6 Discussion

In this section, the results presented in Sects. 5.2–5.4 are discussed in context. Besides the observation that the RTM and the RSHTP approach provide consistent results at the centimeter level in RCR computations of the quasigeoid, we summarize the following findings related to some particular questions:

6.1 Impact of the HC for the height anomaly in the restore step

Through application of the HC according to Eq. (4) in the restore step the agreement with GNSS/leveling data is substantially improved. Only then the results are also consistent with the RSHTP approach at the centimeter level. Neglecting it leads to a very localized systematic positive bias in the deep valleys. This bias can attain 10–20 cm for a degree 2160 RTM (scenario using a high-resolution combined GGM such as EGM2008) and even larger numbers for, e.g., a RTM defined according to a satellite-only model, say, degree 250–300. In a fitted quasigeoid the bias would be shifted into the adjacent mountain ridges with opposite sign since GNSS/leveling benchmarks are available mostly in the valleys. Thus, following up on the work by Klees et al. (2023) and others, our study now also provides the empirical proof that omitting the HC for the height anomaly indeed gives flawed results. This is a relevant finding considering that the HC for the height anomaly has been considered negligible for a long time (Forsberg and Tscherning 1981), and is still up to date in recent studies (e.g., Lin et al. 2023, final paragraph in Section 2).

6.2 Applicability to “short-wavelength” RTM surfaces

One specific question was related to the validity of the classic RTM approach and the HC for “short-wavelength” RTM surfaces, e.g., in combination with a high-resolution GGM of degree 2160. After all, Forsberg and Tscherning (1997) postulated “luckily this HC is quite straightforward if the reference topography is long-wavelength, so that the reference topography above the computation point P may be approximated by a Bouguer plate” – or in the context of Eqs. (6) and (8) a Bouguer shell. However, based on the numerical results we do not get the impression that the short-wavelength RTM imposes any practical problems at all. On the contrary, it features some practical advantages. Firstly, also pointed out by Forsberg and Tscherning (1997), a higher-frequency reference topography implies smaller RTM effects and a quicker decay of the far-zone effects in the first place, resulting a significantly smaller integration radius. Secondly, the HC for the height anomaly gets even larger for long-wavelength RTM (Klees et al. 2022). For example, values up to 26 cm are to be expected in the study area assuming a 100 km (Boxcar filter) RTM surface.

Furthermore, pros and cons of both approaches can be discussed as follows.

6.3 Pros of the RSHTP approach

No RTM surface is introduced at all. Thus, the explicit HC is conceptually avoided. Instead, the RSHTP approach implicitly accounts for the HC since the SH expansion of the topographic potential evaluated at the original data points inherently provides harmonically downward continued functionals, exactly what the HC aims at. In fact, theoretically the RSHTP approach provides this harmonic downward continuation even for the whole internal space of the topographic masses, which makes it also applicable to compute the geoid.

Furthermore, the applied mass reductions preserve a physically consistent Earth model insofar that exactly the same topographic information is used for each computation point. Opposed to that, although the closed-form expressions for the HC have now shown to be theoretically exact by Klees et al. (2023), the HC is still computed from a different spherical shell in each computation point.

The technique allows to directly combine the topographic potential with the GGM at coefficient level up to the desired $n_\text {max}$, i. e., it is inherently spectrally consistent. The assumed linear relationship between RTM surface and the representation of the topographic spectrum included in the GGM is avoided.

As a practical benefit, through computing the combined term $(\cdot )_\text {GGM-SHT}$, only one additional SH analysis but no additional SH synthesis is needed for the SH topographic potential in addition to the GGM, and, unlike the SGM described in Hirt et al. (2019), the SH expansion itself differs from the standard case for the topographic height function only by the additional massline integral. Also, the full-scale part of the RSHTP reduction from the integration in the space domain ($(\cdot )_\text {FST}$) has to be computed only once even for different $n_\text {max}$ of the GGM or of the SH expansion of the topographic potential, respectively.

Furthermore, the absence of the RTM surface is especially convenient in case of multiple large density contrasts (large lakes, ice caps etc.) because the individual contributions of various layers to the $(\cdot )_\text {FST}$ and $(\cdot )_\text {SHT}$ terms can be easily computed separately and stacked (see also the related con of the classic RTM in this regard).

6.4 Cons of the RSHTP approach

Numerical implementation is more sophisticated and requires a fixed-area integration of the DEM to ensure mass consistency between the SH analysis of topographic potential coefficients and the full-scale topographic effect in the space domain. Generally, SH expansions of the topography come at high computation costs. On the other hand, this disadvantage is neutralized with regard to the classic RTM with SH-filtered RTM surface which also requires SH analysis of the topographic height function unless precomputed products such as the MERIT2160 (Hirt et al. 2019) are available.

As discussed in Sect. 3, the SH analysis computed from data of a regional domain violates the orthogonality of the SH basis on the sphere and introduces spectral leakage. According to Slobbe et al. (2012), this error does not smoothly approach zero as the regional domain size increases. Thus, if the RSHTP approach is to be applied in a pure forward modeling from GGM and topography data global SH analysis is indispensable. On the other hand, as shown in Sect. 5.1, the regional approach appears indeed viable in RCR computations. In this real-world example, the total effect of the fixed-area computation (see Fig. 4) is acceptable and does not significantly affect the RCR results compared to the RTM approach (Tables 1, 2, 3, 4).

6.5 Pros of the classic RTM

The far-zone effect of the classic RTM converges to zero, thus a fixed integration radius can be used (significantly larger for the potential than for the gravity) instead of a fixed-area computation. However, the additional HC in terms of the height anomaly is still not yet implemented, e.g., in the widely used TC program of the GRAVSOFT package (Forsberg and Tscherning 2014). Thus, we recommend to check whether this is the case for any specific software in use. Adding it manually is straightforward, either directly in the source code or evaluated separately based on simple algebraic operations on the DEM grids.

6.6 Cons of the classic RTM

In practical terms, the concept of the RTM surface complicates the handling of different large-scale density contrasts which may appear simultaneously and contribute equally to the long-wavelength signal in the GGM. A prominent example for this are the polar regions with ocean bathymetry, ice caps and subglacial lakes. If applied rigorously, i. e., no approximation like rock-equivalent topography etc. is introduced, these density contrasts can be conveniently taken into account by considering individual RTM surfaces for each interface (e.g., rock/ice, ice/water, water/air) (Schwabe et al. 2014). Although these interfaces can be stacked, thereby even coinciding in places (for example, rock/ice and ice/air interface would coincide over the ice-free mountains of Antarctica), for very localized features (smaller lakes, glaciers) this quickly becomes numerically inefficient. An alternative would be to apply the RTM only to large-scale features, similar to the topography/bathymetry where the so-called “marine convention” is frequently used, and then to remove and restore local density anomalies to their complete topographic effect.

Furthermore, the classic RTM approach requires explicit computation of the RTM surface and of the RTM reduction in the space domain for each desired spectral resolution of the RTM (usually according to $n_\text {max}$ of the GGM). In case of the SH-filtered reference topography this implies not only an additional SH analysis but also an additional subsequent SH synthesis for the heights. As discussed above, the advantage of the RSHTP approach in that regard is that the $n_\text {max}$ of the SH topographic potential can be simply changed in the joint SH synthesis with the GGM term as long as the coefficients according to Eq. (17) for a certain DEM have been precomputed once up to an arbitrary desired SH degree.

7 Conclusions

With this novel approach to model the topographic effect we present an alternative to the classic RTM method in remove-compute-restore computations of the quasigeoid. The residual spherical harmonic topographic potential (RSHTP) technique avoids the HC equally for all functionals of the gravity field. It can be considered as a generalization of the “RTM baseline technique” as described by Rexer et al. (2018) and Hirt et al. (2019), where the full-scale effect of the topography in the space domain is combined with an expansion of the topographic potential into spherical harmonics. However, while the “RTM baseline technique” implies a convolution of the topographic height function H, RSHTP makes direct use of a truncated SH expansion of the tesseroid formula, which can be computed analytically.

A case study in the region of the central European Alps demonstrated the practical feasibility of the RSHTP method. This is based on real gravity data in the region of the Swiss and Austrian Alps and external validation of the quasigeoid solutions against independent GNSS/leveling data. Although the intention was primarily to showcase the contribution to improved gravity and quasigeoid computations, it could be just as well applied to, e.g., deflections of the vertical or gravity gradients. This will potentially support the improved prediction or forward modeling of a set of gravity field functionals, e.g., in updates of regional or global data products such as GGMplus (Hirt et al. 2013).

Furthermore, the validity of the classic RTM with HC approach in quasigeoid computations was investigated. All taken together, the significance of the HC for the height anomaly according to Klees et al. (2023) in deep mountain valleys could be confirmed. In our example, the RTM method provides results consistent with the RSHTP method at the centimeter level (i. e., standard deviation better 2 cm, max. residuals better 5 cm in most cases), apart from edge effects and data gaps. On the other hand, neglecting the HC for the height anomalies leads to a systematic bias in the deep valleys of up to 10–20 cm, which is reflected in asymmetric histograms of GNSS/leveling residuals. Thus, the long-accepted assumption that the HC for height anomalies is negligible (Forsberg and Tscherning 1981) is finally disproven.

In principle, the RSHTP reduction is also valid at all interior points within the considered topography. In this context, some similarity with the topographic bias as described by Ågren (2004) is obvious. Thus, Eq. (23) should be readily applicable also to derive the disturbing potential at the geoid, provided the method applied in the compute step includes any form of downward continuation of the residual gravity field down to the geoid. It is planned to study this aspect further in the upcoming activities for the European Alps Geoid project (EAlpG).

Finally, optimized implementation of the technique taking into account both theoretical and practical aspects remains for future investigations.

Proposal for corrections to Wichiencharoen (1982)

Based on MacMillan (1958, pp. 36–39), Wichiencharoen (1982, Table 1) compiled the potential $V'$ and attraction $A'$ on the inner and outer boundary of a spherical shell. The purpose was to study the indirect effect on the geoid, thus, the lower boundary (computation point $P_0$) is the geoid, approximated by a sphere with the mean Earth radius R, and the upper boundary (computation point P) is $r=R+h_p$. Also presented are formulas for the respective effects $V'_s$, $A'_s$ if the spherical shell is condensed at the lower boundary. k (G) is Newton’s gravitational constant, $M_s$ is the total mass of the spherical shell, and an auxiliary variable is defined as $u = h_p / R$. Furthermore, Taylor expansions for $(1+u)^{-1}$ and $(1+u)^{-2}$ are used.

Table 5 Proposal for corrections to Wichiencharoen (1982, Table 1)

It should be noted that the report contains some significant errors:

• Equations 22 and 28 According to the sign convention in Eq. (20), the attraction $A'$ is defined as the gravitational effect $-\frac{\partial V}{\partial r}$. Then, Eqs. (21), (22) and (28) should have a positive sign on the right-hand side, respectively. In Table 1, $A'$ at P has the correct sign if written as $\frac{k M_s}{\left( R+h_p\right) ^2}$ but not if written as $4\pi k \rho h_p \cdot \left( \dots \right)$. Note however that MacMillan (1958, p. 39) defines his attraction A positive toward the center as $\frac{\partial V}{\partial r}$.

• Equation 26 Equation (24) uses the formula derived by MacMillan (1958, p. 39) for the potential in a running point between the two bounding spheres, i. e., inside the masses of the spherical shell. Inserting $r=R$, Eq. (25) for the potential $V'$ in $P_0$ is correctly obtained. However, instead of going out from Eq. (24) again and then inserting $r=R$, the derivative is applied to Eq. (25). Hence, the substantial conclusion from MacMillan (1958, pp. 36–39) that inside the spherical shell the attraction is

  $$\begin{aligned} A' = -\frac{\partial V'}{\partial r} = -\frac{4}{3}\pi k \rho \left( \frac{R^3}{r^2}-r\right) , \end{aligned}$$

  (A1)

  and therefore $A'$ must vanish in $P_0$, is ignored.

• Table 1 $V' - V'_s$

  In the simplified formula, the term $\frac{u}{3}$ is neglected without indication.

To summarize, we propose that Wichiencharoen (1982, Table 1) should read as presented in Table 5.