A new method of variational Bayesian slip distribution inversion

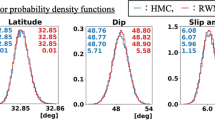
Abstract

For slip distribution inversion with Bayesian theory, traditionally, the Markov Chain Monte Carlo (MCMC) method is well applied to generate a posterior probability density function with a sampling strategy. However, its computational cost may be expensive, and it fails to accommodate large volume data sets and estimate higher dimensional parameters of interest. In this study, we introduce variational inference theory into the study of coseismic slip distribution, and present a variational Bayesian slip distribution inversion approach. Furthermore, synthetic tests show that the variational Bayesian approach can efficiently and accurately invert the designed slip distribution; therefore, we conclude that the proposed algorithm is appropriate to invert the slip distribution parameters, which might be superior to MCMC sampling due to its excellent convergence speed and low computational burden. Taking the Dingri earthquake on March 20, 2020, as an example, we further verify the practicability of the variational Bayesian method in actual earthquakes. Additionally, the inversion results show that the main fault slip region of the Dingri earthquake occurs at depths of 2 ~ 8 km on the surface, the maximum slip amount is 0.54 m, and the coseismic release seismic moment is 5.58 × 10¹⁷ Nm, corresponding to a moment magnitude of Mw 5.79.

Appendices

Appendix A

• I. The relevant definitions of variational inference are expounded from the perspective of Bayesian theory (Jordan et al. 1999; Blei et al. 2017):

  $$ p({\mathbf{m}}|{\mathbf{d}}) = \frac{{p({\mathbf{d}}|{\mathbf{m}})p({\mathbf{m}})}}{{p({\mathbf{d}})}} = \frac{{p({\mathbf{m}},{\mathbf{d}})}}{{p({\mathbf{d}})}} $$

  (A1)

  where $p({\mathbf{d}})$ is expressed as follows:

  $$ p({\mathbf{d}}) = \frac{{p({\mathbf{m}},{\mathbf{d}})}}{{p({\mathbf{m}}|{\mathbf{d}})}} $$

  (A1.1)

  Take logarithmic form on both sides of the Eq. (A1.1):

  $$ \begin{aligned} \log p({\mathbf{d}}) = & \log p({\mathbf{m}},{\mathbf{d}}) - \log p({\mathbf{m}}|{\mathbf{d}}) \\ = & \log (\frac{{p({\mathbf{m}},{\mathbf{d}})}}{{q({\mathbf{m}})}}) - \log (\frac{{p({\mathbf{m}}|{\mathbf{d}})}}{{q({\mathbf{m}})}}) \\ \end{aligned} $$

  (A1.2)

  Solve the expectation for ${\mathbf{m}}$ on both sides of the Eq.(A1.2):

  $$ \begin{aligned} \int\nolimits_{{\mathbf{m}}}{\log p({\mathbf{d}})} q({\mathbf{m}})d{\mathbf{m}} = &\int\nolimits_{{\mathbf{m}}} {q({\mathbf{m}})} \log (\frac{{p({\mathbf{m}},{\mathbf{d}})}}{{q({\mathbf{m}})}})d{\mathbf{m}}\\&- \int\nolimits_{{\mathbf{m}}} {q({\mathbf{m}})} \log (\frac{{p({\mathbf{m}}|{\mathbf{d}})}}{{q({\mathbf{m}})}})d{\mathbf{m}}\\ \log p({\mathbf{d}}) = & \int\nolimits_{{\mathbf{m}}}{q({\mathbf{m}})} \log (p({\mathbf{m}},{\mathbf{d}}))d{\mathbf{m}} \\&-\int\nolimits_{{\mathbf{m}}} {q({\mathbf{m}})} \log (q({\mathbf{m}}))d{\mathbf{m}} \\ & - \int\nolimits_{{\mathbf{m}}}{q({\mathbf{m}})} \log (\frac{{p({\mathbf{m}}|{\mathbf{d}})}}{{q({\mathbf{m}})}})d{\mathbf{m}}\\ \end{aligned} $$

  (A1.3)

  where,$q({\mathbf{m}})$is defined as the variational distribution, which is used to approximate the posterior distribution, $p({\mathbf{m}}|{\mathbf{d}})$;$\log p({\mathbf{d}})$ is defined as the evidence term, which is a constant; $\int\nolimits_{{\mathbf{m}}} {q({\mathbf{m}})}\log (p({\mathbf{m}},{\mathbf{d}}))d{\mathbf{m}} -\int\nolimits_{{\mathbf{m}}} {q({\mathbf{m}})} \log (q({\mathbf{m}}))d{\mathbf{m}}$is defined as the Evidence Lower Bound (ELBO), recorded as ${\text{ELBO(}}q{)}$(Blei et al. 2017):

  $$ \begin{aligned} {\text{ELBO(}}q{)} =\, &\int\nolimits_{{\mathbf{m}}} {q({\mathbf{m}})} \log (p({\mathbf{m}},{\mathbf{d}}))d{\mathbf{m}}\\& -\int\nolimits_{{\mathbf{m}}} {q({\mathbf{m}})} \log (q({\mathbf{m}}))d{\mathbf{m}} \\ =\, & {\text{E}}_{q} [\log p({\mathbf{m}},{\mathbf{d}})] - {\text{E}}_{q} [\log q({\mathbf{m}})] \\ \end{aligned}$$

  (A1.4)

  and $-\int\nolimits_{{\mathbf{m}}} {q({\mathbf{m}})} \log (\frac{{p({\mathbf{m}}|{\mathbf{d}})}}{{q({\mathbf{m}})}})d{\mathbf{m}}$is defined as the Kullback–Leibler (KL) divergence, which represents the closeness, or distance, of the variational distribution,$q({\mathbf{m}})$,to the posterior distribution, $p({\mathbf{m}}|{\mathbf{d}})$,recorded as ${\text{KL}}[q({\mathbf{m}})||p({\mathbf{m}}|{\mathbf{d}})]$(Kullback and Leibler 1951):

  $$ \begin{aligned}{\text{KL}}[q({\mathbf{m}})||p({\mathbf{m}}|{\mathbf{d}})] =\, & -\int\nolimits_{{\mathbf{m}}} {q({\mathbf{m}})} \log (\frac{{p({\mathbf{m}}|{\mathbf{d}})}}{{q({\mathbf{m}})}})d{\mathbf{m}}\\ =\, & {\text{E}}_{q} [\log q({\mathbf{m}})] - {\text{E}}_{q} [\log p({\mathbf{m}}|{\mathbf{d}})] \\ \end{aligned}$$

  (A1.5)

• II. From the perspective of the mean field approximation method, to prove that maximizing the ELBO is equivalent to minimizing the KL divergence. Expound the principle that the variational distribution approximates the posterior probability distribution of the parameters to be solved (Bishop 2006; Blei et al. 2017).

  The Evidence Lower Bound,${\text{ELBO(}}q{)}$, can be expressed as follows:

  $$ \begin{aligned} {\text{ELBO(}}q{)} =\, &{\text{E}}_{q} [\log p({\mathbf{m}},{\mathbf{d}})] - {\text{E}}_{q}[\log q({\mathbf{m}})] \\ = \,& \int_{{\mathbf{m}}} {q({\mathbf{m}})}\log (p({\mathbf{m}},{\mathbf{d}}))d{\mathbf{m}}\\& -\int_{{\mathbf{m}}} {q({\mathbf{m}})} \log (q({\mathbf{m}}))d{\mathbf{m}} \\ = & \int {\prod\limits_{i = 1}^{n}{q_{i} (m_{i} )} } \log (p({\mathbf{m}},{\mathbf{d}}))d{\mathbf{m}}\\&- \int {\prod\limits_{i = 1}^{n} {q_{i} (m_{i} )} } \sum\limits_{i =1}^{n} {\log (q_{i} (m_{i} )} )d{\mathbf{m}} \\ \end{aligned}$$

  (A2)

  Considering the simplification of formula derivation, we denote the first and second items on the right end of the formula (A2) as part1 and part2, respectively.

  $$ \begin{aligned} {\text{part1}} = & \int {\prod\limits_{i = 1}^{n} {q_{i} (m_{i} )} } \log (p({\mathbf{m}},{\mathbf{d}}))d{\mathbf{m}} \\ = & \int_{{m_{1} }} {\int_{{m_{2} }} { \cdots \int_{{m_{n} }} {\prod\limits_{i = 1}^{n} {q_{i} (m_{i} )} } } } \log (p({\mathbf{m}},{\mathbf{d}})dm_{1} dm_{2} \cdots dm_{n} \\ = & \int_{{m_{j} }} {q_{j} } (m_{j} )(\int_{{m_{i \ne j} }} { \cdots \int {\log (p({\mathbf{m}},{\mathbf{d}})} } \prod\limits_{i \ne j}^{n} {q_{i} (m_{i} )} dm_{i} )dm_{j} \\ = & \int_{{m_{j} }} {q_{j} } (m_{j} ){\text{E}}_{{q(\nabla m_{j} )}} [\log (p({\mathbf{m}},{\mathbf{d}})]dm_{j} \\ \end{aligned} $$

  (A2.1)

  where ${\text{E}}_{{q(\nabla m_{j} )}}$ represents the expectation of other parameters except for the j-th type parameter.

  $$ \begin{aligned} {\text{part2}} = & \int {\prod\limits_{i = 1}^{n} {q_{i} (m_{i} )} } \sum\limits_{i = 1}^{n} {\log (q_{i} (m_{i} )} )d{\mathbf{m}} \\ = & \sum\limits_{i = 1}^{n} {\left( {\int_{{m_{i} }} {q_{i} (m_{i} )} \log (q_{i} (m_{i} ))dm_{i} } \right)} \\ \end{aligned} $$

  (A2.2)

  In part2, for the variational approximation of the posterior distribution of the specified parameter,$m_{j}$, the cumulative sum of the remaining items in the sequence can be regarded as a constant and denoted as ${\text{const}}{.}$. Thus, part2 can be expressed as follows:

  $$ {\text{part2}} = \int_{{m_{j} }} {q_{j} (m_{j} )} \log (q_{j} (m_{j} ))dm_{j} + {\text{const}}{.} $$

  (A2.3)

  Hence, the Evidence Lower Bound,${\text{ELBO(}}q_{j} {)}$, only related to $m_{j}$ can be simplified as follows:

  $$ \begin{aligned} {\text{ELBO(}}q_{j} {)} =\, &{\text{part1 - part2}} \\ =\, & \int_{{m_{j} }} {q_{j} } (m_{j}){\text{E}}_{{\nabla m_{j} }} [\log (p({\mathbf{m}},{\mathbf{d}})]dm_{j} \\&- \int_{{m_{j} }} {q_{j} (m_{j})} \log (q_{j} (m_{j} ))dm_{j} + {\text{const}}{.} \\ \end{aligned}$$

  (A2.4)

  At this time, we assume that ${\text{log(}}\tilde{p}_{j} {(}m_{j} {,}{\mathbf{d}}{))} = {\text{E}}_{{q(\nabla m_{j} )}} [\log (p({\mathbf{m}},{\mathbf{d}})]$,then

  $$ \begin{aligned} {\text{ELBO(}}q_{j} {)} = &\int_{{m_{j} }} {q_{j} } (m_{j} ){\text{log(}}\tilde{p}_{j} {(}m_{j}{,}{\mathbf{d}}{))}dm_{j} \\&- \int_{{m_{j} }} {q_{j} (m_{j} )} \log (q_{j} (m_{j} ))dm_{j} + {\text{const}}{.} \\ = & {\text{E}}_{{q_{j}}} [{\text{log(}}\tilde{p}_{j} {(}m_{j} {,}{\mathbf{d}}{))}] \\&-{\text{E}}_{{q_{j} }} [\log (q_{j} (m_{j} ))] + {\text{const}}{.} \\= & - {\text{KL[}}q_{j} (m_{j} )||\tilde{p}_{j} {(}m_{j}{|}{\mathbf{d}}{)]} + {\text{const}}{.} \\ \end{aligned}$$

  (A2.5)

  Since KL divergence is non-negative, maximizing the ELBO means that KL divergence is zero. At this time, the variational distribution fully approximates the posterior probability distribution of the parameters to be solved. That is, the following relationship is satisfied:

  $$ \log (q_{j} (m_{j} )) = {\text{log(}}\tilde{p}_{j} {(}m_{j} {,}{\mathbf{d}}{))} = {\text{E}}_{{q(\nabla m_{j} )}} [\log (p({\mathbf{m}},{\mathbf{d}}))] $$

  (A2.6)

Appendix B

• I. The detailed formula of the variational distribution,$q({\mathbf{s}})$, corresponding to the slip parameter,${\mathbf{s}}$, is derived as follows:

  $$ \begin{aligned} \log q({\mathbf{s}}) =\, & {\text{E}}_{{q(\nabla {\mathbf{s}})}} \left[ {\log p({\mathbf{s}},{{\varvec{\upsigma}}}^{2} ,\alpha^{2} ,{\mathbf{d}})} \right] \\ =\, & {\text{E}}_{{q(\nabla {\mathbf{s}})}} \left[ {\log p({\mathbf{d}}|{\mathbf{s}},{{\varvec{\upsigma}}}^{2} ) + \log p({\mathbf{s}}|\alpha^{2} )} \right] \\ =\, & {\text{E}}_{{q(\nabla {\mathbf{s}})}} \left[ {\log p({\mathbf{d}}|{\mathbf{s}},{{\varvec{\upsigma}}}^{2} )] + {\text{E}}_{{q(\nabla {\mathbf{s}})}} [\log p({\mathbf{s}}|\alpha^{2} )} \right] \\ \end{aligned} $$

  (B1)

  where ${\text{E}}_{{q(\nabla {\mathbf{s}})}} [\log p({\mathbf{d}}|{\mathbf{s}},{{\varvec{\upsigma}}}^{2} )]$ and ${\text{E}}_{{q(\nabla {\mathbf{s}})}} [\log p({\mathbf{s}}|\alpha^{2} )]$ are given by

  $$ \begin{aligned} &{\text{E}}_{{q(\nabla {\mathbf{s}})}} [\log p({\mathbf{d}}|{\mathbf{s}},{{\varvec{\upsigma}}}^{2} )] \\&\quad={\text{E}}_{{q(\nabla {\mathbf{s}})}} \left[ \log \left\{\prod\limits_{k = 1}^{K} \exp \left[ - \tfrac{{\sigma_{k}^{2}}}{2}({\mathbf{d}}{}_{k} \right.\right.\right.\\&\qquad\left.\left.\left.- {\mathbf{G}}_{k} {\mathbf{s}})^{T}(\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1} ({\mathbf{d}}_{k} -{\mathbf{G}}_{k} {\mathbf{s}}) \right] \right\} \right] +{\text{const}}. \\&\quad= {\text{E}}_{{q(\nabla {\mathbf{s}})}} \left[\sum\limits_{k = 1}^{K} \left( - \tfrac{{\sigma_{k}^{2}}}{2}({\mathbf{d}}{}_{k}\right.\right.\\&\left.\left. - {\mathbf{G}}_{k} {\mathbf{s}})^{T}(\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1} ({\mathbf{d}}_{k} -{\mathbf{G}}_{k} {\mathbf{s}}) \right) \right] + {\text{const}}.\\&\quad= - \frac{1}{2}\sum\limits_{k = 1}^{K} \left\{{\text{E}}({{\varvec{\upsigma}}}_{k}^{2} )({\mathbf{d}}{}_{k}^{T}(\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1} {\mathbf{d}}_{k} -{\mathbf{d}}{}_{k}^{T} (\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1}{\mathbf{G}}_{k} {\mathbf{s}} \right.\\&\qquad\left.- {\mathbf{s}}^{T}{\mathbf{G}}_{k}^{T} (\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1}{\mathbf{d}}_{k} + {\mathbf{s}}^{T} {\mathbf{G}}_{k}^{T}(\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1} {\mathbf{G}}_{k} {\mathbf{s}})\right\} + {\text{const}}. \\ &\quad= - \frac{1}{2}\sum\limits_{k =1}^{K} \left\{ {\text{E(}}{{\varvec{\upsigma}}}_{k}^{2}{)}{\mathbf{s}}^{T} {\mathbf{G}}_{k}^{T} (\sum\nolimits_{{\mathbf{d}}}^{k})^{ - 1} {\mathbf{G}}_{k} {\mathbf{s}} \right.\\&\qquad\left.-2{\text{E(}}{{\varvec{\upsigma}}}_{k}^{2} {)}{\mathbf{s}}^{T}{\mathbf{G}}_{k}^{T} (\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1}{\mathbf{d}}_{k} \right\} + {\text{const}}. \\ \end{aligned}$$

  (B1.1)

  and

  $$ \begin{aligned}&{\text{E}}_{{q(\nabla {\mathbf{s}})}} [\log p({\mathbf{s}}|\alpha^{2} )]\\&\quad ={\text{E}}_{{q(\nabla {\mathbf{s}})}} \left[ {\log (\exp [ -\frac{{\alpha^{2} }}{2}({\mathbf{Ls}})^{T} {\mathbf{Ls}}])} \right]+ {\text{const}}. \\&\quad= {\text{E}}_{{q(\nabla {\mathbf{s}})}}\left[ { - \frac{{\alpha^{2} }}{2}({\mathbf{Ls}})^{T} {\mathbf{Ls}}}\right] + {\text{const}}. \\&\quad = - \frac{1}{2}{\text{E}}(\alpha^{2}){\mathbf{s}}^{T} {\mathbf{L}}^{T} {\mathbf{Ls}} + {\text{const}}.\\\end{aligned} $$

  (B1.2)

  Finally, substituting the Eqs. (B1.1) and (B1.2) into the Eq. (B1), the logarithmic form of the analytical solution of the variational distribution,$q({\mathbf{s}})$,can be expressed as follows:

  $$ \begin{aligned}\log q({\mathbf{s}}) =\, &{\text{E}}_{{q(\nabla {\mathbf{s}})}} [\log p({\mathbf{d}}|{\mathbf{s}},{{\varvec{\upsigma}}}^{2} )] \\&+{\text{E}}_{{q(\nabla {\mathbf{s}})}} [\log p({\mathbf{s}}|\alpha^{2} )] \\= & - \frac{1}{2}\sum\limits_{k =1}^{K} \{ {\text{E}}({{\varvec{\upsigma}}}_{k}^{2}){\mathbf{s}}^{T} {\mathbf{G}}_{k}^{T} (\sum\nolimits_{{\mathbf{d}}}^{k})^{ - 1} {\mathbf{G}}_{k} {\mathbf{s}} \\&-2{\text{E}}({{\varvec{\upsigma}}}_{k}^{2} ){\mathbf{s}}^{T}{\mathbf{G}}_{k}^{T} (\sum\nolimits_{{\mathbf{d}}}^{k})^{ - 1}{\mathbf{d}}_{k} \}\\& + \left( { - \frac{1}{2}{\text{E}}(\alpha^{2}){\mathbf{s}}^{T} {\mathbf{L}}^{T} {\mathbf{Ls}}} \right) +{\text{const}}. \\= & - \frac{1}{2}\left\{ {\mathbf{s}}^{T}\sum\limits_{k = 1}^{K} {\text{E}}({{\varvec{\upsigma}}}_{k}^{2}){\mathbf{G}}_{k}^{T} (\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1}{\mathbf{G}}_{k} {\mathbf{s}} + {\mathbf{s}}^{T}{\text{E}}(\alpha^{2} ) {\mathbf{L}}^{T} {\mathbf{Ls}}\right.\\&\left. -2\sum\limits_{k = 1}^{K} {({\text{E(}}{{\varvec{\upsigma}}}_{k}^{2}{)}{\mathbf{s}}^{T} {\mathbf{G}}_{k}^{T} (\sum\nolimits_{{\mathbf{d}}}^{k})^{ - 1} {\mathbf{d}}_{k} )} \right\} + {\text{const}}. \\= & -\frac{1}{2}\left\{ {\mathbf{s}}^{T} (\sum\limits_{k = 1}^{K}{{\text{E}}({{\varvec{\upsigma}}}_{k}^{2} ){\mathbf{G}}_{k}^{T}(\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1} {\mathbf{G}}_{k} +{\text{E}}(\alpha^{2} )} {\mathbf{L}}^{T} {\mathbf{L}}){\mathbf{s}}\right.\\&\left.- 2\sum\limits_{k = 1}^{K}{({\text{E}}({{\varvec{\upsigma}}}_{k}^{2} ){\mathbf{s}}^{T}{\mathbf{G}}_{k}^{T} (\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1}{\mathbf{d}}_{k} )} \right\} + {\text{const}}. \\\end{aligned}$$

  (B1.3)

• II. The detailed formula of the variational distribution,$q({{\varvec{\upsigma}}}^{2} )$, of the hyperparameter,${{\varvec{\upsigma}}}^{2}$, is derived as follows:

  $$ \begin{aligned} \log q({{\varvec{\upsigma}}}^{2} ) =\, & {\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}} [\log p({\mathbf{s}},{{\varvec{\upsigma}}}^{2} ,\alpha^{2} ,{\mathbf{d}})] \\ =\, & {\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}} [\log p({\mathbf{d}}|{\mathbf{s}},{{\varvec{\upsigma}}}^{2} ) + \log p({{\varvec{\upsigma}}}^{2} )] \\ =\, & {\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}} [\log p({\mathbf{d}}|{\mathbf{s}},{{\varvec{\upsigma}}}^{2} )] + {\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}} [\log p({{\varvec{\upsigma}}}^{2} )] \\ \end{aligned} $$

  (B2)

  where ${\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}} [\log p({\mathbf{d}}|{\mathbf{s}},{{\varvec{\upsigma}}}^{2} )]$ is given by

  $$\begin{aligned} &{\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}} [\log p({\mathbf{d}}|{\mathbf{s}},{{\varvec{\upsigma}}}^{2} )] \\&\quad={\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}} \left[ \log \left( {\prod\limits_{k = 1}^{K} {(\sigma_{k}^{2} )^{{{{N_{k} }\mathord{\left/ {\vphantom {{N_{k} } 2}} \right. \kern-0pt} 2}}} } }\right)\right.\\&\qquad+ \log \left( \prod\limits_{k = 1}^{K} \exp [ -\tfrac{{\sigma_{k}^{2} }}{2}({\mathbf{d}}{}_{k} - {\mathbf{G}}_{k}{\mathbf{s}})^{T} \right.\\&\qquad\left.\left.(\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1}({\mathbf{d}}_{k} - {\mathbf{G}}_{k} {\mathbf{s}})] \right)\right] + {\text{const}}{.} \\&\quad = {\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}} \left[ \sum\limits_{k = 1}^{K}\left\{ \frac{{N_{k} }}{2}\log (\sigma_{k}^{2} ) -\tfrac{{\sigma_{k}^{2} }}{2}({\mathbf{d}}{}_{k} - {\mathbf{G}}_{k}{\mathbf{s}})^{T} \right.\right.\\&\qquad\left.\left.(\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1}({\mathbf{d}}_{k} - {\mathbf{G}}_{k} {\mathbf{s}}) \right\}\right] + {\text{const}}{.} \\&\quad= \sum\limits_{k = 1}^{K} \left\{\frac{{N_{k} }}{2}\log (\sigma_{k}^{2} ) - \tfrac{{\sigma_{k}^{2}}}{2}{\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}}[({\mathbf{d}}{}_{k} - {\mathbf{G}}_{k} {\mathbf{s}})^{T}\right.\\&\qquad\left.(\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1} ({\mathbf{d}}_{k} -{\mathbf{G}}_{k} {\mathbf{s}})] \right\} + {\text{const}}{.} \\\end{aligned}$$

  (B2.1)

  where ${\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}} {[}({\mathbf{d}}{}_{k} -{\mathbf{G}}_{k} {\mathbf{s}})^{T} (\sum_{{\mathbf{d}}}^{k} )^{ - 1}({\mathbf{d}}_{k} - {\mathbf{G}}_{k} {\mathbf{s}}){]}$ can be expanded and the specific content is as follows:

  $$\begin{aligned}& {\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}} [({\mathbf{d}}{}_{k} -{\mathbf{G}}_{k} {\mathbf{s}})^{T} (\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1}({\mathbf{d}}_{k} - {\mathbf{G}}_{k} {\mathbf{s}})]\\&\quad ={\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}}[{\mathbf{d}}{}_{k}^{T} (\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1}{\mathbf{d}}_{k} - 2{\mathbf{d}}{}_{k}^{T}\\&\qquad (\sum\nolimits_{{\mathbf{d}}}^{k})^{ - 1} {\mathbf{G}}_{k} {\mathbf{s}} + {\mathbf{s}}^{T}{\mathbf{G}}_{k}^{T} (\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1}{\mathbf{G}}_{k} {\mathbf{s}}] \\ &\quad= {\mathbf{d}}{}_{k}^{T}(\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1} {\mathbf{d}}_{k} -2{\mathbf{d}}{}_{k}^{T} (\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1}\\&\qquad{\mathbf{G}}_{k} {\text{E}}({\mathbf{s}}) +{\text{E}}({\mathbf{s}}^{T} {\mathbf{G}}_{k}^{T}(\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1} {\mathbf{G}}_{k} {\mathbf{s}})\\ \end{aligned}$$

  (B2.2)

  From the expectation calculation formula of quadratic form ${\mathbf{Y}}^{T}{\mathbf{RY}}$, we know that ${\text{E(}}{\mathbf{Y}}^{T} {\mathbf{RY}}) =tr({\mathbf{R}}{\text{D}}({\mathbf{Y}})) +{\text{E(}}{\mathbf{Y}}{)}^{T} {\mathbf{R}}{\text{E(}}{\mathbf{Y}}{)}$, where ${\mathbf{R}}$ is a known invertible matrix, and ${\text{E(}}{\mathbf{Y}}{)}$and ${\text{D}}({\mathbf{Y}})$ are the expectation and variance of vector ${\mathbf{Y}}$,respectively. Therefore, ${\text{E(}}{\mathbf{s}}^{T}{\mathbf{G}}_{k}^{T} (\sum_{{\mathbf{d}}}^{k} )^{ - 1}{\mathbf{G}}_{k}{\mathbf{s}}{)}$ is given by

  $$\begin{aligned} {\text{E(}}{\mathbf{s}}^{T}{\mathbf{G}}_{k}^{T} (\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1}{\mathbf{G}}_{k} {\mathbf{s}}{)} =\,& tr({\mathbf{G}}_{k}^{T}(\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1} {\mathbf{G}}_{k}{\text{D}}({\mathbf{s}})) \\&+ {\text{E(}}{\mathbf{s}}{)}^{T}{\mathbf{G}}_{k}^{T} (\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1}{\mathbf{G}}_{k} {\text{E(}}{\mathbf{s}}{)}\end{aligned}$$

  (B2.3)

  Hence, the final expression of ${\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}} [\log p({\mathbf{d}}|{\mathbf{s}},{{\varvec{\upsigma}}}^{2})]$ is as follows:

  $$ \begin{aligned}& {\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}} [\log p({\mathbf{d}}|{\mathbf{s}},{{\varvec{\upsigma}}}^{2} )] \\&\quad=\,\sum\limits_{k = 1}^{K} \left\{ \frac{{N_{k} }}{2}\log (\sigma_{k}^{2} ) - \tfrac{{\sigma_{k}^{2}}}{2}({\mathbf{d}}{}_{k}^{T} (\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1}{\mathbf{d}}_{k} \right.\hfill \\&- 2{\mathbf{d}}{}_{k}^{T} (\sum\nolimits_{{\mathbf{d}}}^{k})^{ - 1} {\mathbf{G}}_{k} {\text{E}}({\mathbf{s}})+ \;tr({\mathbf{G}}_{k}^{T} (\sum\nolimits_{{\mathbf{d}}}^{k})^{ - 1} {\mathbf{G}}_{k} {\text{D}}({\mathbf{s}})) \\&\left. +{\text{E}}({\mathbf{s}})^{T} {\mathbf{G}}_{k}^{T}(\sum\nolimits_{{\mathbf{d}}}^{k} )^{ - 1} {\mathbf{G}}_{k}{\text{E}}({\mathbf{s}})) \right\} + {\text{const}}{.} \hfill \\\end{aligned} $$

  (B2.4)

  In Eq. (A2), the calculation formula of ${\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}} [\log p({{\varvec{\upsigma}}}^{2})]$ is given by

  $$ \begin{aligned} &{\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}} [\log p({{\varvec{\upsigma}}}^{2} )] \\&\quad= {\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}} \left[ \log \left( \prod\limits_{k = 1}^{K} {(({{\varvec{\upsigma}}}_{k}^{2})^{{a_{k} - 1}} )} ) \right.\right.\\&\qquad\left.\left.+ \prod\limits_{k = 1}^{K} \exp ( -{\text{b}}_{k} {{\varvec{\upsigma}}}_{k}^{2} \right) \right] +{\text{const}}{.} \\ &\quad= {\text{E}}_{{q(\nabla {{\varvec{\upsigma}}}^{2} )}} \left[ {\sum\limits_{k = 1}^{K}{\left\{ {(a_{k} - 1)\log ({{\varvec{\upsigma}}}_{k}^{2} ) -{\text{b}}_{k} {{\varvec{\upsigma}}}_{k}^{2} } \right\}} } \right] +{\text{const}}{.} \\ &\quad= (a_{k} - 1)\log ({{\varvec{\upsigma}}}_{k}^{2} ) - {\text{b}}_{k}{{\varvec{\upsigma}}}_{k}^{2} \\ \end{aligned}$$

  (B2.5)

  Finally, substituting the Eqs. (B2.4) and (B2.5) into the Eq. (B2), the logarithmic form of the analytical solution of the variational distribution,$q({{\varvec{\upsigma}}}^{2})$, can be expressed as follows:

  $$ \begin{gathered} \log q({\varvec{\upsigma}}^{2} ) = {\text{E}}_{{q(\nabla {\varvec{\upsigma }}^{2} )}} [\log p({\mathbf{d}}|{\mathbf{s}},{\varvec{\upsigma }}^{2} )] + {\text{E}}_{{q(\nabla {\varvec{\upsigma }}^{2} )}} [\log p({\varvec{\upsigma }}^{2} )] \hfill \\ \quad \quad \quad \quad = \sum\limits_{{k = 1}}^{K} {\left\{ {\left( {\frac{{N_{k} }}{2} + a{}_{k} - 1} \right)\log (\sigma _{k} ^{2} ) - \left( {\frac{1}{2}{\mathbf{d}}_{k} ^{T} \left( {\sum\nolimits_{{\mathbf{d}}}^{k} } \right)^{{ - 1}} {\mathbf{d}}_{k} - {\mathbf{d}}_{k} ^{T} \left( {\sum\nolimits_{{\mathbf{d}}}^{k} } \right)^{{ - 1}} {\mathbf{G}}_{k} {\text{E(}}{\mathbf{s}})} \right.} \right.} \hfill \\ \quad \quad \quad \quad \quad \quad \left. {\left. { + \frac{1}{2}tr({\mathbf{G}}_{k} ^{T} \left(\sum\nolimits_{{\mathbf{d}}}^{k} \right)^{{ - 1}} {\mathbf{G}}_{k} {\text{D}}({\mathbf{s}})) + \frac{1}{2}{\text{E(}}{\mathbf{s}})^{T} {\mathbf{G}}_{k} ^{T} \left( {\sum\nolimits_{{\mathbf{d}}}^{k} } \right)^{{ - 1}} {\mathbf{G}}_{k} {\text{E(}}{\mathbf{s}}) + b_{k} )} \right)\sigma _{k} ^{2} } \right\} + {\text{const}}{\text{.}} \hfill \\ \end{gathered} $$

  (B2.6)

• III. The detailed formula of the variational distribution,$q(\alpha^{2} )$, of the hyperparameter,$\alpha^{2}$, is derived as follows:

  $$ \begin{aligned} \log q(\alpha^{2} ) =\, &{\text{E}}_{{q(\nabla \alpha^{2} )}} [\log p({\mathbf{s}},{{\varvec{\upsigma}}}^{2} ,\alpha^{2} ,{\mathbf{d}})]\\ =\, & {\text{E}}_{{q(\nabla \alpha^{2} )}} [\log p({\mathbf{s}},|\alpha^{2} ) + \log p(\alpha^{2} )] \\ =\, &{\text{E}}_{{q(\nabla \alpha^{2} )}} [\log p({\mathbf{s}},|\alpha^{2} )] + {\text{E}}_{{q(\nabla \alpha^{2} )}}[\log p(\alpha^{2} )] \\ \end{aligned}$$

  (B3)

  where ${\text{E}}_{{q(\nabla \alpha^{2} )}} [\log p({\mathbf{s}},|\alpha^{2} )]$and ${\text{E}}_{{q(\nabla \alpha^{2} )}} [\log p(\alpha^{2} )]$ are given by

  $$ \begin{aligned} &{\text{E}}_{{q(\nabla \alpha^{2} )}} [\log p({\mathbf{s}},|\alpha^{2} )] \\&\quad={\text{E}}_{{q(\nabla \alpha^{2} )}} \left[ {\frac{M}{2}\log (\alpha^{2} ) - \frac{{\alpha^{2} }}{2}{\mathbf{s}}^{T}{\mathbf{L}}^{T} {\mathbf{Ls}}} \right] + {\text{const}}{.} \\ &\quad=\frac{M}{2}\log (\alpha^{2} ) - \frac{{\alpha^{2}}}{2}{\text{E[}}{\mathbf{s}}^{T} {\mathbf{L}}^{T} {\mathbf{Ls}}{]} +{\text{const}}{.} \\ &\quad= \frac{M}{2}\log (\alpha^{2} ) -\frac{{\alpha^{2} }}{2}(tr({\mathbf{L}}^{T}{\mathbf{L}}{\text{D}}({\mathbf{s}})) \\&\qquad+{\text{E(}}{\mathbf{s}}{)}^{T} {\mathbf{L}}^{T}{\mathbf{L}}{\text{E(}}{\mathbf{s}}{))} + {\text{const}}{.} \\\end{aligned} $$

  (B3.1)

  and

  $$ \begin{aligned} &{\text{E}}_{{q(\nabla \alpha^{2} )}} [\log p(\alpha^{2} )] \\&\quad= {\text{E}}_{{q(\nabla \alpha^{2} )}} [(a_{0} - 1)\log (\alpha^{2} ) - b_{0} \alpha^{2} ] +{\text{const}}{.} \\ &\quad= (a_{0} - 1)\log (\alpha^{2} ) - b_{0}\alpha^{2} + {\text{const}}{.} \\ \end{aligned}$$

  (B3.2)

  Finally, substituting the Eqs. (B3.1) and (B3.2) into the Eq. (B3), the logarithmic form of the analytical solution of the variational distribution,$q(\alpha^{2})$, can be expressed as follows:

  $$ \begin{aligned} \log q(\alpha^{2} ) =\, &{\text{E}}_{{q(\nabla \alpha^{2} )}} [\log p({\mathbf{s}},|\alpha^{2} )] + {\text{E}}_{{q(\nabla \alpha^{2} )}}[\log p(\alpha^{2} )] \\ =\, & (\frac{M}{2} + a_{0} - 1)\log (\alpha^{2} ) - \left(\frac{1}{2}tr({\mathbf{L}}^{T}{\mathbf{L}}{\text{D}}({\mathbf{s}})) \right.\\&\left.+\frac{1}{2}{\text{E}}({\mathbf{s}})^{T} {\mathbf{L}}^{T}{\mathbf{L}}{\text{E}}({\mathbf{s}}) + b_{0} \right)\alpha^{2} +{\text{const}}{.} \\ \end{aligned} $$

  (B3.3)