1 Introduction

Undifferenced ambiguities of GNSS precise point positioning (PPP) are contaminated by various biases originating from both satellites and receivers (Zumberge et al. 1997). These biases are observable-specific which depend on tracking channels and observation frequencies, and divided into the code biases within pseudorange and the phase biases within carrier-phase measurements. They cannot be separated from clocks or ambiguities in a least-squares adjustment, which means that undifferenced ambiguities are bound to lose their integer properties and thus cannot be directly fixed to integers in conventional PPP. Over the past decade, it has been widely recognized that decoupling the phase biases from the undifferenced GNSS data processing is the key to the recovery of integer undifferenced ambiguities. A few approaches have ever since been well-established to compute wide-lane and narrow-lane phase biases in synergy with the legacy ionosphere-free clocks, such as the uncalibrated phase delay method (e.g., Gabor and Nerem 2002; Ge et al. 2008). Since the International GNSS Service (IGS) has begun to release phase bias products in recent years, users can introduce them along with the legacy satellite clock products into PPP to enable undifferenced ambiguity resolution (PPP-AR) (see Banville et al. 2020; Schaer et al. 2021).

An unwritten rule of using such phase bias products is that users’ PPP-AR should follow preferably the frequency choices and observable combinations prescribed by the phase bias providers. In the case of GPS, if the satellite clock and phase bias products are based specifically on the C1W/C2W pseudorange, the same observables should be ingested, as recommended, into users’ PPP-AR. This is to keep consistency between the phase biases and the PPP ambiguities, as well as the compatibility among the satellite clocks, the code and phase biases (see Geng et al. 2019; Odijk et al. 2016, among others). A dilemma is however that if one prefers GPS C1W/C5Q pseudorange and L1W/L5Q carrier-phase for PPP, for example, bias providers would be advised to re-compute their satellite clocks and phase biases using the new four observables, or adapt their legacy satellite products using a clumsy chain of differential code biases (DCBs) to fit the wide-lane, narrow-lane and ionosphere-free combinations (e.g., Elmezayen and El-Rabbany 2019; Wen et al. 2020). Although converting the satellite clocks with DCBs to match other frequency choices is achievable indeed, it has not been reported whether converting the phase biases with DCBs is feasible or not. Regarding the five Galileo and six BDS-3 frequencies of pseudorange and carrier-phase observables (i.e., E1/E5a/E5b/E5/E6 and B1C/B1I/B2a/B2b/B2/B3I), we can conceive of how inconvenient to smoothly switch among the PPP-AR for all eligible frequency choices and observable combinations.

In order to conquer this problem, Laurichesse (2015) cited the protocol of Radio Technical Commission for Maritime Services (RTCM) State Space Representation, and proposed to establish a new framework of observable-specific phase biases (phase OSBs) instead of those explicit or implicit wide-lane and narrow-lane conventions. OSBs mean that each frequency-specific pseudorange and carrier-phase has a bias correction with regard to each tracking channel of each satellite, and users simply need to subtract these biases from the raw measurements to carry out undifferenced GNSS processing. Laurichesse (2015) then mapped wide-lane phase biases and ionosphere-free integer clocks for four GPS Block IIF satellites into the phase OSBs with the aid of IGS legacy clocks and code biases. A preliminary result showed that such phase OSBs were able to recover integer L1/L5 narrow-lane ambiguities once the L1/L5 wide-lane ambiguities were resolved, though the time-variable inter-frequency clock biases (IFCBs) on the L5 carrier-phase were not mentioned therein (Montenbruck et al. 2011). Later, Liu et al. (2020) extended phase OSBs to Galileo and BDS-2 triple-frequency signals. They showed that phase OSBs could be estimated using uncombined triple-frequency PPP corrected for both pre-determined GPS IFCBs and code biases. However, they did not report whether their phase OSBs could enable GPS L1/L5 PPP-AR. In addition, Geng and Guo (2020) computed wide-lane phase OSBs for instantaneous PPP wide-lane ambiguity resolution, which cannot be applied to retrieve integer narrow-lane ambiguities though.

In recent years, the IGS has established a code OSB framework to address the biases experienced disparately by all varieties of pseudorange observables on different tracking channels (Schaer 2016). Villiger et al. (2019) integrated the ionosphere-free clock and geometry-free ionosphere analysis to estimate code OSBs. An ionosphere-free code OSB combination was fixed to zero as the bias datum to enable pseudo-absolute bias conversions, e.g., C1W/C2W for GPS and C1C/C5Q for Galileo. It was reported that the code OSBs could agree well with the legacy DCBs at an RMS error of 0.11 ns. Furthermore, Schaer et al. (2021) generalized the code OSB framework to phase OSBs in order to resolve the consistency, flexibility and standardization in addressing the phase biases from multi-GNSS frequencies and observables. They used GPS/Galileo dual-frequency observations to validate the applicability of their phase/code OSB products to PPP-AR, and mentioned the potential of extending their phase OSBs to multi-frequency observables.

In this study, we aim at formulating a phase OSB framework for all-frequency GPS/Galileo/BDS signals, even though under the threat of time-variable IFCBs, to facilitate PPP-AR over any frequency choices and observable combinations at the user end (i.e., literally all-frequency PPP-AR coined in this study). “All-frequency” PPP-AR is analogous to the concept of all-source positioning and navigation characterized mainly by the smooth reconfiguration in case of any conceivable sensor combination (Haug et al. 2020). Multi-frequency PPP-AR and multi-sensor navigation, on the opposite, are not originally required to achieve this capability. The article is organized as follows: Section 2 describes the method of all-frequency phase OSB estimation and explains why such phase OSBs can enable all-frequency PPP-AR. Section 3 shows the multi-frequency GPS/Galileo data to verify our phase OSBs. Sections 4 and 5 demonstrate and discuss the results before Sect. 6 concludes this study.

2 Method

GNSS multi-frequency observation equations for code division multiple access (CDMA) signals from satellite k to station i in the unit of length can be written as

$$\begin{aligned} \left\{ \begin{array}{l} P_{i,1}^k=\rho _{i,1}^k+c\left( t_i-t^k\right) +\gamma _i^k+d_{i,1}+d_1^k \\ P_{i,2}^k=\rho _{i,2}^k+c\left( t_i-t^k\right) +g_2^2\gamma _i^k+d_{i,2}+d_2^k \\ P_{i,q}^k=\rho _{i,q}^k+c\left( t_i-t^k\right) +g_q^2\gamma _i^k+d_{i,q}+d_q^k \\ L_{i,1}^k=\rho _{i,1}^k+c\left( t_i-t^k\right) -\gamma _i^k+\lambda _1\left( N_{i,1}^k+b_{i,1}+b_1^k\right) \\ L_{i,2}^k=\rho _{i,2}^k+c\left( t_i-t^k\right) -g_2^2\gamma _i^k+\lambda _2\left( N_{i,2}^k+b_{i,2}+b_2^k\right) \\ L_{i,q}^k=\rho _{i,q}^k+c\left( t_i-t^k\right) -g_q^2\gamma _i^k+\lambda _q\left( N_{i,q}^k+b_{i,q}+\mathring{b}_q^k\right) \end{array}\right. \end{aligned}$$
(1)

where \(P_{i,1}^k\), \(P_{i,2}^k\) and \(P_{i,q}^k\) are the pseudorange measurements on frequencies 1, 2 and q, respectively, while \(L_{i,1}^k\), \(L_{i,2}^k\) and \(L_{i,q}^k\) are the carrier-phase measurements; \(\rho _{i,1}^k\), \(\rho _{i,2}^k\) and \(\rho _{i,q}^k\) denote the geometric distance between satellite k and station i including the troposphere delay and the antenna phase center errors for frequencies 1, 2 and q, respectively; c is the speed of light in vacuum; \(t_i\) and \(t^k\) denote the receiver and satellite clocks, respectively; \(\gamma _i^k\) is the slant ionosphere delay on frequency 1; \(g_2=\dfrac{f_1}{f_2}\) and \(g_q=\dfrac{f_1}{f_q}\) where \(f_1\), \(f_2\) and \(f_q\) are the signal frequencies; \(\lambda _1\), \(\lambda _2\) and \(\lambda _q\) are the wavelengths and \(N_{i,1}^k\), \(N_{i,2}^k\) and \(N_{i,q}^k\) are the integer ambiguities; \(d_{i,1}\), \(d_{i,2}\) and \(d_{i,q}\) symbolize the receiver code biases on frequencies 1, 2 and q, respectively, whereas \(d_1^k\), \(d_2^k\) and \(d_q^k\) are the satellite code biases, which are all termed as code OSBs; similarly, \(b_{i,1}\), \(b_{i,2}\) and \(b_{i,q}\) are the receiver phase biases, and \(b_1^k\), \(b_2^k\) and \(\mathring{b}_q^k\) are the satellite phase biases in the unit of cycles, which are all phase OSBs. For brevity, we do not consider the dependence of OSBs on tracking channels in Eq. (1), even for code OSBs (see Villiger et al. 2019).

It should be pointed out that q can represent any third frequency, other than the first two frequencies that define the clock datum in this article. We throughout define the first two frequencies (i.e., 1 and 2) as the baseline frequencies, and the first two pseudorange as the baseline pseudorange. Equation 1 can be taken as a general formulation for dual, triple and multiple frequencies of GNSS observations. We presume that the code and phase OSBs are all time-invariable for brevity; the only exception is that the satellite phase OSB on frequency q, \(\mathring{b}_q^k\), might vary over time, and its difference from the satellite phase OSBs on the baseline frequencies is usually termed as the IFCBs. For simplicity, we model \(\mathring{b}_q^k\) as an epoch-wise parameter in Eq. (1),

$$\begin{aligned} \mathring{b}_q^k\doteq b_q^k+\delta b_q^k \end{aligned}$$
(2)

where \(b_q^k\) denotes the time-constant part of \(\mathring{b}_q^k\) while \(\delta b_q^k\) denotes the temporal or epoch-wise variation with respect to \(b_q^k\). In this sense, the first epoch of \(\delta b_q^k\) is thus supposed to be zero. Note that the term \(\delta b_q^k\) disappears if no time-variable IFCB is present. Neither code nor phase OSBs can be estimated directly using Eq. (1) due to their linear dependency on clocks, ionosphere delays and ambiguities. We need first to reformulate Eq. (1) by combining the OSBs with clocks, ionosphere delays and ambiguities to remove the rank deficiency (Odijk et al. 2016).

Regarding the code OSBs in Eq. (1), the IGS has released their correction products in the Bias-SINEX format (Solution INdependent EXchange) (Schaer 2016). In this study, we use \(D_1^k\), \(D_2^k\) and \(D_q^k\) to denote the satellite code OSB corrections for \(d_1^k\), \(d_2^k\) and \(d_q^k\), respectively. Note that we never presume \(D_1^k=d_1^k\), \(D_2^k=d_2^k\) or \(D_q^k=d_q^k\). Rather, according to Villiger et al. (2019), it is the following relations that hold,

$$\begin{aligned} \left\{ \begin{array}{l} D_1^k-D_2^k=d_1^k-d_2^k \\ D_1^k-D_q^k=d_1^k-d_q^k \\ \alpha D_1^k-\beta D_2^k=0 \end{array}\right. \end{aligned}$$
(3)

where

$$\begin{aligned} \left\{ \begin{array}{l} \alpha =\dfrac{g_2^2}{g_2^2-1} \\ \beta =\dfrac{1}{g_2^2-1} \end{array}\right. \end{aligned}$$
(4)

The first two relations in Eq. (3) defines DCBs while the third defines the bias datum of code OSBs to facilitate the pseudo-absolute bias estimation. In addition, we can derive a satellite-specific, while frequency-independent, constant \({\mathcal {D}}^k\) which satisfies

$$\begin{aligned} {\mathcal {D}}^k\doteq D_1^k-d_1^k=D_2^k-d_2^k=D_q^k-d_q^k \end{aligned}$$
(5)

2.1 All-frequency phase clock/OSB determination

In order to avoid the linear dependency of the bias unknowns on other parameters, we reformulate Eq. (1) as

$$\begin{aligned} \left\{ \begin{aligned} P_{i,1}^k&=\rho _{i,1}^k+c\left( {\bar{t}}_i-{\bar{t}}^k\right) +{\bar{\gamma }}_i^k \\ P_{i,2}^k&=\rho _{i,2}^k+c\left( {\bar{t}}_i-{\bar{t}}^k\right) +g_2^2{\bar{\gamma }}_i^k \\ P_{i,q}^k&=\rho _{i,q}^k+c\left( {\bar{t}}_i-{\bar{t}}^k\right) +g_q^2{\bar{\gamma }}_i^k+{\bar{h}}_{i,q}^k \\ L_{i,1}^k&=\rho _{i,1}^k+c\left( {\bar{t}}_i-{\bar{t}}^k\right) -{\bar{\gamma }}_i^k+\lambda _1{\bar{N}}_{i,1}^k \\ L_{i,2}^k&=\rho _{i,2}^k+c\left( {\bar{t}}_i-{\bar{t}}^k\right) -g_2^2{\bar{\gamma }}_i^k+\lambda _2{\bar{N}}_{i,2}^k \\ L_{i,q}^k&=\rho _{i,q}^k+c\left( {\bar{t}}_i-{\bar{t}}^k\right) -g_q^2{\bar{\gamma }}_i^k+\lambda _q{\bar{N}}_{i,q}^k+\lambda _q\delta b_q^k \end{aligned}\right. \end{aligned}$$
(6)

where

$$\begin{aligned} \left\{ \begin{aligned} {\bar{t}}_i&=t_i+\dfrac{1}{c}\left( \alpha d_{i,1}-\beta d_{i,2}\right) \\ {\bar{t}}^k&=t^k-\dfrac{1}{c}\left( \alpha d_1^k-\beta d_2^k\right) \\ {\bar{\gamma }}_i^k&=\gamma _i^k-\beta \left( d_{i,1}-d_{i,2}+d_1^k-d_2^k\right) \\ {\bar{h}}_{i,q}^k&=g_q^2\beta \left( d_{i,1}-d_{i,2}+d_1^k-d_2^k\right) -\left( \alpha d_{i,1}-\beta d_{i,2}\right) \\&\quad -\left( \alpha d_1^k-\beta d_2^k\right) +d_{i,q}+d_q^k \end{aligned}\right. \nonumber \\ \end{aligned}$$
(7)

\({\bar{t}}^k\) denotes the legacy satellite clock which is aligned with the code biases on the baseline pseudorange. \({\bar{h}}_{i,q}^k\) is an unknown constant to be estimated on the frequency q pseudorange for each satellite tracked by station i. The new ambiguity terms are

$$\begin{aligned} \left\{ \begin{aligned} {\bar{N}}_{i,1}^k&=N_{i,1}^k+b_{i,1}+b_1^k-\dfrac{1}{\lambda _1}\biggl (\left( \alpha +\beta \right) \left( d_{i,1}+d_1^k\right) \\&\quad -2\beta \left( d_{i,2}+d_2^k\right) \biggr ) \\&=N_{i,1}^k+{\bar{b}}_{i,1}+{\bar{b}}_1^k-\dfrac{1}{\lambda _1}\biggl (D_1^k+2\beta \left( D_1^k-D_2^k\right) \biggr ) \\ {\bar{N}}_{i,2}^k&=N_{i,2}^k+b_{i,2}+b_2^k-\dfrac{1}{\lambda _2}\biggl (2\alpha \left( d_{i,1}+d_1^k\right) \\&\quad -\left( \alpha +\beta \right) \left( d_{i,2}+d_2^k\right) \biggr ) \\&=N_{i,2}^k+{\bar{b}}_{i,2}+{\bar{b}}_2^k\\&\quad -\dfrac{1}{\lambda _2}\biggl (D_1^k+\left( \alpha +\beta \right) \left( D_1^k-D_2^k\right) \biggr ) \\ {\bar{N}}_{i,q}^k&=N_{i,q}^k+b_{i,q}+b_q^k\\&\quad -\dfrac{1}{\lambda _q}\biggl (g_q^2\beta \left( d_{i,1}-d_{i,2}+d_1^k-d_2^k\right) \\&\quad +\alpha \left( d_{i,1}+d_1^k\right) -\beta \left( d_{i,2}+d_2^k\right) \biggr ) \\&=N_{i,q}^k+{\bar{b}}_{i,q}+{\bar{b}}_q^k\\&\quad -\dfrac{1}{\lambda _q}\biggl (D_1^k+\left( g_q^2+1\right) \beta \left( D_1^k-D_2^k\right) \biggr ) \end{aligned} \right. \end{aligned}$$
(8)

where the relations in Eq. (3) have been introduced. Note that \({\bar{N}}_{i,q}^k\) absorbs \(b_q^k\), but not \(\delta b_q^k\). A direct least-squares adjustment on Eq. (6) would produce ambiguity-float solutions for all parameters listed in Eqs. (7) and (8) in addition to \(\delta b_q^k\). The terms \({\bar{b}}_{i,1}\), \({\bar{b}}_{i,2}\) and \({\bar{b}}_{i,q}\) stand for the nominal receiver phase OSBs containing all receiver-dependent time-constant code/phase bias terms defined in Eq. (1) on frequencies 1, 2 and q, respectively. In the meantime, the nominal satellite phase OSBs are defined as

$$\begin{aligned} \left\{ \begin{array}{l} {\bar{b}}_1^k=b_1^k+\dfrac{1}{\lambda _1}{\mathcal {D}}^k \\ {\bar{b}}_2^k=b_2^k+\dfrac{1}{\lambda _2}{\mathcal {D}}^k \\ {\tilde{b}}_q^k\doteq {\bar{b}}_q^k+\delta b_q^k=b_q^k +\dfrac{1}{\lambda _q}{\mathcal {D}}^k+\delta b_q^k \end{array}\right. \end{aligned}$$
(9)

Note that the third-frequency phase OSBs \({\tilde{b}}_q^k\) are defined as being able to accommodate time-variable OSBs \(\delta b_q^k\).

Based on the first two sub-equations of Eq. (8), we can first estimate the phase OSBs for the baseline frequencies using

$$\begin{aligned} \left\{ \begin{aligned}&\hat{{\bar{N}}}_{i,1}^k+\dfrac{1}{\lambda _1}\biggl (D_1^k+2\beta \left( D_1^k-D_2^k\right) \biggr )\\&={\check{N}}_{i,1}^k+\check{{\bar{b}}}_{i,1}+\check{{\bar{b}}}_1^k \\&\hat{{\bar{N}}}_{i,2}^k+\dfrac{1}{\lambda _2}\biggl (D_1^k+\left( \alpha +\beta \right) \left( D_1^k-D_2^k\right) \biggr )\\&={\check{N}}_{i,2}^k+\check{{\bar{b}}}_{i,2}+\check{{\bar{b}}}_2^k \end{aligned}\right. \end{aligned}$$
(10)

where the accent “\(\hat{\;\;}\)” denotes a least-squares estimate from Eq. (6). Since \(D_1^k\) and \(D_2^k\) are known code OSB corrections, the left-hand side of Eq. (10) has been known, and the terms on the right-hand side are to be estimated. For simplicity, we presume that \(\left( \check{{\bar{b}}}_{i,1}+\check{{\bar{b}}}_1^k\right) \) and \(\left( \check{{\bar{b}}}_{i,2}+\check{{\bar{b}}}_2^k\right) \) are both fractional, of which the integer parts have been absorbed by \({\check{N}}_{i,1}^k\) and \({\check{N}}_{i,2}^k\), respectively. In this sense, \({\check{N}}_{i,1}^k\) and \({\check{N}}_{i,2}^k\) can then be separated by integer rounding operations and in turn moved to the left-hand side of Eq. (10) (Ge et al. 2008; Schaer et al. 2021). Next, the satellite phase OSBs \(\check{{\bar{b}}}_1^k\) and \(\check{{\bar{b}}}_2^k\) can be estimated as daily constants by presuming one reference receiver’s phase OSBs to be zero.

Of particular note, the satellite phase OSB estimation using Eq. (10) is actually based on ambiguity-float solutions (\(\hat{{\bar{N}}}_{i,1}^k\) and \(\hat{{\bar{N}}}_{i,2}^k\)) from Eq. (6). To achieve a more rigorous phase OSB estimation, one should further fix, or tightly constrain, the ambiguity terms \({\bar{N}}_{i,1}^k\) and \({\bar{N}}_{i,2}^k\) in Eq. (6) to the already known quantities derived from Eq. (10), i.e., the integer \({\check{N}}_{i,1}^k\) and \({\check{N}}_{i,2}^k\) plus the phase OSBs \(\left( \check{{\bar{b}}}_{i,1}+\check{{\bar{b}}}_1^k\right) \) and \(\left( \check{{\bar{b}}}_{i,2}+\check{{\bar{b}}}_2^k\right) \), respectively. To be concrete, such tight constraints can take the undifferenced forms of

$$\begin{aligned} \left\{ \begin{aligned}&\lambda _1\biggl ({\check{N}}_{i,1}^k+\check{{\bar{b}}}_{i,1} +\check{{\bar{b}}}_1^k\biggr )-D_1^k-2\beta \biggl (D_1^k-D_2^k\biggr )\\&\quad =\lambda _1{\bar{N}}_{i,1}^k,\;\lambda _1\sigma _{{\bar{N}}_{i,1}^k}=0.001\,\mathrm {mm} \\&\lambda _2\biggl ({\check{N}}_{i,2}^k+\check{{\bar{b}}}_{i,2} +\check{{\bar{b}}}_2^k\biggr )-D_1^k-\left( \alpha +\beta \right) \biggl (D_1^k-D_2^k\biggr )\\&\quad =\lambda _2{\bar{N}}_{i,2}^k,\; \lambda _2\sigma _{{\bar{N}}_{i,2}^k}=0.001\,\mathrm {mm} \end{aligned}\right. \end{aligned}$$
(11)

where \(\sigma _{{\bar{N}}_{i,1}^k}\) and \(\sigma _{{\bar{N}}_{i,2}^k}\) act as the uncertainties of the two tight constraints on \({\bar{N}}_{i,1}^k\) and \({\bar{N}}_{i,2}^k\), respectively. Equation (11) should be imposed on Eq. (6) as pseudo-observations with super low uncertainties to re-estimate satellite clocks \({\bar{t}}^k\). Then, the ambiguity-float satellite clock term \(\hat{{\bar{t}}}^k\) can be upgraded to \(\check{{\bar{t}}}^k\). Such satellite clocks can be termed as phase clocks, or in other words, ambiguity-fixed clocks, which should be applied along with the satellite phase OSBs (i.e., \(\check{{\bar{b}}}_1^k\) and \(\check{{\bar{b}}}_2^k\)) to enable dual-frequency PPP-AR. Both Geng et al. (2019) and Schaer et al. (2021) have demonstrated the importance of re-estimating satellite clocks after determining the satellite phase OSBs in the first step.

Furthermore, in the re-estimation process of satellite clocks using Eqs. (6) and (11), the ambiguity term \({\bar{N}}_{i,q}^k\) and the time-variable OSB \(\delta b_q^k\) on the third-frequency carrier-phase will also be re-estimated. As a result, the third-frequency phase OSBs need to be re-computed correspondingly. Analogous to the derivation from Eqs. (8) to (10), we have

$$\begin{aligned}&\check{{\bar{N}}}_{i,q}^k+\dfrac{1}{\lambda _q} \biggl (D_1^k+\left( g_q^2+1\right) \beta \left( D_1^k-D_2^k\right) \biggr )\nonumber \\&={\check{N}}_{i,q}^k+\check{{\bar{b}}}_{i,q}+\check{{\bar{b}}}_q^k \end{aligned}$$
(12)

of which the terms on the left-hand side are known, while those on the right-hand side are to be estimated. It is worth emphasizing that \(\check{{\bar{N}}}_{i,q}^k\) differs in nature from \(\hat{{\bar{N}}}_{i,q}^k\), \(\hat{{\bar{N}}}_{i,1}^k\) and \(\hat{{\bar{N}}}_{i,2}^k\) as the \(\check{{\bar{N}}}_{i,q}^k\) is computed under the ambiguity-fixed satellite clocks \(\check{{\bar{t}}}^k\). One should be reminded of the difference between Eqs. (10) and (12). Equation (12) can be used to calculate the time-constant portion (i.e., \(\check{{\bar{b}}}_q^k\)) of the third-frequency satellite phase OSBs. If IFCBs do exist, the final third-frequency satellite phase OSBs should be translated into

$$\begin{aligned} \check{{\tilde{b}}}_q^k=\check{{\bar{b}}}_q^k+\delta {\check{b}}_q^k \end{aligned}$$
(13)

where \(\delta {\check{b}}_q^k\) denotes the re-estimation quantity of \(\delta b_q^k\) under the ambiguity-fixed satellite clocks. At this point, we are aware that both \(\check{{\bar{b}}}_q^k\) and \(\delta {\check{b}}_q^k\) are compatible with the ambiguity-fixed satellite clocks.

In addition, the estimation of phase OSBs using Eqs. (10) and (12) might not be so straightforward since the direct ambiguity estimates from Eq. (6) would be contaminated by ionospheric delays (e.g., Geng and Shi 2017). It is because the pseudorange can hardly constrain the slant ionospheric delays precisely. One can thus use the wide-lane and ionosphere-free combinations between \({\bar{N}}_{i,1}^k\), \({\bar{N}}_{i,2}^k\) and \({\bar{N}}_{i,q}^k\), instead of Eqs. (10) and (12), to address such ionospheric contaminations (see Geng and Shi 2017). Once the wide-lane and narrow-lane phase biases are identified in accordance with the approach proposed by Schaer et al. (2021) among others, the satellite phase OSBs can be computed using

$$\begin{aligned} \begin{bmatrix} \lambda _1{\bar{b}}_1^k\\ \lambda _2{\bar{b}}_2^k\\ \lambda _q{\bar{b}}_q^k \end{bmatrix}= & {} \begin{bmatrix} \dfrac{g_2}{g_2-1} &{} \dfrac{-1}{g_2-1} &{} 0 \\ \dfrac{g_q}{g_q-1} &{} 0 &{} \dfrac{-1}{g_q-1} \\ \alpha &{} -\beta &{} 0 \end{bmatrix}^{-1}\nonumber \\&\begin{bmatrix} \lambda _{12,\mathrm {w}}{\bar{b}}_{12,\mathrm {w}}^k\\ \lambda _{1q,\mathrm {w}}{\bar{b}}_{1q,\mathrm {w}}^k\\ \lambda _{12,\mathrm {n}}{\bar{b}}_{12,\mathrm {n}}^k \end{bmatrix} \end{aligned}$$
(14)

where \({\bar{b}}_{12,\mathrm {w}}^k\), \({\bar{b}}_{1q,\mathrm {w}}^k\) and \({\bar{b}}_{12,\mathrm {n}}^k\) are the wide-lane phase bias on frequencies 1 and 2, the wide-lane phase biases on frequencies 1 and q, and the narrow-lane phase bias on frequencies 1 and 2 in the unit of cycles. \(\lambda _{12,\mathrm {w}}\), \(\lambda _{1q,\mathrm {w}}\) and \(\lambda _{12,\mathrm {n}}\) are their wavelengths, respectively.

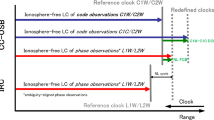
Finally, the ambiguity-fixed satellite clocks \(\check{{\bar{t}}}^k\) along with the daily satellite phase OSBs \(\check{{\bar{b}}}_1^k\) and \(\check{{\bar{b}}}_2^k\) as well as the epoch-wise \(\check{{\tilde{b}}}_q^k\) will enable all-frequency PPP-AR at the user end. Note that \(\check{{\tilde{b}}}_q^k\) can also be modeled as a piece-wise linear parameter for simplicity. Figure 1 describes the complete process of the phase clock/OSB determination in this study. It is worth mentioning that our all-frequency phase clocks/OSBs comply with the common clock/OSB (CC-OSB) model proposed by Schaer et al. (2021) (see Fig. 1 therein).

Fig. 1
figure 1

A schematic diagram for the GNSS phase clock/OSB determination in this study. Green boxes denote data or products while white boxes denote processes

Full size image

2.2 All-frequency PPP-AR

Compared to the conventional wide-lane and narrow-lane phase biases, phase OSBs are more convenient and flexible in enabling PPP-AR over any frequency choices and observable combinations. In the case of uncombined PPP, users only need to subtract the code and phase OSBs from their corresponding pseudorange and carrier-phase observations, that is

$$\begin{aligned} \left\{ \begin{array}{l} {\hat{P}}_{i,1}^k=P_{i,1}^k-D_1^k \\ {\hat{P}}_{i,2}^k=P_{i,2}^k-D_2^k \\ {\hat{P}}_{i,q}^k=P_{i,q}^k-D_q^k \\ {\hat{L}}_{i,1}^k=L_{i,1}^k-\lambda _1\check{{\bar{b}}}_1^k \\ {\hat{L}}_{i,2}^k=L_{i,2}^k-\lambda _2\check{{\bar{b}}}_2^k \\ {\hat{L}}_{i,q}^k=L_{i,q}^k-\lambda _q\check{{\tilde{b}}}_q^k \end{array}\right. \end{aligned}$$
(15)

After the satellite clocks \(\check{{\bar{t}}}^k\) are corrected as well, the resultant PPP ambiguities will retrieve their integer properties. Users do not need to have all observables shown in Eq. (15) to achieve PPP-AR. Rather, any two or more frequencies of pseudorange and carrier-phase from Eq. (15) will ensure a full recovery of integer ambiguities, namely all-frequency PPP-AR. That is to say, even if it is \({\hat{P}}_{i,1}^k\), \({\hat{P}}_{i,q}^k\), \({\hat{L}}_{i,1}^k\) and \({\hat{L}}_{i,q}^k\) that are processed, PPP-AR is still achievable.

In the case of ionosphere-free PPP, on the other hand, the Melbourne-Wübbena combination observable is usually used to resolve wide-lane ambiguities. One can still use any two frequencies of pseudorange and carrier-phase from Eq. (15) to form the Melbourne-Wübbena combination. Note that a further antenna phase center correction is required, especially for Galileo satellites whose antenna phase centers in igs14.atx differ across all frequencies. In particular, we have

$$\begin{aligned} {\hat{L}}_{i,1q,\mathrm {m}}^k= & {} \dfrac{{\hat{L}}_{i,1}^k+z_{i,1 }^k}{\lambda _1}-\dfrac{{\hat{L}}_{i,q}^k+z_{i,q}^k}{\lambda _q}\nonumber \\&-\dfrac{g_q-1}{g_q+1}\biggl (\dfrac{{\hat{P}}_{i,1}^k+z_{i,1}^k}{\lambda _1}+\dfrac{{\hat{P}}_{i,q}^k+z_{i,q}^k}{\lambda _q}\biggr ) \end{aligned}$$
(16)

where \({\hat{L}}_{i,1q,\mathrm {m}}^k\) is the Melbourne-Wübbena combination based on frequencies 1 and q; \(z_{i,1}^k\) and \(z_{i,q}^k\) are the antenna phase center corrections for frequencies 1 and q, respectively, which are mainly subject to phase center offsets (PCOs). From igs14.atx, the frequency-specific horizontal PCOs usually differ by as small as a few millimeters for both receiver and satellite antennas. Therefore, we propose a rule-of-thumb for the \(z_{i,1}^k\) and \(z_{i,q}^k\) computations,

$$\begin{aligned} \left\{ \begin{array}{l} z_{i,1}^k\approx z_{i,1}\sin {\theta _i^k}+z_1^k \\ z_{i,q}^k\approx z_{i,q}\sin {\theta _i^k}+z_q^k \end{array}\right. \end{aligned}$$
(17)

where \(z_{i,1}\) and \(z_{i,q}\) are the receiver antenna’s vertical PCOs on frequencies 1 and q, respectively, whereas \(z_1^k\) and \(z_q^k\) are the satellite antenna’s vertical PCOs; \(\theta _i^k\) is the elevation angle of satellite k with respect to station i. We apply the satellite antenna’s vertical PCOs without regarding the nadir angles, because such angles are small enough (e.g., \(<14^\circ \)). Once the Melbourne-Wübbena wide-lane ambiguities are resolved successfully, the ionosphere-free combination observable based on \({\hat{P}}_{i,1}^k\), \({\hat{P}}_{i,q}^k\), \({\hat{L}}_{i,1}^k\) and \({\hat{L}}_{i,q}^k\) can be used along with the satellite clocks \(\check{{\bar{t}}}^k\) to resolve narrow-lane ambiguities (see Schaer et al. 2021, among others).

2.3 Remarks on the satellite clocks for all-frequency PPP-AR

All-frequency PPP-AR is challenging in concept since one satellite clock product must apply to all eligible frequency choices and observable combinations. Although correcting raw GNSS measurements for code and phase OSBs is quite straightforward, Eq. (15) does not shed light on why the satellite clocks \(\check{{\bar{t}}}^k\) aligned with the baseline pseudorange can be safely applied to all other third-frequency observables without inducing any extra biases to prevent PPP-AR. We demonstrate this point with the raw observables on frequencies 1 and q, while all other cases can be investigated similarly. After the OSB corrections in Eq. (15), we expand \({\hat{P}}_{i,1}^k\), \({\hat{P}}_{i,q}^k\), \({\hat{L}}_{i,1}^k\) and \({\hat{L}}_{i,q}^k\) by substituting the relations in Eqs. (5) and (9), and obtain

$$\begin{aligned} \left\{ \begin{aligned} {\hat{P}}_{i,1}^k&=\rho _{i,1}^k+c\left( t_i-t^k\right) +\gamma _i^k+d_{i,1}-{\mathcal {D}}^k \\ {\hat{P}}_{i,q}^k&=\rho _{i,q}^k+c\left( t_i-t^k\right) +g_q^2\gamma _i^k+d_{i,q}-{\mathcal {D}}^k \\ {\hat{L}}_{i,1}^k&=\rho _{i,1}^k+c\left( t_i-t^k\right) -\gamma _i^k+\lambda _1\left( N_{i,1}^k+b_{i,1}\right) -{\mathcal {D}}^k \\ {\hat{L}}_{i,q}^k&=\rho _{i,q}^k+c\left( t_i-t^k\right) -g_q^2\gamma _i^k+\lambda _q\left( N_{i,q}^k+b_{i,q}\right) -{\mathcal {D}}^k \end{aligned}\right. \end{aligned}$$
(18)

It can be seen that all satellite-dependent code and phase biases are reduced to only \({\mathcal {D}}^k\) for each observable. Similar to the reformulation from Eqs. (1) to 6, we can lump the bias terms (i.e., \(d_{i,1}\), \(d_{i,q}\), \(b_{i,1}\), \(b_{i,q}\) and \({\mathcal {D}}^k\)) into the new clock, ionosphere and ambiguity parameters to be estimated, that is,

$$\begin{aligned} \left\{ \begin{aligned} \breve{t}_i&=t_i+\dfrac{1}{c}\left( a d_{i,1}-e d_{i,q}\right) \\ \breve{t}^k&=t^k+\dfrac{{\mathcal {D}}^k}{c} \\ \breve{\gamma }_i^k&=\gamma _i^k-e\left( d_{i,1}-d_{i,q}\right) \\ \breve{N}_{i,1}^k&=N_{i,1}^k+b_{i,1}-\dfrac{1}{\lambda _1}\biggl (\left( a+e\right) d_{i,1}-2e d_{i,q}\biggr ) \\ \breve{N}_{i,q}^k&=N_{i,q}^k+b_{i,q}-\dfrac{1}{\lambda _q}\biggl (2a d_{i,1}-\left( a+e\right) d_{i,q}\biggr ) \\ a&=\dfrac{g_q^2}{g_q^2-1} \\ e&=\dfrac{1}{g_q^2-1} \end{aligned} \right. \end{aligned}$$
(19)

We can find that neither \(\breve{N}_{i,1}^k\) nor \(\breve{N}_{i,q}^k\) is contaminated by any satellite-dependent biases, and thus single-difference ambiguities can be resolved in this case. However, one remaining question is whether the nominal satellite clock \(\breve{t}^k\) in Eq. (19) is equal to the satellite clock \({\bar{t}}^k\) in Eq. (6). The answer matters critically in whether the ambiguity-fixed satellite clock products \(\check{{\bar{t}}}^k\) aligned with the baseline frequencies can also be applied to all third frequencies.

In order to prove \({\bar{t}}^k=\breve{t}^k\), we have the following derivation with the aid of Eqs. (3) and (5),

$$\begin{aligned} \begin{aligned} {\bar{t}}^k&=t^k-\dfrac{1}{c}\biggl (\alpha d_1^k-\beta d_2^k\biggr ) \\&=t^k-\dfrac{1}{c}\biggl (d_1^k+\beta \left( d_1^k-d_2^k\right) \biggr ) \\&=t^k-\dfrac{1}{c}\biggl (d_1^k-D_1^k+D_1^k+\beta \left( D_1^k-D_2^k\right) \biggr ) \\&=t^k-\dfrac{1}{c}\biggl (d_1^k-D_1^k+\left( \alpha D_1^k-\beta D_2^k\right) \biggr ) \\&=t^k+\dfrac{{\mathcal {D}}^k}{c}=\breve{t}^k \end{aligned} \end{aligned}$$
(20)

At this point, we find that the legacy satellite clock, though governed by the baseline pseudorange, can be converted into the clock compatible with all other third-frequency observables, thanks to the established code OSB framework underpinned by Eq. (3). Equations (18)–(20) therefore confirms the flexibility of the code and phase OSBs in enabling all-frequency PPP-AR.

3 Data and models

One month of 30-s multi-frequency measurements from 122 globally-distributed GPS/Galileo reference stations were collected to compute phase clocks/OSBs for days 306-335 (November) in the year of 2020 (Fig. 2). We then used another 48 stations, which did not overlap the stations in the reference network (Table 1), to test the phase clock/OSB products with the goal of enabling all-frequency PPP-AR (e.g., GPS L1/L5, Galileo E1/E6, etc.). GPS L1/L2/L5 pseudorange measurements from all tracking channels were aligned with C1W/C2W/C5Q using the WUM (Wuhan University) code OSB products. Likewise, all Galileo E1/E5a/E5b/E5/E6 pseudorange were aligned with C1C/C5Q/C7Q/C8Q/C6C. The GPS Block IIF satellites’ L2 antenna phase centers in igs14.atx were duplicated for their L5 signals. Regarding receiver antennas, we presumed that Galileo E1 had the same antenna phase centers as GPS L1, and all other frequencies shared the phase centers of GPS L2. More GNSS data processing details refer to Table 2.

Fig. 2
figure 2

122 stations (blue circles) for the GPS/Galileo phase OSB determination and another 48 stations (red triangles) to test all-frequency PPP

Full size image

Though the uncombined GNSS model was used to estimate the phase clocks/OSBs with multi-frequency measurements, the traditional dual-frequency ionosphere-free model was adopted to carry out daily PPP-AR at the 48 test stations to verify all-frequency PPP-AR. We should ideally have 1440 daily solutions if the GNSS measurements were complete. Since there were only 16 GPS satellites emitting L5 signals at the moment, we processed GPS L5-relevant PPP together with Galileo E1/E5a data to maximize the ambiguity fixing rates. Likewise, Galileo dual-frequency PPP under an incomplete constellation of only 24 satellites was always carried out together with GPS L1/L2 data. In addition, we chose the sequential bias fixing strategy for PPP-AR, and the bias round-off criteria were 0.25 and 0.15 cycles for wide-lane and narrow-lane ambiguities, respectively (Dong and Bock 1989). We should reiterate that it was the GPS L1/L2 and Galileo E1/E5a ambiguity-fixed satellite clocks that were used exclusively for all PPP tests, no matter which frequency choices or observable combinations were processed.

4 Results

4.1 GPS and Galileo phase OSBs

We used the 122 stations in Fig. 2 to estimate GPS/Galileo ambiguity-fixed satellite clocks and satellite phase OSBs for each frequency. Figure 3 shows the 30 days of GPS/Galileo phase OSBs delimited by the vertical grids with respect to each satellite. In panels a) and c), the black, red and blue dot clusters symbolize the phase OSBs for the GPS L1, L2 and L5 signals, respectively; in panels e) and g), the black, red, blue, orange and purple dot clusters denote the phase OSBs for the Galileo E1, E5a, E5a, E5 and E6 signals, respectively. Each colored cluster comprises 30 dots, representing the 30 daily phase OSBs, except for the piece-wise linear GPS L5 OSBs every 15 minutes. The phase OSBs in panels a) and e) were calculated using the WUM daily code OSBs, as plotted in panels b) and f) after removing their 30-day mean (i.e., “mean-removed” dot clusters). For comparison, the phase OSBs in panels c) and g) are computed using the DLR (Deutsches Zentrum für Luft- und Raumfahrt) daily DCBs. These DCBs are converted into code OSBs which are then plotted in panels d) and h) (Villiger et al. 2019).

Ideally from the physical point of view, phase OSBs should be quite stable over a quite long period, although they are estimated as daily quantities in this study. From Fig. 3, however, most phase OSBs vary by up to ±1 ns with peak-to-peak variations of up to 1.3 ns on average over the 30 days. Comparing the phase and code OSBs, we can see that the code OSBs appear to be more stable than their phase counterparts. In practice, the IGS can usually release monthly mean DCB products with little loss of precision, but it is reported that only the Melbourne-Wübbena phase biases appear to be quite stable across days. Equations (10) and (12) have shown that the phase OSB estimation is subject to code OSBs, and thus the temporal variations of code OSBs would be translated into the phase OSB estimates. This explains why the phase and code OSBs need to be converted into wide-lane phase biases prior to a cross comparison in a physical and rigorous sense (Banville et al. 2020). Moreover, Banville et al. (2020), Geng et al. (2019) and Schaer et al. (2021) further demonstrated that it did not make physical sense to quantify the temporal characteristics of narrow-lane phase biases in an isolated manner without considering their linear dependency on satellite clocks.

Table 1 Number of all sorts of receivers within each network in Fig. 2
Full size table
Table 2 Correction models and estimation strategies for GPS/Galileo undifferenced data processing
Full size table
Fig. 3
figure 3

GPS L1/L2/L5 and Galileo E1/E5a/E5b/E5/E6 satellite phase OSBs (ns) over the 30 days of November 2020. The mean-removed C1W/C2W/C5Q and C1C/C5Q/C7Q/C8Q/C6C code OSBs derived from WUM and DLR are plotted in panels b, d, f and h. The phase OSBs in panels a and e are computed using the WUM code OSBs, whereas those in panels (c) and (g) are based on the DLR DCBs. “p2p” stands for “peak-to-peak” which shows the mean peak-to-peak OSB variation during the 30 days for all GPS/Galileo satellites

Full size image

Therefore, in Fig. 3, the visualization of phase OSBs’ mean peak-to-peak variations and their contrast with code OSBs’ variations only confirms the fact that the phase OSBs are affected by code OSBs; larger code OSB temporal variations implicate more significant phase OSB variations. In particular, the temporal stability of the GPS L1 and L2 phase OSBs, as gauged by the mean peak-to-peak variation (i.e., p2pL1 and p2pL2), is 0.74 ns and 1.03 ns in the case of WUM code OSBs, respectively, which then fall to 0.61 ns and 0.84 ns when the DLR code OSBs are used instead. This result can be understood according to the fact that p2pC1W and p2pC2W are reduced from 0.53 and 0.88 ns for the WUM code OSBs to 0.38 and 0.62 ns for the DLR code OSBs, respectively. Analogously, the apparent temporal variations of Galileo phase OSBs in panels e) and g) are also associated with the code OSBs in panels f) and h), respectively. Despite the better performance of DLR based OSBs, it is the phase OSBs in panels a) and e) that are used throughout this study for all-frequency PPP-AR.

In addition, the GPS L5 phase OSBs can be computed every epoch as white-noise parameters, or every 15 minutes as piece-wise linear parameters. Though the latter strategy was already used for this study, we also estimated epoch-wise L5 phase OSBs for comparison. It was found that they only differed from the 15-minute piece-wise linear estimates by less than 4 ps (i.e., 1.2 mm) for each GPS IIF and IIIA satellite.

4.2 Ambiguity residuals after OSB corrections

Next, we applied the GPS/Galileo phase OSBs back to the 122 stations and carried out dual-frequency PPP-AR using the Melbourne-Wübbena and the ionosphere-free combination observables. Figure 4 shows the distribution of the wide-lane and narrow-lane ambiguity fractional-cycle residuals at all 122 stations after the correction of code and phase OSBs. The more residuals approach zero, the higher the ambiguity fixing rates in PPP. Panels a) and b) are for the L1/L2 PPP, whereas panels c) and d) are for the L1/L5 PPP. As expected, 88.7% of wide-lane and 95.6% of narrow-lane ambiguity residuals from the L1/L2 PPP are within ±0.15 cycles, in good conformity with the statistics by Geng and Shi (2017) among others. The narrow-lane ambiguity residuals’ distribution is clearly more favorable than its wide-lane counterpart. However, for the L1/L5 PPP, only 68.9% of wide-lane ambiguity residuals are within ±0.15 cycles which is about 20 percentage point less than that in panel a). The standard deviation of the wide-lane ambiguity residuals is 0.17 cycles which is even 90% larger than that in panel a). We tried to excluded the 37 Trimble receivers (NetR9 and Alloy) and re-plotted the residuals’ distribution as open red bars in panels c) and d). This time we can see that 78.6% of all wide-lane ambiguity residuals are within ±0.15 cycles and the standard deviation improves to 0.11 cycles, both of which are more close to the statistics in panel a). In contrast, the narrow-lane ambiguity residuals for the L1/L5 PPP are negligibly degraded by the Trimble receivers. There is less than one percentage point discrepancy in terms of the ambiguity residuals’ distribution, while the standard deviations differ by 0.01 cycles only, as shown by the solid black and open red bars. Compared to the wide-lane ambiguities, the narrow-lane ambiguity residuals from the L1/L5 PPP perform much more comparably with those from the L1/L2 PPP. We therefore postulate that the Trimble receivers’ L5 pseudorange might be problematic, which will be investigated in Sect. 5.

Fig. 4
figure 4

Distribution of the wide-lane and narrow-lane ambiguity fractional-cycle residuals (cycle) after GPS phase OSB corrections at the 122 stations for all 30 days. Panels (a) and (b) are for the GPS L1/L2 signals, whereas panels (c) and (d) are for the GPS L1/L5 signals. The red open bars in panels (c) and (d) are the distribution for stations without Trimble receivers. \(\sigma \) denotes the standard deviation of all ambiguity residuals; the percentages show the proportions of the residuals within \(\pm 0.1\), \(\pm 0.15\) or \(\pm 0.25\) cycles

Full size image

For completeness, Fig. 5 shows the wide-lane and narrow-lane ambiguity residuals’ distribution for the Galileo satellites observed by the 122 stations. Four sorts of dual-frequency PPP based on the E1/E5a, E1/E5b, E1/E5 and E1/E6 signals are attempted here. In general, all standard deviations of the ambiguity residuals are less than 0.1 cycles, which are quite comparable to the GPS statistics in Fig. 4. Across all panels, around 90% of wide-lane and 95% of narrow-lane ambiguity residuals are within ±0.15 cycles, implying that Galileo PPP-AR is not impaired by the Trimble receivers. Unlike GPS, the distribution of Galileo wide-lane ambiguity residuals performs comparably with their narrow-lane counterpart, which is attributed to the relatively lower noise of Galileo pseudorange (e.g., Geng et al. 2017). Figure 5 demonstrates the high precisions of the Galileo phase OSBs in recovering integer PPP ambiguities almost unanimously for a variety of dual-frequency signals, echoing the achievement in Fig. 4 for GPS. This result is encouraging because only the E1/E5a based satellite clocks need to be computed, but which can still be applied to any other dual-frequency Galileo signals for PPP-AR.

Fig. 5
figure 5

Distribution of the wide-lane and narrow-lane ambiguity fractional-cycle residuals (cycle) after Galileo phase OSB corrections at the 122 stations for all 30 days. The PPP based on the E1/E5a, E1/E5b, E1/E5 and E1/E6 signals are presented in the top to the bottom panels. Refer to Fig. 4 for the meaning of all symbols

Full size image
Fig. 6
figure 6

Wide-lane ambiguity fixing rates (%) for GPS L1/L2 and L1/L5 PPP as well as Galileo E1/E5a and E1/E5b PPP at each of the 48 test stations over the 30 days

Full size image

4.3 PPP ambiguity fixing rates

In this section, we use the 48 test stations in Fig. 2 which do not overlap the 122 stations to more objectively assess the phase OSBs. Again, the Melbourne-Wübbena and the ionosphere-free combination observables were used to enable dual-frequency PPP-AR. Figure 6 shows the wide-lane ambiguity fixing rates of GPS L1/L2, L1/L5, Galileo E1/E5a and E1/E5b PPP in the top left, bottom left, top right and bottom right panels, respectively. Each colored square unit denotes the fixing rate at a given station (horizontal axes) on a particular day (vertical axes) in November, and a blank square denotes loss of GNSS observations. The stations are grouped according to the receiver types. Note that a bluish or reddish square indicates a fixing rate of well over or below 80%. In the first place, the L1/L2 PPP has over 97% of wide-lane ambiguities fixed to integers on average where the Septentrio and Leica receivers perform uniformly better than all other receivers. The E1/E5a, E1/E5b and E1/E5 PPP have even higher mean fixing rates of 98% (Table 3). The Javad and Trimble receivers now perform more comparably with the Septentrio and Leica receivers, probably implying that their Galileo observations have better quality than their GPS observations. On the contrary, the L1/L5 PPP suffers lower fixing rates on wide-lane ambiguities compared to the L1/L2 PPP, except for the Leica receivers. This situation is exceptionally worse regarding the Trimble receivers, of which the wide-lane ambiguity fixing rates are almost all around 75% over the month. Though the Trimble receivers appear to perform generally decently in the GPS L1/L2, Galileo E1/E5a and E1/E5b PPP, they drag down the L1/L5 wide-lane ambiguity fixing rate to 87% on average, about 10 percentage point lower compared to the other PPP tests in Table 3.

Table 3 Dual-frequency PPP-AR performance for GPS and Galileo at the 48 test stations. Column 2 shows the mean wide-lane (before slashes) and narrow-lane (after slashes) ambiguity fixing rates. Columns 3 and 4 show the daily ambiguity-float and ambiguity-fixed positioning RMS errors (mm), respectively, against the IGS weekly solutions for the east, north and up components. Column 5 shows the percentages of incorrectly resolved solutions
Full size table

Correspondingly, we further plotted the narrow-lane ambiguity fixing rates for the GPS L1/L2, L1/L5, Galileo E1/E5a and E1/E5b PPP in Fig. 7. The mean fixing rates for the four PPP-AR tests are comparable to each other (all around 95%) and the failure rates of unresolved solutions are all zero, which also hold in the case of Galileo E1/E5 and E1/E6 PPP shown only in Table 3. Moreover, no clear inferiority against the Trimble receivers for the L1/L5 narrow-lane ambiguity fixing rates is observed. Since the narrow-lane ambiguity precisions are mainly subject to the carrier-phase noise and satellite geometry, the fact of the decent narrow-lane (Fig. 7) but poor wide-lane (Fig. 6) ambiguity fixing rates for the Trimble receivers implies that their L5 pseudorange might undergo yet identified biases. Despite this problem, the overall statistics in Table 3, Figs. 6 and 7 still demonstrate that the GPS/Galileo phase OSBs proposed in this study are able to recover the integer PPP ambiguities at high success rates, even though it is the GPS L1/L2 and Galileo E1/E5a satellite clock products that are applied to the seemingly “incompatible” L1/L5, E1/E5b, E1/E5 and E1/E6 signals.

Fig. 7
figure 7

Narrow-lane ambiguity fixing rates (%) for GPS L1/L2 and L1/L5 PPP as well as Galileo E1/E5a and E1/E5b PPP at each of the 48 test stations over the 30 days

Full size image

Moreover, Table 3 shows the daily positioning RMS errors against the IGS weekly positions for all dual-frequency PPP. Although we always combined GPS with Galileo to more efficiently resolve PPP ambiguities, the ambiguity-fixed position estimates in Table 3 were obtained using only a single satellite system by introducing the hard constraints of the pre-resolved integer ambiguities. We removed the solutions whose horizontal position estimates deviated from the IGS positions by more than 5 cm, and the resultant outlier rates are shown in the last column of Table 3. Favorably, the outliers of all PPP tests account for less than 0.5%, even though there are only 16 satellites contributing to the GPS L1/L5 solutions. It is not surprising that the GPS L1/L2 PPP has the highest positioning precision since it benefits from much more available satellites and maturer correction models (e.g., antenna phase centers, etc.). The RMS errors of the east, north and up components are reduced by 40%, 13% and 6%, respectively, from the ambiguity-float to the ambiguity-fixed solutions. In contrast, the RMS errors of the other PPP tests in Table 3 almost double that of the GPS L1/L2 PPP, imputed in part to the fact that there are as few as 16 GPS satellite emitting L5 signals and 24 Galileo satellites orbiting Earth. Despite this adverse situation, their ambiguity-fixed solutions can still improve the precisions of daily positions, especially in the east component by 30–60%, while less than 20% in the north and up components. This result demonstrates the high applicability of the GPS/Galileo phase OSBs in enabling PPP-AR this is based on the unconventional L1/L5, E1/E5b, E1/E5 and E1/E6 frequency choices.

Fig. 8
figure 8

Double-difference GPS C1W/C2W/C5Q pseudorange residuals (m) derived from ultra-short baseline solutions between a variety of mainstream receivers. The residuals are color coded to denote different satellites. The black curves denote the Gauss filtered (500-epoch window) residuals for each satellite. The receiver types forming the baselines are plotted as the panel titles, whereas the baseline stations, lengths and observation periods are plotted at the bottom of each panel

Full size image

5 Discussions

Figures 4 and 6 show that the Trimble L5 pseudorange might be problematic, resulting in biased Melbourne-Wübbena combination observations. We thus found six ultra-short baselines equipped with the four mainstream receiver types listed in Table 1. Double-difference pseudorange residuals in a differential GNSS positioning are computed and plotted in Fig. 8. Ideally, such residuals should be close to zero; conversely, nonzero biases of the residuals would implicate receiver-relevant problems. Note that all GPS code tracking channels have been aligned with C1W, C2W and C5Q using the WUM code OSBs. The top three panels show the C1W/C2W/C5Q pseudorange residuals for three zero baselines between a Septentrio PolaRx5TR, a Leica GR50 and a Javad TRE_G3TH receiver. The residuals are color coded to distinguish among the satellites. A Gauss filter with a 500-epoch window is applied to suppress high-frequency noise and the filtered residuals are plotted as black curves. We can see that the C1W pseudorange are much more noisy than C2W and C5Q. However, all sorts of pseudorange residuals show minimal biases among the GPS satellites, as illustrated by the black curves all close to zero in the top three panels. This result suggests that the Septentrio, Leica and Javad receivers’ GPS pseudorange are generally compatible with each other, at least for the receiver sub-types we exemplify here. Unfortunately, this favorable situation cannot hold anymore if a Trimble receiver is involved. The bottom three panels of Fig. 8 show three ultra-short baselines between Trimble receivers and the other three receiver types above (i.e., Septentrio, Leica and Javad). This time the biases of up to 0.5 m among the GPS satellites can be found for the C1W and C5Q pseudorange residuals, while the C2W pseudorange residuals perform comparably well with those in the top panels. The bottom panels might unveil that the GPS L1/L5 Melbourne-Wübbena wide-lane ambiguities are more biased than their L1/L2 counterparts in the case of Trimble receivers. However, we must be cautious of this finding because we inspect only a limited group of receivers with a few firmware versions and antennas. The real cause behind those Trimble equipments’ deviant behaviors needs more investigation.

Fig. 9
figure 9

Ionosphere-free carrier-phase residuals (cycle) at station ALBH on day 309 for the GPS L1/L2 (panel a), L2/L5 (panel b), Galileo E1/E5a (panel c) and E5a/E5b PPP (panel d). The residuals are color coded to distinguish among satellites and the black curves denote the Gauss filtered residuals (100-epoch window). \(\sigma \) denotes the standard deviation (cycle) of all residuals and “NL” represents the narrow-lane ambiguity fixing rate

Full size image

Section 4.3 shows the PPP-AR performance for all “ideal” dual-frequency choices. An ideal dual-frequency choice requires that the separation of the two signal frequencies is wide enough to keep the amplified phase noise as low as possible (usually about three times the raw phase noise). This preference rules out those unfavorable choices like GPS L2/L5, Galileo E5a/E5b and E5a/E6 combinations, though they are in theory also feasible for dual-frequency PPP. These unfavorable frequency choices, however, are highly appreciated in composing extra-wide-lane carrier-phase combination observables for near instantaneous ambiguity fixing thanks to their super long wavelengths (up to a few meters) (e.g., Geng and Guo 2020). To verify all-frequency PPP-AR, we also attempted to implement dual-frequency PPP-AR based on such frequency choices. As expected, their wide-lane ambiguity fixing based on the Melbourne-Wübbena combination corrected for phase OSBs achieves 100% success rates at almost all 48 test stations on all days. Such a wide-lane ambiguity fixing, if in concert with the PPP-AR based on ideal dual-frequency signals, will make multi-frequency PPP-AR achievable. However, the narrow-lane ambiguity fixing rates for such unfavorable frequency choices are not as high as those for the ideal frequency choices in Sects. 4.3. Figure 9 exemplifies the ionosphere-free phase residuals in the unit of narrow-lane wavelengths at station ALBH for day 309. All visible satellites are color coded and their residuals are Gauss filtered with a 100-epoch window as denoted by the overlain black curves. Panels a) and c) show the residuals for two ideal frequency choices (GPS L1/L2 and Galileo E1/E5a) of which the standard deviations are 0.09 and 0.08 cycles. More than 96% of residuals are within ±0.25 cycles, and the narrow-lane ambiguity fixing rates reach 99.7% and 100% for the L1/L2 and E1/E5a PPP-AR, respectively.

However, in the case of GPS L2/L5 PPP in panel b), the ionosphere-free phase noise is about 17 times the raw phase noise, while the narrow-lane wavelength is only about 12 cm. The resultant phase residuals have a standard deviation of 0.41 cycles which is almost five times that of GPS L1/L2 PPP. Even worse, the drastically fluctuating black curves imply that some uncalibrated observation biases (e.g., satellite L5 antenna phase centers) are destructively amplified, making only 65% of residuals fall in ±0.25 cycles and only 36.5% of narrow-lane ambiguities fixed to integers. The Galileo E5a/E5b PPP performs moderately better, despite its phase noise being amplified by even 27 times while its narrow-lane wavelength remaining around 12 cm. In panel d), about 60% of the E5a/E5b phase residuals are within ±0.25 cycles, but the black curves fluctuate less drastically than those in panel b). We hence resolved about 71.3% of narrow-lane ambiguities for the E5a/E5b PPP-AR. This result suggests that the phase OSBs in this study are even able to enable PPP-AR for the unfavorable frequency choices, though undermined by hugely amplified observation biases.

We have demonstrated that the phase OSBs are able to allow PPP-AR for any two or more frequencies of GNSS signals. However, it is unknown whether single-frequency PPP-AR is also achievable conceptually. We hence correct the pseudorange and carrier-phase measurements on frequency q for code and phase OSBs and then lump the bias terms into new clock and ambiguity parameters to be estimated, as exemplified by Eqs. (18) and (19), that is,

$$\begin{aligned} \left\{ \begin{aligned} {\hat{P}}_{i,q}^k&=\rho _{i,q}^k+c\left( \grave{t}_i-\breve{t}^k\right) +g_q^2\gamma _i^k \\ {\hat{L}}_{i,q}^k&=\rho _{i,q}^k+c\left( \grave{t}_i-\breve{t}^k\right) -g_q^2\gamma _i^k+\lambda _q\grave{N}_{i,q}^k \end{aligned} \right. \end{aligned}$$
(21)

where

$$\begin{aligned} \left\{ \begin{array}{l} \grave{t}_i=t_i+\dfrac{d_{i,q}}{c} \\ \grave{N}_{i,q}^k=N_{i,q}^k+b_{i,q}-\dfrac{d_{i,q}}{\lambda _q} \end{array} \right. \end{aligned}$$
(22)

Encouragingly, the theoretical form of the satellite clock parameter \(\breve{t}^k\) in single-frequency PPP is the same as the legacy clock \({\bar{t}}^k\) defined by the IGS, as proved by Eq. (20). The ambiguity parameter \(\grave{N}_{i,q}^k\) becomes resolvable once the receiver-dependent biases \(b_{i,q}\) and \(d_{i,q}\) are eliminated in single differencing and the slant ionosphere delays are precisely mitigated in a regional reference network (see Geng et al. 2010; Wübbena et al. 2005).

6 Conclusions and outlook

In order to implement PPP-AR flexibly based on any GNSS frequency choices and observable combinations (i.e., all-frequency PPP-AR), we proposed a method to compute ambiguity-fixed phase clock/OSB products based on code OSBs in an uncombined observation model. Time-variable IFCBs on any third-frequency observables are modeled as piece-wise linear biases to be combined with the time-constant phase OSBs. Such phase and code OSBs could be corrected straightforwardly from raw GNSS measurements, and the integer properties of the resultant PPP ambiguities based on any frequency choices and observable combinations would be fully recovered, even though it was the legacy (but ambiguity-fixed) satellite clocks that were applied throughout.

We used a global GPS/Galileo network in November of 2020 to compute L1/L2/L5 and E1/E5a/E5b/E5/E6 phase OSBs, and found that their temporal stability was subject to the time-variable behaviors of code OSBs. The more stable the code OSBs, the more stable the phase OSBs over time. Once these phase OSB products were applied to dual-frequency PPP, roughly over 95% of wide-lane and narrow-lane ambiguity residuals were within \(\pm 0.25\) cycles and \(\pm 0.15\) cycles, respectively, in any case of GPS L1/L2, L1/L5, Galileo E1/E5a, E1/E5b, E1/E5 and E1/E6 PPP. As a result, the mean fixing rates for both wide-lane and narrow-lane ambiguities reached 95% and the positioning precision in the east component was improved by 30–60% in all dual-frequency PPP tests.

It should be stressed that the key to computing such phase clock/OSB products is the eligible code OSB products of which the bias datum agrees with the satellite clock datum. Only in this case can the ambiguity-fixed clocks on the baseline frequencies be applied to all-frequency PPP-AR. Though multi-frequency PPP-AR is not attempted explicitly in this study, we believe that it is also achievable since the extra-wide-lane ambiguity fixing (e.g., GPS L2/L5, Galileo E5a/E5b, etc.) has turned out to be 100% successful once the phase OSBs are corrected. We believe that all-frequency PPP-AR can easily adapt to the change of users’ GNSS frequency choices and observable combinations, and is more robust whenever a prescribed carrier frequency of signals are lost especially in real time.