1 Introduction

The International Gravity Reference System (IGRS) will be realized by absolute gravity observations and the comparisons between the absolute gravimeters that make the observations (Wilmes et al. 2016; Wziontek et al. 2021). The system will provide an accurate and unified global gravity reference, but the long-term stability of reference stations in the system must be studied, and in areas where the gravity field is not stable and its changes in time must be investigated. Maintaining the gravity system in areas where the gravity field undergoes changes, for example due to glacial isostatic adjustment (GIA) (e.g. Wu and Peltier 1982; Ekman and Mäkinen 1996; Lambert et al. 2001; Teferle et al. 2009), tectonics (e.g. Van Camp et al. 2016), non-tidal sea-level variations (Olsson et al. 2009), hydrological mass variations (Pálinkáš et al. 2013) and other geophysical processes (see, e.g. Van Camp et al. 2017, for an overview), requires gravity monitoring and an understanding of the ongoing processes.

In Northern Europe, the gravity changes continuously due to GIA. Due to the disappearance of past ice loads, the Earth’s crust is continuously rising, causing vertical velocities up to 1 cm/yr in Fennoscandia (Milne et al. 2001). This postglacial rebound (PGR) process has been extensively studied with a variety of techniques, such as tide gauges (Ekman 1996), repeated precise levelling (Mäkinen and Saaranen 1998) and continuous observations using global navigation satellite systems (GNSSs) (Johansson et al. 2002; Kierulf et al. 2014; Lahtinen et al. 2019). Contemporary uplift rates determined by these techniques are used to constrain geophysical models of GIA (e.g. Milne et al. 2004) and create mathematical empirical uplift models (e.g. Vestøl 2006). By combining the geophysical models with the empirical models, semi-empirical models are created for the Fennoscandian area (Ågren and Svensson 2007; Vestøl et al. 2019). Steffen and Wu (2011) give an overview of data and GIA modelling in Fennoscandia.

Additional information on the GIA processes can be obtained by gravity measurements. The ratio between the gravity change rates and uplift rates is of particular interest, as gravity changes reflect not only the effect of the vertical motion but also of mass redistribution in the Earth’s interior related to GIA. The ratio is also used to evaluate the motion of the origin of the global terrestrial reference frame (e.g. Mazzotti et al. 2011; Lambert et al. 2013) and to separate the effect of past and present ice-mass changes (e.g. Van Dam et al. 2017; Omang and Kierulf 2011). The ratio was in an early stage determined at − 0.154 µGal/mm (where 1 µGal = 10–8 m/s2) by Wahr et al. (1995) through modelling over Antarctica and Greenland. Since then, ratios have been determined from gravity and GNSS observations for the different postglacial rebound regions: Fennoscandia (e.g. Ekman and Mäkinen 1996; Mäkinen et al. 2005; Timmen et al. 2012; Ophaug et al. 2016) and Laurentia (e.g. Larson and van Dam 2000; Lambert et al. 2006; Mazzotti et al. 2011). The most recent result for Fennoscandia is by Olsson et al. (2019): they investigated absolute gravity time series from 59 stations covering time spans up to three decades and concluded that the ratio obtained from the absolute gravity time series and the latest land uplift model for the region is in agreement with the modelled relation \(\dot{g} = 0.03 - 0.163\dot{h}\) given in Olsson et al. (2015). It is expected that we will find that the relationship is not linear over the whole area once we get better time series at higher resolution.

The Nordic countries, and in particular Finland, have a long history of absolute gravity measurements. Absolute gravity measurements in Finland started already in the 1960s using a long wire pendulum (Hytönen 1972). Absolute gravity measurements with free-fall instruments started in 1976 and continue to this day. In this paper, we present absolute gravity available in Finland between 1976 and 2019 and use them to estimate gravity rates for GIA studies. Different types of free-fall instruments were used. The data sets start with a measurement by the IMGC instrument in 1976 and two GABL measurements in 1980 and continues in 1988 with 14 years of JILAg data (with sporadic contributions by FG5), 10 years of FG5 data and 6 years of FG5X data. Olsson et al. (2019) essentially used only the FG5 data in their final solution, while we add data to both ends of the time range. We look for a way to include also the IMGC, GABL and JILAg data, which are associated with larger uncertainties, into the solutions. This will considerably extend the time span of the data used. We do not only add more data to the stations treated in Olsson et al. (2019); we add also data from five additional stations which improve the spatial coverage. Overall, we will analyse up to 43 years of absolute gravity measurements on 12 stations in Finland. Using the very long time series, we will look at the time needed for gravity trends to stabilize over time. Then, we will use the gravity trends that have shown to be stable in time to study the relationship between gravity rates and uplift rates, not only from the semi-empirical land uplift model, but also from GNSS time series, including the most recent GNSS solution from Lahtinen et al. (2019). The new ratios between gravity rates and uplift rates we present will give new input for future GIA studies.

The absolute gravity data will be presented and analysed in Sect. 2, together with a description of the land uplift model and GNSS data used later in the study. In Sect. 3, we will estimate and analyse gravity trends for each station. In Sect. 4, we will investigate the gravity change rate conversion times, and in Sect. 5, we will determine and analyse the ratio of gravity velocities and vertical velocities. Section 6 gives a summary and conclusions.

2 Data

2.1 Absolute gravity observations

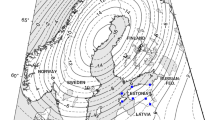
The Finnish absolute-gravity-station network, suitable for repeated measurements with an FG5-type absolute gravimeter, consists currently of 23 stations (see Fig. 1). In this study, we consider only those 12 stations, which have at least 3 measurements made over a time span of at least 3 years (red dots in Fig. 1). At the Metsähovi Geodetic Research Station (MGRS), absolute gravity measurements were taken at four different locations over the years: AA, AB, AC and AG, of which only AB and AC are currently in use. MGRS hosts the gravity laboratory of FGI with, e.g. two co-located superconducting gravimeters. The gravity laboratory of MGRS also houses the National Standards Laboratory for free-fall acceleration of gravity. Stations Vaasa AA and AB are located 15 kms apart. All stations in Finland are co-located with permanent GNSS stations of the Finnish Permanent GNSS Network, FinnRef® (Koivula et al. 2012), except for Kilpisjärvi, Oulu and Vaasa AA. (Table S1 gives more details.)

Fig. 1
figure 1

Absolute gravity stations in Finland. Red dots are stations with more than three absolute gravity observations at least 3 years apart. Grey dots are stations with less observations and are not used in this study. Contour lines show the expected GIA-induced gravity change rate according to the NKG2016LU_gdot model (Olsson et al. 2019)

Full size image

We analyse all absolute gravity observations made at the 12 stations until the end of 2019. Table 1 gives an overview of the organizations and instruments that measured at the stations in Finland between 1976 and 2019. First absolute gravity measurements were taken in 1976 with the IMGC gravimeter at Vaasa AA and Sodankylä (Cannizzo et al. 1978) and in 1980 with the GABL gravimeter in Metsähovi and Sodankylä (Arnautov et al. 1982). The Finnish Geodetic Institute (FGI) performed repeated measurements with the JILAg free-fall-type gravimeter JILAg-5 (Faller et al. 1983; Niebauer et al. 1986) between 1988 and 2002 at Metsähovi, Vaasa, Sodankylä, Joensuu and Virolahti. During this time also the FG5-type gravimeters (Niebauer et al. 1995), FG5-102, FG5-111 and FG5-101, visited Metsähovi and the FG5-111 also Vaasa. Since 2003, the measurements are part of the Nordic Absolute Gravity Project in the Working Group for Geodynamics of the Nordic Geodetic Commission. Within the framework of this project, teams of the Institut für Erdmessung (IfE) visited Finland with the FG5-220 between 2003 and 2008, measuring in Metsähovi, Vaasa and Sodankylä (Gitlein 2009). The FGI measured with the FG5-221 gravimeter between 2003 and 2012. In 2013, the FG5-221 was upgraded to the FG5X-221 model replacing the dropping chamber with a chamber incorporating a recoil compensating driving mechanism of the wagon that carries the test mass before and after the drop (Niebauer et al. 2011). Also, the free-fall distance was increased. The upgrade improved the performance of the instrument resulting in smaller uncertainties. The newest stations Kilpisjärvi, Kivetty, Oulu and Savukoski have only been measured with the FG5X-221. Data of instruments that visited Metsähovi between 2003 and 2019 for comparisons, but did not visit other stations in Finland, were not taken into account.

Table 1 Organizations and instruments that performed absolute gravity measurements used in this study in Finland between 1976 and 2019
Full size table

Details on the data processing are given in the electronic supplementary material. For the compilation of the data for this study, new vertical gravity gradients were calculated for the stations including the newest available gravity gradient measurements. To account for a possible nonlinearity of the gradient, a second-degree polynomial representation of the gradient was introduced for all stations except for Oulu, where gradient data were not sufficient for a second-degree polynomial fit. (Parameters are given in electronic supplementary material Table S2.) Using the new gradient values, all gravity values were transferred from the effective height (Timmen 2003) of the measurements, where the measured gravity value is invariant to the gradient value (~ 84 cm for JILAg, ~ 121 cm for FG5 and ~ 127 cm for FG5X), to the common transfer height chosen close to the effective heights of FG5 or FG5X: 120 cm for stations with FG5 measurements and 127 cm for stations with only FG5X measurements. All data can be found in electronic supplementary material (Table S3). The measurements taken over the years in Metsähovi at the stations AA and AG were transferred to the station AB using relative gravity differences measured between these stations. The gravity transfer from the AC pillar to the AB pillar was recalculated for this study using all gravity differences from absolute gravity measurements made with the FG5(X)-221 instrument in successive days on these pillars between 2003 and 2019.

2.2 Instrument stability and performance

When observing time series with an instrument, it is important to monitor the stability of the instrument in time. The stability of instruments becomes even more important when more than one instrument is used. Possible offsets between instruments must be investigated. Table 2 shows the results of the International and European absolute gravimeter comparisons for the instruments that operated in Finland. The way results are given for different comparisons differs from year to year. To be able to compare the results, we made an attempt to harmonize the way the results are given by showing them in the same way as for the comparison of 2013, 2015 and 2017. There, the offset is the average of the differences found between the measurements and the station reference values and the uncertainties given are the RMS values of the expanded uncertainties of the differences, where the measurement uncertainties as well as the reference value uncertainties are taken into account. For the early comparisons from 1981 to 1997, we present only offsets. At these comparisons, the IMGC and GABL offsets are estimated to have uncertainties in the range of 20 µGal and the JILAg-5 around 10 µGal. FG5 offset uncertainties would be around 5 µGal.

Table 2 International (ICAG) and European (ECAG) absolute gravimeter comparisons and the deviations from the reference value in µgal of participating instruments that operated in Finland between 1976 and 2019
Full size table

The first international comparisons of absolute gravimeters in the 1980s showed large variations between the instruments compared to later comparisons (Boulanger et al. 1983, 1986, 1991). However, the instruments shown here were in agreement when considering their large uncertainties. Due to continuous evolution of the instruments, it is not clear whether the results of IMGC and the GABL in 1989 can be used with confidence to assess measurements in Finland in 1976 and 1980, respectively. Moreover, comparisons before 1994 consisted only from AGs of the pre-FG5 generation, and their reference values are possibly not consistent with later comparisons.

In the 1990s, the FG5 instruments participated for the first time in the international comparisons. For the 1994 comparison, a new offset for the JILAg-5 instrument was calculated afterwards. Due to instrumental problems, results of the JILAg-5 instrument were excluded 2001 from the final comparison results (Vitushkin et al. 2002). No conclusion can be made on possible offsets between the JILAg-5 instrument and the FG5 instruments during this time.

Since 2001, the comparisons are dominated by FG5 instruments. Starting 2009, the international (CCM.G) and European (EURAMET.M.G) comparisons have been divided in a CIPM Key Comparison (KC), as defined by the Mutual Recognition Arrangement of the International Committee for Weight and Measures (CIPM MRA) (CIPM 1999), and a CIPM Pilot study. In the KC only national metrology institutes (NMI) and designated laboratories (DI) can participate, and the Pilot Study is open for any institute (Jiang et al. 2012). The FG5(X)-221 instrument has, as the national standard for the free-fall acceleration, participated in all KCs, whereas the other FG5(X) instruments, that have measured in Finland, have participated in the Pilot Studies. For all comparisons, the results of the instruments that operated in Finland were in agreement with the comparison reference values. The FG5-102 showed a large difference to the comparison value in 2011 (Francis et al. 2013), but this instrument did not visit Finland after 1994, when it performed better in the ICAG1994.

The early IMGC and GABL results differ by 13 µgal (Boulanger et al. 1983). In addition, their relation to later instruments cannot be well established. We therefore give the results of these both instruments large uncertainties of 10 µgal in the trend calculations.

In addition to the international and regional comparisons, also bilateral comparisons and double occupations have frequently taken place in Fennoscandia. Their results are given in electronic supplementary material. We come to the conclusion that overall the ICAG and ECAG results (Table 2) and the results of the bilateral comparisons and double occupations do not allow to conclude consistent and significant offsets or changes in time for the instruments at the times they were operating in Finland.

However, in Chapter 3 we will use the long time series at Metsähovi and other stations to conclude an offset of approximately + 7 µGal for the JILAg-5 measurements with respect to the FG5(X) measurements. This is similar to Timmen et al. (2008) who derived an offset of + 9 µGal for the JILAg-3 with respect to the FG5-220 from the time series at Clausthal, Lambert et al. (2001) who found + 7 µGal for the JILAg-2 relative to the FG5-106 from AG time series in North America, and Pálinkáš et al. (2013) who found up to + 9 µGal for the JILAg-6 from a large number of field stations in Czech Republic, Slovakia and Hungary.

2.3 Absolute gravity measurement uncertainty

The g-software, used for acquisition and postprocessing of FG5(X) data (Micro-g LaCoste 2007), gives 3 numbers related to quality of the measurement value: the set scatter, the measurement precision and the total uncertainty. The measurement precision, i.e. the standard deviation of the measurements, combined with instrumental-related uncertainties forms the total uncertainty (e.g. values used in Olsson et al. 2019). The manufacturer of the FG5 estimated the instrumental contribution to standard uncertainty at 1.1 µGal (Niebauer et al. 1995). This uncertainty budget does not cover all instrumental components, and also site-dependent uncertainties are not included.

The most careful uncertainty estimates for absolute gravity measurements, combining the standard deviation of the measurements with a full set of instrument-related uncertainties and site-dependent uncertainties, are typically those submitted by the owners of the gravimeters in connection with international comparisons of absolute gravimeters, starting with the ICAG 2005, where they have been obligatory. For the FG5(X) gravimeters used in this study, these combined standard uncertainties range from 1.9 to 2.7 µGal for a gravity value provided close to the effective height (i.e. with a near-negligible contribution by the uncertainty of a vertical gravity transfer). For the FG5-221 and its upgrade FG5X-221, the values are mostly 2.6 µGal and 2.3 µGal, respectively. These values are generally representative for pre-2005 FG5 data as well. Long-term and seasonal changes in local hydrography are not covered by the uncertainty budget.

Because of their more complete uncertainty budget, we prefer to base our uncertainty estimates on the comparison results instead of the uncertainty estimates of the g-software. The site-dependent contributions at our stations and those at comparison sites are comparable, and large micro-seismic noise only rarely increases the total uncertainty value. We therefore assign a standard uncertainty of 2.6 µGal to all FG5 measurements and 2.3 µGal to the FG5X-221 measurements.

No uncertainty estimates were routinely produced for the measurements with the JILAg-5, and during the period, it participated in the international comparisons; none were required by them either. However, estimates were calculated in calibration certificates (e.g. for measurements with the purpose of establishing reference gravity stations) and typically resulted in standard uncertainties of around 5 µGal. These uncertainties are valid at the observation height of the JILAg instrument. Taking this and the results of the comparisons (Tables 2, 3) into account as well as the uncertainties of the transfer from the observational height of around 80 cm to the common reference height of 120 cm, we adopt 7 µGal uncertainties for all JILAg-5 measurements.

Table 3 Gravity trends \(\dot{g}\) in µGal/yr
Full size table

The uncertainties of the transfers to the AB pillar in Metsähovi were taken into account for the JILAg and FG5(X) measurements by increasing the uncertainties through error propagation for those measurements accordingly.

For the IMGC and for the GABL, we use 10 µGal from Cannizzo et al. (1978) and Arnautov et al. (1982), respectively.

2.4 Land uplift model NKG2016LU

The NKG2016LU model (Vestøl et al. 2019) is the latest official land uplift model for Northern Europe of the Nordic Geodetic Commission (NKG). It is a semi-empirical land uplift model where a GIA model, developed in the project based on a geophysical approach, was merged using a remove–interpolate–restore technique with an empirical model determined from geodetic GNSS measurements and repeated levelling observations. Interpolation was done through collocation (Vestøl et al. 2019). In contrary to earlier models, such as NKG2005LU (Ågren and Svensson 2007; Vestøl 2006), tide gauge data were not included. An uncertainty grid was estimated for the model based on uncertainties of the different components. The model comes in three versions: NKG2016LU_lev, NKG2016LU_abs (Vestøl et al. 2019) and NKG2016LU_gdot (Olsson et al. 2019). NKG2016LU_lev gives land uplift values relative to the geoid as measured by repeated levelling. NKG2016LU_abs gives the absolute land uplift values in the ITRF2008 reference frame as measured by GNSS. NK2016LU_gdot gives gravity uplift rates. It was determined by multiplying NKG2016LU_abs with the factor − 0.163 µGal/mm. The factor was determined by Olsson et al. (2015) based on geophysical modelling and found valid based on absolute gravity results in Olsson et al. (2019). The uncertainty of the factor was estimated at ±  ~ 0.016 µGal/mm (Ophaug et al. 2016). The NKG2016LU model currently gives the best representation of the GIA-induced land uplift, providing also reliable uplift values for gravity points not located at GNSS or levelling points. We therefore use NKG2016LU_abs and NKG2016LU_gdot as a reference model in this study.

2.5 GNSS observations

In addition to the land uplift model, we use uplift velocities from three GNSS datasets: The first GNSS dataset is one of the latest results of the BIFROST-project (Baseline Inferences for Fennoscandian Rebound Observations, Sea Level, and Tectonics) from Kierulf et al. (2014). Two sets of velocities are given: one in the International Terrestrial Reference Frame 2008, ITRF2008, (used here) and another in a regional reference frame essentially determined by their preferred GIA model. The provided uncertainties include white and flicker noise.

The second GNSS dataset is from Vestøl et al. (2019) and was used in the calculation of the NKG2016LU model. It is the latest BIFROST reprocessing and differs from Kierulf et al. (2014) by, for example, the noise model that here includes white noise and power law noise. Vertical velocities are given in ITRF2008. The estimated uncertainties are, however, too optimistic, and we multiply them with 1.41, as is suggested in Vestøl et al. (2019).

The third GNSS data set is from Lahtinen et al. (2019). It is a product of the joint GNSS Analysis Centre of the NKG. Vertical velocities are given in ITRF2014, and uncertainties include flicker and white noise. The authors conclude that the uncertainties may be too optimistic at single stations.

3 Gravity change rates

Figure 2 shows the time series of all stations. Two sets of trends were estimated through the observed gravity time series. The first set of trends, \(\dot{g}_{1}\), were calculated for each station separately applying a weighted least squares adjustment, using the weights adopted in Sect. 2.3. In this solution, no offsets between instrument types were applied. At stations where measurements are available from different types of instruments, also separate trends were calculated from FG5(X)-only measurements (Joensuu, Metsähovi, Sodankylä, Vaasa AA, Vaasa AB and Virolahti), only JILAg measurements (Metsähovi) or only FG5 and JILAg measurements (Metsähovi and Sodankylä). The standard errors of unit weight of the station-wise trend adjustments including all data varied between 0.1 (Kilpisjärvi) and 1.46 (Sodankylä). The \(\dot{g}_{1}\) trends are shown in Fig. 2 and Table 3.

Fig. 2
figure 2

Observed absolute gravity time series and their trends at stations: a Joensuu, b Kevo, c Kilpisjärvi, d Kivetty, e Kuusamo AB, f Metsähovi, g Oulu, h Savukoski, i Sodankylä, j Vaasa AA, k Vaasa AB, l Virolahti. The different instruments are given as: blue square for IMGC, grey circle for GABL, red diamonds for JILAg-5, blue triangles for FG5-111, yellow triangles for FG5-220 and green triangles for FG5-221 and FG5X-221. For clarity, no distinction was made between the different instruments of the same type in sub-figure f, where all FG5 and FG5X data are represented by green triangles. Solid trend lines include all data with no offsets applied, dashed trend lines only part of the data and orange trend lines all data with offsets applied. Note the different ranges of the axes.

Full size image

To investigate the possible offsets between legacy instruments and the FG5(X) instruments (see Sect. 2.2), we calculate a second set of trends, \(\dot{g}_{2}\). Here the trends of stations with observations of other instruments in addition to FG5(X) observations were estimated in one joint adjustment, where also offsets were estimated for instruments other than FG5(X). The observation equation used in the least squares adjustment is the following:

$$ g_{ijk} = a_{j} + b_{j} t_{i} + c_{k} + \varepsilon_{ijk} , $$
(1)

where \(g_{ijk}\) is the gravity value at epoch i, station j and measured with instrument k. aj and bj are the constant and trend for station j and ck is the offset of instrument k. ck is kept zero for measurements with the FG5 and FG5X instruments. For the observations, we again used the weights that are adopted in Sect. 2.3. The combined adjustment resulted in a standard error of unit weight of 0.83.

The following offsets were found: 31.39 ± 10.90 µGal for the IMGC instrument, 32.59 ± 7.36 µGal for the GABL instrument and 6.76 ± 0.81 µGal for the JILAg-5 instrument. Because the adjustment included only one IMGC measurement in Sodankylä, as a result this measurement did not influence the trend value for Sodankylä. One may argue that the large amount of data in Metsähovi will dominate the offset estimation. When leaving the Metsähovi data out of the adjustment, offset values were found of 33.56 ± 11.05 µGal, 28.66 ± 10.83 µGal and 8.99 ± 2.24 µGal for the IMGC, GABL and JILAg-5 instruments, respectively. Especially for the JILAg-5 instrument, the difference between the offset solutions is significant. Both offsets for the JILAg-5 instruments are at the same level as the offsets found for other JILAg instruments in other studies (Sect. 2.2): Olsson et al. (2019) found an offset of 7.74 ± 0.78 µGal for the offset between the JILAg-5 and FG5, but estimated a rather low trend of − 0.41 ± 0.06 µGal/yr for Metsähovi using the offset. In the final solution of Olsson et al. (2019), the JILAg-5 measurements were left out. Lambert et al. (2001) found for the JILAg-2 an offset of 7.1 ± 1.9 µGal based on 71 JILAg and FG5 observations over 13 years. The offsets found for the JILAg-3 (9.4 ± 1.4 µGal) and JILAg-2 (8.7 ± 1.7 µGal) in Timmen et al. (2008) and Pálinkáš et al. (2013), respectively, are larger, but are based on less data: the result of Timmen et al. (2008) was based on 29 JILAg observations over 16 years, succeeded by only 4 FG5 observations made within one year. The result of Pálinkáš et al. (2013) was based on 11 years of JILAg and FG5 data that were treated within years as simultaneous measurements, assuming no variations due to hydrology or geodynamics between the measurements. The uncertainty of the second JILAg-5 offset solution here, calculated without Metsähovi data, is also very large. Therefore, we will use the first offsets that were calculated in the adjustment that included the Metsähovi data and of which the JILAg-5 offset agreed with the offsets calculated in Olsson et al. (2019) and Lambert et al. (2001).

When estimating also an offset for the FG5X-221 instrument in the combined solution, an offset of − 1.41 ± 0.58 µGal was found. Although the offset is significant when considering its own uncertainty, the offset is smaller than the uncertainties for individual measurements. Considering (a) that the results of the three international comparisons, where the FG5X-221 participated, show no consistency between the years, (b) that in these comparisons both FG5-type and FG5X-type instruments are well represented, and (c) that no group offsets can be seen between these two types of instruments in the comparisons, we at this stage prefer to use the combined solution with no FG5X-offset calculated. The \(\dot{g}_{2}\) trends, estimated with offsets for the IMGC, GABL and JILAg-5 instruments, are also shown in Fig. 2 and Table 3.

From Table 3, it is clear that the time series of the new stations Kilpisjärvi, Kivetty, Oulu and Savukoski are not yet long enough to produce reliable gravity trends. Although the time series of these stations show clear trends (Fig. 2), their estimated trends have large uncertainties and differences with the \(\dot{g}_{NKG}\) values predicted by the NKG2016LU_gdot model are large with large uncertainties (Table 3). For these data, it is clear that a time span of 5 years or less is not enough to determine accurate reliable gravity trends. For the Kevo station, even a longer time span of 12 years has not been enough (Fig. 2b). This station showed a small positive trend of 0.21 ± 0.46 µGal/yr in Olsson et al. (2019) after 6 years. Now, after 12 years, the trend of − 0.22 ± 0.24 µGal/yr is negative and its uncertainty smaller, although when taking their uncertainties into account the trends agree (just). The difference with the trend value from the uplift model is large and significant. The reason is for the unexpected low trend value we find in the local environment of the station. The Kevo station is situated on a sloped peninsula surrounded on three sides by the Kevo Lake 20 m below. This complex hydrologic setting strongly influences the gravity measurements, although they are usually taken around the same time in summer. For the above reasons, the new stations with short time series as well as the Kevo station are excluded from the analyses later in this study.

Also at other stations with longer time series, effects of the local environments are visible. For example, in Joensuu (Fig. 2a) the correlation between the gravity residuals and the groundwater level in a nearby well is 84%. The ground water level was exceptionally high in 2004 and very low, 1.5 m lower, during the measurements in 2006. This is visible as a high gravity value in 2004 and a very low value in 2006. The measurement in 2006 pulled the trend downwards in early trend calculations (Bilker-Koivula et al. 2008). But now, with more data, the 2004 and 2006 observations show up as outliers.

The time series in Metsähovi also show large deviations of the observations around the estimated trends. From studies with the superconducting gravimeter in Metsähovi, it is known that a large part of the variations in gravity can be explained by variations in subsurface water storage and the level of the Baltic Sea (Mäkinen et al. 2014). In a preliminary study by Virtanen et al. (2014), 10 years of superconducting gravity data in Metsähovi were analysed together with the data of the FG5-221. It was shown that most of the variations in the absolute gravity data are also seen in the superconducting time series and they can therefore be attributed to the same environmental signals. Correcting the absolute gravity data for the different environmental signals or alternatively using the superconducting data had only a small effect on the trends estimated from the absolute data, due to the length of the time series. A closer synergy between absolute and superconducting gravity data in Metsähovi is anticipated for future studies.

In most of the \(\dot{g}_{1}\) solutions, a bigger trend value is obtained when all measurements are used in comparison with trends calculated from only FG5(X) or JILAg and FG5(X) measurements. In most cases, these higher trend values do not agree with the trend values of the uplift model, but trends from FG5(X)-only measurements come close (Table 3). In Metsähovi, where a lot of data is available, the trend is derived with high precision when all available data are used in the \(\dot{g}_{1}\) solution and the difference with the uplift model is small. In Fig. 2f, the JILAg data show a larger scatter around the trend than the FG5(X) data; this can partially be explained by the larger uncertainties of the measurements. There is only little overlap with FG5 measurements as the JILAg-5 measurements ended in 2002 and the FG5-221 measurements started in 2003. When looking in Metsähovi at the trends of JILAg-only data or FG5(X)-only data in the \(\dot{g}_{1}\) solution, smaller trends are found, indicating an offset between the instruments, which supports the findings for other JILAg instruments (Sect. 2.2). In the joint solution, \(\dot{g}_{1}\), with offset estimation, a trend for Metsähovi is derived that is close to the trend obtained with FG5(X) only (Table 3). In general, the trends in the \(\dot{g}_{2}\) solution are close to the FG5(X)-only solutions or somewhere in between the FG5(X)-only solution and the \(\dot{g}_{1}\) solutions including JILAg and FG5(X) data.

Only in the case of Virolahti, a very different trend is found when the offset between JILAg and FG5(X) is introduced. The FG5(X) data alone were not yet enough to produce a reliable trend. The \(\dot{g}_{2}\) trend for Virolahti is in agreement with the uplift model.

At both stations in Vaasa, all estimated trends are larger than the trends of the uplift model, but differences with respect to the model are within their uncertainties. The model seems to underestimate the gravity changes at these stations by − 0.17 and − 0.10 µGal/yr lower than the trends of the model (Table 3). A reason for this difference could be their proximity to the centre of the uplift area. Olsson et al. (2015) found that using a simple \(\dot{g}{/}\dot{h}\) ratio for the whole Fennoscandian uplift region, when converting uplift rates from a GIA model to gravity change rates can cause differences with observed gravity velocity of between − 0.04 and 0.04 µGal/yr over the whole area, with an underestimation of \(\dot{g}\) of around − 0.02 µGal/yr close to the centre of the uplift and an overestimation of + 0.02 µGal/yr in the South-Eastern and most Northern part of Finland. Although the sign is right, the underestimation modelled by Olsson et al. (2015) is much smaller than what we see at Vaasa AA and AB. Another effect to consider is the apparent sea level decrease in the Baltic Sea due to the PGR. Olsson et al. (2009) estimated the effect on gravity to be between − 0.0058 µGal/yr and − 0.0377 µGal/yr for Swedish absolute gravity stations and Metsähovi. The Vaasa AA station is only 0.5 km from the sea shore and has an elevation of 3 m and may well experience this effect. However, again the sign is right, but the values are smaller than what we see at Vaasa AA. We suspect that part of the stronger trend at AA may also be related to long-term changes in the subsurface water storage surrounding the point which is not on bedrock. We plan to investigate this assumption in a separate study. The situation is different for Vaasa AB. This station is located inland more than 10 km from the sea shore, and it is founded on bedrock at 34 m elevation.

In Olsson et al. (2019), of the three stations that were part of the \(\dot{g}_{O\_II}\) solution, only the trend of Vaasa AB has a small difference with the trend of the uplift model. There, the stations Joensuu and Sodankylä showed much lower trends than the uplift model, although statistically the Joensuu trend also agreed with the uplift model. With 7 years of more data and a robust trend calculation using offsets, we are confident that we now have 7 stations with reliable trends. When the uncertainties of the estimated trends and of the uplift model are taken into account, all seven \(\dot{g}_{2}\) trends we show here are in agreement with the uplift model and the agreement is at the same level or even better than for the \(\dot{g}_{1}\) FG5(X)-only solutions. This proves that our approach works: When offsets for the older instruments are introduced, the measurements of these instruments can be included in the calculations and can even strengthen the solutions.

4 Gravity change rate convergence

Time series with a lot of data over a long time span give us the possibility to study how long absolute gravity time series are needed to get reliable PGR-related trend rates. Gitlein (2009) and Timmen et al. (2012) detected the gravity trends with an average uncertainty of 0.6 µGal/yr for the time span of 4–5 years of their studies with yearly measurements. Van Camp et al. (2005) estimate that a time span of 15–25 years is needed to determine the gravity change rate with an uncertainty of 0.1 µGal/yr, depending on the noise model. In Table 3, we saw that a time span of 4–5 years is not enough to reliably determine the PGR-induced gravity changes. For longer time series, the uncertainty values of the estimated trends come close to or even reach 0.1 µGal/yr (Table 3).

The longest time series in Finland is for Sodankylä with 43.0 years. When leaving measurements with the early instruments GABL and IMGC out, there are time series, containing JILAg and FG5(X) data, of 31 years in Metsähovi, Sodankylä and Vaasa AA (see Table 3). Even when considering FG5(X)-only measurements, there are 3 stations with over 20 years of measurements. Of the seven stations with solution \(\dot{g}_{2}\) that are in agreement with the land uplift model, only Kuusamo has a time series shorter than 15 years.

For the seven stations of solution \(\dot{g}_{2}\), we calculated for each station time series of trends starting with two measurements and adding one measurement for each new trend calculation. For the “with-offset” datasets, the offsets determined in Sect. 3 were used to correct the data of GABL, IMGC and JILAg-5. The results are shown in Fig. 3.

Fig. 3
figure 3

Gravity trends as a function of the time span between the first and the last measurement in a time series for the dataset \(\dot{g}_{2}\) with offsets for the GABL, IMGC and JILAg instruments applied (blue), for dataset \(\dot{g}_{1}\) with all data and no offsets applied (red), data sets with JILAg and FG5(X) measurements with JILAg offset applied (orange), and with only FG5(X) data (green). The expected gravity change according to the NKG2016LU_gdot model is given as a solid line and its 1σ-uncertainty as dashed lines. Note the different ranges of the axes

Full size image

Figure 3 shows that the trends converge to a stable value faster when the offsets are taken into account. Also, the trend values stabilize closer to the values expected by the land uplift model. In Metsähovi, a clear break in the convergence is seen after 23 years for the dataset containing all data without applying offsets (Fig. 3c). This coincides with the replacement of the JILAg-5 by the FG5-221. For Metsähovi and Sodankylä, where IMGC and GABL measurements took place 8 to 12 years before the JILAg measurements, the trends converge slowly and reach stability between 25 and 30 years (Fig. 3c, d). Without these old data, the trends including FG5(X) and offset-corrected JILAg data converge between 15 and 20 years and in Joensuu and Vaasa AB even faster around 10 years. This means the old IMGC and GABL data are not meaningful for the time series. The convergence of trends from combined JILAg and FG5(X) data takes more time than for FG5(X)-based trends alone, due to the larger uncertainties of the JILAg data. After 10 years, most FG5(X) trends have stabilized. Only in Metsähovi and Sodankylä, more time was needed for the trends to stabilize. In Metsähovi, the FG5(X) time series converges faster when the early FG5 measurements from before 2003 are left out (Fig. 3c).

At the Vaasa AA station, the FG5(X)-only trend values have been stable for over 10 years, but all that time about 0.15 µGal/yr higher than the trend of the land uplift model (Fig. 3e). The trend obtained in Vaasa AA from the absolute gravity measurements is reliable, which is also confirmed by its uncertainty that is smaller than the uncertainty of the uplift model. However, when considering the total uncertainty budget of the trends and the uplift model, the value of the difference, although very consistent, falls still within the uncertainty boundaries. On the contrary, the Vaasa AB trend seems to have settled at a 0.10 to 0.15 µGal/yr smaller value than the NKG2016LU_gdot value, although the latest trend value using all FG5(X) data up till 2019 is 0.10 µGal/yr larger than the uplift model value (Fig. 3f). At this station, the trend and uplift model values fall within each other’s uncertainty boundaries.

The trend value in Sodankylä seems to have stabilized only in recent years to a value close to the uplift model value (Fig. 3d). In Metsähovi, the process has been even slower. Although there are a lot of measurements, the trend value has changed slowly over time and seems to be more stable only since the last 5 years of measurements (Fig. 3c). The value in Metsähovi also seems to have stabilized at a value of around 0.10 µGal/yr lower than the NKG2016LU_gdot value. Figure 2f shows large deviations of the measurements in Metsähovi due to hydrological signals. It may be that the hydrological circumstances in Metsähovi have changed over the years, causing a slow change in gravity. The Metsähovi data must be looked at in more detail in follow-up studies, to see what causes this slow change in the trend values over time.

At Virolahti, the final trend is close to the NKG2016LU_gdot rate, but the time series contains only 4 observations and the trend has a relatively large uncertainty (Fig. 3g). More observations are needed for Virolahti to bring the uncertainty of the trend down and to be able to see to which value the trend will settle.

We must note that we have not corrected the data for any seasonal effects from hydrology. Correcting the time series for hydrological signals can reduce the variation of the gravity time series [see, e.g. Ophaug et al. (2016), Lambert et al. (2006) and Mikolaj et al. (2015)]. We expect that the convergence to a stable trend can go faster when the hydrological signal is removed.

5 Relationship between gravity change rates and land uplift rates

In estimating a linear relationship \(\dot{g} = a + b \dot{h}\) between gravity change rates, \(\dot{g}\), and vertical velocities, \(\dot{h}\), standard regression methods cannot be used as observations of both, \(\dot{g}\) and \(\dot{h}\), contain errors (“errors in variables”). The straight line, \(\dot{g} = a + b \dot{h}\), is instead fitted to the pairs (\(\dot{h}_{i} , \dot{g}_{i}\)) by minimizing the orthogonal “weighted distances” between the line and the pairs (“orthogonal regression”). Here, \(\dot{g}_{i}\) are the observed gravity trends which are subject to error, \(\dot{h}_{i}\) are the observed vertical velocities at the same locations, likewise subject to error, and a and b are the coefficients of the linear relationship we want to estimate, where \(a = \dot{g}_{{\dot{h} = 0}}\) and b the slope which is \(\dot{g}{/}\dot{h}\) for \(a = 0\). Note that we do not assume that \(a = \dot{g}_{{\dot{h} = 0}} = 0\). Thus, the estimates a* and b* are obtained by minimizing the \(\chi^{2}\) merit function, given by:

$$ \chi^{2} \left( {a,b} \right) = \sum\limits_{i = 1}^{N} {\frac{{\left( {\dot{g}_{i} - a - b\dot{h}_{i} } \right)}}{{\sigma_{{_{{\dot{g}_{i} }} }}^{2} + b^{2} \sigma_{{_{{\dot{h}_{i} }} }}^{2} }}} , $$
(2)

with respect to a and b (Press et al. 2012). Here, the \(\sigma_{{\dot{g}_{i} }}\) are the uncertainties of the \(\dot{g}_{i} { }\) and the \(\sigma_{{\dot{h}_{i} }}\) the uncertainties of the \(\dot{h}_{i}\), respectively. In another variant, we use the FREML algorithm by AMC (2002), which is based on Eq. 2, but includes the option to fit a line that goes through \(\dot{g}_{{\dot{h} = 0}} = 0\). In the sequel, the estimates b* are denoted by \(\dot{g}{/}\dot{h}\), and the estimates a* of the intercept by \(\dot{g}_{{\dot{h} = 0}}\). It is equivalent to consider the intercept \(\dot{h}_{{\dot{g} = 0}}\) of the fitted line with the \(\dot{h}\)-axis. Our gravity rates are not the best for estimating axes intercept values, as, in contrary to Olsson et al. (2019), we lack stations close to the border of the uplift area. We estimate the relationship between gravity rates of the \(\dot{g}_{2}\) solution and the vertical rates of the NKG2016LU-abs model (Sect. 2.4) and the GNSS datasets (Sect. 2.5). For the vertical rates, we use two sets of uncertainties. The first set, \(\sigma_{1}\), are the uncertainties of the vertical rates as they are provided with the rates. In the second set, \(\sigma_{2}\), we include the uncertainties of the reference frame origin motion in the uncertainties of the vertical rates by error propagation. For ITRF2008 we use for the uncertainty of the origin motion 0.5 mm/yr (drift) and 0.2 mm/yr (scale) determined by Wu et al. (2011). For ITRF2014, we use 0.33 mm/yr found by Riddell et al. (2017). The rates and their uncertainties are given in Table 4. As the origin motion of the ITRF and the drift of its scale will influence the \(\dot{h}\) in the same way at all our stations in the limited area, their influence is included in the parameter \(a\), that is the intercept \(\dot{g}_{{\dot{h} = 0}}\) or equivalently \(\dot{h}_{{\dot{g} = 0}}\) when using the uncertainty set \(\sigma_{1}\). Results are given in Table 5 and as slopes in Fig. 4. The \(\chi^{2}\)-probability, q, is an indicator for the goodness of fit, with a small value indicating a poor fit.

Table 4 Estimated gravity change rates, \(\dot{g}_{2}\), and vertical rates, \(\dot{h}_{1}\), from the NKG2016LU_abs land uplift model, \(\dot{h}_{2}\), from GPS time series in Kierulf et al. (2014), \(\dot{h}_{3}\), from GNSS time series in Vestøl et al. (2019), and \(\dot{h}_{4}\), from GNSS time series in Lahtinen et al. (2019)
Full size table
Table 5 Ratios, \(b = \dot{g}/\dot{h}\), between gravity change rates, \(\dot{g}_{2}\), and vertical rates, \(\dot{h}_{i}\), of Table 4, and intercept values \(a = \dot{g}_{{\dot{h} = 0}}\) and \(\dot{h}_{{\dot{g} = 0}}\) when the intercept values are estimated and ratios when the intercept is fixed at zero
Full size table
Fig. 4
figure 4

Observed gravity trends plotted versus uplift rates from: a the NKG2016LU_abs land uplift model (Vestøl et al. 2019), b GNSS time series by Kierulf et al. (2014), c GNSS time series of Vestøl et al. (2019) and d GNSS time series of Lahtinen et al. (2019). Closed dots represent the stations of the \(\dot{g}_{2}\) solution and open dots the other stations. Error bars are the 1-\(\sigma_{1}\) uncertainties of Table 4. A linear relation between the \(\dot{g}_{2}\) gravity rates and the vertical rates, \(\dot{g} = a + b \dot{h}\), is shown calculated with the \(\sigma_{1}\) uncertainties and the intercept \(\dot{g}_{{\dot{h} = 0}}\) estimated (solid line). For comparison, the modelled relationship, \(\dot{g} = 0.030 - 0.163 \dot{h}\), of Olsson et al. (2015) is also plotted (dashed line)

Full size image

When the intercept is not fixed and we use the \(\sigma_{1}\) uncertainties, we find \(\dot{g}{/}\dot{h}\) ratios of − 0.211 ± 0.019, − 0.217 ± 0.026, − 0.227 ± 0.024 and − 0.206 ± 0.017 µGal/mm for the relationship with uplift datasets \(\dot{h}_{1}\), \(\dot{h}_{2}\), \(\dot{h}_{3}\) and \(\dot{h}_{4}\), respectively. The fit to the data is very good with the q-values being between 0.7 and 1. The best fit is obtained with the NKG2016LU_abs model, \(\dot{h}_{1}\), with q = 0.980, and second best with the GNSS rates of Lahtinen et al. (2019), \(\dot{h}_{4}\), where q = 0.959. When including the uncertainty of the origin motion, using the \(\sigma_{2}\) uncertainties, goodness-of-fit values increase a little for all four cases. The ratios reduce a bit, but not significantly and their uncertainties increase. However, for all cases the ratios are higher than the ratios based on measurements found for Fennoscandia in the literature (Table 6), when the intercept is estimated as well.

Table 6 Relationship between gravity rates and vertical rates found in the literature for Fennoscandian PGR area or parts of it
Full size table

Not only are the \(\dot{g}{/}\dot{h}\) ratios presented in Table 5 higher than those in Table 6, also the intercepts for \(\dot{g} = 0\) and \(\dot{h} = 0\) are significantly nonzero. When forcing \(a = \dot{g}_{{\dot{h} = 0}} = 0\) in the fit, we find ratios that are smaller and in agreement with values found earlier for Fennoscandia (Table 6) when no intercept is estimated. However, the goodness-of-fit values are close to zero when using the \(\sigma_{1}\) uncertainties. When forcing the slope to go through the origin, it is more correct to use the \(\sigma_{2}\) uncertainties that include the uncertainty of the reference frame origin motion. In that case, the goodness-of-fit values are larger, but still significantly worse than without the forced zero-intercept: between 0.520 for \(\dot{h}_{3}\) and 0.747 for \(\dot{h}_{1}\). The forced zero-intercept has clearly worsened the fit and we can conclude that our data favours a nonzero intercept.

When looking at other solutions for Fennoscandia (Table 6), we see that in the earliest work no intercept values were estimated. Olsson et al. (2019) estimate intercepts that are 0.14 ± 0.14 µGal/yr at most. On the contrary, Ophaug et al. (2016) find negative intercept values that go down to − 0.210 ± 0.183 µGal/yr.

Significantly nonzero intercept values could indicate a misalignment between the origins of the reference frames of the vertical velocities (ITRF2008 for \(\dot{h}_{1}\), \(\dot{h}_{2}\) and \(\dot{h}_{3}\) and ITRF2014 for \(\dot{h}_{4}\)) and the centre of mass. However, Mazzotti et al. (2011), Altamimi et al. (2011) and Altamimi et al. (2016) state that the origins of the reference frames of our vertical references are well aligned with the centre of mass. To study this, we must use the \(\sigma_{1}\) uncertainties that do not include the uncertainties for the reference frame origin motion that is common for all stations in the area. The intercept values we find in Table 5 are larger than what could be possible based on the uncertainties in the origin motion found by Wu et al. (2011) and Riddell et al. (2017). For comparison, Mazzotti et al. (2011) and Lambert et al. (2013), who analysed absolute gravity and GNSS time series in North America, found no evidence for misalignment of the ITRF2005/2008 origin.

The GNSS velocity uncertainties may be underestimated. This could, for example, be the case for the velocities, \(\dot{h}_{4}\) as determined by Lahtinen et al. (2019). However when we increase the uncertainties of the vertical rates, similar size slope and intercept values are obtained, but their uncertainties grow. Unrealistic uncertainties of the vertical rates are needed to change the slope. But, as the results with the \(\sigma_{2}\) uncertainties show, a reasonable scaling of the input uncertainties increases the uncertainties of the intercept values from 36–57% of the value to 64–92% of the intercept value. Then, at the 2σ level the intercepts are not significant any more.

Once we obtain more data for the new stations in Finland, we may be able to strengthen the solution. Currently, when including the trends of all stations, also those with too little data and large uncertainties in the gravity trends, the \(\dot{g}{/}\dot{h}\)-ratios and intercept values and their uncertainties do not change, but the quality of the fit decreases (Table S6 in the electronic supplementary material).

The data must also be combined with data from the surrounding countries, like it was done in Olsson et al. (2019), once more data is collected and trends have improved. However, also in that publication not all stations were included in the final solution. Only 21 out of the 43 stations with enough repeated measurements were included in the final solution. When we calculated ratios and intercept values for the seven stations of our solution using the gravity trends found by Olsson et al. (2019), we find ratios between − 0.189 ± 0.021 (\(\dot{h}_{4}\)) and − 0.221 ± 0.029 (\(\dot{h}_{3} )\) µgal/mm and intercepts between 0.073 ± 0.123 and 0.224 ± 0.165 µGal/yr, when using the \(\sigma_{1}\) uncertainties (see Table S6 in electronic supplementary material). These ratios are also larger than the ratio found in Olsson et al. (2019) when using the 21 stations (Table 6).

The large intercept values and ratios pose an interesting geophysical challenge with respect to load distribution and earth response. The larger values may indicate that in addition to a gravity change due to vertical movement, there is also a gravity change and thus a mass movement, not related to the vertical movements or even GIA. GIA models are usually based on one-dimensional Earth models that do not account for lateral inhomogeneities (see, e.g. Olsson et al. 2015). It will be interesting to compare our findings with more refined GIA models. The Nordic Geodetic Commission has plans for a next-generation semi-empirical land uplift model that will, for example, also incorporate gravity observations (Vestøl et al. 2019). Together with new gravity data of more stations, it will allow for a new evaluation of the relationship between the gravity change rates and the vertical velocities.

6 Summary and conclusions

We analysed repeated absolute gravity observations of 43 years from 12 stations in Finland and calculated trends from the individual time series as well as a joined adjustment of the data in which offsets were estimated for the IMGC, GABL and JILAg-5 instruments. An offset of 6.8 ± 0.8 µGal was determined for the JILAg-5 instrument with respect to the FG5(X) instruments. When offsets estimated for the older instruments were introduced, the measurements of these instruments could be included in the calculations and could even strengthen the solutions. The trends of seven out of 12 stations were found robust and suitable for further analysis. The NKG2016LU_gdot land uplift model was in agreement with the trends of all these seven stations. In spite of the good agreement, the model underestimates the gravity trends in the Vaasa area. The reason for this must be investigated in future studies.

The long time series were used to study the time needed for the trends to stabilize. We found that when offsets were applied for the JILAg-5 data, the trend of JILAg and FG5(X) combined stabilized in between 15 and 20 years and at some stations even faster. The FG5(X) data alone stabilized in general within 10 years. It is expected that stabilization will be even faster when data are corrected for the hydrological signal. Looking at the development of the trend over time gives a good indication if a trend value is reliable or not.

Large slopes and axes intercept values were found for the relationship between gravity rates and uplift rates. Slope values between − 0.206 ± 0.017 and − 0.227 ± 0.024 µGal/mm were found and intercept values of 0.248 ± 0.089 to 0.335 ± 0.136 µGal/yr when using vertical trend uncertainties given with the trends. The intercept values may be exaggerated by extrapolation as we lack stations close to the border of the uplift area. When more data become available for the five stations that were not included in the final solution, we might strengthen the solution in future, but extrapolation remains a problem as the smallest land uplift rates in Finland do not come below 3 mm/yr. Once in the whole Nordic and Baltic area more stations with long and good time series become available, we might be able to get a stronger solution for the relation between gravity change and uplift rates. And together with the next-generation NKG semi-empirical land uplift model, we may be able to better explain our findings.

To improve the data, time series of the newest stations in Finland must be continued, and in future studies hydrological signals and gravity changes induced by geophysical processes other than the post glacial rebound must be investigated.

The absolute gravity stations and the measurements on them that are described here are the contribution of the Finnish Geospatial Research Institute, National Land Survey of Finland, to the International Gravity Reference Frame of the International Association of Geodesy. The Metsähovi Geodetic Research Station is a GGOS Core Station and has the qualifications to become both a Reference Station and a Comparison Station of the IGRF (Wziontek et al. 2021). The other absolute stations provide a high-quality network at national level.