How to account for temporal correlations with a diagonal correlation model in a nonlinear functional model: a plane fitting with simulated and real TLS measurements

Abstract

To avoid computational burden, diagonal variance covariance matrices (VCM) are preferred to describe the stochasticity of terrestrial laser scanner (TLS) measurements. This simplification neglects correlations and affects least-squares (LS) estimates that are trustworthy with minimal variance, if the correct stochastic model is used. When a linearization of the LS functional model is performed, a bias of the parameters to be estimated and their dispersions occur, which can be investigated using a second-order Taylor expansion. Both the computation of the second-order solution and the account for correlations are linked to computational burden. In this contribution, we study the impact of an enhanced stochastic model on that bias to weight the corresponding benefits against the improvements. To that aim, we model the temporal correlations of TLS measurements using the Matérn covariance function, combined with an intensity model for the variance. We study further how the scanning configuration influences the solution. Because neglecting correlations may be tempting to avoid VCM inversions and multiplications, we quantify the impact of such a reduction and propose an innovative yet simple way to account for correlations with a “diagonal VCM.” Originally developed for GPS measurements and linear LS, this model is extended and validated for TLS range and called the diagonal correlation model (DCM).

1 Introduction

Terrestrial laser scanners (TLS) capture a large number of three-dimensional (3D) points rapidly, with high precision and spatial resolution. The point clouds obtained can be visualized in specific commercial software or approximated with parametric models, among which are the increasingly popular and flexible B-spline curves or surfaces (e.g., Bureick et al. 2016; Koch 2010; Neitzel et al. 2019). The main advantage of point cloud modelization strategies over visualization comes from the possibility of performing rigorous test statistics, for example, for deformation analysis purposes (Zhao et al. 2019; Kermarrec et al. 2020a). The mathematical model can be simplified for basic objects, such as ellipsoids, cylinders or planes (e.g., Ahn 2004; Fang et al. 2015; Lehmann 2019). A linearized Gauss–Helmert (Lenzmann and Lenzmann 2004; Neitzel 2010) or Gauß–Markov model (GHM and GMM, respectively, see (Koch 1999) is generally used to estimate the parameters of the corresponding geometric primitives. Among them, planes have a simple geometry and are easy to manufacture and handle. For that reason, they are often used for calibration purpose, i.e., to estimate the uncertainty of the sensors or optimize measurements settings. Exemplarily, Wujanz et al. (2017, 2018) or Schmitz et al. (2019) derive a stochastic model for TLS range measurements using approximations of planar surfaces with different colors and material properties. Heinz et al. (2019) investigated the TLS parameter settings for optimization purposes by scanning a plane. TLS point clouds were further approximated with planes in order to improve the registration in Theiler and Schindler (2012). Plane fitting and segmentation of target surfaces are an important step in applications such as the monitoring of structures (Bolkas and Martinez 2018).

Unfortunately, a bias is introduced when the estimates of a nonlinear problem—such as a popular plane fitting—are derived by a linearized or first-order substitute problem. The second-order effect was obtained analytically by expanding the nonlinear functional model by its second-order Taylor series in Lösler et al. (2020). The authors analyzed the bias between the first- and second-order solution rigorously for a plane fitting and also studied the impact of a large number of poor measurements versus small and precise samples. The empirical results of Heinz et al. (2019) were confirmed mathematically: Both contributions highlighted the advantages of a high discretization of the point clouds regarding an increase in the signal-to-noise ratio, balancing the computation effort and the need for accurate parameter estimation. The simulated measurements in Lösler et al. (2020) were assumed to be spatially correlated by means of a rotational-invariant Taylor–Karman structured matrix (Grafarend and Schaffrin 1979). Modeling correlations as being spatial focuses on the resolution capability of TLS or their effective number of measurements (Kauker and Schwieger 2017; Schmitz et al. 2020). In this contribution, we will adopt a different approach to correlations and come back to the source of the measurements: Range from TLS—phase or time of flight—is a measure of time (Rüeger 1996); their correlations should logically be modeled as being time dependent since they are mainly linked with physical temporal effects such as laser or atmospheric noise, see Lösler et al. (2016) for investigations with total station measurements. For the sake of simplification, we will assume—and shortly justify—that angles are non-correlated and further consider that the measurements are heteroscedastic, i. e., with different variances.

Neglecting correlations in LS adjustment leads to a simplification of VCM and is known to give unrealistic and mainly underestimated a priori or a posteriori dispersion (Jäger et al. 2005, p. 214ff) see Klos et al. (2018) for GPS velocity uncertainty and Kermarrec and Schön (2014) for coordinate estimation using double differences from GPS phase observations. This discrepancy can be linked with the particular structure of the inverse of the VCM (Kermarrec and Schön 2016). Unfortunately, the VCM is involved in the computation of the aforementioned second-order solution (Lösler et al. 2020); we are entitled to think that temporal correlations will affect the corresponding bias and raise the following questions:

• 1. What is the impact of the correlations of TLS range measurements on the second-order solution regarding the first-order one?

• 2. Does the scanning configuration affect the parameter and dispersion biases?

• 3. Will the diagonal VCM that neglects correlations lead to results comparable to the one obtained with fully populated VCM? If not, is it possible to account for temporal correlations by an equivalent diagonal model?

By answering these questions, we aim to give the practitioner some indications about the impact of TLS range correlations on the second-order solution. Our goal is to weigh the benefits of this improved solution against the additional computational burden, in the presence of correlated noise. We will place ourselves, without loss of generality in the controlled framework of simulated TLS point clouds from a plane, which is a popular scanned object.

We intent to draw the attention of the reader to the risk of neglecting correlations in the first- or second-order solution, and propose a powerful yet simple alternative to the use of fully populated VCM in LS adjustment. To that aim, we will investigate the extent to which the DCM proposed for GPS correlations together with a strictly linear functional model can be applied to the nonlinear problem of a plane fitting from TLS measurements. This new model was said, ironically, to account for correlations in an “hidden” way (Kermarrec and Schön 2017a). Up to now it has never been introduced, tested nor validated in engineering geodesy for nonlinear functional models. The DCM avoids computational demanding matrix inversion, which is a non-negligible advantage when the second-order solution is worth computed, for example, regarding small objects and/or a high scanning rate. In this contribution, we propose to validate the use of the DCM in the light of simulations by analyzing real data from a scanned plane. This necessitates to choose a model for temporal correlations of range measurements from TLS: We will adopt to the Matérn model (Matérn 1960). Our proposal is inspired by the work of Kermarrec and Schön (2014) for GPS and based on a first investigations for TLS correlations (Kermarrec et al. 2019). The Matérn covariance function is widely used in geostatistics (Gelfand et al. 2010) for modeling spatiotemporal patterns. For some applications of the model, the interested reader is refereed to Lilly et al. (2017). Its three parameters, i. e., the smoothness, the correlation parameter, and the variance, make the covariance function extremely flexible and able to model all kinds of noise, from Gaussian to flicker or random walk noise. It has been recently implemented for the analysis of GPS coordinate time series in the dedicated software Hector (Bos et al. 2012), highlighting the high interest of this specific community for this process.

The paper is organized as follows: We summarize in Sect. 2 the first- and second-order solution when a linearization of the functional model is performed. We further describe in Sect. 3 the stochastic model chosen for TLS measurements and its simplification with the DCM. In Sect. 4, we present the results derived from both simulated and real TLS measurements from a plane. Sect. 5 concludes our investigations with some recommendations on how and when to account for correlations in LS plane fitting.

2 Mathematical background

2.1 Bias in an implicit functional model

The stochastic properties of the estimates derived by means of the GHM or GMM are related to the solved linearized substitute problem but not the underlying nonlinear problem. The well-known linear property of the expectation is generally invalid for nonlinear functions, i. e.,

$$\begin{aligned} {\text {E}}\left\{ {\varvec{f}}\left( {\mathbf {x}}\right) \right\}\ne & {} {\varvec{f}}\left( {\text {E}} \left\{ {\mathbf {x}} \right\} \right) , \end{aligned}$$

(1)

where ${\text {E}}\left\{ \cdot \right\}$ denotes the expectation operator. The expectation of the function is unequal to the transformed expectation value, if ${\varvec{f}}$ is nonlinear (Carlton and Devore 2017, p. 87). For that reason, the statistical properties of a linear solver cannot be passed to the nonlinear case without limitations, i. e., the derived estimates are biased. Box (1971) derives the bias of the estimates of explicit nonlinear functional models using a second-order truncated Taylor expansion. Similar expressions can be found in (e.g., Teunissen 1990; Fang 2015; Wang and Zhao 2019). Lösler et al. (2020) extend this derivation to the case of implicit nonlinear functional models including ill-posed optimization problems. Implicit functional relationships are known as more general models and, therefore, provide the widest range of application (Neitzel 2010; Lösler et al. 2020).

The second-order truncated Taylor expansion of an explicit functional model ${\varvec{f}}\left( \hat{{\mathbf {x}}} \right) = {\mathbf {y}} + \tilde{\mathbf {e}}$ is given by

$$\begin{aligned} {\varvec{f}}\left( \hat{{\mathbf {x}}} \right)\approx & {} {\varvec{f}}\left( \tilde{\mathbf {x}} \right) + {\mathbf {A}}\Delta {\mathbf {x}} + \frac{1}{2} \left[ \Delta {\mathbf {x}}^{\mathrm {T}} {\mathbf {H}}_i \Delta {\mathbf {x}} \right] _i . \end{aligned}$$

(2)

Here, $\hat{{\mathbf {x}}} = \tilde{\mathbf {x}} + \Delta {\mathbf {x}}$ is the vector of parameters to be estimated, ${\mathbf {A}}$ and ${\mathbf {H}}$ are the Jacobian and the Hessian of ${\varvec{f}}$ evaluated at $\tilde{\mathbf {x}}$, respectively. The vector ${\mathbf {y}}$ contains the measurements and $\tilde{\mathbf {e}}$ is the vector of related true errors with expectation ${\text {E}}\left\{ \tilde{\mathbf {e}}\right\} = {\mathbf {0}}$ and dispersion ${\text {E}}\left\{ \tilde{\mathbf {e}} \tilde{\mathbf {e}}^{\mathrm {T}} \right\} = \Sigma _{\mathbf {e}}$.

Since each $\tilde{\mathbf {e}}$ yields in a certain estimation error $\Delta {\mathbf {x}}$, one can express such dependencies by a corresponding Taylor series. With restriction to the second order, this series reads

$$\begin{aligned} \Delta {\mathbf {x}}= & {} {\mathbf {F}}\tilde{\mathbf {e}} + \frac{1}{2} \left[ \tilde{\mathbf {e}}^{\mathrm {T}} {\mathbf {G}}_i \tilde{\mathbf {e}} \right] _i, \end{aligned}$$

(3)

where ${\mathbf {F}}$ and ${\mathbf {G}}$ are the Jacobian and the Hessian evaluated at $\tilde{\mathbf {e}}$.

By introducing the expectations, one obtains

$$\begin{aligned} {\text {E}} \left\{ \Delta {\mathbf { x}} \right\}= & {} {\text {E}}\left\{ {\mathbf {F}}\tilde{\mathbf {e}} \right\} + \frac{1}{2} {\text {E}}\left\{ \left[ \tilde{\mathbf {e}}^{\mathrm {T}} {\mathbf {G}}_i \tilde{\mathbf {e}} \right] _i \right\} . \end{aligned}$$

(4)

Whereas the linear term becomes zero (e.g., Teunissen 2003, p. 47), i. e.,

$$\begin{aligned} {\text {E}}\left\{ {\mathbf {F}}\tilde{\mathbf {e}} \right\}= & {} {\mathbf {F}}{\text {E}}\left\{ \tilde{\mathbf {e}}\right\} = {\mathbf {0}}, \end{aligned}$$

(5)

the quadratic term leads to (e.g., Teunissen 2003, p. 49)

$$\begin{aligned} {\text {E}}\left\{ \tilde{\mathbf {e}}^{\mathrm {T}} {\mathbf {G}}\tilde{\mathbf {e}} \right\}= & {} {{\,\mathrm{tr}\,}}{\left( {\mathbf {G}}\Sigma _{\mathbf {e}} \right) }. \end{aligned}$$

(6)

It follows that the second-order improved estimates are given by

$$\begin{aligned} {\text {E}}\left\{ \Delta {\mathbf {x}} \right\}= & {} \frac{1}{2} \left[ {{\,\mathrm{tr}\,}}{\left( {\mathbf {G}}_i \Sigma _{\mathbf {e}} \right) } \right] _i, \end{aligned}$$

(7a)

$$\begin{aligned} {\text {E}}\left\{ \Delta {\mathbf {x}} \Delta {\mathbf {x}}^{\mathrm {T}} \right\}= & {} {\mathbf {F}}\Sigma _{\mathbf {e}} {\mathbf {F}}^{\mathrm {T}} + \frac{1}{2} \left[ {{\,\mathrm{tr}\,}}{\left( {\mathbf {G}}_i \Sigma _{\mathbf {e}} {\mathbf {G}}_j \Sigma _{\mathbf {e}} \right) } \right] _{ij}. \end{aligned}$$

(7b)

The least-squares parameters are obtained by minimizing the cost function, i. e.,

$$\begin{aligned} \Omega= & {} \left( {\mathbf {y}} - {\varvec{f}} \left( \hat{\mathbf {x}} \right) \right) ^{\mathrm {T}} \Sigma _{\mathbf {e}}^{\mathrm {-1}} \left( {\mathbf {y}} - {\varvec{f}} \left( \hat{\mathbf {x}} \right) \right) = \min , \end{aligned}$$

(8)

which leads to the necessary condition

$$\begin{aligned} \hat{\mathbf {A}}_{x}^{\mathrm {T}} \Sigma _{\mathbf {e}}^{\mathrm {-1}} \left( {\mathbf {y}} - {\varvec{f}}\left( \hat{\mathbf {x}} \right) \right)= & {} 0, \end{aligned}$$

(9)

where $\hat{\mathbf {A}} = {\mathbf {A}} + \left[ \Delta {\mathbf { x}}^{\mathrm {T}} {\mathbf {H}}_i \right] _i$ is the Jacobian evaluated at $\hat{\mathbf {x}}$ (Box 1971). Substituting Eqs. 2, 3 into Eq. 9 and neglecting the quadratic term yields the Jacobian

$$\begin{aligned} {\mathbf {F}}= & {} \left( {\mathbf {A}}^{\mathrm {T}} \Sigma _{\mathbf {e}}^{\mathrm {-1}} {\mathbf {A}} \right) ^{-1} {\mathbf {A}}^{\mathrm {T}} \Sigma _{\mathbf {e}}^{\mathrm {-1}}. \end{aligned}$$

(10)

For the quadratic term, we finally obtain

$$\begin{aligned} \left[ {{\,\mathrm{tr}\,}}{ \left( {\mathbf {G}}_i \Sigma _{\mathbf {e}} \right) } \right] _i= & {} -{\mathbf {F}} \left[ {{\,\mathrm{tr}\,}}{\left( {\mathbf {F}} \Sigma _{\mathbf {e}} {\mathbf {F}}^{\mathrm {T}} {\mathbf {H}}_i \right) } \right] _i. \end{aligned}$$

(11)

According to Eq. 7, the bias of the estimated parameters and the related dispersion yields

$$\begin{aligned} {\text {E}}\left\{ \Delta {\mathbf {x}} \right\}= & {} -\frac{1}{2} {\mathbf {F}} \left[ {{\,\mathrm{tr}\,}}{ \left( \Sigma _{\mathbf {x}} {\mathbf {H}}_i \right) } \right] _i, \end{aligned}$$

(12a)

$$\begin{aligned} {\text {E}}\left\{ \Delta {\mathbf {x}} \Delta {\mathbf {x}}^{\mathrm {T}} \right\}= & {} \Sigma _{\mathbf {x}} + \frac{1}{2} {\mathbf {F}} \left[ {{\,\mathrm{tr}\,}}{\left( \Sigma _{\mathbf {x}} {\mathbf {H}}_i \Sigma _{\mathbf {x}} {\mathbf {H}}_j \right) } \right] _{ij} {\mathbf {F}}^{\mathrm {T}}, \end{aligned}$$

(12b)

where $\Sigma _{\mathbf {x}} = {\mathbf {F}} \Sigma _{\mathbf {e}} {\mathbf {F}}^{\mathrm {T}} = \left( {\mathbf {A}}^{\mathrm {T}} \Sigma _{\mathbf {e}}^{\mathrm {-1}} {\mathbf {A}}\right) ^{-1}$ is the well-known first-order dispersion of the parameters (Box 1971). It should be emphasized that the Hessian ${\mathbf {G}}$ is not required in explicit representation to derive the bias of the estimates.

As shown by Lösler et al. (2020), the Jacobian in Eq. 10 of an implicit functional model ${\varvec{f}}\left( {\mathbf {x}},{\mathbf {e}}\right) = {\varvec{f}}\left( {\mathbf {u}}\right) = {\mathbf {0}}$, which is solved by minimizing the Lagrangian function, is given by

$$\begin{aligned} \mathbf {F_u}= & {} \left[ \begin{array}{cc} -\Sigma _{\mathbf {x}} {\mathbf {A}}^{\mathrm {T}} {\mathbf {N}}^{\mathrm {-1}} {\mathbf {B}} &{} \Sigma _{\mathbf {x}} {\mathbf {A}}^{\mathrm {T}} {\mathbf {N}}^{\mathrm {-1}} \\ {\mathbf {I}} - \Sigma _{\mathbf {e}} {\mathbf {B}}^{\mathrm {T}} \Sigma _{\mathbf {k}} {\mathbf {B}} &{} \Sigma _{\mathbf {e}} {\mathbf {B}}^{\mathrm {T}} \Sigma _{\mathbf {k}} \end{array} \right] , \end{aligned}$$

(13)

where ${\mathbf {B}}$ is the Jacobian of ${\varvec{f}}$ evaluated at $\tilde{\mathbf {e}}$. The first-order dispersion of the estimated parameters ${\mathbf {x}}$ and the Lagrangian ${\mathbf {k}}$ are given by (cf. Höpcke 1980, p. 161f)

$$\begin{aligned} \Sigma _{\mathbf {x}}= & {} \left( {\mathbf {A}}^{\mathrm {T}} {\mathbf {N}}^{\mathrm {-1}} {\mathbf {A}} \right) ^{-1}, \end{aligned}$$

(14a)

$$\begin{aligned} \Sigma _{\mathbf {k}}= & {} {\mathbf {N}}^{\mathrm {-1}} - {\mathbf {N}}^{\mathrm {-1}} {\mathbf {A}} \Sigma _{\mathbf {x}} {\mathbf {A}}^{\mathrm {T}} {\mathbf {N}}^{\mathrm {-1}} , \end{aligned}$$

(14b)

respectively, where ${\mathbf {N}} = {\mathbf {B}} \Sigma _{\mathbf {e}} {\mathbf {B}}^{\mathrm {T}}$.

In some application, ${{\,\mathrm{nullity}\,}}\left( {\mathbf {A}}^{\mathrm {T}} {\mathbf {N}}^{\mathrm {-1}} {\mathbf {A}} \right) = r > 0$ occurs and, therefore, the inverse in Eq. 14a does not exist. To solve the resulting ill-posed problem, r further parameter constraints are usually introduced and Eq. 14a becomes (e. g. Pázman and Denis 1999)

$$\begin{aligned} \Sigma _{\mathbf {x}}= & {} {\mathbf {U}} - {\mathbf {U}}{\mathbf {R}}^{\mathrm {T}}{\mathbf {S}} . \end{aligned}$$

(15a)

Here, ${\mathbf {R}}$ is the Jacobian of the further parameter constraint equations and

$$\begin{aligned} {\mathbf {U}}= & {} \left( {\mathbf {A}}^{\mathrm {T}} {\mathbf {N}}^{\mathrm {-1}} {\mathbf {A}} + {\mathbf {R}}^{\mathrm {T}} {\mathbf {R}} \right) ^{\mathrm {-1}} , \end{aligned}$$

(15b)

$$\begin{aligned} \mathbf {S^{\mathrm {T}}}= & {} \left( {\mathbf {R}} {\mathbf {U}} \mathbf {R^{\mathrm {T}}}\right) ^{\mathrm {-1}} {\mathbf {R}} {\mathbf {U}} . \end{aligned}$$

(15c)

The extended Jacobian of an implicit functional model ${\varvec{f}}$ containing r parameter constraints to eliminate the rank deficiency reads (Lösler et al. 2020)

$$\begin{aligned} \mathbf {F_u}= & {} \left[ \begin{array}{ccc} -\Sigma _{\mathbf {x}} {\mathbf {A}}^{\mathrm {T}} {\mathbf {N}}^{\mathrm {-1}} {\mathbf {B}} &{} \Sigma _{\mathbf {x}} {\mathbf {A}}^{\mathrm {T}} {\mathbf {N}}^{\mathrm {-1}} &{} {\mathbf {S}}^{\mathrm {T}} \\ {\mathbf {I}} - \Sigma _{\mathbf {e}} {\mathbf {B}}^{\mathrm {T}} \Sigma _{\mathbf {k}} {\mathbf {B}} &{} \Sigma _{\mathbf {e}} {\mathbf {B}}^{\mathrm {T}} \Sigma _{\mathbf {k}} &{} {\mathbf {0}} \end{array} \right] . \end{aligned}$$

(16)

To derive the bias of the estimates having an implicit functional model, the Jacobian $\mathbf {F_u}$ and the Hessian $\mathbf {H_u}$ of the function ${\varvec{f}}$ evaluated at $\tilde{\mathbf {u}}^{\mathrm {T}} = \left[ \begin{array}{cc} \tilde{\mathbf {x}}^{\mathrm {T}}&\tilde{\mathbf {e}}^{\mathrm {T}} \end{array}\right]$ are substituted into Eq. 12, i. e.,

$$\begin{aligned} {\text {E}}\left\{ \Delta {\mathbf {u}} \right\}= & {} -\frac{1}{2} \mathbf {F_u} \left[ {{\,\mathrm{tr}\,}}{ \left( \Sigma _{\mathbf {u}} \mathbf {H_u}_i \right) } \right] _i, \end{aligned}$$

(17a)

$$\begin{aligned} {\text {E}}\left\{ \Delta {\mathbf {u}} \Delta {\mathbf {u}}^{\mathrm {T}} \right\}= & {} \Sigma _{\mathbf {x}} + \frac{1}{2} \mathbf {F_u} \left[ {{\,\mathrm{tr}\,}}{\left( \Sigma _{\mathbf {u}} \mathbf {H_u}_i \Sigma _{\mathbf {u}} \mathbf {H_u}_j \right) } \right] _{ij} {\mathbf {F}}_u^{\mathrm {T}}, \end{aligned}$$

(17b)

where $\Sigma _{\mathbf {u}} = \mathbf {F_u} \Sigma _{\mathbf {e}} \mathbf {F_u}^{\mathrm {T}}$. A detailed derivation can be found in Lösler et al. (2020).

2.2 Special case of a plane fitting

From now on, we will place ourselves in the specific case of estimating a plane from a TLS point cloud recorded in polar coordinates. The nonlinear implicit functional relation of a plane reads

$$\begin{aligned} {\mathbf {n}}^{\mathrm {T}} {\mathbf {P}}_i= & {} d, \end{aligned}$$

(18)

where ${\mathbf {n}}^{\mathrm {T}} = \left[ \begin{array}{ccc} n_1&n_2&n_3\end{array}\right]$ is the normalized normal vector, d is the perpendicular distance from the estimated plane to the origin of the scanner’s local coordinate system. ${\mathbf {P}}_{i,\mathrm {cart}}^{\mathrm {T}}~=~\left[ \begin{array}{ccc} X_i&Y_i&Z_i \end{array}\right]$ is an arbitrary point of the plane. Eq. 18 can be written as $n_1 X_i + n_2 Y_i + n_3 Z_i - d = 0$ by considering the constraint ${\mathbf {n}}^{\mathrm {T}} {\mathbf {n}} = 1$ or $n_1^2 + n_2^2 + n_3^2 = 1$ for the length of the normal vector.

Fig. 1

Polar and Cartesian coordinates. The center of the TLS is the origin of the coordinate system

The raw measurements of a TLS are not Cartesian but polar coordinates: The range r expressed in meter [m], a vertical and a horizontal angle called $\theta$ and $\phi$, respectively, expressed in degree [$^\circ$] or gradian [gon]. They are depicted for one point ${\mathbf {P}}_{i}$ in Fig. 1. The origin of the coordinate system is the center of the TLS. The Cartesian coordinates in Eq. 18 are expressed by means of polar measurements as

$$\begin{aligned} X_i= & {} r_i \sin {\theta _i} \cos {\phi _i}, \end{aligned}$$

(19a)

$$\begin{aligned} Y_i= & {} r_i \sin {\theta _i} \sin {\phi _i}, \end{aligned}$$

(19b)

$$\begin{aligned} Z_i= & {} r_i \cos {\theta _i}, \end{aligned}$$

(19c)

with ${\mathbf {P}}_{i,\mathrm {pol}}^{\mathrm {T}} = \left[ \begin{array}{ccc} \theta _i&\phi _i&r_i \end{array}\right]$.

The first- and second-order dispersion corresponding to a plane fitting are derived from Sect. 2.1 and described in detail by Lösler et al. (2020). The estimates and the a priori dispersions—whether first or second order—depend on the VCM $\Sigma _{\mathbf {e}}$ from Eq. 17. We base our investigations on the approximation that $\Sigma _{\mathbf {e}} \approx \Sigma _{\mathbf {y}}$, where $\Sigma _{\mathbf {y}}$ is the VCM of the raw TLS measurements. In this contribution, we chose to model the covariance function of the measurements to set $\Sigma _{\mathbf {y}}$. Other approaches than modeling are, for example, based on variance component estimation (Teunissen and Amiri-Simkooei 2008). Such iterative implementations are computational demanding and may lead to numerical inaccuracies—up to the non-symmetry of the estimated VCM. In this contribution, we avoid this drawback by following the work of Kermarrec and Schön (2014) and suppose that a physical plausible modeling of the correlation structure is available. Our results can be, thus, read from two different perspectives when the parameters of the chosen model are varied in a plausible range: How (i) an inaccurate stochastic model and/or (ii) correlations affect the biases. We will use the notation $\Sigma _{\mathbf {y}} = \Sigma _{\mathrm {pol}}$ for the sake of readability.

3 Stochastic model for TLS measurements

3.1 Heteroscedasticity

The raw TLS measurements are expressed in polar coordinates, they are heteroscedastic and have different variances $\sigma _r^2$, $\sigma _\theta ^2$, and $\sigma _\phi ^2$.

• 1. The angle measurements are coming from the mechanical rotation of internal mirrors: It is justified to consider their correlation structure as a combination of flicker and white noise (Hooge 1994). Our first investigations with maximum likelihood estimation have confirmed this assumption and shown that the white noise component makes more than 70% of the total noise variance for the scanning scenario used in this contribution. Based on these results, we allowed ourselves to consider them as uncorrelated in a first approximation. Their variance is taken from the manufacturer’s datasheet (Böhler and Marbs 2002). In this contribution, we will use the specification of the Z+F 2016 (Zoller & Fröhlich GmbH, Wangen im Allgäu, Germany) for both, the simulations and the real data analysis.

• 2. The range variance $\sigma _r^2$ will depend on different factors such as the properties of the scanned object (e. g. color, roughness), eventually atmospheric transmission, and the range r or the scanner itself (Soudarissanane et al. 2011). This value can be constant based on the manufacturer’s indications or follow empirical models. Exemplarily, Wujanz et al. (2017) modeled the point-wise range variance depending on the intensity of the reflected signal. Using the 1D mode of a TLS, a power function could be fitted to the range variance versus intensity: $\sigma _r = c_{\mathrm {int}} + \beta _{\mathrm {int}} Int^{\alpha _{\mathrm {int}} }$, where the parameters $\alpha _{\mathrm {int}}$, $\beta _{\mathrm {int}}$ and $c_{\mathrm {int}}$ were determined empirically by regression analysis for different terrestrial laser scanners and Int is the raw intensity expressed in [Inc]. Unfortunately, the intensity value may not be accessible for all TLS. In order to cope with this challenge, further investigations were carried out (e.g., Schmitz et al. 2019). In this contribution, we place ourselves in a simulated framework and vary $\sigma _r^2$ independently of simulated intensity values.

3.2 Temporal correlations

As aforementioned, we consider the temporal range correlations only and neglect the correlations for angle measurements. This approximation seems justified in a first approximation and will be the topic of further investigations.

3.2.1 Why the Matérn model: a justification

Range measurements are a measure of time independent of the TLS under consideration (phase or time of flight) (Rüeger 1996): We will, therefore, consider the TLS range measurements as temporally correlated. Many effects act on correlating the measurements, such as atmospheric turbulence due to the propagation of the laser in a random medium (Wheelon 2001) or to the sensor itself (Llopis et al. 2011; van der Ziel 1970). Phase noise related to fluctuations of the optical phase of the output, quantum noise due to the random phase of photons added by spontaneous emission and optical fiber with scattering phenomena inside the fiber should be considered as factors acting on correlating the measurements, to name but a few.

Such noise, also called stochastic processes, is well described by power-law slopes in the frequency domain, so-called colored noises. By means of differential equations, the different sources of noise can be modeled, leading to different power laws; the resulting “global” noise is a combination of all of them. Exemplarily, a widely assumed model for GPS coordinate time series analysis is a combination of flicker or power-law noise with white noise (Bos et al. 2020). However, many noises exhibit a high-frequency slope with a low-frequency plateau. Such stationary processes are better modeled by a Matérn model (Matérn 1960; Guttorp and Gneiting 2005), which accounts for the short-range dependence—as the fractional Brownian motion (fBm, Mandelbrot and Ness (1968))—but is damped at low frequencies. The property of the process is intuitively related to a common feature of many physical systems: a pressure to grow together with a resistance on that growth (Lilly et al. 2017); this phenomenon leads to a balance or equilibrium between the two forces. The Matérn process accounts for that effect and, as the length of the time series increases, the stochastic model is more adequately modeled with a Matérn model than a purely fractional noise (see, e.g., He et al. 2019). Such processes are widely used in spatial geostatistic (Gneiting et al. 2010; Handcock and Wallis 1994; Stein 1999). The Matérn model is less popular for modeling noise of time series, although its flexibility permits a wide range of applications.

In this contribution, we will model the temporal correlations of TLS range measurements with this process, following the work of the first author on GPS phase correlation and the strong parallel between TLS and GPS measurements and processing (Kermarrec et al. 2019). First investigations based on residual analysis and the empirical mode decomposition have empirically confirmed the theoretical expectation about the noise structure of TLS range measurements (Kermarrec et al. 2020b) (please note that in Tab. 1 of this contribution, the smoothness is given by the third and not the second value; the correlation parameter is the fourth value and should be 1.18, see erratum). The authors could successfully justified the use of the Matérn model. In the next section, we propose introducing the Matérn model in detail, which is a mandatory step to understand the concepts of smoothness and correlation length and their impact on the biases defined in Sect. 2.1.

3.2.2 Statistical description

A Matérn process z is stationary, and its spectrum is of the form

$$\begin{aligned} S_{zz} \left( \omega \right)= & {} \frac{A^2}{\left( \omega ^2 +\alpha ^2 \right) ^{\nu }},\quad \nu \ge \frac{1}{2}. \end{aligned}$$

(20)

The parameter A sets the spectral level, and $\nu$ is called the smoothness of the process and is related to the slope of the power spectral density (psd) as the frequency $\omega \rightarrow \infty$. For $\nu = \frac{1}{2}$ the Matérn model is identical to the exponential model; the limit case as $\nu \rightarrow \infty$, is the Gaussian model. $\nu = 1$ was used exemplarily in Rodríguez-Iturbe and Mejía (1974) to model the volume of rainfall. A smoothness larger than 1 is linked to the mean-square differentiability of the process (Stein 1999), i. e., with the smooth decrease in the covariance function at the origin. The parameter $\alpha$ is a positive range parameter which has units of angular frequency. It acts as a damping of the psd as $\omega \rightarrow 0$ and, thus, controls the transition between two regimes:

$$\begin{aligned} S_{zz} \left( \omega \right)\rightarrow & {} {\left\{ \begin{array}{ll} \frac{A^2}{\left( \alpha ^2 \right) ^\nu } &{} \left| \omega \right| \gg \alpha \\ \frac{A^2}{\left( \omega ^2 \right) ^\nu } &{} \left| \omega \right| \ll \alpha \end{array}\right. } \end{aligned}$$

(21)

To illustrate this property, Fig. 2 shows the psd of different processes corresponding to different set of values $\left[ \alpha ,\nu \right]$. Without lack of generality, we assumed a sampling of 1 s. Changing the sampling does not affect the figure due to the scaling effect. Clearly, the Matérn psd is constant for low frequencies and decreases as a power law at higher frequencies, similarly to a damped fBm. A high smoothness (exemplary $\nu =3$, magenta curve) is linked to a strong decay of the psd as $\left| \omega \right| \gg \alpha$ and a constant regime as $\left| \omega \right| \ll \alpha$. This latter case corresponds to a white noise having the same power level for all frequencies.

For a high correlation parameter (exemplary $\alpha =1.5$), Fig. 2b shows a longer plateau regarding a noise generated with a low $\alpha = 0.5$. This latter has a psd similar to the one of a fBm.

The covariance $C_{zz}$ of a second-order stationary process is related to the spectrum through the inverse Fourier relationship $S_{zz} \left( \omega \right) = \int _{-\infty }^{\infty }{C_{zz}\left( \tau \right) e^{-i\omega \tau } d\tau }$, where $\tau > 0$ is the time difference. For a Matérn process, $C_{zz}\left( \tau \right)$ is given by

$$\begin{aligned} C_{zz} \left( \tau \right)= & {} \sigma ^2 {\mathrm {M}}_{\nu } \left( \alpha \tau \right) . \end{aligned}$$

(22)

We introduce the Matérn function as

$$\begin{aligned} {\mathrm M}_{\nu } \left( x \right)= & {} \frac{2}{\Gamma \left( \nu - \frac{1}{2} \right) 2^{\left( \nu -\frac{1}{2} \right) } } \left| x \right| ^{\left( \nu - \frac{1}{2} \right) } \mathrm {K}_{\left( \nu - \frac{1}{2} \right) } \left( \left| x \right| \right) , \end{aligned}$$

(23)

where $\Gamma$ denotes the gamma function and $\mathrm {K}_{\left( \nu - \frac{1}{2} \right) }$ the decaying modified Bessel function of the second kind of order $\nu ~-~\frac{1}{2}$ (Abramowitz and Stegun 1972). The variance of the process is denoted by $\sigma ^2$.

Figure 2a, c, e shows the covariance function for the same parameter values as Fig. 2b, d, f. Clearly, for $\nu = 3$, the function decreases slowly at the origin compared to the exponential model $\nu = \frac{1}{2}$. The Matérn covariance has asymptotic behavior for large and small timescales (Lilly et al. 2017).

Fig. 2

psd corresponding to a Matérn process. a The covariance function in [$\hbox {m}^2$] versus time in [s] by varying the smoothness parameter and yielding the correlation parameter constant to 1.5. The smoothness affects the mean-squared differentiability of the function at the origin strongly. The corresponding legend is depicted in b, which represents the psd: The slopes change with the smoothness. c The covariance function by varying the correlation parameter and keeping the smoothness parameter to 1. d The psd. The slopes are constant, $\alpha$ affects the cutoff frequency of the psd from which it becomes constant. e The psd by adding white noise to the correlated noise (CN). The CN gives the part of correlated noise regarding white noise; CN=1 corresponds to no white noise. f psd of processes where the variance of the total noise is not scaled

3.2.3 Our proposal to model TLS range temporal correlations

Following the proposal of Kermarrec et al. (2019), we model the temporal correlations of TLS range measurements with a separable covariance function (Gelfand et al. 2010). This function is built as follows:

• 1. We assume that the variance of the range measurements will account for or “catch” all spatial effects, i. e., the impact of surface properties and atmospheric transmission on the signal-to-noise ratio by means of the intensity model proposed by Wujanz et al. (2017).

• 2. The temporal correlations are modeled independently with a Matérn covariance function.

The resulting function is a product of the modeled variance and the chosen covariance function. In this contribution, we assume that the variance of additional white noise is small compared to the correlated one. Increasing the impact of white noise decreases the one of correlations in the LS adjustment: Such cases are less relevant to study, as the results obtained will be similar to the one corresponding to a diagonal VCM. We illustrate this behavior in Fig. 2e, where we show exemplarily the psd of a simulated noise defined as a combination of white noise and a Matérn process. In this example, the total variance is the same for all simulated time series (the green line corresponds to a pure white noise and the blue one to a pure correlated noise). In Fig. 2f, we increased the power of white noise gradually as well as the total variance. From these two figures, we see that only the high-frequency region of the psd is impacted by the additional source of noise, provided that the latter has approximately the same variance as the correlated one (yellow line in Fig. 2f). If the white noise has a smaller variance (red line), its impact on the shape of the psd is less pronounced than in the previous case. Thus, additional white noise will have a similar effect as decreasing the smoothness.

The Matérn parameters can be estimated from time series such as LS residuals with the Whittle maximum likelihood estimator, which we briefly explain in “Appendix A” for the sake of completeness.

3.3 VCM of the raw measurements

3.3.1 Building the VCM

In building the VCM of the raw measurements, we propose to account for the scanning time and model the correlation “linewise”: For a given object extracted from the whole point cloud, we consider that the last point of a scanned line (Fig. 3 for $t=10$), is not directly recorded before the first point of the second line (Fig. 3, $t=11$) after the horizontal angle has been incremented.

Fig. 3

Linewise modeling of correlations: We account for the time for the scanner to come back to the initial elevation as acting as decorrelating the two measurements $t=10$ and $t=11$. We consider a plane as the object being fitted

Fig. 4

Example of a fully populated VCM accounting for temporal range correlations. The values are given in [$\hbox {mm}^2$]. $\hat{{\Sigma }}_{\theta }$, $\hat{{\Sigma }}_{\phi }$ are sorted time-wise, and diagonal is not depicted; 2000 values were simulated

We resume the stochasticity of the TLS measurements in a matrix form, $\hat{\Sigma }_{\mathrm {pol}}$ being the VCM of the polar measurements defined as:

$$\begin{aligned} \hat{{\Sigma }}_{\mathrm {pol}}= & {} \left[ \begin{array}{ccc} {\hat{\Sigma }}_\theta &{}\qquad {\mathbf {0}} &{}\qquad {\mathbf {0}} \\ {\mathbf {0}} &{}\qquad {\hat{\Sigma }}_\phi &{}\qquad {\mathbf {0}} \\ {\mathbf {0}} &{}\qquad {\mathbf {0}} &{}\qquad {\hat{\Sigma }}_r \end{array} \right] , \end{aligned}$$

(24)

where the diagonal block matrices ${\hat{\Sigma }}_\theta$, ${\hat{\Sigma }}_\phi$ are sorted time-wise. Their elements are given by the corresponding variances $\sigma _\theta ^2$, $\sigma _\phi ^2$. ${\hat{\Sigma }}_r$ is the fully populated VCM of the range, and is filled using the proposed Matérn covariance model of Eqs. 22 and 23 with $\sigma ^2 = \sigma _r^2$ as the range variance. The time increment between two measurements is given from the scanning setting chosen, e. g. high, superhigh or extremely high. The corresponding matrix ${\hat{\Sigma }}_r$ is visualized in Fig. 4, for which $\left[ \alpha ,\, \nu \right] = \left[ 0.05,\,1.5\right]$. Clearly, the number of elements of the covariance function that are non-null depends on the chosen set of Matérn parameters.

We denote furthermore $\hat{{\Sigma }}_{\mathrm {pol,diag}}$, the diagonal Matrix corresponding to $\hat{{\Sigma }}_{\mathrm {pol}}$, where diag states for diagonal, i. e., without accounting for temporal correlations.

3.3.2 Impact of the measurement configuration

Each coordinate based functional model can be expressed in polar and Cartesian representation. According to Suchomski (1999), the transformation of the polar coordinates into their Cartesian representations yields biased results, if a linearized substitute problem is used. In this contribution and following Sect. 2, we avoid this drawback: No transformation of the VCM of the raw measurements by means of the propagation law is needed. However, the biases defined in Sect. 2.1 will still depend on the scanning configuration through the Jacobian and Hessian matrices (Eq. 17). The orientation of the scanned object in space will affect the biases of second order described in Sect. 2.1.

3.3.3 The equivalent diagonal model or DCM

Using fully populated VCM in LS adjustment may be computational demanding. Based on the work of Luati and Proietti (2011), Kermarrec and Schön (2016) developed an alternative based on diagonal VCM: the so-called DCM. This model was successfully used in LS adjustment with GPS phase observations for the specific use of ambiguity resolution or coordinates estimation to avoid introducing fully populated matrices (Kermarrec and Schön 2017b). In this section, we propose to shortly summarize the main idea behind this simplified yet powerful stochastic model.

We call $\hat{{\Sigma }}_{\mathrm {equi}}$ the equivalent diagonal matrix to $\hat{{\Sigma }}_{\mathrm {pol}}$.The conditions under which the LS estimate with $\hat{{\Sigma }}_{\mathrm {equi}}$ is identical to the one given by $\hat{{\Sigma }}_{\mathrm {pol}}$ are given in Luati and Proietti (2011) and are based on a decomposition of the design matrix of the linear LS adjustment as a product of the eigenvectors of $\hat{{\Sigma }}_{\mathrm {pol}} \hat{{\Sigma }}_{\mathrm {equi}}^{\mathrm {-1}}$.

In the case of a mean estimator, a necessary and sufficient condition for the equivalence between the generalized LS and the DCM to hold is that each element of the diagonal matrix $\hat{{\Sigma }}_{\mathrm {equi}}^{\mathrm {-1}}$ is the sum of the row elements of the inverse of the fully populated covariance matrix $\hat{{\Sigma }}_{\mathrm {pol}}^{\mathrm {-1}}$. Kermarrec and Schön (2016) tested empirically the generalization of this equivalence for more sophisticated linear functional models: They showed that matrix multiplication involving non-sparse fully populated VCM could be avoided.

Figure 5 explains graphically how to compute the equivalent matrix. We point out that the semi-equivalence holds true for the estimates and their a priori cofactor matrices in a linear model. In this contribution, we will investigate whether it can be used in the second-order solution derived in Sect.2.1.

When the inverse of the VCM exists explicitly, the VCM can be replaced by a simple factor, which we call the Variance Inflation Factor (VIF), see Kermarrec et al. (2020a) and “Appendix B.” An explicit formulation of the inverse exists when the correlation structure can be modeled with a Matérn model corresponding to $\nu = \frac{1}{2}$, which corresponds in one dimension to a so-called autoregressive model of first order AR(1), see (Rao and Toutenburg 1995) or (Rasmussen and Williams 2006). Thus, the use of a VIF will be justified if the simulations show that misspecifying the smoothness do not affect strongly the bias of second order.

Fig. 5

Computation of the equivalent diagonal matrix of the DCM from the inverse of the fully populated VCM

Fig. 6

Example of two simulated planes corresponding to two scanning configurations. The scanning rate for the representation of the TLS plane generated is constant and taken here to $dt=1 \times 10^{-5}\hbox { s}$: This corresponds to a value for which the covariance function reaches the 0 value inside one line and not to the reference value in both cases. Please note that we consider that the main axis of the TLS crosses the plane in its center in all simulated cases

4 Simulations

4.1 Simulated observation

We simulate TLS raw measurements from a plane to study the impact of both scanning configuration and temporal correlations on the first-order and second-order bias in a controlled framework, see Eq. 17 and cf. Sect. 2.2. In the following sections, we propose describing the setup that was adopted to make the simulations as close as possible to a real scenario.

4.1.1 General configuration

The optimal scanning configuration for which the regular points lie on a regular grid corresponding to a null horizontal and vertical tilt regarding the TLS main axis is depicted in Fig. 6. For this reference configuration, we have $\left[ \theta ,\,\phi \right] =\left[ 0,\,0\right] ^\circ$. All planes are generated having the size $1\hbox { m}\times 1\hbox { m}$ and scanned at a distance of $10\hbox { m}$. We chose a temporal spacing between the points of $dt = 5\times 10^{-5}\hbox { s}$ so that the reference number of points per scanning line reaches 25. This value corresponds to the setting “premium, high” or “preview, normal” for the Z+F 2016 used in this contribution for the real data analysis.

4.1.2 Positive definite VCM

In order to study the impact of the scanning configuration on the biases, we generated different point clouds by adapting the horizontal and vertical tilts of the planes. Because we account for the slight increase in distance coming from the tilt, not all the scanning lines have 25 measurements, similarly to a real case scenario. For the sake of comparison—and in order to also ensure that all VCM are positive definite—we need to adapt the scanning rate to reach the reference number of 25 points per scanning line for all configurations. An example of this problematic is presented in Fig. 6: The reference scanning configuration shown in Fig. 6a is compared with the one corresponding to a horizontal tilt of and a vertical tilt of 40% (see Fig. 6b). A temporal spacing of $dt=1 \times 10^{-5}\,{\hbox { s}}$ was chosen for both cases and not the reference value of $dt= 5 \times 10^{-5}\hbox { s}$. Without decreasing dt accordingly, the number of points per scanning line is lower for the case corresponding to Fig. 6b than for the reference one. Unfortunately, when the number of measurements per scanning lines is low and the level of the chosen correlations high, the covariance function will not reach the 0 value inside one line: The corresponding VCM are badly conditioned and cannot be used in the adjustment, i. e., they are not positive definite. This effect is highlighted in Fig. 7a, for which $\alpha = 0.2$. Clearly, the covariance function does not reach the 0 value inside one line of 25 values. Since this effect occurs when the number of points per scanning line is small regarding the correlation length, we avoid it by fixing the minimal number of points per scanning line equal to the number of points chosen for the reference configuration. Concretely dt may be smaller, for some scanning configurations, than the reference value. This allows to compare the results when $\alpha$ is varied, see Sect. 4.2. We note that this effect is not likely to happen with real data as the number of points per line is much higher. We intentionally chose in this contribution to follow the configuration used in Lösler et al. (2020)

4.1.3 Configurations

To answer the first and second scientific questions raised in the introduction, we simulated different configurations by changing the horizontal and vertical tilts of the plane. $\theta$ and $\phi$ are, thus, varied in the range $\left[ 0,20,40,60\right] ^\circ$ independently. An example of the planes obtained is depicted in Fig. 6, for which a distance of 10 m was chosen. The distance between the center of the TLS and the plane was held fixed.

Fig. 7

First line of the covariance function in [$\hbox {m}^2$] for a different value of $\alpha$ and $\nu$. The scanning rate is taken to $dt= 5 \times 10^{-5}\hbox { s}$, which corresponds to 25 points per line

We are aware that the scanning configuration also includes the edge length and the distance to the instrument. These effects on the first- and second-order solutions have already been studied in Lösler et al. (2020), who simulated planes with different edge lengths, at the same distance and scanned with different scanning rates by increasing the number of points per scanning line and/or the number of scanning lines.

Based on their study, we highlight the following points:

• 1. Changing the distance is similar to acting on the a priori variance factor of the measurements. Exemplarily, increasing the distance corresponds to an increase in $\sigma _r^2$ and thus of the bias (Wujanz et al. 2017).

• 2. Acting on the distance is, moreover, linked to varying the scanning rate but for a fixed distance: For a given edge length, increasing dt is related to decreasing the number of grid points, which increases the bias.

• 3. A high bias was found for small edge lengths.

These effects have already been investigated in Lösler et al. (2020). We do not aim to repeat their investigations and, thus, concentrate on the impact of the correlation structure on these biases only and not on their absolute values.

4.2 Stochastic model

We account for the heteroscedasticity and correlations of the TLS measurements as proposed in Sect. 3.1. The setup of the VCM of the measurements is as follows:

• 1. The polar angle variances are held fixed and the measurements are considered to be uncorrelated. The variance is taken from a manufacturer’s datasheet Z+F 2016 and fixed to $\sigma _{\phi } = \sigma _{\theta } = 0.007^\circ$.

• 2. The range variance is varied starting with $\sigma _{r,0} = 1\hbox { mm}$ up to $\sigma _{r,0} = 5\hbox { mm}$. Intermediate results can be easily deduced from these two cases, as well as the one corresponding to more extreme values of $\sigma _{r,0}$.

• 3. The range measurements are temporally correlated. We use the simplified Matérn model described in Sect. 3.2. Different correlation structures are tested corresponding to four different smoothnesses and six correlation parameters.

Table 1 Stochastic and configuration parameters used for the simulations

We summarize the different stochastic and configuration models in Table 1.

4.3 How to compare the results and what is expected?

We define the following ratios in order to provide an answer to the three main questions raised in the introduction:

• To investigate the difference between the second- and first-order solution for the estimated range ${\hat{d}}$ and the standard deviation $\sigma _d$ of the range of the plane:

  $$\begin{aligned} R_{{\hat{d}},2/1}= & {} \frac{{\hat{d}}_{\mathrm {2^{nd}}} - {\hat{d}}_{\mathrm {1^{st}}}}{{\hat{d}}_{\mathrm {2^{nd}}}}, \end{aligned}$$

  (25a)
  $$\begin{aligned} R_{\sigma ,2/1}= & {} \frac{\sigma _{d,\mathrm {2^{nd}}} - \sigma _{d,\mathrm {1^{st}}}}{\sigma _{d,\mathrm {2^{nd}}}}. \end{aligned}$$

  (25b)

• To study how a simplification of the fully populated VCM with its diagonal counterpart $\hat{{\Sigma }}_{\mathrm {pol,diag}}$ will impact the second-order solution:

  $$\begin{aligned} R_{{\hat{d}},2/2\mathrm {diag}}= & {} \frac{{\hat{d}}_{\mathrm {2^{nd}}} - {\hat{d}}_{\mathrm {2^{nd},diag}} }{{\hat{d}}_{\mathrm {2^{nd}}}}, \end{aligned}$$

  (26a)
  $$\begin{aligned} R_{\sigma ,2/2\mathrm {diag}}= & {} \frac{\sigma _{d,\mathrm {2^{nd}}} - \sigma _{d,\mathrm {2^{nd},diag}} }{\sigma _{d,\mathrm {2^{nd}}}}. \end{aligned}$$

  (26b)

• To test whether the DCM using $\hat{{\Sigma }}_{\mathrm {equi}}$ can replace the fully populated VCM in the LS adjustment:

  $$\begin{aligned} R_{{\hat{d}},2/2\mathrm {equi}}= & {} \frac{{\hat{d}}_{\mathrm {2^{nd}}} - {\hat{d}}_{\mathrm {2^{nd},equi}} }{{\hat{d}}_{\mathrm {2^{nd}}}}, \end{aligned}$$

  (27a)
  $$\begin{aligned} R_{\sigma ,2/2\mathrm {equi}}= & {} \frac{\sigma _{d,\mathrm {2^{nd}}} - \sigma _{d,\mathrm {2^{nd},equi}} }{\sigma _{d,\mathrm {2^{nd}}}}. \end{aligned}$$

  (27b)

We call ${\hat{d}}_{\mathrm {2^{nd}}}$, ${\hat{d}}_{\mathrm {2^{nd},diag}}$, ${\hat{d}}_{\mathrm {2^{nd},equi}}$ the second-order solution computed with $\hat{{\Sigma }}_{\mathrm {pol}}$, $\hat{{\Sigma }}_{\mathrm {pol,diag}}$ and $\hat{{\Sigma }}_{\mathrm {equi}}$, respectively, for the range r of the TLS. ${\hat{d}}_{\mathrm {1^{st}}}$ is the corresponding first-order solution. The dispersions $\sigma _{d}$ are defined similarly. All ratios will be given in $\%$, with as many digits as necessary for the sake of comparison. Please note that we always consider the second-order solution as the reference one.

We propose to initially discuss the expected results intuitively to simplify the understanding of the simulations:

• 1. Since we consider having a fixed number of points per line, increasing the correlation parameter $\alpha$ will act as decreasing the impact of correlations: The solution will tend to the one obtained with a diagonal matrix $\hat{{\Sigma }}_{\mathrm {pol,diag}}$.

• 2. Increasing the smoothness will increase the impact on the bias regarding the diagonal solution or for a given $\alpha$. The diagonal solution is close to the one obtained for $\nu$ = $\frac{1}{2}$ as $\alpha$ increases: Exemplarily Fig. 7a, b shows the decay of the covariance function in that specific case, as the time increases.

• 3. We expect that a larger $\sigma _r$ will increase the ratios.

• 4. A suboptimal scanning configuration is expected to decrease the impact of the temporal correlations on the ratios.

In the following, we choose intentionally to present in details the results for two configurations only. Further results will be discussed in text form in order not to overload our contribution.

Fig. 8

Reference scanning configuration $\left[ \theta ,\,\phi \right] = \left[ 0,0\right] ^\circ$ for $\sigma _{r,0} = 1\hbox { mm}$ (left), and $\sigma _{r,0} = 5\hbox { mm}$ (right). For a and b, we have: top: $R_{{\hat{d}},2/1}$, middle: $R_{{\hat{d}},2/2\mathrm {diag}}$, bottom: $R_{{\hat{d}},2/2\mathrm {equi}}$, as mentioned in the corresponding title of the subplots. Please note: For the sake of readability, we intentionally choose the same y-axis for the two $\sigma _{r,0}$

4.4 Results

4.4.1 Reference scanning configuration $\left[ \theta ,\,\phi \right] =\left[ 0,\,0\right] ^{\circ }$

• 1. Difference between the second- and first-order solution $R_{{\hat{d}},2/1}$ and $R_{\sigma ,2/1}$. The corresponding results are presented in Fig. 8a, b (top). Under the reference scanning configuration, $\left[ \theta ,\,\phi \right] = \left[ 0,\,0\right] ^\circ$ and for $\sigma _{r,0} = 1\hbox { mm}$, $R_{{\hat{d}},2/1}$ is nearly constant (around 0.003%) independently of the correlation structure. $R_{\sigma ,2/1}$ is between 1% and 2% for the range of values chosen. Both ratios tend to a constant value, which is reached for $\alpha > 2$. We see clearly that for $\sigma _{r,0} = 5\hbox { mm}$ an increase in correlations is linked to a slight decrease in the ratio, i. e., from 0.0045 to 0.004% for the parameter (magenta line versus blue line) and 0.25% for $R_{\sigma ,2/1}$, for $\alpha = 0.5$, $\nu =\left[ 0.5-1.5\right]$: Accounting for correlations damped the difference between the first- and second-order solution for both parameter and dispersion. This effect can be interesting to avoid computing the second-order solution when small objects are scanned, for which the absolute bias is not negligible. However, we note that the ratios are under 1% and can be considered as small. To summarize, when temporal correlations are accounted for, the ratios decrease so that it becomes less interesting to use the second-order solution. This effect is at the same time a risk when correlations are underestimated and the first-order solution is computed. For that reason, it is still always preferable not to compute the first-order solution for small objects. Please note that we were not considering the absolute value of the differences—which depends on the edge length—and only analyzed how correlations affected the difference.

• 2. Simplification of the fully populated VCM with its diagonal counterpart $R_{{\hat{d}},2/2\mathrm {diag}}$ and $R_{\sigma ,2/2\mathrm {diag}}$ The results are presented in Fig. 8a, b (middle). The impact of the fully populated VCM at the parameter level regarding its diagonal counterpart is nearly negligible. For $R_{\sigma ,2/2\mathrm {diag}}$, the expected high difference between fully populated VCM and diagonal VCM can be confirmed: for $\sigma _{r,0} = 1\hbox { mm}$ and $\left[ \alpha ,\,\nu \right] = \left[ 0.5,1.25\right]$, the ratio $R_{\sigma ,2/2\mathrm {diag}}$ reaches nearly 40% and 60% for $\sigma _{r,0} = 5\hbox { mm}$. For a lower smoothness and high correlation parameter, we have less significant values: For the exponential covariance function $\left[ \alpha ,\,\nu \right] =\left[ 0.5,\,0.5\right]$, the ratio reaches 20% and 50% for $\sigma _{r,0} = 1\hbox { mm}$ and $\sigma _{r,0} = 5\hbox { mm}$, respectively. We note further that the correlation parameter $\alpha$ should be high to reach $R_{\sigma ,2/2\mathrm {diag}} = 0$, particularly for $\sigma _{r,0} = 5\hbox { mm}$: Even low correlations lead to a high ratio. A strong smoothness $\nu$ increases the ratio for a given $\alpha$, which is a logical effect as the VCM is less sparse. This reference case highlights that correlations should not be disregarded for computing the dispersion. This conclusion would be the same if the first-order solution had been used, due to the aforementioned small difference between the first- and second-order solution (see previous point). Not accounting for correlations and using a diagonal VCM is linked to a risk of making a high error in terms of dispersion.

• 3. Simplification of the fully populated VCM with its diagonal counterpart $R_{{\hat{d}},2/2\mathrm {equi}}$ and $R_{\sigma ,2/2\mathrm {equi}}$ derived by the DCM approach Figure 8a, b (bottom) shows the good adequation between the results given with the DCM and the fully populated VCM. At the parameter level, the ratio $R_{{\hat{d}},2/2\mathrm {equi}}$ is not higher than 0.002% for the case corresponding to $\left[ \alpha ,\,\nu \right] = \left[ 0.5,\,1.25\right]$ and $\sigma _{r,0} = 5\hbox { mm}$. $R_{\sigma ,2/2\mathrm {equi}}$ highlights the strength of the approximation with the DCM regarding using the diagonal VCM: $R_{\sigma ,2/2\mathrm {equi}}$ reaches a maximum value of approximately 4% for $\left[ \alpha ,\,\nu \right] = \left[ 0.5,\,1.25\right]$ and $\sigma _{r,0} = 1\hbox { mm}$, about one order of magnitude better than $R_{\sigma ,2/2\mathrm {diag}}$ for the same configuration. We note that $R_{\sigma ,2/2\mathrm {equi}}$ is getting smaller as $\sigma _{0,r}$ increases (Fig. 8b right bottom), which we interpret as coming from the closeness of the range variance to the angle one. Additional tests by increasing the angle variance to $0.01^\circ$ instead of $0.007^\circ$ led to an increase in $R_{\sigma ,2/2\mathrm {equi}}$ comparable with the values given for $\sigma _{r,0} = 1\hbox { mm}$ and the reference angle variance chosen. This study confirms empirically that the equivalence holds true for a nonlinear LS plane fitting: The DCM can be used with high confidence to replace the fully populated VCM. We also mention an important point for computational efficiency: The difference by varying the smoothness for a fixed $\alpha$ is below 0.1%. This result is promising. Indeed, even if the estimated smoothness is higher than 0.5, we can replace it by $\nu = 0.5$ and slightly decrease the estimated $\alpha$ from 0.5 without impacting the results for the parameters and dispersion. Alternatively, one could directly assume that the temporal correlation model follows an AR(1) process and estimate or model the correlation length only: The AR(1) model for one-dimensional time series is corresponding to a Matérn model with $\nu =\frac{1}{2}$ (Rasmussen and Williams 2006). As aforementioned in Sect. 3.3.3, the inverse of the VCM from an AR(1) model can be replaced by a scaled identity in the LS adjustment, see Kermarrec et al. (2020a) for a detailed explanation. The authors recommend using the AR(1) model due to the potential numerical instability of the DCM for high smoothness and low $\alpha$ (see, e. g., Fig. 8, bottom, yellow line). These computational inaccuracies are linked to the high number of relevant values, i. e., not close to zero, on one line of the fully populated VCM. Additionally combined with suboptimal scanning configurations, they can lead to a ratio of up to 1% for $\left[ \theta ,\,\phi \right] = \left[ 60,\,20\right] ^\circ$ and $\left[ \alpha ,\,\nu \right] = \left[ 0.5,\,1.25\right]$. This effect—although of a small magnitude—gives weight to the use of a more stable AR(1) model in the DCM, besides the fact that for that model a close formula for the inverse of the VCM exists.

4.4.2 Impact of the scanning configuration

Fig. 9

$\left[ \theta ,\,\phi \right] = \left[ 40,0\right] ^\circ$. Left (top, middle and bottom, respectively): $R_{{\hat{d}},2/1}$, $R_{{\hat{d}},2/2\mathrm {diag}}$, $R_{{\hat{d}},2/2\mathrm {equi}}$, right: $\sigma _{r,0} = 1\hbox { mm}$, left $\sigma _{r,0} = 5\hbox { mm}$. Right $R_{\sigma ,2/1}$, $R_{\sigma ,2/2\mathrm {diag}}$, $R_{\sigma ,2/2\mathrm {equi}}$, right: $\sigma _{r,0} = 1\hbox { mm}$, left $\sigma _{r,0} = 5\hbox { mm}$, as mentioned in the corresponding title. Please note: For the sake of readability, we intentionally did not choose the same y-axis for the two $\sigma _{r,0}$ for $R_{{\hat{d}},2/1}$, $R_{{\hat{d}},2/2\mathrm {diag}}$, $R_{{\hat{d}},2/2\mathrm {equi}}$

We further analyzed different scanning configurations following Table 1 for the sake of completeness. Without loss of generality, we chose to present the case $\left[ \theta ,\,\phi \right] =\left[ 40,\,0\right] ^\circ$ graphically in Fig. 9. Further results are given in text form.

• 1. Difference between the second- and first-order solution $R_{{\hat{d}},2/1}$ and $R_{\sigma ,2/1}$

  From Fig. 9a (top), the impact of the scanning configuration chosen is shown to affect $R_{{\hat{d}},2/1}$ negatively, which increases by a factor of 10 regarding the reference case (Fig. 8): The difference between the second- and first-order solution still decreases with increasing correlations and tends to 0.03%. On the contrary, $R_{\sigma ,2/1}$ reaches approximately 0.075% in mean over all simulated correlation structure. It is lower than with $\left[ \theta ,\,\phi \right] = \left[ 0,\,0\right] ^\circ$; the scanning configuration lead to a decrease in the impact of the temporal correlations on the second-order solution compared to the first-order one. These results were confirmed for other scanning configuration. Exemplarily for $\left[ \theta ,\,\phi \right] = \left[ 60,\,20\right] ^\circ$, we got a mean of $R_{{\hat{d}},2/1} = 0.06\%$ and $R_{\sigma ,2/1} = 0.08\%$, for $\left[ \theta ,\,\phi \right] = \left[ 40,\,40\right] ^\circ$, $R_{{\hat{d}},2/1} = 0.07\%$ and $R_{\sigma ,2/1} = 0.06\%$. We conclude, therefore, that the non-optimality of the scanning configuration leads to ratios close to 0: The first- and second-order solutions are similar in terms of parameter and dispersion when temporal correlations are additionally considered.

• 2. Simplification of the fully populated VCM with its diagonal counterpart $R_{{\hat{d}},2/2\mathrm {diag}}$ and $R_{\sigma ,2/2\mathrm {diag}}$

  Figure 9a, b (middle) highlights further the non-necessity of accounting for correlations as the scanning configuration becomes worth more: $R_{{\hat{d}},2/2\mathrm {diag}}$ is below $1\times 10^{-5}$ and $R_{\sigma ,2/2\mathrm {diag}}$ is not higher than 1.5% for $\sigma _{r,0} = 5\hbox { mm}$. Similar results were found, for example, for $\left[ \theta ,\,\phi \right] = \left[ 60,\,20\right] ^\circ$ with $R_{\sigma ,2/2\mathrm {diag}}$ reaching maximal 1% or $\left[ \theta ,\,\phi \right] = \left[ 40,\,40\right] ^\circ$ with $R_{\sigma ,2/2\mathrm {diag}} \approx 0.5\%$. As the configuration deviates from the optimal condition, the fully populated VCM can be replaced by its diagonal counterpart.

• 3. Simplification of the fully populated VCM with its diagonal counterpart $R_{{\hat{d}},2/2\mathrm {equi}}$ and $R_{\sigma ,2/2\mathrm {equi}}$ derived by the DCM approach

  The results obtained with the DCM are similar to the previous case. Once more, the equivalent model can replace the fully populated VCM with a high confidence. Even if at the parameter level, $R_{{\hat{d}},2/2\mathrm {equi}}$ is higher than $R_{{\hat{d}},2/2\mathrm {diag}}$, it remains at a level close to 0. Similar to the reference case, $R_{\sigma ,2/2\mathrm {equi}}$ is approximately five times lower than $R_{\sigma ,2/2\mathrm {diag}}$. As $R_{\sigma ,2/2\mathrm {diag}}$, $R_{\sigma ,2/2\mathrm {equi}}$ decreases as the scanning configuration becomes worth more. These conclusions were similar for all other scanning configurations we simulated, and are not discussed further.

4.5 Using the DCM in a real case

To highlight how to use the DCM in real case, a white plane of size $1\hbox { m} \times 1\hbox { m}$ was scanned at a distance of 10 m with a Z+F 2016 using the scanning modus “high” and “superhigh” (premium). This corresponds approximately to a scanning rate as chosen in the simulations. We chose two scanning configurations, i. e., the optimal one with no tilt (see Sect. 4) and a scanning configuration with a slight tilt of $20^\circ$ for $\theta$. The point clouds were preprocessed to avoid edge effects and outliers, and finally cut using a free software. The point clouds obtained resulted in 30 lines of 30 points, similar to our simulated planes. We adopted a standard deviation of $0.004^\circ$ for the angles and $0.2 \hbox { mm}$ for the range. The values were taken from the manufacturer’s datasheet and agree with the one of more accurate model based on the intensity value such as in Wujanz et al. (2017).

Fig. 10

Flowchart of the data analysis procedure

The first-order solution was computed in a first approximation using the corresponding diagonal VCM built as explained in Sect. 3.3. The correlation structure of the range was estimated from the residuals using a Matérn model by fixing the smoothness to $\frac{1}{2}$: This corresponds to an autoregressive process of first order AR(1) in one dimension, see Rasmussen and Williams (2006). Due to the chosen parameterization of the Matérn covariance function, a balance between $\nu$ and $\alpha$ occurs, i. e., the estimated correlation parameter will be smaller than if a higher smoothness would have been estimated, see Stein (1999). As shown in Sect. 4.4.1 within a simulated framework, we are allowed—even for the suboptimal scanning configuration—to make this simplification. A second possibility is to estimate the parameters of a Matérn model and decrease $\alpha$ by 0.5 by keeping $\nu$ fixed to $\frac{1}{2}$: This approximation is valid for the use in the DCM and not for an accurate correlation modeling, it leads to less computational demanding matrix inversion. We make use of the first strategy in this contribution and further adopt a “global” correlation model, i. e., the white noise component is not independently estimated and considered to decrease the correlation length accordingly, see Kermarrec and Schön (2017b). We performed the estimation linewise using the MATLAB function ar. For the optimal scanning configuration, the mean values were 0.11 (respectively, 0.14 for the suboptimal scanning configuration) over the lines with a standard deviation of $1 \times 10^{-3}$, respectively, $3 \times 10^{-3}$ for the correlation coefficient for the setting high. We found for the setting superhigh a higher correlation coefficient of 0.31 with a standard deviation of $0.7 \times 10^{-3}$ (respectively, 0.35 with a standard deviation of $1.5 \times 10^{-3}$ for the suboptimal scanning configuration). The correlation coefficients are nearly independent of the scanning configuration: This validates that temporal correlations can be estimated from the residuals, i. e., at a distance of $10\hbox { m}$ under labor condition, we do not expect atmospheric effects to affect the correlation structure. We are aware that this estimation may be biased due to the small samples under consideration; however, the stable results are a validation that the bias is probably kept small: Otherwise some numerical instability in the parameter estimation would have been visible. An accurate determination of the parameters is beyond the scope of the present paper and would overload it, i. e., we wish to validate the use of the DCM so that a rough approximation is enough here to show its range of application. Simulations having shown that the parameter estimation is not affected by this approximation, we only concentrate on the dispersion for the real data analysis.

4.5.1 Optimal scanning configuration

For the optimal scanning configuration, the first-order dispersion of the range d using the estimated fully populated VCM reaches $0.101\hbox { mm}$ for the setting high (respectively, $0.08\hbox { mm}$ for the setting superhigh). We found an increase lower than $1\%$ for both case using the second-order dispersion, which is coherent with the simulation results for the chosen standard deviation of the range; the value of the correlation coefficient corresponds approximately to $\alpha =1$. Using a diagonal VCM resulted in an underestimated dispersion of $0.076\hbox { mm}$ (respectively, $0.068\hbox { mm}$), which also corresponds to the value found in the simulations (see Fig. 8b, left, middle). We made use of the DCM for the range by means of the VIF computed from the correlation coefficient (see “Appendix B”). The corrected dispersion value reached $0.098\hbox { mm}$ (respectively, 0.079), which is close to the value found using the fully populated VCM, thus, validating the effectiveness of the DCM. The DCM has a similar effect as if the range standard deviation would have been increased by a factor $\sqrt{VIF}$.

4.5.2 Suboptimal scanning configuration

In that case, and following the simulations, the second-order dispersion is not worth computing for the range standard deviation under consideration (see Fig. 9b, left, middle). Using the estimated fully populated VCM, a value of $0.35\hbox { mm}$ for the setting high (respectively, $0.28\hbox { mm}$ for the setting superhigh) was found. This is a slightly higher value than for the optimal scanning configuration. Using a diagonal VCM or the DCM changed the results by less than $0.2\%$ and can replace with a high trustworthiness the fully populated VCM in the computation of the dispersion. Please note, the increased number of digits of the presented results is only used for the sake of comparability. We additionally performed the parameter estimation for all four cases. As shown in the simulation, an improved stochastic model has a low impact on the solution. This effect was confirmed in the real data analysis and is here not presented with the sake not to overload the present contribution.

4.5.3 Conclusion of the real data analysis

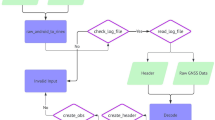
The DCM is a simplification based on the AR(1) model: a Matérn model with a fix smoothness, balanced by a corresponding “decrease” in the estimated correlation parameter. The methodology for using the DCM with real data is summarized in a flowchart form in Fig. 10. Simulations have shown that the DCM can be used with a high trustworthiness, which we validated by means of the real data analysis from a plane fitting. It allows one, in a first approximation, to correct the first- or second-order dispersion adequately, as well as for parameter estimation when needed. Further investigations will concentrate on how to estimate the AR(1) parameter and the white noise component, following, for example, Kargoll et al. (2018).

5 Conclusion

A knowledge of the stochastic properties of TLS errors is of great importance to avoid untrustworthy test decisions for deformation, and unrealistic dispersion or parameter estimation. When a linearization of the functional model is performed, biases are introduced in the LS approximation and a second-order solution may be more appropriate to get realistic estimates. Unfortunately, physical correlations of the raw TLS measurements combined with the scanning configuration are expected to impact this improved solution. We modeled the correlation structure of the TLS range measurements with the Matérn covariance function to analyze this impact. The three model parameters, i. e., smoothness, correlation length and variance, can be trustworthily estimated, even for small samples, by means of the de-biased Whittle likelihood. Alternatively, they could be fixed without further estimation based on empirical investigation or modeling. Accounting for an improved stochastic model for TLS measurements leads to fully populated VCM. The estimation of the second-order solution may become computationally demanding: Some investigations were needed to weight the corresponding benefits against computing the first-order solution only. Based on simulated TLS measurements from a plane scanned with different measurement configurations and considering various correlated noise structures, we have shown that the ratio between the first- and second-order solution was below $2\%$ for the dispersion and $0.05\%$ for the estimation of the range for a reference configuration without tilt of the plane. The ratio was found to decrease as the correlations increased, as well as for suboptimal scanning configurations: There is, thus, a high risk of miss-estimating the dispersion when the first-order solution is computed. This effect is getting higher when correlations are further underestimated. Indeed, we investigated whether a simple diagonal VCM without taking correlations into account would have led to the same LS results and found that the dispersion increased with the level of correlations to reach a ratio of up to $60\%$ between the results obtained with fully populated and diagonal VCM for a range standard deviation of $5\hbox { mm}$. The ratio decreased as the scanning configuration deviated from the reference one. We concluded that accounting for correlations with a fully populated VCM in the LS adjustment is crucial when objects are scanned under optimal scanning conditions, particularly if the first-order solution is computed. This result has driven our research to answer our third scientific question: Is it possible to replace the fully populated VCM with a DCM or equivalent diagonal model for a LS plane fitting? In this contribution, we could successfully confirm the empirical results found for GPS adjustment by modeling various scanning conditions: A fully populated VCM can be resumed to a diagonal matrix, which accounts in a “hidden” way for correlations in a LS adjustment. The ratio differences DCM versus fully populated VCM were smaller than $2\%$, compared with values up to $60\%$ for the corresponding diagonal matrix. We advise making use of an AR(1) model for the correlation structure with the DCM for numerical stability. This assumption further simplifies the computation of the inverse of the VCM, resuming it to a simple factor. Empirical estimations or physical modeling of an accurate correlation structure of TLS range measurements remain the topic of further contributions.

Appendices

Appendix: Estimation of the Matérn parameters in real case

The three parameters of the Matérn covariance function, the variance, the range and the smoothness of the correlation function, have to be estimated in real cases. This estimation can be performed from the residuals of the LS adjustment. The most important parameter is the smoothness, as it impacts strongly on the first values of the inverse of the VCM and, thus, the value of the dispersion (Kermarrec and Schön 2016).

The estimation can be done with MLE, as in the Hector software (Bos et al. 2012) or with the powerful Whittle maximum likelihood, which we propose to describe briefly for the sake of completeness. The poor performance of the MLE for short samples (Sykulski et al. 2019) can be avoided using this estimator, which aims to provide faster estimation with only a slight inaccuracy. In that case, the Whittle likelihood in its discretized form is given by

$$\begin{aligned} l_W \left( H\right)= & {} -\sum _{\omega \in \Omega } \left[ \log {\left( {\tilde{f}}\left( \omega ,H\right) \right) } + \frac{I\left( \omega \right) }{{\tilde{f}}\left( \omega ,H\right) } \right] \end{aligned}$$

(28)

with $\Omega$ as the set of discrete Fourier frequencies, ${\tilde{f}}\left( \omega ,H\right)$ the continuous-time process spectral density and $I\left( \omega \right)$ the periodogram, i. e.,

$$\begin{aligned} I\left( \omega \right)\propto & {} \sum _{j=1}^N \left| z_j e^{-ij\omega } \right| ^2 . \end{aligned}$$

(29)

The Whittle estimator assumes a priori that the power spectrum of the underlying process of the dataset is known and should only be used, if a time series is consistent with the process under consideration. This can be checked visually in a first approximation with the MATLAB function pwelch to estimate the psd of the process.

Appendix: Variance inflation factor

The noise model of TLS range measurements can be approximated with the autoregressive model of the first order AR(1), which assumes a weak stationarity. The correlation matrix of the corresponding process has a Toeplitz structure (Rao and Toutenburg 1995), i. e.,

$$\begin{aligned} {\mathbf {Q}}_{\mathrm {AR(1)}}= & {} \left[ \begin{array}{cccccc} 1 &{} \rho &{} \rho ^2 &{} \ldots &{} \rho ^{n - 1} &{} \rho ^n \\ \rho &{} 1 &{} \rho &{} \ldots &{} \rho ^{n - 2} &{} \rho ^{n - 1} \\ \rho ^2 &{} \rho &{} 1 &{} \ddots &{} \rho ^{n - 3} &{} \rho ^{n - 2} \\ \vdots &{} \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ \rho ^{n - 1} &{} \rho ^{n - 2} &{} \ddots &{} \ddots &{} 1 &{} \rho \\ \rho ^n &{} \rho ^{n - 1} &{} \ldots &{} \ldots &{} \rho &{} 1 \end{array} \right] , \end{aligned}$$

(30)

where $\rho$ is the autocorrelation coefficient, which can be estimated or fixed a priori. The main advantage of the $\mathrm {AR(1)}$ over other correlation models is that an explicit inverse ${{\mathbf {Q}}}_{\mathrm {AR(1)}}^{-1}$ exists, i. e.,

$$\begin{aligned} {\mathbf {Q}}_{\mathrm {AR(1)}}^{-1}= & {} \frac{1}{1 - \rho ^2} \left[ \begin{array}{cccccc} 1 &{} -\rho &{} 0 &{} \ldots &{} 0 &{} 0 \\ -\rho &{} 1 + \rho ^2 &{} -\rho &{} \ddots &{} 0 &{} 0 \\ 0 &{} -\rho &{} 1 + \rho ^2 &{} \ddots &{} 0 &{} 0 \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} 0 \\ 0 &{} 0 &{} 0&{} \ddots &{} 1 + \rho ^2 &{} -\rho \\ 0 &{} 0 &{} 0 &{} \ldots &{} -\rho &{} 1 \end{array} \right] .\nonumber \\ \end{aligned}$$

(31)

Consecutively, the diagonal equivalent matrix, following Sect. 3.3.3 is given by

$$\begin{aligned} {\mathbf {Q}}_{\mathrm {AR(1),equi}}^{-1}= & {} \frac{1}{1 - \rho ^2} \left[ \begin{array}{cccccc} 1 - \rho &{} 0 &{} 0 &{} \ldots &{} 0 &{} 0 \\ 0 &{} \left( 1 - \rho \right) ^2 &{} 0 &{} \ddots &{} 0 &{} 0 \\ 0 &{} 0 &{} \left( 1 - \rho \right) ^2 &{} \ddots &{} 0 &{} 0 \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} 0 \\ 0 &{} 0 &{} 0 &{} \ddots &{} \left( 1 - \rho \right) ^2 &{} 0 \\ 0 &{} 0 &{} 0 &{} \ldots &{} 0 &{} 1 - \rho \end{array} \right] .\nonumber \\ \end{aligned}$$

(32)

Thus, assuming that for large matrices, the first and last terms of the diagonal that have different values than the rest can be neglected, we approximate ${\mathbf {Q}}_{\mathrm {AR(1),equ}}$ by ${\mathbf {Q}}_{\mathrm {AR(1),equi}} = VIF{{\mathbf {I}}}$, where ${\mathbf {I}}$ is the identity matrix and the variance inflation factor is defined as $VIF=\frac{1+\rho }{1-\rho }$. The corresponding VCM $\hat{{\Sigma }}_r$ for the range is obtained by $\hat{{\Sigma }}_{r,\mathrm {equi}} = \sigma _{0,r}^2 VIF {{\mathbf {I}}}$.