Abstract
Vertical surface displacements from continuous Global Positioning System (GPS) stations often show strong seasonal signals, which in some cases may be associated with surface mass loading, including hydrological, and non-tidal oceanic and atmospheric loading. In Antarctica, many GPS stations show vertical motions in phase with seasonal snow accumulation changes, but these variations cannot be fully explained with snow load variations between seasons. Instead we show, for many sites in Antarctica, that a significant component of the annual cycle in vertical GPS coordinates time series may be related to snow/ice inside antennas causing as an artefact apparent seasonal variation, with amplitudes of up to 4 mm. We present a method based on the Empirical Mode Decomposition (EMD) algorithm to remove this artefact signal. The corrected GPS time series show an improvement in the agreement with displacements predicted by elastic modelling using GRACE-derived surface mass loads.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Surface displacement time series, derived from the Global Positioning System (GPS), contain signatures of multiple geophysical phenomena, ranging from global tectonic plate motions (Feigl et al. 1993) to local climatic effects (Davis et al. 2004). While horizontal components of displacements are widely used, vertical displacements were historically less favourable due to their sensitivity to errors in orbital modelling, monument instabilities, tropospheric modelling errors and other reference frame factors (e.g. Herring et al. 2016). However, during recent years numerous improvements have been made in the analysis of GPS data (e.g. Boehm et al. 2006; Steigenberger et al. 2009; Tregoning and Watson 2009). Time series of vertical displacements are now derived with better precision allowing their usage for studying the Earth’s response to various loading effects, including Global Isostatic Adjustment (GIA) (e.g. King et al. 2010), hydrology (e.g. Borsa et al. 2014) and sea level (e.g. Wöppelmann et al. 2009).
Vertical GPS time series often show seasonal variations dominated by yearly and half-yearly periods (van Dam et al. 2007). These variations are mainly associated with the Earth’s response to surface hydrological and atmospheric loading caused by the water transfer between continents and oceans. These displacements could in principle be predicted if the Earth’s rheology and the load are known. Therefore, retrieving accurately the annual signal from vertical GPS displacement signals is a key observation to validate models of induced surface strain due to surface mass variations. However, studies in the literature (Ray et al. 2013) have shown that “spurious” periodic signals in GPS time series signals may exist as a result of systematic error propagation. These variations can potentially bias the estimation of the “real” periodic geophysical signals as well as other parameters estimated from the time series such as the linear secular velocities (Blewitt and Lavallée 2002). Penna and Stewart (2003) showed that unmodelled semidiurnal and diurnal signals at certain tidal periods can propagate into seasonal signals. King and Watson (2010) also showed that multipath and time variable network geometry effects can contribute to draconitic period (351 day) signals present in GPS time series. Therefore, it is likely that site-specific errors can propagate and cause profound changes in the statistical properties of GPS time series. One of the well-known examples of site-specific errors in GPS positioning is related to snow accumulation on the GPS antenna, especially in locations with freezing conditions, such as Antarctica and Greenland. Antenna radomes are commonly used for continuous GPS sites installations in these regions to cover antennas against snow. Jaldehag et al. (1996) showed that variations in the order of several centimetres in the vertical coordinates time series can be explained by the accumulation of snow which delays and scatters the GPS signals. Similarly, O’Keefe et al. (2000) showed that 1.25 cm of wet surface ice loading can lead to a reduction of in the signal-to-noise ratio (SNR) of about 3 dB.
Snow-contaminated positions are usually manifested as discontinuities or anomalous position estimates in the time series. However, it is not clear yet whether they in practice contribute to periodic or quasi-periodic signals, since they are not completely dependent on the annual cycle of surface temperature. The common practice to eliminate anomalous position estimates, within the geodetic community, is to flag snow-contaminated estimates based on the experience and knowledge of the local weather conditions of the GPS site, assuming a certain model of the time series. Larson (2013) developed an algorithm that uses SNR data to determine when the GPS signal has been impacted by snow or ice. This technique considers that SNR time series can be fitted by a seasonal term and a second-order polynomial, and data that are outside a user-defined threshold are removed and their corresponding position flagged as snow contaminated. Despite the success of this model for removing large outliers and improving the positions by \(\sim \)10% mostly within the Plate Boundary Observatory (PBO) network, there were cases where the SNR time series showed large seasonal variations and did not follow the proposed model.
Most of the studies mentioned above considered the impact of snow/ice accumulation on bare GPS antennas or on covering radomes. However, in 2015 the U.S. POLENET-ANET team discovered ice inside a chokering antenna that had been covered by a radome (David Saddler, Personal Communication), then subsequently documented internal antenna snow/ice at many sites and surmised that blowing spindrift snow had entered through basal chokering drain holes (Konfal et al. 2016). To stop intrusion of snow, the POLENET-ANET team covered or blocked the chokering drainage holes (David Saddler, Personal Communication). Changes in daily position time series subsequent to blocking the entry of snow were substantial at many POLENET-ANET GPS sites (Saddler et al. 2018; Wilson et al. 2019). In this paper, we investigate this effect on vertical position time series for selected sites in POLENET-ANET (Polar Earth Observing Network-Antarctic Network) GPS continuous networks in Antarctica. First, we describe the GPS data processing strategy. Then, we assess and discuss the effect of snow intrusion on GPS time series and we introduce a method for removing this effect.
2 GPS data analysis
The GPS position time series used in this study are derived from the processing of networks with globally distributed sites combined with 6 regional networks in Antarctica. The time span of the data extends from 1995 up to mid-2019. We used the GAMIT-GLOBK software (Herring et al. 2016) to process the GPS raw carrier phase data. Satellite orbital parameters were fixed to the International GNSS Service (IGS) Final (or repro2) product values, and we estimated for each day the Earth orientation parameters (EOP), station coordinates and atmospheric zenith delays at each station. We considered the effects of ocean tide loading by using the FES2004 model (Lyard et al. 2006) as well as the non-tidal atmospheric pressure loading deformation (Tregoning and Watson 2009). For the atmospheric modelling, we employed the time-varying a priori Zenith Hydrostatic Delay (ZHD) and Vienna Mapping function (VMF1), derived from the ECMWF model (Boehm et al. 2006). We incorporated the second-order ionospheric effects by using the Ionosphere Map Exchange format (IONEX) files from the IGS. An elevation cut-off angle of 10\(^{\circ }\) was used, and observations were weighted using an elevation-dependent scheme based on the post-fit residuals. The position time series were derived, using a Kalman filter, after combining the loosely constrained estimates of station coordinates and EOP and their covariances from each day of our networks. To allow a stable combination of the subnetworks we used 12 common tie sites between all networks. Then, we realized the ITRF2014 reference frame (Altamimi et al. 2016) by performing a daily six-parameter transformation (3 translations, 3 rotations). The resulting position time series were inspected and corrected manually for outliers, and instrumental and/or earthquake offsets.
3 Effects of snow intrusion in GPS antenna
One characteristic of many GPS time series in Antarctica is the presence of multiple gaps (for example due to lack of observations during winter seasons when solar power is not available and wind turbines may not provide enough current to operate the receiver). Therefore, for this paper we selected a subset of sites (Fig. 1a) from the POLENET-ANET network, which don’t suffer from winter data gaps.
Figure 2 shows the detrended time series of vertical displacements. All the time series show an annual cycle with apparent subsidence during the summer and uplift during winter seasons, in phase with seasonal snowfall changes (Bromwich 1988). However, we observe an abrupt decay of these variations for all the time series, at different epochs between 2016 and 2017. Given that a dominant part of the quasi-annual signal in vertical GPS time series is related to various environmental and climatic sources, its amplitude is likely to be time dependent. However, it is not expected to change so rapidly, and this change coincides with no known sudden climatological shift. Alternatively, if these changes are believed to arise following discontinuity in the realisation of the reference frame, we would expect the reduction of the annual cycle to be synchronised between all the stations. Sharp changes in individual GPS time series properties are more likely to be instrument related, such as antenna or receiver changes.
Almost 60% of the continuous running GPS stations in our processed Antarctic network are equipped with choke-ring antennas (100% of bedrock sites in the U.S. POLENET-ANET network up to 2019) (Fig. 1c). It is a well-known standard antenna designed for geodetic measurements. Most of the sites in Antarctica and Greenland are also equipped with radomes for protection against snow and debris during winter seasons. However, antennas are still not completely isolated against snow intrusions, since by default they are equipped with drainage openings placed in the ground plane in order to provide egress for moisture (Fig. 1b). A closer inspection of the time series metadata shows that the sudden reductions in amplitude coincide with the time of plugging (total/partial plugging, tapping) the choke-ring antenna holes (personal communication from David Saddler) (Fig. 2). Therefore, the only plausible explanation for the halt of the annual signal must be associated with the cessation of snow penetration via the antenna drain holes, which had previously solidified within the radome. Cycles of seasonal accumulation and melting of ice between choke-rings of the antennas caused a scattering and attenuation of the GPS signal, which led to an apparent annual position variation. To test for the significance of the variance change before and after the antenna plugging, we applied the Levene’s test (Levene 1960). The p values for all the sites were below the 0.05 significance level. Thus, the null hypothesis is rejected, supporting our observation of the annual cycle reduction after the closure of antenna drainage holes.
4 Method for removing the apparent annual cycle
Previous studies, in regions of extended winter seasons, explained the variations in GPS surface displacement time series by the seasonal mass loading due to snow accumulation and melting periods. Fu et al. (2012) showed a high correlation between GPS vertical time series in Alaska with the GRACE-modelled loading displacements, suggesting that the hydrological cycle is the main driver for ground deformation in Alaska. Bevis et al. (2012) and Liu et al. (2017) studied the annual signal in the vertical displacements measured at two GPS sites in Greenland and showed that it is largely driven by the Earth’s elastic response to seasonal variations in ice mass and surface atmospheric pressure. Therefore, the oscillations we observe in our time series are likely to be the results of a combination of periodic signals due to such surface load changes and due to antenna snow intrusion effects. To avoid removing real geophysical signal while extracting the snow-related signal, we follow a three-step approach: (i) we remove the surface loading deformation from the GPS time series, then (ii) we use the resulting residuals (GPS-GRACE) to extract the annual signal component associated with the snow intrusion, and (iii) we remove this component from the raw GPS time series.
If we consider that the geophysical processes that produce the annual cycle seen in GPS observations are related to regional-scale surface mass loading effects, then GRACE data could be used to infer the annual vertical elastic deformation displacements. In our study, we use the GRACE solution from the NASA Goddard Space Flight Center (GSFC) (Luthcke et al. 2013; Loomis and Luthcke 2017), provided by the EOST loading service (Gegout et al. 2010). Although the EOST product has been corrected for a GIA model, we detrended the GRACE time series in order to take into account any linear rate residual arising from GIA mismodelling . The monthly time series were interpolated to daily intervals using a cubic spline and then subtracted from the GPS time series, for the lifetime of GRACE up to July 2016. The resulting residual time series are then used to extract the antenna-ice-related (non-loading) annual signal. Visual inspection of the time series might lead to the impression that this signal has a temporally constant amplitude; however, given that it is associated with the seasonal cycle of surface temperature, it is likely to show variable seasonality. For this reason, we use the Empirical Decomposition Mode (EMD) algorithm to estimate the signal. The EMD method has been successfully used in different geophysical signal analysis applications (e.g. Luthcke et al. 2013; Montillet et al. 2013). Unlike other techniques, EMD does not rely on linearity or stationarity assumptions. It is based on decomposing a time series x(t) into a number N of intrinsic mode functions (IMFs) \(c_j(t)\) as:
where \(r_n(t)\) is a nonzero-mean remainder which is a slowly varying function with only a few extrema. In practice, the EMD method works by a sifting process (Huang et al. 1998), which starts with identifying and connecting all the local extrema with a cubic spline. Then, the first component h is extracted by taking the difference between the data and the local mean of the envelope. The resulting component h is treated as data, and the previous two processes are repeated until the residual becomes a monotonic function or a function only containing one internal extremum from which no more IMFs can be extracted. To reduce the edge effects in the EMD decomposition, different techniques were developed. Huang et al. (1998) proposed to extend the original signal by adding artificial waves at either ends to overcome the splines’ uncertain definition at the edges.
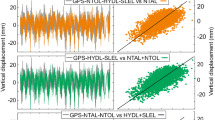
The raw, residuals (GPS-GRACE) and the corrected time series (from top to bottom) of the stations BERP (with a choke-ring antenna and radome) and SCTB (Zephyr geodetic antenna, no radome). The red line is the elastic deformation derived from GRACE. The orange squares are the monthly averaged time series
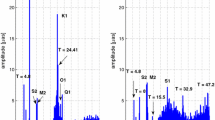
A limitation of the EMD is the so-called mode mixing problem, which corresponds to the presence of signals with disparate scales in one IMF or signals with the same timescales sifted into different IMFs. To overcome this issue, a variation of the algorithm was developed, called the Ensemble Empirical Decomposition Mode (EEMD) (Wu and Huang 2009). The EEMD runs an ensemble of EMDs while adding multiple noise realizations to the signal. In our study, we use 1000 runs while adding Gaussian noise. The visual inspection of the resulting IMFs from the EEMD shows that the first components are mostly high frequency (Fig. 3). We calculated the spectra of all the IMFs, and we selected the components with the highest amplitude at the annual period. The seventh is from the annual cycle, and the eighth has some contribution of the annual cycle with a dominant inter-annual variation. Chambers (2015) suggests that using EMD to identify multidecadal variability and accelerations in tide gauge time series should be done with caution, as it is more likely that multiple modes contribute to explain the physical climate modes. Therefore, in order to obtain a narrow band annual cycle, we combine the seventh and the eight components; then, we apply a single EMD decomposition in a second iteration. The resulting first IMF corresponds to the annual signal component related to snow effects, which we remove from the raw GPS time series.
We used a synthetic time series to investigate the ability of the EDM method for extracting the annual cycle mode. We used a daily time series consisting of a long-term linear rate, semi-annual and annual signals and Gaussian noise (Fig. S1). The annual signal is simulated with a time-varying amplitude and present only in the first 8 years of the total time span to mimic the effect of snow intrusion. The decomposition result shows a weak recovery of the annual signal by the EMD, with standard deviation of the residuals of \(\sigma =2.91\) mm. The EEMD provides a significant improvement where the phase of the seventh is more consistent with the simulated signal, although the amplitude is slightly underestimated (\(\sigma =2.54\) mm). When combining the seventh and the eighth components and applying a single EMD iteration, the annual signal matches quite well the first IMF component (\(\sigma =2.44\) mm). The decomposition introduces a small artefact after the time of cessation of the annual signal, but this is not going to affect our results since we do not correct for snow effects after the plugging time.
We illustrate the method outlined above using time series from two sites, for the same period, with different antenna models. One has a choke-ring antenna with radome and was subject to a plugging of the drain holes (BERP), and a second site is located on Ross Island (SCTB) with a Trimble Zephyr antenna which does not require a radome. Figure 4 shows the raw GPS time series as well as the residual time series (after correction). The reduction of the annual cycle for the BERP time series is evident, compared to the case of the SCTB site, for which the corrected time series is similar to the original one, meaning that the EMD does not degrade the time series in the case of the absence of a snow-related annual signal. Although we note a 4-mm reduction in the power at the annual cycle (Fig. 5) for the site BERP, the power at the other subannual frequencies remains similar to the original time series, indicating that the decomposition did not remove power from any other frequencies. There is a slight increase in the amplitude at the semi-annual period which might be related to a phase shift between GRACE-derived surface displacements and GPS time series. To gain an overall assessment of the effect of applying the EMD correction, we calculated the weighted root-mean-square (WRMS) scatter of all the time series considered in this study. We note a reduction of the scatter in all the time series with varying amounts (Fig. 6), depending on the amplitude of the apparent annual signal which varies according to the amount of snow intrusion at each site. As expected, we obtained a slight further reduction in the WRMS when subtracting the GRACE-derived elastic deformation from the corrected GPS time series. This indicates that the annual signal in the corrected GPS time series is in phase with GRACE and might be related to regional hydrological processes across Antarctica. We also note a decrease in magnitude of the spectral index \((\kappa )\) from − 1.15 to − 0.93 after applying the correction, in agreement with Kłos et al. (2018), who suggested that ignoring the varying seasonal signal leads to an overestimation of the spectral index, resulting in an overestimation of the trend uncertainty.
We found that the highest reduction in the WRMS corresponds to the time series of the stations BERP, CRDI and SUGG (Fig. 6). These time series also have the highest amplitude of the annual signal, indicating that the EMD decomposition performs well when the snow-related signal is dominating the annual frequency. Additionally, one of the limitations of the EMD method is that it is difficult to separate signals when their frequencies are very close together (Huang et al. 1998), which might be the case in our study when the GRACE signal does not reflect the local loading signal at the GPS site and some residuals might be left in the time series.
5 Discussion
Different methods have been proposed to remove time-dependent periodic signals from geodetic time series. Kłos et al. (2018) provides a summary of the performance of different algorithms to estimate time-varying seasonal signals in synthetic time series. They showed that the noise level in time series is one of the important factors influencing the precision of the estimation. Our proposed method takes advantage of the dyadic filter bank behaviour of the EMD. The main structures of the signal are mainly concentrated in the lower-frequency IMFs and are less prevalent in the high-frequency modes (first components). Therefore, we expect a limited impact of the noise on the precision of our estimation of the seasonal signal. Thus, it is unlikely that we are introducing a bias into the estimation of the secular velocity from the corrected time series. Although it is beyond the scope of this paper, it is worth mentioning that the EMD could also be used to detrend geodetic time series and detect multi-decade position changes by investigating IMFs with one extremum during the span of the data (Wu et al. 2007).
A core assumption of our method is that the “genuine” geophysical periodic surface loading signal can be restored from GRACE-derived elastic deformation. However, as mentioned earlier, the lack of available GRACE solutions beyond July 2016 increases the chance of overestimating the snow-related seasonal variations. Fortunately, this was limited in our study since most of the antenna hole taping dates were within few months of early 2016, except SUGG and CRDI which were partially plugged in December 2016.
In this study, we found that the apparent seasonal variations caused by snow intrusions were roughly symmetric and gradual over a timescale of weeks, in contrast to the effects of accumulated frost or ice, which are likely to cause jumps in the vertical displacements within short time span (Kochanski 2015). Although this is highly related to temperature and humidity conditions at the GPS stations, we still do not have a full explanation why those asymmetric sharp variations occur at some sites and not others. In the case of antenna snow intrusion, we observe geographic dependencies of the amplitude of the apparent annual cycle, indicating that seasonal weather conditions at the GPS sites are likely the key elements determining the amount of snow pushed inside GPS radomes. In an attempt to investigate this hypothesis we retrieved the air temperature and wind speed records at the GPS sites from the RINEX meteorological files. These measurements are from a near-surface atmospheric pack attached close to the GPS station. Since the GPS antennas are mounted on masts elevated above the ground by approximately 1.5 m, the snow intrusion inside the antenna will occur only if enough suspended snow particles are blown by wind through the drainage holes. A critical parameter for this mechanism is known as the threshold wind speed, the minimum wind speed initiating snow transport (Schmidt 1986). We used the empirical formula proposed by Li and Pomeroy (1997) to derive the wind speed threshold based on air temperature for dry snow conditions. Figure 7 shows the IMF corresponding to the annual signal removed from GPS time series along with the surface air temperature as well as the wind speed anomalies with respect to the wind speed threshold. We observe a clear correlation between the air temperature and the annual IMF of the position time series with a positive lag, indicating that the start of the uplift signal is typically delayed by a few weeks after the temperature reaches the melting point. Although this might be related to bedrock thermal expansion (Hill et al. 2009), it is unlikely to be significant given the short delay between the air temperature change and the surface displacement. During winter seasons when temperature reaches its lowest, snow starts accumulating inside the antenna and an apparent subsidence signal is then observed. Interestingly, we also observe that the amplitude of the annual cycle of the IMF is correlated with the magnitude and duration of above-threshold wind speed occurrences. For the sites BERP, CRDI and to a lesser extent BURI, when wind speed is frequently and significantly above the threshold, a considerable amount of suspended snow is intruded in the radome. However, for the site DEVI, wind speed is rarely above the threshold, so a very limited amount of snow is transported which explains the small amplitude of the artefactual annual cycle in the GPS time series at this particular site. From these observations, we can conclude that two key elements need to coexist for snow intrusion inside the radome: low temperatures below freezing and high wind speed above the threshold in order to sustain snow particle transport. Following the lead of the U.S. POLENET-ANET project, networks where these two conditions are present should block drainage holes in chokering antennas.
While information about the dates that drainage holes were plugged or taped and details of the monument are well documented for the POLENET-ANET sites, this information is still absent in most of the official GPS archives. Our study shows that it is highly important to have this information in order to detect and identify apparent quasi-periodic surface displacement related to snow effects. Therefore, adding new entries to the current IGS-style log files documenting the changes in the antenna environment will be invaluable to the broad scientific community using high-latitude GNSS data.
We show that snow intrusions into choke-ring GPS antennas can cause the introduction of spurious annual signal in the vertical component, with amplitudes of up to 4 mm. An algorithm based on the EMD method has been proposed to extract this signal. This algorithm improves our GPS time series in Antarctica and results in a good agreement with displacements predicted using elastic modelling of GRACE-derived surface mass loads. For geophysical applications, the presence of these apparent annual signals in vertical surface displacements can have profound implications in obscuring hydrological or tidal loading effects. Moreover, the presence of such signal is likely to introduce error propagation into other frequencies leading to erroneous physical interpretations.
Data availability statement
All the GPS data used in this publication are publicly available in the UNAVCO data portal (https://www.unavco.org/data/data.html) and the CDDIS data repository (https://cddis.nasa.gov/archive/gnss/data/daily). Position time series are available upon request from the author. The identifiers of the GPS data from the U.S. POLENET-ANET network are listed below: Site (DOIs): BERP (https://doi.org/10.7283/T54J0CC2), BURI (https://doi.org/10.7283/T5RB72W7), CRDI (https://doi.org/10.7283/T5C24TQS), DEVI (https://doi.org/10.7283/T57942Z0), FTP4 (https://doi.org/10.7283/T5B27SKD), LWN0 (https://doi.org/10.7283/T5T43RD8), SUGG (https://doi.org/10.7283/T5CV4G1M).
References
Altamimi Z, Rebischung P, Métivier L, Collilieux X (2016) ITRF2014: a new release of the international terrestrial reference frame modeling nonlinear station motions. J Geophys Res Solid Earth 121:6109–6131. https://doi.org/10.1002/2016JB013098
Bevis M et al (2012) Bedrock displacements on Greenland driven by ice mass variations, climate cycles and climate change. Proc Natl Acad Sci 109:11944–11948
Blewitt G, Lavallée D (2002) Effect of annual signals on geodetic velocity. J Geophys Res 107:B2145. https://doi.org/10.1029/2001JB000570
Boehm J, Werl B, Schuh H (2006) Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J Geophys Res 111:B02406. https://doi.org/10.1029/2005JB003629
Borsa AA, Agnew DC, Cayan DR (2014) Ongoing drought-induced uplift in the western United States. Science 345:1587–1590. https://doi.org/10.1126/science.1260279
Bromwich DH (1988) Snowfall in high southern latitudes. Rev Geophys 26(1):149–168. https://doi.org/10.1029/RG026i001p00149
Chambers DP (2015) Evaluation of empirical mode decomposition for quantifying multi-decadal variations and acceleration in sea level records. Nonlin Processes Geophys 22:157–166
Davis JL, Elósegui P, Mitrovica JX, Tamisiea ME (2004) Climate-driven deformation of the solid Earth from GRACE and GPS. Geophys Res Lett 31:L24605. https://doi.org/10.1029/2004GL021435
Feigl KL et al (1993) Space geodetic measurement of crustal deformation in central and southern California, 1984–1992. J Geophys Res 98(B12):21677–21712. https://doi.org/10.1029/93JB02405
Fu Y, Freymueller JT, Jensen T (2012) Seasonal hydrological loading in southern Alaska observed by GPS and GRACE. Geophys Res Lett 39:L15310. https://doi.org/10.1029/2012GL052453
Gegout P, Boy J-P, Hinderer J, Ferhat G (2010) Modeling and observation of loading contribution to time-variable GPS sites positions. IAG Symposia 135(8):651–659. https://doi.org/10.1007/978-3-642-10634-7
Herring TA, Melbourne TI, Murray MH, Floyd MA, Szeliga WM, King RW, Phillips DA, Puskas CM, Santillan M, Wang L (2016) Plate Boundary Observatory and related networks: GPS data analysis methods and geodetic products. Rev Geophys 54:759–808. https://doi.org/10.1002/2016RG000529
Hill EM, Davis JL, Elósegui P, Wernicke BP, Malikowski E, Niemi NA (2009) Characterization of site-specific GPS errors using a short-baseline network of braced monuments at Yucca Mountain, southern Nevada. J Geophys Res 114:B11402. https://doi.org/10.1029/2008JB006027
Huang NE, Shen Z, Long SR, Wu MC, Shih EH, Zheng Q, Tung CC, Liu HH (1998) The empirical mode decomposition method and the Hilbert spectrum for non-stationary time series analysis. Proc R Soc Lond 454A:903–995
Jaldehag RTK, Johansson JM, Davis JL, Elósegui P (1996) Geodesy using the Swedish Permanent GPS network: effects of snow accumulation on estimates of site positions. Geophys Res Lett 23:1601–1604. https://doi.org/10.1029/96GL00970
King MA et al (2010) Improved constraints on models of glacial isostatic adjustment: a review of the contribution of ground-based geodetic observations. Surv Geophys 31(5):465–507. https://doi.org/10.1007/s10712-010-9100-4
King MA, Watson CS (2010) Long GPS coordinate time series: multipath and geometry effects. J Geophys Res 115:B04403. https://doi.org/10.1029/2009JB006543
Kłos A, Bos MS, Bogusz J (2018) Detecting time-varying seasonal signal in GPS position time series with different noise levels. GPS Solut 22:21. https://doi.org/10.1007/s10291-017-0686-6
Kochanski KA (2015) Ice and the apparent variation of GPS station positions for Alaska, B.Sc. thesis, Dept. Earth, Atmospheric and Planetary Sciences, Massachusetts Institute of Technology
Konfal S, Kendrick E, Saddler D, Wilson T, Bevis M (2016) Crustal velocity solutions in polar environments: GPS position errors caused by ice in antennas. SCAR Open Science Conference, Kuala Lumpur, Malaysia
Larson KM (2013) A methodology to eliminate snow- and ice-contaminated solutions from GPS coordinate time series. J Geophys Res Solid Earth 118:4503–4510. https://doi.org/10.1002/jgrb.50307
Levene H (1960) Robust tests for equality of variances. Contributions to probability and statistics: essays in honor of harold hotelling. Stanford University Press, Stanford, pp 278–292
Li L, Pomeroy JW (1997) Probability of occurrence of blowing snow. J Geophys Res 102(D18):21955–21964. https://doi.org/10.1029/97JD01522
Liu L, Khan SA, van Dam T, Ma JHY, Bevis M (2017) Annual variations in GPS-measured vertical displacements near Upernavik Isstrøm (Greenland) and contributions from surface mass loading. J Geophys Res Solid Earth 122:677–691. https://doi.org/10.1002/2016JB013494
Loomis BD, Luthcke SB (2017) J Geod. Mass evolution of mediterranean black, red, and caspian seas from GRACE and altimetry: accuracy assessment and solution calibration 91(2):195–206. https://doi.org/10.1007/s00190-016-0952-3
Luthcke SB, Sabaka TJ, Loomis BD, Arendt AA, McCarthy JJ, Camp J (2013) Antarctica, Greenland and Gulf of Alaska land ice evolution from an iterated GRACE global mascon solution. J Glaciol 59(216):613–631
Lyard F, Lefévre F, Letellier T, Francis O (2006) Modelling the global ocean tides: a modern insight from FES2004. Ocean Dyn 56:394–415. https://doi.org/10.1007/s10236-006-0086-x
Montillet JP, Tregoning P, McClusky S, Yu K (2013) Extracting white noise statistics in GPS coordinate time series. IEEE Geosci Rem Sens Lett 10(3):563–567. https://doi.org/10.1109/LGRS.2012.2213576
O’Keefe K, Stephen J, Lachapelle G, Gonzales RA (2000) Effect of ice loading of a GPS antenna. Geomatica 54(1):63–74
Penna NT, Stewart MP (2003) Aliased tidal signatures in continuous GPS height time series. Geophys Res Lett 30:2184. https://doi.org/10.1029/2003GL018828
Ray J, Griffiths J, Collilieux X, Rebischung P (2013) Subseasonal GNSS positioning errors. Geophys Res Lett 40:5854–5860. https://doi.org/10.1002/2013GL058160
Saddler DM, Wilson TJ, Bevis MG, Smalley R Jr, Dalziel IWD, Matheny P, Konfal SA, Gomez D, Kendrick EC (2018) Analysis of present-day horizontal crustal motions in West Antarctica. AGU Fall Meeting Abstracts G23C–0629
Schmidt RA (1986) Transport rate of drifting snow and the mean wind speed profile. Bound Layer Meteor 34:213–241
Steigenberger P, Rothacher M, Fritsche M, Rülke A, Dietrich R (2009) Quality of reprocessed GPS satellite orbits. J Geod 83:241–248. https://doi.org/10.1007/s00190-008-0228-7
Tregoning P, Watson C (2009) Atmospheric effects and spurious signals in GPS analyses. J Geophys Res 114:B09403. https://doi.org/10.1029/2009JB006344
van Dam T, Wahr J, Lavallée D (2007) A comparison of annual vertical crustal displacements from GPS and gravity recovery and climate experiment (GRACE) over Europe. J Geophys Res 112:B03404. https://doi.org/10.1029/2006JB004335
Wahr AGJ, Zhong S (2013) Computations of the viscoelastic response of a 3-D compressible Earth to surface loading: an application to Glacial Isostatic Adjustment in Antarctica and Canada. Geophys J Int 192:557–572. https://doi.org/10.1093/gji/ggs030
Wilson T, Bevis M, Konfal S, Saddler D, Kendrick E, Matheny P, Barletta V, Smalley R, Dalziel I, Aster R, Nyblade A, Wiens D (2019) Understanding the mismatch between measured and model-predicted crustal motions across West Antarctica: Insights from POLENET-ANET GPS results. Workshop on Glacial Isostatic Adjustment, Ice Sheets, and Sea-level Change - Observations, Analysis, and Modelling, Ottawa, Canada
Wöppelmann G, Letetrel C, Santamaría A, Bouin M-N, Collilieux X, Altamimi Z, Williams SDP, Martín Miguez B (2009) Rates of sea-level change over the past century in a geocentric reference frame. Geophys Res Lett 36:L12607. https://doi.org/10.1029/2009GL038720
Wu ZH, Huang NE (2009) Ensemble empirical mode decomposition: a noise-assisted data analysis method. Adv Adapt Data Anal 1(1):1–41
Wu Z, Huang NE, Long SR, Peng C-K (2007) On the trend, detrending, and variability of nonlinear and nonstationary time series. Proc Natl Acad Sci 104(38):14889–14894. https://doi.org/10.1073/pnas.0701020104
Acknowledgements
GPS data used in this study were obtained from UNAVCO (https://www.unavco.org/instrumentation/networks/status/polenet) and from the International GNSS Service (IGS). We thank David Saddler and Matt King for communicating the database of antenna drainage holes plugging. The package PyEMD (https://github.com/laszukdawid/PyEMD) was used for the EMD analysis. The GPS data processing was performed on the Rocket High Performance Computing service at Newcastle University. AK and PJC are supported by UK Natural Environment Research Council grants NE/K004085/1 and NE/R002029/1. Comments from Terry Wilson, Editor Jürgen Kusche and three anonymous reviewers greatly improved our original manuscript.
Author information
Authors and Affiliations
Contributions
AK designed the research and implemented the calculations. AK and PJC wrote the manuscript.
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Koulali, A., Clarke, P.J. Effect of antenna snow intrusion on vertical GPS position time series in Antarctica. J Geod 94, 101 (2020). https://doi.org/10.1007/s00190-020-01403-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00190-020-01403-6