1 Introduction

The Gravity Recovery And Climate Experiment (GRACE, Tapley et al. 2004) satellite mission was in orbit for over 15 years and provided an invaluable data record for climate and Earth system sciences. Its primary data product was a time series of monthly gravity field snapshots—a proxy for mass distribution in the Earth system.

To recover the gravity field from GRACE data without prior information, a global, homogeneous data distribution is required (Weigelt et al. 2013). Typically, global coverage is reached after about one month. This means that any signal that cannot be represented by a monthly time series has to be reduced from the data before the gravity field is computed; otherwise, the sampling theorem (e.g., Shannon 1949) is not fulfilled. This signal reduction is performed by using geophysical models which provide high-frequency temporal gravity variations. As these models are not perfect, residual high-frequency signal is aliased into the monthly gravity field, deteriorating the solution (Han et al. 2004). This undesired effect is currently among the limiting factors for the overall solution quality for both GRACE and its successor GRACE-FO (Flechtner et al. 2016). There have already been efforts toward improving the dealiasing process which aims at directly improving the dealiasing model coefficients (Zenner et al. 2010, 2012).

The idea we present here is to use information about the uncertainty of these geophysical models within the gravity field recovery process. The overall goal of the approach is to improve the gravity field estimates by incorporating a more realistic stochastic observation model. Assuming random error behavior, a stochastic description of the model uncertainties provides a more appropriate weighting of the observations. Measurements, which are subjected are larger model error, will be downweighted in the adjustment process, which mitigates their impact on the estimated gravity field. Ideally, this reduces temporal aliasing effect, namely the north–south striping patterns in the GRACE solutions, while conserving the full monthly signal. We outline two approaches how this additional information can be efficiently introduced into the least squares adjustment and show their mathematical equivalence. We evaluate our approach using six years of GRACE data, from which two time series of monthly solutions, with and without the derived error model, are computed.

2 Least squares estimation with model errors

The first step in recovering Earth’s gravity field from satellite data in a least squares sense is to relate the acquired observations \({\mathbf {l}}\) with the sought-after gravity field parameters \({\mathbf {x}}\) through a functional model of the form

$$\begin{aligned} {\mathbf {l}}= f({\mathbf {x}}, {\mathbf {y}}). \end{aligned}$$
(1)

There exist a number of representations for the functional model f, which relate the observations to the gravity field through Newton’s second law of motion, for example, integrated variational equations (e.g., Montenbruck and Gill 2000; Beutler and Mervart 2010) or integral equations (e.g., Mayer-Gürr 2006). As depicted in (1), this mapping will not only depend on the gravity field parameters \({\mathbf {x}}\), but also additional model parameters \({\mathbf {y}}\). In practice f will be evaluated using fixed model output, denoted by \({\mathbf {y}}_m\), resulting in a functional model

$$\begin{aligned} {\mathbf {l}}= f({\mathbf {x}}, {\mathbf {y}}_m) = f_m({\mathbf {x}}), \end{aligned}$$
(2)

which only depends on \({\mathbf {x}}\). Taking GRACE/GRACE-FO as an example, \({\mathbf {x}}\) will typically consist of a monthly snapshot of non-tidal gravity variations and satellite specific parameters, whereas \({\mathbf {y}}_m\) is composed of models approximating all other forces acting on the satellite. The force model usually includes Earth and ocean tides, non-tidal gravity field variations in atmosphere and ocean, non-conservative forces such as drag and solar radiation pressure, and the static gravity field. The non-gravitational parameters in \({\mathbf {x}}\) generally include calibration parameters for various instruments aboard the satellite, e.g., accelerometer bias and scale, and the satellite initial state.

In order to estimate the unknown parameters \({\mathbf {x}}\) from the functional model (2) in a least squares sense, we expand \(f_m\) into a Taylor series with respect to \({\mathbf {x}}\) at \({\mathbf {x}}_0\). The resulting power series

$$\begin{aligned} {\mathbf {l}}= f_m({\mathbf {x}}_0) + \frac{\partial f_m }{\partial {\mathbf {x}}}\Bigg |_{\,\,{\mathbf {x}}_0} ({\mathbf {x}}-{\mathbf {x}}_0)+ \cdots \end{aligned}$$
(3)

is then truncated after the linear term. For clarity, we introduce the design matrix \({\mathbf {A}}\), which is the Jacobian of \(f_m\) with respect to \({\mathbf {x}}\) evaluated at \({\mathbf {x}}_0\), and the parameter corrections \({\varDelta }{\mathbf {x}}\) defined as \({\mathbf {x}}- {\mathbf {x}}_0\). Moving the zero-order term of the power series to the left-hand side yields

$$\begin{aligned} {\varDelta }{\mathbf {l}}= {\mathbf {l}}- f_m({\mathbf {x}}_0) = {\mathbf {A}}{\varDelta }{\mathbf {x}}+ {\mathbf {e}}, \end{aligned}$$
(4)

which relates the reduced observations \({\varDelta }{\mathbf {l}}\) to the parameter corrections. The residual vector \({\mathbf {e}}\) is added to the right-hand side of (4) because the system of observation equations will generally be inconsistent due to measurement errors in \({\mathbf {l}}\) and model imperfections. We assume that the residuals \({\mathbf {e}}\) will be correlated, and hence we need to define a metric \({\mathbf {P}}\equiv {\varvec{\Sigma }}^{-1}_{{\mathbf {e}}}\) in order to appropriately minimize the norm of \({\mathbf {e}}\). To obtain the covariance matrix of the residuals, we apply covariance propagation to (4). We assume that the model output

$$\begin{aligned} {\mathbf {y}}_m= {\mathbf {y}}_t+ {\mathbf {y}}_e, \quad {\mathbf {y}}_e\sim {\mathcal {N}}(0, {\varvec{\Sigma }}_{{\mathbf {y}}_m}), \end{aligned}$$
(5)

differs from the true values \({\mathbf {y}}_t\) only by some random errors \({\mathbf {y}}_e\) with a known covariance matrix \({\varvec{\Sigma }}_{{\mathbf {y}}_m}\). Considering these model uncertainties, we find that

$$\begin{aligned} {\varvec{\Sigma }}_{{\mathbf {e}}}= {\varvec{\Sigma }}_{{\mathbf {l}}}+ {\mathbf {B}}{\varvec{\Sigma }}_{{\mathbf {y}}_m}{\mathbf {B}}^\mathrm{T}. \end{aligned}$$
(6)

Here, \({\mathbf {B}}\) is the Jacobian of f with respect to \({\mathbf {y}}\) evaluated at \(({\mathbf {x}}_0, {\mathbf {y}}_m)\). Note that in (6), no uncertainties of \({\mathbf {x}}_0\) and \({\mathbf {A}}\) are considered, as the Taylor series expansion point is purely deterministic. Solving the overdetermined system of observation equations (4) using the covariance matrix (6) leads to the well-known least squares estimate of \({\mathbf {x}}\),

$$\begin{aligned} {\hat{{\mathbf {x}}}}= {\mathbf {x}}_0 + ({\mathbf {A}}^\mathrm{T}{\mathbf {P}}{\mathbf {A}})^{-1} {\mathbf {A}}^\mathrm{T}{\mathbf {P}}{\varDelta }{\mathbf {l}}. \end{aligned}$$
(7)

Alternatively, the model uncertainty can also be incorporated on the parameter level. Linearizing (1) with respect to both \({\mathbf {x}}\) and \({\mathbf {y}}\) at \(({\mathbf {x}}_0, {\mathbf {y}}_m)\) yields

$$\begin{aligned} {\varDelta }{\mathbf {l}}= {\mathbf {l}}- f({\mathbf {x}}_0, {\mathbf {y}}_m) = {\mathbf {A}}{\varDelta }{\mathbf {x}}+ {\mathbf {B}}{\varDelta }{\mathbf {y}}+ {\tilde{{\mathbf {e}}}}, \end{aligned}$$
(8)

which extends the parameter space to include the stochastic model parameter corrections \({\varDelta }{\mathbf {y}}= {\mathbf {y}}-{\mathbf {y}}_m\). We denote the residuals in this approach by \({\tilde{{\mathbf {e}}}}\) because, in line with the standard approach to nonlinear least squares adjustment, the expansion point \(({\mathbf {x}}_0, {\mathbf {y}}_m)\) is purely deterministic; hence,

$$\begin{aligned} {\varvec{\Sigma }}_{{\tilde{{\mathbf {e}}}}}= {\varvec{\Sigma }}_{{\mathbf {l}}}. \end{aligned}$$
(9)

To include the model parameter uncertainty \({\varvec{\Sigma }}_{{\mathbf {y}}_m}\), we introduce the pseudo-observations

$$\begin{aligned} 0 = {\mathbf {I}}{\varDelta }{\mathbf {y}}+ {\mathbf {y}}_e, \quad {\mathbf {y}}_e\sim {\mathcal {N}}(0, {\varvec{\Sigma }}_{{\mathbf {y}}_m}), \end{aligned}$$
(10)

where \({\mathbf {I}}\) is an identity matrix of appropriate dimensions. Combining (8) and (10) leads to the blocked system of observation equations

$$\begin{aligned} \begin{bmatrix} {\varDelta }{\mathbf {l}}\\ 0 \end{bmatrix} = \begin{bmatrix} {\mathbf {A}}&\quad {\mathbf {B}}\\ 0&\quad {\mathbf {I}}\end{bmatrix} \begin{bmatrix} {\varDelta }{\mathbf {x}}\\ {\varDelta }{\mathbf {y}}\end{bmatrix} + \begin{bmatrix} {\tilde{{\mathbf {e}}}}\\ {\mathbf {y}}_e\end{bmatrix}. \end{aligned}$$
(11)

The system of normal equations corresponding to (11) is given by

$$\begin{aligned} \begin{bmatrix} {\mathbf {A}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\mathbf {A}}&{\mathbf {A}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\mathbf {B}}\\ {\mathbf {B}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\mathbf {A}}&\quad {\mathbf {B}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\mathbf {B}}+{\varvec{\Sigma }}_{{\mathbf {y}}_m}^{-1} \\ \end{bmatrix} \begin{bmatrix} {\varDelta }{\hat{{\mathbf {x}}}} \\ {\varDelta }{\hat{{\mathbf {y}}}} \end{bmatrix} = \begin{bmatrix} {\mathbf {A}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\varDelta }{\mathbf {l}}\\ {\mathbf {B}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\varDelta }{\mathbf {l}}\\ \end{bmatrix}, \end{aligned}$$
(12)

or more concisely

$$\begin{aligned} \begin{bmatrix} {\mathbf {N}}_{{\mathbf {x}}{\mathbf {x}}}&{\mathbf {N}}_{{\mathbf {x}}{\mathbf {y}}} \\ {\mathbf {N}}_{{\mathbf {x}}{\mathbf {y}}}^\mathrm{T}&\quad {\mathbf {N}}_{{\mathbf {y}}{\mathbf {y}}}+{\varvec{\Sigma }}_{{\mathbf {y}}_m}^{-1} \\ \end{bmatrix} \begin{bmatrix} {\varDelta }{\hat{{\mathbf {x}}}} \\ {\varDelta }{\hat{{\mathbf {y}}}} \end{bmatrix} = \begin{bmatrix} {\mathbf {n}}_{\mathbf {x}}\\ {\mathbf {n}}_{\mathbf {y}}\\ \end{bmatrix}. \end{aligned}$$
(13)

To show that (7) and (11) give the same estimate of \({\hat{{\mathbf {x}}}}\), we first eliminate \({\varDelta }{\mathbf {y}}\) from the least squares adjustment. Following Niemeier (2008), the coefficient matrix and right-hand side of the resulting system of normal equations

$$\begin{aligned} {\bar{{\mathbf {N}}}}{\varDelta }{\hat{{\mathbf {x}}}}= {\bar{{\mathbf {n}}}} \end{aligned}$$
(14)

can be explicitly written as

$$\begin{aligned} \begin{aligned} {\bar{{\mathbf {N}}}}&= {\mathbf {A}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\mathbf {A}}- {\mathbf {A}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\mathbf {B}}( {\mathbf {B}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\mathbf {B}}+{\varvec{\Sigma }}_{{\mathbf {y}}_m}^{-1})^{-1}{\mathbf {B}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\mathbf {A}}\\&= {\mathbf {A}}^\mathrm{T}[{\tilde{{\mathbf {P}}}}- {\tilde{{\mathbf {P}}}}{\mathbf {B}}( {\mathbf {B}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\mathbf {B}}+{\varvec{\Sigma }}_{{\mathbf {y}}_m}^{-1})^{-1}{\mathbf {B}}^\mathrm{T}{\tilde{{\mathbf {P}}}}]{\mathbf {A}}\end{aligned} \end{aligned}$$
(15)

and

$$\begin{aligned} \begin{aligned} {\bar{{\mathbf {n}}}}&= {\mathbf {A}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\varDelta }{\mathbf {l}}- {\mathbf {A}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\mathbf {B}}( {\mathbf {B}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\mathbf {B}}+{\varvec{\Sigma }}_{{\mathbf {y}}_m}^{-1})^{-1}{\mathbf {B}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\varDelta }{\mathbf {l}}\\&= {\mathbf {A}}^\mathrm{T}[{\tilde{{\mathbf {P}}}}- {\tilde{{\mathbf {P}}}}{\mathbf {B}}( {\mathbf {B}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\mathbf {B}}+{\varvec{\Sigma }}_{{\mathbf {y}}_m}^{-1})^{-1}{\mathbf {B}}^\mathrm{T}{\tilde{{\mathbf {P}}}}]{\varDelta }{\mathbf {l}}, \end{aligned} \end{aligned}$$
(16)

where we introduced the weight matrix \({\tilde{{\mathbf {P}}}}= {\varvec{\Sigma }}_{{\mathbf {l}}}^{-1}\) for brevity. Applying the matrix identity

$$\begin{aligned} \begin{aligned}&({\mathbf {R}} + {\mathbf {U}}{\mathbf {S}}{\mathbf {V}})^{-1} \\&\quad = {\mathbf {R}}^{-1} - {\mathbf {R}}^{-1} {\mathbf {U}}({\mathbf {S}}^{-1} + {\mathbf {V}}{\mathbf {R}}^{-1}{\mathbf {U}})^{-1}{\mathbf {V}}{\mathbf {R}}^{-1} \end{aligned} \end{aligned}$$
(17)

(e.g., Henderson and Searle 1981; Hager 1989) to the bracketed expressions in (15) and (16) yields

$$\begin{aligned} {\bar{{\mathbf {N}}}} = {\mathbf {A}}^\mathrm{T}[{\tilde{{\mathbf {P}}}}^{-1} + {\mathbf {B}}{\varvec{\Sigma }}_{{\mathbf {y}}_m}{\mathbf {B}}^\mathrm{T}]^{-1}{\mathbf {A}}\end{aligned}$$
(18)

and

$$\begin{aligned} {\bar{{\mathbf {n}}}} = {\mathbf {A}}^\mathrm{T}[{\tilde{{\mathbf {P}}}}^{-1} + {\mathbf {B}}{\varvec{\Sigma }}_{{\mathbf {y}}_m}{\mathbf {B}}^\mathrm{T}]^{-1}{\varDelta }{\mathbf {l}}, \end{aligned}$$
(19)

which is exactly the least squares adjustment in (7). This means that to incorporate model uncertainties, one can either augment the covariance matrix of observations, or co-estimate model corrections as stochastic parameters with known prior covariance. An alternative interpretation of this equivalence is that the model errors are either projected into the post-fit residuals, since the weights of contaminated observations are reduced, or the model errors are absorbed by the additional parameters. If the numerical values of the model corrections are of interest, one can solve (11) directly or use

$$\begin{aligned} {\varDelta }{\hat{{\mathbf {y}}}}= ({\mathbf {B}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\mathbf {B}}+{\varvec{\Sigma }}_{{\mathbf {y}}_m}^{-1})^{-1} {\mathbf {B}}^\mathrm{T}{\tilde{{\mathbf {P}}}}({\varDelta }{\mathbf {l}}- {\mathbf {A}}{\varDelta }{\hat{{\mathbf {x}}}}) \end{aligned}$$
(20)

after \({\varDelta }{\hat{{\mathbf {x}}}}\) was determined through (7) or (14).

3 Application to GRACE gravity field recovery

To investigate the impact of using model uncertainties, we estimate monthly gravity field solutions from GRACE data following the least squares adjustment (11). We restrict our study to errors of the atmosphere and ocean dealiasing (AOD) product used to remove high-frequency non-tidal variations in GRACE/GRACE-FO processing (AOD1B, Dobslaw et al. 2017). However, other background models, such as ocean tides, can be treated in a similar fashion. The current release of AOD1B is given as a three-hourly time series of potential coefficients up to a spherical harmonic degree and order of 180. The model is applied to the GRACE observations by linearly interpolating the corresponding nodal points to the observation times. If all model parameters are considered to be subject to uncertainties, \({\varDelta }{\mathbf {y}}\) would be represented by 248 nodal points with 32,757 parameters each, resulting in over 8 million additional parameters per month. To reduce this number and the accompanying computational burden, we restrict the spatial resolution of the co-estimated model corrections to maximum spherical harmonic degree of 40 and parameterize the temporal evolution as daily block means. This implies that higher frequencies in both space and time are treated as error free.

3.1 Derivation of \({\varvec{\Sigma }}_{{\mathbf {y}}_m}\)

To derive the AOD model uncertainty covariance matrix \({\varvec{\Sigma }}_{{\mathbf {y}}_m}\), we make use of the ESA Earth System Model (ESA ESM, Dobslaw et al. 2015, 2016) for satellite gravity mission simulations. The dataset provides six-hourly time series of potential changes from atmosphere (A), ocean (O), hydrosphere (H), cryosphere (I), and solid Earth (S) as well as a time series of estimated atmosphere and ocean model errors (aoErr) up to a spherical harmonic degree of 180. These error estimates correspond to release 05 (RL05) of the AOD1B product; however, the currently employed AOD1B RL06 is a notable improvement over RL05 both in terms of high-frequency variability and also long-term consistency (e.g., Figures 1 to 3 in Dobslaw et al. 2017). The major error characteristics as reflected by spatial and temporal correlations and regional distributions, however, remain largely unchanged. This includes in particular the much higher accuracy over the continents, in particular over the densely populated regions of the world; higher errors in some open-ocean places that are resonant at daily-to-weekly periods (Bellingshausen Basin, North Pacific, Arctic Ocean); and the highest errors at the shelf or in semi-enclosed seas. Error characteristics as represented in ESA ESM are thus perceived as still representative even for RL06, albeit those are now somewhat more conservative than in the case of RL05 (Henryk Dobslaw, personal communication).

AOD product errors do not only arise from uncertainties in atmosphere and ocean models, but in principle also contain unmodeled high-frequency variations from other geophysical subsystems. We therefore chose to also include variations in the hydrosphere, as they exhibit the largest magnitude in frequencies below 30 days, next to the given atmosphere and ocean errors (2.5 mm global RMS, compared to 0.4 mm global RMS of the I component). In order to align the given dealiasing error samples with the parameterization defined for the model error corrections, we apply a temporal low-pass filter, followed by a downsampling to one day, and truncate the potential coefficients at degree and order 40. Specifically, daily averages are computed from the three-hourly potential coefficients, which are then assigned to 12:00 of the corresponding day. To restrict the a priori model uncertainty covariance matrix to sub-monthly variations of the dealiasing errors, we subtract the mean of each calendar month as well as a secular and annual fit from the time series. The resulting residual variations \({\tilde{{\mathbf {y}}}}_{\text {aoErr}}\) and \( {\tilde{{\mathbf {y}}}}_{\text {H}}\) are then interpreted as realizations of the underlying—assumed to be stationary—stochastic daily AOD error process. For a given day \(t_i\), this can be explicitly written as

$$\begin{aligned} {\tilde{{\mathbf {y}}}}_e(t_i) = {\tilde{{\mathbf {y}}}}_{\text {aoErr}}(t_i) + {\tilde{{\mathbf {y}}}}_{\text {H}}(t_i). \end{aligned}$$
(21)

The stationarity assumption implies that the covariance function of \({\tilde{{\mathbf {y}}}}_e(t_i)\) only depends on the lag \(k=|j-i|\) between two epochs \(t_i\) and \(t_j\) (Lütkepohl 2005). Correspondingly, the covariance matrix of the process \({\varvec{\Sigma }}_{{\mathbf {y}}_m}\) is block Toeplitz with a structure

$$\begin{aligned} ({\varvec{\Sigma }}_{{\mathbf {y}}_m})_{ij} = {\left\{ \begin{array}{ll} {\varvec{\Sigma }}(|j-i|) &{} \text {for } i \le j \\ {\varvec{\Sigma }}(|j-i|))^\mathrm{T} &{} \text {otherwise} \end{array}\right. }. \end{aligned}$$
(22)

As the direct estimation of \({\varvec{\Sigma }}_{{\mathbf {y}}_m}\) from the sample suffers from numerical instability for higher lags (e.g., Fan et al. 2016), a parametric method to estimate the spatiotemporal correlations of \({\tilde{{\mathbf {y}}}}_e\) was chosen. Specifically, we approximate the stochastic properties of the process using an autoregressive (AR) representation of the form

$$\begin{aligned} {\mathbf {y}}_e(t_i) = \sum _{k=1}^p \varvec{\Phi }^{(p)}_k{\mathbf {y}}_e(t_{i-k}) + {\mathbf {w}}(t_i),\quad {\mathbf {w}}(t_i) \sim {\mathcal {N}}(0, {\varvec{\Sigma }}^{(p)}_{\mathbf {w}}).\nonumber \\ \end{aligned}$$
(23)

In (23), \(\varvec{\Phi }^{(p)}_k\) are the AR model coefficients and \({\mathbf {w}}(t_i)\) is a white noise sequence. The superscript p of \(\varvec{\Phi }^{(p)}_k\) and \({\varvec{\Sigma }}^{(p)}_{\mathbf {w}}\) denotes that these coefficients and white noise covariance are part of an AR(p) model, where p is the model order. The model coefficients and white noise covariance were determined using Yule–Walker equations for multivariate AR processes (e.g., Lütkepohl 2005; Brockwell and Davis 2010) with empirical covariance estimates from the sample \({\tilde{{\mathbf {y}}}}_e\). The maximum order p for which a stable AR model could be estimated from the given AOD error time series was \(p_{\text {max}}=3\). We obtained the required empirical covariance matrices for the lags \(k = \{0,\ldots ,p_{\text {max}}\}\) through the unbiased estimator

$$\begin{aligned} {\varvec{\Sigma }}(k) = \frac{1}{N}\sum _{j=0}^{N-1} \frac{1}{M_j-k}\sum _{i=k}^{M_j-1} {\tilde{{\mathbf {y}}}}_e(t_{i-k}) {\tilde{{\mathbf {y}}}}_e(t_i)^\mathrm{T} \end{aligned}$$
(24)

(Brockwell and Davis 2010), where \(M_j\) is the number of days in month j and N is the total number of months. After the coefficients were determined, we used the AR model equation (23) to transform the pseudo-observations (10). By separating \({\mathbf {y}}_e\) and \({\mathbf {w}}\) in (23) to the left- and right-hand side, we get

$$\begin{aligned} {\mathbf {w}}(t_i) = {\mathbf {y}}_e(t_i) - \sum _{k=1}^p \varvec{\Phi }^{(p)}_k{\mathbf {y}}_e(t_{i-k}). \end{aligned}$$
(25)

When assembled in chronological order for epochs \(t = \{0,\ldots ,M-1\}\), (25) yields a linear mapping \({\bar{\varvec{\Phi }}}\) relating the full time series of model errors \({\bar{{\mathbf {y}}}}_e\) to the white noise sequence \({\bar{{\mathbf {w}}}}\) through

$$\begin{aligned} {\bar{{\mathbf {w}}}} = {\bar{\varvec{\Phi }}}{\bar{{\mathbf {y}}}}_e. \end{aligned}$$
(26)

To evaluate (25) for epochs of the white noise sequence with \(t < p_{\text {max}}\), epochs of \({\mathbf {y}}_e\) with \(t<0\) are required. These epochs are assumed to be unknown, so warm-up effects are introduced to (26). To mitigate this undesired behavior, we also derived AR models for orders \(p=\{0, \ldots , p_{\text {max}}-1\}\) and placed them in the corresponding rows of \({\bar{\varvec{\Phi }}}\). The structure of \({\bar{\varvec{\Phi }}}\) is then given by

$$\begin{aligned} \begin{bmatrix} {\mathbf {I}}&\quad&\quad&\quad&\quad&\quad \\ -\varvec{\Phi }^{(1)}_1&\quad {\mathbf {I}}&\quad&\quad&\quad&\quad \\ -\varvec{\Phi }^{(2)}_2&\quad -\varvec{\Phi }^{(2)}_1&\quad {\mathbf {I}}&\quad&\quad&\quad \\ -\varvec{\Phi }^{(3)}_3&\quad -\varvec{\Phi }^ {(3)}_2&\quad -\varvec{\Phi }^ {(3)}_1&\quad {\mathbf {I}}&\quad&\quad \\&\quad -\varvec{\Phi }^{(3)}_3&\quad -\varvec{\Phi }^ {(3)}_2&\quad -\varvec{\Phi }^ {(3)}_1&\quad {\mathbf {I}}&\quad \\&\quad&\quad \ddots&\quad \ddots&\quad \ddots&\quad \ddots \\ \end{bmatrix}. \end{aligned}$$
(27)

By applying \({\bar{\varvec{\Phi }}}\) to (10), we finally arrive at the transformed pseudo-observations

$$\begin{aligned} 0 = {\bar{\varvec{\Phi }}} {\varDelta }{\mathbf {y}}+ {\bar{{\mathbf {w}}}},\quad {\bar{{\mathbf {w}}}} \sim {\mathcal {N}}(0, \bar{{\varvec{\Sigma }}}_{{\bar{{\mathbf {w}}}}}), \end{aligned}$$
(28)

with

$$\begin{aligned} \bar{{\varvec{\Sigma }}}_{{\bar{{\mathbf {w}}}}} = \begin{bmatrix} {\varvec{\Sigma }}^{(0)}_{{\mathbf {w}}}&~&~&~&~&~ \\ ~&{\varvec{\Sigma }}^{(1)}_{{\mathbf {w}}}&~&~&~&~ \\ ~&~&{\varvec{\Sigma }}^{(2)}_{{\mathbf {w}}}&~&~&~ \\ ~&~&~&{\varvec{\Sigma }}^{(3)}_{{\mathbf {w}}}&~&~ \\ ~&~&~&~&{\varvec{\Sigma }}^{(3)}_{{\mathbf {w}}}&~ \\ ~&~&~&~&~&\ddots \\ \end{bmatrix}. \end{aligned}$$
(29)

We briefly note that the equality \(\bar{{\varvec{\Sigma }}}_{{\bar{{\mathbf {w}}}}} = {\bar{\varvec{\Phi }}}{\varvec{\Sigma }}_{{\mathbf {y}}_m}{\bar{\varvec{\Phi }}}^\mathrm{T}\) only holds if \({\mathbf {y}}_e\) is an AR(\(p_{\text {max}}\)) process. From a computational perspective, the AR model approximation of \({\varvec{\Sigma }}_{{\mathbf {y}}_m}\) has the benefit that the normal equation coefficient matrix

$$\begin{aligned} {\bar{\varvec{\Phi }}}^\mathrm{T}\bar{{\varvec{\Sigma }}}^{-1}_{{\bar{{\mathbf {w}}}}}{\bar{\varvec{\Phi }}} \end{aligned}$$
(30)

arising from (28) is block-banded with a bandwidth of \(p_{\text {max}}+1\). Hence, for a GRACE monthly solution with \(M=31\) epochs in \({\bar{{\mathbf {w}}}}\) and \(p_{\text {max}}=3\), the block density of the normal equation matrix is only 12%. Furthermore, the inverse of (30) is strictly block Toeplitz, therefore satisfying our assumption of a stationary error process.

3.2 Parameterization of \({\varDelta }{\mathbf {y}}\) and \({\varDelta }{\mathbf {x}}\)

Following the definition of the AOD error process in the previous section, we parameterize the model corrections as daily time series of potential coefficients from degree 2 to 40. The parameter vector \({\varDelta }{\mathbf {y}}\) is therefore given as

$$\begin{aligned} {\varDelta }{\mathbf {y}}= \begin{bmatrix} {\varDelta }{\mathbf {y}}_0^\mathrm{T}&\cdots&{\varDelta }{\mathbf {y}}_{M-1}^\mathrm{T} \\ \end{bmatrix}^\mathrm{T}, \end{aligned}$$
(31)

where M is the number of days in that specific month. Correspondingly, the observation equation coefficient matrix \({\mathbf {B}}\) is block-diagonal. The monthly mean \({\varDelta }{\mathbf {x}}\) is also parameterized as potential coefficients, though from degree 2 to 120. This choice of parametrization introduces a linear dependency between \({\varDelta }{\mathbf {y}}\) and \({\varDelta }{\mathbf {x}}\). The zero-observations (10) however imply that the daily co-estimates \({\varDelta }{\hat{{\mathbf {y}}}}_k\) have zero mean over one month with respect to \({\varvec{\Sigma }}_{{\mathbf {y}}_m}\). We can verify that \({\varDelta }{\hat{{\mathbf {y}}}}\) is centered by computing the sample mean \({\mathbf {m}}\) through the least squares adjustment

$$\begin{aligned} {\varDelta }{\hat{{\mathbf {y}}}}= {\mathbf {F}}{\mathbf {m}}+ {\mathbf {v}},\quad {\mathbf {v}}\sim {\mathcal {N}}(0, {\varvec{\Sigma }}_{{\mathbf {y}}_m}). \end{aligned}$$
(32)

Here \({\mathbf {F}}= [{\mathbf {I}}\cdots {\mathbf {I}}]^\mathrm{T}\), where \({\mathbf {I}}\) is an identity matrix of appropriate dimension. Substituting the estimate (20) into the least squares solution

$$\begin{aligned} {\hat{{\mathbf {m}}}}= ({\mathbf {F}}^\mathrm{T}{\varvec{\Sigma }}_{{\mathbf {y}}_m}^{-1}{\mathbf {F}})^{-1} {\mathbf {F}}^\mathrm{T} {\varvec{\Sigma }}_{{\mathbf {y}}_m}^{-1}{\varDelta }{\hat{{\mathbf {y}}}}\end{aligned}$$
(33)

always yields \({\hat{{\mathbf {m}}}}= {\mathbf {0}}\) for the given design matrices \({\mathbf {A}}\) and \({\mathbf {B}}\). From the first block row of the system of normal equations (13), we find that

$$\begin{aligned} {\varDelta }{\hat{{\mathbf {x}}}} = {\mathbf {N}}_{{\mathbf {x}}{\mathbf {x}}}^{-1}{\mathbf {n}}_{\mathbf {x}}- {\mathbf {N}}_{{\mathbf {x}}{\mathbf {x}}}^{-1}{\mathbf {N}}_{{\mathbf {x}}{\mathbf {y}}} {\varDelta }{\hat{{\mathbf {y}}}}\end{aligned}$$
(34)

which relates the estimates for \({\mathbf {x}}\) and \({\mathbf {y}}\). Here, the matrix \({\mathbf {N}}_{{\mathbf {x}}{\mathbf {y}}} = {\mathbf {A}}^\mathrm{T}{\tilde{{\mathbf {P}}}}{\mathbf {B}}\) is crucial, as it describes how the residual high-frequency gravity field variations \({\varDelta }{\mathbf {y}}\) affect the monthly solution. Since this essentially shows how sub-monthly variations are mapped into the monthly mean, it can be interpreted as a projection representing temporal aliasing effects. Analogous considerations have been carried out by Albertella et al. (1991), Sneeuw and van Gelderen (1997), and Sneeuw (2000), however, with the application of spatial aliasing rather than temporal aliasing. Expanding (34) yields

$$\begin{aligned} {\varDelta }{\hat{{\mathbf {x}}}} = {\mathbf {N}}_{{\mathbf {x}}{\mathbf {x}}}^{-1}{\mathbf {A}}^\mathrm{T}{\tilde{{\mathbf {P}}}}({\varDelta }{\mathbf {l}}- {\mathbf {B}}{\varDelta }{\hat{{\mathbf {y}}}}), \end{aligned}$$
(35)

which offers another insight into how the co-estimation of model corrections affect the estimated monthly solution. As can be seen, the reduced observations \({\varDelta }{\mathbf {l}}\) are further reduced by the estimated parameters \({\varDelta }{\hat{{\mathbf {y}}}}\). We explicitly state that it is crucial; \({\varDelta }{\hat{{\mathbf {y}}}}\) is co-estimated, i.e., the correlations between monthly mean and daily model corrections are taken into account. Since the weighted mean \({\hat{{\mathbf {m}}}}\) of \({\varDelta }{\hat{{\mathbf {y}}}}\) is zero, this means that no monthly signal is reduced from the observations, but rather the estimated high-frequency model corrections.

4 Evaluation of estimated solutions

We now evaluate the impact of incorporating the AOD model uncertainties into the gravity field recovery. As stated in the introduction, the aim of introducing these AOD model uncertainties is to reduce the effects of temporal aliasing without losing monthly gravity field signal. To verify if this goal was achieved, we gauge the high-frequency noise content and the signal level of a series of monthly solutions.

Basis of the evaluation are two time series, “OBS” and “OBS+AOD”, of GRACE monthly solutions in the time span of 2005-01 to 2010-12. We chose this period because we observe a nearly homogeneous observation quality due to the still-active thermal management of the satellites (Tapley et al. 2015), minimal orbit decay, and an extended solar flux quiet period (e.g., Agee et al. 2010). Moreover, this time span contains no large data gaps or orbit repeat cycles. Given these circumstances, we expect a consistent set of solutions without large monthly outliers. For both time series, the monthly gravity field is parameterized up to a spherical harmonic degree of 120 and the processing scheme follows ITSG-Grace2018 (Mayer-Gürr et al. 2018). Whereas OBS only considers a stochastic model for the GRACE observations, OBS+AOD additionally incorporates AOD error information as outlined in the previous section. All other processing steps are identical. The estimated solutions follow the signal definition of the official GRACE products, and hence contain only non-tidal variations in hydrosphere, cryosphere, and solid Earth as well as residual atmosphere and ocean signal.

A widely used metric to quantify the noise level in GRACE solutions is to look at variability over the oceans, as most of the signal in these regions is expected to be removed through ocean tide and dealiasing models (Bonin et al. 2012; Meyer et al. 2016; Jean et al. 2018). In order to minimize residual signal in the noise estimates, we exclude coastal regions and regions where non-tidal ocean signal is expected, like the Arctic Ocean, Antarctic Circumpolar Current, and the Malvinas confluence. The resulting ocean mask covers approximately 46% of the total ocean area and is primarily located in the band of \(\pm \,50^{\circ }\) geographic latitude. We further reduce a climatology consisting of mean, trend, annual, and semi-annual variations from each time series. To gauge the noise level at different spatial scales, we compute the ocean RMS after applying a Gaussian filter with different radii.

Fig. 1
figure 1

Time series of quiet ocean RMS in equivalent water height for the standard solution (OBS) and the solution incorporating dealiasing model errors (OBS+AOD). A 300 km Gaussian filter was applied to both solutions

Full size image

Figure 1 shows the weighted RMS time series, expressed in equivalent water height (EWH), of both solutions for the investigated time span after a 300 km Gaussian filter was applied. As can be observed, the time series incorporating dealiasing errors exhibits lower RMS values throughout with an average RMS reduction of about 25%. Additionally, the month-to-month variation of the RMS values is lower, suggesting a more consistent solution set.

Fig. 2
figure 2

Quiet ocean RMS over the time span from 2005 to 2010 for both time series (top) and RMS reduction in OBS+AOD with respect to OBS (bottom) for different Gaussian filter radii

Full size image

Figure 2 shows the quiet ocean RMS in space and time of both time series for varying filter radii (top) and the corresponding RMS reduction in OBS+AOD with respect to OBS (bottom). We find the largest improvements between filter radii of 250 km to 300 km with a maximum RMS reduction of about 25%. Unsurprisingly, with larger filter radii and the corresponding stronger smoothing, the solutions become similar, as any high-frequency noise is filtered out.

Fig. 3
figure 3

RMS reduction in OBS+AOD w.r.t. OBS for each individual spherical harmonic coefficient

Full size image

In Fig. 3, the RMS reduction of OBS+AOD with respect to OBS for each spherical harmonic coefficient is shown. As can be seen, the RMS in both solutions is nearly identical in below order 15 for all degrees. The largest reduction is found around the orders 46 and 61, which correspond to the third an fourth resonance order, respectively (Cheng and Ries 2017). These (close) multiples of spherical harmonic order 15 are where we would expect temporal aliasing to cause larger errors (Seo et al. 2008).

Fig. 4
figure 4

Basin average time series for the Malvinas confluence zone (top) and the Danube basin (bottom) for OBS+AOD monthly solutions (300 km Gaussian filter applied), the sum of OBS+AOD monthly solutions (300 km Gaussian filter applied) and daily co-estimates, and daily gravity field solutions from ITSG-Grace2018. Note the different y-axis scale

Full size image

Figure 4 shows a comparison of the monthly block means of OBS+AOD, the sum of monthly block means and daily co-estimates, and an independently computed daily GRACE time series in terms of basin average time series. We briefly note that the basin average of the unconstrained monthly solutions and therefore the long wavelength variations of the time series will depend on the applied smoothing, which in this case was performed through a 300 km Gaussian filter. Both daily time series exhibit a similar short-wavelength behavior, from which we conclude that the daily co-estimates indeed pick up sub-monthly geophysical signals. This in turn means that since these high-frequency gravity field variations are absorbed by the additional parameters, their effect on the monthly estimates through temporal aliasing is also reduced.

In order to ensure that the approach does not cause signal attenuation, we examine regions where strong geophysical signals are present. Specifically, we look at river basins with a high signal-to-noise ratio (SNR). To identify river basins which match this criterion, we first derive noise estimates for 405 catchments for which the outlines were kindly provided by the Global Runoff Data Centre (2007). We follow a similar approach to Bonin et al. (2012) and move all basin polygons into quiet ocean areas while conserving their latitude. Leaving the basin polygons on their respective parallel is motivated by the latitude dependency of GRACE errors (Wahr et al. 2006). Following the same argumentation as for the total ocean RMS, the basin average time series for these shifted catchments will be dominated by random errors and can therefore be used to derive basin-specific noise estimates. To inhibit high-frequency spatial noise in smaller catchments and to reduce residual signal, we apply a 300 km Gaussian filter and subtract a climatology before computing basin average time series for all 405 shifted river basins. The temporal RMS over each time series then yields an upper bound for the noise in the corresponding catchment.

The signal level in each of the river basins is derived from the WaterGAP Global Hydrology Model (WGHM, Döll et al. 2003), to which we also applied a 300 km Gaussian filter so it matches the spectral characteristics of the GRACE time series used to compute the noise estimates. Restricting further investigations to river basins where both GRACE solutions exhibit an SNR higher than 10 leaves us with 69 globally distributed river basins. The SNR threshold of 10 was chosen as a trade-off between noise potentially influencing the temporal variability and conserving a large enough number of basins for meaningful conclusions. Since the annual cycle will be the dominant signal in most basins and is contained in the background model, we also examine the intra-annual variability by applying a high-pass filter before computing the temporal RMS.

Fig. 5
figure 5

Temporal variability of OBS+AOD over temporal variability of OBS for river basins with an SNR higher than 10 for the full signal (top) and intra-annual signal (bottom) in equivalent water height

Full size image

Figure 5 shows the temporal variability of both GRACE time series in equivalent water height plotted against each other. The top panel shows the variabilities of the full signal while the bottom panel shows the variabilities of the intra-annual variations. We do observe a good agreement between both time series, suggesting that the signal level of OBS and OBS+AOD matches. The largest discrepancies occur in river basins with an average SNR close to the chosen threshold of 10, where noise might still play a role. A maximum variability reduction of 1.0 cm (from 12.4 cm to 11.4 cm) can be observed in the Cross River (Nigeria). However, the noise in this basin also drops from 2.7 to 2.0 cm. For larger basins, where high-frequency noise is smoothed more effectively, both solutions do agree within 1% to 2%. Figure 6 shows the reduction in variability over the noise reduction in OBS+AOD with respect to OBS for the investigated basins. We can clearly observe a dependency between noise and variability reduction. This suggests that part of the reduced variability of OBS+AOD is due to the overall lower noise floor. With increasing basin area and the corresponding stronger smoothing, both solutions converge. Generally, the variabilities of OBS and OBS+AOD are within 2% for 73% of all river basins, which lead us to conclude that the developed approach does not attenuate the signal level in the monthly solutions.

Fig. 6
figure 6

Reduction in variability over noise reduction in OBS+AOD with respect to OBS for the selected river basins

Full size image

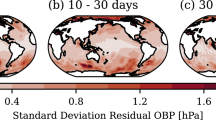
Finally, we investigate the formal error structure of the solutions and the agreement between formal and empirical errors. The incorporation of the dealiasing uncertainties should improve the stochastic description of the observations; hence, we expect more realistic formal errors. The chosen time span of 2005 to 2010 allows us to compute the empirical standard deviation from the time series, as due to the homogeneous data quality and orbit geometry, we have a set of consistent monthly solutions. Since the estimated coefficients contain both signal and noise, we reduce a climatology consisting of mean, trend, annual, and semi-annual variations from each time series beforehand. This simple parametric model cannot capture the full signal, so in lower spherical harmonic degrees, where a larger SNR is expected, we cannot derive reasonable standard deviation estimates. To obtain a comparable quantity from the formal errors, we average the variances over the same time span. In Fig. 7, we can see the averaged formal errors (left column), the empirical standard deviations (middle column), and the ratio between both quantities (right column). Overall, the error structure of both time series is quite similar, with both empirical and formal errors exhibiting higher uncertainties in orders that are approximately integer multiples of 15. This behavior is expected and can be attributed to orbit resonance effects (Seo et al. 2008). The magnitude of the errors in these orders, however, is different between OBS+AOD and OBS. The empirical standard deviation of OBS+AOD is generally lower, while the formal errors are generally higher. This can be clearly seen when examining the ratios of both quantities (Fig. 7, right column), which show that the formal errors underestimate the uncertainties in the resonance orders while overestimating other coefficients. The underestimation is less pronounced in OBS+AOD, which tends to overestimate the empirical errors in other order bands. Overall, the formal errors of OBS+AOD do fit better to the empirical estimates, with a median ratio of 1.01, compared to 0.86 of OBS.

Fig. 7
figure 7

Comparison of average formal errors (left), empirical standard deviation (middle), and the ratio between average formal errors and empirical standard deviation (right) for the standard solution (OBS) and the solution incorporating dealiasing model errors (OBS+AOD)

Full size image

5 Summary and outlook

We presented a computationally efficient method to incorporate background model uncertainties into the gravity field recovery process. Assuming random error behavior, the model uncertainties can either be considered by augmenting the covariance matrix of observations, or by co-estimating constrained model corrections. Since both approaches lead to identical monthly gravity field estimates, which one is chosen mainly depends on implementation aspects. We used the ESA Earth System Model to derive uncertainty estimates for the atmosphere and ocean dealiasing product (AOD) in the form of an autoregressive model. This parametric method allowed us to approximate the spatiotemporal correlations of the AOD errors as a stationary process. Representing the error process as an autoregressive model also has benefits concerning the required computational resources. The resulting system of normal equations is block-banded, compared to the dense block Toeplitz structure of the covariance matrix of a stationary process.

To evaluate our approach, we computed time series of GRACE monthly solutions from L1B data with and without incorporating the derived AOD error model. Variability over the ocean shows a noise reduction over the whole spatial spectrum, with a maximum of 25% for Gaussian filter radii from 250 to 300 km. Also, month-to-month variations of the variability are lower, resulting in a more consistent time series. We confirmed that the lower noise level is not accompanied by signal loss by examining time series of drainage basin averages in regions with high signal-to-noise ratio. These evaluations showed consistent signal levels for both solutions in medium-to-large river basins, where we expect noise to play a minor role. We further found a better agreement between empirical and formal errors when considering AOD model uncertainties. This supports our initial assumption that the use of this additional information does improve the stochastic modeling of the GRACE observables.

We have shown that the current parameterization of the AOD model corrections as daily sets of spherical harmonic coefficients from degree 2 to 40 does significantly improve the estimated monthly gravity field solutions. The approach has been employed in this form for the processing of ITSG-Grace2018 (Mayer-Gürr et al. 2018). The next steps are to increase both spatial and temporal resolution of the error model, and to possibly include the uncertainties of the used global ocean tide model.

The theoretical framework of the approach was developed by Andreas Kvas and Torsten Mayer-Gürr, Andreas Kvas analyzed the GRACE L1B data and wrote this manuscript. The computed gravity field time series are publicly available through PANGEA.