Abstract
This paper presents recently developed strategies for high-fidelity, analytical radiation force modelling for spacecraft. The performance of these modelling strategies is assessed using a new model for the Global Positioning System Block IIR and IIR-M spacecraft. The statistics of various orbit model parameters in a full orbit estimation process that uses tracking data from 100 stations are examined. Over the full year of 2016, considering all Block IIR and IIR-M satellites on orbit, introducing University College London’s grid-based model into the orbit determination process reduces mean 3-d orbit overlap values by 9% and the noise about the mean orbit overlap value by 4%, when comparing against orbits estimated using a simpler box-wing model of the spacecraft. Comparing with orbits produced using the extended Empirical CODE Orbit Model, we see decreases of 4% and 3% in the mean and the noise about the mean of the 3-d orbit overlap statistics, respectively. In orbit predictions over 14-day intervals, over the first day, we see smaller root-mean-square errors in the along-track and cross-track directions, but slightly larger errors in the radial direction. Over the 14th day, we see smaller errors in the radial and cross-track directions, but slightly larger errors in the along-track direction.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
At Global Navigation Satellite System (GNSS) altitudes, the major force that affects satellite trajectories is Earth gravity, but the effects of solar and lunar gravity are also considerable. Next in this hierarchy of forces, as shown in Fig. 3.1 of Montenbruck and Gill (2000), there is solar radiation pressure (SRP), which is caused by the interaction of solar photons with spacecraft surfaces. If this is not accounted for in the force models used for orbit prediction, the calculated position of the spacecraft can be in error at the 100-m level after 12 h (Fliegel and Gallini 1996). For this reason, SRP modelling is an important topic in GNSS orbit determination and precise orbit determination (POD) in general (Montenbruck and Gill 2000; Vallado and McClain 2001; Tapley et al. 2004).
Since the 1980s, various methods for dealing with the problem have been presented in the literature (Colombo 1986; Beutler et al. 1994; Fliegel and Gallini 1996; Springer et al. 1999; Bar-Sever and Kuang 2003; Arnold et al. 2015). Many of these are empirical methods, requiring no a priori knowledge of the spacecraft properties or its operating environment. In global network analyses that incorporate tracking measurements from a large network of one hundred stations or more, such methods can produce spacecraft orbits with cm-level accuracy (Sośnica et al. 2015).
However, in a purely empirical approach, the orbit model parameters can absorb the effects of other un-modelled or mis-modelled processes (e.g. Earth rotation, geocentre variation (Meindl et al. 2013), etc.). This can result in orbit model parameter estimates that are non-physical, which means they cannot improve our understanding of the physical processes that determine the trajectory of the satellites and are therefore limited in their ability to help improve the modelling of those processes. As a result, a number of groups introduced analytical, or physics-based, radiation force modelling into their orbit estimation processes. In this area, the box-wing (BW) approach, first introduced by Marshall and Luthcke (1994) for application to POD of the TOPEX/Poseidon mission, has been particularly influential. The general concept is to model the spacecraft structure using eight flat plates (six for a cuboid representing the spacecraft bus and two for solar panels), with assumed values for the optical and thermal properties of the surfaces, which are then combined with a priori modelling of the spacecraft attitude and the incident radiation fluxes. This approach was applied to the Block II/IIA and Block IIR satellites of the Global Positioning System (GPS) by Rodriguez-Solano et al. (2012). In comparing the performance of their semi-analytical adjustable box-wing model with the Centre for Orbit Determination (CODE) Empirical Orbit Model (ECOM; Beutler et al. 1994), the authors determined that the orbit solutions produced by the two methods were comparable, but that the accelerations produced by the ECOM model were less physically meaningful. More recent efforts that adopt a broadly similar modelling approach include Montenbruck et al. (2015) for Galileo satellites and Montenbruck et al. (2017a) for the QZS-1 satellite of Quasi-Zenith Satellite System (QZSS).
The box-wing models are relatively easy to implement. However, they are not able to fully capture the radiation flux-spacecraft surface interaction in satellites with complex surface geometry where the effects of mutual self-shadowing and reflected radiation can be significant. An alternative class of analytical radiation force modelling methods, in which ray-tracing techniques are combined with detailed spacecraft surface models to account for SRP, Earth radiation pressure (ERP) and thermal re-radiation (TRR), was developed in the early 1990s (Klinkrad et al. 1991), and these methods are able to capture these detailed effects. The models were tested in POD of the European remote sensing satellites ERS-2 and ENVISAT (Doornbos et al. 2002). To distinguish them from the box-wing methods, we refer to these as high-fidelity analytical radiation force modelling methods. In GNSS, high-fidelity SRP modelling for GLONASS satellites was first explored by Ziebart and Dare (2001). This work was motivated by broader efforts to improve GLONASS orbit quality as part of the IGEX-98 campaign (Willis et al. 1999). Work in this area continued over the years at University College London (UCL), where the approach was enhanced with methods to account for TRR (Adhya 2005), ERP (Sibthorpe 2006; Ziebart et al. 2007; Li et al. 2017) and antenna thrust (AT; Ziebart et al. 2007), and validated on a number of additional cases including the GPS Block IIA and Block IIR satellites, the Jason-1 spacecraft of the Ocean Surface Topography Mission and ENVISAT (Ziebart et al. 2005; Sibthorpe 2006). Recent work in this area demonstrated improved accuracy in shadow modelling when using geometric primitives, as opposed to triangular tessellations, to represent curved surfaces when constructing the spacecraft model (Grey and Ziebart 2014). The modelling approach, as presented in Ziebart et al. (2005), was adopted into the operational standards for precise orbit determination of the Jason-1 altimetry satellite (Cerri et al. 2010; Zelensky et al. 2010). Recently, other research groups have explored a broadly similar approach for modelling SRP on Beidou satellites (Tan et al. 2016; Wang et al. 2018), on the Gravity Field and Steady-State Ocean Circulation Explorer (GOCE) satellite (Gini 2014) and on QZS-1 (Darugna et al. 2018).
In this paper, using a new model for the GPS Block IIR and IIR-M satellites, we present developments to the UCL model computation strategies that are designed to extend the validity of the models to all possible orientations of the radiation source(s) with respect to the spacecraft. As such, these next-generation general-purpose models account for the effect of radiation forcing from any number of radiation sources, from any direction, providing a high-fidelity radiation flux–spacecraft interaction model that can be used to deal with both SRP and ERP. A key advantage of this approach is that the final model makes no prior assumptions about the attitude characteristics of the spacecraft and can therefore deal with any deviations from nominal attitude.
2 UCL modelling strategy
Our radiation force modelling strategy comprises three processes:
-
(i)
Computation of the bus model, where the space vehicle bus contribution to the accelerations due to SRP and ERP is dealt with. In this process, the accelerations due to thermal emissions from the multi-layered insulation (MLI) covering the bus are also computed, according to Sect. 4.3.3 of Adhya (2005). The core technique uses a ray-tracing algorithm, where the rays simulate the incident radiation flux for a given geometry of the spacecraft with respect to the radiation source. The output of this process is a set of three grids representing the accelerations in the X, Y and Z-axes of the spacecraft body-fixed system (BFS), where the grid nodes are spaced at 1° intervals in latitude and longitude in the BFS.
-
(ii)
Separate computation of the solar panel model, where the solar panel contributions to the accelerations due to SRP and ERP are dealt with.
-
(iii)
AT modelling, which accounts for the recoil force on the spacecraft due to emission of photons from signal transmitters.
As input, the approach requires a computer model of the spacecraft that holds information about the external geometry and various surface material properties including reflectivity, specularity, absorptivity and emissivity. The models are built from a combination of geometric primitives (polygons, circles, cylinders, spheres, cones and truncated cones), avoiding any need for tessellation, especially on curved surfaces (Ziebart et al. 2003). This produces models with good geometric fidelity without requiring an excessively large number of components, e.g. the UCL model for the GPS IIR/IIR-M bus, as shown in Fig. 6, is made up of 182 components. The solar panels (not shown in Fig. 6) are modelled as two rectangular plates.
For solar flux, the models are computed using a nominal value for the mean solar irradiance at one astronomical unit (AU) of 1368 Wm−2 (Hastings and Garrett 1996). The solar irradiance is known to vary over the solar cycle (with a period of between 9 and 14 years) by 1.4 Wm−2. This represents circa 0.1% variation in the parameter. Little is gained by correcting the nominal value. It is more important to scale the model depending on the probe-Sun distance at the calculation epoch. Taking 1368 Wm−2 as a reference value, the eccentricity of the Earth’s orbit about the Sun modulates the solar irradiance near the Earth to 1415.7 Wm−2 at perihelion (+3.4%) and 1322.6 Wm−2 at aphelion (−3.3%). This gives a variation (between perihelion and aphelion) of circa 100 Wm−2 (the precise value being 91.3 Wm−2), approximately 6.7% of the mean value.
For the Earth radiation flux model, we use data from the Clouds and Earth Radiant Energy System (CERES) (Wielicki et al. 1996) project, which provides the irradiance at the top-of-atmosphere (TOA), an altitude of ~ 30 km above the Earth’s surface, in a grid format spaced at 1-degree intervals in latitude and longitude in an Earth-centred Earth-fixed (ECEF) system. Computationally, it can be expensive and slow to determine the total Earth radiation flux incident on a spacecraft, from the part of the Earth’s surface that is visible to that spacecraft, based on a search of the full CERES grid. To overcome this, we have developed a configurable Earth radiation model that re-organises the CERES data into a grid of triangles wrapped around the TOA surface. The number of triangles used to represent the TOA surface is configured during run-time, based on the number of triangles required to achieve a specified precision level. This approach is outlined in Li et al. (2017). At GNSS altitudes, radiation flux from the Earth is about 15 Wm−2.
In the ray-tracing algorithm, a pixel array (simulating the radiation source) is projected onto the computer simulation of the spacecraft with the force at each ray-surface intersection computed according to:
where
-
\( \varvec{F}_{{\mathbf{n}}} \) is the normal force acting in the direction of the surface normal, \( \hat{\varvec{n}} \),
-
\( \varvec{F}_{{{\mathbf{s}}^{\prime } }} \) is the shear force acting in the \( \hat{\varvec{s}}^{\prime } \) direction, which is along the projection of the total force onto the surface plane,
-
\( \varvec{F}_{{{\mathbf{mli}}}} \varvec{ } \) is the force due to the thermal re-radiation from the MLI on the bus surface, which also acts along the normal direction,
-
E is the mean irradiance of the radiation source at one astronomical unit,
-
A is the area of the surface (determined in this case by the pixel array spacing),
-
c is the speed of light in vacuum,
-
\( \nu \) is the reflectivity of the material,
-
\( \mu \) is the specularity of the material,
-
\( \theta \) is the angle of incidence of the radiation with respect to the surface,
-
\( T_{\text{mli}} \) is the temperature of the MLI,
-
\( \sigma \) is the Stefan–Boltzmann constant,
-
\( \alpha \) is the absorptivity of the MLI material,
-
\( \epsilon_{\text{mli}} \) is the emissivity of the MLI material,
-
\( \epsilon_{\text{eff}} \) is the effective emissivity between the MLI and the spacecraft and
-
\( T_{\text{sc}} \) is the internal temperature of the spacecraft bus.
Note, Eqs. 1 and 2 are derived in Ziebart (2001, 2004) and Eqs. 3 and 4 are developed in detail in Adhya (2005). The acceleration due to AT, \( \varvec{\ddot{x}}_{\text{at}} \left( {\varvec{r},t} \right) \), is calculated according to:
where W is the signal power in Watts, m is the spacecraft mass in kg and \( \hat{\varvec{r}} \) is the unit vector from the geocentre towards the satellite centre of mass (Ziebart et al. 2007).
Equations 1 and 2 are also used for computing the SRP and ERP forces acting on the solar panels, but the spacecraft bus and the solar array are treated separately during force model computation, with the results combined during model implementation, as explained in Sect. 4. A similar approach is used by Darugna et al. (2018), and this is done because it simplifies the model computation process as it is not always practical to incorporate the correct solar panel behaviour into the ray-tracing computations.
2.1 Bus model computation scheme
To produce the complete bus model, the pixel array is rotated around the spacecraft in a systematic way, through a discrete set of points, and the ray-tracing computations are performed from each point. Each computation takes the following form:
where the inputs \( \varphi = {\text{atan}}2\left( {z, \sqrt {\left( {x^{2} + y^{2} } \right)} } \right) \) and \( \lambda = {\text{atan}}2\left( {y,x} \right) \) represent latitude and longitude, respectively, of the radiation source in the spacecraft BFS (as defined in Fig. 1); the outputs \( a_{x} ,a_{y} \) and \( a_{z} \) are acceleration along the X, Y and Z-axes, respectively, in the spacecraft BFS.
Defining latitude and longitude in the spacecraft BFS. Here, \( \varphi \in \left( { - 90^\circ , + 90^\circ } \right) \) and is defined by \( \varphi^{\prime } \in \left( {0^\circ , 180^\circ } \right) \), according to \( \varphi = 90^\circ - \varphi^{\prime } \) where \( \varphi^{\prime } \) is the angle between the Z-axis (in the + Z-direction) and \( \varvec{r}_{\varvec{s}} \), where \( \varvec{r}_{\varvec{s}} \) is the position of the radiation source in the spacecraft BFS; \( \lambda \in \left( { - 180^\circ , + 180^\circ } \right) \) is the angle between the X-axis (in the + X-direction) and the projection of \( \varvec{r}_{\varvec{s}} \) on the X–Y plane and it is positive in the anticlockwise direction and negative in the clockwise direction
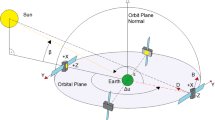
In the computation scheme used in early analyses (Ziebart and Dare 2001), the pixel array was rotated around the spacecraft Y-axis at 12° intervals in the Earth-probe-Sun (EPS) angle, as shown in Fig. 2. The ray-tracing algorithm was executed at 30 points only, and a Fourier series was fitted to the results to represent the final continuous model. The underlying assumption was of spacecraft attitude behaviour fully consistent with the nominal attitude model, in which the Sun is confined to the XZ plane, and the Z-axis points to the geocentre (see Fig. 2). In subsequent studies, e.g. Ziebart et al. (2005), this modelling assumption was maintained but the number of data points computed was increased to 360 by reducing the increment in the EPS angle to 1°.
GNSS satellites on orbit may depart from a nominal attitude state due to limitations of their attitude control systems. Non-GNSS satellites can have attitude laws that are far less constrained than the typical GNSS attitude laws. Thus, as the application of the core technique was considered for non-GNSS missions, the computation scheme was modified. First, the EPS-sweep pixel array orientation scheme was proposed. In this scheme, the pixel array centre points are uniformly distributed around the spacecraft in the central EPS plane (i.e. the spacecraft X–Z plane in this case). Then, each point is rotated by ± 1° about the spacecraft Y-axis, resulting in a new set of points, all inclined at ± 1° with respect to the spacecraft X–Z plane. This process is repeated at 1° steps to populate a full set of pixel-array centre points in 10°-arcs around the spacecraft as shown in Fig. 3. For GNSS satellites, the EPS-sweep method produces pixel arrays that are distributed around the primary parts of the spacecraft BFS within which the Sun moves, but coverage remains incomplete in other directions.
Therefore, an additional computation scheme based on the spiral points algorithm (Saff and Kuijlaars 1997) was introduced, see Fig. 4. With this method, it is possible to efficiently position the radiation source uniformly on a sphere that encloses the spacecraft. As it provides complete coverage in all directions, it can be used to produce a general-purpose model that makes no prior assumptions about the orientation of the spacecraft with respect to the radiation source(s). Currently, the spiral points computation scheme is our preferred model computation method, but there are additional data processing steps required before the outputs of a computation scheme based on this method can be used in a POD process.
2.2 Producing the grid files
The spiral points are not regularly spaced in latitude and longitude. Instead, the points are sorted according to distance along the spiral path, starting at the north pole (\( \varphi = 90^\circ , \lambda = 0^\circ \)) and ending at the south pole (\( \varphi = - 90^\circ , \lambda = 0^\circ \)). This is not a standard method for organising the data. Thus, to provide a final model that is easily integrated into the POD processes of model users, we produce a set of acceleration grids, with grid nodes uniformly spaced at 1° intervals in latitude and longitude in the satellite frame.
To compute the grid values, we use a modified version of Shepard’s method (Shepard 1968)—specifically, an implementation of the modified quadratic Shepard’s method (Franke and Nielson 1980) with a type of full sector search as described in Renka (1988)—to determine the optimal set of gridding parameters. The interpolated values are computed in a two-step process. First, a quadratic surface is fitted around each data point. The quadratic (Q) neighbours parameter determines the radius of a circle large enough to include the nearest Q neighbours. Then, the interpolant at a chosen location is computed using an inverse distance weighted average of the computed quadratic surface fits around each data point. The weighting (W) neighbour’s parameter specifies the number of nearest data points to include for this. There are no clear rules for choosing either the Q or the W parameter for the modified Shepard’s method, in that the optimal choice is data set specific. In this work, for the GPS IIR bus model, we developed a quality assurance process for determining this parameter pair using a two-dimensional search through Q–W space. This is how the process works:
-
(i)
The radiation pressure model is computed using the spiral points scheme and the EPS-sweep scheme.
-
(ii)
The 10,000 spiral points data set is expanded using a padding process, see below.
-
(iii)
Using modified Shepard’s method, 1600 grids are produced from the output of the spiral points computation, for each acceleration component, with all combinations of Q, W pairs considered, where both Q and W range from 11 to 50.
-
(iv)
For each grid file, the interpolated values at each of the 3960 EPS-sweep points are calculated, and the interpolated value is compared with the results from the EPS-sweep computation. This is used to compute the RMS error value, \( E_{\text{rms}} \), for that grid file according to:
$$ E_{\text{rms}} = \sqrt {\frac{1}{3960}\mathop \sum \limits_{k = 1}^{3960} (a_{{{\text{EPS}},i}} - a_{{{\text{grid}},i}} )^{2} } , $$(7)where \( a_{{{\text{EPS}},i}} \) are accelerations at point i according to the EPS-sweep computation and \( a_{{{\text{grid}},i}} \) is an interpolated acceleration at point i derived from the grid file.
-
(v)
Finally, the grid files that minimise the \( E_{\text{rms}} \) quantity for each component (X, Y and Z) are chosen as the optimal grid files for that spacecraft.
2.3 Padding the spiral points data set
The modified Shepard’s method is a general-purpose interpolation algorithm that works with two-dimensional data that are irregularly scattered by using information from a specified set of the nearest neighbour points. As such, in using this method to create the radiation force model grids, we encounter a problem. The algorithm is not able to identify the correct nearest neighbour points in the regions close to the data set boundaries (i.e. \( \varphi = 90^\circ \,{\text{or}} - 90^\circ , \lambda = 180^\circ \, {\text{or}} - 180^\circ \)) when the output from a spiral points computation, labelled using latitude and longitude pairs in a 2-d Cartesian system, is provided as the input. To overcome this, we developed a method that creates an artificially extended spiral points data set that is bounded in the region \( \varphi \in \left( { - 270^\circ , + 270^\circ } \right) \) and \( \lambda \in \left( { - 540^\circ , + 540^\circ } \right) \). The transformation rules that map the raw spiral points data, bounded in the region \( \varphi \in \left( { - 90^\circ , + 90^\circ } \right) \) and \( \lambda \in \left( { - 180^\circ , + 180^\circ } \right) \), to data points in the extended regions are given in Eqs. 8 to 15, where \( f\left( {\varphi ,\lambda } \right) \) is used to populate the extended region using the raw data. A portion of this extended data set around the north pole (\( \varphi = 90^\circ \)) is shown in Fig. 5, where the red data points are the spiral points. The yellow points, the top-padding above the north pole, are reflections of the raw data points about the \( \varphi = 90^\circ \) line, which are then shifted by \( \pm 180^\circ \) in longitude beyond the north pole. Using this, expanded data set gives us a solution to the nearest neighbour problem. Another largely unavoidable issue is caused by the requirement to project the spiral points onto a 2-d Cartesian space, which distorts the apparent distance between points. With the Mercator projection, this effect increases with distance from \( \varphi = 0^\circ \). The impact of this is clearly seen in Fig. 5 where the density of data points becomes sparser approaching \( \varphi = 90^\circ \).
The expanded spiral points data set around the north pole region, i.e. where \( \varphi = 90^\circ \pm 10^\circ \). The red points are the raw data. The raw data are mapped onto the extended regions according to the transformation rules given in Eqs. (8) to (15), where the region labels are also defined
Top-padding (T): \( \varphi > 90^\circ \), \( \lambda \in \left( { - 180^\circ , 180^\circ } \right) \)
Bottom-padding (B): \( \varphi < - 90^\circ \), \( \lambda \in \left( { - 180^\circ , 180^\circ } \right) \)
Left-padding (L): \( \varphi \in \left( { - 90^\circ , 90^\circ } \right), \lambda < - 180^\circ \)
Right-padding (R): \( \varphi \in \left( { - 90^\circ , 90^\circ } \right), \lambda > 180^\circ \)
Top-Left Padding (TL): \( \varphi > 90^\circ , \lambda < - 180^\circ \)
Top-Right Padding (TR): \( \varphi > 90^\circ , \lambda > 180^\circ \)
Bottom-Left Padding (BL): \( \varphi < - 90^\circ , \lambda < - 180^\circ \)
Bottom-Right Padding (BR): \( \varphi \left\langle { - 90^\circ , \lambda } \right\rangle + 180^\circ \)
2.4 Modelling limitations
There are a number of factors limiting the accuracy of the current approach, which include:
-
(a)
Mis-modelling of reflected radiation coming off the bus onto the panels and shadowing from the bus onto the panels (and vice versa). Both of these are due to the separate treatment of the solar panels and the spacecraft bus during model computation. Here, there is a trade-off in modelling accuracy between being able to deal with non-standard solar panel orientations and being able to capture the effects of reflections and self-shadowing of the bus onto the panels. An analysis of this trade-off is not presented here but will be considered carefully in future development work.
-
(b)
No modelling of the time-evolution of the surface material properties.
-
(c)
Incomplete modelling of TRR effects. In the ray-tracing algorithm, we only consider spacecraft bus surfaces that are covered in multi-layer insulation (MLI). This strategy can perform reasonably well on those satellites where the surfaces are mostly covered in MLI, as is the case with the GPS Block IIR and IIR-M bus surfaces. However, it is limited in cases where a significant proportion of the spacecraft surface is not covered in MLI (e.g. the SAR antenna on Sentinel-1; radiators on Galileo spacecraft, etc.). Also, we are not considering the force due to the temperature gradient across the Sun-facing and anti-Sun-facing sides of the solar panels in this study, but this effect has been considered in previous studies (Adhya 2005) and we are working towards developing a simplified approach to account for this.
-
(d)
No modelling of thermal recoil forces due to emissions from radiators and other thermal control system components that actively emit heat. The impact of this will be different between the Block IIR and the Block IIR-M satellites. The thermal control system of the Block IIR-M satellites was updated with additional integral heat pipes due to high heat concentrations in the honeycomb structure of the L-band panel due, in part, to increased signal power needs (Hartman et al. 2000).
3 Model implementation
The UCL radiation force model implementation requires several inputs. Most of these are spacecraft-specific information that includes position, nominal mass, actual mass if available, the grid files for the bus model, solar panel properties (area, surface material properties), attitude information (in the form of attitude control laws or on-board attitude measurements) to enable accurate determination of the spacecraft BFS and solar panel orientation in the BFS.
As explained in Sect. 2, the model for the spacecraft bus is pre-computed, with the results of the computation stored in grids that are uniformly spaced at 1° intervals in latitude and longitude of the Sun position in the spacecraft BFS. To call these models in an orbit determination algorithm, these grids must be read in and stored in a suitable data structure. As a part of this process, it is a good idea to denormalise the grid values according to:
where
-
\( m_{\text{n}} \) is the nominal mass of the spacecraft, i.e. the value used to compute the grid in kg,
-
\( m_{\text{a}} \) is the actual mass of the spacecraft in kg,
-
\( \varvec{\ddot{x}}_{\text{grid}} \) are the grid file accelerations in the spacecraft BFS x, y and z-axes in ms−2,
-
\( \widetilde{{\varvec{\ddot{x}}}}_{grid} \) are denormalised grid file accelerations in ms−2,
-
E is the mean solar irradiance at 1 AU.
This is because our radiation force modelling software was originally developed for solar radiation pressure modelling only. As such, the accelerations given in the grid files are produced using a solar radiation flux model that assumes a constant solar irradiance of 1368 Wm−2 at 1 AU. However, by applying this denormalisation step, it becomes relatively straightforward to use the UCL grids as a general-purpose radiation flux-spacecraft interaction model.
With all required inputs provided, and made accessible, it is possible to compute the accelerations due to the separate model components. The bus model is computed according to:
where \( \kappa \) is the shadow crossing function (equals 1 in full phase of the Sun and 0 in umbra); \( E_{\text{s}} \left( {\varvec{r},t} \right) \) and \( E_{\text{e}} \left( {\varvec{r},t} \right) \) are solar radiation flux and Earth radiation flux, respectively, at the spacecraft’s location \( \varvec{r} \) at time t; \( \varphi_{\text{s}} \) and \( \lambda_{\text{s}} \) are latitude and longitude, respectively, of the Sun’s position in the spacecraft BFS; \( \varphi_{\text{e}} \) and \( \lambda_{\text{e}} \) are latitude and longitude, respectively, of the Earth’s position in the spacecraft BFS. For latitude and longitude values between grid nodes, the accelerations should be calculated using bilinear interpolation. The solar panel’s contribution to accelerations due to radiation forcing is:
Finally, the combined acceleration due to radiation forces, \( \varvec{\ddot{x}}_{\text{rad}} \), is calculated according to:
where \( \varvec{\ddot{x}}_{\text{at}} \left( {\varvec{r},t} \right) \) is the acceleration due to antenna thrust.
4 The GPS IIR/IIR-M model description and data sources
The detailed UCL GPS IIR/IIR-M geometric model is generated from a set of technical drawings that are published in Chapter 5 of Adhya (2005). The primary source for the surface material properties is Fliegel and Gallini (1996). Additional details about how the model was put together are given in Ziebart et al. (2003). According to an unpublished report produced by UCL in collaboration with the Aerospace Corporation, and delivered to the United States Air Force in October 2005, the Block IIR/IIR-M satellites beyond GPS satellite vehicle number (SVN) 51 are equipped with a NAP ultra-high frequency (UHF) antenna (see Fig. 6), which is installed on the same side of the bus as the W-sensor high band antenna used for military applications found on the − X-face. Like the W-sensor high and low band antennae, the NAP UHF antenna is also composed of thin cylindrical components made of aluminium that are covered in black tape (Adhya 2005). Thus, in our model, the same material properties are used, i.e. \( \nu = 0.06 \) and \( \mu = 0 \). The authors were unable to determine the full form on the NAP acronym or the purpose of this antenna.
The computation of the force models for the bus is performed using Version 5.05 of UCL’s Analytical SRP and TRR Modelling Software at a nominal spacecraft mass of 1100 kg and a pixel-array resolution of 1 mm2. The bus model grid files for the IIR/IIR-M spacecraft, with and without the NAP antenna, are provided alongside this article as an electronic supplement.
Most of the values used for our solar panel model, given in Table 1, are taken from Adhya (2005). The combined surface area of the solar panel yoke arms is taken from Fliegel and Gallini (1996) because the drawings in Adhya (2005) provide only their length. For the rear side of the panels, we use surface properties given in Rodríguez-Solano (2009).
In Table 2, we present the statistics for the selected UCL grids for the GPS IIR/IIR-M satellites, both with and without the NAP antenna. The grids chosen are the ones corresponding to the Q, W parameter pairs that minimise the RMS error when the interpolated grid file values are compared against the results of an EPS-sweep computation. The RMS errors of the Z grids are approximately five times higher than the X grids. This is due to the W-band antennae and for those satellites that have them, the NAP antenna. In the EPS-sweep computation, these protruding elements result in significantly larger cross-section boundaries as the pixel array pans across the Z surfaces. By contrast, these elements have almost no effect on cross-section boundaries as the pixel array pans across the X surfaces. Thus, there are larger errors in the ray-tracing algorithm when computing Z accelerations. This is due to the edge-matching effect, which depends upon the cross-section perimeter and is explained in Chapter 10 of Ziebart (2001). This does not affect the Y grids as the pixel arrays do not pan across the Y surfaces in the same way.
For the BW model, we use the values used by the European Space Operations Centre (ESOC) in their POD processing for the International GNSS Service (IGS; Johnston et al. 2017), which are 4.11, 0.0 and 4.25 m2 for the x, y and z faces of the bus, respectively (Garcia-Serrano et al. 2016). The combined surface area of the solar array and yoke arms is 13.91 m2. In the ESOC BW model, for the surface properties of the bus, \( \nu = 0.06 \) and \( \mu = 0 \). The solar panel properties of the BW model and the UCL model are identical.
For the antenna thrust model, we use the IGS model values for signal power (http://acc.igs.org/orbits/thrust-power.txt), which are 85 W for GPS Block IIR and 108 W and 198 W for GPS Block IIR-M satellites.
5 Model validation
We investigate the performance of the new modelling strategy using two software systems: the UCL Orbit Dynamics Library (UCL-ODL) and ESOC’s Navigation Package for Earth Observation Satellites (NAPEOS) software (Springer 2009). The UCL-ODL comprises a set of programs developed by researchers at UCL over the years, for the explicit purpose of studying the impact of force modelling strategies that are developed by the UCL Space Geodesy and Navigation Laboratory. NAPEOS is a GNSS data processing package developed by ESOC and used in its contributions to IGS activities to produce satellite orbits, precise clocks, station coordinates, Earth rotation parameters and so on.
5.1 Analysis of the impact of separate model components using the UCL-ODL
Using the UCL-ODL, we performed a series of sensitivity analyses to investigate the impact of the individual model components and verify the implementation method. In these tests, as the reference trajectory, we used precise IGS final orbits, considering all available IIR and IIR-M satellites over the full month of March 2016. For each satellite, we perform multiple orbit predictions, with separate prediction runs corresponding to separate IGS final orbit files. As such, in this part of the analysis, we consider 13 GPS IIR satellites and 7 GPS IIR-M satellites. For those satellites with a complete set of IGS final orbits during the analysis period, we perform 31 prediction runs from 1 to 31 March 2016. In the orbit propagator, the general force modelling strategy uses Earth Gravity Model 2008 up to degree and order 20 (Pavlis et al. 2012, 2013) and the JPL Development Ephemerides 405 (DE405) for third-body gravitational forcing due to the Sun, Moon, Jupiter and Venus (Standish 1998). The solid Earth tide effect due to the Sun and the Moon is accounted for according to Marsh et al. (1987). General relativistic effects are modelled according to Sect. 3.7.3 of Montenbruck and Gill (2000). The numerical integration is based on an 8th order Runge–Kutta integrator.
In terms of radiation force modelling strategy, the following scenarios were systematically assessed:
-
Base model: SRP-only model using the ESOC BW model (Garcia-Serrano et al. 2016).
-
Test 1: SRP-only, where the bus model comprises grids produced by the UCL ray-tracing software, but only Eqs. 1 and 2 are used.
-
Test 2: Same as Test 1, but here the bus model comprises grids that account for both SRP and the effects of MLI TRR (Eqs. 3 and 4).
-
Test 3: Same as Test 2, but with ERP turned on.
-
Test 4: Same as Test 3, but with AT turned on.
In Fig. 7, we show the impact of different modelling strategies on orbit prediction error over a single 12-h arc for the GPS satellite SVN 46. As smaller and smaller effects are considered in the modelling strategy, the orbit prediction results improve, giving a general indication that the models are performing as we expect. In Table 3, we provide orbit prediction errors statistics for all Block IIR/IIR-M satellites on orbit during the analysis period. The best results, in the sense that the RMS and the maximum 3-d orbit prediction error over a 12-h arc are minimised, at 0.648 m and 1.440 m, respectively, are produced by the method that considers the combined effects of SRP, bus MLI TRR, ERP and AT. For that modelling approach, the full set of statistics for all satellites that were considered in the analysis, are given in Table 4. An interesting observation from these results is that the modelling of the bus MLI TRR, an effect that is not considered by most IGS analysis centres, has a significant impact on reducing orbit prediction error over the arc.
5.2 Analysis of the impact of the new bus model on POD using NAPEOS
To assess the impact of introducing our grid-based model of the spacecraft bus on the quality of orbit estimates, we ran a number of POD analyses using NAPEOS. The analysis uses 100 tracking stations of the IGS Multi-GNSS Experiment (MGEX) (Montenbruck et al. 2017b) and all observed GPS satellites, but the results presented here focus on the 13 GPS Block IIR and 7 Block IIR-M satellites that were on orbit during the analysis period. The data processing method broadly follows ESOC’s IGS analysis strategy (ftp://igs.org/pub/center/analysis/esa.acn) where the basic observables are undifferenced carrier phases and pseudoranges and the integer carrier phase ambiguities are resolved (Ge et al. 2005). The Earth gravity model used is EIGEN-GL05C up to degree and order 12 (Foerste et al. 2008), and the JPL Development Ephemerides 405 (DE405) is used for third-body gravitational forcing due to the Sun, Moon and all solar system planets including Pluto (Standish 1998). The effects of solar Earth tides, ocean tides, solid Earth pole tide, oceanic pole tide and general relativistic corrections are accounted for according to the IERS conventions (Petit and Luzum 2010). The numerical integration uses the Adams–Bashforth/Adams–Moulton 8th order prediction–correction multistep method, as described in Springer (2009).
With the core data processing strategy fixed, we run the POD process using four different orbit modelling strategies, batch processed at 24-h intervals, from 00:00:00 to 23:59:30 in GPS time, thus completely independent from day to day. For the orbits, we generate estimates for the midnight epoch, such that there is an overlap between consecutive solutions at a single point. A full year (2016) is considered, so there are 366 independent solutions and 365 overlap points. In addition to the orbit model parameters, station coordinates and Earth rotation parameters are also estimated. The orbit models considered include:
-
1.
ECOM: No a priori radiation force model, only the reduced ECOM (Springer et al. 1999) and three constrained along-track parameters (constant, cosine and sine with argument of latitude as argument). Here, the along-track parameters are included as soak-up parameters to absorb the effects of orbit mis-modelling, which tends to manifest strongly in the along-track direction, as the results of Sect. 5.1 demonstrate.
-
2.
ECOM + BW: Same estimation strategy as ECOM-only, but here we also include an a priori radiation force model using the ESOC BW model of the GPS IIR and IIR-M spacecraft (Garcia-Serrano et al. 2016).
-
3.
ECOM + UCL: Here, the only difference with the ECOM + BW strategy is that the box is replaced by the grid-based model.
-
4.
ECOM-2: No a priori radiation force model, only the D4B1 extended ECOM (Arnold et al. 2015) along with the three constrained along-track parameters for consistency. Here, our analysis with the ECOM-2 model is not as comprehensive as it might be (as it was not in the scope of our original study plan). This will be addressed in our future work.
In Table 5, we present statistics of the estimated ECOM parameters from methods 1–3. We do not present the statistics for ECOM-2 because comparison between models with different parameterizations cannot be made directly. In general, as the daily solutions are fully independent of each other, smaller absolute values for both the mean and the RMS indicate an improvement in the force modelling. Using the ECOM + UCL model, we see a reduction in the absolute value of both the mean and the RMS values of the \( D_{0} \), \( B_{0} \) and all along-track parameters (except the mean of the \( A_{0} \) parameter that is the same for both), when comparing with results using the ECOM + BW model. We see a reduction in the RMS of the \( Y_{0} \) parameter, but the mean increases. The mean and RMS of the Bsin and Bcos parameters increase, which indicate the presence of systematic effects that the ECOM + UCL combination is not effectively dealing with.
In Table 6, we show the statistics of the orbit overlap differences. A smaller value for both the mean and the RMS indicates an improvement in the force modelling. The RMS values in all components are smallest with ECOM + UCL approach. However, the mean values for both the radial and along-track components are smallest with the ECOM-2 approach and the mean value for the cross-track component is smallest with the ECOM approach. In the 3-d orbit overlap values, we see a drop of 9% and 4% in the mean and RMS values, respectively, when we compare the ECOM + UCL results against ECOM + BW.
The performance of the ECOM, ECOM + BW and ECOM + UCL orbit modelling strategies was also assessed in a series of orbit prediction tests. In these tests, 3 days of independently estimated orbits were used to determine a best fitting orbit represented by position and velocity coordinates and the eight parameters of the ECOM method described above. This best fitting orbit was then propagated into the future for 14 days, after the end of the 3-day fit interval. These predicted orbits were compared against the estimated orbits, on the first day and the last day of the prediction interval. In these tests, ECOM + UCL is the reference model and the orbits estimated using ECOM + UCL are used as the basis of the 3-day orbit fit and as the ground truth. These tests are done over 2016. Thus, the first 1-day prediction interval considered is day 4 of 2016 and the first 14th-day prediction interval is day 17. The results from these tests are presented in Table 7.
Comparing RMS orbit prediction errors using ECOM + UCL against ECOM + BW, after 1-day, we see the errors increase by 0.21 cm in the radial direction but fall by 2.20 cm and 1.81 cm in the along-track and cross-track directions, respectively. For the 14th day predictions, we see a reduction in the RMS orbit prediction errors of 20.35 cm and 13.79 cm in the radial and cross-track directions, but an increase of 15.52 cm in the along-track direction. Overall, these results suggest ECOM + UCL is outperforming ECOM + BW, in the day 1 and day 14 orbit prediction tests, but there are limitations to this analysis that should be addressed in future work for improved confidence in our findings. For example, because we use it as our reference model, it is possible that ECOM + UCL is favoured in these tests. Also, systematic errors, such as those that depend on the elevation of the Sun above the orbital plane, do not show up in the yearly statistics. A more complete picture of the comparative performance of the models should be investigated through time series analysis.
6 Conclusions and discussion
Recent developments to our radiation force modelling strategy were analysed using a new model for the GPS Block IIR and Block IIR-M satellites. Advances to our approach include: an enhanced bus model computation scheme (based on the spiral points algorithm) that uses ray-tracing to determine the radiation flux-spacecraft interaction from 10,000 points distributed uniformly on a sphere surrounding the spacecraft; an improved method (from a numerical stability perspective) for producing grids spaced at \( 1^\circ \times 1^\circ \) intervals in latitude and longitude in the spacecraft frame using a padding process to extend the spiral points data in all directions to reduce the impact of edge effects; a quality assurance process that uses results from an EPS-sweep computation with 3960 points for selecting an optimal set of grids. The models produced, and the proposed implementation method, were refined using a series of verification tests within the UCL-ODL. The impact of introducing UCL’s grid-based model into a full POD process was investigated by analysing the statistics of estimated orbit model parameters, orbit overlaps and orbit prediction errors. Combined, the results provide a good indication that introducing high-fidelity analytical force modelling into the POD process can improve the quality of the estimated orbits and further refinements of the approach to address current limitations are worth pursuing.
One of the difficulties with the high-fidelity approach lies in acquiring the spacecraft data (geometry, surface material properties, attitude history, mass and mass history) that is required to produce accurate models. It is hoped that the results in this paper adds evidence to the case for making this data available to the science and engineering community, where it is possible—especially the detailed geometry and surface material properties. Using an accurate spacecraft model, it is possible to compute the high-fidelity radiation force model. However, the model computation time remains a problem and limits the number of development and testing cycles that we are able to perform. A typical model computation involves a \( 5 \times 5 {\text{m}}^{2} \) pixel array projected onto the spacecraft model at a 1 mm pixel spacing. In such a case, there are \( 2.5 \times 10^{7} \) rays per incoming radiation flux direction, \( 1 \times 10^{4} \) different directions in the spiral points computation scheme, and so this requires \( 2.5 \times 10^{11} \) ray-spacecraft surface interaction calculations. As it stands, this process takes ~ 3 days to compute (job run-time as opposed to CPU time) on the UCL high-performance computing facility, Legion@UCL (can take longer when the facility is under heavy load), followed by ~ 1 day of analyst’s time to work through the process of generating the grids. Therefore, it is worth exploring methods for reducing model production times. We are beginning to explore the use of a graphical processing unit (GPU) to exploit standard computer graphics techniques in the computation of the radiation flux-spacecraft surface interaction—a process that naturally lends itself to being parallelised. This idea is demonstrated in Grey et al. (2017) where an OpenCL implementation of a radiation source-satellite surface interaction model that includes accurate modelling of diffuse reflection and apparent size of illumination source is used to simulate the impact of photoelectron emission on spacecraft surface charging. Also, we are exploring the use of an algorithm that re-organises the UCL spacecraft model components into a k-dimensional tree data structure, to speed up the ray-tracing algorithm by greatly reducing the number of ray-surface interaction tests that need to be performed (Li et al. 2018).
References
Adhya S (2005) Thermal re-radiation modelling for precise prediction and determination of spacecraft orbits. PhD Thesis, University College London
Arnold D, Meindl M, Beutler G et al (2015) CODE’s new solar radiation pressure model for GNSS orbit determination. J Geod 89:775–791. https://doi.org/10.1007/s00190-015-0814-4
Bar-Sever Y, Kuang D (2003) New empirically-derived solar radiation pressure model for GPS satellites. JPL TRS 1992+
Beutler G, Brockmann E, Gurtner W et al (1994) Extended orbit modeling techniques at the CODE processing center of the international GPS service for geodynamics (IGS): theory and initial results. Manuscr Geod 19:367–386
Cerri L, Berthias JP, Bertiger WI et al (2010) Precision orbit determination standards for the Jason Series of Altimeter Missions. Mar Geod 33:379–418
Colombo OL (1986) Ephemeris errors of GPS satellites. Bull Géod 60(1):64–84. https://doi.org/10.1007/BF02519355
Darugna F, Steigenberger P, Montenbruck O, Casotto S (2018) Ray-tracing solar radiation pressure modeling for QZS-1. Adv Sp Res 62(4):935–943. https://doi.org/10.1016/J.ASR.2018.05.036
Doornbos E, Scharroo R, Klinkrad H et al (2002) Improved modelling of surface forces in the orbit determination of ERS and ENVISAT. Can J Remote Sens 28(4):535–543. https://doi.org/10.5589/m02-055
Fliegel HF, Gallini TE (1996) Solar force modeling of block IIR Global Positioning System satellites. J Spacecr Rockets 33(6):863–866. https://doi.org/10.2514/3.26851
Foerste CU, Flechtner F, Schmidt R et al (2008) EIGEN-GL05C—a new global combined high-resolution GRACE-based gravity field model of the GFZ-GRGS cooperation. In: Geophysical research abstracts. Vienna, Austria, vol 10, Abstract No EGU2008-A-06944
Franke R, Nielson G (1980) Smooth interpolation of large sets of scattered data. Int J Numer Methods Eng 15(11):1691–1704
Garcia-Serrano C, Springer T, Dilssner F et al (2016) ESOC’s multi-GNSS processing. In: IGS workshop 2016. Sydney, Australia
Ge M, Gendt G, Dick G, Zhang FP (2005) Improving carrier-phase ambiguity resolution in global GPS network solutions. J Geod 79:103–110. https://doi.org/10.1007/s00190-005-0447-0
Gini F (2014) GOCE precise non-gravitational force modeling for POD applications. Ph.D. Thesis, University of Padua
Grey S, Ziebart M (2014) Developments in high fidelity surface force models and their relative effects on orbit prediction. In: AIAA/AAS astrodynamics specialist conference. American Institute of Aeronautics and Astronautics
Grey S, Marchand R, Ziebart M, Omar R (2017) Sunlight illumination models for spacecraft surface charging. IEEE Trans Plasma Sci 45(8):1898–1905. https://doi.org/10.1109/TPS.2017.2703984
Hartman T, Boyd LR, Koster D et al (2000) Modernizing the GPS Block IIR Spacecraft. In: ION GPS 2000, pp 2115–2121
Hastings D, Garrett H (1996) Spacecraft–environment interactions. Cambridge University Press, Cambridge
Johnston G, Riddell A, Hausler G (2017) The International GNSS Service. In: Teunissen PJG, Montenbruck O (eds) Springer Handbook of Global Navigation Satellite Systems, 1st edn. Springer International Publishing, Cham, pp 967–982. https://doi.org/10.1007/978-3-319-42928-1_33
Klinkrad H, Koeck C, Renard P (1991) Key features of a satellite skin force modelling technique by means of Monte-Carlo ray tracing. Adv Sp Res 11(6):147–150. https://doi.org/10.1016/0273-1177(91)90244-E
Li Z, Ziebart M, Grey S, Bhattarai S (2017) Earth radiation pressure modelling for BeiDou IGSO Satellites. In: China Satellite Navigation conference, Shanghai, 2017
Li Z, Ziebart M, Bhattarai S et al (2018) Fast solar radiation pressure modelling with ray tracing and multiple reflections. Adv Sp Res 61(9):2352–2365. https://doi.org/10.1016/j.asr.2018.02.019
Marsh G, Lerch FJ, Putney BH et al (1987) an improved gravitational model of the Earth’s field: GEM-TI. NASA-TM-4019, REPT-87B0451, NAS 1.15:4019, NASA, USA
Marshall JA, Luthcke SB (1994) Modeling radiation forces acting on Topex/Poseidon for precision orbit determination. J Spacecr Rockets 31(1):99–105. https://doi.org/10.2514/3.26408
Meindl M, Beutler G, Thaller D et al (2013) Geocenter coordinates estimated from GNSS data as viewed by perturbation theory. Adv Sp Res 51(7):1047–1064. https://doi.org/10.1016/J.ASR.2012.10.026
Montenbruck O, Gill E (2000) Satellite orbits : models, methods and applications. Springer, Heidelberg
Montenbruck O, Steigenberger P, Hugentobler U (2015) Enhanced solar radiation pressure modeling for Galileo satellites. J Geod 89:283–297. https://doi.org/10.1007/s00190-014-0774-0
Montenbruck O, Steigenberger P, Darugna F (2017a) Semi-analytical solar radiation pressure modeling for QZS-1 orbit-normal and yaw-steering attitude. Adv Sp Res 59(8):2088–2100. https://doi.org/10.1016/J.ASR.2017.01.036
Montenbruck O, Steigenberger P, Prange L et al (2017b) The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)—achievements, prospects and challenges. Adv Sp Res 59(7):1671–1697. https://doi.org/10.1016/J.ASR.2017.01.011
Pavlis NK, Holmes SA, Kenyon SC, Factor JK (2012) The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J Geophys Res Solid Earth 117:B04406. https://doi.org/10.1029/2011JB008916
Pavlis NK, Holmes SA, Kenyon SC, Factor JK (2013) Erratum: correction to the development and evaluation of the earth gravitational model 2008 (EGM2008). J Geophys Res Solid Earth 118(5):2633. https://doi.org/10.1002/jgrb.50167
Petit G, Luzum B (eds) (2010) IERS Conventions (2010) (IERS Technical Note 36). Verlag des Bundesamts für Kartographie und Geodäsie, Frankfurt am Main
Renka RJ (1988) Multivariate interpolation of large sets of scattered data. ACM Trans Math Sci 4(2):139–148
Rodríguez-Solano CJ (2009) Impact of Albedo Modelling on GPS Orbits. Master Thesis, Technical University of Munich
Rodriguez-Solano CJ, Hugentobler U, Steigenberger P (2012) Adjustable box-wing model for solar radiation pressure impacting GPS satellites. Adv Sp Res 49(7):1113–1128. https://doi.org/10.1016/J.ASR.2012.01.016
Saff EB, Kuijlaars ABJ (1997) Distributing many points on a sphere. Math Intell 19(1):5–11
Shepard D (1968) A two-dimensional interpolation function for irregularly-spaced data. In: Proceedings-1968 ACM national conference
Sibthorpe AJ (2006) Precision non-conservative force modelling for low earth orbiting spacecraft. Ph.D. Thesis, University College London
Sośnica K, Thaller D, Dach R et al (2015) Satellite laser ranging to GPS and GLONASS. J Geod 89(7):725–743. https://doi.org/10.1007/s00190-015-0810-8
Springer T (2009) NAPEOS mathematical models and algorithms. DOPS-SYS-TN-0100-OPS-GN, Issue 1.0, Nov 2009. http://navigation-office.esa.int/products/napeos
Springer TA, Beutler G, Rothacher M (1999) A new solar radiation pressure model for GPS satellites. GPS Solut 2(3):50–62. https://doi.org/10.1007/PL00012757
Standish EM (1998) JPL planetary and lunar ephemerides: DE405/LE405. Interoffice Memorandum 312.F-98-048, Jet Propulsion Laboratory
Tan B, Yuan Y, Zhan B, et al (2016) A new analytical solar radiation pressure model for current BeiDou satellites: IGGBSPM. Sci Rep 6(32967): https://doi.org/10.1038/srep32967
Tapley BD, Schutz BE, Born GH (2004) Statistical orbit determination. Academic Press, Cambridge
Vallado DA, McClain WD (2001) Fundamentals of astrodynamics and applications. Kluwer Academic Publishers, Dordrecht
Wang C, Guo J, Zhao Q, Liu J (2018) Solar radiation pressure models for BeiDou-3 I2-S satellite: comparison and augmentation. Remote Sens 10(1):118. https://doi.org/10.3390/rs10010118
Wielicki BA, Barkstrom BR, Harrison EF et al (1996) Clouds and the Earth’s Radiant Energy System (CERES): an Earth observing system experiment. Bull Am Meteorol Soc 77(5):853–868. https://doi.org/10.1175/1520-0477(1996)077%3c0853:CATERE%3e2.0.CO;2
Willis P, Beutler G, Gurtner W et al (1999) IGEX: international GLONASS experiment—scientific objectives and preparation. Adv Sp Res 23(4):659–663. https://doi.org/10.1016/S0273-1177(99)00147-7
Zelensky NP, Lemoine FG, Ziebart M et al (2010) DORIS/SLR POD modeling improvements for Jason-1 and Jason-2. Adv Sp Res 46(12):1541–1558. https://doi.org/10.1016/J.ASR.2010.05.008
Ziebart M (2001) High precision analytical solar radiation pressure modelling for GNSS spacecraft. Ph.D. Thesis, University of East London
Ziebart M (2004) Generalized analytical solar radiation pressure modeling algorithm for spacecraft of complex shape. J Spacecr Rockets 41(5):840–848. https://doi.org/10.2514/1.13097
Ziebart M, Dare P (2001) Analytical solar radiation pressure modelling for GLONASS using a pixel array. J Geod 75:587–599. https://doi.org/10.1007/s001900000136
Ziebart M, Adhya S, Sibthorpe A, Cross P (2003) GPS Block IIR non-conservative force modelling: computation and implications. In: ION GPS/GNSS 2003. Portland, OR, pp 2671–2678
Ziebart M, Adhya S, Sibthorpe A et al (2005) Combined radiation pressure and thermal modelling of complex satellites: algorithms and on-orbit tests. Adv Sp Res 36(3):424–430. https://doi.org/10.1016/j.asr.2005.01.014
Ziebart M, Sibthorpe A, Cross P, et al (2007) Cracking the GPS-SLR orbit anomaly. In: ION GNSS 2007. Fort Worth, Texas, pp 2033–2038
Acknowledgements
This work is supported financially by the UK Natural Environment Research Council (NE/K010816/1; Grant No. 157630). The collaboration between University College London and PosiTim to test new force modelling strategies in an orbit estimation process is funded, in part, through a European Space Agency project to develop force models for Galileo GNSS spacecraft. The authors acknowledge the use of the UCL Legion High-Performance Computing Facility (Legion@UCL), and associated support services, in the completion of this work. The authors wish to thank three anonymous reviewers for their valuable comments and suggestions which have greatly improved the quality of this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bhattarai, S., Ziebart, M., Allgeier, S. et al. Demonstrating developments in high-fidelity analytical radiation force modelling methods for spacecraft with a new model for GPS IIR/IIR-M. J Geod 93, 1515–1528 (2019). https://doi.org/10.1007/s00190-019-01265-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00190-019-01265-7