1 Introduction

The height anomaly is required if one wishes to transform GNSS-derived ellipsoidal heights to normal heights and vice versa. Height anomalies are the separation between the telluroid and the Earth’s surface or, equivalently, the separation between a geocentric reference ellipsoid and the quasigeoid (e.g. Moritz 2015). Their values come from the solution to Molodensky boundary-value problem (Molodensky et al. 1960, 1962; Heiskanen and Moritz 1967) and can be determined by evaluating Stokes’s integral with the Molodensky gravity anomaly in place of the classical gravity anomaly used to calculate the geoid (e.g. Vaníček 1974).

Molodensky problem has been studied quite extensively from the theoretical point of view (e.g. Pellinen 1962; Brovar 1964; Sansó 1978, 1989; Costea et al. 2014; Foroughi and Tenzer 2014; Banz et al. 2014, among others). The Molodensky free air gravity anomaly is gravity acceleration at the Earth’s surface minus normal gravity at the corresponding point on the telluroid. The gravitational effects of the topography can be expressed as an infinite power series of so-called G terms, derived from convolution integrals of Molodensky free air gravity anomalies and normal heights (e.g. Moritz 1970). These are added to the Molodensky free air anomaly to give what we abbreviate in the following as the Molodensky gravity anomaly. For regional quasigeoid computations, this power series is typically truncated to the first order (e.g. Burša 1965; Rapp 1975; Amod and Merry 2002, Merry 2003) to the so-called \( G_{1} \) term, though higher-order G terms have also been considered (e.g. Sideris and Schwarz 1988; Li et al. 1995; Denker and Tziavos 1999).

The most recent gravimetric quasigeoid model of Australia, AGQG2017 (Featherstone et al. 2018a, b) was computed using Faye gravity anomalies (e.g. Moritz 1968) as an approximation of Molodensky gravity anomalies (cf. Amod and Merry 2002; Mojzeš et al. 2005). Faye gravity anomalies are calculated by adding the planar gravimetric terrain correction to the free air anomaly as an approximation of the \( G_{1} \) term, but the terrain correction is always positive, whereas the \( G_{1} \) term can take both positive and negative values due to the inclusion of the free air anomaly. This approximation will be investigated herein.

McCubbine et al. (2017) provide a mathematical framework to compute planar gravimetric terrain correction uncertainties. The presentation here provides a similar methodology to determine first-order Molodensky gravity anomaly uncertainties based on the assumption that the DEM and free air anomaly errors are zero-mean Gaussian random variables that are spatially independent. This work closes a gap in the existing literature on an error propagation formula. This is extended further to determine the error in the computed quasigeoid (cf. Featherstone et al. 2018a).

We present the computation of G1 terms and their errors on a 1″ × 1″ grid over Australia and 1′ × 1′ grids of quasigeoid heights and their errors, computed using the remove–compute–restore technique with the Featherstone et al. (1998) modified Stokes’s kernel. Here, the computational procedures for the quasigeoid heights are performed deterministically, with the propagated error computations treated completely separately. As such, the propagated errors have no effect on the computed quasigeoid itself.

2 First-order solution to the Molodensky problem

The height anomaly \( \zeta \) can be determined by evaluating Stokes’s integration of Molodensky free air anomalies and an infinite sum of Molodensky \( G_{n} \) terms. The commonly used first-order Stokesian solution is

$$ \zeta = \frac{R}{4\pi \gamma } \iint\limits_{{{\varOmega }}} {({{\Delta }}g_{FA} + G_{1} )S\left( \varPsi \right){{\rm d}{\varOmega }}} $$
(1)

where \( \gamma \) is normal gravity on the telluroid (e.g. Denker and Tziavos 1999), \( {{\Delta }}g_{FA} \) is the Molodensky free air gravity anomaly on the surface of the topography, \( S(\varPsi ) \) is Stokes’s kernel or some modification thereof, and \( G_{1} \) is the first-order Molodensky gravity correction term, given by, e.g. Moritz (2015)

$$\begin{aligned} G_{1} \left( {\phi ,\lambda } \right) &= \frac{{R^{2} }}{2 \pi }\iint \frac{{H^{*} \left( {\phi^{\prime } ,\lambda^{\prime } } \right){{\Delta }}g_{FA} \left( {\phi^{\prime } ,\lambda^{\prime } } \right)}}{{{\text{l}}\left( {\phi ,\lambda ,\phi^{\prime } ,\lambda^{\prime } } \right)^{3} }} \\ &\quad\, - \frac{{H^{*} \left( {\phi ,\lambda } \right){{\Delta }}g_{FA} \left( {\phi^{\prime } ,\lambda^{\prime } } \right)}}{{{\text{l}}\left( {\phi ,\lambda ,\phi^{\prime } ,\lambda^{\prime } } \right)^{3} }}{ \cos }(\phi^{\prime } ){\text{d}}\phi^{\prime } {\text{d}}\lambda^{\prime } .\end{aligned} $$
(2)

In Eq. (2), \( H^{*} \) is the normal height and \( l = 2R{ \sin }({{\Psi }}/2) \) is the distance between the roving point of the integral and each computation point, where R is the mean Earth radius and \( \Psi \) is the spherical distance on the unit sphere. When \( H^{*} \) and \( {{\Delta }}g_{FA} \) are gridded, the \( G_{1} \) convolution integral can be discretised and expressed in spectral form as (cf. Sideris and Schwarz 1986, 1988)

$$ G_{1} = \frac{{{{\Delta }}\phi {{\Delta }}\lambda }}{2 \pi }\left[ {\left( {H^{*} {{\Delta }}g_{FA} } \right)*\frac{1}{{{\text{l}}^{3} }} - H^{*} \left( {{{\Delta }}g_{FA} *\frac{1}{{{\text{l}}^{3} }}} \right)} \right] , $$
(3)

where \( {{\Delta }}\phi \) and \( {{\Delta }}\lambda \) are the latitudinal and longitudinal grid spacings (dimensions of length after discretisation). In the frequency domain, the convolutions become multiplication (since \( f*g = F^{ - 1} \left( {F\left( f \right)F\left( g \right)} \right) \)), which can be efficiently evaluated using the discrete/fast Fourier transform. Wavelet formulations have been proposed by Yu et al. (2001) and Freeden and Mayer (2006), but here we only consider the Fourier case. However, we do make use of the very efficient FFTW algorithm (Frigo and Johnson 2005).

We calculated a 1″ by 1″ (~ 30 m resolution) grid of Molodensky \( G_{1} \) terms over the entire Australian continent. We used the 1″ × 1″ digital elevation model (DEM) provided by Geoscience Australia (Gallant et al. 2011) as normal height values and a 1″ × 1″ grid of Molodensky free air gravity anomalies interpolated from values in the Geoscience Australia land gravity database. The DEM was derived from Shuttle Radar Topography Mission (SRTM) ellipsoidal heights, converted to physical heights using EGM96 (Lemoine et al. 1998) and “hydrologically enforced” using the ANUDEM software (Hutchinson 1989) to ensure that streams and rivers flow in the correct direction.

Similarly to the planar terrain correction presented by McCubbine et al. (2017), we evaluated the convolution integrals out to a maximum distance of 0.5° (~ 50 km) from the computation point. This was done so that the \( G_{1} \) terms could be used to compute quasigeoid solutions that are comparable to those in Featherstone et al. (2018a). We also used a kernel weighting function (McCubbine et al. 2017)

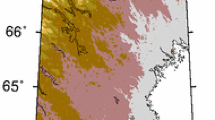
$$ w = \frac{{2l^{4} }}{{\left( {l + \frac{{\Delta l}}{2} } \right)^{2} \left( {l - \frac{{\Delta l}}{2} } \right)^{2} }} , $$
(4)

to estimate kernel values that are more representative of their mean over each 1″ × 1″ cell compared to just the value at each centre. The \( G_{1} \) term values are shown in Fig. 1, generalised to 1′ by 1′ for display purposes. Statistics of the 1″ × 1″ grid are given in the caption.

Fig. 1
figure 1

1″ × 1″ Molodensky \( G_{1} \) terms block-averaged to a 1′ x 1′ resolution. For the 1″ × 1″ grid: [min: − 113.698, max: 139.588, mean: 0.037, STD: 0.998] mGal

Full size image

The 1″ × 1″ DEM and gravity anomaly grids each occupy approximately 80 Gb in ASCII format. These are too large to be read into core memory on a PC, so they were broken into 5° × 5° sub-grids with a 1° overlaps at each edge. The 1° overlap ensures that the sub-grids agree at the boundaries since the integrals were evaluated out to a maximum 0.5° radius from each computation point. For the EW direction, the agreement was exact because the tiles overlap by more than the integration radius. For the NS direction, the agreement was less than 10−4 mGal because the mean latitude of each sub-grid was used to compute the spherical distance. We then computed the \( G_{1} \) term at each sub-grid element and “stitched” the tiles back together using the GMT (Wessel et al. 2013) routine grdblend.

The computations were performed using a Matlab™ script that makes use of highly efficient in-built Fourier transform routines (FFTW; Frigo and Johnson 2005). There were 90 individual DEM and free air anomaly sub-grids in total, and the script took approximately 25 min to run for each tile. The total run time to compute the 1″ × 1″ resolution \( G_{1} \) terms was 37.5 h, a testament to the efficiency of the FFTW.

3 Free air anomaly and DEM error propagation into the G 1 term

For the \( G_{1} \) term error propagation formulas derived in this section, we make the implicit assumption that Eq. (2), and its discretisation given by Eq. (3), do not introduce any error. This is not strictly true, however. For example, Eq. (2) neglects the angle of inclination of the heights between the computation and roving points (Baussus-von Luetzow 1971). Similarly, Eq. (3) discretises the integral so that it is possible to evaluate it numerically, but the topographic heights and gravity field are continuous in reality. However, these equations are widely used and their theoretical deficiencies are well documented elsewhere.

In the following, we consider the propagation of errors in the gravity anomaly data and DEM heights into the \( G_{1} \) term by looking at the Taylor series expansion of Eq. (3) around these terms. The contribution of a single grid element at \( \left( {\phi^{\prime } ,\lambda^{\prime } } \right) \) to the \( G_{1} \) term at \( \left( {\phi ,\lambda } \right) \) is given by

$$\begin{aligned} G_{1}^{\prime } &= \frac{{{{\Delta }}\phi {{\Delta \lambda }}}}{2 \pi }\left[ {\frac{{H^{*} \left( {\phi^{\prime } ,\lambda^{\prime } } \right){{\Delta }}g_{FA} \left( {\phi^{\prime } ,\lambda^{\prime } } \right)}}{{{\text{l}}\left( {\phi ,\lambda ,\phi^{\prime } ,\lambda^{\prime } } \right)^{3} }} }\right. \\ & \qquad \left.{- \frac{{H^{*} \left( {\phi ,\lambda } \right){{\Delta }}g_{FA} \left( {\phi^{\prime } ,\lambda^{\prime } } \right)}}{{{\text{l}}\left( {\phi ,\lambda ,\phi^{\prime } ,\lambda^{\prime } } \right)^{3} }}} \right] \\ & = \frac{{{{\Delta }}\phi^{\prime } {{\Delta }}\lambda^{\prime } }}{2 \pi }\left[ {\frac{{H^{\prime *} {{\Delta }}g_{FA}^{\prime } }}{{{\text{l}}^{3} }} - \frac{{H^{*} {{\Delta }}g_{FA}^{\prime } }}{{{\text{l}}^{3} }}} \right] \end{aligned}$$
(5)

A small change in the normal height and free air anomaly at the roving point (denoted by \( dH^{'} * \) and \( \delta { {d}}g' _{FA} \), respectively) and computation point height (denoted \( \delta H \)) on the \( G_{1}^{\prime } \) value can be evaluated by considering the Taylor series expansion around these terms, which is

$$ \begin{aligned} & G^{\prime }_{1} \left( {H^{\prime *} + dH^{\prime *} ,H^{*} + dH^{*} ,{{\Delta }}g_{FA}^{\prime } + d{{\Delta }}g_{FA}^{\prime } } \right) \\ & \qquad - G_{1}^{\prime } \left( {H^{\prime *} ,H^{*} ,{{\Delta }}g_{FA}^{\prime } } \right) \\ & \quad = \sum\limits_{j = 1}^{\infty } {\frac{1}{j!}\left( {dH^{\prime *} \frac{\partial }{{\partial H^{\prime *} }} + dH^{*} \frac{\partial }{{\partial H^{*} }} + d{{\Delta }}g_{FA}^{\prime } \frac{\partial }{{\partial {{\Delta }}g_{FA}^{\prime } }}} \right)^{j} }\\ & \quad G_{1}^{\prime } \left( {H^{\prime *} ,H^{*} ,{{\Delta }}g_{FA}^{\prime } } \right) \\ & \quad = \frac{{{{\Delta }}\phi {{\Delta \lambda }}}}{2 \pi }\left[ {(dH^{\prime *} - dH^{*} ) \frac{{{{\Delta }}g_{FA}^{\prime } }}{{{\text{l}}^{3} }} + (dH^{\prime *} - dH^{*} ) \frac{{d{{\Delta }}g_{FA}^{\prime } }}{{{\text{l}}^{3} }} }\right.\\ & \qquad\, \left.{+\, d{{\Delta }}g_{FA}^{\prime } \frac{{H^{\prime *} - H^{*} }}{{{\text{l}}^{3} }}} \right] \\ \end{aligned} $$
(6)

By considering the \( dH^{\prime *} \),\( dH^{*} \) and \( d{{\Delta }}g_{FA}^{\prime } \) terms as stochastic quantities (uncertainties), we can the evaluate the variance of \( G_{1}^{\prime } \)

$$\begin{aligned} Var\left( {G_{1}^{\prime } } \right) & = \frac{{{{\Delta }}\phi^{2} {{\Delta \lambda }}^{2} }}{{4 \pi^{2} }}\left[ {\frac{{{{\Delta }}g_{FA}^{\prime 2} }}{{{\text{l}}^{6} }}Var\left( {dH^{\prime *} - dH^{*} } \right) + \frac{1}{{{\text{l}}^{6} }}Var}\right.\\ &\qquad \left.{ \left( {\left( {dH^{\prime *} - dH^{*} } \right)d{{\Delta }}g_{FA}^{\prime } } \right) + \frac{{\left( {H^{\prime *} - H^{*} } \right)^{2} }}{{{\text{l}}^{6} }}Var\left( {d{{\Delta }}g_{FA}^{\prime } } \right)} \right. \\ & \qquad+ \,\frac{{2{{\Delta }}g_{FA}^{\prime } }}{{{\text{l}}^{6} }}Cov\left( {dH^{\prime *} - dH^{*} ,\left( {dH^{\prime *} - dH^{*} } \right)d{{\Delta }}g_{FA}^{\prime } } \right) \\ & \qquad +\, \frac{{2{{\Delta }}g_{FA}^{\prime } \left( {H^{\prime *} - H^{*} } \right)}}{{{\text{l}}^{6} }}Cov\left( {dH^{\prime *} - dH^{*} ,d{{\Delta }}g_{FA}^{\prime } } \right) \\ &\qquad +\, \left. {\frac{{2\left( {H^{\prime *} - H^{*} } \right)}}{{{\text{l}}^{6} }}Cov\left( {\left( {dH^{\prime *} - dH^{*} } \right)d{{\Delta }}g_{FA}^{\prime } ,d{{\Delta }}g_{FA}^{\prime } } \right)} \right] \\ \end{aligned} $$
(7)

To simplify Eq. (7), we have made the following three initial assumptions about the DEM and free air gravity anomaly uncertainties:

  1. (i)

    \( dH^{\prime *} \),\( dH^{*} \) and \( d{{\Delta }}g_{FA}^{\prime } \) are zero-mean Gaussian random variables with variances \( \sigma_{{dH^{\prime *} }}^{2} \), \( \sigma_{{dH^{*} }}^{2} \) and \( \sigma_{{d{{\Delta }}g_{FA}^{\prime } }}^{2} \);

  2. (ii)

    \( d{{\Delta }}g_{FA}^{\prime } \) and DEM values \( dH^{\prime *} \) and \( dH^{*} \) values are spatially independent, i.e. no correlation among values in nearby grid cells;

  3. (iii)

    \( d{{\Delta }}g_{FA}^{\prime } \) are independent to the \( dH^{\prime *} \) values.

None of these assumptions are strictly true, however. For (i), the exact nature of the gravity anomaly and DEM errors are unknown. In the absence of any concrete information to the contrary, we assume them to be random, non-systematic, and equally likely to fall either side of a zero mean for convenience, which leads to the choice of a Gaussian distribution. For (ii), the errors in the DEM are typically correlated out to approximately 100 m (Gallant et al. 2011) and the gravity data used to determine the 1″ × 1″ grid have an Australia-wide average spatial density of around one measurement every 4 \( {\text{km}}^{2} \) (but this varies from place to place: see Fig. 1 in Featherstone et al. 2018a), so neighbouring grid cells may be determined from the same surveys. These effects could be compensated for with additional covariance terms, which, however, are neglected in the following for simplicity (cf. McCubbine et al. 2017). For point (iii), the free air anomalies were determined using a “topographic restoration procedure” (Featherstone and Kirby 2000), which implicitly causes correlated errors between the free air gravity anomalies and DEM; this is addressed in Appendix A, although it drastically increases the complexity of the error variance computation so has not been performed.

Under all the above assumptions, the simplified expression of the \( Var(G'_{1} ) \) (Eq. 7) is given by

$$\begin{aligned} Var\left( {G_{1}^{\prime } } \right) &\cong \frac{{{{\Delta }}\phi^{2} {{\Delta \lambda }}^{2} }}{{4 \pi^{2} {\text{l}}^{6} }}\left[ {{{\Delta }}g_{FA}^{\prime 2} (\sigma_{{dH^{*} }}^{2} + \sigma_{{dH^{\prime *} }}^{2} ) + \sigma_{{d{{\Delta }}g_{FA}^{\prime } }}^{2} }\right.\\ & \qquad \left.{\left( {H^{{\prime *^{2} }} - 2H^{\prime *} H^{*} + H^{{*^{2} }} } \right) + \sigma_{{d{{\Delta }}g_{FA}^{\prime } }}^{2} (\sigma_{dH}^{2} + \sigma_{{dH^{\prime } }}^{2} )} \right] . \end{aligned}$$
(8)

Following McCubbine et al. (2017), the variance of the \( G_{1} \) term convolution integral can then be expressed as a sum of convolutions by

$$ \begin{aligned} Var\left( {G_{1} } \right) & = \frac{{{{\Delta }}\phi^{2} {{\Delta \lambda }}^{2} }}{{4 \pi^{2} }}\left[ {\sigma_{{dH^{*} }}^{2} \left( {{{\Delta }}g_{FA}^{{\prime^{2} }} *\frac{1}{{{\text{l}}^{6} }}} \right) }\right.\\ & \qquad\left.{+ \,\left( {\sigma_{{dH^{\prime *} }}^{2} {{\Delta }}g_{FA}^{{\prime^{2} }} *\frac{1}{{{\text{l}}^{6} }}} \right) + \left( {(\sigma_{{d{{\Delta }}\widehat{g}_{FA} }}^{2} H^{{\prime *^{2} }} )*\frac{1}{{{\text{l}}^{6} }}} \right.} \right. \\ & \qquad - \,\left. {\left. {2H\left( {(\sigma_{{d{{\Delta }}g^{\prime }_{FA} }}^{2} H^{\prime *} )*\frac{1}{{{\text{l}}^{6} }}} \right) + H^{{*^{2} }} \left( {\sigma_{{d{{\Delta }}g_{FA}^{\prime } }}^{2} *\frac{1}{{{\text{l}}^{6} }}} \right)} \right) }\right.\\ & \qquad \left.{+\, \sigma_{{\delta H^{*} }}^{2} \left( {\sigma_{{d{{\Delta }}g_{FA}^{\prime } }}^{2} *\frac{1}{{{\text{l}}^{6} }}} \right) + \left( {\sigma_{{dH^{\prime *} }}^{2} \sigma_{{d{{\Delta }}g_{FA}^{\prime } }}^{2} *\frac{1}{{{\text{l}}^{6} }}} \right)} \right] \\ \end{aligned} . $$
(9)

We calculated \( G_{1} \) error variances using Eq. (9) with the 1″ × 1″ DEM, assuming the height errors at each grid point to be independent with a standard deviation of ± 7.66 m (cf. McCubbine et al. 2017), a gridded 1″ × 1″ free air anomaly, and a 1″ × 1″ gridded free air anomaly errors used for AGQG2017 (Featherstone et al. 2018a). Equation (9) is valid for spatially varying DEM error standard deviations (i.e. error standard deviation values gridded at the same resolution as the free air anomalies and DEM, rather than a constant value), but these estimates are currently unavailable for the DEM used in this study.

Figure 2 shows the square root of the \( G_{1} \) uncertainty values re-gridded at 1′ × 1′ for display purposes; statistics of the 1″ × 1″ grid are given in the caption. The gravity observations used for these calculations have been collected during regional surveys of different extents with varying methodologies and instrumentation. This leads to heterogeneous uncertainties among different survey areas, which results in some spurious linear features at the boundaries in Fig. 2, e.g. at 30°S and 128°E.

Fig. 2
figure 2

1″ × 1″ Molodensky \( G_{1} \) term uncertainty estimates block-averaged to a 1′ x 1′ resolution. For the 1′’ × 1′’ grid: [min: 0, max: 43.715, mean: 0.244, STD: 0.805] mGal

Full size image

Finally, due to the assumptions regarding independence and the fact that the \( G_{1} \) term integral is zero at the computation point, the variance of the Molodensky gravity anomaly \( {{\Delta }}g \) is given by

$$ Var\left( {{{\Delta }}g} \right) = Var\left( {{{\Delta }}g_{FA} } \right) + Var(G_{1} ) $$
(10)

The standard deviation (square root of variance) of the Molodensky gravity anomaly \( Var\left( {{{\Delta }}g} \right) \) is shown in Fig. 3, with the variances of the free air gravity anomalies \( Var\left( {{{\Delta }}g_{FA} } \right) \) taken from Featherstone et al. (2018a). The gridding of the gravity anomaly data also introduces some errors. These are not reflected in the free air anomaly error standard deviation grid here because they are not given by the GMT gridding procedure directly.

Fig. 3
figure 3

1″ × 1″ Molodensky gravity anomaly error standard deviations block-averaged to a 1′ x 1′ resolution. For the 1″ × 1″ grid: [min: 0.003, max: 54.201, mean: 2.026, STD: 2.881] mGal

Full size image

4 Quasigeoid determination and error propagation through Stokes’s integral

The Molodensky \( G_{1} \) term is theoretically superior to the planar terrain correction for computing the height anomaly. We therefore used the \( G_{1} \) term in place of the planar terrain correction values for a series of regional quasigeoid computations, producing a range of solutions by the remove–compute–restore technique with EGM2008 (Pavlis et al. 2012, 2013) as the reference field and Curtin University’s FFTmod1D2011.f software (Hirt et al. 2011).

We used the Featherstone et al. (1998) modified Stokes’s kernel (herein abbreviated to FEO) with modification degrees ranging from 40° to 120° (in 20° increments) and spherical cap radii ranging from 0° to 5° (in 0.5° increments). The FEO kernel modification minimises the L2-norm of the truncation bias and accelerates convergence of the truncation bias per degree by making the error kernel’s derivative continuous at the truncation radius. The quasigeoid solutions were compared to GNSS-levelling data, which are described in Featherstone et al. ((2018a, b)). The standard deviation of the comparisons is shown in Fig. 4. Quasigeoid models produced using planar terrain corrections fit the GNSS-levelling data slightly better for each parameter combination after removal of a plane to account for the predominantly north south tilt in the Australian Height Datum (cf. Featherstone and Filmer 2012).

Fig. 4
figure 4

STD (m) of gravimetric quasigeoid models for parameter sweeps of FEO kernel modification degree and spherical integration cap radius versus GNSS-levelling data after removal of a tilted plane using the G1 term (solid lines) and the planar terrain correction (dashed lines—from Featherstone et al. 2018a), both determined from 1″ × 1″grids

Full size image

The modification degree and integration cap radius together act as partial high pass filters on the integrated signal (Vaníček and Featherstone 1998). In Fig. 4, when the integration cap radius is small (< 1°), it is the dominant high pass filter. This is evidenced by little difference among the quasigeoid solutions with different modification degrees for both the Faye and Molodensky anomalies. As the integration cap radius increases and the power of the filter thus lessens, long-wavelength errors in the terrestrial gravity data pass more into the quasigeoid solutions. This is more prominent for lower modification degrees, again where the filter is less powerful.

The quasigeoid solution using the \( G_{1} \) term that best agrees with the GNSS-levelling data is obtained with a modification degree of 40 and an integration cap radius of 0.5°. This is exactly the same parameter combination found for AGQG2017 (Featherstone et al. 2018a). However, as with AGQG2017, these results must be balanced against the inherent ~ 40 mm precision of the GNSS-levelling data (cf. Featherstone et al. 2018a, Sect. 2.4), which makes any definitive discrimination among the model solutions difficult for the range of the y-axis in Fig. 4.

The quasigeoid solutions using 1″ × 1″ planar terrain corrections always agree better (or at least the same) with the GNSS-levelling data than those determined using the 1″ × 1″ G1 terms. We postulate that the slightly weaker agreement of the quasigeoid solutions determined using the \( G_{1} \) term to the GNSS-levelling data is due to the sparser gravity data coverage in relation to the DEM resolution, i.e. inadequately dense gravity observations used to grid the free air anomaly at 1″ × 1″ for the \( G_{1} \) term computation. This is arguably a limitation of the Molodensky method because it appears to require gravity observations at a spatial density commensurate with the resolution of the DEM used.

To further investigate this postulate, we computed \( G_{1} \) terms and planar terrain corrections using coarser 1′ × 1′ grids of free air anomalies and DEM heights, and used these to determine quasigeoids with the same sweeps of Stokes’s integral parameters as shown in Fig. 4. This test revealed that the \( G_{1} \) terms outperformed the planar terrain corrections in this instance (Fig. 5). Further work should be undertaken to shed more light on this behaviour, however. For example, the resolution of the DEM and gridded free air anomaly data could be varied prior to the computation of planar terrain corrections and \( G_{1} \) terms to test our postulate.

Fig. 5
figure 5

STD (m) of gravimetric quasigeoid models for parameter sweeps of FEO kernel modification degree and spherical integration cap radius versus GNSS-levelling data after removal of a tilted plane using the G1 term (solid lines) and the planar terrain corrections, both determined from 1′ × 1′ grids

Full size image

Gravity anomaly error variances \( \sigma^{2} ({{\Delta }}g) \) were propagated through a modified version of Stokes’s integral to produce error estimates of the quasigeoid heights \( \sigma^{2} ({{\zeta }}) \). Following the methods in Featherstone et al. (2018a), error variances of regional quasigeoid heights determined by the remove–compute–restore procedure can be approximated using global gravity model error variance estimates and gravity anomaly error variances by

$$\begin{aligned} \sigma^{2} \left( {\zeta_{i} } \right) &= \sigma^{2} (\zeta_{i} )_{GGM} + \kappa^{2} \mathop \sum \limits_{{{\varOmega }}} \sigma^{2} \left( {{{\Delta }}g_{j} } \right)\widehat{S}^{2} \left( {\psi_{{{\text{i}},{\text{j}}}} } \right)d{{\varOmega }}^{2} - \kappa^{2} \\ & \quad \times \mathop \sum \limits_{{{\varOmega }}} \sigma^{2} \left( {{{\Delta }}g_{j} } \right)_{GGM} \widehat{S}^{2} \left( {\psi_{{{\text{i}},{\text{j}}}} } \right){{{\rm d}\varOmega }}^{2} \end{aligned}$$
(11)

where \( \widehat{S} \) is the FEO-modified Stokes’s kernel, \( \sigma^{2} (\zeta_{i} )_{GGM} \) and \( \sigma^{2} \left( {{{\Delta }}g_{j} } \right)_{GGM} \) are the reference global gravity model quasigeoid height and gravity anomaly error variances, respectively, \( \kappa = r/4\pi \) for geocentric radius \( r \), point \( i \) is the computation point and point \( j \) is the roving point of the integration.

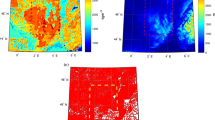
Figure 6a shows the Molodensky gravity anomaly errors supplemented by Sandwell et al. (2013) satellite altimetry gravity anomaly errors offshore. Figure 6b shows their contribution to the quasigeoid height errors (i.e. the second term on the right-hand side of Eq. 11) with the same integration parameters used to generate the quasigeoid model. Figure 6c shows the EGM2008 quasigeoid height error \( \sigma (\zeta_{i} )_{EGM2008} \). Figure 6 (d) shows the final quasigeoid height standard deviation \( \sigma \left( {\zeta_{i} } \right) \) derived via Eq. (11). Both the EGM2008 gravity anomaly and quasigeoid error grids were downloaded from http://earth-info.nga.mil/GandG/wgs84/gravitymod/egm2008/egm08_error.html. These were determined by the EGM2008 development team by propagating error estimates of the raw gravity data used to determine EGM2008 through (an unmodified) Stokes’s integral (Pavlis and Saleh 2005).

Fig. 6
figure 6

a The Molodensky gravity anomaly error standard deviation [min: 0.003 max: 54.201 mean: 2.001 STD: 2.880] mGal. b Stokes’s integral error propagation (i.e. second term in Eq. 11) of the Molodensky gravity anomaly error data evaluated with FEO modification degree of 40 and integration cap radius of 0.5° [min: 0.000 max: 0.080: mean: 0.004 STD: 0.006] m. c The EGM2008 quasigeoid height errors standard deviation [min: 0.038 max: 0.299 mean: 0.057 STD: 0.019] m. d The quasigeoid height standard deviation [min: 0.038 max: 0.270 mean: 0.055 STD: 0.017] m

Full size image

The propagated Molodensky gravity anomaly uncertainties produce quasigeoid uncertainties with a mean of 4 mm and a maximum of 80 mm (Fig. 6). Further, the mean quasigeoid error in the final model is approximately 2 mm less than that of the EGM2008 quasigeoid. This is commensurate with the increased precision seen in the comparison with GNSS-levelling data (Fig. 2).

The error variances of the \( G_{1} \) terms have been propagated independently through Stokes’s integral to assess their contribution to the uncertainty (i.e. evaluating the second term in Eq. (11) with the \( G_{1} \) term error variances in place of the full Molodensky anomaly variances). The standard deviation of these values (i.e. square root of the second term of Eq. 11) is shown in Fig. 7. On comparison with Fig. 6b, onshore, the \( G_{1} \) terms contribute greatly to the uncertainty signal. They account for at least half of the total error, having a maximum value of 27 mm in the South East of Australia. This demonstrates that for a robust uncertainty estimate of the quasigeoid derived using the Molodensky anomaly, the contribution of the \( G_{1} \) terms should not be overlooked.

Fig. 7
figure 7

Stokes’s integral error propagation of the Molodensky G1 term standard deviation [min: 0 max: 0.027 mean: 0.001 STD: 0.002] m

Full size image

5 Concluding remarks

We have presented a 1″ × 1″ grid of first-order Molodensky \( G_{1} \) terms and a grid of corresponding uncertainty estimates for the entire Australian continent. This work closes a gap in the existing literature on the methodology to compute uncertainty estimates for the \( G_{1} \) term. The formulas allow for DEM and gravity anomaly uncertainty estimates to be propagated through the convolution integrals and subsequently into the quasigeoid model.

We combined the \( G_{1} \) terms with an existing grid of free air anomalies to produce Molodensky gravity anomalies. These were used to compute quasigeoid models by the remove–compute–restore procedure with EGM2008 as the reference field. As was the case for AGQG2017 (Featherstone et al. 2018a), the solution that agreed closest with ~ 7000 GPS-levelling data was given by an integration cap radius of 0.5° and a modification degree of 40. The Molodensky quasigeoid solutions appear to be less precise than the Faye ones. Our preliminary tests appear to indicate that this is attributable to the mismatch between the spatial resolution of the gravity data and DEM. For the currently available gravity and DEM data covering Australia, it appears that planar terrain corrections are preferable to Molodensky \( G_{1} \) terms.

We combined the \( G_{1} \) term uncertainty estimates with existing grid of free air anomaly uncertainty estimates and propagated the resulting grid through the modified Stokes’s integral. The Molodensky gravity anomaly uncertainties with mean a of 2 mGal and a maximum of 54 mGal translate into quasigeoid height uncertainties with a mean of 4 mm and a maximum of 80 mm. The largest uncertainty values were found in the South East where the topography varies most strongly. These precision estimates generally agree with what is anticipated of the quasigeoid accuracy in those areas.

Finally, it is important to recall that the derivation of the \( G_{1} \) term uncertainties given here is based on the assumption that the DEM and free air anomaly errors are zero-mean Gaussian random variables and are spatially independent. Refining these assumptions and modifying the error propagation formula may well improve the precision of the derived uncertainty values but could ultimately be costly in terms of their numerical evaluation.