1 Introduction

The GNSS antenna phase centre is a function of the direction of the incoming signal, and it is different for each antenna. It is an error source in precise positioning, and it should be corrected during data processing. With the corrections, the phase observations are reduced to the antenna reference point (ARP), a fixed physical place on an antenna. The phase centre correction (PCC) is normally divided into two parts, phase centre variation (PCV) and phase centre offset (PCO), which should be used together. The act of determining the phase centre corrections (PCC) for a GNSS antenna is called calibration. In this paper, we introduce a method to validate GNSS antenna calibration tables. The goal is to find the residual offsets due to imperfections in the antenna and its calibration table.

Nowadays, accepted calibration methods include field robot calibration and calibration in an anechoic chamber. These calibrations yield individual absolute calibration tables for the measured frequencies. The International GNSS Service (IGS) maintains a list of the institutions offering the approved calibration services (IGS 2017).

The traditional phase centre determination method involves using the ground truth, i.e. the network or the short baseline with known coordinates (Mader 1999; Rothacher et al. 1995). Nowadays, the method is relevant for validating calibrations. However, when comparing the levelled height differences, calibrated baseline distances or reference coordinates with GPS baselines, we may assume that the difference between the resolved GPS baseline and ground truth is antenna related, while it is due to multipath and other site-specific effects.

Stepniak et al. (2015) had used the short baseline at Lamkowko Satellite Observatory for testing antennas. The LAMA IGS station, with an LEIAT504GG LEIS antenna, was at one end of the baseline and the pillar point was at the other end. The reference coordinates for baseline were measured using a reference antenna (ASH700936F_C SNOW). Stepniak et al. (2015) compared 28 different antennas, with the reference using NGS and IGS absolute type calibration tables. For some antennas, only elevation-dependent PCC was available. They discovered discrepancies of up to 5 mm in the horizontal components and 25 mm in the Up component for some antennas, with the antenna models having been converted from relative calibrations. The work of Stepniak et al. (2015) can be considered an antenna test rather than a validation of the calibration tables. However, when the reference antenna has better calibration than the tested antennas, the method works as a validating method, too.

One simple test procedure for an antenna pair is rotation and swapping. If we swap the antennas, we can solve for the relative residual offsets of the antennas in relation to one another or relative to the reference antenna. By rotating one of the antennas between sessions without tilting, we can solve for the absolute North and East residual offsets for the antenna. If the distance between antennas is only a few metres, we can assume that the differences in the baseline coordinates are due to rotation and swapping and thus related to the antenna. Without repetition, there is no redundancy (simple swapping) or little redundancy (swapping, rotating) in the coordinate difference observations and the risk of an incorrect conclusion is high.

The improvement for the method of swapping two antennas is the permutation method, first introduced as a full roving method by Bányai (2005). He used in his example a network of four pillars but only two sessions. The antennas were moved to the next pillars between the sessions. With two sessions, the relative offsets are solvable but the redundancy of observations is poor. Bányai originally introduced the method for antenna calibration, but the phase variation should be also determined in calibration. Thus, the roving method should be considered a means of validating antenna calibration or an observing strategy for local networks, as he concluded. While the proposed observation strategy may work for measurement campaigns, it does not work in the case of permanent networks.

Our approach is based on the full roving method proposed by Bányai (2005). We developed the method further in 2011 (Kallio et al. 2012) and during the EMRP SIB60 project (Pollinger et al. 2015) by increasing the number of permutations and sessions, and thus the redundancy of the observations. We used the version developed in a Metsähovi antenna test in 2011 (Kallio et al. 2012) and introduced it as a permutation method. We also developed the processing strategy using full covariance matrices for session solutions. Our idea was to validate antenna calibration tables after calibration, and if necessary, recalibrate the antenna, or apply additional residual offsets as corrections in campaigns or in a permanent network. We combined the rotation and circulation of antennas on pillars into the same process.

In the following, we introduce the methodology for the permutation method, the measurements taken at the Metsähovi test field and analysis and results based on the measurements. Finally, we further discuss the differences found between antenna calibration tables of different institutions.

2 Methodology

With the permutation method antennas are circulated so that each antenna visits each site at least once. The antenna north arrows are directed towards geodetic North, but in some pillars and sessions the antennas are rotated \(180^{\circ }\), each antenna in turn. The permutation and rotation of antennas can vary depending on the number of antennas and pillars used in the test. With simulations, we can investigate the expected quality before the measurements. We can check and ensure any necessary moves and rotations so as to allow for enough redundancy for reliable offset estimates. Depending on the number of antennas, we choose 3–8 pillars. For the measurements it is important to have at least as many 24-h sessions as there are antennas because each antenna visits every pillar. For three antennas, we recommend the movements and rotations presented in Fig. 1.

Fig. 1
figure 1

Antenna movements and rotation with three antennas (red, green and blue) in six sessions (S1–S6) at the three points (A, B and C); the down arrow means orientation of the antenna towards the South, whereas without the arrow the antenna is oriented towards the North

Full size image

We explain the influence of the antenna change on session coordinates via the offset parameters. The null hypothesis in the statistical test is that the offsets are zeros, which means that the calibration tables are correct. If they differ statistically significantly from zero, we can claim that there are still antenna-dependent properties that were not corrected with the calibration table. We do not handle PCV or PCC separately, but instead obtain offsets that are, under certain circumstances, applicable as additional corrections to the coordinates in field work or when using GNSS for distance measurements.

If certain phenomena are assumed to be dependent upon distances or temperatures, we can vary the distances or temperatures in our experiments. In order to study the dependence of the site coordinates on the antenna, we must vary the antennas; otherwise, the antenna-dependent part remains invisible. With our method, it is possible to solve for the antenna-specific constants. These constants are called residual offsets. When processing the session baseline vectors, the antenna calibration tables are applied. There should not be statistically detectable antenna-dependent offsets with perfect PCC corrections,

We hypothesize that it is possible to separate the antenna-dependent residual offsets from the site-specific residuals of the session solutions by varying the antennas on the site. If we change the antenna on the site, the properties of the new antenna will have influence on the coordinates. The antenna-dependent offsets move with antenna, but the site-specific errors do not; they remain a burden on the site coordinates.

2.1 Swapping

The model for residual offsets in swapping is:

$$\begin{aligned} X_j-X_i+R_{j} O_q- R_{i}O_p=\varDelta X_{ij_1}, \end{aligned}$$
(1)

where \(X_i\) and \(X_j\) are unknown station coordinates for sites i and j, and \(O_p\) and \(O_q\) are unknown offset parameters for antennas p and q on sites i and j, respectively. \(\varDelta X_{ij_1}\) is the coordinate difference observation in session 1. The rotation matrices \(R_{i}\) and \(R_{j}\) are different for each site:

$$\begin{aligned} R_i= \begin{pmatrix} -sin{\varphi }_i cos{\lambda }_i &{} -sin{\lambda }_i &{}cos{\varphi }_i cos{\lambda }_i \\ -sin{\varphi }_i sin{\lambda }_i &{}cos{\lambda }_i &{}cos{\varphi }_i sin{\lambda }_i \\ cos{\varphi }_i &{} 0 &{} sin{\varphi }_i \end{pmatrix}, \end{aligned}$$
(2)

when converting the offset vectors from topocentric to global system at sites i and j. Because every antenna has a different orientation, we must convert the offset parameters in Eq. (1) to the same system as the coordinates. The session solutions and the site coordinates in the equations are in global system, but the offset parameters in antenna system. The antenna system is North, East and Up, if the north arrow of the antenna is pointing to the North and the antenna is levelled. With short baselines, we can neglect the rotation matrices and the offsets can be solved using the global system. The estimated offset vectors can then be converted to topocentric coordinates using the coordinates for the mean point of the test network used in the conversion.

It is easy to see that if we have only two antennas and two sessions, and if we swap the antennas, it results in two equations: Eq. 1 and

$$\begin{aligned} X_j-X_i+R_{j} O_p- R_{i}O_q=\varDelta X_{ij_2}. \end{aligned}$$
(3)

If we subtract these two equations, the coordinate parameters will be eliminated and we can solve for the residual offset difference of the two antennas.

2.2 Rotation

If we, instead of swapping, rotate the antenna q after the first session, we get

$$\begin{aligned} X_j-X_i+R_{j}R_{q_{180}} O_q- R_{i}R_{p_{0}} O_p=\varDelta X_{ij_2}. \end{aligned}$$
(4)

We need extra rotation matrices \(R_{q_{180}}\) and \(R_{p_0}\), which are the rotation around the vertical axis of the antennas. \(R_{p_{0}}\) is a \(3\times 3\) identity matrix and \(R_{q_{180}}\) is \(180^{\circ }\) rotation, which only changes the signs of the horizontal elements of the offset vector. Because the rotation matrices are known, subtracting the equation of the first session from the equation of the second sessions will result in the solution for the horizontal components of the offset parameter of antenna q.

2.3 Mathematical model for residual offset estimation in permutation method

The above examples with two antennas and two sessions have no redundancy and the uncertainty of the resolved offsets remains unknown, but they can be used as quick tests for the antennas. A more complete analysis of the residual offsets can be achieved using the network approach. The permutation method yields redundant measurements. The amount of redundancy depends on the number of antennas, sites and sessions and how the permutation of the antennas has been made. Mathematically, we have two networks: one for points and a different network for antennas. Equation (5) is the functional model for a baseline vector. The total number of similar types of matrix equations in one session is the number of sites minus one.

$$\begin{aligned} X_j-X_i+R_{j}R_{q_{js}} O_q- R_{i}R_{p_{is}} O_p=\varDelta X_{ij_s}. \end{aligned}$$
(5)

The extra rotation matrices \(R_{p_{is}}\) and \(R_{q_{js}}\) represent the rotation around the vertical axis of antennas \(p_{is}\) and \(q_{js}\) in session s at points i and j.

The weighting of observations is done in a session-wise manner. Weights are based on the covariance matrix of the session solution. Because we have coordinate differences as observations, the weight matrix, \(W_{\varDelta X}\), of the session is the inverse of the covariance matrix for the coordinate differences. If we have n sites, we can form \(3(n-1)\) differences and \(3(n-1)\times 3(n-1)\) covariance matrix for coordinate differences for every daily solution,

$$\begin{aligned} C_{\varDelta X}= & {} D\cdot {C_X}\cdot D^T \end{aligned}$$
(6)
$$\begin{aligned} W_{\varDelta X}= & {} {C_{\varDelta X} }^{-1}. \end{aligned}$$
(7)

D is a differencing operator and \(C_X\) is the covariance matrix of coordinates from the session solutions. The normal equations for the least squares process are obtained by stacking the session solutions:

$$\begin{aligned} N= & {} \sum {A_s}^T W_{\varDelta X_s} A_s \end{aligned}$$
(8)
$$\begin{aligned} t= & {} \sum {A_s}^T W_{\varDelta X_s} DX_s. \end{aligned}$$
(9)
$$\begin{aligned} A_s= & {} \begin{pmatrix} {{ \begin{array}{cccccccccccccc} -I &{} I &{} 0 &{} 0 &{} \cdots &{} 0 &{} | &{} \cdots &{} 0 &{} -R_1R_{p_{1s}} &{} 0 &{} 0 &{} \cdots &{} R_2R_{q_{2s}} \\ -I &{} 0 &{} I &{} &{} \cdots &{} &{} | &{} \cdots &{} 0 &{} -R_1R_{p_{1s}} &{} 0 &{} R_3R_{q_{3s}} &{} \cdots &{} 0 \\ -I &{} 0 &{} 0 &{} I &{} \cdots &{} 0 &{} | &{} \cdots &{} 0 &{} -R_1R_{p_{1s}} &{} R_4R_{q_{4s}} &{} 0 &{} \cdots &{} 0 \\ &{} &{} &{} &{} \vdots &{} &{} | &{} &{} &{} \vdots &{} &{} &{} &{} \\ -I &{} 0 &{} 0 &{} 0 &{} \cdots &{} I &{} | &{} \cdots &{} R_nR_{q_{ns}} &{} -R_1R_{p_{1s}} &{} 0 &{} 0 &{} \cdots &{} 0 \end{array} }}\end{pmatrix} \end{aligned}$$
(10)

is the design matrix for one session. In the partitioning of \(A_s\), the left part represents the coordinates. It remains the same in each session. The right part, which is for offsets, changes from session to session depending on which antenna is at which station and the attitude of the antenna.

The normal equation matrix N has not full rank. The reasons for a rank deficiency of four are a lack of the information about network translation and the lack of a fixed Up residual offset. Thanks to the rotations of the antennas at some sites and during certain sessions, the absolute North and East components of the residual offsets can be solved. If there were no rotations of the antennas, the rank deficiency would be six. The unknown parameters

$$\begin{aligned} x= \begin{pmatrix} X_{3n\times 1}\\ O_{3n\times 1}\end{pmatrix}, \end{aligned}$$
(11)

residual offsets, \(O_{3n\times 1}\), as the main products and site coordinates, \(X_{3n\times 1}\), as the by-product can be solved for using the constraint equation in a normal equation group:

$$\begin{aligned} { \begin{pmatrix} N &{} G^{T}\\ G &{}0_{4x4} \end{pmatrix} \begin{pmatrix} x\\ k \end{pmatrix}}= \begin{pmatrix} t\\ 0_{4x0} \end{pmatrix} , \end{aligned}$$
(12)

where the first three rows of the G-matrix are the inner constraint translation of coordinates. The last row of the constraint equation group states that the sum of the Up components of residual offsets is zero. The coordinates are thus the coordinate differences from the mean point of the network (in global orientation), while the Up components of the residual offsets are relative to the mean of all the Up components of all the antennas used in the test. When partitioning of G the left part is for coordinate unknowns and the right part for offsets:

$$\begin{aligned} G={ \begin{pmatrix}{ \begin{array}{rrrrrrcrrrcrrrrrrrrrr} 1 &{}0 &{}0 &{}1 &{} 0 &{} 0 &{} \cdots &{}1 &{} 0 &{} 0 &{}| &{} 0 &{} 0 &{}0 &{} 0 &{}0 &{}0 &{} \cdots &{}0 &{} 0 &{}0 \\ 0&{} 1&{} 0 &{} 0 &{} 1 &{} 0 &{}\cdots &{} 0 &{} 1 &{} 0&{}| &{} 0&{} 0 &{} 0 &{} 0&{} 0 &{}0 &{}\cdots &{} 0&{} 0 &{}0 \\ 0 &{} 0 &{} 1 &{} 0&{} 0 &{} 1 &{} \cdots &{} 0 &{} 0 &{} 1&{}| &{} 0&{} 0&{} 0&{} 0 &{} 0 &{} 0 &{}\cdots &{} 0&{} 0 &{} 0\\ 0&{} 0 &{} 0&{} 0&{}0 &{} 0 &{}\cdots &{} 0&{} 0&{} 0 &{} |&{}0 &{}0 &{} 1&{} 0 &{} 0 &{} 1 &{} \cdots &{} 0&{} 0 &{} 1 \end{array} }\end{pmatrix}} . \end{aligned}$$
(13)

k in Eq. (12) is the additional unknown, in which we are not interested. Iteration is not necessary because the model is linear, but during the processing phase the covariance matrices of daily solutions can be scaled iteratively. We used Förstner’s estimator for the scaling factor (Förstner 1979). Thus, the poor sessions will receive less weight in the adjustment. The alternative is to reject the bad sessions.

Table 1 Achievable precision of the offset parameters: na is the number of antennas, np is the number of points, ns is the number of sessions, \(t_{99}\sigma (NEU)\) is \(1\%\) significance level test statistics for the North, East and Up components of the offsets, respectively, (min r) means minimum local redundancy, and dfr is the degree of freedom in the adjustment
Full size table

2.4 Testing the significance of the offsets

The null hypothesis in the test is that there are no residual offsets:

$$\begin{aligned} H_0:O=0. \end{aligned}$$
(14)

The opposite hypothesis is:

$$\begin{aligned} H_1:O\ne 0. \end{aligned}$$
(15)

The test statistics are as follows:

$$\begin{aligned} F_O=\frac{(O-0)^T {C_{O}}^{-1}(O-0)}{u_{O}}\sim F_{u_{O},r}. \end{aligned}$$
(16)

The null hypothesis is rejected for significance level \(\alpha \) if

$$\begin{aligned} F_O>F(\alpha ,u_0,r). \end{aligned}$$
(17)

Here, O is the \(u_O\)-size vector of the offset parameters, which are tested, and 0 is the zero vector with size \(u_O\). r is redundancy of the adjustment. If the null hypothesis is rejected, we know that at least one of the offsets is significant. The test can be run separately for the North, East and Up components.

For individual offset values, we use t-statistics. If

$$\begin{aligned} \left| O_i \right| >t_{1-\alpha ,r}\sigma _{i}, \end{aligned}$$
(18)

then the single offset value differs significantly from zero.

For the Up components, the test shows whether there are significant residual offsets compared to the mean residual offset of the antennas in the test, while for the North and East components it shows whether or not the absolute residual offsets differ significantly from zero.

Table 2 Antennas and individual absolute calibrations
Full size table

2.5 Achievable precision of the residual offsets

The levels of precision of the estimated offsets are functions of the antenna permutations and rotations at sites and the levels of precision of the session coordinates. The levels of precision of the session coordinates depend on the satellite geometry, antenna, precision of the orbits, troposphere and ionosphere, multipath environment, set-up of the antenna, cut-off angle, etc. We obtain the estimated covariance matrix of the coordinates from the session solutions. The covariance matrix of the estimated parameters is the inverse of the normal equation matrix multiplied by the variance factor. The variation in the centring is invisible in those covariance matrices.

We proved the viability of the method first by calculating the variance propagation of the coordinates in the estimated offsets by varying the number of antennas and pillars and rotations. In each case we calculated the test statistics, redundancy of the adjustment and the minimum local redundancy of the observations. The confidence region depends on the redundancy.

We simulated more than one hundred different configurations. A summary of them can be seen in Table 1. The offset is significant if its absolute value is more than the t test statistics. For example consider the three antenna case. In order to be interpreted as significant with a risk level of \(1\%\), the North and East components should be more than 1.5 times the standard deviation of the observation, while the relative Up component should be 0.9 times the one \(\sigma \) of the observed coordinate difference. With more antennas and pillars, we have more sessions and redundancy. With seven antennas, we can achieve precision levels of 0.7 times one \(\sigma \) for an observation at a significance level of \(1\%\). With good antennas, the standard deviation in the observations of the coordinate differences from a session solution of 24 h may be < 0.1 mm. Thus, according to the simulation it is possible to reach sub-mm level precision for residual offsets. The number of rotations influences the precision and resolvability of the absolute horizontal components of the offsets, while more permutations will give more precise relative offsets.

3 Measurements

3.1 Measurements in 2011

We performed the first antenna test using the permutation method at Metsähovi in 2011 for eight Leica AR25 and nine Ashtech Dorne Margolin Choke Ring antennas, given in Table 2. The antennas were calibrated in Geo++ GmbH. In order to validate the calibration, we used three concrete pillars, on which we permuted a total of 17 antennas. The measurements and results were presented in Kallio et al. (2012). However, the updated data set has been reprocessed here because we completed the data set in autumn 2011 by measuring the rejected sessions and an extra session with two antennas rotated at \(180^{\circ }\).

3.2 The new Revolver network

Our simulations (Sect. 2.5) showed that increasing the number of pillars, and thus number of simultaneously tracking antennas, we can achieve better precision for the residual offsets. To validate the antennas with the permutation method, we constructed a new dedicated pillar network, called Revolver, in May 2014 (Jokela et al. 2016). Distances between the pillars were short, from 2.5 to 5 m. Revolver is a part of the Metsähovi pillar network (Fig. 2).

Antennas were attached to the pillars using a level stainless steel platform, casted permanently on top of the concrete pillars. We levelled the platforms with the spirit level when attaching the platform. The accuracy of the level is from 0.5 to 0.75 mm/m. If we take into account the construction work, the accuracy of the level of the platform is about 1 mm/m.

To attach an antenna to the platform, there is a 3/8” hole for a specifically manufactured bolt. The centring system tolerances follow ISO 286-2 tolerances H7 and h7 for holes and bolts. The maximum influence of centring and tilting on the residual offsets is 0.1 mm. This is the limit value for the accuracy we can achieve due to the centring and tilting uncertainties.

3.3 Measurements in 2014

The eight Ashtech Dorne Margolin Choke Ring antennas in our validation experiment were calibrated by Geo++ in 2009, and as part of the EMRP SIB60 project (Pollinger et al. 2015), at Hannover University IfE using the robot calibration, and at Bonn University in the anechoic chamber, in 2013–2014 (Table 2). Besides three individual absolute calibration sets, we used IGS08-1816 (Schmid et al. 2015) type absolute calibration tables for the antennas. Thus, we obtained four different calibration sets in comparison: IGG, Bonn University, anechoic chamber; IfE, Hannover University, robot; Geo++, robot; and IGS08 type.

Fig. 2
figure 2

Revolver test network is a part of the Metsähovi local network (background photograph: Google Earth 2014.07.26, \(60^\circ 13^\prime 24^{\prime \prime }\), \(24^\circ 23^\prime 38^{\prime \prime }\))

Full size image
Table 3 Antennas on pillars
Full size table

In our measurements from July to August 2014 (DOY 185–224), we used for the first time the new Revolver network and one older concrete pillar about 14 m from Revolver (number 440 in Fig. 2). The session plan is shown in Table 3. Each antenna visited every pillar at least twice, and each antenna was in a \(180^\circ \) rotated position in at least four sessions. Some sessions were repeated. We gathered a total of 23 complete 24-h sessions with a 5-s recording interval and the receivers’ cut-off angle set at zero. We performed the preliminary processing of the data after each session in order to be able to repeat bad sessions. Only one session was repeated for this reason.

The only difference between the sessions was the change of an antenna on the pillar, while at some pillars the orientation of the antenna was changed according to our measurement plan. Other circumstances affecting the coordinates, i.e. receivers, cables, pillars and multipath environment, remained the same from session to session.

4 Validation process

The calibration validating strategy is presented in Fig. 3. It has two mains steps: processing the phase observations for the daily coordinates and using the daily coordinates as observations for residual offset estimation. We processed the daily solutions with Bernese 5.2 (Dach et al. 2015) software separately for each frequency and each calibration set and saved them into SINEX files. After that, the daily coordinates, together with their covariance matrices, were used in residual offset estimation (Sect. 2.3) in our software. The decision to validate the calibrations was based on the statistical testing (Sect. 2.4).

Fig. 3
figure 3

The validating process (the yellow parts were performed with Bernese and the blue parts with our own software)

Full size image
Table 4 Data sets used for validating the calibrations
Full size table

The coordinate variation of the daily solutions was investigated before the main task, validating the calibrations by estimating the residual offsets (Sect. 5.1). The repeatability of the validating process is tested by comparing the validating results of the old (2011) and the new (2014) measurements (Sect. 6.3).The impact of the residual offsets was studied by comparing the daily solutions with and without corrections due to the residual (Sect. 7), and comparing the results with ground truth (Sect. 7.1).

5 Input data for validation, daily solutions with Bernese software

Our data processing strategy was the double-difference approach. We computed separately L1 and L2 solutions with Ife, Hannover University robot, Bonn University chamber, Geo++ individual absolute calibration tables and IGS type absolute calibration tables, and we produced separate solutions with cut-off angles of \(10^\circ \) and \(15^\circ \). Because there seemed to be no significant differences between the solutions with cut-off angles of \(10^\circ \) and \(15^\circ \) in our case, we chose the daily solution sets with cut-off angle of \(10^{\circ }\) for the subsequent residual offset estimation. As a result of the Bernese processing, we get 10 data sets for validation. The data sets are presented in Table 4. The name of the data set is referred to in subsequent figures.

We used the IGS final orbits and Earth orientation parameters. The observables were screened before ambiguity resolution. Ambiguities were solved using the sigma strategy (Dach et al. 2015). The troposphere was modelled using the global mapping function (Boehm et al. 2006). Because of the short distances between pillars, we had no need to estimate the site-specific troposphere parameters. The datum was defined by constraining one of the pillar points (440) to its ITRF2008 coordinates in mid-epoch of the measurement campaign.

During processing we used calibration tables and the antenna orientation files. Bernese software is capable of taking into account the antenna’s orientation when it uses the calibration tables (Dach et al. 2015).

5.1 Investigation of daily variation

We investigated the daily residuals and the influences of the rotations on the coordinates by calculating the network solution without estimating the offset parameters.

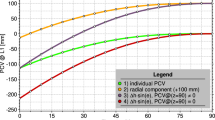
The daily solutions for all the points varied very little in our case, because we had high-quality antennas and calibrations for them. All of the daily solutions were within 1 mm when absolute individual calibration tables were used (Fig. 4).

Fig. 4
figure 4

The daily variation of coordinates on all pillars organized by day of the year. Sample residuals were calculated with L1 frequency and IfE calibration tables

Full size image

We had four pillar points (14000, 14060, 14120 and 540), on which two of the eight antennas in turn were in a \(180\,^{\circ }\) rotated position (Table 3). The pillar-wise variation in the daily solutions in the North component is shown in Fig. 5. A similar effect can be seen in the East component, too.

Fig. 5
figure 5

The daily variation in the North components on pillars 14,000 (green), 14,060 (blue), 14,120 (black) and 504 (red) with the L1 data sets. Dots: antennas were in the normal position; circles: antennas were in a \(180\,^{\circ }\) rotated position

Full size image
Fig. 6
figure 6

The daily variation in the North components on pillars 14,000 (green), 14,060 (blue), 14,120 (black) and 504 (red), organized by antenna with L1 data sets. Dots: antennas were in the normal position; circles: antennas were in a \(180\,^{\circ }\) rotated position

Full size image

The coordinate time series residuals at these pillars show the influence of the residual offsets when the antennas were rotated. The antenna orientation tables were in use during Bernese processing, and so the results should not include any jumps due to the antenna orientation. The jump between sessions when the antenna orientation was different indicates the residual offset of the antennas. The size of the jump is approximately twice the size of residual offset.

Table 5 Residual offsets with 1% significance level t test statistics (the numbers in bold are interpreted as being significant)
Full size table
Fig. 7
figure 7

The new residual offsets (absolute residual offsets for the North and the East components and relative offsets for the Up component) from reprocessed data for all antennas in 2011. The first eight antenna types: 3, 5, 6, 7, 11, 12, 22 and 40, are LEIAR25.R4 LEIT, and the next eight antenna types: 94, 54, 61, 70, 72, 59, 63 and 88, are ASH700936C_M NONE, and the type of the antenna 95 is ASH700936D_M NONE

Full size image

The difference between the rotated and normal position is clearest when the IfE, Hannover University robot calibration tables are used. The variation due to changing the antenna on pillar was small, but still the rotation reveals the remaining systematic offset. The variation with IGS08 type calibrations was larger, and the systematic effect was difficult to see without organizing the residuals by antenna (Fig. 6). The systematic variation when using the Geo++ calibration tables and the IGG, Bonn University chamber calibration tables was small and statistically insignificant.

6 Residual offset estimation

In order to estimate residual offsets, we used in-house software that read coordinates and covariances from the SINEX files and performed least squares network adjustments with additional offset parameters, as explained in Sect. 2.3.

The absolute North and East components and the relative Up component of the offset vector with 99% confidence regions are estimated separately for each data set in Table 4. The estimated residual offsets are presented in Table 5 and in Figs. 7, 8 and 9.

Fig. 8
figure 8

The residual offsets (absolute residual offsets for the North and the East components and relative offsets for the Up component) of L1, using four different calibration sets

Full size image
Fig. 9
figure 9

The residual offsets (absolute residual offsets for the North and the East components and relative offsets for the Up component) of L2, using four different calibration sets

Full size image

6.1 Residual offsets 2011

The completed data set, measured in 2011, were reprocessed with Bernese 5.2 using the parameters presented in 5. The input data for residual offset estimation include 28 SINEX files and 17 antennas for two frequencies. The original configuration (Kallio et al. 2012) did not have any rotated position. In the completed set, two antennas were in the rotated position for test purposes in one session, which made it possible to estimate the absolute residual offsets of all antennas (Fig. 7) for the North and East components. The results were too sensitive to the observations of only one session and not precise enough for decision (Table 5). However, the relative residual offsets were more precise and usable.

We found significant differences between the two antenna types in the L2 residual offsets in the Up component. The relative offsets can be used for the North and the East components in campaigns, in which the tested antennas are used together.

6.2 Residual offsets 2014

The Bernese processing was carried out separately for two frequency and four calibration tables. Thus, we analysed eight different data sets with 23 SINEX files and eight antennas in each of them. In residual offset estimation, we obtained the absolute residual offsets for the North and the East components and the relative residual offsets for the Up components for eight antennas.

The North and the East components of the antenna residual offsets were systematically negative when we used IfE, Hannover University robot calibration tables. The residual offsets were small but statistically significant. If we had only the IfE, Hannover University, robot calibration tables, we might then suspect that the validation procedure generated a bias in all the offsets. However, when we used IGG, Bonn University or Geo++ tables, the North and the East components of the offsets were much smaller and the signs of offsets were opposite to those found on the IGG, Bonn University anechoic chamber table. The IGS08 type calibration tables did not fit for all antennas as well, and the signs of the offsets did not systematically have the same sign.

The differences between the calibration sets were clear, and the residual offsets indicate the systematic effect on the robot or chamber calibration process or when calibrating the robot.

When we look at the Geo++ calibration, antenna 63 had a different sign in the North and East components than the other antennas. The Geo++ calibration of antenna 63 was performed at a different time than the other antennas. We do not know whether the robots were calibrated between antenna calibrations.

6.3 Comparison of the results of antenna tests in 2011 and 2014

The antennas used in the two validation measurements from 2011 and 2014 were different. Seven ASH700936C_M antennas and one ASH700936D_M antenna were used in both campaigns. The Leica antennas used in 2011 are now in permanent stations and were not available during the Revolver measurements. Also, one Ashtech antenna (11,761) is now at a permanent station IGS point METS.

When comparing the two validation tests, the relative offsets were more suitable than the absolute offsets because there was only one session with rotated antenna positions in the data set for the 2011 validation test. The offsets and covariance matrices were converted to refer to the mean of the offsets of the eight antennas. As comparison, we used the Geo++ tables because in 2011 there were antennas that had only Geo++ individual absolute calibration tables.

Fig. 10
figure 10

Comparison of the relative residual offsets achieved in 2011 and 2014. The offsets are relative to the mean of the offsets of the presented eight antenna

Full size image

The relative residual offsets from the reprocessed (2011) and the new (2014) determination are presented alongside one another for those antennas, which were common in both tests with 99% significance error bars, in Fig. 10.

The agreement of the relative residual offsets for the reprocessed three pillar test in 2011 and the results achieved in 2014 in Revolver test field was good. The solutions for the relative residual offsets in the Up component fit particularly well.

The better measurement configuration and more sessions per antenna are the reasons for the smaller confidence regions in 2014 than in 2011. The redundancy, degree of freedom in adjustment, in 2014 was 439, while in the 2011 reprocessing it was 112. The critical values, t-statistics in Table 5, for accepting the zero hypothesis, were quite small in 2014, and even offsets of < 0.1 mm will be interpreted as significant. In 2011 the limit was about 0.5 mm.

7 Impact of correcting residual offsets

Correcting the daily coordinates with residual offsets decreases the variation of coordinates significantly. The millimetre level variation in 2014 campaign shrank to sub-millimetre level (Fig. 11).

7.1 Comparison with ground truth

The validation method does not require the ground truth, but in order to illustrate the influence of the residual offsets on the height differences, we chose two antenna pairs: the antenna pair with the biggest difference in residual offsets in the Up component and the other pair for comparison. We compared GPS height differences with the ground truth measured with precise spirit levelling. We subtracted the actual height differences from the height differences obtained using the daily Bernese solutions before and after correcting the estimated residual offsets. The GPS height differences minus levelled height differences were calculated for different pillar pairs between antenna pairs 63–88 and 94–54 when the IGS08, type L1 calibration set was used in data processing. Also, the geoid height difference between the points was applied.

Fig. 11
figure 11

The daily variation of coordinates in global system on all pillars organized by day of the year. Sample residuals calculated with L1 frequency and IfE calibration tables. Grey: Daily variation without residual offset corrections. Red: Daily variation with residual offset corrections

Full size image
Fig. 12
figure 12

Height differences between antennas compared with the ground truth. The blue points show the difference when using session solutions and the red points the differences when the session solutions have been corrected due to the residual offsets

Full size image

The GPS height difference with and without the residual offset compared with the levelled height difference demonstrated the bias due to the antenna calibration. In Fig. 12, the respective pillar pairs were plotted below the solution.

Most of the peaks in the figures were related to the same pillar 440, which was 12 m outside the Revolver. It was not the same type of pillar as the other pillars, ad it was situated nearer the buildings and a little bit lower. It is important to see that the estimated residual offset was not affected by the systematic bias in the coordinates of that particular pillar point. The same bias was present in the coordinates during every session, it remained “constant” session after session, and it was invisible in the coordinate time series. To observe the site (but not antenna)-specific bias, we used precision levelling, which gave us the ground truth. The residual offset difference between antennas 63 and 88 was approximately 1.5 mm. After applying a correction, the difference from the ground truth was < 0.5 mm. The residual offset difference between antennas 94 and 54 was only 0.4 mm, and the height difference agreed well with ground truth without correction, but was even better after correction. We noted similar behaviour with all possible antenna pairs and calibration tables used in the validation.

8 Comparing and mixing the calibration sets

In order to obtain separate residual offsets for each calibration set, we did not mix the calibration sets in the daily solutions. However, we can compare the calibration sets by comparing the residual offsets of the sets. The North and East components of the offsets are directly comparable, but the Up component is related to the mean of the Up components of the antennas in the data set and shows only how well the antennas in the calibration set fit together.

In order to see the influence of mixing the calibration sets or different calibration sources on the coordinates, we performed the zero baseline calculation. We used the same RINEX data at both ends of the zero baselines and applied three different calibration sets at the other end. For the fixed end of the baseline, we used the anechoic chamber calibration tables from Bonn University. The zero baselines are thus from the anechoic chamber calibration to the robot or type calibrations. Kinematic zero baseline processing was performed with Bernese 5.2 software for all antennas (in days/antenna: 185/63 189/72 191/94 194/88 196/95 198/54 200/59 203/70) for the data from the pillar 14240 separately with L1 and L2 frequencies. The coordinate differences between the tables depend on the satellite geometry. In order to obtain comparable satellite geometry for all days, we applied time shifts of 3:56 min per day relative to day 185 before printing (Fig. 13). Because the same observation data (same RINEX file) were at both ends of the zero baseline vector, the multipath and other site-specific error sources were all eliminated from the coordinate differences of the vector, and we can expect that the difference comes from the antenna tables.

Fig. 13
figure 13

The difference between the robot calibration, or type calibration sets, and the anechoic chamber calibration set for all antennas participating in the 2014 campaign for L1 (left) and L2 (right) frequencies. The figures show the kinematic coordinate differences at zero baseline from the base (data from the IGG, Bonn University tables) and rovers (same data with other calibration tables). Time shifts of about 4 min per day were applied to the solutions before printing

Full size image

The kinematic zero baseline clearly shows the temporal difference between the calibrations in the coordinate domain. The epoch-by-epoch differences in the robot calibration relative to the anechoic chamber calibration for the L1 and L2 frequencies are presented in Fig. 13. The differences in the North and East components were less than a millimetre, but in the Up component the difference could systematically be in the order of several millimetres. The calibration tables from the same source had the same pattern, which depends on the satellite geometry. In the most precise applications, it is not advisable to mix the tables from different calibration sources.

The deviation of the zero baseline components for the different antennas when using the same calibration set suggests the uncertainty of the coordinate differences in short baseline vectors due to the antenna calibration. The deviation within the individual robot calibration sets are small, while the median ranges of differences within the calibration sets for L1 were < 0.8 mm in the North and East components and < 1.6 mm in the Up component. For L2, the ranges were larger: 1–2 mm for the horizontal components and about 2 mm for the Up component. For type calibration, the horizontal ranges were 1–2 mm, but they were no more than 1–1.5 mm in the vertical direction. The relatively small differences in the type calibration set indicate that the ASH700936C_M and ASH700936D_M antennas were similar. If we calculate the mean differences for the North and East components per antenna, we can see that they compared well to the estimated residual offsets of the calibration sets (Figs. 8, 9). The Up component in the robot calibration and type calibration tables was systematically different compared to the anechoic chamber calibrations in the case of our antennas. Temporal differences in the site coordinates could be up to 8 mm in L2 (Fig. 13). The mean difference in the 24-h data for these antennas in L1 was approximately 2 mm, whereas in L2 it was up to 4 mm.

9 Discussion

The limit value for rejecting the antenna table (claiming that it is not valid) should be much larger than the t-statistics. The standard deviation in the single elevation and azimuth-dependent PCC correction, provided by calibration institutions, is 0.2–0.5 mm. The practical limit for rejecting the table could not be < 0.1–0.2 mm.

The influence of the residual offsets on the distances calculated based on the coordinate differences between antennas was insignificant in the case of our antenna set when tables from the same calibration institution were used. The reason was that the differences in residual offsets between antennas were almost zero. The influence on the height differences can be seen if we choose the “wrong” antenna pair, like in Fig. 12 with antennas 63 and 88. The influence of the residual offsets in the Up component can also be seen with respect to the distances when the height difference between the points was large.

The differences between the calibration sets of the different institutions, which we found here, concern the antennas and calibration tables used in the validation. The test gives not a general statement on the quality of the different calibration institute, and the findings may vary for different antennas. The differences give a suggestion of the uncertainty due to the antenna calibration.

10 Conclusion

During the EMRP SIB60 project, we developed an antenna test field and a procedure to validate the antenna calibration tables, which is based on circulating the antennas on concrete pillars. We tested the procedure and compared different calibrations using the data from eight Ashtech choke ring antennas, for which we had individual absolute calibration tables from three different institutes (IfE, Bonn, Geo++) and type calibration tables of IGS08.

We have shown that it is possible to find the residual offsets of antennas at the sub-millimetre level, and it is likewise possible to separate the residual offset from the “constant” biases in the coordinates in our antenna-validating procedure. After using offset corrections, the agreement of the estimated coordinates and ground truth was better and the variation in session solutions was smaller.

We found significant systematic differences between the calibration sets provided by the different institutions. The influence of the difference on the coordinates was small but systematic. We calculated the differences for the eight antennas by computing zero baselines between the calibration tables. The same comparison can easily be performed for other antennas that have different calibrations.