Forward calculation of gravity and its gradient using polyhedral representation of density interfaces: an application of spherical or ellipsoidal topographic gravity effect

Abstract

A density interface modeling method using polyhedral representation is proposed to construct 3-D models of spherical or ellipsoidal interfaces such as the terrain surface of the Earth and applied to forward calculating gravity effect of topography and bathymetry for regional or global applications. The method utilizes triangular facets to fit undulation of the target interface. The model maintains almost equal accuracy and resolution at different locations of the globe. Meanwhile, the exterior gravitational field of the model, including its gravity and gravity gradients, is obtained simultaneously using analytic solutions. Additionally, considering the effect of distant relief, an adaptive computation process is introduced to reduce the computational burden. Then features and errors of the method are analyzed. Subsequently, the method is applied to an area for the ellipsoidal Bouguer shell correction as an example and the result is compared to existing methods, which shows our method provides high accuracy and great computational efficiency. Suggestions for further developments and conclusions are drawn at last.

Appendices

A Appendix

In order to map the partition on the icosahedral facets outward to a certain surface, geocentric radiuses of the surface under an equal-angle grid are firstly determined (Fig. 14). As for the terrain surface of the Earth, discussed by Balmino et al. (2011) and Tenzer et al. (2009), given some systematic approximations adopted, the geocentric radius R could be expressed as $R=r+H+N$ without introducing large error, in which r means the geocentric radius of the Earth’s reference sphere or ellipsoid, H and N are the corresponding altitude and geoid undulation. If the radius r is latitude-dependent, the Earth’s ellipticity can be easily taken into account by $r=ab\sqrt{{a}^{2}\hbox {sin}^{2}{\theta }_{c}{+b}^{2}\cos ^{2}{\theta }_{c}}$, where $\theta _c$ is the geocentric colatitude, a and b are the semimajor and semiminor axes of the Earth’s reference ellipsoid, respectively.

Fig. 14

A diagrammatic sketch of the relationship between the PGIM’s vertices and an equal-angle grid. In which, m is a vertex of the PGIM, and $e_{1}$ to $e_{4}$ are four data points of the equal-angle grid. The geocentric radius of m is interpolated by these four points’ radiuses

After determining geocentric radiuses under the equal angular grid, radiuses of the PGIM’s vertices are interpolated using the spherical bilinear interpolation method (Wang et al. 2006) as following. Geocentric radius ${r}_{ave}$ of a PGIM’s vertex ${m}\left( {\phi _{m}, {\theta }_{m} } \right)$ could be determined by grid points closed to m. Provided $e_{1}(\phi _{1},\theta _{1},r_{1}),e_{2}(\phi _{2},\theta _{2},r_{2}),e_{3} (\phi _{3},\theta _{3},r_{3})$ and $e_{4}(\phi {4},\theta {4},r_{4})$ are four data points of the equal angular grid which form the smallest spherical quadrangular region with m in it (Fig. 14). The interpolation can be performed as:

$$\begin{aligned}&r_{\mathrm {ave}} \left( {\phi _{m} ,\theta _{m} } \right) =\left( \hbox {Acos}\phi _{m} +B\theta _{m} +C\theta _{m} \cos \phi _{m} +D \right) /\varDelta \nonumber \\ \end{aligned}$$

(1)

$$\begin{aligned}&{A} =\Delta {\theta }_{1} \left( {r}_{4} {-r}_{2} \right) +{\theta }_{2} \left( {r}_{1} {-r}_{3} \right) \end{aligned}$$

(2)

$$\begin{aligned}&{B}=\left( {r}_{1} {-r}_{2} \right) \cos \phi _{1} +\left( {r}_{4} {-r}_{3} \right) \cos \phi _{2} , \end{aligned}$$

(3)

$$\begin{aligned}&{C}= r_{3}+r_{2} {-r}_{1} {-r}_{4} , \end{aligned}$$

(4)

$$\begin{aligned}&{D}=\theta _{2} \cos \phi _{2} {r}_{3} {-\theta }_{2} \cos \phi _{1} {r}_{1}+\theta _{1} \cos \phi _{1} {r}_{2}\nonumber \\&\qquad \quad -\,\theta _{1} \cos \phi _{2} {r}_{4} , \end{aligned}$$

(5)

$$\begin{aligned}&\varDelta =\left( {\theta }_{2} {-\theta }_{1} \right) \left( {\cos \phi _{2} -\cos \phi _{1} } \right) . \end{aligned}$$

(6)

Discussed by Du et al. (2012), the interpolation could be taken as an average and error reduction process of the equal angular data set. The error of the interpolation is very low if the resolution of the original grid data is very high. And Tsoulis et al. (2003) pointed out that the resulting surfaces had the geometrical constraint to pass through the exact positions of the original data. Therefore, the error introduced by the interpolation is ignored here.

B Appendix

The exterior gravitational potential, along with its vectors and gradient tensors, of a polyhedron can be forward calculated using the algorithm proposed by Werner and Scheeres (1996). The algorithm is derived in closed form so that there is no error produced during the process of forward calculating theoretically. Assuming the distribution of density inside a polyhedron, expressed as $\rho$ in the following equations, is constant, all facets of the polyhedron are triangles and vertices of a facet are ordered anticlockwise as one observes the facet from outside of the polyhedron. Then the polyhedron’s exterior gravitational potential V, gradient $\nabla {V}$ and gradient tensors $\nabla \nabla {V}$ are given as below, in which G is the gravitational constant. Gradient directions here are x, y and z in the Cartesian coordinate system.

$$\begin{aligned}&V=\frac{1}{2}{G}\rho \left( {\sum \nolimits _{e=1}^{n}} \vec {r}_{e}\cdot {\mathbf{E}}_{e} \cdot \vec {r}_{e} \cdot {L}_{e}\right. \nonumber \\&\qquad \left. +{\sum \nolimits _{f=1}^{m}} \vec {r}_{f}\cdot {\mathbf{F}}_{f}\cdot \vec {{r}_{f} }\cdot {\omega }_{f} \right) , \end{aligned}$$

(7)

$$\begin{aligned}&\nabla V = -G \rho \left( {\sum \nolimits _{e=1}^{n}{\mathbf{E}}_{e}\cdot \vec {{r}_{e} }\cdot L_{e} +\sum \nolimits _{{f=1}}^{m} {\mathbf{F}}_{f} \cdot \vec {r}_{f} \cdot {\omega }_{f} } \right) , \nonumber \\ \end{aligned}$$

(8)

$$\begin{aligned}&\nabla \nabla V = -G\rho \left( \sum \nolimits _{e=1}^{n} {\mathbf{E}}_{e} \cdot {L}_{e} +\sum \nolimits _{f=1}^{m} {\mathbf{F}}_{f} \cdot {\omega }_{f} \right) . \end{aligned}$$

(9)

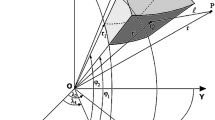
in which m and n represent number of facets and edges of the polyhedron, respectively. This feature indicates that the exterior gravitational fields of a polyhedron could be expressed as a sum of effect of all its facets and edges. For instance, as the sketch of a polyhedron shown in Fig. 15, $\vec {{r}_{f} }$ and $\vec {{r}_{e} }$ stand for two vectors from the observation point P to a triangular facet of the polyhedron, ABC, and one of its edges, CA. Meanwhile, ${\mathbf{F}}_{f}$ and ${\mathbf{E}}_{e}$ represent tensor products of facet and edge accordingly. ${\omega }_{f}$ and ${L}_{e}$ are two coefficients decided by the relative position between the observing point P and the face and edge. The expressions mentioned above are given by

Fig. 15

A diagrammatic sketch of a tetrahedron ABCD placed in the Cartesian coordinate. P is the observation point, $\vec {r}$ represents vector, and $\vec {n}$ is a normal vector

$$\begin{aligned} {\mathbf{E}}_{e}= & {} {\hat{n}}_{1} {\hat{n}}_{ca} +{\hat{n}}_{2} {\hat{n}}_{ac},\end{aligned}$$

(10)

$$\begin{aligned} {\mathbf{F}}_{f}= & {} {\hat{n}}_{f} {\hat{n}}_{f} , \end{aligned}$$

(11)

$$\begin{aligned} {L}_{e}= & {} \frac{{\bar{r}}_{i} +{\bar{r}}_{j}+ d_{ij}}{{r}_{i} + {r}_{j} {-d}_{ij}} , \end{aligned}$$

(12)

$$\begin{aligned} \omega _{f}= & {} 2\tan ^{-1}\nonumber \\&\times \frac{\vec {r}_{i} \cdot \vec {r}_{j}\times \vec {r}_{k}}{{\bar{r}_{i}}{\bar{r}}_{j} \bar{r}_{k}+ \bar{r}_{i}\left( {\vec {r}_{j} \cdot \vec {r}_{k} } \right) + \bar{r}_{j} \left( {\vec {r}_{k} \cdot \vec {r}_{i} } \right) + \bar{r}_{k} \left( {\vec {r}_{i} \cdot \vec {r}_{j} } \right) }.\nonumber \\ \end{aligned}$$

(13)

In equations above, $\vec {r}_{i}$, $\vec {r}_\mathrm{j}$ and $\vec {r}_\mathrm{k}$ represent three vectors from P to the face’s vertices C, A and B, with its module $\bar{r}_{i}$, $\bar{r}_{j}$ and $\bar{r}_{k}$, respectively. $\vec {n}_\mathrm{f}$ stands for the outside normal vector of the face ABC. It equals the normalized vector of $\overrightarrow{AB}\times \overrightarrow{BC}$. $d_{ij}$ represents the distance between the ends of vectors $\vec {r}_\mathrm{i}$ and $\vec {r}_{j}$ which equals the length of edge CA here. Moreover, $\overrightarrow{n}_{1}$ and $\overrightarrow{n}_{2}$ are two outside normal vectors of edge CA that lie on the face ABC and face ACD, respectively. These two vectors could be obtained by the cross-product between a face’s outside normal vector and one of its edge’s normal vector accordingly. For instance, $\overrightarrow{n}_{1}$ equals $\overrightarrow{n}_{f} \times \overrightarrow{n}_{ca}$. Expressions such as $\mathbf{F}_{f} ={\hat{n}} _{f} {\hat{n}} _\mathrm{f}$ means the tensor product of two normal vectors which is a $3\times 3$ matrix. For each facet of the polyhedron, it has a ${\mathbf{F}}_{f}$ and $\omega _{f}$ associated with. And each edge has an individual ${\mathbf{E}}_e$ and ${\mathbf{L}}_{e}$. Subsequently, the gravitational field of the polyhedron could be obtained by calculating the sum of effects of all its facets and edges.

As all computations are conducted in the Cartesian coordinate, the outcome gravitational fields are with respect to the Cartesian coordinate as well. A coordinate transformation matrix R is added into Eqs. (8) and (9), as we need to forward calculate the gravitational fields of a polyhedron in directions reference to the spherical coordinate. Given the position of the observation point P in spherical coordinates $\left( {\phi _P ,\theta _P ,\bar{r}_{P}}\right)$, then R is given by

$$\begin{aligned} {\mathbf{R}}=\left| {{\begin{array}{ccc} {\sin \theta _P \cos \phi _P }&{}\quad {\sin \theta _P \sin \phi _P }&{}\quad {\cos \theta _P } \\ {\cos \theta _P \cos \phi _P }&{}\quad {\cos \theta _P \sin \phi _P }&{}\quad {-\hbox {sin}\theta _P } \\ {-\hbox {sin}\phi _P }&{}\quad {\cos \phi _P }&{}\quad {0} \\ \end{array}}} \right| . \end{aligned}$$

(14)

Subsequently, gradient and gradient tensors of a polyhedron’s gravitational potential oriented in the directions $\phi$, $\theta$ and r are expressed as below.

$$\begin{aligned} \nabla V&=-G\rho \left( \sum \nolimits _{e=1}^n {\mathbf{E}}_{e} \cdot \vec {r}_{e}\cdot {\mathbf{R}}^\mathrm{T}\cdot {L}_{e} \right. \nonumber \\&\qquad \left. +\,\sum \nolimits _{f=1}^{m} {\mathbf{F}}_{f}\cdot \vec {r}_{f} \cdot {\mathbf{R}}^\mathrm{{T}}\cdot \omega _{f} \right) , \end{aligned}$$

(15)

$$\begin{aligned} \nabla \nabla V&=-G\rho \left( \sum \nolimits _{{e=1}}^{n} {\mathbf{R}}\cdot {\mathbf{E}}_{e}\cdot {\mathbf{R}}^\mathrm{{T}}\cdot {L}_{e} \right. \nonumber \\&\qquad \left. +\,\sum \nolimits _{f=1}^{m} {\mathbf{R}}\cdot {\mathbf{F}}_{f} \cdot {\mathbf{R}}^\mathrm{{T}}\cdot \omega _{f} \right) . \end{aligned}$$

(16)