1 Introduction

GPS-based high-low satellite-to-satellite tracking (hl-SST) is a well-established method to map the Earth’s gravity field since the launch of the CHAllenging Minisatellite Payload (CHAMP) satellite mission (Reigber et al. 1998). Later on, hl-SST was also exploited by the Gravity Recovery And Climate Experiment, GRACE (Tapley et al. 2004), and the Gravity Field and Steady-State Ocean Circulation Explorer, GOCE (Drinkwater et al. 2006) satellite missions. This technique is particularly useful to map the long-wavelength part of the Earth’s gravity field (Reigber et al. 2003).

Until now, gravity field is typically modelled on the basis of satellite kinematic orbits computed as an intermediate product (e.g. Baur et al. 2014). In the last decade, several techniques have been developed to exploit the kinematic orbits for gravity field modelling (e.g. Baur et al. 2014). In the context of this study, we will focus on the average acceleration approach (Ditmar and van Eck van der Sluijs 2004). This approach has been successfully applied in the compilation of a number of gravity field models, including the DEOS_CHAMP-01C_70 model, derived from CHAMP data (Ditmar et al. 2006), and the DGM-1S model, which is based on data from the GRACE and GOCE satellite gravity missions (Farahani et al. 2013). These models use kinematic orbits that were derived from GPS hl-SST data by a precise point positioning approach (Švehla and Rothacher 2005) followed by a three-point double-differentiation scheme. Hereafter, this approach is referred to as the ‘orbit method’. In this approach, the quality of the gravity field model critically depends on the quality of the kinematic orbits.

In general, kinematic orbits are sensitive to the observation geometry and various systematic errors, e.g. mismodelling of the antenna phase centre variations (PCV) and the high-order ionosphere-induced errors. In recent years, dedicated algorithms were developed to mitigate the impact of those errors on the kinematic orbits and corresponding gravity field solutions (Jäggi et al. 2009, 2011, 2015; Bock et al. 2011). However, the kinematic orbits may still suffer from some unknown or mismodelled systematic errors, as well as artefacts that are difficult to be modelled for Low Earth Orbiters (LEO), e.g. hardware delays from both the GPS satellites and GPS receivers, near-field multipath effects, etc.

The GPS carrier phase measurements were already applied to derive relative vehicle accelerations in airborne gravimetry (Jekeli and Garcia 1997). In this research, we propose to use a somewhat similar approach in gravity field modelling from GPS data collected by satellites. The basic idea is to estimate average satellite accelerations directly from the GPS carrier phase measurements using an epoch-differenced scheme. Hereafter, this approach is referred to the ‘phase method’. The main benefit of this approach is that no phase ambiguity solutions are needed and that systematic errors, which do not change much from epoch to epoch, are largely eliminated. It is worth mentioning that the phase method still requires knowledge of the satellite orbit, as will be shown later. However, this orbit only plays a supporting role.

We demonstrate the added value of the proposed approach using GPS data collected by the GOCE mission. The GOCE satellite was equipped, among others, with two 12-channel dual-frequency Lagrange GPS hl-SST instruments (Intelisano et al. 2008), each consisting of a geodetic-quality GPS receiver and a helix antenna. In this study, GPS data collected in the nominal phase of the GOCE mission spanning the time interval from November 2009 to July 2012 are used and the days with data problems are excluded as proposed in (Visser et al. 2014). The average satellite accelerations derived both from the kinematic orbits and directly from GPS phase measurements are exploited to recover the gravity field. In order to demonstrate the strength of the proposed method more convincingly, we consider two variants of kinematic orbits. One is the officially provided kinematic orbit, i.e. the SST_PKI_2 product (EGG-C 2010; Bock et al. 2014), hereafter denoted as the ESA (European Space Agency) orbit and the orbit method in this case is denoted as the ‘orbit-ESA method’. The other one is computed in house by the PANDA (Position And Navigation Data Analyst) software (Liu and Ge 2003), which was developed at Wuhan University; hereafter, this orbit is denoted as the WHU orbit and the orbit method in this case is denoted as the ‘orbit-WHU method’. To ensure a fair comparison of the orbit method and the phase method, the carrier phase data and measurement models used in the latter one are identical to those adopted when deriving the WHU kinematic orbit.

To assess the quality of the obtained gravity solutions, the gravity field model DGM-1S is used. It is based on GRACE K-Band Ranging (KBR) and GOCE gradiometry data (Farahani et al. 2013), and therefore has a much higher accuracy than the hl-SST-based solutions obtained with either method. In addition, we make an attempt to identify some mass transport signals in the obtained solutions.

The outline of the paper is the following. In Sect. 2, we provide a review of the average acceleration approach and present the functional model of deriving average accelerations from kinematic orbits and GPS phase measurements. In addition, we discuss in that section the inversion of average accelerations into gravity field parameters, with a focus on the data weighting scheme. In Sect. 3, noise in the average satellite accelerations obtained with both the phase and the orbit method is analysed. In Sect. 4, we assess the quality of the derived gravity field models. Finally, Sects. 5 and 6 are left for discussion and conclusions, respectively.

2 Theory

In this research, the average acceleration approach (Ditmar and van Eck van der Sluijs 2004) is used to estimate a model of the Earth’s gravity field. The processing of both kinematic orbits and phase measurements consists of three steps: (1) transforming the input data (kinematic orbits or phase measurements) into a set of residual satellite accelerations with respect to an a priori mean gravity field model; (2) least-squares inversion of the residual accelerations into residual SH coefficients; and (3) restoring the coefficients of the a priori model to obtain the final gravity field model. As the third step is straightforward, we focus below on the first two steps. In Sect. 2.1, we describe the functional models used to derive average satellite accelerations from either kinematic orbits or phase measurements. In Sect. 2.2, we address practical aspects of the computation of the residual accelerations. as well as the inversion of residual accelerations into SH coefficients, with a major focus on the data weighting scheme.

2.1 Functional models

2.1.1 Functional model of the orbit method

Three-dimensional (3-D) average satellite acceleration \({\bar{{\mathbf{a}}}}(t)\) are derived from 3-D satellite position \(\mathbf{r}(t)\) with a 3-point differentiation scheme:

$$\begin{aligned} {\bar{{\mathbf{a}}}}(t)=\frac{\mathbf{r}(t+\Delta t)-2\mathbf{r}(t)+\mathbf{r}(t-\Delta t)}{\left( {\Delta t} \right) ^{2}}, \end{aligned}$$
(1)

where t is the measurement epoch and \(\Delta t\) is the sampling interval. The average acceleration vector \({\bar{{\mathbf{a}}}}(t)\) obtained from Eq. (1) can be interpreted as a 3-D pointwise acceleration vector \(\mathbf{a}(t)\) averaged with weight \(\frac{\Delta t-\left| s \right| }{\left( {\Delta t} \right) ^{2}}\) in the time interval \(s\in \left[ {-\Delta t,\Delta t} \right] \) (Ditmar and van Eck van der Sluijs 2004):

$$\begin{aligned} {\bar{{\mathbf{a}}}}(t)= & {} \int \limits _{-\Delta t}^{\Delta t} {\frac{\Delta t-\left| s \right| }{\left( {\Delta t} \right) ^{2}}\mathbf{a}(t+s\hbox {)d}s} \nonumber \\= & {} \int \limits _{-\Delta t}^{\Delta t} {\frac{\Delta t-\left| s \right| }{\left( {\Delta t} \right) ^{2}}\mathbf{a}^{(g)}(t+s\hbox {)d}s} \nonumber \\&+\int \limits _{-\Delta t}^{\Delta t} {\frac{\Delta t-\left| s \right| }{\left( {\Delta t} \right) ^{2}}\mathbf{a}^{(ng)}(t+s)\hbox {d}s} , \end{aligned}$$
(2)

where \(\mathbf{a}^{(g)}\) and \(\mathbf{a}^{(ng)}\) are gravitational and non-gravitational acceleration of the satellite, respectively. Equation (2) explains the conceptual link between the orbit-based average satellite accelerations on the one hand and the gravitational and non-gravitational forces acting on the satellite on the other hand. Further details of this approach have been presented in (Ditmar and van Eck van der Sluijs 2004).

Fig. 1
figure 1

OMCs of the epoch-differenced carrier phase observations (a) and errors caused by fixing the LEO positions to an a priori kinematic orbit (b) for DOY 306, 2009. The errors of the kinematic orbit are approximated by differences between the kinematic orbit and the reduced-dynamic orbit

Full size image

2.1.2 Functional model of the phase method

The raw observables of dual-frequency GPS carrier phase measurements collected by a GPS receiver on board a LEO are generally expressed as:

$$\begin{aligned} L_1 (t)= & {} \rho (t)+c\cdot \delta t_r (t)-I+\lambda _1 N_1 +M_1 (t)+\varepsilon _1 (t) \nonumber \\ L_2 (t)= & {} \rho (t)+c\cdot \delta t_r (t)-\frac{f_1^{2}}{f_2 ^{2}}I+\lambda _2 N_2 \nonumber \\&+\,M_2 (t)+\varepsilon _2 (t) \end{aligned}$$
(3)

with \(L_{i}\) the carrier phase measurement on frequency \(f_{i}\) (\(i=1,2\)) in unit of length; t the measurement epoch; \(\rho \left( t \right) =\Vert \mathbf{r}^{s}\left( {t-\tau _r^s \left( t \right) } \right) -\mathbf{r}_r \left( t \right) \Vert \) the geometric distance between the phase centre of the GPS satellite emitting antenna \(\mathbf{r}^{s}\left( {t-\tau _r^s \left( t \right) } \right) \) and LEO receiving antenna \(\mathbf{r}_r \left( t \right) \), and \(\tau _r^s \left( t \right) \) the true travel time; c the speed of light in vacuum; \(\delta t_r \) the receiver clock offset; I the ionosphere path delay of first order on \(f_{1}\); \(\lambda _i \) the signal wavelength on frequency \(f_{i}\); and \(N_{i}\) the carrier phase ambiguity. It should be mentioned that antenna phase centre corrections related to both GPS satellite and LEO GPS receiver, GPS satellite clock offsets, the second-order relativistic correction for nonzero orbit ellipticity, gravitational bending, and phase wind up must be applied in the distance computation. The hardware delays from both the receivers and GPS satellites, higher-order ionospheric errors, the carrier phase multipath, and other systematic errors are grouped into the term \(M_{i}\). Finally, \(\varepsilon _i \) denotes the random noise. In GPS positioning applications, the ionosphere-free linear combination (subscript ’IF’) is commonly used to eliminate the first-order ionosphere path delay:

$$\begin{aligned} L_{\textit{IF}} (t)= & {} \frac{f_1^{2}}{f_1^{2}-f_2^{2}}L_1 (t)-\frac{f_2^{2}}{f_1^{2}-f_2^{2}}L_2 (t)\nonumber \\\approx & {} {2.546}L_1 (t)-1.546L_2 (t). \end{aligned}$$
(4)

Inserting Eq. (3) into Eq. (4) yields

$$\begin{aligned} L_{\textit{IF}} (t)= & {} \rho (t)+c\cdot \delta t_r (t)+\lambda _{\textit{IF}} N_{\textit{IF}}\nonumber \\&+\,M_{\textit{IF}} (t)+\varepsilon _{\textit{IF}} (t), \end{aligned}$$
(5)

where \(\lambda _{IF} =\lambda _1 \), \(N_{IF} =\frac{f_1^{2}}{f_1^{2}-f_2^{2}}N_1 -\frac{f_1 f_2 }{f_1^{2}-f_2^{2}}N_2 \) is the corresponding carrier phase ambiguity, \(M_{IF}\) is the systematic error, and \(\varepsilon _{IF} \) denotes the random noise. It should be noted that the ambiguity \(N_{IF}\) is no longer an integer quantity. Furthermore, the noise is roughly a factor of three higher than in the original single-frequency measurements of Eq. (3). In this study, GPS satellite positions and clock offsets are taken from the International GNSS Service (IGS) (Dow et al. 2009) or its analysis centres and considered to be known quantities. Linearization around the approximate positions of the LEO’s centre of mass (COM) yields

$$\begin{aligned} L_{\textit{IF}} (t)= & {} \rho _0 (t)-\mathbf{e}(t)\cdot \delta \mathbf{r}(t)+c\cdot \delta t_r (t)\nonumber \\&+\lambda _{\textit{IF}} N_{\textit{IF}} +M_{\textit{IF}} (t)+\varepsilon _{IF} (t), \end{aligned}$$
(6)

where \(\rho _0(t)=\Vert \mathbf{r}^{s}({t-\tau _r^s(t)})-\mathbf{r}_{0r}(t)\Vert \) is the approximate geometric distance; \(\mathbf{r}_{0r}(t)=\mathbf{r}_{0com}(t)+R(t)\cdot \mathbf{r}_{pco} \) is the approximate GPS receiver phase centre position vector, and \(\mathbf{r}_{0com} \) is the approximate LEO COM position vector taken from an a priori orbit, \(\mathbf{r}_{pco} \) is the phase centre offset with respect to LEO COM and R is the rotation matrix from the frame of \(\mathbf{r}_{pco} \) to that of \(\mathbf{r}_{0com} \); \(\mathbf{e}(t)=\frac{\mathbf{{r}}^{s}({t-\tau _r^s(t)})-\mathbf{r}_{0r}(t)}{\Vert \mathbf{r}^{s}({t-\tau _r^s(t)})-\mathbf{r}_{0r}(t)\Vert }\) is the so-called line-of-sight vector; and \({\updelta }\) r(t) is the LEO COM position correction vector. We rewrite Eq. (6) as

$$\begin{aligned} l_{IF} (t)=A\hbox {(t)}{} \mathbf{X}(t), \end{aligned}$$
(7)

where \(l_{IF} \left( t \right) =L_{IF} \left( t \right) -\rho _0 \left( t \right) \) is the residual observation (observed minus computed value); X is the unknown parameter vector, which consists of three LEO position coordinate corrections (one for each component) per epoch, one receiver clock offset correction per epoch and one ambiguity correction per GPS tracking arc without cycle slips; and A is the corresponding design matrix.

The ionosphere-free phase observations are linearized epoch by epoch according to Eqs. (6) and (7). Considering a GPS tracking arc without gaps, the epoch-differenced observations can be established as

$$\begin{aligned} l_{IF} (t,t-\Delta t)= & {} l_{IF} (t)-l_{IF} (t-\Delta t) \nonumber \\= & {} A(t)\mathbf{X}(t)-A(t-\Delta t)\mathbf{X}(t-\Delta t) \nonumber \\= & {} A(t)(\mathbf{X}(t)-\mathbf{X}(t-\Delta t))+(A(t)\nonumber \\&-\,A(t-\Delta t))\mathbf{X}(t-\Delta t) \nonumber \\= & {} A(t)\hbox {d}{} \mathbf{X}(t,t-\Delta t)\nonumber \\&+\,\hbox {d}A(t,t-\Delta t)\mathbf{X}(t-\Delta t), \end{aligned}$$
(8)

where dX is the parameter correction difference vector consisting of three LEO position correction differences, i.e. \({\updelta }{} \mathbf{r}\left( t \right) -{\updelta }{} \mathbf{r}\left( {t-\Delta t} \right) \), and one receiver clock offset correction difference; and dA is the design matrix difference. It should be mentioned that the ambiguity parameter disappears in the epoch-differenced observation equations when no cycle slip occurs, whereas systematic errors common to adjacent epochs, e.g. hardware delays from the receiver and GPS satellites, are reduced to a large extent. For satellite acceleration computation, only the position correction differences are of interest, which are included in the first term of the last line of Eq. (8). In addition, the parameters from the previous epoch, i.e. \(\mathbf{X}\left( {t-\Delta t} \right) \), are also kept in the epoch-differenced observation equation. However, they cannot be accurately estimated in the case of an epoch-differenced scheme. As proposed in (Bock 2003), one can fix the satellite positions to a high-precision a priori orbit and assume them to be known. To avoid introducing possible biases towards a background gravity field model, we adopt for this purpose a kinematic orbit (i.e. \({{\varvec{r}}}_{0\mathrm{com}}(t)=\hbox {kinematic orbit}\)), unless the opposite is explicitly stated. The exploited kinematic orbit is a part of the SST_PKI_2 product (EGG-C 2010; Bock et al. 2014).

Strictly speaking, only one initial kinematic position is needed in this case, as the position at the current epoch can be calculated as the sum of the initial position and the estimated position differences. Then, the obtained positions can be used as the a priori orbit for the subsequent epoch. However, we did not adopt this scheme, because errors in the derived position differences would accumulate, and the orbit obtained in this way would likely be too inaccurate.

To quantify the impact of errors in the adopted kinematic orbit, we assume that they can be approximated by differences between the kinematic and the reduced-dynamic orbit of the SST_PRD_2 product (i.e. \(\mathbf{r}_{\mathrm{kin}}-\mathbf{r}_{\mathrm{rdy}}\), where \(\mathbf{r}_{\mathrm{kin}}\) and \(\mathbf{r}_{\mathrm{rdy}}\) are the positions taken from the kinematic orbit and reduced-dynamic orbit, respectively). In this way, the errors caused by fixing the LEO positions to the kinematic orbit can be formulated as \(\hbox {d}A(\mathbf{r}_{\mathrm{kin}}-\mathbf{r}_{\mathrm{rdy}})\) according to Eq. (8). As an example, we consider the data collected on day of year (DOY) 306, 2009. The 3-D RMS difference between the kinematic orbit and reduced-dynamic orbit on that day is 1.6 cm. Figure 1 shows the observation minus computed (OMCs) of the resulting 30-s sampling epoch-differenced carrier phase observations and their errors. The error standard deviation is 0.36 mm, i.e. one order of magnitude smaller than the standard deviation of the OMCs of the epoch-differenced ionosphere-free phase observations, which is 7.50 mm for that day.

Table 1 Data and models used for gravity field recovery
Full size table

As the precision of the kinematic orbit from the SST_PKI_2 product is, in general, about 2 cm in each dimension (Bock et al. 2014), i.e. about 3.5 cm in three dimensions, the resulting errors caused by fixing the satellite positions to this kinematic orbit would be about 0.8 mm, i.e. still about one order of magnitude smaller than the standard deviation of noise in the 30-s sampling epoch-differenced ionosphere-free phase measurements.

One may argue that such a comparison is somewhat unfair because noise in the epoch-differenced phase observations, unlike noise in kinematic positions, is likely frequency-dependent (relatively high at high frequencies and low at low frequencies). Then, low-frequency noise in kinematic positions still may play a role. To prove the opposite, we also produced a gravity field solution with the proposed phase method using the reduced-dynamic orbit as the a priori orbit (i.e. \({{\varvec{r}}}_{0com}(t)=\hbox {reduced-dynamic orbit}\)). The differences between these two solutions turned out to be negligible (see Sect. 5 for further details).

Now, only the parameter correction differences remain to be estimated, which include three position correction differences and one receiver clock offset correction difference. After a least-squares adjustment, the actual position differences are restored by adding back the approximate position differences as given by Eq. (9):

$$\begin{aligned} \hbox {d}{} \mathbf{r}(t,t-\Delta t)= & {} \mathbf{r}(t)-\mathbf{r}(t-\Delta t) \nonumber \\= & {} \mathbf{r}_0 (t)-\mathbf{r}_0 (t-\Delta t)+\,\delta \mathbf{r}(t)-\delta \mathbf{r}(t-\Delta t)\nonumber \\ \end{aligned}$$
(9)

As the carrier phase measurements \(L_{IF} \left( t \right) \) is used in both \(l_{IF} \left( {t,t-\Delta t} \right) \) and \(l_{IF} \left( {t+\Delta t,t} \right) \), errors in subsequent epoch-differenced phase measurements are correlated. However, we neglect this correlation, because this allows us to derive the position differences epoch by epoch and makes the practical implementation more straightforward and efficient.

Finally, according to Eq. (1), the average satellite accelerations can be derived from the position differences as

$$\begin{aligned} {\bar{{\mathbf{a}}}}(t)= & {} \frac{\left( {\mathbf{r}(t+\Delta t)-\mathbf{r}(t)} \right) -\left( {\mathbf{r}(t)-\mathbf{r}(t-\Delta t)} \right) }{\left( {\Delta t} \right) ^{2}}\nonumber \\= & {} \frac{\hbox {d}{} \mathbf{r}(t+\Delta t,t)-\hbox {d}{} \mathbf{r}(t,t-\Delta t)}{\left( {\Delta t} \right) ^{2}}, \end{aligned}$$
(10)

where \(\hbox {d}{} \mathbf{r}\left( {t+\Delta t,t} \right) \) and \(\hbox {d}{} \mathbf{r}\left( {t,t-\Delta t} \right) \) are the two successive position difference vectors.

2.2 Computation and inversion of residual accelerations

Before using the ‘observed’ satellite accelerations, which reflect the sum of the accelerations acting on the satellite, for gravity field modelling, one must convert them into residual accelerations by subtracting their a-priori counterparts, which are based on background force models, in line with Eq. (2). The background force models used to compute the a priori satellite accelerations, the exploited reference frames, as well as the data and the associated corrections used to produce the observed accelerations, are listed in Table 1. In particular, a high-quality global gravity model (GGM) (here DGM-1S) is used as background gravity field, unless the opposite is explicitly stated. Using a high-quality mean GGM somewhat simplifies both the computational procedure and the analysis of the results obtained. In particular, this concerns the estimation of stochastic properties of data noise (see Sect. 2.2).

We also did additional test computations, when the background gravity model was defined as EGM96, which is much less accurate than DGM-1S. In this way, we showed that the choice of the background gravity model has a negligible influence on the gravity field solutions obtained with either method and does not change the performance of the methods (see Sect. 5 for more details).

Both the raw GPS measurements and the kinematic orbits from the SST_PKI_2 product are provided with 1-s sampling, whereas the WHU kinematic orbits are computed with 5-s sampling. The accelerations derived from them suffer from strong high-frequency noise, which requires the application of frequency-dependent data weighting (FDDW) when they are inverted into gravity field parameters (Klees et al. 2003; Ditmar and van Eck van der Sluijs 2004). To represent the dependence of noise on frequency, we consider noise power spectral density (PSD), which implies that noise in the average accelerations is stationary (Klees et al. 2003). On the other hand, it turned out that the actual noise may occasionally suffer from non-stationarity, which leads to unsatisfactory results of data inversion even if FDDW is used. As a solution, we down-sampled the input data sets by picking up the epochs every 30 s, so that resulting noise in derived satellite accelerations is less frequency-dependent. It turned out that noise non-stationarity in that case does not play a substantial role anymore, even if is still present. To fully exploit information in the GPS data, six acceleration data sets are produced, each set being shifted by 5 s with respect to the previous one. Then, all the six data sets are jointly inverted in the course of gravity field recovery. To that end, we use the method of preconditioned conjugate gradients with a block-diagonal preconditioning matrix, which facilitates a rapid convergence of iterations (Ditmar and Klees 2002).

The reduced-dynamic orbits in the official SST_PRD_2 products are provided with 10-s sampling. They are interpolated to the kinematic orbit epochs with an eleventh-order Legendre interpolation scheme and then used to geo-locate the satellite for the computation of the satellite accelerations, i.e. the right-hand side of Eq. (2). To take non-gravitational accelerations into account, the common-mode accelerometer observations from the sensitive axes are used after a 5-s resampling; the instrument biases per component are estimated once per day, together with the gravity field parameters.

3 Residual average accelerations

Due to the high accuracy of the exploited background force models, the obtained residual accelerations are dominated by noise. Therefore, we treat the residual accelerations in this section as realizations of data noise. As mentioned in Sect. 2.2, six acceleration sets in total are produced with each method. As the properties of these data sets are similar, only one of them is discussed below.

3.1 Analysis in the time and spatial domain

Prior to the least-squares estimation of the gravity field parameters, the residual average accelerations are cleaned from outliers. To this end, the residual accelerations exceeding a given threshold (here, 3 times the corresponding standard deviation) are identified. Then, all 3 components of the identified residual accelerations are discarded as outliers. The procedure is iterated until no more outliers are found. As a result, 14, 18, and 17% of data are excluded in the case of the orbit-ESA method, the orbit-WHU method and the phase method, respectively. The mean values and standard deviations of the cleaned residual accelerations are listed in Table 2 obviously shows that the standard deviations clearly show an improvement in the precision of all three components of the accelerations derived with the phase method. The improvement is particularly noticeable for the cross-track component. In comparison with the orbit-ESA method, the improvement reaches 36%. In comparison with the orbit-WHU method, the improvement is more modest: 16%. This is likely because of the same carrier phase data and measurement models adopted for the orbit-WHU method and the phase method. Note that the code measurements used in deriving the WHU kinematic orbits have only a minor effect on the orbit precision, since the weights assigned to those measurements are 40,000 times lower than the weights assigned to the phase measurements.

Table 2 Mean values and standard deviations of residual average accelerations (\(\upmu \hbox {m}/\hbox {s}^{2}\))
Full size table
Fig. 2
figure 2

Root mean square (RMS) errors of the residual average accelerations (\(\upmu \hbox {m}/\hbox {s}^{2}\)) per geographical \(1^{{\circ }}\times 1^{{\circ }}\) bin for the orbit-ESA method (a–c), the orbit-WHU method (d–f) and the phase method (g–i). The plots in the left column, middle column and right column show the along-track component, cross-track component, and radial component, respectively

Full size image

The standard deviations listed in Table 2 also reveal that the accelerations derived from the WHU kinematic orbit seem to be more precise, as compared to those derived from the ESA kinematic orbit. As different software packages were used when deriving the orbits, the specific factors responsible for this difference are not clear to us yet. This is, however, out of the scope of this paper and will not be discussed hereafter. Furthermore, the standard deviations of the radial component are larger than those of the other two components in all three cases. In the case of the orbit method, this can be explained by a relatively low precision of the GPS positioning in the radial direction. On average, the positioning precision in the radial direction is a factor of three lower than the precision in the two other directions, as can be seen from the orbit covariance information in the SST_PCV_2 products (EGG-C 2010). A similar explanation is likely applicable also to the position differences in the case of the phase method.

Fig. 3
figure 3

Same as Fig. 2, but for the differences of RMS errors: between the orbit-ESA method and the phase method (\(\hbox {RMS}^{\mathrm{(orbit-ESA)}}\)-\(\hbox {RMS}^{\mathrm{(phase)}})\) (a–c); between the orbit-WHU method and the phase method (\(\hbox {RMS}^{\mathrm{(orbit-WHU)}}\)-\(\hbox {RMS}^{\mathrm{(phase)}})\) (d–f); and between the orbit-ESA method and the orbit-WHU method (\(\hbox {RMS}^{\mathrm{(orbit-ESA)}}\)-\(\hbox {RMS}^{\mathrm{(orbit-WHU)}})\) (g–i). The plots in the left column, middle column and right column show the along-track component, cross-track component, and radial component, respectively

Full size image

Figure 2 shows the RMS errors of the residual accelerations per geographical \(1{^{\circ }}\times 1{^{\circ }}\) bin for all three cases. Again, the errors are larger for the radial component, as compared to the other two components, in all three cases. We also see that the geographical distribution of the RMS errors is highly inhomogeneous in all cases. The largest RMS errors are observed near the geomagnetic poles. This is consistent with the findings of Van den IJssel et al. (2011), Bock et al. (2014), and Jäggi et al. (2015), who showed that L2 losses and systematic errors in the orbit cause errors in the gravity field solutions near the geomagnetic poles and along the geomagnetic equator. The errors along the geomagnetic equator are not obvious in Fig. 2. However, it is likely that some systematic errors in that area are still present, which accumulate in deriving gravity field solutions, as will be shown later. Several factors may contribute to the observed geographical distribution of errors: (1) un-modelled higher-order ionospheric terms, which can cause large errors due to a high electron density near the poles and the equator; (2) ionospheric scintillation effects, which usually cause rapid fluctuations in amplitude and phase of the GPS signal and lead to a degradation in the quality of the observations: signal-to-noise ratio (SNR) dropping, frequent cycle slips, and L2 losses; (3) a weak observation geometry over the polar regions due to the GPS constellation design.

Figure 3 further shows the differences between the RMS errors per geographical \(1{^{\circ }}\times 1{^{\circ }}\) bin. Figure 3a–c shows the differences between the orbit-ESA method and the phase method, Fig. 3d–f presents the differences between the orbit-WHU method and the phase method, and Fig. 3g–i shows the differences between the orbit-ESA method and the orbit-WHU method. It is clear that the RMS errors related to the phase method are smaller than the errors related to the orbit-ESA method at all three components. A similar comparison with the orbit-WHU method shows a clear improvement at the cross-track component only; improvements at the other two components are not so obvious. This is consistent with the statistics presented in Table 2.

Figure 4 displays the number (a–c) and percentage (d–f) of excluded epochs per geographical \(1{^{\circ }}\times 1{^{\circ }}\) bin for all three cases. One can see a similar pattern in all cases: More observations are excluded near the geomagnetic poles, which can be attributed to the large noise in residual accelerations there, as explained before. Figure 4g–i shows the difference between the number of excluded epochs per \(1{^{\circ }}\times 1{^{\circ }}\) bin for the two methods. It is obvious that more data are discarded near the geomagnetic poles in the case of the phase method. At other latitudes, less data are excluded in the case of the phase method. An exception is a narrow stripe along the Earth equator, which is particularly obvious in Fig. 4g. An analysis showed that this is caused by cycle slips in the carrier phase measurements at the moments when the satellite crosses the equator during its ascending arcs (the reasons for that are not clear to us). We remind that the phase method does not work at the epochs with cycle slips. However, this concerns only about 0.2% of the total number of data. We do not make further investigations on this issue, but assume that its impact onto global gravity field recovery is negligible due to the small number of such events and the application of an outlier detection scheme.

Fig. 4
figure 4

Number (top row) and percentage (middle row) of excluded epochs per geographical \(1{^{\circ }}\times 1{^{\circ }}\) bin for the orbit-ESA method (a, d), the orbit-WHU method (b, e), and the phase method (c, f). Plots (g–i) in the bottom row display the differences between the shown numbers (\(\hbox {g}=\hbox {a}-\hbox {c}\); \(\hbox {h}=\hbox {b}-\hbox {c}\); \(\hbox {f}=\hbox {a}-\hbox {b}\))

Full size image
Fig. 5
figure 5

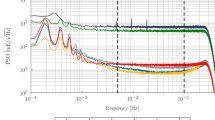
Noise \(\hbox {PSD}^{1/2}\)s of the residual average accelerations derived from the ESA kinematic orbit (dotted lines), the WHU kinematic orbit (dashed lines), and GPS phase measurements (solid lines). The along-track, cross-track, and radial components are plotted in red, green, and blue, respectively

Full size image

3.2 Analysis in the spectral domain

Figure 5 shows the square root PSD, hereafter referred to as \(\hbox {PSD}^{1/2}\), of the residual average accelerations. These noise spectra are computed for the entire time interval considered in this study (November 2009–July 2012). In general, the \(\hbox {PSD}^{1/2}\)s show similar features in all cases. Noise at the radial component is higher than at the other two components, which have been already discussed in Sect. 3.1. Furthermore, noise in all cases increases with frequency beyond \(3\times 10^{-3}\) Hz. This is explained by the fact that double-differentiation in the time domain corresponds to the multiplication of \(\hbox {PSD}^{1/2}\) with \(\omega ^{2}\) in the frequency domain, where \(\omega \) denotes angular frequency.

Fig. 6
figure 6

Left column residual SH coefficients (\(\log _{10}\) representation of the absolute values, i.e. \(\log _{10 }{\vert }\hbox {C}_\mathrm{lm}{\vert }\)) based on average accelerations obtained with a the orbit-ESA method, b the orbit-WHU method, and c the phase method. Right column the differences between two sets of residual SH coefficients, d \(\log _{10} {\vert }\hbox {C}_{\mathrm{lm}}^{(\mathrm{orbit-ESA})}{\vert } - \log _{10}{\vert }\hbox {C}_{\mathrm{lm}}^{(\mathrm{phase})}{\vert }\), e \(\log _{10} {\vert }\hbox {C}_{\mathrm{lm}}^{(\mathrm{orbit-WHU})}{\vert } - \log _{10}{\vert }\hbox {C}_{\mathrm{lm}}^{(\mathrm{phase})}{\vert }\), and f \(\log _{10} {\vert }\hbox {C}_{\mathrm{lm}}^{(\mathrm{orbit-ESA})}{\vert } - \log _{10}{\vert }\hbox {C}_{\mathrm{lm}}^{(\mathrm{orbit-WHU})}{\vert }\)

Full size image

At the same time, the \(\hbox {PSD}^{1/2}\)s of the average accelerations obtained in different ways show some differences. It can be seen that the \(\hbox {PSD}^{1/2}\)s in the case of the phase method are lower than those in the case of the orbit method for all three components in the entire frequency range. This can be attributed to a higher precision of the phase method. On average, the improvements are 5, 21, 5% for the along-track, cross-track, and radial component, respectively, as compared to the orbit-WHU method, and 22, 39, 24% as compared to the orbit-ESA method. Again, the cross-track component benefits the most from the phase method. This is very close to the values obtained by the analysis in the time domain (cf. Sect. 3.1)

4 Recovered gravity field

4.1 Analysis in the spectral domain

The mean gravity field over the period November 2009–July 2012 is recovered to degree 150 using all three variants of average accelerations. Figure 6a–c shows the residual SH coefficients for the three solutions. These coefficients reveal similar patterns. Due to the polar gaps in the GOCE satellite ground tracks, the zonal and near-zonal coefficients show in all cases a clear degradation, as compared to other coefficients (Sneeuw and van Gelderen 1997). Furthermore, noise in SH coefficients increases with degree, which can be primarily explained by the downward continuation effect.

Figure 6d displays the differences between the residual coefficients of the phase method and the orbit-ESA method. Positive differences are observed in general, which indicates an overall higher quality of the solution obtained with the phase method, as compared to the orbit-ESA method. Exceptions are the zonal and near-zonal terms, which are influenced by the polar gaps. As mentioned in Sect. 3.1, more data are discarded near the geomagnetic poles in the case of the phase method, particularly as compared to the orbit-ESA method (see Fig. 4g). This likely aggravates the negative impact of the polar gaps on the gravity field solutions in that case. Figure 6e shows the differences between the residual coefficients of the phase method and the orbit-WHU method. The differences are not so clear as in Fig. 6d, so that they can hardly be used to draw conclusions regarding the relative performance of the phase method and the orbit-WHU method.

Figure 7 shows the obtained residual solutions in terms of geoid heights per degree. To account for the polar gap problem, the low-order terms for which \(m\le \left| {0.5\pi -I} \right| l\) (with I being the orbit inclination in radians) are excluded according to the rule of thumb proposed by Van Gelderen and Koop (1997). As can be seen from the plot, the degree amplitudes in the case of the phase method are, in general, smaller than in the case of the orbit method in the entire degree range, but especially at low degrees. This also confirms a better performance of the phase method in the context of gravity field modelling. Furthermore, the total gravity field signal, which is represented by the solid black line, suggests that the gravity field can be recovered to a slightly higher maximum degree when the phase method is applied.

An inspection of the residual solutions in terms of cumulative geoid heights reveals that the accuracy of the obtained gravity field model in the case of the phase method is higher by 4–15%, as compared to the orbit-WHU method, and by 14–35%, as compared to the orbit-ESA method (cf. Table 3).

Fig. 7
figure 7

Geoid height differences with respect to DGM-1S per degree, obtained with the orbit-ESA method (in red), the orbit-WHU method (in green), and the phase method (in blue). Low-order coefficients are excluded. The black line represents the DGM-1S total gravity field signal

Full size image
Table 3 Cumulative geoid height differences (cm) with respect to DGM-1S up to degree 50, 100, and 150
Full size table

4.2 Analysis in the spatial domain in terms of geoid heights

Figure 8 presents the obtained residual gravity field solutions in the spatial domain in terms of geoid heights. A 300-km Gaussian filter is applied to focus on the long- to medium-wavelength parts of the spectrum. Pronounced errors along the geomagnetic equator can be observed in the solutions obtained with the orbit method (Fig. 8a, b), particularly when the ESA orbit was used as input. This can be traced back to high electron density, coupled with large short-term variations in the ionosphere over the geomagnetic equator (Jäggi et al. 2015). On the other hand, these errors are reduced in the case of the phase method (Fig. 8c). This indicates that the ionosphere-induced errors may impact the kinematic orbits in a different manner, as compared to the raw phase measurements, and a direct differentiation of raw phase measurements in the case of the phase method mitigates those errors. Of course, this is only a conjecture, but an investigation of this issue in more detail is beyond the scope of this study. A further comparison of the plots reveals that the geoid heights are systematically smaller for the phase method (Fig. 8d–f), which also confirms its better performance.

The RMS residual geoid heights (without Gaussian smoothing) outside the polar gaps (at latitudes lower than \(\pm 83.4{^{\circ }})\) are 46.2, 41.6, and 39.7 cm for the orbit-ESA method, the orbit-WHU method, and the phase method, respectively. This is remarkably consistent with the results in the spectral domain.

Fig. 8
figure 8

Residual gravity field solutions with respect to DGM-1S in terms of geoid heights obtained with the orbit-ESA method (a), the orbit-WHU method (b), and the phase method (c). Plots (d–f) show the differences of the absolute value of the residual geoid heights: \(\hbox {d}={\vert }\hbox {a}{\vert }-{\vert }\hbox {c}{\vert }\), \(\hbox {e}={\vert }\hbox {b}{\vert }-{\vert }\hbox {c}{\vert }\), \(\hbox {f}={\vert }\hbox {a}{\vert }-{\vert }\hbox {b}{\vert }\) (thus, positive numbers indicate a better performance of the phase method and vice versa). The 300-km Gaussian smoothing is applied in all cases

Full size image

4.3 Analysis in the spatial domain in terms of mass anomalies

We also make an attempt to identify some mass transport signals in the obtained solutions. To this end, we analyse mean mass anomalies in the considered time interval (November 2009–July 2012), smoothed with a 700-km Gaussian filter to suppress high-frequency noise. These mass anomalies reflect the deviation of mass distribution in the considered time interval from the mean mass distribution in February 2003–December 2010 (the interval covered by the background mean field DGM-1S). The results are compared with the mean mass anomaly in November 2009–July 2012 derived from the optimally filtered monthly solutions, which are based on KBR data from the GRACE satellite mission. The solutions were produced in house using a methodology similar to that exploited in the production of the Delft Mass Transport model DMT (Liu et al. 2010; Farahani 2013; Farahani et al. 2014, 2016). For brevity, these solutions are referred below to as ‘DMT solutions’. Those monthly solutions describe deviations from the DGM-1S mean field, which is consistent with the mean field used in this study. The solutions are processed with the statistically optimal Wiener-type filter based on full signal and noise covariance matrices (Klees et al. 2008) in order to make the result as close to the reality as possible. We note that an attempt to filter unconstrained DMT solutions consistently with GOCE GPS solutions (i.e. by applying the 700-km Gaussian filter) leads to unsatisfactory results: the solutions in that case suffered from artefacts elongated in the north–south direction due to a poor sensitivity of the GRACE mission in the cross-track direction (not shown). In addition, we consider the GRACE gravity product release 5 (RL05), generated by the University of Texas at Austin’s Center of Space Research (CSR, Bettadpur 2012) and post-processed by the DDK5 filter (Kusche et al. 2009). To ensure a consistency with the DMT and the GPS-based solutions, DGM-1S is first subtracted from the monthly CSR solutions. After that, the monthly mass anomalies in November 2009–June 2012 are averaged to produce the mean mass anomaly in the considered time interval. At the last stage, a 400-km Gaussian filter is applied to mitigate the artefacts elongated in the north–south direction.

Fig. 9
figure 9

Mean mass anomaly over the period November 2009–July 2012 in terms of EWH (cm) based on: a GOCE GPS data processed with the orbit-ESA method; b GOCE GPS data processed with the orbit-WHU method; c GOCE GPS data processed with the phase method; d DMT model; e CSR DDK5 model with 400-km Gaussian smoothing. 700-km Gaussian smoothing has been applied to the solutions based on GOCE GPS data

Full size image

Figure 9 presents the obtained maps of mass anomalies in terms of equivalent water heights (EWH). One can see that the GPS-based solutions are very noisy in some areas. For instance, around the geomagnetic equator, mass anomalies have a similar amplitude over the continents and the oceans. Such a behaviour is clearly unphysical and reveals a low accuracy of GPS-based solutions (particularly, those obtained with the orbit method, Fig. 9a, b). Furthermore, strong noise is observed in GPS-based solutions in the vicinity of the poles. On the other hand, noise at the intermediate latitudes seems to be at a much lower level. To facilitate the further analysis, we zoom in onto two specific regions: North America and south-west Africa (Figs. 10, 11, respectively).

Both the DMT and CSR solutions show positive mass anomalies around the Hudson Bay in the northern part of North America (Fig. 10d, e). Since the DGM-1S model reflects the mean gravity field in the past time interval which starts much earlier than that considered in our study, the observed mass anomaly reveals a mass increase over time. This increase can be explained by the glacial isostatic adjustment in that area (Tamisiea et al. 2007; Wu et al. 2010; Sasgen et al. 2012). An evidence of this anomaly can also be seen in the GPS-based solutions, particularly in the solutions obtained with the orbit-WHU method (Fig. 10b) and the phase method (Fig. 10c).

In south-west Africa, both the DMT and CSR solutions clearly show positive mass anomalies (Fig. 11d, e). This is likely caused by the change from drought to wetter conditions in the Okavango and Zambezi basins in 2003–2012 (Ahmed et al. 2014; Hassan and Jin 2016). Again, the GPS-based solutions seem to be capable of reproducing those anomalies, particularly in the solutions obtained with the orbit-WHU method (Fig. 11b) and the phase method (Fig. 11c).

To compare the accuracy of the GPS-based solutions quantitatively, the RMS differences (in terms of EWH) between the optimally filtered DMT solution and the Gaussian-filtered GPS-based solutions are calculated for different Gaussian filter radii. Importantly, the results of data processing inside the polar gaps of the GOCE ground tracks are neither predictable nor representative due to the absence of data there. Therefore, we exclude the polar regions from the quantitative comparison by limiting the range of considered latitudes to \(\pm \hbox {N}^{\circ }\), where the value of N\(^{\circ }\) is defined as a function of the Gaussian filter radius: \(\hbox {N}^{\circ }=83.4^{\circ }-\hbox {radius}/40,000\times 360^{\circ }\). In view of the 6.6 degree radius of the polar gaps, this means that the influence of the polar gaps is fully avoided. Figure 12a shows the RMS differences from the DMT model in all cases. It is obvious that the phase method presents smaller RMS differences as compared to the orbit method. Figure 12b further shows the reduction of the RMS differences from the DMT model, when the phase method is applied instead of the orbit-ESA or the orbit-WHU method. As can be seen, the phase method reduces the RMS difference for all Gaussian filter radii under consideration. The maximum reduction is observed for the Gaussian smoothing radius of about 500-km, reaching about 45 and 22% in comparison with the orbit-ESA method and the orbit-WHU method, respectively. Thus, the solution obtained with the phase method is closer to the DMT solution, indicating a higher quality of the phase method.

It is worth adding that we also made an attempt to compare the methods in individual regions, such as North America and the south-west part of Africa. It turned out, however, that the relative performance of the phase method and the orbit-WHU method is rather sensitive to the definition of the target region. It is always possible to define the region such that either of the two methods shows a higher performance. Therefore, we refrain from discussing the regional comparison as not sufficiently representative.

Fig. 10
figure 10

Same as Fig. 9, but for the territory of North America

Full size image
Fig. 11
figure 11

Same as Fig. 9, but for south-west Africa

Full size image
Fig. 12
figure 12

Analysis of the mean mass anomalies (in terms of EWH) over the period November 2009–July 2012 obtained with different data processing methods. Plot a shows the RMS differences from the DMT model as a function of the Gaussian filter radius for the phase method (in green), the orbit-ESA method (in red), and the orbit-WHU method (in blue). Plot b shows the reduction (in percentages) of the RMS differences from the DMT model as a function of the Gaussian filter radius, when the phase method is applied instead of the orbit-ESA method (in red) or instead of the orbit-WHU method (in blue). The percentage is calculated as: \(( {\hbox {RMS}_{\mathrm{orbit}} -\hbox {RMS}_{\mathrm{phase}} } )/\hbox {RMS}_{\mathrm{orbit}} \times 100\)

Full size image

5 Discussion

For the results presented until now, a kinematic a priori orbit is used in the phase method. In order to demonstrate the robustness of the obtained results, we derived the satellite accelerations exploited in the phase method using a different a priori orbit (namely, a reduced-dynamic orbit), cf. Sect. 2.1.2. The residuals with respect to DGM-1S in terms of cumulative geoid heights up to degree 50, 100, and 150 are listed in Table 4. It can be seen that the usage of different a priori orbits in the phase method has a negligible impact on the gravity solutions: not more than 2%. Furthermore, we present the residuals with respect to DGM-1S in terms of geoid heights, as well as the differences of the obtained residuals with respect to those obtained when a kinematic obit was used as the a priori one (Fig. 13). One can see that residuals in the spatial domains are also nearly the same in these two cases. This confirms that the phase method is not sensitive to the choice of the a priori orbit.

In addition, we inverted all three variants of the derived accelerations using a relatively inaccurate background model of the mean gravity field, namely EGM96 (Lemoine et al. 1998). It should be noted that the background gravity model and stochastic model of data noise had to be refined iteratively in the case of the inaccurate background model. Once the iterations converged, there were little differences between the noise stochastic models obtained with different background models (not shown). When EGM96 is used as the background model of the mean gravity field, the residuals with respect to DGM-1S in terms of cumulative geoid heights in the case of the phase method are reduced by 5–15%, as compared to the orbit-WHU method and by 14–30%, as compared to the orbit-ESA method (Table 4). This is rather similar to the results obtained when DGM-1S is used as the background model of the mean gravity field. Thus, a better performance of the phase method, as compared to the orbit method, is not specific for a particular choice of the background model. Figure 14 further presents the residual geoid heights with respect to DGM-1S when EGM96 was used as the background model, as well as the differences of the residual geoid heights with respect to those obtained when DGM-1S was used as the background model. An inspection of these residual geoid heights also shows little sensitivity to the choice of the background model. From Table 4, it follows that these differences are indeed modest: only 0.3–1.1% when the cumulative geoid height errors up to degree 150 are considered. In the case of the cumulative geoid height errors up to degree 50, these differences are larger: 8–14%. In the spatial domain, large differences are mainly observed over polar regions for all three cases (Fig. 15). A likely explanation for the observed differences is a bias towards the background model in both methods due to the polar gaps of the GOCE satellite ground tracks. We did not make a further investigation of this difference, as it is common to both methods and thus does not alter the conclusions regarding a higher performance of the phase method.

Table 4 Residuals with respect to DGM-1S in terms of cumulative geoid heights up to degree 50, 100, and 150 cm
Full size table
Fig. 13
figure 13

a Residual geoid heights with respect to DGM-1S in case of the phase method when a reduced-dynamic a priori orbit is used and b the differences of absolute residual geoid heights from its counterpart in Fig. 8c where a kinematic a priori orbit is used (\(\hbox {b}={\vert }\hbox {a}{\vert }-{\vert }\hbox {Fig}.~8 \hbox {c}{\vert }\)). The 300-km Gaussian smoothing is applied

Full size image
Fig. 14
figure 14

Residual geoid heights with respect to DGM-1S for the orbit-ESA method (a), the orbit-WHU method (b), and the phase method (c) when EGM96 is used as the background model. d–f Show the differences of the absolute values of the residual geoid heights in (a–c) from their counterparts in Fig. 8a–c obtained when DGM-1S is used as the background model (\(\hbox {d}={\vert }\hbox {a}{\vert } -{\vert }\hbox {Fig}.~8\hbox {a}{\vert }\); \(\hbox {e}={\vert }\hbox {b}{\vert }-{\vert }\hbox {Fig}.~8\hbox {b}{\vert }\); \(\hbox {f}={\vert }\hbox {c}{\vert }-{\vert }\hbox {Fig}.~8\hbox {c}{\vert }\)). Plots d, e, f are associated with the orbit-ESA method, the orbit-WHU method and the phase method, respectively

Full size image
Fig. 15
figure 15

Differences of the absolute values of the residual geoid heights between the solutions using different background models of the mean gravity field (DGM-1S and EGM96): \({\vert }\hbox {RES}_{\mathrm{EGM96}}{\vert }-{\vert } \hbox {RES}_{\mathrm{DGM-1S}}{\vert }\). Plots (a, d), (b, e) and (c, f) hold for the orbit-ESA method, the orbit-WHU method, and the phase method, respectively. Plots (a–c) show the differences in the southern hemisphere and plots (d–f) in the northern hemisphere

Full size image

6 Conclusions

In this study, we developed a new method for deriving average satellite acceleration, which is based on raw GPS carrier phase measurements. We applied this method to the GPS data collected by the GOCE satellite mission. As the data processing is based on an epoch-differenced scheme applied to the original phase measurements, there is no need to estimate ambiguity parameters, and the data processing becomes simpler, as compared to the orbit method. Furthermore, as systematic errors common to adjacent epochs are mostly eliminated, more precise accelerations are obtained with the phase method. An analysis of residual satellite accelerations in the time and spectral domain showed that the phase method resulted in lower noise than the orbit method in all three acceleration components. The cross-track component benefits the most from the phase method with an improvement of about 20%.

The derived average accelerations were applied to recover the mean gravity field in November 2009–July 2012 complete to degree 150. In general, gravity field parameters were estimated with the phase method more accurately. The zonal and near-zonal terms were an exception. This was likely due to a larger number of outliers excluded over the polar regions in the case of the phase method, which may enhance polar gap effect. The residual geoid heights obtained with the phase method showed overall smaller degree amplitudes, and the cumulative geoid heights up were reduced by 4–15% (depending on the maximum degree), as compared to the orbit method. In addition, the residual geoid heights in the spatial domain revealed larger errors associated with the geomagnetic equator in the case of the orbit method. Finally, the performance of the two methods was compared in terms of mass anomalies, using the DMT model as the reference. Both methods showed an ability to recover the signals related to a long-term mass redistribution, yielding the best results for the intermediate latitudes. An inspection of obtained mass anomalies allowed us to conclude that the signatures produced with the phase method are more consistent with solutions based on GRACE KBR data.

The obtained results imply that GPS data processed with the phase method might be a valuable source of information about mass transport. Remarkably, the sensitivity of GPS observations is more isotropic than that of KBR observations acquired by GRACE. Even more, the GPS observations are more sensitive in the cross-track direction than in the along-track direction (cf. Table 2; Fig. 5). Therefore, combining GRACE KBR data with GPS data delivered by various satellites and processed with the phase method may increase the accuracy and resolution of mass transport modelling. Furthermore, usage of the latter data may facilitate mass transport modelling even in the absence of GRACE KBR data (in the months when GRACE data are not delivered due to the degradation of GRACE satellite systems, as well as during the gap between the GRACE mission and its successor, if such a gap takes place). In view of that, we recommend to further study the potential of GPS data in mass transport modelling. In particular, it will be important to consider GPS data delivered by other satellite missions (e.g. SWARM) and to compare the proposed technique with those considered in the previous publications (e.g. Baur 2013; Weigelt et al. 2013).

One can see that we have made two simplifications in the proposed phase method when deriving satellite position differences from the epoch-differenced phase measurements (cf. Sect. 2.1.2). First, the error correlations between the subsequent epoch-differenced phase measurements are neglected when deriving the satellite position differences. One may argue that neglecting the error correlations is a drawback of the adopted scheme. At least, the estimates are not optimal from the statistical point of view. Thus, further efforts are needed in order to identify potential benefits of making a statistically optimal estimation of satellite accelerations in the context of the phase method. The second simplification in the phase method is fixing the satellite positions at the previous epoch to a high-precision a priori orbit. It goes without saying that the phase method in the present form benefits from a high-precision a priori orbit. However, we do not tend to conclude that this is the explanation of the better performance of the phase method, as compared to the orbit method. We believe that some systematic errors that do not change much from epoch to epoch are mitigated or even cancelled out in the epoch-differenced phase measurements obtained with the adopted scheme. Thus, they do not propagate into the derived position differences and the satellite average accelerations. On the other hand, those errors still propagate into the orbit during the parameter adjustment. This may explain the better performance of the phase method.