1 Introduction

Kinematic orbit positions often serve as observations for gravity field estimation. Hence, their accuracy directly affects the quality of the gravity field estimates. We present a new method for kinematic orbit determination based on raw GPS measurements. The method can be seen as a variation of precise point positioning (PPP) (Witchayangkoon 2000). In contrast to currently used approaches, we directly use raw global positioning system (GPS) observations, as they are observed. No linear combinations or observation differences are used. Code and phase measurements on both frequencies are directly incorporated in a least squares adjustment. To achieve highest accuracies, a careful treatment of all errors affecting GPS observations is absolutely necessary. A major aspect of PPP is the knowledge of precise transmitter position and clock information. Besides this, errors like antenna center variations (ACV), relativistic effects, phase wind-up, and the ionosphere have to be taken into account. If these effects are handled properly, a position accuracy in the range of a few centimeters is achievable.

Several satellite missions to study Earth’s gravity field have been launched in the past two decades. These missions, starting with CHAMP (challenging minisatellite payload) (Reigber et al. 2001), followed by GRACE (gravity recovery and climate experiment) (Tapley et al. 2004) and GOCE (gravity field and steady-state ocean circulation explorer) (Drinkwater et al. 2007), have been very successful and have provided new insights into Earth’s gravity field. These three missions rely on diverse measurement techniques, all of them being equipped with a GPS receiver. The high accuracy kinematic orbits can be used as observations to determine Earth’s gravity field. This method is known as satellite-to-satellite tracking in high-low mode (SST-hl). It was the observation principle used for the CHAMP mission and served as a supplement to other measurements in case of GOCE and GRACE. A major advantage is that the principle can be transferred to any other low earth orbiter (LEO) equipped with a GNSS (global navigation satellite system) receiver.

In recent years, the scientific community has focused on the time variable component of the gravity field. GRACE is able to observe variations in the gravity field due to its highly accurate microwave ranging system. These results are of high interest to different communities like hydrology, glaciology, and geology (Cazenave and Chen 2010) and form the basis for research concerning climate change, sea level change, deglaciation and is, therefore, also of socio-economical interest. Until recently, it was not possible to observe these variations in the gravity field through any other measurement technique, except for signals at large spatial scales. Facing a possible gap between the GRACE mission and its successor GRACE follow-on (Flechtner et al. 2014), an additional observation method becomes very important. First successful application of SST-hl to derive mass variations was done by Prange (2010). Recent investigations (Weigelt et al. 2013; Baur 2013; Zehentner and Mayer-Gürr 2014) indicate that it is possible to derive at least variations at medium scales (800–1000 km). We will use static and time variable gravity field results based on our kinematic orbits as a tool to validate our orbit determination method. For gravity field recovery, we incorporate the short arc integral approach introduced by Mayer-Gürr (2006). For a detailed description, we recommend the reader to take a look at Mayer-Gürr et al. (2006) or Mayer-Gürr et al. (2010).

This paper is structured into five major sections. After the introduction, Sect. 2 describes the methodology used for precise kinematic orbit determination; in Sect. 3, the input for some real data applications and the work flow to compute the kinematic orbits is explained; Sect. 4 shows the validation of the produced kinematic orbits by means of orbit comparisons and gravity field estimates; finally, Sect. 5 summarizes the main points and draws some conclusions.

2 Method

Current approaches for POD (precise orbit determination) rely on the ionosphere-free linear combination or on observation differences of GNSS signals. State-of-the-art approaches are, for example, given by Bock et al. (2011), van den IJssel et al. (2015) or Prange (2010). They all rely on observation combinations, which are utilized to mitigate systematic errors like the ionospheric influence. Our approach is founded on the basic rule that all observations shall be used as they are observed, including code and phase observations on all frequencies. This means no forming of linear combinations or differences, like single or double differences. A main drawback of linear combinations is the fact that the measurement noise is increased (Dach et al. 2007). If the original observations are used, the noise level is unchanged, but in contrast to linear combinations systematic errors are not eliminated or reduced. Thus, all systematic influences must be known beforehand, or at least estimated as parameters in the least squares adjustment. This approach was first described in Zehentner and Mayer-Gürr (2014).

2.1 Basic observation equation

The basic observation equations for code and phase measurements, according to Hoffmann-Wellenhof et al. (2008) are

$$\begin{aligned} R = \rho + c \delta t \end{aligned}$$
(1)

and

$$\begin{aligned} \lambda \Phi = \rho + c \delta t + \lambda n \end{aligned}$$
(2)

where R and \(\Phi \) denote the code and the phase measurement, respectively. On the right hand side are the parameters \(\rho \), the range between receiver and transmitter containing the unknown receiver position, the receiver clock error \(\delta t\) and in case of phase observations the unknown number of cycles n, called ambiguity, times the specific wavelength \(\lambda \) of the used carrier frequency. In addition to this basic set of parameters several further influences must be considered, for example the ionospheric influence or the transmitter clock error. Some of these influences can be modeled to a sufficient accuracy and reduced from the observations. We take into account relativistic effects and space–time curvature (Hoffmann-Wellenhof et al. 2008) as well as the phase wind-up correction (Kouba 2009). Other influences, like the transmitter clock error, must be known beforehand. The transmitter clock information is for instance provided by the International GNSS Service (IGS) (Dow et al. 2009), which also offers highly accurate post-processed GPS orbit information. Remaining errors, like the ionospheric delay or antenna center variations, are not known with sufficient accuracy and have to be estimated. The parametrization of these errors is given in Sect. 2.2.

Based on the basic observation equations, with extensions described in the subsequent paragraphs, the design matrix for the least-squares adjustment is set up. Observation equations are set up for each measurement individually. Due to the introduction of precise GPS orbits and clocks, the presented method can be seen as a variation of the PPP approach. The equation system is set up for a certain time span, e.g., one day, and solved iteratively by incorporating a variance component estimation to adjust the observation weights and account for outliers.

2.2 Additional parameters

Antenna center variations GPS measurements, both code or phase, are always related to the electronic center of the antenna. This electronic center is, however, not a physically defined point inside the antenna, but depends on several parameters:

  • antenna type

  • carrier frequency

  • observation type

  • signal direction (azimuth, elevation)

  • surrounding (multipath effects).

To relate all measurements to a common point, a mean antenna center is defined. Individual observations deviate from this mean antenna center by a constant offset, and azimuth and elevation-dependent variations. This constant offset is different for each carrier frequency. The azimuth and elevation-dependent differences, termed the antenna center variations or ACVs, vary for different frequencies and observation types. ACVs are present at both the receiver and the transmitter side. To estimate ACVs, the observation equations must be extended by additional parameters.

We parametrize receiver ACVs with a spherical harmonics expansion based on Legendre polynomials, similar to the representation used for gravity field modeling. Two restrictions have to be applied to the ACV estimation: firstly, the degree 0 and 1 terms of the spherical harmonics expansion must be omitted. These harmonics correspond to a scale and a shift with respect to the origin of the coordinate system (Hofmann-Wellenhof and Moritz 2006), thus they are not estimable due to their correlation with the clock error and the receiver position. Secondly, the spherical harmonics expansion must be limited to terms which are symmetric to the equator, due to the missing observations on the satellite-facing hemisphere of the antenna.

$$\begin{aligned} \mathrm{ACV}(\alpha , E)&= \sum _{n=2}^{N} \sum _{m=0}^{n} (c_{nm} \cos (m\alpha ) P_{nm} (\cos E) \nonumber \\&\quad + s_{nm} \sin (m\alpha ) P_{nm} (\cos E)). \end{aligned}$$
(3)

ACVs in Eq. (3) depend on azimuth \(\alpha \) and elevation E. The \(P_{nm}\) are the Legendre polynomials and their associated coefficients \(c_{nm}\) and \(s_{nm}\).

For transmitters, a parametrization with spherical harmonics is not applicable, because the view angle of a GNSS transmitter is restricted to approximately 14\(^\circ \)–17\(^\circ \), depending on the involved receivers. For a receiver on the ground, a view angle of 14\(^\circ \) is sufficient; in case of a LEO, the view angle is related to the altitude of the satellite. We use radial basis functions on a regular grid to parametrize transmitter ACVs. The principles of radial basis functions can, for example, be found in Eicker (2008). For the necessary regular distribution of the basis functions over the surface of the transmitter antenna, the triangle vertex algorithm as given by Kenner (1976) and Eicker (2008) was chosen.

The transmitter ACVs were parametrized as:

$$\begin{aligned} \mathrm{ACV}(\alpha , E) = \sum _{i=1}^I a_i \Phi _i (\cos \psi ) \end{aligned}$$
(4)

where

$$\begin{aligned} \Phi _i (\cos \psi ) = \sum _{n=2}^N \sqrt{2n+1} \cdot P_n (\cos \psi ). \end{aligned}$$
(5)

Equation (4) also depends on azimuth \(\alpha \) and elevation E, more specifically on the spherical distance \(\psi \) between the current point and the position of the basis functions. The basis functions \(\Phi _i\) are represented by a sum of Legendre functions \(P_n\) and associated to a specific coefficient \(a_i\). The subscript i represents the index of the used basis function. The sum in Eq. (5) starts from degree 2. This is due to the fact that degree 0 and 1 again correspond to a scale or shift and they cannot be separated from other parameters, like the position of the transmitter.

Ionospheric influence The ionosphere is a dispersive medium with respect to the signal frequencies used in GNSS. This means that code measurements are delayed, whereas phase measurements are advanced. The classical approach to treating this error source is the elimination of its effect through use of the ionosphere-free linear combination. Another approach is to estimate the total electron content (TEC) along the signal path, denoted as the slant TEC (STEC), which can be added to the observation equations as a parameter. This means that in every epoch for each tracked satellite, an individual STEC parameter is set up in the least squares adjustment. Following Hoffmann-Wellenhof et al. (2008), Eqs. (1) and (2) are expanded as follows:

$$\begin{aligned} R = \rho + c \delta t + \Delta I_{g}^{(1)} \mathrm{STEC} \end{aligned}$$
(6)

and

$$\begin{aligned} \Phi = \rho + c \delta t + \lambda n + \Delta I_{p}^{(1)} \mathrm{STEC}, \end{aligned}$$
(7)

with \(\Delta I_{g}^{(1)} = {\frac{40.3}{f^2}}\) and \(\Delta I_{p}^{(1)} =-\Delta I_{g}^{(1)}\). This parametrization only takes into account the first-order term of the ionospheric influence. Although this covers approximately 99 % of the error, it is not sufficient for high accuracy applications. As shown by Fritsche et al. (2005), it is necessary to include second- and third-order terms if centimeter or even millimeter accuracy is needed. The second- and third-order terms as given by Fritsche et al. (2005) are

$$\begin{aligned} \begin{aligned} \Delta I_{g}^{(2)} \mathrm{STEC}&= {\frac{7527 c}{f^3}} (\mathbf{B_0 \cdot k}) \cdot \mathrm{STEC} \\ \Delta I_{g}^{(3)} \mathrm{STEC}&= {\frac{2437}{f^4}} N_{\mathrm{max}} \eta \cdot \mathrm{STEC} \end{aligned} \end{aligned}$$
(8)

for code observations and

$$\begin{aligned} \begin{aligned} \Delta I_{p}^{(2)} \mathrm{STEC}&= - {\frac{1}{2}} \Delta I_{g}^{(2)} \mathrm{STEC} \\ \Delta I_{p}^{(3)} \mathrm{STEC}&= - {\frac{1}{3}} \Delta I_{g}^{(3)} \mathrm{STEC} \end{aligned} \end{aligned}$$
(9)

for phase observations. Where the first-order term can have magnitudes in the range of several meters, the magnitude of the second- and third-order terms still range from a few millimeters up to several centimeters.

The representations in Eqs. (8) and (9) depend on the carrier frequency f, the speed of light c, the peak electron density \(N_{\mathrm{max}}\), a shape parameter \(\eta \), and the magnetic field vector \(\mathbf{B_0}\). Fritsche et al. (2005) provide a value for the shape parameter (0.66) and an approximation formula to obtain \(N_\mathrm{max}\). Not shown in Eqs. (8) and (9) is a part of the third-order term we omit, as its magnitude is far below one millimeter as shown by Brunner and Gu (1991). To obtain the magnetic field vector, we make use of the International Geomagnetic Reference Field (IGRF) (Finlay et al. 2010) provided by the International Association of Geomagnetism and Aeronomy. It is given in a spherical harmonics expansion up to degree and order 13 at 5-year intervals with linear interpolation between two consecutive models.

An electromagnetic signal traveling through the ionosphere is not only advanced or delayed, but it is also bent due to the varying refractive index within the ionosphere. According to Hoque and Jakowski (2008), this gives rise to two effects on GPS signal propagation. First, the so-called bending effect arises due to the signal not traveling along a straight path between transmitter and receiver and thus the measured distance is too long. This effect was already investigated by Brunner and Gu (1991) or Hoque and Jakowski (2008). Petrie et al. (2010) give a nice review of available mitigation procedures. Second, the dispersive nature of the ionosphere means that GPS L1 and L2 signals travel along slightly different paths through the ionosphere and thus represent different STEC values. Hoque and Jakowski (2008) call this effect the TEC difference range error. Hoque and Jakowski (2008) provide empirical correction formulas for both effects, which we use to correct the observations. The correction for the bending effect can be computed by

$$\begin{aligned} b_\mathrm{gm}= \frac{7.5 \cdot 10^{-5} \cdot \mathrm{STEC}^2 \cdot \exp (-2.13 \beta )}{f^4 HF_2 \cdot (h_\mathrm{m}F_2)^{1/8}} \end{aligned}$$
(10)

where \(b_{\mathrm{gm}}\) is the correction in units of meters depending on the squared STEC in TEC units (1 TEC unit = \(10^{16}\) electrons/m\(^2\)), the elevation angle \(\beta \) in radians, the signal frequency f in GHz, the \(F_2\) layer scale height \(HF_2\) in kilometers, and the peak ionization height \(h_\mathrm{m}F_2\) in kilometers.

The correction for the TEC difference range error is given as:

$$\begin{aligned} \Delta \mathrm{TEC} = \frac{0.1108 \cdot \mathrm{STEC}^2 \cdot \exp (-2.1844 \beta )}{f^2 HF_2 \cdot (h_\mathrm{m}F_2)^{0.3}}. \end{aligned}$$
(11)

The resulting \(\Delta \) TEC will be in TEC units, if \(HF_2\) and \(h_\mathrm{m}F_2\) are in kilometers, frequency f is in Hertz, STEC is in electrons/m\(^2\), and \(\beta \) is in radians. To transform the correction into units of length, the following formula can be applied:

$$\begin{aligned} \Delta \mathrm{TEC [m]} = \frac{40.3}{f^2} \Delta \mathrm{TEC}. \end{aligned}$$
(12)

The values needed to evaluate Eqs. (10) and (11) are the STEC, the peak ionization height and the layer scale height. The STEC is an estimated parameter in the least squares adjustment, and for the peak ionization height and the layer scale height we use global mean values.

2.3 Extended observation equation

The basic observation equations, given in Eqs. (1) and (2), are now extended by the parameters for the ionosphere and the ACVs. In addition, the observations are corrected for known influences. This leads to

$$\begin{aligned} R + \Delta R= & {} \rho + c \delta t + \left( \Delta I_g^{(1)} + \Delta I_g^{(2)} + \Delta I_g^{(3)}\right) \mathrm{STEC} \nonumber \\&+\, \mathrm{ACV}^R_r + \mathrm{ACV}^R_t \end{aligned}$$
(13)

and

$$\begin{aligned}&\lambda \Phi + \Delta \Phi \nonumber \\&\quad = \rho + c \delta t + \lambda n + \left( \Delta I_p^{(1)} + \Delta I_p^{(2)} + \Delta I_p^{(3)}\right) \mathrm{STEC}\nonumber \\&\qquad +\, ACV^{\Phi }_r + ACV^{\Phi }_t. \end{aligned}$$
(14)

\(\Delta R\) and \(\Delta \Phi \) include all known corrections, like phase wind-up, relativistic effects, transmitter clock error, bending correction, differential code biases and the TEC difference range correction. \(\Delta I_g^{(1)}\), \(\Delta I_g^{(2)}\), \(\Delta I_g^{(3)}\), \(\Delta I_p^{(1)}\), \(\Delta I_p^{(2)}\), and \(\Delta I_p^{(3)}\) are the factors for the first-, second- and third-order ionospheric terms, given in Eqs. (6)–(9). \(\mathrm{ACV}^R_r\) and \(\mathrm{ACV}^{\Phi }_r\) are the receiver ACVs for code and phase observations. Finally, \(\mathrm{ACV}^R_t\) and \(\mathrm{ACV}^{\Phi }_t\) are the transmitter ACVs for code and phase observations. These extended observation equations are the basis to set up the least squares adjustment and estimate the sought parameters: receiver position, receiver clock error, STEC, ambiguities, and ACVs. For phase observations, the appropriate wavelength \(\lambda \) has to be applied, according to the used frequency. Hence, the incorporation of new frequencies (e.g., GPS L5) is straight forward.

2.4 Observation weighting

A key aspect in the context of a least-squares adjustment is observation weighting. With increasingly realistic weighting schemes, the quality of the estimated parameters as well as the corresponding variance and covariance information improves. In case of precise orbit determination, two different observation types with different accuracies—the code and the phase observations—are combined in one least-squares adjustment. Thus, a realistic weighting scheme is required. In the context of GPS processing, elevation-dependent weights for observations are commonly used. Therefore, a fixed a priori standard deviation for a certain observation type is scaled according to the elevation. We introduce a more realistic scheme which is dependent on both azimuth and elevation. To take the elevation and azimuth dependency into account, we generate an accuracy map for each observation type based on residuals from a previous iteration with fixed observation weights. The antenna hemisphere is divided into a regular grid and each residual is assigned to one of the grid cells according to azimuth and elevation. For each cell, the standard deviation of the observations is computed by taking into account the redundancies coming from the least-squares adjustment. Figure 1 gives an example of such an accuracy map derived for the satellite mission GOCE. The structure of the map shows that there are deviations in the observation accuracy from a simple elevation-dependent weighting scheme.

Fig. 1
figure 1

Accuracy map for observation type L1C for the satellite GOCE given in millimeters. The plot covers the complete hemisphere down to an elevation angle of 0\(^\circ \)

Full size image

In addition to the azimuth and elevation-dependent weighting scheme, we make use of variance component estimation Koch (2004) to account for possible outliers. The method uses observation residuals and redundancies to estimate an empirical variance for a group of observations. We estimate these variances for each satellite in view, at each epoch, and separately for code and phase observations. The weight for such a group of observations is calculated by

$$\begin{aligned} \hat{\sigma }_k^{2} = \frac{\mathbf {\varOmega _{k}}}{r_{k}} \end{aligned}$$
(15)

where \(\mathbf \varOmega _k\) is the squared sum of residuals \(\hat{e}\) given by

$$\begin{aligned} \mathbf {\varOmega _{k}}=\hat{\mathbf{e}}_k^{T} \hat{\mathbf{e}}_{k} = (\mathbf{A}_{k} \hat{\mathbf{x}} - \mathbf{l}_{k})^{T} (\mathbf{A}_{k} \hat{\mathbf{x}} - \mathbf{l}_{k}) \end{aligned}$$
(16)

and \(r_k\) is the redundancy

$$\begin{aligned} r_k = m_k - \frac{1}{\sigma _k^2} \text {trace}(\mathbf{N}_k \mathbf{N}^{-1}) \end{aligned}$$
(17)

here, \(\mathbf{N}_k\) is the normal equation matrix of the group, \(\mathbf N\) is the full normal equation matrix and \(m_k\) is the number of observations in the group.

The estimated a posteriori variance is compared to the given a priori value. If there is a significant difference, the observation weight is changed according to the empirical variance. The decision on the significance of a difference is made by application of a modified Huber M-estimator (Koch 2004). This method implicitly realizes an outlier detection and removal algorithm. The weight of huge outliers is continuously reduced after each iteration. Practically, such an outlier ends up with a weight close to zero and, therefore, does not contribute to the estimation of the parameters. The only requirement is that the redundancy at each epoch is high enough to reliably detect outliers. Modern spaceborne GPS receivers are tracking up to 12 satellites simultaneously and due to the fully populated GPS transmitter constellation the average number of tracked satellites is in the range of 8 to 10.

3 Real data applications

3.1 Input data

We investigate the performance of our method for precise kinematic orbit determination by applying it to real observation data from GRACE and GOCE. The GRACE time series starts in January 2003 and ends in November 2014, whereas for GOCE we processed the whole lifespan of the satellite from November 2009 to October 2013. Precise orbit and clock information is taken from the Center for Orbit Determination in Europe (CODE) (Dach et al. 2009). Precise orbit positions are given at 15-min intervals. Clock corrections are provided with different sampling rates. If available high-rate clock corrections with sampling rates of 5 s were used (Bock et al. 2009). For periods in which no 5 s sampled corrections were available, 30 s precise clocks were utilized. In addition to precise ephemerides, we used differential code biases also provided by CODE.

Used observations are the code and phase measurements on the original two carrier frequencies of GPS. For GRACE, six observation types are available: three code (C/A, P1 and P2) and three phase (L1C, L1P and L2P) measurements. The receiver of GOCE provides the same three code observations but only L1C and L2P phase observations. In both cases, we used the P1, P2, L1C and L2P observations. To fully exploit the observation data, we used the highest available sampling rate, which is 10 s for GRACE and 1 s for GOCE. For a priori observation weights, we introduced uniform values, except for the final orbit computation where we introduced azimuth and elevation-dependent observation weights. The only preprocessing step was to find cycle slips, which was done by finding jumps in the Melbourne–Wübbena combination. In case of a detected jump, a new ambiguity was set up for this GPS satellite. All computed solutions are float solutions.

3.2 Orbit processing

Figure 2 shows the necessary computational steps to achieve the final orbit solution.

Fig. 2
figure 2

Flow chart of the orbit estimation procedure

Full size image

The first step was to estimate ACVs for all three receivers. This was done individually for each satellite by setting up the daily normal equations and eliminating all epoch-dependent parameters and the phase ambiguities. Then, normal equations of a longer time span were combined and solved to get the ACV parameters. To guarantee a mean value of 0 for the ACVs, the parameters were regularized separately for each observation type. The weights of each daily solution and the regularization matrix were determined by variance component estimation. For each receiver, we estimated a common correction for L1 and L2 phase observations, and two individual parameter sets for the P1 and P2 code observations. For GRACE, a maximum degree of 50 for the spherical harmonics expansion was sufficient. The ACV estimation for GOCE was done up to maximum degree and order 60. For example, maximum spherical harmonic degree 60 corresponds to a half-wavelength resolution of 3\(^\circ \). For each GRACE satellite, we had to estimate two sets of ACV parameters, as we observed that the ACVs differ depending on whether the occultation antenna is switched on or off. The same effect was already observed by Montenbruck and Kroes (2003) with CHAMP data. To avoid mapping of transmitter ACVs into the estimated receiver ACVs, nadir angle-dependent values provided by the IGS were introduced in this first orbit computation.

The second step was to estimate ACVs for all transmitters active during the used time span. The previously estimated receiver ACVs were now introduced as known corrections. One set of ACV parameters was set up for each individual transmitter, without introducing any a priori values, e.g., the IGS values. The separation of transmitters was based on the satellite vehicle number (SVN), based on the assumption that the ACVs are constant for a certain SVN, even if the transmitted pseudo-random noise code (PRN) is changed. Similar to our approach for the receivers, we estimated a common correction for L1 and L2 phase observations and individual corrections for P1 and P2 code observations. Triangle vertex level for localization of the radial basis functions was 20 and restricted to a nadir angle of 17\(^\circ \). For details on the triangle vertex distribution, see Eicker (2008). This results in 101 parameters per observation type and transmitter.

The adjustment was carried out by setting up daily normal equations and eliminating position, clock and ambiguity parameters. The stored normal equations and regularization matrices were then combined to solve for the ACVs. The weight for each normal equation and the regularization was determined by means of variance component estimation. The regularization was applied individually for each observation type and each transmitter to guarantee a zero mean value of the ACVs. GPS antenna center offsets were taken from the IGS antex files. Therefore, we had to distinguish between the two definitions IGS05 and IGS08 to be consistent with the precise GPS orbit and clock information from CODE. Figure 3 shows three examples of estimated phase ACVs, displayed up to a nadir angle of 17\(^\circ \). The chosen examples show a satellite of Block IIR-A (SVN 44), Block IIR-M (SVN 55) and Block IIF (SVN 66). From Fig. 3, it can be seen that transmitter ACVs are not only nadir dependent but also depend on the azimuth and, thus, a nadir angle-dependent representation, as used by the IGS, is not sufficient to cover all the variability of the transmitter ACVs.

Fig. 3
figure 3

Example of estimated transmitter ACVs for L1 and L2 phase observations for SVN 44 (left), 55 (middle) and 66 (right) given in millimeters. Maximum nadir angle shown is 17\(^\circ \)

Full size image

The estimated ACVs were introduced as corrections to the observations for the third orbit computation. The observation residuals of this solutions were then used to generate accuracy maps for each observation type, as described in Sect. 2.4. Together with the ACVs, the accuracy maps were used in the fourth and final step to compute the final kinematic orbit, along with the covariance matrix for each epoch.

4 Results

4.1 Orbit comparisons

One problem in orbit validation is that there are no absolute reference values available for the satellite position. One possibility is to compare with a dynamic or reduced-dynamic orbit. These products incorporate different force models, like an a priori gravity field model. They are far smoother than kinematic orbits, but they heavily depend on the choice of the background models which can introduce additional errors. Therefore, they cannot serve as an absolute reference, but they can help to characterize the noise level of the kinematic orbit.

We investigated the differences with respect to a reduced-dynamic orbit. For the GRACE satellites, the L1B data product GNV1B provided by the Jet Propulsion Laboratory (JPL) (Case et al. 2010) was chosen. For GOCE, we used a reduced-dynamic orbit solution produced by the Astronomical Institute at the University of Bern (AIUB) (Bock et al. 2011), which is provided in the GOCE level 2 SST_PSO (Gruber et al. 2008) product.

When comparing a kinematic and a reduced-dynamic orbit, the differences do not show white noise behavior, as it can be seen in Fig. 4. Long-term deviations are not only caused by errors in the kinematic orbit, but also originate from deficiencies in the reduced-dynamic orbit modeling. To mitigate these deviations, we applied a moving average filter to the differences and subtracted the filtered time series from the original. This approach was also used by Weinbach and Schön (2012) to investigate the noise of kinematic orbits.

Fig. 4
figure 4

Example of position differences between GRACE A kinematic and reduced-dynamic orbit for 3 h on 01.01.2012 in centimeters

Full size image

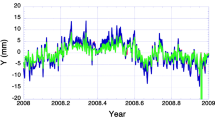
As filter length we chose 5 min, which corresponds to 31 epochs for GRACE orbits at 10 s sampling and 301 epochs for the GOCE orbits at 1 s sampling. Thus, effects with a wavelength longer than 5 min are filtered out and mainly high frequency noise remains. After the filter process, the root mean square error (rms) of the remaining differences was computed for each day. To account for large outliers deviations, larger than 5 cm in the residual time series were rejected from the computation of the rms. For most of the days, the amount of rejected epochs was below 1 %. Figures 5, 6 and 7 show the results obtained for GRACE and GOCE. Figure 8 shows the same investigation carried out with the kinematic orbit for GOCE computed at AIUB (Bock et al. 2011).

Fig. 5
figure 5

Daily rms values of filtered position differences between kinematic and reduced-dynamic orbits for GRACE A

Full size image
Fig. 6
figure 6

Daily rms values of filtered position differences between kinematic and reduced-dynamic orbits for GRACE B

Full size image
Fig. 7
figure 7

Daily rms values of filtered position differences between kinematic (ITSG) and reduced-dynamic orbits for GOCE

Full size image
Fig. 8
figure 8

Daily rms values of filtered position differences between kinematic (AIUB) and reduced-dynamic orbits for GOCE

Full size image

Figures 5, 6, 7, and 8 clearly show that the noise level for the radial component is higher. This is an inherent property of GPS. Due to the observation geometry, the vertical component is worse determined than the horizontal components. This is already known from ground-based applications, where a rule of thumb states that the vertical component is worse by a factor of 1.5 to 2 (Hoffmann-Wellenhof et al. 2008). For GRACE, a degradation of the accuracy occurs for the time frame 2007 until the beginning of 2008 (Figs. 5, 6). This is due to the fact that for this time span only 30 s sampled precise GPS clocks are available, which were interpolated to the 10 s observation sampling. In general, it can be seen that the rms values for all three components are stable and do not show large time dependency, for example, related to the 11-year solar cycle.

The lesson to learn from Figs. 5, 6, 7 and 8 is to know the average high frequency noise level of the different orbits. Therefore, Table 1 lists mean rms values for all satellites. These values give an indication of the noise level of the kinematic orbits in the absence of long wavelength systematic errors. As it can be seen from Figs. 7, 8, and Table 1, the kinematic GOCE orbit computed at AIUB performs slightly worse than our orbit.

Table 1 Mean daily rms values for along, cross and radial components of all three satellite missions over the entire time frame
Full size table

4.2 Gravity field results

Based on our kinematic orbits for the satellites GRACE and GOCE, we computed a time series of monthly gravity fields. For gravity recovery, the short arc integral approach (Mayer-Gürr 2006) was used. The main parameter settings and data products are listed in Table 2.

Table 2 Data and parameters used in the gravity field estimation
Full size table

All monthly solutions were produced independently for each satellite. This provides the opportunity to combine different solutions on the basis of normal equations. Finally, we produced a time series of GOCE only solutions (ITSG-GO) and of GRACE only solutions (ITSG-GR). For validation purposes, GRACE solutions from CSR (CSR-RL05) (Bettadpur 2012) are used. We also computed GOCE monthly solutions based on the kinematic orbits produced at AIUB in the frame of the high-level processing facility (HPF) (Visser et al. 2006). These solutions are similar to those included in the GOCE time-wise model release 4, except for the maximum degree and order, as they were produced in-house applying the same approach. From here on, these solutions are denoted as AIUB-GO.

Figure 9 displays difference degree amplitudes with respect to the static gravity field GOCO03S (Mayer-Gürr et al. 2012) for 10 monthly solutions computed with GOCE orbits. Shown months are Nov. and Dec. 2009, Mar. and Oct. 2010, Apr., Aug. and Dec. 2011, and Jan., Mar. and May 2012. The blue solutions are based on the ITSG orbits; the red solutions were computed with kinematic orbits produced at AIUB (Bock et al. 2011). Apart from the orbit products, the different solutions are based on the same input data and parameter settings. This makes it possible to compare the performance of the different orbit determination methods. Figure 9 shows that the ITSG solutions perform better over the whole spectrum. The largest differences are visible in low degrees, approximately from degree 10 to 20. This can be attributed to the fact that azimuth and nadir-dependent ACVs were used for the transmitters. This has already been shown by Zehentner and Mayer-Gürr (2014).

Fig. 9
figure 9

Degree amplitudes of coefficient differences of 10 monthly gravity field solutions (11.2009, 12.2009, 03.2010, 10.2010, 04.2011, 08.2011, 12.2011, 01.2012, 03.2012, and 05.2012) based on GOCE orbits compared to the GOCO03S model. Solutions were computed with ITSG orbits (blue) and for the same months with AIUB orbits (red). A polar gap of 7\(^\circ \) is taken into account through the rule described by Sneeuw and van Gelderen (1997)

Full size image

The validation of the monthly gravity field models can be also done by comparing them with monthly GRACE solutions derived from highly accurate microwave measurements. A direct comparison is not feasible, due to the high noise level of the SST-hl solutions in contrast to the GRACE solutions. As an alternative approach, we derived gravity variations for selected regions and compared them to values derived from a GRACE time series. In particular, we studied the two most prominent regions where variations can be expected: the Amazon River basin, which exhibits the highest annual variations due to the changing water content; and Greenland, which also exhibits annual variation, but more importantly features the biggest trend in terms of mass change. This trend is due to the massive ice loss caused by the global climate change (Velicogna 2009; Cazenave and Chen 2010).

The GOCO03S (Mayer-Gürr et al. 2012) model served as a reference for our investigations. The difference between GOCO03S and each monthly solution was filtered by a 500 km Gaussian filter to suppress high frequency noise. As we do not aim at the estimation of absolute values of mass change, we omit corrections for leakage effects or glacial isostatic adjustment. Information about the necessary steps to retrieve absolute mass change estimates can be found in Baur (2012). We computed equivalent water heights on a regular grid with a spacing of 0.5\(^\circ \). These grid values were then averaged for each of the two regions to derive a single value for each month and each solution, the area mean values in terms of equivalent water height. Figures 10 and 11 show the results derived from the ITSG solutions based on both GRACE orbits compared to the CSR RL05 solutions (Bettadpur 2012).

Fig. 10
figure 10

Area mean values over the amazon river basin derived from ITSG-GR (blue) and CSR-RL05 (red) monthly gravity fields in terms of water height. To filter high frequency noise, a 500 km Gaussian filter was applied

Full size image
Fig. 11
figure 11

Area mean values over Greenland derived from ITSG-GR (blue) and CSR-RL05 (red) monthly gravity fields in terms of water height. To filter high frequency noise, a 500 km Gaussian filter was applied

Full size image

Figures 10 and 11 clearly demonstrate the ability to derive the annual signal in the Amazon River basin and the trend in Greenland from our kinematic orbits. At this stage, it must be emphasized that each monthly gravity field solution is a stand-alone solution. This means we did not apply a Kalman-filter approach or any post-processing of coefficients, in contrast to other recent publications, for example, by Weigelt et al. (2013) or Baur (2013).

Figure 12 shows area mean values for Greenland derived from our GOCE solution ITSG-GO and the solutions based on AIUB GOCE orbits (AIUB-GO) in terms of geoid height. Both SST-hl solutions are much noisier than the CSR time series, but compared to each other the ITSG solution performs better with less deviations with respect to the reference (CSR-RL05). The results indicate that it is possible to derive a trend estimate for Greenland from the GOCE solution, even though only observations from a single satellite mission are used and the time span is rather short.

Fig. 12
figure 12

Area mean values over Greenland derived from ITSG-GO (blue), CSR-RL05 (red) and AIUB-GO (green) monthly gravity fields in terms of geoid height. To filter high frequency noise, a 500 km Gaussian filter was applied

Full size image

4.3 Other satellite missions

As mentioned in the introduction, the principle of SST-hl can be transferred to any satellite mission carrying a geodetic GPS receiver. This allowed us to compute kinematic orbits and gravity fields for several satellites which are not originally dedicated to the study of Earth’s gravity field. We used data from the satellite missions Swarm (Friis-Christensen et al. 2006), TerraSAR-X (Werninghaus et al. 2007), Tandem-X (Krieger et al. 2007), MetOpA, MetOpB (Edwards et al. 2006) and Cosmic (Rocken et al. 2000). For each satellite, the previously described work flow was used to generate kinematic orbits. This includes estimation of transmitter and receiver ACVs as well as generation of individual accuracy maps for each satellite. Due to high computational burden, the estimation of transmitter ACVs was skipped for MetOpA, MetOpB and Cosmic. Instead transmitter ACVs derived from GRACE data were used.

The gravity field computation follows the same approach we applied to GRACE and GOCE data, described in the previous section. The only difference being that these non-dedicated missions do not provide accelerometer measurements which are used to compensate for non-gravitational forces acting on the satellite. Figure 13 shows degree variances of monthly solutions based on data from different satellite missions.

Fig. 13
figure 13

Degree variances of monthly gravity field solutions from Swarm (March 2014), TerraSAR-X (July 2013), Tandem-X (July 2013), MetOpA (July 2013), MetOpB (July 2013) and COSMIC (July 2013). For comparison also monthly GOCE (July 2013) and GRACE (July 2013) solutions are displayed. A polar gap of 18\(^\circ \) is taken into account through the rule described by Sneeuw and van Gelderen (1997)

Full size image

Figure 13 shows that in principle all missions can be used to estimate Earth’s gravity field. The worst results are achieved with Cosmic data, even though the shown solution is a combination of all five active COSMIC satellites. This is mainly due to the fact that the quality of the GPS observations is very low compared to other missions. Additionally, the attitude determination of the Cosmic satellites is rather poor, with an accuracy of approximately 2\(^\circ \) (Hwang et al. 2008) in each axis, and the orbits of the satellites feature a high altitude of 800 km in combination with a low inclination of 72\(^\circ \).

The results obtained with the satellites MetOpA and B are also clearly inferior to solutions based on, for example, TerraSAR-X or Tandem-X. The reasons can be found in the high orbital altitude of approximately 800 km and a slightly worse positioning accuracy. The degradation in positioning accuracy can be attributed to the fact that the receivers of MetOpA and MetOpB are restricted to a maximum number of 8 tracked GPS satellites.

We achieved promising results with the two radar satellites TerraSAR-X and Tandem-X. Especially for the low degrees (2–10), the accuracy is comparable to the results obtained with GRACE or GOCE. The gravity field solutions obtained with Swarm data are slightly inferior compared to TerraSAR-X or Tandem-X. Only by combining data of all three Swarm satellites, a similar accuracy can be achieved, even though two of the satellites are orbiting at a lower altitude of 430 km. This indicates a slightly worse positioning accuracy for the Swarm satellites, possibly also due to the fact that the Swarm GPS receivers are only tracking a maximum of 8 GPS satellites simultaneously.

5 Conclusions

Based on the presented results, we conclude that the presented approach for precise orbit determination is applicable. The main advantage of our method is the fact that observations are directly used as they are observed by the receiver. This preserves the original measurement accuracy and gives the possibility to fully exploit the contained information of each individual observation type. The inclusion of new observables (new L5 signal) is straight forward, because the observation equations are set up individually and no combinations are used. The approach also includes a realistic observation weighting scheme as well as a sophisticated handling of different error sources. Precise knowledge of these errors, for example receiver and transmitter ACVs or precise transmitter orbits and clocks, can be seen as the Achilles’ heel of our approach. Furthermore, ionospheric modeling shall be reviewed and maybe adopted for LEO positioning. Validation shows that the produced orbit solutions feature the same or better accuracies as compared to existing methods. Gravity field estimates based on our kinematic orbits are slightly better than solutions based on kinematic orbits published by other research institutions. An important aspect is that the orbits show the potential to assess time variations in Earth’s gravity field. We also showed that the principle of SST-hl can be transferred to any satellite mission equipped with a geodetic GNSS receiver.

With further work towards optimizing the orbit computation and a detailed analysis of remaining errors, SST-hl can be a great opportunity to fill a possible gap between GRACE and its successor GRACE follow-on. Apart from being a gap filler, we demonstrated that SST-hl can be seen as an additional viable method to quantify changes in Earth’s gravity field and thus can contribute to a better understanding of processes in the system Earth. All orbits presented here are freely available at: ftp://ftp.tugraz.at/outgoing/ITSG/tvgogo/orbits.