Rescue of the historical sea level record of Marseille (France) from 1885 to 1988 and its extension back to 1849–1851

Abstract

This paper describes the historical sea level data that we have rescued from a tide gauge, especially devised originally for geodesy. This gauge was installed in Marseille in 1884 with the primary objective of defining the origin of the height system in France. Hourly values for 1885–1988 have been digitized from the original tidal charts. They are supplemented by hourly values from an older tide gauge record (1849–1851) that was rediscovered during a survey in 2009. Both recovered data sets have been critically edited for errors and their reliability assessed. The hourly values are thoroughly analysed for the first time after their original recording. A consistent high-frequency time series is reported, increasing notably the length of one of the few European sea level records in the Mediterranean Sea spanning more than one hundred years. Changes in sea levels are examined, and previous results revisited with the extended time series. The rate of relative sea level change for the period 1849–2012 is estimated to have been $1.08\pm 0.04$ mm/year at Marseille, a value that is slightly lower but in close agreement with the longest time series of Brest over the common period ($1.26\pm 0.04$ mm/year). The data from a permanent global positioning system station installed on the roof of the solid tide gauge building suggests a remarkable stability of the ground ($-0.04\pm 0.25$ mm/year) since 1998, confirming the choice made by our predecessor geodesists in the nineteenth century regarding this site selection.

Introduction

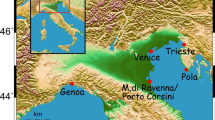
The main tide gauge at Marseille on the southeast coast of France (Fig. 1) has been maintained since 1885. It was especially devised to accurately define the origin of the French national height system (the ‘Nivellement Général de la France’ or NGF) by providing direct measurements of the mean sea level (MSL) through an original recording device designated as a ‘totalisateur’, an ingenious mechanical integrator capable of providing MSL values over specified sampling periods such as a day or week, as described below (Reitz 1878). Those measurements of MSL taken between February 1885 and December 1896 were used to define the datum for the geodetic levelling of mainland France. However, although the mean sea surface had appeared the most suitable equipotential reference level against which a national height system could be referenced, a certain concern about its actual stability and uniformity was raised. It is worth reminding ourselves that the first theories of past ice ages had just emerged a couple of decades before (e.g. Agassiz 1840), and evidence was being accumulated to assess them. The above concern kept French geodesists recording the mean sea levels beyond 1896 as a datum control of the NGF levelling, subsequently supporting early studies of long-term changes in mean sea levels (e.g. Vignal 1935; Gutenberg 1941).

Fig. 1

Observing locations of the rescued historical tide gauge records at Marseille, France. The insert shows the stations mentioned in the text

Today, Marseille is one of the few European tide gauge records in the Mediterranean Sea spanning more than one hundred years. The scarcity of long tide gauge records and the spatial variability of the rates of sea level change along the coasts of the world make the Marseille record particularly interesting in the study of long-term ocean and climate variability (e.g. Woodworth 2006; Marcos and Tsimplis 2007a; Church and White 2011). In line with this interest, the Marseille tide gauge has been committed to the core network of stations of the Global Sea Level Observing System (GLOSS) since its inception in 1985 (Merrifield et al. 2010). It has also been contributing data to the Permanent Service for Mean Sea Level (PSMSL; Holgate et al. 2013). However, only mean sea levels have been provided so far, because the ‘totalisateur’ was the primary recording device, and the classical recorder (tidal charts) was considered a backup that was used occasionally to control the ‘totalisateur’ and had never been exploited, except for the years 1985–1986. The latter years were digitized by the French hydrographic agency (SHOM) for a specific campaign of depth soundings and their reduction to the nautical chart datum.

The interest for high-frequency sea level data (at least hourly) has been repeatedly expressed by the scientific community (IOC 2012). Within this context, the French mapping agency (IGN) decided to undertake the digitisation of the circa 1200 nine-metre-long tidal charts recorded between 1885 and 1988 and to install a modern acoustic tide gauge in July 1998, providing sea levels at 10-min sampling intervals. This acoustic gauge was later on replaced by a radar gauge in April 2009 with a 1-min sampling rate and real-time transmission capabilities (Martín Míguez et al. 2008a). In 1988, the classical recording device stopped due to the last gauge attendant retiring and the nine-metre-long paper rolls for the tidal charts becoming difficult to acquire. Nevertheless, the tide gauge has continued operating, and MSL readings have been taken with the ‘totalisateur’ recording device with a roughly weekly sampling interval until present.

The publication of the recovered 1885–1988 hourly data set and the results of the metrological work undertaken to assess its quality was further delayed in 2009 by the discovery of an older tide gauge record (1849–1851) while analysing the documentation collected from historical archives. In this study, we finally present both sea level records providing assessments of their quality and examining to what extent the sea level time series are consistent since 1849 at Marseille. The article is organized as follows. It begins by giving an overview of the background for the establishment of the tide gauges as well as some details of the construction and operation of the main one (Sect. 2). The ingenious system that provides direct readings of the true mean sea level since 1885 (the ‘totalisateur’ or mechanical integrator) is described in Sect. 3. The issue of assessing the quality of the recovered hourly data is then addressed in Sect. 4, implementing standard procedures (IOC 1985) as well as specific ones devised for our case study of the data sets. The connection of the data sets to a common datum is assessed. Finally, the sea level variations since 1849 are revisited based on the updated and extended Marseille time series.

Historical background and local setting

The problem of the origin of the national height systems was discussed in the mid-nineteenth century. The question of whether a mean sea level would be more logical than a low tide level was raised in France in 1847 when the first attempt to define the reference level for all French levelling networks in the mainland was undertaken (Bourdalouë 1847). Eventually, the concept of the geoid was defined as that equipotential surface of the Earth’s gravity field that most closely coincides with the mean sea level. The choice of that particular surface was motivated at that time by the belief that the average level of the sea was uniform and stable over long periods of time. In 1864, the International Association of Geodesy (IAG) urged maritime countries to carry out continuous sea level observations at as many sites as possible and to link them by precise levelling. The foreseen purpose was to provide the future means by which the zero level for all European levelling networks could be established (Lallemand 1890).

In France, a ministerial decree of 13 July 1860 stated that the origin of the (first) unified levelling network (nowadays designated as NGF-Bourdalouë) was the 0.40 m graduation mark of the marble tide staff located at Fort Saint-Jean in the old harbour of Marseille (Fig. 1). That graduation mark was supposedly at the mean sea level of that harbour. However, it remains an enigma how it was actually determined. Little information has been found on the tide staff itself, which was likely installed between 1846 (the date of the project to construct a canal in the old harbour) and 1856 (Délestrac 1856). Its destruction is, however, precisely dated as 21 August 1944 when the north pillar of the transporter bridge was exploded by the German Kriegsmarine, hitting the marble tide staff and breaking it. Nevertheless, early concerns about the accuracy of that mean sea level determination, progress in levelling techniques, the above-mentioned IAG (1864) recommendation and the necessity of densification shortly led to the idea of establishing a second national levelling network and height system in France (Lallemand and Prévot 1927), nowadays designated as NGF-Lallemand.

A great deal of attention was then given to the determination of an accurate mean sea level for the origin of the second national height system (Bouquet de la Grye 1890; Lallemand and Prévot 1927). The choice of Marseille in the Mediterranean Sea was maintained, considering both the small tidal range of about 10 cm and the land stability of the region. The region of Marseille is indeed considered to have been tectonically stable, at least during the late Pleistocene (Guieu 1977). Global positioning system (GPS) data have further confirmed the stability of the tide gauge station (Sect. 5). The location of the tide gauge was chosen to be on the open sea and away from any freshwater supply. It is about 1.9 km south of the Fort Saint-Jean tide staff (Fig. 1).

Considerable efforts were subsequently invested to establish that tide gauge station: the sole instrument cost 10,450 Francs (of that epoch) and the buildings 37,600 Francs, not mentioning the studies and the many meetings of the NGF levelling committee (Bernard 1899; Lallemand and Prévot 1927). Two solidly grounded buildings comprise the station: one for the tide gauge and the other for the dedicated gauge attendant (Fig. 2). They were built in 1883, whereas the instrument was assembled in Marseille between November 1884 and January 1885, starting observations on 3 February 1885. Further details on that instrument are provided in Sect. 3.

Fig. 2

Overview of the main components of the main tide gauge station operational at Marseille, France, since February 1885 (a); sketch of the tide gauge building with the exact location of the recording and floating devices, the stilling well and the fundamental benchmark (b)

Figure 2a shows the entrance that leads to the stilling well through a channel that was carved 0.60 m deep below the low tide. In between, the stilling well and the entrance of the channel were set a bronze door, a small brick wall and a steel sheet; all of them having holes at their base that can be opened or closed at will. These obstacles were intended to mechanically filter out high-frequency wave action or lapping while keeping the semi-diurnal tide and the longer period signals unchanged (Bernard 1899).

An instrument devised for Geodesy

Description

To our knowledge, only two other similar instruments were operating at that time, all of them (including that of Marseille) built by the same firm of Dennert & Pape in Altona, near Hamburg, Germany. They were installed the same year 1880, in Cadiz, Spain, and in Helgoland, a British possession at that time (Fig. 1). Both Cadiz and Helgoland tide gauges stopped recording a long time ago, in 1924 (Marcos et al. 2011) and presumably in 1901 (Rohde 1982), respectively. Only Marseille has kept operational since its installation in 1885.

Figure 3a shows an overview sketch of the Marseille tide gauge. The gauge was firmly set above the stilling well on the upper floor (Fig. 2b). Briefly, it is a high-precision mechanical floating gauge supplemented with a mechanical integrator. The mechanical integrator (‘totalisateur’) is located on the left part of the sketch in Fig. 3a (left of the platinum ribbon) and is further detailed in Fig. 3b with frontal (bottom right) and lateral (bottom left) views. A most important part of the tide gauge is the ‘40.500 litres’ (original unit) copper float of 0.9 m in diameter and 0.2 m in width. It is connected with a pulley mechanism to the recording devices, that is, the pen carriage tracing out the sea level variations on a paper chart and the roller carriage of the ‘totalisateur’. The paper roll is set on a 48-h rotating cylinder driven by a mechanical clock, resulting in a paper speed of 12 mm/h or about 105 m per year. The graphical recording is a duplicate one. Originally, two pens with diamond points were simultaneously tracing out the sea level variations on a specific blackened glazed paper which was split into two tidal charts while rotating: one was kept on-site, whereas the other was sent to Paris for archiving. The tide gauge has a reduction ratio of 10 (ratio of the amplitude of sea level variations in the open sea to that recorded).

Fig. 3

Overview of the Marseille tide gauge (a), whose mechanical integrator (‘totalisateur’) is depicted in the frontal (bottom right) and the side (bottom left) views (b)

The design of the Marseille tide gauge was supplemented with substantial original instructions from Charles Lallemand (Lallemand and Prévot 1927). However, the most ingenious part is definitely the mechanical integrator (Reitz 1878). This mechanical integrator was designated as the ‘totalisateur’ in French, hence giving its name to the tide gauge. Figure 3a indicates how it works. As the float rises and falls with the sea level in the stilling well, its vertical movement is reduced by a factor of 10 and horizontally translated to the rack and its pen carriage. The horizontal movement further transforms into a vertical one of the carriage holding the rollers ($r1$) and ($r2$). The platinum ribbon is intended to ensure the rigorous mechanical translation of the rack movement. The rollers are made of agate (SiO3) while the integrator disk ($Q$) upon which they are in contact is made of glass, ensuring an exact contact so that there is no slipping or hooking on it. The integrator disk rotates with the chart cylinder driven by the same mechanical clock. Its axis is aligned to that joining the rollers ($r1$) and ($r2$).

For the sake of simplicity, Fig. 3b illustrates the principle of the mechanical integrator mechanism with only one roller ($r$). The diameter of the roller ($r$) is a given constant $(\lambda )$. Both the integrator disk ($Q$) and the roller ($r$) are equipped with loop counters. Provided there is no slipping or hooking on the integrator disk, the following relationship (E1) holds:

$$\begin{aligned} \frac{\lambda }{2}\times \delta n=z\times \delta N \end{aligned}$$

(E1)

with $(\delta n)$ the difference of the readings ($n1$–$n0$) on the roller counter of ($r$) between two successive epochs (t0) and ($t1$), ($z$) the sea level variations (reduced by a factor of 10) between those two epochs and $(\delta N)$ the corresponding difference ($N1$–$N0$) on the disk counter of ($Q$). The latter quantity $(\delta N)$ is proportional to the time difference ($\delta t$ or $t1$–$t0$) between the two epochs, K being equal to 1/2 if expressed in days (one loop every two days):

$$\begin{aligned} \left\{ {{\begin{array}{l} {\delta N=K\times \delta t} \\ {K=1/2} \\ \end{array} }} \right. \end{aligned}$$

(E2)

From Eqs. (E1) and (E2) can be derived the integration of the sea level curve between two epochs ($t0$) and ($t1$) and subsequently its rigorous mathematical mean (Zm) by simply subtracting the corresponding readings on the loop counter ($n1$–$n0$) and dividing by the elapsed time ($t1$–$t0$) as follows:

$$\begin{aligned} \begin{array}{l} z_m \!=\!\frac{10}{t_1 \!-\!t_0 }\int \limits _{t_0 }^{t_1 } {z\cdot \delta t\,{=}\,} \frac{10\lambda }{2\cdot (t_1 \!-\!t_0 )}\int \limits _{t_0 }^{t_1 } {\frac{\delta n}{\delta N}\cdot \delta t=\frac{10\lambda }{2K\cdot (t_1 -t_0 )}\int \limits _{n_0 }^{n_1 } {\delta n} } \\ z_m =\frac{10\lambda }{2K}\cdot \frac{n_1 -n_0 }{t_1 -t_0 } \end{array} \end{aligned}$$

(E3)

The factor of 10 corresponds to the mechanical reduction factor (see above). Consequently, the ‘totalisateur’ directly yields mean sea levels between two epochs following the rigorous mathematical definition (integration of a curve), at any desired frequency determined by the time interval between the operator’s readings. Further description on the mechanical integrator can be found in old German from the original publication by Reitz (1878) or in French (Bernard 1899; Lallemand and Prévot 1927). Coulomb (2014) provides an extensive and comprehensive review of the substantial amount of material gathered so far (correspondence, account, photographs, sketches, etc.).

Data sets and datum relationship

Table 1 summarizes the various tide gauge data sets that are presently available for Marseille. A data set is defined here as a comprehensive set of sea level observations that are related to the same location and gauge.

Table 1 Overview of tide gauge data sets at Marseille

The earliest sea level observations at Marseille date back to 1849 from one of the first self-recording float tide gauges devised in France (Chazallon 1859). Figure 1 shows its location in the Harbour of La Joliette, about 3 km north of the ‘totalisateur’ tide gauge. Values every half an hour from November 1849 to May 1851 were recently rediscovered in the form of handwritten tabulations. The associated tidal charts have not been found so far. Surprisingly, the tabulated data were expressed in ‘apparent solar time’, in spite of ‘mean solar time’ being the legal time since 1816 in France. Pouvreau (2008) reports on this anachronism, which lasted between 1846 and 1860 in the recording of tide gauges under Chazallon’s supervision. Indeed, using a variable time scale such as the apparent solar time requires daily corrections to adjust from the naturally linear time scale of a mechanical clock. In the case study of Marseille, the historical documentation states that the Chazallon tide gauge recorded in mean solar time, whereas the tabulated data had been corrected to be in apparent solar time. Consequently, the following corrections have been applied to the tabulated (only the hourly values were digitized) Marseille 1849–1851 record:

• correction from apparent solar time to mean solar time at Marseille by applying the ‘equation of time’ given in Savoie (2001);

• correction from mean solar time to universal time (UT) by subtracting 21.575 min, a value corresponding to the difference in longitude between Marseille and Greenwich.

The latest data sets come from an acoustic and a radar tide gauge (sets 3 and 4 in Table 1, respectively). These gauges have provided high-frequency sea level data directly in digital form and UT system from October 1998 to April 2009 and from April 2009 to the present, respectively. The radar gauge replaced the acoustic one in April 2009, mostly because of repeated malfunctioning of the acoustic sensor since November 2000 (discussed later on in Sect. 4.4). The sea levels of the above-mentioned modern and oldest data sets (data sets 1, 3 and 4 in Table 1) are referred to a common nautical chart datum, the so-called ‘Zéro hydrographique’ (ZH). These observations were undertaken under the supervision of French hydrographers, whose golden rule since the early nineteenth century has been to refer to that datum for sea level observations (Beautemps-Beaupré 1829). The ZH is usually represented by a local set of tide gauge benchmarks, including tide staffs installed in such a way that their zero graduation marks coincide with the nautical chart datum ZH, whatever the practical realization of the ZH (Wöppelmann et al. 2006a). Considering that both the Fort Saint-Jean marble staff and the Chazallon tide gauge were contemporary and their zero set to be at the ZH, it is reasonable to speculate that levelling operations had connected them, ensuring the same datum.

The main data set comes from the ‘totalisateur’ tide gauge, which has been working continuously from February 1885 to the present, with short interruptions due to mechanical failures or maintenance. Actually, two separate records result from this tide gauge: one from the mechanical integrator (‘totalisateur’), which consists of tabulated MSL readings from the loop counters (daily), and the second from the tidal charts (continuous curve). The main record has been that of the mechanical integrator, to which most of the geodesists’ attention has been focused. Its MSL data from 1885 onward have been readily provided to the international community and public data banks such as the PSMSL. The modern tide gauges have taken over the MSL provision since 1998, despite the readings performed on the integrator continuing on a roughly weekly basis since 1988, instead of a daily basis when there was a dedicated gauge attendant. The tidal charts were barely exploited, but scrupulously archived in Marseille and Paris. Chart recording eventually stopped in August 1988 with the retirement of the last gauge attendant, the difficulty to acquire the specific nine-metre-long and 17-cm-width paper rolls, and the somehow lack of interest for sea level observations at the French mapping agency. However, under the pressure of the national committee representative of the International Union of Geodesy and Geophysics (IUGG), the tidal charts were gathered and digitized with variable efforts depending on the human resources available at the French mapping agency. The years 1909 (important works at the tide gauge), 1913 (missing tidal charts at both the Marseille and Paris archives), 1921 and 1924 (tidal curves illegible) were not digitized.

In agreement with its geodetic rationale, the internal reference of the mechanical integrator was referred to the French national levelling datum (NGF-Lallemand), once it was established using MSL data from February 1885 to December 1896 (Lallemand and Prévot 1927). The fundamental benchmark for France, which defines that datum, is a brass bolt covered with a very hard alloy of platinum and iridium. It is embedded in a granite block set in the bottom floor of the tide gauge building (Fig. 2b). Figure 4 summarizes the relative position of the NGF datums and the most significant reference levels at Marseille that we have dealt with. For the sake of completeness, the PSMSL datum (RLR in Fig. 4) and the GPS antenna reference point are indicated as well. The nautical chart datum ZH is defined at Marseille as 0.329 m below NGF-Lallemand or 1.989 m below the fundamental benchmark. It corresponds to the zero graduation mark of the Fort Saint-Jean marble tide staff. It is worth noting here for future historical studies that there is about 1 mm difference between the heights expressed in NGF-Lallemand and those expressed in NGF-IGN69 which arises from the type of heights (orthometric versus normal heights, respectively). Most precisely, the height of the fundamental benchmark is 1.660 m in NGF-Lallemand and 1.6607 m in NGF-IGN69.

Fig. 4

Datum and reference levels associated with the tide gauge records in Marseille. ‘$h$’ is the ‘tide gauge constant’ (see text)

Figure 4 also shows the relationship between the tide gauge (TG) index or rack index and the centre separating the two integrator rollers (Fig. 3a), which corresponds to the zero of the mechanical integrator. They are mechanically linked to be 1 metre. By calibrating the TG index, the MSL readings on the ‘totalisateur’ can be referred to the levelling datum as follows:

$$\begin{aligned} \hbox {MSL}=h-(1{,}000+\eta )-\frac{10\lambda }{2K}\times \frac{{\left( {\delta n^{\prime }+\delta n^{\prime \prime }} \right) }/2}{\delta T} \end{aligned}$$

(E4)

where (h) is known as the tide gauge constant which relates the TG index to the levelling datum, $(\eta )$ is intended to take into account any mechanical distortion of the rack or the platinum ribbon (none observed since 1909), and the last term comes from (E3) by averaging the difference of readings over the time interval $\delta T$ from two rollers instead of one in (E3), that is, $\delta n$’ on roller ($r1$) and $\delta n$” on ($r2$). The negative sign corresponds to the roller carriage falling while the float rises and vice versa (Fig. 3a).

Assessing the quality of the recovered data

Calibration procedures and internal control

Sounding probes are the means by which the ‘totalisateur’ tide gauge has historically been calibrated. The calibration consists in determining the tide gauge constant (h) in equation (E4) by comparing the sea level readings on the TG index to that obtained using a sounding probe referenced to the fundamental benchmark and hence to the levelling datum (Bonnetain et al. 2009). Under a perfect functioning and ideal environmental conditions, without important changes in the tide gauge components such as the length of the wire or the platinum ribbon, the tide gauge constant remains unchanged, as its name suggests. However, changing components of the tide gauge ultimately occur over long-term periods due to mechanical failures or maintenance, which require to recalibrate the instrument and recalculate the constant. Fortunately, such changes are generally documented in the log books where the daily MSL readings of the ‘totalisateur’ were reported. In addition, mechanical devices cannot be assumed to be free of drift, which will be reflected in drifts in the resulting data due to parts wearing out. Consequently, routinely monitoring of tide gauges for drifts by comparison to readings taken from tide staffs and/or sounding probes is recommended (IOC 1985), even though no noticeable change has occurred. The IOC (1985) also recommends carrying out a test specifically designed by the French engineer C. van de Casteele (1903–1977) for assessing the performance of mechanical tide gauges (Lennon 1968). Basically, this test consists of establishing a diagram plotting readings taken with a reference probe against its differences with the tide gauge readings over a complete tidal cycle (12h25min). Further details can be found in Martín Míguez et al. (2008b), who have extended the test to modern tide gauges.

In Marseille, the on-site presence of a gauge attendant certainly ensured the best possible control of the instruments. In particular, the detailed quality controls reported in the next sections show a couple of periods where the malfunctioning of the tide gauge could be related to the gauge attendant not being well or newly appointed with no supervision or overlap with the former gauge attendant. Nonetheless, as was mentioned above, the chart recording was mostly scrupulously carried out and readily archived with little exploitation, contrary to the ‘totalisateur’ recording which received the geodesist’s exclusive attention. In this line of evidence, the first obvious quality control of the recovered hourly data is to compute monthly mean sea levels and to compare them to the historically quality controlled ones from the ‘totalisateur’. The monthly averages were selected in this exercise mainly because the tidal charts were replaced monthly. Any malfunctioning in the chart recording or problem with the tidal chart setting will thus likely affect the whole monthly data and its average.

Figure 5 illustrates the main results obtained in controlling and correcting (where possible if the error was understood) the recovered data from the tidal charts by comparison to the MSL data from the ‘totalisateur’ recording. The final step of this exercise (Fig. 5d) shows a standard deviation of 1.6 cm for the monthly differences, which can be considered an excellent result taking into account the factor of 10 reduction from the charts. Indeed, it means that the tidal charts were set to the reference level to within 1-2 mm each month, and the digitisation process did not introduce significantly larger systematic errors within each month. Figure 5a corresponds to the rough comparison with the data issued from the digitization process. In Fig. 5b, basic errors such as erroneous dating or mixing up the zero level used for the chart digitization were detected and corrected (Philippe 2003). There were four people involved in the digitization process, which lasted several years, although they were not working simultaneously or digitizing the tidal charts chronologically. It was puzzling to figure out the required correction to obtain Fig. 5c. The issue was found to be an erroneous scaling factor setting of 0.5 or 0.75 in the preliminary step of digitizing the data (Philippe 2003). Figure 5d is finally obtained after applying the tide gauge constants (h) that were reported in the log books of the tabulated MSL readings.

Fig. 5

Differences between monthly averages in sea level obtained from the digitized tidal charts minus those obtained from the mechanical integrator readings (‘totalisateur’): a directly after the tidal chart digitization; b after detecting basic errors (time shifts of 12 h, erroneous dating, mixing up the zero level used for the chart digitization); c after correcting for erroneous scale factors of 0.5 and 0.75 during the digitization; and d after applying the tide gauge calibration constants

‘Buddy checking’ with Genova

The comparison with the adjacent long-term sea level record of Genova, Italy, provides an external means to further evaluate the quality of the Marseille MSL data. The Genova MSL record is considered as mostly reliable (Tsimplis and Spencer 1997; Woodworth 2003). It was obtained from the Revised Local Reference (RLR) data set of the PSMSL and covers a substantial common period with the Marseille record, except for the long data gap between 1910 and 1927 and unfortunate unavailability of Genova data after 1996.

Figure 6a shows that the inter-annual signal structure is very similar in the two records, as might be expected from two sites located only 310 km apart along the same coastline (Fig. 1). The linear trends of Marseille and Genova over the common periods of 1885–1996 (‘totalisateur’) or 1885–1988 (tidal charts) are statistically identical at $1.25\pm 0.10$ mm/year. The conclusions from the comparison with Genova apply both to the MSL data from the ‘totalisateur’ and to the tidal charts recordings. The numerical differences using the ‘totalisateur’ or the chart data are found to be not statistically significant, as one would expect from the previous section. The zero-lag correlation coefficients of the de-trended monthly and annual MSL time series over the common period 1885–1996 are 0.85 and 0.89, respectively, significant at the 99 % confidence level. By differencing both MSL records, most of the spatially coherent sea level variability is removed, leaving a time series which will mostly reflect instrumental errors and local variability in either of the tide gauge records (Fig. 6b).

Fig. 6

Comparison between annual mean sea levels at Marseille and Genova (a); and differences between both time series (b)

The clear peak in 1951–1952 has been noticed in previous studies (e.g. Tsimplis and Spencer 1997; Woodworth 2003), but little explanation had been obtained on the origin of the malfunctioning. By examining the historical documentation, we have found that it corresponds to a period from August 1951 to November 1952 when the gauge attendant had serious health problems and the supervising engineer in Paris had just taken over the responsibility of the levelling department. In November 1952, the float was found submerged at the bottom of the stilling well. From this event onward, the attention seems to recover to its previous quality. There is no evidence in the historical documentation that the gradually increasing difference of sea levels evident between 1956 and 1959 in Fig. 6b is a result of instrument malfunctioning in Marseille. It might be real or due to errors in the Genova record. The root mean square (RMS) of the de-trended annual MSL differences is 0.026 m and reduces to 0.020 m if the data from 1951 to 1952 are discarded. No significant reduction is obtained by discarding the 1956–1959 data. Both RMS values are within the range of 0.01–0.03 m reported by Woodworth (2003) for ‘high-quality’ records.

Tidal analysis and tidal residuals

Tidal analysis was first applied to the hourly sea level record on a yearly basis. For each year, a classical harmonic analysis was separately performed using the standard tidal analysis package t_tide (Pawlowicz et al. 2002), which enables to search for up to 146 tidal constituents. In this study, we considered only those constituents with a signal-to-noise ratio larger than 2 (Table 2). Confidence intervals of amplitudes and phase lags of each constituent were determined based on a correlated bivariate white noise model (Pawlowicz et al. 2002). Tides at Marseille are small ($\sim$0.1 m) and are dominated by the semi-diurnal oscillation, M2 being the major constituent; its yearly amplitudes and phase lags together with the associated confidence intervals are plotted in Fig. 7. As noted by others (e.g. Agnew 1986; Pugh 1987), changes in the tidal constituents may indicate malfunctioning of the instrument. In particular, whenever the stilling well gets obstructed by sediments collected in its bottom, there can be expected to be an attenuation of the amplitude of tidal variations and a phase shift of the tidal oscillations. These features are clearly observed during the periods 1926–1928 and 1937–1940 (Fig. 7), with variations that can reach 50 % decrease in the amplitude of M2.

Table 2 Main ocean tide constituents at Marseille

Fig. 7

Evolution of the M2 ocean tide constituent: a amplitude in mm; and b phase lag in degrees

By analysing the historical documentation (Guillot et Bezault 1928), we found out that important maintenance works were carried out in July 1928, in particular in the channel leading to the stilling well (Fig. 2a). This channel had not been cleaned since 1916 and was found to be substantially cluttered with sediments. The second period 1937–1940 could not be related to a clear specific event, although it might be worth mentioning that a new gauge attendant was appointed in 1938 and the urgent need for a cleaning of the channel was expressed in 1941. Additionally, a smaller decrease of about 1 cm in amplitude with increasing phase lag is also noted in 2009, suggesting a similar but less serious obstruction problem. This was confirmed later on by the cleaning operation carried out on 27 October 2010. A more thorough analysis, described in the following, was devised to determine timing errors in the time series.

The years 1941–1956 were identified as the longest continuous period of time with highly stable yearly values of tidal amplitudes and phase lags (Fig. 7). This 16-year-long period was consequently used to estimate the most reliable tidal constituents for Marseille showing a signal-to-noise ratio larger than 2. They are listed in Table 2 with their 95 % confidence levels. Annual and semi-annual cycles were not included since they mostly originate from non-astronomical forcing. The largest constituent is M2 displaying an amplitude of 6.8 cm, followed by K1, S2, O1, N2 and P1, with amplitudes between 1 and 3 cm. The remaining constituents show amplitudes smaller than 1 cm. The associated uncertainties are always about 1 mm. Uncertainties in the phase lag of the major constituents (those with amplitudes larger than 1 cm) are smaller than 5 degrees.

The main tidal constituents listed in Table 2 were used to build the tidal prediction hourly time series for the years when observations exist. A careful comparison between the predicted tides and the observations was then performed in order to identify and remove, where possible, the effects of timing errors. The procedure developed for this purpose consists in computing the time lag of maximum correlation between the tidal and the observed signals for each month. The choice of monthly batches corresponds to the frequency of tidal chart replacement. As the timing errors are expected to be smaller than the sampling rate of 1 h (digitized sea levels), the time series were first linearly interpolated onto a 1-min time interval. The data gaps were kept the same as in the original observational record to avoid the introduction of spurious information.

Figure 8a plots the monthly time lags corresponding to the maximum correlation. Vertical lines in Fig. 8 denote particular events or periods that were eventually found meaningful to explain the evidenced discrepancies between observations and tidal predictions. From 1885 to 1911, a delay of about 28 min on average with respect to the tidal prediction is evidenced. This delay roughly corresponds with the changes in the legal time system definition. It first changed from Local Mean Time in Marseille to Local Mean Time in Paris on 15 March 1891 and later on to Greenwich Mean Time on 10 March 1911. The total time difference amounts to 21.575 min (Sect. 3.2). From our results, there is no evidence that the first legal time system change was taken into account in the Marseille tide gauge recording. No clear record was either found on the second legal time system change in spite of being actually effective in our results (Fig. 8a). Consequently, the digitized hourly sea levels from Februry 1885 to March 1911 were corrected by $-21.575$ min (Fig. 8b) in agreement with the known time difference between the Marseille and the Greenwich locations.

Fig. 8

a Time lags derived from the maximum autocorrelation obtained using the observed tide gauge signal and the tidal predictions based on the hourly data between 1941 and 1956; b same but taking into account of the difference between local mean time in Marseille and local mean time in Greenwich (or Universal Time) and discarding the periods where there is indication that the stilling well was obstructed (see text)

The largest time lags were found for the periods 1925–1928 and 1937–1940, coincident with the periods when the above tidal analysis showed noticeable changes in the M2 yearly amplitudes and phase lags (Fig. 7) attributed to a channel and stilling well obstruction. The changes are evidenced in fine detail using our approach that computes the time lags of the observations with respect to the astronomical tide or clock (Fig. 8a). The results from this approach confirm that a stilling well obstruction occurred between May 2009 and October 2010. It was finally confirmed by the cleaning carried out on 27 October 2010. Data demonstrating such obstruction behaviour needs to be rejected from any subsequent sea level analysis focused on the high-frequency domain of the spectrum. We therefore removed those three periods from the final quality controlled hourly data set of the Marseille tide gauge (Fig. 8b). They should be flagged in the public data banks that make Marseille tide gauge data available such as the GLOSS data centres.

The most enigmatic results arise from the period 1957 to 1988 during which an apparent cyclic-like behaviour is evidenced in the time lags (Fig. 8) and in the phase lags of M2 (Fig. 7). A tentative (speculative) explanation could come from the obstacles set between the stilling well and the entrance of the channel (Fig. 2a). As mentioned in Sect. 2, they comprise holes at their base that could be opened or closed at will. However, little information is known about their setting of how much they were actually opened or closed. However, it is worth reminding that these timing errors have little influence on the monthly and annual averages.

The era of modern tide gauges

The era of modern tide gauges is out of the scope of this data archaeology study. However, for the sake of completeness and revisiting changes in sea level while updating and extending the Marseille record back to 1849, the hourly data of the acoustic and radar tide gauge were included in the above quality controlled analysis. Those particular data sets would certainly benefit from a future and dedicated study. The results displayed in Fig. 8 reveal substantial timing shifts starting in November 2000 that gradually recover around October 2006. The tide gauge station underwent building works between November 2000 and April 2001, well after the acoustic tide gauge was installed (October 1998), which apparently altered the timing of the observations. No other maintenance or building work has been reported. Without any further information and understanding, the data cannot objectively be corrected for the observed time lags.

It is also worth noting a sudden but small increase of nearly 1 cm in the M2 amplitude in the years 2010–2012 (Fig. 7), not accompanied by any significant change in its phase lag, however. The harmonic analysis suggests that these recent estimates are reliable and stable after the installation and setting up of the new radar tide gauge in April 2009. The reasons for such an increase in the M2 amplitude remain thus unclear. The aforementioned tentative explanation of varying opening in the water admission through the channel towards the stilling well cannot hold here as the tidal analysis shows estimates of M2 amplitude and phase lag for the years 1849–1851 in close agreement with the float gauge all over its 1885–1988 period, thus rather pointing to an instrument problem of the radar gauge or its calibration.

Revisiting changes in sea levels at Marseille

Long-term trends and acceleration

Monthly mean sea levels at Marseille were computed by averaging our quality controlled hourly observations for each calendar month (Fig. 9) following the PSMSL recommendations (http://www.psmsl.org), that is, monthly averages were computed only if at least 15 days of complete observations were available within a given month; otherwise, it was taken as a data gap. Where available, the monthly mean sea levels from the ‘totalisateur’ supplemented the missing data from the tidal chart recording, mainly between August 1988 and October 1998. Figure 9 also shows the annual mean sea levels computed from the monthly values.

Fig. 9

a Monthly mean sea level time series at Marseille from 1849 to present. In black are the mean sea levels computed from the hourly data, whereas in red are supplied the mean sea levels for the period 1988–1998 from the ‘totalisateur’ recording device (see text). b Yearly mean sea level time series at Marseille (black) and Brest (blue) and 5-years running averages (thick lines)

Monthly time series were first deseasonalized by fitting annual and semi-annual signals using harmonic analysis and removing these fitted signals. The MSL trend from 1849 to 2012 was then computed from the deseasonalized data by means of a robust linear regression and resulted in an estimate of $1.08\,{\pm }\,0.04$ mm/year (uncertainties correspond to standard errors hereinafter). This estimate is in agreement with previously reported trends, although over shorter multi-decadal periods. Marcos and Tsimplis (2008) estimated a linear trend of $1.2\pm 0.1$ mm/year in Marseille and in the nearby Genova tide gauge for a period starting in 1885. They also found significant correlations between Marseille monthly sea levels and the rest of available tide gauges in the western Mediterranean, suggesting that this location is representative of the low-frequency sea level variability of the entire sub-basin. This was corroborated by Tsimplis et al. 2008 who found that Marseille is located in an area where sea level correlations are highest among most of the western Mediterranean.

Mean sea level acceleration in Marseille was computed by fitting a quadratic function to the monthly time series, resulting in $-$0.15 $\pm$ 0.11 mm/year/century. When only the twentieth century is considered the acceleration increases (in absolute value) up to $-1.28 \pm 0.25$ mm/year, consistent with the value reported by Marcos and Tsimplis (2008). The negative acceleration reflects the overall behaviour of long-term sea level changes in Southern Europe during the twentieth century, as described by Woodworth (2003) and Marcos and Tsimplis (2008): until 1960, sea level was rising at rates of about 1.2-1.5 mm/year (Tsimplis and Baker 2000). During the following 1960–1990 period, all tide gauges in the region recorded a gradual sea level drop at an average rate of $-$1.3 mm/year (Tsimplis and Baker 2000), which was attributed to increasing atmospheric pressure over the region and ocean temperature and salinity changes associated to large scale NAO variations (Tsimplis and Josey 2001; Tsimplis et al. 2005). After 1990, mean sea levels have started rising again (Fenoglio-Marc 2001; Tsimplis et al. 2005; Marcos and Tsimplis 2008). As explained by Woodworth et al. (2009), the negative acceleration found in Marseille is not in conflict with the positive global average reported by Church and White (2011) with a value for twice the quadratic coefficient of 0.9 $\pm$ 0.3 mm/year/century since 1880, as there are significant differences regionally. It is also worth noting from the above-mentioned accelerations and from Fig. 9b, the importance of the period over which the acceleration is computed (Rahmstorf and Vermeer 2011).

Marseille time series was compared with the longest sea level record of Brest updated by Wöppelmann et al. (2006b) and made available through the French SONEL data bank (http://www.sonel.org). Some features of the comparison must be stressed (Fig. 9b). First, during the second half of the nineteenth century, both sea level time series show no sea level rise (note that in Marseille only one complete year is available from the oldest tide gauge, corresponding to 1850). Second, during the period 1910–1920, the Brest record is characterized by a rapid increase–decrease of sea level centred in 1915, which was attributed to atmospheric forcing by Douglas (2008), and does not affect the Marseille record. Finally, from 1980 onward, the Marseille record remains on average 5 cm below the Brest record. Consistently, the sea level trend derived for Brest over the common period 1849–2012 is 1.26 $\pm$ 0.04 mm/year, slightly larger than that from Marseille. The main reason is the sea level drop in Marseille lasting 30 years until the early 1990s, as explained above. From 1990 onward, sea level trends at both stations are virtually identical (Fig. 9b).

It is worth remembering here that tide gauges measure sea level relative to the nearby land upon which their benchmarks are installed, thus including the contribution of any vertical land movement in their records. Without independent estimates of these land movements, tide gauges cannot determine whether the sea level is rising or the land is sinking (or both), no matter how accurately and consistently their measurements are performed (e.g. Woodworth 2006). It has been common practice to correct tide gauge trends for the vertical motion of the land associated with postglacial rebound using geophysical models of the Glacial Isostatic Adjustment (GIA), despite it having shown that significant discrepancies exist among the different model predictions (e.g. King et al. 2012). The installation of continuously operating GPS stations at or nearby tide gauges has opened the possibility for an independent assessment of any vertical land movement irrespective of its cause (e.g. Wöppelmann et al. 2007). In Marseille, the co-located GPS station (Fig. 2a) has exhibited a vertical velocity of $-0.16\pm 0.13$ mm/year since 1998 (Santamaría-Gómez et al. 2012), hence suggesting that the Marseille tide gauge is grounded on a stable site (Bouquet de la Grye 1890). This was further corroborated by Wöppelmann and Marcos (2012) using an advanced independent approach of combining tide gauge and satellite altimetry sea level data to infer vertical land motion, which resulted in an estimate of 0.17 $\pm$ 0.20 mm/year, not statistically different from the GPS solution. The stability of the Marseille tide gauge station encouraged Tsimplis et al. (2011) to choose this time series as the ‘beacon’ station to check the consistency of Mediterranean Sea coastal sea level records not vertically referenced.

Other sea level signals

Sea level variability in Marseille was explored in the frequency domain using spectral analysis of the monthly time series. Since a continuous time series was required to perform the analysis, the period 1941–1987 of the monthly record was chosen as the longest period of time during which data gaps are at maximum 3 months long. These were linearly interpolated without notably affecting the analysis (a spline interpolation was also tested leading to the same results). The power spectrum in Fig. 10 was computed using a 512-point Kaiser–Bessel window with a window half length overlapping for the time series of 564 months. The window was chosen with the aim of having the highest possible resolution in frequency, as the interest was first focused on the long-term rather than on the high-frequency (intra-annual and monthly) oscillations. The power spectrum in Fig. 10 shows noisy and peaky signals below 1 year, with only the annual and the semi-annual oscillations clearly defined. It also reveals other frequency bands and peaks of lower frequency, whose energy content is smaller than the seasonal cycle.

Fig. 10

Power spectra ($\hbox {cm}^{2}$ month) of Marseille monthly mean sea levels from 1941 to 1987. Vertical red lines are drawn as guidelines at 6, 12 and 14 months

The seasonal sea level cycle is one of the most prominent features of sea level variability. The mean seasonal cycle in Marseille, computed from harmonic analysis of the entire time series, resulted in amplitudes of 4 cm and 2.6 cm for the annual and semi-annual cycles, respectively. The annual cycle peaked in October on average, whereas the semi-annual peaked in January (and six months later). Overall, the seasonal cycle accounts for 16 % of the total sea level monthly variance. These results are in agreement with those reported by Marcos and Tsimplis (2007b), who carried out a comprehensive analysis of the seasonal sea level cycle in the Mediterranean Sea using the longest tide gauge records. They also noted that the seasonal sea level cycle is far from constant, in particular inter-annual variations of the annual amplitudes reach up to 8 cm in Marseille due to the differential ocean heating from year to year. Marcos and Tsimplis (2007b) also pointed out that changes in the seasonal cycle in Marseille were consistent with other tide gauges in the western Mediterranean.

The power spectrum also reveals energy at other frequency bands. The next peak after the annual cycle was found around 14 months, coinciding with the period of the pole tide (Haubrick and Munk 1959) and with energy about one order of magnitude smaller than that of the annual cycle. The pole tide is the oceanic response to the Earth’s free nutation, whose frequency was established to 0.84 $\hbox {year}^{-1}$ or period of 14.28 months (Haubrick and Munk 1959). A harmonic analysis of the monthly time series that fitted the seasonal signals together with a harmonic signal of 14.28 months resulted in an oscillation of 7 mm amplitude. This value is in agreement with the average amplitude of the pole tide reported by Haubrick and Munk (1959) of around 10 mm that was obtained using the longest tide gauge records available at that time, and with a maximum value at $45^{\circ }\hbox {N}$ of around 5 mm (Trupin and Wahr 1990).

Significant energy content is also found at inter-annual scales, between 1 and 5 years (Fig. 10). Sea level variability in the Mediterranean Sea at these time scales is mostly concentrated in the winter season and is of atmospheric origin (Gomis et al. 2008). In particular, in Marseille, about 40 % of the yearly sea level variance is accounted for by the atmospheric contribution of pressure and wind (Marcos and Tsimplis 2008). The monthly variance in winter was found to be almost threefold that in summer.

The length of the period used to compute the power spectrum does not allow being conclusive about signals with periods longer than 5 years. For example, nothing can be said from this analysis about the nodal tide of 18.6 years. However, the spectrum clearly shows energy around 100 months, which could be related to the presence of the 11-year solar cycle oscillation. Woodworth (1985) already suggested a small response of the Mediterranean tide gauges (including Marseille) to the sunspots cycle, using maximum entropy spectral analysis.

Tide gauges with high-frequency (at least 1 h) sampling rates have also been used extensively to study sea level extremes. The time series of Marseille is part of the sparse and invaluable worldwide data set of sea level records longer than 100 years with high-frequency sampling. Letetrel et al. (2010) took advantage of these features to characterize the sea level extremes and their evolution over the period 1885–2008 using a local regression model based on the Generalized Pareto Distribution. Interestingly, they found that temporal changes in extreme events, originated by winter atmospheric perturbations, do not always follow changes in mean sea level at inter-annual and decadal scales.

Conclusion: an extended sea level time series

Originally devised for geodesy, the interest in the Marseille tide gauge record has gradually shifted from this community to meteorologists, oceanographers and climatologists. This shift is natural as the coastline is at the interface of the major Earth sub-systems that are the solid earth continents, the oceans and the atmosphere. In addition, Marseille data are now extending over 160 years and covering three centuries, hence being particularly interesting for studying long-term trends in sea levels in the context of recent climate change. The broadened interest also results from an instrument that was devised to be robust and of the highest mechanical precision design. In this respect, it is of historical curiosity in quoting the Ing. Reitz correspondence to Ing. Lallemand on 1 June 1883: “we started working from the principle that gauges likely foreseen to operate during centuries should be extremely robust”. Even though the former Cadiz and Helgoland copies did not exceed a hundred years of recording, they lasted several decades, however (Marcos et al. 2011; Rohde 1982). Yet, our experience on the recovered data of the Marseille tide gauge copy indicates that the most important issue in the recording of high-quality sea level data is definitely the care and maintenance of the gauge. At Marseille, a gauge attendant ensured this maintenance daily for over a century (1885–1988).

Despite the broad use of Marseille MSL time series over the past decades, little was known by most users on the origin of those mean sea levels recorded by an ingenious device rigorously complying with the mathematical definition of a mean (mechanical integrator; Sect. 3). Moreover, many have wondered why the hourly values were missing or more precisely why they never pre-existed the mean sea levels. In this study, we have reported the principle of the mechanical integrator from the historical documentation available in French and in German. The ‘mysteriously missing’ hourly values have been recovered from the classical tidal charts (1885–1988) which constituted a secondary recording system, never really exploited but scrupulously archived. These have been supplemented with hourly values from 1849 to 1851 rediscovered in tabulated ledgers during a fortunate survey in 2009. All the recovered hourly data have been thoroughly scrutinized for errors and datum consistency using a series of quality control procedures (Sect. 4). Their reliability has been assessed, identifying values that can be considered suspect such as those from July 1925 to July 1928, March 1937 to November 1940 and August 1951 to November 1952. The historical documentation suggests that the suspect data are almost certainly a result of the gauge being relatively poorly maintained, either due to a gauge attendant being unwell or newly appointed without proper supervision or due to a lack of interest and control from the supervising headquarters in Paris. In this respect, it is interesting to note that since 1988 despite the floating gauge being visited every week or so by an agent from Aix-en-Provence to perform the readings on the mechanical integrator, long periods of gauge outage and frequent breaks have occurred mostly due to the lack of a dedicated and well-trained gauge attendant. It can even affect the modern gauge operating within the historical infrastructure such as between May 2009 and October 2010 (channel obstruction, Fig. 8).

As a result, aside from the above-mentioned periods of apparent gauge malfunctioning and the original missing data for 1909, 1913, 1921 and 1924, a consistent high-frequency time series from 1849 to present is achieved, increasing notably the length of one of the few European sea level records in the Mediterranean Sea spanning three centuries. The extended and cleaned record of Marseille hourly sea levels is provided in computer-accessible form in the supplementary material and in SONEL (http://www.sonel.org) and its associated REFMAR (refmar.shom.fr) portal at the French hydrographic agency, supplying data to the PSMSL and GLOSS. This will enable any future researcher to make ready use of the data sets, without the need to consult the original tidal charts for which now permission has become difficult to obtain as the tide gauge and its buildings have been classified as an Historic Monument, including the tidal charts. Despite its exceptional longevity, it is unlikely that the floating gauge will pass another century operating as it has been since 1885 since the expertise in high-precision mechanics has become rare and expensive.