Abstract
We present an adaptive grid refinement algorithm to solve probabilistic optimization problems with infinitely many random constraints. Using a bilevel approach, we iteratively aggregate inequalities that provide most information not in a geometric but in a probabilistic sense. This conceptual idea, for which a convergence proof is provided, is then adapted to an implementable algorithm. The efficiency of our approach when compared to naive methods based on uniform grid refinement is illustrated for a numerical test example as well as for a water reservoir problem with joint probabilistic filling level constraints.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Probabilistic programming or optimization under probabilistic constraints (or chance constraints) has become a standard model of stochastic optimization whenever inequality constraints are affected by random parameters. The typical form of such probabilistic program is
where \(x\in {\mathbb {R}}^{n}\) denotes a decision variable, \(f:{\mathbb {R}} ^{n}\rightarrow {\mathbb {R}}\) is some cost function, \(\xi : \varOmega \rightarrow {\mathbb {R}}^s\) refers to an s-dimensional random vector defined on a probability space \(\left( \varOmega , {\mathscr {A}},{\mathbb {P}}\right) \), \(g:{\mathbb {R}}^{n}\times \) \({\mathbb {R}} ^{s}\rightarrow {\mathbb {R}}^{m}\) is some constraint mapping representing a finite system of random inequalities and p is some safety level. To provide a simple illustration, x might be the supply vector for different goods to be produced and \(\xi \) might represent the demand vector of these same goods. Most often, one is faced with a here and now situation, which means that the decision has to be taken prior to the observation of the random vector. For instance, the baker has to decide early in the morning how many breads, cakes etc. to bake much in advance of noting the real customer demand of these products. The natural constraint to be imposed by the baker is demand satisfaction for all goods, i.e. the inequality system \(g_{i}\left( x,\xi \right) {:}{=}\xi _{i}-x_{i}\le 0\) for \(i=1,\ldots ,m\). However, as this inequality system is stochastic and the realization of the random parameter is not known at the time the optimization problem has to be solved in x, it does not make sense to use this system as a constraint in the optimization problem. Therefore, the dependence of the problem on the concrete realizations of \(\xi \) has to be removed. A simple remedy would consist in replacing the random vector by its expectation and solve the problem
The drawback of this approach is that the inequality will be satisfied only for the average demand. A given decision on the production may then lead to frequent demand violation and the baker will be faced with unhappy customers. Passing to another extreme, the baker might decide to satisfy the customers demand in any circumstances, which amounts to solving a problem under worst case constraints
where ‘supp \(\xi \)’ denotes the support of the random vector \(\xi \). Then, the customer will be happy all the time. However, the baker will have to provide such an enormous amount of goods in order to satisfy all unforeseen demand, that it will cause possibly enormous costs. Moreover, most of the time unused products have to be thrown away afterwards. Observe that given a uncountable support this last problem—in contrast to the previous ones—has an infinite number of constraints, hence one is dealing with semi-infinite optimization here. As an introduction to that topic we refer to the survey article (López and Still 2007) or the monograph (Stein 2003). Observe also that both models above exploit only minimal information about the random distribution of \(\xi \), namely its first moment in (2) and its support in (3).
A good compromise between these models consists in declaring a decision to be feasible if the probability of satisfying the random inequality system \( g_{i}\left( x,\xi \right) \le 0\) is at least some specified level \(p\in \left[ 0,1\right] \) typically close to but different from one (note that the choice \(p=1\) would boil down to the worst case model (3)). This yields the probabilistic constraint in (1). Such constraint allows one to find a good trade-off between costs and safety by yielding quite robust and cheap solutions. Moreover, the model exploits the full distributional information about x and provides a probabilistic interpretation of the optimal decision found. Probabilistic or chance constraints have been introduced around 60 years ago by Charnes et al. (1958). Major theoretical breakthrough has been achieved in the pioneering work of Prékopa, whose monograph (Prékopa 1995) is still a standard reference in probabilistic programming. More recent presentation can be found in Shapiro et al. (2014) and van Ackooij (2020). Applications of probabilistic programming are abundant in engineering sciences, notably power management, telecommunications and chemical engineering. In the last 10–20 years, much progress has been achieved in the algorithmic treatment of these optimization problems (e.g., Adam et al. 2020; Bremer et al. 2015; Curtis et al. 2018; Dentcheva and Martinez 2013; Geletu et al. 2017; Hong et al. 2011; Luedtke and Ahmed 2008; Pagnoncelli et al. 2009). At the same time, the traditional model (1) has been continuously extended from a classical operations research setting towards infinite dimensions (PDE constrained optimization) (Farshbaf-Shaker et al. 2018, 2019; Geletu et al. 2017), dynamic models (multistage) (Andrieu et al. 2010; González Grandón et al. 2019; Guigues and Henrion 2017; Liu et al. 2016; Martínez-Frutos and Periago Esparza 2018) and infinite inequality systems (González Grandón et al. 2017; Heitsch 2020; van Ackooij et al. 2016). This latter aspect will be in the focus of the present paper.
There are two main sources for infinite random inequality systems. The first one is uniformity in time or space. For instance, one application of this paper will be concerned with the time continuous control of a water reservoir under random inflow. A crucial constraint in this problem consist in keeping the level of the reservoir above a critical value c with given probability throughout the considered time horizon \(\left[ 0,T\right] \). This leads us to the consideration of an optimization problem with probabilistic constraints of the type
where \(g_{t}\left( x,\xi \right) \) refers to the water level at time t depending on the water release (decision to be determined here and now) and on the random inflow (to be observed later, e.g., precipitation). The only but crucial difference with (1) consists in passing from the finite index i to the continuous index t. In another context, such as risk-averse PDE constrained optimization, one might deal with uniform probabilistic state constraints, where the index could refer now to a point in a given space domain (e.g., Farshbaf-Shaker et al. 2018, p. 832). A second source of infinite random inequality systems is the simultaneous presence of different kinds of uncertainty, namely uncertainty endowed with stochastic information—which allows one to estimate distributions of the random parameter and to derive probabilities—and non-stochastic uncertainty which at most gives an idea about the support of the random vectors. The first type is usually dealt with in the context of probabilistic constraints as in (1), whereas the second one falls into the class of robust optimization problems (see, e.g., Ben-Tal et al. (2009)). For instance in problems of optimal gas transport, one is simultaneously faced with stochastic uncertainty (given by uncertain gas loads for which large historical data bases exist) and with robust uncertainty (given by unknown friction coefficients of pipes which are under ground and can hardly be estimated) (González Grandón et al. 2017). The resulting probabilistic constraint then may take the form
where \(\xi \) is the random load and \(\varPhi \) is the uncertain friction coefficient which is allowed to vary arbitrarily within some given uncertainty set \({\mathscr {U}}\). This constellation of a probabilistic constraint involving a robust one motivated the choice of the acronym probust for such constraints in Van Ackooij et al. (2020). Observe that mathematically, though different in interpretation, (4) and (5) are the same.
We note that in a more general context the index sets in (4) and (5) could even depend themselves on the decision and/or random vector, so that one would consider, e.g., \({\mathscr {U}}\left( x,\xi \right) \) or \({\mathscr {U}}\left( x\right) \). Such models—without the probabilistic aspect—would bring one towards inequality systems considered in generalized semi-infinite programming (see, e.g., Guerra Vázquez et al. 2008; Stein 2003). An application of probabilistic constraints involving decision-dependent index sets is presented in the context of the capacity maximization problem in gas networks (Heitsch 2020).
It has to be mentioned that, similarly to the case of finite inequality systems, one has to distinguish between joint probabilistic constraints, where the probability is taken uniformly over all random inequalities as in (1), and individual probabilistic constraints, where each random inequality is turned into an individual probabilistic constraint. In the context of (4), for instance, such individual model would read as
Examples for applications of continuously indexed individual constraints are First Order Stochastic Dominance Constraints (Dentcheva and Ruszczyński 2010) and Distributionally Robust Chance Constraints (Zymler et al. 2013). In the water reservoir context, (6) just ensures that the water level stays above c with given probability p at each time \(t\in \left[ 0,T\right] \) individually. Usually, one is interested, however, in keeping the level above c with given probability p uniformly throughout the time horizon \(\left[ 0,T\right] \) which corresponds to (4) and is a much stronger requirement.
A first theoretical analysis of optimization problems subject to probust constraints can be found in Farshbaf-Shaker et al. (2018) (continuity properties and existence and stability of solutions) and in Van Ackooij et al. (2020) (differentiability and gradient formulae). As far as the numerical solution of such problems is concerned, early attempts using worst case analysis allowed for an analytical reduction of the continuously indexed constraint to a conventional one with a single (but now moving) index. Such favorable situation is exceptional, however. For instance, in the capacity maximization problem for gas networks considered in Heitsch (2020), it was assumed that the network is a tree. As soon as cycles are involved, such analytical reduction is no longer possible and numerical techniques have to be developed. The purpose of the present work is to propose efficient algorithmic solution schemes for probust problems which are based on adaptive grid refinement strategies and clearly outperform a brute force uniform discretization of the index set. The basic idea of grid refinement is the selection of new gridpoints (actually indices representing inequalities) according to their importance with respect to the given probability distribution. This leads to an alternating two-phase algorithm where the upper level iterates on the decision x with the current grid fixed and the lower level iterates on finding a new grid point with the current decision x fixed. The resulting grids are highly non-uniform in general and provide a satisfactory approximation of the probabilistic constraint with much fewer points than uniform grids.
The paper is organized as follows: In Sect. 2, the algorithmic details of our solution approach are presented. We start with a brief review of the spheric-radial decomposition of Gaussian random vectors which is a successful tool for solving conventional (finitely indexed) probabilistic programs as (1) for Gaussian (more generally: elliptically symmetric) distributions. We then propose and illustrate a conceptual two-level (alternating) algorithm for adaptive grid refinement. This is followed by the description of an implementable algorithm whose superiority over uniform grid generation methods is demonstrated for a numerical example. Section 3 provides a convergence proof for the conceptual algorithm mentioned above. Finally in Sect. 4, our adaptive algorithm will be applied to a simplified model of water reservoir control. Results will be compared on the algorithmic level with a standard approach using uniform grids and on the modeling level with a simplifying reduction to expected inflows according to (2) or time-wise individual chance constraints according to (6).
2 Algorithmic solution approaches
In this paper, we consider optimization problems with probust constraints:
Here, \(f:{\mathbb {R}}^{n}\rightarrow {\mathbb {R}}\) is some objective function depending on a decision vector \(x\in {\mathbb {R}}^{n}\), \(\xi \) is an s-dimensional random vector defined on some probability space \(\left( \varOmega ,{\mathscr {A}},{\mathbb {P}}\right) \), \(g:{\mathbb {R}}^{n}\times {\mathbb {R}}^{s}\times {\mathbb {R}}^{d}\rightarrow {\mathbb {R}}\) is a random constraint function indexed by \(t\in T\subseteq {\mathbb {R}}^{d}\). Finally, \(X\subseteq {\mathbb {R}}^{n}\) is some abstract deterministic constraint set, given for instance by box constraints. It is clear that, for a numerical solution of (7), the infinite inequality system has to be turned into a finite one in the one or other way. Then, one is dealing with a conventional probabilistic constraint as in (1), a problem which could be solved with standard methods of nonlinear optimization such as SQP. The basic ingredient for the numerical treatment of probust constraints will therefore consist in the efficient computation of values and gradients of the probability function
An appropriate tool to achieve this goal in the case that \(\xi \) has a Gaussian or, more generally an elliptically symmetric distribution (e.g. Student) is the so-called spheric-radial decomposition (e.g., Farshbaf-Shaker et al. 2019; González Grandón et al. 2017; Heitsch 2020; Van Ackooij et al. 2020). As this is the working horse for all probability computations in this paper, we start with a short introduction here and refer to more detailed presentations in Van Ackooij and Henrion (2014, 2017).
2.1 Spheric-radial decomposition
In this section we show how values and gradients of the probability function \({\tilde{\varphi }}\) in (8) can be approximated efficiently when \(\xi \) obeys an s-dimensional Gaussian distribution according to \(\xi \sim {\mathscr {N}}\left( \mu ,\varSigma \right) \) with expectation \(\mu \) and covariance matrix \(\varSigma \). The principle of spheric-radial decomposition of a Gaussian random vector expresses the fact that, for any Borel measurable subset \(C\subseteq {\mathbb {R}}^{s}\) one has the representation
where \({\mathbb {S}}^{s-1}\) is the unit sphere in \({\mathbb {R}}^{s}\), \(\nu _{\chi }\) is the one-dimensional Chi-distribution with d degrees of freedom, \(\nu _{\eta }\) is the uniform distribution on \({\mathbb {S}}^{s-1}\) and L is a root of \(\varSigma \) (i.e., \(\varSigma =LL^{T}\)). Applied to (8), this yields the expression
For the ease of presentation, we shall assume that the constraint mappings \( g_{i}\) in (8) are convex in their second argument \(\xi \). This will be the case, for instance, in the numerical example considered in Sect. 2.5 and in the application we are going to discuss in Sect. 4. For applications of the spheric-radial decomposition to probabilistic constraints without this convexity assumptions, we refer, for instance, to Heitsch (2020); Van Ackooij and Pérez-Aros (2020).
As an immediate consequence of Van Ackooij and Henrion (2014, Prop 3.11), we then have the following observation:
Proposition 1
Let \(x\in {\mathbb {R}}^{n}\) be such that \({\tilde{\varphi }}\left( x\right) >\frac{1}{2}\) and that there exists some \(z\in {\mathbb {R}}^{s}\) with \(g_{i}\left( x,z\right) <0\) for all \(i=1,\ldots ,m\). Then, \(g_{i}\left( x,\mu \right) <0\) for all \(i=1,\ldots ,m\).
Clearly, if the probability level p in problem (1) is larger than \(\frac{1}{2}\), then \({\tilde{\varphi }} \left( x\right) >\frac{1}{2}\) will be satisfied at every feasible point of that problem. Recall that \(p>\frac{1}{2}\) is not a restrictive assumption, because in general the probability levels will be chosen close to one (e.g. 0.9). In particular, under this first assumption of the Proposition, there must exist some \(z\in {\mathbb {R}}^{s}\) with \(g_{i}\left( x,z\right) \le 0\) for all \(i=1,\ldots ,m\) (otherwise, \({\tilde{\varphi }} \left( x\right) =0\)). Now, the second assumption of the Proposition slightly strengthens this fact towards a strict inequality. It will be satisfied in all properly modeled applications. The benefit of Proposition 1 is the following:
Corollary 1
Under the assumptions of Proposition 1, the integrand in (9) can be explicitly represented for any fixed \(x\in {\mathbb {R}}^{n}\) and \(w\in {\mathbb {S}}^{s-1}\) as
Here, \(F_{\chi }\) is the cumulative distribution function of the one-dimensional Chi-distribution with d degrees of freedom,
and \(\rho \left( x,w\right) \) is the unique solution in r of the equation \( e\left( r\right) =0\), where
Proof
Fix some arbitrary \(x\in {\mathbb {R}}^{n}\) and \(w\in {\mathbb {S}}^{s-1}\). If \( w\in I(x)\), then, by definition of I(x) and since the support of the Chi-distribution is the non-negative reals,
Otherwise, there exists some \(r \ge 0\) such that \(e(r) >0\). On the other hand, \(e(0) < 0\) as a consequence of Proposition 1. Moreover, by the assumed convexity of g in its second argument, e is a convex function too. Hence, there exists a unique solution \(\rho \left( x,w\right) \) of the equation \(e\left( r\right) =0\) and one has that
\(\square \)
The integral (9) can be numerically approximated by a finite sum
where \(\left\{ w^{\left( 1\right) },\ldots ,w^{\left( K\right) }\right\} \subseteq {\mathbb {S}}^{s-1}\) is a sample of the uniform distribution on \( {\mathbb {S}}^{s-1}\). A simple way to get such a sample is based on the observation that the normalization \(\theta /\left\| \theta \right\| \) to unit length of a standard Gaussian distribution \(\theta \sim {\mathscr {N}} \left( 0,I_{s}\right) \) is uniformly distributed on \({\mathbb {S}}^{s-1}\). Hence, one may sample \({\mathscr {N}}\left( 0,I_{s}\right) \) using Monte-Carlo or better Quasi Monte-Carlo simulation in order to generate some scenarios \(\big \{{\tilde{w}}^{\left( 1\right) },\ldots ,{\tilde{w}}^{\left( K\right) }\big \}\) and then pass to their normalized version \(w^{\left( j\right) }{:}{=}{\tilde{w}}^{\left( j\right) }/\big \Vert {\tilde{w}}^{\left( j\right) }\big \Vert , j=1,\ldots ,K\).
Combining (10) with Corollary 1, we arrive at the following implementable approximation of our probability function:
The crucial step in this approximation is the efficient solution of the equation \(e\left( r\right) =0\) for given x and \(w^{\left( j\right) }\) in order to determine \(\rho \left( x,w^{\left( j\right) }\right) \). This is particularly easy if the constraint mappings \(g_{i}\) in (8) are linear in \(\xi \) (as in the application in Sect. 4) or quadratic (as in Heitsch 2020; Farshbaf-Shaker et al. 2019) or polynomial of low order. As for the one-dimensional cumulative distribution function \( F_{\chi }\), highly precise numerical approximations are available.
In order to also derive an approximation of the gradient \(\nabla {\tilde{\varphi }}\) we are led to differentiate the approximation (11) of \({\tilde{\varphi }}\) with respect to x:
Here, \(f_{\chi }\) denotes the density of the given Chi-distribution (note that \(F_{\chi }^{\prime }=f_{\chi }\)). The question of whether the gradient of the approximation is an approximation of the gradient is of theoretical nature and shall not be discussed here. It can be answered positively under mild conditions, see, e.g., Van Ackooij and Henrion (2017). Moreover, the function \(\rho \) may turn out to be non-differentiable at arguments \(\big ( x,w^{\left( j\right) }\big ) \) for which the maximum
is attained by more than one index. Therefore, in a strict sense, one would have to consider (Clarke-) subdifferentials rather than ordinary derivatives as in Van Ackooij and Henrion (2017). Fortunately, classical differentiability of \(\rho \) is typically given for almost all arguments. The derivative itself is easily computed by applying the Implicit Function Theorem to the equation
at \(r{:}{=}\rho \big ( x,w^{\left( j\right) }\big ) \), where \(i^{*}\) is defined to be the (assumed) unique index with
One then obtains that
Combining this with (12), yields a fully explicit approximation of the gradient of the probability function:
Observe that both the value in (11) and the gradient in (13) of \(\varphi \) can be simultaneously updated at some given iterate of the decision x with each given sample \(w^{\left( j\right) }\). In particular, the possibly time-consuming determination of the value \(\rho \big ( x,w^{\left( j\right) }\big ) \) has to be executed only once for both quantities. The precision of both computations (11) and (13) can be controlled by choosing an appropriate sample size K. In most applications we found a sample of size 10.000 based on Quasi Monte-Carlo simulation of the standard Gaussian distribution (see above) to be sufficient at least in the early phase of iterations when solving an optimization problem numerically. Close to the solution it may be beneficial to increase this sample size say to 50.000.
2.2 Uniform discretization schemes
Having described the computation of values and gradients of the probability function \(\varphi \) related to finitely many random inequalities in (8), we have the necessary ingredients to solve the optimization problem (1), where the probabilistic constraint is defined via finitely many random inequalities. Turning now to the probust problem (7) involving infinitely many random inequalities, we will make recourse to the finite case by choosing appropriate discretization schemes for the index set T. A simple approach for solving (7) would consist in selecting a sufficiently large number of indices from the index set T and then turning (7) into an optimization problem with conventional probabilistic constraints as given in (1). One could either select indices randomly or establish a uniform grid. In the case of a rectangle
such uniform grid of order \(\left( N_{1},\ldots ,N_{p}\right) \) would consist of the finite index set
Then (7) reduces to the problem
with finitely many random inequalities which is of type (1) and, hence, can be solved say with an SQP method for nonlinear optimization using the tools provided in Sect. 2.1. If we do so without further refinement, in particular with a fixed sample size K for the spheric-radial decomposition, then we refer to this approach as to (FUG-FS), meaning fixed uniform grid—fixed sampling.
At this point one can already think about some refinements of this naive approach still on the level of uniform grids. Accepting the idea that a highly precise and computationally expansive approximation of problem (7) may be needed only when the iterate x is close to a solution, we could content ourselves with much coarser uniform grids \( T_{U}^{N_{1}^{\prime },\ldots ,N_{p}^{\prime }}\) with \(N_{j}^{\prime }\) significantly smaller than \(N_{j}\) in the beginning, but increasing towards \( N_{j}\) in the course of iterations. At the same time, in the beginning we could choose a much smaller sample size \(K^{\prime }<K\) for controlling the precision of the probability function \(\varphi \) and its gradient when applying the spheric-radial decomposition and turning to a large K only in the terminal phase of the iterations. We will refer to this as to (IUG-IS), meaning increasing uniform grid—increasing sampling. It is intuitively clear that the indices \(t\in T\) in (7) describing the infinite inequality system do not have the same importance in the probabilistic context as in the deterministic one (without random vector). More precisely, their importance will crucially hinge on the geometric position of the (x-depending) set of feasible scenarios
with respect to the probability distribution of \(\xi \). This position will make some indices (inequalities) account for smaller, some for bigger probabilities. Therefore it should not come as a surprise that a uniform grid will typically waste a lot of probability-based information and that an appropriately adapted grid has the potential of clearly outperforming it. In the following, we will formulate and illustrate first a conceptual algorithm for adaptive grid refinement and then propose an implementable version thereof.
2.3 A conceptual algorithmic framework for adaptive grid refinement
Denote the probability function associated with (7) by
so that (7) can be rewritten as
Similarly, for any finite inner approximation \(I\subseteq T\), denote
yielding the approximate optimization problem
which is of type (1) with \(m{:}{=}\#I\) and, hence, algorithmically accessible via nonlinear optimization based on the information provided in Sect. 2.1. Clearly, since for any fixed \(x\in {\mathbb {R}}^{n}\),
it follows that

In other words, the feasible set of (15) is an outer approximation of the original feasible set in (7) and, hence, the optimal value of (15) is a lower bound on that of (7). Now, as this observation holds true for any finite index set I , one could reasonably decide on a choice \(I^{*}\) among all finite index sets sharing the same cardinality, which minimizes the value of \(\varphi ^{I} \) because this one, \(\varphi ^{I^{*}}\), will provide the best available upper estimate for \(\varphi \). Of course, one has to take into account that this choice of \(I^*\) is typically not possible in a uniform sense (i.e., for all \(x \in {\mathbb {R}}^n\)). But one could locally adapt this choice to the sequence of iterates x generated in the solution process, thereby organizing the choice in a manner that the obtained sequence of index sets \(I^*\) increases in size. In this way an adaptive grid can be generated which sequentially collects the (locally) most informative indices and potentially leads to much faster convergence of solutions than uniform grids of comparative size—or put differently: to comparable convergence of solutions as uniform grids of much larger size. This idea suggests a conceptual two-level algorithm for solving the probust problem (7).
We emphasize that both, the upper and the lower level in Algorithm 1 can be solved by means of nonlinear optimization methods using the information from Sect. 2.1. The difference between both problems is that in step 2 the x-variable is fixed and optimization is carried out over the t-variable and in step 3 the t-variable is fixed and optimization takes place with respect to the x-variable.
We are going to illustrate this conceptual algorithm for the following simple example, which, for the purpose of visualization is in dimension two both with respect to decisions x and to the random vector \(\xi \) (i.e., \(n=s=2\)):
Formally, here one is dealing with is a system of two continuously indexed systems but this easily recast in the form of (7) upon putting
Moreover, we choose \(X{:}{=}{\mathbb {R}}^{2}\). Figure 1a shows the set M of feasible decisions \(x=\left( x_{1},x_{2}\right) \) defined by the probabilistic constraint (17). Since its graphical representation cannot be achieved due to the underlying infinite number of random inequalities, we have shown its presumably very tight approximation on the basis of a uniform grid on \(\left[ 0,2\pi \right] \) consisting of 101 points. The optimal solution of problem (17) (which is nothing but the norm-minimal feasible point) is denoted by \(x^{*}\) in the figure. As a starting point of our algorithm we choose \(x^{0}{:}{=}\left( 1,1\right) \). Entering step 2 of the algorithm (the lower level problem), we have to minimize the one-dimensional probability function
which is plotted in Fig. 1b and achieves its minimum at \( t_{0}^{*}\approx 2.24\). Using this first index created, we pass to step 3 (the upper level problem) and solve the optimization problem
The feasible set \(M^{1}\) of decisions \(x=\left( x_{1},x_{2}\right) \) satisfying the probabilistic constraint above is illustrated in Fig. 1a. It can be interpreted as the best approximation of the true feasible set M based on a single index in \(\left[ 0,2\pi \right] \). The upper level problem is easily solved graphically, because, given the objective, we have to look for the norm-minimal feasible point \(x^{\left( 1\right) }\in \) \( M^{1} \) which is determined by the unique circle centered at the origin and touching the boundary of the feasible set (see Fig. 1a). With this first iterate in the space of decisions we re-enter step 2 and solve the new lower level problem which amounts to minimizing over \([0,2\pi ]\) the probability function
Here, the previously computed index \(t_{0}^{*}\) is kept and a new one t is added, so that it minimizes the joint probability of two inequalities. From Fig. 1b, we identify the new index as \( t_{1}^{*}\approx 3.14\). This creates the next upper level problem
whose feasible set \(M^{2}\) and optimal solution \(x^{\left( 2\right) }\in \) \( M^{2}\) (norm minimal element of \(M^{2}\)) are illustrated in Fig. 1a. Proceeding this way one generates a sequence of lower and upper level problems whose solutions are depicted in Fig. 1. It can be seen that the sequence \(M^k\) of feasible is decreasing and approximates M fairly well already after 3 iterations. Similarly, the iterates \(x^{k}\) of the upper level problem quickly converge to the solution \(x^*\) of the given probust problem.
The meaning of the lower level problem is illustrated in Fig. 2 in the two-dimensional space of realizations of the random vector \(\xi =\left( \xi _{1},\xi _{2}\right) \) (not to be confused with the two-dimensional space of decisions x from Fig. 1a). The diagrams show the evolution of the solution sets
of the continuously indexed inequality system with decision fixed as the kth iterate \(x^{(k)}\) of the decision vector generated in Algorithm 1 (set colored in black). Observe that this set changes with x and its probability is smaller than the desired level p as long as \(x^{(k)}\) is not feasible for the probust constraint as in Fig. 1a (i.e., \( x^{(k)} \notin M\)). It is only in the limit—as \(x^{(k)}\rightarrow x^{*} \)—that \({\mathbb {P}}\left( \xi \in Z^{k}\right) \rightarrow p\). The figure also indicates in each step the finitely indexed approximations
before entering the lower level problem (set colored in gray) and after adding the inequalities (two at a time because we are dealing with two inequality systems in our example) corresponding to the new index \( t_{k}^{*}\) (cuts colored in black). In each step, the new inequalities minimize the probability of the resulting finite inequality system. In other words, the new inequalities cut off an area of maximum of probability. Note that \( Z^{k}\subseteq {\tilde{Z}}^{k}\subseteq {\hat{Z}}^{k}\) and that in a probabilistic sense, \({\tilde{Z}}^{k}\) is the best reduction of \({\hat{Z}}^{k}\) by a single new index towards the continuously indexed set \(Z^{k}\). This probabilistic sense reveals itself in Fig. 2 by the fact that the new cuts do not necessarily correspond what we might expect as a good approximation of \(Z^{k}\) in a geometric sense. In the course of these first four iterations, a clear tendency to improve the geometric approximation in the anti-diagonal direction at the cost of the diagonal direction. This effect can be explained from the chosen distribution of the random vector, where we assumed a negative correlation between its components. Therefore, probability is stronger reduced by cuts whose normals are anti-diagonal. In Sect. 3, we will present a convergence proof for Algorithm 1.
2.4 Efficient implementable adaptive grid refinement
The solution algorithm presented in the previous section is of conceptual nature only, as it relies on two full optimization problems in each of its iterations. In order to design an implementable version of this algorithm, one has to make sure that only finitely many substeps are taken in each iteration. This could be guaranteed, for instance, if one replaces the exact solution of the upper and lower level problems in Algorithm 1 by \(\varepsilon \)-solutions for some sufficiently small \(\varepsilon \). Indeed, the convergence result we prove in Sect. 3 applies even to this generalized form of Algorithm 1 provided that the tolerances of the two subproblems tend to zero.
Still, a solution of both problems at high accuracy would bear the risk of unnessecary numerical efforts and of wasting the potential advantages of aggregating indices according to their probabilistic importance over a simple uniform grid construction. Therefore, our approach with respect to the upper level problem will simply rely on making just a few single steps (only one in example (17)) with a nonlinear optimization solver (e.g., SQP or active-set method) and only in the very last iteration (after the improvement of the objective becomes small in a predefined sense) making a complete solve of the upper level problem. Moreover, we adopt the idea of working with a comparatively small sample size in the spheric-radial decomposition in the initial phase and using a large size only in this mentioned final solve, when highly precise solutions for the overall problem are generated. This idea has already been employed in the uniform grid approach (IUG-IS) introduced in Sect. 2.2.
An major challenge is to keep the computational effort for the lower level problem small. If this is not achieved, any progress made on the upper level is counteracted by the lower level making the determination of few informative indices such costly, that even their small number does not pay the whole approach. We will therefore propose two strategies to reduce the time spent for the lower level so that its contribution to the overall computing time becomes negligible. The first measure consists in not solving the lower level exactly but rather finding approximate solutions which are defined on an appropriate enlargement of the current grid. The idea is particularly easily implemented for one-dimensional index sets T such as time intervals: given any current finite grid \(I_{k}\subseteq T\) when entering the lower level problem, we define another finite grid \({\hat{I}}\subseteq T\) by collecting all mid points between neighbors of the current grid. Hence, if
then
Instead of solving the lower level continuous optimization problem
as in step 2 of Algorithm 1, we find by finite enumeration the solution of
The new index \(t_{k}^{*}\) solving this finite substitute of the original lower level problem is then joined to the current grid to define the new grid \(I_{k+1}{:}{=}I_{k}\cup \left\{ t_{k}^{*}\right\} \) used in the next upper level problem as in step 3 of Algorithm 1.
The construction above requires that—unlike the empty set in Algorithm 1—the initial grid should contain at least two elements. In particular, the two endpoints of the interval should be contained in the initial grid because the new grids will always be contained in the convex hull of the initial grid. When starting with two grid points, then \({\hat{I}}\) solely consists of their average and so no enumeration is necessary in (19), this average is necessarily the newly created index. It is therefore reasonable to have both end points of T and the midpoint in the starting grid. From then on, new grids may freely develop which concentrate in certain more interesting regions of the index set as shown in the numerical example of Sect. 2.5. The procedure is illustrated in the left part of Fig. 3. Here, the black points represent the initial grid \(I_{k}\), when entering the lower level in iteration k and the gray points generate the grid \({\hat{I}}\) of associated midpoints. Among these, the one minimizing the probability function
related with problem (18) is chosen (encircled). This corresponds to the finite enumeration of function values of \(\varphi _{k}\) in (19) (thin lines in Fig. 3). In the next iteration, the new grid \(I_{k+1}\) is enlarged by the previously determined best point and two new mid points enter the new set \({\hat{I}}\) of candidates. Continuing this way, the current grid (as well as the midpoints may concentrate in regions where the (changing) probability function is small.
An important aspect in the implementation of these idea is keeping upper and lower level synchronous. It may turn out that the aggregation of just one new index in the lower level as described so far is too slow when compared to the progress in the upper level. Therefore, it is recommended to collect more than one new index at a time in the lower level. The procedure is the same as before: one selects the best candidate from \({\hat{I}}\), adds it to \( I_{k}\), removes it from \({\hat{I}}\), generates the two new midpoints entering \({\hat{I}}\) and selects again the best candidate from \({\hat{I}}\) now with a changed probability function. The only difference is that now the change of the probability function is not due to a new iterate \(x^{k+1}\) of the upper level (\(x^{k}\) remains fixed) but due to a changed grid \(I_{k}\), say \(\tilde{ I}_{k}\), in (19). After this step has been repeated a defined number of times within step 2 of Algorithm 1, the new grid \( I_{k+1} \) (entering step 3) is defined to be the last grid \({\tilde{I}}_{k}\) obtained in the described manner. The effect of multiple aggregation will become evident in the numerical example of Sect. 2.5. The described heuristic way of updating grid indices could fail to approximate the lower level problem unless the maximum distance of successive grid points is small enough with respect to the Lipschitz constant of the probability function minimized in the lower level. Therefore, rather than starting with an empty grid, we advise to use a coarse uniform grid of, e.g., 10 points from the very beginning.
A generalization of the presented ideas to higher dimensional index sets T could rely on mid points of appropriate triangulations of T or on Quasi Monte-Carlo sequences.
The second measure to reduce the computational burden of the lower level problem consists in saving information on the grid \(I_{k}\) in problem (19): a naive approach would make \(\#{\hat{I}}\) independent calls of the probability
to find the minimum. Doing so, one would repeat each time the effort in the spheric-radial decomposition related with indices from the given grid \({\tilde{t}}\in I_{k}\) (black points in Fig. 3). It therefore appears to be promising to save this information and to make the necessary updates in the spheric-radial decomposition only for the respectively added candidate from \({\hat{I}}\) (gray points in Fig. 3). To be more precise, we revisit the spheric-radial decomposition in Sect. 2.1 and recall that—following (11)—at a given iterate \(x_{k}\) of decisions and a fixed index \(t\in {\hat{I}}\), we have to compute for all sampled directions \(w^{\left( j\right) }\) (\(j=1,\ldots ,K\)) the critical radius \(\rho \left( x_{k},w^{\left( j\right) }\right) \), which according to Corollary 1 is defined as the unique solution in r of the equation
Here, we have adapted the abstract notation of Sect. 2.1 (involving finitely many functions \(g_{i}\)) to the concrete setting of (7) (involving a single function g but indexed by finitely many values of t). It is easy to see that
For each sample \(w^{\left( j\right) }\) and each fixed \(t\in {\hat{I}}\), such function call consumes the time \(\alpha \left( \#I_{k}+1\right) +\beta \), where \(\alpha \) is the average time needed for solving an equation
in r and \(\beta \) is the average computation time for a call of the cumulative distribution function \(F_{\chi }\) (see (11)). Since this computation has to be repeated for each of the \({\tilde{K}}\) samples \( w^{\left( j\right) }\) for which the sum in (11) has to be evaluated and each \(t\in {\hat{I}}\), the overall computation time would amount to
where we have used that \(\#{\hat{I}}=\#I_{k}-1\) (one average less than grid points). The ratio between \(\alpha \) and \(\beta \) may strongly differ according to the complexity of the function g. If g is linear in its second argument (the random vector)—as it will be the case in our numerical example and in the application to reservoir problems—then \( \alpha \) will be quite small compared with \(\beta \) because finding the zero above is just the computation of a quotient. If g happens to be quadratic in the second argument, then the zero is found by solving a quadratic equation which is more time consuming etc.
Alternatively, we can make use of the following updating scheme
where \(r_{t}\) is the solution in r of the equation \(g\big ( x_{k},\mu +r_{t}Lw^{\left( j\right) }\big ) =0\). This decomposition allows us to compute \({\tilde{\rho }}\big ( x_{k},w^{\left( j\right) }\big ) \) only once and to save this value along with its contribution \(F_{\chi }\big ( \tilde{ \rho }\big ( x_{k},w^{\left( j\right) }\big ) \big ) \) to the overall probability according to (11) for each sample \(w^{\left( j\right) }\). This leads for each sample to a computation time of \(\alpha \#I_{k}+\beta \). Then, for an arbitrary new candidate \(t\in {\hat{I}}\) only one additional equation has to be solved to compute \(r_{t}\), so that \(\rho \big ( x_{k},w^{\left( j\right) }\big ) \) is obtained by simple comparison of the saved value \({\tilde{\rho }}\big ( x_{k},w^{\left( j\right) }\big ) \) with \(r_{t}\). Hence, for each sample \(w^{\left( j\right) }\) and each fixed \( t\in {\hat{I}}\) , the additional time needed for computing \(\rho \big ( x_{k},w^{\left( j\right) }\big ) \) equals \(\alpha \).
As for the computation of the final contribution of sample \(w^{\left( j\right) }\) to the overall probability according to (11), one has to compute the Chi-distribution function \(F_{\chi }\big ( \rho \big ( x_{k},w^{\left( j\right) }\big ) \big ) \) only in case that \(\rho \big ( x_{k},w^{\left( j\right) }\big ) <{\tilde{\rho }}\big ( x_{k},w^{\left( j\right) }\big ) \) because otherwise \(F_{\chi }\big ( \rho \big ( x_{k},w^{\left( j\right) }\big ) \big ) =F_{\chi }\big ( {\tilde{\rho }} \big ( x_{k},w^{\left( j\right) }\big ) \big ) \) with the latter value already saved before. Therefore, if \(\tau \in \left[ 0,1\right] \) denotes the average ratio of samples \(w^{\left( j\right) }\) for which \(\rho \big (x_{k},w^{\left( j\right) }\big ) <{\tilde{\rho }}\big ( x_{k},w^{\left( j\right) }\big ) \), this final contribution consumes time \(\tau \beta \) per sample \(w^{\left( j\right) }\) and per index \(t\in {\hat{I}}\). Summarizing, the total computing time for all \({\tilde{K}}\) samples and all indices \(t\in \hat{I }\) amounts to
The efficiency of this updating idea can be measured by the ratio of the computing times in (22) and (23):
Since the numerator here is quadratic in the grid size and the denominator only linear, it follows that the efficiency tends to infinity with the grid size. This explains the strikingly growing gain in the reduction of computing time of the lower level observed with increasing grid size in the numerical example of Sect. 2.5.
Observe that, while \(\alpha \) and \(\beta \) can be easily determined from numerical experiments, the coefficient \(\tau \) remains unknown. Intuitively, it may be assumed rather close to zero in practice because a set of more or less random new inequalities will rarely dominate a set of given ones in most directions. To provide a concrete comparison between the naive and the refined method, consider a small grid size of 10 points in a setting where \( \alpha =\beta \), i.e., the computing time for solving a single equation (21) in r and for calling the Chi-distribution function are equal. Then, in the worst (highly unlikely) case of \(\tau =1\), the efficiency amounts according to the calculus above to 3.7 while the ratio improves towards 5.4 in the best case (\(\tau =0\)). For a grid size of 100 points, these ratios improve towards 33.8 and 50.5, respectively.
Finally, we mention that, similar to the solution of the upper level problem, we use a smaller sample size in the spheric-radial decomposition when solving the lower level problem in the beginning and turn to a large sample size only in the final solution step, when high precision is desired. This is the reason to call our approach (AG-IS), meaning adaptive grid—increasing sampling.
2.5 A numerical example
As a numerical example for comparing the different solution approaches (FUG-FS), (IUG-IS), (AG-IS) presented in Sections 2.2 and 2.4 and for illustrating the use of our adaptive grid refinement strategy, we consider a small stochastic optimization problem with probabilistic constraints having 2-dimensional decision vector and variable m-dimensional Gaussian random vector distributed according to \(\xi \sim {\mathscr {N}}(0,\varSigma )\):
This probabilistic constraint considered here can be recast in the form of (7) by putting
We start our numerical comparison with a two-dimensional Gaussian random vector with mean \(\left( 2,2\right) \) and covariance matrix equal to the identity (independent components with unit variance). Table 1 opposes the results of the two uniform grid approaches (FUG-FS), (IUG-IS) to those of the adaptive grid procedure (AG-IS). The quantity labeled ‘|grid|’ denotes in all cases the size of the final grid which was used in the last step, when all methods performed a full high precision optimization with the Matlab built-in SQP solver. Note that (FUG-FS) did nothing else but this final step with the fixed (uniform) grid of indicated size, whereas (IUG-IS) and (AG-IS) started with smaller, then increasing to the final size grids (uniform and adaptive, respectively) and also with smaller sample sizes for the spheric-radial decomposition but for the last step, where all three methods employed a common large sample size.
All three methods used a common reasonable starting point obtained from a plain optimization using a coarse uniform 11-point grid. The quantity ‘opt’ refers to the optimal value obtained for the objective function of the problem. This value is monotonically increasing with the size of hierarchically ordered grids because the upper approximation of the feasible set becomes better when the grid gets finer. Hence, the optimal value associated with the true solution of the problem is the limit of this increasing sequence.
When comparing the results, we may observe first that between the uniform grid strategies (IUG-IS) seems to perform slightly better than (FUG-FS) at least for larger grids. When comparing both of them with the adaptive grid strategy (AG-IS), one has to compare grids leading to solutions of approximately equal precision (optimal objective value). For instance, the objective value for a uniform grid of 400 points is approximately reached with an adaptive grids of 42 points and with a CPU time of 0.42 s which is also less than one tenth of the uniform grid methods. A similar ratio is observed for the highest precision obtained with a uniform grid consisting of 2.500 points.
The values ’\(t_{low}\)’ and ’\(t_{up}\)’ decompose the total time of the adaptive grid method (AG-IS) into time spent for the lower and upper level problem, respectively. It becomes evident that the key for the small total time is keeping the effort for the lower level much smaller than that for the upper level.
Adaptive grid refinement by algorithm AG-IS observed for the example of Table 1
Figure 4 shows the development of the adaptive grids \( I_{k}\) in the course of iterations, starting with a uniform grid of size 11 which was used to determine the starting point. It can be seen, how the grid points start concentrating first in the first quarter of the time interval before also gathering in the third quarter. These are obviously the regions which are most informative from a probabilistic perspective. Observe that the finest grid represented here (131 points) carries—according to Table 1—as much information as a uniform grid with approximately 2.000 points.
Table 2 provides a more detailed account of the improvement measures for the lower level problem discussed in detail in Sect. 2.4. The data are provided for three varying mean vectors but the same covariance matrix as in the example considered before. The final grid size is fixed as 211. The ‘naive’ approach would disregard both the lower/upper level synchronization and the update strategy (just direct independent calls of probability values). This blows up the time spent for the lower level to an unacceptable degree. Instead of keeping the lower level effort much beyond the upper level one, just the opposite is observed. For instance, in the case of the mean vector \(\left( 2,2\right) \) also considered in Table 1, the time spent for the lower level (206.87 s) even exceeds by far the time which would have been expected for any of the uniform grid methods in order to reach comparable precision. This underlines the need to well tune the solution approach for the lower level. The following columns illustrate the effect of synchronization by aggregating a different number k of new grid points at a time in the lower level problem while applying the update strategy presented at the end of Sect. 2.4. In any case, the CPU time spent for the lower level is extremely reduced which supports the conclusion that updating is the measure of biggest impact to improve the efficiency of the lower level. At the same time, some significant additional gain becomes evident by appropriate synchronization. From the different examples, one may guess that a simultaneous aggregation of approximately 10 new indices in each step of the lower level leads to another reduction of the total time spent by around one half. Further increase of k will then deteriorate this favorable synchronization.
Motivated by the results of Table 1, an extended numerical study showed that the contrast in efficiency between the naive uniform grid approaches on the one hand and our adaptive grid method on the other can be amplified to the extreme in principle. It turned out that the two main factors influencing this contrast are the geometric position of the solution sets to the random inequalities (the sets \(Z^{k}\) in Fig. 2) with respect to the given distribution and the dimension of the random vector. In order to estimate these factors separately, we started in fixed dimension \( s=2\) of the random vector to vary its parameters \(\mu \) and \(\varSigma \) and then, in a second step, increased the dimension to \(s=10\). Similar to what we did in the discussion of Table 1, the efficiency of the adaptive approach was computed as the ratio of CPU times spent in order to reach a fixed threshold of the objective (recall that the objective values related with hierarchically increasing grids form an increasing sequence). For the two uniform grid methods (FUG-FS) and (IUG-IS), we selected the smaller of the two CPU times. The value of the ratio was stabilized by averaging it over a set of different thresholds for the objective. The results are displayed in Table 3.
Ignoring for a moment the column related to higher dimension \(s=10\) and just comparing values for the case \(s=2\), we observe that the efficiency of the adaptive approach strongly depends on the distribution parameters \(\mu \) and \( \varSigma \), it varies in a range between 2 and 12. The following geometric explanation can be given with the help of Fig. 2, where \(\mu =(0,0)\) and correlation − 0.5 were considered (efficiency 3.4): The solution sets of the random inequalities (the sets \(Z^{k}\) in Fig. 2) move with changing decision vector \(x^{k}\), but they were chosen intentionally in our example in a way that they stay centered around (0, 0) and only change their shape. Now, if one imagines, that the mean vector of the given distribution is far from the center, then it is clear that the face of the set \(Z^{k}\) which is closer to \(\mu \) gets much more importance with respect to probability than the opposite face. That is why in the adaptive approach an index selection is favored that leads to cuts near the closer face. Accordingly, indices show a tendency to aggregate rather than to uniformly distribute (see Fig. 4). In contrast, the uniform grid methods evenly spread their cuts, thus wasting a lot of effort with indices not much contributing in a probabilistic sense. Not surprisingly, this effect can be arbitrarily amplified by shifting the mean further away from the center of the sets \(Z^{k}\). This is confirmed by the data in Table 3, where the efficiency is largest in the last row. Another, minor, contrast is added by correlations between the components of the random vector. A positive correlation amplifies the efficiency because the distribution is stretched along the direction of the more and more shifted mean, while a negative correlation weakens the efficiency. For other shift directions of the mean, these circumstances would change of course. It is not surprising that the weakest efficiency of the adaptive approach (1.9) occurs when \(\mu =(0,0)\) and the components are uncorrelated. Then, no special preference for certain faces of the sets \(Z^{k}\) arise and the advantage over a uniform grid tends to disappear. Note that in general applications the solution sets of the inequality system will move completely independently of the given distribution so that a perfect central position is extremely unlikely and a high efficiency of the adaptive grid may be expected.
Turning to the effect of dimension s of the random vector, we confined ourselves to the case of independent components. For the exceptional central case, the efficiency is even slightly below one (probably related to some overhead effect). As soon as the mean deviates from its central position, a clear increase in efficiency due to higher dimension becomes visible reaching a value as high as 56.1. This underlines the promising benefit of using the proposed grid adaptation in real life applications.
The algorithmic approach proposed by us has evidently two major limitations concerning the index set T so far: First, the dimension of T is currently restricted to one and, second, T is assumed to be fixed while it could move as T(x) with the decision in general (analogously to generalized semi-infinite programming). Both issues are subject of future work.
3 Convergence proof for the conceptional algorithm
In this section we provide a convergence proof for the conceptual algorithm presented in Sect. 2.3. Actually, we are going to show convergence in a broader setting by allowing \(\varepsilon \)-optimal solutions of both the lower and upper level problem in Algorithm 1. In this way, convergence can be guaranteed even if the two subproblems are not solved exactly in each step. In the following we assume that \(T\subseteq {\mathbb {R}}^d\) is compact. Furthermore, it will be useful to introduce the grid-dependent sets
as well as the associated grid-dependent probability functions:
Our optimization problem (7) can then be written as
We impose the following basic assumptions on (25):
Lemma 1
The following properties hold true for all \(x\in {\mathbb {R}}^n\), \(M\subseteq T\):
Proof
(28) is evident. (29) follows from the continuity of g. To prove (30), let \(x\in {\mathbb {R}}^n\) and \(M\subseteq T\) be given arbitrarily. Define
By (28) we have \(Z(x,M\cup \{t_k\})\subseteq Z(x,M)\) which implies that Z(x, M) is a disjoint union of \(Z(x,M\cup \{t_k\})\) and \(Z_k\) for all k. Due to the assumption \(\varphi (x,M\cup \{t_k\}) = \varphi (x,M)\) we obtain that \({\mathbb {P}}(\xi \in Z_k) = 0\) for all \(k\in {\mathbb {N}}\). Thus, we have \({\mathbb {P}}(\xi \in \cup _{k\in {\mathbb {N}}}Z_k) = 0\). Moreover, it holds \(Z(x,M\cup \{t_k\}) = Z(x,M) \setminus Z_k\) for any \(k\in {\mathbb {N}}\) such that
Hence, \({\mathbb {P}}(\xi \in Z(x,M\cup (\cup _{k\in {\mathbb {N}}}\{t_k\}))) = {\mathbb {P}}(\xi \in Z(x,M))\) which proves (30). To see (31), fix an arbitrary \(x\in {\mathbb {R}}^{n}\) and observe that by \( Z\left( x,\left\{ t_{1},\ldots ,t_{k}\right\} \right) \) being a decreasing sequence of sets (see (28)) and by probability measures being continuous from above, the assertion follows from the identity
Finally, (26) and (27) allow us to invoke (Farshbaf-Shaker et al. 2018, Prop. 1–3), in order to derive the continuity in x of the function \(\varphi \left( x,K\right) \) for each given compact set \(K\subseteq T \). In particular,
Since \(\varphi \left( x,M\right) =\varphi \left( x,\mathrm {cl\,}M\right) \) for all \(x\in {\mathbb {R}}^{n}\) as a consequence of (29), we have proven (32). \(\square \)
We recall that Algorithm 1 presented in Sect. 2.3 for the solution of (25) constructs a sequence of points \(x_{k}\in X\) and a sequence of indices \(t_{k}\in T \) according to the following alternating scheme:
Here we have changed for later notational convenience the order of upper and lower level problems when compared with Algorithm 1. This does not change, of course, the sequence of iterates. As mentioned above, our aim is to guarantee convergence even in the case that these problems are solved approximately only. Therefore, we shall assume that \(x_{k}\in X\) and \(t_{k}\in T\) are found as solutions of the following approximate problems


where \(\{\delta _k\},\{\tau _k\}\) are sequences of positive numbers. More precisely, this means that
and
Theorem 1
Let \(\delta _k\downarrow 0,\tau _k\downarrow 0\) be two sequences. Let \(\left\{ x_{k},t_{k}\right\} \) be a sequence of solutions generated by the alternating sequence of problems \((U_k),(L_k)\). Then, every cluster point of \( \left\{ x_{k}\right\} \) is a solution of (25).
Proof
Let \({\bar{x}}\) be a cluster point of \(\left\{ x_{k}\right\} \) so that \( x_{k_{l}}\rightarrow {\bar{x}}\) for some subsequence (note that we cannot keep w.l.o.g. the original sequence because in the definition of problem \(\left( U_{k}\right) \) we have to keep all indices t generated from the original sequence, not just those representing the subsequence). Since \(x_{k_{l}}\in X \) as a solution of \(\left( U_{k_{l}}\right) \) and X is closed, we infer that \({\bar{x}}\in X\). The main claim in this proof is the inequality
We postpone the proof of (33) to the end of this proof. Taking (33) for granted, \({\bar{x}}\) is feasible in (25). If \({\bar{x}}\) wasn’t a solution of (25), then there would exist some \(x^{*}\in X\) such that \(\varphi \left( x^{*},T \right) \ge p\) and \(f\left( x^{*}\right) <f\left( {\bar{x}}\right) \). By continuity of f, we may choose some \(l\in {\mathbb {N}}\) such that \(f\left( x_{k_{l}}\right) -\delta _{k_l} >f\left( x^{*}\right) \) with the sequence \(\delta _k\) introduced in the statement of this theorem. As a consequence of (28), one has that
whence \(x^{*}\) is feasible in \(\left( U_{k_{l}}\right) \). Therefore, \(f\left( x_{k_{l}}\right) \le f\left( x^{*}\right) +\delta _{k_l}\) which is a contradiction.
For the remainder of the proof we are going to verify (33). In a first step, we prove the relation
To do so, fix an arbitrary \(m\in {\mathbb {N}}\). Since \(x_{k_{l}}\) is feasible in \(\left( U_{k_{l}}\right) \), we get that
From (32) we derive that
As m was arbitrarily fixed, this last relation holds true for all \(m\in {\mathbb {N}}\). Now, (31) yields (34):
In a second step we verify the statement
Assume that (35) fails to hold. Because \(Z\left( {\bar{x}},G\cup \{t\} \right) \subseteq Z\left( {\bar{x}},G\right) \) by (28) it is sufficient to lead the assumption
to a contradiction. Put \(\varepsilon {:}{=}\varphi \left( {\bar{x}},G\right) -\varphi \left( {\bar{x}},G\cup \left\{ t^{*}\right\} \right) >0 \). Applying (31) upon joining the fixed element \(t^{*}\) to the sequence of indices considered there, we infer that
Accordingly, we find an index \(\alpha \in {\mathbb {N}}\), such that
By virtue of (32), there exists some \(\beta \in {\mathbb {N}}\), such that
Hence,
Now, the monotonicity of \(\varphi \) based on (28) yields that
Since \(t_{k_{l}+1}\) is a solution of the lower level problem \(\left( L_{k_{l}}\right) \) introduced above, we arrive at
As \(\tau _k\downarrow 0\), there exists some \(\rho \in {\mathbb {N}}\) such that \(\tau _k\le \frac{\varepsilon }{4}\) for all \(k\ge \rho \). Therefore,
Owing to (32), there exists some \(\gamma \in {\mathbb {N}}\) with \(\left| \varphi \left( x_{k_{l}},G\right) -\varphi \left( {\bar{x}},G\right) \right| <\frac{\varepsilon }{4}\) for all \(l\ge \gamma \). With \(l^{*}{:}{=}\max \left\{ \alpha ,\beta ,\gamma ,\rho \right\} \) we arrive at the desired contradiction
Therefore, (35) holds true. In the final step of the proof, we show the statement
which proves the desired relation (33) due to (34). Because T is a compact subset of the separable space \({\mathbb {R}}^d\), there exists \({\tilde{T}}\subseteq T\) that is countable and dense in T, i.e.
Due to (35) it holds \(\varphi ( {\bar{x}},G\cup \{{\tilde{t}}_k\}) = \varphi \left( {\bar{x}},G\right) \) for all \(k\in {\mathbb {N}}\). By virtue of (30), (28) and (29) we get the relation
On the other hand, \( \varphi ( {\bar{x}},G) \ge \varphi ( {\bar{x}},T)\) by (28) which proves (36) and the proof is complete. \(\square \)
Remark 1
If in (26) the function g is in addition convex in the second variable z, then the condition (27) can be replaced by the simpler uniform Slater condition
which implies condition (27).
Corollary 2
If the uniform Slater condition is satisfied in the water reservoir problem (41) presented in Sect. 4 below, then every cluster point of the sequence of iterates \( \left\{ x_{k}\right\} \) generated by the conceptual algorithm from Sect. 2.3 is a solution.
Corollary 3
If X is compact, and (25) admits a unique solution (there must be at least one), then the sequence of iterates \(\left\{ x_{k}\right\} \) converges to this solution.
Proof
Denote by \(x^{*}\in X\) the unique solution of (25). If \( \left\{ x_{k}\right\} \) did not’t converge to x, then there would exist an open neighborhood U of \(x^{*}\) and a subsequence \(\left\{ x_{k_{l}}\right\} \) with \(x_{k_{l}}\notin U\) for all \(l\in {\mathbb {N}}\). By compactness of X, one has \(x_{k_{l_{m}}}\rightarrow _{m}{\bar{x}}\) for a further subsequence. By Theorem 1, it follows that \({\bar{x}}\) is a solution of (25), whence \({\bar{x}}=x^{*}\in U\). This yields the contradiction \(x_{k_{l_{m}}}\in U\) for m large enough. \(\square \)
Remark 2
The set X in the water reservoir problem (41) presented in the next section is compact. With some additional effort, it can be shown that the (nonempty) solution set of (41) is unique. Hence, the sequence of iterates \(\left\{ x_{k}\right\} \) generated by the conceptual algorithm from Sect. 2.3 converges to this unique solution.
4 An application to probabilistic water reservoir control under time-continuous inflow
The importance of probabilistic programming in the context of water reservoir management has been recognized a long time ago [see, e.g. the basic monograph (Loucks et al. 1981) or (Chattopadhyay 1988; Edirisinghe et al. 2000; Loiaciga 1988; Prékopa and Szántai 1978, 1979; Van Ackooij et al. 2014)]. Many papers originally considered models with individual probabilistic constraints
which in a suitable structure with separated randomness allow for simple quantile-based reformulations via linear programming. Here, in contrast with (1), each random inequality is turned into a probabilistic constraint individually. On the level of continuously indexed random inequality systems, this difference corresponds to that between (4) and (6). The shortcoming of the individual against the joint probabilistic constraint has already been discussed in the introduction. Suffice it here to refer to a water management application, where random filling levels of the reservoir stayed in a given critical range with probability 90% individually at each time of a finite interval, whereas they stayed in the critical range throughout the whole time interval (the actually desirable property) only with probability 32% (Van Ackooij et al. 2010, p. 548). Therefore, we consider in the following a strongly simplified water reservoir problem with joint probabilistic constraints. The new challenging aspect will arise from dealing with a continuously indexed infinite random inequality system in the context of a probust constraint of type (4). More precisely, we will assume a reservoir with time-continuous random inflow. This will lead, for any release policy (the control to be optimized) to a time-continuous random filling level in the reservoir. Keeping this level within certain limits at high probability will lead us exactly to (4). As for the controlled release, we shall suppose that it is piecewise constant, which partly corresponds to common practice. It would not be harmful to pass to a time-continuous control here as well [leading to probabilistic constraints with infinite-dimensional decisions as in Farshbaf-Shaker et al. (2019)].
4.1 Water reservoir model under time-continuous inflow
In the following model, a single water reservoir with lower level constraint and designed for hydro power generation over a time interval [0, T] is considered. The model is strongly simplified, in order to keep the presentation concise and to focus on the aspect of probust constraints and their algorithmic solution as proposed in Sect. 2. Accordingly, we will neither insist on a careful statistical analysis of the stochastic inflow process nor on incorporating all technological or physical details from real life reservoirs. Rather, one might think about an abstract reservoir with stochastic inflow and controlled release subject to critical levels to be respected (beyond water reservoirs, this could be batteries charged by solar power in minigrids or a bank account in finance).
The stochastic process of water inflow to the reservoir is denoted by \({\tilde{\xi }}\). The time-dependent release of water \({\tilde{x}}\) is controlled and should maximize a given price function. Fixing the initial reservoir level as \(l_0\), the level as a function of time evolves according to
Throughout the time horizon, a minimum level \(\underline{l}\le l_0\) has to be respected. Since, the current water level is stochastic, one may not expect a sure satisfaction of the minimum level, no matter what release function is chosen. Therefore, it makes sense, to formulate a joint probabilistic level constraint as
with some risk level \(p\in (0,1)\). We assume that the reservoir serves the generation of hydro power. The profit of water release will depend on a price signal \({\tilde{c}}\) that may change over time as a function of demand.
Adding an upper bound \({\bar{x}}\) for the water release corresponding to the operational limits of turbines, we end up at the following first version of an optimization problem:
Here, we suppose that the decision x on water release is taken in a completely static way, i.e. neglecting the increasing information on the realization of the stochastic inflow process. We may imagine the situation of a day ahead market on which the offered hourly energy supply (i.e., the water release) is fixed one day in advance, thus completely ignoring the inflows of the next day.
In the following, we pass to a finite-dimensional version of this problem. First, we discretize the time interval as
and define the water release to have constant velocity on each subinterval \([t_{i-1},t_{i})\):
Accordingly, the profit to be maximized reduces to the finite-dimensional expression
where \(c=(c_{1},\ldots ,c_{n})\) and
Second, the random process is reduced to a finite sum of randomly weighted fixed deterministic processes \(\alpha _{j}\) \((j=1,\ldots ,s)\) and \(\beta \):
It is assumed that the random vector \(\xi =(\xi _{1},\ldots ,\xi _{s})\) obeys a centered multivariate Gaussian distribution, i.e., \(\xi \sim {\mathscr {N}}\left( 0,\varSigma \right) \) for some covariance matrix \(\varSigma \).
Note that, while the release is piecewise constant, the inflow in (40) is still continuous in time. Therefore the reservoir level in (37) is also continuous in time and can be written as:
where
Finally, we add some simple deterministic constraints in the following set:
The first part of constraints just relates to an upper bound for the water release corresponding to the maximum operating limit of the given system of turbines. The second part—a so-called ‘cycling constraint’—makes sure that the total water release is not bigger than the expected cumulative inflow of water which equals B(T). In this way, optimization in the given time interval [0, T] is not carried out at the expense of a future time horizon.
Summarizing, under our assumptions the optimization problem (39) reduces to:
where for all \(x\in {\mathbb {R}}^n\) and all \(t\in [0,T]\),
Clearly, (41) is a special instance of the optimization problem (7) with probust constraints and can be solved algorithmically with the approaches discussed in Sect. 2.
4.2 Water reservoir instance
In the following, we are going to apply the adaptive algorithm defined in Sect. 2 in order to solve an instance of the water reservoir problem presented above. We will use the following problem data:
Note that adding cosine terms in the functions \(A_j\) makes the initial water level stochastic too (with expected value \(l_0\)) which we feel to be more realistic if the decision on water release has to be taken well ahead of the given time interval, e.g., on a day-ahead market.
We want to take the opportunity to also oppose the model with joint chance constraints to those simplifying models relying on expected values (2) or individual chance constraints (6), respectively. Both of these models will reduce to ordinary linear semi-infinite programs (see, e.g., Goberna and López (2000) and Goberna and López (2017) for an introduction and overview), but fail to have the desired robustness property. We therefore start by making these additional models more precise.
Contrary to (41), the expected-value model replaces the joint chance constraint by just the continuously indexed inequality inside the probability but with the random vector substituted by its expectation. Since this expectation is zero because \(\xi \) has a centered Gaussian distribution, the resulting optimization problem takes the form
where for all \(x\in {\mathbb {R}}^n\) and all \(t\in [0,T]\),
Observe, that b is affine linear in x, so that (43) represents an ordinary linear semi-infinite program.
As for the model with individual chance constraints, it requires that the stochastic level constraint be satisfied with given probability p for each time t individually:
With the aid of the function b introduced above, we can reformulate this constraint for a fixed \(t \in [0,T]\) as:
Owing to \(\xi \sim {\mathscr {N}}(0,\varSigma )\), the transformation law for Gaussian distributions yields that
Therefore, the chance constraint \({\mathbb {P}}(g(x,\xi ,t) \le 0)\ge p\) can be written as
where \(\varPhi \) is the distribution function of \({\mathscr {N}}(0,1)\). Upon inverting this function, one arrives at the following fully explicit redescription of the individual chance constraint:
Eventually, the optimization problem with individual chance constraints gets the form
which is an ordinary linear semi-infinite program exactly like the expected-value problem (43). Note that our model (41) with (infinitely many) joint probabilistic constraints falls outside this class of linear semi-infinite programs because taking the probability of a joint system of random inequalities inevitably introduces nonlinearities even to originally linear constraints. This leads to the substantially larger numerical effort based on the algorithm presented here. On the other hand, we shall see, that the robustness at low costs of the obtained solutions pay this effort.
Upper left: Plot of optimal release policies for the models of joint (red) and individual (blue) chance constraints (both with \(p=0.9\)) as well as for expected-value (black) constraints (upper left). The appropriate scaled price signal (without reference to the ‘Release’ axis) is represented by a thin line. Simulation of 20 filling level scenarios under joint chance constraint (upper right), expected-value constraint (bottom left) and individual chance constraint (bottom right). Violating scenarios are colored in red, the critical lower level \(\underline{l}=2\) corresponds to the dashed line (Color figure online)
Figure 5 illustrates the three optimal solutions for release profiles under joint chance constraint, expected-value constraint and individual chance constraint. It can be seen that all three profiles try to follow the price signal (weights of objective) in order to maximize the profit. Of course, they cannot do so perfectly in order to meet the respective constraints imposed. The profits realized for these solutions are 89.13 (expected-value constraint), 86.59 (individual chance constraints) and 85.04 (joint chance constraint). This decay is clear from the fact that the corresponding constraints are increasingly restrictive. Note, however, that the loss in profit for the model with joint chance constraint is not very large. Indeed the release profiles look comparatively similar. On the other hand, the impact on the probability of satisfying uniformly over time the lower level constraint is remarkable. These probabilities calculate as 90% for joint chance constraint (corresponding to the imposed level), 72% for individual chance constraints (when imposing an individual probability of 90% for each time step separately) and only 29.7% for expected value constraints. These findings are supported by the three additional diagrams in Fig. 5. Here, a posterior check of solutions was carried out by simulating 20 inflow profiles according to the chosen distribution and applying the respective release policy. The diagrams then show the resulting 20 level profiles for the reservoir. For the solution under joint chance constraint, there is just one violating scenario (two would be expected on average for repeated simulations according to the probability of 90%). The solution under individual chance constraints does what it is expected to do: at each time separately, there are only few violating profiles (two on average according to the chosen individual probability of 90%). On the other hand, seven profiles are violating in the sense of a uniform condition, i.e., violate the level at some time. The situation is even worse for expected-value constraints, with thirteen violating scenarios. Note that in all cases the average final level coincides with the average initial level due to the cycling constraint.
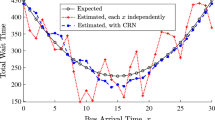
Figure 6 displays the numerical results for the three grid discretization approaches presented in Sect. 2 in the water reservoir problem with joint chance constraints. The left picture shows the dependence of the optimal value on the grid size for the uniform and adaptive grid control. It turns out that a grid size of above 50 is sufficient for a high accurate solution of the reservoir problem when applying the adaptive grid control. The right picture of Fig. 6 plots the CPU times vs. optimal value. Note that any optimal value must be larger than the true optimal value of the problem because the discretization of the continuous inequality system leads to larger feasible sets in the maximization problem. Therefore, the smaller the computed value is (the more it is to the right), the more precise is the solution. Since the curves from the original data exhibited some noisy behavior due to random effects in the iteration processes, they were smoothened afterwards by a moving average. A clear dominance of the adaptive grid approach even growing when approaching the solution becomes evident. Among the two uniform discretization schemes, the one with increasing grid and sample performs slightly better than the one with a naive fixed uniform grid.
5 Conclusions
In the present paper we introduce an adaptive discretization framework to solve probust optimization problems and show that this approach converges under quite mild assumptions. Furthermore, we demonstrate that an implementable version of this methodology is efficient and outperforms uniform discretization approaches. This is verified for numerical examples as well as in the application of water reservoir management under time-continuous random inflow.
References
Adam L, Branda M, Heitsch H, Henrion R (2020) Solving joint chance constrained problems using regularization and Bender’s decomposition. Ann Oper Res 292:683–709
Andrieu L, Henrion R, Römisch W (2010) A model for dynamic chance constraints in hydro power reservoir management. Eur J Oper Res 207:579–589
Bank B, Guddat J, Klatte D, Kummer B, Tammer K (1982) Non-linear parametric optimization. Akademie Verlag, Berlin
Ben-Tal A, El Ghaoui L, Nemirovski A (2009) Robust optimization. Princeton University Press, Princeton
Bremer I, Henrion R, Möller A (2015) Probabilistic constraints via SQP solver: application to a renewable energy management problem. Comput Manag Sci 12:435–459
Calafiore GC, Campi MC (2006) The scenario approach to robust control design. IEEE Trans Autom Control 51:742–753
Charnes A, Cooper WW, Symonds GH (1958) Cost horizons and certainty equivalents: an approach to stochastic programming of heating oil. Manag Sci 4:235–263
Chattopadhyay S (1988) A realistic linear decision rule for reservoir management. Water Resour Manag 2:21–34
Curtis F, Wächter A, Zavala V (2018) A sequential algorithm for solving nonlinear optimization problems with chance constraints. SIAM J Optim 28:930–958
Dentcheva D, Martinez G (2013) Regularization methods for optimization problems with probabilistic constraints. Math Program 138:223–251
Dentcheva D, Ruszczyński A (2010) Robust stochastic dominance and its application to risk-averse optimization. Math Program 123:85–100
Edirisinghe NCP, Patterson EI, Saadouli N (2000) Capacity planning model for a multipurpose water reservoir with target-priority operation. Ann Oper Res 100:273–303
Farshbaf-Shaker MH, Henrion R, Hömberg D (2018) Properties of chance constraints in infinite dimensions with an application to PDE constrained optimization. Set-Valued Var Anal 26:821–841
Farshbaf-Shaker MH, Gugat M, Heitsch H, Henrion R (2020) Optimal Neumann boundary control of a vibrating string with uncertain initial data and probabilistic terminal constraints. SIAM J Control Optim 58(4):2288–2311
Geletu A, Hoffmann A, Klöppel M, Li P (2017) An inner-outer approximation approach to chance constrained optimization. SIAM J Optim 27:1834–1857
Geletu A, Hoffmann A, Schmidt P, Li P (2020) Chance constrained optimization of elliptic PDE systems with a smoothing convex approximation. ESAIM Control Optim Calc Var 26:70
Goberna MA, López MA (2000) Linear semi-infinite optimization. Wiley, Hoboken
Goberna MA, López MA (2017) Recent contributions to linear semi-infinite optimization. 4OR Q J Oper Res 15:221–264
González Grandón T, Heitsch H, Henrion R (2017) A joint model of probabilistic/robust constraints for gas transport management in stationary networks. Comput Manag Sci 14:443–460
González Grandón T, Henrion R, Pérez-Aros P (2020) Dynamic probabilistic constraints under continuous random distributions. Math. Program. appeared online https://doi.org/10.1007/s10107-020-01593-z
Guerra Vázquez F, Rückmann J-J, Stein O, Still G (2008) Generalized semi-infinite programming: a tutorial. J Comput Appl Math 217(2):394–419
Guigues V, Henrion R (2017) Joint dynamic probabilistic constraints with projected linear decision rules. Optim Methods Softw 32:1006–1032
Heitsch H (2020) On probabilistic capacity maximization in a stationary gas network. Optimization 69:575–604
Hong L, Yang Y, Zhang L (2011) Sequential convex approximations to joint chance constrained programs: a Monte Carlo approach. Oper Res 59:617–630
Liu X, Kucukyavuz S, Luedtke J (2016) Decomposition algorithms for two-stage chance constrained programs. Math Program 157:219–243
Loiaciga HA (1988) On the use of chance constraints in reservoir design and operation modeling. Water Resour Res 24:1969–1975
López M, Still G (2007) Semi-infinite programming. Eur J Oper Res 180:491–518
Loucks P, Stedinger JR, Haith DA (1981) Water resource systems planning and analysis. Prentice Hall, Englewood Cliffs
Luedtke J, Ahmed S (2008) A sample approximation approach for optimization with probabilistic constraints. SIAM J Optim 19:674–699
Martínez-Frutos J, Periago Esparza F (2018) Optimal control of PDEs under uncertainty. Springer, Cham
Pagnoncelli B, Ahmed S, Shapiro A (2009) Sample average approximation method for chance constrained programming: theory and applications. J Optim Theory Appl 142:399–416
Prékopa A (1995) Stochastic programming. Kluwer, Dordrecht
Prékopa A, Szántai T (1978) Flood control reservoir system design using stochastic programming. Math Program Study 9:138–151
Prékopa A, Szántai T (1979) On optimal regulation of a storage level with application to the water level regulation of a lake. Eur J Oper Res 3:175–189
Shapiro A, Dentcheva D, Ruszczyński A (2014) Lectures on stochastic programming. MOS-SIAM series on optimization, vol 9, 2nd ed. Modeling and theory. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA
Stein O (2003) Bi-level strategies in semi-infinite programming. Springer, Berlin
van Ackooij W (2020) A discussion of probability functions and constraints from a variational perspective. Set-Valued Var Anal 28:585–609
Van Ackooij W, Henrion R (2014) Gradient formulae for nonlinear probabilistic constraints with Gaussian and Gaussian-like distributions. SIAM J Optim 24:1864–1889
Van Ackooij W, Henrion R (2017) (Sub-) Gradient formulae for probability functions of random inequality systems under Gaussian distribution. SIAM-ASA J Uncertain 5:63–87
Van Ackooij W, Pérez-Aros P (2020) Gradient formulae for nonlinear probabilistic constraints with non-convex quadratic forms. J Optim Theory Appl 185:239–269
Van Ackooij W, Henrion R, Möller A, Zorgati R (2010) On probabilistic constraints induced by rectangular sets and multivariate normal distributions. Math Methods Oper Res 71:535–549
Van Ackooij W, Zorgati R, Henrion R, Mö ller A (2014) Joint chance constrained programming for hydro reservoir management. Optim Eng 15:509–531
van Ackooij W, Frangioni A, de Oliveira W (2016) Inexact stabilized Benders’ decomposition approaches with application to chance-constrained problems with finite support. Comput Math Appl 65:637–669
Van Ackooij W, Henrion R, Pérez-Aros P (2020) Generalized gradients for probabilistic/robust (probust) constraints. Optimization 69:1451–1479
Zymler S, Kuhn D, Rustem B (2013) Distributionally robust joint chance constraints with second-order moment information. Math Program 137:167–198
Acknowledgements
The authors gratefully acknowledge the valuable comments and suggestions by an anonymous reviewer which led to an improved version of Theorem 1. The second author thanks the Deutsche Forschungsgemeinschaft for their support within project B04 in the Sonderforschungsbereich/Transregio TRR 154. In addition, the third author acknowledges support by the FMJH Program Gaspard Monge in optimization and operations research including support to this program by EDF.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Berthold, H., Heitsch, H., Henrion, R. et al. On the algorithmic solution of optimization problems subject to probabilistic/robust (probust) constraints. Math Meth Oper Res 96, 1–37 (2022). https://doi.org/10.1007/s00186-021-00764-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00186-021-00764-8
Keywords
- Probabilistic constraints
- Probust constraints
- Chance constraints
- Bilevel optimization
- Semi-infinite optimization
- Adaptive discretization
- Reservoir management