A non-cooperative game theory approach to cost sharing in networks

Abstract

This paper considers networks in which nodes have communication needs between them. The cost of building or maintaining an edge with a given capacity is the same across any pair of agents. It is known that feasibility is reached by any maximal-capacity spanning tree. A multi-stage non-cooperative game is considered in which, at each stage, every agent simultaneously decides either to propose building a connection to another agent or to wait for a better opportunity. The required capacity between any pair of agents can be seen as being to their benefit if and only if, in the resulting tree, there exists a path between them such that every edge provides at least this required capacity. On the other hand, the agents who decide to connect have to pay for the link by equally splitting the cost. The problem is analyzed in a context in which the preferences of the agents regarding benefits and costs are lexicographic. The concepts of capacity synthesis equilibrium (CSE) and strong capacity synthesis equilibrium (strong CSE) are introduced and a mechanism to reach some of these equilibria is presented. We also analyze CSEs and strong CSEs in relation to the Nash equilibria of the benefit capacity synthesis game.

1 Introduction

A version of the well-known network synthesis problem (Ahuja et al. 1993; Tamir 1991) is the capacity synthesis problem, in which a set of agents share a network for exchanging information, for transporting commodities along roads or shipping channels, for establishing commercial channels with limited capacity of human or material resources, etc. For capacity synthesis problems, a required capacity between any pair of agents (bandwidth, road-width, depth of the channel, etc.) is needed. A feasible graph for the capacity synthesis problem is one in which any pair of agents is connected by a path whose edges all hold the capacity of at least the required capacity between them. Among these feasible graphs, we are interested on those with minimum cost. At this respect, we assume that the cost of building or maintaining y units of capacity between any two pairs of agents is the same. Without loss of generality, the cost of y units of capacity can be set to be $y.

In order to find such a graph with minimum cost of building or maintaining, it is assumed that: (i) capacity cannot be obtained across multiple paths; (ii) the same edge can be used jointly by any pair of agents if their required capacity is at most the capacity of the edge; and (iii) the cost of building or maintaining a given capacity between any two pair of agents is the same.

It is well known, and easy to show, that a feasible network with minimum total cost is obtained by using a maximal spanning tree with respect to the capacities.

The capacity synthesis problem is then related to the minimum-cost spanning tree (mcst) problem, for which a number of efficient algorithms, such as Kruskal (1956) and Prim (1957) (see Wu and Chao 2004 for a review), have been developed to produce minimum-cost trees. These algorithms can be adapted to generate maximal-capacity spanning trees by simply applying them from the largest capacity demand downward instead of from the cheapest link upward.

If the problem of allocating the costs among the users is considered, then the situation can be addressed from the perspective of game theory. With respect to the minimum-cost spanning tree problem, many contributions can be found in the literature that address the cooperative approach, beginning with the seminal papers by Bird (1976) and Granot and Huberman (1984). Some last relevant results in mcst cooperative games can be seen in Bogomolnaia and Moulin (2010), Trudeau and Vidal-Puga (2017), Norde (2019) or Bergantiños and Vidal-Puga (2015).

Among the contributions to cost sharing in the capacity synthesis problem from the point of view of cooperative game theory, the papers by Bogomolnaia et al. (2010) and Moulin (2013) provide some relevant referents.

In this paper the capacity synthesis problem is addressed from a non-cooperative perspective, where the focus is on the analysis of the stability and the efficiency of a maximal-capacity spanning tree formation. The analysis is based on the multi-stage non-cooperative game inspired by that introduced in Bergantiños and Lorenzo (2004), and used later in Fernández et al. (2009). In this approach, we assume that the agents only play pure strategies, and that agents’ decisions depend on the agents who are already connected and on how are they connected, but do not depend on the order in which agents are connected. Hence, at each stage, every agent simultaneously decides whether to propose a new connection or to wait for a better opportunity. If two agents propose to connect with each other, then the connection is made and each pays half of the link cost. If the procedure provides a maximal-capacity spanning tree, then this can be regarded as a efficiency property.

The attainment of the required capacity between any pair of agents can be seen as a benefit for said agents if, in the resulting tree, there exists a path between them in which every edge holds at least their required capacity. We introduce a family of profiles of strategies, called $\sigma$-strategies, which provide a maximal-capacity spanning tree and, at the same time are strong Nash equilibria for the so-called game of benefits.

Finally, we consider that the preferences of the agents regarding benefits and costs are lexicographic, and introduce the concept of capacity synthesis equilibrium (CSE) and Strong capacity synthesis equilibrium (Strong CSE). We show that the $\sigma$-strategies are also Strong CSEs.

The rest of the paper is organized as follows. In Sect. 2, the capacity synthesis problem is described. In Sect. 3, the benefit capacity synthesis game and the cost capacity synthesis game are introduced and $\sigma$-strategies are analysed in relation to the Nash equilibria of the benefit capacity synthesis game. When the costs that each agent has to pay are also taken into account, the concept of capacity synthesis equilibrium (CSE) arises. We show that a $\sigma$-strategy is a Strong CSE. Finally, Sect. 4 provides some concluding remarks. For the sake of readability, we have included an Appendix with various significant examples

2 Capacity synthesis problem

Given a set of agents $N=\{1,\dots ,n\}$, $n\in \text{ I }\!\text{ N }$, all located at different places (nodes), an edge between two agents (or nodes) $i,j\in N$, with $i\ne j$, designates an undirected pair (i, j). When $n\ge 2$, the set of all undirected edges, $N(2)=\{(i,j), i,j\in N\}$, has the cardinality ${n \atopwithdelims ()2}=n(n-1)/2$. We similarly define S(2) for any subset $S\subset N$, when $|S|\ge 2$, and $S(2)=\emptyset$ if $|S|<2$.

An undirected graph, G, on N is a pair $(S, E_S)$ where $S\subseteq N$ and $E_S$ is a subset of S(2). We say that $G_1\equiv (S_1,E_{S_1})$ is a subgraph of $G_2\equiv (S_2,E_{S_2})$ if $S_1\subseteq S_2$ and $E_{S_1}\subseteq E_{S_2}$. A path, $\gamma _{ij}$, on $G\equiv (S,E_S)$, between the nodes in S, i and j, is the edge (i, j) (if $(i,j)\in E_S$) or any sequence of different edges in $E_S$, starting at i and ending at j: $\gamma _{ij}\equiv \{(l_0,l_1), (l_1, l_2),\ldots ,(l_{k-1}, l_k),(l_k, l_{k+1})\}$, where $l_0=i$, $l_{k+1}=j$ and $k\ge 1$. A cycle on G is a path in which the starting and the ending node coincide. An undirected graph on N, $\Gamma \equiv (S,E_S)$, $S\subset N$, is a tree if it connects all the nodes in S, and it has no cycles. A spanning tree is a tree connecting all agents in N. Finally, a forest is a set of unconnected trees which contain all the nodes in N. Note that, since a single unconnected node is also considered a tree, some of the trees in a forest may consist of a single unconnected node.

A capacity synthesis problem is a pair (N, t), where $t=[t_{ij}]_{(i,j)\in N(2)}$ is a symmetric non-negative matrix with its diagonal elements equal to zero. Each non-diagonal element in matrix t represents the capacity requirement between the corresponding nodes.

A capacity network for (N, t) is a pair, (G, c), where $G\equiv (N,E_N)$ is an undirected graph on N in which each edge, $e\in E_N$, has a non-negative capacity $c_e$ (when $e=(i,j)$, this capacity can also be denoted as $c_{ij}$). The capacity network, (G, c), is feasible for (N, t) if it supports the capacity requests t: any two nodes $i,j\in N$, with $t_{ij}>0$, are connected in G by at least one path, $\gamma _{ij}$, where all the edges belonging to it, equal or exceed the required capacity between i and j, that is, $c_e \ge t_ {ij}$, for all $e\in \gamma _{ij}$.

A minimal-cost capacity network for (N, t) is a feasible capacity network for (N, t), that minimizes the total cost $\sum _{e\in E_N}c_e$ among all feasible networks for (N, t). We write V(N, t) or simply V(t) for this minimal cost.

As shown in Ahuja et al. (1993), a minimal-cost capacity network is a tree. Although a minimal-cost capacity network may specify edge capacities that are not inherited from the corresponding capacity requests¹, it can be observed that, among the minimal-cost capacity networks, (G, c), for a given problem (N, t), one or more can be found in which $c_{ij}=t_{ij}$, for all $(i,j)\in E_N$. Moreover, in Ahuja et al. (1993) it is shown that for a spanning tree, $\Gamma$, the three following statements are equivalent:

• The capacity network $(\Gamma , t)$ is feasible for (N, t).

• The aggregate capacity $t(\Gamma )=\sum _{e\in \Gamma }t_e$ is maximal among all spanning trees on N.

• The capacity network $(\Gamma , t)$ is a minimal-cost capacity network for (N, t).

A tree, $\Gamma$, that verifies the three above equivalent statements is called a maximal-capacity spanning tree (MCST) for (N, t) (see Bogomolnaia et al. 2010). Such a tree always exists, but may not be unique.

On the basis of the above results, we restrict our analysis to feasible capacity networks, (G, t), in which each edge e that connects agents i and j has a capacity $c_e=c_{ij}=t_{ij}$. Moreover, the problem consists of the construction of an MCST from the complete graph associated with the capacity synthesis problem (N, t). This MCST, as mentioned above, is a minimal-cost capacity network.

In what follows, for the sake of simplicity, we slightly abuse notation and denote by (N, t) the complete graph associated with the capacity synthesis problem (N, t).

Finally, the results in Ahuja et al. (1993) for the minimum-cost spanning tree problem can be rewritten here as the following optimality conditions for the MCST.

Proposition 2.1

(MCST optimality conditions) Given a spanning tree, $\Gamma$, on (N, t), the following statements are equivalent:

• 1. $\Gamma$ is an MCST for (N, t).

• 2. If any edge $(i,j)\in \Gamma$ is deleted, then $t_{ij}\ge t_{kl}$ holds for every possible edge $(k,l)\ne (i,j)$ that connects the two unconnected trees in the resulting forest (cut optimality condition).

• 3. If the edge $(k,l)\notin \Gamma$, then $t_{ij}\ge t_{kl}$ holds for every (i, j) in the path, $\gamma _{kl}$ in $\Gamma$, connecting k and l (path optimality condition).

2.1 MCST algorithms

Let F be a forest whose set of edges are all strictly included in some MCST on (N, t). Let $e=(i,j)$ be one of the edges in the complete graph, (N, t), with the highest capacity among all the edges that do not belong to F, and connect two unconnected trees in F, namely $\Gamma$ and $\Gamma '$, where $i\in \Gamma$ and $j\in \Gamma '$. Consider $F'=F\cup \{e\}$.

Proposition 2.2

$F'$ is a forest which is contained in at least one MCST.

Proof

It is easy to see that $F'$ is a forest. Let $\overline{\Gamma }$ be an MCST for (N, t) containing F. If $e=(i,j)\in E_{\overline{\Gamma }}$ then the proof ends. Otherwise, if we add e to $E_{\overline{\Gamma }}$, then the cycle $\gamma _{ij}\cup \{e\}$ is created, where $\gamma _{ij}$ is the unique path in $\overline{\Gamma }$ that connects i and j. In this cycle, since e leaves $\Gamma$, there exists another edge $e'$ in $\gamma _{ij}$ that reaches $\Gamma$ from outside. Since $e=(i,j)$ is one of the edges in the complete graph, (N, t), with the highest capacity among all the edges that do not belong to F and connects two unconnected trees in F, then $t_e\ge t_{e'}$. On the other hand, the path optimality condition ensures that $t_e\le t_{e'}$, and therefore $t_e= t_{e'}$. Then, if we remove the edge $e'$ from $E_{\overline{\Gamma }}\cup \{e\}$, then the cycle disappears and a new tree is obtained $(\overline{\Gamma }\backslash \{e'\})\cup \{e\}$. This tree is a spanning tree on N which contains $F'$. Moreover, it is an MCST, since the capacity of e is equal to the capacity of $e'$. $\square$

Proposition 2.2 permits us to design algorithms to generate MCSTs inspired by Kruskal’s algorithm²:

• At stage 0, the forest $F_0$ consists of the n isolated nodes.

• At each stage, k, $k=1,2,\ldots , n-1$, add one of the edges, $e_k$ in (N, t), that has a higher capacity among those that join two trees of $F_{k-1}$, that is, among those that do not generate a cycle, when added to $F_{k-1}$.

• The procedure ends after $n-1$ stages.

Notice that, at the different stages, k, $k=1,2,\ldots , n-1$, of the procedure explained above, several edges may be candidates for their addition to $F_{k-1}$, and only one of them has to be selected.

Example 2.3

Consider $N=\{1,2,3,4\}$, and $t= \left( \begin{array}{cccc} 0 &{}\quad 5 &{}\quad 5 &{}\quad 3 \\ 5 &{}\quad 0 &{}\quad 1 &{}\quad 5 \\ 5 &{}\quad 1 &{}\quad 0 &{}\quad 6\\ 3 &{}\quad 5 &{}\quad 6 &{}\quad 0\\ \end{array} \right)$

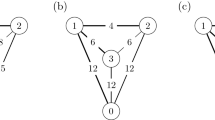
At stage 0, . At the first stage, agents 3 and 4 connect because they need the highest capacity. At the second stage, agent 1 may connect to agent 2 or to agent 3, or agent 2 may connect to agent 4; all these connections have capacity 5. Suppose that agent 1 connects to agent 3 at this stage to form $F_2=\{\{(3,4), (1,3)\},\{2\}\}$. At the third and final stage, agent 2 may connect either to agent 1 or to agent 4; both connections have capacity 5. Suppose that agent 2 connects to agent 1 to obtain the MCST, $F_3=\Gamma$, in Fig. 1. $\lhd$

Fig. 1

$\Gamma =\{(3,4),(1,3),(1,2)\}$ is a MCST

The other possible MCSTs that result when the ties are solved differently are $\Gamma '=\{(1,2),(2,4),(3,4)\}$ and $\Gamma ''=\{(1,3),(3,4),(2,4)\}$, in Fig. 2.

Fig. 2

Other possible MCSTs

3 Capacity synthesis non-cooperative games

Parallel to the design of an MCST for the capacity synthesis problem, (N, t), the question that arises is how to allocate the total cost, V(t), among the agents. Game theory provides tools to answer this question. For instance, Bogomolnaia et al. (2010) use cooperative game theory in their approach and provide several solutions for the associated cost sharing problem. However, in many real-life situations, agents make their decisions independently and therefore it is convenient to address the problem from a non-cooperative point of view.

A non-cooperative game associated with a capacity synthesis problem, (N, t), in which the set of agents is the set of players, can be defined as follows: At an initial stage, all the agents are unconnected, $F_0=\{\{1\},\{2\},\ldots ,\{n\}\}$; now, the strategies, $x_i$, of any player, $i\in N$, consist of either proposing to only one agent $j\in N$, $j\ne i$, to build the edge (i, j) with the required capacity, $t_{ij}$, and paying half of the connection cost each, or waiting for a different situation at this point (all the agents make their decisions simultaneously); the edge (i, j) will be built if at this stage both players, i and j, propose building this connection, otherwise the connection will remain unbuilt. In subsequent stages, every player simultaneously decides either to propose a connection to one of the agents to which they are still unconnected, or to wait and to retain from proposing any link at this stage. However, at these non-initial stages simultaneous connections may generate cycles: in order to prevent cycles, some of the edges for which the corresponding agents propose the connection are not built (the discarded edges may be decided by a referee, a lottery, or even by agreement among the agents involved). The game finishes when, at a certain stage, no more agents connect or when all agents are already connected in a spanning tree. If, when the game finishes, the resulting forest is not a spanning tree, then all agents have to pay a relatively high penalty cost, as compared with the total sum of the costs of their required connections.

Formally, at stage k, $k\ge 1$, the strategy, $x_i$, of an agent, $i\in N$, is a map $x_i:{{\mathcal {F}}}\longrightarrow N\setminus \{i\}\cup w$, where ${{\mathcal {F}}}$ is the set of all possible forests, F, in the graph (N, t), and w means “wait and do not propose any link at this point”. If, for each $F\in {{\mathcal {F}}}$, $\Gamma _i(F)$ denotes the tree in F to which agent i belongs, then

$$\begin{aligned} x_i(F)= \left\{ \begin{array}{cl} j\in N\setminus \Gamma _i(F), &{} \text{ if } i \text{ proposes } \text{ connecting } \text{ to } \text{ agent } j, \\ w, &{} \text{ otherwise. } \\ \end{array} \right. \end{aligned}$$

A profile of strategies for the whole set of agents is $x=(x_i)_{i\in N}$. Let $X_i$ denote the set of possible strategies of agent i, and let $X=\prod _{i\in N}X_i$ be the set of possible profiles of strategies for the agents in N. Finally, let $F^x$ denote the forest that results when the profile of strategies $x\in X$ is played.

When the game finishes, if a path, $\gamma _{ij}$, with capacity $t_{ij}$ (all the edges in $\gamma _{ij}$ have a capacity greater than or equal to $t_{ij}$), has been built, then both agents, i and j, consider $t_{ij}$ as a benefit. Thus, when the profile of strategies x is played, the aggregate benefit obtained by agent $i\in N$ is $p_i(x)=\sum _{j\ne i}p_{ij}(x)$, where $p_{ij}(x)=t_{ij}$ if the aforementioned path is in the forest $F^{x}$, induced by x, and $p_{ij}(x)=0$ otherwise. Agents play their strategies seeking to maximize their aggregate benefit. Notice that if $F^{x}$ is an MCST, then all the agents in N reach the upper bound of their benefit levels, and $p_i(x)=t_i=\sum _{j\ne i}t_{ij}$.

On the other hand, let $c_i(x)$ be the connection cost assigned to agent i when the profile of strategies, $x\in X$, is played. If $F^x=\Gamma ^x$ is a spanning tree, then this cost is, for each $i\in N$, $c_i(x)={1\over 2}\sum _{j\in N\setminus \{i\}:\,(i,j)\in \Gamma ^x}t_{ij}$ ; otherwise, $c_i(x)$ is a high penalty cost, for every $i\in N$. When the agents play their strategies, they also take into account the minimization of their connection costs.

Therefore, two different non-cooperative games may be defined, namely the benefit capacity synthesis game and the cost capacity synthesis game:

Definition 3.1

A benefit capacity synthesis non-cooperative game is a triplet (N, X, p), where N is the set of players, X is the set of possible profiles of strategies for the players in N, and $p: X\longrightarrow \text{ I }\!\text{ R}^n_+$ is the vector-valued function that associates to each strategy $x\in X$, the vector of benefits, p(x), obtained by the players when x is played.

Definition 3.2

A cost capacity synthesis non-cooperative game is a triplet (N, X, c), where N is the set of players, X is the set of possible profiles of strategies for the players in N, and $c: X\longrightarrow \text{ I }\!\text{ R}^n_+$ is the vector-valued cost function that associates to each profile of strategies, $x\in X$, the vector of costs, c(x), incurred by the players when x is played.

Example 2.3 (Continued) For instance, if players face the forest $F=\{\{(1,2),(1,3)\},\{4\}\}$, which has been formed after the two previous stages, and they play $x_1(F)=w$, $x_2(F)=w$, $x_3(F)=4$, and $x_4(F)=3$, then the spanning tree $\Gamma ^x$, in Fig. 3, is formed. These decisions guarantee that each agent ensures the required capacity with all the other agents ($p_{ij}(x)=t_{ij}$, $\forall i,j\in N$), and in fact provide an MCST, as shown in Table 1, where the aggregate benefits obtained by each player in the benefit game, (N, X, p), and the costs borne by each player in the cost game, (N, X, c), are also specified in the two last columns of the table.

Table 1 p(x) and c(x)

Fig. 3

$\Gamma ^{x}=\{(1,2),(1,3),(3,4)\}$

Nevertheless, if players face the forest $F'=\{\{(1,2),(2,3)\},\{4\}\}$, which has been formed after the two previous stages, then none of the possible decisions of players provides an MCST, even if agent 4 connects to 3 through the edge with the maximum capacity, that is, $x'_3(F')=4$ and $x'_4(F')=3$. The resulting spanning tree, $\Gamma ^{x'}$ is represented in Fig. 4, and the corresponding benefits and costs are shown in Table 2.

Table 2 $p(x')$ and $c(x')$

Fig. 4

$\Gamma ^{x'}=\{(1,2),(2,3),(3,4)\}$

The sets of strategies for the benefit capacity synthesis game, and for the cost capacity synthesis game are the same set, but the payoffs of the agents reflect different awards in each game. In the analysis that follows, we will assume that agents have lexicographic preferences regarding the payoffs of the aforementioned games, that is, they are mainly interested in connecting with other agents with their required capacities in order to generate a feasible spanning tree for the capacity synthesis problem (N, t). Among the strategies which are tied with respect to this first goal, the agents are interested in choosing those connections for which they pay the least.

Notice that, in general, a profile of strategies, $x\in X$, always induces a forest, $F^{x}$, which may not necessarily be a spanning tree; even in the case in which it is a spanning tree, it may not be feasible for the capacity synthesis problem, (N, t), as shown in the previous example.

In the next section we identify a class of profiles of strategies that always provide MCSTs for each capacity synthesis problem (N, t), and reciprocally, given an MCST, at least one profile of strategies providing this MCST, always exists in this class. The profiles of strategies in this class are called $\sigma$ -strategies . We will also show that these $\sigma$-strategies have some desirable properties in relation to the benefit capacity synthesis game and to the cost capacity synthesis game.

3.1 $\sigma$-strategies

In the two games defined above, namely the benefit capacity synthesis game and the cost capacity synthesis game, a $\sigma$-strategy generates the connections gradually, by choosing at each stage one of the edges with higher capacity from among those that join two trees in the forest formed in previous stages. Since several edges might be candidates for their construction at any given stage, in order to solve the ties, an agenda or ordering of the edges, $\sigma$, which we will call a ranking, is used. From among the edges that are candidates for their construction at a specific stage, the candidate with the best position in the ranking is selected.

Consider the set of positive integers $M=\left\{ 1,2,\ldots ,{n \atopwithdelims ()2}\right\}$, and let $\sigma : M \longrightarrow N(2)$ denote a permutation function that reflects the ranking of the edges: this function associates the edge $\sigma (r)\in N(2)$ to each position of the ranking, $r=1,2,\ldots ,{n \atopwithdelims ()2}$. For any forest $F\in {{\mathcal {F}}}$, let ${\bar{E}}_{F}$ denote the set of edges, $e\in N(2)\setminus E_F$, which connect two trees in F, and let ${\bar{E}}_F^*$ denote the set of edges in ${\bar{E}}_F$ with maximum capacity. A $\sigma$-strategy, $x^{\sigma }$, can therefore be defined as follows:

Definition 3.3

Given a capacity synthesis problem, (N, t), and a permutation function, $\sigma$, a $\sigma$-strategy, $x^{\sigma }$, is, for each $i\in N$, $x^{\sigma }_i: {{\mathcal {F}}}\longrightarrow N\setminus \{i\}\cup w$, such that

Remark 3.4

Given a permutation function, $\sigma$, on the set of edges, it is easy to see that the graph, $\Gamma ^{x^{\sigma }}$, induced by the $\sigma$-strategy, $x^{\sigma }$, is in fact an MCST, and reciprocally, given an MCST, $\Gamma$, a $\sigma$-strategy exists such that $\Gamma ^{x^{\sigma }}=\Gamma$. However, notice that a given MCST can be generated by different profiles of strategies, some of which may not be $\sigma$-strategies. For instance, those strategies in Examples 4, 5, and 6 in the Appendix. In Examples 4 and 5, when facing the forest with all the nodes unconnected, the edge with the largest capacity is not constructed, and in Example 6, it is built together with another two edges. Therefore, they are not $\sigma$-strategies, although the MCSTs which they generate coincide with those obtained when an appropriate $\sigma$-strategy is played. As a consequence, if we call MCST-strategies the set of strategies that generate an MCST, then the set of $\sigma$-strategies is a proper subset of the set of MCST-strategies. This is illustrated in Fig. 5.

Fig. 5

MCST-strategies and $\sigma$-strategies

In the next subsection, the relationship between the concepts of Nash Equilibria and $\sigma$-strategies is explored.

3.2 $\sigma$-strategies and Nash equilibria

For each agent $i\in N$, and each strategy $x\in X$, let $(x_{-i}; x'_i)$ denote the profile of strategies in which agent i deviates from x by using the strategy $x'\in X$, that is, $(x_{-i}; x'_i)_i=x'_i$, and $(x_{-i}; x'_i)_j=x_j$ for every $j\in N$, $j\ne i$.

Definition 3.5

The profile of strategies $x\in X$ is a Nash equilibrium (NE) for the benefit (for the cost) capacity synthesis non-cooperative game (N, X, p) ((N, X, c)), if no agent $i\in N$ exists for which there is a profile of strategies, $(x_{-i}; x'_i)\in X$, $x'_i\ne x_i$, such that $p_i(x)< p_i(x_{-i}; x'_i)$ $(c_i(x)> c_i(x_{-i}; x'_i))$ holds.

Notice that if $x\in X$ is a profile of strategies that originates an MCST, that is, x is an MCST-strategy, then $p_i(x)=\sum _{j\ne i}t_{ij}$, since an MCST is feasible for (N, t). Note, on the other hand, that $\sum _{j\ne i}t_{ij}$ is an upper bound for the benefit that agent $i\in N$ can obtain. Therefore, any MCST-strategy constitutes an NE for the game (N, X, p) because none of the agents can improve their benefit level by deviating unilaterally from x. In particular, $\sigma$-strategies are NEs for the game (N, X, p).

Nevertheless, an NE for the benefit capacity synthesis non-cooperative game does not necessarily provide an MCST tree, as shown in Example 1 in the Appendix.

We now consider the stronger notion of Strong Nash equilibria (Strong NEs) and analyse the relationship with NEs and MCST-strategies.

For each coalition $S\subset N$, and each strategy $x\in X$, let $x_S$ denote the projection of x on S, and let $(x_{-S}; x'_S)\in X$ denote the profile of strategies in which agents in S deviate from x by using the profile of strategies $x'\in X$, that is, $(x_{-S}; x'_S)_i=x'_i$ for every $i\in S$, and $(x_{-S}; x'_S)_j=x_j$ for every $j\notin S$.

Definition 3.6

The profile of strategies $x\in X$ is a Strong NE for the benefit (for the cost) capacity synthesis non-cooperative game (N, X, p) ((N, X, c)), if no coalition $S\subseteq N$, $S\ne \emptyset$, exists for which there is a profile of strategies, $(x_{-S}; x'_S)\in X$, $x'_S\ne x_S$, such that $p_i(x)< p_i(x_{-S}; x'_S)$ $(c_i(x)> c_i(x_{-S}; x'_S))$ holds, for every $i\in S$.

A Strong NE for the benefit capacity synthesis non-cooperative game (N, X, p) is always an NE, although there are NEs that are not Strong NEs for the benefit capacity synthesis non-cooperative game, as Example 1 in the Appendix also shows.

Notice that if a strategy $x\in X$ generates an MCST, $\Gamma ^x$, then x is a Strong NE for the benefit capacity synthesis non-cooperative game (N, X, p), since every agent, $i\in N$, reaches their maximum level of benefit, $p_i(x)=\sum _{j\ne i}t_{ij}$, and no coalition can improve this individual upper bound of the benefit level of its members. As a consequence, for any permutation function, $\sigma$, the corresponding $\sigma$-strategy, $x^{\sigma }$, is a Strong NE for the benefit capacity synthesis game. Nevertheless, Strong NEs may exist which are not MCST-strategies. For instance in Example 7, in the Appendix, the profile of strategies $x\in X$ is a Strong NE which does not generate a MCST.

The chain of contents is represented in Fig. 6.

Fig. 6

NEs, strong NEs, MCST-strategies, and $\sigma$-strategies

3.3 Capacity synthesis equilibria

As mentioned before, in a capacity synthesis problem, agents are mainly interested in reaching their capacity requirements in relation with all the other agents, and the agent benefit is understood as the sum of the capacities reached. In an equilibrium, no agent exists for which a unilateral deviation implies a strict improvement of their benefit level. However, among the equilibrium profiles, a unilateral deviation may imply that the agent that deviates obtains the same benefit, but pays strictly less. In what follows, we assume that the agents exhibit lexicographic preferences on the profiles of strategies described as: for $i\in N$, $x\succ _i x'$ if and only if $p_i(x)>p_i(x')$, or $p_i(x)=p_i(x')$ and $c_i(x)<c_i(x')$. We introduce the concept of capacity synthesis equilibrium (CSE), and Strong capacity synthesis equilibrium (Strong CSE).

Definition 3.7

The profile of strategies $x\in X$ is a CSE for the capacity synthesis problem, (N, t), if no agent, $i\in N$, exists for which there is a profile of strategies, $(x_{-i};x'_i)$, $x'_i\ne x_i$, such that, either,

• (i) $p_i(x)< p_i(x_{-i}; x'_i)$, or

• (ii) $p_i(x)= p_i(x_{-i}; x'_i)$ and $c_i(x)> c_i(x_{-i}; x'_i)$.

Definition 3.8

The profile of strategies $x\in X$ is a Strong CSE for the capacity synthesis problem, if no coalition $S\subseteq N$, $S\ne \emptyset$, exists for which there is a profile of strategies, $(x_{-S};x'_S)$, $x'_S\ne x_S$, such that, for each $i\in S$, either,

• (i) $p_i(x)< p_i(x_{-S}; x'_S)$, or

• (ii) $p_i(x)= p_i(x_{-S}; x'_S)$ and $c_i(x)> c_i(x_{-S}; x'_S)$.

Notice that a Strong CSE for the capacity synthesis problem is always a CSE. Note also that a CSE is an NE for the benefit capacity synthesis game, but there are NEs, which can even be MCST-strategies for the game (N, X, p) that are not CSEs, as shown in Example 4 in the Appendix.

In the following result, we establish that $\sigma$-strategies are always CSEs. Moreover, they are Strong CSEs for the capacity synthesis problem.

Proposition 3.9

For any permutation function $\sigma$, the $\sigma$-strategy, $x^{\sigma }$, is a Strong CSE for the capacity synthesis problem.

Proof

Given a $\sigma$-strategy, $x^{\sigma }$, assume, on the contrary, that a non-empty coalition, $S^*$, and a profile of strategies $(x^{\sigma }_{-S^*}; x'_{S^*})\in X$, $x'_{S^*}\ne x^{\sigma }_{S^*}$ exist, such that, for each $i\in S^*$, either,

• (i) $p_i(x^{\sigma })< p_i(x^{\sigma }_{-S^*}; x'_{S^*})$, or

• (ii) $p_i(x^{\sigma })= p_i(x^{\sigma }_{-S^*}; x'_{S^*})$ and $c_i(x^{\sigma })> c_i(x^{\sigma }_{-S^*}; x'_{S^*})$.

1.- First, since $\Gamma ^{x^{\sigma }}$ is an MCST, every agent $i\in N$ reaches her maximum possible benefit level, $p_i(x^{\sigma })=\sum _{j\ne i}t_{ij}$. Therefore, for any coalition $S\subseteq N$, the inequality $p_i(x^{\sigma })\ge p_i(x^{\sigma }_{-S}; x'_S)$ holds for every $i\in S$. Particularly, for $S^*\subseteq N$. Therefore, since (i) does not hold for any agent in $S^*$, (ii) must hold, that is, with $(x^{\sigma }_{-S^*}; x'_{S^*})$, every agent in $S^*$ obtains her maximal benefit, $p_i(x^{\sigma }_{-S^*}; x'_{S^*})=\sum _{j\ne i}t_{ij}$, and pays strictly less, $c_i(x^{\sigma }_{-S^*}; x'_{S^*})<c_i(x^{\sigma })$.

2.- Notice that a spanning tree, $\Gamma ^{(x^{\sigma }_{-S^*}; x'_{S^*})}$, is also formed when $(x^{\sigma }_{-S^*}; x'_{S^*})$ is played, since if on the contrary, an unconnected forest would result, and no agent would obtain her maximal benefit. Particularly, agents in $S^*$. This contradicts our assumption above ($p_i(x^{\sigma }_{-S^*}; x'_{S^*})=\sum _{j\ne i}t_{ij}$ for every $i\in S^*$).

3.- We define a reduced problem $(N^{F_0},t^{F_0})$:

Since $\Gamma ^{x^\sigma }\ne \Gamma ^{(x^{\sigma }_{-S^*}; x'_{S^*})}$, let $F_0=\left\{ \Gamma _{F_0}^1, \Gamma _{F_0}^2,,\ldots ,\Gamma _{F_0}^r\right\}$ be the forest which results if only the edges that belong to both, $\Gamma ^{x^\sigma }$ and $\Gamma ^{(x^{\sigma }_{-S^*}; x'_{S^*})}$ are included. Notice that $r\ge 2$. Consider the reduced problem $(N^{F_0},t^{F_0})$, where the trees in $F_0$ are considered as nodes (the set of these r nodes is denoted by $N^{F_0}$), and $t^{F_0}$ is a symmetric matrix such that, for each pair of trees $\Gamma _{F_0}^j, \Gamma _{F_0}^l\in F_0$ (nodes of $N^{F_0}$), $t_{\Gamma _{F_0}^j\Gamma _{F_0}^l}=\max \{t_{k_jk_l},\,\text{ where } \,k_j\in \Gamma _{F_0}^j,\,\text{ and }\,k_l\in \Gamma _{F_0}^l\}$.

4.- Denote by $\Gamma _{F_0}^{x^\sigma }$ and $\Gamma _{F_0}^{(x^{\sigma }_{-S^*}; x'_{S^*})}$ the projections of $\Gamma ^{x^\sigma }$ and $\Gamma ^{(x^{\sigma }_{-S^*}; x'_{S^*})}$ on $N^{F_0}$:

Let $\Gamma _{F_0}^{x^\sigma }$ be the tree on $N^{F_0}$ that results when including only the edges belonging to $\Gamma ^{x^\sigma }$, which link the nodes in $N^F_0$ (the trees of $F_0$). Analogously, consider $\Gamma _{F_0}^{(x^{\sigma }_{-S^*}; x'_{S^*})}$. We say that $\Gamma _{F_0}^{x^\sigma }$ and $\Gamma _{F_0}^{(x^{\sigma }_{-S^*}; x'_{S^*})}$ are the projections of $\Gamma ^{x^\sigma }$ and $\Gamma ^{(x^{\sigma }_{-S^*}; x'_{S^*})}$ on $N^{F_0}$, respectively. Notice that, since $\Gamma ^{x^\sigma }$ is a MCST, the capacity of the edge in $\Gamma _{F_0}^{x^\sigma }$ linking $\Gamma _{F_0}^j$ and $\Gamma _{F_0}^l$, $j,l\in \{1,2,\ldots r\}$, is $t_{\Gamma _{F_0}^j\Gamma _{F_0}^l}$. Note also that the agents corresponding to the nodes at any extreme of the edges of $\Gamma _{F_0}^{(x^{\sigma }_{-S^*}; x'_{S^*})}$, are all deviating from $x^{\sigma }$ (moreover, with respect to the edges of $\Gamma _{F_0}^{x^\sigma }$, at least one of the agents corresponding to the node at some extreme of each edge is also deviating). Then, all these mentioned agents belong to $S^*$ and therefore, they all should obtain their maximal benefit and they all should pay strictly less by deviating.

5.- Denote by $t^*_{F_0}$ the maximum value among the capacities of the edges in $\Gamma _{F_0}^{x^\sigma }$: Notice that $t^*_{F_0}$ is also the maximum value among the components of matrix $t^{F_0}$.

6.- By playing $x^{\sigma }$, an edge with capacity $t^*_{F_0}$ should have been built:

When $x^{\sigma }$ is played, the links are built starting with the one with greatest capacity and continuing in decreasing order, solving the ties with the ranking $\sigma$. Let $(k'_{F_0},k''_{F_0})$ be the link in $\Gamma _{F_0}^{x^\sigma }$ with capacity $t^*_{F_0}$ and the highest position in the ranking $\sigma$ among the edges of the tree $\Gamma _{F_0}^{x^\sigma }$, and denote by $\Gamma '_{F_0}$ and $\Gamma ''_{F_0}$ the trees in $F_0$ to whom $k'_{F_0}$ and $k''_{F_0}$ belong, respectively (we denote $(k'_{F_0},k''_{F_0})$ and $(\Gamma '_{F_0},\Gamma ''_{F_0})$ or $t_{k'_{F_0}k''_{F_0}}$ and $t_{\Gamma '_{F_0}\Gamma ''_{F_0}}$ indistintly). It may be the case that some edges with a capacity greater than or equal to $t^*_{F_0}$ have already been built, but they belong to some tree of the forest $F_0$.

7.- We are going to prove the following result: On the tree $\Gamma _{F_0}^{(x^{\sigma }_{-S^*}; x'_{S^*})}$, all the edges in the path $\gamma _{\Gamma '_{F_0}\Gamma ''_{F_0}}$, connecting $\Gamma '_{F_0}$ and $\Gamma ''_{F_0}$, have capacity $t^*_{F_0}$. Moreover, on the tree $\Gamma ^{(x^{\sigma }_{-S^*}; x'_{S^*})}$, all the edges in the path $\gamma _{k'_{F_0}k''_{F_0}}$, connecting $k'_{F_0}$ and $k''_{F_0}$, have a capacity greater than or equal to $t^*_{F_0}$:

Assume, on the contrary, that there exists an edge in the path $\gamma _{\Gamma '_{F_0}\Gamma ''_{F_0}}$ or an edge belonging to $\gamma _{k'_{F_0}k''_{F_0}}\setminus \gamma _{\Gamma '_{F_0}\Gamma ''_{F_0}}$ with a capacity strictly lower than $t^*_{F_0}$. In this case, the agents at the nodes $k'_{F_0}\in \Gamma '_{F_0}$ and $k''_{F_0}\in \Gamma ''_{F_0}$ do not get their required capacity, since $p_{k'_{F_0}k''_{F_0}}(x^{\sigma }_{-S}; x'_S)=0$. On the other hand, these agents are deviating from $x^{\sigma }$ when $(x^{\sigma }_{-S^*}; x'_{S^*})$ is played, that is, they belong to $S^*$. This contradicts that assumption that $p_i(x^{\sigma }_{-S}; x'_S)=\sum _{j\ne i}t_{ij}$ for every $i\in S^*$.

8.- Either of the two following cases may occur:

8.1.- Case (a): All the trees in $F_0$ are connected through the path $\gamma _{\Gamma '_{F_0}\Gamma ''_{F_0}}$.

Consider a node, $k^j_{F_0}\in \Gamma ^j_{F_0}$, at an extreme of an edge included in $\gamma _{\Gamma '_{F_0}\Gamma ''_{F_0}}$. Inside $\Gamma _{F_0}^j$, the trees $\Gamma ^{x^\sigma }$ and $\Gamma ^{(x^{\sigma }_{-S^*}; x'_{S^*})}$ coincide. Therefore, with respect to the edges which constitute $\Gamma ^j_{F_0}$, $k^j_{F_0}$ pays the same cost both, when $(x^{\sigma }_{-S^*}; x'_{S^*})$ is played or when $x^{\sigma }$ is played. As a consequence, the possible savings of $k^j_{F_0}$ by deviating from $x^{\sigma }$ to $(x^{\sigma }_{-S^*}; x'_{S^*})$ should come from the fact that some of the edges in $\Gamma _{F_0}^{x^\sigma }$, with an extreme on $k^j_{F_0}$, are not in $\Gamma _{F_0}^{(x^{\sigma }_{-S^*}; x'_{S^*})}$. But, with respect to the path $\gamma _{\Gamma '_{F_0}\Gamma ''_{F_0}}=\Gamma _{F_0}^{(x^{\sigma }_{-S^*}; x'_{S^*})}$, $k^j_{F_0}$ pays $t^*_{F_0}$ when it belongs to two edges in this path $\gamma _{\Gamma '_{F_0}\Gamma ''_{F_0}}$ , and $\frac{t^*_{F_0}}{2}$ otherwise.

This means that at least 2 arcs in the tree $\Gamma ^{x^\sigma }_{F_0}$ in which agent $k^j_{F_0}$ is involved, must disappear when agents in $S^*$ deviate from $x^{\sigma }$ to $(x^{\sigma }_{-S^*}; x'_{S^*})$ in order for this agent to strictly reduce her cost. Since this reasoning can be applied to all the agents at the extremes of the arcs in $\gamma _{\Gamma '_{F_0}\Gamma ''_{F_0}}$, this contradicts the fact that $\Gamma _{F_0}^{x^\sigma }$ should have $r-1$ arcs.

8.2.- Case (b): Not all the trees in $F_0$ are connected through the path $\gamma _{\Gamma '_{F_0}\Gamma ''_{F_0}}$. In this case, we will successively reduce the problem $(N^{F_0},t^{F_0})$ via a procedure, with m stages, $m\ge 1$, consisting of joining, at each stage, q, $1\le q\le m$, two trees, $\Gamma '_{F_{q-1}}$ and $\Gamma ''_{F_{q-1}}$, through an edge which has the maximum capacity among all those of $\Gamma _{F_{q-1}}^{x^\sigma }$.

At stage 1, consider the forest with $r-1$ trees, $F_1$, where the trees in $F_0$ considered in 6.- are linked, that is, there is a new tree $\Gamma ^*_{F_1}=\Gamma '_{F_0}\cup \Gamma ''_{F_0}\cup \{(\Gamma '_{F_0},\Gamma ''_{F_0})\}$, and the other trees in $F_1$ are the remaining trees in $F_0$. In the reduced problem $(N^{F_1},t^{F_1})$, the trees in $F_1$ are considered as nodes, and $t^{F_1}$ is a symmetric matrix where, for each pair of trees $\Gamma _{F_1}^j, \Gamma _{F_1}^l\in F_1$, $t_{\Gamma _{F_1}^j\Gamma _{F_1}^l}=\max \{t_{k_jk_l},\,\text{ where }\,k_j\in \Gamma _{F_1}^j,\,\text{ and }\,k_l\in \Gamma _{F_1}^l\}$. Let $\Gamma _{F_1}^{x^\sigma }$ be the projection of $\Gamma _{F_0}^{x^\sigma }$ on $N^{F_1}$, which coincides with the projection of $\Gamma ^{x^\sigma }$ on $N^{F_1}$.

As reasoned in 8.1.- Case (a), when agents in $S^*$ deviate from $x^{\sigma }$ to $(x^{\sigma }_{-S^*}; x'_{S^*})$, at least two links in $\Gamma _{F_0} ^{x^\sigma }$ starting on the intermediate trees of $\gamma _{\Gamma '_{F_0}\Gamma ''_{F_0}}$, $\Gamma _{F_0}^j$, $j\in \{1,2,\ldots ,r\}$, $\Gamma _{F_0}^j\notin \{\Gamma '_{F_0},\,\Gamma ''_{F_0}$}, should disappear in order for the agents in $S^*$ involved to pay strictly less. Notice that these links which should disappear, also belong to $\Gamma _{F_1} ^{x^\sigma }$. Moreover, when agents in $S^*$ deviate from $x^{\sigma }$ to $(x^{\sigma }_{-S^*}; x'_{S^*})$, at least two links in $\Gamma _{F_1} ^{x^\sigma }$ starting on $\Gamma _{F_1}^*$, should disappear in order for the agents in $S^*$ involved to pay strictly less, as is justified in what follows: Let ${\hat{k}}'_{F_0}\in \Gamma '_{F_0}$ and ${\hat{k}}''_{F_0}\in \Gamma ''_{F_0}$ be the agents from which the edges in the path $\gamma _{\Gamma '_{F_0}\Gamma ''_{F_0}}$ exit $\Gamma '_{F_0}$ and $\Gamma ''_{F_0}$, respectively. When $(x^{\sigma }_{-S^*}; x'_{S^*})$ is played, they both pay $\frac{t^*_{F_0}}{2}$ each, apart from what they pay because of the links inside $\Gamma '_{F_0}$ and $\Gamma ''_{F_0}$, respectively. Therefore, even though $k'_{F_0}={\hat{k}}'_{F_0}$ and $k''_{F_0}={\hat{k}}''_{F_0}$ hold, at least two links (one starting on ${\hat{k}}'_{F_0}$ which exits $\Gamma '_{F_0}$, and another starting on ${\hat{k}}''_{F_0}$ which exits $\Gamma ''_{F_0}$) should disappear from $\Gamma _{F_1} ^{x^\sigma }$, when agents in $S^*$ deviate from $x^{\sigma }$ to $(x^{\sigma }_{-S^*}; x'_{S^*})$, in the case that they pay strictly less. Notice that if $k'_{F_0}={\hat{k}}'_{F_0}$ and/or $k''_{F_0}={\hat{k}}''_{F_0}$ does not hold, more than two links in $\Gamma _{F_1} ^{x^\sigma }$ should disappear in order for the agents in $\Gamma ^*_{F_1}$ who deviate to get the saving (more than two).

Denote by $F_1(\gamma _{\Gamma '_{F_0}\Gamma ''_{F_0}})$ the subforest in $F_1$ which consists of $\Gamma ^*_{F_1}$ and the intermediate trees in $\gamma _{\Gamma '_{F_0}\Gamma ''_{F_0}}$.

Let $t^*_{F_1}$ be the maximum value among the capacities of the edges in $\Gamma _{F_1}^{x^\sigma }$. Notice that $t^*_{F_1}$ is also the maximum value among the components of matrix $t^{F_1}$. Consider $(k'_{F_1},k''_{F_1})$, the link in $\Gamma _{F_1}^{x^\sigma }$ with capacity $t^*_{F_1}$ and the highest position in the ranking $\sigma$ among the edges of the tree $\Gamma _{F_1}^{x^\sigma }$, and denote by $\Gamma '_{F_1}$ and $\Gamma ''_{F_1}$ the trees in $F_1$ to whom $k'_{F_1}$ and $k''_{F_1}$ belong, respectively (we denote $(k'_{F_1},k''_{F_1})$ and $(\Gamma '_{F_1},\Gamma ''_{F_1})$ or $t_{k'_{F_1}k''_{F_1}}$ and $t_{\Gamma '_{F_1}\Gamma ''_{F_1}}$ indistintly).

Notice that the projection of $\Gamma _{F_0}^{(x^{\sigma }_{-S^*}; x'_{S^*})}$ on $N^{F_1}$ might contain a cycle. If that happens consider the tree that results when $\Gamma _{F_0}^{(x^{\sigma }_{-S^*}; x'_{S^*})}$ is projected on $N^{F_1}$, and one of the edges in $\gamma _{\Gamma '_{F_0}\Gamma ''_{F_0}}$, with a extreme in either $\Gamma '_{F_0}$ or $\Gamma ''_{F_0}$, has been removed from the above mentioned projection. Denote this tree by $\Gamma _{F_1}^{(x^{\sigma }_{-S^*}; x'_{S^*})}$, and consider the path, $\gamma _{\Gamma '_{F_1}\Gamma ''_{F_1}}$, in $\Gamma _{F_1}^{(x^{\sigma }_{-S^*}; x'_{S^*})}$, connecting $\Gamma '_{F_1}$ and $\Gamma ''_{F_1}$.

A similar reasoning to that in 8.1.- Case (a) can be applied to conclude that, when agents in $S^*$ deviate from $x^{\sigma }$ to $(x^{\sigma }_{-S^*}; x'_{S^*})$, at least two links in $\Gamma _{F_1} ^{x^\sigma }$ starting on the trees connected by $\gamma _{\Gamma '_{F_1}\Gamma ''_{F_1}}$ should disappear in order for the agents in $S^*$ involved to pay strictly less.

If every tree in $F_1$ either, is connected by the path $\gamma _{\Gamma '_{F_1}\Gamma ''_{F_1}}$, or belongs to $F_1(\gamma _{\Gamma '_{F_0}\Gamma ''_{F_0}})$, then $\Gamma _{F_1}^{x^\sigma }$ should have more than $r-2$ arcs, since at least two links in $\Gamma _{F_1} ^{x^\sigma }$, starting on every tree in $F_1$, should disappear in order for the agents in $S^*$ involved to pay strictly less; this is a contradiction.

Otherwise, the procedure explained above in detail for stage 1, can be repeated until at stage m, $m\ge 1$, every tree in $F_m$ either is connected by the path $\gamma _{\Gamma '_{F_m}\Gamma ''_{F_m}}$ or belongs to $\bigcup _{q=1}^m F_q(\gamma _{\Gamma '_{F_{q-1}}\Gamma ''_{F_{q-1}}})$. Then, similarly, we can conclude that $\Gamma _{F_m}^{x^\sigma }$ should have more than $r-m$ edges, which is a contradiction. $\square$

Remark 3.4, Proposition 3.9 and the examples in the Appendix illustrate that the relationship between the concepts addressed in this paper is as represented in Fig. 7.

Fig. 7

$\sigma$-strategies, MCST strategies, CSEs and NEs for (N, X, p)

Remark 3.10

Super strong Nash equilibria (Dubey 1986) is a refinement of the concept of Strong Nash equilibria, where no coalition of players can deviate so that all members weakly benefit, and at least one member strictly benefits. This means that the set of Super Strong NEs for (N, X, p) is included in the set of Strong NEs for (N, X, p).

Notice that MCST strategies are obviously Super Strong Nash equilibria for the benefit capacity synthesis non-cooperative game and conversely, a Super Strong Nash equilibria provides a MCST, since otherwise, the grand coalition could deviate from their original strategy to a MCST strategy and obtain an aggregate benefit greater than the initial one for all its members, being strictly greater for at least one of them. Therefore, the set of Super Strong CSEs is a subset of the set of MCST strategies. As a consequence, Strong CSEs may exist which are not Super Strong CSEs. For instance the one in Example 3 in the Appendix.

On the other hand, it is not difficult to show that $\sigma$-strategies are always Super Strong CSEs, but Super Strong CSEs may exist which are not $\sigma$-strategies, as shown in Example 5 in the Appendix.

Finally, it is worth mentioning that the set of Super Strong CSEs is not the intersection of the Strong CSEs set and the MCST strategies set, as shown in the following example:

Example 3.11

Consider $N=\{1,2,3,4\}$, and $t= \left( \begin{array}{cccc} 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 0 &{}\quad 2 &{}\quad 2 \\ 1 &{}\quad 2 &{}\quad 0 &{}\quad 1 \\ 1 &{}\quad 2 &{}\quad 1 &{}\quad 0 \end{array} \right)$.

If agents play the profile of strategies $x\in X$, in Table 3, the tree $\Gamma ^x$, in Fig. 8, is generated. $\Gamma ^x$ is a MCST, as shown in Table 4

This profile of strategies is a Strong CSE, but it is not a Super Strong CSE since if the coalition $S=\{1,2\}$ deviates from x to $(x_{-S};x'_S)\in X$, as indicated in Table 5, then Agents 1 and 2 obtain the same benefit, Agent 1 pays the same quantity but Agent 2 pays less, as shown in Fig. 11 and Table 6.

Table 3 Profile of strategies $x\in X$

Table 4 p(x) and c(x)

Fig. 8

$\Gamma ^{x}$

Table 5 Profile of strategies $(x_{-S};x'_S)\in X$

Table 6 $p(x_{-S},x'_{S})$ and $c(x_{-S},x'_{S})$

Fig. 9

$\Gamma ^{(x_{-S},x'_{S})}$

4 Concluding remarks

Game theory has been widely applied to the analysis of combinatorial cost sharing problem. The earliest and most highly studied example is the minimum-cost spanning tree problem. Nevertheless game theorists have paid less attention to the capacity synthesis problem (specially regarding non-cooperative approaches), even though it appears to provide a more realistic representation of many strategic decision situations.

In the analysis presented in this paper, we explore the stability of the MCST formation, by taking into account that agents attain an aggregate benefit from their connections, but at the same time, provided that the MCST is constructed, these agents also consider the cost. We have shown that $\sigma$-strategies, apart from providing MCSTs, are stable, not only if benefits are considered as the payoffs of the non-cooperative game, but also if costs are taken into account when lexicographic preferences with respect to these two criteria are assumed.

On the other hand, $\sigma$-strategies provide a useful tool for solving the cost sharing problem. First of all, the costs provided by any $\sigma$-strategy (and the average of the costs over all the rankings of the players) constitute a core cost allocation in the corresponding cooperative game, since they are Bird cost allocations. Secondly, it would be interesting to analyse which properties remain and which properties fail to hold when considering only MCSTs provided by a $\sigma$-strategy, as compared with those present when the rules in Bogomolnaia et al. (2010) are applied.

Notice that the different equilibrium concepts involved in the present paper are compared in terms of the strategies played by the agents. It could be interesting to extend that comparison to the final payoffs (benefits and costs) obtained by the agents. In this sense, it is worth to point out that NEs of the benefit capacity synthesis non-cooperative game may exist which provide dominated vectors of aggregate benefits. For instance, consider the NE, $x\in X$, in Example 1 (Table 9) in the Appendix. The spanning tree generated by x is shown in Fig. 10, and the vector of aggregate benefits (in Table 10) is $p(x)=(10\,\,\,10\,\,\,3\,\,\,7)^t$. It is easy to see that the profile of strategies, $x'\in X$, in Example 1 (Table 11) is also a NE. However, the vector of aggregate benefits for $x'$ is $p(x')=(10\,\,\,10\,\,\,6\,\,\,10)^t$, which dominates p(x). Nevertheless, notice that any MCST strategy of the benefit capacity synthesis non-cooperative game provides non-dominated vectors of aggregate benefits, since with a MCST strategy, all the agents in N reach the upper bound of their benefit levels.

With respect to the cost capacity synthesis non-cooperative game, a similar situation may happen: NEs of the cost capacity synthesis non-cooperative game may exist which provide dominated vectors of aggregate costs. For instance, consider the capacity synthesis problem in Example 2.3, and the profile of strategies, $x\in X$, in Table 7, below.

Table 7 Profile of strategies $x\in X$

Notice that x is a NE for the cost capacity synthesis non-cooperative game. The spanning tree, $\Gamma ^x$, generated by x is the one in Example 2.3 (continued) (Fig. 3), and the aggregate vector of costs of the players is $c(x)=(5\,\,\,2.5\,\,\,5.5\,\,\,3)^t$. However, if the NE $x'\in X$, in Table 8 below is played, the vector of aggregate costs for $x'$ is $c(x')=(4\,\,\,0.5\,\,\,3\,\,\,1.5)^t$, which dominates c(x).

Table 8 Profile of strategies $x\in X$

Nevertheless, all MCST strategies provide aggregate vector of costs which constitute allocations of a fixed quantity, V(t). Therefore, they are all non-dominated vectors. As a consequence, $\sigma$-strategies always provide both, non-dominated vectors of aggregate benefits and non-dominated vectors of aggregate costs.

Appendix

The profile of strategies $x\in X$, in Example 1, is a NE which is not a Strong NE, and therefore it is not a MCST strategy. On the other hand, $x\in X$ is a CSE which is not a Strong CSE (see Fig. 23).

Example 1

Consider $N=\{1,2,3,4\}$, and $t= {\left( \begin{array}{cccc} 0 &{}\quad 5 &{}\quad 1 &{}\quad 4 \\ 5 &{}\quad 0 &{}\quad 2 &{}\quad 3 \\ 1 &{}\quad 2 &{}\quad 0 &{}\quad 3\\ 4 &{}\quad 3 &{}\quad 3 &{}\quad 0\\ \end{array} \right) }$.

Suppose that agents play the profile of strategies, $x\in X$, in Table 9.

Table 9 Profile of strategies $x\in X$

This profile of strategies generates the spanning tree, $\Gamma ^{x}$, in Fig. 10, which is not an MCST, as shown in Table 10:

Fig. 10

$\Gamma ^{x}$

Table 10 p(x) and c(x)

Nevertheless, $x\in X$ is a Nash equilibrium for the game (N, X, p) because if any agent deviates from x, while the remaining agents maintain their strategies, then this agent fails to improve her benefit.³

Notice that x is also a CSE. However, it is not a Strong CSE. Moreover, it is not a Strong NE, as shown in what follows. If coalition $S=\{3,4\}$ deviates from x to $x'=(x_{-S}; x'_S)$, as given in Table 11, then the tree $\Gamma ^{(x_{-S}; x'_S)}$ in Fig. 11 is generated, and all the agents in S improve their benefits, as shown in Table 12.

Table 11 Profile of strategies $(x_{-S}; x'_S)\in X$

Fig. 11

$\Gamma ^{(x_{-S}; x'_S)}$

Table 12 $p(x_{-S}; x'_S)$ and $c(x_{-S}; x'_S)$

$\lhd$

The profile of strategies $x\in X$, in Example 2, is a NE which is neither a Strong NE nor a CSE (see Fig. 23).

Example 2

Consider $N=\{1,2,3,4,5\}$, and $t= {\left( \begin{array}{ccccc} 0 &{}\quad 5 &{}\quad 1 &{}\quad 4 &{}\quad 1\\ 5 &{}\quad 0 &{}\quad 2 &{}\quad 3 &{}\quad 1 \\ 1 &{}\quad 2 &{}\quad 0 &{}\quad 3 &{}\quad 1 \\ 4 &{}\quad 3 &{}\quad 3 &{}\quad 0 &{}\quad 1 \\ 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 0 \\ \end{array} \right) }$.

Suppose that agents play the profile of strategies, $x\in X$, in Table 13.

Table 13 Profile of strategies $x\in X$

The spanning tree generated by the profile of strategies x, $\Gamma ^x$, in Fig. 12, is not an MCST, as shown in Table 14.

Fig. 12

$\Gamma ^{x}$

Table 14 p(x) and c(x)

The profile of strategies $x\in X$ is not a CSE, because if Agent 2 deviates from x to $(x_{-2};x'_2)\in X$, as given in Table 15, then Agent 2 obtains the same benefit but pays less, as shown in Fig. 13 and Table 16.

Table 15 Profile of strategies $(x_{-2};x'_2)\in X$

Table 16 p(x) and c(x)

It is easy to see that the profile of strategies $x\in X$ is an NE, but it is not a Strong NE, because if coalition $S=\{3,4\}$ deviates from x to $(x_{-S};x''_{S})$, as given in Table 17, then the MCST, $\Gamma ^{(x_{S};x''_S)}$, that is generated, coincides with that in Fig. 13, which is an MCST. Therefore both agents in S improve their benefits, as is also shown in Table 16.

Table 17 Profile of strategies $(x_{-S};x'_S)\in X$

Fig. 13

$\Gamma ^{(x_{-2};x'_2)}$

$\lhd$

The profile of strategies $x\in X$, in Example 3, is a Strong CSE and therefore a Strong NE, but it is not a MCST stragety (see Fig. 23).

Example 3

$N=\{1,2,3,4\}$, and $t=\left( {\begin{array}{cccc} 0 &{}\quad 4 &{}\quad 1 &{}\quad 1 \\ 4 &{}\quad 0 &{}\quad 1 &{}\quad 3 \\ 1 &{}\quad 1 &{}\quad 0 &{}\quad 3\\ 1 &{}\quad 3 &{}\quad 3 &{}\quad 0\\ \end{array} } \right)$.

Suppose that agents play the profile of strategies, $x\in X$, as given in Table 18, and generate $\Gamma ^x$, as given in Fig. 14, which is not an MCST, as shown in Table 19, where it can be observed that the required capacity between Agents 2 and 4 is not reached.

Table 18 Profile of strategies $x\in X$

Fig. 14

$\Gamma ^{x}$

Table 19 p(x) and c(x)

It is easy to see that x is an NE for the game (N, X, p). Moreover, it is a Strong NE: Since Agents 1 and 3 already obtain their required capacity in their connections with all the players, only one coalition exists, coalition $S=\{2,4\}$, such that all their members can strictly improve their aggregate benefit by deviating from x; however, none of the deviations from x of the agents in $S=\{2,4\}$ can guarantee a strict improvement of the aggregate benefit of both Agent 2 and Agent 4.

It is also easy to observe that x is a CSE. Moreover, it is a Strong CSE.

$\lhd$

The profile of strategies $x\in X$, in Example 4, is a MCST strategy, but it is not a CSE (see Fig. 23).

Example 4

$N=\{1,2,3,4\}$, and $t=\left( {\begin{array}{cccc} 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 0 &{}\quad 2 &{}\quad 1 \\ 1 &{}\quad 2 &{}\quad 0 &{}\quad 1 \\ 1 &{}\quad 1 &{}\quad 1 &{}\quad 0 \end{array} } \right)$.

Suppose that agents play the profile of strategies $x\in X$, in Table 20, to generate $\Gamma ^{x}$, in Fig. 15, which is an MCST, as shown in Table 21.

Table 20 Profile of strategies $x\in X$

Fig. 15

$\Gamma ^x$

Table 21 p(x) and c(x)

If Agent 3 deviates from x to $(x_{-3};x'_3)$, as given in Table 22, then another MCST, $\Gamma ^{(x_{-3};x'_3)}$, as given in Fig. 16, is generated.

Table 22 Profile of strategies $(x;x'_3)\in X$

As shown in Table 23, the deviation of Agent 3 from $x_3$ to $x'_3$ does not mean an improvement in her benefit level. Nevertheless, Agent 3 does improve her cost assignment.

Table 23 $p(x_{-3};x'_3)$ and $c(x_{-3};x'_3)$

Fig. 16

$\Gamma ^{(x_{-3}; x'_3)}$

Therefore $x\in X$ is an MCST-strategy (and therefore a Strong NE) for the game (N, X, p), but it is not a CSE for the capacity synthesis problem.

$\lhd$

The profile of strategies $x\in X$, in Example 5, is a MCST strategy which is a Strong CSE, but it is not a $\sigma$-strategy (see Fig. 23).

Example 5

$N=\{1,2,3,4\}$, $t=\left( {\begin{array}{cccc} 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 0 &{}\quad 2 &{}\quad 2 \\ 1 &{}\quad 2 &{}\quad 0 &{}\quad 1 \\ 1 &{}\quad 2 &{}\quad 1 &{}\quad 0 \end{array} } \right)$.

If agents play the profile of strategies $x\in X$, as given in Table 24, then the MCST $\Gamma ^x$, as given in Fig. 17, is generated, as shown in Table 25.

Table 24 Profile of strategies $x\in X$

Fig. 17

$\Gamma ^{x}$

Table 25 p(x) and c(x)

Strategy x is not a $\sigma$-strategy, because the first edge which is built is (1, 2), but it does constitute a Strong CSE, which is also a Super Strong CSE.

$\lhd$

The profile of strategies $x\in X$, in Example 6, is a MCST strategy which is a CSE, but it is not a Strong CSE (see Fig. 23).

Example 6

Consider $N=\{1,2,3,4,5,6\}$ and $t=\left( { \begin{array}{cccccc} 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1\\ 1 &{} \quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1\\ 1 &{}\quad 1 &{}\quad 0 &{}\quad 2 &{}\quad 1 &{}\quad 1\\ 1 &{}\quad 1 &{}\quad 2 &{}\quad 0 &{}\quad 1 &{}\quad 1\\ 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 2\\ 1 &{} \quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 2 &{}\quad 0\\ \end{array} } \right)$.

If agents play the profile of strategies $x\in X$, shown in Table 26, then the MCST $\Gamma ^x$, as given in Fig. 18, is generated.

Fig. 18

$\Gamma ^{x}$

Table 26 Profile of strategies $x\in X$

Table 27 p(x) and c(x)

Table 28 Profile of strategies $(x_{-S};x'_S)\in X$

As shown in Table 27, the profile of strategies $x\in X$ is an MCST strategy.

It is easy to observe that x is a CSE. Nevertheless, it is not a Strong CSE: If agents in coalition $S=\{4,5\}$ deviate from x to $(x_{-S};x'_S)$, as given in Table 28, another MCST, $\Gamma ^{(x_{-S}; x'_S)}$, given in Fig. 19, is generated, and Agent 4 and Agent 5 both do strictly improve their cost assignment, as shown in Table 29.

$\lhd$

The profile of strategies $x\in X$, in Example 7, is a Strong NE, which is a CSE, but it is neither a MCST strategy nor a Strong CSE (see Fig. 23).

Example 7

Consider $N=\{1,2,3,4,5,6\}$ and $t=\left( { \begin{array}{cccccc} 0 &{}\quad 4 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1\\ 4 &{}\quad 0 &{}\quad 1 &{}\quad 2 &{}\quad 1 &{}\quad 1\\ 1 &{}\quad 1 &{}\quad 0 &{}\quad 3 &{}\quad 1 &{}\quad 1\\ 1 &{}\quad 2 &{}\quad 3 &{}\quad 0 &{}\quad 1 &{}\quad 1\\ 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 3\\ 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 3 &{}\quad 0\\ \end{array} } \right)$.

If agents play the profile of strategies $x\in X$, as given in Table 30, then a spanning tree, $\Gamma ^x$, as given in Fig. 20, is generated, which is not an MCST, as shown in Table 31.

Fig. 19

$\Gamma ^{(x_{-S}; x'_S)}$

Table 29 $p(x_{-S};x'_S)$ and $c(x_{-S};x'_S)$

Table 30 Profile of strategies $x\in X$

The profile of strategies $x\in X$ is a Strong NE, because neither Agent 2, nor Agent 4, nor coalition $S=\{2,4\}$ (which are the only coalitions in which members can all improve their benefits) can deviate from x to obtain more benefits for all their agents. Finally, $x\in X$ is a CSE, but it is not a Strong CSE: If agents in coalition $S=\{3,5\}$ deviate from x to $(x_{-S};x'_S)$, as given in Table 32, then the spanning tree, $\Gamma ^{(x_{-S};x'_S)}$, as given in Fig. 21, is generated. With this profile of strategies, agents in S obtain the same benefits, but both pay less, as shown in Table 33.

Fig. 20

$\Gamma ^{x}$

Table 31 p(x) and c(x)

Table 32 Profile of strategies $(x_{-S};x'_S)\in X$

Fig. 21

$\Gamma ^{(x_{-S};x'_S)}$

Table 33 $p(x_{-S};x'_S)$ and $c(x_{-S};x'_S)$

Finally, notice that x is also a CSE, but it is not a Strong CSE.

$\lhd$

The profile of strategies $x\in X$, in Example 8, is a Strong NE which is neither a MCST strategy nor a CSE (see Fig. 23).

Example 8

If, as given in Example 7, the profile of strategies $x'\in X$, as given in Table 34, is played, then the spanning tree generated, $\Gamma ^{x'}$, is the same as that generated by $x\in X$, $\Gamma ^x$, in Fig. 21.

Table 34 Profile of strategies $x'\in X$

If agent 3 deviates from $x'$ to $(x'_{-3};x''_3)\in X$, as given in Table 35, then the spanning tree $\Gamma ^{(x'_{-3};x''_3)}$, as given in Fig. 22, is generated, and Agent 3 obtains the same benefit, but pays strictly less, as shown in Table 36. Therefore, $x'\in X$ is a Strong NE, which is not a CSE.

Table 35 Profile of strategies $(x'_{-3};x''_3)\in X$

Fig. 22

$\Gamma ^{(x_{-3};x'_3)}$

Table 36 $p(x_{-3};x'_3)$ and $c(x_{-3};x'_3)$

Fig. 23

Examples which illustrate the contents

$\lhd$

Figure 23 presents a graphic schema of how the examples are located.