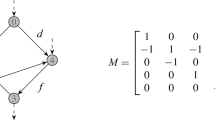A bilevel optimization approach to decide the feasibility of bookings in the European gas market

Abstract

The European gas market is organized as a so-called entry-exit system with the main goal to decouple transport and trading. To this end, gas traders and the transmission system operator (TSO) sign so-called booking contracts that grant capacity rights to traders to inject or withdraw gas at certain nodes up to this capacity. On a day-ahead basis, traders then nominate the actual amount of gas within the previously booked capacities. By signing a booking contract, the TSO guarantees that all nominations within the booking bounds can be transported through the network. This results in a highly challenging mathematical problem. Using potential-based flows to model stationary gas physics, feasible bookings on passive networks, i.e., networks without controllable elements, have been characterized in the recent literature. In this paper, we consider networks with linearly modeled active elements such as compressors or control valves. Since these active elements allow the TSO to control the gas flow, the single-level approaches for passive networks from the literature are no longer applicable. We thus present a bilevel model to decide the feasibility of bookings in networks with active elements. While this model is well-defined for general active networks, we focus on the class of networks for which active elements do not lie on cycles. This assumption allows us to reformulate the original bilevel model such that the lower-level problem is linear for every given upper-level decision. Consequently, we derive several single-level reformulations for this case. Besides the classic Karush–Kuhn–Tucker reformulation, we obtain three problem-specific optimal-value-function reformulations. The latter also lead to novel characterizations of feasible bookings in networks with active elements that do not lie on cycles. We compare the performance of our methods by a case study based on data from the GasLib.

1 Introduction

The main goal of the European entry-exit gas market is to decouple transport and trading of gas. The transmission system operator (TSO), who operates the network, and gas traders interact via so-called bookings. A booking represents a mid- to long-term capacity-right contract between gas traders and the TSO. It grants traders the right to inject and withdraw gas up to the booked capacities at certain nodes of the network. After signing these booking contracts, gas traders can nominate on a daily basis the actual quantities of gas within their booked capacities that should be shipped through the network by the TSO. In total, these so-called nominations have to be balanced and represent the quantities of gas that are injected at entry nodes or withdrawn at exit nodes in a single time period.

By signing a booking contract, the TSO is obliged to guarantee that every balanced and booking-compliant load flow can be transported through the network, which follows from the European directive (Directive 2009) and the subsequent regulation (European Parliament Council 2009) on the entry-exit gas market. Indeed, this condition decouples transport and trading, since after signing the booking contracts, the gas traders can nominate any balanced quantity of gas without considering any transport requirements of the network. However, from a mathematical point of view, deciding the feasibility of a booking poses a significant challenge since infinitely many different balanced load flows have to be checked for being transportable through the network.

First mathematical results regarding bookings are obtained in the PhD theses by Hayn (2016) and Willert (2014). Some structural properties of bookings are analyzed in Willert (2014). Further, Hayn (2016) studies the problem of deciding the feasibility of a booking as a quantifier elimination problem and presents an algorithm that decides the feasibility of a booking in an active network up to a certain tolerance. The remaining literature regarding bookings focuses on the case of passive networks. In Fügenschuh et al. (2014), the so-called reservation-allocation problem is studied for linear flow problems, which is closely related to the feasibility of a booking. Later on, in Labbé et al. (2020), a characterization of feasible bookings is obtained, in which for each pair of nodes, a nonlinear optimization problem needs to be solved to global optimality. These nonlinear problems compute the maximum pressure difference between the corresponding two nodes that can be obtained within the considered booking. If these maximum pressure differences satisfy certain pressure bounds, the booking is feasible and otherwise, it is infeasible. This characterization can be used to decide the feasibility of a booking in polynomial time for passive, tree-shaped networks (Labbé et al. 2020) or passive, single-cycle networks (Labbé et al. 2021). However, the problem is coNP-hard on passive networks in general (Thürauf 2020). Moreover, optimizing over the set of feasible bookings is hard even on tree-shaped networks (Schewe et al. 2020). We note that deciding the feasibility of bookings can also be seen as a special two-stage robust or adjustable robust optimization problem in which the uncertainty set consists of balanced and booking-compliant load flows. Exploiting this point of view, the authors of Aßmann (2019); Aßmann et al. (2019); Robinius et al. (2019) derive methods that can be used to decide the feasibility of bookings in passive networks. Moreover, results of booking feasibility are not restricted to the European entry-exit gas market, but can also be applied to other potential-based network problems such as network expansion under demand uncertainties. This is demonstrated, e.g., in Robinius et al. (2019), where a robust diameter selection for hydrogen networks is computed that is protected against unknown future demand fluctuations.

Unfortunately, all these results in passive networks cannot be used directly to decide the feasibility of bookings in active networks. Switching from passive to active networks makes the problem even more challenging as it introduces binary decisions for switching on or off active elements such as compressors or control valves. These binary decisions have to be taken individually for each balanced load flow within the booking bounds, since the TSO is able to change the settings of the active elements. This additional degree of freedom leads us to consider the following bilevel structure. The upper-level adversarial player tries to find a balanced and booking-compliant load flow that cannot be transported. The TSO, acting as the lower-level player, uses the active elements to transport this “worst-case” load flow of the upper level through the network. Consequently, if the upper-level player finds a balanced and booking-compliant load flow that cannot be transported by the TSO in the lower level, then the booking is infeasible. Otherwise, it is feasible. For an introduction to bilevel optimization, we refer to the books Bard (1998); Dempe (2002) and the recent survey article see above Kleinert et al. (2021). In general, bilevel optimization has been successfully applied to many different problems in the context of energy networks; see Wogrin et al. (2020). Moreover, it has specifically been applied to find scenarios that lead to severe transport situations in passive gas networks with linear flow models; see, e.g., Hennig and Schwarz (2016).

In this paper, we present a first stepping stone towards deciding the feasibility of bookings in networks with linearly modeled active elements and a nonlinear model for stationary gas transport. First, a bilevel model for validating bookings on networks with active elements is derived. Since even linear bilevel optimization is computationally hard, see Hansen et al. (1992); Jeroslow (1985), and since we additionally consider nonlinear gas transport models, we assume that no active element is part of a cycle of the network; see, e.g., Aßmann et al. (2019), where this assumption is used as well. This allows us to reformulate our model as a bilevel problem with mixed-integer nonlinear upper level and a linear lower level. We then develop different approaches to solve this challenging bilevel problem. First, the classic Karush–Kuhn–Tucker (KKT) approach is applied. We provide provably correct bounds on the lower-level primal and dual variables to be used in the linearization of the KKT complementarity constraints. Then, three closed-form expressions of the lower-level optimal value function are studied. Using these closed-form formulas, we set up optimal-value-function reformulations of the presented bilevel model, which then lead to novel characterizations of feasible bookings in active networks. The obtained approaches are evaluated in a computational study for some instances of the GasLib (Schmidt et al. 2017). The results show that the nonlinear gas flow model is computationally very challenging, which only allows for a limited comparison of the methods. Thus, we also conducted a computational study for a simplified linear flow model.

The remainder of this paper is structured as follows. In Sect. 2, we formally introduce the problem of deciding the feasibility of a booking in networks with active elements. In Sect. 3, we then illustrate why the methods for the case of passive networks cannot be applied and how active elements make the problem even more challenging. We present a bilevel model for deciding the feasibility of a booking for active networks in Sect. 4. While this model is well-defined for general active networks, we afterward focus on networks in which the active elements do not lie on cycles. This assumption allows us to reformulate the original bilevel model such that the lower-level problem is linear for every given upper-level decision. Based on the reformulated bilevel model, we provide the single-level KKT reformulation in Sect. 5 and discuss various optimal-value-function reformulations and characterizations of feasible bookings in active networks in Sect. 6. We then compare our methods in a computational study in Sect. 7. Finally, we summarize our results and discuss possible directions for future research in Sect. 8.

2 Problem description

We now formalize the problem of deciding the feasibility of a booking in gas networks including compressors and control valves. We follow and extend the problem description in Labbé et al. (2021), which deals with the feasibility of a booking for a single-cycle network without active elements. To this end, we consider linearly modeled active elements and stationary gas flows.

We model a gas network by a weakly connected and directed graph $G =(V, A)$ with nodes $V$ and arcs $A$. The set of nodes is partitioned into entry nodes $V_+$, at which gas is injected, exit nodes $V_-$, at which gas is withdrawn, and the remaining inner nodes $V_0$. The set of arcs is partitioned into pipes $A_{\mathrm {pipe}}$ and active elements $A _{\mathrm {act}}$, which can actively control the pressure. Further, the set of active elements is split into compressors $A _\mathrm {cm}$, which can increase the pressure, and control valves $A _\mathrm {cv}$, which can decrease the pressure.

We now introduce our framework for deciding the feasibility of a booking.

Definition 2.1

A load flow is a vector $\ell =(\ell _u)_{u \in V} \in \mathbb {R}_{\ge 0}^{V}$ with $\ell _u =0$ for all $u \in V_0$. The set of load flows is denoted by $L$.

A load flow leads to an actual flow situation in the gas network. More precisely, $\ell _u$ denotes the amount of gas that is injected at an entry $u \in V_+$ and that is withdrawn at an exit $u \in V_-$. Since we consider stationary gas flows, the quantities of gas injected and withdrawn from the network have to be balanced. This leads to the definition of a nomination.

Definition 2.2

A nomination is a balanced load flow $\ell$, i.e., $\sum _{u \in V_+}\ell _u = \sum _{u \in V_-} \ell _u$. The set of nominations is given by

$$\begin{aligned} N\mathrel {{\mathop :}{=}}\left\{ \ell \in L:\sum _{u \in V_+}\ell _u = \sum _{u \in V_-} \ell _u \right\} . \end{aligned}$$

A booking, on the other hand, represents a mid- to long-term contract in the European entry-exit gas market between the gas traders and the TSO that allows gas traders to inject or withdraw gas at certain nodes up to the booked capacity. To do so, the TSO is obliged to guarantee that all possibly infinitely many booking-compliant nominations can be transported through the network.

Definition 2.3

A booking is a load flow $b\in L$. A nomination $\ell$ is called booking-compliant w.r.t. the booking $b$ if $\ell \le b$ holds, where “$\le$” is meant component-wise throughout this paper. The set of booking-compliant nominations is given by $N(b) \mathrel {{\mathop :}{=}}\{\ell \in N:\ell \le b\}$.

In the following, we consider stationary gas flows based on the Weymouth pressure loss equation (Weymouth 1912). In line with the corresponding literature Schewe et al. (2020), Thürauf (2020), and Labbé et al. (2021), we model gas flow physics using potential-based flows, which for active networks consist of arc flows $q =(q _a)_{a \in A}$, node potentials $\pi =(\pi _u)_{u \in V}$, and controls $\Delta =(\Delta _a)_{a \in A _{\mathrm {act}}}$. In the context of gas networks with horizontal pipes, potentials represent squared gas pressures at the nodes, i.e., $\pi _u = p^2_u$ for $u \in V$. We note that potential-based flow models are also capable of handling non-horizontal pipes; see Gross et al. (2019). For modeling active elements, a variety of different modeling approaches exist that range from simple linear to sophisticated mixed-integer nonlinear ones; see Fügenschuh et al. (2015). In this paper, we focus on linearly modeled active elements similar to Aßmann (2019). A compressor or control valve $a \in A _{\mathrm {act}}$ linearly increases, respectively decreases, potentials by $\Delta _a \in [0, {\Delta }^+_a ]$, where ${\Delta }^+_a \ge 0$ is an upper bound on its capability to increase or decrease the potential. The compressor or control valve can only be active if a minimal quantity of flow passes the arc in the “correct” direction, i.e., if $q _a > m_a$ holds for some given threshold value $m_a \ge 0$. We model an active element $a =(u,v) \in A _{\mathrm {act}}$ by

$$\begin{aligned} \pi _u- \pi _v&= {\left\{ \begin{array}{ll} -\Delta _a,&{} \text {if }a \in A _\mathrm {cm},\\ \Delta _a,&{} \text {if }a \in A _\mathrm {cv}, \end{array}\right. } \\ \Delta _a&\in [0, {\Delta }^+_a \chi _a (q)], \end{aligned}$$

where the indicator function $\chi _a (q)$ is given by

$$\begin{aligned} \chi _a (q) \mathrel {{\mathop :}{=}}{\left\{ \begin{array}{ll} 1,&{} \text {if }q _a >m_a,\\ 0,&{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

We note that modeling the indicator function $\chi _a$ introduces binary variables in general, which we explicitly consider in Sect. 4. We can now formally define the feasibility of a nomination and a booking.

Definition 2.4

A nomination $\ell \in N$ is feasible if $(q,\pi , \Delta )$ exists that satisfies

$$\begin{aligned}&\sum _{a \in \delta ^{\mathrm {out}}(u)} q _a- \sum _{a \in \delta ^{\mathrm {in}}(u)}q _a = {\left\{ \begin{array}{ll} \ell _u,&{} \ u \in V_+, \\ -\ell _u,&{} \ u \in V_-, \\ 0,&{} \ u \in V_0, \end{array}\right. } \end{aligned}$$

(1a)

$$\begin{aligned}&\pi _{u} - \pi _{v} = \Lambda _a q _a |q _a |, \quad a = (u,v) \in A_{\mathrm {pipe}}, \end{aligned}$$

(1b)

$$\begin{aligned}&\pi _u- \pi _v = {\left\{ \begin{array}{ll} -\Delta _a,&{} \ a =(u,v) \in A _\mathrm {cm},\\ \Delta _a,&{} \ a =(u,v) \in A _\mathrm {cv}, \end{array}\right. } \end{aligned}$$

(1c)

$$\begin{aligned}&\Delta _a \in [0, {\Delta }^+_a \chi _a (q)], \quad a \in A _{\mathrm {act}}, \end{aligned}$$

(1d)

$$\begin{aligned}&\pi _u \in [{\pi }^-_u, {\pi }^+_u ], \quad u \in V, \end{aligned}$$

(1e)

where $\delta ^{\mathrm {out}}(u)$ and $\delta ^{\mathrm {in}}(u)$ denote the sets of arcs leaving and entering node $u \in V$, $\Lambda _a >0$ is a pipe-specific potential drop coefficient for all $a \in A_{\mathrm {pipe}}$, $0 < {\pi }^-_u \le {\pi }^+_u$ are potential bounds for all $u \in V$, and $0 \le {\Delta }^+_a$ is an upper bound on the operation of each active element $a \in A _{\mathrm {act}}$.

Constraints (1a) ensure flow conservation at every node of the network. For pipes $a \in A_{\mathrm {pipe}}$, Constraints (1b) link the arc flow to the incident node potentials. For active elements $a \in A _{\mathrm {act}}$, Constraints (1c) determine the potentials incident to the active element according to its control $\Delta _a$. Moreover, Constraints (1d) ensure that the active elements operate in the allowed ranges, which are due to technical restrictions. Finally, the potentials have to satisfy certain potential bounds, see Constraints (1e). The feasibility of a booking is then defined as follows.

Definition 2.5

A booking $b\in L$ is feasible if all booking-compliant nominations $\ell \in N(b)$ are feasible, i.e., a booking $b$ is feasible if

$$\begin{aligned} \forall \ell \in N(b) \ \exists (q, \pi , \Delta ) \text { satisfying } (\text {1}). \end{aligned}$$

(2)

Consequently, for checking the feasibility of a booking, possibly infinitely many booking-compliant nominations have to be checked for feasibility.

From a robust optimization perspective, Problem (2) can be seen as a special two-stage robust or adjustable robust optimization problem, see Ben-Tal et al. (2009); Yanıkoğlu et al. (2019) for more details. Here, the uncertainty set consists of all booking-compliant nominations $N(b)$. Moreover, the robust problem consists only of so-called “wait-and-see” decisions given by (2.4) and no “here-and-now” decisions are made. The switch from passive to active networks makes Problem (2) even more challenging since it introduces binary “wait-and-see” decisions due to the indicator functions $\chi _a$ for all $a \in A _{\mathrm {act}}$.

3 Why active elements are difficult

In this section, we first review a known characterization of the feasibility of a booking in passive networks as obtained in Labbé et al. (2020). Afterward, we show that this characterization cannot be applied to the considered case with active elements, which illustrates the need for new methods to decide the feasibility of a booking in active networks.

In passive networks, the feasibility of a given booking $b$ can be characterized by computing the maximum potential difference for each pair of nodes; see Theorem 10 in Labbé et al. (2020). For each pair of nodes $({w_1}, {w_2}) \in V ^2$, the authors introduce the nonlinear optimization problem

$$\begin{aligned} \varphi _{{w_1}{w_2}}(b) \mathrel {{\mathop :}{=}}\max _{\ell , q, \pi } \quad&\pi _{{w_1}} - \pi _{{w_2}} \end{aligned}$$

(3a)

$$\begin{aligned} \text {s.t.}\quad&\sum _{a \in \delta ^{\mathrm {out}}(u)} q _a- \sum _{a \in \delta ^{\mathrm {in}}(u)}q _a = {\left\{ \begin{array}{ll} \ell _u,&{} \ u \in V_+, \\ -\ell _u,&{} \ u \in V_-, \\ 0,&{} \ u \in V_0, \end{array}\right. }\end{aligned}$$

(3b)

$$\begin{aligned}&\pi _{u} - \pi _{v} = \Lambda _a q _a |q _a |, \quad a = (u,v) \in A, \end{aligned}$$

(3c)

$$\begin{aligned}&0 \le \ell _u \le b_u, \quad u \in V. \end{aligned}$$

(3d)

The feasibility of a booking is then characterized by constraints on the optimal value $\varphi _{{w_1}{w_2}}(b)$ of (3).

Theorem 3.1

(Theorem 10 in Labbé et al. (2020)) Let $G =(V, A)$ be a weakly connected and passive network and let $b\in L$ be a booking. Then, the booking $b$ is feasible if and only if for each pair of nodes $({w_1}, {w_2}) \in V ^2$, the corresponding optimal value $\varphi _{{w_1}{w_2}}(b)$ satisfies

$$\begin{aligned} \varphi _{{w_1}{w_2}}(b) \le {\pi }^+_{{w_1}} - {\pi }^-_{{w_2}}. \end{aligned}$$

(4)

For passive tree-shaped or passive single-cycle networks, this characterization can be checked in polynomial time; see Labbé et al. (2020, 2021); Robinius et al. (2019). However, the problem of validating a booking on general passive networks is known to be coNP-hard (Thürauf 2020).

Unfortunately, the characterization given in Theorem 3.1 does not hold if active elements are present in the network, which we demonstrate by the following counterexample. To this end, we consider a tree $G =(V,A)$ with corresponding lower and upper potential bounds ${\pi }^-$ and ${\pi }^+$:

$$\begin{aligned}&V:= \{s, v, t\}, \quad A:= \{(s, v), (v, t)\}, \\&{\pi }^-_{s} = {\pi }^+_{s} = 5, \quad {\pi }^-_{v} = 0, \ {\pi }^+_{v} = 10, \quad {\pi }^-_{t} = 5, \ {\pi }^+_{t} = 7, \end{aligned}$$

where $s\in V_+$ is an entry node, $t\in V_-$ is an exit node, and $v\in V_0$ is an inner node. Furthermore, $(s, v) \in A _\mathrm {cm}$ is a compressor that operates in the range $\Delta _{(s, v)} \in [0,2]$ if $q _{(s, v)} > m_{(s, v)} =0$ and otherwise, it is switched to bypass mode, i.e., $\Delta _{(s, v)} = 0$. The arc $(v, t) \in A_{\mathrm {pipe}}$ is a pipe with potential drop coefficient $\Lambda _{(v, t)} = 1$. A graphical representation is given in Figure 1.

Fig. 1

Network of the counterexample consisting of three nodes, one compressor, and one pipe, together with relevant node and arc parameters

We consider the booking $(b_{s}, b_{v}, b_{t}) = (1,0,1)$. By construction, every feasible point of (3) satisfies $0 \le q _a \le 1$ for all $a \in A$. To apply the passive characterization (4) to the active network $G =(V,A)$, we set the active element to bypass mode and interpret it as a pipe with $\Lambda _{(s, v)} = 0$. Consequently, it follows that the characterization conditions (4) are directly satisfied for every pair of nodes except of $(s, t)$. For the latter pair of nodes, the booking-compliant nomination $(\ell _{s}, \ell _{v}, \ell _{t}) = (1,0,1)$ is the optimal solution of (3) w.r.t. $(s, t)$ with objective value $\varphi _{st}(b) = 1$ and therefore violates the corresponding condition (4). Consequently, the booking is infeasible. However, this is not correct here since the compressor can be used to compensate the potential loss. In particular, for every booking-compliant nomination $\ell \in N(b)$, we can explicitly construct a corresponding feasible point of (2.4) as follows: The zero nomination is feasible due to $\pi _u = 5$ for all $u \in V$, $q _a = 0$ for all $a \in A$, $\Delta _{(s, v)} = 0$, and $\chi _{(s, v)}(q) = 0$. Thus, we now consider an arbitrary nonzero nomination $\ell \in N(b)$. The corresponding flows $q$ are unique since $G$ is a tree. We thus can construct the following feasible point of (2.4):

$$\begin{aligned} \pi _{s} = 5, \ \pi _{v} = 7, \ \pi _{t} = 7 - q _{(v, t)}^2, \quad \Delta _{(s, t)} = 2, \ \chi _{(s, v)}(q) = 1, \end{aligned}$$

where $\pi _{t} = 7 - q _{(v, t)}^2 \in [5,7]$ holds due to $0 \le q _a \le 1$ for all $a \in A$. This small counterexample illustrates that the existing characterization for deciding the feasibility of a booking in passive networks cannot be applied directly to the case of networks with active elements.

Furthermore, the introduction of active elements may lead to a disconnected set of feasible nominations, which is proven to be connected for the case of passive networks; see Schewe et al. (2020). We can observe this effect in our small counterexample by setting the threshold value $m_{(s, v)}=0.5$. Then, the set of nominations $N(b)$ splits into infeasible nominations $\{(\ell _s, \ell _v, \ell _t)=(x,0,x):x \in (0,0.5]\}$ and the set of feasible nominations $\{(\ell _s, \ell _v, \ell _t)=(x,0,x):x \in (0.5,1]\} \cup \{(0,0,0)\}$, which are not connected. Consequently, the booking $(b_{s}, b_{v}, b_{t}) = (1,0,1)$ is infeasible. We additionally note that the maximum potential difference between $s$ and $t$ is 0.25, which is obtained by the nomination (0.5, 0, 0.5) that differs from the optimal solution $\varphi _{st}(b)$ given by (1, 0, 1) of the passive characterization (4). Consequently, the usual monotonicity property of passive network, namely that more flow between a pair of nodes leads to a larger potential difference, is not satisfied in active networks anymore.

In the following section, we adapt the method of computing maximum potential differences to decide the feasibility of a booking in active networks using a bilevel approach. Choosing the tool of bilevel optimization is based on the following intuition. First, an arbitrary booking-compliant nomination is chosen. Afterward, the TSO controls the active elements to transport the nomination through the network. If this is possible for every booking-compliant nomination, then the booking is feasible. Otherwise, it is infeasible. We explore this bilevel perspective to derive new methods to decide the feasibility of a booking in networks with active elements.

4 Bilevel modeling

We adapt the methodology of Labbé et al. (2020) to validate a booking on networks with active elements by adequately computing nominations with maximum potential difference. As previously discussed, an analogous single-level optimization problem is not sufficient if active elements are present. Here, we consider a max-min bilevel optimization problem. The leader chooses a booking-compliant nomination $\ell \in N(b)$ that maximally violates potential bounds. The goal of the follower, i.e., the TSO, is to transport this nomination while minimizing the violation. The TSO determines flows $q$, potentials $\pi$, and controls $\Delta$ of the active elements according to (2.4), where the potential bound intervals are adjusted using auxiliary variables $y,z\in \mathbb {R}$. More precisely, for every node $u \in V$ it is required that $\pi _u \in [{\pi }^-_u-y, {\pi }^+_u + z]$. The bilevel problem is thus given by

$$\begin{aligned} \sup _{\ell \in N(b)} \min _{q,\pi ,\Delta , y, z} \quad&y+ z \end{aligned}$$

(5a)

$$\begin{aligned} \text {s.t.}\quad&\text {(1a)--(1b)}, \nonumber \\&\pi _u + y\ge {\pi }^-_u, \quad u \in V, \end{aligned}$$

(5b)

$$\begin{aligned}&\pi _u- z\le {\pi }^+_u, \quad u \in V. \end{aligned}$$

(5c)

In this bilevel model, we use “sup” instead of “max” in the upper level, since bilevel-optimal solutions might not be attainable. In fact, the bilevel-feasible region may not be closed in the presence of continuous linking variables, i.e., of variables of the upper level that appear in the lower level, and integer decisions at the lower level; see Moore and Bard (1990); Vicente et al. (1996); Köppe et al. (2010). In (5), the linking variables are given by the nomination $\ell$ and the binary decisions of the lower level are induced by the indicator functions $\chi _a$ for all $a \in A _{\mathrm {act}}$. However, we observe in the following that under the structural assumption 1 considered in this paper, the supremum is indeed attained.

In Problem (5), the leader chooses a booking-compliant nomination and maximizes the sum of the violation $y\in \mathbb {R}$ of lower potential bounds and the violation $z\in ~\mathbb {R}$ of upper potential bounds. The follower transports the nomination through the network and chooses a control of the active elements to minimize the total potential bound violation, as modeled by (5b) and (5c). This max-min problem, where leader and follower share the same objective function, is part of a special class of bilevel optimization problems, which includes, e.g., interdiction-like problems; see Wood (2011); Smith and Song (2020) and Section 6 of Kleinert et al. (2021). If the optimal value of (5) is positive, then there exists an infeasible nomination. In this case, the leader has chosen a nomination such that the follower cannot route flows without violating the potential bounds. In contrast, if the optimal value is nonpositive, then the corresponding booking is feasible. From the perspective of the TSO, this objective value measures how close within or how far outside of its physical capabilities the network is operated given a “worst-case” nomination w.r.t. the considered booking. The following result proves the correctness of Problem (5).

Proposition 4.1

Let $G = (V, A)$ be a weakly connected network with linearly modeled active elements $A _{\mathrm {act}}\subseteq A$. Then, the booking $b\in L$ is feasible if and only if the optimal value of (5) is nonpositive.

Proof

If the optimal value of (5) is positive, it is clear that there exists a bilevel-feasible point $(\ell ,q,\pi ,y,z)$ such that the nomination $\ell$ violates either a lower potential bound ($y>0$) or an upper potential bound ($z>0$). Thus, the booking is infeasible in that case.

Suppose now that for every feasible point $(\ell , q, \pi , \Delta , y, z)$ of (5), it holds that $y+z\le 0$. If $y, z\le 0$, all booking-compliant nominations can be transported within the original potential bounds and the booking is feasible. If $y>0$ and $z\le -y$, the nomination $\ell$ violates at least one lower potential bound $\pi _u = {\pi }^-_u-y< {\pi }^-_u$ for $u \in V$. Without changing flows $q$ or the controls $\Delta$, we consider new potentials ${\tilde{\pi }}_u \mathrel {{\mathop :}{=}}\pi _u + y$ for all $u \in V$. Adapting the corresponding auxiliary variables ${\tilde{y}}\mathrel {{\mathop :}{=}}0$ and ${\tilde{z}}\mathrel {{\mathop :}{=}}y+z\le 0$, we have constructed a new solution $(\ell , q, {\tilde{\pi }}, \Delta , {\tilde{y}}, {\tilde{z}})$ of the same objective value without any violation of lower or upper potential bounds. The symmetric case of $z>0$ and $y\le -z$ can be treated analogously. $\square$

It has been discussed in Sect. 3 that the problem of validating the feasibility of a booking when considering active elements is difficult in general. This is reflected in Problem (5), which is a bilevel problem with nonlinear and nonconvex lower level and for which optimal solutions may not be attainable. Thus, to tackle this highly challenging problem we need to make the following structural assumption that allows us to derive a practically more tractable reformulation of the bilevel model considered so far.

Assumption 1

No active element is part of an undirected cycle in $G$.

Fig. 2

Stylized gas network satisfying Assumption 1 (left) and its reduced network (right)

We note that this assumption is also used in Aßmann et al. (2019); Aßmann (2019). Figure 2 shows on the left a stylized gas network satisfying Assumption 1. Intuitively, Assumption 1 implies that there cannot be any flow along a cycle in the network. More precisely, flow in pipes always leads to a potential drop due to (1b), which for flows along a cycle would lead to mismatching starting and end potentials on that cycle. Such a mismatch could however be fixed by using active elements that act on that cycle in order to match starting and end potentials. Assumption 1 eliminates this possibility and allows us to show the uniqueness of the flows corresponding to any given nomination. To this end, we extend the results of Maugis (1977); Collins et al. (1978); Ríos-Mercado et al. (2002) for passive networks.

Theorem 4.2

Suppose that Assumption 1 holds. Then, for a given nomination $\ell \in N$, every feasible point $(q, \pi )$ of (1a) and (1b) admits the same unique flows $q _a$ for all $a \in A$ and the same unique potential differences $\pi _u- \pi _v$ for all $(u,v)\in A_{\mathrm {pipe}}$.

Proof

We prove that flows $q$ are uniquely determined by the nomination $\ell$. The uniqueness of potential differences on pipes then directly follows from (1b). First, observe that by Assumption 1, the removal of an active element $a \in A _{\mathrm {act}}$ decomposes the network $G =(V, A)$ into two smaller networks. Moreover, after removing all active elements $A _{\mathrm {act}}$, the network $G$ is split into disconnected and passive components.

If $A _{\mathrm {act}}= \emptyset$, the network $G$ is passive and the result follows from Maugis (1977); Collins et al. (1978). By induction on $|A _{\mathrm {act}}|$, we show that the result also holds true in general. Thus, suppose that the result holds for networks with at most $|A _{\mathrm {act}}| - 1$ active elements. We remove an arbitrary active element $a \in A _{\mathrm {act}}$ from $G$, which results in two networks with fewer active elements $G _1=(V _1,A _1)$ and $G _2=(V _2,A _2)$. We assume w.l.o.g. that $a = (s, t)$ with $s\in V _1$ and $t\in V _2$. For every node $u \in V$, we define

$$\begin{aligned} \sigma _u \mathrel {{\mathop :}{=}}{\left\{ \begin{array}{ll} 1,&{}\text {if }u \in V_+,\\ -1,&{}\text {if }u \in V_-,\\ 0,&{}\text {if }u \in V_0. \end{array}\right. } \end{aligned}$$

Then, the balancedness of supply and demand of nomination $\ell$ implies that the arc flow $q _a$ is uniquely given by

$$\begin{aligned} q _a = \sum _{u \in V _1} \sigma _u \ell _u = -\sum _{u \in V _2} \sigma _u \ell _u. \end{aligned}$$

Starting from the nomination $\ell$, we now construct another nomination ${\tilde{\ell }}$ for $G _1$ that is balanced over $V _1$. We define ${\tilde{\ell }}_u \mathrel {{\mathop :}{=}}\ell _u$ for all $u \in V _1\setminus \{s\}$ and

$$\begin{aligned} {\tilde{\ell }}_s\mathrel {{\mathop :}{=}}\left|\sigma _s\ell _s- \sum _{w \in V _1} \sigma _w \ell _w \right|. \end{aligned}$$

All nodes in $V _1\setminus \{s\}$ keep the same nomination value. The modification at node $s$ might change its role, i.e., it can either be an entry, an exit, or an inner node. Thus, we also define ${\tilde{\sigma }}_u \mathrel {{\mathop :}{=}}\sigma _u$ for all $u \in V _1\setminus \{s\}$ and

$$\begin{aligned} {\tilde{\sigma }}_s\mathrel {{\mathop :}{=}}{\left\{ \begin{array}{ll} 1,&{} \text {if } \sigma _s\ell _s- \sum _{w \in V _1} \sigma _w \ell _w > 0,\\ -1,&{} \text {if } \sigma _s\ell _s- \sum _{w \in V _1} \sigma _w \ell _w <0,\\ 0,&{} \text {if } \sigma _s\ell _s- \sum _{w \in V _1} \sigma _w \ell _w =0, \end{array}\right. } \end{aligned}$$

which exactly corresponds to the sign of $\sigma _s\ell _s- \sum _{w \in V _1} \sigma _w \ell _w$. In particular, we have produced a nomination for $G _1$, since

$$\begin{aligned} \sum _{u \in V _1} {\tilde{\sigma }}_u {\tilde{\ell }}_u = \sum _{u \in V _1\setminus \{s\}} \sigma _u \ell _u + \sigma _s\ell _s- \sum _{w \in V _1} \sigma _w \ell _w = 0. \end{aligned}$$

By the induction hypothesis, the restriction of $q$ to $A _1$ is uniquely determined. Symmetrical arguments can be applied to show that the restriction of $q$ to $A _2$ is also unique. Finally, the result follows given the fact that $A = A _1 \cup A _2 \cup \{a \}$. $\square$

The latter result implies that, once a nomination is given, most lower-level decisions in (5) are already fixed by physics. The lower-level problem can thus be reduced to only include the remaining decision variables. Therefore, consider the collection of passive subnetworks obtained by removing all active elements from $G$, which we denote by ${\mathcal {G}}\mathrel {{\mathop :}{=}}\{G _0, G _1, \dots , G _{|A _{\mathrm {act}}|}\}$. For convenience, we sometimes denote an active arc $a \in A _{\mathrm {act}}$ by $a =(G _i,G _j)$ if $a =(u,v)$ for $u \in V (G _i)$ and $v \in V (G _j)$. Then, by Assumption 1, the graph ${\tilde{G}}=({\mathcal {G}}, A _{\mathrm {act}})$ obtained by merging passive subnetworks into single nodes is a tree. In line with Ríos-Mercado and Borraz-Sánchez (2015); Ríos-Mercado et al. (2002), we call ${\tilde{G}}$ the reduced network. Figure 2 illustrates a network (left) and its associated reduced network (right).

Using the rationale of Ríos-Mercado et al. (2002), it follows by Theorem 4.2 that the potentials corresponding to a nomination $\ell \in N$ are determined as soon as a reference potential in an arbitrary passive subnetwork $G _j\in {\mathcal {G}}$ and the controls $\Delta _a$ of all active elements $a \in A _{\mathrm {act}}$ are fixed. Exploiting this uniqueness of flows and potentials, the following result presents an equivalent reformulation of Problem (5). Therein, the upper level consists of a potential-based flow over $G$ where all active elements are inactive, i.e., $\pi _u = \pi _v$ for all $(u,v)\in A _{\mathrm {act}}$. The TSO then reacts by using the active elements, as well as a constant shift $\tau _j$ to be applied to the potentials of all the nodes $u \in V (G _j$) for every passive subnetwork $G _j\in {\mathcal {G}}$. Intuitively, in addition to choosing a worst-case nomination, the upper-level player thus already fixes all physical quantities that are uniquely determined by the nomination, i.e., all flows and the potential differences on pipes. The lower level, on the other hand, consists of a problem containing only those decision variables that the TSO influences. In addition, this new bilevel structure allows us to linearly model the indicator function $\chi _a$ for the activation of an element $a \in A _{\mathrm {act}}$ using binary variables.

Theorem 4.3

Consider the bilevel problem

$$\begin{aligned} \max _{\ell , q, \pi , s} \quad&y+ z\end{aligned}$$

(6a)

$$\begin{aligned} \text {s.t.}\quad&(\text {1a}), (\text {1b}), \end{aligned}$$

(6b)

$$\begin{aligned}&\ell \in N(b), \end{aligned}$$

(6c)

$$\begin{aligned}&\pi _u = \pi _v, \quad (u, v)\in A _{\mathrm {act}}, \end{aligned}$$

(6d)

$$\begin{aligned}&q _a \le m_a (1-s_a)+ Ms_a, \quad a \in A _{\mathrm {act}}, \end{aligned}$$

(6e)

$$\begin{aligned}&s_a \in \{0,1\}, \quad a \in A _{\mathrm {act}}, \end{aligned}$$

(6f)

$$\begin{aligned}&(\Delta , \tau , y, z) \in {\mathcal {R}}(\ell , q, \pi , s), \end{aligned}$$

(6g)

where $M\mathrel {{\mathop :}{=}}\min \{\sum _{u \in V_+} b_u, \sum _{u \in V_-} b_u \}$ is an upper bound on the flow on any arc and the set of lower-level solutions ${\mathcal {R}}(\ell , q,\pi , s)$ is given by

$$\begin{aligned} {{\,\mathrm{arg\,min}\,}}_{\Delta , \tau , y, z} \quad&y+ z\end{aligned}$$

(7a)

$$\begin{aligned} \text {s.t.}\quad&\tau _i - \tau _j = {\left\{ \begin{array}{ll} - \Delta _a,&{} \quad a = (G _i, G _j) \in A _\mathrm {cm},\\ \Delta _a,&{} \quad a = (G _i, G _j) \in A _\mathrm {cv}, \end{array}\right. } \end{aligned}$$

(7b)

$$\begin{aligned}&\Delta _a \in [0,{\Delta }^+_a s_a ], \quad a \in A _{\mathrm {act}}, \end{aligned}$$

(7c)

$$\begin{aligned}&\tau _j + y\ge {\pi }^-_u-\pi _u, \quad u \in V (G _j),\ G _j\in {\mathcal {G}}, \end{aligned}$$

(7d)

$$\begin{aligned}&\tau _j - z\le {\pi }^+_u- \pi _u, \quad u \in V (G _j),\ G _j\in {\mathcal {G}}. \end{aligned}$$

(7e)

Under Assumption 1, Problems (5) and (6) admit the same optimal value.

Proof

Let $(\ell , q, \pi , \Delta , y,z)$ be a bilevel-feasible point of (5). In Ríos-Mercado et al. (2002), it is shown that for a passive network, all potentials are uniquely determined once a reference potential is fixed. In particular, all solutions of (1a) and (1b) are equivalent up to a constant shift in every passive subnetwork. Thus, potentials in every passive subnetwork $G _j\in {\mathcal {G}}$ are of the form $\pi _u = \pi _u (\ell ) + \tau _j$ for all $u \in V (G _j)$, where $\pi (\ell )$ is a solution of (1b) and (6d). Moreover, $\tau _j\in \mathbb {R}$ is an arbitrary shift of the potentials in $G _j$. Constraints (7b) then also hold, since the potentials $\pi$ satisfy (1c). It remains to model the indicator function $\chi$. For every $a \in A _{\mathrm {act}}$, we set $s_a =1$ if and only if $q _a > m_a$. Since $q _a \le M$, it follows that (6e) is satisfied. Consequently, $(\ell , q, \pi (\ell ), s, \Delta , \tau , y, z)$ is bilevel feasible for (6) and admits the same objective value.

For the converse, first note that for every $a \in A _{\mathrm {act}}$, Constraints (6e) guarantee that $s_a =1$ holds if $q _a >m_a$. Assume now that $q _a \le m_a$. Then, the leader’s decision on $s_a$ is arbitrary. However, the lower level with $s_a =1$ is a relaxation of the lower level with $s_a =0$. Upper and lower level have the same objective function with opposing optimization directions. Consequently, there is a bilevel-optimal solution of (6) with $s_a =0$, and thus satisfying $s_a =\chi _a (q)$. Let $(\ell , q, \pi , s, \Delta , \tau , y, z)$ be a bilevel-optimal solution of (6) with $s_a = \chi _a (q)$ for all $a \in A _{\mathrm {act}}$. Theorem 4.2 states that the flows $q$ corresponding to $\ell$ and solving the System (1a) and (1b) are unique. If we denote these unique flows by $q (\ell )$, then $q = q (\ell )$ and every bilevel-feasible point of (5) also admits flows $q (\ell )$. Let us now define ${\tilde{\pi }}_u \mathrel {{\mathop :}{=}}\pi _u + \tau _j$ for all $u \in V (G _j)$ and $G _j\in {\mathcal {G}}$. Then, $(\ell , q, {\tilde{\pi }}, \Delta , y, z$) is bilevel-feasible for (5) and admits the same objective function value. $\square$

Since the integer decisions are at the upper level of Problem (6) and all variables of the lower level (7) are continuous, all bilevel-optimal solutions are indeed attained, which allows us to use “max” in (6). As a consequence of Theorem 4.3, the optimal solution of (5) is then attained under Assumption 1 as well. Hence, in this case, the “sup” in (5) can be replaced by a “max”.

To summarize, in this section we first presented a bilevel optimization model of the adversarial interplay of checking the feasibility of a booking. In the resulting Problem (5), the upper-level player selects the worst possible nomination w.r.t. a violation of the potential bounds. The lower-level player, i.e., the TSO, determines flows, potentials, and a control of the active elements to minimize the violation. Exploiting the structure resulting from Assumption 1, we deduced that many of the physical quantities of the TSO’s problem are already uniquely determined by the upper-level nomination. These observations led to Problem (6), where only variables that the TSO can actively control remain in the lower-level problem. Moving flow and potential variables to the upper level has, in particular, allowed us to linearly model the indicator functions $\chi$. Note also that in Problem (6), the upper level is a mixed-integer nonlinear problem (MINLP), but the lower level is a linear problem (LP) for fixed upper-level decisions. In the next section, we will focus on Problem (6) and derive the classical KKT reformulation.

5 Karush–Kuhn–Tucker reformulation

Problem (6) is a bilevel problem with mixed-integer variables. In general, these problems are strongly NP-hard, see, e.g., Hansen et al. (1992). Many approaches for bilevel problems with mixed-integer variables rely on the fact that the linking variables, i.e., the variables of the upper level that appear in the lower level, are all integers. This is not the case here since, in addition to the binaries $s_a$ for $a \in A _{\mathrm {act}}$, the potentials $\pi _u$ for $u \in V$ link the upper and the lower level. However, we observe that the lower level of (6) is linear for every fixed upper-level decision. As a consequence, we can characterize the optimal solutions of the lower level using its KKT conditions.

5.1 Reformulation

Let us first consider the lower level’s dual problem for a fixed upper-level decision $(\ell , q, \pi , s)$. We introduce dual variables $\alpha _a$ for $a \in A _{\mathrm {act}}$ for constraints (7b), ${\delta }^-_u$ and ${\delta }^+_u$ for $u \in V$ corresponding to (7d) and (7e), and finally $\beta _a$ for $a \in A _{\mathrm {act}}$ associated to the upper bound on $\Delta _a$. The dual problem is then given by

$$\begin{aligned} \max _{\alpha , \beta , {\delta }^+, {\delta }^-}\quad&-\sum _{a \in A _{\mathrm {act}}} {\Delta }^+_a s_a \beta _a + \sum _{u \in V} \left( ({\pi }^-_u- \pi _u) {\delta }^-_u-({\pi }^+_u- \pi _u){\delta }^+_u \right) \end{aligned}$$

(8a)

$$\begin{aligned} \text {s.t.}\quad&\sum _{a \in \delta ^{\mathrm {out}}(G _j)} \alpha _a- \sum _{a \in \delta ^{\mathrm {in}}(G _j)} \alpha _a = \sum _{u \in V (G _j)}({\delta }^+_u- {\delta }^-_u), \quad G _j\in {\mathcal {G}}, \end{aligned}$$

(8b)

$$\begin{aligned}&\alpha _a \le \beta _a,\ \beta _a \ge 0, \quad a \in A _\mathrm {cm}, \end{aligned}$$

(8c)

$$\begin{aligned}&-\alpha _a \le \beta _a,\ \beta _a \ge 0, \quad a \in A _\mathrm {cv}, \end{aligned}$$

(8d)

$$\begin{aligned}&\sum _{u \in V} {\delta }^+_u = 1,\ \sum _{u \in V} {\delta }^-_u = 1, \end{aligned}$$

(8e)

$$\begin{aligned}&{\delta }^+_u, {\delta }^-_u \ge 0, \quad u \in V. \end{aligned}$$

(8f)

Let ${\tilde{G}}$ be the reduced network obtained from $G$ by merging all passive subnetworks. The dual problem (8) can then be interpreted as a flow problem on ${\tilde{G}}$. From that point of view, $\alpha$ represents dual flows, $\beta$ are the capacities on arcs corresponding to active elements, and $\sum _{u \in V (G _j)}{\delta }^+_u$ and $\sum _{u \in V (G _j)}{\delta }^-_u$ are the supply and demand at each node $G _j$. Constraints (8b) ensure dual flow balance. Note that the dual arc flows have an unconstrained sign, with the same interpretation as before, i.e., $\alpha _a >0$ corresponds to flow in the direction of arc $a \in A _{\mathrm {act}}$, while $\alpha _a <0$ represents flow in the opposite direction. For compressors $a \in A _\mathrm {cm}$, dual flows are bounded from above, i.e., flow in the direction of the arc is bounded, whereas for control valves $a \in A _\mathrm {cv}$, arc flows are bounded from below, i.e., flow in the opposite direction of the arc is bounded. Finally, total supply and demand equal one; see (8e).

The KKT conditions for the lower level consist of primal feasibility (7b)–(7e), dual feasibility (8b)–(8f), and the complementarity constraints

$$\begin{aligned} {\delta }^-_u (\tau _j+y+\pi _u- {\pi }^-_u)&=0, \quad u \in V (G _j),\ G _j\in {\mathcal {G}}, \end{aligned}$$

(9a)

$$\begin{aligned} {\delta }^+_u (\tau _j-z+\pi _u- {\pi }^+_u)&=0, \quad u \in V (G _j),\ G _j\in {\mathcal {G}}, \end{aligned}$$

(9b)

$$\begin{aligned} \beta _a (\Delta _a-{\Delta }^+_a s_a)&=0, \quad a \in A _{\mathrm {act}}, \end{aligned}$$

(9c)

$$\begin{aligned} (-\alpha _a +\beta _a)\Delta _a&=0, \quad a \in A _\mathrm {cm}, \end{aligned}$$

(9d)

$$\begin{aligned} (\alpha _a +\beta _a)\Delta _a&=0, \quad a \in A _\mathrm {cv}. \end{aligned}$$

(9e)

Consequently, Problem (6) can be reformulated as the MINLP

$$\begin{aligned} \max _{\xi } \quad&y+ z \end{aligned}$$

(10)

$$\begin{aligned} \qquad \text {s.t.}\quad \;&\text {(6b)--(6f),} \end{aligned}$$

(UL)

$$\begin{aligned}&\qquad \qquad \; \text {(7b)--(7e), } \end{aligned}$$

(LLP)

$$\begin{aligned}&\qquad \qquad \; \text {(8b)--(8f),} \nonumber \\&\qquad \qquad \; (\text {9}), \end{aligned}$$

(LLD)

where $\xi =(\ell , q, \pi , s, \Delta , \tau , y, z, \alpha , \beta , {\delta }^+, {\delta }^-)$ is the vector of upper-level, lower-level primal, and lower-level dual variables. Here, Constraint (UL) groups all upper-level constraints. Constraint (LLP) and Constraint (LLD) group lower-level primal and dual constraints, respectively.

5.2 Big-M linearization

A standard way of reformulating the KKT complementarity conditions (9) is via big-M linearizations; see Fortuny-Amat and McCarl (1981). For a dual variable $\lambda \ge 0$ and a primal constraint $c(x)\ge 0$, the complementarity condition $\lambda c(x) =0$ is replaced by

$$\begin{aligned} \lambda \le M_{\text {d}}u, \quad c(x)\le M_{\text {p}}(1-u), \end{aligned}$$

where $u\in \{0,1\}$ is an auxiliary binary variable and $M_{\text {d}}, M_{\text {p}}\ge 0$ are upper bounds for $\lambda$ and c(x), respectively. It is shown in Kleinert et al. (2020) that determining a bilevel-correct big-M is a hard task if problem-specific knowledge is lacking. In the following, by exploiting the structure of Problem (6), we obtain provably correct bounds on lower-level primal and dual variables that can be used for a linearization of (9). First, let us consider the lower-level’s dual variables.

Lemma 5.1

Let $(\ell , q, \pi , s)$ be feasible for (UL). Then, there is a corresponding optimal solution  $(\alpha , \beta , {\delta }^+, {\delta }^-)$ of the lower level’s dual problem (8) with $\alpha _a \in [-1,1]$ and $\beta _a \in [0,1]$ for all $a \in A _{\mathrm {act}}$ as well as ${\delta }^+_u, {\delta }^-_u \in [0,1]$ for all $u \in V$.

Proof

If follows directly from (8e) and (8f) that ${\delta }^+_u, {\delta }^-_u \in [0,1]$ holds for all $u \in V$. Following the interpretation of the lower level’s dual problem as a flow problem on ${\tilde{G}}$, it holds that $|\alpha _a |\le 1$ for all $a \in A _{\mathrm {act}}$, since the total demand and supply are both 1 and ${\tilde{G}}$ is a tree under Assumption 1. Finally, by optimality it follows that $\beta _a \le 1$ holds if for an arc $a \in A _{\mathrm {act}}$ the inequality ${\Delta }^+_a s_a > 0$ is satisfied. Otherwise, if ${\Delta }^+_a s_a = 0$ holds for an arc $a \in A _{\mathrm {act}}$, then $\beta _a$ can be chosen arbitrarily in [0, 1]. $\square$

Next, we derive bounds for lower-level primal variables such that an optimal solution satisfying them always exists.

Lemma 5.2

Let $(\ell , q, \pi , s, \Delta ,\tau , y, z)$ be a bilevel-feasible point of (6), then for any ${\tilde{\varepsilon }},\varepsilon \in \mathbb {R}$, the point $(\ell , q, \pi +{\tilde{\varepsilon }}, s, \Delta , \tau + \varepsilon , y-\varepsilon -{\tilde{\varepsilon }}, z+ \varepsilon + {\tilde{\varepsilon }})$ is also bilevel feasible with the same objective value.

Proof

Let $(\ell , q, \pi , s, \Delta ,\tau , y, z)$ be a bilevel-feasible point of (6) and consider arbitrary but fixed ${\tilde{\varepsilon }}, \varepsilon \in \mathbb {R}$. We now check the feasibility of the point $(\ell , q, \pi +{\tilde{\varepsilon }},s, \Delta ,\tau +\varepsilon , y-\varepsilon - {\tilde{\varepsilon }}, z+ \varepsilon +{\tilde{\varepsilon }})$ for (6).

Since we have not changed the upper-level variables $\ell$, $q$, and $s$, and have only shifted the potential $\pi$ by ${\tilde{\varepsilon }}$, upper-level feasibility follows from Theorem 7.1 in (Koch et al. 2015, Chapter 7). We now turn to the lower level. Since the lower-level variables $\Delta$ stay unchanged, Constraint (7c) holds. Moreover, Constraints (7b), (7d), and (7e) are satisfied due to

$$\begin{aligned} \tau _i + \varepsilon -\tau _j - \varepsilon + \omega _a \Delta _a&= \tau _i -\tau _j + \omega _a \Delta _a = 0,&\quad a = (G _i, G _j) \in A _{\mathrm {act}}, \\ \tau _j + \varepsilon + y- \varepsilon - {\tilde{\varepsilon }}&= \tau _j + y-{\tilde{\varepsilon }}\ge {\pi }^-_u-\pi _u- {\tilde{\varepsilon }},&\quad u \in V (G _j),\ G _j\in {\mathcal {G}}, \\ \tau _j + \varepsilon - z- \varepsilon -{\tilde{\varepsilon }}&= \tau _j - z-{\tilde{\varepsilon }}\le {\pi }^+_u- \pi _u-{\tilde{\varepsilon }},&\quad u \in V (G _j),\ G _j\in {\mathcal {G}}. \end{aligned}$$

This shows the feasibility of the considered point. Additionally, the objective values of both points are equal, which directly follows by construction. $\square$

Corollary 5.3

There is an optimal solution $(\ell , q, \pi ,s,\Delta ,\tau , y, z)$ of (6) that satisfies

$$\begin{aligned} \min _{u \in V} \ \{\pi _u \} = 0 \quad \text {and} \quad \min _{G _j\in {\mathcal {G}}} \ \{\tau _j\} = 0. \end{aligned}$$

Using this result, we can bound the values $\pi$ and $\tau$ in an optimal solution.

Lemma 5.4

There is an optimal solution $(\ell , q, \pi ,s, \Delta ,\tau , y, z)$ of the bilevel problem (6) that satisfies

$$\begin{aligned} 0&\le \pi _u \le \sum _{a \in A} \Lambda _a M^2, \quad u \in V, \\ 0&\le \tau _j \le \sum _{a \in {A _{\mathrm {act}}}} {\Delta }^+_a, \quad G _j\in {\mathcal {G}}, \end{aligned}$$

where $M\mathrel {{\mathop :}{=}}\min \{\sum _{u \in V_+} b_u, \sum _{u \in V_-} b_u \}$ is an upper bound on the flow on any arc.

Proof

Corollary 5.3 implies that there is an optimal solution $(\ell , q, \pi ,s,\Delta ,\tau , y, z)$ of the bilevel problem (6) with $u \in V$ and $G _j\in {\mathcal {G}}$ that satisfies

$$\begin{aligned} \min _{v \in V} \ \{\pi _v \} = \pi _u = 0 , \quad \min _{G _i\in {\mathcal {G}}} \ \{\tau _i\} = \tau _j = 0. \end{aligned}$$

(11)

For an arbitrary node $v \in V$, we now consider a path , which consists of the arcs  corresponding to an undirected path from $u$ to $v$ in $G$. Additionally, for an arc , we introduce , which evaluates to 1, if $a$ is directed from $u$ to $v$, and otherwise it evaluates to $-1$. Consequently, Constraint (1b) and Condition (11) imply

In analogy, for an arbitrary $G _i\in {\mathcal {G}}$, Constraints (7b) and Condition (11) imply

$\square$

Finally, it remains to determine big-M bounds for $y$ and $z$. However, these can be obtained by carefully combining the lower and upper bounds given in Lemma 5.4. It suffices to observe that for a lower-level primal optimal solution, we obtain

$$\begin{aligned} y=\max _{\begin{array}{c} G _j\in {\mathcal {G}},\\ u \in V (G _j) \end{array}} \left\{ {\pi }^-_u-\pi _u-\tau _j\right\} , \quad z=\max _{\begin{array}{c} G _j\in {\mathcal {G}},\\ u \in V (G _j) \end{array}} \left\{ \pi _u + \tau _j-{\pi }^+_u \right\} . \end{aligned}$$

6 Optimal-value-function reformulations and characterizations of feasible bookings

As an alternative to the KKT reformulation of Sect. 5, the bilevel problem (6) can also be reformulated using the lower level’s optimal value function; see, e.g., Dempe (2002). Let $\varphi (\ell , q, \pi ,s)$ be the optimal value of (7) for given upper-level decisions $(\ell , q, \pi , s)$. Note that the lower level (7) is feasible for every $(\ell , q, \pi , s)$, i.e., (LLP) always admits a feasible point. Thus, (6) is equivalent to

$$\begin{aligned} \max _{\ell , q, \pi , s}\left\{ \varphi (\ell , q, \pi , s):(\right\} \text {UL}). \end{aligned}$$

(12)

By strong duality of the lower level, $\varphi$ is also the optimal value function of the lower level’s dual problem (8). The latter is a linear problem with objective function parameterized by $\pi$ and $s$. Thus, $\varphi$ is a piecewise-linear and convex function. More precisely, given that the lower level is always feasible and bounded, the same holds for the lower-level’s dual problem. The optimal value function $\varphi$ can thus be expressed as the maximum over the lower level’s dual objective function evaluated in a potentially exponential number of vertices of the feasible set of the lower level’s dual problem. Consequently, the single-level reformulation (12) is a convex maximization problem over a nonconvex feasible set, which is a highly intractable problem class, in general.

6.1 The optimal value function

We exploit the special structure of the lower level under Assumption 1 to express $\varphi$ by polynomially many vertices of the polyhedral feasible set of the lower level’s dual problem. To this end, let ${\tilde{G}}$ be the reduced network corresponding to $G$. Additionally, for every two passive subnetworks $G _i, G _j\in {\mathcal {G}}$, there exists a unique, undirected path joining them, which we denote by . Choosing any $G _k$ as the root of ${\tilde{G}}$, we can partition the active elements into arcs pointing away from or towards $G _k$, i.e., $A _{\mathrm {act}}=A _{\mathrm {act}}^{k, \rightarrow }\cup A _{\mathrm {act}}^{k, \leftarrow }$. Formally, we define

In the following, we prove that for given ${\delta }^+$ and ${\delta }^-$, the flow variables $\alpha$ can be uniquely determined using the conservation constraints (8b). Given that (8b) contains $|A _{\mathrm {act}}|+1$ many linear equations and that the system is of rank $|A _{\mathrm {act}}|$, we can eliminate an arbitrarily chosen row. We denote by $G _0$ the passive subnetwork in ${\mathcal {G}}$ for which we delete the corresponding equation in (8b). Then, $G _0$ can be interpreted as the root of ${\tilde{G}}$ and we can consider subtrees of ${\tilde{G}}$ w.r.t. $G _0$. If we remove an arc $a \in A _{\mathrm {act}}$ in $G$, then the network decomposes into two subnetworks. For $a \in A _{\mathrm {act}}$ and $G _j \in {\mathcal {G}}$, the set $\mathcal {G}_{a}({G _j})$ denotes all passive sub-components that are contained in the subnetwork, which contains $G _j$ after removing arc $a$. In particular, the subtree of ${\tilde{G}}$ “following” $a$ is obtained by $\mathcal {G}_{a}({G _j})$ if $a =(G _i,G _j)\in A _{\mathrm {act}}^{0, \rightarrow }$ and by $\mathcal {G}_{a}({G _i})$ if $a =(G _i,G _j)\in A _{\mathrm {act}}^{0, \leftarrow }$. The solution of (8b) is then given by the following lemma.

Lemma 6.1

Constraints (8b) are equivalent to

$$\begin{aligned}&\alpha _a = -\sum _{G _l\in \mathcal {G}_{a}({G _j})} \sum _{u \in V (G _l)} \left( {\delta }^+_u- {\delta }^-_u \right) ,&a =(G _i,G _j)\in A _{\mathrm {act}}^{0, \rightarrow }, \end{aligned}$$

(13a)

$$\begin{aligned}&\alpha _a = \sum _{G _l\in \mathcal {G}_{a}({G _i})} \sum _{u \in V (G _l)} \left( {\delta }^+_u- {\delta }^-_u \right) ,&a =(G _i,G _j)\in A _{\mathrm {act}}^{0, \leftarrow }. \end{aligned}$$

(13b)

Proof

For given supplies ${\delta }^+$ and demands ${\delta }^-$, we already noted that $\alpha$ can be interpreted as a flow. Due to Constraints (8e), Constraints (8b), which ensure flow conservation in ${\tilde{G}}$, always admit feasible flows. For an arc $a =(G _i,G _j)\in A _{\mathrm {act}}^{0, \rightarrow }$, the flow $\alpha _a$ is determined by the net demand

$$\begin{aligned} D\mathrel {{\mathop :}{=}}\sum _{G _l\in \mathcal {G}_{a}({G _j})} \sum _{u \in V (G _l)} \left( {\delta }^+_u- {\delta }^-_u \right) \end{aligned}$$

of the subtree “following” $a$. If $D\ge 0$, a surplus in supply needs to leave the subtree over $a$ flowing from $G _j$ to $G _i$. Respecting the sign convention on the flow along directed arcs, it then holds $\alpha _a = -|D| = -D$. If $D<0$, a surplus in demand needs to be shipped over $a$ into the subtree, thus $\alpha _a = |D| = -D$. Similar arguments apply to $a =(G _i,G _j)\in A _{\mathrm {act}}^{0, \leftarrow }$. $\square$

With this result at hand, we can explicitly determine the vertices of the polyhedral feasible set of the lower level’s dual problem (8).

Theorem 6.2

The vertices of the polyhedron (8) are given by (13) and

$$\begin{aligned} \beta _a&= \max \{\alpha _a, 0\}, \quad a \in A _\mathrm {cm},\\ \beta _a&= \max \{-\alpha _a, 0\}, \quad a \in A _\mathrm {cv},\\ {\delta }^+_{w_1}&=1,\ {\delta }^+_u = 0, \quad u \in V \setminus \{{w_1}\},\\ {\delta }^-_{w_2}&=1,\ {\delta }^-_u = 0, \quad u \in V \setminus \{{w_2}\}, \end{aligned}$$

for all pairs of nodes $({w_1},{w_2})\in V ^2$.

Proof

By Lemma 6.1, Constraints (13) uniquely determine $\alpha$ as a function of ${\delta }^+$ and ${\delta }^-$. Furthermore, for every feasible point of (8), the constraints

$$\begin{aligned} \beta _a&\ge \max \{\alpha _a, 0\}, \quad a \in A _\mathrm {cm},\\ \beta _a&\ge \max \{-\alpha _a, 0\}, \quad a \in A _\mathrm {cv}, \end{aligned}$$

hold and have to be active at a vertex. It is therefore sufficient to determine the vertices of (8e) and (8f) in the space of ${\delta }^+$ and ${\delta }^-$, which are given by

$$\begin{aligned} {\delta }^+_{w_1}&=1,\ {\delta }^+_u = 0, \quad u \in V \setminus \{{w_1}\},\\ {\delta }^-_{w_2}&=1,\ {\delta }^-_u = 0, \quad u \in V \setminus \{{w_2}\}, \end{aligned}$$

for any pair of nodes $({w_1},{w_2})\in V ^2$. This concludes the proof. $\square$

Using this result and the network structure, we now elaborate on a representation of these vertices as follows. For any two nodes ${w_1}\in G _{j_1}$ and ${w_2}\in G _{j_2}$, we introduce for any $a = (G _i, G _j)\in A _{\mathrm {act}}^{0, \rightarrow }$,

$$\begin{aligned} \alpha _a ({w_1},{w_2})&\mathrel {{\mathop :}{=}}{\left\{ \begin{array}{ll} -1,&{} \text {if }G _{j_1}\in \mathcal {G}_{a}({G _j}), G _{j_2}\notin \mathcal {G}_{a}({G _j}), \\ 1,&{} \text {if }G _{j_1}\notin \mathcal {G}_{a}({G _j}), G _{j_2}\in \mathcal {G}_{a}({G _j}), \\ 0,&{} \text {otherwise,} \end{array}\right. } \end{aligned}$$

and for any $a = (G _i, G _j)\in A _{\mathrm {act}}^{0, \leftarrow }$,

$$\begin{aligned} \alpha _a ({w_1},{w_2})&\mathrel {{\mathop :}{=}}{\left\{ \begin{array}{ll} 1,&{} \text {if }G _{j_1}\in \mathcal {G}_{a}({G _i}), G _{j_2}\notin \mathcal {G}_{a}({G _i}), \\ -1,&{} \text {if }G _{j_1}\notin \mathcal {G}_{a}({G _i}), G _{j_2}\in \mathcal {G}_{a}({G _i}), \\ 0,&{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

Furthermore, for any $a \in A _{\mathrm {act}}$, we define

$$\begin{aligned} \beta _a ({w_1}, {w_2}) \mathrel {{\mathop :}{=}}{\left\{ \begin{array}{ll} \max \{\alpha _a ({w_1}, {w_2}), 0\},&{}\text {if }a \in A _\mathrm {cm}, \\ \max \{-\alpha _a ({w_1}, {w_2}), 0\},&{}\text {if }a \in A _\mathrm {cv}. \end{array}\right. } \end{aligned}$$

Before we give a closed-form expression of the lower-level optimal value function $\varphi$, we discuss an alternative way of representing $\alpha _a ({w_1}, {w_2})$ and $\beta _a ({w_1},{w_2})$. Recall that the set of active elements $A _{\mathrm {act}}$ is partitioned into the set of compressors $A _\mathrm {cm}$ and the set of control valves $A _\mathrm {cv}$. The sets $A _{\mathrm {act}}^{k, \rightarrow }$ and $A _{\mathrm {act}}^{k, \leftarrow }$ can be partitioned similarly. For all $a \in A _{\mathrm {act}}$, we then obtain

Consequently, it also holds

Using this representation of $\beta _a ({w_1}, {w_2})$, we obtain the closed form of the lower-level optimal value function stated in the following result.

Corollary 6.3

The optimal value function $\varphi$ of (7) is given by

(14)

Similar to the results obtained in Labbé et al. (2020) for passive networks, we can now establish a characterization of feasible bookings for networks (under Assumption 1) with linearly modeled active elements.

Theorem 6.4

Let $G = (V, A)$ be a weakly connected network satisfying Assumption 1. Then, the booking $b\in L$ is feasible if and only if $\phi _{{w_1}{w_2}}(b) \le {\pi }^+_{w_1}- {\pi }^-_{w_2}$ is satisfied for every pair of nodes $({w_1}, {w_2})\in V ^2$ with ${w_1}\in V (G _{j_1})$ and ${w_2}\in V (G _{j_2})$, where we define

Proof

As a consequence of Proposition 4.1 and Theorem 4.3, the booking $b$ is feasible if and only if the solutions of (12) satisfy $\varphi (\ell , q, \pi , s) \le 0$. By Corollary 6.3, the latter holds if and only if

for every pair of nodes $({w_1}, {w_2})\in V ^2$.

Observe that $\phi _{{w_1}{w_2}}(b) - ({\pi }^+_{w_1}- {\pi }^-_{w_2})$ is a lower bound for the solutions of (12). Thus, if the booking is feasible, $\phi _{{w_1}{w_2}}(b) \le {\pi }^+_{w_1}- {\pi }^-_{w_2}$ holds for every pair of nodes $({w_1}, {w_2})\in V ^2$. On the contrary, if the booking is infeasible, there exists a feasible point $(\ell , q, \pi , s)$ of (UL) and a pair of nodes $({w_1}, {w_2})\in V ^2$ such that $\varphi (\ell , q, \pi , s) > 0$ holds, i.e.,

In particular, we also have $\phi _{{w_1}{w_2}}(b) > {\pi }^+_{w_1}- {\pi }^-_{w_2}$. $\square$

The optimal-value-function reformulation  (12), where $\varphi$ is given by (14), requires optimizing a piecewise-linear function with $|V |^2$ pieces over a nonlinear and nonconvex feasible domain. Using the characterization given in Theorem 6.4, all $|V |^2$ linear pieces can be optimized in individual subproblems.

6.2 Reduced optimal value function

Since the lower level mainly controls active elements that link passive subnetworks, it is possible to give a coarser interpretation of the lower-level optimal value function. The main intuition now is to consider the lower level as a problem on the reduced network ${\tilde{G}}$. By grouping all nodes of a passive subnetwork, we can rewrite the lower-level optimal value function, yielding

(15)

Then, applying the same arguments as in the proof of Theorem 6.4, we deduce a characterization with fewer subproblems to be solved.

Corollary 6.5

Let $G = (V, A)$ be a weakly connected network satisfying Assumption 1. Then, the booking $b\in L$ is feasible if and only if $\phi _{j_1j_2} (b) \le 0$ is satisfied for every pair of passive subnetworks $(G _{j_1}, G _{j_2})\in {\mathcal {G}}^2$, where $\phi _{j_1j_2} (b)$ is defined by

We introduce variables $\theta ^+_{j}$ and $\theta ^-_{j}$ for every $G _j \in {\mathcal {G}}$ that satisfy

$$\begin{aligned} \theta ^+_{j}&= \max _{u \in V (G _j)} \left\{ \pi _u- {\pi }^+_u \right\} , \end{aligned}$$

(16a)

$$\begin{aligned} \theta ^-_{j}&= \max _{u \in V (G _j)} \left\{ {\pi }^-_u- \pi _u \right\} . \end{aligned}$$

(16b)

The optimal value function (15) then is a piecewise-linear function with $(|A _{\mathrm {act}}|+1)^2$ pieces. For $G _j\in {\mathcal {G}}$, $\theta ^+_{j}$ and $\theta ^-_{j}$ are also piecewise-linear functions with each $|V (G _j)|$ pieces. The characterization in Corollary 6.5 requires optimizing $(|A _{\mathrm {act}}|+1)^2$ pieces of (15) separately, under the additional Constraint (16a) for $G _{j_1}\in {\mathcal {G}}$ and Constraint (16b) for $G _{j_2}\in {\mathcal {G}}$.

6.3 Separable optimal value function

Still considering the lower level as a problem defined on the reduced network ${\tilde{G}}$, we derive a third closed-form expression of the lower-level optimal value function $\varphi$. We can go one step further to reduce the number of subproblems in a characterization from $(|A _{\mathrm {act}}|+1)^2$ to $|A _{\mathrm {act}}|+1$. Instead of considering every pair of subnetworks $(G _{j_1},G _{j_2})\in {\mathcal {G}}^2$ directly, the intuition is to first consider a third subnetwork $G _k$ acting as an intermediary and then to treat $(G _{j_1},G _k)$ and $(G _k,G _{j_2})$ separately. Note that for any three subnetworks $G _{j_1}, G _k, G _{j_2}\in {\mathcal {G}}$, it holds that

(17)

where equality holds if $G _k$ lies on the path . Figure 3 illustrates this relation for $G _{j_1}=G _3, G _k=G _0, G _{j_2}=G _2$. Here, the arc $(G _0, G _1)$ appears in the right-hand side of (17), while clearly not lying on .

Fig. 3

Illustration of (17)

The previous observation allows us to prove the following result.

Lemma 6.6

For every $G _k\in {\mathcal {G}}$, it holds $\varphi \ge \varphi ^k$, where we define

(18)

for every feasible point $(\ell , q, \pi , s)$ of (UL).

Proof

Given that ${\Delta }^+_a s_a \ge 0$ for all $a \in A _{\mathrm {act}}$, (17) implies that $\varphi (\ell , q, \pi , s)$ is bounded from below by

For given $G _k$, the elements of the latter $\max$-operator are separable w.r.t. $(G _{j_1}, {w_1})$ and $(G _{j_2}, {w_2})$. Consequently, the joint $\max$-operator can be split, which concludes the proof. $\square$

Based on this result, we can derive the third closed form of the lower-level optimal value function $\varphi$ by considering all $G _k\in {\mathcal {G}}$ and $\varphi ^k$.

Theorem 6.7

The optimal value function $\varphi$ of (7) is given by

$$\begin{aligned} \max _{G _k\in {\mathcal {G}}} \ \varphi ^k, \end{aligned}$$

(19)

where $\varphi ^k$ is defined in (18).

Proof

By Lemma 6.6, $\varphi \ge \max _{G _k\in {\mathcal {G}}}\varphi ^k$ holds. Let $(\ell , q, \pi , s)$ be feasible for (UL). Furthermore, let $(G _{j_1}, G _{j_2}, {w_1}, {w_2})$ be the maximizer defining $\varphi (\ell , q, \pi , s)$. For $G _k$ on the path , equality holds in (17). Thus,

$$\begin{aligned} \max _{G _k\in {\mathcal {G}}} \ \varphi ^k(\ell , q, \pi , s) = \varphi (\ell , q, \pi , s). \square \end{aligned}$$

Again, we can solve several subproblems independently and obtain the third characterization.

Corollary 6.8

Let $G = (V, A)$ be a weakly connected network satisfying Assumption 1. Then, the booking $b\in L$ is feasible if and only if $\phi _{k} (b) \le 0$ is satisfied for a passive subnetwork $G _k\in {\mathcal {G}}$, where

$$\begin{aligned} \phi _{k} (b)= \max _{\ell , q, \pi , s} \left\{ \varphi ^k(\ell , q, \pi , s):(\text {UL})\right\} . \end{aligned}$$

We introduce variables $\vartheta ^+_{k}$ and $\vartheta ^-_{k}$ for every $G _k\in {\mathcal {G}}$ that satisfy

(20a)

(20b)

The optimal value function $\varphi$ as defined in Theorem 6.7 then is a piecewise-linear function with $|A _{\mathrm {act}}|+1$ pieces. For $G _k\in {\mathcal {G}}$, $\vartheta ^+_{k}$ and $\vartheta ^-_{k}$ are also piecewise linear with $|V |$ pieces each. The characterization of Corollary 6.8 considers $|A _{\mathrm {act}}|+1$ linear objectives. For each subproblem for $G _k\in {\mathcal {G}}$, only the additional constraints (20) corresponding to $G _k$ are required.

As a closing remark, we discuss how the formulations and characterizations presented in this section can be implemented using standard linearization techniques for the max-operators.

Remark 6.9

(Linerization of max-operators) We have seen that the lower-level optimal value function is a piecewise-linear function that is convex and that needs to be maximized over a nonconvex domain. To model the max-operators involved in the different models of $\varphi$, we make use of the following classical technique. For a finite index set $I$, we want to model $\max _{i\in I} \{f_i\}$. To this end, we introduce binary variables $u_i$ for all $i\in I$ and let $L, U\in \mathbb {R}$ be chosen such that $L\le f_i\le U$ holds for every $i\in I$. Then, $g=\max _{i\in I} \{f_i\}$ holds if and only if

$$\begin{aligned}&f_i\le g\le f_i+ (U-L)(1-u_i), \quad i\in I, \end{aligned}$$

(21a)

$$\begin{aligned}&\sum _{i\in I} u_i= 1,\ u_i\in \{0,1\}, \quad i\in I. \end{aligned}$$

(21b)

This reformulation can be applied to all three variants (14), (15), and (19) of the lower-level optimal value function. The appropriate big-M values $L,U\in \mathbb {R}$ can be easily derived from the results of Sect. 5.2. By doing so, the three representations of the lower-level optimal value function $\varphi$ (and the characterizations derived from them) can be modeled as MINLPs.

7 Computational experiments

In this section, we evaluate the performance of the different approaches developed in this paper. In Sect. 7.3, the presented nonlinear potential-based flow model is studied. In order to better evaluate the performance of our methods and to eliminate challenging nonlinearities, we additionally study a simplified linear potential-based flow model in Sect. 7.4. We compare the KKT reformulation with the three optimal-value-function reformulations and the three characterizations derived in Sect. 6. The columns Method and Definition of Table 1 give a short overview regarding the considered methods including their abbreviations used throughout this section.

Table 1 Overview of methods and model statistics

7.1 Data

Our case study is based on two instances of the GasLib (Schmidt et al. 2017) and different corresponding bookings. On the one hand, we study GasLib-134 (version 2), which is a tree-shaped network with 134 nodes, one compressor, and one control valve. It roughly represents the Greek gas network. The flow thresholds $m$ are set to 0 for the compressor and to $-10^{-2}$ for the control valve. The latter value is chosen to guarantee the feasibility of the zero nomination in GasLib-134. Since the zero nomination is always booking-compliant, its feasibility is a necessary condition for the feasibility of any booking. Bookings for networks in the GasLib can be obtained by setting the corresponding nominations contained in the GasLib as bookings. For GasLib-134, these nominations reflect actual demand scenarios over several years in the past. We selected three random nominations over the year to consider different demands. In particular, we study bookings derived from the nominations 2011-11-06, 2012-07-22, and 2014-10-24.

On the other hand, we consider the GasLib-40 network for which we have replaced one compressor by a pipe to satisfy Assumption 1. This results in a network with six fundamental cycles, 40 nodes, and five compressors. All flow thresholds $m$ are set to 0. As before, we derive one booking, denoted by 0–0, from the single GasLib nomination. This booking then serves as a base for the generation of additional bookings. To do so, we slightly vary the booking at entries and exits as follows. For parameters $\mu _1,\mu _2\in (0,100)$ and node $u \in V$, we obtain a new booking ${\tilde{b}}$, denoted ${\mu _1}-{\mu _2}$, by uniformly sampling a random integer in

$$\begin{aligned} {\tilde{b}}_u \in {\left\{ \begin{array}{ll} \left[ \frac{100-\mu _1}{100}b_u, \frac{100+\mu _1}{100}b_u \right] , &{}\text {if }u \in V_+,\\ \left[ \frac{100-\mu _2}{100}b_u, \frac{100+\mu _2}{100}b_u \right] , &{}\text {if }u \in V_-,\\ \{0\},&{} \text {if }u \in V_0, \end{array}\right. } \end{aligned}$$

where $b$ is the initial booking 0–0. For GasLib-40, we generate three additional bookings for $(\mu _1,\mu _2)\in \{(10,10),(1,20),(10,5)\}$. Note that in this way, we obtain bookings that are not balanced, which is in contrast to the bookings derived from GasLib nominations.

7.2 Computational setup

All models have been implemented in Python  3.8.0 using Pyomo  5.7.1 (Hart et al. 2017). We performed all computations using the Kaby Lake nodes with 32 GB RAM of the compute cluster Regionales Rechenzentrum Erlangen (2021). The time limit is 2 h.

In Sect. 7.3, when treating nonlinear gas physics, we use ANTIGONE  1.1 (Misener and Floudas 2014) and BARON  17.4 Tawarmalani and Sahinidis 2005) within GAMS  24.8 (GAMS Development Corporation 2020) to solve the occurring MINLPs. We perform the computations on a single thread and set the optCr parameter in GAMS to $10^{-4}$. In Sect. 7.4, we use Gurobi  9.0.1 (LLC Gurobi Optimization 2020) to solve linear approximations of the gas physics. We again perform computations on a single thread and set Gurobi parameters IntFeasTol to $10^{-9}$ and NumericFocus to 3.

We now discuss some statistics of our models, which are summarized in Table 1. To solve the single-level reformulations, a single optimization problem needs to be solved, whereas characterizations require solutions of multiple subproblems. The columns Subproblems present the number of optimization problems to be solved for each method w.r.t. the GasLib-134 and GasLib-40 networks. As we can see in Table 1, the number of subproblems drastically differs for the considered characterizations. This is due to the fact that F-CHAR consists of $|V |^2$ many subproblems, whereas the other two characterizations R-CHAR and S-CHAR consist of $(|A _{\mathrm {act}}|+1)^2$ and  $(|A _{\mathrm {act}}|+1)$ subproblems. A reduced number of subproblems comes, however, at the cost of additional binary variables. All models are implemented in their linearized form, i.e., KKT ’s complementarity constraints have been linearized as discussed in Sect. 5.2 and for all other models, the linearization (6.9) of the max-operators is used. The Binaries columns indicate the maximum number of additional binary variables (other than the $|A _{\mathrm {act}}|$ binary variables $s$) required for the linearization of a subproblem. Among all optimal-value-function reformulations, i.e., F-OVF, R-OVF, and S-OVF, we can observe that R-OVF contains the smallest number of binary variables, which is comparable to the number of binary variables for KKT. Regarding the characterizations, there is a clear trade-off between the number of subproblems and the number of binary variables, for which we later see that the large number of subproblems in F-CHAR is a computational disadvantage.

We finally note that all subproblems of the characterizations are solved iteratively without warm-starts. Thus, we do not exploit that all characterizations can be fully parallelized since all subproblems can be solved independently. The actual parallelization of the approaches based on the characterizations is out of the scope of this paper. However, to take this aspect into account during the discussion of our results, we discuss, besides the total sequential time, also an idealized parallel time, i.e., the maximum time required to solve a single subproblem.

7.3 The nonlinear case

Table 2 lists the results for the GasLib-134 network and the 2011-11-06 booking. Method indicates the method from Table 1. Vio. represents the obtained violation, i.e., for single-level reformulations the optimal value of the problem and for the characterizations the maximum violation of any bound on the optimal solutions of the corresponding subproblems. Thus, this column denotes the measure of feasibility of a booking. Positive values indicate violated potential bounds and thus the infeasibility of a booking. On the other hand, nonpositive values indicate that all booking-compliant nominations can be transported within the potential bounds, which implies the feasibility of a booking. Sol. gives the running time in seconds for single-level reformulations. Min., Med., and Max. denote the minimum, median, and maximum running times (in seconds) necessary for solving a single characterization subproblem and checking whether the corresponding bound on the optimal solution is satisfied. Finally, Total reports the total time, which for characterizations is equal to the time spent in the sequential treatment of all subproblems. If an instance could not be solved within the time limit of ${2}\,\hbox {h}$, then we represent it by “–” in the corresponding row of the table.

Table 2 Results for GasLib-134 and the 2011-11-06 booking in the nonlinear case

Unfortunately, the solvers do not give consistent results although all violations are negative, i.e., the booking seems to be feasible. The runs using BARON for R-OVF and S-OVF deviate from the common answer of all other combinations of methods and solvers. In particular, the optimal solution has been cut off from the search space at some point during the spatial branching. Consequently, we have to interpret the obtained results by BARON with great caution. On the other hand, we can analyze the trend presented by ANTIGONE. F-OVF and F-CHAR need the most time, which is expected since they have the most binary variables and subproblems, respectively. Although, the idealized parallel time of F-CHAR, i.e., 3.17s, is faster than the total time of KKT, it should not be forgotten that for GasLib-134, we need to solve 17,956 subproblems. Here, the only method slightly outperforming KKT is R-OVF. The latter has approximately the same number of additional binary variables as KKT, while S-OVF requires more binary variables. Concerning the corresponding methods using the characterizations, we observe that R-CHAR and S-CHAR are outperformed both w.r.t. the total sequential time and the idealized parallel time. Although, they require fewer subproblems to be solved than F-OVF, they admit additional binary variables to be branched on. For some subproblems, the solvers struggle to prove optimality. While the median time is good, there exist some outlier problems that require a long time to close the duality gap. As for the bookings 2012-07-22 and 2014-10-24, the general trends are similar although there are some outliers. KKT performs comparatively slow when considering the 2012-07-22 booking and using ANTIGONE. Similarly, S-OVF performs worse with ANTIGONE, whereas BARON follows the previous trend. For the sake of brevity, we include the tables corresponding to GasLib-134 and the 2012-07-22 and 2014-10-24 bookings in “Appendix A”.

For GasLib-40, we are not able to generate meaningful results within the time limit of 2 h. We generally have to conclude that the problem at hand is numerically very unstable and hard to handle for the used nonlinear solvers. Some models could still be solved relatively fast, in particular the KKT model. However, the solvers often incorrectly certify optimality or get stuck in suboptimal solutions, not being able to close the duality gap. One possible explanation for this higher instability could be the cyclic structure of GasLib-40. To test this hypothesis, we generated variants of GasLib-134 with added cycles and compared them to the original tree network for the 2011-11-06 booking. We considered the GasLib-134 network with two, four, and six fundamental cycles added inside the passive subnetwork between both active elements. On the one hand, discrepancies between the results of ANTIGONE and BARON become more frequent with an increasing number of cycles. Furthermore, on the example of solving KKT using ANTIGONE, the running times for the GasLib-134 network with two, four, and six cycles are 42.64s, 871.41s, and 6553.46s, respectively. We thus observe a significant increase compared to the running time of 6.93s for the original GasLib-134 network.

The spatial branching on the nonlinear gas physics in addition to the branching on linearized piecewise-linear functions leads to very challenging problems, which would require further tuning of the MINLP solvers. This is, however, out of the scope of this case study. To compare our methods, we have thus resorted to analyzing linear approximations of gas physics as presented in the next section.

7.4 The linear case

Except for the nonlinear gas physics at the right-hand side of (1b), all considered models are linear with mixed-integer variables. In this section, we consider linear approximations of gas physics to obtain mixed-integer linear problems (MILP) to be solved by Gurobi. To this end, we replace $|q _a |$ for every $a \in A_{\mathrm {pipe}}$ by $cM$, where $c\in (0, 1]$ is a scaling factor and $M\mathrel {{\mathop :}{=}}\min \{\sum _{u \in V_+} b_u, \sum _{u \in V_-} b_u \}$ is an upper bound on the flow on each arc. Thus, we replace Constraints (1b) with

$$\begin{aligned} \pi _{u} - \pi _{v} = \xi _a q _a, \quad \xi _a = c\Lambda _a M, \quad a = (u,v) \in A_{\mathrm {pipe}}. \end{aligned}$$

Table 3 shows the results for GasLib-134 and the 2011-11-06  booking, where Appr. indicates the different scaling factors $c\in \{0.2, 0.4, 0.6, 0.8, 1.0\}$. F-OVF is clearly outperformed by the shown methods. The same holds for F-CHAR both w.r.t. the total sequential time and the idealized parallel time. Consequently, we choose to omit both methods in the tables.

Table 3 Results for GasLib-134 and the 2011-11-06 booking in the linear case

Table 4 Results for GasLib-40 and the 0–0 booking in the linear case

First, we observe that all methods present consistent results in the linear case. Additionally, for increasing scaling factors $c$, the resulting violations also increase. This trend is easily explained by the fact that a large scaling factor leads to a larger potential drop along all pipes, which again results in larger overall potential differences. In particular, the booking is feasible for $c\in \{0.2, 0.4\}$ and becomes infeasible for larger scaling factors. We observe that for all scaling factors, KKT is performing well. Although slightly faster, R-OVF does not significantly outperform KKT. Similarly, S-OVF admits running times comparable to KKT, but is the slowest among the presented methods, which can be explained by its large number of binary variables necessary for the complete linearization of the optimal value function (19). Concerning the methods using the characterizations, the sequential time necessary to solve R-CHAR and S-CHAR is of the same order of magnitude as KKT. When considering the idealized parallel time, R-CHAR and S-CHAR are the clear winners. To obtain these idealized parallel times, 9 and 3 subproblems need to be solved in parallel, respectively. In that regard, R-CHAR is the fastest method for four scaling factors and only takes a little longer for $c=0.4$, where S-CHAR is slightly faster. Again, similar trends can be observed for the remaining bookings of GasLib-134. We therefore do not explicitly discuss the corresponding results, but list them in “Appendix B”.

Table 4 shows the results for GasLib-40 and booking 0–0. In contrast to GasLib-134, F-OVF and F-CHAR are more competitive for GasLib-40, which has fewer nodes and thus both methods require fewer binary variables (for the linearizations) or subproblems; see Table 1. However, the cyclic structure of GasLib-40 makes the problem of checking the feasibility of a booking more challenging. In our experiments, S-OVF is not able to find a provably optimal solution and has thus been omitted from this table. For $c\in \{0.4, 0.6, 0.8, 1.0\}$, the optimal solution was found by S-OVF, however the duality gap could not be closed during the time limit. Overall, we observe more variability in running times across different scaling factors $c$ for all methods. In terms of total time, i.e., the sequential time for characterizations, KKT is the fastest method. In terms of idealized parallel time, i.e., the maximum time necessary to solve a single subproblem, all three characterizations outperform KKT. Note that we still have to solve 1600 subproblems for F-CHAR, although all individual computations can be done in at most 0.5s for $c\in \{0.2, 0.4, 0.6, 1.0\}$ and in roughly 1s for $c=0.8$. If computations can be fully parallelized, i.e., a sufficient number of cores are available to solve all subproblems in parallel, R-CHAR is the most adequate method for GasLib-40 to obtain a beneficial trade-off between the small number of subproblems to be solved and the number of additional binary variable in each subproblem. On the other hand, S-CHAR requires more time for each subproblem, at the benefit of very few subproblems to be solved and can thus still outperform KKT if fewer parallel computing resources are available.

To eliminate the possibility that the interpretation of the previous results are purely linked to the balancedness of bookings generated from nominations of the GasLib, we have additionally studied the three perturbed bookings 10–10, 1–20, and 10–5. Qualitatively, the results follow the discussion of the booking 0–0. The corresponding tables are thus listed in “Appendix C”.

As a final discussion, note that all of the methods studied in this paper also allow for preemptive decisions without the need to solve the models to optimality. For each single-level reformulation, whenever a relaxation produces a nonpositive value, we can stop the computation and certify that the booking is feasible. Similarly, whenever a feasible point of positive violation is found, the booking is infeasible with the certificate given by the corresponding infeasible nomination. For showing the infeasibility of a booking, the same logic can be extended to characterizations. As soon as a feasible point of one subproblem with positive violation has been found, we can stop and certify that the booking is infeasible. This can be useful especially in practice, since TSOs generally have additional knowledge regarding their networks and are aware of their bottlenecks. With this knowledge at hand, it could be possible to check specific individual subproblems to identify infeasible nominations that lead to a rejection of the considered booking request. In case of a feasible booking, all subproblems must be solved. They can however be terminated early, based on a nonpositive value of a relaxation.

8 Conclusion

The problem of deciding the feasibility of a booking in the European entry-exit gas market has been studied mostly for passive networks up to now. In this paper, we considered networks with linearly modeled active elements that do not lie on cycles of the network. By doing so, we present a first stepping stone towards the study of more general networks and more general models of active elements. The approaches for verifying the feasibility of a booking in passive networks are not directly applicable to the case of networks with active elements, as discussed in Sect. 3. Thus, we have then presented a bilevel optimization model, in which the upper-level player chooses a nomination that is most difficult to transport and the TSO at the lower level uses the active elements to transport this nomination. Consequently, the bilevel structure results from the fact that the TSO takes a decision individually for every nomination by controlling the active elements appropriately. We studied both the classical KKT reformulation and problem-specific optimal-value-function reformulations. More precisely, we have given three optimal-value-function reformulations giving rise to three equivalent characterizations of feasible bookings, which generalize the characterization in Labbé et al. (2020) for passive networks. Our case studies show that the KKT approach is already a very well performing method to check the feasibility of a booking. It also shows that the more problem-specific approaches of Sect. 6 can sometimes outperform the KKT approach, especially when parallel computing resources are available. It should, however, be noted that the applicability of these methods depends on the structure of the network at hand. In particular, the number of binary variables for the linearizations and the number of subproblems to be solved in the characterizations vary significantly. They are determined by the number of active elements and nodes. Thus, the best-performing method among the various optimal-value-function reformulations and characterizations strongly depends on the considered network.

In general, the methods developed in this paper can be used as a decision-support system in the planning departments of TSOs that decide on the signing or the rejection of booking requests. In practice, the validation of such a booking request is usually based on checking expert scenarios via simulation tools. In this regard, our methods can help to automatically generate such expert scenarios that are hard to transport within the technical restrictions of the network. Obviously, this is only possible if the network satisfies the assumptions made in this paper and, thus, there is still a lot to do in order to automate the process of validating bookings.

For future work, it will be interesting to study networks without specific assumptions on the location of the active elements, as well as more general models for the active elements. However, even in the setting of this paper, some challenges still need to be tackled. It is required to develop problem-specific solution approaches, especially for the case of nonlinear gas physics. Similar to the studies in Robinius et al. (2019); Labbé et al. (2020) for tree-shaped and in Labbé et al. (2021) for single-cycle networks, algorithms to solve the nonlinear subproblems of the characterizations presented in this paper can be beneficial. Finally, the analyses of the European gas market models studied in Böttger et al. (2021); Schewe et al. (2020) can be extended to take into account linearly modeled active elements by integrating the novel characterizations of feasible bookings presented in this paper.

Appendices

Appendix A: Results for the nonlinear case

See Tables 5 and 6.

Table 5 Results for GasLib-134 and the 2012-07-22 booking

Table 6 Results for GasLib-134 and the 2014-10-24 booking

Appendix B: Results for GasLib-134 in the linear case

See Tables 7 and 8.

Table 7 Results for GasLib-134 and the 2012-07-22 booking

Table 8 Results for GasLib-134 and the 2014-10-24 booking

Table 9 Results for GasLib-40 and the 10–10 booking

Appendix C: Results for GasLib-40 in the linear case

See Table 9, 10 and 11.

Table 10 Results for GasLib-40 and the 1–20 booking

Table 11 Results for GasLib-40 and the 10–5 booking