1 Introduction

The problem of packing rectangles into rectangular containers or to cut them from rectangular stock sheets arises in a variety of industrial applications. Thereby, one typically aims at determining a feasible solution where the wasted material or space is minimized. Consider for example the paper (Haessler 1971), glass (Hahn 1968), wood (Bouaine et al. 2018), or metal industry (Jakobs 1996). Here, rectangular pieces are needed for the production of certain goods, which are typically cut from given stock pieces (He et al. 2012). Another common application arising in logistics is to load pallets or containers (Huang and Chen 2007). Furthermore, similar problems appear in the production and operation of microchips, namely in the layout of processor chips (Wu and Chan 2005) and the dynamic allocation of memory as well as in multiprocessor scheduling (He et al. 2012). Finally, the editing and lay-outing of newspapers (Wei et al. 2009) or the arrangement of products on supermarket shelves (Problem description 2019) belong to this class of problems, too. They are typically modeled as some special variant of the two-dimensional Knapsack Problem (2D-KP), which we introduce in Sect. 2 and discuss in depth in Sect. 3.

However, for practitioners it is often useful when they are presented not only one optimal but a set of diverse “near-optimal” solutions from which she or he can choose. This holds especially for those tasks where it is hard to formalize or model important side constraints. Consider, for example, the last two examples from above. If a supermarket wants to investigate the buying behavior of its customers, an arrangement of the products minimizing the empty space is certainly desirable. Nevertheless, such a result on its own is not very meaningful for the particular task. Instead, the company needs to conduct tests with a variety of arrangements to assess whether they increase the purchasing rates or not (Kök et al. 2015). Similarly, when it comes to the layout of texts, pictures, or ads on a newspaper page, the result does not necessarily have to be minimal w.r.t. the resulting empty space, but has to come in some aesthetic appeal. Thus, presenting the user with a selection of assortments that cover some minimum threshold of the available area can be advantageous in all areas where experiences and subjective perceptions have an impact on the solution that is finally chosen.

Problems of this kind motivate the Maximum Diversity Assortment Selection Problem (MDASP), which we introduce in Sect. 2. Next, we review the literature on two inherent subproblems in Sect. 3: The above mentioned 2D-KP and the Maximum Diversity Problem (MDP), where a predefined number of elements has to be selected from a given set such that the diversity among them is maximized. Before discussing a mixed-integer quadratic programming (MIQP) model for MDASP in Sect. 5, we introduce MIQP formulations to determine upper bounds on the maximum diversity in Sect. 4. Furthermore, we present a generic two-stage heuristic in Sect. 6. Finally, we present extensive computational experiments in Sect. 7 and conclude with an outlook on future research in Sect. 8.

2 Definitions and problem setup

For MDASP we are given a rectangle with width \(w \in {\mathbb {Z}}_{\ge 0}\) and height \(h \in {\mathbb {Z}}_{\ge 0}\), which we call container. Furthermore, we are given a set of rectangles \({\mathcal {R}} :=\{R_1,\ldots ,R_n\}\) and each of them is associated with its width \(w_i \in {\mathbb {Z}}_{\ge 0}\) and its height \(h_i \in {\mathbb {Z}}_{\ge 0}\). Next, an assortment is a subset \({\mathcal {A}} \subseteq {\mathcal {R}}\) of rectangles, i.e., \({\mathcal {A}} \in {\mathcal {P}}({\mathcal {R}})\) where \({\mathcal {P}}({\mathcal {R}})\) denotes the powerset of \({\mathcal {R}}\). We call an assortment \({\mathcal {A}}\) feasible if it can be placed in the container \({\mathcal {C}}\) without overlapping, i.e., if we can assign a bottom-left corner coordinate \((x_i,y_i) \in {\mathbb {R}}^2\) to each rectangle \(R_i \in {\mathcal {A}}\) such that \(\left[ x_i,x_i + w_i \right) \times \left[ y_i,y_i + h_i \right) \subseteq [0,w) \times [0,h)\) and for all \(R_i,R_j \in {\mathcal {A}}\) with \(i \ne j\) we have \(\left[ x_i,x_i + w_i \right) \times \left[ y_i,y_i + h_i \right) \cap \left[ x_j,x_j + w_j \right) \times \left[ y_j,y_j + h_j \right) = \emptyset \), see Iori et al. (2020). In the sequel, we denote the set of all feasible assortments by \({\mathcal {F}}\). Next, each assortment \({\mathcal {A}}\) has an associated value \(v({\mathcal {A}}) = \sum \nolimits _{R_i \in {\mathcal {A}}} w_i h_i\), which is the sum of the areas of the rectangles it contains. We call an assortment \({\mathcal {A}}^*\) optimal if it is feasible and if \(v({\mathcal {A}}^*) \ge v({\mathcal {A}})\) holds for every \({\mathcal {A}} \in {\mathcal {F}}\). Determining an optimal assortment is called the two-dimensional Knapsack Problem (2D-KP). Note that we otherwise allow an arbitrary placement of the rectangles inside the container, i.e., we do not impose any further conditions, and we do not allow the rotation of rectangles. An example can be found in Fig. 1.

Fig. 1
figure 1

Container \({\mathcal {C}}\) with rectangle set \({\mathcal {R}}\). Assortment \({\mathcal {A}}_1\) is feasible and \({\mathcal {A}}_2\) is even optimal. On the other hand, assortments \({\mathcal {A}}_3\) and \({\mathcal {A}}_4\) are not feasible

Full size image

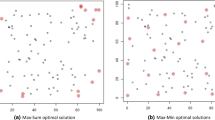
For MDASP we are furthermore given a threshold value \({\underline{v}}\in [0,v({\mathcal {C}})]\), with \(v({\mathcal {C}}) := wh\) denoting the area of the container, as well as a natural number \(m \in {\mathbb {N}}\) with \(m \ge 2\). We call an assortment \({\mathcal {A}}\) \({\underline{v}}\)-good if it is feasible and if \(v({\mathcal {A}}) \ge {\underline{v}}\), and we denote the set of \({\underline{v}}\)-good assortments by \({\mathcal {F}}_{{\underline{v}}} \subseteq {\mathcal {F}}\). Furthermore, a selection is a multi-subset \({\mathcal {S}}\) of assortments, i.e., we allow that an assortment is contained more than once in \({\mathcal {S}}\), of cardinality \(|{\mathcal {S}}| = m\). We call \({\mathcal {S}}\) feasible if all of its assortments are \({\underline{v}}\)-good, i.e., if \({\mathcal {A}} \in {\mathcal {F}}_{{\underline{v}}}\) for all \({\mathcal {A}}\in {\mathcal {S}}\). Additionally, we are given a diversity function \(\delta \) for selections and call \(\delta ({\mathcal {S}})\) the diversity of selection \({\mathcal {S}}\). The two diversity functions that we consider in this paper are based on the Hamming distances between assortment pairs contained in \({\mathcal {S}}\) and are discussed in Sect. 2.1. Finally, a selection \({\mathcal {S}}^*\) is called optimal if it is feasible and if \(\delta ({\mathcal {S}}^*) \ge \delta ({\mathcal {S}})\) holds for all feasible selections \({\mathcal {S}}\). An example selection is shown in Fig. 2. In the following, we denote an MDASP instance \({\mathcal {I}}\) as a quintuple \({\mathcal {I}} := ({\mathcal {C}}, {\mathcal {R}}, m, {\underline{v}}, \delta )\).

Fig. 2
figure 2

Example for a selection of size \(m = 6\) to the instance leung8 w.r.t. \(\delta _{min}\), and a given threshold of \({\underline{v}}= 0.923\) which is the optimal value to the corresponding 2D-KP. The instance contains 30 rectangles, and the obtained selection has a diversity of 0.778, which was the most diverse selection that we obtained for this instance. Nevertheless, the best bound we found on this instance had a value of 0.916, compare with computational results in Sect. 7

Full size image

Lemma 1

MDASP is NP-hard.

Proof

We prove this by reducing from 2D-KP, which is NP-hard, see Fekete and Schepers (2004) or Garey and Johnson (1979). Given an instance of 2D-KP with container \({\mathcal {C}}\) and rectangle set \({\mathcal {R}}\), for arbitrary m and \(\delta \) there exists a feasible assortment of value at least \({\underline{v}}\) if and only if there exists a feasible selection for the MDASP instance \({\mathcal {I}} := ({\mathcal {C}}, {\mathcal {R}}, m, {\underline{v}}, \delta )\). \(\square \)

2.1 Diversity of selections

A common distance measure applied to the subsets of a common superset is the Hamming distance (Hamming 1950). For two assortments \({\mathcal {A}}\) and \({\mathcal {A}}'\), the (normalized) Hamming distance is defined as

$$\begin{aligned} d_{H}({\mathcal {A}},{\mathcal {A}}') := \frac{|{\mathcal {A}}\,\triangle \,{\mathcal {A}}'|}{|{\mathcal {A}}| + |\mathcal {A'}|} = \frac{|({\mathcal {A}}\,\cup \,{\mathcal {A}}')\setminus ({\mathcal {A}}\,\cap \,{\mathcal {A}}')|}{|{\mathcal {A}}| + |\mathcal {A'}|}, \end{aligned}$$

where \(\triangle \) represents the symmetric difference of sets. Furthermore, we define \(d_{H}({\mathcal {A}},{\mathcal {A}}') = 0\) in case that \({\mathcal {A}} = \mathcal {A'} = \emptyset \). Note that we consider the normalized Hamming distance, i.e., we divide by \(|{\mathcal {A}}|+|{\mathcal {A}}'|\), in order to ensure that the number of rectangles forming the assortments has no impact on the distance. An example demonstrating this rationale is depicted in Fig. 3.

Fig. 3
figure 3

The Hamming distance without normalization between \({\mathcal {A}}_1\) and \({\mathcal {A}}_2\) is 2, while the distance between \({\mathcal {A}}_3\) and \({\mathcal {A}}_4\) is 4. Using normalization, \({\mathcal {A}}_1\) and \({\mathcal {A}}_2\) have maximum distance 1, while the distance between \({\mathcal {A}}_3\) and \({\mathcal {A}}_4\) is \(\frac{1}{3}\)

Full size image

Lemma 2

Let \({\mathcal {I}} := ({\mathcal {C}}, {\mathcal {R}}, m, {\underline{v}}, \delta )\) be an MDASP instance. For any two assortments \({\mathcal {A}} \subseteq {\mathcal {R}}\) and \({\mathcal {A}}' \subseteq {\mathcal {R}}\) we have \(d_H({\mathcal {A}},{\mathcal {A}}')\in [0,1].\)

Based on the Hamming distance, we define two diversity functions for selections. Therefore, we denote the index set of the assortments of a selection by \(M := \{1,\dots ,m\}\) and introduce the Minimum-Distance-Diversity as

$$\begin{aligned} \delta _{min} ({\mathcal {S}}) := \min \limits _{\begin{array}{c} i,j \in M\\ i < j \end{array}} \{ d_H ({\mathcal {A}}_i, {\mathcal {A}}_j) \} \end{aligned}$$

and the Average-Distance-Diversity as

$$\begin{aligned} \delta _{avg} ({\mathcal {S}}) := \frac{2}{m (m - 1)} \sum \limits _{i = 1}^{m-1} \sum \limits _{j = i+1}^{m}d_H({\mathcal {A}}_i,{\mathcal {A}}_j). \end{aligned}$$

Lemma 3

Let \({\mathcal {I}} := ({\mathcal {C}}, {\mathcal {R}}, m, {\underline{v}}, \delta )\) be an MDASP instance and let \({\mathcal {S}}\) be a selection. Then \( 0 \le \delta _{min} ({\mathcal {S}}) \le \delta _{avg} ({\mathcal {S}}) \le 1.\)

Proof

$$\begin{aligned} \delta _{min} ({\mathcal {S}})= & {} \min \limits _{\begin{array}{c} i,j \in M\\ i< j \end{array}} \{ d_H ({\mathcal {A}}_i, {\mathcal {A}}_j) \} \\= & {} \frac{2}{m (m - 1)} \sum \limits _{k = 1}^{m-1} \sum \limits _{l = k+1}^{m}\min \limits _{\begin{array}{c} i,j \in M\\ i < j \end{array}} \{ d_H ({\mathcal {A}}_i, {\mathcal {A}}_j) \} \\\le & {} \frac{2}{m (m - 1)} \sum \limits _{k = 1}^{m-1} \sum \limits _{l = k+1}^{m}d_H({\mathcal {A}}_k,{\mathcal {A}}_l) = \delta _{avg} ({\mathcal {S}}) \end{aligned}$$

\(\square \)

3 Related work and subproblems

MDASP has first been introduced in the 11th AIMMS-MOPTA Optimization Modeling Competition (AIMMS-MOPTA optimization 2019; Problem description 2019), which is part of the MOPTA conference series annually held at Lehigh University. To the best of our knowledge, there exists no previous work regarding it. Therefore, we give an overview of the literature concerning its two inherent subproblems instead: The two-dimensional Knapsack Problem (2D-KP) and the Maximum Diversity Problem (MDP).

As discussed in Sect. 1, the packing and cutting of rectangular items into or from rectangular containers arises in the context of many different applications. Thus, the 2D-KP is a topic that has been under investigation for a long time. According to Dowsland and Dowsland (1992), the first mathematical formulation of the problem was given by Kantorovich (1960) in 1939. Similar problem formulations were given by other authors during the 1950’s as the work of Kantorovich was not translated until 1960.

For a general overview over 2D-KP, we refer to the survey papers (Cheng et al. 1994; Crainic et al. 2012; Dyckhoff 1990; Hinxman 1980; Hopper and Turton 2001), and in particular to the most recent one by Iori et al. (2020). Further, it is important to note that the two-dimensional Cutting Stock Problem (2CSP) is closely related to 2D-KP. In fact, solution algorithms for 2CSP can also be applied to 2D-KP. However, as there exists a variety of different variants of 2D-KP, we want to emphasize the work of Wäscher et al. (2007) and Lodi et al. (1999) regarding their classification. The former is based on the typology used in Dyckhoff (1990). Here, the different rectangular packing problems are identified as, e.g., Bin Packing, Knapsack, or Cutting Stock Problems, and additionally classified according to their dimensionality and objective as well as by the size, shape, and characteristics of the rectangles. On the other hand, the classification of Lodi et al. is based on the side constraints that need to be satisfied, e.g., if the rectangles can be placed freely in the container or are allowed to be rotated. Further, there exist a weighted and an unweighted variant of 2D-KP. In the weighted case each rectangle is assigned a certain value, and the objective of the problem is to maximize the sum of the values of all placed rectangles. In the unweighted case, the value of each rectangle corresponds to its area. Thus, the objective here can either be seen as maximizing the area of all placed rectangles or as minimizing the empty or wasted space in the container. In this article we consider the unweighted variant of 2D-KP where the rectangles can be placed freely and are not allowed to be rotated.

In the literature, many mixed-integer programming (MIP) models exist for 2D-KP. For further details regarding MIP in general, we refer to Achterberg (2007). Hadjiconstantinou and Christofides (1995) introduced a formulation using the straightforward technique of discretizing the container. For each integer coordinate tuple in the container there exists a binary variable indicating if the corresponding point is already covered by a placed rectangle. Other MIP models featuring fewer variables and constraints using the relative positions of pairs of rectangles were introduced by Belov et al. (2009) and Egeblad and Pisinger (2009). The former approach is based on variables and corresponding constraints indicating whether two rectangles overlap when projected onto the x- or y-axis, from which at most one is allowed for a feasible assortment. The idea of the latter model is to use binary variables for each pair of rectangles to ensure that one of them is placed either over, under, left, or right of the other. Several other MIP formulations can be found in Beasley (1985), Gilmore and Gomory (1965), Hatefi (2017), Hifi (2001).

Furthermore, a variety of problem-specific Branch-and-Bound approaches has been developed (Christofides and Whitlock 1977; Clautiaux et al. 2007; Hifi and Zissimopoulos 1997). To improve their performance, Boschetti et al. (2002) present an upper bound, which can be used to significantly reduce the number of feasibility checks that have to be performed. Additionally, Fekete et al. (2007) introduce an approach to reduce the time that is needed for checking the feasibility of subsets of rectangles, i.e., whether it can be placed into the container and therefore forms a feasible assortment. They use graph structures to model equivalence classes of assortments and can determine if a certain rectangle subset is feasible or not by checking it for cycles and cliques. Their approach relies on a similar idea as the sequence-pair representation of rectangle-packings (Murata et al. 2003). Here, a possible packing is represented by two directed graphs encoding a sequence of the rectangles inside the container from left to right and from bottom to top, respectively. This idea was incorporated into solution approaches for 2D-KP, e.g., into the heuristics presented in Egeblad and Pisinger (2009), which extends (Pisinger 2007), where the representation is combined with a simulated annealing approach.

Next, we give a brief overview of the broad variety of heuristics and meta-heuristics that have been applied to 2D-KP. We start with deterministic algorithms, which are typically embedded in an iterative procedure applying different randomized orderings of the rectangles. The first type of heuristic used for 2D-KP are quasi-human algorithms that are inspired by the behavior of humans when solving a given problem. Consider, for example, the Least-Flexible-First algorithms of Wu et al. (2002), Wu and Chan (2005), and Huang and Chen (2007). The basic idea is to pack rectangles that are less flexible due to their size in the beginning, in order to have more flexibility when finishing up the packing. On the other hand, Wei et al. (2009) presented a Least-Waste-First heuristic where the rectangles are placed such that empty areas where no further rectangles can be placed are avoided. The third kind of placing procedures are so-called Best-Fit algorithms. In general, these heuristics are based on an evaluation function. Here, the rectangles are not only chosen and placed in a way such that the resulting empty space is as small as possible, but they also have to fit “well” with respect to the already placed ones. Examples for this type of heuristic can be found in the work of He et al. (2012), de Armas et al. (2012), and in particular in the IBHP heuristic of Shiangjen et al. (2018). The last deterministic approach we mention here is the Dynamic Decomposition algorithm of Wang (2017). His idea is to sequentially decompose the container into smaller parts, pack them with rectangles, and rearrange them afterwards.

As mentioned above, several meta-heuristics have also been applied to 2D-KP. The approaches can roughly be partitioned into Greedy Randomized Adaptive Search Procedures (GRASPs) (MirHassani and Jalaeian Bashirzadeh 2015; Perboli et al. 2011; Álvarez Valdés et al. 2005), TABU Searches (Álvarez Valdés et al. 2007), Genetic Algorithms (Beasley 2004; Bortfeldt and Winter 2009), and Simulated Annealing approaches (Egeblad and Pisinger 2009; Leung et al. 2012). Further, there exist hybrid heuristics that combine deterministic algorithms and meta-heuristics (Gonçalves 2007; Gonçalves and Resende 2006; Hadjiconstantinou and Iori 2007).

The second problem, which is implicitly contained in MDASP, is to select a predefined number of elements from a given set such that the diversity among them is maximized. In our case this is the set of \({\underline{v}}\)-good solutions \({\mathcal {F}}_{{\underline{v}}}\). This problem is known as the Maximum Diversity Problem or as Maximum Dispersion Problem (MDP) and is usually subdivided into the MAX-SUM and the MAX-MIN case. In the first case, the sum of the distances between the selected elements is maximized, while in the second case, one aims at maximizing the minimum distance between the chosen elements. This directly corresponds to our diversity measures \(\delta _{avg}\) and \(\delta _{min}\).

Surveys on MDP have been published by Martí et al. (2013) and Sandoya et al. (2018). As for 2D-KP, there exists a variety of exact approaches to model and solve MDP, including MIP and IQP formulations (Ghosh 1996; Kuo et al. 1993) as well as special Branch-and-Bound approaches (Martí et al. 2010). Furthermore, different meta-heuristics have been used to tackle the problem, including for example GRASP heuristics (Resende et al. 2010; Silva et al. 2007, 2004), TABU Searches (Duarte and Martí 2007), and the Iterated Greedy Approach (Lozano et al. 2011). Finally, there also exist hybrid algorithms (Gallego et al. 2009; Santos et al. 2005) and greedy heuristics (Ravi et al. 1994).

4 Upper bounds on the diversity

In this section, we introduce two MIQP formulations to derive upper bounds on the maximum diversity of MDASP instances w.r.t. \(\delta _{min}\) and \(\delta _{avg}\). The basic idea is to relax the problem by including assortments for which there may not exist a feasible placement in the container but that satisfy the \({\underline{v}}\)-criterion, i.e., assortments contained in \({\mathcal {G}}_{{\underline{v}}} := \{{\mathcal {A}} \in {\mathcal {P}}({\mathcal {R}})\, | \, {\underline{v}}\le v({\mathcal {A}}) \le v({\mathcal {C}})\}\).

To simplify notation, we use an alternative expression for the Hamming distance in the following, namely

$$\begin{aligned} d_{H}({\mathcal {A}},{\mathcal {A}}')= & {} \frac{|{\mathcal {A}}\,\triangle \,{\mathcal {A}}'|}{|{\mathcal {A}}| + |\mathcal {A'}|} = \frac{|{\mathcal {A}}| + |\mathcal {A'}| - 2 \, |{\mathcal {A}} \cap {\mathcal {A}}'|}{|{\mathcal {A}}| + |\mathcal {A'}|} = 1 - \frac{2 \, |{\mathcal {A}} \cap {\mathcal {A}}'|}{|{\mathcal {A}}| + |\mathcal {A'}|}. \end{aligned}$$

4.1 Bounding the minimum-distance-diversity \(\delta _{min}\)

Lemma 4

Let \({\mathcal {I}} := ({\mathcal {C}}, {\mathcal {R}}, m, {\underline{v}}, \delta _{min})\) be an instance of MDASP and let \({\mathcal {S}}\) denote a feasible selection for \({\mathcal {I}}\). Then

$$\begin{aligned} \delta _{min}({\mathcal {S}}) \le 1 - \min \limits _{ \{{\mathcal {A}}_1,\dots ,{\mathcal {A}}_m\} \subseteq {\mathcal {G}}_{{\underline{v}}}} \max \limits _{\begin{array}{c} i,j \in \{1,\dots ,m\}\\ i < j \end{array}} \left\{ \frac{2 \, |{\mathcal {A}}_i \cap {\mathcal {A}}_j|}{|{\mathcal {A}}_i| + |{\mathcal {A}}_j|} \right\} . \end{aligned}$$

Proof

From the definition of \(\delta _{min}\) and since \({\mathcal {F}}_{{\underline{v}}} \subseteq {\mathcal {G}}_{{\underline{v}}}\) it follows that

$$\begin{aligned} \delta _{min}({\mathcal {S}})&\le \max \limits _{ \{{\mathcal {A}}_1,\dots ,{\mathcal {A}}_m\} \subseteq {\mathcal {F}}_{{\underline{v}}}} \min \limits _{\begin{array}{c} i,j \in \{1,\dots ,m\}\\ i< j \end{array}} \{ d_{H}({\mathcal {A}}_i, {\mathcal {A}}_j)\} \nonumber \\&= \max \limits _{ \{{\mathcal {A}}_1,\dots ,{\mathcal {A}}_m\} \subseteq {\mathcal {F}}_{{\underline{v}}}} \min \limits _{\begin{array}{c} i,j \in \{1,\dots ,m\}\\ i< j \end{array}} \left\{ 1 - \frac{2 \, |{\mathcal {A}}_i \cap {\mathcal {A}}_j|}{|{\mathcal {A}}_i| + |{\mathcal {A}}_j|} \right\} \nonumber \\&= \max \limits _{ \{{\mathcal {A}}_1,\dots ,{\mathcal {A}}_m\} \subseteq {\mathcal {F}}_{{\underline{v}}}} \left\{ 1 - \max \limits _{\begin{array}{c} i,j \in \{1,\dots ,m\}\\ i< j \end{array}} \left\{ \frac{2 \, |{\mathcal {A}}_i \cap {\mathcal {A}}_j|}{|{\mathcal {A}}_i| + |{\mathcal {A}}_j|} \right\} \right\} \nonumber \\&= 1 - \min \limits _{ \{{\mathcal {A}}_1,\dots ,{\mathcal {A}}_m\} \subseteq {\mathcal {F}}_{{\underline{v}}}} \max \limits _{\begin{array}{c} i,j \in \{1,\dots ,m\}\\ i< j \end{array}} \left\{ \frac{2 \, |{\mathcal {A}}_i \cap {\mathcal {A}}_j|}{|{\mathcal {A}}_i| + |{\mathcal {A}}_j|} \right\} \nonumber \\&\le 1 - \min \limits _{ \{{\mathcal {A}}_1,\dots ,{\mathcal {A}}_m\} \subseteq {\mathcal {G}}_{{\underline{v}}}} \max \limits _{\begin{array}{c} i,j \in \{1,\dots ,m\}\\ i < j \end{array}} \left\{ \frac{2 \, |{\mathcal {A}}_i \cap {\mathcal {A}}_j|}{|{\mathcal {A}}_i| + |{\mathcal {A}}_j|} \right\} . \end{aligned}$$
(1)

\(\square \)

The following MIQP formulation \(\text {UB}_{min}\) determines expression (1), i.e., an optimal selection with respect to \(\delta _{min}\) in \({\mathcal {G}}_{{\underline{v}}}\). Its variables and their meanings are listed in Table 1.

$$\begin{aligned}&\max \quad 1 - z \quad \end{aligned}$$
(2)
$$\begin{aligned}&\text {s.t.} \quad \quad \sum \limits _{R_i \in {\mathcal {R}}} w_i h_i c_{i a} \ge {\underline{v}}\qquad \qquad \quad \forall \, a \in M \end{aligned}$$
(3)
$$\begin{aligned}&\qquad \qquad \sum \limits _{R_i \in {\mathcal {R}}} \, w_i h_i c_{i a} \le v({\mathcal {C}}) \,\, \qquad \qquad \forall \, a \in M \end{aligned}$$
(4)
$$\begin{aligned}&\sum \limits _{R_i \in {\mathcal {R}}} \, (c_{i a} + c_{i b}) = \, t_{a b}\, \, \qquad \qquad \forall \, a, b \in M \text { with } a < b \end{aligned}$$
(5)
$$\begin{aligned}&c_{i a} + c_{i b} \le 1 + s_{i a b}\,\,\qquad \qquad \forall \, R_i \in {\mathcal {R}}, \,\, \qquad \qquad \forall a,b \in M \text { with } a < b \end{aligned}$$
(6)
$$\begin{aligned}&\sum \limits _{R_i \in {\mathcal {R}}} \, s_{i a b} \le \frac{1}{2} \, z \,t_{a b}\,\,\qquad \qquad \qquad \qquad \forall \, a, b \in M \text { with } a < b \end{aligned}$$
(7)
$$\begin{aligned}&c_{i a} \in \{0,1\} \qquad \, \forall \, R_i \in {\mathcal {R}},\qquad \qquad \, \forall a \in M \end{aligned}$$
(8)
$$\begin{aligned}&s_{i a b} \in \{0,1\}\, \, \qquad \qquad \forall \, R_i \in {\mathcal {R}}, \,\, \qquad \qquad \forall a, b \in M \text { with } a < b \end{aligned}$$
(9)
$$\begin{aligned}&t_{a b} \in [0, \dots , 2|{\mathcal {R}}|] \qquad \qquad \forall \, a, b \in M \text { with } a < b \end{aligned}$$
(10)
$$\begin{aligned}&z \in [0,1] \end{aligned}$$
(11)

Constraints (3) and (4) ensure that the generated assortments are contained in \({\mathcal {G}}_{{\underline{v}}}\). Additionally, \(t_{a b}\) is equal to \(|{\mathcal {A}}_a|+|{\mathcal {A}}_b|\) due to constraint (5). Further, we have \(s_{i a b} = 1\) if assortments \({\mathcal {A}}_a\) and \({\mathcal {A}}_b\) share rectangle \(R_i\) due to constraint (6). Therefore, z is equal to the maximum value of \(\frac{2 \, |{\mathcal {A}}_a \cap {\mathcal {A}}_b|}{|{\mathcal {A}}_a|+|{\mathcal {A}}_b|}\) among all pairs \(a,b \in M\) with \(a < b\) due to constraints (7) and because we minimize it in the objective function (2). Note that we intentionally choose the \(s_{iab}\) variables to be binary as the gap of the MIQP was tighter for a majority of the instances when the time limit was hit. This may be because the solver may not figure out that the variables are implicitly binary and thus benefits from the additional integrality conditions.

Table 1 Variables for MIQP model \(\text {UB}_{min}\)
Full size table

4.2 Bounding the average-distance-diversity \(\delta _{avg}\)

The results from the previous subsection can also be adapted to \(\delta _{avg}\).

Lemma 5

Let \(({\mathcal {C}}, {\mathcal {R}}, m, {\underline{v}}, \delta _{avg})\) be an instance of MDASP and let \({\mathcal {S}}\) denote a feasible selection. It holds that

$$\begin{aligned} \delta _{avg}({\mathcal {S}}) \le 1 - \min \limits _{ \{{\mathcal {A}}_1,\dots ,{\mathcal {A}}_m\} \subseteq {\mathcal {G}}_{{\underline{v}}}} \frac{2}{m \, (m - 1)} \sum \limits _{i = 1}^{m-1} \sum \limits _{j = i+1}^{m} \frac{2 \, |{\mathcal {A}}_i \cap {\mathcal {A}}_j|}{|{\mathcal {A}}_i| + |{\mathcal {A}}_j|}. \end{aligned}$$

Proof

From the definition of \(\delta _{avg}\) and since \({\mathcal {F}}_{{\underline{v}}} \subseteq {\mathcal {G}}_{{\underline{v}}}\) it follows that

$$\begin{aligned} \delta _{avg}({\mathcal {S}})&\le \max \limits _{ \{{\mathcal {A}}_1,\dots ,{\mathcal {A}}_m\} \subseteq {\mathcal {F}}_{{\underline{v}}}} \frac{2}{m \, (m - 1)} \sum \limits _{i = 1}^{m-1} \sum \limits _{j = i+1}^{m}d_H({\mathcal {A}}_i,{\mathcal {A}}_j) \nonumber \\&= \max \limits _{ \{{\mathcal {A}}_1,\dots ,{\mathcal {A}}_m\} \subseteq {\mathcal {F}}_{{\underline{v}}}} \frac{2}{m \, (m - 1)} \sum \limits _{i = 1}^{m-1} \sum \limits _{j = i+1}^{m} \left( 1 - \frac{2 \, |{\mathcal {A}}_i \cap {\mathcal {A}}_j|}{|{\mathcal {A}}_i| + |{\mathcal {A}}_j|} \right) \nonumber \\&= \max \limits _{ \{{\mathcal {A}}_1,\dots ,{\mathcal {A}}_m\} \subseteq {\mathcal {F}}_{{\underline{v}}}} \frac{2}{m \, (m - 1)} \left( \frac{m \, (m-1)}{2} - \sum \limits _{i = 1}^{m-1} \sum \limits _{j = i+1}^{m} \frac{2 \, |{\mathcal {A}}_i \cap {\mathcal {A}}_j|}{|{\mathcal {A}}_i| + |{\mathcal {A}}_j|} \right) \nonumber \\&= \max \limits _{ \{{\mathcal {A}}_1,\dots ,{\mathcal {A}}_m\} \subseteq {\mathcal {F}}_{{\underline{v}}}} \left\{ 1 - \frac{2}{m \, (m - 1)} \sum \limits _{i = 1}^{m-1} \sum \limits _{j = i+1}^{m} \frac{2 \, |{\mathcal {A}}_i \cap {\mathcal {A}}_j|}{|{\mathcal {A}}_i| + |{\mathcal {A}}_j|} \right\} \nonumber \\&= 1 - \min \limits _{ \{{\mathcal {A}}_1,\dots ,{\mathcal {A}}_m\} \subseteq {\mathcal {F}}_{{\underline{v}}}} \frac{2}{m \, (m - 1)} \sum \limits _{i = 1}^{m-1} \sum \limits _{j = i+1}^{m} \frac{2 \, |{\mathcal {A}}_i \cap {\mathcal {A}}_j|}{|{\mathcal {A}}_i| + |{\mathcal {A}}_j|} \nonumber \\&\le 1 - \min \limits _{ \{{\mathcal {A}}_1,\dots ,{\mathcal {A}}_m\} \subseteq {\mathcal {G}}_{{\underline{v}}}} \frac{2}{m \, (m - 1)} \sum \limits _{i = 1}^{m-1} \sum \limits _{j = i+1}^{m} \frac{2 \, |{\mathcal {A}}_i \cap {\mathcal {A}}_j|}{|{\mathcal {A}}_i| + |{\mathcal {A}}_j|}. \end{aligned}$$
(12)

\(\square \)

The following MIQP formulation \(\text {UB}_{avg}\) determines expression (12), i.e., an optimal selection w.r.t. \(\delta _{avg}\) in \({\mathcal {G}}_{{\underline{v}}}\):

$$\begin{aligned}&\max \quad 1 - \frac{2}{m \, (m-1)} \sum \limits _{a=1}^{m-1} \sum \limits _{b=a+1}^{m} \, z_{a b} \end{aligned}$$
(13)
$$\begin{aligned}&\text {s.t.}\quad (3)-(6) \, \nonumber \\&\sum \limits _{R_i \in {\mathcal {R}}} \, s_{i a b} = \frac{1}{2} z_{a b} t_{a b} \qquad \text { for all } a, b \in M \text { with } a < b\end{aligned}$$
(14)
$$\begin{aligned}&(8)-(10) \nonumber \\&\qquad \, \,z_{a b} \in [0,1] \qquad \qquad \text {for all } a, b \in M \text { with } a < b. \end{aligned}$$
(15)

Most of the variables and constraints here are identical to the ones used in \(\text {UB}_{min}\). However, here we introduce individual continuous variables (15) for each assortment pair \({\mathcal {A}}_a\) and \({\mathcal {A}}_b\) to determine their individual contributions using constraints (14) to the objective function (13).

4.3 Relations between diversity functions and their bounds

If we consider two MDASP instances that only differ by the diversity function, we can make the following observations.

Lemma 6

Let \({\mathcal {I}}_1 = ({\mathcal {C}}, {\mathcal {R}}, m, {\underline{v}}, \delta _{min})\) and \({\mathcal {I}}_2 = ({\mathcal {C}}, {\mathcal {R}}, m, {\underline{v}}, \delta _{avg})\) be MDASP instances with optimal selections \({\mathcal {S}}_{1}\) and \({\mathcal {S}}_{2}\), respectively. Then it holds that \(\delta _{min}({\mathcal {S}}_{1}) \le \delta _{avg}({\mathcal {S}}_{2})\).

Proof

Applying Lemma 3 yields \( \delta _{min}({\mathcal {S}}_{1}) \le \delta _{avg}({\mathcal {S}}_{1}) \le \delta _{avg}({\mathcal {S}}_{2})\). \(\square \)

Corollary 1

Let \({\mathcal {I}}_1 = ({\mathcal {C}}, {\mathcal {R}}, m, {\underline{v}}, \delta _{min})\) and \({\mathcal {I}}_2 = ({\mathcal {C}}, {\mathcal {R}}, m, {\underline{v}}, \delta _{avg})\) be two instances of MDASP. Then any upper bound on the diversity of \({\mathcal {I}}_2\) is an upper bound on the diversity of \({\mathcal {I}}_1\) as well.

This result can directly be applied to our MIQP model \(\text {UB}_{avg}\).

Corollary 2

Let \({\mathcal {I}} = ({\mathcal {C}}, {\mathcal {R}}, m, {\underline{v}}, \delta _{min})\) be an instance of MDASP and let \({\mathcal {S}}\) denote a feasible selection. We have \(\delta _{min}({\mathcal {S}})\le \text {UB}_{avg}^*({\mathcal {I}})\), where \(\text {UB}_{avg}^*({\mathcal {I}})\) is the optimal solution value for the corresponding MIQP model.

However, this bound cannot be tighter than the one we derive using \(\text {UB}_{min}\).

Lemma 7

Let \({\mathcal {I}} = ({\mathcal {C}}, {\mathcal {R}}, m, {\underline{v}}, \delta _{min})\). We have \(\text {UB}_{min}^*({\mathcal {I}}) \le \text {UB}_{avg}^*({\mathcal {I}}),\) where \(\text {UB}_{min}^*({\mathcal {I}})\) and \(\text {UB}_{avg}^*({\mathcal {I}})\) denote the optimal solution values for the corresponding MIQP models.

Proof

Let \({\mathcal {S}}_{1},{\mathcal {S}}_{2}\) be optimal selections for \(\text {UB}_{min}({\mathcal {I}})\) and \(\text {UB}_{avg}({\mathcal {I}})\), respectively. By Lemma 6 and by the optimality of \({\mathcal {S}}_{2}\), it follows that

$$\begin{aligned} \text {UB}_{min}^*({\mathcal {I}}) = \delta _{min}({\mathcal {S}}_{1}) \le \delta _{avg}({\mathcal {S}}_{2}) = \text {UB}_{avg}^*({\mathcal {I}}). \end{aligned}$$

\(\square \)

5 An MIQP model for MDASP

The rationale behind the following MIQP model for MDASP is the following. We construct a selection within \({\mathcal {G}}_{{\underline{v}}}\) by using either formulation \(\text {UB}_{min}\) or \(\text {UB}_{avg}\), depending on the diversity function of the instance, see Sect. 4 for more details. However, for each assortment we additionally add the constraints of a MIP formulation for 2D-KP in order to ensure its feasibility, i.e., we guarantee that the selection is actually a subset of \({\mathcal {F}}_{{\underline{v}}}\) and therefore feasible itself. In the following example formulation (P) for \(\delta _{min}\), we use the inequalities of the MIP model of Egeblad and Pisinger (2009). It features the variables listed in Table 2.

$$\begin{aligned}&{\text {(P)}} \nonumber \\&\max \qquad 1 - z \qquad \end{aligned}$$
(16)
$$\begin{aligned}&\text {s.t.}\qquad \sum \limits _{R_i \in {\mathcal {R}}} w_i h_i c_{i a} \ge {\underline{v}}\qquad \forall \, a \in M \end{aligned}$$
(17)
$$\begin{aligned}&\sum \limits _{R_i \in {\mathcal {R}}} \, w_i h_i c_{i a} \le w h \,\, \forall \, a \in M \end{aligned}$$
(18)
$$\begin{aligned}&\sum \limits _{R_i \in {\mathcal {R}}} \, (c_{i a} + c_{i b}) = \, t_{a b} \,\, \forall \, a, b \in M \text { with } a < b \end{aligned}$$
(19)
$$\begin{aligned}&c_{i a} + c_{i b} \le 1 + s_{i a b} \,\, \forall \, R_i \in {\mathcal {R}}, \,\, \forall \, a, b \in M \text { with } a < b\end{aligned}$$
(20)
$$\begin{aligned}&\sum \limits _{R_i \in {\mathcal {R}}} \, s_{i a b} \le \frac{1}{2} \, z \, t_{a b}\,\, \forall \, a, b \in M \text { with } a < b \end{aligned}$$
(21)
$$\begin{aligned}&l_{ija} + r_{ija} + u_{ija} + o_{ija} \ge c_{ia} + c_{ja} - 1 \qquad \forall \, R_i, R_j \in {\mathcal {R}} \text { with } i < j,\,\, \forall a \in M \nonumber \\ \end{aligned}$$
(22)
$$\begin{aligned}&x_{ia} - x_{ja} + w \, l_{ija} \le w - w_{i} \,\, \forall \, R_i, R_j \in {\mathcal {R}} \text { with } i < j, \,\, \forall a \in M\end{aligned}$$
(23)
$$\begin{aligned}&x_{ja} - x_{ia} + w \, r_{ija} \le w - w_{j} \,\, \forall \, R_i, R_j \in {\mathcal {R}} \text { with } i < j, \,\, \forall a \in M \end{aligned}$$
(24)
$$\begin{aligned}&y_{ia} - y_{ja} + h \, u_{ija} \le h - h_{i}\,\, \forall \, R_i, R_j \in {\mathcal {R}} \text { with } i < j, \,\, \forall a \in M \end{aligned}$$
(25)
$$\begin{aligned}&y_{ja} - y_{ia} + h \, o_{ija} \le h - h_{j} \,\, \forall \, R_i, R_j \in {\mathcal {R}} \text { with } i < j, \,\, \forall a \in M \end{aligned}$$
(26)
$$\begin{aligned}&0 \le x_{ia} \le w - w_{i}\,\, \forall \, R_i \in {\mathcal {R}}, \,\, \forall a \in M \end{aligned}$$
(27)
$$\begin{aligned}&0 \le y_{ia} \le h - h_{i}\,\, \forall \, R_i \in {\mathcal {R}}, \,\, \forall a \in M \end{aligned}$$
(28)
$$\begin{aligned}&l_{ija},r_{ija},u_{ija},o_{ija} \in \{0,1\} \,\, \forall \, R_i, R_j \in {\mathcal {R}} \text { with } i < j, \,\, \forall a \in M \end{aligned}$$
(29)
$$\begin{aligned}&c_{i a} \in \{0,1\} \qquad \forall \, R_i \in {\mathcal {R}}, \,\, \forall a \in M \end{aligned}$$
(30)
$$\begin{aligned}&s_{i a b} \in \{0,1\}\,\, \forall \, R_i \in {\mathcal {R}},\,\, \forall a, b \in M \text { with } a < b \end{aligned}$$
(31)
$$\begin{aligned}&t_{a b} \in [0, \dots , 2|{\mathcal {R}}|] \qquad \forall \, a, b \in M \text { with } a < b \end{aligned}$$
(32)
$$\begin{aligned}&z \in [0,1] \end{aligned}$$
(33)
Table 2 Variables for MIQP model (P) for MDASP
Full size table

The objective function (16), constraints (17)–(21) and variables (30)–(33) correspond to model \(\text {UB}_{min}\) and construct a selection with maximum Minimum-Distance-Diversity in \({\mathcal {G}}_{{\underline{v}}}\). On the other hand, constraints (22)–(28) and variables (27)–(29) originate from the MIP formulation of Egeblad and Pisinger (2009) for 2D-KP and ensure that the contained assortments are actually feasible. Thereby, constraint (22) ensures that if rectangles \(R_i\) and \(R_j\) are used in assortment \({\mathcal {A}}_a\), i.e., \(c_{ia} = c_{ja} = 1\), then at least one of the four variables \(l_{ija}\), \(r_{ija}\), \(u_{ija}\), or \(o_{ija}\) has to be equal to 1. This implies that \(R_i\) has to be placed left of \(R_j\) (23), right of \(R_j\) (24), under \(R_j\) (25), or over \(R_j\) (26), which guarantees that the two rectangles do not overlap. Furthermore, by the definition of the positioning variables \(x_{ia}\) and \(y_{ia}\), see (27) and (28), each rectangle is placed within the container. Note that the constraints ensuring the feasibility of the assortments, i.e., (22)–(28), are similar to the constraints in the formulation of Padberg (2000).

5.1 A benders decomposition algorithm

Next, we describe a Benders decomposition approach for the introduced MIQP formulation for MDASP. For details regarding Benders decompositions, we refer to Benders (2005) and Geoffrion (1972). To derive it, we subdivide the model into its two subproblems. The higher-level problem consists in constructing a diverse selection of assortments in \({\mathcal {G}}_{{\underline{v}}}\). The lower-level problems ensure the feasibility of the contained assortments. Thus, in our case the higher-level problem is \(\text {UB}_{min}\) or \(\text {UB}_{avg}\), depending on the diversity function, and the lower-level problem is any MIP formulation or exact approach for 2D-KP to check the feasibility of the single assortments, e.g., the variables and constraints from Egeblad and Pisinger (2009) in example (P). If a solution for the higher-level problem has been found, but an assortment \({\mathcal {A}}\) is identified as infeasible by a lower-level problem, corresponding no-good-cuts

$$\begin{aligned} \sum \limits _{R_i \in {\mathcal {A}}} x_{ia} \le |{\mathcal {A}}|-1, \forall a \in M \end{aligned}$$

are added to the higher-level problem, which is then solved again. These cuts ensure that no assortment containing \({\mathcal {A}}\) as a subset is considered as feasible by the higher-level problem. Note that this separation problem, i.e., the lower-level problem, is NP-hard itself as we need solve an instance of 2D-KP.

6 A generic two-stage heuristic

Next, we present a generic two-stage heuristic for MDASP, see Algorithm 1. In its first stage, we use any heuristic or exact solution approach for 2D-KP to sample the space of \({\underline{v}}\)-good assortments. We denote this sample set by \({\mathcal {F}}_s \subseteq {\mathcal {F}}\) in the following. Afterwards, we consider this subset in any exact or heuristic solution approach for MDP in order to determine a feasible selection of size m with respect to the diversity measure \(\delta \). Note that unless we are able to sample the complete set of \({\underline{v}}\)-good assortments, i.e., \({\mathcal {F}}_{{\underline{v}}}\), and do apply an exact MDP approach, the algorithm does not necessarily determine an optimal solution.

figure a

For many MDP approaches from the literature the distances between the assortments have to be known prior to their execution. However, depending on the size of \({\mathcal {F}}_{s}\), determining them can be quite time-consuming. Thus, we introduce a new heuristic for MDP that does not rely on the prior availability of these distances.

Our algorithm, which is stated as Algorithm 2, is based on the idea of a random exchange, i.e., we start with a selection \({\mathcal {S}}_{b}\) of m randomly chosen assortments and then iteratively check if a complete or partial exchange with another k assortments increases the diversity of the selection. A similar idea was suggested by Ghosh (1996). However, in his approach the exchange is based on an evaluation of all assortments. We avoid this by selecting the assortments completely at random and only determine the distances between the considered \(m+k\) assortments in \({\mathcal {S}}_{c}\). Afterwards, we use an exact MDP formulation, depending on the diversity function that should be maximized, to choose m assortments from \({\mathcal {S}}_{c}\) with maximum diversity, see Kuo et al. (1993) for example. Note that the diversity cannot decrease. The number k of assortments considered for an exchange increases with every 100 iterations that did not lead to an increase of the diversity, see line 5 of the algorithm. This count is reset whenever a more diverse selection is found. The idea here is, in particular when considering \(\delta _{min}\), that the diversity of the selection may depend on distances between multiple assortments. In this case, the exchange of only one assortment does not lead to an increase in the diversity. Thus, it is necessary to consider the replacement of more than one assortment at once. Algorithm 2 terminates after \(\Delta \) unsuccessful iterations.

figure b

7 Computational experiments

In this section, we report on the results of our computational experiments. We conducted them using the two instances from the MOPTA competition (Problem description 2019) as well as modified 2D-KP and 2CSP instances, which are widely known from the literature. We evaluate the results for directly solving an instantiation of the MIQP formulation and when applying the Benders approach, which were both presented in Sect. 5, and for an instantiation of our generic two-stage heuristic from Sect. 6. We compare the three approaches w.r.t. the diversity of the best solution they determined. Additionally, we present the results of our upper bound computations using the formulations described in Sect. 4.

Before doing this, we investigate different exact and heuristic approaches for 2D-KP regarding the best generated solution and the total number of generated assortments. This is necessary in order to decide which MIP formulation to use within the MIQP model and which heuristic to employ in the first stage of the heuristic. For the latter we are particularly interested in the number of generated assortments that satisfy the \({\underline{v}}\)-criterion.

For our experiments, we considered \({\underline{v}}= (1 - \varepsilon ) v^*\) with \(\varepsilon = 0.05\) as threshold. Here, \(v^*\) denotes the best solution value which we determined during the 2D-KP runs. Thus, obtaining good solutions for 2D-KP obviously is a crucial task as the value of the best solution found by any of the approaches serves as the threshold value for all successive computational experiments.

7.1 Computational setup

All heuristic algorithms for 2D-KP were implemented in Ada 2012 using the GNAT Pro 19 compiler (AdaCore: GNAT 2019) and were run on an Intel(R) Xeon(TM) E5-2690 v4 CPU with 2.60GHz, four cores, and 32 GB RAM. The Benders approach was coded with Python v3.6 (Python Software Foundation 2020), and for the MIP and MIQP models Gurobi v9.0 (Gurobi Optimization 2019) was used as solver. For all computations, we set a time limit of 3,600 seconds. Additionally, for the computation of the upper bounds the focus of Gurobi was set to primarily improve the bounds.

7.2 Test instances

Since MDASP is a novel optimization problem, an important task was to come up with test instances. Before explaining how we derived test instances using 2D-KP and 2CSP instances, we first of all explain how the two test instances for the MOPTA competition were created.

7.2.1 Generation of MOPTA instances

For the AIMMS-MOPTA competition, data generation procedures were devised to produce problems of any size, that could exhibit some variety in the shape of the rectangles, as measured by the aspect ratio (height-width ratio), and in the size of the rectangles, as measured by the surface.

The generation procedure for the first data set has seven parameters (n, \(w_\text {min}\), \(w_\text {max}\), \(\theta _1\), \(h_\text {min}\), \(h_\text {max}\), \(\theta _2)\). It first generates samples \(w_i\) and \(h_i\) of real-valued random variables \({\mathcal {W}}_i\) and \({\mathcal {H}}_i\) representing the width and height of rectangle i for \(i=1,\dots , n\). \({\mathcal {W}}_i\) and \({\mathcal {H}}_i\) follow independent bounded power law distributions with shape parameters \(\theta _1\) and \(\theta _2\) respectively, restricted to the domain \([w_\text {min}, w_\text {max}]\) \(\times \) \([h_\text {min}, h_\text {max}]\):

$$\begin{aligned}&{\mathbb {P}}(w \le {\mathcal {W}}_i \le w+dw, h \le {\mathcal {H}}_i \le h+dh) \propto w^{\theta _1} h^{\theta _2} dw\;dh + o(dw\;dh) \nonumber \\&\quad \text { for } w\in [w_\text {min}, w_\text {max}), h \in [h_\text {min}, h_\text {max}). \end{aligned}$$
(34)

This can be done by drawing some \(u_i\), \(v_i\) uniformly in [0, 1] and setting

$$\begin{aligned} w_i&= \left( (w_\text {max}^{\theta _1+1}-w_\text {min}^{\theta _1+1}) u_i + w_\text {min}^{\theta _1+1}\right) ^{1/(\theta _1+1)}, \end{aligned}$$
(35)
$$\begin{aligned} h_i&= \left( (h_\text {max}^{\theta _2+1}-h_\text {min}^{\theta _2+1}) v_i + h_\text {min}^{\theta _2+1}\right) ^{1/(\theta _2+1)}. \end{aligned}$$
(36)

The real-valued samples are then rounded up to the next integer. The data set was generated using \(n=200\), \(w_\text {min}=40\), \(w_\text {max}=200\), \(\theta _1=1.8\), \(h_\text {min}=40\), \(h_\text {max}=200\), \(\theta _2=0.8\). The container had width 300 and height 400. Having \(\theta _1, \theta _2 > 0\) means that large rectangles are favored over small rectangles in the generation process.

The generation procedure for the second data set has seven parameters (n, \(s_\text {min}\), \(s_\text {max}\), \(\theta _3\), \(\ell _\text {min}\), \(\ell _\text {max}\), \(\theta _4)\). It first generates samples \(s_i\) and \(\ell _i\) of real-valued random ratios \({\mathcal {S}}_i\) and lengths \({\mathcal {L}}_i\), \(i=1,\dots ,n\), following independent bounded power law distributions with shape parameters \(\theta _3\) and \(\theta _4\) respectively, restricted to the domain \([s_\text {min}, s_\text {max}]\times [\ell _\text {min}, \ell _\text {max}]\), defined similarly to (34):

$$\begin{aligned}&{\mathbb {P}}(s \le {\mathcal {S}}_i \le s+ds, \ell \le {\mathcal {L}}_i \le \ell +d\ell ) \propto s^{\theta _3} \ell ^{\theta _4} ds\;d\ell + o(ds\;d\ell ) \\&\quad \text { for } s\in [s_\text {min}, s_\text {max}), \ell \in [\ell _\text {min}, \ell _\text {max}). \end{aligned}$$

It then derives width and height samples \(w_i, h_i\) using a conditional rule: if \(s_i \ge 1\), set \(w_i=\ell _i/s_i\) and \(h_i=\ell _i\) (tall rectangles); if \(s_i<1\), set \(w_i=\ell _i\) and \(h_i = s_i \ell _i\) (flat rectangles). The values are then rounded up to the next integer. The data set was generated using \(n=40\), \(s_\text {min}=0.25\), \(s_\text {max}=2\), \(\theta _3=0.5\), \(\ell _\text {min}=20\), \(\ell _\text {max}=200\), \(\theta _4=1\). The container was a square of sides of length 500.

The two data generation procedures are not equivalent. It can be checked that when \({\mathcal {W}}_i\), \({\mathcal {H}}_i\) follow truncated power laws, the distribution of the products \({\mathcal {W}}_i {\mathcal {H}}_i\) or the ratios \({\mathcal {H}}_i /{\mathcal {W}}_i\) do not themselves follow power laws. Thus, the two generation procedures control the distribution of the aspect ratios and surfaces in two different ways.

For both data sets, the parameters were determined after some tuning to make sure the problems were sufficiently challenging. This was done by estimating the computational time needed to obtain a pool of \(\epsilon \)-optimal solutions to the two-dimensional knapsack problem formulated following (Hadjiconstantinou and Christofides 1995). To estimate the times, simplified instances were solved, obtained by scaling down by a factor 50 the dimensions of the container and rectangles and rounding them up to the next integer. Scale-and-round was used to reduce the number of binary variables needed to formulate the problems while hopefully preserving the relative degree of difficulty among the generated problems. The generation of a solution pool takes more time than the generation of a single solution but was deemed useful to measure the complexity of describing the set of good solutions from which a maximally-diverse solution is subsequently selected.

7.2.2 Derivation of instances from 2D-KP and 2CSP

As mentioned, we additionally created new MDASP instances based on 2D-KP and 2CSP instances, of which plentiful exist in the literature. In particular, we used the test instance packages listed in Table 3 to generate test instances for MDASP. Most of them can be found on the website of Wei and Wenbin (2019), while the remaining ones were directly taken from the corresponding sources.

Table 3 Packages of test instances given in the literature and by the AIMMS-MOPTA Competition. \(|{\mathcal {R}}|_{min}\) is the smallest number of rectangles among all instances of the considered package, while \(|{\mathcal {R}}|_{max}\) is the maximum cardinality of \({\mathcal {R}}\) among all instances of the package
Full size table

As mentioned above, except for the two instances from the competition, all other instances originate from 2D-KP or 2CSP. Therefore, in many cases the sum of the areas over all rectangles approximately equals the area of the given container, because here the focus often is on the placement of the rectangles within the container. Hence, if we simply declare them to be MDASP instances, the number of \({\underline{v}}\)-good assortments, for \({\underline{v}}= (1-\varepsilon ) v^*\) with \(\varepsilon = 0.05\), and the maximum diversities would often be rather small. On the other hand, if we consider an instance with a set of rectangles \({\mathcal {R}}\) for which the sum of the areas is much bigger than the area of the container, \({\mathcal {F}}_{{\underline{v}}}\) may contain many assortments having Hamming distance 1. Thus, we decided to modify the instances in order to ensure that \({\mathcal {F}}_{{\underline{v}}}\) has suitable size by scaling down the container and to thereby guarantee that at least one rectangle has to be contained in at least two assortments of each feasible selection.

Lemma 8

Let \({\mathcal {I}}\) be an instance of MDASP. Furthermore, let the total area of the given rectangles in \({\mathcal {R}}\) be \(A_{{\mathcal {R}}} := \sum _{R_i \in {\mathcal {R}}} w_i h_i\). If

$$\begin{aligned} m {\underline{v}}> A_{{\mathcal {R}}} \end{aligned}$$

holds, then at least one rectangle is contained in at least two assortments of each feasible selection.

Proof

Assume there exist m feasible assortments \({\mathcal {A}}_1, \ldots , {\mathcal {A}}_m\) such that the intersection of each pair of differing assortments is empty, i.e., \({\mathcal {A}}_i \cap {\mathcal {A}}_j = \varnothing \) for all \(i, j \in \{1, \ldots , m\}\) with \(i \ne j\). Further, let \({\mathcal {A}}_U := \bigcup _{i \in \{1, \ldots , m\}} {\mathcal {A}}_i\) be the union of the considered assortments. Since all assortments are feasible, we have \(v({\mathcal {A}}_i) \ge {\underline{v}}\) for all \(i \in \{1, \ldots , m\}\). Then it follows that

$$\begin{aligned} A_{\mathcal {R}} = \sum \limits _{R_i \in {\mathcal {R}}} w_i h_i \ge \sum \limits _{R_i \in {\mathcal {A}}_U} w_i h_i = \sum \limits _{i = 1}^m v({\mathcal {A}}_i) \ge m {\underline{v}}, \end{aligned}$$

which is a contradiction. \(\square \)

However, as we assume \({\underline{v}}= (1 - \varepsilon ) v^*\) in the following and do not want to rely on determining \(v^*\) for every instance, we consider the area of the container \(v({\mathcal {C}})\) instead. Hence, the goal is to scale the container such that

$$\begin{aligned} {m \cdot v({\mathcal {C}})} > {A_{\mathcal {R}}}. \end{aligned}$$

On the other hand, we additionally want to avoid instances with \(A_{\mathcal {R}} \le v({\mathcal {C}})\) since this could imply that \({\mathcal {F}}_{{\underline{v}}}\) consists of only few assortments for a small \(\varepsilon \). Therefore, we additionally request that

$$\begin{aligned} {v({\mathcal {C}})} < {A_{{\mathcal {R}}}}. \end{aligned}$$

Summing up, our goal is to scale the containers such that

$$\begin{aligned} 1< p := \frac{m \cdot v({\mathcal {C}})}{A_{{\mathcal {R}}}} < m. \end{aligned}$$

Our scaling procedure works as follows: If \(p \notin (1,m)\), let \(s_r := \frac{h}{w}\) be the side-ratio of \({\mathcal {C}}\), and let \(w_{max} := \max _{R_i \in {\mathcal {R}}} \{w_i\}\) and \(h_{max} := \max _{R_i \in {\mathcal {R}}} \{h_i\}\) be the maximal width and height among all rectangles in \({\mathcal {R}}\). Then, we determine the minimum value of \(p \in {\mathbb {N}}\) with \(p \ge 2\) such that \({\mathcal {C}}\) is scaled, the side-ratio \(s_r\) is preserved, and each rectangle of \({\mathcal {R}}\) still fits into the resulting container. This can be done by determining

$$\begin{aligned} p_{min} = \bigg \lceil \max \left( 2, \frac{m \cdot s_r \cdot w_{max}^2}{A_{\mathcal {R}}}, \frac{m \cdot h_{max}^2}{s_r \cdot A_{\mathcal {R}}} \right) \bigg \rceil . \end{aligned}$$

The formula can be derived from \(p = \frac{m\cdot w \cdot h}{A_{\mathcal {R}}}\), \(s_r \cdot w = h\), and the fact that the rectangles with maximum width and height still have to fit into the container.

If \(p_{min} \in \{2,\dots ,m-1\}\), we determine the corresponding integral width and height

$$\begin{aligned} w_{new} = \bigg \lceil \sqrt{\frac{p_{min} \cdot A_{\mathcal {R}}}{m \cdot s_r}}\bigg \rceil \text { and } h_{new} = \bigg \lceil \sqrt{\frac{p_{min} \cdot s_r \cdot A_{\mathcal {R}}}{m}}\bigg \rceil , \end{aligned}$$

and scale \({\mathcal {C}}\) accordingly. Otherwise, we use the original container. Note that if this procedure led to a container with a greater area than the original one, we eventually decided to leave \({\mathcal {C}}\) unchanged. This applies to eleven of the instances from the packages 2csp, OKP, and others. We decided to do that in order to preserve instance specific properties and to allow only assortments that would have been feasible w.r.t. the original container.

Note that if a certain instance is not equipped with a container, we proceed analogously by setting \(s_r\) to the average side-ratio of the rectangles in \({\mathcal {R}}\), which was done for the instances of the area package. Finally, we removed instances that occured twice after the scaling procedure and ended up with a test set consisting of 1,199 instances. All scaled instances that were used for evaluating the presented solution approaches are available as csv files at https://cloud.zib.de/s/P3FBm9Wbn499LHY.

7.3 Evaluating solution approaches for 2D-KP

In the remainder of this manuscript, we use the following abbreviations for 2D-KP algorithms: Concerning the heuristics we use LWF, GRASP, and IBHP for the Least-Waste-First heuristic of Wei et al. (2009), the GRASP algorithm of Álvarez Valdés et al. (2005), and the IBHP heuristic of Shiangjen et al. (2018), respectively. Regarding MIP formulations, by HC95 we refer to the IP model of Hadjiconstantinou and Christofides (1995), BKRS09 abbreviates the IP model of Belov et al. (2009), and EP09 corresponds to the MIP formulation of Egeblad and Pisinger (2009). Recall that we used a time limit of 3,600 seconds for any computation, so it may happen that the heuristics lead to better results than the exact approaches.

7.3.1 Evaluation with respect to the best generated assortment

First of all, we compare the above mentioned 2D-KP algorithms w.r.t. the value of their best generated assortment for each instance in the test set. The exact results can be found as a csv file at https://cloud.zib.de/s/bn8bd7Wfwj5KgT9. In Table 4, we present summarized results for the different instance packages. Note that the number of instances on which the different approaches obtained the best assortment do not have to sum up to 1,199 as we counted instances on which two or more algorithms achieved the best solution multiple times. Additionally, one should keep in mind that we compare three exact approaches and three heuristics.

Table 4 Number of instances on which the algorithms obtained an assortment with biggest value
Full size table

The IBHP heuristic outperformed all other approaches w.r.t. the number of instances on which it determined an assortment with biggest value. This is the case for 1,018 of 1,199 instances, i.e., on 84.9% of the test set. The second-best approach in this context is the LWF heuristic with 310 of the 1,199 instances (25.9%), followed by approach EP09 (17.1%), and the GRASP heuristic (16.7%). Thus, when comparing all instances at once, it seems that IBHP is best suited for obtaining the best generated assortment. However, if we look at the different instance packages in more detail, we can observe that while on packages with \(|{\mathcal {R}}|_{max} > 197\) the best generated assortments were indeed obtained by IBHP, EP09 delivered the best results on packages with \(|{\mathcal {R}}|_{max} \le 22\). This meets the expectation of the observer as the exact approaches are likely to perform worse with a growing number of rectangles.

Furthermore, the reasons for the results of the heuristic approaches may be due to their underlying basic ideas. GRASP relies on the idea of improving an initially generated assortment by randomly exchanging and moving the contained rectangles. On the other hand, IBHP and LWF apply sophisticated placing procedures where the rectangles are scored and placed in a manner such that wasted space is avoided if possible. However, the placing procedure in IBHP works faster than the evaluation within LWF, because here every rectangle is scored based on the question if it could cause wasted space in the next step. Thus, LWF spends more computing time when determining the scores for the rectangles, which IBHP can use to generate a greater variety of assortments.

If we compare the MIP approaches with each other, we observe that EP09 leads to the best results, although HC95 solved bigger instances in terms of the cardinality of \({\mathcal {R}}\). This behavior might be explained by the ideas behind the MIP models. HC95 relies on binary variables indicating whether a certain position inside the container is covered by a placed rectangle or not. This can be advantageous for instances with a small container. In contrast, EP09 and BKRS09 make use of the relative positions of the rectangles in their models. In our experiments the constraints modelling the relative positions in EP09 seem to be more effective than representing the relative positions by intersections in the projections onto the axes, which is the idea behind BKRS09.

7.3.2 Evaluation with respect to the number of generated assortments

Next, we compare the three heuristic approaches for 2D-KP w.r.t. the number of assortments that were generated. We do this, since in the first stage of the generic two-stage heuristic, the space of feasible \({\underline{v}}\)-good assortments \({\mathcal {F}}_{{\underline{v}}}\) has to be sampled and therefore the number of generated assortments is an important factor. Note that we do not consider the MIP approaches in this context, as they did not generate many feasible solutions during the solving process, even for small instances. The total number of generated assortments and the number of \({\underline{v}}\)-good assortments, for \({\underline{v}}= (1-\varepsilon )v^*\) with \(\varepsilon = 0.05\), can be found as a csv file at https://cloud.zib.de/s/bn8bd7Wfwj5KgT9. Note that for the number of \({\underline{v}}\)-good solutions we only counted undominated assortments, i.e., assortments which were not contained in any other. For the total number of assortments, we did not remove the dominated ones, as their number was too big to complete the removing process within one week of computation time per instance.

First, we compare the different algorithms w.r.t. the total number of generated assortments. In this case, IBHP obtained the most solutions on 921 of the 1,199 instances, i.e., on 76.8%, while the GRASP algorithm obtained the most on the remaining 278 ones (23.2%), see Table 5. If we take a closer look on the properties of the different instances, we can observe that GRASP obtained the most assortments on packages with \(|{\mathcal {R}}|_{max} \le 197\) and Burke.

Table 5 Number of instances on which the heuristics generated the most assortments in total and the most undominated \({\underline{v}}\)-good assortments, for \({\underline{v}}= (1-\varepsilon )v^*\) with \(\varepsilon = 0.05\)
Full size table

Next, if we consider the subset of \({\underline{v}}\)-good assortments and remove the dominated ones from it, which we were able to achieve within a week for each of the instances, the described situation intensifies, see Table 5. In this case, IBHP obtained the most assortments on 1,003 of the 1,199 instances (83.7%). The biggest instance on which GRASP delivers results superior to IBHP consists of 500 rectangles and the percentage of instances where it performs best decreases to 19.4%. Interestingly, LWF was able to generate the biggest set of assortments on 11 instances.

This behavior can again be explained by the subroutines on which the heuristics rely. As the scoring procedure within LWF consumes much time, IBHP and GRASP produce a greater variety of assortments. Further, recall that GRASP did not perform as good as IBHP in our evaluation w.r.t. the value of the best generated assortment, see Sect. 7.3.1. Consequently, it obtains a smaller number of generated assortments in total as its search is limited to a smaller solution subspace. This is in line with the fact that the number of instances on which GRASP obtains the most assortments decreases when considering only \({\underline{v}}\)-good assortments. Recall that we consider\({\underline{v}}= (1-\varepsilon )v^*\), where \(v^*\) is the best solution value found by any of the approaches, which gives IBHP an advantage. The former observations may be explained by the randomness regarding its improvement procedure, which can, in contrast to a more guided approach like IBHP, be a drawback when considering instances with many rectangles.

7.4 Evaluation with respect to diversity

Based on the results from the two previous subsections, we instantiated the generic two-stage heuristic (2SH) with IBHP and the random exchange heuristic presented in Sect. 6 and use MIP formulation EP09 for the instantiation of the MIQP model.

Next, we are going to compare the results of the solution approaches, discussed in Sects. 5 and 6. Therefore, we generated instances of MDASP from the scaled 2D-KP instances by setting \(m = 6\), \(\delta \in \{\delta _{min}, \delta _{avg}\}\), and \({\underline{v}}= (1-\varepsilon )v^*\) with \(\varepsilon = 0.05\), i.e., we created two test instances for each container and set of rectangles. Hence, we ran every solution approach on 2,398 instances of MDASP. Recall that we always consider \(v^*\) to be equal to the value of the best generated assortment of the corresponding 2D-KP instance, see Sect. 7.3.1. Thus, we ran the MIQP formulation, the corresponding Benders decomposition approach (BD), and the two-stage heuristic for \(\delta _{min}\) as well as for \(\delta _{avg}\). The detailed results we obtained can be found as a csv file at https://cloud.zib.de/s/bn8bd7Wfwj5KgT9.

7.4.1 Evaluation with respect to \(\delta _{min}\)

First, we evaluate the results w.r.t. \(\delta _{min}\). Here, the heuristic delivered the best results on 1,124 of the 1,199 instances, i.e., on 93.7% of the instances and thus was the best performing approach among all considered algorithms, see Table 6. The second-best performing one in this context was the Benders approach, solving 60 instances best, i.e., 5.0%. However, the MIQP formulation was able to solve ten instances to optimality, while the heuristic obtained only four optimal selections, see Table 7.

Table 6 Number of instances on which the solution approaches obtained the best diversity w.r.t. \(\delta _{min}\) and \(\delta _{avg}\)
Full size table
Table 7 Minimum and maximum cardinality of \({\mathcal {R}}\) of the instances that are solved best by the approaches w.r.t. \(\delta _{min}\) and \(\delta _{avg}\)
Full size table

When we consider the maximum number of rectangles contained in the instances and investigate the single packages in more detail, one can observe that the heuristic performs well on any type of test instance, and outperforms the other approaches on 20 of the 23 packages. However, it performs less well on packages where the instances consist only of few rectangles, see for example HC, ngcut, and PB. Meanwhile, the Benders approach \(\text {BD}\) is especially strong when solving instances of this type and led to the best results on small instances, even if the biggest instance on which it could obtain the best diversity value consisted of 29 rectangles only. Furthermore, it was able to generate the most diverse selections on all instance packages with 22 rectangles or less. Finally, the biggest instance, w.r.t. the number of contained rectangles, for which the most diverse solution was found by the MIQP formulation, consisted of 50 rectangles.

Possible reasons for these results are on the one hand that the exact approaches, i.e., MIQP and BD, are likely to perform worse with an increasing number of rectangles. However, the exact approaches benefit from their ability to choose “less dense” assortments over “dense” ones. By this we mean that it may be advantageous to remove rectangles from an assortment as long as it stays \({\underline{v}}\)-good in order to increase the diversity of the selection. The two-stage heuristic relying on IBHP does not consider this as it aims at filling up empty space in the constructed assortments by adding rectangles as long as possible. Nevertheless, this ability seems to be advantageous for instances with few rectangles and in particular for those, which were originally designed in a way that nearly all rectangles can be placed.

7.4.2 Evaluation with respect to \(\delta _{avg}\)

For \(\delta _{avg}\), we make similar observations. Here, the heuristic obtained the best result on 1,092 instances, while the Benders approach could solve slightly more instances better than it did in the case of \(\delta _{min}\), i.e., 8.6%. Thus, this approach seems to perform better in the Average-Distance-Diversity case and its dominance on small instances w.r.t. the cardinality of \({\mathcal {R}}\) intensifies. Meanwhile, the MIQP formulation could solve nearly the same amount of instances, see Table 6. Additionally, the Benders approach is now able to obtain the best result on instances with a size of up to 120 rectangles.

The obtained results can be explained analogously to the \(\delta _{min}\) case, with the additional comment that the Benders approach performed better when considering \(\delta _{avg}\) instead of \(\delta _{min}\). This may be due to the corresponding objective functions. When we are considering \(\delta _{min}\), changing one assortment in a selection does often not affect the overall diversity of the selection since the objective function aims at maximizing the minimum distance between the assortments. However, for \(\delta _{avg}\), the goal is to maximize the sum of the distances between the assortments, so an exchange of assortments in a selection has nearly always a direct influence on the objective function. Hence, the search, which relies on a branch-and-bound tree, is more guided in the latter case.

Thus, we conclude again that the two-stage algorithm using IBHP and the random exchange heuristic is the best approach for deriving good solutions for MDASP instances, but when considering the Average-Distance-Diversity and an instance consisting of only a few rectangles, i.e., of less than 22, then the Benders approach is the solution approach of choice.

7.5 Evaluation of upper bounds

Finally, we look at the bounds obtained by MIQPs \(\text {UB}_{min}\) and \(\text {UB}_{avg}\) from Sect. 4. Recall that \(\text {UB}_{min}\) is only valid for \(\delta _{min}\), while \(\text {UB}_{avg}\) determines a valid bound for both diversity functions. It is important to note that any upper bound derived during the solving process is also valid. The results can be found as a csv file at https://cloud.zib.de/s/bn8bd7Wfwj5KgT9.

7.5.1 Evaluation with respect to \(\delta _{min}\)

We start our evaluation with a comparison of both bounds on the instances w.r.t. \(\delta _{min}\). The minimum distance between any bound and the best result of any solution approach to MDASP is in both cases equal to 0, due to instance ngcut01 since the maximum diversity that could be obtained coincides with the value of the bounds. Furthermore, the maximum distance between the bounds and best obtained diversity is 1, as for the biggest instances w.r.t. the number of contained rectangles, only selections with diversity equal to 0 are obtained, while the bounds are equal to 1.

Table 8 Average distance between the bounds and the best obtained diversity. \(\delta ^*\) signifies the value of the most diverse selection that could be obtained by any solution approach to MDASP
Full size table
Table 9 Number of instances per package on which the presented bounds performed best w.r.t. \(\delta _{min}\)
Full size table

Concerning the average distance between the bounds and the best obtained diversity, we can conclude that both bounds are nearly equally strong, with a slight advantage for \(\text {UB}_{avg}\). But \(\text {UB}_{min}\) leads to better results on instances with less than 500 rectangles, making it better suited for smaller instances, while \(\text {UB}_{avg}\) performs best on instances with \(|{\mathcal {R}}| \ge 500\), see Table 8. Furthermore, \(\text {UB}_{min}\) was the best bound for 552 instances, and \(\text {UB}_{avg}\) for 730 instances. On how many instances each bound performed best can be found in Table 9.

Note that, due to Lemma 7, \(\text {UB}_{min}\) should take on smaller values than \(\text {UB}_{avg}\) but since not all bounds could obtain their optimal value, we end up with \(\text {UB}_{avg}\) determining better bounds than \(\text {UB}_{min}\) on more than half of the instances, see Table 9. In fact, the MIQP formulations of \(\text {UB}_{min}\) and \(\text {UB}_{avg}\) were only able to obtain optimal solutions on 29 and 56 instances, respectively.

One possible explanation why \(\text {UB}_{avg}\) obtained better results than \(\text {UB}_{min}\) could again be due to the objective functions of the underlying MIQPs. While \(\text {UB}_{avg}\) minimizes a sum of variables, \(\text {UB}_{min}\) aims at minimizing a single value which often works worse in practice.

7.5.2 Evaluation with respect to \(\delta _{avg}\)

Finally, we present the results obtained by \(\text {UB}_{avg}\) for the instances w.r.t. \(\delta _{avg}\). The minimum distance between \(\text {UB}_{avg}\) and the value of a most diverse selection is again equal to 0, due to instance ngcut01. We also obtain a maximum distance of 1 between \(\text {UB}_{avg}\) and the best diversity due to instance zdf16.

The average distances to the best obtained diversities generated by the solution approaches to MDASP are depicted in the right column of Table 8. As expected, the distances between \(\text {UB}_{avg}\) and the value of the most diverse selection are smaller than in the case of \(\delta _{min}\) since the diversity of a selection w.r.t. \(\delta _{avg}\) is bigger than or equal to its diversity w.r.t. \(\delta _{min}\), see Lemma 3. Furthermore, \(\text {UB}_{avg}\) seems to work best on packages with instances consisting of 1,000 rectangles or less. Nevertheless, it also obtains its biggest distance on a package with instances consisting of less than 100 rectangles, i.e., on package OKP. This suggests that either the solution approaches fail on determining selections with great diversity or that the relaxation of the conditions that the considered assortments have to fulfill is too weak. But this issue occurs for the bounds on \(\delta _{min}\) as well. However, with an average distance of 0.232 to all considered instances, \(\text {UB}_{avg}\) achieves better results for \(\delta _{avg}\) than any bound on \(\delta _{min}\).

8 Conclusion and outlook

In this article, we introduced the Maximum Diversity Assortment Selection Problem (MDASP), which is a novel generalization of the two-dimensional Knapsack Problem (2D-KP). First, we mathematically defined MDASP and introduced two diversity-functions for selections based on the Hamming distance. Afterwards, we presented an overview of the literature focusing on its two inherent subproblems 2D-KP and MDP. Next, we introduced two MIQPs that can be used to determine upper bounds on the diversity of MDASP instances. Based on them, we presented an exact MIQP formulation for MDASP, a Benders decomposition approach for it, as well as a generic two-stage heuristic. Furthermore, we compared different solution approaches for 2D-KP with respect to the best assortment value and the number of generated assortments. Finally, we investigated the presented solution approaches for MDASP with respect to the maximum diverse selections they determined.

As a main result, the generic two-stage heuristic instantiated with IBHP and the random exchange for MDP delivered the best results with respect to the diversity among the presented solution approaches for MDASP. However, the Benders approaches led to more diverse selections on instances consisting of only few rectangles, especially with respect to \(\delta _{avg}\). Again, it is important to note that it is an exact algorithm, in contrast to the heuristic.

There are many directions for further research concerning MDASP. First of all, we are currently working on a possible improvement of the Benders decomposition approach by using the algorithm presented by Fekete et al. (2007) for determining the maximality of an assortment. Additionally, it would be beneficial to experiment with other cuts than the no-good-cuts in order to improve the performance of the overall Benders approach. For example, one could try to use a variant of “Combinatorial Benders Cuts” as suggested by Côté et al. (2014). Additionally, it would be interesting to test a sequence-pair representation based formulation within the presented MIQP approaches and try to speed up the computations and improve the LP bound by that.

Furthermore, we are investigating the structures of the solutions created by the different heuristics. The idea here would be to combine them in order to further broaden the variety in the set of generated \({\underline{v}}\)-good solutions. In this context, a modification of the shift strategy of IBHP, adapting the strength of the GRASP heuristic for small instances, would be of great advantage. Additionally, it would be interesting if a heuristic exchange of rectangles with similar widths and heights could be integrated into the current approaches in order to improve the diversity between the constructed assortments.