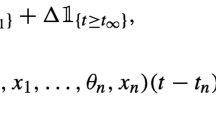First-order sensitivity of the optimal value in a Markov decision model with respect to deviations in the transition probability function

Abstract

Markov decision models (MDM) used in practical applications are most often less complex than the underlying ‘true’ MDM. The reduction of model complexity is performed for several reasons. However, it is obviously of interest to know what kind of model reduction is reasonable (in regard to the optimal value) and what kind is not. In this article we propose a way how to address this question. We introduce a sort of derivative of the optimal value as a function of the transition probabilities, which can be used to measure the (first-order) sensitivity of the optimal value w.r.t. changes in the transition probabilities. ‘Differentiability’ is obtained for a fairly broad class of MDMs, and the ‘derivative’ is specified explicitly. Our theoretical findings are illustrated by means of optimization problems in inventory control and mathematical finance.

1 Introduction

Already in the 1990th, Müller (1997a) pointed out that the impact of the transition probabilities of a Markov decision process (MDP) on the optimal value of a corresponding Markov decision model (MDM) can not be ignored for practical issues. For instance, in most cases the transition probabilities are unknown and have to be estimated by statistical methods. Moreover in many applications the ‘true’ model is replaced by an approximate version of the ‘true’ model or by a variant which is simplified and thus less complex. The result is that in practical applications the optimal (strategy and thus the optimal) value is most often computed on the basis of transition probabilities that differ from the underlying true transition probabilities. Therefore the sensitivity of the optimal value w.r.t. deviations in the transition probabilities is obviously of interest.

Müller (1997a) showed that under some structural assumptions the optimal value in a discrete-time MDM depends continuously on the transition probabilities, and he established bounds for the approximation error. In the course of this the distance between transition probabilities was measured by means of some suitable probability metrics. Even earlier, Kolonko (1983) obtained analogous bounds in a MDM in which the transition probabilities depend on a parameter. Here the distance between transition probabilities was measured by means of the distance between the respective parameters. Error bounds for the expected total reward of discrete-time Markov reward processes were also specified by Van Dijk (1988) and Van Dijk and Puterman (1988). In the latter reference the authors also discussed the case of discrete-time Markov decision processes with countable state and action spaces.

In this article, we focus on the situation where the ‘true’ model is replaced by a less complex version (for a simple example, see Subsection 1.4.3 in the supplemental article Kern et al. (2020)). The reduction of model complexity in practical applications is common and performed for several reasons. Apart from computational aspects and the difficulty of considering all relevant factors, one major point is that statistical inference for certain transition probabilities can be costly in terms of both time and money. However, it is obviously of interest to know what kind of model reduction is reasonable and what kind is not. In the following we want to propose a way how to address the latter question.

Our original motivation comes from the field of optimal logistics transportation planning, where ongoing projects like SYNCHRO-NET (https://www.synchronet.eu/) aim at stochastic decision models based on transition probabilities estimated from historical route information. Due to the lack of historical data for unlikely events, transition probabilities are often modeled in a simplified way. In fact, events with small probabilities are often ignored in the model. However, the impact of these events on the optimal value (here the minimal expected transportation costs) of the corresponding MDM may nevertheless be significant. The identification of unlikely but potentially cost sensitive events is therefore a major challenge. In logistics planning operations engineers have indeed become increasingly interested in comprehensibly quantifying the sensitivity of the optimal value w.r.t. the incorporation of unlikely events into the model. For background see, for instance, Holfeld and Simroth (2017) and Holfeld et al. (2018). The assessment of rare but risky events takes on greater importance also in other areas of applications; see, for instance, Komljenovic et al. (2016), Yang et al. (2015) and references cited therein.

By an incorporation of an unlikely event into the model we mean, for instance, that under performance of an action a at some time n a previously impossible transition from one state x to another state y gets now assigned small but strictly positive probability $\varepsilon$. Mathematically this means that the transition probability $P_n((x,a),\,\cdot \,)$ is replaced by $(1-\varepsilon )P_n((x,a),\,\bullet \,)+\varepsilon Q_n((x,a),\,\bullet \,)$ with $Q_n((x,a),\,\bullet \,):=\delta _y[\,\bullet \,]$, where $\delta _y$ is the Dirac measure at y. More generally one could consider a change of the whole transition function (the family of all transition probabilities) ${\varvec{P}}$ to $(1-\varepsilon ){\varvec{P}}+\varepsilon {\varvec{Q}}$ with $\varepsilon >0$ small. For operations engineers it is here interesting to know how this change affects the optimal value, ${{{\mathcal {V}}}}_{0}({\varvec{P}})$. If the effect is minor, then an incorporation can be seen as superfluous, at least from a pragmatic point of view. If on the other hand the effect is significant, then the engineer should consider the option to extend the model and to make an effort to get access to statistical data for the extended model.

At this point it is worth mentioning that a change of the transition function from ${\varvec{P}}$ to $(1-\varepsilon ){\varvec{P}}+\varepsilon {\varvec{Q}}$ with $\varepsilon >0$ small can also have a different interpretation than an incorporation of an (unlikely) new event. It could also be associated with an incorporation of an (unlikely) divergence from the normal transition rules. See Sect. 4.5 for an example.

In this article, we will introduce an approach for quantifying the effect of changing the transition function from ${\varvec{P}}$ to $(1-\varepsilon ){\varvec{P}}+\varepsilon {\varvec{Q}}$, with $\varepsilon >0$ small, on the optimal value ${{{\mathcal {V}}}}_{0}({\varvec{P}})$ of the MDM. In view of $(1-\varepsilon ){\varvec{P}}+\varepsilon {\varvec{Q}}={\varvec{P}}+\varepsilon ({\varvec{Q}}-{\varvec{P}})$, we feel that it is reasonable to quantify the effect by a sort of derivative of the value functional ${{{\mathcal {V}}}}_{0}$ at ${\varvec{P}}$ evaluated at direction ${\varvec{Q}}-{\varvec{P}}$. To some extent the ‘derivative’ $\dot{{{\mathcal {V}}}}_{0;{\varvec{P}}}({\varvec{Q}}-{\varvec{P}})$ specifies the first-order sensitivity of ${{{\mathcal {V}}}}_{0}({\varvec{P}})$ w.r.t. a change of ${\varvec{P}}$ as above. Take into account that

$$\begin{aligned} {{\mathcal {V}}}_{0}({\varvec{P}}+\varepsilon ({\varvec{Q}}-{\varvec{P}})) - {{\mathcal {V}}}_{0}({\varvec{P}})\,\approx \,\varepsilon \cdot \dot{{\mathcal {V}}}_{0;{\varvec{P}}}({\varvec{Q}}-{\varvec{P}}) \qquad \text{ for } \varepsilon >0 \text{ small }. \end{aligned}$$

(1)

To be able to compare the first-order sensitivity for (infinitely) many different ${\varvec{Q}}$, it is favourable to know that the approximation in (1) is uniform in ${\varvec{Q}}\in {{\mathcal {K}}}$ for preferably large sets ${{\mathcal {K}}}$ of transition functions. Moreover, it is not always possible to specify the relevant ${\varvec{Q}}$ exactly. For that reason it would be also good to have robustness (i.e. some sort of continuity) of $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}({\varvec{Q}}-{\varvec{P}})$ in ${\varvec{Q}}$. These two things induced us to focus on a variant of tangential ${{\mathcal {S}}}$-differentiability as introduced by Sebastião e Silva (1956) and Averbukh and Smolyanov (1967) (here ${{\mathcal {S}}}$ is a family of sets ${{\mathcal {K}}}$ of transition functions). In Section 3 we present a result on ‘${{\mathcal {S}}}$-differentiability’ of ${{\mathcal {V}}}_0$ for the family ${{\mathcal {S}}}$ of all relatively compact sets of admissible transition functions and a reasonably broad class of MDMs, where we measure the distance between transition functions by means of metrics based on probability metrics as in Müller (1997a).

The ‘derivative’ $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}({\varvec{Q}}-{\varvec{P}})$ of the optimal value functional ${{\mathcal {V}}}_{0}$ at ${\varvec{P}}$ quantifies the effect of a change from ${\varvec{P}}$ to $(1-\varepsilon ){\varvec{P}}+\varepsilon {\varvec{Q}}$, with $\varepsilon >0$ small, assuming that after the change the strategy $\pi$ (tuple of the underlying decision rules) is chosen such that it optimizes the target value ${{\mathcal {V}}}_{0}^{\pi }({\varvec{P}}')$ (e.g. expected total costs or rewards) in $\pi$ under the new transition function ${\varvec{P}}':=(1-\varepsilon ){\varvec{P}}+\varepsilon {\varvec{Q}}$. On the other hand, practitioners are also interested in quantifying the impact of a change of ${\varvec{P}}$ when the optimal strategy (under ${\varvec{P}}$) is kept after the change. Such a quantification would somehow answers the question: How much different does a strategy derived in a simplified MDM perform in a more complex (more realistic) variant of the MDM? Since the ‘derivative’ $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^\pi ({\varvec{Q}}-{\varvec{P}})$ of the functional ${{\mathcal {V}}}_{0}^\pi$ under a fixed strategy $\pi$ turns out to be a building stone for the derivative $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}({\varvec{Q}}-{\varvec{P}})$ of the optimal value functional ${{\mathcal {V}}}_{0}$ at ${\varvec{P}}$, our elaborations cover both situations anyway. For fixed strategy $\pi$ we obtain ‘${{\mathcal {S}}}$-differentiability’ of ${{\mathcal {V}}}_0^\pi$ even for the broader family ${{\mathcal {S}}}$ of all bounded sets of admissible transition functions.

The ‘derivative’ which we propose to regard as a measure for the first-order sensitivity will formally be introduced in Definition 7. This definition is applicable to quite general finite time horizon MDMs and might look somewhat cumbersome at first glance. However, in the special case of a finite state space and finite action spaces, a situation one faces in many practical applications, the proposed ‘differentiability’ boils down to a rather intuitive concept. This will be explained in Section 1 of the supplemental article Kern et al. (2020) with a minimum of notation and terminology. In Section 1 of the supplemental article Kern et al. (2020) we will also reformulate a backward iteration scheme for the computation of the ‘derivative’ (which can be deduced from our main result, Theorem 1) in the discrete case, and we will discuss an example.

In Section 2 we formally introduce quite general MDMs in the fashion of the standard monographs Bäuerle and Rieder (2011), Hernández-Lerma and Lasserre (1996), Hinderer (1970), Puterman (1994). Since it is important to have an elaborate notation in order to formulate our main result, we are very precise in Section 2. As a result, this section is a little longer compared to the respective sections in other articles on MDMs. In Section 3 we carefully introduce our notion of ‘differentiability’ and state our main result concerning the computation of the ‘derivative’ of the value functional.

In Section 4 we will apply the results of Section 3 to assess the impact of one or more than one unlikely but substantial shock in the dynamics of an asset on the solution of a terminal wealth problem in a (simple) financial market model free of shocks. This example somehow motivates the general set-up chosen in Sections 2–3. All results of this article are proven in Sections 3–5 of the supplemental article Kern et al. (2020). For the convenience of the reader we recall in Section 6 of the supplemental article Kern et al. (2020) a result on the existence of optimal strategies in general MDMs. Section 7 of the supplemental article Kern et al. (2020) contains an auxiliary topological result.

2 Formal definition of Markov decision model

Let E be a non-empty set equipped with a $\sigma$-algebra ${{\mathcal {E}}}$, referred to as state space. Let $N\in {\mathbb {N}}$ be a fixed finite time horizon (or planning horizon) in discrete time. For each point of time $n=0,\ldots ,N-1$ and each state $x\in E$, let $A_n(x)$ be a non-empty set. The elements of $A_n(x)$ will be seen as the admissible actions (or controls) at time n in state x. For each $n=0,\ldots ,N-1$, let

$$\begin{aligned} A_n:=\bigcup _{x\in E} A_n(x) \quad \text{ and } \quad D_n:=\big \{(x,a)\in E\times A_n:\,a\in A_n(x)\big \}. \end{aligned}$$

The elements of $A_n$ can be seen as the actions that may basically be selected at time n whereas the elements of $D_n$ are the possible state-action combinations at time n. For our subsequent analysis, we equip $A_n$ with a $\sigma$-algebra ${{\mathcal {A}}}_n$, and let ${{\mathcal {D}}}_n:=({{\mathcal {E}}}\otimes {{\mathcal {A}}}_n)\cap D_n$ be the trace of the product $\sigma$-algebra ${{\mathcal {E}}}\otimes {{\mathcal {A}}}_n$ in $D_n$. Recall that a map $P_n:D_n\times {{\mathcal {E}}}\rightarrow [0,1]$ is said to be a probability kernel (or Markov kernel) from $(D_n,{{\mathcal {D}}}_n)$ to $(E,{{\mathcal {E}}})$ if $P_n(\,\cdot \,,B)$ is a $({{\mathcal {D}}}_n,{{\mathcal {B}}}([0,1]))$-measurable map for any $B\in {{\mathcal {E}}}$, and $P_n((x,a),\,\bullet \,)\in {{\mathcal {M}}}_1(E)$ for any $(x,a)\in D_n$. Here ${{\mathcal {M}}}_1(E)$ is the set of all probability measures on $(E,{{\mathcal {E}}})$.

2.1 Markov decision process

In this subsection, we will give a formal definition of an E-valued (discrete-time) Markov decision process (MDP) associated with a given initial state, a given transition function and a given strategy. By definition a (Markov decision) transition (probability) function is an N-tuple

$$\begin{aligned} {\varvec{P}}= (P_0,\ldots ,P_{N-1}) \end{aligned}$$

whose n-th entry $P_n$ is a probability kernel from $(D_n,{{\mathcal {D}}}_n)$ to $(E,{{\mathcal {E}}})$. In this context $P_n$ will be referred to as one-step transition (probability) kernel at time n (or from time n to $n+1$) and the probability measure $P_n((x,a),\,\bullet \,)$ is referred to as one-step transition probability at time n (or from time n to $n+1$) given state x and action a. We denote by ${{\mathcal {P}}}$ the set of all transition functions.

We will assume that the actions are performed by a so-called N-stage strategy (or N-stage policy). An (N-stage) strategy is an N-tuple

$$\begin{aligned} \pi = (f_0,\ldots ,f_{N-1}) \end{aligned}$$

of decision rules at times $n=0,\ldots ,N-1$, where a decision rule at time n is an $({{\mathcal {E}}},{{\mathcal {A}}}_n)$-measurable map $f_n:E\rightarrow A_n$ satisfying $f_n(x)\in A_n(x)$ for all $x\in E$. Note that a decision rule at time n is (deterministic and) ‘Markovian’ since it only depends on the current state and is independent of previous states and actions. We denote by ${\mathbb {F}}_n$ the set of all decision rules at time n, and assume that ${\mathbb {F}}_n$ is non-empty. Hence a strategy is an element of the set ${\mathbb {F}}_0\times \cdots \times {\mathbb {F}}_{N-1}$, and this set can be seen as the set of all strategies. Moreover, we fix for any $n=0,\ldots ,N-1$ some $F_n\subseteq {\mathbb {F}}_n$ which can be seen as the set of all admissible decision rules at time n. In particular, the set ${\varPi }:=F_0\times \cdots \times F_{N-1}$ can be seen as the set of all admissible strategies.

For any transition function ${\varvec{P}}=(P_n)_{n=0}^{N-1}\in {{\mathcal {P}}}$, strategy $\pi =(f_n)_{n=0}^{N-1}\in {\varPi }$, and time point $n\in \{0,\ldots ,N-1\}$, we can derive from $P_n$ a probability kernel $P_n^{\pi }$ from $(E,{{\mathcal {E}}})$ to $(E,{{\mathcal {E}}})$ through

$$\begin{aligned} P_n^{\pi }(x,B) := P_n\big ((x,f_n(x)),B\big ), \qquad x\in E,\,B\in {{\mathcal {E}}}. \end{aligned}$$

(2)

The probability measure $P_n^\pi (x,\,\bullet \,)$ can be seen as the one-step transition probability at time n given state x when the transitions and actions are governed by ${\varvec{P}}$ and $\pi$, respectively.

Now, consider the measurable space

$$\begin{aligned} ({\varOmega },{{\mathcal {F}}}) := (E^{N+1},{{\mathcal {E}}}^{\otimes (N+1)}). \end{aligned}$$

For any $x_0\in E$, ${\varvec{P}}=(P_n)_{n=0}^{N-1}\in {{\mathcal {P}}}$, and $\pi \in {\varPi }$ define the probability measure

$$\begin{aligned} {\mathbb {P}}^{x_0,{\varvec{P}};\pi } := \delta _{x_0}\otimes P_0^\pi \otimes \cdots \otimes P_{N-1}^\pi \end{aligned}$$

(3)

on $({\varOmega },{{\mathcal {F}}})$, where $x_0$ should be seen as the initial state of the MDP to be constructed. The right-hand side of (3) is the usual product of the probability measure $\delta _{x_0}$ and the kernels $P_0^\pi ,\ldots ,P_{N-1}^\pi$; for details see display (16) in Section 2 of the supplemental article Kern et al. (2020). Moreover let ${\varvec{X}}=(X_0,\ldots ,X_N)$ be the identity on ${\varOmega }$, i.e.

$$\begin{aligned} X_n(x_0,\ldots ,x_N) := x_n, \qquad (x_0,\ldots ,x_N)\in E^{N+1},\,n=0,\ldots ,N. \end{aligned}$$

(4)

Note that, for any $x_0\in E$, ${\varvec{P}}=(P_n)_{n=0}^{N-1}\in {{\mathcal {P}}}$, and $\pi \in {\varPi }$, the map ${\varvec{X}}$ can be regarded as an $(E^{N+1},{{\mathcal {E}}}^{\otimes (N+1)})$-valued random variable on the probability space $({\varOmega },{{\mathcal {F}}},{\mathbb {P}}^{x_0,{\varvec{P}};\pi })$ with distribution $\delta _{x_0}\otimes P_0^\pi \otimes \cdots \otimes P_{N-1}^\pi$.

It follows from Lemma 1 in the supplemental article Kern et al. (2020) that for any $x_0,{\widetilde{x}}_0, x_1,\ldots ,x_n\in E$, ${\varvec{P}}=(P_n)_{n=0}^{N-1}\in {{\mathcal {P}}}$, $\pi =(f_n)_{n=0}^{N-1}\in {\varPi }$, and $n=1,\ldots ,N-1$

• (i) ${\mathbb {P}}^{x_0,{\varvec{P}};\pi }[X_{0}\in \,\bullet \,]=\delta _{x_0}[\,\bullet \,]$,

• (ii) ${\mathbb {P}}^{x_0,{\varvec{P}};\pi }[X_{1}\in \,\bullet \,\Vert X_0={\widetilde{x}}_0]=P_0\big ((x_0,f_0(x_0)),\,\bullet \,\big )$,

• (iii) ${\mathbb {P}}^{x_0,{\varvec{P}};\pi }[X_{n+1}\in \,\bullet \,\Vert (X_0,X_1,\ldots ,X_n)=({\widetilde{x}}_0,x_1,\ldots ,x_n)]$$= P_n\big ((x_n,f_n(x_n)),\,\bullet \,\big )$,

• (iv) ${\mathbb {P}}^{x_0,{\varvec{P}};\pi }[X_{n+1}\in \,\bullet \,\Vert X_n=x_n]= P_n\big ((x_n,f_n(x_n)),\,\bullet \,\big )$.

The formulation of (ii)–(iv) is somewhat sloppy, because in general a (regular version of the) factorized conditional distribution of X given Y under ${\mathbb {P}}^{x_0,{\varvec{P}};\pi }$ (evaluated at a fixed set $B\in {{\mathcal {E}}}$) is only ${\mathbb {P}}_Y^{x_0,{\varvec{P}};\pi }$-a.s. unique. So assertion (iv) in fact means that the probability kernel $P_n((\,\cdot \,,f_n(\,\cdot \,)),\,\bullet \,)$ provides a (regular version of the) factorized conditional distribution of $X_{n+1}$ given $X_n$ under ${\mathbb {P}}^{x_0,{\varvec{P}};\pi }$, and analogously for (ii) and (iii). Note that the factorized conditional distribution in part (ii) is constant w.r.t. ${\widetilde{x}}_0\in E$. Assertions (iii) and (iv) together imply that the temporal evolution of $X_n$ is Markovian. This justifies the following terminology.

Definition 1

(MDP) Under law ${\mathbb {P}}^{x_0,{\varvec{P}};\pi }$ the random variable ${\varvec{X}}=(X_0,\ldots ,X_N)$ is called (discrete-time) Markov decision process (MDP) associated with initial state $x_0\in E$, transition function ${\varvec{P}}\in {{\mathcal {P}}}$, and strategy $\pi \in {\varPi }$.

2.2 Markov decision model and value function

Maintain the notation and terminology introduced in Sect. 2.1. In this subsection, we will first define a (discrete-time) Markov decision model (MDM) and introduce subsequently the corresponding value function. The latter will be derived from a reward maximization problem. Fix ${\varvec{P}}\in {{\mathcal {P}}}$, and let for each point of time $n=0,\ldots ,N-1$

$$\begin{aligned} r_n : D_n\longrightarrow {\mathbb {R}}\end{aligned}$$

be a $({{\mathcal {D}}}_n,{{\mathcal {B}}}({\mathbb {R}}))$-measurable map, referred to as one-stage reward function. Here $r_n(x,a)$ specifies the one-stage reward when action a is taken at time n in state x. Let

$$\begin{aligned} r_N : E\longrightarrow {\mathbb {R}}\end{aligned}$$

be an $({{\mathcal {E}}},{{\mathcal {B}}}({\mathbb {R}}))$-measurable map, referred to as terminal reward function. The value $r_N(x)$ specifies the reward of being in state x at terminal time N.

Denote by ${\varvec{A}}$ the family of all sets $A_n(x)$, $n=0,\ldots ,N-1$, $x\in E$, and set ${\varvec{r}}:=(r_n)_{n=0}^N$. Moreover let ${\varvec{X}}$ be defined as in (4) and recall Definition 1. Then we define our MDM as follows.

Definition 2

(MDM) The quintuple $({\varvec{X}},{\varvec{A}},{\varvec{P}},{\varPi },{\varvec{r}})$ is called (discrete-time) Markov decision model (MDM) associated with the family of action spaces ${\varvec{A}}$, transition function ${\varvec{P}}\in {{\mathcal {P}}}$, set of admissible strategies ${\varPi }$, and reward functions ${\varvec{r}}$.

In the sequel we will always assume that a MDM $({\varvec{X}},{\varvec{A}},{\varvec{P}},{\varPi },{\varvec{r}})$ satisfies the following Assumption (A). In Sect. 3.1 we will discuss some conditions on the MDM under which Assumption (A) holds. We will use ${\mathbb {E}}_{n,x_n}^{x_0,{\varvec{P}};\pi }$ to denote the expectation w.r.t. the factorized conditional distribution ${\mathbb {P}}^{x_0,{\varvec{P}};\pi }[\,\bullet \,\Vert X_n=x_n]$. For $n=0$, we clearly have ${\mathbb {P}}^{x_0,{\varvec{P}};\pi }[\,\bullet \,\Vert X_0=x_0]={\mathbb {P}}^{x_0,{\varvec{P}};\pi }[\,\bullet \,]$ for every $x_0\in E$; see Lemma 1 in the supplemental article Kern et al. (2020). In what follows we use the convention that the sum over the empty set is zero.

Assumption (A)

$\sup _{\pi =(f_n)_{n=0}^{N-1}\in {\varPi }}{\mathbb {E}}_{n,x_n}^{x_0,{\varvec{P}};\pi }[\,\sum _{k=n}^{N-1}|r_k(X_k,f_k(X_k))|+ |r_N(X_N)|\,]<\infty$ for any $x_n\in E$ and $n=0,\ldots ,N$.

Under Assumption (A) we may define in a MDM $({\varvec{X}},{\varvec{A}},{\varvec{P}},{\varPi },{\varvec{r}})$ for any $\pi =(f_n)_{n=0}^{N-1}\in {\varPi }$ and $n=0,\ldots ,N$ a map $V_{n}^{{\varvec{P}};\pi }:E\rightarrow {\mathbb {R}}$ through

$$\begin{aligned} V_n^{{\varvec{P}};\pi }(x_n) := {\mathbb {E}}_{n,x_n}^{x_0,{\varvec{P}};\pi }\Big [\sum _{k=n}^{N-1} r_k(X_k,f_k(X_k)) + r_N(X_N)\Big ]. \end{aligned}$$

(5)

As a factorized conditional expectation this map is $({{\mathcal {E}}},{{\mathcal {B}}}({\mathbb {R}}))$-measurable (for any $\pi \in {\varPi }$ and $n=0,\ldots ,N$). Note that for $n=1,\ldots ,N$ the right-hand side of (5) does not depend on $x_0$; see Lemma 2 in the supplemental article Kern et al. (2020). Therefore the map $V_n^{{\varvec{P}};\pi }(\cdot )$ need not be equipped with an index $x_0$.

The value $V_{n}^{{\varvec{P}};\pi }(x_n)$ specifies the expected total reward from time n to N of ${\varvec{X}}$ under ${\mathbb {P}}^{x_0,{\varvec{P}};\pi }$ when strategy $\pi$ is used and ${\varvec{X}}$ is in state $x_n$ at time n. It is natural to ask for those strategies $\pi \in {\varPi }$ for which the expected total reward from time 0 to N is maximal for all initial states $x_0\in E$. This results in the following optimization problem:

$$\begin{aligned} V_0^{{\varvec{P}};\pi }(x_0) \longrightarrow \max \ \text{(in } \pi \in {\varPi })\,! \end{aligned}$$

(6)

If a solution $\pi ^{{\varvec{P}}}$ to the optimization problem (6) (in the sense of Definition 4 ahead) exists, then the corresponding maximal expected total reward is given by the so-called value function (at time 0 ).

Definition 3

(Value function) For a MDM $({\varvec{X}},{\varvec{A}},{\varvec{P}},{\varPi },{\varvec{r}})$ the value function at time $n\in \{0,\ldots ,N\}$ is the map $V_{n}^{{\varvec{P}}}:E\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} V_n^{{\varvec{P}}}(x_n) := \sup _{\pi \in {\varPi }}V_n^{{\varvec{P}};\pi }(x_n). \end{aligned}$$

(7)

Note that the value function $V_{n}^{{\varvec{P}}}$ is well defined due to Assumption (A) but not necessarily $({{\mathcal {E}}},{{\mathcal {B}}}({\mathbb {R}}))$-measurable. The measurability holds true, for example, if the sets $F_{n},\ldots ,F_{N-1}$ are at most countable or if conditions (a)–(c) of Theorem 2 in the supplemental article Kern et al. 2020) are satisfied; see also Remark 1(i) in the supplemental article Kern et al. (2020).

Definition 4

(Optimal strategy) In a MDM $({\varvec{X}},{\varvec{A}},{\varvec{P}},{\varPi },{\varvec{r}})$ a strategy $\pi ^{{\varvec{P}}}\in {\varPi }$ is called optimal w.r.t. ${\varvec{P}}$ if

$$\begin{aligned} V_0^{{\varvec{P}};\pi ^{{\varvec{P}}}}(x_0) = V_0^{{\varvec{P}}}(x_0)\quad \text{ for } \text{ all } x_0\in E. \end{aligned}$$

(8)

In this case $V_0^{{\varvec{P}};\pi ^{{\varvec{P}}}}(x_0)$ is called optimal value (function), and we denote by ${\varPi }({\varvec{P}})$ the set of all optimal strategies w.r.t. ${\varvec{P}}$. Further, for any given $\delta >0$, a strategy $\pi ^{{\varvec{P}};\delta }\in {\varPi }$ is called $\delta$-optimal w.r.t. ${\varvec{P}}$ in a MDM $({\varvec{X}},{\varvec{A}},{\varvec{P}},{\varPi },{\varvec{r}})$ if

$$\begin{aligned} V_0^{{\varvec{P}}}(x_0) - \delta \le V_0^{{\varvec{P}};\pi ^{{\varvec{P}};\delta }}(x_0) \quad \text{ for } \text{ all } x_0\in E, \end{aligned}$$

(9)

and we denote by ${\varPi }({\varvec{P}};\delta )$ the set of all $\delta$-optimal strategies w.r.t. ${\varvec{P}}$.

Note that condition (8) requires that $\pi ^{{\varvec{P}}}\in {\varPi }$ is an optimal strategy for all possible initial states $x_0\in E$. Though, in some situations it might be sufficient to ensure that $\pi ^{{\varvec{P}}}\in {\varPi }$ is an optimal strategy only for some fixed initial state $x_0$. For a brief discussion of the existence and computation of optimal strategies, see Section 6 of the supplemental article Kern et al. (2020).

Remark 1

(i) In practice, the choice of an action can possibly be based on historical observations of states and actions. In particular one could relinquish the Markov property of the decision rules and allow them to depend also on previous states and actions. Then one might hope that the corresponding (deterministic) history-dependent strategies improve the optimal value of a MDM $({\varvec{X}},{\varvec{A}},{\varvec{P}},{\varPi },{\varvec{r}})$. However, it is known that the optimal value of a MDM $({\varvec{X}},{\varvec{A}},{\varvec{P}},{\varPi },{\varvec{r}})$ can not be enhanced by considering history-dependent strategies; see, e.g., Theorem 18.4 in Hinderer (1970) or Theorem 4.5.1 in Puterman (1994).

(ii) Instead of considering the reward maximization problem (6) one could as well be interested in minimizing expected total costs over the time horizon N. In this case, one can maintain the previous notation and terminology when regarding the functions $r_n$ and $r_N$ as the one-stage costs and the terminal costs, respectively. The only thing one has to do is to replace “$\sup$” by “$\inf$” in the representation (7) of the value function. Accordingly, a strategy $\pi ^{{\varvec{P}};\delta }\in {\varPi }$ will be $\delta$-optimal for a given $\delta >0$ if in condition (9) “$-\delta$” and “$\le$” are replaced by “$+\delta$” and “$\ge$”. $\square$

3 ‘Differentiability’ in ${\varvec{P}}$ of the optimal value

In this section, we show that the value function of a MDM, regarded as a real-valued functional on a set of transition functions, is ‘differentiable’ in a certain sense. The notion of ‘differentiability’ we use for functionals that are defined on a set of admissible transition functions will be introduced in Sect. 3.4. The motivation of our notion of ‘differentiability’ was discussed subsequent to (1). Before defining ‘differentiability’ in a precise way, we will explain in Sect. 3.2–3.3 how we measure the distance between transition functions. In Sect. 3.5–3.6 we will specify the ‘Hadamard derivative’ of the value function. At first, however, we will discuss in Sect. 3.1 some conditions under which Assumption (A) holds true. Throughout this section, ${\varvec{A}}$, ${\varPi }$, and ${\varvec{r}}$ are fixed.

3.1 Bounding functions

Recall from Section 2 that ${{\mathcal {P}}}$ stands for the set of all transition functions, i.e. of all N-tuples ${\varvec{P}}=(P_n)_{n=0}^{N-1}$ of probability kernels $P_n$ from $(D_n,{{\mathcal {D}}}_n)$ to $(E,{{\mathcal {E}}})$. Let $\psi :E\rightarrow {\mathbb {R}}_{\ge 1}$ be an $({{\mathcal {E}}},{{\mathcal {B}}}({\mathbb {R}}_{\ge 1}))$-measurable map, referred to as gauge function, where ${\mathbb {R}}_{\ge 1}:=[1,\infty )$. Denote by ${\mathbb {M}}(E)$ the set of all $({{\mathcal {E}}},{{\mathcal {B}}}({\mathbb {R}}))$-measurable maps $h\in {\mathbb {R}}^E$, and let ${\mathbb {M}}_\psi (E)$ be the set of all $h\in {\mathbb {M}}(E)$ satisfying $\Vert h\Vert _{\psi }:=\sup _{x\in E}|h(x)|/\psi (x)<\infty$. The following definition is adapted from Bäuerle and Rieder (2011), Müller (1997a), Wessels (1977). Conditions (a)–(c) of this definition are sufficient for the well-definiteness of $V_{n}^{{\varvec{P}};\pi }$ (and $V_{n}^{{\varvec{P}}}$); see Lemma 1 ahead.

Definition 5

(Bounding function) Let ${{\mathcal {P}}}'\subseteq {{\mathcal {P}}}$. A gauge function $\psi :E\rightarrow {\mathbb {R}}_{\ge 1}$ is called a bounding function for the family of MDMs $\{({\varvec{X}},{\varvec{A}},{\varvec{P}},{\varPi },{\varvec{r}}):{\varvec{P}}\in {{\mathcal {P}}}'\}$ if there exist finite constants $K_1,K_2,K_3>0$ such that the following conditions hold for any $n=0,\ldots ,N-1$ and ${\varvec{P}}=(P_n)_{n=0}^{N-1}\in {{\mathcal {P}}}'$.

• (a) $|r_n(x,a)| \le K_1 \psi (x)$ for all $(x,a)\in D_n$.

• (b) $|r_N(x)| \le K_2 \psi (x)$ for all $x\in E$.

• (c) $\int _E\psi (y)\,P_n\big ((x,a),dy\big )\le K_3 \psi (x)$ for all $(x,a)\in D_n$.

If ${{\mathcal {P}}}'=\{{\varvec{P}}\}$ for some ${\varvec{P}}\in {{\mathcal {P}}}$, then $\psi$ is called a bounding function for the MDM $({\varvec{X}},{\varvec{A}},{\varvec{P}},{\varPi },{\varvec{r}})$.

Note that the conditions in Definition 5 do not depend on the set ${\varPi }$. That is, the terminology bounding function is independent of the set of all (admissible) strategies. Also note that conditions (a) and (b) can be satisfied by unbounded reward functions.

The following lemma, whose proof can be found in Subsection 3.1 of the supplemental article Kern et al. (2020), ensures that Assumption (A) is satisfied when the underlying MDM possesses a bounding function.

Lemma 1

Let ${{\mathcal {P}}}'\subseteq {{\mathcal {P}}}$. If the family of MDMs $\{({\varvec{X}},{\varvec{A}},{\varvec{P}},{\varPi },{\varvec{r}}):{\varvec{P}}\in {{\mathcal {P}}}'\}$ possesses a bounding function $\psi$, then Assumption (A) is satisfied for any ${\varvec{P}}\in {{\mathcal {P}}}'$. Moreover, the expectation in Assumption (A) is even uniformly bounded w.r.t. ${\varvec{P}}\in {{\mathcal {P}}}'$, and $V_n^{{\varvec{P}};\pi }(\cdot )$ is contained in ${\mathbb {M}}_\psi (E)$ for any ${\varvec{P}}\in {{\mathcal {P}}}'$, $\pi \in {\varPi }$, and $n=0,\ldots ,N$.

3.2 Metric on set of probability measures

In Sect. 3.4 we will work with a (semi-) metric (on a set of transition functions) to be defined in (11) below. As it is common in the theory of probability metrics (see, e.g., p. 10 ff in Rachev 1991), we allow the distance between two probability measures and the distance between two transition functions to be infinite. That is, we adapt the axioms of a (semi-) metric but we allow a (semi-) metric to take values in ${{\overline{{\mathbb {R}}}}}_{\ge 0}:={\mathbb {R}}_{\ge 0}\cup \{\infty \}$ rather than only in ${\mathbb {R}}_{\ge 0}:=[0,\infty )$.

Let $\psi$ be any gauge function, and denote by ${{\mathcal {M}}}_1^\psi (E)$ the set of all $\mu \in {{\mathcal {M}}}_1(E)$ for which $\int _E \psi \,d\mu <\infty$. Note that the integral $\int _E h\,d\mu$ exists and is finite for any $h\in {\mathbb {M}}_\psi (E)$ and $\mu \in {{\mathcal {M}}}_1^\psi (E)$. For any fixed ${\mathbb {M}}\subseteq {\mathbb {M}}_\psi (E)$, the distance between two probability measures $\mu ,\nu \in {{\mathcal {M}}}_1^\psi (E)$ can be measured by

$$\begin{aligned} d_{{\mathbb {M}}}(\mu ,\nu ) := \sup _{h\in {\mathbb {M}}}\Big |\int _E h\,d\mu - \int _E h\,d\nu \Big |. \end{aligned}$$

(10)

Note that (10) indeed defines a map $d_{{\mathbb {M}}}:{{\mathcal {M}}}_1^\psi (E)\times {{\mathcal {M}}}_1^\psi (E)\rightarrow {\overline{{\mathbb {R}}}}_{\ge 0}$ which is symmetric and fulfills the triangle inequality, i.e. $d_{{\mathbb {M}}}$ provides a semi-metric. If ${\mathbb {M}}$ separates points in ${{\mathcal {M}}}_1^\psi (E)$ (i.e. if any two $\mu ,\nu \in {{\mathcal {M}}}_1^\psi (E)$ coincide when $\int _E h\,d\mu =\int _E h\,d\nu$ for all $h\in {\mathbb {M}}$), then $d_{{\mathbb {M}}}$ is even a metric. It is sometimes called integral probability metric or probability metric with a $\zeta$-structure; see Müller (1997b), Zolotarev (1983). In some situations the (semi-) metric $d_{\mathbb {M}}$ (with ${\mathbb {M}}$ fixed) can be represented by the right-hand side of (10) with ${\mathbb {M}}$ replaced by a different subset ${\mathbb {M}}'$ of ${\mathbb {M}}_\psi (E)$. Each such set ${\mathbb {M}}'$ is said to be a generator of $d_{\mathbb {M}}$. The largest generator of $d_{\mathbb {M}}$ is called the maximal generator of $d_{\mathbb {M}}$ and denoted by ${\overline{{\mathbb {M}}}}$. That is, ${\overline{{\mathbb {M}}}}$ is defined to be the set of all $h\in {\mathbb {M}}_\psi (E)$ for which $|\int _Eh\,d\mu -\int _Eh\,d\nu |\le d_{\mathbb {M}}(\mu ,\nu )$ for all $\mu ,\nu \in {{\mathcal {M}}}_1^\psi (E)$.

We now give some examples for the distance $d_{{\mathbb {M}}}$. The metrics in the first four examples were already mentioned in Müller (1997a, b). In the last three examples $d_{\mathbb {M}}$ metricizes the $\psi$-weak topology. The latter is defined to be the coarsest topology on ${{\mathcal {M}}}_1^\psi (E)$ for which all mappings $\mu \mapsto \int _E h\,d\mu$, $h\in {\mathbb {C}}_\psi (E)$, are continuous. Here ${\mathbb {C}}_\psi (E)$ is the set of all continuous functions in ${\mathbb {M}}_\psi (E)$. If specifically $\psi \equiv 1$, then ${{\mathcal {M}}}_1^\psi (E)={{\mathcal {M}}}_1(E)$ and the $\psi$-weak topology is nothing but the classical weak topology. In Section 2 in Krätschmer et al. (2017) one can find characterizations of those subsets of ${{\mathcal {M}}}_1^\psi (E)$ on which the relative $\psi$-weak topology coincides with the relative weak topology.

Example 1

Let $\psi :\equiv 1$ and ${\mathbb {M}}:={\mathbb {M}}_{{{{\text {TV}}}}}$, where ${\mathbb {M}}_{{{{\text {TV}}}}}:=\{\mathbb {1}_B : B\in {{\mathcal {E}}}\}\subseteq {\mathbb {M}}_\psi (E)$. Then $d_{\mathbb {M}}$ equals the total variation metric $d_{{{{\text {TV}}}}}(\mu ,\nu ) := \sup _{B\in {{\mathcal {E}}}}|\mu [B] - \nu [B]|$. The set ${\mathbb {M}}_{{{{\text {TV}}}}}$ clearly separates points in ${{\mathcal {M}}}_1^{\psi }(E)={{\mathcal {M}}}_1(E)$. The maximal generator of $d_{{{{\text {TV}}}}}$ is the set ${\overline{{\mathbb {M}}}}_{{{{\text {TV}}}}}$ of all $h\in {\mathbb {M}}(E)$ with ${{\text {sp}}}(h):=\sup _{x\in E} h(x) - \inf _{x\in E} h(x)\le 1$; see Theorem 5.4 in Müller (1997b). $\square$

Example 2

For $E={\mathbb {R}}$, let $\psi :\equiv 1$ and ${\mathbb {M}}:={\mathbb {M}}_{\text {Kolm}}$, where ${\mathbb {M}}_{\text {Kolm}}:=\{\mathbb {1}_{(-\infty ,t]} : t\in {\mathbb {R}}\}\subseteq {\mathbb {M}}_\psi ({\mathbb {R}})$. Then $d_{\mathbb {M}}$ equals the Kolmogorov metric $d_{\text {Kolm}}(\mu ,\nu ) := \sup _{t\in {\mathbb {R}}}|F_{\mu }(t) - F_{\nu }(t)|$, where $F_\mu$ and $F_\nu$ refer to the distribution functions of $\mu$ and $\nu$, respectively. The set ${\mathbb {M}}_{\text {Kolm}}$ clearly separates points in ${{\mathcal {M}}}_1^{\psi }({\mathbb {R}})={{\mathcal {M}}}_1({\mathbb {R}})$. The maximal generator of $d_{\text {Kolm}}$ is the set ${\overline{{\mathbb {M}}}}_{\text {Kolm}}$ of all $h\in {\mathbb {R}}^{\mathbb {R}}$ with ${\mathbb {V}}(h)\le 1$, where ${\mathbb {V}}(h)$ denotes the total variation of h; see Theorem 5.2 in Müller (1997b). $\square$

Example 3

Assume that $(E,d_E)$ is a metric space and let ${{\mathcal {E}}}:={{\mathcal {B}}}(E)$. Let $\psi :\equiv 1$ and ${\mathbb {M}}:={\mathbb {M}}_{\text {BL}}$, where ${\mathbb {M}}_{\text {BL}}:=\{h\in {\mathbb {R}}^E: \Vert h\Vert _{\text {BL}}\le 1 \}\subseteq {\mathbb {M}}_\psi (E)$ with $\Vert h\Vert _{\text {BL}}:=\max \{\Vert h\Vert _{\infty },\,\Vert h\Vert _{\text {Lip}}\}$ for $\Vert h\Vert _{\infty }:=\sup _{x\in E}|h(x)|$ and $\Vert h\Vert _{\text {Lip}}:=\sup _{x,y\in E:\,x\ne y}|h(x)-h(y)|/d_E(x,y)$. Then $d_{\mathbb {M}}$ is nothing but the bounded Lipschitz metric $d_{\text {BL}}$. The set ${\mathbb {M}}_{\text {BL}}$ separates points in ${{\mathcal {M}}}_1^{\psi }(E)={{\mathcal {M}}}_1(E)$; see Lemma 9.3.2 in Dudley (2002). Moreover it is known (see, e.g., Theorem 11.3.3 in Dudley 2002) that if E is separable then $d_{\text {BL}}$ metricizes the weak topology on ${{\mathcal {M}}}_1^\psi (E)={{\mathcal {M}}}_1(E)$. $\square$

Example 4

Assume that $(E,d_E)$ is a metric space and let ${{\mathcal {E}}}:={{\mathcal {B}}}(E)$. For some fixed $x'\in E$, let $\psi (x):= 1 + d_E(x,x')$ and ${\mathbb {M}}:={\mathbb {M}}_{{{{\text {Kant}}}}}$, where ${\mathbb {M}}_{{{\text {Kant}}}}:=\{h\in {\mathbb {R}}^E: \Vert h\Vert _{\text {Lip}}\le 1 \}\subseteq {\mathbb {M}}_\psi (E)$ with $\Vert h\Vert _{\text {Lip}}$ as in Example 3. Then $d_{\mathbb {M}}$ is nothing but the Kantorovich metric $d_{{{{\text {Kant}}}}}$. The set ${\mathbb {M}}_{{{{\text {Kant}}}}}$ separates points in ${{\mathcal {M}}}_1^{\psi }(E)$, because ${\mathbb {M}}_{\text {BL}}$ ($\subseteq {\mathbb {M}}_{{{{\text {Kant}}}}}$) does. It is known (see, e.g., Theorem 7.12 in Villani 2003) that if E is complete and separable then $d_{{{{\text {Kant}}}}}$ metricizes the $\psi$-weak topology on ${{\mathcal {M}}}_1^\psi (E)$.

Recall from Vallender (1974) that for $E={\mathbb {R}}$ the $L^1$-Wasserstein metric $d_{{{{{\text {Wass}}}}}_1}(\mu ,\nu ) := \int _{-\infty }^\infty |F_\mu (t) - F_\nu (t)|\,dt$ coincides with the Kantorovich metric. In this case the $\psi$-weak topology is also referred to as $L^1$-weak topology. Note that the $L^1$-Wasserstein metric is a conventional metric for measuring the distance between probability distributions; see, for instance, Dall’Aglio (1956), Kantorovich and Rubinstein (1958), Vallender (1974) for the general concept and Bellini et al. (2014), Kiesel et al. (2016), Krätschmer et al. (2012), Krätschmer and Zähle (2017) for recent applications. $\square$

Although the Kantorovich metric is a popular and well established metric, for the application in Section 4 we will need the following generalization from $\alpha =1$ to $\alpha \in (0,1]$.

Example 5

Assume that $(E,d_E)$ is a metric space and let ${{\mathcal {E}}}:={{\mathcal {B}}}(E)$. For some fixed $x'\in E$ and $\alpha \in (0,1]$, let $\psi (x):= 1 + d_E(x,x')^\alpha$ and ${\mathbb {M}}:={\mathbb {M}}_{{{{\text {H}}}{\ddot{\text {o}}{{\text {l}}}}},\alpha }$, where ${\mathbb {M}}_{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }:=\{h\in {\mathbb {R}}^E: \Vert h\Vert _{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }\le 1 \}\subseteq {\mathbb {M}}_\psi (E)$ with $\Vert h\Vert _{{{{\text {H}}}\ddot{{{\text {o}}}}{{\text {l}}}},\alpha }:=\sup _{x,y\in E:\,x\ne y}|h(x)-h(y)|/d_E(x,y)^\alpha$. The set ${\mathbb {M}}_{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }$ separates points in ${{\mathcal {M}}}_1^{\psi }(E)$ (this follows with similar arguments as in the proof of Lemma 9.3.2 in Dudley 2002). Then $d_{{\mathbb {M}}}$ provides a metric on ${{\mathcal {M}}}_1^\psi (E)$ which we denote by $d_{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }$ and refer to as Hölder-$\alpha$metric. Especially when dealing with risk averse utility functions (as, e.g., in Section 4) this metric can be beneficial. Lemma 9 in Section 7 of the supplemental article Kern et al. (2020) shows that if E is complete and separable then $d_{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }$ metricizes the $\psi$-weak topology on ${{\mathcal {M}}}_1^\psi (E)$. $\square$

3.3 Metric on set of transition functions

Maintain the notation from Sect. 3.2. Let us denote by $\overline{{\mathcal {P}}}_\psi$ the set of all transition functions ${\varvec{P}}=(P_n)_{n=0}^{N-1}\in {{\mathcal {P}}}$ satisfying $\int _E\psi (y)\,P_n((x,a),dy)<\infty$ for all $(x,a)\in D_n$ and $n=0,\ldots ,N-1$. That is, $\overline{{\mathcal {P}}}_\psi$ consists of those transition functions ${\varvec{P}}=(P_n)_{n=0}^{N-1}\in {{\mathcal {P}}}$ with $P_n((x,a),\,\bullet \,)\in {{\mathcal {M}}}_1^\psi (E)$ for all $(x,a)\in D_n$ and $n=0,\ldots ,N-1$. Hence, for the elements ${\varvec{P}}=(P_n)_{n=0}^{N-1}$ of $\overline{{\mathcal {P}}}_\psi$ all integrals of the shape $\int _E h(y)\,P_n((x,a),dy)$, $h\in {\mathbb {M}}_\psi (E)$, $(x,a)\in D_n$, $n=0,\ldots ,N-1$, exist and are finite. In particular, for two transition functions ${\varvec{P}}=(P_n)_{n=0}^{N-1}$ and ${\varvec{Q}}=(Q_n)_{n=0}^{N-1}$ from $\overline{{\mathcal {P}}}_\psi$ the distance $d_{\mathbb {M}}(P_n((x,a),\,\bullet \,),Q_n((x,a),\,\bullet \,))$ is well defined for all $(x,a)\in D_n$ and $n=0,\ldots ,N-1$ (recall that ${\mathbb {M}}\subseteq {\mathbb {M}}_\psi (E)$). So we can define the distance between two transition functions ${\varvec{P}}=(P_n)_{n=0}^{N-1}$ and ${\varvec{Q}}=(Q_n)_{n=0}^{N-1}$ from $\overline{{\mathcal {P}}}_\psi$ by

$$\begin{aligned} d_{\infty ,{\mathbb {M}}}^{\phi }({\varvec{P}},{\varvec{Q}}):=\max _{n=0,\ldots ,N-1}\sup _{(x,a)\in D_n}\,\frac{1}{\phi (x)}\cdot d_{{\mathbb {M}}}\Big (P_n\big ((x,a),\,\bullet \,\big ),Q_n\big ((x,a),\,\bullet \,\big )\Big )\nonumber \\ \end{aligned}$$

(11)

for another gauge function $\phi :E\rightarrow {\mathbb {R}}_{\ge 1}$. Note that (11) defines a semi-metric $d_{\infty ,{\mathbb {M}}}^{\phi }:\overline{{\mathcal {P}}}_\psi \times \overline{{\mathcal {P}}}_\psi \rightarrow {\overline{{\mathbb {R}}}}_{\ge 0}$ on $\overline{{\mathcal {P}}}_\psi$ which is even a metric if ${\mathbb {M}}$ separates points in ${{\mathcal {M}}}_1^\psi (E)$.

Maybe apart from the factor $1/\phi (x)$, the definition of $d_{\infty ,{\mathbb {M}}}^{\phi }({\varvec{P}},{\varvec{Q}})$ in (11) is quite natural and in line with the definition of a distance introduced by Müller (1997a, p. 880). In Müller (1997a), Müller considers time-homogeneous MDMs, so that the transition kernels do not depend on n. He fixed a state x and took the supremum only over all admissible actions a in state x. That is, for any $x\in E$ he defined the distance between $P((x,\,\cdot \,),\,\bullet \,)$ and $Q((x,\,\cdot \,),\,\bullet \,)$ by $\sup _{a\in A(x)}d_{{\mathbb {M}}}(P((x,a),\,\bullet \,),Q((x,a),\,\bullet \,))$. To obtain a reasonable distance between $P_n$ and $Q_n$ it is however natural to take the supremum of the distance between $P_n((x,\,\cdot \,),\,\bullet \,)$ and $Q_n((x,\,\cdot \,),\,\bullet \,)$ w.r.t. $d_{\mathbb {M}}$ uniformly over a and over x.

The factor $1/\phi (x)$ in (11) causes that the (semi-) metric $d_{\infty ,{\mathbb {M}}}^{\phi }$ is less strict compared to the (semi-) metric $d_{\infty ,{\mathbb {M}}}^1$ which is defined as in (11) with $\phi :\equiv 1$. For a motivation of considering the factor $1/\phi (x)$, see part (iii) of Remark 2 and the discussion afterwards.

3.4 Definition of ‘differentiability’

Let $\psi$ be any gauge function, and fix some ${{\mathcal {P}}}_\psi \subseteq \overline{{\mathcal {P}}}_\psi$ being closed under mixtures (i.e. $(1-\varepsilon ){\varvec{P}}+\varepsilon {\varvec{Q}}\in {{\mathcal {P}}}_\psi$ for any ${\varvec{P}},{\varvec{Q}}\in {{\mathcal {P}}}_\psi$, $\varepsilon \in (0,1)$). The set ${{\mathcal {P}}}_\psi$ will be equipped with the distance $d_{\infty ,{\mathbb {M}}}^{\phi }$ introduced in (11). In Definition 7 below we will introduce a reasonable notion of ‘differentiability’ for an arbitrary functional ${{\mathcal {V}}}:{{\mathcal {P}}}_\psi \rightarrow L$ taking values in a normed vector space $(L,\Vert \cdot \Vert _L)$. It is related to the general functional analytic concept of (tangential) ${{\mathcal {S}}}$-differentiability introduced by Sebastião e Silva (1956) and Averbukh and Smolyanov (1967); see also Fernholz (1983), Gill (1989), Shapiro (1990) for applications. However, ${{\mathcal {P}}}_{\psi }$ is $\textit{not}$ a vector space. This implies that Definition 7 differs from the classical notion of (tangential) ${{\mathcal {S}}}$-differentiability. For that reason we will use inverted commas and write ‘${{\mathcal {S}}}$-differentiability’ instead of ${{\mathcal {S}}}$-differentiability. Due to the missing vector space structure, we in particular need to allow the tangent space to depend on the point ${\varvec{P}}\in {{\mathcal {P}}}_\psi$ at which ${{\mathcal {V}}}$ is differentiated. The role of the ‘tangent space’ will be played by the set

$$\begin{aligned} {{\mathcal {P}}}_{\psi }^{{\varvec{P}};\pm } := \{{\varvec{Q}}-{\varvec{P}}:\,{\varvec{Q}}\in {{\mathcal {P}}}_\psi \} \end{aligned}$$

whose elements ${\varvec{Q}}-{\varvec{P}}:=(Q_0-P_0,\ldots ,Q_{N-1}-P_{N-1})$ can be seen as signed transition functions. In Definition 7 we will employ the following terminology.

Definition 6

Let ${\mathbb {M}}\subseteq {\mathbb {M}}_\psi (E)$, $\phi$ be another gauge function, and fix ${\varvec{P}}\in {{\mathcal {P}}}_\psi$. A map ${{\mathcal {W}}}:{{\mathcal {P}}}_{\psi }^{{\varvec{P}};\pm }\rightarrow L$ is said to be $({\mathbb {M}},\phi )$-continuous if the mapping ${\varvec{Q}}\mapsto {{\mathcal {W}}}({\varvec{Q}}-{\varvec{P}})$ from ${{\mathcal {P}}}_\psi$ to L is $(d_{\infty ,{\mathbb {M}}}^{\phi },\Vert \cdot \Vert _L)$-continuous.

For the following definition it is important to note that ${\varvec{P}}+ \varepsilon ({\varvec{Q}}- {\varvec{P}})$ lies in ${{\mathcal {P}}}_\psi$ for any ${\varvec{P}},{\varvec{Q}}\in {{\mathcal {P}}}_\psi$ and $\varepsilon \in (0,1]$.

Definition 7

(‘${{\mathcal {S}}}$-differentiability’) Let ${\mathbb {M}}\subseteq {\mathbb {M}}_\psi (E)$, $\phi$ be another gauge function, and fix ${\varvec{P}}\in {{\mathcal {P}}}_{\psi }$. Moreover let ${{\mathcal {S}}}$ be a system of subsets of ${{\mathcal {P}}}_{\psi }$. A map ${{\mathcal {V}}}:{{\mathcal {P}}}_{\psi }\rightarrow L$ is said to be ‘${{\mathcal {S}}}$-differentiable’ at ${\varvec{P}}$ w.r.t. $({\mathbb {M}},\phi )$ if there exists an $({\mathbb {M}},\phi )$-continuous map $\dot{{\mathcal {V}}}_{{\varvec{P}}}:{{\mathcal {P}}}_{\psi }^{{\varvec{P}};\pm }\rightarrow L$ such that

$$\begin{aligned} \lim _{m\rightarrow \infty }\Big \Vert \frac{{{\mathcal {V}}}({\varvec{P}}+\varepsilon _m({\varvec{Q}}-{\varvec{P}}))-{{\mathcal {V}}}({\varvec{P}})}{\varepsilon _m} - \dot{{\mathcal {V}}}_{{\varvec{P}}}({\varvec{Q}}-{\varvec{P}})\Big \Vert _L=0 \quad \text{ uniformly } \text{ in } {\varvec{Q}}\in {{\mathcal {K}}}\nonumber \\ \end{aligned}$$

(12)

for every ${{\mathcal {K}}}\in {{\mathcal {S}}}$ and every sequence $(\varepsilon _m)\in (0,1]^{{\mathbb {N}}}$ with $\varepsilon _m\rightarrow 0$. In this case, $\dot{{\mathcal {V}}}_{{\varvec{P}}}$ is called ‘${{\mathcal {S}}}$-derivative’ of ${{\mathcal {V}}}$ at ${\varvec{P}}$ w.r.t. $({\mathbb {M}},\phi )$.

Note that in Definition 7 the derivative is not required to be linear (in fact the derivative is not even defined on a vector space). This is another point where Definition 7 differs from the functional analytic definition of (tangential) ${{\mathcal {S}}}$-differentiability. However, non-linear derivatives are common in the field of mathematical optimization; see, for instance, Römisch (2004), Shapiro (1990).

Remark 2

(i) At least in the case $L={\mathbb {R}}$, the ‘${{\mathcal {S}}}$-derivative’ $\dot{{\mathcal {V}}}_{{\varvec{P}}}$ evaluated at ${\varvec{Q}}- {\varvec{P}}$, i.e. $\dot{{\mathcal {V}}}_{{\varvec{P}}}({\varvec{Q}}-{\varvec{P}})$, can be seen as a measure for the first-order sensitivity of the functional ${{\mathcal {V}}}: {{\mathcal {P}}}_{\psi }\rightarrow {\mathbb {R}}$ w.r.t. a change of the argument from ${\varvec{P}}$ to $(1-\varepsilon ){\varvec{P}}+ \varepsilon {\varvec{Q}}$, with $\varepsilon >0$ small, for some given transition function ${\varvec{Q}}$.

(ii) The prefix ‘${{\mathcal {S}}}$-’ in Definition 7 provides the following information. Since the convergence in (12) is required to be uniform in ${\varvec{Q}}\in {{\mathcal {K}}}$, the values of the first-order sensitivities $\dot{{\mathcal {V}}}_{{\varvec{P}}}({\varvec{Q}}-{\varvec{P}})$, ${\varvec{Q}}\in {{\mathcal {K}}}$, can be compared with each other with clear conscience for any fixed ${{\mathcal {K}}}\in {{\mathcal {S}}}$. It is therefore favorable if the sets in ${{\mathcal {S}}}$ are large. However, the larger the sets in ${{\mathcal {S}}}$, the stricter the condition of ‘${{\mathcal {S}}}$-differentiability’.

(iii) The subset ${\mathbb {M}}$ ($\subseteq {\mathbb {M}}_\psi (E)$) and the gauge function $\phi$ tell us in a way how ‘robust’ the ‘${{\mathcal {S}}}$-derivative’ $\dot{{\mathcal {V}}}_{{\varvec{P}}}$ is w.r.t. changes in ${\varvec{Q}}$: The smaller the set ${\mathbb {M}}$ and the ‘steeper’ the gauge function $\phi$, the less strict the metric $d_{\infty ,{\mathbb {M}}}^{\phi }({\varvec{P}},{\varvec{Q}})$ (given by (11)) and the more robust $\dot{{\mathcal {V}}}_{{\varvec{P}}}({\varvec{Q}}-{\varvec{P}})$ in ${\varvec{Q}}$. It is thus favorable if the set ${\mathbb {M}}$ is small and the gauge function $\phi$ is ‘steep’. However, the smaller ${\mathbb {M}}$ and the ‘steeper’ $\phi$, the stricter the condition of $({\mathbb {M}},\phi )$-continuity (and thus of ‘${{\mathcal {S}}}$-differentiability’ w.r.t. $({\mathbb {M}},\phi )$). More precisely, if ${\mathbb {M}}_1\subseteq {\mathbb {M}}_2$ and $\phi _1\ge \phi _2$ then $({\mathbb {M}}_1,\phi _1)$-continuity implies $({\mathbb {M}}_2,\phi _2)$-continuity.

(iv) In general the choice of ${{\mathcal {S}}}$ and the choice of the pair $({\mathbb {M}},\phi )$ in Definition 7 do not necessarily depend on each other. However in the specific settings (b) and (c) in Definition 8, and in particular in the application in Section 4, they do. $\square$

In the general framework of our main result (Theorem 1) we can not choose $\phi$ ‘steeper’ than the gauge function $\psi$ which plays the role of a bounding function there. Indeed, the proof of $({\mathbb {M}},\psi )$-continuity of the map $\dot{{\mathcal {V}}}_{{\varvec{P}}}:{{\mathcal {P}}}_{\psi }^{{\varvec{P}};\pm }\rightarrow {\mathbb {R}}$ in Theorem 1 does not work anymore if $d_{\infty ,{\mathbb {M}}}^{\psi }$ is replaced by $d_{\infty ,{\mathbb {M}}}^{\phi }$ for any gauge function $\phi$ ‘steeper’ than $\psi$. And here it does not matter how exactly ${{\mathcal {S}}}$ is chosen.

In the application in Section 4, the set $\{{\varvec{Q}}_{{\varDelta },\tau }: {\varDelta }\in [0,\delta ]\}$ should be contained in ${{\mathcal {S}}}$ (for details see Remark 10). This set can be shown to be (relatively) compact w.r.t. $d_{\infty ,{\mathbb {M}}}^{\phi }$ for $\phi (x)=\psi (x)$ ($:=1+u_{\alpha }(x)$) but not for any ‘flatter’ gauge function $\phi$. So, in this example, and certainly in many other examples, relatively compact subsets of ${{\mathcal {P}}}_\psi$ w.r.t. $d_{\infty ,{\mathbb {M}}}^{\psi }$ should be contained in ${{\mathcal {S}}}$. It is thus often beneficial to know that the value functional is ‘differentiable’ in the sense of part (b) of the following Definition 8.

The terminology of Definition 8 is motivated by the functional analytic analogues. Bounded and relatively compact sets in the (semi-) metric space $({{\mathcal {P}}}_\psi ,d_{\infty ,{\mathbb {M}}}^{\phi })$ are understood in the conventional way. A set ${{\mathcal {K}}}\subseteq {{\mathcal {P}}}_\psi$ is said to be bounded (w.r.t. $d_{\infty ,{\mathbb {M}}}^{\phi }$) if there exist ${\varvec{P}}'\in {{\mathcal {P}}}_\psi$ and $\delta >0$ such that $d_{\infty ,{\mathbb {M}}}^{\phi }({\varvec{Q}},{\varvec{P}}')\le \delta$ for every ${\varvec{Q}}\in {{\mathcal {K}}}$. It is said to be relatively compact (w.r.t. $d_{\infty ,{\mathbb {M}}}^{\phi }$) if for every sequence $({\varvec{Q}}_m)\in {{\mathcal {K}}}^{{\mathbb {N}}}$ there exists a subsequence $({\varvec{Q}}'_m)$ of $({\varvec{Q}}_m)$ such that $d_{\infty ,{\mathbb {M}}}^{\phi }({\varvec{Q}}_m',{\varvec{Q}})\rightarrow 0$ for some ${\varvec{Q}}\in {{\mathcal {P}}}_\psi$. The system of all bounded sets and the system of all relatively compact sets (w.r.t. $d_{\infty ,{\mathbb {M}}}^{\phi }$) are the larger the ‘steeper’ the gauge function $\phi$ is.

Definition 8

In the setting of Definition 7 we refer to ‘${{\mathcal {S}}}$-differentiability’ as

• (a) ‘Gateaux–Lévy differentiability’ if ${{\mathcal {S}}} = {{\mathcal {S}}}_{{{\text {f}}}} := \{{{\mathcal {K}}}\subseteq {{\mathcal {P}}}_\psi : {{\mathcal {K}}} \text{ is } \text{ finite }\}$.

• (b) ‘Hadamard differentiability’ if ${{\mathcal {S}}} = {{\mathcal {S}}}_{{{\text {rc}}}} := \{{{\mathcal {K}}}\subseteq {{\mathcal {P}}}_\psi : {{\mathcal {K}}} \text{ is } \text{ relatively } \text{ compact }\}$.

• (c) ‘Fréchet differentiability’ if ${{\mathcal {S}}} = {{\mathcal {S}}}_{{{\text {b}}}} := \{{{\mathcal {K}}}\subseteq {{\mathcal {P}}}_\psi : {{\mathcal {K}}} \text{ is } \text{ bounded }\}$.

Clearly, ‘Fréchet differentiability’ (of ${{\mathcal {V}}}$ at ${\varvec{P}}$ w.r.t. $({\mathbb {M}},\phi )$) implies ‘Hadamard differentiability’ which in turn implies ‘Gateaux–Lévy differentiability’, each with the same ‘derivative’.

The last sentence before Definition 8 and the last sentence in part (iii) of Remark 2 together imply that ‘Hadamard (resp. Fréchet) differentiability’ w.r.t. $({\mathbb {M}},\phi _1)$ implies ‘Hadamard (resp. Fréchet) differentiability’ w.r.t. $({\mathbb {M}},\phi _2)$ when $\phi _1\ge \phi _2$.

The following lemma, whose proof can be found in Subsection 3.2 of the supplemental article Kern et al. (2020), provides an equivalent characterization of ‘Hadamard differentiability’.

Lemma 2

Let ${\mathbb {M}}\subseteq {\mathbb {M}}_\psi (E)$, $\phi$ be another gauge function, and ${{\mathcal {V}}}:{{\mathcal {P}}}_\psi \rightarrow L$ be any map. Fix ${\varvec{P}}\in {{\mathcal {P}}}_\psi$. Then the following two assertions hold.

(i) If ${{\mathcal {V}}}$ is ‘Hadamard differentiable’ at ${\varvec{P}}$ w.r.t. $({\mathbb {M}},\phi )$ with ‘Hadamard derivative’ $\dot{{\mathcal {V}}}_{{\varvec{P}}}$, then we have for each triplet $({\varvec{Q}}, ({\varvec{Q}}_m), (\varepsilon _m))\in {{\mathcal {P}}}_\psi \times {{\mathcal {P}}}_\psi ^{{\mathbb {N}}}\times (0,1]^{{\mathbb {N}}}$ with $d_{\infty ,{\mathbb {M}}}^{\phi }({\varvec{Q}}_m,{\varvec{Q}})\rightarrow 0$ and $\varepsilon _m\rightarrow 0$ that

$$\begin{aligned} \lim _{m\rightarrow \infty }\Big \Vert \frac{{{\mathcal {V}}}({\varvec{P}}+\varepsilon _m({\varvec{Q}}_m-{\varvec{P}}))-{{\mathcal {V}}}({\varvec{P}})}{\varepsilon _m} - \dot{{\mathcal {V}}}_{{\varvec{P}}}({\varvec{Q}}-{\varvec{P}})\Big \Vert _L = 0. \end{aligned}$$

(13)

(ii) If there exists an $({\mathbb {M}},\phi )$-continuous map $\dot{{\mathcal {V}}}_{{\varvec{P}}}:{{\mathcal {P}}}_{\psi }^{{\varvec{P}};\pm }\rightarrow L$ such that (13) holds for each triplet $({\varvec{Q}}, ({\varvec{Q}}_m), (\varepsilon _m))\in {{\mathcal {P}}}_\psi \times {{\mathcal {P}}}_\psi ^{{\mathbb {N}}}\times (0,1]^{{\mathbb {N}}}$ with $d_{\infty ,{\mathbb {M}}}^{\phi }({\varvec{Q}}_m,{\varvec{Q}})\rightarrow 0$ and $\varepsilon _m\rightarrow 0$, then ${{\mathcal {V}}}$ is ‘Hadamard differentiable’ at ${\varvec{P}}$ w.r.t. $({\mathbb {M}},\phi )$ with ‘Hadamard derivative’ $\dot{{\mathcal {V}}}_{{\varvec{P}}}$.

3.5 ‘Differentiability’ of the value functional

Recall that ${\varvec{A}}$, ${\varPi }$, and ${\varvec{r}}$ are fixed, and let $V_{n}^{{\varvec{P}};\pi }$ and $V_{n}^{{\varvec{P}}}$ be defined as in (5) and (7), respectively. Moreover let $\psi$ be any gauge function and fix some ${{\mathcal {P}}}_\psi \subseteq \overline{{\mathcal {P}}}_\psi$ being closed under mixtures.

In view of Lemma 1 (with ${{\mathcal {P}}}':=\{{\varvec{P}}\}$), condition (a) of Theorem 1 below ensures that Assumption (A) is satisfied for any ${\varvec{P}}\in {{\mathcal {P}}}_\psi$. Then for any $x_n\in E$, $\pi \in {\varPi }$, and $n=0,\ldots ,N$ we may define under condition (a) of Theorem 1 functionals ${{\mathcal {V}}}_{n}^{x_n;\pi }:{{\mathcal {P}}}_\psi \rightarrow {\mathbb {R}}$ and ${{\mathcal {V}}}_{n}^{x_n}:{{\mathcal {P}}}_\psi \rightarrow {\mathbb {R}}$ by

$$\begin{aligned} {{\mathcal {V}}}_{n}^{x_n;\pi }({\varvec{P}}) := V_{n}^{{\varvec{P}};\pi }(x_n)\quad \text{ and } \quad {{\mathcal {V}}}_{n}^{x_n}({\varvec{P}}) := V_{n}^{{\varvec{P}}}(x_n), \end{aligned}$$

(14)

respectively. Note that ${{\mathcal {V}}}_{n}^{x_n}({\varvec{P}})$ specifies the maximal value for the expected total reward in the MDM (given state $x_n$ at time n) when the underlying transition function is ${\varvec{P}}$. By analogy with the name ‘value function’ we refer to ${{\mathcal {V}}}_{n}^{x_n}$ as value functional given state $x_n$at time n. Part (ii) of Theorem 1 provides (under some assumptions) the ‘Hadamard derivative’ of the value functional ${{\mathcal {V}}}_{n}^{x_n}$ in the sense of Definition 8.

Conditions (b) and (c) of Theorem 1 involve the so-called Minkowski (or gauge) functional $\rho _{{\mathbb {M}}}:{\mathbb {M}}_\psi (E)\rightarrow {\overline{{\mathbb {R}}}}_{\ge 0}$ (see, e.g., Rudin (1991, p. 25)) defined by

$$\begin{aligned} \rho _{{\mathbb {M}}}(h) := \inf \big \{\lambda \in {\mathbb {R}}_{>0}:\, h/\lambda \in {\mathbb {M}}\big \}, \end{aligned}$$

(15)

where we use the convention $\inf \emptyset :=\infty$, ${\mathbb {M}}$ is any subset of ${\mathbb {M}}_\psi (E)$, and we set ${\mathbb {R}}_{>0}:=(0,\infty )$. We note that Müller (1997a) also used the Minkowski functional to formulate his assumptions.

Example 6

For the sets ${\mathbb {M}}$ (and the corresponding gauge functions $\psi$) from Examples 1–5 we have $\rho _{{\overline{{\mathbb {M}}}}_{{{{\text {TV}}}}}}(h) = {{\text {sp}}}(h)$, $\rho _{{\overline{{\mathbb {M}}}}_{\text {Kolm}}}(h) = {\mathbb {V}}(h)$, $\rho _{{\mathbb {M}}_{\text {BL}}}(h) = \Vert h\Vert _{{{\text {BL}}}}$, $\rho _{{\mathbb {M}}_{{{{\text {Kant}}}}}}(h) = \Vert h\Vert _{{{\text {Lip}}}}$, and $\rho _{{\mathbb {M}}_{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }(h) = \Vert h\Vert _{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }$, where as before ${\overline{{\mathbb {M}}}}_{{{{\text {TV}}}}}$ and ${\overline{{\mathbb {M}}}}_{\text {Kolm}}$ are used to denote the maximal generator of $d_{{{{\text {TV}}}}}$ and $d_{\text {Kolm}}$, respectively. The latter three equations are trivial, for the former two equations see Müller (1997a, p. 880). $\square$

Recall from Definition 4 that for given ${\varvec{P}}\in {{\mathcal {P}}}_\psi$ and $\delta >0$ the sets ${\varPi }({\varvec{P}};\delta )$ and ${\varPi }({\varvec{P}})$ consist of all $\delta$-optimal strategies w.r.t. ${\varvec{P}}$ and of all optimal strategies w.r.t. ${\varvec{P}}$, respectively. Generators ${\mathbb {M}}'$ of $d_{\mathbb {M}}$ were introduced subsequent to (10).

Theorem 1

(‘Differentiability’ of ${{\mathcal {V}}}_{n}^{x_n;\pi }$ and ${{\mathcal {V}}}_{n}^{x_n}$) Let ${\mathbb {M}}\subseteq {\mathbb {M}}_\psi (E)$ and ${\mathbb {M}}'$ be any generator of $d_{\mathbb {M}}$. Fix ${\varvec{P}}=(P_n)_{n=0}^{N-1}\in {{\mathcal {P}}}_\psi$, and assume that the following three conditions hold.

• (a) $\psi$ is a bounding function for the MDM $({\varvec{X}},{\varvec{A}},{\varvec{Q}},{\varPi },{\varvec{r}})$ for any ${\varvec{Q}}\in {{\mathcal {P}}}_\psi$.

• (b) $\sup _{\pi \in {\varPi }}\rho _{{\mathbb {M}}'}(V_n^{{\varvec{P}};\pi }) < \infty$ for any $n=1,\ldots ,N$.

• (c) $\rho _{{\mathbb {M}}'}(\psi ) < \infty$.

Then the following two assertions hold.

• (i) For any $x_n\in E$, $\pi =(f_n)_{n=0}^{N-1}\in {\varPi }$, $n=0,\ldots ,N$, the map ${{\mathcal {V}}}_{n}^{x_n;\pi }:{{\mathcal {P}}}_\psi \rightarrow {\mathbb {R}}$ defined by (14) is ‘Fréchet differentiable’ at ${\varvec{P}}$ w.r.t. $({\mathbb {M}},\psi )$ with ‘Fréchet derivative’ $\dot{{\mathcal {V}}}_{n;{\varvec{P}}}^{x_n;\pi }:{{\mathcal {P}}}_{\psi }^{{\varvec{P}};\pm }\rightarrow {\mathbb {R}}$ given by

  $$\begin{aligned}&\dot{{\mathcal {V}}}_{n;{\varvec{P}}}^{x_n;\pi }({\varvec{Q}}-{\varvec{P}}) \nonumber \\&\quad := \sum _{k=n+1}^{N-1}\sum _{j=n}^{k-1}\int _E\cdots \int _E r_k(y_k,f_k(y_k))\,P_{k-1}\big ((y_{k-1},f_{k-1}(y_{k-1})),dy_k\big ) \nonumber \\&\qquad \cdots (Q_j-P_j)\big ((y_j,f_{j}(y_j)),dy_{j+1}\big )\cdots P_n\big ((x_n,f_n(x_n)),dy_{n+1}\big )\nonumber \\&\qquad + \sum _{j=n}^{N-1}\int _E\cdots \int _E r_N(y_N)\,P_{N-1}\big ((y_{N-1},f_{N-1}(y_{N-1})),dy_N\big )\nonumber \\&\qquad \cdots (Q_j-P_j)\big ((y_j,f_{j}(y_j)),dy_{j+1}\big )\cdots P_n\big ((x_n,f_n(x_n)),dy_{n+1}\big ). \end{aligned}$$

  (16)

• (ii) For any $x_n\in E$ and $n=0,\ldots ,N$, the map ${{\mathcal {V}}}_{n}^{x_n}:{{\mathcal {P}}}_\psi \rightarrow {\mathbb {R}}$ defined by (14) is ‘Hadamard differentiable’ at ${\varvec{P}}$ w.r.t. $({\mathbb {M}},\psi )$ with ‘Hadamard derivative’ $\dot{{\mathcal {V}}}_{n;{\varvec{P}}}^{x_n}:{{\mathcal {P}}}_{\psi }^{{\varvec{P}};\pm }\rightarrow {\mathbb {R}}$ given by

  $$\begin{aligned} \dot{{\mathcal {V}}}_{n;{\varvec{P}}}^{x_n}({\varvec{Q}}-{\varvec{P}}) := \lim _{\delta \searrow 0}\,\sup _{\pi \in {\varPi }({\varvec{P}};\delta )}\dot{{\mathcal {V}}}_{n;{\varvec{P}}}^{x_n;\pi }({\varvec{Q}}-{\varvec{P}}). \end{aligned}$$

  (17)

  If the set of optimal strategies ${\varPi }({\varvec{P}})$ is non-empty, then the ‘Hadamard derivative’ admits the representation

  $$\begin{aligned} \dot{{\mathcal {V}}}_{n;{\varvec{P}}}^{x_n}({\varvec{Q}}-{\varvec{P}}) = \sup _{\pi \in {\varPi }({\varvec{P}})}\dot{{\mathcal {V}}}_{n;{\varvec{P}}}^{x_n;\pi }({\varvec{Q}}-{\varvec{P}}). \end{aligned}$$

  (18)

The proof of Theorem 1 can be found in Section 4 of the supplemental article Kern et al. (2020). Note that the set ${\varPi }({\varvec{P}};\delta )$ shrinks as $\delta$ decreases. Therefore the right-hand side of (17) is well defined. The supremum in (18) ranges over all optimal strategies w.r.t. ${\varvec{P}}$. If, for example, the MDM $({\varvec{X}},{\varvec{A}},{\varvec{P}},{\varPi },{\varvec{r}})$ satisfies conditions (a)–(c) of Theorem 2 in the supplemental article Kern et al. (2020), then by part (iii) of this theorem an optimal strategy can be found, i.e. ${\varPi }({\varvec{P}})$ is non-empty. The existence of an optimal strategy is also ensured if the sets $F_0,\ldots ,F_{N-1}$ are finite (a situation one often faces in applications). In the latter case the ‘Hadamard derivative’ $\dot{{\mathcal {V}}}_{n;{\varvec{P}}}^{x_n}({\varvec{Q}}-{\varvec{P}})$ can easily be determined by computing the finitely many values $\dot{{\mathcal {V}}}_{n;{\varvec{P}}}^{x_n;\pi }({\varvec{Q}}-{\varvec{P}})$, $\pi \in {\varPi }({\varvec{P}})$, and taking their maximum. The discrete case will be discussed in more detail in Subsection 1.5 of the supplemental article Kern et al. (2020).

If there exists a unique optimal strategy $\pi ^{{\varvec{P}}}\in {\varPi }$ w.r.t. ${\varvec{P}}$, then ${\varPi }({\varvec{P}})$ is nothing but the singleton $\{\pi ^{{\varvec{P}}}\}$, and in this case the ‘Hadamard derivative’ $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}$ of the optimal value (functional) ${{\mathcal {V}}}_0^{x_0}$ at ${\varvec{P}}$ coincides with $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0;\pi ^{{\varvec{P}}}}$.

Remark 3

(i) The ‘Fréchet differentiability’ in part (i) of Theorem 1 holds even uniformly in $\pi \in {\varPi }$; see Theorem 1 in the supplemental article Kern et al. (2020) for the precise meaning.

(ii) We do not know if it is possible to replace ‘Hadamard differentiability’ by ‘Fréchet differentiability’ in part (ii) of Theorem 1. The following arguments rather cast doubt on this possibility. The proof of part (ii) is based on the decomposition of the value functional ${{\mathcal {V}}}_{n}^{x_n}$ in display (26) of the supplemental article Kern et al. (2020) and a suitable chain rule, where this decomposition involves the sup-functional ${\varPsi }$ introduced in display (27) of the supplemental article Kern et al. (2020). However, Corollary 1 in Cox and Nadler (1971) (see also Proposition 4.6.5 in Schirotzek 2007) shows that in normed vector spaces sup-functionals are in general not Fréchet differentiable. This could be an indication that ‘Fréchet differentiable’ of the value functional indeed fails. We can not make a reliable statement in this regard.

(iii) Recall that ‘Hadamard (resp. Fréchet) differentiability’ w.r.t. $({\mathbb {M}},\psi )$ implies ‘Hadamard (resp. Fréchet) differentiability’ w.r.t. $({\mathbb {M}},\phi )$ for any gauge function $\phi \le \psi$. However, for any such $\phi$ ‘Hadamard (resp. Fréchet) differentiability’ w.r.t. $({\mathbb {M}},\phi )$ is less meaningful than w.r.t. $({\mathbb {M}},\psi )$. Indeed, when using $d_{\infty ,{\mathbb {M}}}^{\phi }$ with $\phi \le \psi$ instead of $d_{\infty ,{\mathbb {M}}}^{\psi }$, the sets ${{\mathcal {K}}}$ for whose elements the first-order sensitivities can be compared with each other with clear conscience are smaller and the ‘derivative’ is less robust.

(iv) In the case where we are interested in minimizing expected total costs in the MDM $({\varvec{X}},{\varvec{A}},{\varvec{P}},{\varPi },{\varvec{r}})$ (see Remark 1(ii)), we obtain under the assumptions (and with the same arguments as in the proof of part (ii)) of Theorem 1 that the ‘Hadamard derivative’ of the corresponding value functional is given by (17) (resp. (18)) with “$\sup$” replaced by “$\inf$”. $\square$

Remark 4

(i) Condition (a) of Theorem 1 is in line with the existing literature. In fact, similar conditions as in Definition 5 (with ${{\mathcal {P}}}':=\{{\varvec{Q}}\}$) have been imposed many times before; see, for instance, Bäuerle and Rieder (2011, Definition 2.4.1), Müller (1997a, Definition 2.4), Puterman (1994, p. 231 ff), and Wessels (1977).

(ii) In some situations, condition (a) implies condition (b) in Theorem 1. This is the case, for instance, in the following four settings (the involved sets ${\mathbb {M}}'$ and metrics were introduced in Examples 1–5).

• (1) ${\mathbb {M}}':={\overline{{\mathbb {M}}}}_{{{{\text {TV}}}}}$ and $\psi :\equiv 1$.

• (2) ${\mathbb {M}}':={\overline{{\mathbb {M}}}}_{\text {Kolm}}$ and $\psi :\equiv 1$, as well as for $n=1,\ldots ,N-1$

  • $\int _{{\mathbb {R}}}V_{n+1}^{{\varvec{P}};\pi }(y)\,P_n((\,\cdot \,,f_n(\,\cdot \,)),dy)$, $\pi =(f_n)_{n=0}^{N-1}\in {\varPi }$, are increasing,

  • $r_n(\,\cdot \,,f_n(\,\cdot \,))$, $\pi =(f_n)_{n=0}^{N-1}\in {\varPi }$, and $r_N(\cdot )$ are increasing.

• (3) ${\mathbb {M}}':={\mathbb {M}}_{\text {BL}}$ and $\psi :\equiv 1$, as well as for $n=1,\ldots ,N-1$

  • $\sup _{\pi =(f_n)_{n=0}^{N-1}\in {\varPi }}\sup _{x\not =y}d_{\text {BL}}(P_n((x,f_n(x)), \,\bullet \,),P_n((y,f_n(y)),\,\bullet \,))/d_E(x,y)<\infty$,

  • $\sup _{\pi =(f_n)_{n=0}^{N-1}\in {\varPi }}\Vert r_n(\,\cdot \,,f_n(\,\cdot \,)) \Vert _{\text {Lip}}<\infty$ and $\Vert r_N\Vert _{\text {Lip}}<\infty$.

• (4) ${\mathbb {M}}':={\mathbb {M}}_{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }$ and $\psi (x):=1+d_E(x,x')^\alpha$ for some $x'\in E$ and $\alpha \in (0,1]$. (recall that ${\mathbb {M}}_{{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }}={\mathbb {M}}_{{{{\text {Kant}}}}}$ for $\alpha =1$), as well as for $n=1,\ldots ,N-1$

  • $\sup _{\pi =(f_n)_{n=0}^{N-1}\in {\varPi }}\sup _{x\not =y} d_{{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }}(P_n((x,f_n(x)),\,\bullet \,),P_n((y,f_n(y)),\,\bullet \,))/d_E(x,y)^\alpha <\infty$,

  • $\sup _{\pi =(f_n)_{n=0}^{N-1}\in {\varPi }}\Vert r_n(\,\cdot \,,f_n(\,\cdot \,))\Vert _{{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }}<\infty$ and $\Vert r_N\Vert _{{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }}<\infty$

The proof of (a)$\Rightarrow$(b) relies in setting 1) on Lemma 1 (with ${{\mathcal {P}}}':=\{{\varvec{P}}\}$) and in settings 2)–4) on Lemma 1 (with ${{\mathcal {P}}}':=\{{\varvec{P}}\}$) along with Proposition 1 of the supplemental article Kern et al. (2020). The conditions in setting 2) are similar to those in parts (ii)–(iv) of Theorem 2.4.14 in Bäuerle and Rieder (2011), and the conditions in settings 3) and 4) are motivated by the statements in Hinderer (2005, p. 11f).

(iii) In many situations, condition (c) of Theorem 1 holds trivially. This is the case, for instance, if ${\mathbb {M}}'\in \{{\overline{{\mathbb {M}}}}_{{{{\text {TV}}}}},{\overline{{\mathbb {M}}}}_{\text {Kolm}},{\mathbb {M}}_{\text {BL}}\}$ and $\psi :\equiv 1$, or if ${\mathbb {M}}':={\mathbb {M}}_{{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }}$ and $\psi (x):=1+d_E(x,x')^\alpha$ for some fixed $x'\in E$ and $\alpha \in (0,1]$.

(iv) The conditions (b) and (c) of Theorem 1 can also be verified directly in some cases; see, for instance, the proof of Lemma 7 in Subsection 5.3.1 of the supplemental article Kern et al. (2020). $\square$

In applications it is not necessarily easy to specify the set ${\varPi }({\varvec{P}})$ of all optimal strategies w.r.t. ${\varvec{P}}$. While in most cases an optimal strategy can be found with little effort (one can use the Bellman equation; see part (i) of Theorem 2 in Section 6 of the supplemental article Kern et al. 2020), it is typically more involved to specify all optimal strategies or to show that the optimal strategy is unique. The following remark may help in some situations; for an application see Sect. 4.4.

Remark 5

In some situations it turns out that for every ${\varvec{P}}\in {{\mathcal {P}}}_\psi$ the solution of the optimization problem (6) does not change if ${\varPi }$ is replaced by a subset ${\varPi }'\subseteq {\varPi }$ (being independent of ${\varvec{P}}$). Then in the definition (7) of the value function (at time 0) the set ${\varPi }$ can be replaced by the subset ${\varPi }'$, and it follows (under the assumptions of Theorem 1) that in the representation (18) of the ‘Hadamard derivative’ $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}$ of ${{\mathcal {V}}}_0^{x_0}$ at ${\varvec{P}}$ the set ${\varPi }({\varvec{P}})$ can be replaced by the set ${\varPi }'({\varvec{P}})$ of all optimal strategies w.r.t. ${\varvec{P}}$ from the subset ${\varPi }'$. Of course, in this case it suffices to ensure that conditions (a)–(b) of Theorem 1 are satisfied for the subset ${\varPi }'$ instead of ${\varPi }$. $\square$

3.6 Two alternative representations of $\dot{{\mathcal {V}}}_{n;{\varvec{P}}}^{x_n;\pi }$

In this subsection we present two alternative representations (see (19) and (20)) of the ‘Fréchet derivative’ $\dot{{\mathcal {V}}}_{n;{\varvec{P}}}^{x_n;\pi }$ in (16). The representation (19) will be beneficial for the proof of Theorem 1 (see Lemma 3 in Subsection 4.1 of the supplemental article Kern et al. 2020) and the representation (20) will be used to derive the ‘Hadamard derivative’ of the optimal value of the terminal wealth problem in (28) below (see the proof of Theorem 3 in Subsection 5.3 of the supplemental article Kern et al. 2020).

Remark 6

(Representation I) By rearranging the sums in (16), we obtain under the assumptions of Theorem 1 that for every fixed ${\varvec{P}}=(P_n)_{n=0}^{N-1}\in {{\mathcal {P}}}_\psi$ the ‘Fréchet derivative’ $\dot{{\mathcal {V}}}_{n;{\varvec{P}}}^{x_n;\pi }$ of ${{\mathcal {V}}}_{n}^{x_n;\pi }$ at ${\varvec{P}}$ can be represented as

$$\begin{aligned} \dot{{\mathcal {V}}}_{n;{\varvec{P}}}^{x_n;\pi }({\varvec{Q}}-{\varvec{P}})&= \sum _{k=n}^{N-1}\int _E\cdots \int _E\int _E V_{k+1}^{{\varvec{P}};\pi }(y_{k+1})\,(Q_k - P_k)\big ((y_k,f_k(y_k)),dy_{k+1}\big ) \nonumber \\&\quad P_{k-1}\big ((y_{k-1},f_{k-1}(y_{k-1})),dy_{k}\big ) \cdots P_n\big ((x_n,f_n(x_n)),dy_{n+1}\big ) \end{aligned}$$

(19)

for every $x_n\in E$, ${\varvec{Q}}=(Q_n)_{n=0}^{N-1}\in {{\mathcal {P}}}_\psi$, $\pi =(f_n)_{n=0}^{N-1}\in {\varPi }$, and $n=0,\ldots ,N$. $\square$

Remark 7

(Representation II) For every fixed ${\varvec{P}}=(P_n)_{n=0}^{N-1}\in {{\mathcal {P}}}_\psi$, and under the assumptions of Theorem 1, the ‘Fréchet derivative’ $\dot{{\mathcal {V}}}_{n;{\varvec{P}}}^{x_n;\pi }$ of ${{\mathcal {V}}}_{n}^{x_n;\pi }$ at ${\varvec{P}}$ admits the representation

$$\begin{aligned} \dot{{\mathcal {V}}}_{n;{\varvec{P}}}^{x_n;\pi }({\varvec{Q}}-{\varvec{P}})=\dot{V}_n^{{\varvec{P}},{\varvec{Q}};\pi }(x_n) \end{aligned}$$

(20)

for every $x_n\in E$, ${\varvec{Q}}=(Q_n)_{n=0}^{N-1}\in {{\mathcal {P}}}_\psi$, $\pi =(f_n)_{n=0}^{N-1}\in {\varPi }$, and $n=0,\ldots ,N$, where $(\dot{V}_k^{{\varvec{P}},{\varvec{Q}};\pi })_{k=0}^N$ is the solution of the following backward iteration scheme

$$\begin{aligned} \begin{aligned} \dot{V}_N^{{\varvec{P}},{\varvec{Q}};\pi }(\cdot )&\,:=\, 0, \\ \dot{V}_k^{{\varvec{P}},{\varvec{Q}};\pi }(\cdot )&\,:=\, \int _E \dot{V}_{k+1}^{{\varvec{P}},{\varvec{Q}};\pi }(y)\,P_k\big ((\,\cdot \,,f_k(\cdot )),dy\big ) \\&\qquad + \int _E V_{k+1}^{{\varvec{P}};\pi }(y)\,(Q_k - P_k)\big ((\,\cdot \,,f_k(\cdot )),dy\big ),\qquad k=0,\ldots ,N-1. \ \end{aligned} \end{aligned}$$

(21)

Indeed, it is easily seen that $\dot{V}_n^{{\varvec{P}},{\varvec{Q}};\pi }(x_n)$ coincides with the right-hand side of (19). Note that it can be verified iteratively by means of condition (a) of Theorem 1 and Lemma 1 (with ${{\mathcal {P}}}':=\{{\varvec{Q}}\}$) that $\dot{V}_n^{{\varvec{P}},{\varvec{Q}};\pi }(\cdot )\in {\mathbb {M}}_\psi (E)$ for every ${\varvec{Q}}\in {{\mathcal {P}}}_\psi$, $\pi \in {\varPi }$, and $n=0,\ldots ,N$. In particular, this implies that the integrals on the right-hand side of (21) exist and are finite. Also note that the iteration scheme (21) involves the family $(V^{{\varvec{P}};\pi }_k)_{k=1}^N$ which itself can be seen as the solution of a backward iteration scheme:

$$\begin{aligned} V_N^{{\varvec{P}};\pi }(\cdot ):= & {} r_N(\cdot ), \\ V_k^{{\varvec{P}};\pi }(\cdot ):= & {} r_k(\,\cdot \,,f_k(\cdot )) + \int _E V_{k+1}^{{\varvec{P}};\pi }(y)\,P_k\big ((\,\cdot \,,f_k(\cdot )),dy\big ),\qquad k=1,\ldots ,N-1; \end{aligned}$$

see Proposition 1 of the supplemental article Kern et al. (2020). $\square$

4 Application to a terminal wealth optimization problem in mathematical finance

In this section we will apply the theory of Sections 2–3 to a particular optimization problem in mathematical finance. At first, we introduce in Sect. 4.1 the basic financial market model and formulate subsequently the terminal wealth problem as a classical optimization problem in mathematical finance. The market model is in line with standard literature as Bäuerle and Rieder (2011, Chapter 4) or (Föllmer and Schied 2011, Chapter 5). To keep the presentation as clear as possible we restrict ourselves to a simple variant of the market model (only one risky asset). In Sect. 4.2 we will see that the market model can be embedded into the MDM of Sect. 2. It turns out that the existence (and computation) of an optimal (trading) strategy can be obtained by solving iteratively N one-stage investment problems; see Sect. 4.3. In Sect. 4.4 we will specify the ‘Hadamard derivative’ of the optimal value functional of the terminal wealth problem, and Sect. 4.5 provides some numerical examples for the ‘Hadamard derivative’.

4.1 Basic financial market model, and the target

Consider an N-period financial market consisting of one riskless bond $B=(B_0,\ldots ,B_N)$ and one risky asset $S=(S_0,\ldots ,S_N)$. Further assume that the value of the bond evolves deterministically according to

$$\begin{aligned} B_0= 1,\qquad B_{n+1} = {\mathfrak {r}}_{n+1} B_n, \qquad n=0,\ldots ,N-1 \end{aligned}$$

for some fixed constants ${\mathfrak {r}}_1,\ldots ,{\mathfrak {r}}_N\in {\mathbb {R}}_{\ge 1}$, and that the value of the asset evolves stochastically according to

$$\begin{aligned} S_0>0,\qquad S_{n+1} = {\mathfrak {R}}_{n+1} S_n, \qquad n=0,\ldots ,N-1 \end{aligned}$$

for some independent ${\mathbb {R}}_{\ge 0}$-valued random variables ${\mathfrak {R}}_1,\ldots ,{\mathfrak {R}}_N$ on some probability space $({\varOmega },{{{\mathcal {F}}}},{\mathbb {P}})$ with (known) distributions ${\mathfrak {m}}_1,\ldots ,{\mathfrak {m}}_N$, respectively.

Throughout Section 4 we will assume that the financial market satisfies the following Assumption (FM), where $\alpha \in (0,1)$ is fixed and chosen as in (24) below. In Examples 7 and 8 we will discuss specific financial market models which satisfy Assumption (FM).

Assumption (FM)

The following three assertions hold for any $n=0,\ldots ,N-1$.

• (a) $\int _{{\mathbb {R}}_{\ge 0}}y^\alpha \,{\mathfrak {m}}_{n+1}(dy)<\infty$.

• (b) ${\mathfrak {R}}_{n+1}>0$${\mathbb {P}}$-a.s.

• (c) ${\mathbb {P}}[{\mathfrak {R}}_{n+1} \ne {\mathfrak {r}}_{n+1}]=1$.

Note that for any $n=0,\ldots ,N-1$ the value ${\mathfrak {r}}_{n+1}$ (resp. ${\mathfrak {R}}_{n+1}$) corresponds to the relative price change $B_{n+1}/B_n$ (resp. $S_{n+1}/S_n$) of the bond (resp. asset) between time n and $n+1$. Let ${{\mathcal {F}}}_0$ be the trivial $\sigma$-algebra, and set ${{\mathcal {F}}}_n:=\sigma (S_0,\ldots ,S_n)=\sigma ({\mathfrak {R}}_1,\ldots ,{\mathfrak {R}}_n)$ for any $n=1,\ldots ,N$.

Now, an agent invests a given amount of capital $x_0\in {\mathbb {R}}_{\ge 0}$ in the bond and the asset according to some self-financing trading strategy. By trading strategy we mean an $({{\mathcal {F}}}_n)$-adapted ${\mathbb {R}}_{\ge 0}^2$-valued stochastic process $\varphi =(\varphi _n^0,\varphi _n)_{n=0}^{N-1}$, where $\varphi _n^0$ (resp. $\varphi _n$) specifies the amount of capital that is invested in the bond (resp. asset) during the time interval $[n,n+1)$. Here we require that both $\varphi _n^0$ and $\varphi _n$ are nonnegative for any n, which means that taking loans and short sellings of the asset are excluded. The corresponding portfolio process $X^{\varphi }=(X_0^{\varphi },\ldots ,X_N^{\varphi })$ associated with $\varphi =(\varphi _n^0,\varphi _n)_{n=0}^{N-1}$ is given by

$$\begin{aligned} X_0^{\varphi } := \varphi _0^0+\varphi _0 \quad \text{ and } \quad X_{n+1}^{\varphi } := \varphi _n^0{\mathfrak {r}}_{n+1} + \varphi _n{\mathfrak {R}}_{n+1},\qquad n=0,\ldots ,N-1. \end{aligned}$$

A trading strategy $\varphi =(\varphi _n^0,\varphi _n)_{n=0}^{N-1}$ is said to be self-financing w.r.t. the initial capital $x_0$ if $x_0=\varphi _0^0+\varphi _0$ and $X_n^{\varphi }=\varphi _n^0+\varphi _n$ for all $n=1,\ldots ,N$. It is easily seen that for any self-financing trading strategy $\varphi =(\varphi _n^0,\varphi _n)_{n=0}^{N-1}$ w.r.t. $x_0$ the corresponding portfolio process admits the representation

$$\begin{aligned} X_0^{\varphi } = x_0 \quad \text{ and } \quad X_{n+1}^{\varphi } = {\mathfrak {r}}_{n+1} X_n^{\varphi } + \varphi _n({\mathfrak {R}}_{n+1}-{\mathfrak {r}}_{n+1}) \quad \text{ for } n=0,\ldots ,N-1.\nonumber \\ \end{aligned}$$

(22)

Note that $X_n^{\varphi }-\varphi _n$ corresponds to the amount of capital which is invested in the bond between time n and $n+1$. Also note that it can be verified easily by means of Remark 3.1.6 in Bäuerle and Rieder (2011) that under condition (c) of Assumption (FM) the financial market introduced above is free of arbitrage opportunities.

In view of (22), we may and do identify a self-financing trading strategy w.r.t. $x_0$ with an $({{\mathcal {F}}}_n)$-adapted ${\mathbb {R}}_{\ge 0}$-valued stochastic process $\varphi =(\varphi _n)_{n=0}^{N-1}$ satisfying $\varphi _0\in [0,x_0]$ and $\varphi _n\in [0,X_n^{\varphi }]$ for all $n=1,\ldots ,N-1$. We restrict ourselves to Markovian self-financing trading strategies $\varphi =(\varphi _n)_{n=0}^{N-1}$ w.r.t. $x_0$ which means that $\varphi _n$ only depends on n and $X_n^{\varphi }$. To put it another way, we assume that for any $n=0,\ldots ,N-1$ there exists some Borel measurable map $f_n:{\mathbb {R}}_{\ge 0}\rightarrow {\mathbb {R}}_{\ge 0}$ such that $\varphi _n = f_n(X_n^{\varphi }).$ Then, in particular, $X^{\varphi }$ is an ${\mathbb {R}}_{\ge 0}$-valued $({{\mathcal {F}}}_n)$-Markov process whose one-step transition probability at time $n\in \{0,\ldots ,N-1\}$ given state $x\in {\mathbb {R}}_{\ge 0}$ and strategy $\varphi =(\varphi _n)_{n=0}^{N-1}$ (resp. $\pi =(f_n)_{n=0}^{N-1}$) is given by ${\mathfrak {m}}_{n+1}\circ \eta _{n,(x,f_n(x))}^{-1}$ with

$$\begin{aligned} \eta _{n,(x,f_n(x))}(y) := {\mathfrak {r}}_{n+1}x + f_n(x)(y - {\mathfrak {r}}_{n+1}), \qquad y\in {\mathbb {R}}_{\ge 0}. \end{aligned}$$

(23)

The agent’s aim is to find a self-financing trading strategy $\varphi =(\varphi _n)_{n=0}^{N-1}$ (resp. $\pi =(f_n)_{n=0}^{N-1}$) w.r.t. $x_0$ for which her expected utility of the discounted terminal wealth is maximized. We assume that the agent is risk averse and that her attitude towards risk is set via the power utility function $u_\alpha :{\mathbb {R}}_{\ge 0}\rightarrow {\mathbb {R}}_{\ge 0}$ defined by

$$\begin{aligned} u_\alpha (y) := y^\alpha \end{aligned}$$

(24)

for some fixed $\alpha \in (0,1)$ (as in Assumption (FM)). The coefficient $\alpha$ determines the degree of risk aversion of the agent: the smaller the coefficient $\alpha$, the greater her risk aversion. Hence the agent is interested in those self-financing trading strategies $\varphi =(\varphi _n)_{n=0}^{N-1}$ (resp. $\pi =(f_n)_{n=0}^{N-1}$) w.r.t. $x_0$ for which the expectation of $u_\alpha (X_N^{\varphi }/B_N)$ under ${\mathbb {P}}$ is maximized.

In the following subsections we will assume for notational simplicity that ${\mathfrak {r}}_{1},\ldots ,{\mathfrak {r}}_{N}$ are fixed and that ${\mathfrak {m}}_1,\ldots ,{\mathfrak {m}}_N$ are a sort of model parameters. In this case the factor $1/B_N$ in $u_\alpha (X_N^{\varphi }/B_N)$ in display (25) is superfluous; it indeed does not influence the maximization problem or any ‘derivative’ of the optimal value. On the other hand, if also the (Dirac-) distributions of ${\mathfrak {r}}_{1},\ldots ,{\mathfrak {r}}_{N}$ would be allowed to be variable, then this factor could matter for the derivative of the optimal value w.r.t. changes in the (deterministic) dynamics of $B_N$.

4.2 Embedding into MDM, and optimal trading strategies

The setting introduced in Sect. 4.1 can be embedded into the setting of Sections 2–3 as follows. Let ${\mathfrak {r}}_1,\ldots ,{\mathfrak {r}}_N\in {\mathbb {R}}_{\ge 1}$ be a priori fixed constants. Let $(E,{{\mathcal {E}}}) := ({\mathbb {R}}_{\ge 0},{{\mathcal {B}}}({\mathbb {R}}_{\ge 0}))$ and $A_n(x) := [0,x]$ for any $x\in {\mathbb {R}}_{\ge 0}$ and $n=0,\ldots ,N-1$. Then $A_n = {\mathbb {R}}_{\ge 0}$ and $D_n = D := \{(x,a)\in {\mathbb {R}}_{\ge 0}^2:\,a\in [0,x]\}.$ Let ${{\mathcal {A}}}_n := {{\mathcal {B}}}({\mathbb {R}}_{\ge 0})$. In particular, ${{\mathcal {D}}}_n = {{\mathcal {B}}}({\mathbb {R}}_{\ge 0}^2)\cap D$ and the set ${\mathbb {F}}_n$ of all decision rules at time n consists of all those Borel measurable functions $f_n:{\mathbb {R}}_{\ge 0}\rightarrow {\mathbb {R}}_{\ge 0}$ which satisfy $f_n(x)\in [0,x]$ for all $x\in {\mathbb {R}}_{\ge 0}$ (in particular ${\mathbb {F}}_n$ is independent of n). For any $n=0,\ldots ,N-1$, let the set $F_n$ of all admissible decision rules at time n be equal to ${\mathbb {F}}_n$. Let as before ${\varPi }:=F_0\times \cdots \times F_{N-1}$.

Moreover let $r_n:\equiv 0$ for any $n=0,\ldots ,N-1$, and

$$\begin{aligned} r_N(x) := u_\alpha (x/B_N), \qquad x\in {\mathbb {R}}_{\ge 0}. \end{aligned}$$

(25)

Consider the gauge function $\psi :{\mathbb {R}}_{\ge 0}\rightarrow {\mathbb {R}}_{\ge 1}$ defined by

$$\begin{aligned} \psi (x) := 1 + u_\alpha (x). \end{aligned}$$

(26)

Let ${{\mathcal {P}}}_\psi$ be the set of all transition functions ${\varvec{P}}=(P_n)_{n=0}^{N-1}\in {{\mathcal {P}}}$ consisting of transition kernels of the shape

$$\begin{aligned} P_n\big ((x,a),\,\bullet \,\big ) := {\mathfrak {m}}_{n+1}\circ \eta _{n,(x,a)}^{-1}\,[\,\bullet \,], \qquad (x,a)\in D_n,\,n=0,\ldots ,N-1 \end{aligned}$$

(27)

for some ${\mathfrak {m}}_{n+1}\in {{\mathcal {M}}}_1^{\alpha }({\mathbb {R}}_{\ge 0})$, where ${{\mathcal {M}}}_1^{\alpha }({\mathbb {R}}_{\ge 0})$ is the set of all $\mu \in {{\mathcal {M}}}_1({\mathbb {R}}_{\ge 0})$ satisfying $\int _{{\mathbb {R}}_{\ge 0}}u_\alpha \,d\mu <\infty$, and the map $\eta _{n,(x,a)}$ is defined as in (23). In particular, ${{\mathcal {P}}}_\psi \subseteq \overline{{\mathcal {P}}}_\psi$ (with $\overline{{\mathcal {P}}}_\psi$ defined as in Sect. 3.3), and $(1-\varepsilon ){\varvec{P}}+\varepsilon {\varvec{Q}}\in {{\mathcal {P}}}_\psi$ for all ${\varvec{P}},{\varvec{Q}}\in {{\mathcal {P}}}_\psi$ and $\varepsilon \in (0,1)$ (i.e. ${{\mathcal {P}}}_\psi$ is closed under mixtures). Moreover it can be verified easily that $\psi$ given by (26) is a bounding function for the MDM $({\varvec{X}},{\varvec{A}},{\varvec{Q}},{\varPi },{\varvec{r}})$ for any ${\varvec{Q}}\in {{\mathcal {P}}}_\psi$ (see Lemma 7(i) of the supplemental article Kern et al. 2020). Note that ${\varvec{X}}$ plays the role of the portfolio process $X^{\varphi }$ from Sect. 4.1. Also note that for some fixed $x_0\in {\mathbb {R}}_{\ge 0}$, any self-financing trading strategy $\varphi =(\varphi _n)_{n=0}^{N-1}$ w.r.t. $x_0$ may be identified with some $\pi =(f_n)_{n=0}^{N-1}\in {\varPi }$ via $\varphi _n=f_n(X_n^{\varphi })$.

Then, for every fixed $x_0\in {\mathbb {R}}_{\ge 0}$ and ${\varvec{P}}\in {{\mathcal {P}}}_\psi$ the terminal wealth problem introduced in the second to last paragraph of Sect. 4.1 reads as

$$\begin{aligned} {\mathbb {E}}^{x_0,{\varvec{P}};\pi }[r_N(X_N)] \longrightarrow \max \ (\text{ in } \pi \in {\varPi })\,! \end{aligned}$$

(28)

A strategy $\pi ^{{\varvec{P}}}\in {\varPi }$ is called an optimal (self-financing) trading strategy w.r.t. ${\varvec{P}}$(and $x_0$) if it solves the maximization problem (28).

Remark 8

In the setting of Sect. 4.1 we restrict ourselves to Markovian self-financing trading strategies $\varphi =(\varphi _n)_{n=0}^{N-1}$ w.r.t. $x_0$ which may be identified with some $\pi =(f_n)_{n=0}^{N-1}\in {\varPi }$ via $\varphi _n=f_n(X_n^{\varphi })$. Of course, one could also assume that the decision rules of a trading strategy $\pi$ also depend on past actions and past values of the portfolio process $X^{\varphi }$. However, as already discussed in Remark 1(i), the corresponding history-dependent trading strategies do not lead to an improved optimal value for the terminal wealth problem (28). $\square$

4.3 Computation of optimal trading strategies

In this subsection we discuss the existence and computation of solutions to the terminal wealth problem (28), maintaining the notation of Sect. 4.2. We will adapt the arguments of Section 4.2 in Bäuerle and Rieder (2011). As before ${\mathfrak {r}}_1,\ldots ,{\mathfrak {r}}_N\in {\mathbb {R}}_{\ge 1}$ are fixed constants.

Basically the existence of an optimal trading strategy for the terminal wealth problem (28) can be ensured with the help of a suitable analogue of Theorem 4.2.2 in Bäuerle and Rieder (2011). In order to specify the optimal trading strategy explicitly one has to determine the local maximizers in the Bellman equation; see Theorem 2(i) in Section 6 of the supplemental article Kern et al. (2020). However this is not necessarily easy. On the other hand, part (ii) of Theorem 2 ahead (a variant of Theorem 4.2.6 in Bäuerle and Rieder 2011) shows that, for our particular choice of the utility function (recall (24)), the optimal investment in the asset at time $n\in \{0,\ldots ,N-1\}$ has a rather simple form insofar as it depends linearly on the wealth. The respective coefficient can be obtained by solving the one-stage optimization problem in (29) ahead. That is, instead of finding the optimal amount of capital (possibly depending on the wealth) to be invested in the asset, it suffices to find the optimal fraction of the wealth (being independent of the wealth itself) to be invested in the asset.

For the formulation of the one-stage optimization problem note that every transition function ${\varvec{P}}\in {{\mathcal {P}}}_\psi$ is generated through (27) by some $({\mathfrak {m}}_1,\ldots ,{\mathfrak {m}}_N)\in {{\mathcal {M}}}_1^{\alpha }({\mathbb {R}}_{\ge 0})^N$. For every ${\varvec{P}}\in {{\mathcal {P}}}_\psi$, we use $({\mathfrak {m}}_1^{{\varvec{P}}},\ldots ,{\mathfrak {m}}_N^{{\varvec{P}}})$ to denote any such set of ‘parameters’. Now, consider for any ${\varvec{P}}\in {{\mathcal {P}}}_\psi$ and $n=0,\ldots ,N-1$ the optimization problem

$$\begin{aligned} v_n^{{\varvec{P}};\gamma } := \int _{{\mathbb {R}}_{\ge 0}}u_\alpha \Big (1+\gamma \Big (\frac{y}{{\mathfrak {r}}_{n+1}} - 1\Big )\Big )\,{\mathfrak {m}}_{n+1}^{{\varvec{P}}}(dy)\,\longrightarrow \,\max \ (\text{ in } \gamma \in [0,1])\,! \end{aligned}$$

(29)

Note that $1+\gamma (y/{\mathfrak {r}}_{n+1}-1)$ lies in ${\mathbb {R}}_{\ge 0}$ for any $\gamma \in [0,1]$ and $y\in {\mathbb {R}}_{\ge 0}$, and that the integral on the left-hand side (exists and) is finite (this follows from displays (34)–(36) in Subsection 5.1 of the supplemental article Kern et al. 2020) and should be seen as the expectation of $u_\alpha (1+\gamma ({\mathfrak {R}}_{n+1}/{\mathfrak {r}}_{n+1} - 1))$ under ${\mathbb {P}}$.

The following lemma, whose proof can be found in Subsection 5.1 of the supplemental article Kern et al. (2020), shows in particular that

$$\begin{aligned} v_n^{{\varvec{P}}} := \sup _{\gamma \in [0,1]}v_n^{{\varvec{P}};\gamma } \end{aligned}$$

is the maximal value of the optimization problem (29).

Lemma 3

For any ${\varvec{P}}\in {{\mathcal {P}}}_\psi$ and $n=0,\ldots ,N-1$, there exists a unique solution $\gamma _n^{{\varvec{P}}}\in [0,1]$ to the optimization problem (29).

Part (i) of the following Theorem 2 involves the value function introduced in (7). In the present setting this function has a comparatively simple form:

$$\begin{aligned} V_n^{{\varvec{P}}}(x_n) = \sup _{\pi \in {\varPi }}{\mathbb {E}}_{n,x_n}^{x_0,{\varvec{P}};\pi }[r_N(X_N)] \end{aligned}$$

(30)

for any $x_n\in {\mathbb {R}}_{\ge 0}$, ${\varvec{P}}\in {{\mathcal {P}}}_\psi$, and $n=0,\ldots ,N$.

Part (ii) involves the subset ${\varPi }_{{{\text {lin}}}}$ of ${\varPi }$ which consists of all linear trading strategies, i.e. of all $\pi \in {\varPi }$ of the form $\pi =(f_n^{\varvec{\gamma }})_{n=0}^{N-1}$ for some $\varvec{\gamma }=(\gamma _n)_{n=0}^{N-1}\in [0,1]^N$, where

$$\begin{aligned} f_n^{\varvec{\gamma }}(x) := \gamma _n\,x,\qquad x\in {\mathbb {R}}_{\ge 0},\,n=0,\ldots ,N-1. \end{aligned}$$

(31)

In part (i) and elsewhere we use the convention that the product over the empty set is 1.

Theorem 2

(Optimal trading strategy) For any ${\varvec{P}}\in {{\mathcal {P}}}_\psi$ the following two assertions hold.

• (i) The value function $V_n^{{\varvec{P}}}$ given by (30) admits the representation

  $$\begin{aligned} V_n^{{\varvec{P}}}(x_n) = {\mathfrak {v}}_n^{{\varvec{P}}} u_\alpha (x_n/B_n) \end{aligned}$$

  for any $x_n\in {\mathbb {R}}_{\ge 0}$ and $n=0,\ldots ,N-1$, where ${\mathfrak {v}}_n^{{\varvec{P}}} := \prod _{k=n}^{N-1}v_k^{{\varvec{P}}}$.

• (ii) For any $n=0,\ldots ,N-1$, let $\gamma _n^{{\varvec{P}}}\in [0,1]$ be the unique solution to the optimization problem (29) and define a decision rule $f_n^{{\varvec{P}}}:{\mathbb {R}}_{\ge 0}\rightarrow {\mathbb {R}}_{\ge 0}$ at time n through

  $$\begin{aligned} f_n^{{\varvec{P}}}(x) := \gamma _n^{{\varvec{P}}}x,\qquad x\in {\mathbb {R}}_{\ge 0}. \end{aligned}$$

  (32)

  Then $\pi ^{{\varvec{P}}}:=(f_n^{{\varvec{P}}})_{n=0}^{N-1}\in {\varPi }_{{{\text {lin}}}}$  forms an optimal trading strategy w.r.t. ${\varvec{P}}$. Moreover, there is no further optimal trading strategy w.r.t. ${\varvec{P}}$ which belongs to ${\varPi }_{{{\text {lin}}}}$.

The proof of Theorem 2 can be found in Subsection 5.2 of the supplemental article Kern et al. (2020). The second assertion of part (ii) of Theorem 2 will be beneficial for part (ii) of Theorem 3 ahead; for details see Remark 9. The following two Examples 7 and 8 illustrate part (ii) of Theorem 2.

Example 7

(Cox–Ross–Rubinstein model) Let ${\mathfrak {r}}_1=\cdots ={\mathfrak {r}}_N={\mathfrak {r}}$ for some ${\mathfrak {r}}\in {\mathbb {R}}_{\ge 1}$. Moreover let ${\varvec{P}}\in {{\mathcal {P}}}$ be any transition function defined as in (27) with ${\mathfrak {m}}_1=\cdots ={\mathfrak {m}}_N={\mathfrak {m}}_{{\varvec{P}}}$ for some ${\mathfrak {m}}_{{\varvec{P}}} := p_{{\varvec{P}}}\delta _{{\textsf {u} }_{{\varvec{P}}}} + (1-p_{{\varvec{P}}})\delta _{{\textsf {d} }_{{\varvec{P}}}}$, where $p_{{\varvec{P}}}\in [0,1]$ and ${\textsf {d} }_{{\varvec{P}}},{\textsf {u} }_{{\varvec{P}}}\in {\mathbb {R}}_{>0}$ are some given constants (depending on ${\varvec{P}}$) satisfying ${\textsf {d} }_{{\varvec{P}}}<{\mathfrak {r}}<{\textsf {u} }_{{\varvec{P}}}$. Then ${\varvec{P}}\in {{\mathcal {P}}}_\psi$ and conditions (a)–(c) of Assumption (FM) are clearly satisfied. In particular, the corresponding financial market is arbitrage-free and the optimization problem (29) simplifies to (up to the factor ${\mathfrak {r}}^{-\alpha }$)

$$\begin{aligned} \big \{p_{{\varvec{P}}}\, u_\alpha ({\mathfrak {r}} + \gamma ({\textsf {u} }_{{\varvec{P}}}-{\mathfrak {r}})) + (1-p_{{\varvec{P}}})\, u_\alpha ({\mathfrak {r}} + \gamma ({\textsf {d} }_{{\varvec{P}}}-{\mathfrak {r}}))\big \}\,\longrightarrow \max \ (\text{ in } \gamma \in [0,1])\,!\nonumber \\ \end{aligned}$$

(33)

Lemma 3 ensures that (33) has a unique solution, $\gamma _{{\textsf {CRR} }}^{{\varvec{P}}}$, and it can be checked easily (see, e.g., Bäuerle and Rieder (2011, p. 86)) that this solution admits the representation

$$\begin{aligned} \gamma _{{\textsf {CRR} }}^{{\varvec{P}}} = \left\{ \begin{array}{lll} 0 &{} , &{} p_{{\varvec{P}}}\in [0,p_{{\varvec{P}},0}]\\ \frac{{\mathfrak {r}}}{({\mathfrak {r}} - {\textsf {d} }_{{\varvec{P}}})({\textsf {u} }_{{\varvec{P}}} - {\mathfrak {r}})}\cdot \frac{p_{{\varvec{P}}}^{\kappa _\alpha }({\textsf {u} }_{{\varvec{P}}} - {\mathfrak {r}})^{\kappa _\alpha } - (1-p_{{\varvec{P}}})^{\kappa _\alpha }({\mathfrak {r}} - {\textsf {d} }_{{\varvec{P}}})^{\kappa _\alpha }}{p_{{\varvec{P}}}^{\kappa _\alpha }({\textsf {u} }_{{\varvec{P}}} - {\mathfrak {r}})^{\kappa _\alpha \alpha } + (1-p_{{\varvec{P}}})^{\kappa _\alpha }({\mathfrak {r}} - {\textsf {d} }_{{\varvec{P}}})^{\kappa _\alpha \alpha }} &{} , &{} p_{{\varvec{P}}}\in (p_{{\varvec{P}},0},p_{{\varvec{P}},1})\\ 1 &{} , &{} p_{{\varvec{P}}}\in [p_{{\varvec{P}},1},1] \end{array} \right. , \nonumber \\ \end{aligned}$$

(34)

where $\kappa _\alpha :=(1-\alpha )^{-1}$ and

$$\begin{aligned} p_{{\varvec{P}},0} := \frac{{\mathfrak {r}} - {\textsf {d} }_{{\varvec{P}}}}{{\textsf {u} }_{{\varvec{P}}} - {\textsf {d} }_{{\varvec{P}}}}~(>0) \quad \text{ and } \quad p_{{\varvec{P}},1} := \frac{{\textsf {u} }_{{\varvec{P}}}^{1-\alpha }({\mathfrak {r}} - {\textsf {d} }_{{\varvec{P}}})}{{\textsf {u} }_{{\varvec{P}}}^{1-\alpha }({\mathfrak {r}} - {\textsf {d} }_{{\varvec{P}}}) + {\textsf {d} }_{{\varvec{P}}}^{1-\alpha }({\textsf {u} }_{{\varvec{P}}} - {\mathfrak {r}})}~(<1). \end{aligned}$$

Note that only fractions from the interval [0, 1] are admissible, and that the expression in the middle line in (34) lies in (0, 1) when $p_{{\varvec{P}}}\in (p_{{\varvec{P}},0},p_{{\varvec{P}},1})$. Thus, part (ii) of Theorem 2 shows that the strategy $\pi ^{{\varvec{P}}}_{\textsf {CRR} }$ defined by (32) (with $\gamma _n^{{\varvec{P}}}$ replaced by $\gamma _{{\textsf {CRR} }}^{{\varvec{P}}}$) is optimal w.r.t. ${\varvec{P}}$ and unique among all $\pi \in {\varPi }_{{{\text {lin}}}}({\varvec{P}})$. $\square$

In the following example the bond and the asset evolve according to the ordinary differential equation and the Itô stochastic differential equation

$$\begin{aligned} d{\mathfrak {B}}_t = \nu {\mathfrak {B}}_t\,dt \quad \text{ and } \quad d{\mathfrak {S}}_t = \mu {\mathfrak {S}}_t\,dt+\sigma {\mathfrak {S}}_t\,d{\mathfrak {W}}_t, \end{aligned}$$

respectively, where $\nu ,\mu \in {\mathbb {R}}_{\ge 0}$ and $\sigma \in {\mathbb {R}}_{>0}$ are constants and ${\mathfrak {W}}$ is a one-dimensional standard Brownian motion. We assume that the trading period is (without loss of generality) the unit interval [0, 1] and that the bond and the asset can be traded only at N equidistant time points in [0, 1], namely at $t_{N,n}:=n/N$, $n=0,\ldots ,N-1$. Then, in particular, the relative price changes ${\mathfrak {r}}_{n+1}:=B_{n+1}/B_n={\mathfrak {B}}_{t_{N,n+1}}/{\mathfrak {B}}_{t_{N,n}}$ and ${\mathfrak {R}}_{n+1}:=S_{n+1}/S_n={\mathfrak {S}}_{t_{N,n+1}}/{\mathfrak {S}}_{t_{N,n}}$ are given by

$$\begin{aligned} \exp \big \{\nu (t_{N,n+1}-t_{N,n})\big \} \end{aligned}$$

and

$$\begin{aligned} \exp \big \{(\mu - \tfrac{\sigma ^2}{2})(t_{N,n+1}-t_{N,n}) + \sigma ({\mathfrak {W}}_{t_{N,n+1}} - {\mathfrak {W}}_{t_{N,n}})\big \}, \end{aligned}$$

respectively. In particular, ${\mathfrak {r}}_{n+1}=\exp (\nu /N)$ and ${\mathfrak {R}}_{n+1}$ is distributed according to the log-normal distribution ${{\text {LN}}}_{(\mu - \sigma ^2/2)/N,\sigma ^2/N}$ for any $n=0,\ldots ,N-1$.

Example 8

(Black–Scholes–Merton model) Let ${\mathfrak {r}}_1=\cdots ={\mathfrak {r}}_N={\mathfrak {r}}$ for ${\mathfrak {r}}:=\exp (\nu /N)$, where $\nu \in {\mathbb {R}}_{\ge 0}$. Moreover let ${\varvec{P}}\in {{\mathcal {P}}}$ be any transition function defined as in (27) with ${\mathfrak {m}}_1=\cdots ={\mathfrak {m}}_N={\mathfrak {m}}_{{\varvec{P}}}$ for ${\mathfrak {m}}_{{\varvec{P}}}:={{\text {LN}}}_{(\mu _{{\varvec{P}}} - \sigma _{{\varvec{P}}}^2/2)/N,\sigma _{{\varvec{P}}}^2/N}$, where $\mu _{{\varvec{P}}}\in {\mathbb {R}}_{\ge 0}$ and $\sigma _{{\varvec{P}}}\in {\mathbb {R}}_{>0}$ are some given constants (depending on ${\varvec{P}}$) satisfying $\mu _{{\varvec{P}}}>(1-\alpha )\sigma _{{\varvec{P}}}^2$. Then ${\varvec{P}}\in {{\mathcal {P}}}_\psi$ and it is easily seen that conditions (a)–(c) of Assumption (FM) hold. In particular, the corresponding financial market is arbitrage-free and the optimization problem (29) now reads as

$$\begin{aligned} \int _{{\mathbb {R}}_{\ge 0}}u_\alpha \Big (1+\gamma \Big (\frac{y}{{\mathfrak {r}}} - 1\Big )\Big ){\mathfrak {f}}_{(\mu _{{\varvec{P}}} - \sigma _{{\varvec{P}}}^2/2)/N,\sigma _{{\varvec{P}}}^2/N}(y)\,\ell (dy)\longrightarrow \max \ (\text{ in } \gamma \in [0,1])\,!\nonumber \\ \end{aligned}$$

(35)

where ${\mathfrak {f}}_{(\mu _{{\varvec{P}}} - \sigma _{{\varvec{P}}}^2/2)/N,\sigma _{{\varvec{P}}}^2/N}$ is the standard Lebesgue density of the log-normal distribution ${{\text {LN}}}_{(\mu _{{\varvec{P}}} - \sigma _{{\varvec{P}}}^2/2)/N,\sigma _{{\varvec{P}}}^2/N}$. Lemma 3 ensures that (35) has a unique solution, $\gamma _{{\textsf {BSM} }}^{{\varvec{P}}}$, and it is known (see, e.g., Merton 1969; Pham 2009) that this solution is given by

$$\begin{aligned} \gamma _{{\textsf {BSM} }}^{{\varvec{P}}} = \left\{ \begin{array}{lll} 0 &{} , &{} \nu \in [\mu _{{\varvec{P}}},\infty ) \\ \frac{1}{1-\alpha }\frac{\mu _{{\varvec{P}}} - \nu }{\sigma _{{\varvec{P}}}^2} &{} , &{} \nu \in (\nu _{{\varvec{P}},\alpha },\mu _{{\varvec{P}}}) \\ 1 &{} , &{} \nu \in [0,\nu _{{\varvec{P}},\alpha }] \end{array} \right. , \end{aligned}$$

(36)

where $\nu _{{\varvec{P}},\alpha }:=\mu _{{\varvec{P}}} - (1 - \alpha )\sigma _{{\varvec{P}}}^2\,(\in (0,\mu _{{\varvec{P}}}))$. Note that only fractions from the interval [0, 1] are admissible, and that the expression in the middle line in (36) is called Merton ratio and lies in (0, 1) when $\nu \in (\nu _{{\varvec{P}},\alpha },\mu _{{\varvec{P}}})$. Thus, part (ii) of Theorem 2 shows that the strategy $\pi ^{{\varvec{P}}}_{\textsf {BSM} }$ defined by (32) (with $\gamma _n^{{\varvec{P}}}$ replaced by $\gamma _{{\textsf {BSM} }}^{{\varvec{P}}}$) is optimal w.r.t. ${\varvec{P}}$ and unique among all $\pi \in {\varPi }_{{{\text {lin}}}}({\varvec{P}})$. $\square$

4.4 ‘Hadamard derivative’ of the optimal value functional

Maintain the notation and terminology introduced in Sects. 4.1–4.3. In this subsection we will specify the ‘Hadamard derivative’ of the optimal value functional of the terminal wealth problem (28) at (fixed) ${\varvec{P}}$; see part (ii) of Theorem 3. Recall that $\alpha \in (0,1)$ introduced in (24) is fixed and determines the degree of risk aversion of the agent.

By the choice of the gauge function $\psi$ (see (26)) we may choose ${\mathbb {M}}:={\mathbb {M}}':={\mathbb {M}}_{{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }}$ (with ${\mathbb {M}}_{{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }}$ introduced in Example 5) in the setting of Sect. 3.5. Note that $\psi$ coincides with the corresponding gauge function in Example 5 with $x':=0$. That is, in the end the metric $d_{\infty ,{\mathbb {M}}_{{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }}}^\psi$ (as defined in (11)) on ${{\mathcal {P}}}_\psi$ is used to measure the distance between transition functions.

For the formulation of Theorem 3 recall from (14) the definition of the functionals ${{\mathcal {V}}}_0^{x_0;\pi }$ and ${{\mathcal {V}}}_0^{x_0}$, where the maps $V_0^{{\varvec{P}};\pi }$ and $V_0^{{\varvec{P}}}$ are given by (5) and (7), respectively. In the specific setting of Sect. 4.2 we know from (30) that

$$\begin{aligned} {{\mathcal {V}}}_0^{x_0;\pi }({\varvec{P}}) \,=\, V_0^{{\varvec{P}};\pi }(x_0) \,=\, {\mathbb {E}}^{x_0,{\varvec{P}};\pi }[r_N(X_N)] \quad \text{ and } \quad {{\mathcal {V}}}_0^{x_0}({\varvec{P}}) \,=\, \sup _{\pi \in {\varPi }}{{\mathcal {V}}}_0^{x_0;\pi }({\varvec{P}})\nonumber \\ \end{aligned}$$

(37)

for any $x_0\in {\mathbb {R}}_{\ge 0}$, ${\varvec{P}}\in {{\mathcal {P}}}_\psi$, and $\pi \in {\varPi }$.

Further recall that any $\varvec{\gamma }=(\gamma _n)_{n=0}^{N-1}\in [0,1]^N$ induces a linear trading strategy $\pi _{\varvec{\gamma }}:=(f_n^{\varvec{\gamma }})_{n=0}^{N-1}\in {\varPi }_{{{\text {lin}}}}$ through (31). Let $v_n^{{\varvec{P}};\gamma _n}$ be defined as on the left-hand side of (29), and set $v_n^{{\varvec{P}};\varvec{\gamma }}:=v_n^{{\varvec{P}};\gamma _n}$ for any $n=0,\ldots ,N-1$. Moreover, for any $n=0,\ldots ,N-1$ denote by $\gamma _n^{{\varvec{P}}}$ the unique solution to the optimization problem (29) (Lemma 3 ensures the existence of a unique solution). Finally set $\varvec{\gamma }^{{\varvec{P}}}:=(\gamma _n^{{\varvec{P}}})_{n=0}^{N-1}$.

Theorem 3

(‘Differentiability’ of ${{\mathcal {V}}}_0^{x_0;\pi _{\varvec{\gamma }}}$ and ${{\mathcal {V}}}_0^{x_0}$) In the setting above let $x_0\in {\mathbb {R}}_{\ge 0}$, $\varvec{\gamma }\in [0,1]^N$, and ${\varvec{P}}\in {{\mathcal {P}}}_\psi$. Then the following two assertions hold.

• (i) The map ${{\mathcal {V}}}_0^{x_0;\pi _{\varvec{\gamma }}}:{{\mathcal {P}}}_\psi \rightarrow {\mathbb {R}}$ defined by (37) is ‘Fréchet differentiable’ at ${\varvec{P}}$ w.r.t. $({\mathbb {M}}_{{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }},\psi )$ with ‘Fréchet derivative’ $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0;\pi _{\varvec{\gamma }}}:{{\mathcal {P}}}_{\psi }^{{\varvec{P}}; \pm }\rightarrow {\mathbb {R}}$ given by

  $$\begin{aligned} \dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0;\pi _{\varvec{\gamma }}}({\varvec{Q}}-{\varvec{P}}) \,=\, \dot{{\mathfrak {v}}}_0^{{\varvec{P}},{\varvec{Q}};\pi _{\varvec{\gamma }}}\,u_\alpha (x_0), \end{aligned}$$

  (38)

  where $\dot{{\mathfrak {v}}}_0^{{\varvec{P}},{\varvec{Q}};\pi _{\varvec{\gamma }}}:= \sum _{k=0}^{N-1}v_{N-1}^{{\varvec{P}};\varvec{\gamma }}\cdots (v_k^{{\varvec{Q}};\varvec{\gamma }} - v_k^{{\varvec{P}};\varvec{\gamma }})\cdots v_0^{{\varvec{P}};\varvec{\gamma }}$.

• (ii) The map ${{\mathcal {V}}}_0^{x_0}:{{\mathcal {P}}}_\psi \rightarrow {\mathbb {R}}$ defined by (37) is ‘Hadamard differentiable’ at ${\varvec{P}}$ w.r.t. $({\mathbb {M}}_{{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }},\psi )$ with ‘Hadamard derivative’ $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}:{{\mathcal {P}}}_{\psi }^{{\varvec{P}};\pm }\rightarrow {\mathbb {R}}$ given by

  $$\begin{aligned} \dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}({\varvec{Q}}-{\varvec{P}}) \,=\, \sup _{\pi \in {\varPi }_{{{\text {lin}}}}({\varvec{P}})}\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0;\pi }({\varvec{Q}}-{\varvec{P}}) \,=\, \dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0;\pi _{\varvec{\gamma }^{{\varvec{P}}}}}({\varvec{Q}}-{\varvec{P}}). \end{aligned}$$

  (39)

Remark 9

Basically Theorem 1 yields the first “$=$” in (39) with ${\varPi }_{{{\text {lin}}}}({\varvec{P}})$ replaced by ${\varPi }({\varvec{P}})$. Since part (ii) of Theorem 2 ensures that for any ${\varvec{P}}\in {{\mathcal {P}}}_\psi$ there exists an optimal trading strategy which belongs to ${\varPi }_{{{\text {lin}}}}$, we may replace for any ${\varvec{P}}\in {{\mathcal {P}}}_\psi$ in the representation (30) of the value function $V_0^{{\varvec{P}}}(x_0)$ (or, equivalently, in the representation (37) of the value functional ${{\mathcal {V}}}_0^{x_0}({\varvec{P}})$) the set ${\varPi }$ by ${\varPi }_{{{\text {lin}}}}$ ($\subseteq {\varPi }$). Therefore one can use Theorem 1 to derive the first “$=$” in (39). The second “$=$” in (39) is ensured by the second assertion in part (ii) of Theorem 2. For details see the proof which is carried out in Subsection 5.3 of the supplemental article Kern et al. (2020). $\square$

4.5 Numerical examples for the ‘Hadamard derivative’

In this subsection we quantify by means of the ‘Hadamard derivative’ (of the optimal value functional ${{\mathcal {V}}}_0^{x_0}$) the effect of incorporating an unlikely but significant jump in the dynamics $S=(S_0,\ldots ,S_N)$ of an asset price on the optimal value of the corresponding terminal wealth problem (28). At the end of this subsection we will also study the effect of incorporating more than one jump.

We specifically focus on the setting of the discretized Black–Scholes–Merton model from Example 8 with (mainly) $N=12$. That is, we let ${\mathfrak {r}}_1=\cdots ={\mathfrak {r}}_N={\mathfrak {r}}$ for ${\mathfrak {r}}:=\exp (\nu /N)$, where $\nu \in {\mathbb {R}}_{\ge 0}$. Moreover let ${\varvec{P}}$ correspond to ${\mathfrak {m}}_1=\cdots ={\mathfrak {m}}_N={\mathfrak {m}}_{{\varvec{P}}}$ for ${\mathfrak {m}}_{{\varvec{P}}}:={{\text {LN}}}_{(\mu _{{\varvec{P}}} - \sigma _{{\varvec{P}}}^2/2)/N,\sigma _{{\varvec{P}}}^2/N}$, where $\mu _{{\varvec{P}}}\in {\mathbb {R}}_{\ge 0}$ and $\sigma _{{\varvec{P}}}\in {\mathbb {R}}_{>0}$ are chosen such that $\mu _{{\varvec{P}}} > (1-\alpha )\sigma _{{\varvec{P}}}^2$. In fact we let specifically $\mu _{{\varvec{P}}}=0.05$ and $\sigma _{{\varvec{P}}}=0.2$. This set of parameters is often used in numerical examples in the field of mathematical finance; see, e.g., Lemor et al. (2006, p. 898). For the initial state we choose $x_0=1$. For the drift $\nu$ of the bond we will consider different values, all of them lying in $\{0.01,0.02,0.03,0.035,0.04\}$. Moreover, we let (mainly) $\alpha \in \{0.25,0.5,0.75\}$. Recall that $\alpha$ determines the degree of risk aversion of the agent; a small $\alpha$ corresponds to high risk aversion.

By a price jump at a fixed time $n\in \{0,\ldots ,N-1\}$ we mean that the asset’s return ${\mathfrak {R}}_{n+1}$ is not anymore drawn from ${\mathfrak {m}}_{{\varvec{P}}}$ but is given by a deterministic value ${\varDelta }\in {\mathbb {R}}_{\ge 0}$ esstentially ‘away’ from 1. As appears from Table 1, in the case $N=12$ it seems to be reasonable to speak of a ‘jump’ at least if ${\varDelta }\le 0.8$ or ${\varDelta }\ge 1.25$. The probability under ${\mathfrak {m}}_{{\varvec{P}}}$ for a realized return smaller than 0.8 (resp. larger than 1.25) is smaller than 0.0001. A realized return of $\le 0.5$ (resp. $\ge 1.5$) is practically impossible; its probability under ${\mathfrak {m}}_{{\varvec{P}}}$ is smaller than $10^{-30}$ (resp. $10^{-10}$). That is, the choice ${\varDelta }=0.5$ or ${\varDelta }=1.5$ doubtlessly corresponds to a significant price jump.

Table 1 Some quantiles of the distribution ${\mathfrak {m}}_{{\varvec{P}}}$ of the asset’s return in the discretized ($N=12$) Black–Scholes–Merton model ($\mu _{{\varvec{P}}}=0.05$, $\sigma _{{\varvec{P}}}=0.2$)

If at a fixed time $\tau \in \{0,\ldots ,N-1\}$ a formerly nearly impossible ‘jump’ ${\varDelta }$ can now occur with probability $\varepsilon$, then instead of ${\mathfrak {m}}_{\tau +1}={\mathfrak {m}}_{{\varvec{P}}}$ one has ${\mathfrak {m}}_{\tau +1}=(1-\varepsilon ){\mathfrak {m}}_{{\varvec{P}}}+\varepsilon \delta _{\varDelta }$. That is, instead of ${\varvec{P}}$ the transition function is now given by $(1-\varepsilon ){\varvec{P}}+\varepsilon {\varvec{Q}}_{{\varDelta },\tau }$ with ${\varvec{Q}}_{{\varDelta },\tau }$ generated through (27) by ${\mathfrak {m}}_{n+1}={\mathfrak {m}}_{{\varvec{Q}}_{{\varDelta },\tau ;n}}$, $n=0,\ldots ,N-1$, where

$$\begin{aligned} {\mathfrak {m}}_{{\varvec{Q}}_{{\varDelta },\tau ;n}} := \left\{ \begin{array}{lll} \delta _{{\varDelta }}, &{} &{}\quad n=\tau \\ {\mathfrak {m}}_{{\varvec{P}}}, &{} &{}\quad \text{ otherwise } \end{array} \right. . \end{aligned}$$

(40)

By part (ii) of Theorem 3 the ‘Hadamard derivative’ $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}$ of the optimal value functional ${{\mathcal {V}}}_0^{x_0}$ evaluated at ${\varvec{Q}}_{{\varDelta },\tau }-{\varvec{P}}$ can be written as

$$\begin{aligned} \dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}({\varvec{Q}}_{{\varDelta },\tau }-{\varvec{P}})= & {} \sum _{k=0}^{N-1}v_{N-1}^{{\varvec{P}};\varvec{\gamma }^{{\varvec{P}}}_{\textsf {BSM} }}\cdots (v_k^{{\varvec{Q}}_{{\varDelta },\tau };\varvec{\gamma }^{{\varvec{P}}}_{\textsf {BSM} }} - v_k^{{\varvec{P}};\varvec{\gamma }^{{\varvec{P}}}_{\textsf {BSM} }})\cdots v_0^{{\varvec{P}};\varvec{\gamma }^{{\varvec{P}}}_{\textsf {BSM} }} \nonumber \\= & {} v_{N-1}^{{\varvec{P}};\varvec{\gamma }^{{\varvec{P}}}_{\textsf {BSM} }}\cdots (v_\tau ^{{\varvec{Q}}_{{\varDelta },\tau };\varvec{\gamma }^{{\varvec{P}}}_{\textsf {BSM} }} - v_\tau ^{{\varvec{P}};\varvec{\gamma }^{{\varvec{P}}}_{\textsf {BSM} }})\cdots v_0^{{\varvec{P}};\varvec{\gamma }^{{\varvec{P}}}_{\textsf {BSM} }} \end{aligned}$$

(41)

with $\varvec{\gamma }^{{\varvec{P}}}_{\textsf {BSM} }:=(\gamma ^{{\varvec{P}}}_{\textsf {BSM} },\ldots ,\gamma ^{{\varvec{P}}}_{\textsf {BSM} })$, where $\gamma ^{{\varvec{P}}}_{\textsf {BSM} }$ is given by (36). The involved factors are

$$\begin{aligned}&v_n^{{\varvec{P}};\varvec{\gamma }^{{\varvec{P}}}_{\textsf {BSM} }} \nonumber \\&\quad = \left\{ \begin{array}{lll} 1 &{} , &{} \nu \in [\mu _{{\varvec{P}}},\infty ) \\ \int _{{\mathbb {R}}_{\ge 0}}u_\alpha \big (1+\frac{1}{1-\alpha }\frac{\mu _{{\varvec{P}}} - \nu }{\sigma _{{\varvec{P}}}^2}(\frac{y}{{\mathfrak {r}}} - 1)\big ){\mathfrak {f}}_{(\mu _{{\varvec{P}}} - \sigma _{{\varvec{P}}}^2/2)/N,\sigma _{{\varvec{P}}}^2/N}(y)\,\ell (dy) &{} , &{} \nu \in (\nu _{{\varvec{P}},\alpha },\mu _{{\varvec{P}}}) \\ {\mathfrak {r}}^{-\alpha }\,\exp \big \{\frac{\alpha }{N}(\mu _{{\varvec{P}}} - \frac{\sigma _{{\varvec{P}}}^2}{2}) + \frac{(\alpha \sigma _{{\varvec{P}}})^2}{2N}\big \} &{} , &{} \nu \in [0,\nu _{{\varvec{P}},\alpha }], \end{array} \right. \end{aligned}$$

(42)

$$\begin{aligned} v_n^{{\varvec{Q}}_{{\varDelta },\tau };\varvec{\gamma }^{{\varvec{P}}}_{\textsf {BSM} }} = \left\{ \begin{array}{lll} 1 &{} , &{} \nu \in [\mu _{{\varvec{P}}},\infty ) \\ \int _{{\mathbb {R}}_{\ge 0}}u_\alpha \big (1 + \frac{1}{1-\alpha }\frac{\mu _{{\varvec{P}}} - \nu }{\sigma _{{\varvec{P}}}^2}(\frac{y}{{\mathfrak {r}}}-1)\big )\,{\mathfrak {m}}_{{\varvec{Q}}_{{\varDelta },\tau ;n}}(dy) &{} , &{} \nu \in (\nu _{{\varvec{P}},\alpha },\mu _{{\varvec{P}}}) \\ {\mathfrak {r}}^{-\alpha }\,\int _{{\mathbb {R}}_{\ge 0}}u_\alpha (y)\,{\mathfrak {m}}_{{\varvec{Q}}_{{\varDelta },\tau ;n}}(dy) &{} , &{} \nu \in [0,\nu _{{\varvec{P}},\alpha }] \end{array} \right. \nonumber \\ \end{aligned}$$

(43)

for $n=0,\ldots ,N-1$, where $\nu _{{\varvec{P}},\alpha }:=\mu _{{\varvec{P}}} - (1 - \alpha )\sigma _{{\varvec{P}}}^2$ ($\in (0,\mu _{{\varvec{P}}})$).

Note that $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}({\varvec{Q}}_{{\varDelta },\tau }-{\varvec{P}})$ is independent of $\tau$, which can be seen from (40)–(43). That is, the effect of a jump is independent of the time at which the jump takes place. Also note that $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}({\varvec{Q}}_{{\varDelta },\tau }-{\varvec{P}})\equiv 0$ when $\nu \in [\mu _{{\varvec{P}}},\infty )$. This is not surprising, because in this case the optimal fraction $\gamma ^{{\varvec{P}}}_{\textsf {BSM} }$ to be invested into the asset is equal to 0 (see (36)) and the agent performs a complete investment in the bond at each trading time n.

Remark 10

As mentioned before, the ‘Hadamard derivative’ $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}$ evaluated at ${\varvec{Q}}_{{\varDelta },\tau }-{\varvec{P}}$ can be seen as the first-order sensitivity of the optimal value ${{\mathcal {V}}}_0^{x_0}({\varvec{P}})$ w.r.t. a change of ${\varvec{P}}$ to $(1-\varepsilon ){\varvec{P}}+\varepsilon {\varvec{Q}}_{{\varDelta },\tau }$, with $\varepsilon >0$ small. It is a natural wish to compare these values for different ${\varDelta }\in {\mathbb {R}}_{\ge 0}$. In Subsection 5.4 of the supplemental article Kern et al. (2020) it is proven that the family $\{{\varvec{Q}}_{{\varDelta },\tau }: {\varDelta }\in [0,\delta ]\}$ is relatively compact w.r.t. $d_{\infty ,{\mathbb {M}}_{{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }}}^\psi$ (the proof does not work if $d_{\infty ,{\mathbb {M}}_{{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }}}^\psi$ is replaced by $d_{\infty ,{\mathbb {M}}_{{{{{\text {H}}}{\ddot{{{\text {o}}}}{{\text {l}}}}},\alpha }}}^\phi$ for any gauge function $\phi$ ‘flatter’ than $\psi$) for any fixed $\delta \in {\mathbb {R}}_{>0}$ (and $\tau \in \{0,\ldots ,N-1\}$, $\alpha \in (0,1)$). As a consequence the approximation (1) with ${\varvec{Q}}={\varvec{Q}}_{{\varDelta },\tau }$ holds uniformly in ${\varDelta }\in [0,\delta ]$, and therefore the values $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}({\varvec{Q}}_{{\varDelta },\tau }-{\varvec{P}})$, ${\varDelta }\in [0,\delta ]$, can be compared with each other with clear conscience. $\square$

Fig. 1

‘Hadamard derivative’ $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}({\varvec{Q}}_{{\varDelta },\tau }-{\varvec{P}})$ (for ${\varDelta }=1.5)$ and negative ‘Hadamard derivative’ $-\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}({\varvec{Q}}_{{\varDelta },\tau }-{\varvec{P}})$ (for ${\varDelta }=0.5)$ for $N=12$, $\nu =0.01$, $\mu _{{\varvec{P}}}=0.05$, and $\sigma _{{\varvec{P}}}=0.2$ in dependence of the risk aversion parameter $\alpha$

By Remark 10 and (41) we are able to compare the effect of incorporating different ‘jumps’ ${\varDelta }$ in the dynamics $S=(S_0,\ldots ,S_N)$ of an asset price on the optimal value (functional) ${{\mathcal {V}}}_0^{x_0}({\varvec{P}})$. As appears from Fig. 1 the negative effect of incorporating a ‘jump’ ${\varDelta }=0.5$ in the dynamics $S=(S_0,\ldots ,S_N)$ of an asset price is larger than the positive effect of incorporating a ‘jump’ ${\varDelta }=1.5$ for every choice of the agent’s degree of risk aversion. Figure 1 also shows the unsurprising effect that a high risk aversion (small value of $\alpha$) leads to a negligible sensitivity.

Next we compare the values of $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}({\varvec{Q}}_{{\varDelta },\tau }-{\varvec{P}})$ for trading horizons $N\in \{4,12,52\}$ in dependence of the drift $\nu$ of the bond and the ‘jump’ ${\varDelta }$. This choices of N correspond respectively to a quarterly, monthly, and weekly time discretization. We will restrict ourselves to ‘jumps’ ${\varDelta }\le 0.8$. On the one hand, this ensures that the ‘jumps’ are significant; see the discussion above. On the other hand, as just discerned from Fig. 1, the effect of jumps ‘down’ are more significant than jumps ‘up’.

Fig. 2

‘Hadamard derivative’ $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}({\varvec{Q}}_{{\varDelta },\tau }-{\varvec{P}})$ for $\alpha =0.5$, $\mu _{{\varvec{P}}}=0.05$, and $\sigma _{{\varvec{P}}}=0.2$ in dependence of the ‘jump’ ${\varDelta }$ and the drift $\nu$ of the bond, showing $N=4$ in the first, $N=12$ in the second, and $N=52$ in the third column

From Fig. 2 one can see that for each trading time N and any ${\varDelta }\in [0,0.8]$ the (negative) effect of incorporating a ‘jump’ ${\varDelta }$ in the dynamics $S=(S_0,\ldots ,S_N)$ of an asset price is the smaller the smaller the spread between the drift $\mu _{{\varvec{P}}}$ of the asset and the drift $\nu$ of the bond. There is only a tiny (nearly invisible) difference between the ‘Hadamard derivative’ $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}({\varvec{Q}}_{{\varDelta },\tau }-{\varvec{P}})$ for the trading times $N\in \{4,12,52\}$. So the fineness of the discretization seems to play a minor part.

Next we compare the values of $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}({\varvec{Q}}_{{\varDelta },\tau }-{\varvec{P}})$ for the drift $\nu \in \{0.02,0.03,0.04\}$ of the bond in dependence of the risk aversion parameter $\alpha$ and the ‘jump’ ${\varDelta }$.

Fig. 3

‘Hadamard derivative’ $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}({\varvec{Q}}_{{\varDelta },\tau }-{\varvec{P}})$ for $N=12$, $\mu _{{\varvec{P}}}=0.05$, and $\sigma _{{\varvec{P}}}=0.2$ in dependence of the ‘jump’ ${\varDelta }$ and risk aversion parameter $\alpha$, showing $\nu =0.02$ in the first, $\nu =0.03$ in the second, and $\nu =0.04$ in the third column

Fig. 4

‘Hadamard derivative’ $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}({\varvec{Q}}_{{\varDelta },\varvec{\tau }(\ell )}-{\varvec{P}})$ for $N=12$ in dependence on $\ell \in \{1,\ldots ,N\}$ and ${\varDelta }\in [0,0.8]$ showing $\alpha =0.25$ and $\nu =0.02$ (left), $\alpha =0.5$ and $\nu =0.03$ (middle), and $\alpha =0.75$ and $\nu =0.04$ (right)

As appears from Fig. 3, for any ${\varDelta }\in [0,0.8]$ the (negative) effect of incorporating a ‘jump’ ${\varDelta }$ in the dynamics $S=(S_0,\ldots ,S_N)$ of an asset price is the smaller the higher the agent’s risk aversion, no matter what the drift $\nu \in \{0.02,0.03,0.04\}$ of the bond looks like. Take into account that the extent of this effect is influenced via (41)–(43) by the optimal fraction $\gamma ^{{\varvec{P}}}_{\textsf {BSM} }$ to be invested into the asset which in turn depends on the risk aversion parameter $\alpha$ (see (36)).

Finally, let us briefly touch on the case where more than one jump may appear. More precisely, instead of ${\varvec{Q}}_{{\varDelta },\tau }$ (with $\tau \in \{0,\ldots ,N-1\}$) consider the transition function ${\varvec{Q}}_{{\varDelta },\varvec{\tau }(\ell )}$ (with $1\le \ell \le N$, $\varvec{\tau }(\ell )=(\tau _1,\ldots ,\tau _\ell )$, $\tau _1,\ldots ,\tau _\ell \in \{0,\ldots ,N-1\}$ pairwise distinct) which is still generated by means of (40) but with the difference that at the $\ell$ different times $\tau _1,\ldots ,\tau _\ell$ the distribution ${\mathfrak {m}}_{{\varvec{P}}}$ is replaced by $\delta _{\varDelta }$. Just as in the case $\ell =1$, it turns out that it does not matter at which times $\tau _1,\ldots ,\tau _\ell$ exactly these $\ell$ jumps occur. Figure 4 shows the value of $\dot{{\mathcal {V}}}_{0;{\varvec{P}}}^{x_0}({\varvec{Q}}_{{\varDelta },\varvec{\tau }(\ell )}-{\varvec{P}})$ in dependence on $\ell$ and ${\varDelta }$. It seems that for any fixed ${\varDelta }\in [0,0.8]$ the first-order sensitivity increases approximately linearly in $\ell$.

5 Supplement

The supplement Kern et al. (2020) illustrates the setting of Sects. 2–3 in the case of finite state space and finite action spaces, and contains the proofs of the results from Sects. 3–4. Moreover, supplemental definitions and results to Sect. 2 are given and the existence of optimal strategies in general MDMs is discussed. Finally, a supplemental topological result is shown.