Continuity and monotonicity of solutions to a greedy maximization problem

Abstract

Motivated by an application to resource sharing network modelling, we consider a problem of greedy maximization (i.e., maximization of the consecutive minima) of a vector in ${\mathbb {R}}^n$, with the admissible set indexed by the time parameter. The structure of the constraints depends on the underlying network topology. We investigate continuity and monotonicity of the resulting maximizers with respect to time. Our results have important consequences for fluid models of the corresponding networks which are optimal, in the appropriate sense, with respect to handling real-time transmission requests.

1 Introduction

Starting from seminal papers of Rybko and Stolyar (1992), Dai (1995), Bramson (1996a, b, 1998) and other authors, fluid models have become a standard tool in investigating long-time behaviour of complicated queueing systems. Such models are useful for establishing stability and obtaining hydrodynamic or diffusion limits for multiclass queueing networks and resource sharing networks with various service protocols. Using a similar methodology in the case of real-time earliest deadline first (EDF) networks with resource sharing is hindered by the lack of suitable fluid model equations. To overcome this difficulty, Kruk (2017) suggested the definition of fluid models for these systems by means of an optimality property, called local edge minimality, which is known to characterize the EDF discipline in stochastic resource sharing networks. It turns out that the success of this approach depends on establishing suitable local properties of a vector-valued mapping $F:[0,\infty )\rightarrow {\mathbb {R}}^n$, resulting from a greedy maximization (i.e., maximization of the consecutive minima) of a vector in ${\mathbb {R}}^n$ over the admissible set $A_t$, depending on the underlying network topology and indexed by the time parameter. A convenient way to describe the value F(t) for a given $t\ge 0$ is to define it as the maximal element of $A_t$ with respect to a suitable “min-sensitive” partial ordering. Roughly speaking, the function F, when well behaved, determines the so-called frontiers (i.e., the left endpoints of the supports) of the states in the corresponding locally edge minimal fluid model [see Definition 3 and formula (10), to follow]. Recall that in a stochastic EDF queueing system, the frontier is the largest lead time of a customer who has ever been in service. The idea of using frontiers for the asymptotics of EDF systems dates back to the paper of Doytchinov et al. (2001) on a G/G/1 queue, and it has been used several times since then. However, both the application of this notion to resource sharing networks and our approach to determining the frontiers by finding maximal elements of partially ordered sets appear to be new.

In this paper, for any $t\ge 0$, we construct the value of F(t) as a solution of a nested sequence of nonlinear multiple resource allocation problems in a t-dependent admissible set. While none of these problems is hard to solve, their number and forms vary with t in a complex, discontinuous way, making the analysis of the resulting mapping F on $[0,\infty )$ rather involved. Examples illustrating our construction and some related issues can be found in Sects. 3.2, 4 and 5.4 , to follow. We investigate key properties of F, namely, its continuity and monotonicity. Our main results are described in more detail in Sect. 2.4, to follow, after the introduction of indispensable notation. These results are used in our forthcoming paper to establish fundamental properties of locally edge minimal fluid models, like their existence, uniqueness and stability.

Our work is closely related to perturbation analysis of optimization problems, see, e.g., Bonnans and Shapiro (2000). A typical problem in this area is to minimize a real-valued function f(x, u) over $x\in X$, subject to $G(x,u)\in K$, where $u\in U$ is a parameter, $G:X\times U\rightarrow Y$ and K is a suitable (usually closed and convex) subset of Y. The underlying spaces X, Y, U may be fairly general, e.g., Banach. [See problem ($P_u$) on p. 260 of Bonnans and Shapiro (2000)]. The aim is to investigate, under suitable assumptions, continuity of the optimal value function and the corresponding solution set with respect to the parameter u. Our problem does not fall readily within the scope of this theory because, as we have already mentioned, for each parameter t, we consider a nested sequence of optimization problems (as opposed to a single one), varying discontinuously with t, where each problem determines the form (the target function, the constraints and even the dimension) of the next one. Moreover, in perturbation analysis of problems like ($P_u$), one typically assumes that f, G are fairly regular (say $C^2$), together with suitable second order sufficient conditions, assuring, roughly speaking, some type of strong convexity of the associated Lagrangian function in the vicinity of the solution of the unperturbed problem. See, e.g, Theorems 5.5.53 and 5.5.57 in Bonnans and Shapiro (2000) for representative samples of such results in the context of nonlinear programming. In our analysis, we consider constraints which are not necessarily $C^2$ and problems for which second order sufficient conditions of the form mentioned above typically do not hold.

Another topic related to our study is theory of separated continuous linear programs (SCLP), used for optimal control of fluid models for some multiclass processing networks, see Weiss (2008) and the references given there. In contrast to SCLP, our problem is, in general, nonlinear. Moreover, due to qualitatively different target functions, our construction of F(t) appears to be of a different nature than algorithms used to solve SCLP, which are more akin to the classic simplex method of linear programming.

We hope that the theory developed in this paper will be useful not only in the asymptotic analysis of EDF-like disciplines, but also in the case of other “greedy“ scheduling policies for resource sharing networks, for example Longest Queue First (Dimakis and Walrand 2006) or Shortest Remaining Processing Time (Verloop et al. 2005). Some ideas related to the latter applications are sketched in Sect. 6.

1.1 Notation

For sets A, B, we write $A \subsetneq B$ if A is a proper subset of B. For a finite set A, let |A| denote the cardinality of A. Let ${\mathbb {N}}$ denote the set of positive integers, let ${\mathbb {R}}$ denote the set of real numbers and let $(-\infty ,+\infty ]={\mathbb {R}}\cup \{+\infty \}$. The nonnegative real numbers $[0,\infty )$ will be denoted by ${\mathbb {R}}_+$. For $a,b\in {\mathbb {R}}$, we write $a\vee b$ ($a\wedge b$) for the maximum (minimum) of a and b, $a^+$ for $a \vee 0$. Vector inequalities are to be interpreted componentwise, i.e., for $a,b\in {\mathbb {R}}^n$, $a=(a_1,..,a_n)$, $b=(b_1,\ldots ,b_n)$, $a\le b$ if and only if $a_i\le b_i$ for all $i=1,\ldots ,n$. For $a=(a_1,..,a_n)\in {\mathbb {R}}^n$, we write $\min a$ for $\min _{i=1,\ldots ,n} a_i$ and ${\mathrm{Argmin}}\;a$ for $\{i\in \{1,\ldots ,n\}: a_i = \min a\}$. For $a=(a_1,..,a_n)\in {\mathbb {R}}^n$ and a set $A\subsetneq \{1,\ldots ,n\}$ with $\{1,\ldots ,n\}{\setminus }A= \{i_1,\ldots ,i_k\}$, where $k=n-|A|$ and $i_1<i_2<\cdots <i_k$, we identify $(a_i)_{i\notin A}$ with $(a_{i_1},\ldots a_{i_k})\in {\mathbb {R}}^k$. By convention, a sum of the form $\sum _{i=n}^m$ ($\bigcup _{i=n}^m$) with $n>m$ or, more generally, a sum of numbers (resp., sets) over the empty set of indices equals zero (resp., $\emptyset$). For a set $A \subseteq {\mathbb {R}}$, let ${\overline{A}}$ denote the closure of A.

The following additional notation will be used in Sect. 6.2. For $x\le 0$, the set [0, x) is empty. For a Borel set $B\subseteq {\mathbb {R}}_+$, we denote the indicator of the set B by ${\mathbb {I}}_{B}$. We also define the real valued function $\chi (x)=x$, for $x\in {\mathbb {R}}_+$. Denote by ${{\mathbf {M}}}$ the set of all finite, nonnegative measures on ${{\mathcal {B}}}({\mathbb {R}}_+)$, the Borel subsets of ${\mathbb {R}}_+$. The set ${{\mathbf {M}}}$ is endowed with the weak topology. For $\xi \in {{\mathbf {M}}}$ and $B\in {\mathcal {B}}({\mathbb {R}}_+)$, $\xi _{|B}$ will denote the truncation of $\xi$ to B, i.e., the measure on ${\mathcal {B}}({\mathbb {R}}_+)$ given by $\xi _{|B}(C)=\xi (B \cap C)$ for all $C\in {\mathcal {B}}({\mathbb {R}}_+)$. For $\xi \in {{\mathbf {M}}}$ and a Borel measurable function $g:{\mathbb {R}}_+\rightarrow {\mathbb {R}}$ that is integrable with respect to $\xi$, define $\langle g,\xi \rangle =\int _{{\mathbb R}_+}g(x)\xi (dx).$ For $\mu \in {{\mathbf {M}}}$, let $l_\mu = \sup \{x\in {\mathbb {R}}_+: \mu ([0,x))=0 \}.$ Let ${{\mathbf {M}}}_a$ denote those elements of ${{\mathbf {M}}}$ that do not charge the origin. We say that a measure $\xi \in {{\mathbf {M}}}$ has a finite first moment if $\langle \chi ,\xi \rangle <\infty$. Let ${{\mathbf {M}}}_{\chi }$ denote the set of all such measures and let ${{\mathbf {M}}}_0={{\mathbf {M}}}_{\chi }\cap {{\mathbf {M}}}_a$.

2 The mapping F

2.1 “Min-sensitive” partial ordering on ${\mathbb {R}}^n$

We define the relation “$\eqslantless$” inductively on ${\mathbb {R}}^n$ as follows.

Definition 1

For $a,b\in {\mathbb {R}}$, we write $a \eqslantless b$ iff $a\le b$. If $n\ge 2$, for $a,b\in {\mathbb {R}}^n$, $a=(a_1,..a_n)$, $b=(b_1,\ldots ,b_n)$, we write $a \eqslantless b$ if one of the following four cases holds.

• (i) $a=b$,

• (ii) $\min a < \min b$,

• (iii) $\min a = \min b$ and ${\mathrm{Argmin}}\;b \subsetneq {\mathrm{Argmin}}\;a$,

• (iv) $\min a = \min b$, ${\mathrm{Argmin}}\;a = {\mathrm{Argmin}}\;b \subsetneq \{1,\ldots ,n\}$ and $(a_i)_{i \notin {\mathrm{Argmin}}\;a} \eqslantless (b_i)_{i \notin {\mathrm{Argmin}}\;b}$ in ${\mathbb {R}}^{|{\mathrm{Argmin}}\;a|}$.

Remark 1

Clearly, if $a \eqslantless b$, then $\min a \le \min b$. The converse is, in general, false, unless $n=1$. For example, the relation $(0,1) \eqslantless (1,0)$ does not hold.

The proof of the following lemma is elementary and it is left to the reader.

Lemma 1

The relation “$\eqslantless$” is a partial ordering on ${\mathbb {R}}^n$.

Remark 2

For $a,b\in {\mathbb {R}}^n$, the inequality $a\le b$ implies $a \eqslantless b$. In dimensions greater than one the converse is in general, false, for example, $(0,2) \eqslantless (1,1)$.

2.2 The mapping definition

Let $I,J\in {\mathbb {N}}$ and let $\mathbf{I}=\{1,\ldots ,I\}$, $\mathbf{J}=\{1,\ldots ,J\}$. For $i\in \mathbf {I}$, let $h_i:{\mathbb {R}}\rightarrow {\mathbb {R}}$ be a continuous, nonnegative, nondecreasing function with $\lim _{x\rightarrow \infty } h_i(x)=\infty$ and

$$\begin{aligned} x^*_i:=\sup \{x\in {\mathbb {R}}:h_i(x)=0\} \in (-\infty , 0]. \end{aligned}$$

(1)

In other words, each $h_i$ is the cumulative distribution function of an atomless, $\sigma$-finite measure in ${\mathbb {R}}$, with finite, nonpositive infimum of its support. Let $G_j$, $j\in \mathbf{J}$, be a family of distinct, nonempty subsets of $\mathbf{I}$ (not necessarily pairwise disjoint) such that $\mathbf{I}= \bigcup _{j\in \mathbf{J}} G_j$.

Definition 2

For $t\ge 0$, we denote by $F(t)=(F_i(t))_{i\in \mathbf{I}}$ the maximal element of the set

$$\begin{aligned} A_t = \Big \{a=(a_1,\ldots ,a_I)\in {\mathbb {R}}^I:\; a_i \le t, \; i\in \mathbf{I}, \; \sum _{i\in G_j} h_i(a_i) \le t, \; j \in \mathbf{J} \Big \}, \end{aligned}$$

with respect to the relation “$\eqslantless$”.

Somewhat informally, F(t) may be thought of as the result of “greedy” maximization of a vector $a\in {\mathbb {R}}^I$, subject to the constraints defining the set $A_t$, in the following sense. We first maximize $\min a$ over $a\in A_t$, then we maximize the “next minimum” $\min \{ a_i, i\notin {\mathrm{Argmin}}\;a\}$ over the set of maximizers of the previous problem, and we continue in this way until all the entries of the maximizer $a^*=F(t)$ are determined. In Sect. 3.1 we formalize and describe in detail this nested max-min procedure which implies, in particular, the existence and uniqueness of the maximizer F(t).

Remark 3

A seemingly more general version of Definition 2, in which for a fixed (possibly positive) $t_0\in {\mathbb {R}}$ and $t\ge t_0$, the set $A_t$ is replaced by

$$\begin{aligned} A_t^{t_0} = \Big \{a=(a_1,\ldots ,a_I)\in {\mathbb {R}}^I:\; a_i \le t, \; i\in \mathbf{I}, \; \sum _{i\in G_j} h_i(a_i) \le t-t_0, \; j \in \mathbf{J} \Big \}, \end{aligned}$$

and the half-line $(-\infty ,0]$ in (1) is replaced by $(-\infty , t_0]$, may be easily reduced to the case considered in Definition 2 by the change of variables $y=x-t_0$, $s=t-t_0$ and by using ${\tilde{h}}_i(y)=h_i(x)=h_i(y+t_0)$ instead of $h_i$.

2.3 Motivation: fluid models for resource sharing networks

The need for investigating the properties of the mapping F defined above arises in the theory of fluid models for real-time networks with resource sharing. Below, we briefly (and somewhat informally) describe this connection. The reader may consult (Kruk 2017) for more details and references.

Consider a network with a finite number of resources (nodes), labelled by $j=1,\ldots ,J$, and a finite set of routes, labelled by $i=1,\ldots ,I$. Let $\mathbf{I}=\{1,\ldots ,I\}$, $\mathbf{J}=\{1,\ldots ,J\}$. For $j\in \mathbf{J}$, let $G_j \subseteq \mathbf{I}$ be the set of routes using the resource j. For convenience, we assume that all the resources have a unit service rate. By a flow on route i we mean a continuous transmission of a file through the resources used by this route. We assume that a flow takes simultaneous possession of all the resources on its route during the transmission. Each flow in the network has a deadline for transmission completion. Networks of this type may be used to model, e.g., voice and video transmission, manufacturing systems with order due dates or emergency health care services. In what follows, by the lead time of a flow we mean the difference between its deadline and the current time.

As in Kruk (2016, 2017), the time evolution of such a system may be described by the process ${\mathfrak {X}}(t,s)=(Z(t,s),D(t,s),T(t,s),Y(t,s))$, $t\ge 0, s\in {\mathbb {R}},$ where the component processes Z, D, T, Y are defined as follows. For $t\ge 0$ and $s\in {\mathbb {R}}$, $Z(t,s)=(Z_i(t,s))_{i\in \mathbf{I}}$, where $Z_i(t,s)$ is the number of flows on route i with lead times at time t less than or equal to s which are still present in the system at that time. Similarly, the vectors $D(t,s)=(D_i(t,s))_{i\in \mathbf{I}}$, $T(t,s)=(T_i(t,s))_{i\in \mathbf{I}}$ denote the number of departures (i.e., transmission completions) and the cumulative transmission time by time t corresponding to each route i of flows with lead times at time t less than or equal to s. Let $Y_i(t,s)=t-T_i(t,s)$, $i\in \mathbf{I}$, denote the cumulative idleness by time t with regard to transmission of flows on route i with lead times at time t less than or equal to s and let $Y(t,s)=(Y_i(t,s))_{i\in \mathbf{I}}$. The process ${\mathfrak {X}}$ satisfies the following network equations, valid for ${\tilde{t}}\ge t\ge 0$, $s\in {\mathbb {R}}$:

$$\begin{aligned}&Z(t,s)= Z(0,t+s)+E(t,s)-D(t,s), \qquad \;\; \qquad \end{aligned}$$

(2)

$$\begin{aligned}&D_i(t,s)=S_i(T_i(t,s),t,s), \qquad T_{i}(t,s) +Y_i(t,s)=t, \qquad i\in \mathbf{I}, \end{aligned}$$

(3)

$$\begin{aligned}&\sum _{i\in G_j } \big ( T_i({\tilde{t}}, s-{\tilde{t}})- T_i(t,s-t) \big ) \le {\tilde{t}}-t, \qquad j\in \mathbf{J}, \qquad \end{aligned}$$

(4)

where $E(t,s)=(E_i(t,s))_{i\in \mathbf{I}}$ is the corresponding external arrival process and $S_i(t',t,s)$ denotes the number of transmission completions of flows on route $i\in \mathbf{I}$ having lead times at time t less than or equal to s, by the time the system has spent $t'$ units of time transmitting these flows.

Fluid models are deterministic, continuous analogs of resource sharing networks, in which individual flows are replaced by a divisible commodity (fluid), moving along I routes with J resources (nodes). They usually arise from formal functional law of large numbers approximations of the corresponding stochastic flow level models. The analogs of the network Eqs. (2)–(4) are the following fluid model equations, valid for ${\tilde{t}}\ge t\ge 0$, $s\in {\mathbb {R}}$:

$$\begin{aligned}&{\overline{Z}}(t,s)= {\overline{Z}}(0,t+s)+ \alpha (t+ (s\wedge 0))^+ -{\overline{D}}(t,s), \qquad \;\;\; \end{aligned}$$

(5)

$$\begin{aligned}&{\overline{D}}_i(t,s)={\overline{T}}_i(t,s)/m_i, \qquad {\overline{T}}_{i}(t,s) +{\overline{Y}}_i(t,s)=t, \qquad i\in \mathbf{I}, \end{aligned}$$

(6)

$$\begin{aligned}&\sum _{i\in G_j} \big ( {\overline{T}}_i({\tilde{t}}, s-{\tilde{t}})- {\overline{T}}_i(t,s-t) \big ) \le {\tilde{t}}-t, \qquad j\in \mathbf{J}, \qquad \;\; \end{aligned}$$

(7)

where $m_i$ is the mean transmission time of a flow on route i and $\alpha =(\alpha _i)_{i\in \mathbf{I}}$ is the vector of flow arrival rates. A system

$$\begin{aligned} \overline{{\mathfrak {X}}}(t,s)=({\overline{Z}}(t,s),{\overline{D}}(t,s), {\overline{T}}(t,s),{\overline{Y}}(t,s)), \qquad t\ge 0, \; s\in {\mathbb {R}}, \end{aligned}$$

(8)

with continuous, nonnegative components, satisfying the Eqs. (5)–(7), together with some natural monotonicity assumptions, is called a fluid model for the resource sharing network under consideration.

Definition 3

Let $\overline{{\mathfrak {X}}}$ be a fluid model of the form (8). For $t\ge 0$ and $i\in \mathbf{I}$, the quantity ${\overline{F}}_i^{\overline{{\mathfrak {X}}}} (t):=\inf \left\{ s\in {\mathbb {R}}: {\overline{Z}}_i(t,s)>0\right\} \wedge 0$ will be called the frontier on route i at time t.

To proceed further, we will introduce a class of fluid models which is, in some sense, optimal with respect to handling real-time transmission requests. To this end, we define a partial ordering “$\ll$” on the space of real functions on ${\mathbb {R}}$, which is extremely sensitive to the behaviour of the functions under comparison for small arguments.

Definition 4

(Kruk 2017, Definition 5) Let $f, g:{\mathbb {R}}\rightarrow {\mathbb {R}}$ be such that for some $a\in {\mathbb {R}}$ we have $f\equiv g$ on $(-\infty ,a]$ and let $c= \sup \{ a\in {\mathbb {R}}: f(x)=g(x) \; \forall x \le a\}.$ We write $f \ll g$ if either $c=\infty$ (i.e., $f\equiv g$ on ${\mathbb {R}}$), or $c<\infty$ and there exists $\epsilon >0$ such that $f\le g$ on $[c,c+\epsilon ]$.

Definition 5

(see Kruk 2017, Definition 11) A fluid model $\overline{{\mathfrak {X}}}$ of the form (8) for a resource sharing network with $\sum _{i\in \mathbf{I}} {\overline{Z}}_i(0,\cdot )\equiv 0$ on $(-\infty ,c]$ for some $c\in {\mathbb {R}}$ is called locally edge minimal at a time $t_0\ge 0$ if there exists $h>0$ such that for any fluid model $\overline{{\mathfrak {X}}}'$ with the same $\alpha$, $m_i$, $G_i$ and the same initial state ${\overline{Z}}'(0,\cdot )={\overline{Z}}(0,\cdot )$, satisfying $\overline{{\mathfrak {X}}}'(t_0,\cdot )=\overline{{\mathfrak {X}}}(t_0,\cdot ),$ we have $\sum _{i\in \mathbf{I}} {\overline{Y}}_i(t,\cdot )\ll \sum _{i\in \mathbf{I}} {\overline{Y}}_i'(t,\cdot )$ (equivalently, $\sum _{i\in \mathbf{I}} {\overline{Z}}_i(t,\cdot )\ll \sum _{i\in \mathbf{I}} {\overline{Z}}_i'(t,\cdot )$) for every $t\in (t_0,t_0+h)$. The fluid model $\overline{{\mathfrak {X}}}$ is called locally edge minimal, if it is locally edge minimal at every $t_0\ge 0$.

The intuition behind these notions is that a locally edge minimal fluid model tries to transmit as much “customer mass” corresponding to the earliest deadlines as possible, and hence its idleness with respect to such mass is as small as possible. Accordingly, such a model may be thought of as a “macroscopic” counterpart of a resource sharing network working under the earliest-deadline-first (EDF) protocol. Indeed, the EDF service discipline in such a network may be characterized by an analogous notion of local edge minimality, see Kruk (2017), Definition 8 and Theorems 5–7.

In a forthcoming paper, we show that existence and local uniqueness of a fluid model ${\overline{{\mathfrak {X}}}}$ for given data $\alpha$, $m_i$, $G_i$, and initial state ${\overline{Z}}(0,\cdot )$, which is locally edge minimal at a time $t_0\ge 0$, is related to continuity and local monotonicity of the mapping F introduced in Sect. 2.2, with

$$\begin{aligned} h_i(x)=m_i [{\overline{Z}}_i(0,x+t_0) - {\overline{Z}}_i(0,x^*_i+t_0)]^+ + \alpha _i m_i [(x+t_0)^+-(x^*_i+t_0)^+]^+,\nonumber \\ \end{aligned}$$

(9)

and $x^*_i={\overline{F}}_i^{\overline{{\mathfrak {X}}}}(t_0)$ for $i\in \mathbf{I}$. In fact, if F is well behaved, then the frontiers of a fluid model ${\overline{{\mathfrak {X}}}}$ which is locally edge minimal at $t_0$ are given by the formula

$$\begin{aligned} {\overline{F}}_i^{\overline{{\mathfrak {X}}}}(t) = F_i(t-t_0)-(t-t_0), \qquad i\in \mathbf{I}, \end{aligned}$$

(10)

for $t\ge t_0$ sufficiently close to $t_0$. This means that, up to a suitable time shift, F represents the vector of the earliest deadlines of the fluid masses present in the system, which translates to the corresponding frontiers according to (10). Since the initial distribution ${\overline{Z}}(0,\cdot )$ is, in general, nonlinear, the analysis of the function F corresponding to nonlinear $h_i$ is indispensable for the investigation of the transient behaviour of such fluid models. However, it turns out that for large $t_0$, the points $x^*_i+t_0$ are also large, so under a natural assumption that the supports of ${\overline{Z}}_i(0,\cdot )$ are bounded above, the functions $h_i$ in (9) are linear on $[x^*_i, \infty )$. Consequently, the linear case, investigated in Sect. 5.1 of this paper, is of considerable importance, because it determines the long-time behaviour of the corresponding locally edge minimal fluid model, for example, its stability or the form of its invariant manifold. In particular, one of remarkable implications of the formulae developed in Sect. 5.1 is stability of locally edge minimal fluid models, regardless of the underlying resource sharing network topology. Results along this line may be found in our forthcoming paper.

2.4 Overwiev of the main results

In this paper, we investigate key properties of the mapping $F: [0,\infty )\rightarrow {\mathbb {R}}^I$, in particular those which are relevant to the theory of locally edge minimal fluid models. In Sect. 3, we present a detailed construction of F(t) and we provide some illustrating examples. The main result of Sect. 4 is Theorem 1, stating that if each function $h_i$ is strictly increasing in $[x^*_i,\infty )$, then the corresponding map F is continuous. This basic regularity result, together with the method of partions, introduced in Sect. 3.4, is useful in proving various refinements, like Lipschitz continuity of F for Lipschitz $h_i$ (Sect. 5.2) or an upgrade of the local monotonicity result from linear to $C^1$ functions $h_i$ (Sect. 5.3). The main contribution of Sect. 5 is the explicit evaluation of the mapping F near zero in the linear case, implying, in particular, its local monotonicity in a neighbourhood of zero for piecewise linear $h_i$. As we have already mentioned, the latter fact is then generalized to (piecewise) $C^1$ functions. Finally, in Sect. 5.4, we show that, somewhat surprisingly, the mapping F may fail to be globally monotone, even if the corresponding functions $h_i$ are linear in $[x^*_i,\infty )$.

3 The mapping construction algorithm

3.1 Construction

Fix $t\ge 0$. We define the vector $F(t)=(F_i(t))_{i\in \mathbf{I}}$ as follows.

Let $f^{(1)}=f^{(1)}(t)$ be the supremum of $x\le t$ satisfying the constraints

$$\begin{aligned} \sum _{i\in G_j} h_i(x) \le t, \qquad \quad j \in \mathbf{J}. \end{aligned}$$

(11)

If $f^{(1)}=t$, we take $F_i(t)=t$ for each $i\in \mathbf{I}$, $\mathbf{I}^{(1)}=\mathbf{I}$, $\mathbf{J}^{(1)}=\mathbf{J}$, $\mathbf{N}^{(1)}=\emptyset$ and $k_{max}=k_{max}(t)=1$. In what follows, we assume that $f^{(1)}<t$. By continuity of $h_i$, $x=f^{(1)}$ satisfies (11) and the set $\mathbf{J}^{(1)} = \big \{ j\in \mathbf{J}: \sum _{i\in G_j} h_i(f^{(1)}) = t \big \}$ of active constraints is nonempty. (Indeed, if $\mathbf{J}^{(1)} =\emptyset$, then $f=f^{(1)}+\epsilon$ also satisfies (11) for $\epsilon >0$ small enough, which contradicts the definition of $f^{(1)}$.) Let $\mathbf{I}^{(1)} = \bigcup _{j\in \mathbf{J}^{(1)}} G_j$ and

$$\begin{aligned} \mathbf{N}^{(1)}= \{ j\in \mathbf{J}: G_j \subseteq \mathbf{I}^{(1)}\}{\setminus }{} \mathbf{J}^{(1)}. \end{aligned}$$

(12)

For $i\in \mathbf{I}^{(1)}$, put $F_i(t)=\sup \{ x\le t:h_i(x)=h_i(f^{(1)})\}.$ If $\mathbf{I}^{(1)}=\mathbf{I}$, this completely determines the vector F(t). In this case, let $k_{max}=1$. Otherwise, let $\mathbf{K}^{(1)}=\mathbf{J}{\setminus }(\mathbf{J}^{(1)}\cup \mathbf{N}^{(1)})$ and let $f^{(2)}=f^{(2)}(t)$ be the supremum of $x\le t$ satisfying the constraints

$$\begin{aligned} \sum _{i\in G_j\cap \mathbf{I}^{(1)}} h_i(F_i(t)) + \sum _{i\in G_j{\setminus }{} \mathbf{I}^{(1)}} h_i(x) \le t, \qquad \qquad j \in \mathbf{K}^{(1)}. \end{aligned}$$

(13)

Note that $G_j{\setminus }{} \mathbf{I}^{(1)}\ne \emptyset$ for $j \in \mathbf{K}^{(1)}$, so the second sum in (13) is taken over a nonempty set of indices. We also have $f^{(1)} < f^{(2)}$ by definition. If $f^{(2)}=t$, we take $\mathbf{I}^{(2)} = \mathbf{I}{\setminus }{} \mathbf{I}^{(1)}$, $\mathbf{J}^{(2)}=\mathbf{K}^{(1)}$, $\mathbf{N}^{(2)}=\emptyset$, $F_i(t)=t$ for each $i\in \mathbf{I}^{(2)}$ and $k_{max}=2$. If $f^{(2)}<t$, then $x=f^{(2)}$ satisfies (13) and the set $\mathbf{J}^{(2)}$ of active constraints in (13) (i.e., those $j \in \mathbf{K}^{(1)}$, for which equality holds in (13) with $x=f^{(2)}$) is nonempty. In this case, let $\mathbf{I}^{(2)} = \bigcup _{j\in \mathbf{J}^{(2)}} G_j{\setminus }{} \mathbf{I}^{(1)}$,

$$\begin{aligned} \mathbf{N}^{(2)}= \{ j\in \mathbf{J}: G_j \subseteq \mathbf{I}^{(1)}\cup \mathbf{I}^{(2)}\}{\setminus }(\mathbf{J}^{(1)}\cup \mathbf{J}^{(2)} \cup \mathbf{N}^{(1)}) \end{aligned}$$

and put $F_i(t)=\sup \{ x\le t:h_i(x)=h_i(f^{(2)})\}$ for $i \in \mathbf{I}^{(2)}$. If $\mathbf{I}^{(1)}\cup \mathbf{I}^{(2)}=\mathbf{I}$, the definition of the vector F(t) is complete and we take $k_{max}=2$, otherwise we let $\mathbf{K}^{(2)}=\mathbf{J}{\setminus }( \mathbf{J}^{(1)} \cup \mathbf{J}^{(2)} \cup \mathbf{N}^{(1)} \cup \mathbf{N}^{(2)})$, and we continue our construction as follows.

Suppose that for some $k\ge 2$, we have defined numbers $f^{(1)}<f^{(2)}<\cdots<f^{(k)}<t$, nonempty, disjoint subsets $\mathbf{J}^{(1)}$,...,$\mathbf{J}^{(k)}$ of $\mathbf{J}$, disjoint (not necessarily nonempty) subsets $\mathbf{N}^{(1)}$,...,$\mathbf{N}^{(k)}$ of $\mathbf{J}$ with

$$\begin{aligned} \Big (\bigcup _{l=1}^k \mathbf{J}^{(l)} \Big ) \cap \Big (\bigcup _{l=1}^k \mathbf{N}^{(l)} \Big ) = \emptyset , \qquad \qquad \bigcup _{l=1}^k (\mathbf{J}^{(l)} \cup \mathbf{N}^{(l)}) \ne \mathbf{J}, \end{aligned}$$

(14)

and nonempty, disjoint subsets $\mathbf{I}^{(1)}$, ...,$\mathbf{I}^{(k)}$ of $\mathbf{I}$ with $\bigcup _{l=1}^k \mathbf{I}^{(l)} \ne \mathbf{I}$ such that for $l=1,..,k$,

$$\begin{aligned} \mathbf{N}^{(l)}= & {} \left\{ j\in \mathbf{J}: G_j \subseteq \bigcup _{p=1}^l \mathbf{I}^{(p)}\right\} {\setminus }\left( \bigcup _{p=1}^l \mathbf{J}^{(p)} \cup \bigcup _{p=1}^{l-1} \mathbf{N}^{(p)}\right) , \quad \;\; \\&\quad \sum _{i\in G_ j} h_i(F_i(t)) = t, \qquad j\in \mathbf{J}^{(l)}, \qquad \nonumber \end{aligned}$$

(15)

$$\begin{aligned}&\quad \sum _{i\in G_j\cap \bigcup _{p=1}^{l}{} \mathbf{I}^{(p)}} h_i(F_i(t)) + \sum _{i\in G_j{\setminus }\bigcup _{p=1}^{l} \mathbf{I}^{(p)}} h_i(f^{(l)}) < t, \qquad j\in \mathbf{K}^{(l)},\qquad \qquad \end{aligned}$$

(16)

where

$$\begin{aligned} F_i(t)=\sup \{ x\le t:h_i(x)=h_i(f^{(p)})\}, \qquad i\in \mathbf{I}^{(p)}, \; p=1,\ldots ,l, \end{aligned}$$

(17)

and $\mathbf{K}^{(l)}= \mathbf{J}{\setminus }\bigcup _{p=1}^l (\mathbf{J}^{(p)} \cup \mathbf{N}^{(p)})$. Note that $\mathbf{K}^{(l)}\ne \emptyset$ by (14) and $G_j{\setminus }\bigcup _{p=1}^{l} \mathbf{I}^{(p)} \ne \emptyset$ for $j\in \mathbf{K}^{(l)}$, $l=1,\ldots ,k$, by (15), so that the second sum in (16) is taken over a nonempty set of indices. (Such numbers and sets were defined in the last paragraph for $k=2$.) Let $f^{(k+1)}=f^{(k+1)}(t)$ be the supremum of $x\le t$ satisfying the constraints

$$\begin{aligned} \sum _{i\in G_j\cap \bigcup _{p=1}^{k}{} \mathbf{I}^{(p)}} h_i(F_i(t)) + \sum _{i\in G_j{\setminus }\bigcup _{p=1}^{k} \mathbf{I}^{(p)}} h_i(x) \le t, \qquad j \in \mathbf{K}^{(k)}. \end{aligned}$$

(18)

The inequality (16) implies that $f^{(k+1)}>f^{(k)}$. If $f^{(k+1)}=t$, we take $\mathbf{I}^{(k+1)}= \mathbf{I}{\setminus }\bigcup _{l=1}^k \mathbf{I}^{(l)}$, $\mathbf{J}^{(k+1)}=\mathbf{K}^{(k)}$, $\mathbf{N}^{(k+1)}=\emptyset$ and $F_i(t)=t$ for each $i\in \mathbf{I}^{(k+1)}$, so the definition of the vector F(t) is complete. In this case, we put $k_{max}=k+1$. If $f^{(k+1)}<t$, then $x=f^{(k+1)}$ satisfies (18) and the set $\mathbf{J}^{(k+1)}$ of active constraints in (18) (i.e., these $j \in \mathbf{K}^{(k)}$, for which equality holds in (18) with $x=f^{(k+1)}$) is nonempty. In this case, let $\mathbf{I}^{(k+1)} = \bigcup _{j\in \mathbf{J}^{(k+1)}} G_j{\setminus }\bigcup _{l=1}^k \mathbf{I}^{(l)}$, define $\mathbf{N}^{(k+1)}$ by (15) with $l=k+1$ and put $F_i(t)=\sup \{ x\le t: h_i(x)=h_i(f^{(k+1)})\}$ for $i\in \mathbf{I}^{(k+1)}$. This ends the $k+1$th step of our construction. If $\bigcup _{l=1}^{k+1} \mathbf{I}^{(l)}=\mathbf{I}$, the definition of the vector F(t) is complete. In this case, put $k_{max}=k+1$. Otherwise, we make another (i.e., the $k+2$th) step of our algorithm, taking $k+1$ instead of k and proceeding as above.

When the construction terminates after $k_{max}$ steps, we have defined the vector F(t).

Remark 4

The index $k_{max}$ and the sets $\mathbf{I}^{(k)}$, $\mathbf{J}^{(k)}$, $\mathbf{N}^{(k)}$, $\mathbf{K}^{(k)}$ defined above depend on the time t. In what follows, when we want to stress this dependence, we write $k_{max}(t)$, $\mathbf{I}^{(k)}(t)$, $\mathbf{J}^{(k)}(t)$, $\mathbf{N}^{(k)}(t)$, $\mathbf{K}^{(k)}(t)$, respectively.

Remark 5

Let ${\bar{h}}(x)= \max _{j\in \mathbf{J}} \sum _{i\in G_j} h_i(x)$, $x\in {\mathbb {R}}$. If ${\bar{h}}$ is strictly increasing in $[\min _{i\in \mathbf{I}} x^*_i,\infty )$, then, by definition,

$$\begin{aligned} f^{(1)}(t) = {\bar{h}}^{-1}(t) \wedge t, \qquad \qquad t\ge 0. \end{aligned}$$

(19)

Remark 6

If $i\in \mathbf{I}^{(k)}(t)$ for some $k\in \{1,\ldots ,k_{max}(t)\}$ and if the function $h_i$ is strictly increasing in $[x^*_i,\infty )$, then [compare (17)],

$$\begin{aligned} F_i(t) = f^{(k)}(t) \vee x^*_i. \end{aligned}$$

(20)

Remark 7

In general, some of the sets $\mathbf{N}^{(k)}$, $k=1,\ldots ,k_{max}$, may be nonempty, see Example 1, to follow. If $j\in \mathbf{N}^{(k)}$ for some k, then

$$\begin{aligned} \sum _{i\in G_j} h_i(F_i(t)) = \sum _{l=1}^k \sum _{i\in G_j\cap \mathbf{I}^{(l)}} h_i(f^{(l)}(t))< t. \end{aligned}$$

This strict inequality may be interpreted as an indication of “unavoidable bottleneck idleness” in the corresponding locally edge minimal fluid network - transferring higher priority fluids by other resources does not allow j to use its full capacity on the time interval [0, t]. This phenomenon is well known in the theory of resource sharing networks and it was discussed in detail, e.g., by Gurvich and Van Mieghem (2015), Gurvich and Van Mieghem (2017). A mild sufficient condition for all the sets $\mathbf{N}^{(k)}$ to be empty is that for each $j\in \mathbf{J}$, $G_j{\setminus }\bigcup _{j'\ne j} G_{j'} \ne \emptyset$. This corresponds to the so-called local traffic condition for the underlying network topology, under which every resource has at least one route using only that resource (Harrison et al. 2014; Kang et al. 2009). The latter requirement is satisfied, e.g., by linear networks, for which $I=J+1$ and $G_j=\{1,j+1\}$, $j=1,\ldots ,J$. There are, however, some important systems that do not satisfy the local traffic assumption, for example ring networks, used as counterexamples for stability of the LQF protocol (Birand et al. 2012; Dimakis and Walrand 2006).

3.2 Examples

In this subsection, we provide two examples illustrating the construction of the mapping $F:[0,\infty )\rightarrow {\mathbb {R}}^I$ defined in Sect. 3.1. The first one has relatively simple structure, yielding time-independent $k_{max}$, $\mathbf{J}^{(k)}$, $\mathbf{I}^{(k)}$, $\mathbf{N}^{(k)}$ in $(0,\infty )$ and linear function F. The second one, in which $k_{max}$, $\mathbf{J}^{(k)}$, $\mathbf{I}^{(k)}$ vary in time and F is nonlinear, indicates some of the difficulties encountered in more general situations.

Example 1

Let $h_i(x)=x^+$ for $x\in {\mathbb {R}}$ and $i\in \mathbf{I}$. Then $x^*_i=0$ for each $i\in \mathbf{I}$. For $t\ge 0$ and $j\in \mathbf{J}$, (11) takes the form $|G_j| \; x^+\le t$, so its maximal solution is $f^{(1)}(t)= t/\max \{|G_j|:j\in \mathbf{J}\}$. Hence, for $t=0$ we have $f^{(1)}(0)=0$, $\mathbf{J}^{(1)}(0)=\mathbf{J}$, $\mathbf{I}^{(1)}(0)=\mathbf{I}$, $\mathbf{N}^{(1)}(0)=\emptyset$, $k_{\max }(0)=1$ and $F_i(0)=0$ for all i. In what follows, we assume that $t>0$. Then $\mathbf{J}^{(1)}(t) = \{ j\in \mathbf{J}: |G_j| = \max \{|G_{j'}|:j'\in \mathbf{J} \} \}$ and $F_i(t) = \frac{t}{\max \{|G_j|:j\in \mathbf{J}\}}$ for $i\in \mathbf{I}^{(1)}(t)=\bigcup _{j\in \mathbf{J}^{(1)}(t)} G_j$.

In the remainder of this example, the time argument in $\mathbf{J}^{(k)}(t)$, $\mathbf{I}^{(k)}(t)$, $\mathbf{N}^{(k)}(t)$, $\mathbf{K}^{(k)}(t)$, will be skipped. If $|G_j|=|G_{j'}|$ for every $j,j'\in \mathbf{J}$, then $\mathbf{J}^{(1)}=\mathbf{J}$, $\mathbf{N}^{(1)}=\emptyset$ and the definition of F is complete. Otherwise, let $\mathbf{N}^{(1)}$ be given by (12). For j belonging to the set

$$\begin{aligned} \mathbf{K}^{(1)}= \{j\in \mathbf{J}: |G_j| < \max _{j'\in \mathbf{J}} |G_{j'}|, G_j{\setminus }{} \mathbf{I}^{(1)} \ne \emptyset \}, \end{aligned}$$

the constraint (13) takes the form $\frac{|G_j\cap \mathbf{I}^{(1)}| \; t}{\max \{|G_{j'}|:j'\in \mathbf{J}\}} + |G_j{\setminus }{} \mathbf{I}^{(1)} | \; x^+\le t,$ yielding the maximal solution

$$\begin{aligned} f^{(2)}(t) = \min _{j\in \mathbf{K}^{(1)}} \frac{1-\frac{|G_j\cap \mathbf{I}^{(1)}| }{\max \{|G_{j'}|:j'\in \mathbf{J}\}}}{|G_j{\setminus }\mathbf{I}^{(1)} |} \; t. \end{aligned}$$

(21)

Moreover, $\mathbf{J}^{(2)}$ is the set of $j\in \mathbf{K}^{(1)}$ attaining the minimum in (21) and $F_i(t)= f^{(2)}(t)$ for $i\in \mathbf{I}^{(2)} = \bigcup _{j\in \mathbf{J}^{(2)}} G_j{\setminus }{} \mathbf{I}^{(1)}$. If $\mathbf{I}^{(1)} \cup \mathbf{I}^{(2)}= \mathbf{I}$ (in particular, if the minimum in (21) is attained at every $j\in \mathbf{K}^{(1)}$), then the construction of F is complete. Otherwise we proceed similarly, until we get $f^{(3)}(t)$,...,$f^{(k_{max})}(t)$, and hence all $F_i(t)$, $i\in \mathbf{I}$, in the form of linear functions of t, with slopes depending (in an increasingly complicated way) on the sets $G_j$, describing the topology of the corresponding network.

Observe that in this example some sets $\mathbf{N}^{(k)}$ may, in general, be nonempty. The simplest such case occurs for $I=J=2$, $G_1=\{1\}$ and $G_2=\{1,2\}=\mathbf{I}$. Then $\mathbf{J}^{(1)}=\{2\}$, $\mathbf{I}^{(1)}=\mathbf{I}$, and hence $\mathbf{N}^{(1)}=\{1\}$ and $k_{max}=1$.

In general, the main difficulty in analyzing the properties of the mapping F, already indicated in Remark 4, is the time dependence of the index $k_{max}$ and the sets $\mathbf{I}^{(k)}$, $\mathbf{J}^{(k)}$, $k=1,\ldots ,k_{max}$. The following example, corresponding to a simple linear network topology pictured in Fig. 1, illustrates this point. Note that, by Remark 7, in this case the sets $\mathbf{N}^{(k)}$ are empty.

Fig. 1

Two-node linear network

Fig. 2

Coordinate mappings of F from Example 2. $F_1$ = solid, $F_2$ = x-marks, $F_3$ = circles

Example 2

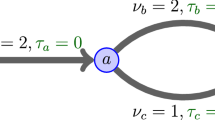
Let $I=3$, $J=2$, $G_1=\{1,2\}$ and $G_2=\{1,3\}$ (see Fig. 1). Furthermore, for $x\in {\mathbb {R}}$, let $h_1(x)=(x+2)^+$, $h_2(x)=(x+1)^+$ and $h_3(x)=5x^+$, so that $x^*_1=-2$, $x^*_2=-1$, $x^*_3=0$.

Let $0\le t \le 1$. Then the maximal solution of (11) is $f^{(1)}(t)= t-2$ and we have $\mathbf{J}^{(1)}(t)=\mathbf{J}$. Thus, $\mathbf{I}^{(1)}(t)=\mathbf{I}$, $k_{max}(t)=1$, and (20) implies that

$$\begin{aligned} F_1(t) = t-2, \qquad \quad F_2(t)=-1, \qquad \quad F_3(t)=0. \end{aligned}$$

(22)

For $1< t < 7/2$, the maximal solution of (11) is $f^{(1)}(t)= t/2-3/2$, $\mathbf{J}^{(1)}(t)=\{1\}$, so $\mathbf{I}^{(1)}(t)=G_1=\{1,2\}$. Furthermore, $\mathbf{K}^{(1)}(t)=\{2\}$ and the maximal solution of (13) is $f^{(2)}(t)= (t-1)/10$, so $\mathbf{J}^{(2)}(t)=\{2\}$, $\mathbf{I}^{(2)}(t)=\{3\}$, $k_{max}(t)=2$ and (20) yields

$$\begin{aligned} F_1(t) = F_2(t)= \frac{t-3}{2}, \qquad \quad F_3(t)=\frac{t-1}{10}. \end{aligned}$$

(23)

For $t = 7/2$ we still have $f^{(1)}(t)= t/2-3/2$, but $\mathbf{J}^{(1)}(t)=\mathbf{J}$, $\mathbf{I}^{(1)}(t)=\mathbf{I}$, $k_{max}(t)=1$. However, (23) still holds. Note that $F_1(7/2)=F_2(7/2)=F_3(7/2)=1/4$.

Finally, for $t>7/2$, the maximal solution of (11) is $f^{(1)}(t)= t/6-1/3$, $\mathbf{J}^{(1)}(t)=\{2\}$ and $\mathbf{I}^{(1)}(t)=G_2=\{1,3\}$. Thus, $\mathbf{K}^{(1)}(t)=\{1\}$ and the maximal solution of (13) is $f^{(2)}(t)=5t/6-8/3$, so $\mathbf{J}^{(2)}(t)=\{1\}$, $\mathbf{I}^{(2)}(t)=\{2\}$, $k_{max}(t)=2$ and (20) yields

$$\begin{aligned} F_1(t) = F_3(t)= \frac{t}{6}- \frac{1}{3}, \qquad \quad F_2(t)= \frac{5t}{6}- \frac{8}{3}. \end{aligned}$$

(24)

It is easy to see that the mapping F given by (22)–(24) is continuous and nondecreasing on $[0,\infty )$, see Fig. 2. This example also indicates that there is, in general, no hope for obtaining any global results about the auxiliary functions $f^{(p)}$, $p>1$. Here, $f^{(2)}$ is linear and strictly increasing in (1, 7/2) and $(7/2,\infty )$, but it does not even exist in $[0,1]\cup \{7/2\}$.

3.3 Relations with minimax multiple resource allocation problems

By construction, for a fixed $t\ge 0$, $f^{(1)}=f^{(1)}(t)$ is the value function of the following multiple resource allocation problem (MRP) with nonlinear constraints:

$$\begin{aligned} \text{ maximize } \;\;\; \min _{i\in \mathbf{I}} a_i \qquad \qquad \qquad \qquad \\ \text{ subject } \text{ to } \;\;\; a_i \le t, \; i\in \mathbf{I}, \quad \sum _{i\in G_j} h_i(a_i) \le t, \; j\in \mathbf{J}. \end{aligned}$$

[By (1), we may also add constraints $a_i \ge \min _{i\in \mathbf{I}} x^*_i$, $i\in \mathbf{I}$.] Moreover, both the I-tuple $(f^{(1)},\ldots ,f^{(1)})$ and F(t) are optimal solutions for this problem. If the functions $h_i(x)$, $x\ge x^*_i$, are linear, then the above task is a well-studied multiple resource allocation problem, see, e.g., Katoh and Ibaraki (1998), Section 8 (in particular Subsection 8.1) and the references given there. Parametric analysis of linear resource allocation problems was developed by Luss (1992).

Similarly, if $k_{max}(t)\ge 2$, then $f^{(2)}=f^{(2}(t)$ is the value function of the MRP

$$\begin{aligned} \text{ maximize } \;\;\; \min _{i\in \mathbf{I}{\setminus }\mathbf{I}^{(1)}(t)} a_i \qquad \qquad \qquad \qquad \text{ subject } \text{ to } \; \\ a_i \le t, \;\; i\notin \mathbf{I}^{(1)}(t), \sum _{i\in G_j{\setminus }{} \mathbf{I}^{(1)}(t)} h_i(a_i) \le t-\sum _{i\in G_j\cap \mathbf{I}^{(1)}(t)} h_i(F_i(t)), \;\; j\in \mathbf{K}^{(1)}(t), \end{aligned}$$

and the $I-|\mathbf{I}^{(1)}(t)|$-tuples $(f^{(2)},\ldots ,f^{(2)})$, $(F_i(t))_{i\notin \mathbf{I}^{(1)}(t)}$ are optimal solutions for this MRP. Continuing in this way, we can describe F(t) in terms of solutions to a nested sequence of $k_{max}(t)$ nonlinear MRPs, parametrized by t. However, as Example 2 indicates, $k_{max}(t)$, $\mathbf{J}^{(k)}(t)$, $\mathbf{I}^{(k)}(t)$, vary with t, so the form (in fact, even the number) of these problems changes discontinuously with time. This is the main difficulty which has to be overcome in the subsequent analysis.

3.4 Partitions and inverses

Let ${\mathcal {J}}$ be the set of “ordered partitions” of the set $\mathbf{J}$, i.e., finite sequences of subsets of $\mathbf{J}$ in the form $(J_1,\ldots ,J_k)$, where $J_i\ne \emptyset$, $i=1,\ldots ,k$, $J_i\cap J_l = \emptyset$, $1\le i <l\le k$, and $\bigcup _{i=1}^k (J_i \cup N_i) = \mathbf{J}$, $(\bigcup _{i=1}^k J_i) \cap (\bigcup _{i=1}^k N_i) =\emptyset$, where the sets $N_1,\ldots ,N_k$ are defined recursively as

$$\begin{aligned} N_l = \left\{ j\in \mathbf{J}: G_j \subseteq \bigcup _{p=1}^l \bigcup _{j'\in J_p} G_{j'}\right\} {\setminus }\left( \bigcup _{p=1}^l J_p \cup \bigcup _{p=1}^{l-1} N_p\right) , \qquad l=1,\ldots k, \end{aligned}$$

[compare the first relation in (14) and (15)]. Fix $T>0$ and let

$$\begin{aligned} {\mathcal {T}}^{\mathcal {D}} = \{t\in [0,T]: \mathbf{J}^{(p)}(t) =J_p, p=1,\ldots ,k\}, \quad {\mathcal {D}}= (J_1,\ldots ,J_k)\in {\mathcal {J}}. \end{aligned}$$

(25)

We label the nonempty sets of the form ${\mathcal {T}}^{\mathcal {D}}$, ${\mathcal {D}} \in {\mathcal {J}}$, as ${\mathcal {T}}_1,\ldots {\mathcal {T}}_d$. Clearly, $\bigcup _{i=1}^d {\mathcal {T}}_i = [0,T]$.

For a function $g:{\mathbb {R}}\rightarrow [0,\infty )$ with $\lim _{x\rightarrow \infty } g(x)=\infty$, let $g^{-1}$ denote its (generalized) right-continuous inverse (see, e.g., Whitt 2002, Section 13.6),

$$\begin{aligned} g^{-1}(t) = \inf \{s\ge 0: g(s)>t\}, \qquad \quad t\ge 0. \end{aligned}$$

If the function g is nondecreasing and $g(x_0)=0$ for some $x_0\in {\mathbb {R}}$, then

$$\begin{aligned} g^{-1}(t) = \sup \{s\ge 0: g(s)\le t\}, \qquad \quad t\ge 0. \end{aligned}$$

Fix ${\mathcal {D}}= (J_1,\ldots ,J_k)\in {\mathcal {J}}$. For $t\in {\mathcal {T}}^{\mathcal {D}}$, we can write $f^{(p)}(t)$, $p=1,\ldots ,k_{max}(t)$, (and hence F(t)) in closed form, using the inverse functions introduced above. To see this, let $t\in {\mathcal {T}}^{\mathcal {D}}$ and note that $k=k_{max}(t)$. Choose $j_1,\ldots ,j_k \in \mathbf{J}$ so that $j_p \in J_p = \mathbf{J}^{(p)}(t)$ for each $j=1,\ldots ,k$. Then

$$\begin{aligned} f^{(1)}(t) = \Big ( \sum _{i\in G_{j_1}} h_i \Big )^{-1}(t) \; \wedge \; t, \end{aligned}$$

(26)

and for $p=2,\ldots ,k$, we have the recursive formulae

$$\begin{aligned} f^{(p)}(t) = \Big ( \sum _{i\in G_{j_p} \cap I_p} h_i \Big )^{-1} \Big ( t - \sum _{l=1}^{p-1} \sum _{i\in G_{j_p} \cap I_l} h_i(f^{(l)}(t)) \Big ) \; \wedge \; t, \end{aligned}$$

(27)

where

$$\begin{aligned} I_1 = \bigcup _{j \in J_1} G_j = \mathbf{I}^{(1)}(t) , \quad I_p = \bigcup _{j \in J_p} G_j{\setminus }\bigcup _{l=1}^{p-1} I_l= \mathbf{I}^{(p)}(t), \quad p=2,\ldots ,k. \; \end{aligned}$$

(28)

(Actually, the minimization with t in (26)–(27) is necessary only in the case of $f^{(k)}(t)$.)

4 Continuity

In general, the function F may have jumps, as the following one-dimensional example indicates.

Fig. 3

Function $h_1$ from Example 3 (thin) and the corresponding mapping F (thick)

Example 3

Let $I=J=1$ and let $h_1(x) = (x^+\wedge 1)+(x-2)^+$, $x\in {\mathbb {R}}$. Then $F_1(t)=f^{(1)}(t)=t/2$ for $0\le t<2$ and $F_1(t)=f^{(1)}(t)=t/2+1$ for $t\ge 2$.

Clearly, the discontinuity of $F_1=f^{(1)}$ at $t=2$ in this example is caused by a “flat spot”, i.e., the interval [1, 2] on which $h_1$ takes the constant value 2, resulting in the jump of $h_1^{-1}$ [see (26) and Fig. 3]. In our queueing application, this corresponds to the lack of “customer mass” with deadlines in the interval [1, 2] in the system, causing the frontier to jump over this empty interval. The following theorem assures that in the absence of such “flat spots”, the function F is actually continuous.

Theorem 1

Assume that for every $i\in \mathbf{I}$, the function $h_i$ is strictly increasing in $[x^*_i,\infty )$. Then the mapping F is continuous in $[0,\infty )$.

In the proof of this result, we will use the following elementary lemma. For the sake of completeness, we provide its justification.

Lemma 2

Let (X, d) be a metric space. Let $y\in X$ and let $\{x_n\}$ be a sequence of elements of X such that every subsequence $\{x_{n_k}\}$ of $\{x_n\}$ contains a further subsequence $\{x_{n_{k_l}}\}$ converging to y. Then $\lim _{n\rightarrow \infty } x_n=y$.

Proof

Suppose that the sequence $\{x_n\}$ does not converge to y. This means that there exist $\epsilon >0$ and a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ such that $d(x_{n_k},y)\ge \epsilon$ for all k. However, we have assumed the existence of a subsequence $\{x_{n_{k_l}}\}$ of $\{x_{n_k}\}$ such that $\lim _{l\rightarrow \infty } d(x_{n_{k_l}},y)=0$, so we have a contradiction. $\square$

The proof of Theorem 1 is long and somewhat involved, so we only sketch it here, moving most of the technical details to the “Appendix”. It is convenient to introduce additional notation

$$\begin{aligned} \mathbf{D}^{(p)} = \mathbf{J}^{(p)} \cup \mathbf{N}^{(p)}, \qquad p=1,\ldots ,k_{max}. \end{aligned}$$

(29)

Clearly, the sets $\mathbf{D}^{(p)}=\mathbf{D}^{(p)}(t)$ depend on the time t, see Remark 4.

Sketch of the proof of Theorem 1

Let $t_n>0$ be such that $t_n \rightarrow t_0$ as $n\rightarrow \infty$. We may assume that $t_n\le t_0+1$ for all n. Our aim is to show that $F(t_n)\rightarrow F(t_0)$, i.e., for every $i\in \mathbf{I}$, we have

$$\begin{aligned} \lim _{n\rightarrow \infty } F_i(t_n) = F_i(t_0). \end{aligned}$$

(30)

Without loss of generality (passing to a subsequence if necessary) we may assume that for every $m,n\ge 1$, we have $k_{max}(t_m)=k_{max}(t_n)$ and $\mathbf{J}^{(p)}(t_m)=\mathbf{J}^{(p)}(t_n)$ (hence $\mathbf{I}^{(p)}(t_m)=\mathbf{I}^{(p)}(t_n)$, $\mathbf{N}^{(p)}(t_m)=\mathbf{N}^{(p)}(t_n)$) for $p=1,\ldots ,k_{max}(t_m)$. Consequently, in what follows, we will simply write $k_{max}$, instead of $k_{max}(t_n)$, $n\ge 1$, $\mathbf{J}^{(p)}$ instead of $\mathbf{J}^{(p)}(t_n)$, $n\ge 1$, e.t.c..

By definition, for $n\ge 1$ and $p=1,\ldots ,k_{max}$, $\min _{i\in \mathbf{I}} x^*_i \le f^{(p)}(t_n) \le t_n \le t_0+1$. Hence, by Lemma 2, without loss of generality (passing to a subsequence if necessary) we may assume that the sequences $\{f^{(p)}(t_n)\}$, $p=1,\ldots ,k_{max}$, converge. Let

$$\begin{aligned} f^{(p)}_\infty :=\lim _{n\rightarrow \infty } f^{(p)}(t_n), \qquad \qquad p=1,\ldots ,k_{max}. \end{aligned}$$

(31)

Remark 5 implies that $f^{(1)}$ is continuous, hence

$$\begin{aligned} f^{(1)}(t_0)=f^{(1)}_\infty \le f^{(2)}_\infty \le \ldots \le f^{(k_{max})}_\infty \le t_0. \end{aligned}$$

(32)

First suppose that $t_0=0$. We have

$$\begin{aligned} f^{(1)}(0)=\min _{i\in \mathbf{I}} x^*_i, \end{aligned}$$

(33)

$\mathbf{J}^{(1)}(0)=\mathbf{J}$, $\mathbf{I}^{(1)}(0)=\mathbf{I}$, $k_{max}(0)=1$ and $F_i(0)=x^*_i$ for all $i\in \mathbf{I}$. Let $i\in \mathbf{I}$. Then $i\in \mathbf{I}^{(k)}$ for some $k\in \{1,\ldots ,k_{max}\}$. By the definition of $f^{(k)}$, $0\le h_i(f^{(k)}(t_n))\le t_n$, and hence, as $t_n \downarrow 0$, by (1),

$$\begin{aligned} F_i(t_n)= & {} \sup \{ x \le t_n:h_i(x)=h_i(f^{(k)}(t_n))\} \\\rightarrow & {} \sup \{ x \le 0:h_i(x)=0\} \; = \; x^*_i \; = \; F_i(t_0), \end{aligned}$$

so $F_i$ is continuous at 0. Hence, in what follows, we will assume that $t_0>0$.

We will first consider the case in which $f^{(1)}(t_n)=t_n$ for all $n\ge 1$. Then $f^{(1)}(t_0)=t_0$ and thus, for each $i\in \mathbf{I}$, $F_i(t_n)=t_n\rightarrow t_0 = F_i(t_0).$ Similarly, if $f^{(1)}(t_0)=t_0$ then $f^{(1)}(t_n) \rightarrow t_0$, so for each $i\in \mathbf{I}$, the inclusion $F_i(t_n)\in [f^{(1)}(t_n),t_n]$ implies that $F_i(t_n)\rightarrow t_0 = F_i(t_0)$. Therefore, we may additionally assume

$$\begin{aligned} f^{(1)}(t_n)<t_n, \qquad n\ge 0. \end{aligned}$$

(34)

We prove (30) inductively for $i\in \mathbf{I}^{(l)}(t_0)$, $l=1,\ldots ,k_{max}(t_0)$. In the lth inductive step, we define

$$\begin{aligned} b_l= & {} \min \{p=1,\ldots ,k_{max}: \mathbf{D}^{(p)}{\setminus }\bigcup _{k=1}^{l-1} \mathbf{D}^{(k)}(t_0) \ne \emptyset \}, \end{aligned}$$

(35)

$$\begin{aligned} p_l= & {} \max \{p=1,\ldots ,k_{max}: \mathbf{D}^{(p)} \cap \ \mathbf{J}^{(l)}(t_0) \ne \emptyset \}. \end{aligned}$$

(36)

It is easy to check that

$$\begin{aligned} \mathbf{I}^{(l)}(t_0)=\bigcup _{p=b_l}^{p_l} B_p^{(l)}, \end{aligned}$$

(37)

where $B_p^{(l)}=\mathbf{I}^{(p)} \cap \mathbf{I}^{(l)}(t_0)$. We show that there exists ${\bar{p}}_l\in \{b_l,\ldots ,p_l \}$ such that

$$\begin{aligned} f^{(p)}_\infty = f^{(l)}(t_0), \qquad \qquad p=b_l,\ldots ,{\bar{p}}_l. \end{aligned}$$

(38)

By (20) and (38), for $i\in B_p^{(l)}$, $p=b_l,\ldots ,{\bar{p}}_l$, as $n\rightarrow \infty$, we have

$$\begin{aligned} F_i(t_n) = f^{(p)}(t_n)\vee x^*_i \rightarrow f^{(l)}(t_0) \vee x^*_i = F_i(t_0). \end{aligned}$$

(39)

We also argue that if ${\bar{p}}_l<p_l$, then for $i\in B_p^{(l)}$, $p={\bar{p}}_l+1,\ldots ,p_l$, we have $f^{(l)}(t_0) < f^{(p)}_\infty \le x^*_i,$ so by (20), as $n\rightarrow \infty$,

$$\begin{aligned} F_i(t_n) = f^{(p)}(t_n)\vee x^*_i \rightarrow f^{(p)}_\infty \vee x^*_i = x^*_i = f^{(l)}(t_0) \vee x^*_i= F_i(t_0). \end{aligned}$$

(40)

Finally, the Eqs. (37), (39)–(40) imply (30) for every $i\in \mathbf{I}^{(l)}(t_0)$.

The details of the above inductive argument may be found in the “Appendix”. $\square$

5 Monotonicity

In this section, we investigate monotonicity of the mapping F. It turns out that, in general, F fails to be globally nondecreasing, even if the functions $h_i$ are piecewise linear, see Sect. 5.4. However, under suitable assumptions on $h_i$, monotonicity of F in some neighbourhood of 0 may be established. More precisely, our goal is to find $T>0$ such that for every $0\le t<{\tilde{t}}<T$ and $i\in \mathbf{I}$, we have

$$\begin{aligned} F_i(t)\le F_i({\tilde{t}}). \end{aligned}$$

(41)

This is done in Sect. 5.1 for piecewise linear $h_i$, $i\in \mathbf{I}$, and in Sect. 5.3 for piecewise $C^1$ functions $h_i$.

5.1 Local monotonicity in the linear case

In this subsection we assume that for all $i\in \mathbf{I}$,

$$\begin{aligned} h_i(x)= \rho ^i (x-x^*_i)^+, \quad \qquad x\in {\mathbb {R}}, \end{aligned}$$

(42)

where $\rho ^i$, $i\in \mathbf{I}$, are given positive constants. Without loss of generality we also assume that

$$\begin{aligned} x^*_1\le x^*_2 \le \ldots \le x^*_I. \end{aligned}$$

(43)

Let $m^*\in \{1,\ldots I\}$ and $0=n_{0}<1\le n_1<n_2<\cdots <n_{m^*}=I$ be such that

$$\begin{aligned} x^*_1=\cdots =x^*_{n_1}<x^*_{n_1+1}=\cdots =x^*_{n_2}<\cdots <x^*_{n_{m^*-1}+1}=\cdots =x^*_{n_{m^*}}. \end{aligned}$$

(44)

Let $y^*_k=x^*_{n_k}$, $k=1,\ldots ,m^*$, and let $y^*_{m^*+1}=\infty$. By (33) and (44), we have $f^{(1)}(0)=x^*_1=y^*_1$. It follows from Remark 5 that $f^{(1)}(\cdot )$ is continuous and strictly increasing in $[0,\infty )$. Let $t^*_1= (f^{(1)})^{-1}(y_{2}^*)$ if $m^*\ge 2$ and $t^*_1=\infty$ otherwise. Let

$$\begin{aligned} a^{(1)}= \max _{j\in \mathbf{J}} \sum _{i \in G_j \cap \{1,\ldots ,n_1\}} \rho ^i. \end{aligned}$$

(45)

We have

$$\begin{aligned} \mathbf{J}^{(1)}(t)= & {} \{j\in \mathbf{J}: \sum _{i \in G_j \cap \{1,\ldots ,n_1\}} \rho ^i = a^{(1)}\}, \qquad t\in (0,t^*_1), \end{aligned}$$

(46)

$$\begin{aligned} f^{(1)}(t)= & {} (x^*_1+ t/a^{(1)}) \wedge t = (y^*_1+ t/a^{(1)}) \wedge t, \qquad t\in [0,t^*_1), \end{aligned}$$

(47)

(see Remark 5). Using (47), we get $t^*_1=a^{(1)} (y^*_2-y^*_1)$. Note that $\mathbf{J}^{(1)}$ (and hence $\mathbf{I}^{(1)}$, $\mathbf{N}^{(1)}$) is constant in $(0,t^*_1)$.

If $x^*_1=0$ and $a^{(1)}\le 1$, then $m^*=1$ and $t^*_1=\infty$. In this case, (47) implies that $f^{(1)}(t)=t$ for $t\ge 0$, so $F_i(t)=t$ for all $t\ge 0$, $i\in \mathbf{I}$. In the remainder of this section we assume that either $x^*_1<0$, or $a^{(1)}> 1$. In particular, we have

$$\begin{aligned} f^{(1)}(t)= x^*_1+ t/a^{(1)}=y^*_1+ t/a^{(1)} , \qquad \qquad t \in [0,t^*_1 \wedge {\bar{t}}_1), \end{aligned}$$

(48)

where ${\bar{t}}_1=\infty$ if $a^{(1)}\ge 1$ and ${\bar{t}}_1=a^{(1)} x^*_1/(a^{(1)}-1)$ otherwise.

In what follows, we consider only $t\in [0, t^*_1 \wedge {\bar{t}}_1)$. If $\mathbf{I}^{(1)}=\mathbf{I}$, then $k_{max}=1$, and hence the numbers $f^{(k)}(t)$, $k=1,..,k_{max}$, have already been defined. Assume that $\mathbf{I}^{(1)}\ne \mathbf{I}$. Then we continue our construction by induction as follows.

Assume that for some $k\ge 1$, there exist strictly positive numbers $t^*_l$, ${\bar{t}}_l$, $l=1,\ldots ,k$, such that for all $0< t < {\underline{t}}_k:=\min _{1\le l \le k} (t^*_l \wedge {\bar{t}}_l)$ the sets $\mathbf{I}^{(l)}=\mathbf{I}^{(l)}(t)$, $\mathbf{J}^{(l)}=\mathbf{J}^{(l)}(t)$, $\mathbf{N}^{(l)}=\mathbf{N}^{(l)}(t)$, $l=1,\ldots ,k$, do not depend on t and $\bigcup _{l=1}^k \mathbf{I}^{(l)} \ne \mathbf{I}$, i.e., $k_{max}(t)>k$. For $l=1,\ldots ,k$, let $i^{(l)}=\min (\mathbf{I}{\setminus }\bigcup _{p=1}^{l-1} \mathbf{I}^{(p)})$ and let $m^{(l)}\in \{1,\ldots ,m^*\}$ be such that $x^*_{i^{(l)}}=y^*_{m^{(l)}}$. By definition, $1=i^{(1)}<i^{(2)}<\cdots < i^{(k)}\le I$ and $1=m^{(1)}\le m^{(2)}\le \cdots \le m^{(k)}\le m^*$. Furthermore, we assume that for each $l=1,\cdots ,k$, there exists a constant $a^{(l)}>0$ such that

$$\begin{aligned} f^{(l)}(t)= x^*_{i^{(l)}}+ t/a^{(l)}=y^*_{m^{(l)}}+ t/a^{(l)} < y^*_{m^{(l)}+1} , \qquad \;\;\; t \in [0,{\underline{t}}_k) . \end{aligned}$$

(49)

(For notational convenience, for $l>1$, we have defined $f^{(l)}(0)$ in (49) by continuity, i.e., as $f^{(l)}(0+)=x^*_{i^{(l)}}$, although $\mathbf{J}^{(1)}(0)=\mathbf{J}$ and hence $f^{(l)}(0)$ has not been defined by the algorithm from Sect. 3.1.) Note that all the above assumptions have already been verified for $k=1$.

By (20), (42) and (49), for $t \in (0,{\underline{t}}_k)$, $j\in \mathbf{K}^{(k)}$, the Eq. (16) implies

$$\begin{aligned} t> \sum _{p=1}^k \sum _{i\in G_j \cap \mathbf{I}^{(p)}} \rho ^i (f^{(p)}(t) -x^*_i)^+ = \sum _{p=1}^k \sum _{i\in G_j \cap \mathbf{I}^{(p)} \cap \{ n_{m^{(p)}-1}+1,\cdots ,n_{m^{(p)}} \}} \frac{\rho ^i \; t}{a^{(p)}},\nonumber \\ \end{aligned}$$

(50)

while the Eq. (18) takes the form

$$\begin{aligned} t\ge & {} \sum _{p=1}^k \sum _{i\in G_j \cap \mathbf{I}^{(p)}} \rho ^i (f^{(p)}(t) -x^*_i)^+ + \sum _{i\in G_j{\setminus }\bigcup _{p=1}^{k} \mathbf{I}^{(p)}} \rho ^i (x-x^*_i)^+ \nonumber \\= & {} \sum _{p=1}^k \sum _{i\in G_j \cap \mathbf{I}^{(p)} \cap \{ n_{m^{(p)}-1}+1,\ldots ,n_{m^{(p)}} \}} \rho ^i \frac{t}{a^{(p)}} + \sum _{i\in G_j{\setminus }\bigcup _{p=1}^{k} \mathbf{I}^{(p)}} \rho ^i (x-x^*_i)^+,\nonumber \\ \end{aligned}$$

(51)

which, in turn, is equivalent to

$$\begin{aligned} \sum _{i\in G_j{\setminus }\bigcup _{p=1}^{k} \mathbf{I}^{(p)}} \rho ^i(x-x^*_i)^+ \le b^{(k+1)}_j \ t, \end{aligned}$$

(52)

where

$$\begin{aligned} b^{(k+1)}_j= 1- \sum _{p=1}^k \frac{1}{a^{(p)}} \sum _{i\in G_j\cap \mathbf{I}^{(p)} \cap \{n_{m^{(p)}-1}+1,\ldots ,n_{m^{(p)}}\}} \rho ^i, \qquad j \in \mathbf{K}^{(k)}. \end{aligned}$$

By (50), $b^{(k+1)}_j>0$ for each $j \in \mathbf{K}^{(k)}$. Let $i^{(k+1)}=\min (\mathbf{I}{\setminus }\bigcup _{p=1}^{k} \mathbf{I}^{(p)})$, let $m^{(k+1)}\in \{1,\ldots ,m^*\}$ be such that $x^*_{i^{(k+1)}}=y^*_{m^{(k+1)}}$ and let

$$\begin{aligned} a^{(k+1)}_j= & {} \frac{1}{b^{(k+1)}_j} \sum _{i\in G_j\cap \{n_{m^{(k+1)}-1}+1,\ldots ,n_{m^{(k+1)}} \}{\setminus }\bigcup _{p=1}^{k} \mathbf{I}^{(p)}} \rho ^i, \qquad j \in \mathbf{K}^{(k)}, \\ a^{(k+1)}= & {} \max _{j \in \mathbf{K}^{(k)}} a^{(k+1)}_j. \end{aligned}$$

Recall that $f^{(k+1)}(t)$ is the supremum of $x\le t$ satisfying the constraints (52). By an argument similar to the one used for $f^{(1)}$ above, one may check that $f^{(k+1)}(\cdot )$ is continuous and strictly increasing in $(0,{\underline{t}}_k)$. Let $t^*_{k+1}=\infty$ if either $m^{(k+1)}=m^*$, or $f^{(k+1)}({\underline{t}}_k-)\le y_{m^{(k+1)}+1}^*$, and $t^*_{k+1}= (f^{(k+1)})^{-1}(y_{m^{(k+1)}+1}^*)$ otherwise. By definition, $f^{(k+1)}(0):=f^{(k+1)}(0+)=x^*_{i^{(k+1)}}=y^*_{m^{(k+1)}}$ [see the notational remark following (49)], and, more generally, for $t\le {\underline{t}}_k \wedge t^*_{k+1}$, we have

$$\begin{aligned} \mathbf{J}^{(k+1)}(t)= & {} \{j\in \mathbf{K}^{(k)}: a^{(k+1)}_j = a^{(k+1)}\} \qquad \text{ if } t>0, \nonumber \\ f^{(k+1)}(t)= & {} (x^*_{i^{(k+1)}}+ t/a^{(k+1)}) \wedge t = (y^*_{m^{(k+1)}}+ t/a^{(k+1)}) \wedge t. \qquad \end{aligned}$$

(53)

Using (53), we get $t^*_{k+1}=a^{(k+1)} (y^*_{m^{(k+1)}+1}-y^*_{m^{(k+1)}})$ unless $t^*_{k+1}=\infty$. Note that $\mathbf{J}^{(k+1)}$ (and hence $\mathbf{I}^{(k+1)}$, $\mathbf{N}^{(k+1)}$) is constant in $(0,{\underline{t}}_k \wedge t^*_{k+1})$.

If $y^*_{m^{(k+1)}}=0$ and $a^{(k+1)}<1$, then $m^{(k+1)}=m^*$ and $t^*_{k+1}=\infty$. In this case, (53) implies that $f^{(k+1)}(t)=t$ for $t \in [0, {\underline{t}}_k)$, so $k_{max}(t)=k+1$, $F_i(t)=t$ for such t and $i\in \mathbf{I}{\setminus }\bigcup _{p=1}^{k} \mathbf{I}^{(p)}$. In what follows, we assume that either $y^*_{m^{(k+1)}}<0$, or $a^{(k+1)}\ge 1$. In particular,

$$\begin{aligned} f^{(k+1)}(t)= x^*_{i^{(k+1)}}+ t/a^{(k+1)}=y^*_{m^{(k+1)}}+ t/a^{(k+1)} , \qquad t \in [0,{\underline{t}}_k \wedge t^*_{k+1} \wedge {\bar{t}}_{k+1}), \nonumber \\ \end{aligned}$$

(54)

where ${\bar{t}}_{k+1}=\infty$ if $a^{(k+1)}\ge 1$ and ${\bar{t}}_{k+1}=a^{(k+1)} x^*_{i^{(k+1)}}/(a^{(k+1)}-1)$ otherwise.

This ends the $k+1$th step of our construction. If $\bigcup _{l=1}^{k+1} \mathbf{I}^{(l)}=\mathbf{I}$, then for $0< t < {\underline{t}}_{k+1}=\min _{1\le l \le k+1} (t^*_l \wedge {\bar{t}}_l)$, we have $k_{max}(t)=k+1$ and the definition of $f^{(p)}(t)$, $p=1,\ldots ,k_{max}(t)$, is complete. Otherwise, we make another (i.e., the $k+2$th) step of our algorithm, taking $k+1$ instead of k and proceeding as above.

When the construction terminates, in the time interval $(0, {\underline{t}}_{k_{max}})$, we have the sets $\mathbf{I}^{(l)}=\mathbf{I}^{(l)}(t)$, $l=1,\ldots ,k_{max}$, constant in t, and $f^{(l)}(t)$, $l=1,\ldots ,k_{max}$, in the form of strictly increasing linear functions. Let $i\in \mathbf{I}$ and let $k\in \{1,\ldots ,k_{max}\}$ be such that $i\in \mathbf{I}^{(k)}$. Let $0\le t< {\tilde{t}} < {\underline{t}}_{k_{max}}$. Then, by (20), $F_i(t) = f^{(k)}(t) \vee x^*_i \le f^{(k)}({\tilde{t}}) \vee x^*_i = F_i({\tilde{t}}),$ and (41) follows.

Remark 8

Since the above argument is local in time, it actually requires only that for each $i\in \mathbf{I}$, (42) holds in some neighborhood of $x^*_i$, i.e., for all $x < X^*_i$, where $X^*_i>x^*_i$ are given constants. (Without loss of generality we may further assume that $X^*_{i'}=X^*_{i''}$ if $i',i''\in \mathbf{I}$ and $x^*_{i'}=x^*_{i''}$.) We only have to restrict t in each step of our construction to the interval $[0,{\underline{t}}_k')$ with ${\underline{t}}_k'=\min _{1\le l \le k} (t^*_l \wedge {\bar{t}}_l \wedge \bar{{\bar{t}}}_l)$, where $\bar{{\bar{t}}}_l=\infty$ if $f^{(l)}({\underline{t}}_l-)\le X^*_{i^{(l)}}$ and $\bar{{\bar{t}}}_l= (f^{(l)})^{-1}(X^*_{i^{(l)}})$ otherwise. In this case, (41) holds for all $i\in \mathbf{I}$ and $0\le t<{\tilde{t}} < {\underline{t}}_{k_{max}}'$.

5.2 Reduction lemmas and Lipschitz continuity

In this subsection we consider the case of general $h_i$, assuming only that each $h_i$ is strictly increasing in $[x^*_i,\infty )$. Fix $T>0$ and recall the sets ${\mathcal {T}}_1,\ldots {\mathcal {T}}_d$ from Sect. 3.4. The following lemma reduces the problem of establishing monotonicity of F to showing its monotonicity under the additional assumption that $k_{max}$ and the sets $\mathbf{J}^{(p)}$, $\mathbf{I}^{(p)}$, $p=1,\ldots ,k_{max}$, are constant in t.

Lemma 3

Assume that for $k=1,\ldots ,d$, the mapping F is nondecreasing on ${\mathcal {T}}_k$. Then F is nondecreasing on [0, T].

Proof

First note that F is nondecreasing on $\overline{{\mathcal {T}}_k}$ for each $k=1,\ldots ,d$. Indeed, let t, ${\tilde{t}}$ be such that $t< {\tilde{t}}$ and $t,{\tilde{t}} \in \overline{{\mathcal {T}}_k}$ for some k. Then for each $n \in {\mathbb {N}}$, there exist $t_n, {\tilde{t}}_n \in {\mathcal {T}}_k$ such that $t_n< {\tilde{t}}_n$ and $t_n \rightarrow t$, ${\tilde{t}}_n \rightarrow {\tilde{t}}$ as $n\rightarrow \infty$. By assumption, $F(t_n)\le F({\tilde{t}}_n)$ for each n. Letting $n\rightarrow \infty$, by Theorem 1 we get $F(t)\le F({\tilde{t}})$, so F is indeed monotone on $\overline{{\mathcal {T}}_k}$.

Let $0\le t< {\tilde{t}}\le T$ and let $k_0$ be such that $t \in {\mathcal {T}}_{k_0}$. Let $t_1= \sup \{ s \le {\tilde{t}}: s\in {\mathcal {T}}_{k_0}\}$. Then $t_1 \in \overline{{\mathcal {T}}_{k_0}}$, so $F(t)\le F(t_1)$. If $t_1 = {\tilde{t}}$, we have (41) and the proof is complete. Assume that $t_1 < {\tilde{t}}$. In this case, $(t_1,{\tilde{t}}] \cap {\mathcal {T}}_{k_0} = \emptyset$ by the definition of $t_1$. However, there exist $k_1 \ne k_0$ and a sequence $s_n \in {\mathcal {T}}_{k_1}$ such that $s_n \downarrow t_1$. Let $t_2= \sup \{ s \le {\tilde{t}}: s\in {\mathcal {T}}_{k_1}\}$. Then $t_1,t_2 \in \overline{{\mathcal {T}}_{k_1}}$, so $F(t_1)\le F(t_2)$, and hence $F(t)\le F(t_2)$. If $t_2 = {\tilde{t}}$, the proof is complete, otherwise $(t_2,{\tilde{t}}] \cap ({\mathcal {T}}_{k_0} \cup {\mathcal {T}}_{k_1}) = \emptyset$. Let $k_2 \notin \{ k_0, k_1\}$ and a sequence $s_n \in {\mathcal {T}}_{k_2}$ be such that $s_n \downarrow t_2$. Put $t_3= \sup \{ s \le {\tilde{t}}: s\in {\mathcal {T}}_{k_2}\}$. As above, we have $F(t_2)\le F(t_3)$, and hence $F(t)\le F(t_3)$. After a finite number $l\le d$ of such steps we get $F(t)\le F(t_l)$ and $t_l={\tilde{t}}$, so (41) holds. $\square$

A slight modification of the above argument yields

Lemma 4

Assume that for $k=1,\ldots ,d$, the mapping F is Lipschitz continuous on ${\mathcal {T}}_k$. Then F is Lipschitz on [0, T].

This lemma, together with (26)–(28), may be used to provide a simple proof of the following result.

Theorem 2

Assume that there exist $0<c<C<\infty$ such that

$$\begin{aligned} c(y-x) \le h_i(y)-h_i(x) \le C (y-x), \qquad x^*_i \le x \le y, \quad i\in \mathbf{I}. \end{aligned}$$

(55)

Then F is Lipschitz continuous in $[0,\infty )$.

Proof

Fix $T>0$. We will argue that F is Lipschitz in [0, T] (with the Lipschitz constant independent on T). According to Lemma 4, it suffices to show this in each ${\mathcal {T}}_l$, $l=1,\ldots ,d$. Fix ${\mathcal {D}}= (J_1,\ldots ,J_k)\in {\mathcal {J}}$. By (55), for $0\le x \le y$, we have $(y-x)/(CI) \le g(y)-g(x) \le (y-x)/c$, where g is any of the inverses appearing in (26)–(27). Hence, the function $f^{(1)}$ defined by (26) is Lipschitz in ${\mathcal {T}}^{\mathcal {D}}$. Using this fact, together with (27), (55), and proceeding by induction, we show Lipschitz continuity of $f^{(p)}$, $p=2,\ldots ,k$, in ${\mathcal {T}}^{\mathcal {D}}$. From this, we get Lipschitz continuity of F in ${\mathcal {T}}^{\mathcal {D}}$ by (20). $\square$

Example 3 indicates that the lower bound in (55) is necessary for Theorem 2 to hold.

5.3 Local monotonicity in the $C^1$ case

In this subsection, we assume that for each $i\in \mathbf{I}$, $h_i\in C^1([x^*_i,\infty ))$ and

$$\begin{aligned} \rho ^i:=h_i'(x^*_i)>0, \end{aligned}$$

(56)

where $h_i'(x^*_i)$ denotes the right derivative of $h_i$ at $x^*_i$. Again, with no loss of generality we may assume (43). Define $m^*$, $n_0,\ldots ,n_{m^*}$, $y^*_1,\ldots ,y^*_{m^*}$ as in Sect. 5.1. Because our concern here is local monotonicity of F, without loss of generality we may assume that $h_i'(x)>0$ for all $i\in \mathbf{I}$ and $x\ge x^*_i$ (compare Remark 8).

The main idea of our analysis for this case is to consider it as a small perturbation of the linear problem considered in Sect. 5.1, with $\rho ^i$ given by (56). In particular, let ${\underline{t}}_{k_{max}}$ be as in in Sect. 5.1 and let $k_{max}^L$ be the constant $k_{max}(t)$, $0<t<{\underline{t}}_{k_{max}}$, defined there. Furthermore for $k=1,\ldots ,k_{max}^L$, let $a^{(k)}$ be as in Sect. 5.1 and let $\mathbf{J}^{(k)}_L$, $\mathbf{I}^{(k)}_L$, $\mathbf{N}^{(k)}_L$, $\mathbf{K}^{(k)}_L$, $f^{(k)}_L$, denote the sets $\mathbf{J}^{(k)}(t)$, $\mathbf{I}^{(k)}(t)$, $\mathbf{N}^{(k)}(t)$, $\mathbf{K}^{(k)}(t)$, $t\in (0,{\underline{t}}_{k_{max}})$, and the function $f^{(k)}$ for the above-mentioned linear problem, respectively.

Fix $0<T\le {\underline{t}}_{k_{max}}/2$ and the partition ${\mathcal {D}} = (J_1,\ldots ,J_k) \in {\mathcal {J}}$ such that there exists a sequence $t_n\downarrow 0$ such that $t_n\in {\mathcal {T}}^{\mathcal {D}}$ for all n. Since $f^{(1)}(t)<\cdots<f^{(k-1)}(t)<t$ for $t\in {\mathcal {T}}^{\mathcal {D}}$, using (26)–(27) and proceeding by induction, it is easy to see that $f^{(1)}$,..., $f^{(k-1)}$ are the truncations of $C^1$ functions to ${\mathcal {T}}^{\mathcal {D}}$, and $f^{(k)}$ is the truncation to ${\mathcal {T}}^{\mathcal {D}}$ of a function in the form $g(t)\wedge t$, where g is $C^1$. Therefore, in order to prove that the functions $f^{(p)}$, $p=1,\ldots ,k=k_{max}$, (and hence, by (20), $F_i$, $i\in \mathbf{I}$) are nondecreasing in an intersection of ${\mathcal {T}}^{\mathcal {D}}$ and a neighborhood of zero, it suffices to check that

$$\begin{aligned} (f^{(p)})'(0):= \lim _{t\downarrow 0, t\in {\mathcal {T}}^{\mathcal {D}}} \frac{f^{(p)}(t)-f^{(p)}(0)}{t}>0, \qquad p=1,\ldots ,k, \end{aligned}$$

(57)

where $f^{(p)}(0):=f^{(p)}(0+)=\lim _{n\rightarrow \infty }f^{(p)}(t_n)$. Consequently, by Lemma 3, if we verify (57), then the proof of monotonicity of the mapping F in a neighborhood of zero is complete. In what follows, we consider only $t \in {\mathcal {T}}^{\mathcal {D}}$.

We will first consider the case of $x^*_1=y^*_1=0$ (hence $m^*=1$, $n_1=I$) and $a^{(1)}\le 1$. Then for every $j\in \mathbf{J}$ and $t>0$ small enough,

$$\begin{aligned} \sum _{i\in G_j} h_i(t) \le a^{(1)} t +o(t), \end{aligned}$$

(58)

with equality for $j\in \mathbf{J}^{(1)}_L$. If $a^{(1)}<1$, then (58) implies that $f^{(1)}(t)=t$, and hence $F_i(t)=t$, $i\in \mathbf{I}$, for t small enough. If $a^{(1)}=1$, then, by (58), $f^{(1)}(t)=t+o(t)$. Since $f^{(1)}(t)<f^{(p)}(t) \le t$ for $p=2,\ldots ,k$, this implies $(f^{(1)})'(0) =(f^{(2)})'(0) =\cdots =(f^{(k)})'(0) =1$. Therefore, in the remainder of the proof we may assume that either $x^*_1<0$, or $a^{(1)}> 1$.

By (33), we have $f^{(1)}(0)= x^*_1=y^*_1$. We claim that

$$\begin{aligned}&J_1 \subseteq \mathbf{J}^{(1)}_L, \qquad \qquad \qquad \qquad \qquad \qquad \end{aligned}$$

(59)

$$\begin{aligned}&f^{(1)}(t)= f^{(1)}_L(t)+o(t)=x^*_1+ t/a^{(1)}+o(t)=y^*_1+ t/a^{(1)}+o(t), \;\; \end{aligned}$$

(60)

[compare (48)]. Suppose that (59) is false and let $j\in J_1{\setminus }{} \mathbf{J}^{(1)}_L$, $j'\in \mathbf{J}^{(1)}_L$. Then, by (45)–(46), for small $t>0$ we have

$$\begin{aligned} t = \sum _{i \in G_{j} \cap \{1,\ldots ,n_1\}} h_i(f^{(1)}(t)) = \sum _{i \in G_{j} \cap \{1,\ldots ,n_1\}} \rho ^i(f^{(1)}(t)-x^*_1) + o(f^{(1)}(t)-x^*_1) \qquad \\ < \sum _{i \in G_{j'} \cap \{1,\ldots ,n_1\}} \rho ^i(f^{(1)}(t)-x^*_1) + o(f^{(1)}(t)-x^*_1) = \sum _{i \in G_{j'} \cap \{1,\ldots ,n_1\}} h_i(f^{(1)}(t)) \le t. \end{aligned}$$

We have obtained a contradiction, proving (59). Using (46) and (59), for $j\in J_1$, for small $t>0$, we get

$$\begin{aligned} t = \sum _{i \in G_{j} \cap \{1,\ldots ,n_1\}} h_i(f^{(1)}(t)) = (a^{(1)}+o(t)) (f^{(1)}(t)-x^*_1), \end{aligned}$$

yielding (60). If $k=1$, then (60) implies (57) and our proof is complete, otherwise we proceed by induction as follows.

Assume that for some $1\le l<k$ there are indices $r\in \{1,..,l\wedge k^L_{max}\}$, $0=p_0<1 \le p_1<p_2<\cdots <p_r= l$ such that

$$\begin{aligned}&\bigcup _{p=p_{s-1}+1}^{p_s} J_p \subseteq \mathbf{J}^{(s)}_L, \qquad s=1,\ldots ,r, \qquad \qquad \end{aligned}$$

(61)

$$\begin{aligned}&\bigcup _{p=p_{s-1}+1}^{p_{s}} I_p = \mathbf{I}^{(s)}_L, \qquad s=1,\ldots ,r-1. \qquad \;\; \end{aligned}$$

(62)

where the sets $I_p$ are as in (28). We also assume that for $p=p_{s-1}+1,\ldots p_s$, $s=1,\ldots ,r$, we have

$$\begin{aligned} f^{(p)}(t)= f^{(s)}_L(t) + o(t) = x^*_{i^{(s)}}+ t/a^{(s)}+o(t)=y^*_{m^{(s)}}+ t/a^{(s)}+o(t). \quad \end{aligned}$$

(63)

By (59)–(60), the above assumptions hold for $l=1$ (hence $r=1$, $p_1=1$). Note that in this case (62) is vacuously true.

For $p=0,\ldots ,k-1$, let $K_p=\{j'\in \mathbf{J}: G_j {\setminus }\bigcup _{q=1}^p I_q \ne \emptyset \}$. Clearly, $K_0=\mathbf{J}$. Moreover, (28) implies that $K_p=\mathbf{K}^{(p)}(t)$ for $p=1,\ldots k-1$. We claim that

$$\begin{aligned} K_l \subseteq K_{p_{r-1}} = \mathbf{K}_L^{(r-1)}. \end{aligned}$$

(64)

Indeed, the inclusion in (64) is obvious, since $p_{r-1}<l$. By (62), $\bigcup _{p=1}^{p_{r-1}} I_p = \bigcup _{s=1}^{r-1} \mathbf{I}^{(s)}_L$, hence $\bigcup _{p=1}^{p_{r-1}} \mathbf{D}^{(p)}(t)=\bigcup _{s=1}^{r-1}{} \mathbf{D}^{(s)}_L$, yielding the equality in (64).

By (28) and (61) with $s=r$, $\bigcup _{p=p_{r-1}+1}^{l} I_p \subseteq \bigcup _{j\in \mathbf{J}^{(r)}_L} G_j \subseteq \bigcup _{s=1}^{r} \mathbf{I}^{(s)}_L$. This, together with (62) and the fact that the sets $I_p$ are disjoint, yields

$$\begin{aligned} \bigcup _{p=p_{r-1}+1}^{l} I_p \subseteq \mathbf{I}^{(r)}_L. \end{aligned}$$

(65)

We first assume that the inclusion in (65) is strict. Then

$$\begin{aligned} \mathbf{J}^{(r)}_L \cap K_l \ne \emptyset . \end{aligned}$$

(66)

Indeed, if (66) is false, then $\mathbf{J}^{(r)}_L \subseteq \bigcup _{p=1}^{l} \mathbf{D}^{(p)}(t)$, and hence $\mathbf{I}^{(r)}_L \subseteq \bigcup _{p=1}^{l} I_p$. The latter inclusion, together with (62) and the fact that the sets $I_p$ are disjoint, yields $\mathbf{I}^{(r)}_L \subseteq \bigcup _{p=p_{r-1}+1}^{l} I_p$, contrary to the case assumption, so (66) follows. By (1), (17)–(18), (56), (62)–(63) and (65), for small $t>0$, $f^{(l+1)}(t)$ is the supremum of $x\le t$ satisfying the constraints

$$\begin{aligned} t\ge & {} \sum _{p=1}^l \sum _{i\in G_j \cap I_p} [\rho ^i (f^{(p)}(t)-x^*_i) + o((f^{(p)}(t)-x^*_i)^+)] \nonumber \\&+ \sum _{i\in G_j{\setminus }\bigcup _{p=1}^l I_p} [\rho ^i (x-x^*_i)^+ + o((x-x^*_i)^+)] \nonumber \\= & {} \sum _{s=1}^{r-1} \sum _{i\in G_j \cap \mathbf{I}^{(s)}_L} [\rho ^i (f^{(s)}_L(t) -x^*_i+ o(t) ) + o((f^{(s)}_L(t) -x^*_i+ o(t) )^+)] \nonumber \\&+ \sum _{i\in G_j \cap \bigcup _{p=p_{r-1}+1}^{l} I_p} [\rho ^i (f^{(r)}_L(t) -x^*_i+ o(t) ) + o((f^{(r)}_L(t) -x^*_i+ o(t) )^+)] \nonumber \\&+ \sum _{i\in G_j{\setminus }\bigcup _{p=1}^l I_p} [\rho ^i (x-x^*_i)^+ + o((x-x^*_i)^+)] \nonumber \\= & {} \sum _{s=1}^{r-1} \sum _{i\in G_j \cap \mathbf{I}^{(s)}_L \cap \{ n_{m^{(s)}-1}+1,\ldots ,n_{m^{(s)}} \}} \frac{\rho ^i t}{a^{(s)}} \nonumber \\&+ \sum _{i\in G_j \cap (\bigcup _{p=p_{r-1}+1}^{l} I_p) \cap \{ n_{m^{(r)}-1}+1,\ldots ,n_{m^{(r)}} \}} \frac{\rho ^i t}{a^{(r)}} \; + \; o(t) \nonumber \\&+ \sum _{i\in G_j{\setminus }\bigcup _{p=1}^l I_p} [\rho ^i (x-x^*_i)^+ + o((x-x^*_i)^+)], \end{aligned}$$

(67)

for $j\in K_l$. Recall that in the corresponding linear problem, for small $t>0$, we have

$$\begin{aligned} t\ge & {} \sum _{s=1}^{r-1} \sum _{i\in G_j \cap \mathbf{I}^{(s)}_L} \rho ^i (f^{(s)}_L(t) -x^*_i)^+ \; + \sum _{i\in G_j{\setminus }\bigcup _{s=1}^{r-1} \mathbf{I}^{(p)}_L} \rho ^i (f^{(r)}_L(t)-x^*_i)^+ \nonumber \\= & {} \sum _{s=1}^{r-1} \sum _{i\in G_j \cap \mathbf{I}^{(s)}_L \cap \{ n_{m^{(s)}-1}+1,\ldots ,n_{m^{(s)}} \}} \frac{\rho ^i \; t}{a^{(s)}} \; + \sum _{i\in G_j{\setminus }\bigcup _{s=1}^{r-1} \mathbf{I}^{(s)}_L} \rho ^i \Big (\frac{ t}{a^{(r)}}+x^*_{i^{(r)}}-x^*_i\Big )^+ \nonumber \\= & {} \sum _{s=1}^{r-1} \sum _{i\in G_j \cap \mathbf{I}^{(s)}_L \cap \{ n_{m^{(s)}-1}+1,\ldots ,n_{m^{(s)}} \}} \frac{\rho ^i \; t}{a^{(s)}} \nonumber \\&+ \sum _{i\in G_j \cap (\bigcup _{p=p_{r-1}+1}^{l} I_p) \cap \{ n_{m^{(r)}-1}+1,\ldots ,n_{m^{(r)}} \}} \frac{\rho ^i t}{a^{(r)}} \nonumber \\&+ \sum _{i\in G_j{\setminus }\bigcup _{p=1}^l I_p} \rho ^i \Big (\frac{ t}{a^{(r)}}+x^*_{i^{(r)}}-x^*_i\Big )^+ \end{aligned}$$

(68)

for $j\in \mathbf{K}^{(r-1)}_L$, with equality for $j\in \mathbf{J}^{(r)}_L$ [compare (49), (51)]. Note that the second equality in (68) follows from (65). Comparing (67) to (68) and using (64), (66), we get the inclusion $J_{l+1} \subseteq \mathbf{J}^{(r)}_L$ and (63) for $p=l+1$, $s=r$. This ends the inductive step in the case of strict inclusion in (65).

It remains to analyze the case in which

$$\begin{aligned} \bigcup _{p=p_{r-1}+1}^{l} I_p = \mathbf{I}^{(r)}_L. \end{aligned}$$

(69)

Then (62) holds for $s=1,\ldots ,r$, so $\bigcup _{p=1}^l I_p=\bigcup _{s=1}^{r} \mathbf{I}^{(p)}_L$ and $K_l=\mathbf{K}^{(r)}_L$ (this is the equality in (64), with r in the place of $r-1$). Also, (62) for $s\le r$, together with the inequality $l<k$, implies that $r<k^L_{max}$. The counterpart of (67) in this case is

$$\begin{aligned} t\ge & {} \sum _{s=1}^{r} \sum _{i\in G_j \cap \mathbf{I}^{(s)}_L \cap \{ n_{m^{(s)}-1}+1,\ldots ,n_{m^{(s)}} \}} \frac{\rho ^i t}{a^{(s)}} \; + \; o(t) \nonumber \\&+ \sum _{i\in G_j{\setminus }\bigcup _{p=1}^l I_p} [\rho ^i (x-x^*_i)^+ + o((x-x^*_i)^+)], \end{aligned}$$

(70)

for $j\in K_l$. If $r+1=k^L_{max}$, $y_{m^{(r+1)}}=y_{m^*}=0$ and $a^{(r+1)}<1$, then $f^{(r+1}_L(t) =t$ for small $t>0$ and the counterpart of (68) is

$$\begin{aligned} t > \sum _{s=1}^{r} \sum _{i\in G_j \cap \mathbf{I}^{(s)}_L \cap \{ n_{m^{(s)}-1}+1,\ldots ,n_{m^{(s)}} \}} \frac{\rho ^i \; t}{a^{(s)}} + \sum _{i\in G_j{\setminus }\bigcup _{p=1}^l I_p} \rho ^i t \end{aligned}$$

(71)

for $j\in \mathbf{K}^{(r)}_L=K_l$. Comparing (70) to (71) we see that $f^{(l+1)}(t)=t$ and $l+1=k_{max}(t)=k$, so our inductive proof of (57) is complete. If $y_{m^{(r+1)}}<0$ or $a^{(r+1)}\ge 1$, then the counterpart of (68) is

$$\begin{aligned} t \ge \sum _{s=1}^{r} \sum _{i\in G_j \cap \mathbf{I}^{(s)}_L \cap \{ n_{m^{(s)}-1}{+}1,\ldots ,n_{m^{(s)}} \}} \frac{\rho ^i t}{a^{(s)}} {+} \sum _{i\in G_j{\setminus }\bigcup _{p=1}^l I_p} \rho ^i \Big (\frac{ t}{a^{(r+1)}}+x^*_{i^{(r+1)}}-x^*_i\Big )^+,\nonumber \\ \end{aligned}$$

(72)

for $j\in \mathbf{K}^{(r)}_L=K_l$, with equality for $j\in \mathbf{J}^{(r)}_L$. Comparing (70) to (72), we get (63) for $p=l+1$, $s=r+1$, and $J_{l+1} \subseteq \mathbf{J}^{(r+1)}_L$, yielding (61) for $s=r+1$, and the proof of the inductive step is complete.

5.4 Lack of global monotonicity

It is not hard to prove that, without any additional assumptions on the functions $h_i$, (41) holds for every $0\le t < {\tilde{t}}$ and $i \in \mathbf{I}^{(1)}(t)$. In spite of this, the mapping F is, in general, not monotone on $[0,\infty )$, even if $h_i$, $i \in \mathbf{I}$, are given by (42), as the following example shows.

Fig. 4

Complex four-node, seven-route network with nonlinear mapping F

Example 4

Let $I=7$, $J=4$, $G_1=\{1,3,6\}$, $G_2=\{2,4,7\}$, $G_3=\{3,4,5,6,7\}$ and $G_4=\{6,7\}$. The corresponding network topology is pictured in Fig. 4. Next, let

$$\begin{aligned} h_1(x)= & {} h_2(x) \; =\; 2(x+11)^+, \\ h_3(x)= & {} h_4(x) \; =\; (x+11)^+,\nonumber \end{aligned}$$

(73)

$$\begin{aligned} h_5(x)= & {} x^+, \\ h_6(x)= & {} h_7(x) \; =\; 2(x+10)^+,\nonumber \end{aligned}$$

(74)

so that $x^*_1=x^*_2=x^*_3=x_4^*=-11$, $x^*_5=0$, $x^*_6=x^*_7=-10$. One may easily check that for $0\le t \le 8$, $\mathbf{J}^{(1)}(t) = \{1,2\}$, $\mathbf{J}^{(2)}(t)=\{3\}$, $\mathbf{I}^{(1)}(t) = \{1,2,3,4,6,7\}$, $\mathbf{I}^{(2)}(t)=\{5\}$, $\mathbf{N}^{(1)}(t) = \{4\}$ and $\mathbf{N}^{(2)}(t) =\emptyset$. Moreover,

$$\begin{aligned} f^{(1)}(t) =\frac{t}{3}-11, \qquad \;f^{(2)}(t) =\frac{t}{3}, \qquad \;\; \;\;0\le t\le 3, \end{aligned}$$

(75)

$$\begin{aligned} f^{(1)}(t) =\frac{t-53}{5}, \qquad f^{(2)}(t) =\frac{8-t}{5}, \qquad 3\le t\le 8, \end{aligned}$$

(76)

hence

$$\begin{aligned} F_5(t)=\frac{8-t}{5}, \qquad 3\le t\le 8, \end{aligned}$$

(77)

and the mapping F fails to be nondecreasing.

The “network topology” in the above example may be somewhat simplified, at the price of making some of the functions $h_i(x)$, $x\ge x^*_i$, nonlinear. Namely, let $I=5$, $J=3$, $G_1=\{1,3\}$, $G_2=\{2,4\}$ and $G_3=\{3,4,5\}$. Assume (73)–(74) and let $h_3(x) = h_4(x) = (x+11)^+ + 2(x+10)^+,$ so that $x^*_1=x^*_2=x^*_3=x_4^*=-11$, $x^*_5=0$. (Somewhat informally, this network structure has been obtained from the previous one by removing the fourth server and merging the routes 3, 6 (resp., 4, 7) into a single route 3 (resp., 4), see Fig. 5). It is easy to verify that in this case for $0\le t \le 8$, $\mathbf{J}^{(1)}(t) = \{1,2\}$, $\mathbf{J}^{(2)}(t)=\{3\}$, $\mathbf{I}^{(1)}(t) = \{1,2,3,4\}$, $\mathbf{I}^{(2)}(t)=\{5\}$ and (75)–(77) still hold. Note that this network satisfies the local traffic condition and hence $\mathbf{N}^{(1)}(t) = \mathbf{N}^{(2)}(t) =\emptyset$ for all t.

Fig. 5

Simplified three-node, five-route network with nonlinear mapping F

6 Related minimax problems and fluid models

In this section, we briefly, and somewhat informally, discuss two fluid models related to the one defined in Sect. 2.3. In both of them, the state dynamics may be locally described by appropriate vector-valued mappings of essentially the same nature as the function F considered above. Consequently, it is natural to expect that the methods developed in this paper will turn out be useful in the investigation of key properties of these maps.

6.1 Locally queue length minimal fluid models

If the service discipline in a resource sharing network does not take the customer timing requirements into account, the second argument in the network Eqs. (2)–(4), and hence in the corresponding fluid model Eqs. (5)–(7), is superfluous. Neglecting it [or putting large s into (5)–(8) and letting $s\rightarrow \infty$], we get the fluid model

$$\begin{aligned} \overline{{\mathfrak {X}}}(t)=({\overline{Z}}(t),{\overline{D}}(t), {\overline{T}}(t),{\overline{Y}}(t)), \qquad t\ge 0, \end{aligned}$$

(78)

with continuous, nonnegative components, subject to appropriate monotonicity assumptions, satisfying the following equations, valid for ${\tilde{t}}\ge t\ge 0$:

$$\begin{aligned} {\overline{Z}}(t)= {\overline{Z}}(0)+ \alpha t -{\overline{D}}(t), \qquad \qquad \qquad \;\;\;\; \end{aligned}$$

(79)

$$\begin{aligned} {\overline{D}}_i(t)={\overline{T}}_i(t)/m_i, \qquad {\overline{T}}_{i}(t) +{\overline{Y}}_i(t)=t, \qquad i\in \mathbf{I}, \end{aligned}$$

(80)

$$\begin{aligned} \sum _{i\in G_j} \big ( {\overline{T}}_i({\tilde{t}})- {\overline{T}}_i(t) \big ) \le {\tilde{t}}-t, \qquad j\in \mathbf{J}. \qquad \;\; \end{aligned}$$

(81)

Recall Definition 1. To proceed further, we define a partial ordering “$\leqslant$” on ${\mathbb {R}}^n$ such that for any $a,b\in {\mathbb {R}}^n$, $a\leqslant b$ if and only if $-b \eqslantless -a$.

Definition 6

A fluid model $\overline{{\mathfrak {X}}}$ of the form (78) for a resource sharing network is called locally queue length minimal at a time $t_0\ge 0$ if there exists $h>0$ such that for any fluid model $\overline{{\mathfrak {X}}}'$ with the same $\alpha$, $m_i$, $G_i$, satisfying $\overline{{\mathfrak {X}}}'(t_0)=\overline{{\mathfrak {X}}}(t_0)$, we have ${\overline{Z}}(t) \leqslant {\overline{Z}}'(t)$ (equivalently, ${\overline{D}}'(t) \eqslantless {\overline{D}}(t)$) for every $t\in (t_0,t_0+h)$. The fluid model $\overline{{\mathfrak {X}}}$ is called locally queue length minimal if it is called locally queue length minimal at every $t_0\ge 0$.

The intuition behind this definition is that a locally queue length minimal fluid model tries to minimize the maximal queue lengths by transmitting as much “customer mass” from the longest queues as possible. Thus, such a model may be regarded as a “macroscopic” counterpart of a resource sharing network working under the Longest Queue First (LQF) protocol. More precisely, it corresponds to a “strong” variant of LQF in which the transmission is scheduled on as many routes having the longest queue lengths as possible, instead of using a random tie-breaking rule considered, e.g., in Dimakis and Walrand (2006). Since LQF is usually implemented on a packet level, the model (78)–(81) may be simplified further by putting $m_i=1$, $i\in \mathbf{I}$ (and hence removing the superfluous function ${\overline{D}}$).

The state dynamics of a fluid model in a neighbourhood of a time point $t_0\ge 0$ at which this model is locally queue length minimal may be described by local behaviour near 0 of the mapping H defined below.

Definition 7

Let $h_i(x)= m_i (x+{\overline{Z}}_i(t_0))^+$, $i\in \mathbf{I}$, $x\in {\mathbb {R}}$. For $t\ge 0$, let

$$\begin{aligned} B_t = \Big \{a=(a_1,\ldots ,a_I)\in {\mathbb {R}}^I:\; a_i \le \alpha _i t, \; i\in \mathbf{I}, \; \sum _{i\in G_j} h_i(a_i) \le t, \; j \in \mathbf{J} \Big \}, \end{aligned}$$

and let $H(t)=(H_i(t))_{i\in \mathbf{I}}$ be the element maximizing the vector $a-\alpha t$ over $a\in B_t$ with respect to the relation “$\eqslantless$”.

In fact, for a fluid model which is locally queue length minimal at $t_0$ and for small $t\ge 0$, we have ${\overline{Z}}_i(t_0+t)=\alpha t -H(t)$. In particular, monotonicity of H translates into a natural viability condition ${\overline{Z}}_i(t_0+{\tilde{t}})-{\overline{Z}}_i(t_0+t)\le \alpha _i ({\tilde{t}}-t)$ for all $0\le t\le {\tilde{t}}$, $i\in \mathbf{I}$, which is, in some sense, a counterpart of monotonicity of the “frontier” mapping F in a locally edge minimal fluid model.

In the case of $\alpha _i=1$, $i\in \mathbf{I}$, we have $B_t=A_t$ and $H(t)=F(t)$, where $A_t$ and F(t) are as in Definition 2. More generally, if $\alpha _i=\alpha _{i'}$ for each $i,i'\in \mathbf{I}$ such that ${\overline{Z}}_i(t_0)={\overline{Z}}_{i'}(t_0)$, then H(t) can be (locally) retrieved from F(t) by a suitable linear change of variables. Note that even without any additional assumptions, since the functions $h_i$ in Definition 7 are piecewise linear, the mapping H is linear in a neighbourhood of 0 and it can be expressed in closed form by mimicking the approach of Sect. 5.1.

6.2 SRPT fluid models

To be in line with existing measure-valued fluid models for single-server SRPT queues (Down et al. 2009; Kruk and Sokołowska 2016), we conside a fluid model for a SRPT resource sharing network in which the state descriptor is a vector of measures, rather than the corresponding distribution functions [compare (8)]. In what follows, we will use the additional notation from Sect. 1.1.

As before, let $\alpha _i$ be the flow arrival rate to route $i\in \mathbf{I}$. For $i\in \mathbf{I}$, let $\nu _i\in {{\mathbf {M}}}_0$ be a probability measure, representing the incoming flow (or fluid) transmission time distribution on route i, and let $\xi _i\in {{\mathbf {M}}}_0$ be the initial measure, modelling the transmission time requirements of the fluid present on route i at time zero. To simplify the analysis, we assume that all the distributions $\nu _i$, $\xi _i$ are continuous. For $i\in \mathbf{I}$, let

$$\begin{aligned} v^*_i=\sup \{x\in {\mathbb {R}}_+: (\xi _i+\nu _i)([0,x])<\xi ({\mathbb {R}}_+)+1 \}. \end{aligned}$$

Let $\alpha =(\alpha _i)_{i\in \mathbf{I}}$, $\nu =(\nu _i)_{i\in \mathbf{I}}$ and $\xi =(\xi _i)_{i\in \mathbf{I}}$. For $j\in \mathbf{J}$, let $\rho _j=\sum _{i\in G_j} \alpha _i \langle \chi , \nu _i \rangle$ be the traffic intensity at resource j.

Definition 8

A continuous function $\zeta =(\zeta _1,\ldots ,\zeta _I):{\mathbb {R}}_+\rightarrow {{\mathbf {M}}}^I$ with $\zeta (0)=\xi$ is called a SRPT-like fluid model for a resource sharing network if

• (i) for all $t\ge 0$ and $i\in \mathbf{I}$, $\zeta _i(t)= (\xi _i+\alpha _i t\nu _i)_{|[l_{\zeta _i(t)},\infty )}$,

• (ii) for ${\tilde{t}} \ge t\ge 0$ and $j\in \mathbf{J}$, $\sum _{i\in G_j} (\langle \chi ,\zeta _i(t) \rangle - \langle \chi ,\zeta _i({\tilde{t}}) \rangle ) \le (1-\rho _j)({\tilde{t}}-t),$

• (iii) the function $L^\zeta (t)=(l_{\zeta _i(t)})_{i\in \mathbf{I}}$ is nondecreasing on $(0,\infty )$, i.e., $L^\zeta (t)\le L^\zeta ({\tilde{t}})$ for all ${\tilde{t}} \ge t> 0$.

Here the condition (ii) imposes the resource capacity constraints, while (iii) is a natural viability condition, assuring that the fluid model does not “get back” the fluid mass which has already been transmitted. The condition (i), stating that the fluid mass departed from each route had transmission time requirements less than the left edge of the support of the current measure-valued state descriptor for this route, is specific to the intra-route SRPT discipline. See (C3) in Definition 2.2 of Down et al. (2009) and the following discussion for more details. However, the conditions (i)–(iii) of Definition 8 do not imply that the bandwidth is being assigned to the routes according to the global SRPT across all traffic classes. In fact, SRPT-like fluid models may arise as fluid limits of networks with various bandwidth allocations to the routes, e.g., fixed priorities or proportional fairness, as long as SRPT is implemented locally, i.e., within each route. “Local SRPT” policies of this type were proposed by Aalto and Ayesta (2009) in order to improve the delay performance of the system. Note that by (i), given the fluid model data $\alpha$, $\nu$ and $\xi$, the left edge mapping $L^\zeta$ determines the corresponding SRPT-like fluid model uniquely. In order to capture the “global” SRPT scheduling on the level of a fluid model, we extend the relation “$\eqslantless$” from Definition 1 to $(-\infty ,+\infty ]^n$ and we introduce the following notion.

Definition 9

A SRPT-like fluid model $\zeta$ for a resource sharing network is called locally left edge maximal at a time $t_0\ge 0$ if there exists $h>0$ such that for any SRPT-like fluid model $\zeta '$ with the same $\alpha$, $\nu _i$, $\xi _i$, $G_i$, satisfying $\zeta '(t_0)=\zeta (t_0)$, we have $L^{\zeta '}(t) \eqslantless L^{\zeta }(t)$ (equivalently, $(\langle \chi , \zeta _i(t) \rangle )_{i\in \mathbf{I}} \eqslantless (\langle \chi , \zeta _i'(t) \rangle )_{i\in \mathbf{I}}$) for every $t\in (t_0,t_0+h)$. The fluid model $\zeta$ is called locally left edge maximal if it is called locally left edge maximal at every $t_0\ge 0$.

The intuition behind this definition is that a locally left edge maximal fluid model tries to maximize the minima of the left edges of the supports of the measure-valued state descriptors across all routes by transmitting as much “fluid mass” located at the minimal edges as possible. Consequently, such a model may be regarded as a “macroscopic” counterpart of a resource sharing network working under the SRPT protocol.

It is natural to describe the local dynamics of the function $L^{\zeta }$ corresponding to a fluid model $\zeta$ which is locally left edge maximal at a time $t_0$ by means of a mapping similar to F and H from Definitions 2 and 7 , respectively. To fix ideas, let $t_0=0$.

Definition 10

For $t\ge 0$, we denote by $L(t)=(L_i(t))_{i\in \mathbf{I}}$ the maximal element of the set

$$\begin{aligned} C_t = \Big \{ (a_1,\ldots ,a_I)\in (-\infty ,+\infty ]^I: a_i \le v^*_i, i\in \mathbf{I}, \sum _{i\in G_j} (h_i(a_i) +t g_i(a_i))\le t, j \in \mathbf{J} \Big \} \end{aligned}$$

with respect to the relation “$\eqslantless$”, where $h_i(x) = \langle \chi {\mathbb {I}}_{[0,x)}, \xi _i \rangle$ and $g_i(x) = \alpha _i \langle \chi {\mathbb {I}}_{[0,x)}, \nu _i \rangle$ for $i\in \mathbf{I}$, $x\in (-\infty ,+\infty ]$.

If L is suitably well behaved (in particular, locally monotone, see Definition 8 (iii)), then $L=L^\zeta$ in a neighbourhood of the origin.

In the case of $l_{\xi _i} < l_{\nu _i}$, $i\in \mathbf{I}$, for small $t\ge 0$ we have

$$\begin{aligned} C_t = \Big \{(a_1,\ldots ,a_I)\in (-\infty ,+\infty ]^I:\; a_i \le v^*_i, \; i\in \mathbf{I}, \; \sum _{i\in G_j} h_i(a_i) \le t, \; j \in \mathbf{J} \Big \}, \end{aligned}$$

and hence the mapping L is a minor variant of F. If all the distributions $\xi _i$, $\nu _i$ are uniform on some intervals or, more generally, if they possess step-like densities in ${\mathbb {R}}_+$, then L is piecewise linear and it can be evaluated by mimicking the approach of Sect. 5.1. In the absence of such additional assumptions, the local behaviour of the mapping L does not appear to be easily reducible to the properties of F, due to the additional terms $t g_i(x)$ in the definition of $C_t$. However, the main difficulty here is precisely the one we have already dealt with in the case of F. Indeed, the problem of evaluating L(t) (as well as F(t)) is a nested sequence of “conventional” optimization problems, varying discontinuously with t, in which each problem determines the form of its successor. Consequently, we expect that the methods developed in this paper will be useful also in the qualitative analysis of L. In particular, we conjecture that if for any $i\in \mathbf{I}$, the function $h_i+g_i$ is strictly increasing in $(l_{\xi _i+\nu _i}, v^*_i)$, then continuity of the mapping L may be established along the lines of the proof of Theorem 1; and if the distributions $\xi _i$, $\nu _i$ possess continuous densites, then the approach of Sect. 5.3 can be used to investigate local monotonicity of L. Note that it is natural to consider non-uniform (e.g., exponential) distributions $\xi _i$, $\nu _i$ here, so the functions $h_i$, $g_i$ under consideration are typically nonlinear, although they are often piecewise $C^1$. Finally, Example 4 can be modified by using, say, $h_i(x):=h_i(x-11)\wedge 100$, and adding any $\nu _i$ with $l_{\nu _i}>100$, to demonstrate that the mapping L may fail to be nondecreasing in $(0,\infty )$.

7 Further research directions

The results obtained in this paper may be regarded as introductory in nature and there are several important issues regarding our mapping F that remain to be addressed. First, one would like to relax the assumptions on regularity of $h_i$ necessary for local monotonicity of F. Example 4 shows that “kinks” of $h_i$ may create problems in this regard, so it is not immediately clear that the monotonicity result of Sect. 5.3 may be carried over even to the Lipschitz case. A remedy for this problem may be creating a “differential” version of the algorithm from Sect. 3.1, determining the derivatives of $f^{(p)}$, rather than their values, for Lipschitz $h_i$, in a way similar to our analysis for the linear case. This, however, in the absence of $C^1$ regularity of $h_i$, yields an ODE system with discontinuous right-hand side, so even establishing existence of solutions to such a system may be challenging.

Another direction that appears to be important for applications is to skip the assumption of strict monotonicity of $h_i$. As Example 3 indicates, this results in jumps of the corresponding process F. However, from the point of view of the queueing application described in Sect. 2.3, with the functions $h_i$ given by (9), this is not necessarily a problem, because some $F_i$ may “jump over the flat spots”, containing no mass of the corresponding initial distributions ${\overline{Z}}_i(0,\cdot )$, without causing discontinuity of the resulting locally edge minimal fluid model. Similarly, it may be useful to investigate functions $h_i$ with upward jumps, corrresponding to distributions with atoms. This would open an avenue to using techniques similar to those developed in our forthcoming paper, but for pre-limit stochastic networks, rather than for the corresponding fluid limits.

Example 4 shows that there is no hope for global monotonicity of F in the general case. However, it is plausible that for some simple network topologies (e.g., linear or tree networks), the mapping F is monotone on $[0,\infty )$. This would greatly simplify the analysis of the corresponding fluid limits, and aid the investigation of the pre-limit stochastic networks.

Finally, it may be interesting to replace the relation “$\eqslantless$” and/or the set $A_t$ in the definition of F(t) by a different partial ordering and/or admissible set, and to investigate properties and possible applications of the resulting mappings. In particular, the functions H, L defined in Sect. 6 and their applications to queueing network modelling should be subject to further research.

Appendix: Inductive proof of Theorem 1

We continue the argument starting in Sect. 4. As we have already explained, we may assume that $t_0>0$ and that (31), (34) hold.

1.1 The base case: $i\in \mathbf{I}^{(1)}(t_0)$

For $j\in \mathbf{J}^{(1)}$, we have $\sum _{i\in G_j} h_i(f^{(1)}(t_n)) =t_n$, so $\sum _{i\in G_j} h_i(f^{(1)}(t_0)) =t_0$. Consequently, $\mathbf{J}^{(1)} \subseteq \mathbf{J}^{(1)}(t_0)$, and thus $\mathbf{I}^{(1)} \subseteq \mathbf{I}^{(1)}(t_0)$. Let $i\in \mathbf{I}^{(1)}$. Then $i\in \mathbf{I}^{(1)}(t_0)$, so, by (20), $F_i(t_n)= f^{(1)}(t_n) \vee x^*_i \rightarrow f^{(1)}(t_0) \vee x^*_i = F_i(t_0)$ as $n\rightarrow \infty$. We have shown that for $i\in \mathbf{I}^{(1)}$, we have (30).

If $\mathbf{I}^{(1)} = \mathbf{I}^{(1)}(t_0)$ (in particular, if $\mathbf{I}^{(1)} =\mathbf{I}$), we have (30) for every $i\in \mathbf{I}^{(1)}(t_0)$. Assume that $\mathbf{I}^{(1)} \ne \mathbf{I}^{(1)}(t_0)$. Then

$$\begin{aligned} \mathbf{J}^{(1)}(t_0){\setminus }{} \mathbf{D}^{(1)}\ne \emptyset , \end{aligned}$$

(82)

because $\bigcup _{j\in \mathbf{D}^{(1)}} G_j = \mathbf{I}^{(1)}$ [see (29)], while $\bigcup _{j\in \mathbf{J}^{(1)}(t_0)} G_j = \mathbf{I}^{(1)}(t_0)$. Let

$$\begin{aligned} p_1=\max \{p=1,\ldots ,k_{max}: \mathbf{D}^{(p)} \cap \mathbf{J}^{(1)}(t_0) \ne \emptyset \}. \end{aligned}$$

(83)

By (82), we have $p_1\ge 2$. For $p=1,\ldots ,p_1$, let

$$\begin{aligned} A_p^{(1)}=\mathbf{D}^{(p)} \cap \mathbf{J}^{(1)}(t_0), \qquad \qquad B_p^{(1)}=\mathbf{I}^{(p)} \cap \mathbf{I}^{(1)}(t_0). \end{aligned}$$

(84)

Clearly,

$$\begin{aligned} \mathbf{J}^{(1)}(t_0)=\bigcup _{p=1}^{p_1} A_p^{(1)} \end{aligned}$$

(85)

and $\bigcup _{p=1}^{p_1} B_p^{(1)}\subseteq \mathbf{I}^{(1)}(t_0)$. We will check that

$$\begin{aligned} \mathbf{I}^{(1)}(t_0)=\bigcup _{p=1}^{p_1} B_p^{(1)}. \end{aligned}$$

(86)

Indeed, let $i\in \mathbf{I}^{(1)}(t_0)$. Then $i\in G_j$ for some $j\in \mathbf{J}^{(1)}(t_0)$, so, by (85), $j\in A_p^{(1)} \subseteq \mathbf{D}^{(p)}$ for some $p\in \{1,\ldots ,p_1\}$. Consequently, for some $q\in \{1,\ldots ,p\}$, we have $i\in \mathbf{I}^{(q)}$ and hence $i\in B_q^{(1)}$. Thus, $\mathbf{I}^{(1)}(t_0)\subseteq \bigcup _{p=1}^{p_1} B_p^{(1)}$ and (86) follows. Moreover, the above argument justifies the inclusion

$$\begin{aligned} \mathbf{I}^{(1)}(t_0)\subseteq \bigcup _{p=1}^{p_1} \bigcup _{j\in A_p^{(1)}} G_j = \bigcup _{p=1}^{p_1} \bigcup _{j\in A_p^{(1)}} \bigcup _{q=1}^p (G_j \cap \mathbf{I}^{(q)}), \end{aligned}$$

(87)

where the equality follows from the inclusion $A_p^{(1)} \subseteq \mathbf{D}^{(p)}$.

Let $p\in \{2,\ldots ,p_1\}$ be such that $A_{p}^{(1)}\ne \emptyset$ and let $j\in A_{p}^{(1)}$. Since $j\in \mathbf{J}^{(1)}(t_0)$ and (34) holds, we have

$$\begin{aligned} \sum _{i\in G_j} h_i(f^{(1)}(t_0)) = t_0. \end{aligned}$$

(88)

If $f^{(p)}(t_n)=t_n$ for infinitely many n, then, by the definition of $f^{(p)}$ [compare (17)–(18)] and the inequality $f^{(1)}<f^{(p)}$, for these n we have

$$\begin{aligned} \sum _{i\in G_j\cap \bigcup _{k=1}^{p-1} \mathbf{I}^{(k)}} h_i(f^{(1)}(t_n)) + \sum _{i\in G_j\cap \mathbf{I}^{(p)}} h_i(t_n)\le & {} \nonumber \\ \sum _{k=1}^{p-1} \sum _{i\in G_j\cap \mathbf{I}^{(k)}} h_i(f^{(k)}(t_n)) + \sum _{i\in G_j\cap \mathbf{I}^{(p)}} h_i(t_n)\le & {} t_n. \end{aligned}$$

(89)

Letting $n\rightarrow \infty$ in (89), we get

$$\begin{aligned} \sum _{i\in G_j\cap \bigcup _{k=1}^{p-1} \mathbf{I}^{(k)}} h_i(f^{(1)}(t_0)) + \sum _{i\in G_j\cap \mathbf{I}^{(p)}} h_i(t_0) \le t_0. \end{aligned}$$

(90)

The relations (88) and (90), together with the inequalities $f^{(1)}(t_0)\le t_0$, $t_0>0\ge \max _{i\in \mathbf{I}} x^*_i$, imply that $f^{(1)}(t_0)=t_0$, which contradicts (34). Consequently, since $A_{p_1}^{(1)}\ne \emptyset$ by (83)–(84), in the remainder of our proof we may assume that for $p\le p_1$,

$$\begin{aligned} f^{(p)}(t_n)<t_n, \qquad n\ge 1. \end{aligned}$$

(91)

Since $j\in A_{p}^{(1)} \subseteq \mathbf{D}^{(p)} = \mathbf{J}^{(p)} \cup \mathbf{N}^{(p)} \subseteq \mathbf{K}^{(p-1)}$, for every n we have

$$\begin{aligned} \sum _{k=1}^{p-1} \sum _{i\in G_j\cap \mathbf{I}^{(k)}} h_i(f^{(k)}(t_n)) + \sum _{i\in G_j\cap \mathbf{I}^{(p)}} h_i(f^{(p-1)}(t_n)) < t_n, \end{aligned}$$

(92)

[compare (16)–(17)], and

$$\begin{aligned} \sum _{k=1}^{p-1} \sum _{i\in G_j\cap \mathbf{I}^{(k)}} h_i(f^{(k)}(t_n)) + \sum _{i\in G_j\cap \mathbf{I}^{(p)}} h_i(f^{(p)}(t_n)) \le t_n, \end{aligned}$$

(93)

with equality for $j\in C_{p}^{(1)} := \mathbf{J}^{(p)} \cap \mathbf{J}^{(1)}(t_0) \subseteq A_{p}^{(1)}$. Note that (92) and the above-mentioned equality in (93) imply that for $n\ge 1$, $j\in C_{p}^{(1)}$,

$$\begin{aligned} f^{(p)}(t_n) > f^*_{j,p}:=\min \{x^*_i: i \in G_j\cap \mathbf{I}^{(p)} \} . \end{aligned}$$

(94)

By (31) and (94),

$$\begin{aligned} f^{(p)}_\infty \ge f^*_{j,p}, \qquad \qquad j\in C_{p}^{(1)}. \end{aligned}$$

(95)

Letting $n\rightarrow \infty$ in (93) for $j\in A_{p}^{(1)}$ and using (31), we get

$$\begin{aligned} \sum _{i\in G_j\cap \mathbf{I}^{(1)}} h_i(f^{(1)}(t_0)) + \sum _{k=2}^{p-1} \sum _{i\in G_j\cap \mathbf{I}^{(k)}} h_i(f^{(k)}_\infty ) + \sum _{i\in G_j\cap \mathbf{I}^{(p)}} h_i(f^{(p)}_\infty ) \le t_0. \end{aligned}$$

(96)

This, together with (88), (32) and monotonicity of $h_i$, yields the equality in (96) for each $j\in A_{p}^{(1)}$ and the equations

$$\begin{aligned} h_i(f^{(k)}_\infty ) = h_i(f^{(1)}(t_0)), \qquad i\in G_j\cap \mathbf{I}^{(k)}, \;\; k=2,..,p, \;\; j\in A_p^{(1)}. \end{aligned}$$

(97)

By (87) and (97) with $p=p_1$, we have

$$\begin{aligned} h_i(f^{(k)}_\infty ) = h_i(f^{(1)}(t_0)), \qquad i\in B_k^{(1)}, \;\; k=2,..,p_1. \end{aligned}$$

(98)

The relations (32), (94)–(95), (97) (with $k=p$) and the properties of the functions $h_i$, in turn, imply that either

$$\begin{aligned} f^{(2)}_\infty = \cdots =f^{(p)}_\infty =f^{(1)}(t_0), \end{aligned}$$

(99)

or

$$\begin{aligned} f^{(1)}(t_0)<f^{(p)}_\infty = f^*_{j,p}, \qquad \qquad j\in C_{p}^{(1)}, \end{aligned}$$

(100)

provided that $C_{p}^{(1)}\ne \emptyset$. In the latter case, $f^*_{j,p}$ does not depend on $j\in C_{p}^{(1)}$ and hence it will be denoted by $f^*_{p}$.

The above argument implies that if $f^{(1)}(t_0)\ge \min _{j\in C_{p}^{(1)}} f^*_{j,p}$ (or if $f^*_{j,p}\ne f^*_{j',p}$ for some $j,j'\in C_{p}^{(1)}$), then (100) cannot hold, and hence (99) holds. Similarly, if $C_{p}^{(1)}\ne \emptyset$ and

$$\begin{aligned} f^{(1)}(t_0)< \min _{j\in C_{p}^{(1)}} f^*_{j,p}=f^*_{p}, \end{aligned}$$

(101)

then, by (95) and (100),

$$\begin{aligned} f^{(p)}_\infty = f^*_{p}. \end{aligned}$$

(102)

Let ${\bar{p}}_1=\max \{p\in \{1,\ldots ,p_1\}: f^{(p)}_\infty =f^{(1)}(t_0)\}.$ We have shown that

$$\begin{aligned} f^{(k)}_\infty =f^{(1)}(t_0), \qquad \qquad k=1,\ldots ,{\bar{p}}_1, \end{aligned}$$

(103)

and that if ${\bar{p}}_1<p_1$, then for every $p>{\bar{p}}_1$ such that $C_p^{(1)}\ne \emptyset$, the relations (101)–(102) hold. It may be the case that ${\bar{p}}_1<p_1$ and for some ${\tilde{p}}\in \{{\bar{p}}_1+1,\ldots ,p_1\}$, we have $C_{{\tilde{p}}}^{(1)}= \emptyset$. In this case, if $i\in B_{{\tilde{p}}}^{(1)}$, then (32) and (98) imply that

$$\begin{aligned} f^{(1)}(t_0) < f^{({\tilde{p}})}_\infty \le x_i^*, \qquad \qquad i\in B_{{\tilde{p}}}^{(1)}. \end{aligned}$$

(104)

Fix $i\in \mathbf{I}^{(1)}(t_0)$. If $i\in B_{p}^{(1)}$ for some $p\le {\bar{p}}_1$, then, by (20) and (103),

$$\begin{aligned} F_i(t_n) = f^{(p)}(t_n) \vee x^*_i \rightarrow f^{(1)}(t_0) \vee x^*_i = F_i(t_0), \qquad n\rightarrow \infty , \end{aligned}$$

so (30) holds. If $i\in B_{p}^{(1)}$ for some $p> {\bar{p}}_1$, then there exists $k\in \{p,\ldots ,p_1\}$ such that $i\in G_j\cap \mathbf{I}^{(p)}$ for some $j\in A_k^{(1)}$ [see (87)]. If $C_p^{(1)}\ne \emptyset$, then, by (102), $f^{(p)}_\infty =f^*_p$ and, by the same argument as in (104),

$$\begin{aligned} f^{(1)}(t_0) \le f^*_p \le x_i^*, \qquad \qquad i\in B_{p}^{(1)}. \end{aligned}$$

(105)

Thus, since $i\in \mathbf{I}^{(1)}(t_0)$, by (1), (20), (102) and (105), as $n\rightarrow \infty$,

$$\begin{aligned} F_i(t_n) = f^{(p)}(t_n) \vee x^*_i \rightarrow f^*_p \vee x^*_i = x^*_i = f^{(1)}(t_0) \vee x^*_i = F_i(t_0), \end{aligned}$$

(106)

and again (30) holds. Finally, if $C_p^{(1)}= \emptyset$, then reasoning as in (106), but using (104) instead of (105), we get $\lim _{n\rightarrow \infty } F_i (t_n)=F_i(t_0)$. Since, by (86), every $i\in \mathbf{I}^{(1)}(t_0)$ belongs to some $B_p^{(1)}$, $p\le p_1$, the above argument shows that (30) is true for all $i\in \mathbf{I}^{(1)}(t_0)$.

If $\mathbf{D}^{(1)}(t_0)=\mathbf{J}$, then $\mathbf{I}^{(1)}(t_0)=\mathbf{I}$ and (30) holds for each $i\in \mathbf{I}$. In what follows, we assume that $\mathbf{K}^{(1)}(t_0)\ne \emptyset$. For future reference note that

$$\begin{aligned} \bigcup _{p=1}^{{\bar{p}}_1} \mathbf{J}^{(p)} \subseteq \mathbf{J}^{(1)}(t_0). \end{aligned}$$

(107)

Indeed, let $j\in \mathbf{J}^{(p)}$ for some $p\le {\bar{p}}_1$. By (91),

$$\begin{aligned} \sum _{i\in G_j} h_i(F_i(t_n))=\sum _{k=1}^{p} \sum _{i\in G_j\cap \mathbf{I}^{(k)}} h_i(f^{(k)}(t_n)) = t_n, \end{aligned}$$

which, together with (103), implies that

$$\begin{aligned} \sum _{i\in G_j} h_i(f^{(1)}(t_0))= \sum _{k=1}^{p} \sum _{i\in G_j\cap \mathbf{I}^{(k)}} h_i(f^{(1)}(t_0)) = t_0, \end{aligned}$$

and hence $j\in \mathbf{J}^{(1)}(t_0)$. We also have $\bigcup _{p=1}^{{\bar{p}}_1} \mathbf{D}^{(p)} \subseteq \mathbf{D}^{(1)}(t_0).$ Indeed, (107) implies $\bigcup _{p=1}^{{\bar{p}}_1} \mathbf{I}^{(p)} = \bigcup _{p=1}^{{\bar{p}}_1} \bigcup _{j\in \mathbf{J}^{(p)}} G_j \subseteq \bigcup _{j\in \mathbf{J}^{(1)}(t_0)} G_j = \mathbf{I}^{(1)}(t_0).$ Thus, for $j\in \mathbf{D}^{(p)}$, $p\le {\bar{p}}_1$, we have $G_j \subseteq \bigcup _{k=1}^{p} \mathbf{I}^{(k)} \subseteq \mathbf{I}^{(1)}(t_0)$, and hence $j\in \mathbf{D}^{(1)}(t_0)$.

1.2 Inductive assumption

Fix $m\in \{1,\ldots ,k_{max}(t_0)-1\}$. For $l=1,\ldots ,m$, let $b_l$, $p_l$ be given by (35)–(36). By definition, $b_1=1$ and $b_l\le p_l$ for each $l=1,\ldots ,m$. For $l=1,\ldots ,m-1$, let $q_{l}=b_{l+1}-1$, so that by (35) we have

$$\begin{aligned} \bigcup _{p=1}^{q_{l}} \mathbf{D}^{(p)} \subseteq \bigcup _{k=1}^{l} \mathbf{D}^{(k)}(t_0), \qquad \quad \bigcup _{p=1}^{q_{l}} \mathbf{I}^{(p)} \subseteq \bigcup _{k=1}^{l} \mathbf{I}^{(k)}(t_0). \end{aligned}$$

(108)

For $p=b_l,\ldots ,p_l$, $l=1,\ldots ,m$, let

$$\begin{aligned} A_p^{(l)}=\mathbf{D}^{(p)} \cap \mathbf{J}^{(l)}(t_0), \quad B_p^{(l)}=\mathbf{I}^{(p)} \cap \mathbf{I}^{(l)}(t_0), \quad C_p^{(l)}=\mathbf{J}^{(p)} \cap \mathbf{J}^{(l)}(t_0). \;\; \end{aligned}$$

(109)

The definitions (35)–(36) imply that

$$\begin{aligned} \mathbf{J}^{(l)}(t_0)=\bigcup _{p=b_l}^{p_l} A_p^{(l)}. \end{aligned}$$

(110)

[see also (108)]. Using (108) and (110), one may easily check (37).

Suppose that for $l=1,\ldots ,m$, the following assertions hold.

There exist indices ${\bar{p}}_l\in \{b_l,\ldots ,p_l \}$ such that (38) holds and

$$\begin{aligned} \bigcup _{p=b_l}^{{\bar{p}}_l} \mathbf{D}^{(p)} \subseteq \bigcup _{p=1}^{l}{} \mathbf{D}^{(p)}(t_0). \quad \qquad \qquad \end{aligned}$$

(111)

Note that (35) and (111) imply

$$\begin{aligned} 1=b_1\le {\bar{p}}_1<b_2 \le {\bar{p}}_2<\cdots <b_m \le {\bar{p}}_m. \end{aligned}$$

(112)

If ${\bar{p}}_l<p_l$, then for every $p\in \{{\bar{p}}_l+1,\ldots ,p_l\}$ such that $C_p^{(l)}\ne \emptyset$, we have

$$\begin{aligned} f^{(l)}(t_0) < f^{(p)}_\infty =f^*_p, \end{aligned}$$

(113)

where $f^*_p$ is the common value of $f^*_{j,p}$ [defined in (94)] for $j\in C_p^{(l)}$ and, moreover, $f^*_p\le x^*_i$ for $i\in B_{p}^{(l)}$. If $C_{{\tilde{p}}}^{(l)}=\emptyset$ for some ${\tilde{p}}\in \{ {\bar{p}}_l+1,\ldots , p_l\}$, then

$$\begin{aligned} f^{(l)}(t_0) < f^{({\tilde{p}})}_\infty \le x^*_i, \qquad i\in B_{{\tilde{p}}}^{(l)}. \end{aligned}$$

(114)

For $j\in A_p^{(l)}$, $p=b_l,\ldots ,p_l$ and $r=1,..,l$,

$$\begin{aligned} h_i(f^{(k)}_\infty )= h_i(f^{(r)}(t_0)), \qquad i\in G_j \cap B^{(r)}_k, \;\;\; k=b_r,\ldots ,p_r\wedge p. \end{aligned}$$

(115)

For $r=1,\ldots ,m$ and $k=b_r,\ldots ,p_r$, $B^{(r)}_k \subseteq \mathbf{I}^{(r)}(t_0) \subseteq \bigcup _{j \in \mathbf{J}^{(r)}(t_0)} G_j = \bigcup _{p=b_r}^{p_r} \bigcup _{j \in A^{(r)}_p} G_j,$ where the equality follows from (110). Hence, (115) implies

$$\begin{aligned} h_i(f^{(k)}_\infty )= h_i(f^{(r)}(t_0)), \qquad i\in B^{(r)}_k, \;\; k=b_r,\ldots ,p_r, \;\; r=1,\ldots ,m. \end{aligned}$$

(116)

Because $f^{(1)}(t_0)<\cdots <f^{(l)}(t_0)\le f^{(k)}_\infty$ for $k=b_l,\ldots ,p_l$, (115) implies also that for $p=b_l,\ldots ,p_l$,

$$\begin{aligned} h_i(f^{(k)}_\infty )= h_i(f^{(l)}(t_0)), \qquad i\in G_j \cap \mathbf{I}^{(k)}, \;\; k=b_l,\ldots ,p, \;\; j\in A_p^{(l)}. \end{aligned}$$

(117)

Finally, we assume that (30) holds for all $i\in \bigcup _{k=1}^{m} \mathbf{I}^{(k)}(t_0)$.

Note that all the above assumptions have already been verified in the case of $m=1$.

1.3 Inductive step

Define $b_{m+1}$ by (35) with $l=m+1$ and let $q_m=b_{m+1}-1$. By definition, we have (108) for $l=m$, so $\mathbf{K}^{(m)}(t_0) \subseteq \mathbf{K}^{(q_m)}$. The inclusion (111) implies that

$$\begin{aligned} b_{m+1}> {\bar{p}}_m. \end{aligned}$$

(118)

Also, for $j\in \mathbf{K}^{(q_m)}$ (and hence for $j\in \mathbf{K}^{(m)}(t_0)$), we have

$$\begin{aligned} \sum _{p=1}^{q_m}\sum _{i\in G_j \cap \mathbf{I}^{(p)}} h_i(F_i (t_n)) + \sum _{i\in G_j{\setminus }\bigcup _{p=1}^{q_m}{} \mathbf{I}^{(p)}} h_i(f^{(b_{m+1})}(t_n))= & {} \nonumber \\ \sum _{p=1}^{q_m}\sum _{i\in G_j \cap \mathbf{I}^{(p)}} h_i(f^{(p)} (t_n)) + \sum _{i\in G_j{\setminus }\bigcup _{p=1}^{q_m}{} \mathbf{I}^{(p)}} h_i(f^{(b_{m+1})}(t_n))\le & {} t_n. \qquad \end{aligned}$$

(119)

If

$$\begin{aligned} f^{(b_{m+1})}(t_n)=t_n, \end{aligned}$$

(120)

for some n, then $k_{max}=b_{m+1}$, $\mathbf{J}^{(b_{m+1})} = \mathbf{K}^{(q_{m})}$, $\mathbf{N}^{(b_{m+1})} = \emptyset$ and $F_i(t_n)=t_n$ for all $i\in \mathbf{I}^{(b_{m+1})} = \mathbf{I}{\setminus }\bigcup _{k=1}^{q_m} \mathbf{I}^{(k)}$. If (120) holds for infinitely many n, then letting $n\rightarrow \infty$ in (119) along this subsequence, by (108) for $l=m$, monotonicity of $h_i$, the inequality $F_i(t_0)\le t_0$ for all $i\in \mathbf{I}$, and the inductive assumption (30) for $i\in \bigcup _{k=1}^{m} \mathbf{I}^{(k)}(t_0)$, we get

$$\begin{aligned} \sum _{i\in G_j \cap \bigcup _{p=1}^{m} \mathbf{I}^{(p)}(t_0)} h_i(F_i (t_0)) + \sum _{i\in G_j{\setminus }\bigcup _{p=1}^{m}\mathbf{I}^{(p)}(t_0)} h_i(t_0)\le & {} \nonumber \\ \sum _{p=1}^{q_m}\sum _{i\in G_j \cap \mathbf{I}^{(p)}} h_i(F_i (t_0)) + \sum _{i\in G_j{\setminus }\bigcup _{p=1}^{q_m}{} \mathbf{I}^{(p)}} h_i(t_0)\le & {} t_0 \end{aligned}$$

(121)

for all $j\in \mathbf{K}^{(m)}(t_0)$. This, in turn, implies that $F_i(t_0)=t_0$ for all $i\in \mathbf{I}^{(m+1)}(t_0)= \mathbf{I}{\setminus }\bigcup _{p=1}^{m}{} \mathbf{I}^{(p)}(t_0) \subseteq \mathbf{I}{\setminus }\bigcup _{k=1}^{q_m} \mathbf{I}^{(k)}$, where the inclusion follows from the second inclusion in (108) for $l=m$. Hence, for all $i\in \mathbf{I}^{(m+1)}(t_0)$ (and thus for all $i\in \mathbf{I}$), we have (30) along a subsequence $\{t_n\}$ satisfying (120). Consequently, in the remainder of the proof we may assume that $f^{(b_{m+1})}(t_n)<t_n$ for each $n\ge 1,$ and thus equality holds in (119) for $j\in \mathbf{J}^{(b_{m+1})}$.

We claim that

$$\begin{aligned} f^{(b_{m+1})}_\infty =f^{(m+1)}(t_0), \end{aligned}$$

(122)

$$\begin{aligned} \mathbf{J}^{(b_{m+1})}{\setminus }\bigcup _{p=1}^{m}{} \mathbf{J}^{(p)}(t_0) \subseteq \mathbf{J}^{(m+1)}(t_0). \end{aligned}$$

(123)

Letting $n\rightarrow \infty$ in (119), we get

$$\begin{aligned} \sum _{p=1}^{q_m}\sum _{i\in G_j \cap \mathbf{I}^{(p)}} h_i(F_i (t_0)) + \sum _{i\in G_j{\setminus }\bigcup _{p=1}^{q_m}{} \mathbf{I}^{(p)}} h_i(f^{(b_{m+1})}_\infty )\le & {} t_0 \end{aligned}$$

(124)

for $j\in \mathbf{K}^{(q_m)}$, with equality for $j\in \mathbf{J}^{(b_m+1)}$ [compare (121)]. For $k=1,\ldots ,m$, by (38) and (118), we have

$$\begin{aligned} f^{(k)}(t_0)=f^{(b_{k})}_\infty \le f^{(m)}(t_0)=f^{(b_{m})}_\infty \le f^{(b_{m+1})}_\infty , \end{aligned}$$

(125)

so for $i\in \mathbf{I}^{(k)}(t_0)$, $h_i(F_i(t_0))=h_i(f^{(k)}(t_0)) \le h_i(f^{(b_{m+1})}_\infty )$. This, together with (108) for $l=m$ and (124) implies

$$\begin{aligned} \sum _{i\in G_j \cap \bigcup _{p=1}^{m} \mathbf{I}^{(p)}(t_0)} h_i(F_i (t_0)) + \sum _{i\in G_j{\setminus }\bigcup _{p=1}^{m}\mathbf{I}^{(p)}(t_0)} h_i(f^{(b_{m+1})}_\infty ) \le t_0 \end{aligned}$$

(126)

for $j\in \mathbf{K}^{(q_m)}$ (hence for $j\in \mathbf{K}^{(m)}(t_0)$), and thus

$$\begin{aligned} f^{(b_{m+1})}_\infty \le f^{(m+1)}(t_0). \end{aligned}$$

(127)

In order to prove the opposite inequality, we will first check that

$$\begin{aligned} \mathbf{J}^{(b_{m+1})}{\setminus }\bigcup _{p=1}^{m}{} \mathbf{J}^{(p)}(t_0) \ne \emptyset . \end{aligned}$$

(128)

Suppose, to the converse, that

$$\begin{aligned} \mathbf{J}^{(b_{m+1})}\subseteq \bigcup _{p=1}^{m}{} \mathbf{J}^{(p)}(t_0) . \end{aligned}$$

(129)

Then $\mathbf{I}^{(b_{m+1})} \subseteq \bigcup _{j\in \mathbf{J}^{(b_{m+1})}} G_j \subseteq \bigcup _{p=1}^{m} \bigcup _{j\in \mathbf{J}^{(p)}(t_0) } G_j = \bigcup _{p=1}^{m}{} \mathbf{I}^{(p)}(t_0) ,$ and thus, by the second inclusion in (108) for $l=m$, $\bigcup _{p=1}^{b_{m+1}}{} \mathbf{I}^{(p)} \subseteq \bigcup _{p=1}^{m}{} \mathbf{I}^{(p)}(t_0)$. Consequently, for $j\in \mathbf{N}^{(b_{m+1})}$, $G_j \subseteq \bigcup _{p=1}^{m}\mathbf{I}^{(p)}(t_0)$, and hence $\mathbf{N}^{(b_{m+1})} \subseteq \bigcup _{p=1}^{m}{} \mathbf{D}^{(p)}(t_0)$. This, together with (129), implies that $\mathbf{D}^{(b_{m+1})} \subseteq \bigcup _{p=1}^{m}{} \mathbf{D}^{(p)}(t_0)$, which contradicts the definition of $b_{m+1}$. We have proved (128).

Fix $j\in \mathbf{J}^{(b_{m+1})}{\setminus }\bigcup _{p=1}^{m}\mathbf{J}^{(p)}(t_0)$. Then equality holds in (124). We will check that equality holds in (126) as well. Suppose that $i\in G_j \cap \bigcup _{p=1}^{m} \mathbf{I}^{(p)}(t_0){\setminus }\bigcup _{p=1}^{q_m}{} \mathbf{I}^{(p)}$. Then $i\in \mathbf{I}^{(k)}(t_0) \cap \mathbf{I}^{(r)}$ for some $k\le m$ and $r\ge b_{m+1}$. Letting $n\rightarrow \infty$ in the equality $h_i(F_i(t_n))=h_i(f^{(r)}(t_n))$, and using the inductive assumption (30) for $i\in \bigcup _{p=1}^{m} \mathbf{I}^{(p)}(t_0)$, we get $h_i(f^{(k)}(t_0) )= h_i(F_i(t_0))= h_i(f^{(r)}_\infty )$, while $f^{(k)}(t_0)\le f^{(m)}(t_0) \le f^{(b_{m+1})}_\infty \le f^{(r)}_\infty$ by (125). Hence $h_i(F_i(t_0))=h_i(f^{(b_{m+1})}_\infty )$, so (108) for $l=m$ and the equality in (124) imply that equality holds in (126) as well. Arguing as in (94), we get $f^{(m+1)}(t_0)>\min \{ x^*_i:i\in G_j{\setminus }\bigcup _{p=1}^{m}{} \mathbf{I}^{(p)}(t_0) \},$ so (127) and the equality in (126) imply that $f^{(b_{m+1})}_\infty = f^{(m+1)}(t_0)$. We have proved (122). Replacing $f^{(b_{m+1})}_\infty$ by $f^{(m+1)}(t_0)$ in the equality in (126) we get $j\in \mathbf{J}^{(m+1)}(t_0)$, so (123) holds as well.

Let $i\in \mathbf{I}^{(b_{m+1})}{\setminus }\bigcup _{p=1}^{m}\mathbf{I}^{(p)}(t_0)$. We will show that (30) holds. Since $i\in \mathbf{I}^{(b_{m+1})}$, we have $i\in G_j$ for some $j\in \mathbf{J}^{(b_{m+1})}$. If $j\in \bigcup _{p=1}^{m}{} \mathbf{D}^{(p)}(t_0)$, then $i\in \bigcup _{p=1}^{m}{} \mathbf{I}^{(p)}(t_0)$, contrary to the choice of i, so $j\in \mathbf{J}^{(b_{m+1})}{\setminus }\bigcup _{p=1}^{m}\mathbf{D}^{(p)}(t_0) \subseteq \mathbf{J}^{(b_{m+1})}{\setminus }\bigcup _{p=1}^{m}{} \mathbf{J}^{(p)}(t_0)$ and hence, by (123), $j\in \mathbf{J}^{(m+1)}(t_0)$. Then $G_j \subseteq \bigcup _{p=1}^{m+1}{} \mathbf{I}^{(p)}(t_0)$, so $i\in \mathbf{I}^{(m+1)}(t_0)$. Consequently, by (20) and (122),

$$\begin{aligned} F_i(t_n) = f^{(b_{m+1})}(t_n)\vee x^*_i \rightarrow f^{(m+1)}(t_0) \vee x^*_i = F_i(t_0), \end{aligned}$$

(130)

as $n\rightarrow \infty$, so (30) holds.

If $\mathbf{I}^{(m+1)}(t_0) \subseteq \mathbf{I}^{(b_{m+1})}$, we have (30) for each $i\in \mathbf{I}^{(m+1)}(t_0)$. Assume that

$$\begin{aligned} \mathbf{I}^{(m+1)}(t_0){\setminus }{} \mathbf{I}^{(b_{m+1})} \ne \emptyset \end{aligned}$$

(131)

and let $p_{m+1}$ be given by (36) with $l=m+1$. By (108) for $l=m$ and (131), $b_{m+1}<p_{m+1}$. For $p=b_{m+1},\ldots ,p_{m+1}$, define the sets $A^{(m+1)}_p$, $B^{(m+1)}_p$, $C^{(m+1)}_p$ by (109) with $l=m+1$. By the definitions of $b_{m+1}$, $p_{m+1}$ and (108) for $l=m$, we have (110) for $l=m+1$. Clearly, $\bigcup _{p=b_{m+1}}^{p_{m+1}} B_p^{(m+1)}\subseteq \mathbf{I}^{(m+1)}(t_0)$. We will check that (37) holds for $l=m+1$. Indeed, let $i\in \mathbf{I}^{(m+1)}(t_0)$. Then $i\in G_j$ for some $j\in \mathbf{J}^{(m+1)}(t_0)$, so, by (110) with $l=m+1$, $j\in A_p^{(m+1)} \subseteq \mathbf{D}^{(p)}$ for some $p\in \{b_{m+1},\ldots ,p_{m+1}\}$. Consequently, we have $i\in \mathbf{I}^{(q)}$ for some $q\le p$. However, $q>q_m$ by the second inclusion in (108) with $l=m$, and hence $i\in B_q^{(m+1)}$ for some $q\in \{b_{m+1},\ldots ,p_{m+1}\}$. Thus, $\mathbf{I}^{(m+1)}(t_0)\subseteq \bigcup _{p=b_{m+1}}^{p_{m+1}} B_{p}^{(m+1)}$ and (37) with $l=m+1$ follows.

We will first consider the case in which $f^{(m+1)}(t_0)=t_0$. Then $\mathbf{I}^{(m+1)}(t_0) = \mathbf{I}{\setminus }\bigcup _{p=1}^{m}\mathbf{I}^{(p)}(t_0)$ and $F_i(t_0)=t_0$ for each $i\in \mathbf{I}^{(m+1)}(t_0)$. Moreover, by (122),

$$\begin{aligned} f^{(b_{m+1})}_\infty =t_0. \end{aligned}$$

(132)

Let $i\in \mathbf{I}^{(m+1)}(t_0)$. Then $i\in \mathbf{I}^{(p)}$ for some $p\ge b_{m+1}$ by the second inclusion in (108) with $l=m$, and thus $f^{(b_{m+1})}(t_n) \vee x^*_i \; \le \; F_i(t_n) \; \le \; t_n,$ which, by (132), implies that $F_i(t_n) \rightarrow t_0=F_i(t_0)$, so (30) holds for all i.

It remains to consider the case of

$$\begin{aligned} f^{(m+1)}(t_0)<t_0. \end{aligned}$$

(133)

Let $p\in \{b_{m+1},\ldots ,p_{m+1}\}$ be such that $A_{p}^{(m+1)}\ne \emptyset$ and let $j\in A_{p}^{(m+1)}$. Since $j\in \mathbf{J}^{(m+1)}(t_0)$ by (109) with $l=m+1$, the relation (133) implies

$$\begin{aligned} \sum _{k=1}^{m+1} \sum _{i\in G_j \cap \mathbf{I}^{(k)}(t_0)} h_i(f^{(k)}(t_0)) = t_0. \end{aligned}$$

(134)

Suppose that $f^{(p)}(t_n)=t_n$ for infinitely many n, and thus $p=k_{max}$. Then $\mathbf{N}^{(p)}=\emptyset$, so $\mathbf{J}^{(p)}=\mathbf{D}^{(p)}$ and $A^{(l)}_p=C^{(l)}_p$ for each $l\le m+1$. If $p_l=k_{max}$ for some $l\le m$, then $p_l=p\ge b_{m+1}$, and $C^{(l)}_{p_l}=A^{(l)}_{p_l}\ne \emptyset$ by (36), (109). Hence, by (112), (118), (113), as $n\rightarrow \infty$, we have $0<t_0\leftarrow t_n = f^{(p_l)}(t_n) \rightarrow f^*_{p_l}\le 0$, contradiction. Thus, $p>\max \{p_l, l\le m\}$, so by (109) and (37), $\mathbf{I}^{(p)} \cap \bigcup _{l=1}^{m} \mathbf{I}^{(l)}(t_0)= \emptyset$. Consequently, for $j\in A^{(m+1)}_p \subseteq \mathbf{J}^{(m+1)}(t_0)$, $G_j \cap \mathbf{I}^{(p)}\subseteq \mathbf{I}^{(m+1)}(t_0)$ and the definition of $f^{(p)}$ [compare (18)], together with (37) for $l=1,\ldots ,m+1$, imply

$$\begin{aligned} t_n\ge & {} \sum _{k=1}^{p-1} \sum _{i\in G_j\cap \mathbf{I}^{(k)}} h_i(f^{(k)}(t_n)) + \sum _{i\in G_j\cap \mathbf{I}^{(p)}} h_i(t_n) \\\ge & {} \sum _{l=1}^m \sum _{i\in G_j\cap \mathbf{I}^{(l)}(t_0)} h_i(f^{(b_l)}(t_n)) + \sum _{k=b_{m+1}}^{p-1} \sum _{i\in G_j\cap \mathbf{I}^{(k)}\cap \mathbf{I}^{(m+1)}(t_0)} h_i(f^{(b_{m+1})}(t_n)) \\&+ \sum _{i\in G_j\cap \mathbf{I}^{(p)}} h_i(t_n) . \end{aligned}$$

Letting $n\rightarrow \infty$ and using (38), (122), we get

$$\begin{aligned}&\sum _{l=1}^m \sum _{i\in G_j\cap \mathbf{I}^{(l)}(t_0)} h_i(f^{(l)}(t_0)) + \sum _{k=b_{m+1}}^{p-1} \sum _{i\in G_j\cap \mathbf{I}^{(k)}\cap \mathbf{I}^{(m+1)}(t_0)} h_i(f^{(m+1)}(t_0)) \\&\quad + \sum _{i\in G_j\cap \mathbf{I}^{(p)}} h_i(t_0) \le t_0, \end{aligned}$$

which, together with (134), implies that $f^{(m+1)}(t_0)=t_0$, contrary to (133). Consequently, since $A_{p_{m+1}}^{(m+1)}\ne \emptyset$ by (36) and (109) with $l=m+1$, in the remainder of the proof we may assume that (91) holds for $p=b_{m+1},\ldots ,p_{m+1}$. This, in turn, implies (92), (94) and the equality in (93) for $j\in C_p^{(m+1)}$, $p\in \{b_{m+1},\ldots ,p_{m+1}\}$, by the same argument as in the case of $j\in C_p^{(1)}$, $p\le p_1$.

The relation (94) implies

$$\begin{aligned} f^{(p)}_\infty \ge f^*_{j,p}, \quad \qquad j\in C_p^{(m+1)}, \quad p=b_{m+1},\ldots ,p_{m+1}. \end{aligned}$$

(135)

For $j\in A_p^{(m+1)}$, $p=b_{m+1},\ldots ,p_{m+1}$, letting $n\rightarrow \infty$ in (93), we get (96). This, in turn, together with (134), (32), (35)–(36), (38), (122) and monotonicity of $h_i$, yields (115) for $j\in A_p^{(m+1)}$, $p=b_{m+1},\ldots ,p_{m+1}$ and $r=1,..,m+1$. Consequently, (117) holds with $l=m+1$ and $p=b_{m+1},\ldots ,p_{m+1}$.

Using (135) and (117) (with l, p as above) instead of (95) and (97), respectively, in analogy to the development of (99)–(104), (105), we can derive the following facts. Let

$$\begin{aligned} {\bar{p}}_{m+1}=\max \{ p\in \{b_{m+1},\ldots ,p_{m+1}\}: f^{(p)}_\infty = f^{(m+1)}(t_0) \}. \end{aligned}$$

Then (38) holds with $l=m+1$. If ${\bar{p}}_{m+1}<p_{m+1}$, then for every $p\in \{{\bar{p}}_{m+1}+1,\ldots ,p_{m+1}\}$ such that $C_p^{(m+1)}\ne \emptyset$, we have (113) with $l=m+1$, where $f^*_p$ is the common value of $f^*_{j,p}$ for $j\in C_p^{(m+1)}$. Moreover, for such p,

$$\begin{aligned} f^*_p\le x^*_i, \qquad i\in B_{p}^{(m+1)}. \end{aligned}$$

(136)

If $C_{{\tilde{p}}}^{(m+1)}=\emptyset$ for some ${\tilde{p}}\in \{ {\bar{p}}_{m+1}+1,\ldots , p_{m+1}\}$, then (114) holds with $l=m+1$.

Let $i\in \mathbf{I}^{(m+1)}(t_0)$. We will check that (30) holds. By (37) with $l=m+1$, $i\in B^{(m+1)}_p$ for some $p\in \{b_{m+1},\ldots ,p_{m+1}\}$. If $p\le {\bar{p}}_{m+1}$, then (30) follows from (38) with $l=m+1$ by an argument similar to (130). If ${\bar{p}}_{m+1}<p\le p_{m+1}$, then the argument is analogous to the proof of the corresponding case ${\bar{p}}_1<p\le p_1$ for $i\in \mathbf{I}^{(1)}(t_0)$ (see (106) and the paragraph surrounding it); we just use (113) with $l=m+1$, (136), (114) with $l=m+1$, instead of (102), (105), (104), respectively.

If $m+1=k_{max}(t_0)$, then (30) holds for all $i\in \mathbf{I}$ and we are done. Assume that $\mathbf{K}^{(m+1)}(t_0)\ne \emptyset$. For the sake of the next inductive step, we will show (111) for $l=m+1$. Let $j\in \mathbf{J}^{(p)}{\setminus }\bigcup _{k=1}^m \mathbf{J}^{(k)}(t_0)$ for some $b_{m+1}\le p\le {\bar{p}}_{m+1}$. Since (91) holds for this p, we have $t_n= \sum _{k=1}^{p} \sum _{i\in G_j\cap \mathbf{I}^{(k)}} h_i(f^{(k)}(t_n)).$ Letting $n\rightarrow \infty$ and using (109), (37), (35) with $l=m+1$, (116) and (38) with $l=m+1$, we get

$$\begin{aligned} t_0= & {} \sum _{k=1}^{p} \sum _{i\in G_j\cap \mathbf{I}^{(k)}} h_i(f^{(k)}_\infty )\\= & {} \sum _{l=1}^m \sum _{k=b_l}^{p\wedge p_l} \sum _{i\in G_j\cap \mathbf{I}^{(k)} \cap \mathbf{I}^{(l)}(t_0)} h_i(f^{(k)}_\infty ) + \sum _{k=b_{m+1}}^{p} \sum _{i\in G_j\cap \mathbf{I}^{(k)}{\setminus } \bigcup _{l=1}^m \mathbf{I}^{(l)}(t_0)} h_i(f^{(k)}_\infty ) \\= & {} \sum _{l=1}^m \sum _{k=b_l}^{p\wedge p_l} \sum _{i\in G_j\cap B_k^{(l)}} h_i(f^{(l)}(t_0)) + \sum _{k=b_{m+1}}^{p} \sum _{i\in G_j\cap \mathbf{I}^{(k)}{\setminus }\bigcup _{l=1}^m \mathbf{I}^{(l)}(t_0)} h_i(f^{(m+1)}(t_0)) \\= & {} \sum _{l=1}^{m} \sum _{i\in G_j\cap \mathbf{I}^{(l)}(t_0)} h_i(f^{(l)}(t_0)) + \sum _{i\in G_j{\setminus }\bigcup _{l=1}^m \mathbf{I}^{(l)}(t_0)} h_i(f^{(m+1)}(t_0)), \end{aligned}$$

so $j\in \mathbf{J}^{(m+1)}(t_0)$. We have shown that $\bigcup _{p=b_{m+1}}^{{\bar{p}}_{m+1}} \mathbf{J}^{(p)} \subseteq \bigcup _{p=1}^{m+1}{} \mathbf{J}^{(p)}(t_0)$, so

$$\begin{aligned} \bigcup _{p=b_{m+1}}^{{\bar{p}}_{m+1}} \mathbf{I}^{(p)} \subseteq \bigcup _{p=b_{m+1}}^{{\bar{p}}_{m+1}} \bigcup _{j\in \mathbf{J}^{(p)}} G_j \subseteq \bigcup _{p=1}^{m+1} \bigcup _{j\in \mathbf{J}^{(p)}(t_0)} G_j = \bigcup _{p=1}^{m+1}{} \mathbf{I}^{(p)}(t_0). \end{aligned}$$

(137)

Let $j\in \mathbf{D}^{(p)}$ for some $b_{m+1}\le p\le {\bar{p}}_{m+1}$. By (108) for $l=m$ and (137),

$$\begin{aligned}&G_j = \Big (G_j \cap \bigcup _{p=1}^{q_{m}} \mathbf{I}^{(p)}\Big ) \cup \Big (G_j \cap \bigcup _{p=b_{m+1}}^{p} \mathbf{I}^{(p)}\Big ) \subseteq \bigcup _{p=1}^{m}{} \mathbf{I}^{(p)}(t_0) \\&\quad \; \cup \bigcup _{p=1}^{m+1}\mathbf{I}^{(p)}(t_0) = \bigcup _{p=1}^{m+1}{} \mathbf{I}^{(p)}(t_0). \end{aligned}$$

Thus, $j\in \bigcup _{p=1}^{m+1}{} \mathbf{D}^{(p)}(t_0)$ and (111) with $l=m+1$ follows.

In summary, we have shown that either (30) holds for all $i\in \mathbf{I}$, or all the assertions of the inductive assumption, including (30) for $i\in \mathbf{I}^{(l)}$, are true for $l=1,\ldots ,m+1$. This ends the inductive proof of (30) for each $i\in \mathbf{I}$.