Abstract
In problems of portfolio selection the reward-risk ratio criterion is optimized to search for a risky portfolio offering the maximum increase of the mean return, compared to the risk-free investment opportunities. In the classical model, following Markowitz, the risk is measured by the variance thus representing the Sharpe ratio optimization and leading to the quadratic optimization problems. Several polyhedral risk measures, being linear programming (LP) computable in the case of discrete random variables represented by their realizations under specified scenarios, have been introduced and applied in portfolio optimization. The reward-risk ratio optimization with polyhedral risk measures can be transformed into LP formulations. The LP models typically contain the number of constraints proportional to the number of scenarios while the number of variables (matrix columns) proportional to the total of the number of scenarios and the number of instruments. Real-life financial decisions are usually based on more advanced simulation models employed for scenario generation where one may get several thousands scenarios. This may lead to the LP models with huge number of variables and constraints thus decreasing their computational efficiency and making them hardly solvable by general LP tools. We show that the computational efficiency can be then dramatically improved by alternative models based on the inverse ratio minimization and taking advantages of the LP duality. In the introduced models the number of structural constraints (matrix rows) is proportional to the number of instruments thus not affecting seriously the simplex method efficiency by the number of scenarios and therefore guaranteeing easy solvability.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Portfolio selection problems are usually tackled with the mean-risk models that characterize the uncertain returns by two scalar characteristics: the mean, which is the expected return, and the risk—a scalar measure of the variability of returns. In the original Markowitz model (Markowitz 1952) the risk is measured by the standard deviation or variance. Several other risk measures have been later considered thus creating the entire family of mean-risk (Markowitz-type) models. In particular, downside risk measures (Fishburn 1977) are frequently considered instead of symmetric measurement by the standard deviation. While the original Markowitz model forms a quadratic programming problem, many attempts have been made to linearize the portfolio optimization procedure (cf. Mansini et al. 2014, and references therein). The LP solvability is very important for applications to real-life financial decisions where the constructed portfolios have to meet numerous side constraints including the minimum transaction lots, transaction costs and mutual funds characteristics (Mansini et al. 2015). A risk measure can be LP computable in the case of discrete random variables, i.e., in the case of returns defined by their realizations under specified scenarios. This applies to a wide class of risk measures called recently polyhedral (Eichhorn and Römisch 2005), as represented by convex polyhedral functions for discrete random variables. Several such polyhedral risk measures have been applied to portfolio optimization (Mansini et al. 2014). Typical risk measures are deviation type. The simplest polyhedral risk measures are dispersion measures similar to the variance. Konno and Yamazaki (1991) introduced the portfolio selection model with the mean absolute deviation (MAD). Young (1998) presented the Minimax model while earlier Yitzhaki (1982) introduced the mean-risk model using Gini’s mean (absolute) difference (GMD) as the risk measure. The Gini’s mean difference turns out to be a special aggregation technique of the multiple criteria LP model (Ogryczak 2000) based on the pointwise comparison of the absolute Lorenz curves. The latter makes the quantile shortfall risk measures directly related to the dual theory of choice under risk (Quiggin 1982). Recently, the second order quantile risk measures have been introduced in different ways by many authors (Artzner et al. 1999; Rockafellar and Uryasev 2002). The measure, usually called the Conditional Value at Risk (CVaR) or Tail VaR, represents the mean shortfall at a specified confidence level. The CVaR measures maximization is consistent with the second order stochastic dominance (Ogryczak and Ruszczyński 2002a). The LP computable portfolio optimization models are capable to deal with non-symmetric distributions. Some of them, like the downside mean semideviation (half of the MAD) can be combined with the mean itself into optimization criteria (safety or underachievement measures) that remain in harmony with the second order stochastic dominance. Some, like the conditional value at risk (CVaR) (Rockafellar and Uryasev 2002) having a great impact on new developments in portfolio optimization, may be interpreted as such a combined functional while allowing to distinguish the corresponding deviation type risk measure.
Some polyhedral risk measures, like the mean below-target deviation, Minimax or CVaR, represent typical downside risk focus. On the other hand, measures like MAD or GMD are rather symmetric. Nevertheless, all they can be extended to enhance downside risk focus (Michalowski and Ogryczak 2001; Krzemienowski and Ogryczak 2005) while preserving their polyhedrality.
Having given the risk-free rate of return \(r_0\), a risky portfolio \({\mathbf x}\) may be sought that maximizes ratio between the increase of the mean return \(\mu ({\mathbf x})\) relative to \(r_0\) and the corresponding increase of the risk measure \(\varrho ({\mathbf x})\), compared to the risk-free investment opportunities. Namely, a performance measure of the reward-risk ratio is defined \({(\mu ({\mathbf x}) - r_0})/{\varrho ({\mathbf x})}\) to be maximized. The optimal solution of the corresponding problem is usually called the tangency portfolio as it corresponds to the tangency point of the so-called capital market line drawn from the intercept \(r_0\) and passing tangent to the risk/return frontier. For the polyhedral risk measures the reward-risk ratio optimization problem can be converted into an LP form (Mansini et al. 2003). The reward-risk ratio is well defined for the deviation type risk measures. Therefore while dealing with the CVaR or Minimax risk model we must replace this performance measure (coherent risk measure) \(C({\mathbf x})\) with its complementary deviation representation \(\mu ({\mathbf x}) - C({\mathbf x})\) (Chekhlov et al. 2002; Mansini et al. 2003). The reward-risk ratio optimization with polyhedral risk measures can be transformed into LP formulations. Such an LP model, for instance for the MAD type risk measure, contains then T auxiliary variables as well as T corresponding linear inequalities. Actually, the number of structural constraints in the LP model (matrix rows) is proportional to the number of scenarios T, while the number of variables (matrix columns) is proportional to the total of the number of scenarios and the number of instruments \(T + n\). Hence, its dimensionality is proportional to the number of scenarios T. It does not cause any computational difficulties for a few hundreds scenarios as in computational analysis based on historical data. However, real-life financial analysis must be usually based on more advanced simulation models employed for scenario generation (Carino et al. 1998). One may get then several thousands scenarios (Pflug 2001) thus leading to the LP model with huge number of auxiliary variables and constraints and thereby hardly solvable by general LP tools. Similar difficulty for the standard minimum risk portfolio selection have been effectively resolved by taking advantages of the LP duality to reduce the number of structural constraints to the number of instruments (Ogryczak and Śliwiński 2011a, b). For the linearized reward-risk ratio models such an approach does not work. Although, for the CVaR risk measure we have shown (Ogryczak et al. 2015) that while taking advantages of possible inverse formulation of the reward-risk ratio optimization as ratio \({\varrho ({\mathbf x})}/{(\mu ({\mathbf x}) - r_0)}\) to be minimized and the LP dual of the linearized problem one can get the number of constraints limited to the number of instruments.
In this paper we analyze efficient optimization of reward-risk ratio for various polyhedral risk measures by taking advantages of possible inverse formulation of the reward-risk ratio optimization as a risk-reward ratio \({\varrho ({\mathbf x})}/{(\mu ({\mathbf x}) - r_0)}\) to be minimized, we show that (under natural assumptions) this ratio optimization is consistent with the SSD rules, despite that the ratio does not represent a coherent risk measure (Artzner et al. 1999). Further, while transforming this ratio optimization to an LP model, we use the LP duality equivalence to get a model formulation providing much higher computational efficiency. The number of structural constraints in the introduced model is proportional to the number of instruments n while only the number of variables is proportional to the number of scenarios T thus not affecting so seriously the simplex method efficiency. Therefore, the model can effectively be solved with general LP solvers even for very large numbers of scenarios. Indeed, the computation time for the case of fifty thousand scenarios and one hundred instruments is then below a minute.
2 Portfolio optimization and risk measures
The portfolio optimization problem considered in this paper follows the original Markowitz’ formulation and is based on a single period model of investment. At the beginning of a period, an investor allocates the capital among various securities, thus assigning a nonnegative weight (share of the capital) to each security. Let \(J = \{ 1,2,\ldots ,n \} \) denote a set of securities considered for an investment. For each security \(j \in J\), its rate of return is represented by a random variable \(R_j\) with a given mean \(\mu _j = {\mathbb E}\{ R_j \}\). Further, let \({\mathbf x}= (x_j)_{j=1,2,\ldots ,n}\) denote a vector of decision variables \(x_j\) expressing the weights defining a portfolio. The weights must satisfy a set of constraints to represent a portfolio. The simplest way of defining a feasible set Q is by a requirement that the weights must sum to one and they are nonnegative (short sales are not allowed), i.e.
Hereafter, we perform detailed analysis for the set Q given with constraints (1). Nevertheless, the presented results can easily be adapted to a general LP feasible set given as a system of linear equations and inequalities, thus allowing one to include short sales, upper bounds on single shares or portfolio structure restrictions which may be faced by a real-life investor.
Each portfolio \(\mathbf{x}\) defines a corresponding random variable \(R_{{\mathbf x}} = \sum _{j=1}^{n}R_j x_j\) that represents the portfolio rate of return while the expected value can be computed as \(\mu ({\mathbf x}) = \sum _{j=1}^{n}\mu _j x_j\). We consider T scenarios with probabilities \(p_t\) (where \(t=1,\ldots ,T\)). We assume that for each random variable \(R_j\) its realization \(r_{jt}\) under the scenario t is known. Typically, the realizations are derived from historical data treating T historical periods as equally probable scenarios (\(p_t=1/T\)). Although the models we analyze do not take advantages of this simplification. The realizations of the portfolio return \(R_{{\mathbf x}}\) are given as \(y_t = \sum _{j=1}^n r_{jt} x_j\).
The portfolio optimization problem is modeled as a mean-risk bicriteria optimization problem where the mean \(\mu (\mathbf{x})\) is maximized and the risk measure \(\varrho (\mathbf{x})\) is minimized. In the original Markowitz model, the standard deviation \(\sigma (\mathbf{x}) = [ {\mathbb E}\{ ( R_\mathbf{x} - \mu (\mathbf{x}) )^2 \}]^{1/2}\) was used as the risk measure. Actually in most optimization models the variance \(\sigma ^2(\mathbf{x}) = {\mathbb E}\{ ( R_\mathbf{x} - \mu (\mathbf{x}) )^2 \}\) can be equivalently used. The latter simplifies the computations as
where \(\mathbf{C}\) is \(n\times n\) symmetric matrix with elements
i.e. the covariance matrix for random variables \(R_j\). It can be argued that the variability of rate of return above the mean should not be penalized since the investors concern of an underperformance rather than the overperformance of a portfolio. This led Markowitz (1959) to propose downside risk measures such as downside standard deviation and semivariance \(\bar{\sigma }^2({\mathbf x}) = \sum _{t=1}^{T} ( \max \{0, \mu ({\mathbf x})- \sum _{j=1}^{n}r_{jt}x_j\})^2 p_t\) to replace variance as the risk measure. Consequently, one observes growing popularity of downside risk models for portfolio selection Sortino and Forsey (1996). Several other risk measures \(\varrho ({\mathbf x})\) have been later considered thus creating the entire family of mean-risk models (cf., Mansini et al. 2014, 2015). These risk measures, similar to the standard deviation, are not affected by any shift of the outcome scale and are equal to 0 in the case of a risk-free portfolio while taking positive values for any risky portfolio. Several risk measures applied to portfolio optimization belong to a wide class of risk measures called recently polyhedral (Eichhorn and Römisch 2005), as represented by convex polyhedral (piece-wise linear) functions for discrete random variables. Such risk measures can be LP computable in the case of discrete random variables, i.e., in the case of returns defined by their realizations under specified scenarios. The LP solvability of the portfolio optimization problems is very important for applications to real-life financial decisions where the constructed portfolios have to meet numerous side constraints including the minimum transaction lots, transaction costs and mutual funds characteristics (Mansini et al. 2015).
Typical risk measures are deviation type and most of them are not directly consistent with the stochastic dominance order or other axiomatic models of risk-averse preferences (Rothschild and Stiglitz 1970) and coherent risk measurement (Artzner et al. 1999). In stochastic dominance, uncertain returns (modeled as random variables) are compared by pointwise comparison of some performance functions constructed from their distribution functions. The first performance function \(F^{(1)}_{{\mathbf x}}\) is defined as the right-continuous cumulative distribution function: \(F^{(1)}_{{\mathbf x}}(\eta ) = F_{{\mathbf x}}(\eta ) = {\mathbb P}\{ R_{{\mathbf x}} \le \eta \}\) and it defines the First order Stochastic Dominance (FSD). The second function is derived from the first as \( F^{(2)}_{{\mathbf x}}(\eta ) = \int _{-\infty }^{\eta } F_{{\mathbf x}}(\xi ) \ d\xi \) and it defines the Second order Stochastic Dominance (SSD). We say that portfolio \( {{\mathbf x}^\prime }\) dominates \({{\mathbf x}^{{\prime \prime }}}\) under the SSD (\( R_{{\mathbf x}^\prime } \succ _{_{SSD}} R_{{\mathbf x}^{{\prime \prime }}}\)), if \(F^{(2)}_{{\mathbf x}^\prime }(\eta ) \le F^{(2)}_{{\mathbf x}^{{\prime \prime }}}(\eta )\) for all \(\eta \), with at least one strict inequality. A feasible portfolio \({\mathbf x}^0 \in Q\) is called SSD efficient if there is no \({\mathbf x}\in Q\) such that \(R_{{\mathbf x}} \succ _{_{SSD}} R_{{\mathbf x}^0}\). Stochastic dominance relates the notion of risk to a possible failure of achieving some targets. As shown by Ogryczak and Ruszczyński (1999), function \(F^{(2)}_{{\mathbf x}}\), used to define the SSD relation, can also be presented as follows:
and thereby its values are LP computable for returns represented by their realizations \(y_t\).
The simplest shortfall criterion for a specific target value \(\tau \) is the mean below-target deviation
The mean below-target deviation, when minimized, is LP computable for returns represented by their realizations \(y_t\) as:
When the mean \(\mu ({\mathbf x})\) is used instead of the fixed target the value \(F^{(2)}_{{\mathbf x}}(\mu ({\mathbf x}))\) defines the risk measure known as the downside mean semideviation from the mean
The downside mean semideviation is always equal to the upside one and therefore we refer to it hereafter as to the mean semideviation (SMAD). The mean semideviation is a half of the mean absolute deviation (MAD) from the mean (Ogryczak and Ruszczyński 1999) \(\delta ({\mathbf x}) = {\mathbb E}\{ | R_\mathbf{x} - \mu (\mathbf{x}) | \}= 2 \bar{\delta }({\mathbf x}).\) Hence the corresponding portfolio optimization model is equivalent to those for the MAD optimization. However, to avoid misunderstanding, we will use the notion SMAD for the mean semideviation risk measure and the corresponding optimization models. Many authors pointed out that the SMAD model opens up opportunities for more specific modeling of the downside risk (Speranza 1993). Since \(\bar{\delta }({\mathbf x}) = F^{(2)}_{{\mathbf x}}(\mu ({\mathbf x}))\), the mean semideviation (4) is LP computable (when minimized), for a discrete random variable represented by its realizations \(y_t\). Although, due to the use of distribution dependent target value \(\mu ({\mathbf x})\), the mean semideviation cannot be directly considered an SSD consistent risk measure. SSD consistency (Ogryczak and Ruszczyński 1999) and coherency (Mansini et al. 2003) of the SMAD model can be achieved with maximization of complementary risk measure \(\mu _\delta ({\mathbf x}) =\mu ({\mathbf x}) - \bar{\delta }({\mathbf x})= {\mathbb E}\{ \min \{ \mu ({\mathbf x}), R_{{\mathbf x}} \} \}\), which also remains LP computable for a discrete random variable represented by its realizations \(y_t\).
An alternative characterization of the SSD relation can be achieved with the so-called Absolute Lorenz Curves (ALC) (Ogryczak and Ruszczyński 2002a), i.e. the second order quantile functions:
where the quantile function \(F_{{\mathbf x}}^{(-1)}(p) = \inf \ \{ \eta : F_{{\mathbf x}}(\eta ) \ge p \}\) is the left-continuous inverse of the cumulative distribution function \(F_{{\mathbf x}}\). As \(F_{{\mathbf x}}\) and \(F_{{\mathbf x}}^{(-1)}\) represent a pair non-decreasing inverse functions, their integrals \(F_{{\mathbf x}}^{(2)}\) and \(F^{(-2)}_{{\mathbf x}}\) are a pair of convex conjugent functions (Rockafellar 1970), i.e.
Therefore, pointwise comparison of ALCs is equivalent to the SSD relation (Ogryczak and Ruszczyński 2002a) in the sense that \(R_{{\mathbf x}^\prime } \succeq _{_{SSD}} R_{{\mathbf x}^{{\prime \prime }}}\) if and only if \(F^{(-2)}_{{\mathbf x}^\prime }(\beta ) \ge F^{(-2)}_{{\mathbf x}^{\prime \prime }}(\beta )\) for all \(0 < \beta \le 1\). Moreover, following (2) and (6), the ALC values can be computed by optimization:
where for a discrete random variable represented by its realizations \(y_t\) problem (7) becomes an LP.
For any real tolerance level \(0 < \beta \le 1\), the normalized value of the ALC defined as
is the Worst Conditional Expectation or Tail VaR which is now commonly called the Conditional Value-at-Risk (CVaR). This name was introduced by (Rockafellar and Uryasev 2000) who considered (similar to the Expected Shortfall by (Embrechts et al. 1997)) the measure CVaR defined as \({\mathbb E}\,\{ R_{{\mathbf x}} | R_{{\mathbf x}}\le F^{(-1)}_{{\mathbf x}}(\beta ) \}\) for continuous distributions showing that it could then be expressed by a formula analogous to (7) and thus be potentially LP computable. The approach has been further expanded to general distributions in (Rockafellar and Uryasev 2002). For additional discussion of relations between various definitions of the measures we refer to Ogryczak and Ruszczyński (2002b). The CVaR measure is an increasing function of the tolerance level \(\beta \), with \(M_1({\mathbf x})=\mu ({\mathbf x})\). For any \(0< \beta < 1\), the CVaR measure is SSD consistent (Ogryczak and Ruszczyński 2002a) and coherent (Artzner et al. 1999). Opposite to deviation type risk measures, for coherent measures larger values are preferred and therefore the measures are sometimes called safety measures (Mansini et al. 2003). Due to (7), for a discrete random variable represented by its realizations \(y_t\) the CVaR measures are LP computable. It is important to notice that although the quantile risk measures (VaR and CVaR) were introduced in banking as extreme risk measures for very small tolerance levels (like \(\beta =0.05\)), for the portfolio optimization good results have been provided by rather larger tolerance levels (Mansini et al. 2003). For \(\beta \) approaching 0, the CVaR measure tends to the Minimax measure
introduced to portfolio optimization by Young (1998). Note that the maximum (downside) semideviation
and the conditional \(\beta \)-deviation
respectively, represent the corresponding deviation polyhedral risk measures. They may be interpreted as the drawdown measures (Chekhlov et al. 2002). For \(\beta =0.5\) the measure \(\Delta _{0.5}({\mathbf x})\) represents the mean absolute deviation from the median (Mansini et al. 2003).
The commonly used approach to implement the Markowitz-type mean-risk models is based on the use of a specified lower bound \(\mu _0\) on expected return while minimizing the risk criterion. An alternative specific approach to portfolio optimization looks for a risky portfolio offering the maximum increase of the mean return, compared to the risk-free target \(\tau \). Namely, given the risk-free rate of return \(\tau \), a risky portfolio \({\mathbf x}\) that maximizes the ratio \({(\mu ({\mathbf x}) - \tau )}/{\varrho ({\mathbf x})}\) is sought. This leads us to the following ratio optimization problem:
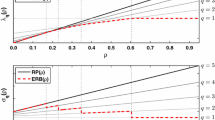
We illustrate ratio optimization (12) in Fig. 1. The approach is well appealing with respect to the preferences modeling and applied to standard portfolio selection or (extended) index tracking problems (with a benchmark as the target). For the classical Markowitz modeling of risk with the standard deviation one gets the Sharpe ratio (Sharpe 1966):
Many approaches have replaced the standard deviation in the Sharpe ratio with an alternative risk measure. First of all, Sortino ratio (Sortino and Price 1994) replaces the standard deviation with the downside standard deviation:
Further, for the reward-risk ratio may be optimized for various polyhedral risk measures. For the latter, the reward-risk ratio optimization problem can be converted into an LP form (Mansini et al. 2003).
When the risk-free return \(r_0\) is used instead of the target \(\tau \) than the ratio optimization (12) corresponds to the classical Tobin’s model (Tobin 1958) of the modern portfolio theory (MPT) where the capital market line (CML) is the line drawn from the risk-free rate at the intercept that passes tangent to the mean-risk efficient frontier. Any point on this line provides the maximum return for each level of risk. The tangency (tangent, super-efficient) portfolio is the portfolio of risky assets on the efficient frontier at the point where the CML is tangent to the efficiency frontier. It is a risky portfolio offering the maximum increase of the mean return while comparing to the risk-free investment opportunities. Namely having given the risk-free rate of return \(r_0\) one seeks a risky portfolio \({\mathbf x}\) that maximizes the ratio \({(\mu ({\mathbf x}) -r_0})/{\varrho ({\mathbf x})}\).
Instead of the reward-risk ratio maximization one may consider an equivalent model of the risk-reward ratio minimization (see Fig. 2):
Actually, this is a classical model for the tangency portfolio as considered by Markowitz (1959) and used in statistics books (Pratt et al. 1995).
Both the ratio optimization models (12) and (15) are theoretically equivalent. However, the risk-reward ratio optimization (15) enables easy control of the denominator positivity by simple inequality \({\mu ({\mathbf x}) \ge \tau + \varepsilon }\) added to the problem constraints. In the standard reward-risk ratio optimization the corresponding inequality \({\varrho ({\mathbf x}) \ge \tau + \varepsilon }\) with convex risk measures requires complex discrete model even for LP computable risk measures (Guastaroba et al. 2016). Model (15) may also be additionally regularized for the case of multiple risk-free solutions. Regularization \(({\varrho ({\mathbf x}) + \varepsilon })/({\mu ({\mathbf x}) - \tau })\) guarantees that the risk-free portfolio with the highest mean return will be selected then.
Moreover, since
the risk-reward ratio formulation allows us to justify SSD consistency of the many ratio optimization approaches. Indeed, the following theorem is valid (Ogryczak et al. 2015):
Theorem 1
If risk measure \(\varrho ({\mathbf x})\) is mean-complementary SSD consistent, i.e.
then the risk-reward ratio optimization (15) and equivalently (12) is SSD consistent, i.e.
provided that \(\mu ({\mathbf x})> \tau > \mu ({\mathbf x}) - \varrho ({\mathbf x})\).
The risk-reward ratio models can usually be easily reformulated into simpler and computationally more efficient forms. Note that both the Sharpe ratio optimization (13) and the Sortino ratio optimization (14) represent complex nonlinear problems. When switching on the risk-reward ratio optimization they can easily be reformulated into classical quadratic optimization with linear constraint. Actually, the risk-reward ratio model equivalent to the Sharpe ratio maximization takes the form:
Applying the Charnes and Cooper transformation 1962 with substitutions: \(\displaystyle \tilde{x}_j={x_j}/({z-\tau })\), \(\displaystyle v={z}/({z-\tau })\) and \(\displaystyle v_0={1}/({z-\tau })\) the problem can be reformulated into the following convex quadratic program (Cornuejols and Tütüncü 2007):
The risk-reward ratio model equivalent to the Sortino ratio maximization takes the form:
By substitutions: \(\displaystyle \tilde{d}_{t} = {d_{t}}/({z-\tau })\), \(\displaystyle \tilde{x}_j={x_j}/({z-\tau })\), \(\displaystyle v={z}/({z-\tau })\) and \(\displaystyle v_0={1}/({z-\tau })\) it can be reformulated into the following convex quadratic program:
Note that possible formulation of the Sortino index optimization with the corresponding risk-reward ratio based on the standard semideviation allows us to justify its SSD consistency. Indeed, as the standard semideviation is a mean-complementary SSD consistent risk measure (Ogryczak and Ruszczyński 1999), applying Theorem 1 we get the following assertion.
Corollary 1
The Sortino index optimization is SSD consistent provided that \(\mu ({\mathbf x})> \tau > \mu ({\mathbf x}) - \bar{\sigma }({\mathbf x})\).
In the following section we analyze efficient computation of tangency portfolio for various polyhedral risk measures taking advantages of possible inverse formulation as the risk-reward ratio optimization model
Note that due to Theorem 1 (under natural assumptions) this ratio optimization is consistent with the SSD rules in the following sense.
Corollary 2
Let \({\mathbf x}^0\) be an optimal portfolio to the risk-reward ratio optimization problem (20) that satisfies condition \(\mu ({{\mathbf x}^0}) - \varrho ({{\mathbf x}^0}) \le \tau \). For any deviation risk measure \(\varrho ({\mathbf x})\) which is mean-complementary SSD consistent, portfolio \({\mathbf x}^0\) is SSD nondominated with the exception of alternative optimal portfolios having the same values of mean return \(\mu ({{\mathbf x}^0})\) and risk measure \(\varrho ({{\mathbf x}^0})\).
We analyze the risk-reward ratio optimization model (20) for the most popular polyhedral risk measures such as SMAD, CVaR, Minimax and mean below-target deviation. We show that this ratio optimization is consistent with the SSD rules, despite that the ratio does not represent a coherent risk measure (Artzner et al. 1999). The most important, we demonstrate that while transforming this ratio optimization to an LP model and taking advantages of the LP duality we get model formulations providing high computational efficiency and scalable with respect to the number of scenarios. Actually, the number of structural constraints in the introduced LP models is proportional to the number of instruments n while only the number of variables is proportional to the number of scenarios T thus not affecting so seriously the simplex method efficiency. Therefore, the models can effectively be solved with general LP solvers even for very large numbers of scenarios. The simplex method applied to a primal problem actually solves both the primal and the dual (Vanderbei 2014). Since the dual of the dual is the primal, applying the simplex method to the dual also solves both the primal and the dual problem. Therefore, one can take advantages of smaller dimensionality of the dual model without need of any additional computations to recover the primal solution (the optimal portfolio).
3 Computational LP models for basic polyhedral risk measures
3.1 SMAD model
For the SMAD model, the downside mean semideviation from the mean \(\bar{\delta }({\mathbf x})\) may be considered as a basic risk measure. The risk-reward ratio model (20) for the SMAD risk measurement may be formulated as follows:
Note that the downside mean semideviation is a mean-complementary SSD consistent risk measure (Ogryczak and Ruszczyński 1999), thus applying Theorem 1 one gets:
Corollary 3
The SMAD risk-reward ratio optimization (21) is SSD consistent provided that \(\mu ({\mathbf x})> \tau > \mu ({\mathbf x}) - \bar{\delta }({\mathbf x})\).
The ratio model (21) can be linearized by the Charnes and Cooper substitutions (Charnes and Cooper 1962; Williams 2013): \(\displaystyle \tilde{d}_{t} = {d_{t}}/({z-\tau })\), \(\displaystyle \tilde{x}_j={x_j}/({z-\tau })\), \(\displaystyle v={z}/({z-\tau })\) and \(\displaystyle v_0={1}/({z-\tau })\) leading to the following LP formulation:
The original values of \(x_j\) can be then recovered dividing \(\tilde{x}_j\) by \(v_0\).
After eliminating defined by equations variables v and \(v_0\), one gets the most compact formulation:
with \(T+n\) variables and \(T+2\) constraints.
Taking the LP dual to model (23) one gets the model:
containing T variables \(u_{t}\) corresponding to inequalities (23b), nonnegative variable q corresponding to inequality (23d) and unbounded (free) variable h corresponding to equation (23c), but only n structural constraints. Indeed, the T constraints corresponding to variables \(d_{t}\) from (23) take the form of simple upper bounds (SUB) on \(u_{t}\) (24d) thus not affecting the problem complexity. Hence, similar to the standard portfolio optimization model based on the SMAD measure (Ogryczak and Śliwiński 2011b), the number of constraints in (24) is proportional to the portfolio size n, thus it is independent from the number of scenarios. The same remains valid for the model transformed to the so-called canonical form (Dantzig 1963) or computational form (Maros 2003) with explicit slack variables:
Exactly, there are \(T +n +2\) variables and n constraints in the computational form. This guarantees a high computational efficiency of the simplex method for the dual model, even for very large number of scenarios.
The optimal portfolio weights are easily recovered from the dual variables (shadow prices) corresponding to the inequalities (24b) or equations (25b). Exactly, the dual variables to (24b) represent optimal values of \(\tilde{x}_j\) from (23) while the optimal values of the original \(x_j\) variables from model (21) can be recovered as normalized values \(\tilde{x}_j\), thus dividing \(\tilde{x}_j\) by \(\sum _{j=1}^n \tilde{x}_j\).
For finding a primal solution having known only a dual solution or vice versa, the following Complementary Slackness Theorem (see, e.g. Vanderbei 2014), is generally used.
Theorem 2
(Complementary Slackness) Suppose that \({\mathbf x}= (x_1,\ldots , x_n )\) is primal feasible and that \({\mathbf y}= (y_1 ,\ldots , y_m )\) is dual feasible. Let \((w_1 , w_2 ,\ldots , w_m )\) denote the corresponding primal slack variables (residuals), and let \((s_1 , s_2 , \ldots , s_n )\) denote the corresponding dual slack variables (residuals). Then \({\mathbf x}\) and \({\mathbf y}\) are optimal for their respective problems if and only if
Following Theorem 2, a primal solution \(\tilde{x}_j\) may be found as a solution to the system:
where inequalities (27a) and (27b) lead to the linear system
In the case of the unique primal optimal solution, it is simply given as a solution of linear equations (23c), (27c) and (28). In general, finding a solution of the system (27) is more complex and thereby finding a primal solution having known only a dual solution could be a quite complex problem. Solving such a system of linear inequalities and equations, in general, may require the use of the simplex method restricted to finding a feasible solution (the so-called Phase I, e.g. Vanderbei 2014) or with an additional objective if a special property of solutions is sought.
The problem is much simpler, however, for the basic solutions (vertices) used in the simplex method. Basic solutions are characterized by a structure of basic variables with linearly independent columns of coefficients and nonbasic variables fixed at their bounds (either lower or upper). The simplex method while generating sequence of basic solutions, takes this advantage and when applied to a primal problem it actually solves both the primal and the dual (Maros 2003; Vanderbei 2014). Since the dual of the dual is the primal, applying the simplex method to the dual also solves both the primal and the dual problem. Exactly, in the simplex method a sequence of basic feasible solutions and complementary dual vectors (satisfying complementary slackness conditions (26)) is built. A complementary basic dual vector may be infeasible during the solution process while its feasibility is reached at the optimality. Hence, having the basic optimal solution of the dual problem (24) defined by the basis index set B consisted of variable q and \(n-1\) of variables \(u_t\), h and corresponding slacks \(s_j\), one has defined the primal optimal solution as the unique solution of the linear system:
of n equations with n variables. Recall that in the simplex method this solution is already found as the so-called simplex multipliers (Maros 2003) during the pricing step. Therefore, the dual solutions are directly provided by any linear programming solver (see e.g. (IBM 2016)). Thus one can take advantages of smaller dimensionality of the dual model without need of any additional computations to recover the primal solution (the optimal portfolio).
The downside mean semideviation is a risk relevant measure. Therefore, assuming that only risky assets are considered for a portfolio, the corresponding reward-risk ratio (12) does not need any nonconvex constraint to enforce positive values of the risk measure. Nevertheless, the reward-risk ratio optimization for the SMAD measure results in an LP model that contains \(T+n\) variables and \(T+2\) constraints (Mansini et al. 2003) and its dimensionality cannot be reduced with any dual reformulation.
3.2 CVaR model
In the CVaR model, one needs to use the complementary deviational risk measure, the drawdown measure \(\varrho ({\mathbf x})=\Delta _{\beta }({\mathbf x})\) for the reward-risk ratio optimization. Hence, the CVaR risk-reward ratio model (20) based on the CVaR risk measure takes the following form:
Note that the CVaR measure is a SSD consistent measure (the drawdown measure is mean-complementary SSD consistent) (Ogryczak and Ruszczyński 2002a), thus following Theorem 1 we get:
Corollary 4
The CVaR risk-reward ratio optimization (30) is SSD consistent provided that \(\mu ({\mathbf x})> \tau > M_{\beta }({\mathbf x})\).
Fractional ratio model (30) can be linearized by substitutions: \(\displaystyle \tilde{d}_{t} = {d_{t}}/({z-\tau })\), \(\displaystyle \tilde{y} = {y}/({z - \tau })\), \(\displaystyle \tilde{x}_j={x_j}/({z-\tau })\), \(\displaystyle v={z}/({z-\tau })\) and \(\displaystyle v_0={1}/({z-\tau })\) leading to the following LP formulation:
After eliminating defined by equations variables v and \(v_0\), one gets the most compact formulation:
with \(T+n+1\) variables and \(T+2\) constraints.
Taking the LP dual to model (32) we get the following model:
containing T variables \(u_{t}\) corresponding to inequalities (32b), nonnegative variable q corresponding to inequality (32d) and unbounded (free) variable h corresponding to equation (32c), but only \(n+1\) structural constraints. Indeed, the T constraints corresponding to variables \(d_{t}\) from (32) take the form of simple upper bounds on \(u_{t}\) (33d) not affecting the problem complexity. Thus similar to the standard portfolio optimization with the CVaR measure (Ogryczak and Śliwiński 2011a), the number of constraints in (33) is proportional to the number of instruments n, thus it is independent from the number of scenarios. The same remains valid for the model transformed to the canonical form with explicit slack variables:
Exactly, there are \(T +n +2\) variables and \(n+1\) equations in the canonical form. This guarantees a high computational efficiency of the simplex method for the dual model, even for very large number of scenarios.
The optimal portfolio weights, i.e., the optimal values of the original \(x_j\) variables from model (30) can be recovered as normalized values \(\tilde{x}_j\) of dual variables corresponding to inequalities (33c) (or equations (34c)), thus dividing \(\tilde{x}_j\) by \(\sum _{j=1}^n \tilde{x}_j\). The simplex method when applied to a primal problem, it actually solves both the primal and the dual (Maros 2003; Vanderbei 2014). Since the dual of the dual is the primal, applying the simplex method to the dual also solves both the primal and the dual problem. Therefore, the dual solutions are directly provided by any linear programming solver (see e.g. IBM 2016). Thus one can take advantages of smaller dimensionality of the dual model without need of any additional complex computations to recover the primal solution (the optimal portfolio).
When the simplex method generates the basic optimal solution of the dual problem (33) defined by the basis index set B consisted of variable q and n of variables \(u_t\), h and corresponding slacks \(s_j\), the provided primal optimal solution is defined as the unique solution of the linear system:
of \(n+1\) equations with \(n+1\) variables: \(\tilde{y}\) and \(\tilde{x}_j\) for \(j=1,\ldots ,n\).
If one needs to find another primal solutions, which is usually not a case of portfolio optimization, we consider, then the full complementary slackness system must be solved. Following Theorem 2, a primal solution \(\tilde{x}_j\) (together with \(\tilde{y}\)) may be found as a solution to the system:
Solving such a system of linear inequalities and equations, in general, may require the use of the simplex method restricted to finding a feasible solution (Phase I) or with an additional objective if a special property of solutions is sought.
3.3 Minimax model
The Minimax portfolio optimization model representing a limiting case of the CVaR model for \(\beta \) tending to 0 is even simpler than the general CVaR model. The risk-reward ratio optimization model (20) using the maximum downside deviation \(\Delta ({\mathbf x})\) can be written as the following problem:
The Minimax risk measure is SSD consistent (the maximum downside deviation measure is mean-complementary SSD consistent) (Mansini et al. 2003), thus applying Theorem 1 we get the following assertion.
Corollary 5
The Minimax risk-reward ratio optimization (37) is SSD consistent provided that \(\mu ({\mathbf x})> \tau > M({\mathbf x})\).
Fractional model (37) is linearized by substitutions: \(\displaystyle \tilde{y} = {y}/({z - \tau })\), \(\displaystyle \tilde{x}_j={x_j}/({z-\tau })\), \(\displaystyle v={z}/({z-\tau })\) and \(\displaystyle v_0={1}/({z-\tau })\) leading to the following LP formulation:
After eliminating defined by equations variables v and \(v_0\), one gets the most compact formulation:
with \(n+1\) variables and \(T+2\) constraints.
The LP dual to model (39), built with T variables \(u_{t}\) corresponding to inequalities (39b), nonnegative variable q corresponding to inequality (39d) and unbounded (free) variable h corresponding to equation (39c), gets the following problem:
containing only \(n+1\) structural constraints. Thus similar to the standard Minimax optimization (Ogryczak and Śliwiński 2011b), the number of constraints in (40) is proportional to the portfolio size n while being independent from the number of scenarios. The same remains valid for the model transformed to the canonical form with explicit slack variables:
Exactly, there are \(T +n +2\) variables and \(n+1\) equations in the canonical form. This guarantees a high computational efficiency of the dual model even for a very large number of scenarios.
The optimal portfolio, i.e., the optimal values of the original \(x_j\) variables from model (37) can be recovered as normalized values \(\tilde{x}_j\) of dual variables corresponding to inequalities (40c) (or equations (41c)), thus dividing \(\tilde{x}_j\) by \(\sum _{j=1}^n \tilde{x}_j\). The simplex method when applied to an LP problem, it actually solves both the primal and the dual (Maros 2003; Vanderbei 2014). Hence, applying the simplex method to the dual also solves both the primal and the dual problem. Therefore, the dual solutions are directly provided by any linear programming solver (see e.g. IBM 2016). Thus one can take advantages of smaller dimensionality of the dual model without need of any additional computations to recover the primal solution (the optimal portfolio).
When the simplex method generates the basic optimal solution of the dual problem (40) defined by the basis index set B consisted of variable q and n of variables \(u_t\), h and corresponding slacks \(s_j\), the provided primal optimal solution is defined as the unique solution of the linear system:
of \(n+1\) equations with \(n+1\) variables: \(\tilde{y}\) and \(\tilde{x}_j\) for \(j=1,\ldots ,n\).
If one needs to find another primal solutions, which is usually not a case of portfolio optimization, we consider, then the full complementary slackness system must be solved. Following Theorem 2, a primal solution \(\tilde{x}_j\) (together with \(\tilde{y}\)) may be found as a solution to the system:
Solving such a system of linear inequalities and equations, in general, may require the use of the simplex method restricted to finding a feasible solution (Phase I) or with an additional objective if a special property of solutions is sought.
3.4 Mean below-target deviation and Omega ratio
The risk-reward ratio model based on the mean below-target deviation risk measure \(\bar{\delta }_{\tau }({\mathbf x})\) (downside mean semideviation from the threshold \(\tau \)) turns out to be equivalent to the so-called Omega ratio optimization. The Omega ratio is a relatively recent performance measure introduced by Keating and Shadwick (2002) which captures both the downside and upside potential of a portfolio. The Omega ratio can be defined as the ratio between the expected value of the profits and the expected value of the losses, where for a predetermined threshold \(\tau \), portfolio returns over the target \(\tau \) are considered as profits, whereas returns below the threshold are considered as losses. Following Ogryczak and Ruszczyński (1999), for any target value \(\tau \) the following equality holds:
Thus, we can write:
Therefore, the Omega maximization is equivalent to the risk-reward ratio model based on the mean below-target deviation thus minimizing \(\frac{{\delta }_\tau ({\mathbf x})}{\mu ({\mathbf x}) - \tau }\). Hence, the Omega ratio model (20) takes the form:
The mean below-target deviation is a mean-complementary SSD consistent risk measure (Ogryczak and Ruszczyński 1999). Hence, from Theorem 1 we get the following assertion.
Corollary 6
The Omega ratio optimization (44) is SSD consistent provided that \(\mu ({\mathbf x})> \tau > \mu ({\mathbf x}) - {\delta }_\tau ({\mathbf x})\).
Fractional model (44) can be linearized by substitutions: \(\displaystyle \tilde{d}_{t} = {d_{t}}/({z-\tau })\), \(\displaystyle \tilde{x}_j={x_j}/({z-\tau })\), \(\displaystyle v={z}/({z-\tau })\) and \(\displaystyle v_0={1}/({z-\tau })\) leading to the formulation:
After eliminating variables v and \(v_0\) defined by equations, one gets the most compact formulation:
with \(T+n\) variables and \(T+2\) constraints.
Taking the LP dual to model (46) one gets the following model:
containing T variables \(u_{t}\) corresponding to inequalities (46b), nonnegative variable q corresponding to inequality (46d) and unbounded (free) variable h corresponding to equation (46c), but only n structural constraints. Indeed, the T constraints corresponding to variables \(d_{t}\) from (46) take the form of simple upper bounds on \(u_{t}\) (47c) thus not affecting the problem complexity. Hence, similar to the standard portfolio optimization model based on the SMAD measure (Ogryczak and Śliwiński 2011b), the number of constraints in (47) is proportional to the portfolio size n, thus it is independent from the number of scenarios. The same remains valid for the model transformed to the canonical or computational form (Maros 2003) with explicit slack variables:
Exactly, there are \(T +n +2\) variables and n constraints in the computational form. This guarantees a high computational efficiency of the simplex method for the dual model, even for very large number of scenarios.
The optimal portfolio weights are easily recovered from the dual variables (shadow prices) corresponding to the inequalities (47b) or equations (48b). Exactly, the dual variables to (47b) represent optimal values of \(\tilde{x}_j\) from (46) while the optimal values of the original \(x_j\) variables from model (44) can be recovered as normalized values \(\tilde{x}_j\), thus dividing \(\tilde{x}_j\) by \(\sum _{j=1}^n \tilde{x}_j\). The simplex method when applied to an LP problem, it actually solves both the primal and the dual (Maros 2003; Vanderbei 2014). Hence, applying the simplex method to the dual also solves both the primal and the dual problem. Therefore, the dual solutions are directly provided by any linear programming solver (see e.g. IBM 2016) and one can take advantages of smaller dimensionality of the dual model without need of any additional computations to recover the primal solution (the optimal portfolio).
When the simplex method generates the basic optimal solution of the dual problem (47) defined by the basis index set B consisted of variable q and n of variables \(u_t\), h and corresponding slacks \(s_j\), the provided primal optimal solution is defined as the unique solution of the linear system:
of \(n+1\) equations with \(n+1\) variables: \(\tilde{y}\) and \(\tilde{x}_j\) for \(j=1,\ldots ,n\).
If one needs to find another primal solutions, which is usually not a case of portfolio optimization we consider, the full complementary slackness system must be solved. Following Theorem 2, a primal solution \(\tilde{x}_j\) (together with \(\tilde{y}\)) may be found as a solution to the system:
Solving such a system of linear inequalities and equations, in general, may require the use of the simplex method restricted to finding a feasible solution (Phase I) or with an additional objective if a special property of solutions is sought.
The mean below-target deviation is not a risk relevant measure. Therefore, the corresponding reward-risk ratio (12) and the standard Omega ratio optimization models need a nonconvex constraint to enforce positive values of the risk measure. The latter requires introduction of additional constraints and auxiliary binary variables to deal with those critical situations where the risk measure at the denominator of the reward-risk ratio may take null value (Guastaroba et al. 2016). Moreover, the reward-risk ratio optimization for the mean below-target deviation measure results in a Mixed Integer LP model that contains \(T+n\) variables and \(T+2\) constraints (Mansini et al. 2003) and its dimensionality cannot be reduced with any dual reformulation.
3.5 Computational tests
In order to test empirically increase of the efficiency while taking advantages of inverse ratio models with dual reformulations, we have run computational tests on the large scale tests instances developed by Lim et al. (2009). They were originally generated from a multivariate normal distribution for 50, 100 or 200 securities with the number of scenarios 50 000 just providing an adequate approximation to the underlying unknown continuous price distribution. All computations were performed with primal simplex algorithm of the CPLEX 12.6.3 package on a PC with the Intel Xeon E5-2680 v2 CPU and 32GB RAM. All computations were performed as a single thread in order to be independent on the scalability of the CPLEX algorithms and yield time results that are easier to compare.
Our earlier experience has shown that the computational performances of the primal LP model for the risk-reward ratio optimization are similar to those of LP models for reward-risk ratio optimization. Actually, they have almost identical numbers of variables and constraints. However, for the mean below-target deviation measure which is not strictly risk relevant, the latter ratio optimization not always can be represented by LP models since the positivity of the risk measure (in denominator) may be an active constraint. Explicit use of this constraint generate additional integer programming relations and dramatically increases the computational complexity. We experienced this phenomenon while studying the standard approach to the Omega ratio maximization (Guastaroba et al. 2016), which corresponds to the reward-risk maximization for the mean below-target deviation. Generally, the reward-risk models are computationally not simpler that the primal risk reward models. Therefore, in our experimental study we have focused on computational advantages of the usage of dual models while comparing them to the primal ones.
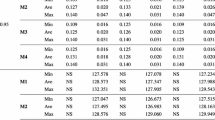
In Table 1 there are presented computation times for all the above primal and dual models. All results are presented as the averages of 10 different test instances of the same size. For the large scale test problems the solution times of the dual CVaR models (33) ranging from 7 to 110 s are 20 to 60 times shorter than those for the primal models.
It was explicitly forbidden for CPLEX to automatically select best LP optimizer in order to guarantee comparable results between all the LP problems, as CPLEX tried to solve different problems (depending mostly on their size) with different algorithms. However, in general, dual simplex algorithm offered similar or worse performance, while barrier algorithm provided better performance overall.
The Minimax models are computationally very easy. Running the computational tests we were able to solve the large scale test instances of the dual model (40) in times below 15 s. In fact, even the primal model could be solved in reasonable time up to 50 s for large scale test instances.
The SMAD and Omega models are computationally very similar each other and both similar to the CVaR models. Indeed, the dual models can be solved in not more than 92 s for the large scale test instances and those times are 18–35 times shorter than for the primal models. Additionally, in case of the primal problem for SMAD risk measure CPLEX offered an automatic dual problem formulation during presolve step which resulted in exactly the same performance figures compared to the dual problem. That behavior was blocked by turning off certain settings during the comparison computations.
4 Conclusions
We have presented the reward-risk ratio optimization models for the several polyhedral risk measures and analyzed their properties. Taking advantages of possible inverse formulation of the risk-reward ratio optimization (15) we get a model well defined and SSD consistent under natural restriction on the target value selection. Thus, this ratio optimization is consistent with the SSD rules, despite that the ratio does not represent a coherent risk measure (Artzner et al. 1999).
We show that while transforming the risk-reward ratio optimization to an LP model, we can take advantages of the LP duality to get a model formulation providing higher computational efficiency. In the introduced dual model, similar to the direct polyhedral risk measures optimization (Ogryczak and Śliwiński 2011b), the number of structural constraints is proportional to the number of instruments while only the number of variables is proportional to the number of scenarios, thus not affecting so seriously the simplex method efficiency. The model can effectively be solved with general LP solvers even for very large numbers of scenarios. Actually, the dual portfolio optimization problems of fifty thousand scenarios and two hundred instruments can be solved with the general purpose LP solvers in less than 2 min. On the other hand, such efficiency cannot be achieved with LP models corresponding to the standard reward-risk ratio optimization even if these LP models can be applied without additional discrete constraints.
We have studied in details the risk-return ratio models for the basic polyhedral risk measures of the SMAD, CVaR, Minimax and mean below-target deviation (Omega index optimization). Similar computationally efficient dual reformulations may be also achieved for more complex polyhedral risk measures. In particular for the measures with enhanced downside risk focus (Michalowski and Ogryczak 2001; Krzemienowski and Ogryczak 2005; Mansini et al. 2007).
References
Artzner P, Delbaen F, Eber J-M, Heath D (1999) Coherent measures of risk. Math Finance 9:203–228
Carino DR, Myers DH, Ziemba WT (1998) Concepts, technical issues and uses of the Russel–Yasuda Kasai financial planning model. Oper Res 46:450–463
Charnes A, Cooper WW (1962) Programming with linear fractional functionals. Naval Res Logist 9:181–186
Chekhlov A, Uryasev S, Zabarankin M (2002) Drawdown measure in portfolio optimization. Int J Theor Appl Finance 26:1443–1471
Cornuejols G, Tütüncü R (2007) Optimization methods in finance. Cambridge University Press, Cambridge
Dantzig GB (1963) Linear programming and extensions. Princeton University Press, Princeton
Eichhorn A, Römisch W (2005) Polyhedral risk measures in stochastic programming. SIAM J Optim 16:69–95
Embrechts P, Klüppelberg C, Mikosch T (1997) Modelling extremal events for insurance and finance. Springer, New York
Fishburn P (1977) Mean-risk analysis with risk associated with below target returns. Am Econ Rev 67:116–126
Guastaroba G, Mansini R, Ogryczak W, Speranza MG (2016) Linear Programming Models based on Omega Ratio for the Enhanced Index Tracking Problem. Eur J Oper Res 251:938–956
IBM CORPORATION (2016) User’s Manual for CPLEX. http://www.ibm.com/support/knowledgecenter/en/SSSA5P_12.6.3/ilog.odms.studio.help/Optimization_Studio/topics/PLUGINS_ROOT/ilog.odms.studio.help/pdf/usrcplex.pdf
Keating C, Shadwick WF (2002) A universal performance measure. J Perform Meas 6:59–84
Konno H, Yamazaki H (1991) Mean-absolute deviation portfolio optimization model and its application to Tokyo stock market. Manag Sci 37:519–531
Krzemienowski A, Ogryczak W (2005) On extending the LP computable risk measures to account downside risk. Comput Optim Appl 32:133–160
Lim C, Sherali HD, Uryasev S (2009) Portfolio optimization by minimizing conditional value-at-risk via nondifferentiable optimization. Comput Optim Appl 46:391–415
Mansini R, Ogryczak W, Speranza MG (2003) On LP solvable models for portfolio optimization. Informatica 14:37–62
Mansini R, Ogryczak W, Speranza MG (2007) Conditional value at risk and related linear programming models for portfolio optimization. Ann Oper Res 152:227–256
Mansini R, Ogryczak W, Speranza MG (2014) Twenty years of linear programming based portfolio optimization. Eur J Oper Res 234:518–535
Mansini R, Ogryczak W, Speranza MG (2015) Linear and mixed integer programming for portfolio optimization. Springer, Cham, Switzerland
Markowitz HM (1952) Portfolio selection. J Finance 7:77–91
Markowitz HM (1959) Portfolio selection: efficient diversification of investments. Wiley, New York
Michalowski W, Ogryczak W (2001) Extending the MAD portfolio optimization model to incorporate downside risk aversion. Naval Res Logist 48:185–200
Maros I (2003) Computational techniques of the simplex method. Kluwer AP, Boston
Ogryczak W (2000) Multiple criteria linear programming model for portfolio selection. Ann Oper Res 97:143–162
Ogryczak W, Przyłuski M, Śliwiński T (2015) Portfolio optimization with reward-risk ratio measure based on the conditional value-at-risk, Lecture notes. In: Engineering and computer science: proceedings of the world congress on engineering and computer science 2015, WCECS 2015, 21–23 October, 2015, San Francisco, USA, pp 913–918
Ogryczak W, Ruszczyński A (1999) From stochastic dominance to mean-risk models: semideviations as risk measures. Eur J Oper Res 116:33–50
Ogryczak W, Ruszczyński A (2002a) Dual stochastic dominance and related mean-risk models. SIAM J Optim 13:60–78
Ogryczak W, Ruszczyński A (2002b) Dual stochastic dominance and quantile risk measures. Int Trans Oper Res 9:661–680
Ogryczak W, Śliwiński T (2011a) On solving the dual for portfolio selection by optimizing Conditional Value at Risk. Comput Optim Appl 50:591–595
Ogryczak W, Śliwiński T (2011b) On dual approaches to efficient optimization of LP computable risk measures for portfolio selection. Asia-Pac J Oper Res 28:41–63
Pflug GCh (2001) Scenario tree generation for multiperiod financial optimization by optimal discretization. Math Program 89:251–271
Pratt J, Raiffa H, Schlaifer R (1995) Introduction to statistical decision theory. MIT Press, Cambridge, MA
Quiggin J (1982) A theory of anticipated utility. J Econ Behav Organ 3:323–343
Rockafellar RT (1970) Convex analysis. Princeton University Press, Princeton
Rockafellar RT, Uryasev S (2000) Optimization of conditional value-at-risk. J Risk 2:21–41
Rockafellar RT, Uryasev S (2002) Conditional value-at-risk for general loss distributions. J Bank Finance 26:1443–1471
Rothschild M, Stiglitz JE (1970) Increasing risk: I. A definition. J Econ Theory 2:225–243
Sharpe WF (1966) Mutual fund performance. J Bus 39:119–138
Sortino FA, Forsey HJ (1996) On the use and misuse of downside risk. J Portf Manag Winter 1996:35–42
Sortino FA, Price LN (1994) Performance measurement in a downside risk framework. J Invest 3:59–64
Speranza MG (1993) Linear programming models for portfolio optimization. Finance 14:107–123
Tobin J (1958) Liquidity preference as behavior towards risk. Rev Econ Stud 25:65–86
Vanderbei RJ (2014) Linear programming: foundations and extensions, 3rd edn. Springer, New York
Williams HP (2013) Model building in mathematical programming, 5th edn. Wiley, Chichester
Yitzhaki S (1982) Stochastic dominance, mean variance, and Gini’s mean difference. Am Econ Rev 72:178–185
Young MR (1998) A minimax portfolio selection rule with linear programming solution. Manag Sci 44:673–683
Acknowledgements
The research was partially supported by the National Science Centre (Poland) under the grant DEC-2012/07/B/HS4/03076.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ogryczak, W., Przyłuski, M. & Śliwiński, T. Efficient optimization of the reward-risk ratio with polyhedral risk measures. Math Meth Oper Res 86, 625–653 (2017). https://doi.org/10.1007/s00186-017-0613-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00186-017-0613-1
Keywords
- Portfolio optimization
- Reward-risk ratio
- Tangency portfolio
- Polyhedral risk measures
- Fractional programming
- Linear programming
- Computation