An optimal reinsurance problem in the Cramér–Lundberg model

Abstract

In this article we consider the surplus process of an insurance company within the Cramér–Lundberg framework with the intention of controlling its performance by means of dynamic reinsurance. Our aim is to find a general dynamic reinsurance strategy that maximizes the expected discounted surplus level integrated over time. Using analytical methods we identify the value function as a particular solution to the associated Hamilton–Jacobi–Bellman equation. This approach leads to an implementable numerical method for approximating the value function and optimal reinsurance strategy. Furthermore we give some examples illustrating the applicability of this method for proportional and XL-reinsurance treaties.

1 Introduction

The determination of optimal insurance contracts is a classical topic in insurance mathematics. The first results are stated in a static utility theoretic framework and concern the relation between a risk facing individual and the insurer. The goal is the construction of an optimal insurance arrangement for the first party with a certain constraint stemming from the second party. Classical contributions in this context are Kenneth (1973), Raviv (1979) and Borch (1974), where one finds a collection of pioneering articles. A more recent paper by Guerra and Centeno (2008) studies this problem for exponential utility and provides the link to the maximization of the so-called adjustment coefficient which is the decay rate of the ruin probability for increasing initial capital. The idea of using reinsurance for maximizing the adjustment coefficient was introduced by Waters (1983), further studied by Centeno (1986, (2002) and Schmidli and Hald (2004), and can be considered as the motivation for studying optimal reinsurance.

The first paper to study dynamic optimal reinsurance in the classical risk model for the minimization of the ruin probability is Schmidli (2001), who dealt with the case of proportional reinsurance treaties. This approach was extended to excess of loss contracts by Hipp and Vogt (2003). A general presentation on ruin probability minimization by means of reinsurance in the classical and diffusion risk model can be found in Schmidli (2008). Furthermore, this reference provides some asymptotic studies of the behaviour of optimal strategies, which in certain situations coincide with the ones maximizing the adjustment coefficient. Some additional results with a focus on non-proportional reinsurance contracts are given in Hipp and Taksar (2010).

Using a different criterion to assess the performance of an insurance portfolio, Eisenberg (2010) thoroughly covers a variety of capital injection minimization problems under both the classical risk model and its diffusion approximation where the insurer has the possibility to dynamically reinsure its risk. The incorporation of dynamic reinsurance to the classical problem of maximizing the dividend pay-outs of an insurance company prior to ruin in a compound Poisson framework was treated by Azcue and Muler (2005) for general reinsurance schemes and by Mnif and Sulem (2005) for excess of loss reinsurance. In a diffusion setting, the corresponding problem was studied by Højgaard and Taksar (1999) in the case of proportional reinsurance. Combining dividend pay-outs maximization with proportional risk exposure reduction, Schäl (1998) formulated a piecewise deterministic Markov model where only jumps but not the deterministic flow can be controlled. In contrast to the aforementioned references which deal with optimal reinsurance for continuous time risk processes, Schäl (2004) investigates a discrete time insurance model controlled by reinsurance and investments in a financial market with the intention to either maximize the expected exponential utility or minimize the ruin probability. An analogous problem was treated by Irgens and Paulsen (2004), where the authors examine the purpose of maximizing the expected utility of terminal wealth by use of optimal investment and reinsurance.

Finally, we would like to mention a new approach linking ruin theoretical concepts with the framework of worst-case optimization theory explored by Korn et al. (2012). Embedded in a differential game setup, the authors applied a worst-case scenario approach to maximize the expected utility of the surplus of an insurance company at some given deterministic terminal time by dynamic proportional reinsurance.

In this contribution, we will study the use of dynamic reinsurance for maximizing a particular economic performance measure which for a diffusion risk model was introduced by Højgaard and Taksar (1998a, (1998b).

For its definition, let $X^{{\mathbbm {u}}}= (X_t^{{\mathbbm {u}}})_{t \ge 0}$ be a surplus process comprising a reinsurance strategy ${\mathbbm {u}}$. The performance measure of this particular strategy is defined by

$$\begin{aligned} V^{{\mathbbm {u}}}(x)= \mathbb {E}_x\left[ \int _0^{\tau _x^{{\mathbbm {u}}}}e^{-\delta t} X_t^{{\mathbbm {u}}}\,dt\right] , \end{aligned}$$

(1)

where $\delta >0$ denotes a discount or preference rate and $\tau ^{{\mathbbm {u}}}$ is the time of ruin of $X^{{\mathbbm {u}}}$. In Taksar (2000) this measure is motivated by the following arguments: the surplus of the insurance company is kept on a bank account and interest gains are immediately distributed as dividends, thus maximizing expected discounted dividend payments is equivalent to maximizing (1). Another way to motivate this value function in a Markovian environment is to introduce a random life time $S\sim Exp(\delta )$ which is independent of all other model ingredients. Then one observes

$$\begin{aligned} V^{{\mathbbm {u}}}(x)=\frac{1}{\delta }\mathbb {E}_x\left[ X^{{\mathbbm {u}}}_{S} \mathbbm {1}_{\{S<\tau ^{{\mathbbm {u}}}_x\}}\right] , \end{aligned}$$

(2)

which tells that the performance measure is proportional to the expected surplus at a random exponential time S. This means that a dynamic reinsurance strategy is used for maximizing the surplus at some exogenous point in time. Cost functions of the form (1), or more generally involving a running costs function $l(X_t)$, are also studied by Cai et al. (2009) in an uncontrolled piecewise-deterministic compound Poisson environment.

The structure of the manuscript is as follows. In Sect. 2, we give a precise mathematical formulation of the problem, introducing the controlled surplus process and the value function. The analytical characterization of the value function is presented in Sect. 3. It starts with a collection of basic properties and employs the dynamic programming approach for achieving a final statement. Section 4 includes some comments on the numerical procedure obtained from the analytical results and two illustrative examples. Finally, a conclusion is stated in Sect. 5.

2 Problem statement

In the sequel, we will always work on a probability space $\left( \varOmega ,\mathcal {F},P\right)$ which carries all stochastic quantities to be defined in the following. In the Cramér–Lundberg model (also known as compound Poisson model or classical risk model), the surplus process $X= \left( X_t\right) _{t\ge 0}$ of a homogeneous insurance portfolio is modeled as

$$\begin{aligned} X_t = x+ct-\sum _{i=1}^{N_t}Y_i. \end{aligned}$$

(3)

Starting with an initial deterministic surplus $X_0=x \ge 0$, the surplus process increases linearly due to premiums that are collected continuously over time at a constant rate $c>0$. On the other hand, it decreases due to claims happening at the arrival times of a homogeneous Poisson process $N = \left( N_t\right) _{t\ge 0}$ with intensity $\lambda > 0$. The claims $\{ Y_i\}_{i \in \mathbb {N}}$ constitute a sequence of positive independently and identically distributed random variables with a density function $f_Y(\cdot )$ and finite mean $\mu$. Later on we will use Y as a representative random variable from this distribution. In addition, the sequence $\{ Y_i\}_{i \in \mathbb {N}}$ and N are assumed to be independent. The flow of information is given by the filtration $\{\mathcal {F}_t\}_{t\ge 0}$ which is generated by the surplus process X. In the remainder of the manuscript, we will use the symbol $\mathbb {E}$ for the expectation with respect to the probability measure P, for the conditional expectation $\mathbb {E}(\cdot \,\vert \,X_0=x)$ we will use the expression $\mathbb {E}_x$.

Fundamental quantities in this framework are the time of ruin

$$\begin{aligned} \tau _x = \inf \{t\ge 0\,\vert \,X_t<0\;\text{ and }\;X_0=x\}, \end{aligned}$$

and the probability of ruin

$$\begin{aligned} \psi (x) = P\left( \tau _x<\infty \right) , \end{aligned}$$

for initial capital $x \ge 0$. In some of the proofs below we will compare pathwise, i.e., we fix an $\omega \in \varOmega$, processes starting at different initial values x and y. Therefore it will be necessary to add the initial value in the definition of the time of ruin, for example $\mathbb {E}_x(X_{\tau _y})$ denotes the expected value of the surplus started at x stopped at the time of ruin as if the surplus would have started in y ($x>y$) (thinking along the same path). Certainly, we have, using $\theta =\inf \{t\ge 0\,\vert \,X_t<x-y\}, \mathbb {E}_x(X_{\tau _y})=\mathbb {E}_x(X_{\theta })$, but we believe that out of the context our notation will be more intuitive.

It is well known, that for avoiding almost sure ruin, it is necessary to choose a premium intensity fulfilling the net-profit condition $c>\lambda \mu$. Therefore, based on the expected value premium principle we set $c=(1+\eta )\lambda \mu$ with a safety loading $\eta >0$. For further details on classical problems in risk theory and related topics we refer to Asmussen and Albrecher (2010).

Assume now that in order to reduce the risk exposure of the portfolio, the insurer (cedent) has the possibility to take reinsurance in a dynamic way. Namely, at each time t, the insurer transfers a portion of the premium income to a reinsurer, who in turn commits to cover a part of the occurred claims. The dynamic reinsurance setup we are going to use follows the presentation from Schmidli (2008).

Formally, a reinsurance scheme is given by a monotone increasing function $r: [0,\infty ) \rightarrow [0,\infty )$ which fulfills $0 \le r(y) \le y$. Then r is the retention function with the meaning that for a claim of size Y, the amount r(Y) is paid by the insurer and $Y-r(Y)$ is taken by the reinsurer. For introducing a control possibility a family of available schemata $\mathfrak {R}$ is parameterized by a control parameter u from a compact set $\mathcal {U}'$. This means that for $u\in \mathcal {U}'$ the chosen reinsurance contract is given by $r(\cdot ,u)\in \mathfrak {R}$, where $r:[0,\infty )\times \mathcal {U}'\rightarrow \mathbb {R}^+$ with $0\le r(y,u)\le y$. In addition we assume that r(y, u) is continuous in both arguments. After fixing the family $\mathfrak {R}$, the set of available reinsurance schemes is given by

$$\begin{aligned} \mathcal {R}=\{r(\cdot ,u)\in \mathfrak {R}\,\vert u \in \mathcal {U}',\, 0 \le r(y,u) \le y,\, r\;\text{ continuous, } \text{ and } \text{ increasing } \text{ in }\,y\}. \end{aligned}$$

For later use we denote by $\rho (y,u)$ the generalized inverse of r(y, u) in the $y-$component, which due to monotonicity exists. Naturally, when employing reinsurance there are premiums to be paid. We assume that the reinsurer uses a deterministic premium function $\pi : L^1(\varOmega ,P) \rightarrow [0,\infty )$, such that when fixing $u\in \mathcal {U}'$ the premium is based on $\pi (Y-r(Y,u))$. From an aggregated risk perspective, if the insurer chooses reinsurance $u\in \mathcal {U}'$ at time t, the premium at rate $\lambda \, \pi (Y-r(Y,u))$ is paid to the reinsurer. Consequently the premium income of the insurer reduces to $c(u)= c- \lambda \, \pi (Y-r(Y,u))$. In the sequel, we shall always assume that c(u) is continuous and that full reinsurance leads to a negative premium income, i.e., $c<\lambda \pi (Y)$.

The premium function $\pi$ may be based on the expected value principle,

$$\begin{aligned} \pi \left( Y- r(Y,u) \right) =(1+\theta )\,\mathbb {E}\left[ Y-r(Y,u) \right] , \end{aligned}$$

where $\theta >\eta$ denotes the safety loading of the reinsurer, or on the variance principle,

$$\begin{aligned} \pi \left( Y- r(Y,u) \right) =\mathbb {E}\left[ Y-r(Y,u) \right] + \alpha \, Var\left[ Y-r(Y,u) \right] , \end{aligned}$$

for $\alpha Var\left[ Y\right] >\eta \mu$.

Possible concrete choices for $\mathfrak {R}$ and $\mathcal {U}'$ are the classical situations of proportional reinsurance and excess-of-loss reinsurance. In the first case we have $r(y,u) = uy$ and $u \in \mathcal {U}'=\left[ 0,1\right]$, in the second case $r(y,u)= \min (y,u)$ and $u \in \mathcal {U}'=\left[ 0,\infty \right]$. Notice, that in the latter case, an infinite retention level is equivalent to no reinsurance. In the following we will restrict the set of control parameters to the set $\mathcal {U}=\{u\in \mathcal {U'}\;\vert \;c(u)\ge 0\}$ for avoiding a negative premium rate. Since $\mathcal {U}'$ is supposed to be compact and $c(\cdot )$ is continuous we have that $\mathcal {U}$ is compact.

Remark 1

The idea of a dynamic reinsurance strategy can be explained as follows. At each time instant t, the insurer chooses a control parameter $u=u_t$ $\in \mathcal {U}$ which specifies a reinsurance scheme $r(\cdot ,u)$ from an available set of schemes. The choice of u simultaneously determines the extent to which the insurer wants to reduce its risk exposure and the additional cost this protection incurs, taking the form of a reinsurance premium. Namely, if a claim occurs at time t, the insurer pays $r(Y,u_t)$ and the reinsurer pays the rest, i.e. $Y-r(Y,u_t)$. In exchange of this risk transfer, the insurer pays to the reinsurer a reinsurance premium at a rate $\lambda \pi \left( Y-r(Y,u_t)\right)$.

Let ${\mathbbm {u}}=(u_t)_{t\ge 0}$ be a $\mathcal {U}$-valued stochastic process which is $\{\mathcal {F}_t\}_{t\ge 0}$ previsible and called a reinsurance strategy. Then the dynamics of the controlled surplus process $X^{{\mathbbm {u}}} =(X_t^{{\mathbbm {u}}})_{t \ge 0}$ are described by

$$\begin{aligned} X_t^{{\mathbbm {u}}} = x + \int _0^t \left[ c - \lambda \pi (Y-r(Y,u_s))\right] ds - \sum _{i=1}^{N_t} r(Y_i,u_{T_i}). \end{aligned}$$

(4)

Remark 2

From Rogers and Williams (1994, p.182) we can deduce that the previsibility of ${\mathbbm {u}}$ induces the fact that it is progressively measurable and thus also measurable as a function in time. Since the premium rate $c(\cdot )$ is assumed to be continuous and bounded by c, the integral $\int _0^t c(u_s)\,ds$ exists at least in the Lebesgue sense. Because jumps of the process $X^{{\mathbbm {u}}}$ occur according to the fundamental Poisson process and behaves continuously between jump times, the process $X^{{\mathbbm {u}}}$ is right continuous with existing limits from the left, i.e., cádlág. Consequently, $X^{{\mathbbm {u}}}$ is progressively measurable as well and for fixed $\omega , X^{{\mathbbm {u}}}(\omega )$ is measurable in t. Again, integrals of the form $\int _0^t X_s\,ds$ certainly do exist in the Lebesgue sense.

The time of ruin $\tau ^{{\mathbbm {u}}}_x$ denotes the time the controlled surplus process $X^{{\mathbbm {u}}}$ first becomes negative,

$$\begin{aligned} \tau ^{{\mathbbm {u}}}_x = \inf \{ t \ge 0: X_t^{{\mathbbm {u}}} < 0 \mid X^{{\mathbbm {u}}}_0=x\}. \end{aligned}$$

From now one we call a stochastic process ${\mathbbm {u}}=\{ u_t\}_{t \ge 0}$ admissible reinsurance strategy if it fulfills all the previously made assumptions. In this context the previsibility is crucial. That is, at claim time $T_i$, the reinsurance parameter is chosen based on the information up to time $T_i-$. The previsibility of the reinsurance strategy is a natural assumption in this setting, otherwise the insurer could change the reinsurance parameter to full reinsurance at the claim occurrence time. The reinsurer would then pay all claims while all premiums would be collected by the insurer. Let $\mathfrak {U}$ denote the set of admissible reinsurance strategies. Associated to an admissible reinsurance strategy ${\mathbbm {u}}$ and an initial reserve $x \ge 0$, we define its performance criterion as the expected cumulative discounted surplus process until ruin,

$$\begin{aligned} V^{{\mathbbm {u}}}(x) = \mathbb {E}_x\left[ \int _0^{\tau ^{{\mathbbm {u}}}_x} e^{-\delta s} X^{{\mathbbm {u}}}_s\, ds\right] , \end{aligned}$$

with $\delta > 0$ a discount or preference rate. In the sequel, we will refer to $V^{{\mathbbm {u}}}(x)$ as the return function. The optimization problem then consists of finding the optimal return function, or value function, defined as

$$\begin{aligned} V(x) = \sup _{{\mathbbm {u}}\in \mathfrak {U}} V^{{\mathbbm {u}}}(x), \end{aligned}$$

(5)

and an optimal admissible reinsurance strategy ${\mathbbm {u}}^{\star }$ leading to the value function, i.e. a strategy which delivers the maximal return function (5).

3 Main results

In this section, we first derive some elementary bounds, which allow for a rough characterization of the value function. In a next step, we are able to prove the existence of a solution to an integro-differential equation which is closely related to the problem’s Hamilton–Jacobi–Bellman equation. Finally, a verification argument provides the bridge between these analytical results and the stochastic optimization problem of interest.

3.1 Some elementary bounds

Proposition 1

For $x \ge 0$, the value function V(x) admits the following bounds:

• (a) $V(x)\le \frac{x}{\delta }+\frac{c}{\delta ^2}$,

• (b) $V(x) \ge \frac{x}{\delta } - \frac{\lambda \pi \left( Y\right) -c}{\delta ^2} \left[ 1-e^{\frac{-\delta x}{\lambda \pi \left( Y\right) -c}}\right]$.

Proof

Let ${\mathbbm {u}}=\{ u_t\}_{t \ge 0}$ be an arbitrary admissible strategy. Since $c(u_s) \le c$ for all $s \ge 0$, we get from (4) that

$$\begin{aligned} X_t^{{\mathbbm {u}}} \le x + ct, \end{aligned}$$

holds for all $t \ge 0$. Since $\delta >0$, this implies that,

$$\begin{aligned} V^{{\mathbbm {u}}}(x) \le \int _0^{\infty } e^{-\delta t} (x + ct)dt = \frac{x}{\delta }+\frac{c}{\delta ^2}. \end{aligned}$$

Taking the supremum over all admissible strategies ${\mathbbm {u}}$ shows that the value function V(x) satisfies inequality (a).

It remains now to validate inequality (b). The choice of the admissible strategy ${{\mathbbm {u}}}_0$ which corresponds to buying continuously full reinsurance until the time of ruin leads to a deterministic reserve $X^{{{\mathbbm {u}}}_0}$

$$\begin{aligned} X_t^{{{\mathbbm {u}}}_0} = x + \left( c-\lambda \pi \left( Y\right) \right) t, \end{aligned}$$

with negative drift. As a consequence, the time of ruin $\tau _x^{{\mathbbm {u}}^0}$ can be explicitly computed, that is, $\tau _x^{{{\mathbbm {u}}}_0} = \frac{x}{\lambda \pi \left( Y\right) -c}$. The underlying return function $V^{{{\mathbbm {u}}}_0}(x)$ is given by

$$\begin{aligned} V^{{{\mathbbm {u}}}_0}(x) = \frac{x}{\delta } - \frac{\lambda \pi \left( Y\right) -c}{\delta ^2} \left[ 1-e^{\frac{-\delta x}{\lambda \pi \left( Y\right) -c}}\right] . \end{aligned}$$

The following result presents bounds on increments of the value function and also provides its continuity.

Proposition 2

For $x >y \ge 0$, the value function satisfies:

• (a) $V(x)-V(y) \le \frac{x-y}{\delta } + C(x,y)\,V(x-y)$, where $C(x,y)\rightarrow 0$ as $\vert \,x-y\,\vert \rightarrow 0,$

• (b) $V(x) -V(y) \ge \frac{x-y}{\delta +\lambda }.$

Proof

For given $x>0$ and given $\epsilon >0$, consider an admissible $\epsilon$-optimal strategy ${\mathbbm {u}}$ such that

$$\begin{aligned} V(x) \le \mathbb {E}_x \left[ \int _0^{\tau _x^{{\mathbbm {u}}}} e^{-\delta t}X_t^{{\mathbbm {u}}} dt\right] + \epsilon . \end{aligned}$$

Since ${\mathbbm {u}}$ is also admissible for initial capital y with $x>y\ge 0$ (up to time $\tau _y^{{\mathbbm {u}}}$), we have

$$\begin{aligned} V(x)-V(y) \le \mathbb {E}_x \left[ \int _0^{\tau _x^{{\mathbbm {u}}}}e^{-\delta t}X_t^{{\mathbbm {u}}} dt \right] - \mathbb {E}_y \left[ \int _0^{\tau _y^{{\mathbbm {u}}}} e^{-\delta t}X_t^{{\mathbbm {u}}} dt \right] + \epsilon , \end{aligned}$$

(6)

where $\mathbb {E}_x,\,\mathbb {E}_y$ indicate the starting value of the corresponding process. Now we are going to use a pathwise argument, let $\mathscr {E} =\{\omega \in \varOmega \,\vert \,\tau _x^{{\mathbbm {u}}}(\omega ) = \tau _y^{{\mathbbm {u}}}(\omega )\}$. Notice that on $\mathscr {E}$ the paths (for fixed $\omega$) of the reserves started in x and y move parallel with a distance $x-y>0$ and get ruined at the same point in time. Therefore, we can rewrite the above inequality in the following way,

$$\begin{aligned} V(x)-V(y)&\le \mathbb {E}_x \left[ \int _0^{\tau _y^{{\mathbbm {u}}}} e^{-\delta t}X_t^{{\mathbbm {u}}} dt \right] -\mathbb {E}_y\left[ \int _0^{\tau _y^{{\mathbbm {u}}}}e^{-\delta t}X_t^{{\mathbbm {u}}}dt\right] \nonumber \\&\quad + \mathbb {E}_x\left[ \mathbbm {1}_{\mathscr {E}^c}\int _{\tau _y^{{\mathbbm {u}}}}^{\tau _x^{{\mathbbm {u}}}} e^{-\delta t}X_t^{{\mathbbm {u}}}dt\right] +\epsilon \nonumber \\&\le \frac{(x-y)}{\delta }+\mathbb {E}_x\left[ \mathbbm {1}_{\mathscr {E}^c}\int _{\tau _y^{{\mathbbm {u}}}}^{\tau _x^{{\mathbbm {u}}}} e^{-\delta t}X_t^{{\mathbbm {u}}}dt\right] +\epsilon \nonumber \\&\le \frac{(x-y)}{\delta }+\mathbb {E}\left[ \mathbbm {1}_{\mathscr {E}^c}\right] V(x-y)+\epsilon . \end{aligned}$$

(7)

The first inequality is just a restatement of (6). It incorporates the fact that the two values, the values of the strategy ${\mathbbm {u}}$ for surplus processes started in x and y, only differ on $\mathscr {E}^c$. This difference is given by the third expectation, in which $\mathbb {E}_x$ indicates that the surplus within the integral is started at x. The second inequality follows from the observation that

$$\begin{aligned} \mathbb {E}_x\left[ \int _0^{\tau _y^{{\mathbbm {u}}}} e^{-\delta t}X_t^{{\mathbbm {u}}} dt\right] -\mathbb {E}_y\left[ \int _0^{\tau _y^{{\mathbbm {u}}}}e^{-\delta t}X_t^{{\mathbbm {u}}}dt\right]&=\mathbb {E}\left[ \int _0^{\tau _y^{{\mathbbm {u}}}}e^{-\delta t}(x-y)dt\right] \\&\le \int _0^{\infty }e^{-\delta t}(x-y)dt. \end{aligned}$$

The last inequality uses $X_{\tau _y^{{\mathbbm {u}}}}^{{\mathbbm {u}}}\le x-y$ for the reserve started in x and that consequently the corresponding expectation is smaller than $V(x-y)$. Define $\theta =\inf \{t\ge 0\,\vert \,X_t^{{\mathbbm {u}}}<x-y\}$ and $C(x,y):=\mathbb {E}\left[ \mathbbm {1}_{\mathscr {E}^c}\right] =P(\tau _y^{{\mathbbm {u}}}<\tau _x^{{\mathbbm {u}}})=P_x(\theta <\tau _x^{{\mathbbm {u}}})$. Observing that $C(x,y)\rightarrow 0$ if $\vert \, x-y\,\vert \rightarrow 0$ yields (a).

Let us now prove inequality (b). Let $y\ge 0$ and $\epsilon >0$ be given, consider an admissible strategy $\bar{{\mathbbm {u}}}$ such that $V^{\bar{{\mathbbm {u}}}}(y)+\epsilon \ge V(y)$. For $x>y$, we have,

$$\begin{aligned} V(x)-V(y)&\ge \mathbb {E}_x \left[ \int _0^{\tau _x^{\bar{{\mathbbm {u}}}}} e^{-\delta t}X_t^{\bar{{\mathbbm {u}}}} dt \right] - \mathbb {E}_y\left[ \int _0^{\tau _y^{\bar{{\mathbbm {u}}}}}e^{-\delta t}X_t^{\bar{{\mathbbm {u}}}}dt\right] -\epsilon .\\ \end{aligned}$$

Again, let $\mathscr {E} =\{\tau _x^{\bar{{\mathbbm {u}}}} = \tau _y^{\bar{{\mathbbm {u}}}}\}$ and let $T_1$ be the time of the first claim occurrence. We can write

$$\begin{aligned}&V(x)-V(y) \ge \mathbb {E}_x\left[ \int _0^{\tau _y^{\bar{{\mathbbm {u}}}}} e^{-\delta t}X_t^{\bar{{\mathbbm {u}}}} dt \right] -\mathbb {E}_y \left[ \int _0^{\tau _y^{\bar{{\mathbbm {u}}}}} e^{-\delta t}X_t^{\bar{{\mathbbm {u}}}}dt\right] \\&\quad +\mathbb {E}_x \left[ \mathbbm {1}_{\mathscr {E}^c} \int _{\tau _y^{\bar{{\mathbbm {u}}}}}^{\tau _x^{\bar{{\mathbbm {u}}}}} e^{-\delta t}X_t^{\bar{{\mathbbm {u}}}} dt \right] -\epsilon \ge \mathbb {E}\left[ \int _0^{T_1}e^{-\delta t}(x-y)dt\right] -\epsilon = \frac{x-y}{\delta +\lambda } -\epsilon . \end{aligned}$$

From the arbitrariness of $\epsilon >0$, we get the result.

Additionally, we can derive the following.

Lemma 1

The value function V is locally Lipschitz continuous.

Proof

For given $x >0$ and $\epsilon >0$, consider an admissible strategy ${\mathbbm {u}}=(u_t^x)_{t\ge 0}$ such that

$$\begin{aligned} V(x) \le \mathbb {E}_x \left[ \int _0^{\tau _x^{{\mathbbm {u}}}} e^{-\delta t}X_t^{{\mathbbm {u}}} dt\right] + \epsilon . \end{aligned}$$

Let $u\in \mathcal {U}$ such that the net drift of the surplus is positive, i.e., $c(u)>\lambda \mathbb {E}(r(Y,u))>0$. Furthermore, we set $\theta _x=\inf \{t\ge 0\,\vert \,X_t^u\ge x\;\text{ with }\;X_0^u=y\}$. Now we can define an admissible strategy ${\mathbbm {u}}^y=(u^y_t)_t\ge 0$ for initial capital y, with $0\le y\le x$, by $u_t^y=u$ for $0\le t<\theta _x$ and $u_t^y=u^x_{t-\theta _x}$ for $t\ge \theta _x$. Notice, if the first claim occurs at $T_1>\frac{x-y}{c(u)}$, then level x is directly reached from level y. We have,

$$\begin{aligned} V(y)&\ge \mathbb {E}_y\left( \int _0^{\tau _y^{{\mathbbm {u}}^y}} e^{-\delta t} X_t^{{\mathbbm {u}}^y}\,dt\right) \\&\ge P\left( T_1>\frac{x-y}{c(u)}\right) \left( \int _0^{\frac{x-y}{c(u)}} e^{-\delta t} [y+c(u)t]\,dt+e^{-\delta \frac{x-y}{c(u)}}(V(x)-\epsilon )\right) . \end{aligned}$$

Finally, after explicitly evaluating the last estimate we derive for $x>y\ge 0$,

$$\begin{aligned} 0\le V(x)-V(y)&\le V(x)\left( 1-e^{-(\delta +\lambda )\frac{x-y}{c(u)}}\right) \\&\quad -e^{-\lambda \frac{x-y}{c(u)}} \left( \frac{c+\delta y-(c+\delta x)e^{-\delta \frac{x-y}{c(u)}}}{\delta ^2}\right) +\epsilon \\&=V(x)\left( \frac{\delta +\lambda }{c(u)}(x-y)+\mathcal {O}(x-y)^2\right) \\&\quad +\frac{x}{c(u)}(x-y)+\mathcal {O}(x-y)^2+\epsilon . \end{aligned}$$

This implies that V is locally Lipschitz continuous.

Finally, we can summarize the following elementary properties of the value function V(x). Notice that absolute continuity follows from the local Lipschitz continuity mentioned in the previous Lemma.

Corollary 1

The value function V is strictly positive, linearly bounded, monotone increasing and absolutely continuous.

Remark 3

Suppose we assume in the proof of part (a) of Proposition 2, that for all $u\in \mathcal {U}$ the random variable r(Y, u) admits a bounded density $f_r^u$. Then, we can formally derive

$$\begin{aligned} P(\tau _y^{{\mathbbm {u}}}<\tau _x^{{\mathbbm {u}}})&=\int _0^\infty P(\tau _y^{{\mathbbm {u}}}<\tau _x^{{\mathbbm {u}}}\,\vert \, X^{{\mathbbm {u}}}_{\tau _y^{{\mathbbm {u}}}-}=w)P(X^{{\mathbbm {u}}}_{\tau _y^{{\mathbbm {u}}}-}=w)dw\\&=\int _0^\infty P(w<r(Y,u_{\tau _y^{{\mathbbm {u}}}})\le w+x-y) P(X^{{\mathbbm {u}}}_{\tau _y^{{\mathbbm {u}}}-}=w)dw\\&=\int _0^{\infty }\int _{w}^{w+x-y}f_r^{u_{\tau _y^{{\mathbbm {u}}}}}(z)dz\,P(X^{{\mathbbm {u}}}_{\tau _y^{{\mathbbm {u}}}}=w)dw\le (x-y)\overline{f_r}, \end{aligned}$$

where $\overline{f_r}$ denotes a bound of $f_r$. Since $P(\tau _y^{{\mathbbm {u}}}<\tau _x^{{\mathbbm {u}}})=\mathbb {E}\left[ \mathbbm {1}_{\mathscr {E}^c}\right]$, we get from (7) that the value function is globally Lipschitz continuous. For example, this case appears when dealing with proportional reinsurance.

For further investigations, we need to improve on the lower bound from Proposition 1. When dealing with a contraction operator later on, the refined bound will allow us to describe the growth behaviour of the value function in a more precise way.

We start with showing that for

$$\begin{aligned} g(x)=\left\{ \begin{array}{c@{\quad }c} \frac{x}{\delta }, &{} x\ge 0,\\ 0,&{} x<0, \end{array}\right. \end{aligned}$$

$\mathcal {L}g(x)-\delta g(x)+x>0$ holds for all $x\ge 0$, where $\mathcal {L}g(x) := cg'(x) + \lambda \left( \int _0^x g(x-y)dF_Y(y) -g(x)\right)$ is the infinitesimal generator of the uncontrolled process X. For that purpose, we define

$$\begin{aligned} H(x):&= \mathcal {L}g(x)-\delta g(x)+x=x+\frac{c}{\delta }-(\delta +\lambda )\frac{x}{\delta }+\lambda \int _0^x\frac{x-y}{\delta }\,dF_Y(y), \end{aligned}$$

which can be rewritten as

$$\begin{aligned} H(x) = \frac{c}{\delta } + \frac{\lambda }{\delta }\left( x(F_Y(x)-1) \right) - \frac{\lambda }{\delta } \int _0^x y\, dF_Y(y). \end{aligned}$$

From $H'(x)= \frac{\lambda }{\delta }(F_Y(x)-1) \le 0$ for all $x \ge 0$, we have that H(x) is monotone decreasing. Determination of the boundary values, $H(0) = \frac{c}{\delta }>0$ and $\lim _{x \rightarrow \infty } H(x) = \frac{c- \lambda \mu }{\delta } >0$, implies that it is strictly positive as well.

Lemma 2

The value function V is bounded from below by $\frac{x}{\delta }+\frac{c-\lambda \mu }{\delta (\delta +\lambda )}$, i.e.,

$$\begin{aligned} V(x)\ge \frac{x}{\delta }+\frac{c-\lambda \mu }{\delta (\delta +\lambda )}. \end{aligned}$$

(8)

Proof

Since g(x) is differentiable we can apply Dynkin’s formula and get

$$\begin{aligned} \mathbb {E}_x\left( e^{-\delta t \wedge \tau }g(X_{t \wedge \tau }) \right) = g(x) +\mathbb {E}_x\left( \int _0^{t \wedge \tau } e^{-\delta s} \left[ \mathcal {L}g(X_s)-\delta g(X_s)\right] ds\right) . \end{aligned}$$

From above, we already know that $\mathcal {L}g(X_s)-\delta g(X_s)\ge -X_s+\frac{c-\lambda \mu }{\delta }$, using this estimate, we arrive at,

$$\begin{aligned} \mathbb {E}_x\left[ e^{-\delta t \wedge \tau }g(X_{t \wedge \tau }) \right] +\mathbb {E}_x\left[ \int _0^{t \wedge \tau }e^{-\delta s}X_s\,ds\right]&\ge g(x)+\mathbb {E}_x\left[ \int _0^{t \wedge \tau }e^{-\delta s}\frac{c-\lambda \mu }{\delta }ds\right] \\&\ge g(x)+\mathbb {E}_x\left[ \int _0^{t \wedge T_1}e^{-\delta s}\frac{c-\lambda \mu }{\delta }ds\right] , \end{aligned}$$

where $T_1$ denotes the time of the first claim occurrence. Using linear boundedness of $g(X_{t \wedge \tau })$ in t and monotone convergence, we arrive at

$$\begin{aligned} \mathbb {E}_x\left[ \int _0^{\tau }e^{-\delta s}X_s\,ds\right] \ge g(x)+\frac{c-\lambda \mu }{\delta (\delta +\lambda )}. \end{aligned}$$

From its definition, we get

$$\begin{aligned} V(x)\ge \mathbb {E}_x\left[ \int _0^{\tau }e^{-\delta s}X_s\,ds\right] \ge \frac{x}{\delta }+\frac{c-\lambda \mu }{\delta (\delta +\lambda )}. \end{aligned}$$

Remark 4

By well known methods, as outlined in Asmussen and Albrecher (2010, Ch.I.4, Ch.IX.3), $f(x):= \mathbb {E}_x\left[ \int _0^{\tau }e^{-\delta s}X_s\,ds\right]$ can be computed explicitly for Erlang distributed claims.

3.2 Characterization of the value function

Based on the elementary properties of the value function which are collected in Corollary 1, we can work out the dynamic programming approach for solving the optimization problem.

We start with observing that V fulfills the dynamic programming principle, that is, for every $\mathcal {F}_t$-adapted stopping time $S \ge 0$ the following relation is valid:

$$\begin{aligned} V(x) = \sup _{u \in \mathfrak {U}}\mathbb {E}_x\left[ \int _0^{\tau ^u_x \wedge S} e^{-\delta t}X_t^u dt+e^{-\delta (\tau ^u_x\wedge S)}V\left( X^u_{\tau ^u_x\wedge S}\right) \right] . \end{aligned}$$

(9)

The proof of this fact is mainly based on the continuity of V and follows standard arguments from the corresponding literature, see for instance the proof of Azcue and Muler (2014, Prop.2.3).

The following Lemma shows that at least in some weak sense V fulfills the associated Hamilton–Jacobi–Bellman equation.

Lemma 3

The value function V defined in (5) is a.e. a solution to:

$$\begin{aligned} 0=\sup _{u\in \mathcal {U}}\{x+c(u)V'(x)-(\delta +\lambda )V(x)+\lambda \,\int _0^{\rho (x,u)}V(x-r(y,u))\,dF_Y(y)\}. \end{aligned}$$

(10)

Proof

In a first step we show that (10) is smaller equal to zero. Fix $x>0, h>0$ and let $u\in \mathcal {U}$. Define $\tilde{{\mathbbm {u}}}=(u_t)_{t\ge 0}$ such that $u_t=u$ for $t\in [0,h]$ and $u_t=\tilde{u}_{t-h}$ for $t>0$ for some $\tilde{u}\in \mathfrak {U}$. If necessary, we choose h small enough such that $x+c(u)h>0$. Let $T_1$ denote the time of the first claim occurrence and set $S=\min \{T_1,h\}$. Then, (9) yields

$$\begin{aligned} 0&\ge \mathbb {E}_x \left[ \int _0^{S} e^{-\delta t} \left( x+c(u)t\right) \, dt + e^{-\delta S}\,V \left( X_{S} ^{\tilde{{\mathbbm {u}}}}\right) -V(x)\right] . \end{aligned}$$

(11)

Since u is a constant control which applies on the time horizon [0, S] we can apply Rolski et al. (1999, Th.11.2.2) and get that $V\in \mathcal {D}(\mathcal {A}^u)$, i.e., V lies in the domain of the generator. In the present situation the generator $\mathcal {A}^u$ of the constantly controlled process $X^u$ is given by

$$\begin{aligned} \mathcal {A}^ug(x)=c(u)g'(x)-\lambda g(x)+\lambda \int _0^{\rho (x,u)}g(x-r(x,y))dF_Y(y). \end{aligned}$$

The particular result from Rolski et al. (1999, Th.11.2.2) applies, because the map $t\mapsto V(x+c(u)t)$ is absolutely continuous, the so-called active boundary is empty and the bounds from Proposition 1 and Proposition 2 guarantee the asked for integrability condition. Therefore we can apply Dynkin’s formula, identifying $V'$ with the measurable density of V, and can rewrite (11) to

$$\begin{aligned} 0&\ge \mathbb {E}_x \left[ \int _0^{S} e^{-\delta t} \left( x+c(u)t\right) \, dt\right. \\&\quad \left. +\int _0^S\,e^{-\delta t}\Bigg (c(u)V'(x+c(u)t)-(\delta +\lambda )V( x+c(u)t)\right. \\&\quad \left. +\,\lambda \int _0^{\rho (x+c(u)t,u)}V(x+c(u)t-r(y,u))dF_Y(y)\Bigg )dt\right] . \end{aligned}$$

After regrouping and division by h we have

$$\begin{aligned} 0 \ge \;&\frac{1}{h}\,\mathbb {E}_x \left[ \int _0^{S} e^{-\delta t}\Bigg (x+c(u)t-(\delta +\lambda )V(x+c(u)t)\right. \\&\left. \quad +\,\lambda \int _0^{\rho (x+c(u)t,u)}V(x+c(u)t-r(y,u))dF_Y(y)\Bigg )\,dt\right] \\&\quad +\frac{1}{h}\mathbb {E}_x\left[ \int _0^S\,e^{-\delta t} c(u)V'(x+c(u)t)dt\right] . \end{aligned}$$

The integral in the first expectation can be interpreted in the Riemann sense, V is continuous, such that sending $h\rightarrow 0$ leads to

$$\begin{aligned} 0 \ge \;&x-(\delta +\lambda )V(x)-(\delta +\lambda )V(x)+\lambda \int _0^{\rho (x,u)}V(x-r(y,u))dF_Y(y)\\&+\lim _{h \searrow 0}\frac{1}{h}\,\mathbb {E}_x\left[ \int _0^S\,e^{-\delta t}c(u)V'(x+c(u)t)\,dt\right] . \end{aligned}$$

The second limitation procedure needs a bit more care since the integrands as functions in t are only measurable and the respective integral is interpreted in the Lebesgue sense. For this purpose consider

$$\begin{aligned}&\lim _{h \searrow 0}\frac{1}{h}\,\mathbb {E}_x\left[ \int _0^S\,e^{-\delta t}c(u)V'(x+c(u)t)\,dt\right] \\&\quad =\lim _{h\searrow 0}e^{-\lambda h}\frac{1}{h}\,\int _0^h e^{-\delta t}c(u)V'(x+c(u)t)\,dt\\&\quad \quad + \lim _{h\searrow 0}\frac{1}{h}\,\int _0^h\lambda e^{-\lambda s}\int _0^s e^{-\delta t}c(u)V'(x+c(u)t)\,dt\,ds\\&\quad =c(u)V'(x)\quad \text{ a.e. }, \end{aligned}$$

where in the second equality we used Lebesgue’s Differentiation Theorem from Wheeden and Zygmund (1977, Th.7.16) which applies since the measurable density $V'$ certainly is locally integrable in the Lebesgue sense because of the bounds on the function V and its increments. One may notice that

$$\begin{aligned} \lim _{h\searrow 0}\frac{1}{h}\,\int _0^h\lambda e^{-\lambda s}\int _0^s e^{-\delta t}c(u)V'(x+c(u)t)\,dt\,ds=0\quad \text{ a.e. }, \end{aligned}$$

since the ds integrand equals zero for $s=0$. The choice of the control parameter $u\in \mathcal {U}$ was arbitrary, such that we have

$$\begin{aligned} 0&\ge \;\sup _{u\in \mathcal {U}}\{x+c(u)V'(x)-(\delta +\lambda )V(x)\\&\quad +\lambda \,\int _0^{\rho (x,u)}V(x-r(y,u))\,dF_Y(y)\}\quad \text{ a.e. } \end{aligned}$$

We can turn to the second step, showing that (10) is also larger or equal to zero. Set again $S=\min \{T_1,h\}$ for some $h>0$ and let the strategy ${\mathbbm {u}}^1=(u^1_t)_{t\ge 0}$ be $h^2-$optimal for the right hand side of (9), that is

$$\begin{aligned} V(x)&=\sup _{u \in \mathfrak {U}}\mathbb {E}_x\left[ \int _0^{S} e^{-\delta t} (x+\int _0^t c(u_s)ds) dt+e^{-\delta S}V(X^u_{S})\right] \\&<\; \mathbb {E}_x\left[ \int _0^S e^{-\delta t}(x+\int _0^t c(u_s^1)ds) dt+e^{-\delta S}V(X^{{\mathbbm {u}}^1}_{S})\right] +h^2+\epsilon \,h, \end{aligned}$$

where we added the term $\epsilon \,h$ with some arbitrary $\varepsilon >0$ for achieving strict positivity. In the above equation we can use $T_1\sim \text{ Exp }(\lambda )$ and regroup a little bit to arrive at

$$\begin{aligned} 0<&\mathbb {E}_x\left[ \int _0^S e^{-\delta t}(x+\int _0^t c(u_s^1)ds) dt\right] +(e^{-(\delta +\lambda )h}-1)\mathbb {E}_x\left[ V(x+\int _0^h c(u_s^1)ds)\right] \\&+\mathbb {E}_x\left[ \int _0^h\lambda e^{-\lambda t}\int _0^{\rho (x+\int _0^t c(u_s^1)ds,u^1_t)}V(x+\int _0^t c(u_s^1)ds-r(y,u_t^1)dF_Y(y)\,dt\right] \\&+\mathbb {E}_x\left[ V(x+\int _0^h c(u_s^1)ds)-V(x)\right] +h^2+\epsilon \,h\\&=:A+B+C+D+h^2+\epsilon \,h. \end{aligned}$$

We kept $\mathbb {E}_x$ since ${\mathbbm {u}}^1$ is still stochastic on the time interval under consideration. In the following we divide $A,\,B,\,C,\,D$ by h and study the limits as h tends to zero - for interchanging limitation and expectation we will repeatedly make use of the dominated convergence Theorem. We start with discussing B:

$$\begin{aligned} \lim _{h\searrow 0}\frac{e^{-(\delta +\lambda )h}-1}{h}\,\mathbb {E}_x\left[ V(x+\int _0^h c(u_s^1)ds)\right] =-(\delta +\lambda )V(x), \end{aligned}$$

which follows from continuity of V. Next we deal with C:

$$\begin{aligned}&\lim _{h\searrow 0}\frac{1}{h}\, \mathbb {E}_x\left[ \int _0^h\lambda e^{-\lambda t}\int _0^{\rho (x+\int _0^t c(u_s^1)ds,u^1_t)}V(x+\int _0^t c(u_s^1)ds-r(y,u_t^1)dF_Y(y)\,dt\right] \\&\quad =\lambda \int _0^{\rho (x,u^1_0)}V(x-r(y,u_0^1)dF_Y(y)\quad \text{ a.e. }, \end{aligned}$$

which is derived by an application of Wheeden and Zygmund (1977, Th.7.16). For part D we exploit a similar procedure together with the absolute continuity of V,

$$\begin{aligned}&\lim _{h\searrow 0}\frac{1}{h}\,\mathbb {E}_x\left[ V(x+\int _0^h c(u_s^1)ds)-V(x)\right] \\&\quad = \lim _{h\searrow 0}\frac{1}{h}\,\mathbb {E}_x\left[ \int _0^{\int _0^h c(u_s^1)ds)}V'(x+y)dy\right] \\&\quad =\lim _{h\searrow 0}\frac{1}{h}\,\mathbb {E}_x\left[ \int _0^{h}c(u_t^1)V'(x+\int _0^t c(u_s^1)ds)dt\right] =c(u^1_0)V'(x)\quad \text{ a.e. } \end{aligned}$$

Part A is resolved in the same way and delivers

$$\begin{aligned} \lim _{h\searrow 0}\frac{1}{h}\,\mathbb {E}_x\left[ \int _0^S e^{-\delta t}(x+\int _0^t c(u_s^1)ds) dt\right] =x. \end{aligned}$$

Finally we arrive at

$$\begin{aligned} 0&\le \,x+c(u^1_0)V'(x)-(\delta +\lambda )V(x)\\&\quad +\lambda \int _0^{\rho (x,u^1_0)}V(x-r(y,u_0^1)dF_Y(y)+\varepsilon \quad \text{ a.e. }, \end{aligned}$$

which concludes the proof since $\varepsilon$ was arbitrary.

At this point, we know that the value function is in some sense a solution to the associated HJB-equation. What remains to be done for a complete analytical characterization is a complement on uniqueness. For accomplishing such a result we are going to rewrite (10) in a way similar Schmidli as (2008, p. 47) did, when transforming equation (2.14) into (2.15).

Suppose x is meaningful in the sense that $V'(x)$ exists. Since the set $\mathcal {U}$ is compact and all corresponding terms are continuous in u, a maximizer u(x) exists such that the supremum equal to zero is attained. Replacing the $\sup _u$ by u(x) in (10) we have

$$\begin{aligned} 0= x+c(u(x))V'(x)-(\delta +\lambda )V(x)+\lambda \,\int _0^{\rho (x,u(x))}V(x-r(y,u(x)))\,dF_Y(y), \end{aligned}$$

(12)

from which we can observe, using the lower bound (8) on V(x), that $c(u(x))V'(x)>0\;\Rightarrow \;c(u(x))>0$. Hence, in the supremum we can replace the set $\mathcal {U}$ by the set $\tilde{\mathcal {U}}=\{u\in \mathcal {U}\,\vert \,c(u)>0\}$. Since V(x) is monotone, we can rewrite (10) into the equivalent form:

$$\begin{aligned} V'(x)=\inf _{u\in \tilde{\mathcal {U}}}\left\{ \frac{(\delta +\lambda )V(x)-x-\lambda \int _0^{\rho (x,u)}V(x-r(y,u))dF_Y(y)}{c(u)}\right\} . \end{aligned}$$

(13)

Formally, we know that a.e. V(x) is a solution to (13). In addition, for x such that $V'(x)$ exists, we have the following,

$$\begin{aligned} V'(x)&= \inf _{u \in \mathcal {\tilde{U}}} \left\{ \frac{(\delta + \lambda )V(x)-x-\lambda \int _0^{\rho (x,u)}V\left( x-r(y,u)\right) dF_Y(y)}{c(u)}\right\} \nonumber \\&\le \frac{(\delta + \lambda )V(x)-x-\lambda \int _0^x V\left( x-y\right) dF_Y(y)}{c}\nonumber \\&\le \frac{(\delta + \lambda )\left( \frac{x}{\delta }+ \frac{c}{\delta ^2} \right) -x- \lambda \int _0^x \frac{x-y}{\delta }dF_Y(y)}{c}\nonumber \\&\le \frac{\frac{(\delta + \lambda )c}{\delta ^2} + \frac{\lambda \mu }{\delta }+M(x)}{c}, \end{aligned}$$

(14)

where $M(x):= \frac{\lambda }{\delta }x\left( 1-F_Y(x)\right)$. Clearly, $M(x) \ge 0$ for all $x \ge 0$. Moreover, we have $\frac{\lambda }{\delta }\mu \ge \frac{\lambda }{\delta }\int _x^{\infty }x dF_Y(z)=M(x)$, which can be used in (14), leading to

$$\begin{aligned} V'(x) \le \frac{\frac{(\delta + \lambda )c}{\delta ^2} + \frac{2\lambda \mu }{\delta }}{c}. \end{aligned}$$

(15)

Reinspecting (12) gives a positive lower bound on c(u(x)),

$$\begin{aligned} c(u(x))V'(x)&=(\delta +\lambda )V(x)-x-\lambda \,\int _0^{\rho (x,u(x))}V(x-r(y,u(x)))\,dF_Y(y)\\&= \delta V(x)-x+\lambda \left( V(x)-\int _0^{\rho (x,u(x))}V(x-r(y,u(x)))\,dF_Y(y)\right) \\&\ge \frac{c-\lambda \mu }{\delta +\lambda }, \end{aligned}$$

where the last inequality is due to Lemma 2. Together with (15) we have

$$\begin{aligned} c(u(x))\ge \frac{c-\lambda \mu }{\delta +\lambda }\left( \frac{\frac{(\delta + \lambda )c}{\delta ^2} + \frac{2\lambda \mu }{\delta }}{c} \right) ^{-1}=:L>0. \end{aligned}$$

As a consequence, we can redefine the crucial set for taking the supremum (resp. $\inf$) $\tilde{\mathcal {U}}=\{u\in \mathcal {U}\,\vert \,c(u)\ge L\}$. One may notice that in (13) the infimum is taken again over a compact set and that the denominator is uniformly bounded away from zero.

The first step towards a unique characterization of the value function is given in the following theorem the proof of which relies on the fixed point property of a certain operator (inspired by a similar approach used in Azcue and Muler (2005, (2014)).

Theorem 1

Let $f(0)>0$ be some given initial value, then there exists a unique a.e. differentiable solution to

$$\begin{aligned} g'(x)=\inf _{u\in \tilde{\mathcal {U}}}\left\{ \frac{(\delta +\lambda )g(x)-x-\lambda \int _0^{\rho (x,u)}g(x-r(y,u)dF_Y(y)}{c(u)}\right\} , \end{aligned}$$

with $g(0)=f(0)$.

Proof

Let $x_0 \ge 0$ and a continuous function $f:[0,x_0]\rightarrow \mathbb {R}$ be given. Fix $h>0$ and set $\mathcal {C}=\{g:[x_0,x_0+h]\rightarrow \mathbb {R}\,\vert \, g\,\text{ is } \text{ continuous } \text{ and }\, g(x_0)=f(x_0)\}$. The operator

$$\begin{aligned}&\mathcal {T}g(x)= f(x_0) \\&\quad + \int _{x_0}^x \inf _{u \in \mathcal {\tilde{U}}} \left\{ \frac{(\delta + \lambda )g(s)-s-\lambda \int _0^{\rho (s-x_0,u)}g(s-r(y,u))dF_Y(y) -\lambda \int _{\rho (s-x_0,u)}^{\rho (s,u)}f(s-r(y,u))dF_Y(y)}{c(u)} \right\} ds, \end{aligned}$$

is defined on $\mathcal {C}$ and $x\in [x_0,x_0+h]$ and clearly $\mathcal {T}g\in \mathcal {C}$. Since for all $s\in [x_0,x_0+h]$ all terms involving u are continuous in it and the infimum is taken over a compact set, we know that a minimizer u(s) exists.

Now let $g_1,\,g_2\,\in \mathcal {C}$ and $u^1(s),\,u^2(s)$ be the corresponding minimizers, we get

$$\begin{aligned}&\mathcal {T}g_1(x)-\mathcal {T}g_2(x)\\&\quad \le \int _{x_0}^x\frac{(\delta +\lambda )[g_1(s)-g_2(s)]-\lambda \int _0^{\rho (s-x_0,u^2(s))}[g_1(s-r(y,u^2(s)))-g_2(s-r(y,u^2(s)))]dF_Y(y)}{c(u^2(s))}ds \\&\quad \le h\frac{(\delta +2 \lambda )}{L}\sup _{s\in [x_0,x_0+h]}\vert \,g1(s)-g_2(s)\,\vert . \end{aligned}$$

Interchanging the roles of $g_1$ and $g_2$ and choosing $h=\frac{L}{2(\delta +2\lambda )}$ we get,

$$\begin{aligned} \left| \,\mathcal {T}g_1(x)-\mathcal {T}g_2(x)\,\right| \le \frac{1}{2}\sup _{s\in [x_0,x_0+h]}\vert \,g_1(s)-g_2(s)\,\vert ,\quad \forall \,x\in [x_0,x_0+h], \end{aligned}$$

such that $\mathcal {T}$ is a contraction on $\mathcal {C}$ and that consequently an unique fixed point of it exists. Since h and the contraction factor do not depend on $x_0$, we can iterate this procedure on the intervals $[0,h],\,[h,2h],\ldots$. Finally, we observe that these fixed points, on the end points of the intervals $[k\,h,(k+1)\,h]$ continuously pasted, induce an unique solution to (13) with given initial value f(0). By construction, this solution is absolutely continuous on $\mathbb {R}^+$, since one may alter the grid for the construction procedure.

We are now able to finalize the analytical characterization of V.

Theorem 2

Suppose $g:\mathbb {R}\rightarrow \mathbb {R}$ with $g(x)=0$ for $x<0$ is linearly bounded by $\frac{x}{\delta }+\frac{c}{\delta ^2}$ and an absolutely continuous solution to (13), then $g(x)=V(x)$. The optimal strategy ${\mathbbm {u}}^*=(u^*_t)_{t\ge 0}$ is induced by the pointwise minimizer u(x) of (13) such that $u_t^*=u(X_{t-}^{{\mathbbm {u}}^*})$.

Remark 5

One can use verbatim the proof from Schmidli (2008, Lem.2.12) to show that the function u defining the optimal strategy is measurable. Consequently the process $(u_t^*)_{t\ge 0}$ is previsible and constitutes an admissible strategy.

Proof

Let $t>0$ and ${\mathbbm {u}}=(u_t)_{t\ge 0}\in \mathfrak {U}$, since the paths of $(X_t^{{\mathbbm {u}}})_{t\ge 0}$ are of bounded variation, we can use the Stieltjes integral to obtain

$$\begin{aligned} e^{-\delta t\wedge \tau _x^{{\mathbbm {u}}}}g(X_{t\wedge \tau _x^{{\mathbbm {u}}}}^{{\mathbbm {u}}})-g(x)= & {} \int _0^{t\wedge \tau _x^{{\mathbbm {u}}}}e^{-\delta s}\left[ -\delta g(X_s^{{\mathbbm {u}}})+c(u_s)g'(X_s^{{\mathbbm {u}}})\right] ds \nonumber \\&+\sum _{T_i\le t\wedge \tau _x^{{\mathbbm {u}}}}e^{-\delta T_i}\left[ g(X_{T_i}^{{\mathbbm {u}}})-g(X_{T_i-}^{{\mathbbm {u}}})\right] . \end{aligned}$$

(16)

The process $M=(M_t)_{t\ge 0}$ defined by

$$\begin{aligned} M_t= & {} \sum _{T_i\le t}e^{-\delta T_i}\left[ g(X_{T_i}^{{\mathbbm {u}}})-g(X_{T_i-}^{{\mathbbm {u}}})\right] \\&-\lambda \int _0^t e^{-\delta s}\left[ \int _0^{\rho (X_s^{{\mathbbm {u}}},u_s)}g(X_s^{{\mathbbm {u}}}-r(y,u_s))dF_Y(y)-g(X_s^{{\mathbbm {u}}})\right] ds, \end{aligned}$$

is a zero-mean martingale, due to compensation. Therefore, taking expectations in (16) leads to

$$\begin{aligned} \mathbb {E}_x\left[ e^{-\delta t\wedge \tau _x^{{\mathbbm {u}}}}g(X_{t\wedge \tau _x^{{\mathbbm {u}}}}^{{\mathbbm {u}}})\right]= & {} g(x)+ \mathbb {E}_x\left[ \int _0^{t\wedge \tau _x^{{\mathbbm {u}}}}e^{-\delta s}\left[ -(\delta +\lambda )g(X_s^{{\mathbbm {u}}})+c(u_s)g'(X_s^{{\mathbbm {u}}})\right. \right. \\&\left. \left. +\,\lambda \int _0^{\rho (X_s^{{\mathbbm {u}}},u_s)}g(X_s^{{\mathbbm {u}}}-r(y,u_s))dF_Y(y)\right] ds\right] . \end{aligned}$$

Remember that for $g'(X_s^{{\mathbbm {u}}})$ we have (at least a.e.)

$$\begin{aligned} g'(X_s^{{\mathbbm {u}}})=\inf _{v\in \tilde{\mathcal {U}}}\frac{(\delta +\lambda )g(X_s^{{\mathbbm {u}}})-X_s^{{\mathbbm {u}}}-\lambda \int _0^{\rho (X_s^{{\mathbbm {u}}},v)}g(X_s^{{\mathbbm {u}}}-r(y,v))dF_Y(y)}{c(v)}, \end{aligned}$$

which yields for the particular control parameter $u_s$,

$$\begin{aligned} \mathbb {E}_x\left[ e^{-\delta t\wedge \tau _x^{{\mathbbm {u}}}}g(X_{t\wedge \tau _x^{{\mathbbm {u}}}}^{{\mathbbm {u}}})\right] \le g(x)- \mathbb {E}_x\left[ \int _0^{t\wedge \tau _x^{{\mathbbm {u}}}}e^{-\delta s}X_s^{{\mathbbm {u}}}ds\right] . \end{aligned}$$

(17)

From Schmidli (2008, Lem.2.9), we know that either ruin occurs or the controlled surplus tends (linearly bounded) to infinity. Therefore, using bounded convergence in (17) results in

$$\begin{aligned} \mathbb {E}_x\left[ \int _0^{t\wedge \tau _x^{{\mathbbm {u}}}}e^{-\delta s}X_s^{{\mathbbm {u}}}ds\right] \le g(x), \end{aligned}$$

hence, $V(x)\le g(x)$. One observes that in (17) we have equality for the strategy ${\mathbbm {u}}^*$, defined in the statement of the theorem, such that finally $V(x)=g(x)$.

The combination of the statement of the last theorem with the uniqueness result and the properties of the value function enables us to state a complete characterization.

Corollary 2

The value function V is the unique solution to (10) in the set of absolutely continuous function $g:\mathbb {R}\rightarrow \mathbb {R}$ with $g(x)=0$ for $x<0$ which are bounded by $\frac{x}{\delta }+\frac{c}{\delta ^2}$. In particular just the initial value V(0) for equation (13) allows for a solution g(x) with the property $\lim _{x\rightarrow \infty }\frac{g(x)}{x}=\frac{1}{\delta }$.

4 Numerical examples

In this section, we will illustrate the theoretical results and sketch a numerical solution method by means of two examples. Furthermore, for the particular case of proportional reinsurance and a reinsurer using the expected value premium principle, we can refine the analytical results and state the asymptotic behaviour of the optimal strategy as the initial capital tends to infinity. Since an explicit solution to (10) is unfortunately out of reach, for deriving a solution one needs to rely on a numerical method. Luckily, the theoretical characterization stated in Theorem 2 and Corollary 2 constitutes an implementable procedure.

These results tell that an iterated application of the operator $\mathcal {T}$, defined in the proof of Theorem 1, on some linear function $g(x)=\frac{x}{\delta }+g_0$ leads to an approximation of the value function if and only if $g_0=V(0)$ is correctly chosen, cf. Corollary 2. Consequently, the first step in the procedure asks for a good guess of $g_0$, which can (and needs) to be improved in later steps. For determining a meaningful approximation of $g_0$, we exploit the idea of policy improvement, see for instance Bäuerle and Rieder (2011).

The starting point is the value $V^{sr}(x)$ corresponding to the situation of no reinsurance, which in our parameter setting can be explicitly determined. Based on this value $V^{sr}$, we compute a strategy ${\mathbbm {u}}^1=\{u^1_t\}$ with $u^1_t=u^1(X_t^{\mathbbm {u}})$ from the HJB-equation (10) via

$$\begin{aligned} u^1(x)&={{\mathrm{arg\,max}}}_{u\in \tilde{\mathcal {U}}}\left\{ x+c(u)\frac{\partial }{\partial x} V^{sr}(x)-(\delta +\lambda )V^{sr}(x)\right. \\&\quad \left. +\,\lambda \,\int _0^{\rho (x,u)}V^{sr}(x-r(y,u))\,dF_Y(y)\right\} . \end{aligned}$$

In a next step we determine a good approximation for $V^{{\mathbbm {u}}^1}(0)$, which can be done by using the Monte-Carlo method with direct simulations of the controlled surplus process from (4).

Now we know that $V^{{\mathbbm {u}}^1}(0)$ corresponds to an admissible strategy but does not necessarily equal V(0). But with $V^{{\mathbbm {u}}^1}(0)$ at hand we can determine $V^{{\mathbbm {u}}^1}(x)$ for $x\ge 0$ either by an iteration of an operator, similar to $\mathcal {T}$ but without the infimum in its definition, or by a finite-difference method. We use this value $V^{{\mathbbm {u}}^1}$ as the starting point of iterations of $\mathcal {T}$. After a number of iterations, one can improve the initial value again by using the same method as illustrated above, but with the function obtained from the iterations as basis for the policy improvement step. This newly obtained value $V^{{\mathbbm {u}}^2}$ then serves as the basis for new iterations of $\mathcal {T}$.

Remark 6

Alternatively, one can execute a policy iteration procedure on the basis of the original HJB-equation (10). Our experience showed that the obtained strategies are very close to the ones determined via the first method. Unfortunately, the quality of the simultaneously generated return functions is not always trustworthy, a fact which originates from the presence of the control parameter in front of the sensitive derivative term and inside the integral. Nevertheless, the use of these strategies allows for a considerable acceleration of the whole procedure.

In this way we create, by the use of policy iterations at intermediate steps, an increasing sequence of initial values and also determine candidates for a fixed point of $\mathcal {T}$. To decide whether an initial value is significantly too small one can check the behaviour of the function obtained from the corresponding iterations of $\mathcal {T}$. If an initial value is far away from V(0) we observe a violation of the lower bound from Lemma 2 for relatively small values of x. We can accept an initial value $V^*(0)$ as a good guess for V(0) if the function $V^*$ obtained from iterations stays within the theoretically given bounds. If additionally $V^*$ matches the value of the implicitly given strategy, we can accept it as an valid approximation of the value function.

Remark 7

Instead of starting the iteration procedure always at predetermined values $V^{{\mathbbm {u}}}$, we can also start with $g(x)=\frac{x}{\delta }+V^{{\mathbbm {u}}}(0)$ and all previously stated arguments still apply.

Our experience showed that this procedure leads to trustworthy results and representative illustrations of our theoretical findings. Certainly, a theoretical numerical analysis would be necessary and highly interesting but this is out of the scope of this publication.

4.1 Example: proportional reinsurance

In the following, we are going to use the model parameters given by: $Y_i\mathop {\sim }\limits ^{iid} f_Y(y)$ with $f_Y(y)=\gamma ^2 y\,e^{-\gamma y}$, i.e. $Gamma(2,\gamma )$ distributed claim amounts. The insurer’s premium rate is determined via the expected value principle and reads as $c=(1+\eta )\lambda \mu$ with $\mu =\frac{2}{\gamma }$ and $\eta >0$. For the reinsurer, we assume the same premium principle but with a safety loading $\theta >\eta$. The concrete numbers are given in Table 1.

Table 1 Set of parameters for proportional reinsurance

The considered reinsurance schema is $r(y,u)=u\,y$ for a control parameter $u\in (\underline{u},1]$ with $\underline{u}=\inf \{u\in [0,1]\;\vert \;c(u)>0\}$, as discussed before the statement of Theorem 1.

For deriving numerical approximations to the value function and to the optimal strategy, we implemented the program we have illustrated in the introduction to this section. In contrast to the case of excess of loss reinsurance, the proportional situation turned out to be numerically demanding, requiring lots of computational efforts for arriving at passably satisfying results.

The strategy obtained from 20 policy iterations steps, starting from $V^{sr}$, is depicted in Fig. 1. In the remark following below, the shape of this strategy is discussed in some detail. Figure 2 contains the graphs of $V^{sr}$ (dotted line), $V^1$ (dashed line) and $V^{20}$ (full line). $V^1$ is computed from 30 iterations of $\mathcal {T}$ starting with g and an initial value $g_{0}=212$ corresponding to the strategy obtained from 1 policy improvement step based on $V^{sr}$. The function $V^{20}$ is derived from 30 operator iterations, but using the initial value $g_{0}=226.436$ associated to the strategy from Fig. 1.

Fig. 1

Numerically obtained proportional reinsurance strategy

Fig. 2

Iteration procedure in the proportional case

In Table 2, we present some exemplary function values from the iterations of $\mathcal {T}$ towards the computation of $V^{20}$.

Table 2 Function values obtained from the application of $\mathcal {T}^n$

Remark 8

We would like to discuss $\lim _{x\rightarrow \infty }u^*(x)$, which by the numerical computations is suggested to be one. Here, we exclusively deal with the case of proportional reinsurance and the expected value premium principle for both insurer and reinsurer, $c(u)=\lambda \mu (u(1+\theta )-(\theta -\eta ))$ for safety loadings $\theta >\eta$. From the definition of the value function, we have

$$\begin{aligned} V(x)&\ge \mathbb {E}_x\left( \int _0^\tau e^{-\delta t}X_t\,dt\right) \\&= \mathbb {E}_x\left( \frac{x}{\delta }(1-e^{-\delta \tau })+ \lambda \mu \eta \int _0^\tau t\,e^{-\delta t}dt +\int _0^\tau e^{-\delta t}M_tdt\right) .\\&=\mathbb {E}_x\left( \frac{x}{\delta }(1-e^{-\delta \tau })+\frac{\eta \lambda \mu }{\delta ^2}\left( 1-e^{-\delta \tau }(1+\delta \tau )\right) +\int _0^\tau e^{-\delta t}M_tdt\right) . \end{aligned}$$

Above, we introduced the martingale $M=(M_t)_{t\ge 0}$ which is the compensated compound Poisson process:

$$\begin{aligned} M_t=\lambda \mu t-\sum _{k=1}^{N_t}Y_k,\quad M_0=0. \end{aligned}$$

Now, we can regard $\int _0^\tau e^{-\delta t}M_t dt$ pathwise as a Stieltjes integral and apply integration by parts, Wheeden and Zygmund (1977, Th.2.21), to arrive at

$$\begin{aligned} \mathbb {E}_x\left( \int _0^\tau e^{-\delta t}M_t dt\right) =\mathbb {E}_x\left( -\frac{e^{-\delta \tau }}{\delta }M_{\tau -}+\int _0^\tau \frac{e^{-\delta t}}{\delta }dM_t\right) =\mathbb {E}_x\left( -\frac{e^{-\delta \tau }}{\delta }M_{\tau -}\right) . \end{aligned}$$

(18)

In (18), the integral with respect to the martingale is itself a martingale, leading to the second equality.

At the same time, using an $\varepsilon -$optimal strategy $u^*$ for initial capital $x>0$, we have

$$\begin{aligned} V(x)-\varepsilon \le&\frac{x}{\delta }+ \mathbb {E}_x\left( \int _0^{\tau ^{u^*}} e^{-\delta t}\left( \int _0^t\lambda \mu (u_s^*(1+\theta )-(\theta -\eta ))ds-\sum _{k=1}^{N_t}u_{T_k}^* Y_k\right) dt\right) \nonumber \\ \le&\frac{x}{\delta }+\frac{\eta \lambda \mu }{\delta ^2}+ \mathbb {E}_x\left( \int _0^{\tau ^{u^*}} e^{-\delta t}M_t^* dt\right) \nonumber \\ =&\frac{x}{\delta }+\frac{\eta \lambda \mu }{\delta ^2}-\mathbb {E}_x\left( \frac{e^{-\delta \tau ^{u^*}}}{\delta }M_{\tau ^{u^*}-}^*\right) . \end{aligned}$$

(19)

If we suppose that $u^*$ is a Markov control, then we certainly have that $M_t^*=\int _0^t\lambda \mu u_s^*ds-\sum _{k=1}^{N_t}u_{T_k}^* Y_k$ is a zero mean $\mathcal {F}^X_t$ martingale and the same integration by parts procedure as before applies. Consequently, we have for x large such that $\tau$ and $\tau ^{u^*}$ ($M_t$ is linearly bounded) are tending almost surely to infinity that:

$$\begin{aligned} V(x)\sim \frac{x}{\delta }+\frac{\eta \lambda \mu }{\delta ^2}\quad \text{ as }\;x\rightarrow \infty . \end{aligned}$$

Now, we proceed with determining $\lim _{x\rightarrow \infty }u^*(x)$. Here, $u^*(x)$ denotes the pointwise maximizer in u of the HJB-equation (10), which due to continuity exists. Plugging in $c(u)=\lambda \mu (u(1+\theta )-(\theta -\eta ))$ and regrouping, we see that

$$\begin{aligned}&u^*(x)=\frac{(\delta +\lambda )V(x)-x+\lambda \mu (\theta -\eta )V'(x)-\lambda \int _0^{\frac{x}{u^*(x)}}V(x-u^*(x)y)dF_Y(y)}{\lambda \mu (1+\theta )V'(x)}\\&\quad \approx \,(\ge )\frac{(\delta +\lambda )(\frac{x}{\delta }+\frac{\eta \lambda \mu }{\delta ^2})-x +\lambda \mu (\theta -\eta )\frac{1}{\delta } -\lambda \int _0^{\frac{x}{u^*(x)}}\left[ \frac{x-u^*(x)y}{\delta }+\frac{\eta \lambda \mu }{\delta ^2}\right] dF_Y(y)}{\lambda \mu (1+\theta )\frac{1}{\delta }}\\&\quad \approx \,(\ge )\frac{ \frac{\lambda x}{\delta }(1-F_Y(x/u^*(x)))+\frac{\lambda \mu }{\delta }(\theta -\eta ) +\frac{\lambda u^*(x)}{\delta }\int _0^{\frac{x}{u^*(x)}} ydF_Y(y)+(\delta +\lambda )\frac{\eta \lambda \mu }{\delta ^2}-\frac{\lambda ^2\mu \eta }{\delta ^2}F(x/u^*(x))}{\frac{\lambda \mu }{\delta }(1+\theta )}. \end{aligned}$$

We wrote “$\approx \,(\ge )$” because in the integral, $V(x-u^*(x)y)\le \frac{x-u^*(x)y}{\delta } +\frac{\eta \lambda \mu }{\delta ^2}$, compare with (19). But since we have more or less a similar lower bound if $x\rightarrow \infty$, it becomes “$\approx$”.

If we now assume that $\lim _{x\rightarrow \infty }u^*(x)=u^*$ exists, it should fulfill

$$\begin{aligned} u^*\approx \frac{\theta +u^*}{1+\theta }, \end{aligned}$$

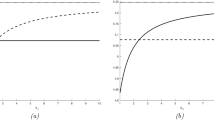
which can be fulfilled only if $u^*=1$. The two plots in Figs. 3 and 4 illustrate the sharp linear upper bound together with V(x) and $f(x)=\mathbb {E}_x\left( \int _0^\tau e^{-\delta t}X_t\,dt\right)$ for exponentially $\nu$ distributed claims and the following set of parameters given in Table 3.

Fig. 3

Illustrative optimal strategy for exponentially distribted claims

Fig. 4

The sharp upper bound for proportional reinsurance and expected value principle for premiums

4.2 Example: XL-reinsurance

As a second example, we consider the case of dynamic XL-reinsurance with $Exp(\nu )$ distributed claim amounts. The particular numbers chosen are close to the ones chosen by Hipp and Vogt (2003) and can be found in Table 4.

Table 3 Set of parameters

Table 4 Set of parameters

Fig. 5

Numerical optimal XL strategy

The numerically determined approximative optimal strategy is displayed in Fig. 5. The corresponding value function’s numerical approximation (full line) is shown in Fig. 6 together with $V^1$ (dashed line). It is remarkable to observe that this strategy consists of $u(x)=\infty$, i.e. buying no reinsurance, followed by taking exactly $u(x)=x$ and finally $u(x)\approx const.$ as the maximizing retention level for large initial capital x.

Fig. 6

Value function for XL-reinsurance

Remark 9

(Comparison with ruin probability minimization) When numerically determining the approximative optimal strategies, one observes some similarities but also differences to the situation of optimal dynamic reinsurance strategies for minimizing ruin probabilities, see Schmidli (2008, Ch. 2.3.1) and Hipp and Vogt (2003). In both situations, proportional and XL, the behaviour for small initial capital is similar, one finds that for some $x_0>0$ on $[0,x_0]$, it is optimal to take no reinsurance. From that point on, a certain amount of reinsurance is bought. For larger x, the reinsurance choice is either returning to the no reinsurance case (proportional) or converging towards a constant level (XL).

Here, the proportional case is in contrast to the situation when minimizing the ruin probability. There, for small claims the optimal reinsurance choice converges to a finite value as x tends to infinity. This different behaviour may be explained by the underlying performance measure which in the present framework is profit orientated. Because of discounting, a ruin event late in time does not bother the insurer which implies that above a certain surplus level (large enough for having early ruin just with a low probability) one is focusing on the maximal drift and not buying reinsurance. The question: “ why does the numerically optimal XL strategy behave differently?” is interesting as a future research project on its own. The answer to this question may be based on the comparison of solutions to integro-differential equations.

5 Conclusion

In this paper, we studied a dynamic optimal reinsurance problem which is derived from an economical valuation criterion in risk theory. An interplay between analytical and probabilistic arguments allowed us to characterize the associated value function and finally the theoretical results were complemented by numerical examples. Based on the alternative interpretation of the studied value function, which is given in (2), we can state, that our results suggest that reinsurance can accelerate the process of building up a free reserve and that the use of reinsurance is beneficial in the economical context.