Refining analytic approximation based estimation of mixed multinomial probit models by parameter selection

Abstract

Applying analytic approximations for computing multivariate normal cumulative distribution functions has led to a substantial improvement in the estimability of mixed multinomial probit models, both in terms of accuracy and especially in terms of computation time. This paper makes a contribution by presenting a possible way to improve the accuracy of estimating mixed multinomial probit model covariances based on the idea of parameter selection using cross-validation. Comparisons to the MACML approach indicate that the proposed parameter selection approach is able to recover covariance parameters more accurately, even when there is a moderate degree of independence between the random coefficients. The approach also estimates parameters efficiently, with standard errors tending to be smaller than those of the MACML approach, which can be observed by means of a real data case.

1 Introduction

Statistical discrete choice methods are an effective way to describe, understand and predict individual choice behavior. The decision makers may be individuals, households, firms, or any other decision-making entity, and the alternatives may represent competing products, courses of action, or other options or elements about which a decision must be made. These methods are used in empirical social research and beyond, for example in the transport sector (Train 2009; Savolainen et al. 2011).

Many different approaches can be considered to explain the role of individual features and to predict choice probabilities when individuals choose from a finite set of discrete alternatives. A widely used model in applied econometrics of discrete choice analysis is the multinomial logit model introduced by Luce (1965) and McFadden (1973). Although this approach has a simple and elegant structure, it also requires the assumption of independence from irrelevant alternatives, which means that the ratio of the choice probabilities of two alternatives is independent of the characteristics of the other alternatives in the choice set. As a result, extensions to the multinomial logit model were introduced that relaxed the assumption of independently and identically distributed errors across alternatives. Common extensions are the class of generalized extreme value models proposed by McFadden (1978) and the multinomial probit model, which allow for comparatively flexible error covariance structures up to certain limits of identifiability (Train 2009). In mixed multinomial probit modeling, random coefficients can be considered which are able to reflect random taste variation across decision makers.

However, in the absence of a closed form likelihood due to resulting multidimensional normal integrals within the process of model building, this essential advantage was usually counterbalanced by computationally burdensome simulation-based estimation approaches for mixed multinomial probit models in the past, especially when considering large choice set and many choice occasions. A way to overcome this drawback is to apply analytic approximations for multidimensional normal integrals. Instead of the actual likelihood in its non-closed form, an analytic approximation of this likelihood is used, which can be maximized efficiently over a given parameter space using gradient-based standard optimization methods. This is proposed by Joe (1995), who refines the analytic approximation method of Solow (1990), but without testing it in the context of estimating probit models. Bhat (2011) takes up this idea with the introduction of his marginal approximate composite maximum likelihood (MACML) approach for mixed multinomial probit models, which is based on the analytic approximation method of Solow (1990) and Joe (1995) (SJ).

In a companion simulation study Bhat and Sidharthan (2011) examine the performance of the MACML approach in the context of estimating parameters of mixed multinomial probit models for cross-sectional and panel data. The results indicate that the analytic approximation based estimators provide parameter estimates, which are very close to the true parameter values. The reported estimation errors are smaller than those of the applied maximum simulated likelihood approach (MSL). Furthermore, the MACML approach provides smaller standard errors and is noted to be much faster¹ than the considered MSL approach.

Patil et al. (2017) provide a simulation evaluation where different estimation techniques for a mixed multinomial probit model with five alternatives are compared. They consider cross-sectional and panel data sets for scenarios with and without correlation among the random coefficients and compare a range of different approaches: the MACML approach; the Geweke–Hajivassiliou–Keane (GHK) simulator with Halton sequences and full information maximum likelihood; the GHK approach implemented in conjunction with the composite marginal likelihood estimation approach; the GHK approach with sparse grid nodes and weights, implemented in conjunction with the composite marginal likelihood estimation approach; and a Bayesian Markov Chain Monte Carlo approach (MCMC). The results suggest that the MACML approach provides the best performance in terms of estimation accuracy and estimation time for all data-generating settings among the considered approaches. Batram and Bauer (2019) provide similar results compared to the MSL approach as part of a simulation evaluation for a cross-sectional mixed multinomial probit model with six alternatives. In addition, they consider different analytic approximation methods for the MACML approach: the SJ approximation method; the method of Mendell and Elston (1974) (ME) together with a modification of this method by Trinh and Genz (2015) (BME); and a selected method of Bhat (2018) (TVBS), who presents four new algorithms.

A closer look at the MACML results shows that there are differences between the parameters in terms of estimation errors: the estimation of the covariances between the random coefficients results in higher estimation errors than the estimation of their mean values (Bhat and Sidharthan 2011; Patil et al. 2017; Batram and Bauer 2019). To avoid singularities during optimization, the correlations between the random coefficients are not estimated directly, but via the corresponding Cholesky decomposition. Here again differences in the estimation errors become apparent. While the results of Bhat and Sidharthan (2011) and Batram and Bauer (2019) suggest that the estimation errors are smaller when there is no correlation between two random coefficients than when they are correlated, on closer examination the opposite seems to be the case. This apparent contradiction results from the fact that Bhat and Sidharthan (2011) and Batram and Bauer (2019) report an absolute percentage bias for each parameter, where the estimated absolute bias is adjusted by the true parameter value. Although this procedure may be justified with regard to the comparability of estimation errors, it is not applicable in the case of no correlation between two random coefficients. In these cases Bhat and Sidharthan (2011) and Batram and Bauer (2019) waive the adjustment² and report the difference in absolute value between mean estimate and the true value.

As a result, for Bhat and Sidharthan (2011) it appears at first that the reported mean estimation errors in the case of no correlation between two random coefficients are smaller than when they are correlated, 0.029 versus 0.076. However, if only mean absolute estimation errors are considered for all parameters to be estimated, this impression seems to be reversed, 0.029 versus 0.023. The absolute errors in the case of the true zero Cholesky parameters are thus on average over 25% higher than those of the non-zero entries. This observation is confirmed by Batram and Bauer (2019), where those errors are on average more than 30% larger. For ME, BME, and TVBS the absolute errors for the true zero Cholesky parameters are even higher: 35%, 45%, and almost 50%, respectively. Batram and Bauer (2019) provide standard and normalized MACML estimation results, where in the latter case choice proportions are normalized to sum to one. This approach results in a substantial increase in computation time. However, it also leads to significantly more accurate estimation results for ME and BME. The performance of SJ and TVBS are more or less unaffected by the normalization. The reported values refer to standard MACML estimation results for SJ and TVBS and normalized MACML estimation results for ME and BME.

This paper introduces a refined method for estimating the covariances between the random coefficients of the mixed multinomial probit model for cross-sectional data. In particular, the estimation of the zero entries of the Cholesky decomposition shall be improved by parameter selection, where the selection mechanism is based on the idea of cross-validation.

The remainder of this study is structured as follows: Sect. 2 presents the mixed multinomial probit model for cross-sectional data. Section 3 introduces the proposed parameter selection approach. The theoretical part of this study is followed by an application part in Sect. 4, in which the effectiveness of the previously introduced parameter selection approach is examined by means of its ability to recover parameters from finite samples. Section 4.1 presents the experimental design. The estimation results are provided in Sect. 4.2 and allow for comparisons to the MACML approach. Other estimation approaches are not considered based on the results of Patil et al. (2017). The application part is closed with a real data case, which is located in an online appendix.³ Sect. 5 concludes.

2 Mixed multinomial probit model

In the following the mixed multinomial probit model for cross-sectional data is presented. The notation refers to Bhat (2011).

If individuals $\left\{ 1,\ldots ,Q\right\}$ are considered who are choosing from a set of alternatives $\left\{ 1,\ldots ,I\right\}$, then the utility that individual q associates with alternative i can be modeled as $u_{qi}=\beta _{q}^{\intercal }x_{qi}+\epsilon _{qi}$, where $x_{qi}$ denotes a K-dimensional vector of exogenous characteristics of alternative i and $\beta _{q}$ is its individually specific valuation. For each individual $q\in \left\{ 1,\ldots ,Q\right\}$ the coefficient vector $\beta _{q}$ is assumed to be drawn from a multivariate normal distribution, i.e. $\beta _{q}\sim {\mathcal {N}}(b,\Omega )$. Thus, the mixed multinomial probit model overcomes limitations of the ordinary probit model by allowing for random taste variation. Furthermore, $\epsilon _{qi}$ is assumed to be independent and identically distributed with $\epsilon _{qi}\sim {\mathcal {N}}(0,\frac{1}{2})$ for model identification purpose, since the decision on one particular alternative is scale invariant. The variance is set to one-half to normalize the variances of the latent utility differences errors, which are typically not identified. This can be seen in the following.

In the case where individual q decides to choose alternative m, the corresponding utility differences are given by $y_{qim}:=u_{qi}-u_{qm}=\beta _{q}^{\intercal }(x_{qi}-x_{qm})+\epsilon _{qi}-\epsilon _{qm}$, where $i=1,\ldots ,I$ and $i\ne m$. Note that individual q chooses alternative m, if and only if $y_{qim}< 0$ holds for all $i\ne m$. In practice, $y_{qim}$ can not be observed and $y_{qim}^{*}:= \mathbb {1}_{\left\{ y_{qim}< 0\right\} }$ has to be examined instead. The likelihood contribution of individual q for choosing alternative m depends upon the proportion of K to I. If $K<I-2$, it is convenient to state the likelihood as

where $z_{qim}:=x_{qi}-x_{qm}$, $\lambda :=\sqrt{2}\epsilon _{qm}$, and $\phi _{K}(\beta \mid b, \Omega )$ denotes the K-variate normal density function at $\beta$ with mean b and positive definite covariance matrix $\Omega$. The standard univariate normal density and cumulative distribution function are denoted by $\phi (\cdot )$ and $\Phi (\cdot )$, respectively. In case of $K>I-2$, let $y_{qm}:=\begin{pmatrix} y_{qm1}, \ldots , y_{qm(m-1)}, y_{qm(m+1)}, \ldots , y_{qmI} \end{pmatrix}^{\intercal } \in \mathbb {R}^{I-1}$, $Z_{qm}:=\begin{pmatrix} x_{q1}-x_{qm}, \ldots , x_{q(m-1)}-x_{qm}, x_{q(m+1)}-x_{qm}, \ldots , x_{qI}-x_{qm} \end{pmatrix} \in \mathbb {R}^{K\times (I-1)}$, and the error differences $\epsilon _{qm}:=\big ( \epsilon _{q1}-\epsilon _{qm}, \ldots , \epsilon _{q(m-1)}-\epsilon _{qm}, \epsilon _{q(m+1)}-\epsilon _{qm}, \ldots , \epsilon _{qI}-\epsilon _{qm} \big )^{\intercal } \in \mathbb {R}^{I-1}$. The vector of utility differences can then be expressed as $y_{qm}=Z_{qm}^{\intercal }\beta _{q}+\epsilon _{qm}.$ Since $\beta _{q}$ and $\epsilon _{qm}$ are assumed to be normally distributed, $y_{qm}$ is also normally distributed with expectation $\mathbb {E}(y_{qm})=Z_{qm}^{\intercal }b$ and covariance matrix

$$\begin{aligned} \mathbb {V}(y_{qm})=Z_{qm}^{\intercal }\Omega Z_{qm}+ \begin{pmatrix} 1 &{} 0.5 &{} \dots &{} 0.5 \\ 0.5 &{} 1 &{} \ddots &{} \vdots \\ \vdots &{} \ddots &{} \ddots &{} 0.5 \\ 0.5 &{} \dots &{} 0.5 &{} 1 \end{pmatrix} =:\Sigma _{q}. \end{aligned}$$

Then the likelihood contribution of individual q for choosing alternative m is given by $L_{q}\left( b,\Omega \right) =\Phi _{I-1}\left( -Z_{qm}^{\intercal }b \mid 0,\Sigma _{q}\right) ,$ where $\Phi _{I-1}\left( -Z_{qm}^{\intercal }b \mid 0,\Sigma _{q}\right)$ denotes the $(I-1)$-variate normal cumulative distribution function at $-Z_{qm}^{\intercal }b$ with zero mean and covariance matrix $\Sigma _{q}$, whose invertibility is guaranteed by $K>I-2$. However, due to singularity problems during the estimation process, a direct estimation of the entries of $\Omega$ is usually avoided. Instead, the entries of L, the lower triangular matrix of the Cholesky decomposition $\Omega =L L^{\intercal }$, are estimated (Bhat and Sidharthan 2011; Patil et al. 2017; Batram and Bauer 2019). These can be merged into the vector $l:=\begin{pmatrix} L_{11}&L_{21}&L_{22}&L_{31}&\dots&L_{KK} \end{pmatrix}$. Thus, $L_{q}\left( b,\Omega \right)$ becomes $L_{q}\left( b,l \right)$.

Given the likelihood contribution for individual q who chooses alternative m, the log-likelihood can be stated as ${\mathcal {L}}\left( b,l\right) =\sum _{q=1}^{Q}{{\mathcal {L}}_{q}\left( b,l\right) },$ where ${\mathcal {L}}_{q}\left( b,l\right) :=\log \left( L_{q}\left( b,l\right) \right)$ and alternative m now represents the chosen alternative for every individual. These alternatives may of course vary across individuals. Since the normal cumulative distribution function cannot be expressed in closed form, the estimation of b and l is usually based on simulation approaches, which typically suffer from computational loads. This shortcoming can be addressed by the use of analytic approximation methods (Joe 1995; Bhat 2011). While Bhat and Sidharthan (2011) and Patil et al. (2017) rely on the SJ approach, Batram and Bauer (2019) additionally consider ME, BME, and TVBS. Among these approaches, SJ provides a very good ratio between computation time and accuracy. Hence, SJ is also applied in this paper.

3 Parameter selection approach

The estimation method proposed in the following is intended to improve the estimation of true zero Cholesky parameters of the mixed multinomial probit model outlined in Sect. 2. The approach is based on the idea of parameter selection and cross-validation.

Consider again the case $K>I-2$ from Sect. 2, where K denotes the number of exogenous characteristics for each alternative $i\in \left\{ 1,\ldots ,I\right\}$ together with the corresponding log-likelihood

$$\begin{aligned} {\mathcal {L}}\left( b,l\right) =\sum _{q=1}^{Q}{{\mathcal {L}}_{q}\left( b,l\right) } =\sum _{q=1}^{Q}{\log \left( L_{q}\left( b,l\right) \right) }, \end{aligned}$$

where $L_{q}\left( b,l\right) =\Phi _{I-1}\left( -Z_{qm}^{\intercal }b \mid 0,\Sigma _{q}\right)$ as described in Sect. 2. Now let |l| denote the length of l and consider $p\in \left\{ 0,1\right\} ^{|l|}$. The set of individuals $\left\{ 1,\ldots ,Q\right\}$ is randomly divided into c subsets $Q_{1},\ldots ,Q_{c}$. Then for $j=1,\ldots ,c$ one can obtain $\left( b^{j},l^{j}_{p}\right) =\text {argmax}\sum _{q \notin Q_{j}}{{\mathcal {L}}_{q}(b,l)}$ s.t. $l_{i}=0$ if and only if $p_{i}=0$ for $i=1,\ldots ,|l|$. This maximization problem can be handled by quasi-newton procedures using SJ and yields estimations $\hat{b}^{j}$ and $\hat{l}^{j}_{p}$ for $j=1,\ldots ,c$. Finally, a c-fold cross-validation score can be obtained by

$$\begin{aligned} {\mathcal {F}}\left( p\right) =\frac{1}{c}\sum _{j=1}^{c}{\sum _{q\in Q_{j}}{{\mathcal {L}}_{q}\left( \hat{b}^{j},\hat{l}^{j}_{p}\right) }}. \end{aligned}$$

Maximizing ${\mathcal {F}}\left( p\right)$ with respect to p yields a suitable binary representation $p^{*}=\text {argmax} \ {\mathcal {F}}\left( p\right)$ of the Cholesky parameters to be selected before maximizing the log-likelihood ${\mathcal {L}}\left( b,l\right)$, where the i-th Cholesky parameter is selected if and only if $p^{*}_{i}=1$.

In order to solve this non-linear binary maximization problem, an appropriate optimization method has to be chosen. Arora et al. (1994) and Alves and Climaco (2007) provide reviews of methods for discrete-integer-continuous variable optimization. However, the very nature of the optimization problem does neither allow for sequential linearization nor any relaxation approaches. It is apparently not possible to provide any gradient information. Hence, a stochastic search method is applied, namely a binary genetic algorithm (Holland 1992; Goldberg 1989).

This optimization procedure is a metaheuristic over a given parameter space. It is motivated by genetics and the natural process of selection and evolution. A binary genetic algorithm provides some advantages: it does not require convexity of the optimization problem and is, at least in theory, capable of finding a global optimum. On the other hand, it can be computationally quite burdensome, especially if the evaluation of the objective function is costly. Furtunately, due to the SJ approximation approach, the c-fold cross-validation score can be evaluated quite efficiently for reasonable values⁴ of c. In this paper, $c=5$ is chosen because this value fits the available computational capacity and corresponds to the widely used ratio of training and test data splitting in machine learning, which means that 80% of the data is used for training and 20% for testing. The reason for this split is based on the well-known Pareto principle. However, this is only a widely used rule of thumb. Research on the optimality of the data splitting ratio has not yet led to a consensus (Picard and Berk 1990; Dobbin and Simon 2011; Afendras and Markatou 2019).

Regarding genetic optimization, the objective function is usually denoted as fitness. In the present case, the parameter space is given by $\left\{ 0,1\right\} ^{|l|}$ and the fitness corresponds to the c-fold cross-validation score ${\mathcal {F}}\left( p\right)$. The entire optimization procedure is based on the bio-inspired operators: selection, crossover, and mutation.

At each step of the optimization procedure there is a current population consisting of m different binary-valued vectors $p^{1},\ldots ,p^{m}\in \left\{ 0,1\right\} ^{|l|}$. The selection of a member $p^{'}\in \left\{ p^{1},\ldots ,p^{m}\right\}$ is made with a certain probability according to its fitness regarding the current population. The selection operator copies vectors from the current population to the next, with numerous different strategies for implementing this selection process, cf. Haupt and Haupt (2004) for a review.

In a second step, the crossover operator splits and merges two selected vectors of the current population to exchange characteristics. This entails randomly selecting a start and end position on a pair of mating vectors and exchanging the sub-vector of 0’s and 1’s between these positions on one vector with that from the mating vector.

Finally, the mutation operator completes the genetic refinement process. It corresponds to selecting a few members of the population, randomly determining positions on the selected vectors, and switching the 0 or 1 at these positions. This step safeguards the process from locking into a local optimum during selection and crossover.

The outlined steps are repeated for successive populations until no further improvement of the fitness is attainable. The member with the highest level of fitness in the last population is the optimum vector $p^{*}$, cf. Haupt and Haupt (2004) for a more detailed discussion.

4 Accuracy comparison between the proposed parameter selection approach and the original estimation method

Within the following subsections, the ability of the proposed parameter selection approach to recover parameters from finite samples in cross-sectional mixed multinomial probit models is evaluated. The results are compared to those of the original MACML estimation approach by Bhat (2011).

4.1 Experimental design

The underlying utility function of the multinomial mixed probit model outlined in Sect. 2 is given by $u_{qi}=\beta _{q}^{\intercal }x_{qi}+\epsilon _{qi}$. According to the simulation studies of Bhat and Sidharthan (2011) and Patil et al. (2017), two 5-dimensional cross-sectional designs are taken into account. Thus a set of 5 alternatives is considered together with 5 independent exogeneous variables. For each choice occasion q and each alternative i the realizations of these exogeneous variables are given by $x_{qi}$. They are drawn from a standard univariate normal distribution. Likewise, the error terms $\epsilon _{qi}$ are drawn from a univariate normal distribution with variance of one-half to normalize the variances of the latent utility error differences. The random coefficient vector $\beta _{q}$ follows a multivariate normal distribution with mean b and covariance matrix $\Omega =LL^{\intercal }$, where L denotes the lower Cholesky matrix of the corresponding decomposition. The covariance parameters are not estimated directly, but using the corresponding lower Cholesky matrix, cf. Section 2.

The covariance matrix design $\Omega _{Bhat}$ is considered first, since it has already been well-discussed in the literature and therefore serves as a benchmark case (Bhat and Sidharthan 2011; Patil et al. 2017). In this example, 15 Cholesky parameters have to be estimated, of which 4 have a true value of zero, corresponding to a proportion of more than 25%:

$$\begin{aligned} \Omega _{\text {Bhat}} =\begin{pmatrix} 1.00 &{}\quad -0.50 &{}\quad 0.25 &{}\quad 0.75 &{}\quad 0.00 \\ -0.50 &{}\quad 1.00 &{}\quad 0.25 &{}\quad -0.50 &{}\quad 0.00 \\ 0.25 &{}\quad 0.25 &{}\quad 1.00 &{}\quad 0.33 &{}\quad 0.00 \\ 0.75 &{}\quad -0.50 &{}\quad 0.33 &{}\quad 1.00 &{}\quad 0.00 \\ 0.00 &{}\quad 0.00 &{}\quad 0.00 &{}\quad 0.00 &{}\quad 1.00 \end{pmatrix}. \end{aligned}$$

The corresponding lower Cholesky matrix $L_{\text {Bhat}}$ has a similar structure due to the arrangement of the variables in $\Omega _{\text {Bhat}}$. The block-diagonal structure is preserved by the Cholesky decomposition:

$$\begin{aligned} L_{\text {Bhat}} =\begin{pmatrix} 1.00 &{}\quad 0.00 &{}\quad 0.00 &{}\quad 0.00 &{}\quad 0.00 \\ -0.50 &{}\quad 0.87 &{}\quad 0.00 &{}\quad 0.00 &{}\quad 0.00 \\ 0.25 &{}\quad 0.43 &{}\quad 0.87 &{}\quad 0.00 &{}\quad 0.00 \\ 0.75 &{}\quad -0.14 &{}\quad 0.24 &{}\quad 0.60 &{}\quad 0.00 \\ 0.00 &{}\quad 0.00 &{}\quad 0.00 &{}\quad 0.00 &{}\quad 1.00 \end{pmatrix}. \end{aligned}$$

Block-diagonal covariance matrix designs are natural restrictions of the general unstructured covariance matrix design in mixed multinomial probit modeling (Baragatti 2011). In some cases of seemingly unstructered covariance matrices, reordering of the underlying variables can be considered to impose a block-diagonal structure. In addition to $\Omega _{Bhat}$, another more taylor-made block-diagonal covariance matrix design is considered to test the parameter selection procedure:

$$\begin{aligned} \Omega _{\text {Block}} =\begin{pmatrix} 1.00 &{}\quad 075 &{}\quad 0.00 &{}\quad 0.00 &{}\quad 0.00 \\ 0.75 &{}\quad 1.00 &{}\quad -0.50 &{}\quad 0.00 &{}\quad 0.00 \\ 0.00 &{}\quad -0.50 &{}\quad 1.00 &{}\quad 0.00 &{}\quad 0.00 \\ 0.00 &{}\quad 0.00 &{}\quad 0.00 &{}\quad 1.00 &{}\quad 0.50 \\ 0.00 &{}\quad 0.00 &{}\quad 0.00 &{}\quad 0.50 &{}\quad 1.00 \end{pmatrix}. \end{aligned}$$

In this case, also 15 Cholesky parameters have to be estimated, of which now 7 have a true value of zero, corresponding to a proportion of almost 50%. The corresponding lower Cholesky matrix is given by:

$$\begin{aligned} L_{\text {Block}} =\begin{pmatrix} 1.00 &{}\quad 0.00 &{}\quad 0.00 &{}\quad 0.00 &{}\quad 0.00 \\ 0.75 &{}\quad 0.66 &{}\quad 0.00 &{}\quad 0.00 &{}\quad 0.00 \\ 0.00 &{}\quad -0.76 &{}\quad 0.65 &{}\quad 0.00 &{}\quad 0.00 \\ 0.00 &{}\quad 0.00 &{}\quad 0.00 &{}\quad 1.00 &{}\quad 0.00 \\ 0.00 &{}\quad 0.00 &{}\quad 0.00 &{}\quad 0.50 &{}\quad 0.87 \end{pmatrix}. \end{aligned}$$

For every covariance matrix design considered the corresponding random coefficient mean values are the same and chosen to be $b=\begin{pmatrix} 1.5&-1.0&2.0&1.0&-2.0 \end{pmatrix}^{\intercal }$ due to Bhat and Sidharthan (2011) and Patil et al. (2017).

In each case, 20 random data sets of size 2500 are generated, corresponding to 2500 individual choice occasions.

For the considered experimental designs MACML benchmark estimates are provided using SJ. In addition, the analytic approximation based estimator using the SJ approximation method together with the genetic algorithm parameter selection procedure outlined in Sect. 3 is applied. Here the cross-validation parameter is set to $c=5$, which corresponds to a widely used ratio of training and test data splitting in machine learning as discussed in Sect. 3.

Bhat and Sidharthan (2011), Patil et al. (2017) and Batram and Bauer (2019) provide relative estimation errors by computing mean parameter estimates across data sets and reporting an absolute percentage bias for each parameter, i.e. $|(\text {mean estimate}-\text {true value})/\text {true value}| \cdot 100$. In doing so, they weight the deviation of the mean estimated value from the true value by its size which, from a theoretical point of view, facilitates comparisons between different parameter values. However, from a more technical perspective, it is not immediately clear why normalization should be required, since larger parameter values are not necessarily accompanied by increased biases. The results of Bhat and Sidharthan (2011) and Batram and Bauer (2019) show that this is not the case and that they are not even accompanied by increased standard errors. Moreover, it is not possible to compute an absolute percentage bias for true zero parameters, which prevents the opportunity for appropriate comparisons in these cases.

In contrast, this study does not only provide average estimation results, but also focuses on the empirical cumulative distributions of the absolute errors, i.e. $|\text {estimate}-\text {true value}|$, aggregated in pairs according the two estimation methods considered. Aggregation is performed over parameters and data sets for each covariance matrix design, where zero and non-zero parameters are considered separately to examine the effects of the parameter selection procedure. Wilcoxon–Mann–Whitney paired tests with large sample normal approximation are used to test for differences in the results (Wilcoxon 1945; Mann and Whitney 1947).

Furthermore, mean absolute estimation errors (MAE) are reported for each parameter, i.e. $|\text {estimate}-\text {true value}|$ averaged across data sets. These errors are easily traceable and yield properly comparable results also for zero parameters. The result is likely to be a higher reported MAE for each parameter compared to an absolute bias due to Bhat and Sidharthan (2011) and Patil et al. (2017), since the triangle inequality applies. In addition, MAE standard deviations are reported. Sensitivity and specificity values are provided to give information about the proportion of correctly neglected and selected parameters, respectively.⁵

4.2 Results

Table 1 provides the estimation results for the covariance matrix design due to Bhat and Sidharthan (2011) and Patil et al. (2017).

Table 1 Estimation results for $L_{\text {Bhat}}$ for SJ without and with parameter selection (cross-validation parameter $c=5$), including mean absolute errors (MAE) and standard deviations based on 20 data sets and 2500 observations per data set

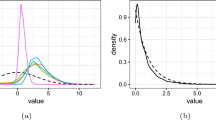
The difference in the accuracy of the estimation results in terms of absolute errors across all parameters is just over 7% in favor of the parameter selection procedure. However, a closer look at the true zero Cholesky entries shows that there are considerable differences. In the case of the SJ approximation without parameter selection, the mean absolute error here is 0.113, whereas in the case of the parameter selection procedure, the mean absolute error is only 0.036, which is less than one third. Small differences in favor of the parameter selection procedure are also apparent in the estimated mean values. Figure 1 shows the empirical cumulative distribution functions of the absolute error differences between SJ without and with parameter selection.

The differences in estimated mean values are significant ($\text {s}=3129$, $\text {z}=2.075$, $p\text {-value}=0.019$). This also applies to the Cholesky parameters ($\text {s}=28520$, $\text {z}=3.953$, $p-\text {value}=0.000$). However, this observation is solely due to the differences in the true zero Cholesky values ($\text {s}=3036$, $\text {z}=6.789$, $p\text {-value}=0.000$). There is little difference in the true non-zero entries ($\text {s}=3635$, $\text {z}=0.013$, $p\text {-value}=0.990$). The mean absolute errors are almost the same here.

The more accurate estimation results of the parameter selection procedure are accompanied by a significant increase in computation time, which is given in minutes and shows the main shortcoming of the approach. The values for sensitivity and specificity are well above 80% even with this comparatively small scaling of the experimental design.

Fig. 1

Empirical cumulative distribution functions of the absolute error differences between SJ estimates without and with parameter selection for $L_{\text {Bhat}}$, estimated by trust region with cross-validation parameter $c=5$ for 20 data sets and 2500 observations per data set split up according to mean values (l.) and Cholesky parameters (r.)

Table 2 provides the estimation results for the covariance matrix $\Omega _{\text {Block}}$. As before, the difference in the accuracy of the estimation results in terms of absolute errors across all parameters is in favor of the parameter selection approach. However, the difference is now over 20%. Again, the greatest differences can be seen in the true zero Cholesky parameters. In the case of the SJ approximation without parameter selection, the mean absolute error here is now 0.097, whereas in the case of the parameter selection procedure, the mean absolute error is now only 0.017, which is less than 20%. Figure 2 shows again the empirical cumulative distribution functions of the absolute error differences between SJ without and with parameter selection.

The significant differences in the estimated Cholesky values ($\text {s}=33709$, $\text {z}=7.404$, $p\text {-value}=0.000$) are now again due to the fact that the differences in the true zero parameters are significant ($\text {s}=9681$, $\text {z}=9.871$, $p\text {-value}=0.000$). This does not apply to the non-zero entries ($\text {s}=1049$, $\text {z}=0.987$, $p\text {-value}=0.324$). The mean absolute errors are almost the same here, 0.167 and 0.161 for SJ without and with parameter selection, respectively. No significant differences can be observed in the mean values either ($\text {s}=2936$, $\text {z}=1.413$, $p\text {-value}=0.158$).

Table 2 Estimation results for $L_{\text {Block}}$ for SJ without and with parameter selection (cross-validation parameter $c=5$), including mean absolute errors (MAE) and standard deviations based on 20 data sets and 2500 observations per data set

Fig. 2

Empirical cumulative distribution functions of the absolute error differences between SJ estimates without and with parameter selection for $L_{\text {Block}}$, estimated by trust region with cross-validation parameter $c=5$ for 20 data sets and 2500 observations per data set split up according to mean values (l.) and Cholesky parameters (r.)

The values for sensitivity and specificity are increased compared to before even reach one in case of specificity, which means that no true non-zero parameter has been incorrectly neglected.

Even though the proposed parameter selection approach is computationally intensive compared to the original estimation method, the results presented here show that it seems to work, at least with respect to the intended improved accuracy of the estimation results.

5 Conclusion

Applying analytic approximations for multivariate normal cumulative distribution functions to estimate mixed multinomial probit models has led to a significant improvement in both accuracy of the estimation results and computation time (Bhat and Sidharthan 2011; Patil et al. 2017). The proposed estimation approach of this paper can help to further reduce estimation errors in the estimation of the covariances of the random coefficients of the model.

However, the achieved improvements in the accuracy of the estimation results are accompanied by considerable increases of the computational load, which is mainly due to the underlying discrete optimization problem of the proposed parameter selection approach and the applied meta-heuristic optimization method. Therefore, the proposed procedure is unsuitable for fast repeated calculations, which are necessary in some application areas. Using a different parameter selection approach or another discrete optimization method could possibly reduce computation times and facilitate an extension of the parameter selection procedure to mixed multinomial probit models for panel data. In this regard, it would maybe be beneficial to investigate the impact of memetic algorithms on the computation time in future research.

The enclosed simulation results indicate that more accurate estimation results can already be obtained by the proposed parameter selection approach than with conventional estimation via an analytic approximation, if only a moderate degree of independence between the random coefficients is present. With greater independence, even more accurate estimation results are possible. The online appendix of this study contains an application to a conjoint analysis study of preferences between alternative vehicles, which shows that the proposed parameter selection approach can provide plausible and efficient estimation results. In particular, with respect to real data, a question for future research may be whether the proposed method is able to reduce parameter identification fragility.