Functional single-index composite quantile regression

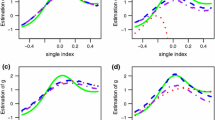
Abstract

The functional single-index model is a very flexible semiparametric model when modeling the relationship between a scalar response and functional predictors. However, the efficiency of the model may be affected by non-normal errors. So, in this paper, we propose functional single index composite quantile regression. The unknown slope function and link function are estimated by using B-spline basis functions. The convergence rates of the estimators are established. Some simulation studies and an application of NIR spectroscopy dataset are presented to illustrate the performance of the proposed methodologies.

Appendix. Proof of the main results

Proof of Theorem 3.1

Let $\theta =(\gamma ^{\top },\lambda ^\top )^{\top }$, $\theta _0=(\gamma _0^{\top },\lambda _0^{\top })^{\top }$, $\delta =n^{-\frac{d}{2d+1}}$, $T_{1}=\delta ^{-1}(\gamma -\gamma _{0})$, $T_{1}=\delta ^{-1}(\lambda -\lambda _{0})$ and $T=(T_{1}^{\top }, T_{2}^{\top })^{\top }$. We next show that, for any given $\epsilon >0$, there exists a sufficient large constant $L=L_{\epsilon }$ such that

$$\begin{aligned} P\left\{ \inf _{\Vert T\Vert =L} Q(\theta _{0}+\delta T)>Q(\theta _{0})\right\} \ge 1-\epsilon . \end{aligned}$$

(A.1)

This implies with the probability at least $1-\epsilon$ that there exists a local minimizer in the ball $\{\theta _{0}+\delta T:\Vert T\Vert \le L\}$.

By the Knight’s identity (Knight 1998), we have

$$\begin{aligned}&Q(\theta _{0}+\delta T)-Q(\theta _{0})\\&\quad =\sum _{k=1}^{K}\sum _{i=1}^{n}\rho _{\tau _k}(Y_i-\mathbf {B}_1^{\top }(\Phi _{i}^{\top }\gamma )\lambda ) -\sum _{k=1}^{K}\sum _{i=1}^{n}\rho _{\tau _k}(Y_i-\mathbf {B}_1^{\top }(\Phi _{i}^{\top }\gamma _0)\lambda _0)\\&\quad =\sum _{k=1}^{K}\sum _{i=1}^{n}\{\mathbf {B}_1^{\top }(\Phi _{i}^{\top }\gamma )\lambda -\mathbf {B}_1^{\top }(\Phi _i^{\top }\gamma _0)\lambda _0\}[I(\varepsilon _i\le 0)-\tau ]\\&\qquad +\sum _{k=1}^{K}\sum _{i=1}^{n}\int _{\mathbf {B}_1^{\top }(\Phi _i^{\top }\gamma _0)\lambda _0-\varvec{g}_0(\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )}^ {\mathbf {B}_1^{\top }(\Phi _i^{\top }\gamma )\lambda -\varvec{g}_0(\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )} [I(\varepsilon _i\le t)-I(\varepsilon _i\le 0)]dt\\&\quad \equiv A_1+A_2. \end{aligned}$$

For $A_2$, we have

$$\begin{aligned} A_2&=\sum _{k=1}^{K}\sum _{i=1}^{n}\int _{\mathbf {B}_1^{\top }(\Phi _i^{\top }\gamma _0)\lambda _0 -\varvec{g}_0(\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )}^ {\mathbf {B}_1^{\top }(\Phi _i^{\top }\gamma )\lambda -\varvec{g}_0(\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )} [I(\varepsilon _i\le t)-I(\varepsilon _i\le 0)]dt\\&=\sum _{k=1}^{K}\sum _{i=1}^{n}\int _{\mathbf {B}_1^{\top }(\Phi _i^{\top }\gamma _0)\lambda _0 -\varvec{g}_0(\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )}^ {\mathbf {B}_1^{\top }(\Phi _i^{\top }\gamma )\lambda -\varvec{g}_0(\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )} [tf(0|X)]dt+o_p(1)\\&=\sum _{k=1}^{K}\sum _{i=1}^{n}f(0|X)\left\{ \mathbf {B}_1^{\top }(\Phi _i^{\top }\gamma )\lambda -\mathbf {B}_1^{\top }(\Phi _i^{\top }\gamma _0)\lambda _0\right\} ^2+o_p(1)\\&\equiv \sum _{k=1}^{K}\sum _{i=1}^{n}f(0|X)\left\{ A_{21}+A_{22}\right\} ^2+o_p(1). \end{aligned}$$

Let $u_0=\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle$, using Taylor expansion to $A_{21}$ and $A_{22}$ at $(u_0,\lambda _0)$ respectively, by conditions (C1)-(C3), we have

$$\begin{aligned} A_2&=\sum _{k=1}^{K}\sum _{i=1}^{n}f(0|X)\left\{ A_{21}+A_{22}\right\} ^2+o_p(1)\\&=\sum _{k=1}^{K}\sum _{i=1}^{n}f(0|X)\Big \{-\mathbf {B}_1^{\top }(\Phi _i^{\top }\gamma _0)\lambda _0 +\mathbf {B}_1^{\top }(\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )\lambda _0 +\mathbf {B}_1^{\top }(\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )(\lambda -\lambda _0)\\&\quad +\mathbf {B}_1^{(1)\top }(\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )\lambda _0(\Phi _i^{\top }\gamma -\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )\Big \}^2+o_p(1)\\&=\sum _{k=1}^{K}\sum _{i=1}^{n}f(0|X)\Big \{-\mathbf {B}_1^{(1)\top }(\langle \varvec{X}_i(t), \varvec{\gamma }_0(t)\rangle )\lambda _0(\Phi _i^{\top }\gamma _0-\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )\\&\quad +\mathbf {B}_1^{\top }(\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )(\lambda -\lambda _0) +\mathbf {B}_1^{(1)\top }(\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )\lambda _0(\Phi _i^{\top }\gamma -\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )\Big \}^2+o_p(1)\\&=\sum _{k=1}^{K}\sum _{i=1}^{n}f(0|X)\Big \{\mathbf {B}_1^{(1)\top }(\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )\lambda _0\Phi _i^{\top }(\gamma \!-\!\gamma _0) +\mathbf {B}_1^{\top }(\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )(\lambda \!-\!\lambda _0)\Big \}^2\!\!+\!o_p(1)\\&=\delta ^2\sum _{k=1}^{K}\sum _{i=1}^{n}f(0|X)\Big \{\mathbf {B}_1^{(1)\top }(\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )\lambda _0\Phi _i^{\top }T_1 +\mathbf {B}_1^{\top }(\langle \varvec{X}_i(t),\varvec{\gamma }_0(t)\rangle )T_2\Big \}^2+o_p(1)\\&=O_p(n\delta ^{2})\Vert T\Vert ^2. \end{aligned}$$

Similarly, we can get $A_1=O_p(n\delta )\Vert T\Vert$. Then, $A_1+A_2=O_p(n\delta ^2)\Vert T\Vert ^2$ uniformly in $||T\Vert =L$ when L is sufficiently large. Therefore, similar to Yu et al. (2020), (A.1) holds, and there exists local minimizers $\hat{\gamma }$ and $\hat{\lambda }$ such that $\Vert \hat{\gamma }-\gamma _0\Vert =O_p(\delta )$ and $\Vert \hat{\lambda }-\lambda _0\Vert =O_p(\delta )$. Then, similar to the argument in Yu et al. (2020), we can finish the proof of this theorem. $\square$