$\ell _2$-penalized approximate likelihood inference in logit mixed models for regional prevalence estimation under covariate rank-deficiency

Abstract

Regional prevalence estimation requires the use of suitable statistical methods on epidemiologic data with substantial local detail. Small area estimation with medical treatment records as covariates marks a promising combination for this purpose. However, medical routine data often has strong internal correlation due to diagnosis-related grouping in the records. Depending on the strength of the correlation, the space spanned by the covariates can become rank-deficient. In this case, prevalence estimates suffer from unacceptable uncertainty as the individual contributions of the covariates to the model cannot be identified properly. We propose an area-level logit mixed model for regional prevalence estimation with a new fitting algorithm to solve this problem. We extend the Laplace approximation to the log-likelihood by an $\ell _2$-penalty in order to stabilize the estimation process in the presence of covariate rank-deficiency. Empirical best predictors under the model and a parametric bootstrap for mean squared error estimation are presented. A Monte Carlo simulation study is conducted to evaluate the properties of our methodology in a controlled environment. We further provide an empirical application where the district-level prevalence of multiple sclerosis in Germany is estimated using health insurance records.

1 Introduction

Regional prevalence estimation is an essential element of modern epidemiologic research (Branscum et al. 2008; Stern 2014; Burgard et al. 2019). Policymakers and health care providers need reliable information on regional disease distributions to plan comprehensive health programs. Depending on the disease of interest, corresponding figures may not be recorded in registries and must be estimated from survey data instead. However, national health surveys often lack in sufficient local observations due to limited resources. As a result, regional prevalence estimates based on survey data can be subject to unacceptable uncertainty due to large sampling variances. Small area estimation (SAE) solves this problem by linking a response variable of interest to statistically related covariates by means of a suitable statistical model. The observations from multiple regions are combined and jointly used for model parameter estimation. Regional prevalence estimates are obtained via model prediction, which allows for an increase in the effective sample size relative to classical direct estimation. See Rao and Molina (2015) for an overview on SAE.

In practice, the efficiency advantage of SAE methods over direct estimators is mainly determined by two aspects: (i) finding a suitable model type to describe the response variable, and (ii) having covariate data with explanatory power. Regarding the first aspect, since regional prevalence is usually stated as proportion (number of sick persons divided by the total number of persons), binomial, Poisson or negative binomial mixed models are canonical choices. The binomial-logit approach has been used for regional proportion estimation in the past, for instance by Molina et al. (2007), Ghosh et al. (2009), Chen and Lahiri (2012), Erciulescu and Fuller (2013), López-Vizcaíno et al. (2013), López-Vizcaíno et al. (2015), Burgard (2015), Militino et al. (2015), Chambers et al. (2016), Hobza and Morales (2016), Liu and Lahiri (2017) and Hobza et al. (2018). The Poisson or negative binomial mixed models were applied to estimate small area counts or proportions by Berg (2010), Chambers et al. (2014), Dreassi et al. (2014), Tzavidis et al. (2015) and Boubeta et al. (2016, 2017), among others. Marino et al. (2019) propose a semiparametric approach allowing for a flexible random effects structure in unit-level models. Ranalli et al. (2018) introduced benchmarking for logistic unit-level. Concerning the second aspect, medical routine data provided by official statistics or health insurance companies have been found to be promising data bases for regional prevalence estimation. Exemplary applications were provided by Tamayo et al. (2016), Burgard et al. (2019), and Breitkreutz et al. (2019).

However, using medical routine data as covariates can be problematic, especially within logit mixed models. Medical treatment frequencies are typically recorded and coded into diagnosis groups, for instance on ICD-3 level (World Health Organization 2018). This context-related segmentation can induce strong correlation between medical treatment frequencies for diseases that are closely related in terms of comorbidity, such as diabetes and hypertension (Long and Dagogo-Jack 2011). If two or more diagnoses from the auxiliary data set are strongly correlated, the space spanned by the covariates can become rank-deficient. In that case, it is not possible to accurately separate the individual contributions of the covariates to the description of the response variable. Model parameter estimates suffer from high variance and model predictions for regional prevalence are not reliable. This is particularly problematic for logit mixed models, as model parameter estimation already relies on approximate inference in the absence of rank-deficiency (Breslow and Clayton 1993). The respective likelihood integral does not have a closed-form solution, which requires techniques like the Laplace approximation to find a proper substitute as objective function. Therefore, when approximate inference is to be performed on a rank-deficient covariate space, methodological adjustments are required to allow for reliable results.

In this paper, we propose a modification to the maximum likelihood Laplace (ML-Laplace) algorithm for model parameter estimation (e.g. Demidenko 2013; Hobza et al. 2018) in a logit mixed model under covariate rank-deficiency. We draw from theoretical insights on ridge regression (Hoerl and Kennard 1970) and extend the Laplace approximation to the log-likelihood function by the squared $\ell _2$-norm of the regression parameters ($\ell _2$-penalty). This adjustment reduces the variance of model parameter estimates considerably and improves approximate inference in the presence of strong covariate correlation. To the best of our knowledge, $\ell _2$-penalization has only been studied for standard ML estimation in fixed effect logit models, for instance by Schaefer et al. (1984), Cessie and Houwelingen (1992), and Pereira et al. (2016). We are not aware of corresponding studies for logit mixed models based on ML-Laplace estimation, especially not in the context of SAE.

An area-level binomial logit mixed model for regional prevalence estimation is presented. Following Jiang and Lahiri (2001) and Jiang (2003), we derive empirical best predictors (EBPs) under the model and present a parametric bootstrap estimator for their mean squared error (MSE). Thereafter, we state the Laplace approximation to the log-likelihood function and demonstrate $\ell _2$-penalized approximate likelihood ($\ell _2$-PAML) estimation of the model parameters. We further show how the tuning parameter for the $\ell _2$-penalty can be chosen in practice. A Monte Carlo simulation study is conducted to study the behavior of $\ell _2$-PAML estimation under different degrees of covariate correlation. And finally, the proposed methodology is applied to regional prevalence estimation in Germany. We use health insurance records of the German Public Health Insurance Company (AOK) and inpatient diagnosis frequencies of the Diagnosis-Related Group Statistics (DRG-Statistics) to estimate district-level multiple sclerosis prevalence.

The remainder of the paper is organized as follows. In Sect. 2, we present the model and its EBP. We further address MSE estimation. In Sect. 3, we present the Laplace approximation and the technical details for $\ell _2$-PAML. Section 4 contains a Monte Carlo simulation study. Section 5 covers the application to regional prevalence estimation. Section 6 closes with some conclusive remarks.

2 Model

2.1 Formulation

For the subsequent derivation, we rely on model-based inference in a finite population setting. Let U be a finite population of size $|U| = N$. Suppose that U is partitioned into D domains $U_d$ of size $|U_d| = N_d$. That is to say, $U = \cup _{d=1}^D U_d$, $U_{d_1}\cap U_{d_2}=\emptyset$, $d_1\ne d_2$, and $\sum _{d=1}^D N_d = N$. Let S be a sample of size $|S| = n$ that is drawn from U. For simplicity, assume the sampling scheme is such that there are domain-specific subsamples $S_d$ of size $|S_d|= n_d$ with fixed $n_d > 0$ for all $d=1, ..., D$. Thus, we have $S = \cup _{d=1}^D S_d$ and $\sum _{d=1}^D n_d = n$. Let y be a dichotomous response variable with potential outcomes $\lbrace 0, 1 \rbrace$. Denote the realization of y for some individual $i \in U_d$ by $y_{id}$. Note that we use the same symbol for a random variable and its realizations in order to avoid overloading the notation. Define $y_d = \sum _{i \in s_d} y_{id}$ as the sample total (count) of y in domain $U_d$. Let $x = \lbrace x_1, ..., x_p \rbrace$ be a set of covariates statistically related to y. Denote $\varvec{x}_d$ as a $1\times p$ vector of aggregated (domain-level) realizations of x. Suppose that corresponding information is retrieved from administrative records and not calculated from the sample S. In what follows, we present an area-level logit mixed model for estimating the domain totals $Y_d = \sum _{i \in U_d} y_{id}$ or proportions $p_d = Y_d / N_d$ of the response variable. Let us consider a set of random effects such that $\{v_{d}:\,\,d=1,\ldots ,D\}$ are independent and identically distributed according to $v_d \sim N(0,1)$. In matrix notation, we have normally distributed random effects

$$\begin{aligned} \varvec{v}=\underset{1\le d \le D}{\text{ col }}(v_{d})\sim N_D(\varvec{0},\varvec{I}_D) \end{aligned}$$

(1)

and, hence, their probability density function (PDF) is stated as

$$\begin{aligned} f_v(\varvec{v})=(2\pi )^{-D/2}\exp \Big \{-\frac{1}{2}\,\varvec{v}^\prime \varvec{v}\Big \}. \end{aligned}$$

(2)

The model assumes that the distribution of the response variable $y_{d}$, conditioned to the random effect $v_{d}$, is

$$\begin{aligned} y_{d}| {v_{d}}\sim \text{ Bin }({n}_{d},p_{d}),\quad d=1,\ldots ,D, \end{aligned}$$

(3)

and that the natural parameter fulfills

$$\begin{aligned} \eta _{d}=\log \frac{p_{d}}{1-p_{d}}=\varvec{x}_{d}\varvec{\beta }+\phi v_{d},\quad d=1,\ldots ,D, \end{aligned}$$

(4)

where $\phi >0$ is an standard deviation parameter, $\varvec{\beta }=\hbox {col}_{1\le r \le p}(\beta _r)$ is the vector of regression parameters and $\varvec{x}_{d}=\hbox {col}^\prime _{1\le r \le p}(x_{dr})$. We complete the model definition by assuming that the domain-specific sample counts $y_{d}$ are independent when conditioned on the random effects $\varvec{v}$. Therefore, the conditional PDF of $\varvec{y}=\text{ col}_{1\le d \le D}({y}_{d})$ given $\varvec{v}$ is stated as

$$\begin{aligned} P(\varvec{y}|\varvec{v})=\prod _{d=1}^DP(y_{d}|v_d),\quad P(y_{d}|\varvec{v})=P(y_{d}|v_d)=\left( {\begin{array}{c}{n}_{d}\\ y_{d}\end{array}}\right) p_{d}^{y_{d}} (1-p_{d})^{{n}_{d}-y_{d}}, \end{aligned}$$

(5)

where

$$\begin{aligned} p_{d} = \frac{\exp \left\{ \varvec{x}_{d}\varvec{\beta }+\phi v_{d}\right\} }{1+\exp \left\{ \varvec{x}_{d}\varvec{\beta }+\phi v_{d}\right\} }= \frac{\exp \{\eta _{d}\}}{1+\exp \{\eta _{d}\}},\quad 1-p_{d}=\frac{1}{1+\exp \{\eta _{d}\}}. \end{aligned}$$

(6)

Further, the unconditional PDF of $\varvec{y}$ is

$$\begin{aligned} P(\varvec{y})=\int _{R^{D}} P(\varvec{y}|\varvec{v}) f_{v}(\varvec{v})\,d\varvec{v}=\int _{R^{D}} \psi (\varvec{y},\varvec{v})\,d\varvec{v}, \end{aligned}$$

(7)

with

$$\begin{aligned} \psi (\varvec{y},\varvec{v})= & {} (2\pi )^{-\frac{D}{2}}\exp \left\{ \frac{-\varvec{v}^\prime \varvec{v}}{2}\right\} \prod _{d=1}^D \frac{\left( {\begin{array}{c}{n}_{d}\\ y_{d}\end{array}}\right) \exp \left\{ y_{d}(\varvec{x}_{d}\varvec{\beta }+\phi v_{d})\right\} }{\left[ 1+\exp \left\{ \varvec{x}_{d}\varvec{\beta }+\phi v_{d}\right\} \right] ^{{n}_{d}}} \nonumber \\= & {} (2\pi )^{-\frac{D}{2}}\prod _{d=1}^D\left( {\begin{array}{c}{n}_{d}\\ y_{d}\end{array}}\right) \exp \left\{ \frac{-\varvec{v}^\prime \varvec{v}}{2}\right\} \exp \left\{ \sum _{k=1}^p\big (\sum _{d=1}^Dy_{d}x_{dk}\big )\beta _k+\phi \sum _{d=1}^Dy_{d}v_{d}\right. \nonumber \\&\quad \!\!-\left. \sum _{d=1}^D{n}_{d} \log \left( 1+\exp \left\{ \varvec{x}_{d}\varvec{\beta }+\phi v_{d}\right\} \right) \right\} . \end{aligned}$$

(8)

2.2 Prediction

Hereafter, we obtain EBPs under the area-level logit mixed model introduced in Sect. 2.1. For this, we first derive best predictors (BPs) in a preliminary setting where all model parameters $\varvec{\theta } := (\varvec{\beta }', \phi )$ are assumed to be known. Then, the EBPs are obtained by replacing the full parameter vector $\varvec{\theta }$ by consistent estimators $\hat{\varvec{\theta }} := (\hat{\varvec{\beta }}', {\hat{\phi }})$. Note that calculating the EBP requires Monte Carlo integration over the random effect PDF, which can be computationally infeasible for some applications. Therefore, we also state two alternative predictors that do not rely on Monte Carlo integration and are easier to apply in practice. We start with the EBPs. Recall the definition of the conditional PDF $P(\varvec{y}|\varvec{v})$ from the last section. For the domain-specific component $P(y_d | v_d)$, we can write

$$\begin{aligned} P({y}_{d}|v_{d})= & {} \left( {\begin{array}{c}{n}_{d}\\ y_{d}\end{array}}\right) p_{d}^{y_{d}} (1-p_{d})^{{n}_{d}-y_{d}} = \frac{\left( {\begin{array}{c}{n}_{d}\\ y_{d}\end{array}}\right) \exp \left\{ y_{d}(\varvec{x}_{d}\varvec{\beta }+\phi v_{d})\right\} }{\left[ 1+\exp \left\{ \varvec{x}_{d}\varvec{\beta }+\phi v_{d}\right\} \right] ^{{n}_{d}}} \nonumber \\= & {} \exp \left\{ \log \left( {\begin{array}{c}{n}_{d}\\ y_{d}\end{array}}\right) +y_{d}(\varvec{x}_{d}\varvec{\beta }+\phi v_{d}) -{n}_{d}\log \big [1+\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_{d}\}\big ]\right\} .\quad \end{aligned}$$

(9)

The probability density function of $\varvec{v}$ is

$$\begin{aligned} f(\varvec{v})=\prod _{d=1}^Df(v_{d}),\quad f(v_{d})=(2\pi )^{-1/2}\exp \big \{-\frac{1}{2}\, v_{d}^2\big \}. \end{aligned}$$

(10)

The BP of $p_{d}=p_{d}(\varvec{\theta },v_d)$ is given by the conditional expectation ${\hat{p}}_{d}(\varvec{\theta })=E_\theta [p_{d}|\varvec{y}]$. Due to the conditional independence of the response realizations given the random effects, we have $E_\theta [p_{d}|\varvec{y}]=E_\theta [p_{d}|{y}_{d}]$ and

$$\begin{aligned} E_\theta [p_{d}|{y}_{d}]= & {} \frac{\int _{R}\frac{\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_{d}\}}{1+\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_{d}\}} P({y}_{d}|v_{d})f(v_{d})\,dv_{d}}{\int _{R}P({y}_{d}|v_{d})f(v_{d})\,dv_{d}} =\frac{{{{\mathcal {N}}}}_{d}(y_{d},\varvec{\theta })}{{{{\mathcal {D}}}}_{d}(y_{d},\varvec{\theta })} =\frac{N_{d}(y_{d},\varvec{\theta })}{D_{d}(y_{d},\varvec{\theta })},\nonumber \\ \end{aligned}$$

(11)

where ${{{\mathcal {N}}}}_{d}={{{\mathcal {N}}}}_{d}(y_{d},\varvec{\theta })$, ${{{\mathcal {D}}}}_{d}={{{\mathcal {D}}}}_{d}(y_{d},\varvec{\theta })$, $N_{d}=N_{d}(y_{d},\varvec{\theta })$ and $D_{d}=D_{d}(y_{d},\varvec{\theta })$ are functions of the model parameters and the domain-specific sample counts. They are stated as follows:

$$\begin{aligned} {{{\mathcal {N}}}}_{d}= & {} \int _{R}\frac{\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_{d}\}}{1+\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_{d}\}} \exp \left\{ \log \left( {\begin{array}{c}{n}_{d}\\ y_{d}\end{array}}\right) +y_{d}\varvec{x}_{d}\varvec{\beta }+\phi y_{d}v_{d}\right. \\&-\left. {n}_{d}\log \left[ 1+\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_{d}\}\right] \right\} f(v_{d})\,dv_{d}, \\ {{{\mathcal {D}}}}_{d}= & {} \int _{R}\exp \left\{ \log \left( {\begin{array}{c}{n}_{d}\\ y_{d}\end{array}}\right) +y_{d}\varvec{x}_{d}\varvec{\beta }+\phi y_{d}v_{d} - {n}_{d}\log \left[ 1+\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_{d}\}\right] \right\} f(v_{d})\,dv_{d}, \\ N_{d}= & {} \int _{R}\frac{\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_{d}\}}{1+\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_{d}\}} \exp \left\{ \phi y_{d}v_{d}-{n}_{d}\log \left[ 1+\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_{d}\}\right] \right\} f(v_{d})\,dv_{d}, \\ D_{d}= & {} \int _{R}\exp \left\{ \phi y_{d} v_{d} - {n}_{d}\log \left[ 1+\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_{d}\}\right] \right\} f(v_{d})\,dv_{d}. \end{aligned}$$

We can conclude that the EBP of $p_{d}$ is ${\hat{p}}_{d}({{\hat{\varvec{\theta }}}})$. However, its quantification requires integration over the random effect PDF $f(v_d)$. As the logit mixed model belongs to the family of generalized linear mixed models, this cannot be performed analytically. Instead, we apply Monte Carlo integration and approximate the EBP as follows:

• 1. Estimate ${\hat{\varvec{\theta }}}=({{\hat{\varvec{\beta }}}},{\hat{\phi }})$.

• 2. For $k=1,\ldots ,K$, generate $v_{d}^{(k)}$ i.i.d. N(0, 1) and $v_{d}^{(K+k)}=-v_{d}^{(k)}$.

• 3. Calculate ${\hat{p}}_{d}({{\hat{\varvec{\theta }}}})={\hat{N}}_{d}/{\hat{D}}_{d}$, where

  $$\begin{aligned} {\hat{N}}_{d}= & {} \frac{1}{2K}\sum _{k=1}^{2K}\left\{ \frac{\exp \{\varvec{x}_{d}{{\hat{\varvec{\beta }}}}+{{\hat{\phi }}} v_{d}^{(k)}\}}{1+\exp \{\varvec{x}_{d}{{\hat{\varvec{\beta }}}}+{{\hat{\phi }}} v_{d}^{(k)}\}} \exp \big \{{{\hat{\phi }}} y_{d}v_{d}^{(k)}-{n}_{d}\log \big [1+\exp \{\varvec{x}_{d}{{\hat{\varvec{\beta }}}}+{{\hat{\phi }}} v_{d}^{(k)}\}\big ] \big \}\right\} , \\ {\hat{D}}_{d}= & {} \frac{1}{2K}\sum _{k=1}^{2K}\exp \left\{ {{\hat{\phi }}} y_{d} v_{d}^{(k)} - {n}_{d}\log \left[ 1+\exp \{\varvec{x}_{d}{{\hat{\varvec{\beta }}}}+{{\hat{\phi }}} v_{d}^{(k)}\}\right] \right\} . \end{aligned}$$

The EBP of $p_d$ can be used to obtain the predictor ${\hat{Y}}_d = N_d {\hat{p}}({\hat{\varvec{\theta }}})$ of the domain total $Y_d$.

We now state two alternative predictors that do not rely on Monte Carlo integration. The first is a synthetic predictor. It is characterized by a regression-synthetic prediction from the area-level logit mixed model without considering the random effect. On that note, the synthetic predictor of $p_d$ is obtained according to

$$\begin{aligned} {\tilde{p}}_d^{syn}=\frac{\exp \{\varvec{x}_{d}{\hat{\varvec{\beta }\}}}}{1+\exp \{\varvec{x}_{d}{\hat{\varvec{\beta }\}}}}, \end{aligned}$$

(12)

which constitutes the synthetic predictor ${\tilde{Y}}_d^{syn} = N_d {\tilde{p}}_d^{syn}$ for $Y_d$. The plug-in predictor is obtained along the same lines, but includes the random effects $v_d$ as well as the variance parameter $\phi$. For the prediction of $p_d$, we have

$$\begin{aligned} {\tilde{p}}_d^{plug} =\frac{\exp \{\varvec{x}_{d}{{\hat{\varvec{\beta }}}}+{\hat{\phi }}{\hat{v}}_d\}}{1+\exp \{\varvec{x}_{d}{{\hat{\varvec{\beta }}}}+{\hat{\phi }}{\hat{v}}_d\}}, \end{aligned}$$

(13)

where ${\hat{v}}_d$ is a predictor for the random effect $v_d$. We describe how to calculate the corresponding predictors in Sect. 3. Finally, the plug-in predictor of $Y_d$ is ${\tilde{Y}}_d^{plug} = N_d {\tilde{p}}_d^{plug}$.

2.3 Mean squared error estimation

In order to assess the reliability of the obtained predictions for $p_d$, we use the mean squared error. It is generally characterized by $MSE({\hat{p}}_d) = E[({\hat{p}}_d - p_d)^2]$. However, $MSE({\hat{p}}_d)$ cannot be quantified directly and must be estimated instead. For this, we apply a parametric bootstrap as demonstrated by González-Manteiga et al. (2007) and Boubeta et al. (2016). It is performed as follows.

• 1. Fit the model to the sample and calculate the estimator ${{\hat{\varvec{\theta }}}}=({\hat{\varvec{\beta }}}',{\hat{\phi }})$.

• 2. Repeat B times with $b=1, ..., B$:

  • (a) Generate $v_d^{(b)}\sim N(0,1)$, $y_d^{(b)}\sim \text{ Bin }({n}_{d},p_{d}^{(b)})$, $d=1,\ldots ,D$, where $p_d^{(b)}=\frac{\exp \left\{ \varvec{x}_{d}{{\hat{\varvec{\beta }}}}+{{\hat{\phi }}} v_{d}^{(b)}\right\} }{1+\exp \left\{ \varvec{x}_{d}{{\hat{\varvec{\beta }}}}+{{\hat{\phi }}} v_{d}^{(b)}\right\} }$.

  • (b) For each bootstrap sample, calculate the estimator ${\hat{\varvec{\theta }}}^{(b)}$ and the EBP ${\hat{p}}_d^{(b)}={\hat{p}}_d^{(b)}({\hat{\varvec{\theta }}}^{(b)})$ as stated above.

• 3. Output: $mse({\hat{p}}_d)=\frac{1}{B}\sum _{b=1}^B\big ({\hat{p}}_d^{(b)}-p_d^{(b)}\big )^2$.

3 Penalized model parameter estimation

In this section, it is demonstrated how model parameter estimation in the area-level logit mixed model under covariate rank-deficiency is performed. The foundation of our estimation strategy is the ML-Laplace algorithm (e.g. Demidenko 2013; Hobza et al. 2018). That is to say, the integrals in the likelihood function are approximated via the Laplace method and the result is maximized with a Newton-Raphson algorithm. However, in light of the comments in Sect. 1 and prior to maximization, we extend the approximated likelihood function by the squared $\ell _2$-norm of $\varvec{\beta }$ to account for the negative effects of covariate rank-deficiency. With this, we obtain a penalized version approximated likelihood, which is then maximized to obtain reliable model parameter estimates. We refer to this procedure as $\ell _2$-penalized approximate maximum likelihood ($\ell _2$-PAML) estimation.

3.1 Laplace approximation

We first perform the Laplace approximation of the likelihood function. Let $h: R\mapsto R$ be a continuously twice differentiable function with a global maximum at $x_0$. This is to say, assume that $h'(x_0)=0$ and $h''(x_0)<0$. A Taylor series expansion of h(x) around $x_0$ yields

$$\begin{aligned} h(x)= & {} h(x_0)+h'(x_0)(x-x_0)+\frac{1}{2}h''(x_0)(x-x_0)^2+o\big (|x-x_0|^2\big ) \nonumber \\&\approx h(x_0)+\frac{1}{2}h''(x_0)(x-x_0)^2. \end{aligned}$$

(14)

The univariate Laplace approximation is

$$\begin{aligned} \int _{-\infty }^{\infty }e^{h(x)}\,dx\approx & {} \int _{-\infty }^{\infty }e^{h(x_0)}\exp \Big \{-\frac{1}{2}\big (-h''(x_0)\big )(x-x_0)^2\Big \}\,dx \nonumber \\= & {} (2\pi )^{1/2}\big (-h''(x_0)\big )^{-1/2}e^{h(x_0)}\int _{-\infty }^{\infty } \frac{\exp \Big \{-\frac{1}{2}\Big (\frac{x-x_0}{(-h''(x_0))^{-1/2}}\Big )^2\Big \}}{(2\pi )^{1/2}\big (-h''(x_0)\big )^{-1/2}}\,dx\nonumber \\= & {} (2\pi )^{1/2}\big (-h''(x_0)\big )^{-1/2}e^{h(x_0)}. \end{aligned}$$

(15)

Let us now approximate the log-likelihood of the area-level logit mixed model. Recall that $v_1,\ldots ,v_D$ are independent and identically distributed according to $v_d \sim N(0,1)$, and that

$$\begin{aligned} y_{d}|_{v_{d}}\overset{ind}{\sim }\text{ Bin }({n}_{d},p_{d}),\quad p_{d}=p_{d}(v_d)=\frac{\exp \left\{ \varvec{x}_{d}\varvec{\beta }+\phi v_{d}\right\} }{1+\exp \left\{ \varvec{x}_{d}\varvec{\beta }+\phi v_{d}\right\} },\quad d=1,\ldots ,D. \end{aligned}$$

Thus, $y_1,\ldots ,y_D$ are unconditionally independent with marginal probability density

$$\begin{aligned} P(y_d)= & {} \int _{-\infty }^{\infty }P(y_{d}|v_d)f(v_d)\,dv_d \nonumber \\= & {} \int _{-\infty }^{\infty }\left\{ \left( {\begin{array}{c}{n}_{d}\\ y_{d}\end{array}}\right) \exp \Big \{y_{d}(\varvec{x}_{d}\varvec{\beta }+\phi v_d\} -{n}_{d}\log \big (1+\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_d\}\big )\Big \}\right\} \nonumber \\&\cdot (2\pi )^{-1/2}\exp \{-\frac{1}{2}v_d^2\}\,dv_d = (2\pi )^{-1/2}\left( {\begin{array}{c}{n}_{d}\\ y_{d}\end{array}}\right) \nonumber \\&\cdot \int _{-\infty }^{\infty }\exp \Big \{-\frac{v_d^2}{2}+y_{d}(\varvec{x}_{d}\varvec{\beta }+\phi v_d) -{n}_{d}\log \big (1+\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_d\}\big )\Big \}\,dv_d \nonumber \\= & {} (2\pi )^{-1/2}\left( {\begin{array}{c}{n}_{d}\\ y_{d}\end{array}}\right) \int _{-\infty }^{\infty }\exp \big \{h(v_d)\big \}\,dv_d, \end{aligned}$$

(16)

where

$$\begin{aligned} h(v_d)=-\frac{v_d^2}{2}+y_{d}(\varvec{x}_{d}\varvec{\beta }+\phi v_d) -{n}_{d}\log \big (1+\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_d\}\big ). \end{aligned}$$

(17)

Note that for the maximizer of $h(\cdot )$, denoted by $v_{0d}$, the first derivative is $h'(v_{0d}) = 0$, and the second derivative is characterized by $h''(v_{0d})<0$. By applying (15) in $v_d=v_{0d}$, we get

$$\begin{aligned} P(y_d)&\approx \left( {\begin{array}{c}{n}_{d}\\ y_{d}\end{array}}\right) \cdot \Big (1+\phi ^2{n}_{d}p_{d}(v_{0d})(1-p_{d}(v_{0d}))\Big )^{-1/2} \nonumber \\&\quad \cdot \exp \Big \{-\frac{v_{0d}^2}{2}+y_{d}(\varvec{x}_{d}\varvec{\beta }+\phi v_{0d})- {n}_{d}\log \big (1+\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_{0d}\}\big )\Big \}.\quad \quad \end{aligned}$$

(18)

From there, we can state the log-likelihood function under the model, which is given by

$$\begin{aligned} l = \sum _{d=1}^D l_d = \log P(y_d). \end{aligned}$$

Using the results of the Laplace approximation, we obtain

$$\begin{aligned}&l_{d} \approx l_{0d}(\varvec{\theta })=\log \left( {\begin{array}{c}{n}_{d}\\ y_{d}\end{array}}\right) -\frac{1}{2}\log \xi _{0d}-\frac{v_{0d}^2}{2} \nonumber \\&\quad \quad \quad +y_{d}(\varvec{x}_{d}\varvec{\beta }+\phi v_{0d}) {n}_{d}\log \big (1+\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_{0d}\}\big ), \end{aligned}$$

(19)

where $p_{0d}=p_{d}(v_{0d})$ and $\xi _{0d}=1+\phi ^2{n}_{d}p_{0d}(1-p_{0d})$.

3.2 $\ell _2$-penalized approximate maximum likelihood

The approximated log-likelihood function is expanded by the squared $\ell _2$-norm of the regression coefficients $\varvec{\beta }$ to account for strong correlation between covariates in $\varvec{x}_1,\ldots ,\varvec{x}_D$. We obtain the penalized maximum likelihood problem

$$\begin{aligned} {\hat{\varvec{\theta }}} = \underset{\varvec{\theta }\in {\mathbb {R}}^{p+1}}{\text {argmax}}\ l^{pen}(\varvec{\theta }),\quad l^{pen}(\varvec{\theta }) = \sum _{d=1}^D l_{0d}(\varvec{\theta }) - \lambda \Vert \varvec{\beta }\Vert _2^2, \end{aligned}$$

(20)

where $l_{0d}(\varvec{\theta })$ is defined in (19) and $\lambda > 0$ is a predefined tuning parameter. Maximization is performed via a Newton-Raphson algorithm. However, note that the Laplace approximations of $l_1, ..., l_D$ depends on the maximizers of $h(v_1), ..., h(v_D)$, which in turn depend on $l_1, ..., l_D$. Therefore, the maximization of (20) must contain two steps that are performed iteratively and conditional on each other. The first step is the approximation of the log-likelihood by maximizing $h(v_1), ..., h(v_D)$. The second step is the maximization of $l^{pen}(\varvec{\theta })$ given the results of the first step. This is demonstrated hereafter.

3.2.1 Step 1: Log-likelihood approximation

In order to maximize $h(v_d)$, we need to quantify its first and second derivatives. These are

$$\begin{aligned} h'(v_d)= & {} -v_d+\phi \big \{y_{d}-{n}_{d}p_{d}(v_d)\big \} \end{aligned}$$

(21)

$$\begin{aligned} h''(v_d)= & {} -\Big (1+\phi ^2{n}_{d}p_{d}(v_d)(1-p_{d}(v_d))\Big ) \end{aligned}$$

(22)

for all $d=1, ..., D$. The Newton-Raphson algorithm maximizes $h(v_d)=h(v_d,\varvec{\theta })$, defined in (17), for fixed $\varvec{\theta }=(\varvec{\beta }^\prime ,\phi )=\varvec{\theta }_0$. The updating equation is

$$\begin{aligned} v_d^{(k+1)}=v_d^{(k)}-\frac{h'(v_d^{(k)},\varvec{\theta }_0)}{h''(v_d^{(k)},\varvec{\theta }_0)}, \end{aligned}$$

(23)

where k denotes an iteration of the procedure.

3.2.2 Step 2: Penalized maximization

We continue with maximizing the penalized approximate log-likelihood function. Regarding the first partial derivatives of $l^{pen}$ with respect to $\beta _1, ..., \beta _p$ and $\phi$, it holds that

$$\begin{aligned} \frac{\partial p_{0d}}{\partial \beta _r}= & {} x_{dr}p_{0d}(1-p_{0d})=x_{dr}(p_{0d}-p_{0d}^2),\,\, \frac{\partial p_{0d}}{\partial \phi }\\= & {} v_{0d}p_{0d}(1-p_{0d})=v_{0d}(p_{0d}-p_{0d}^2), \\ \eta _{0dr}= & {} \frac{\partial \xi _{0d}}{\partial \beta _r}= \phi ^2{n}_{d}x_{dr}[p_{0d}-3p_{0d}^2+2p_{0d}^3], \\ \eta _{0d}= & {} \frac{\partial \xi _{0d}}{\partial \phi }=2\phi {n}_{d}p_{0d}(1-p_{0d})+\phi ^2{n}_{d}(1-2 p_{0d}) \frac{\partial p_{0d}}{\delta \phi } \\= & {} \phi {n}_{d} p_{0d}(1-p_{0d})[2+\phi (1-2p_{0d})v_{0d}]. \end{aligned}$$

For the domain-specific likelihood component $l_{0d}$, this yields to

$$\begin{aligned} \frac{\partial l_{0d}}{\partial \beta _r}=-\frac{1}{2}\frac{\eta _{0dr}}{\xi _{0d}}+(y_{d}-{n}_{d}p_{0d})x_{dr},\quad \frac{\partial l_{0d}}{\partial \phi }=-\frac{1}{2}\frac{\eta _{0d}}{\xi _{0d}}+(y_{d}-{n}_{d}p_{0d})v_{0d}. \end{aligned}$$

With the application of these equations to all domain-specific likelihood components $l_{01}, ..., l_{0D}$ and the consideration of the $\ell _2$-penalty, we finally obtain

$$\begin{aligned} \frac{\partial l^{pen}}{\partial \beta _r} = \sum _{d=1}^D \frac{\partial l_{0d}}{\partial \beta _r} - 2\lambda \beta _r, \quad \frac{\partial l^{pen}}{\partial \phi } = \sum _{d=1}^D \frac{\partial l_{0d}}{\partial \phi }. \end{aligned}$$

(24)

For the second partial derivatives, it holds that

$$\begin{aligned} \frac{\partial \eta _{0dr}}{\partial \beta _s}= & {} \phi ^2{n}_{d}x_{dr}x_{djs}[p_{0d}(1-p_{0d})-6p_{0d}^2(1-p_{0d})+6p_{0d}^3(1-p_{0d})] \\= & {} \phi ^2{n}_{d}x_{dr}x_{djs}p_{0d}(1-p_{0d})[1-6p_{0d}+6p_{0d}^2], \\ \frac{\partial \eta _{0dr}}{\partial \phi }= & {} 2\phi {n}_{d} x_{dr}p_{0d}(1-p_{0d})(1-2p_{0d})+\phi ^2{n}_{d} x_{dr}(1-6p_{0d}+6p_{0d}^2)\frac{\partial p_{0d}}{\partial \phi } \\= & {} \phi {n}_{d} x_{dr}p_{0d}(1-p_{0d})[2(1-2p_{0d})+\phi v_{0d}(1-6p_{0d}+6p_{0d}^2)], \\ \frac{\partial \eta _{0d}}{\partial \beta _r}= & {} \phi ^2v_{0d}{n}_{d}x_{dr}p_{0d}(1-p_{0d})[1-6p_{0d}+6p_{0d}^2], \\ \frac{\partial \eta _{0d}}{\partial \phi }= & {} 2{n}_{d} p_{0d}(1-p_{0d})+2\phi {n}_{d} 1-2p_{0d})\frac{\partial p_{0d}}{\partial \phi } \\&+2\phi {n}_{d}(1-2p_{0d})p_{0d}(1-p_{0d})v_{0d} + \phi ^2{n}_{d} v_{0d}(1-6p_{0d}+6p_{0d}^2)\frac{\partial p_{0d}}{\partial \phi } \\= & {} {n}_{d} p_{0d}(1-p_{0d})[2+2\phi (1-2p_{0d})v_{0d}+2\phi (1-2p_{0d})v_{0d}\\&+ \phi ^2 v_{0d}^2(1-6p_{0d}+6p_{0d}^2)]. \end{aligned}$$

For the domain-specific likelihood component $l_{0d}$, this yields to

$$\begin{aligned} \frac{\partial ^2 l_{0d}}{\partial \beta _r^2}= & {} -\frac{1}{2}\frac{\frac{\partial \eta _{0dr}}{\partial \beta _r}\xi _{0d}-\eta _{0dr}^2}{\xi _d^2} -{n}_{d}x_{dr}^2 p_{0d}(1-p_{0d}), \\ \frac{\partial ^2 l_{0d}}{\partial \beta _s\partial \beta _r}= & {} -\frac{1}{2}\frac{\frac{\partial \eta _{0dr}}{\partial \beta _s}\xi _{0d}-\eta _{0dr}\eta _{0ds}}{\xi _d^2} -{n}_{d}x_{dr}x_{djs}p_{0d}(1-p_{0d}), \\ \frac{\partial ^2 l_{0d}}{\partial \phi \partial \beta _r}= & {} -\frac{1}{2}\frac{\frac{\partial \eta _{0dr}}{\partial \phi }\xi _{0d}-\eta _{0dr}\eta _{0d}}{\xi _d^2} -v_{0d}{n}_{d}x_{dr}p_{0d}(1-p_{0d}), \\ \frac{\partial ^2 l_{0d}}{\partial \phi ^2}= & {} -\frac{1}{2}\frac{\frac{\partial \eta _{0d}}{\partial \phi }\xi _{0d}-\eta _{0d}^2}{\xi _d^2} -v_{0d}^2{n}_{d}p_{0d}(1-p_{0d}). \end{aligned}$$

As for the first partial derivatives applying these equations to all domain-specific likelihood components $l_{01}, ..., l_{0D}$ and considering the $\ell _2$-penalty, we end up with

$$\begin{aligned} \begin{aligned} \frac{\partial ^2 l^{pen}}{\partial \beta _r^2}&= \sum _{d=1}^D \frac{\partial ^2 l_{0d}}{\partial \beta _r^2} - 2\lambda , \quad \frac{\partial ^2 l^{pen}}{\partial \beta _s\partial \beta _r} = \sum _{d=1}^D \frac{\partial ^2 l_{0d}}{\partial \beta _s\partial \beta _r}, \\ \frac{\partial ^2 l^{pen}}{\partial \phi \partial \beta _r}&= \sum _{d=1}^D \frac{\partial ^2 l_{0d}}{\partial \phi \partial \beta _r}, \quad \frac{\partial ^2 l^{pen}}{\partial \phi ^2} = \sum _{d=1}^D \frac{\partial ^2 l_{0d}}{\partial \phi ^2}. \end{aligned} \end{aligned}$$

(25)

For $r,s=1,\ldots ,p+1$, define the components of the score vector

$$\begin{aligned} U_{0r}= \frac{\partial l^{pen}}{\partial \beta _r},\quad U_{0p+1}= \frac{\partial l^{pen}}{\partial \phi },\, \end{aligned}$$

(26)

as well as the Hessian matrix

$$\begin{aligned} H_{0rs}= H_{0sr}=\frac{\partial ^2 l^{pen}}{\partial \beta _s\partial \beta _r},\quad H_{rp+1}=H_{p+1r}=\frac{\partial ^2 l^{pen}}{\partial \phi \partial \beta _r},\quad H_{0p+1p+1}= \frac{\partial ^2 l^{pen}}{\partial \phi ^2}.\nonumber \\ \end{aligned}$$

(27)

In matrix form, we have $\varvec{U}_0=\varvec{U}_0(\varvec{\theta })=\underset{1\le r \le p+1}{\text{ col }}(U_{0r})$ and $\varvec{H}_0=\varvec{H}_0(\varvec{\theta })=(H_{0rs})_{r,s=1,\ldots ,p+1}$. The Newton-Raphson algorithm maximizes $l^{pen}(\varvec{\theta })$, with fixed $v_d=v_{0d}$, $d=1,\ldots ,D$. Let k denote the index of iterations. The corresponding updating equation is

$$\begin{aligned} \varvec{\theta }^{(k+1)}=\varvec{\theta }^{(k)}-\varvec{H}_0^{-1}(\varvec{\theta }^{(k)})\varvec{U}_0(\varvec{\theta }^{(k)}). \end{aligned}$$

(28)

3.2.3 Complete $\ell _2$-PAML algorithm

The final algorithm containing both steps is performed as follows.

• 1. Set the initial values $k=0$, $\varvec{\theta }^{(0)}$, $\varvec{\theta }^{(-1)}=\varvec{\theta }^{(0)}+\varvec{1}$, $v_d^{(0)}=0$, $v_d^{(-1)}=1$, $d=1,\ldots ,D$.

• 2. Until $\Vert \varvec{\theta }^{(k)}-\varvec{\theta }^{(k-1)}\Vert _2<\varepsilon _1$, $\vert v_d^{(k)}-v_d^{(k-1)}\vert <\varepsilon _2$, $d=1,\ldots ,D$, do

  • (a) Apply algorithm (23) with seeds $v_d^{(k)}$, $d=1,\ldots ,D$, convergence tolerance $\varepsilon _2$ and $\varvec{\theta }=\varvec{\theta }^{(k)}$ fixed. Output: $v_d^{(k+1)}$, $d=1,\ldots ,D$.

  • (b) Apply algorithm (28) with seed $\varvec{\theta }^{(k)}$, convergence tolerance $\varepsilon _1$ and $v_{0d}=v_d^{(k+1)}$ fixed, $d=1,\ldots ,D$. Output: $\varvec{\theta }^{(k+1)}$.

  • (c) $k\leftarrow k+1$.

• 3. Output: ${\hat{\varvec{\theta }}}=\varvec{\theta }^{(k)}$, ${\hat{v}}_d=v_d^{(k)}$, $d=1,\ldots ,D$.

We remark that the output of the $\ell _2$-PAML algorithm gives estimates ${\hat{\varvec{\theta }}}$ of the model parameters $\varvec{\theta }$ and mode predictions ${\hat{v}}$ of the random effects $v_d$, $d=1, ..., D$.

3.3 Tuning parameter choice and information criterion

In the technical descriptions of Sect. 3.2, we assumed that the tuning parameter $\lambda$ had been defined prior to model parameter estimation. In practice, it has to be found empirically from the sample data. Note that this aspect is crucial for the effectiveness of the proposed method. On the one hand, if $\lambda$ is chosen too small, the $\ell _2$-PAML approach cannot sufficiently stabilize model parameter estimates in the presence of covariate rank-deficiency. On the other hand, if $\lambda$ is chosen too large, the shrinkage induced by penalization dominates the optimization problem and resulting model parameter estimates are heavily biased. Finding an appropriate value for the tuning parameter is often done via grid search, as can be seen for instance in Bergstra and Bengio (2012) and Chicco (2017). We define a sequence of candidate values $\{\lambda _q\}_{q=1}^Q$, where $\lambda _q > \lambda _{q+1}$. For each candidate value $\lambda _q$ model parameter estimation as demonstrated in Sect. 3.2 is performed. The results of model parameter estimation have to be evaluated by a suitable goodness-of-fit measure. For our application, we choose the non-corrected Bayesian information criterion (BIC; Schwarz 1978). Alternative measures would be the generalized cross-validation criterion (Craven and Wahba 1979) or the Akaike information criterion (Akaike 1974). For given candidate value $\lambda _q$, let ${\hat{\varvec{\beta }}}(\lambda _q)$ and ${\hat{\phi }}(\lambda _q)$ be the estimators of $\varvec{\beta }$ and $\phi$, respectively. Further, let ${\hat{v}}_{d}(\lambda _q)$ be the mode predictor of $v_d$. The Laplace non-corrected BIC is given by

$$\begin{aligned} BIC(\lambda _q)=p \log (D)-2l^{app}(\lambda _q), \end{aligned}$$

(29)

where the second term is the Laplace approximation (19) to the log-likelihood, that is

$$\begin{aligned} l^{app}(\lambda _q)= & {} l^{app}\left( {\hat{\varvec{\beta }}}(\lambda _q),{\hat{\phi }}(\lambda _q),{\hat{v}}_1(\lambda _q),\ldots ,{\hat{v}}_D(\lambda _q)\right) \\= & {} \sum _{d=1}^D\log \left( {\begin{array}{c}{n}_{d}\\ y_{d}\end{array}}\right) + \sum _{d=1}^D\bigg \{-\frac{1}{2}\log {\hat{\xi }}_{d}(\lambda _q)-\frac{{\hat{v}}_{d}(\lambda _q)^2}{2}\\&+ \Big \{y_{d}(\varvec{x}_{d}{\hat{\varvec{\beta }}}(\lambda _q) +{\hat{\phi }}(\lambda _q) {\hat{v}}_{d}(\lambda _q)) \\&-{n}_{d}\log \big (1+\exp \{\varvec{x}_{d}{\hat{\varvec{\beta }}}(\lambda _q)+{\hat{\phi }}(\lambda _q) {\hat{v}}_{d}(\lambda _q)\}\big )\Big \}\bigg \}, \end{aligned}$$

where

$$\begin{aligned} {\hat{\xi }}_{d}(\lambda _q)= & {} 1+{\hat{\phi }}(\lambda _q)^2{n}_{d}{\hat{p}}_{d}(\lambda _q)(1-{\hat{p}}_{d}(\lambda _q)),\\ {\hat{p}}_{d}(\lambda _q)= & {} \frac{\exp \left\{ \varvec{x}_{d}{\hat{\varvec{\beta }}}(\lambda _q)+{\hat{\phi }}(\lambda _q){\hat{v}}_{d}(\lambda _q)\right\} }{1+\exp \left\{ \varvec{x}_{d}{\hat{\varvec{\beta }}}(\lambda _q)+{\hat{\phi }}(\lambda _q){\hat{v}}_{d}(\lambda _q)\right\} }. \end{aligned}$$

For all $\lambda _1, ..., \lambda _Q$, the following algorithm is performed:

• 1. Apply the $\ell _2$-PAML algorithm to obtain $\hat{\varvec{\theta }}(\lambda _q)$ and ${\hat{v}}_1(\lambda _q), ..., {\hat{v}}_D(\lambda _q)$.

• 2. Calculate ${\hat{p}}_d(\lambda _q)$ and ${\hat{\xi }}_d(\lambda _q)$, $d=1, ..., D$.

• 3. Calculate $BIC(\lambda _q)$ according to (29).

After the algorithm is finalized, the optimal tuning parameter $\lambda ^{opt}$ can be defined as the candidate value that minimizes the BIC.

However, due to the non-convexity of the underlying optimization problem for $\ell _2$-PAML estimation, the behavior of the BIC along the tuning parameter sequence can be volatile to the extent that it may be characterized by multiple local minima. Therefore, we further apply cubic spline smoothing by defining $BIC(\lambda ) = f(\lambda ) + \epsilon _q$, where $f(\lambda )$ is a twice differentiable function and $\epsilon _q \sim N(0, \psi )$. The cubic spline estimate ${\hat{f}}$ of the function f is obtained from solving the optimization problem

$$\begin{aligned} \underset{f \in {\mathcal {F}}}{\text {min}} \ \sum _{q=1}^Q \left[ BIC(\lambda _q) - f(\lambda _q) \right] ^2 + \delta \int f''(\lambda )^2 \ \text {d} \lambda , \end{aligned}$$

(30)

where ${\mathcal {F}} = \{f:f \ \text {is twice differentiable} \}$ denotes the class of twice differentiable functions and $\delta > 0$ is a smoothing parameter. After ${\hat{f}}$ has been obtained, the optimal tuning parameter value $\lambda ^{opt}$ is defined as the minimizer of the smoothed function, that is

$$\begin{aligned} \lambda ^{opt} = \underset{\lambda \in \{\lambda _q\}_{q=1}^Q}{\text {argmin}} \ {\hat{f}}(\lambda ). \end{aligned}$$

(31)

4 Simulation

4.1 Setup

Hereafter, the performance of the $\ell _2$-PAML approach is evaluated under controlled conditions. For this, we conduct a Monte Carlo simulation study with $K=500$ iterations that are indexed by $k=1, ..., K$. We generate synthetic data according to

$$\begin{aligned}&y_d \sim \text {Bin}(n_d, p_d), \,\,\, p_d=\frac{\exp \left\{ \beta _0+\varvec{x}_d\varvec{\beta }_1+\phi v_d\right\} }{1+\exp \left\{ \beta _0 + \varvec{x}_d \varvec{\beta }_1 + \phi v_d \right\} },\\&\quad \beta _0=-0.2, \,\, \varvec{\beta }_1 = 0.3\varvec{1}_5,\quad d=1, ...,D, \end{aligned}$$

where $n_d = 100$, $\varvec{1}_5$ as column vector of five ones, and $\phi =0.4$. The random effect $v_d$ is drawn from a standard normal, as defined in Sect. 2.1. For the covariate vector $\varvec{x}_d$, we consider four different settings $\{\text {A, B, C, D}\}$ with respect to the dependency between the auxiliary variables. This is done in order to test the methodology under different covariate correlation situations. In the A-setting, we have orthogonal covariates that are generated according to $x_{rd} \sim U(0.7, 1.2)$, $r=1, ..., 5$. For the remaining three settings, we choose

$$\begin{aligned} \quad x_{1d} \sim U(0.7, 1.2), \quad x_{rd} = \alpha (z_d + \rho x_{1d}), \quad z_{d} \sim U(0,0.2), \quad r=2, ..., 5, \end{aligned}$$

where $\rho$ is a parameter controlling the dependency between $x_{1d}$ and $x_{rd}$, and $\alpha$ is a parameter harmonizing the variance of the random variables over settings. In the B-setting, there is medium correlation with 20-50$\%$ on a percentage scale for the product-moment correlation coefficient. For the C-setting, we have correlation with about 50-75$\%$. And in the D-setting, we have a strong correlation with 80-90$\%$. Note that the latter mimics situations of quasi rank-deficiency, which are of special interest. In addition to covariate correlation, we let the total number of areas D vary over scenarios in order to evaluate the method under different degrees of freedom. Overall, we consider 8 simulation scenarios:

$$\begin{aligned} \begin{array}{ll} \mathbf{A}.1 : D= 50 , &{} \mathbf{A}.2 : D= 100, \\ \mathbf{B}.1 : D= 50, \rho = 0.3, \alpha = 2.0, &{} \mathbf{B}.2 : D= 100, \rho = 0.3, \alpha =2.0, \\ \mathbf{C}.1 : D= 50, \rho = 0.9, \alpha =1.5, &{} \mathbf{C}.2 : D= 100, \rho = 0.9, \alpha =1.5, \\ \mathbf{D}.1 : D= 50, \rho = 1.5, \alpha = 0.7, &{} \mathbf{D}.2 : D= 100, \rho = 1.5, \alpha = 0.7.\\ \end{array} \end{aligned}$$

The objective is to estimate the domain proportion $p_d$, $d=1, ..., D$. We compare two model parameter estimation approaches for the logit mixed model described in Sect. 2.1: a non-penalized approach that is obtained from maximizing $l^{app}$ (Laplace-ML), and the $\ell _2$-penalized approach through maximizing $l^{pen}$ ($\ell _2$-PAML), as described in Sect. 3. We evaluate the simulation outcomes with respect to three aspects: (i) model parameter estimation, (ii) domain proportion prediction, and (iii) MSE estimation based on the parametric bootstrap in Sect. 2.3. The results are summarized in the following subsections.

4.2 Model parameter estimation results

The target of this subsection is to study the fitting behavior of the $\ell _2$-PAML algorithm. Define $\varvec{\theta }:= (\beta _0, \varvec{\beta }_1', \phi )$. For a given estimator ${\hat{\theta }}_r \in \hat{\varvec{\theta }}$ of the model parameter $\theta _r$, $r=1, ..., p+1$, we consider the following performance measures:

$$\begin{aligned} Bias({\hat{\theta }}_r)= & {} \frac{1}{K} \sum _{k=1}^K \left( {\hat{\theta }}_r^{(k)} - \theta _r \right) , MSE({\hat{\theta }}_r) = \frac{1}{K} \sum _{k=1}^K \left( {\hat{\theta }}_r^{(k)} - \theta _r \right) ^2, \end{aligned}$$

(32)

where $\theta _r^{(k)}$ is the value that ${\hat{\theta }}_r$ takes in the k-th iteration of the simulation and $\theta _r$ denotes the true value. As $\theta _r = 0.3$ for all components of $\varvec{\beta }_1$, we average the performance measures for the regression parameters. Table 1 contains the results for model parameter estimation.

Table 1 Model Parameter Estimation Results

We start with the regression parameters $\varvec{\beta }= (\beta _0, \varvec{\beta }_1')'$. It can be seen that the $\ell _2$-PAML algorithm obtains more efficient estimates than the ML-Laplace approach. Its MSE is significantly smaller in all considered scenarios. The largest efficiency gains are obtained in the D-scenarios, which include strong covariate correlation. This could be expected from theory, as the $\ell _2$-penalty was introduced by Hoerl and Kennard (1970) in order to improve the fitting behavior in these settings. However, we also see that under orthogonal covariates (A-scenarios), the $\ell _2$-PAML algorithm still outperforms the ML-Laplace approach. This is because approximate likelihood inference introduces additional uncertainty to model parameter estimation. Here, the $\ell _2$-penalty stabilizes the shape of the objective function, which allows for efficiency gains even without covariate correlation. Yet, the increased efficiency comes at the cost of an increased bias. The slope parameters $\varvec{\beta }_1$, which are penalized while applying the $\ell _2$-PAML algorithm, are estimated with larger bias relative to the ML-Laplace method. Please note that this is in line with theory. Hoerl and Kennard (1970) showed that the $\ell _2$-penalty affects the bias-variance trade-off the researcher typically encounters in ML estimation. It increases the bias in order to reduce the variance, which ultimately allows for a smaller MSE when the regularization parameter $\lambda$ is chosen appropriately.

Fig. 1

Absolute deviation of regression parameter estimates

This is also becomes evident when looking at the distribution of regression parameter estimates. Figure 1 shows boxplots of the absolute deviation $|{\hat{\beta }}_r - \beta _r|$, $\beta _r \in \varvec{\beta }_1$, over all Monte Carlo iterations and for different simulation scenarios. In each quarter, the distribution yielded by the $\ell _2$-PAML algorithm is displayed on the left, while the the one obtained by the ML-Laplace algorithm is located on the right. We see that the boxes and whiskers of the $\ell _2$-PAML algorithm are much shorter than those of the ML-Laplace method. This implies that the deviations from the true value are much smaller under penalization for the vast majority of cases. Accordingly, the fitting behavior is overall stabilized.

Concerning $\phi$, the results are different. The standard deviation parameter estimation is not influenced by the covariate correlation. An intuitive explanation for this phenomenon is that $p_{0d}$ is not affected by the collinearity of $\varvec{x}_d$, and that the diagonal element $H_{0p+1p+1}$ of the Hessian matrix depends on $\varvec{x}_d$ only through $p_{0d}$. This is why, we expect that the asymptotic behavior of the ML-Laplace and $\ell _2$-PAML estimators of $\phi$ will be not (or almost not) affected by the covariate correlation.

Concerning the comparison of the two fitting algorithms, the $\ell _2$-PAML approach increases the efficiency of regression parameter estimation. On the other hand, the efficiency of standard deviation parameter estimation is impaired relative to the ML-Laplace approach. In general, both methods overestimate the true value. This is likely due the involved Laplace approximation in both algorithms. It is known to induce bias to model parameter estimation, as for instance addressed by Jiang (2007), p. 131. However, the bias for the $\ell _2$-PAML algorithm is larger, as it implements additional shrinkage of the regression parameters through the $\ell _2$-penalty. The regression parameter estimates are drawn to zero (to some extent), which causes a larger proportion of the target variable’s variance to be attributed to the random effect. This leads to a stronger overestimation of the random effect standard deviation. Nevertheless, we will see in the next subsection that the efficiency advantage in regression parameter estimation overcompensates the loss in standard devation parameter estimation accuracy.

4.3 Domain proportion prediction results

The target of this subsection is to investigate the behavior of the EBP of $p_d$, $d=1, ..., D$. We consider absolute bias, MSE, relative absolute bias, and relative root mean squared error as performance measures. For a domain proportion prediction in the k-th iteration of the simulation study, define

$$\begin{aligned} {\bar{p}}_d= & {} \frac{1}{K}\sum _{k=1}^K p^{(k)}_d,\, RB_d=\frac{\sum _{k=1}^K |{\hat{p}}_d^{(k)}-p_d^{(k)}|}{K|{\bar{p}}_d|},\, \\ RE_d= & {} \frac{\sqrt{\frac{1}{K}\sum _{k=1}^K({\hat{p}}_d^{(k)}-p^{(k)}_d)^2}}{|{\bar{p}}_d|},\,d=1,\ldots ,D. \end{aligned}$$

Further, let

$$\begin{aligned} B_d=\frac{1}{K}\sum _{k=1}^K|{\hat{p}}_d^{(k)}-p_d^{(k)}|,\,\, E_d= \frac{1}{K}\sum _{k=1}^K({\hat{p}}_d^{(k)}-p^{(k)}_d)^2,\,\,\, d=1,\ldots ,D. \end{aligned}$$

The performance measures are then given by

$$\begin{aligned} ABias= & {} \frac{1}{D}\sum _{d=1}^DB_d,\,\, RABias=\frac{1}{D}\sum _{d=1}^DRB_d,\,\, \\ MSE= & {} \frac{1}{D}\sum _{d=1}^DE_d,\,\, RRMSE =\frac{1}{D}\sum _{d=1}^DRE_d. \end{aligned}$$

The results obtained from the simulation study are summarized in Table 2. We observe that $\ell _2$-PAML improves domain total prediction performance in terms of all considered performance measures and for all implemented simulation scenarios, including those without covariate correlation. This is in line with the simulation results for model parameter estimation from the last subsection. The $\ell _2$-penalty stabilizes the estimation performance even for orthogonal covariates due to the necessary Laplace approximation. However, the strongest efficiency gains in terms of the MSE relative to the ML-Laplace algorithm are obtained in the C- and D-scenarios, where we have strong covariate correlation. Against the backhground of Hoerl and Kennard (1970), this could be expected from theory, as $\ell _2$-penalization is known to be particularly useful in the presence of (quasi-)multicollinearity. Overall, we can conclude that the $\ell _2$-PAML algorithm not only improves model parameter estimation, but also domain total prediction in any setting.

Table 2 Domain Proportion Prediction Results

4.4 Mean squared error estimation results

The target of this subsection is to study the performance of the parametric bootstrap for MSE estimation. We employ $B=500$ bootstrap replicates in order to approximate the prediction uncertainty under the model. For a MSE estimate in the k-th iteration of the simulation study, define

$$\begin{aligned} MSE_d = \frac{1}{K} \sum _{k=1}^K ({\hat{Y}}_d^{(k)} -Y_d^{(k)})^2, \quad mse_d = \frac{1}{K} \sum _{k=1}^K mse({\hat{Y}}_d^{(k)}), \quad mse = \frac{1}{D} \sum _{d=1}^D mse_d, \end{aligned}$$

where ${\hat{Y}}_d^{(k)}$ and $mse({\hat{Y}}_d^{(k)})$ are the EBP of $Y_d$ and its bootstrap MSE estimator (see Sect. 2.3), respectively. We consider the following performance measures

$$\begin{aligned} RBias = \frac{1}{D} \sum _{d=1}^D \frac{mse_d - MSE_d}{MSE_d}, \quad RRMSE = \frac{1}{D} \sum _{d=1} \frac{\sqrt{\frac{1}{D} \sum _{d=1}^D (mse_d - MSE_d)^2}}{MSE_d}. \end{aligned}$$

Table 3 summarizes the simulation results. We see that the parametric bootstrap estimator shows a decent performance overall. There is a slight tendency for underestimation. However, with a relative bias of less then 4.3$\%$ for approximate likelihood inference with a generalized linear mixed model, this is negligible. With regards to the RRMSE, we see that the parametric bootstrap is more efficient under orthogonal covariates (A-scenarios) and medium correlation (B-scenarios). In the C- and D-scenarios, which employ stronger covariate correlation, the RRMSE becomes larger. This is in line with the results of Sect. 4.2. In these scenarios, the model parameter estimates are subject to larger variation, which affects the bootstrap due to its parametric construction. Yet, with respect to practice, a RRMSE ranging from 8.5$\%$ to 17.2$\%$ is a solid result for uncertainty estimation.

Table 3 Mean Squared Error Estimation Results

5 Application

5.1 Data description and model specification

In what follows, we apply the $\ell _2$-PAML approach to estimate the regional prevalence of multiple sclerosis in Germany. For this, we consider the German population of the year 2017. It is segmented into 401 administrative districts and contains about 82 million individuals. The districts correspond to the domains in accordance with Sect. 2.1. The required demographic information is retrieved from the German Federal Statistical Office and based on the methodological standards described in Statistisches Bundesamt (2016). As model response y, we define a binary variable with realizations

$$\begin{aligned} y_{id} = {\left\{ \begin{array}{ll} 1 &{} \text {person has multiple sclerosis} \\ 0 &{} \text {else} \end{array}\right. } \end{aligned}$$

for some $i \in U_d$. The objective is to estimate $p_d = Y_d / N_d$ with $Y_d = \sum _{i \in U_d} y_{id}$ for all German districts. In order to define whether a person has multiple sclerosis, we rely on an intersectoral disease profile provided by the Scientific Institute Institute of the AOK (WIdO). It is based on multiple aspects, including medical descriptions, inpatient diagnoses, and ambulatory diagnoses. The necessary sample counts for y are based on health insurance records provided by the AOK. In particular, we use district-level prevalence figures of the AOK insurance population in 2017 that are based on the intersectoral disease profiles. The AOK insurance population is the biggest statutory health insurance population of the country with roughly 26 million individuals in 2017 (AOK Bundesverband 2018). Note that the German health insurance system has a rather unique separation between statutory and private health insurance. Usually, this has to be accounted for in order to produce reliable prevalence estimates. However, Burgard et al. (2019) showed that model-based inference using covariate data with sufficient explanatory power can overcome this issue.

As auxiliary data source, we use district-level inpatient diagnosis frequencies of the German DRG-Statistics that are provided by the German Federal Statistical Office (Statistisches Bundesamt 2017). The data set contains figures on how often a given disease has been recorded in hospitals within a year. Both main and secondary diagnoses are considered. With respect to diagnosis grouping, the records are provided on the ICD-3 level (World Health Organization 2018). Note that the DRG-Statistics are a full census of all German hospitals. Thus, the corresponding records cover the entire population, as required for the model derivation in Sect. 2.1. However, a drawback of the data set’s richness is that we have to choose a suitable set of predictors x out of approximately 3 000 potential covariates. Naturally, it is not feasible to apply an exhaustive stepwise strategy that is often used in the context of variable selection, as for instance demonstrated by Yamashita et al. (2007).

Instead, we apply a heuristic strategy based on the premise that the objective is to find a covariate subset with sufficient explanatory power for our purpose. First, we isolate the 20 variables of the DRG-Statistics that have the strongest correlation with the AOK records on G35, which is multiple sclerosis on the ICD-3 level. The variables are arranged in decreasing order with respect to their correlation. Next, we use the $\ell _2$-PAML algorithm from Sect. 3.2 to perform model parameter estimation for p covariates, where $p \in \{2, 3, ..., 20\}$. That is to say, we start with the 2 covariates that have the strongest correlation to G35, and then sequentially increase the number of predictors up to 20. For every result of model parameter estimation, we calculate the Laplace non-corrected BIC in (29). Then, we select the covariate subset that corresponds to the model fit which minimizes the BIC. The BIC curve over all considered covariate set cardinalities is displayed in Fig. 2. We see that the curve has an odd evolution over the covariate sets. This can be attributed to three reasons. Firstly, due to the non-linearity of the link function, the covariate sorting is guaranteed to organize the covariates in descending order with regards to their relevance for the target variable. Secondly, due to the strong correlation between them, the covariate contributions interfer with each other. That is to say, when including an additional covariate into the active set, the contributions of the previously contained covariates can change considerably. And finally, as already addressed in Sect. 3.3, the non-convexity of the optimization problem further leads to irregularities in the BIC curve.

Fig. 2

BIC over covariate set cardinalities

Despite these issues, the BIC curve has a clear minimum that is located at $p=9$. Therefore, we isolate the 9 DRG-Statistics variables that have the strongest correlation with the AOK records on G35. Thereafter, we perform a parametric bootstrap to estimate the standard deviation of each model parameter estimate ${\hat{\theta }}_j \in {\hat{\varvec{\theta }}}$, $j=1, ..., p+1$, to evaluate its significance in terms of the p-value. The parametric bootstrap is described as follows:

• 1. Fit the model to the sample and calculate the estimator ${{\hat{\varvec{\theta }}}}=({\hat{\varvec{\beta }}}',{\hat{\phi }})$.

• 2. Repeat B times with $b=1, ..., B$:

  • (a) Generate $v_d^{(b)}\sim N(0,1)$, $y_d^{(b)}\sim \text{ Bin }({n}_{d},p_{d}^{(b)})$, $d=1,\ldots ,D$, where $p_d^{(b)}=\frac{\exp \left\{ \varvec{x}_{d}{{\hat{\varvec{\beta }}}}+{{\hat{\phi }}} v_{d}^{(b)}\right\} }{1+\exp \left\{ \varvec{x}_{d}{{\hat{\varvec{\beta }}}}+{{\hat{\phi }}} v_{d}^{(b)}\right\} }$.

  • (b) For each bootstrap sample, calculate the estimator ${\hat{\varvec{\theta }}}^{(b)}$.

• 3. Output: $sd({\hat{\theta }}_j)=\sqrt{\frac{1}{B}\sum _{b=1}^B\big ({\hat{\theta }}_j^{(b)}- \frac{1}{B} \sum _{k=1}^B {\hat{\theta }}_j^{(k)} \big )^2}$, $j=1, ..., p+1$.

Based on the estimated standard deviations, we calculate test statistics for a sequence of t-tests under the null hypothesis $H_0: \theta _j = 0$, $j=1, ..., p+1$. For a given $\theta _j \in \varvec{\theta }$, the test statistic is given by $t_j = {\hat{\theta }}_j/sd({\hat{\theta }}_j)$ and follows a standard normal distribution. The test statistic values are located in the pdf of the standard normal to obtain their respective p-values. We delete every predictor that corresponds to a model parameter that is not relevant on at least a 10$\%$ significance level. The entire procedure is summarized hereafter:

• 1. Find the 20 covariates with the strongest correlation to y

• 2. Perform model parameter estimation for $p \in \{2, 3, ..., 20\}$ predictors

• 3. Find the number of predictors that minimizes the BIC

• 4. For the BIC-minimal predictor set, perform a parametric bootstrap to estimate standard deviations for the model parameter estimates

• 5. Perform t-tests to evaluate their significance and delete insignificant predictors

The proposed strategy yields us the final covariate set x which consists of $p=5$ predictors. The selected covariates are briefly characterized as follows:

• $X_1$: G43 (Migraine, secondary diagnosis)

• $X_2$: M20 (Acquired deformities of fingers and toes, main diagnosis)

• $X_3$: E66 (Overweight and obesity, main diagnosis)

• $X_4$: E04 (Other nontoxic goiter, main diagnosis)

• $X_5$: G35 (Multiple sclerosis, secondary diagnosis)

Please note that the association of these variables with multiple sclerosis is the result of district-level correlation. It does not directly imply person-level comorbidities in a medical sense. Applying the $\ell _2$-PAML algorithm on the final covariate set yields us the final model specification that we use for regional prevalence estimation. It is summarized in Table 4. The confidence intervals for the parameters are calculated according to ${\hat{\theta }}_j \pm t_{(D, 1-\alpha /2)} sd({\hat{\theta }}_j)$, $j=1, ..., p+1$, where $t_{(\cdot )}$ is the corresponding quantile of t-distribution with D degrees of freedom and significance level $\alpha$. The BIC value of the upper model specification is 979754 and therefore even better than the optimal fit with $p=9$ in Fig. 2. This suggests that the used model specification was a reasonable choice given the considered data basis. Further, observe that the estimated value for the standard deviation parameter $\phi$ is considerably larger than all slope parameters $\beta _1, ..., \beta _5$. This implies that the random effects $v_1, ..., v_D$ are clearly evident in the empirical distribution of $p_1, ..., p_D$. Therefore, we can conclude that using a mixed effect model in this context was a necessary choice.

Table 4 Estimation results for final model specification

We further look at the internal correlation structure of the considered predictors in order to assess the demand for $\ell _2$-penalization in the application. For this, we look at the empirical correlation matrix for the five selected DRG-Statistics variables. It is given as follows:

$$\begin{aligned} \varvec{\varrho }_{xx} = \begin{pmatrix} 1.00\quad &{} 0.95\quad &{} 0.93\quad &{} 0.85\quad &{} 0.94 \\ 0.95\quad &{} 1.00\quad &{} 0.94\quad &{} 0.87\quad &{} 0.95 \\ 0.93\quad &{} 0.94\quad &{} 1.00\quad &{} 0.88\quad &{} 0.95 \\ 0.85\quad &{} 0.87\quad &{} 0.88\quad &{} 1.00\quad &{} 0.88 \\ 0.94\quad &{} 0.95\quad &{} 0.95\quad &{} 0.88\quad &{} 1.00 \end{pmatrix} \end{aligned}$$

We observe that (beside the main diagonal elements), the correlation values range from 0.85 to 0.95, or 85$\%$ to 95$\%$ on a percentage scale. This suggests that the internal correlation structure is very strong and comparable to the D-scenarios of our simulation study. Therefore, we conclude that using $\ell _2$-penalization is reasonable in this context. However, note that some of this correlation is due to the size as a result of district-level aggregation. Again, this does not directly resemble medical comorbidity on an individual level.

5.2 Results

Let us now investigate the results of prevalence estimation. The national prevalence $\sum _{d=1}^D Y_d / \sum _{d=1}^D N_d \cdot 100\%$ is estimated at 0.296$\%$. Based on the parametric bootstrap, we calculate a 95$\%$ confidence interval of $[0.293\%; 0.300\%]$. This implies that the estimated total number of persons with multiple sclerosis ranges approximately from 239 000 to 246 000, which is in line with reference figures on this topic. The Central Research Institute of Ambulatory Health Care in Germany estimated that in 2017 about 240 000 individuals had multiple sclerosis (Müller 2018). The regional distribution of prevalence estimates on the district-level is displayed in Fig. 3. We observe a prevalence discrepancy between the western and eastern parts of Germany. The estimated prevalence in western Germany are overall higher than in eastern Germany. Further, we observe regional clustering with higher prevalence in the central-northern and central-southern parts of Germany. This is also consistent with reference studies. Similar patterns have been found by Central Research Institute of Ambulatory Health Care in Germany (Müller 2018) and Petersen et al. (2014). Overall, the estimates are plausible in both level and geographic distribution.

Fig. 3

Results of prevalence estimation

Figure 3 shows the distributions of district-level prevalence estimates for the EBPs under both $\ell _2$-PAML and the classical ML-Laplace method. The ML-Laplace results are displayed in black, the $\ell _2$-PAML results are plotted in red. We see that the means of the distributions are almost identical. However, the $\ell _2$-PAML distribution shows considerably less variance than the ML-Laplace distribution. This is in line with both theory and the simulation study, which both suggest stabilizing effects through $\ell _2$-penalization.

Fig. 4

Comparision of the EBPs

This is further evident when looking at the summarizing quantiles of both predictive distributions. They are displayed in Table 5 . We see that the $\ell _2$-PAML estimates are more more focussed around the mean and do not show as strong of outliers at the tails of the distribution compared to ML-Laplace.

Table 5 Quantiles of the EBP distributions

Figure 5 displays the root mean squared error estimates $rmse({\hat{p}}_d) = \sqrt{mse({\hat{p}}_d)}$ for the prevalence estimates in Fig. 3, where $mse({\hat{p}}_d)$ is obtained from the parametric bootstrap procedure described in Sect. 2.3. It becomes evident that there are no obvious spatial patterns in the RMSE estimates. We neither observe a particular dependency on the domain sizes nor on the prevalence estimates themselves. However, with respect to the overall level of RMSE estimates, we can conclude that our estimates are more efficient than direct estimates ${\hat{p}}_d^{dir} = y_d / n_d$, $d=1, ..., D$, that are exclusively obtained from the health insurance records. Their standard deviation is given by $sd({\hat{p}}_d^{dir}) = \sqrt{{\hat{p}}_d^{dir}(1-{\hat{p}}_d^{dir})}$.

Fig. 5

Results of RRMSE estimation

A one-to-one comparison of $rmse({\hat{p}}_d)$ and $sd({\hat{p}}_d^{dir})$ per domain is visualized in Fig. 6. The ordinate measures $sd({\hat{p}}_d^{dir})$ and the abscissa measures $rmse({\hat{p}}_d)$. The red line marks the bisector, which indicates equality between the two. We observe that $rmse({\hat{p}}_d)$ is always smaller than $sd({\hat{p}}_d^{dir})$ by quite a margin. Thus, given the reasonable performance of the parametric bootstrap for MSE estimation in the simulation, we can conclude that our estimates mark an improvement over the direct estimates. There is a slight positive relation between the two measures. That is to say, a relatively large $sd({\hat{p}}_d^{dir})$ is accompanied by a relatively large $rmse({\hat{p}}_d)$ on expectation. However, the trend is only vaguely visible.

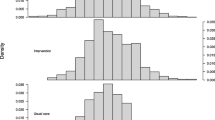
Finally, let us look at the distribution of random effect predictions over domains. They are visualized in Fig.7. The bars of the histogram correspond to the probability density of the mode predictors in the respective interval of the support. The red line is the result of a kernel density estimation over their realized values. We observe that the distribution is very close to normal. This is in line with the theoretical developments from Sect. 2.1. Overall, it can be concluded that the $\ell _2$-PAML approach in the area-level logit mixed model was a sensible choice for the considered application.

Fig. 6

Comparision of estimation uncertainty

Fig. 7

Distribution of random effect mode predictions

6 Conclusion

Regional prevalence estimation is an important issue to monitor the health of the population and for planning capacities of a health care system. A good covariate on the prevalence of a disease can be typically obtained from medical treatment records such as the DRG-Statistics in Germany. We proposed a new small area estimator for regional prevalence that copes with two major issues in this context. First, typically health surveys do not have a large sample and the sample size is mainly dedicated to allow for the estimation of national figures. Within regional entities, therefore, the sample size is very small. Applying classical design based or model assisted estimators on these small sample sizes leads to very high standard errors for many regions. Our small area estimator is capable of overcoming this issue by using a model based approach. The second problem we tackle is, that the best covariates at hand, typically have high correlations between each other. This leads to numerical problems inhibiting the exploitation of these covariates. To overcome this problem we propose to use a $\ell _2$-penalization approach. This leads to the need for revising the parameter estimation procedure and to adapt it to the new requirements. We provide therefore a novel Laplace approximation to a logit mixed model with $\ell _2$ regularization. This estimation procedure is applicable for other purposes such as classical logit mixed model estimation with $\ell _2$-penalization.

The prevalence estimation maps of Sect. 5 show some clusters of small areas with high or low prevalence. This fact indicates that modeling spatial correlation by introducing, for example, simultaneous autoregressive random effects, might benefit the final predictions. Combining this additional generalization with the robust penalized approach is thus desirable. However, it is not an easy theoretical task and deserves future independent research. In a Monte Carlo simulation study we show that the proposed estimation approach $\ell _2$-PAML yields stable parameter estimates even under strong correlations of the covariates. This simulation results underpin the theoretical arguments. Finally, we applied this newly derived estimator to the prediction of district-level multiple sclerosis prevalence and obtained estimates with a considerably low root mean squared error. Hence, we recommend using our new approach for the regional prevalence estimation.