A modification of Chao’s lower bound estimator in the case of one-inflation

Abstract

For zero-truncated count data, as they typically arise in capture-recapture modelling, the nonparametric lower bound estimator of Chao is a frequently used estimator of population size. It is a simple, nonparametric estimator involving only counts of one and counts of two. The estimator is asymptotically unbiased if the count distribution is a member of the power series family and is providing a lower bound estimator if the distribution is a mixture of a member of the power series family. However, if there is one-inflation Chao’s estimator can severely overestimate as we show here. This is also illustrated by routinely collected country-wide data on family violence in the Netherlands. A new lower bound estimator is developed which involves only counts of twos and threes, thus avoiding the overestimation caused by one-inflation. We show that the new estimator is asymptotically unbiased for a power series distribution with and without one-inflation and provides a lower bound estimator under a mixture of power series distributions with and without one-inflation. For all estimators bias-adjusted versions are developed that reduce the bias considerably when the sample size is small. A simulation study compares the modified Chao estimator with the conventional estimator as well as with an estimator suggested by Chiu and Chao more recently.

1 Introduction

The size N of a target population needs to be determined. For this purpose a trapping experiment or study is done where members of the target population are identified at T occasions where T might be known or not. For each member i the count of identifications $X_i$ is returned where $X_i$ takes values in $\{0,1,2,\ldots ,T\}$ for $i=1,\ldots ,N$. However, zero-identifications are not observed, they remain hidden in the experiment. Hence, a zero–truncated sample $X_1,\ldots ,X_n$ is observed, where we have assumed without loss of generality that $X_{n+1}=\cdots =X_N=0$ (for a general introduction into the topic see Borchers et al. 2004; Bunge and Fitzpatrick 1993; Bunge et al. 2014). One way to undertake capture-recapture modelling is on the basis of a zero-truncated count distribution $f_1, f_2, \ldots , f_T$ where $f_x$ is the frequency of count x with T being the largest observed count and $n=f_1+\cdots +f_T$ is the observed sample size. The frequency of zero-counts (of hidden members of the target population) remains unobserved and needs to be estimated. For this purpose Chao’s (1987) conventional estimator $f_1^2/(2f_2)$ for the unobserved frequency $f_0$ of zero-counts is frequently used. Chao’s estimator $n+f_1^2/(2f_2)$ of the population size N is asymptotically unbiased if count X follows a Poisson distribution and represents a lower bound if X follows a mixture of Poisson distributions. In fact, it is pointed out in Chao and Colwell (2017) that the result of asymptotic unbiasedness of Chao’s estimator holds under the weaker condition that only the rare counts need to follow a Poisson distribution, more precisely the counts of ones and twos, the singletons and doubletons, and the unseen units need to follow a Poisson distribution. Chiu et al. (2014) present a bias-improved lower bound but do not address the problem of one-inflation. The purpose of this note is to present a modification of the Chao estimator in the case of one-inflation as it can severely over-estimate in this case. This is in considerable contrast to the expectation of users of the estimator as it is expected that it provides a meaningful lower bound , i.e. a lower bound that is relatively close to the true population size.

One-inflation can occur when the population under study has a subpopulation that cannot be captured anymore after the first capture. Below we discuss an example of police data on perpetrators of domestic violence. Here it is realistic to assume that some individuals in the population refrain from domestic violence after their first contact with the police, in other words their probability to have another capture is zero. A second example is hospital admissions of drug users: the first hospital admission may lead to a change in drug use. In animal studies the idea may be relevant in trap avoidance, where an animal avoids the trap after being captured for the first time. Recently, the problem of one-inflation has received some attention in the literature. Chiu and Chao (2016) consider estimating microbial diversity in the presence of sequencing errors. Bunge et al. (2012) consider estimating population diversity with unreliable low frequency counts (see also Bunge et al. 2014; Willis 2016). All have in common that the frequency $f_1$ of observed singletons is inflated. Whereas in Bunge et al. (2012) several approaches are suggested to deal with inflated singletons including a mixture model and left-censoring, Chiu and Chao (2016) and Willis (2016) suggest a sort of double estimation procedure. First, the observed frequency $f_1$ is re-estimated (Willis 2016) or bias-adjusted (Chiu and Chao 2016) and then incorporated in the ratio-estimator of Willis and Bunge (2015) or the Chao estimator (Chiu and Chao 2016). In addition, Puig and Kokonendji (2018) suggest several lower bound estimators for count distributions with log-convex probability generating functions including compound and mixed Poisson distributions. These, however, do not cover the case of one-inflation. Here, we will develop a lower bound estimator generalizing the original Chao (1987) estimator without dealing with the frequency $f_1$ of singletons measured with error.

To layout the most general setting we consider discrete distributions of the power series family with density

$$\begin{aligned} p_x(\theta )=a_x \theta ^x/\eta (\theta ), \end{aligned}$$

(1)

where $a_x$ is a known, nonnegative coefficient, $\theta$ a positive parameter and $x=0,1,\ldots$ ranges over the set of nonnegative integers; $\eta (\theta )= \sum _{x=0}^\infty a_x \theta ^x$ is the normalizing constant. The power series distributional family contains the Poisson, the binomial, the geometric, the negative-binomial with known shape parameter, the log-series and others. The coefficient $a_x$ defines the specific member of the power series, for example $a_x=1/x!$ defines the Poisson, $a_x={T \atopwithdelims ()x}$ for $x=0,\ldots ,T$ with positive integer T defines the binomial ($a_x=0$ for $x>T$) and $a_x=1$ gives the geometric. Assume further that the target population of interest is not homogeneous so that a more adequate modelling is achieved with the general mixture model for the power series family

$$\begin{aligned} m_x= \int _\theta p_x(\theta ) f(\theta ) d\theta . \end{aligned}$$

(2)

whereas the modelling capacity of the power series distribution is limited, mixtures of power series distributions experience enhanced flexibility in model fitting. The mixture (2) has two parts, the mixture kernel $p_x(\theta )$ and the mixing distribution $f(\theta )$. If we leave the mixing distribution unspecified, the nonparametric estimate is discrete (Lindsay 1995) and connects to clustering.

However, when mixed power series distributions are used to model the zero-truncated distribution, problems may arise due to the lack of identifiability of the mixing distribution (see Link 2003); in addition, boundary problems in maximum likelihood estimation may occur for finite mixture models as outlined by Wang and Lindsay (2005). Hence a renewed interest in lower bound estimation has emerged (Mao 2006; Mao and Lindsay 2007). The original idea of Chao (1987, 1989) was to keep the mixing distribution unspecified and to apply nonparametric inference based on the Cauchy-Schwarz inequality in the context of zero-truncated count mixture modelling which arises naturally in capture-recapture experiments or studies. Here we take up this idea again and develop it further for one-inflated count distributions. The associated zero-truncated densities will be denoted as $p_x^+(\theta )=p_x(\theta )/[1-p_0(\theta )]$ and $m_x^+(\theta )=m_x(\theta )/[1-m_0(\theta )]$ for the zero–truncated power series and the zero–truncated mixture of power series distributions, respectively.

2 Mixtures of power series distributions and the monotonicity of the probability ratio

The power series (1) has an important property. If we consider ratios of neighboring probabilities multiplied by the inverse ratios of their coefficients then

$$\begin{aligned} r_x= \frac{a_x}{a_{x+1}} \frac{p_{x+1}}{p_x}= \theta , \end{aligned}$$

(3)

in other words, the ratio $r_x$ is constant over the range of x with value equal to the unknown parameter $\theta$. Note that $r_x$ is also identical to the zero-truncated quantities $\frac{a_x}{a_{x+1}} \frac{p^+_{x+1}}{p^+_x}$. A nonparametric estimate of $r_x$ is readily available with ${\hat{r}}_x = \frac{a_x}{a_{x+1}} \frac{f_{x+1}}{f_x}$ where $f_x$ is the frequency of observations with count value x. The graph $x \rightarrow {\hat{r}}_x$ is called ratio plot and was developed in Böhning et al. (2013) as a diagnostic device providing evidence for the aptness of a distribution. The coefficient $a_x$ determines the type of ratio plot. For example, if $a_x=1/x!$ we investigate for a Poisson distribution and we call the associated ratio plot Poisson ratio plot, or if $a_x=1$ we call it the geometric ratio plot. The ratio plot might be used as guidance for choosing the component density in the mixture. We follow the paradigm that the more horizontal the ratio plot the more homogeneous is the population w.r.t. the component density, and this would indicate a preference of the distribution with more horizontal pattern in the associated ratio plot.

Table 1 Frequencies of the number of times perpetrators have been identified in a domestic violence incident in the Netherlands in the year 2009

2.1 Example 1

We apply the ratio plot to family violence data for the Netherlands in the year 2009 provided by Van der Heijden et al. (2014). Here the perpetrator study is reported with the data given in Table 1. There were 15, 169 perpetrators identified being involved in a domestic violence incident exactly once, 1957 exactly twice, and so forth. In total, there were 17, 662 different perpetrators identified in the Netherlands for 2009. The data represent the Netherlands except the police region for The Hague. It is known that domestic violence is largely a hidden activity and many incidents remain unreported (Summers and Hoffman 2002). In Fig. 1, we see the geometric ratio plot ${\hat{r}}_x=f_{x+1}/f_x$ against x for the family violence data in the Netherlands. Clearly, the ratio plot shows some monotone increasing trend. We will see in the following that this monotone pattern can be associated with some form of population heterogeneity. In addition, it is apparent that the first ratio $f_2/f_1$ is too small to be in agreement with the line pattern we see in the ratio plot. This indicates an inflation of ones or singletons in the data. In conclusion, we observe two aspects in Fig. 1: the occurrence of heterogeneity and of one-inflation.

Fig. 1

Geometric ratio plot for perpetrator domestic violence identifications in the Netherlands 2009

We return to the question how unobserved heterogeneity is associated with the ratio plot, or in other words, how unobserved heterogeneity can be identified in the ratio plot. It was shown in (2) that the occurrence of unobserved heterogeneity leads to the mixture of power series distributions. We can likewise consider the ratio plot for mixtures

$$\begin{aligned} r_x= \frac{a_x}{a_{x+1}} \frac{m_{x+1}}{m_x}, \end{aligned}$$

(4)

where we use the coefficients $a_x$ associated with the mixture kernel, for example, in the case of a Poisson kernel $a_x=1/x!$ or the case of a geometric kernel $a_x=1$. The estimate of $r_x$ will not change, however, the interpretation of the observed pattern in the ratio plot will. This is mainly due to the following result (Chao 1987, and more general Böhning and Del Rio Vilas 2008):

Theorem 1

Let $m_x= \int _\theta p_x(\theta ) f(\theta ) d\theta$ where $p_x(\theta )$ is a member of the power series family and $f(\theta )$ an arbitrary density. Then, for $r_x= \frac{a_x}{a_{x+1}} \frac{m_{x+1}}{m_x}$ we have the following monotonicity:

$$\begin{aligned} r_x \le r_{x+1} \end{aligned}$$

for all $x=0,1,\ldots$.

This result says that in the case of a mixture of power series distributions the ratio plot will no longer show a horizontal line pattern but will be increasing monotonously. Hence, if a monotone pattern occurs in the ratio plot this may be taken as indication for presence of heterogeneity which can be captured by a nonparametric mixture (2). For this general form of allowing population heterogeneity the estimator of Chao had been developed. If on top of this general heterogeneity one-inflation occurs, Chao’s estimator needs modification which we will discuss in the next section.

3 Modified Chao estimation

As a consequence of the result in Theorem 1 we have that $\frac{a_0}{a_{1}} \frac{m_{1}}{m_0} \le \frac{a_1}{a_{2}} \frac{m_{2}}{m_1}$, or

$$\begin{aligned} \frac{a_0a_{2}}{a_1^2} \frac{m_{1}^2}{m_2}\le {m_0}. \end{aligned}$$

(5)

Replacing the theoretical quantities $m_x$ by their sample estimates $f_x/N$ leads to Chao’s estimate for $f_0$ (Chao 1987, 1989)

$$\begin{aligned} {\hat{f}}_0 = \frac{a_0a_{2}}{a_1^2} \frac{f_{1}^2}{f_2}. \end{aligned}$$

(6)

By comparing (5) with (6) it can be seen that (6) provides a lower bound of the part of the population that is missed. The estimate (6) is most popular and frequently used in capture-recapture estimation, in particular in connection with the Poisson density ($a_x=1/x!$) in the mixture (2). However, it should be noted that other bounds are possible as well using the monotonicity result in Theorem 1. Note that also

$$\begin{aligned} \frac{a_1}{a_{2}} \frac{m_{2}}{m_1} \le \frac{a_2}{a_{3}} \frac{m_{3}}{m_2} \end{aligned}$$

(7)

holds, or equivalently

$$\begin{aligned} \frac{a_1a_{3}}{a_2^2} \frac{m_{2}^2}{m_3}\le {m_1}. \end{aligned}$$

(8)

This bound has never been used nor elaborated on, as it seems pointless since we have observed counts of one, and no bounds seem to be required. If we replace $m_1$ in (5) with the bound given in (8) we yield

$$\begin{aligned} \frac{a_0a_{2}}{a_1^2} \left( \frac{a_1a_{3}}{a_2^2} \frac{m_{2}^2}{m_3}\right) ^2 \frac{1}{m_2}\le {m_0}. \end{aligned}$$

(9)

The bound can be simplified to

$$\begin{aligned} \frac{a_0a_{3}^2}{a_2^3} \frac{m_{2}^3}{m_3^2}\le {m_0}. \end{aligned}$$

(10)

Plugging in frequencies leads to

$$\begin{aligned} {\hat{f}}_0^{\mathrm{new}} = \frac{a_0a_{3}^2}{a_2^3} \frac{f_{2}^3}{f_3^2}. \end{aligned}$$

(11)

Note that we can expect ${\hat{f}}_0^{\mathrm{new}}$ to be smaller than ${\hat{f}}_0$ in the mean as

$$\begin{aligned} \frac{a_0a_{3}^2}{a_2^3} \frac{m_{2}^3}{m_3^2} \le \frac{a_0a_{2}}{a_1^2} \frac{m_{1}^2}{m_2} \le m_0. \end{aligned}$$

(12)

Specific forms of the modified Chao estimator arise for mixtures of particular power series members. We have

$$\begin{aligned} {\hat{f}}_0^{\mathrm{new}}= {\left\{ \begin{array}{ll}\frac{2}{9} \frac{f_{2}^3}{f_3^2}, &{}\quad \text{ if } m_x \text{ is } \text{ a } \text{ Poisson } \text{ mixture },\\ \frac{f_{2}^3}{f_3^2}, &{}\quad \text{ if } m_x \text{ is } \text{ a } \text{ geometric } \text{ mixture },\\ \frac{(T-2)^2}{T(T-3)} \frac{2}{9} \frac{f_{2}^3}{f_3^2}, &{}\quad \text{ if } m_x \text{ is } \text{ a } \text{ binomial } \text{ mixture. } \end{array}\right. } \end{aligned}$$

Note that for T becoming large the lower bound for the Poisson mixture and the binomial mixture will agree. Furthermore, if the mixture reduces to a power series distribution (i.e. there is no mixing involved), both estimators, ${\hat{f}}_0^{\mathrm{new}}$ and ${\hat{f}}_0$, are asymptotically unbiased. Note that, similar to the original Chao estimator (Chao and Colwell 2017), for asymptotic unbiasedness the assumption of a power series distribution can be relaxed to hold only for the rare counts, the doubletons and tripletons, i.e. counts of twos and counts of threes, and the unseen units.

The question arises why the bound ${\hat{f}}_0^{\mathrm{new}}$ could be of interest, as, according to (12), it will typically provide an even lower bound than the conventional Chao lower bound estimator ${\hat{f}}_0$. This question is the topic of the next section.

4 One-inflation

In practice, counts of one, the singletons, occur often more frequently than compatible with a nonparametric mixture model. For example, in the family violence study a portion of the perpetrators having a contact with the police the first time might take this as a serious motivation for a change in behavior and it will never happen again. As Fig. 1 indicates, there appear to be two processes going on. The first process can be viewed as a mixture of geometric distributions (as the linear trend in the ratios of frequencies for counts larger than one indicates) . The second process is an inflation of ones (as the much lower ratio $f_2/f_1$ supports). In these instances, it is more appropriate to allocate extra-mass at counts of one. Hence, we assume that the following one-inflation model holds:

$$\begin{aligned} m_x^\prime ={\left\{ \begin{array}{ll} (1-\pi ) +\pi m_1&{} \quad \text{ for } x=1\\ \pi m_x &{} \quad \text{ for } x=0,2,3,\ldots \end{array}\right. }, \end{aligned}$$

(13)

where $m_x$ is the mixture of a power series member. Note that (13) can be written as $m_x^\prime =(1-\pi )\delta _1(x)+ \pi m_x$ for $x=0,1,2,\ldots$ and $\delta _y(x) = 1$ for $x=y$ and zero otherwise. For a one-inflation model, more singletons will occur than compatible with the nonparametric mixture model as the one-inflation model is outside the class of nonparametric mixtures. Hence Chao’s estimator is no longer a lower bound estimator as Theorem 1 no longer holds. In fact, Chao’s estimator can experience serious overestimation as also becomes clear when considering its form which involves $f_1^2$. Note that one-inflation models behave differently than zero-inflation models as every zero-inflated power series distribution can be written as the mixture $(1-\pi )\delta _0(x) + \pi m_x = (1-\pi ) a_x 0^x/\eta (\theta )+ \pi m(x)$ which is within the class of nonparametric mixtures of power series distributions.

Here comes now the advantage of the new lower bound estimator.

Theorem 2

Assume a one-inflation model $m_x^\prime$ as given in (13), where $m_x= \int _\theta p_x(\theta ) f(\theta ) d\theta$ where $p_x(\theta )$ is a member of the power series family and $f(\theta )$ an arbitrary density. Then

$$\begin{aligned} \frac{a_0a_{3}^2}{a_2^3} \frac{{m_{2}^\prime }^3}{{m_3^\prime }^2}\le {m_0^\prime }. \end{aligned}$$

(14)

We provide a short proof of the result in the appendix. As a consequence of this theorem we can expect ${\hat{f}}_0^{\mathrm{new}}$ to be a lower bound estimator in the mean under heterogeneity of the parameter of the power series distribution and under one-inflation.

Consider the case of a power series distribution with one-inflation, in other words $m_x^\prime =(1-\pi )\delta _1(x)+ \pi p_x$. Then, the conventional Chao estimator has asymptotic bias

$$\begin{aligned} \frac{a_0a_{2}}{a_1^2} \frac{[(1-\pi ) +\pi p_1]^2}{\pi p_2}N - a_0/\eta (\theta ) N \end{aligned}$$

whereas the newly suggested estimator is asymptotically unbiased, even if the power series distribution is one-inflated.

4.1 Example 2

To illustrate the potential of large bias with the conventional Chao estimator consider the following synthetic example. 500 counts were simulated from a Poisson with parameter 1 and merged with 500 extra-ones so that in total $N=1000$ is the population size. The frequency distribution as follows: $f_0=186$, $f_1=690$, $f_2=95$, $f_3=32$, $f_{4+}=7$, so that the observed sample size is $n=814$. The associated ratio plot is presented in Fig. 2 and shows clear evidence of one-inflation. In this case, ignoring the fact that $f_0$ is known, ${\hat{f}}_0^{\mathrm{new}}=186$, corresponding exactly to the observed $f_0$, which compares to the conventional Chao estimator ${\hat{f}}_0=2{,}434$, the latter giving a serious overestimate of the true $f_0=186$.

Fig. 2

Poisson ratio plot for the synthetic data of Example 2

4.2 Example 3

Vergne et al. (2014) discuss count modelling of highly pathogenic avian influenza H5N1 in Thailand. These outbreaks have enormous social and economic impact on the society. The first outbreaks of highly pathogenic avian influenza H5N1 were reported in Thailand in January 2004. For around two years, a large epidemic occurred through-out the country, causing massive mortality in chickens and ducks. The economic consequences of these outbreaks were dramatic, as more than 65 million birds were culled and over US$ 130 million was spent compensating farmers losses during 2004 and 2005 (Vergne et al. 2014). Vergne et al. (2014) also provide the distribution of the number of outbreaks per subdistrict in Thailand from July 3rd 2004 to May 5th 2005. See also Table 2. According to this table, there are 6587 subdistricts in Thailand which reported no outbreaks. However, it can be assumed that there were a considerable number of subdistricts affected by the pathogenic avian influenza H5N1 but reported no outbreaks. Hence, it is of considerable interest to have an estimate of this number. This can be accomplished by treating the distribution as zero-truncated. Fig. 3 shows the associated geometric ratio plot based upon the first five frequencies (we restrict the plotting on the larger frequencies), ignoring the zero-counts. The geometric ratio plot shows evidence for a geometric distribution, except for $x=1$ which is lower than the other ratio indicating one-inflation. This becomes even more clear if we use the concept of geometric ratio plot under the null, a diagnostic tool developed in Böhning and Punyapornwithaya (2018). The idea is to plot the logarithm of ${\hat{r}}_x = \frac{a_x}{a_{x+1}} \frac{f_{x+1}}{f_x}$ against x as before but also include a pointwise 95% confidence band which is computed on the basis of power series distribution which is assumed to be valid. If the distribution is valid then the band should contain all empirical log-ratios. Figure 4 shows the geometric ratio plot under the null for the H5N1 data set. Clearly, the first point is below the confidence band indicating one-inflation.

Table 2 Frequency distribution of the count of reported outbreaks per subdistrict in Thailand from July 3rd 2004 to May 5th 2005

Fig. 3

Geometric ratio plot for the H5N1 outbreak data of Example 3

Fig. 4

Geometric ratio plot under the null for the H5N1 outbreak data of Example 3

Again, we assume an arbitrary mixture of geometric distributions with one-inflation as the analysis of the ratio plots suggests. We find ${\hat{f}}_0^{\mathrm{new}}=551$ and ${\hat{f}}_0=1044$. We note that the conventional Chao estimator is about twice as large as the modified Chao estimator, an effect we would expect if there is one-inflation. We conclude that we estimate at least 550 subdistricts of the 6587 subdistricts to be affected by the outbreak.

4.3 Example 1 (revisited)

We return to Example 1 of the domestic violence study of Sect. 2. A likelihood ratio test, testing a simple geometric against a one-inflated geometric, leads to a value of 98.9 which is highly significant given that the null-distribution is a $\chi ^2$-mixture $0.5 \chi ^2_0 +0.5 \chi ^2_1$. We also include the geometric ratio plot under the null for the domestic violence data in Fig. 5. There is clear evidence that the first ratio is outside the confidence band, indicating one-inflation.

Fig. 5

Geometric ratio plot under the null for the domestic violence data of Example 1

To be more general, we assume an arbitrary mixture of geometric distributions with one-inflation as the analysis of the ratio plots suggests (even though the remaining points are inside the confidence band there is a clear monotone increasing pattern visible). We find ${\hat{f}}_0^{\mathrm{new}}=48,527$ and ${\hat{f}}_0=117,577$. Note that the conventional Chao estimator is much larger than the modified Chao estimator, an effect we typically expect if there is one-inflation. The size of the estimated hidden domestic violence is as expected since dark number research estimates the number of reported domestic crimes between 15% and 30% (Summers and Hoffman 2002). Our estimates given here are likely on the conservative side.

5 Bias reduction

The Chao estimators can have severe bias when the sample size is small. To understand the occurrence of bias we go back to the original Chao estimator as developed in (5). As the arguments used in bias-reduction are not readily available in the published literature we outline them here. We try to estimate $N m_1^2/m_2= E(f_1)^2/E(f_2)$ using $f_1^2/f_2$. However, the latter estimates $E(f_1^2/f_2)$ which is not necessarily close to $E(f_1)^2/E(f_2)$ unless $f_1/N$ and $f_2/N$ are close to $m_1$ and $m_2$, respectively. Hence the idea of bias reduction is to express $E(f_1)^2$, which we cannot estimate directly, as $f_1^2$, by means of $E(f_1)$ and $E(f_1^2)$ which we can estimate directly as $f_1$ and $f_1^2$. Indeed, we use that

$$\begin{aligned} \text{ Var }(f_1)=E(f_1^2)-E(f_1)^2 = E(f_1), \end{aligned}$$

by means of a Poisson assumption. It follows that $E(f_1)^2 = E(f_1^2)- E(f_1)$ which can be estimated as $f_1^2-f_1$ leading to the numerator of the bias-corrected Chao estimator. Turning to the denominator, we note that our interest is in $1/\lambda =1/E(f_2)$, but using $1/f_2$ will estimate $E(1/f_2)$ if the latter exists. Alternatively, $1/(1+f_2)$ will estimate $E[1/(1+f_2)]$ which can be evaluated using the Poisson assumption for $f_2$ as

$$\begin{aligned} E \left( \frac{1}{f_2+1}\right) = \sum _{f_2=0}^\infty \frac{1}{(f_2+1)} \times \exp (-\lambda ) \lambda ^{f_2}/f_2!=1/\lambda +\exp (-\lambda )/\lambda \approx \frac{1}{E(f_2)}, \end{aligned}$$

with the approximation error less than 0.001 for $\lambda > 5$.

This leads to the bias-corrected Chao estimator

$$\begin{aligned} {\hat{N}}_{\text{ Chao-C }} = n+ \frac{a_0a_2}{a_1^2} \frac{f_1(f_1-1)}{f_2+1}. \end{aligned}$$

(15)

In a similar way, we derive the bias correction for the modified Chao estimator leading to

$$\begin{aligned} {\hat{N}}_{\text{ Chao-N }} = n+\frac{a_0a_3^2}{a_2^3} \frac{f_2^3-3f_2^2+2f_2}{(f_3+1)(f_3+2)}, \end{aligned}$$

(16)

but leave the details for Appendix 2.

6 Variance estimation

It is useful to put the proposed estimator into a likelihood framework. Evidently, the estimator (11) uses only counts of ones and twos. Hence it seems reasonable to consider a binomially truncated likelihood

$$\begin{aligned} \log L = f_2 \log (p) +f_3 \log (1-p), \end{aligned}$$

(17)

where $p=P(X=2|X=2 \text{ or } X=3)=a_2/(a_2+a_3\theta )$. The log-likelihood (17) is maximized for ${\hat{p}}=f_2/(f_2+f_3)$, or, ${\hat{\theta }}= \frac{a_2(1-{\hat{p}})}{a_3 {\hat{p}}}= \frac{a_2 f_3}{a_3 f_2}$. Furthermore, it is easy to see that $E(f_0|f_2,f_3;p_2)=\frac{a_0}{a_2\theta ^2+a_3\theta ^3}(f_2+f_3)$. Replacing $\theta$ by its estimate ${\hat{\theta }}$ gives

$$\begin{aligned} {\hat{f}}_0 = \frac{a_0}{a_2 {\hat{\theta }}^2+a_3 {\hat{\theta }}^3}(f_2+f_3)= \frac{a_0a_3^2}{a_2^3} \frac{f_2^3}{f_3^2}, \end{aligned}$$

which corresponds to the proposed estimator (11).

To continue developing a variance estimate we write (11) as $T({\hat{\theta }}) (f_2+f_3)$ with $T({\hat{\theta }}) = \frac{a_0}{a_2 {\hat{\theta }}^2+a_3 {\hat{\theta }}^3}$. We will use the fact that $Var(X)=E[Var(X|Y)] +Var[E(X|Y)]$ for any two random variables X and Y. This conditioning technique is helpful in the capture-recapture context (Böhning 2008; Van der Heijden et al. 2003). We apply this here by using $X=T({\hat{\theta }}) (f_2+f_3)$ and $Y= f_2+f_3$. The first term E[Var(X|Y)] can be approximated as

$$\begin{aligned} (f_2+f_3)^2 Var[T({\hat{\theta }})] \approx (f_2+f_3)^2 Var({\hat{\theta }})T^\prime ({\hat{\theta }})^2. \end{aligned}$$

As $T^\prime ({\hat{\theta }})^2 = \frac{a_0^2a_3^6}{a_2^8}\frac{f_2^8}{f_3^6}\frac{(2f_2+3f_3)^2}{(f_2+f_3)^4}$ and $Var({\hat{\theta }}) \approx \frac{a_2^2}{a_3^2}\frac{(f_2+f_3)f_3}{f_2^2}$ we yield for the first term

$$\begin{aligned} \frac{a_0^2a_3^4}{a_2^6}\frac{f_2^5}{f_3^5}\frac{(2f_2+3f_3)^2}{(f_2+f_3)}. \end{aligned}$$

The second term Var[E(X|Y)] can be approximated by $T({\hat{\theta }})^2 (f_2+f_3)$ since $E[T({\hat{\theta }})^2 (f_2+f_3)|(f_2+f_3)] \approx T(\theta )(f_2+f_3)$, so that the result follows from $Var(f_2+f_3) =E(f_2+f_3)$ under the conventional Poisson assumption. The latter is then estimated by the moment estimate $f_2+f_3$. In total we yield

$$\begin{aligned} \frac{a_0^2a_3^4}{a_2^6}\frac{f_2^5}{f_3^5}\frac{(2f_2+3f_3)^2}{(f_2+f_3)} + \frac{a_0^2 a_3^4}{a_2^6}\frac{f_2^6}{f_3^4(f_2+f_3}. \end{aligned}$$

(18)

Note that (18) can be written in a simple form as

$$\begin{aligned} {\hat{f}}_0^2 \left( 1+\frac{(2f_2+3f_3)^2}{f_2f_3}\right) /(f_2+f_3), \end{aligned}$$

(19)

where ${\hat{f}}_0$ is given by (11). As we have seen in the previous section, it is necessary to stabilize the estimator (11), it is also necessary to use a bias-corrected version of the variance estimator. We suggest to use

$$\begin{aligned} {\hat{f}}_{0,b}^2 \left( 1+\frac{(2f_2+3f_3)^2}{(f_2+1)(f_3+1)}\right) /(f_2+f_3) \end{aligned}$$

(20)

as a variance estimator for ${\hat{f}}_0$, where ${\hat{f}}_{0,b} = \frac{a_0a_3^2}{a_2^3} \frac{f_2^3-3f_2^2+2f_2}{(f_3+1)(f_3+2)}$ is the bias-corrected estimator of $f_0$ developed in the previous section in (16).

To investigate the performance of our variance estimator (20) we provide a small simulation study comparing the estimated standard error according to (20) with the true standard error estimated from the simulation. The results are provided in Table 3. It can be seen that the approximation is excellent for the larger population size $N=1000$ and reasonable for the small population size $N=50$ where it provides a conservative estimate. A more detailed investigation of the proposed variance estimator is given in Kaskasamkul (2018).

Table 3 Ratio of estimated standard error using (20) to the true, simulated standard error for various geometric distributions with and without one-inflation

We are now able to give a more realistic estimation of the hidden frequency $f_0$ for our examples. This is done in Table 4. All estimates appear to be realistic. In the synthetic examples the standard error is relatively large, likely due to the small frequencies in the upper counts.

Table 4 Estimates of the frequency of hidden units with standard error and approximative normal 95% confidence interval; all examples use a geometric mixture kernel in the mixture (2) except the synthetic example which uses a Poisson

7 Simulation

In the first part, we concentrate on the comparison of the the bias-adjusted conventional Chao estimator (15) and the bias-adjusted modified Chao estimator (16). In the second part, we compare the bias-adjusted modified Chao estimator (16) with a previously suggested estimator by Chiu and Chao (2016).

7.1 Comparison of the modified Chao estimator with the conventional Chao estimator

In the following we will focus on the bias-adjusted conventional Chao estimator (15) and the bias-adjusted modified Chao estimator (16). Bias will occur for any member of the power series family as sampling distribution for X. However, the bias-reduction has been developed under a Poisson assumption for the frequency $f_x$. To demonstrate how well the bias reduction works (outside the Poisson sampling for X) we consider as basic sampling the geometric. The latter, as mixture of a Poisson with an exponential, seems to be an attractive distribution as it can incorporate some basic form of heterogeneity (the one that can be modelled by an exponential). We look at two population sizes $N=50$ and 1000 and consider five different scenes with different parameter constellations for each of them.

• 1. Scene 1 is the homogeneous geometric distribution with four parameters $\theta = 0.1, 0.2, 0.3, 0.4$ denoted as populations 1–4.

• 2. Scene 2 is as scene 1 but with 20% one-inflation. More precisely this means that with probability $\pi =0.8$ the count is taken from a homogeneous geometric and with probability $1-\pi =0.2$ it is taken as a count of one.

• 3. Scene 3 is as scene 1 but with 50% one-inflation.

• 4. Scene 4 allows heterogeneity in the parameter of the geometric in addition to 20% one-inflation. The count is taken with probability $\pi =0.8$ from an equally weighted mixture of two geometric distributions. The following six two-component mixture populations were considered: $\theta _2 =0.2,0.3, 0.4$ with $\theta _1=0.1$, $\theta _2 =0.3, 0.4$ with $\theta _1=0.2$ and $\theta _2 =0.4$ with $\theta _1=0.3$ and denoted as populations 1 to 6. Here $\theta _1$ is parameter of the geometric from the first component and $\theta _2$ is the parameter of the geometric from the second component.

• 5. Scene 5 is as in scene 4 but with 50% one-inflation.

Fig. 6

Relative bias (left panels) and relative standard deviation (right panels) of the conventional (Chao-C) and the modified (Chao-N) Chao estimator for $N=50$ and 1000 (from the top to the bottom panel)

The results of the simulation study are presented in Fig. 6. For a generic estimator ${\hat{N}}$ of population size we define relative bias as

$$\begin{aligned} \frac{1}{B} \sum _{i=1}^B\left( {\hat{N}}_i - N\right) /N =\left( \bar{{\hat{N}} }-N\right) /N \end{aligned}$$

and relative standard deviation as

$$\begin{aligned} \sqrt{\frac{1}{B} \sum _{i=1}^B ({\hat{N}}_i - \bar{{\hat{N}} })^2}/N \end{aligned}$$

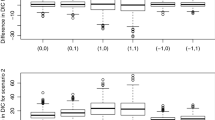
to allow for comparisons across different sized populations. It is clear that the modified Chao estimator ${\hat{N}}_{\text{ Chao-N }}$ with bias-reduction avoids the overestimation bias of the conventional Chao estimator ${\hat{N}}_{\text{ Chao-C }}$ that clearly occurs for all populations with one-inflation as the left panels in Fig. 6 indicate. It becomes also transparent that the larger the one-inflation the higher the overestimation bias of ${\hat{N}}_{\text{ Chao-C }}$. Furthermore, in a way surprisingly, also the relative standard deviation is smaller for ${\hat{N}}_{\text{ Chao-N }}$ in comparison to ${\hat{N}}_{\text{ Chao-C }}$, most significantly for the one-inflation scenes, as the right panels in Fig. 6 show.

Fig. 7

Comparison of the modified Chao estimator $n+f_2^3/f_2^2$ with its bias-corrected version (16) for a geometric distribution with parameters $\theta =0.1, 0.2, 0.3, 0.4$ (upper panels) and with 20% one-inflation (lower panels)

In Fig. 7 we provide a comparison of the modified Chao estimator $n+\frac{a_0a_3^2}{a_2^3}\frac{f_2^3}{f_3^2}$ with its bias-corrected version ${\hat{N}}_{\text{ Chao-N }} = n+\frac{a_0a_3^2}{a_2^3} \frac{f_2^3-3f_2^2+2f_2}{(f_3+1)(f_3+2)}$ (given in (16)) on the basis of a geometric distribution. Clearly, the bias-corrected version is performing well.

7.2 Comparison to previously suggested estimators

Chiu and Chao (2016) also discusses the case of spurious singletons. Using the Cauchy-Schwarz inequality they derived the inequality $E(f_1) \ge$$(2E(f_2)^2)/$$(3E(f_3))$, for large observed sample size (Chiu and Chao 2016; eq. (4a)). They propose further to estimate this quantity by ${\hat{f}}_1 = 2f_2^2/(3f_3)$ and use this estimate in the conventional Chao estimator ${\hat{f}}_{0,\text{ CC* }}= {\hat{f}}_1^2/(2f_2) = (2f_2^3)/(9f_3^2)$ which corresponds exactly to our proposed estimator in the Poisson case. In Eq. (6b) Chiu and Chao (2016) suggest to use the bias-corrected version ${\hat{f}}_1({\hat{f}}_1 -1)/(2f_2+2)$ and we also suggest here to use the bias-corrected estimate of ${\hat{f}}_1 = f_2(f_2-1)/(2f_3+2)$ with the same line of argument as for the bias-correction for ${\hat{f}}_0$. These bias corrections are utmost important, in particular, when working with higher moment estimates as could be seen in the previous section.

In our general power series framework, the bias-corrected Chiu–Chao estimator takes the form

$$\begin{aligned} {\hat{N}}_{\text{ CC }} = n+ \frac{a_0a_2}{a_1^2} \frac{{\hat{f}}_{1,\text{ CC }}({\hat{f}}_{1,\text{ CC }}-1)}{f_2+1}, \end{aligned}$$

(21)

where

$$\begin{aligned} {\hat{f}}_{1,\text{ CC }}= \frac{a_1a_3}{a_2^2} \frac{f_2(f_2-1)}{f_3+1}. \end{aligned}$$

Chiu and Chao suggested also a different bias-correction in eq. (5) which we did not consider as it is undefined if $f_3$ or $f_4$ is zero. Also, they suggest a population size estimator which replaces n by $n-f_1+ {\hat{f}}_1$ which we did not consider here, mainly to achieve a fair comparison. In our context, we consider the singletons as true counts of ones. There are just more than compatible with any Power series mixture which is the source of a potential severe bias. We will take up this point again in the discussion. In this context it is important to see the difference of one-inflation models to zero-inflation models. Whereas the latter is also a Power series mixture, and hence, Chao’s conventional estimator is also a lower bound for zero-inflation models, one-inflation models are not in the family of the Power series mixture and hence Chao’s estimator is no longer a lower bound, as we have seen in the examples.

We expect that ${\hat{N}}_{\text{ Chao-N }}$ and ${\hat{N}}_{\text{ CC }}$ behave quite similarly. Indeed, there are only small differences in their values for all examples (see column 2 in Table 4). Nevertheless, we compared ${\hat{N}}_{\text{ Chao-N }}$ and ${\hat{N}}_{\text{ CC }}$ in a simulation study for a variety of scenarios. We look here at the setting of geometrically distributed counts with and without 20% one-inflation. The results are presented in Fig. 8. Both estimators behave very similar and identical for larger population sizes above 1000. For the smaller population sizes ${\hat{N}}_{\text{ Chao-N }}$ seems to show benefits, in particular with respect to relative standard error. The graphs for Poisson counts with and without one-inflation look similar and are not presented here.

Fig. 8

Relative bias (left panels) and relative standard deviation (right panels) of the bias-adjusted modified Chao estimator (squares) and the bias-adjusted Chiu–Chao estimator (bullets) for $N=50,100$, 1000 and 10, 000 for geometrically distributed counts (top panel) and with 20% one-inflation (bottom panels)

8 Discussion

We have focussed here on one-inflation as this appears to be the most relevant case in practice. Often in the application the occurrence of one-inflation can be well explained and interpreted. For example, in the case of family violence in the Netherlands, one-inflation might occur because many perpetrators might change their behavior after their first identification by the police. However, in principle, it is also possible to extend the approach to higher inflated counts such as two -inflation. To demonstrate this, it follows from Theorem 1 that $\frac{a_0}{a_1}\frac{m_1}{m_0} \le \frac{a_3}{a_4}\frac{m_4}{m_3}$, or ${m_0} \ge \frac{a_0 a_4}{a_1 a_3}\frac{m_1 m_3}{m_4}$. Replacing the theoretical probabilities by their associated frequencies gives the lower bound. Also, a bound can be developed for the situation there is inflation for both, ones and twos. The ratio plot may be helpful again to gain insights on the form of inflation. However, the most practical case occurs with the inflation of counts of ones. In addition, these zero-truncated count distributions as they arise in capture-recapture settings have often very little information in the upper tail, so that there comes in a natural restriction in considering types of higher inflated counts.

One-inflation can occur in several ways. Here, we view the occurrence of ones as true ones, whether they arise from the Power series mixture or as extra-ones. For example, we imagine in the case of family violence that some of the perpetrators change their behavior after they have been identified by the police the very first time, and then never re-occur in the police database. This might lead to extra-ones in the sample. In any case, here is no doubt about the observed sample size n. Another scenario is the case where we think of the singletons as being misclassified, so that some of these might be truly doubletons or tripletons etc. In this case, the observed sample size of different units is overestimated and needs to be corrected, for example, using $n-f_1+{\hat{f}}_1$ as suggested in Chiu and Chao (2016). Which estimator to use, will depend on the application at hand.

Appendices

Appendix 1

We now give a proof of Theorem 2.

Proof

For the non-inflated component we have that

$$\begin{aligned} \frac{a_0a_{3}^2}{a_2^3} \frac{{m_{2}}^3}{{m_3}^2}\le {m_0}, \end{aligned}$$

and multiplying both sides with $\pi$ gives

$$\begin{aligned} \frac{a_0a_{3}^2}{a_2^3} \frac{{(\pi m_{2})}^3}{{(\pi m_3)}^2}\le {\pi m_0}, \end{aligned}$$

which is the result as $m_x^\prime =\pi m_x$ for $x \ne 1$. $\square$

Appendix 2

Here we give some details on the bias-reduction for the modified Chao estimator. We note that

$$\begin{aligned} E[f_2-E(f_2)]^3 = E(f_2^3)-3 E(f_2^2)E(f_2)+ 2 E(f_2)^2. \end{aligned}$$

Using a Poisson assumption for $f_2$, $E[f_2-E(f_2)]^3 =E(f_2)$, we yield

$$\begin{aligned} E(f_2)=E(f_2^3)-3 E(f_2^2)E(f_2)+ 2 E(f_2)^2. \end{aligned}$$

Using the Poisson assumption once more, we have that $E(f_2)^2=E(f_2^2)-E(f_2)$ so that

$$\begin{aligned} 2E(f_2)^3=E(f_2)-E(f_2^3)+3[E(f_2)+E(f_2)^2]E(f_2). \end{aligned}$$

It follows that

$$\begin{aligned} E(f_2)^3= E(f_2^3)-E(f_2)-3E(f_2)^2, \end{aligned}$$

using the Poisson assumption again for $E(f_2)^2$

$$\begin{aligned} E(f_2)^3= E(f_2^3)-E(f_2)-3E(f_2^2)+3E(f_2) \end{aligned}$$

$$\begin{aligned} = E(f_2^3)+2E(f_2)-3E(f_2^2), \end{aligned}$$

which can be validly estimated by $f_2^3-3f_2^2+2f_2$.

Fig. 9

$E[1/(f+1)(f+2)]^2$ and $1/E(f)^2$ as a function of E(f)

For the denominator we note that $E[1/(f_3+1)(f_3+2)]^2$ can be evaluated using the Poisson assumption as (with the abbreviations $f=f_3$ and $\lambda =E(f)$)

$$\begin{aligned} E \left( \frac{1}{(f+1)(f+2)}\right)= & {} \sum _{f=0}^\infty \frac{1}{(f+1)(f+2)} \times \exp (-\lambda ) \lambda ^f/f!\\= & {} \exp (-\lambda ) \frac{1}{\lambda ^2} \sum _{f=0}^\infty \lambda ^{f+2}/(f+2)!\\= & {} \exp (-\lambda ) \frac{1}{\lambda ^2}[\exp (\lambda ) -1-\lambda )]\\= & {} \frac{1}{\lambda ^2}-\frac{\exp (-\lambda )}{\lambda ^2} -\frac{\exp (-\lambda )}{\lambda }, \end{aligned}$$

which is an excellent approximation of $\frac{1}{\lambda ^2}$ if $\lambda \ge 5$ (see also Fig. 9).