1 Introduction

Consider the following general scenario of a model selection. Let \(\{ \mathcal{M }_{\underline{i}}\}_{\underline{i}\in I}\) be a list of models, where \(I\subset 2^{\mathrm{full}}\) and \({\mathrm{full}}=\{1,2,\ldots ,m\}\), consisting of densities described by finite-dimensional parameter \(\theta ^{\underline{i}}\), such that for every \(\underline{i} \in I\) we have \(\mathcal{M }_0\subseteq \mathcal{M }_{\underline{i}} \subseteq \mathcal{M }_{\mathrm{full}}\) for some minimal model \(\mathcal{M }_0\). In the case of a correct specification of the list of models the density \(f\) from which iid sample of size \(n\) is available belongs to a model \(\mathcal{M }_{\underline{t}}\) for some \(\underline{t}\in I\) of cardinality \(|\underline{t}|\) such that \(f\in \mathcal{M }_{\underline{j}}\) implies \(\mathcal{M }_{\underline{t}}\subseteq \mathcal{M }_{\underline{j}}\). Throughout, \(|\underline{i}|\) will denote cardinality of set \(\underline{i}\). Pokarowski and Mielniczuk (2011) considered general parametric models \(\mathcal{M }_{\underline{i}}\) and introduced (unscaled) minimal p-value criterion \(M_m^n\) based on asymptotic p-values of likelihood ratio test statistics \(\varLambda _{n,0,\underline{i}}\) for testing \(H_0: f\in \mathcal{M }_0\) versus \(H_1: f\in \mathcal{M }_{\underline{i}}\setminus \mathcal{M }_0\). It is proved there that under mild conditions on the regularity of the models and for a general lists of parametric models of fixed size \(m\) which does not depend on the sample size the introduced minimal p-value criterion (mPVC) is consistent in the sense considered for selection rules, i.e. that \(P(M_m^n=\underline{t})\rightarrow 1\). Moreover, it is shown that Bayesian Information Criterion BIC (cf. Schwarz 1978) is an approximation of mPVC.

In the present paper we focus on a special family of models, namely exponential models and generalize and strengthen these consistency results to the case of possibly growing families and allow for misspecification of the true density. We also consider maximal p-value criterion (MPVC) as well as greedy versions of both mPVC and MPVC.

We note that permitting that the size of the list of models grows together with the sample size is of interest as it makes possible to handle nonparametric situations, e.g. the case when logarithm of the underlying density has infinite orthonormal expansion. Therefore, beside results on consistency of introduced rules and on Kullback–Leibler distance from the ensuing post-model-selection estimator to the true density when it belongs to one of the underlying models, we were able to prove similar results in the case when the list of models is misspecified. In particular, Theorem 3 states that the selector based on the minimal p-value criterion is then conservative in a sense defined in Sect. 3.1.

BIC-based selection of an appropriate exponential model was applied by Ledwina (1994) to construct data-adaptive Neyman smooth tests. It turned out to be a powerful tool in many testing problems (cf. e.g. Inglot and Ledwina 1996; Kallenberg and Ledwina 1997). In the present paper we investigate usefulness of such approach in a parallel problem of estimation. In particular, in Sect. 4 we compare numerically performance of post-model-selection estimators based on p-values with those based on BIC. It is important to stress that unlike in testing problems, which usually consider nested family of models, we deal here with an arbitrary family of exponential models.

The presented approach can lead also to effective methods of estimating functionals of density which compare favorably with kernel plug-in method. In particular, Mielniczuk and Wojtyś (2010) investigated this problem in the case of Fisher information with BIC applied as a selection criterion, and a similar method may be used also to approximate entropy of a density, which is usually estimated with the use of a kernel estimate truncated from below.

Moreover, let us note that the construction of selection criteria using p-values is quite general and can be applied in other scenarios. In particular, an analogous approach may be used to choose the most parsimonious linear model from a growing list of linear models provided that a design matrix satisfies mild regularity conditions.

Organization of the paper is as follows. In Sect. 2 we introduce exponential families of densities, define p-value criteria and state auxiliary lemmas. Section 3 contains main results on consistency and conservativeness of mPVC and MPVC criteria as well as their greedy counterparts. The results concern both the situation when an underlying density belongs to one of the exponential models considered (correct specification of family of models) and the opposite misspecification case. We also show how these results can be applied to bound convergence rates of ensuing post-model-selection estimators of density with respect to Kullback–Leibler distance. In Sect. 4 behavior of post-model-selection estimators is studied by means of numerical experiments.

2 Model selection procedures based on \({\varvec{p}}\)-values in exponential families of densities and auxiliary results

2.1 Minimal and maximal p-value selection criteria

We specify \(\{ \mathcal{M }_{\underline{i}}\}_{\underline{i}\in I}\) to be a list of exponential models. Let \(B=(b_j(x))_{j=0}^\infty \) be some orthonormal system in \(L^2([0,1],\lambda )\), where \(\lambda \) is the Lebesgue measure on \([0,1]\) and \(b_0\equiv 1\). Observe that equality \(\sum \nolimits _{j=0}^k a_j b_j(x) = 0 \lambda \)-a.e. for some constants \((a_j)_{j=0}^k\) and \(k\in \mathbb{N }\) implies \(a_j=0\) for \(j=0,1,\ldots ,k\). For fixed \(m\in \mathbb{N }\) and every nonempty subset \(\underline{i}\) of \(\{1,\ldots ,m\}\) define regular exponential family of densities on [0,1] of the form

$$\begin{aligned} \mathcal{M }_{\underline{i}} = \left\{ f_\theta (x)=\exp \left\{ \sum \limits _{j\in \underline{i}} \theta _j b_j(x) - \psi _{\underline{i}}(\theta )\right\} : \theta _j\in \mathbb{R }\;\text{ for }\; j\in \underline{i}\right\} , \end{aligned}$$
(1)

where \(\theta =(\theta _j)_{j\in \underline{i}}, \psi _{\underline{i}}(\theta ) = \log \int _0^1 \exp \{{\sum }_{j\in \underline{i}} \theta _j b_j(x)\} dx\) is normalizing constant corresponding to model \(\mathcal{M }_{\underline{i}}\) under consideration. Let \(1\!\mathrm{l}(\cdot )\) be an indicator function and \(\mathcal{M }_0=\{ f_0 (x)=1\!\mathrm{l}(x\in [0,1]) \}\) the smallest (null) model consisting of the uniform density only. We refer to van der Vaart (2000), Sect. 4.2, and Wainwright and Jordan (2008) for an introduction to exponential families.

Let \(f\in L^2([0,1],\lambda )\) be some unknown density on \([0,1]\) and consider the problem of choosing one of the above \(2^m\) models in order to estimate \(f\) with the use of a random sample \(X_1,\ldots ,X_n\sim f\). We consider the following model selection criteria which are proposed in Pokarowski and Mielniczuk (2011) and are based on the idea of likelihood ratio goodness of fit tests. Namely, for a fixed \(m\in \mathbb{N }\) and for every nonempty \(\underline{i} \subset \{1,\ldots ,m\}\) consider testing null hypothesis:

$$\begin{aligned} H_0: f\in \mathcal{M }_0 \end{aligned}$$

versus

$$\begin{aligned} H_1: f\in \mathcal{M }_{\underline{i}}\setminus \mathcal{M }_{0} \end{aligned}$$

with test statistic

$$\begin{aligned} \varLambda _{n,0,\underline{i}} = 2\log \prod _{j=1}^n f_{\hat{\theta }_\mathrm{{ML}}^{\underline{i}}}(X_j), \end{aligned}$$
(2)

calculated for the random sample \(X_1,\ldots ,X_n\sim f\), where \(\hat{\theta }_\mathrm{{ML}}^{\underline{i}}\) is the maximum likelihood estimator of parameter \(\theta \) in family \(\mathcal{M }_{\underline{i}}\) based on \(X_1,\ldots ,X_n\). Note that since for \(\underline{i} =\emptyset \) estimator \(f_{\hat{\theta }_\mathrm{{ML}}^{\underline{i}}}\) is equal to \(f_0(x)=1\!\mathrm{l}(x\in [0,1])\), the statistic \(\varLambda _{n,0,\underline{i}}\) is the likelihood ratio test statistic (LRT) for the above testing problem.

In order to compute p-value of (2) knowledge of the distribution of likelihood ratio statistic under the null hypothesis is needed. Since its exact distribution is not known in the case of the exponential family (1), we use its asymptotically valid approximation by chi-squared distribution. Namely Wilks’ theorem (cf. e.g. Theorem 5.6.3 in Sen and Singer 1993) implies that likelihood ratio statistic defined as in (2) has an asymptotic \(\chi _{|\underline{i}|}^2\) distribution provided \(H_0: f\in \mathcal{M }_0\) holds.

For \(x\in \mathbb{R }\) and \(k\in \mathbb{N }\) denote

$$\begin{aligned} p(x|k)=1-F_k(x), \end{aligned}$$
(3)

where \(F_k\) is the cumulative distribution function of \(\chi _k^2\) distribution. We consider \(p(\varLambda _{n,0,\underline{i}} \,|\, |\underline{i}|)\) as an approximate p-value of the test statistic (2), i.e. the conditional probability that, given \(\varLambda _{n,0,\underline{i}}\), a random variable having \(\chi ^2_{|\underline{i}|}\) distribution exceeds \(\varLambda _{n,0,\underline{i}}\). Observe that if \(G_n\) is c.d.f. of \(\varLambda _{n,0,\underline{i}}\) then c.d.f. of random variable \(p(\varLambda _{n,0,\underline{i}}||\underline{i}|)\) equals \(1-G_n(F_{|\underline{i}|}^{-1}(1-x))\) and if \(H_0\) holds is approximately c.d.f. of the uniform distribution. As the best fitted model for \(f\) we choose the one having the smallest scaled p-value:

$$\begin{aligned} \hat{\underline{i}}_\mathrm{mPVC} = \mathop {\arg \min }\limits _{\underline{i}\subset \{1,\ldots ,m\}} p(\varLambda _{n,0,\underline{i}} \,|\, |\underline{i}|)e^{a_n|\underline{i}|}, \end{aligned}$$

where \(a_n\ge 0, a_n/n\rightarrow 0\) as \(n\rightarrow \infty \) and we put \(p(\varLambda _{n,0,0} \,|\, 0):=n^{-1/2}\). In the case of ties the model \(\mathcal{M }_{\underline{i}}\) having the smallest number of parameters \(|\underline{i}|\) is chosen. Model selection criterion based on choosing the smallest p-value is introduced in Pokarowski and Mielniczuk (2011) where it is called minimal  p -value criterion (mPVC). Its original definition considered only the case \(a_n=0\). In this case from among pairs \(\{H_0,H_{\underline{i}}\}\) we choose the pair for which we are most inclined to reject \(H_0\), i.e. we select a model corresponding to the most convincing alternative hypothesis. If \(a_n>0\) the scaling factor is interpreted as an additional penalization for the complexity of the model.

As an alternative method maximal  p -value criterion (MPVC) is also proposed in Pokarowski and Mielniczuk (2011), which involves test statistics for a family of \(2^m\) null hypotheses of the form

$$\begin{aligned} H_0: f\in \mathcal{M }_{\underline{i}} \end{aligned}$$

versus

$$\begin{aligned} H_1: f\in \mathcal{M }_{\mathrm{full}}{\setminus }\mathcal{M }_{\underline{i}}, \end{aligned}$$

where \({\mathrm{full}}=\{1,\ldots ,m\}\) corresponds to the largest considered model. In this case we choose the model for which likelihood ratio statistic

$$\begin{aligned} \varLambda _{n,\underline{i},\mathrm{full}} = 2\log \prod _{j=1}^n \frac{f_{\hat{\theta }_\mathrm{{ML}}^{\mathrm{full}}}(X_j)}{f_{\hat{\theta }_\mathrm{{ML}}^{\underline{i}}}(X_j)} \end{aligned}$$
(4)

attains the largest scaled p-value:

$$\begin{aligned} \hat{\underline{i}}_\mathrm{MPVC} = \mathop {\arg \max }\limits _{\underline{i}\subset \{1,\ldots ,m\}} p( \varLambda _{n,\underline{i},\mathrm{full}} \,|\, m -|\underline{i}| ) e^{-a_n|\underline{i}|}, \end{aligned}$$
(5)

where \(a_n\ge 0, a_n/n\rightarrow 0\) as \(n\rightarrow \infty \) and, as before, \(p( \varLambda _{n,\underline{i},\mathrm{full}} \,|\, m-|\underline{i}| )\) is an approximate p-value defined as in (3). We also put \(p( \varLambda _{n,\mathrm{full},\mathrm {full}} \,|\, 0 ):=1.\) Here we use the fact that likelihood ratio statistic (4) has under \(H_0: f\in \mathcal{M }_{\underline{i}}\) and for fixed \(m\) an asymptotic \(\chi _{m-|\underline{i}|}^2\) distribution. The motivation is similar to the motivation of mPVC, namely we choose a model which we are the least inclined to reject when compared to the full model.

The aim of the paper is to study properties of the above criteria when fixed \(m\) is replaced by \(m_n\) possibly depending on \(n\). In other words, the number of models is allowed to change with the sample size. Such assumption allows us to consider the case when unknown density \(f\) belongs to one of the models only ultimately as well as the case when the logarithm of \(f\) has infinite expansion with respect to \((b_i)_1^\infty \). We assume throughout that the size \(m_n\) of the list is nondecreasing function of \(n\). In the paper we establish conditions under which consistency properties of mPVC and MPVC hold in such settings. In particular it turns out that under the introduced scaling conditions MPVC rule in general is conservative. The assumption \(a_n\rightarrow \infty \) is a sufficient condition for consistency of MPVC (cf. Theorems 5 and 6). This is a difference between mPVC and MPVC criteria as mPVC may be consistent for \(\mathrm{lim sup}\, a_n<\infty \). In the following we use the notation \(m_n\) wherever possible, however in some formulas in order to avoid subscripts of multiple levels we abbreviate the symbol \(m_n\) to \(m\).

Observe that both \(p\)-value criteria are strictly monotone functions of the maximized likelihood of a model provided the number of degrees of freedom is fixed. The same property holds for BIC and AIC criteria. It follows that if two criteria enjoying this property choose models having the same number of parameters, e.g. if \(|\hat{\underline{i}}_\mathrm{mPVC}|=|\hat{\underline{i}}_\mathrm{MPVC}|\), and these models are uniquely determined then the chosen models necessarily coincide.

Before presenting the main results of the paper, we provide several auxiliary results concerning the properties of likelihood ratio statistic \(\varLambda _n\), which are crucial to prove the consistency of mPVC and MPVC in the case of exponential families of growing dimensions. Some of them, in particular Lemmas 3 and 4, are of independent interest. In their statements the notions of relative entropy and information projection will be used. Thus, let \(D(f||g)\) denote relative entropy (or Kullback–Leibler distance) between densities \(f\) and \(g\), which is equal to \(\int _{-\infty }^\infty f\log (f/g)\) if \(f\) is absolutely continuous with respect to \(g\), and \(\infty \) otherwise.

For the sake of simplicity of notation in the following we use the symbol \(\hat{f}_{\underline{i}}\) to denote the maximum likelihood estimator of density \(f\) in family \(\mathcal{M }_{\underline{i}}\), i.e. \(\hat{f}_{\underline{i}}=f_{\hat{\theta }_\mathrm{{ML}}^{\underline{i}}}\). Maximum likelihood estimator \(\hat{\theta }_\mathrm{ML}^{\underline{i}}\), if it exists, satisfies \(E_{\hat{f}_{\underline{i}}}(b_j(X))=\frac{1}{n}\sum _{i=1}^n b_j(X_i)\) for \(j\in \underline{i}\). It easily follows that \(\varLambda _{n,0,\underline{i}}\) defined in (2) satisfies

$$\begin{aligned} \frac{1}{2n}\varLambda _{n,0,\underline{i}} = \hat{\theta }_\mathrm{{ML}}^{\underline{i}} {\tiny \, ^\circ \, }\bar{b}_n^{\underline{i}} - \psi _{\underline{i}}(\hat{\theta }_\mathrm{ML}^{\underline{i}})=D(\hat{f}_{\underline{i}}||f_0), \end{aligned}$$
(6)

where \(\bar{b}_n^{\underline{i}} = ( n^{-1}\sum _{i=1}^n b_j(X_i))_{j\in \underline{i}}\), while \(\varLambda _{n,\underline{i},\mathrm{full}}\) defined in (4) equals \(2n(D(\hat{f}_{\mathrm{full}}||f_0) - D(\hat{f}_{\underline{i}}||f_0))\). Thus as \(p\)-value \(p(\varLambda _{n,0,\underline{i}} \,|\, |\underline{i}|)\) is a strictly monotone function of \(\varLambda _{n,0,\underline{i}}\) for a fixed \(|\underline{i}|\) it follows that on the stratum \(|\underline{i}|=j\) mPVC criterion chooses an alternative \(\underline{i}\) such that \(\hat{f}_{\underline{i}}\) has the largest KL distance from the uniform density.

2.2 Information projection and basic assumptions

Suppose that \(\theta _{\underline{i}}^* \in \mathbb{R }^{|\underline{i}|}\) is the unique vector which satisfies the equation \( \int b^{\underline{i}} f_{\theta _{\underline{i}}^*} = \int b^{\underline{i}} f\) where \(b^{\underline{i}}(x)=(b_j(x))_{j\in \underline{i}}\). Then \(f_{\theta _{\underline{i}}^*}\) minimizes \(D(f||\cdot )\) on \(\mathcal{M }_{\underline{i}}\). The density \(f_{\underline{i}}^* := f_{\theta _{\underline{i}}^*}\) is called an information projection of \(f\) onto the exponential family \(\mathcal{M }_{\underline{i}}\). It is also characterized by the Pythagorean-like equality \(D(f||g)=D(f||f_{{\underline{i}}}^*)+D(f_{{\underline{i}}}^*||g)\) valid for any \(g\in \mathcal{M }_{\underline{i}}\). This implies uniqueness of the projection. For more of its properties see e.g. Barron and Sheu (1991).

Moreover, define the Kullback–Leibler distance between density \(f\) and the set \(\mathcal{M }\) of densities as

$$\begin{aligned} D(f,\mathcal{M })=\inf \{ D(f||g):\ g\in \mathcal{M }\} \end{aligned}$$

and let \(\underline{t}_m^*\) be defined as

$$\begin{aligned} \underline{t}_m^* = \{j: \theta _{{\mathrm{full}},j}^*\ne 0 \}, \end{aligned}$$

i.e. \(\underline{t}_m^*\) is the set of indices of nonzero coefficients of the parameter \(\theta _{\mathrm{full}}^*\in \mathbb{R }^m\) of information projection of \(f\) onto \(\mathcal{M }_{\mathrm{full}}\). As \(f^*_\mathrm{full}=f^*_{\underline{t}_m^*}\) it follows that \(\underline{t}_m^*\) is the minimal with respect to inclusion set of indices such that

$$\begin{aligned} \underline{t}_m^* = \mathop {\arg \min }\limits _{\underline{i} \subset \{1,\ldots ,m\}} D(f,\mathcal{M }_{\underline{i}}). \end{aligned}$$

Indeed, the fact that every other model which attains the minimum of \(D(f,\cdot )\) includes \(\mathcal{M }_{\underline{t}_m^*}\) as its subset is implied by Pythagorean-like equality mentioned above and assumed linear independence of the system \((b_i)_{i=0}^\infty \) with \(b_0\equiv 1\). Our aim in the paper is to identify \(\underline{t}_m^*\) for a given family \(\{\mathcal{M }_{\underline{i}}\}_{\underline{i}\subset \{1,\ldots ,m_n\}}\) using the introduced model selection criteria.

In the following \(f\) will denote an arbitrary density on [0,1]. Assumptions (A1), (A2) and (A5) below are general assumptions about \(f\) whereas (A6) stipulates that \(\log f\) has an expansion with respect to functions \((b_i)_{i=0}^\infty \) which converges in \(L^2[0,1]\). Existence of information projection is discussed in Theorem 3.3 in Wainwright and Jordan (2008). Assumption (A3) concerns growth of \(||b_j||_\infty \), where \(||b||_\infty =\sup _{x\in [0,1]}|b(x)|\) denotes supremum norm of \(b\), and (A4) constrains growth of \(m_n\). For all main results (A6) will be assumed.

  1. (A1)

    for every \(m_n\in \mathbb{N }\) and \(\underline{i}\subset \{1,\ldots ,m_n\}\) the information projection \(f_{\underline{i}}^*\) exists,

  2. (A2)

    the sequence \((\max _{\underline{i} \subset \{1,\ldots ,m_n\}}|| \log f_{\underline{i}}^* ||_\infty )_n\) is bounded in \(n\in \mathbb{N }\),

  3. (A3)

    \(V_k=\max \nolimits _{j=1,\ldots ,k}||b_j||_\infty = O(k^\omega )\) for some \(\omega \ge 0\) as \(k\rightarrow \infty \),

  4. (A4)

    \(n/m_n^{2+4\omega }\rightarrow \infty \) as \(n\rightarrow \infty \),

  5. (A5)

    \(||f||_\infty < \infty \) and \(\inf _{x\in [0,1]} f(x)>0\),

  6. (A6)

    \(f(x)=\exp \{ \sum \nolimits _{j=1}^\infty \theta _jb_j(x) - \psi (\theta ) \}\) for \(x\in [0,1]\) and some \(\theta \in l^2\) such that \(\psi (\theta )<\infty \), where \(\psi (\theta )=\log \int _0^1 \exp \{ \sum \nolimits _{j=1}^\infty \theta _jb_j(x) \} dx\).

The lemmas below are stated under minimal subsets of assumptions from (A1) to (A6). Their proofs rely on methods developed by Barron and Sheu (1991). In particular Lemma 2 is an extension of a result proved there to the case when quantities considered in (8)–(9) are maximized over all subsets of \(\{1,\ldots ,m_n\}\). Such properties are useful when selection rule \(\hat{\underline{i}}\) based on an exhaustive search of all subsets is considered. Lemmas 3–5 are to the best of our knowledge new.

Let \((\theta _j)_{j=1}^\infty \) be the vector of coefficients given in the representation (A6) of \(f\). We use throughout the following notation:

$$\begin{aligned} \underline{t}:=\{j: \theta _j\ne 0 \} \end{aligned}$$

for the set of indices of nonzero coefficients of \((\theta _j)_{j=1}^\infty \). Note that if \(f\) belongs to an exponential family set \(\underline{t}\) corresponds to the minimal model containing it discussed in the Introduction. For every vector \(v\in \mathbb{R }^\infty \) let

$$\begin{aligned} v^{\underline{i}} := (v_j)_{j\in \underline{i}} \end{aligned}$$

be the vector formed from \((v_j)_{j=1}^\infty \) by choosing only those coordinates whose indices are elements of the set \(\underline{i}, \underline{i}\subset \mathbb{N }\). Moreover for \(m\in \mathbb{N }\) we set \(v^m=v^{\{1,\ldots ,m\}}\).

If \(f\) belongs to some exponential family of distributions \(\mathcal{M }_{\underline{t}}\), i.e. \(|\underline{t}|<\infty \), and the maximal element of \(\underline{t}\) denoted as \(\max \underline{t} \le m_n\) then \(\underline{t} = \underline{t}_m^*\) since in this case \(\theta _{\mathrm{full}}^* = \theta ^{\mathrm{full}}\). Observe also that if \(\underline{t}\) is infinite then \(f\) does not belong to any exponential model (1). We recall that \(m=m_n\) may depend on a sample size \(n\).

2.3 Auxiliary lemmas

In this subsection we give several auxiliary lemmas which are crucial to prove the consistency of mPVC and MPVC in the case of exponential families of growing dimensions. The proofs of them are defered to the Appendix.

Lemma 1

If conditions (A2), (A5) and (A6) hold then sequence \((\max _{\underline{i} \subset \{1,\ldots ,m_n\}}||\theta _{\underline{i}}^*||)_n\) is bounded in \(n\in \mathbb{N }\).

Lemma 2

If conditions (A1)–(A4) hold then \(P(\hat{\theta }_\mathrm{{ML}}^{\underline{i}}\) exists for every \(\underline{i}\subset \{1,\ldots ,m_n\}) \rightarrow 1\) as \(n\rightarrow \infty \) and

$$\begin{aligned} \max \limits _{\underline{i}:\,\underline{i} \subset \{1,\ldots ,m_n\}} D(f_{\underline{i}}^*||\hat{f}_{\underline{i}})= O_P\left( {m_n^{1+2\omega }}/{n}\right) ,\end{aligned}$$
(7)
$$\begin{aligned} \max \limits _{\underline{i}:\,\underline{i} \subset \{1,\ldots ,m_n\}} D(\hat{f}_{\underline{i}}||f_{\underline{i}}^*)= O_P\left( {m_n^{1+2\omega }}/{n}\right) . \end{aligned}$$
(8)

Lemmas 3 and 4 concern the asymptotic properties of likelihood ratio statistic \(\varLambda _{n,0,\underline{i}}\) in the case of exponential families of growing dimensions and as such are of independent interest. For \(\underline{i}\subset \{1,\ldots ,m_n\}\) define

$$\begin{aligned} \lambda _{\underline{i}}=\theta _{\underline{i}}^*{\tiny \, ^\circ \, }E_f(b^{\underline{i}}(X)) - \psi _{\underline{i}}(\theta _{\underline{i}}^*). \end{aligned}$$

Observe that in view of the definition of \(f_{\underline{i}}^*\) we have \(\lambda _{\underline{i}} = \int f \log f_{\underline{i}}^* = \int f_{\underline{i}}^*\log f_{\underline{i}}^*= D(f_{\underline{i}}^* || f_{0})\). The last equality implies \(\lambda _{\underline{i}}\ge 0\).

Lemma 3

If conditions (A1)–(A6) hold then:

  1. (i)
    $$\begin{aligned} \quad \, \max \limits _{\underline{i}: \underline{i} \subset \{1,\ldots ,m_n\}} \left| \frac{1}{2n}\varLambda _{n,0,\underline{i}} - \lambda _{\underline{i}} \right| = O_P\left( \left( \frac{m_n^{1+2\omega }}{n}\right) ^{1/2}\right) \quad \text{ as }\; n\rightarrow \infty . \end{aligned}$$
    (9)

    Moreover,

  2. (ii)

    if \({\underline{t}}_m^* \not \subset {\underline{i}}\) then \(\lambda _{{\underline{i}}}<\lambda _{{\underline{t}}_m^*}\),

  3. (iii)

    if \({\underline{t}}_m^* \subset {\underline{i}}\) then \(\lambda _{{\underline{i}}}=\lambda _{{\underline{t}}_m^*}\).

Remark 1

Note that \(\hat{f}_{\underline{i}}\) and \(f_{\underline{i}}^*\) do not depend on the specific system of functions \((b_j(x))_{j\in \underline{i}}\) provided the systems span the same linear space. In particular we will investigate in Lemma 4 the behavior of the quantities \(D(f_{\underline{i}}^*||\hat{f}_{\underline{i}})\) and \(\varLambda _{n,0,\underline{i}}\) considering an additional system of functions \((\tilde{b}_j(x))_{j=0}^\infty \) orthonormal in \(L^2([0,1],f)\), such that \(\tilde{b}_0(x)\equiv 1\) and that \(sp(b_i, i\in {\underline{i}_k} )=sp(\tilde{b}_i, i\in {\underline{i}_k}), k=1,2\), where \(sp(B)\) stands for a linear space spanned by functions from system \(B\) and \({\underline{i}_1}\subset {\underline{i}_2}=\{1,\ldots ,m_n\}\). Such system can be obtained by Gram-Schmidt orthonormalisation procedure. Obviously \(\tilde{b}_j\) depend on \(f\) but it follows from Lemma 7 in the Appendix that in order to bound \(D(f_{\underline{i}}^*||\hat{f}_{\underline{i}})\) using the constructed system it is enough to evaluate the constant \(A_m(f)\) appearing there. Such useful approach was used by Barron and Sheu (1991) (cf. proof of (6.7) in their paper) and it yields better rates of convergence of \(D(f_{\underline{i}}^*||\hat{f}_{\underline{i}})\) than a direct method based on Yurinski (1976) inequality.

Lemma 4

If conditions (A1)–(A5) hold then

$$\begin{aligned} \mathop {\max }\limits _{\underline{i}: \underline{t}_m^* \subset \underline{i} \subset \{ 1,\ldots ,m_n\}}|\varLambda _{n,0,\underline{i}}-\varLambda _{n,0,\underline{t}_{m_n}^* }| = \varLambda _{n,0,\mathrm{full}}-\varLambda _{n,0,\underline{t}_{m_n}^* }= O_P(m_n)\quad \text{ as } n\rightarrow \infty . \end{aligned}$$

Lemma 5

If assumptions (A1), (A2), (A5) and (A6) hold and \(|\underline{t}|<\infty \) then there exists a constant \(a>0\) such that for every \(n\in \mathbb{N }\)

$$\begin{aligned} \min \limits _{\underline{i}:\,\underline{i}\subset \{1,\ldots ,m_n \}: \underline{t}\not \subset \underline{i}} D(f||f_{\underline{i}}^*) > a. \end{aligned}$$

3 Main results

Sections 3.1 and 3.2 deal with consistency of minimal and maximal p-value criterions, respectively. In Sect. 3.3 greedy counterparts of the criteria are introduced and their consistency is proved. We state first a lemma of a different character than those presented in Sect. 2. It concerns bounds for a tail of the \(\chi ^2_k\) distribution. Recall that \(p(x|k)\) is the p-value defined in (3).

For \(x>0\) and \(k\in \mathbb{N }\) let

$$\begin{aligned} C(x,k)=e^{-x/2}\left( \frac{x}{2}\right) ^{k/2-1} \left( \varGamma \left( \frac{k}{2}\right) \right) ^{-1} \end{aligned}$$

and

$$\begin{aligned} B(x,k)=(x/(x-k+2))C(x,k). \end{aligned}$$

Lemma 6

We have

  1. (i)

    for \(k=1\) and \(x>0, B(x,1)\le p(k|1)\le C(x,1)\);

  2. (ii)

    for \(k>1\) and \(x>0, p(x|k)\ge C(x,k)\) and for \(k>1\) and \(x>k-2, p(x|k)\le B(x,k);\)

Part (i) of the above lemma was proved by Gordon (1941) whereas part (ii) follows from Inglot and Ledwina (2006) after noticing that the product \(c(k)\mathcal{E }_k(x)\) of the functions defined there equals \(C(x,k)\).

For all the results below we assume that assumption (A6) holds, i.e. the logarithm of the underlying density \(f\) has \(L^2\) expansion w.r.t. system \((b_i)_{i=0}^\infty \).

3.1 Minimal p-value criterion mPVC

The first main result states that if \(m\) is held constant then \(\hat{\underline{i}}_\mathrm{mPVC}\) identifies with probability tending to 1 the indices corresponding to the nonzero coefficients of the information projection of \(f\) on \(\mathcal{M }_\mathrm{full}\).

Theorem 1

(mPVC consistency) If conditions (A1), (A5) and (A6) hold and \(m_n=m\) is constant then \({\lim \nolimits _{n\rightarrow \infty }}P(\hat{\underline{i}}_\mathrm{mPVC} = \underline{t}_m^*)=1\).

Proof

Assume that \(|\underline{t}_m^*|>1\) and let \(\tilde{\varLambda }_{n,0,\underline{i}}=\max (\varLambda _{n,0,\underline{i}},2)\). We have

$$\begin{aligned}&P \left( \, \mathop {\min }_{\underline{i}:\underline{t}_{m}^{*}\not \subset \underline{i}\subset \{1,\ldots ,m_{n}\}}\,\,\, p(\varLambda _{n,0,\underline{i}} \,|\, |\underline{i}|) e^{a_n|\underline{i}|} < p({\varLambda }_{n,0,\underline{t}_m^*} \,|\, |\underline{t}_m^*|) e^{a_n|\underline{t}_m^*|} \right) \\&\quad \le P \left( \, \mathop {\min }_{\underline{i}:\underline{t}_{m}^{*}\not \subset \underline{i}\subset \{1,\ldots ,m_n\}}\,\,\, p(\tilde{\varLambda }_{n,0,\underline{i}} \,|\, |\underline{i}|) e^{a_n|\underline{i}|} \le p(\varLambda _{n,0,\underline{t}_m^*} \,|\, |\underline{t}_m^*|) e^{a_n|\underline{t}_{m}^{*}|} \right) . \end{aligned}$$

Lemma 6(ii) implies for \(\varLambda _{n,0,\underline{t}_m^*}>|\underline{t}_m^*|-2\),

$$\begin{aligned} p\left( \varLambda _{n,0,\underline{t}_m^*}\, | \, |\underline{t}_m^*|\right) \le C\left( \varLambda _{n,0,\underline{t}_m^*},|\underline{t}_m^*|\right) \frac{\varLambda _{n,0,\underline{t}_m^*}}{\varLambda _{n,0,\underline{t}_m^*}-|\underline{t}_m^*|+2}. \end{aligned}$$

Parts (i) and (ii) of Lemma 6 yield

$$\begin{aligned} p(\tilde{\varLambda }_{n,0,\underline{i}}\, | \, |\underline{i}|) \ge C(\tilde{\varLambda }_{n,0,\underline{i}},|\underline{i}|)\frac{\tilde{\varLambda }_{n,0,\underline{i}}}{\tilde{\varLambda }_{n,0,\underline{i}}+1}. \end{aligned}$$

Moreover, since \(\left| \frac{1}{2n}\tilde{\varLambda }_{n,0,\underline{i}}-\lambda _{\underline{i}}\right| \le \left| \frac{1}{2n}\varLambda _{n,0,\underline{i}}-\lambda _{\underline{i}}\right| +\frac{1}{2n}\), Lemma 3(i), (ii) and the fact that \(m\) is constant yield that for some \(\varepsilon >0\)

$$\begin{aligned} P \left( \max \limits _{\underline{i} :\underline{t}_m^* \not \subset \underline{i} \subset \{1,\ldots ,m\}} \,\, \frac{1}{2n} \tilde{\varLambda }_{n,0,\underline{i}} < \frac{1}{2n}\varLambda _{n,0,\underline{t}_m^*} - \varepsilon \right) \rightarrow 1. \end{aligned}$$

Note that condition \(|\underline{t}_m^*|>0\) yields \(\varLambda _{n,0,\underline{t}_m^*} \stackrel{\mathcal{P }}{\longrightarrow }\infty \) as \(\frac{1}{2n}\varLambda _{n,0,\underline{t}_m^*} \stackrel{\mathcal{P }}{\longrightarrow }D(f_{\underline{t}_m^*}^*||f_0) > 0\). Thus the definition of \(C(x,p)\) together with \(a_n/n\rightarrow 0\), the fact that \(\tilde{\varLambda }_{n,0,\underline{i}}^{(|\underline{i}|-2)/2}\ge 1\) for \(|\underline{i}|\ge 2\) and the inequalities above imply

$$ \begin{aligned} P \left( \min \limits _{\underline{i} : |\underline{i}|>1 \, \& \, \underline{t}_m^* \not \subset \underline{i} \subset \{1,\ldots ,m\}} \, p(\varLambda _{n,0,\underline{i}}\, | \, |\underline{i}|) e^{a_n|\underline{i}|} \le p\left( \varLambda _{n,0,\underline{t}_m^*}\, | \, |\underline{t}_m^*|\right) e^{a_n|\underline{t}_m^*|} \right) \rightarrow 0. \end{aligned}$$

In order to obtain analogous convergence for \(\underline{i}\) such that \(|\underline{i}|=1\) we reason similarly using inequality

$$\begin{aligned} e^{-x/2}\left( \frac{x}{2}\right) ^{-1/2}\frac{x}{x+1}\ge \frac{2}{3} e^{-x/2-\ln (x/2)/2}\ge \frac{2}{3}e^{-x} \end{aligned}$$

for \(x=\tilde{\varLambda }_{n,0,\underline{i}}\ge 2.\)

On the other hand for \(\underline{i}\subset \{1,\ldots ,m\}\) such that \(\underline{t}_m^*\subsetneq \underline{i}\) we have

$$\begin{aligned}&\log \left( e^{- \frac{\varLambda _{n,0,\underline{i}}}{2}} \left( \frac{\varLambda _{n,0,\underline{i}}}{2} \right) ^{\frac{|\underline{i}|-2}{2}} \varGamma \left( \frac{|\underline{i}|}{2} \right) ^{-1} e^{a_n|\underline{i}|} \right) \\&\quad - \log \left( e^{- \frac{\varLambda _{n,0,\underline{t}_m^*}}{2}} \left( \frac{\varLambda _{n,0,\underline{t}_m^*}}{2} \right) ^{\frac{|\underline{t}_m^*|-2}{2}} \varGamma \left( \frac{|\underline{t}_m^*|}{2}\right) ^{-1} \left( 1\!+\!\frac{|\underline{t}_m^*|\!-\!2}{\varLambda _{n,0,\underline{t}_m^*}\!-\!|\underline{t}_m^*|\!+\!2}\right) e^{a_n| \underline{t}_m^*|} \right) \\&\ge \frac{1}{2}\log n + a_n - \max \limits _{ \underline{i}:\, \underline{t}_m^* \subset \underline{i} } \frac{1}{2}\left| \varLambda _{n,0,\underline{i}} - \varLambda _{n,0,\underline{t}_m^*}\right| +\frac{|\underline{i}|-2}{2} \log \frac{\varLambda _{n,0,\underline{i}}}{2n}\\&\quad -\frac{|\underline{t}_m^*|-2}{2}\log \frac{\varLambda _{n,0,\underline{t}_m^*}}{2n} - \log \frac{\varGamma \left( m/2\right) }{\varGamma \left( |\underline{t}_m^*|/2\right) } -\log \left( 1+\frac{\underline{t}_m^*-2}{\varLambda _{n,0,\underline{t}_m^*}- |\underline{t}_m^*|+2}\right) . \end{aligned}$$

which implies, in view of Lemma 4 and Lemma 6(i) by noting that \(|\underline{i}|>1\) and bounding \(p(\varLambda _{n,0,\underline{i}}\, | \, |\underline{i}|)\) from below and \(p(\varLambda _{n,0,\underline{t}_m^*}\, | \, |\underline{t}_m^*|)\) from above, that

$$\begin{aligned} P \left( \min \limits _{\underline{i} : \underline{t}_m^* \subsetneq \underline{i} \subset \{1,\ldots ,m\}} \,\, p(\varLambda _{n,0,\underline{i}}\, | \, |\underline{i}|) e^{a_n|\underline{i}|} \le p\left( \varLambda _{n,0,\underline{t}_m^*}\, | \, |\underline{t}_m^*|\right) e^{a_n|\underline{t}_m^*|} \right) \rightarrow 0. \end{aligned}$$

The proof in the case \(|\underline{t}_m^*|=1\) is similar. If \(|\underline{t}_m^*|=0\), i.e. projected \(f\) on the full model \(f_{\mathrm{full}}^*\equiv 1\), then \(\varLambda _{n,0,\underline{t}_m^*}=0\) and Lemma 4 implies that \( \max \limits _{\underline{i} \subset \{ 1,\ldots ,m\}}\varLambda _{n,0,\underline{i}}=O_P(1) \). Thus

$$\begin{aligned} P \left( \min _{\underline{i}:\underline{i}\subset \{1,\ldots ,m\} } p(\varLambda _{n,0,\underline{i}} \,|\, |\underline{i}|) e^{a_n|\underline{i}|} <n^{-1/2} \right) \rightarrow 0. \end{aligned}$$

\(\square \)

In the case of a correct specification of the list of models we call a selection rule \(\hat{\underline{i}}=\hat{\underline{i}}(X_1,\ldots ,X_n)\) conservative if \(P(\underline{t}\subset \hat{\underline{i}})\rightarrow 1\) when \(n\rightarrow \infty \). Theorem below states the conditions for conservativeness and consistency of mPVC criterion when the true density \(f\) belongs to one of the models on the list. Observe that some growth conditions on \(m_n\) have to be imposed in this context as the method of calculating approximate p-values relies on Wilks’ theorem and the quality of approximation \(\varLambda _{n,0,\underline{i}}\) by \(\chi ^2_{|\underline{i}|}\) deteriorates when \(|\underline{i}|\) increases together with \(n\).

Theorem 2

(mPVC consistency) Assume (A1)–(A6), \(|\underline{t}|<\infty \) and \(\lim \nolimits _{n\rightarrow \infty }m_n\ge \max \underline{t}\). Then

  1. (i)

    \(\lim \nolimits _{n\rightarrow \infty }P(\underline{t} \subset \hat{\underline{i}}_\mathrm{mPVC} )=1\),

  2. (ii)

    if \(m_n \log m_n = o(\log n + a_n)\) as \(n\rightarrow \infty \) then \(\lim \nolimits _{n\rightarrow \infty }P(\hat{\underline{i}}_\mathrm{mPVC} =\underline{t})=1\).

Proof

Consider the case when \(|\underline{t}|>0\). Assume first that \(\underline{i}\) is such that \(\underline{t}\not \subset \underline{i} \subset \{1,\ldots ,m_n\}\). It is sufficient to show that with \(\tilde{\varLambda }_{n,0,\underline{i}}=\max (\varLambda _{n,0,\underline{i}},2)\)

$$\begin{aligned} P \left( \min _{\underline{i}:\underline{t}\not \subset \underline{i}\subset \{1,\ldots ,m_n\}}\,\,\, p(\tilde{\varLambda }_{n,0,\underline{i}} \,|\, |\underline{i}|) e^{a_n|\underline{i}|} \le p(\varLambda _{n,0,\underline{t}} \,|\, |\underline{t}|) e^{a_n|\underline{t}|} \right) \rightarrow 0. \end{aligned}$$
(10)

Lemma 6 yields for \(\tilde{\varLambda }_{n,0,\underline{i}}>0\) and \(|\underline{i}|>0\)

$$\begin{aligned} p(\tilde{\varLambda }_{n,0,\underline{i}} \,|\, |\underline{i}|) \ge e^{-\tilde{\varLambda }_{n,0,\underline{i}}/2}(\tilde{\varLambda }_{n,0,\underline{i}}/2)^{|\underline{i}|/2-1} \varGamma (|\underline{i}|/2)^{-1} \tilde{\varLambda }_{n,0,\underline{i}}/(\tilde{\varLambda }_{n,0,\underline{i}}+1) \end{aligned}$$
(11)

and for \(\varLambda _{n,0,\underline{t}} > |\underline{t}|-2\) and \(|\underline{t}|>1\)

$$\begin{aligned} p(\varLambda _{n,0,\underline{t}} \,|\, |\underline{t}|) \le e^{-\varLambda _{n,0,\underline{t}}/2}(\varLambda _{n,0,\underline{t}}/2)^{|\underline{t}|/2-1} \varGamma (|\underline{t}|/2)^{-1}\varLambda _{n,0,\underline{t}}/(\varLambda _{n,0,\underline{t}}-|\underline{t}|+2). \nonumber \\ \end{aligned}$$
(12)

Assume that \(|\underline{t}|>1\). The case \(|\underline{t}|=1\) is analogous. As \(\min _{\underline{i}:\,\underline{t}\not \subset \underline{i}}\tilde{\varLambda }_{n,0,\underline{i}}>0, \varLambda _{n,0,\underline{t}}\stackrel{\mathcal{P }}{\longrightarrow }\infty \) (since \(f\not \equiv 1\)) and \(|\underline{t}|<\infty \), the assumptions of Lemma 6 are satisfied with probability tending to \(1\) as \(n\rightarrow \infty \). Observe that \(D(f||f_{\underline{i}}^*) = D(f_{\underline{t}}||f_{\underline{i}}^*)=\lambda _{\underline{t}}-\lambda _{\underline{i}}\). We have

$$\begin{aligned} \frac{1}{2n} \varLambda _{n,0,\underline{t}} - \frac{1}{2n} \tilde{\varLambda }_{n,0,\underline{i}}&= \left( \frac{1}{2n} \varLambda _{n,0,\underline{t}} - \lambda _{\underline{t}} \right) - \left( \frac{1}{2n} \tilde{\varLambda }_{n,0,\underline{i}} - \lambda _{\underline{i}} \right) + (\lambda _{\underline{t}}-\lambda _{\underline{i}})\\&\ge \left( \frac{1}{2n} \varLambda _{n,0,\underline{t}} - \lambda _{\underline{t}} \right) - \max \limits _{\underline{i}:\, \underline{t} \not \subset \underline{i} \subset \{1,\ldots ,m_n\}} \left| \frac{1}{2n} \tilde{\varLambda }_{n,0,\underline{i}} - \lambda _{\underline{i}} \right| \\&+ \min \limits _{\underline{i}\subset \{1,\ldots ,m_n\}:\, \underline{t} \not \subset \underline{i}} D(f||f_{\underline{i}}^*). \end{aligned}$$

As in the proof of Theorem 1 Lemmas 3(i), (ii) and 5 imply that there exists \(\varepsilon >0\) such that

$$\begin{aligned} P \left( \min _{\underline{i}:\, t\not \subset \underline{i} \subset \{1,\ldots ,m_n\}} \, \frac{1}{2n} \varLambda _{n,0,\underline{t}} - \frac{1}{2n} \varLambda _{n,0,\underline{i}} > \varepsilon \right) \rightarrow 1. \end{aligned}$$
(13)

It is easily seen that the inequality \(\varGamma (p/2)\le (\lceil p/2\rceil -1)!\) for \(p\in \mathbb{N }\setminus \{1\}\) implies

$$\begin{aligned} \max _{\underline{i}:\, \underline{i}\subset \{1,\ldots ,m_n\}} \log \frac{\varGamma (|\underline{i}|/2)}{\varGamma (|\underline{t}|/2)}=O(m_n\log m_n)=o(n). \end{aligned}$$

Moreover,

$$\begin{aligned}&\displaystyle \frac{|\underline{t}|-2}{2}\log \frac{\varLambda _{n,0,\underline{t}}}{2}=O_p(\log n);\\&\displaystyle \min \limits _{\underline{i}:\, \underline{t}\not \subset \underline{i}\subset \{1,\ldots ,m_n\}} \log \left( \frac{\tilde{\varLambda }_{n,0,\underline{i}}}{\tilde{\varLambda }_{n,0,\underline{i}}+1} \frac{\varLambda _{n,0,\underline{t}}-|\underline{t}|+2}{\varLambda _{n,0,\underline{t}}}\right) = O_p(1); \end{aligned}$$

for \(L(n,\underline{i}):=\frac{|\underline{i}|-2}{2}\log (\frac{\tilde{\varLambda }_{n,0,\underline{i}}}{2})\) we have \(L(n,\underline{i})\ge 0\) for \(|\underline{i}|\ge 2\) and Lemma 3 easily implies \(\min _{\underline{i}: |\underline{i}|=1}L(n,\underline{i})\ge -cn\) with probability tending to 1 for any positive \(c\). Thus using the assumption \(a_n/n\rightarrow 0\), bounds (11) and (12) and the relations above, we obtain equation (10) and it follows that \(\lim \nolimits _{n\rightarrow \infty }P(\underline{t} \subset \hat{\underline{i}}_{\mathrm{mPVC}} )=1\).

Assume now that \(\underline{t} \subsetneq \underline{i} \subset \{1,\ldots ,m_n\}\), where \(f\not \equiv 1\). As \(\lambda _{\underline{i}}= \lambda _{\underline{t}}>0\), Lemma 6 may be applied to both p-values. As in proof of Theorem 1 we have

$$\begin{aligned}&\log \left( e^{- \frac{\varLambda _{n,0,\underline{i}}}{2}} \left( \frac{\varLambda _{n,0,\underline{i}}}{2} \right) ^{\frac{|\underline{i}|-2}{2}} \varGamma \left( \frac{|\underline{i}|}{2} \right) ^{-1} e^{a_n|\underline{i}|} \right) \\&\quad - \log \left( e^{- \frac{\varLambda _{n,0,\underline{t}}}{2}} \left( \frac{\varLambda _{n,0,\underline{t}}}{2} \right) ^{\frac{|\underline{t}|-2}{2}} \varGamma \left( \frac{|\underline{t}|}{2} \right) ^{-1} \frac{\varLambda _{n,0,\underline{t}}}{\varLambda _{n,0,\underline{t}}-|\underline{t}|+2} e^{a_n|\underline{t}|} \right) \\&\ge \frac{1}{2}\log n \!+\! a_n \!-\! \max \limits _{ \underline{i}:\, \underline{t} \subset \underline{i} } \frac{1}{2}\left| \varLambda _{n,0,\underline{i}} - \varLambda _{n,0,\underline{t}}\right| +\frac{|\underline{i}|-2}{2} \log \frac{\varLambda _{n,0,\underline{i}}}{2n}\\&\quad - \frac{|\underline{t}|-2}{2}\log \frac{\varLambda _{n,0,\underline{t}}}{2n} - \log \frac{\varGamma \left( m_n/2\right) }{\varGamma \left( |\underline{t}|/2\right) } + \log \left( \frac{\varLambda _{n,0,\underline{t}}-|\underline{t}|+2}{\varLambda _{n,0,\underline{t}}} \right) . \end{aligned}$$

Lemma 4 implies \(\max \nolimits _{ \underline{i}:\, \underline{t} \subset \underline{i} \subset \{1,\ldots ,m_n\}} |\varLambda _{n,0,\underline{i}} - \varLambda _{n,0,\underline{t}}| = O_P(m_n).\)

Moreover observe that

$$\begin{aligned}&\frac{|\underline{i}|-2}{2} \log \frac{\varLambda _{n,0,\underline{i}}}{2n} - \frac{|\underline{t}|-2}{2}\log \frac{\varLambda _{n,0,\underline{t}}}{2n}\\&\qquad = \frac{|\underline{i}|-2}{2} \left( \log \frac{\varLambda _{n,0,\underline{i}}}{2n}-\log \frac{\varLambda _{n,0,\underline{t}}}{2n}\right) + \frac{|\underline{i}|-|\underline{t}|}{2}\log \frac{\varLambda _{n,0,\underline{t}}}{2n}. \end{aligned}$$

The first term in the above decomposition is positive as \(|\underline{i}| \ge 2\) and \(\underline{t}\subset \underline{i}\) and the second is easily seen to be larger than \(-c\log n\) with probability tending to 1 for any positive \(c\). Finally, using the fact that \( \log \varGamma (\frac{m_n}{2})/\varGamma (\frac{|\underline{t}|}{2}) = O(m_n\log m_n) \) together with the assumption \(m_n \log m_n = o(\log n + a_n)\) we obtain

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }P\left( \min _{\underline{i}: \, \underline{t} \subset \underline{i} \subset \{1,\ldots ,m_n\}} \, p(\varLambda _{n,0,\underline{i}} \,|\, |\underline{i}|) e^{a_n|\underline{i}|}> p(\varLambda _{n,0,\underline{t}} \,|\, |\underline{t}|) e^{a_n|\underline{t}|} \right) = 1. \end{aligned}$$

The proof in the case \(|\underline{t}|=1\) is similar. Consider now the case when \(f\equiv 1\), i.e. the minimal model is true. We will show that

$$\begin{aligned} P \left( \min _{\underline{i}:\underline{i}\subset \{1,\ldots ,m_n\}} p(\varLambda _{n,0,\underline{i}} \,|\, |\underline{i}|) e^{a_n|\underline{i}|} <n^{-1/2} \right) \rightarrow 0. \end{aligned}$$

As Lemma 4 yields that when the minimal model is true \(\mathrm{max}_{\underline{i}\subset \{1,\ldots ,m_n\}}\varLambda _{n,0,\underline{i}} =O_P(m_n)\) it is enough to show that for any \(C>0\)

$$\begin{aligned} n^{1/2}\min _{k=1,\ldots ,m_n} e^{a_n k}P(Z_k>Cm_n)\rightarrow \infty , \end{aligned}$$

where \(Z_k\) pertains to \(\chi _k^2\) distribution. This is easily shown using Lemma 6, assumption \(m_n\log m_n=o(a_n+\log n)\) and the fact that \(\mathrm{max}_{k\le m_n} \log \varGamma (k/2)=O(m_n\log m_n)\). \(\square \)

Remark 2

Careful examination of the previous proof yields that under conditions of Theorem 2

$$\begin{aligned} P(\underline{t} \not \subset \hat{\underline{i}}_\mathrm{mPVC}) \le C (m_n^{1+2\omega }/n)^{1/2} \end{aligned}$$

for some absolute constant \(C>0\).

Theorem 3 below states that any index \(i_0\) corresponding to a nonzero coefficient in the expansion of \(\log f\) will be eventually included in \(\hat{\underline{i}}_\mathrm{mPVC}\). We call a selection rule \(\hat{\underline{i}}\) conservative for \(f\) satisfying assumption (A6) if for any \(M\in \mathbb{N }P({\underline{t}}\cap \{1,\ldots ,M\}\subset \hat{\underline{i}})\rightarrow 1.\) Note that this notion coincides with the usual definition of conservativeness under correct specification given above Theorem 2 when \(|\underline{t}|<\infty \). In Theorem 3 \(\underline{t}\) can be either infinite or finite. However, an interesting part of the result corresponds to the former case, i.e. when \(\log \,f\) has infinite expansion w.r.t. system \((b_i)_{i=0}^\infty \). As it was noticed before this corresponds to misspecification case when density \(f\) does not belong to any model \(\mathcal{M }_{m_n},\,n=1,2,\ldots \). For finite \(\underline{t}\) Theorem 3 coincides with Theorem 2(i).

Theorem 3

Assume (A1)–(A6), moreover that (i) \(\sum _{i=1}^\infty \theta _ib_i(x)\) is uniformly convergent on \([0,1]\) and (ii) \(a_n|t_{m_n}(f)|=o(n)\), where \(\underline{t}_{m_n} = \underline{t} \cap \{1,\ldots ,m_n\}\). If \(\lim \nolimits _{n\rightarrow \infty }m_n\ge \max \underline{t}\) then \(\hat{\underline{i}}_\mathrm{mPVC}\) is conservative.

Proof

It is enough to prove that for any \(i_0\in \underline{t}\) \(P(i_0\in \hat{\underline{i}}_\mathrm{mPVC}) \rightarrow 1\) as \(n\rightarrow \infty \). The proof proceeds analogously to the proof of Theorem 2 (a). In the following we prove that there exists \(\varepsilon >0\) such that

$$\begin{aligned} \max \limits _{\underline{i}: i_0\not \in \underline{i}\subset \{1,\ldots ,m_n \}} \lambda _{\underline{i}} < \lambda _{\underline{t}_{m_n}} - \varepsilon \,\, \quad \text{ as } n\rightarrow \infty . \end{aligned}$$
(14)

First note that reasoning analogously as in the proof of Lemma 5 we have

$$\begin{aligned} \mathop {\lim \inf }\limits _{n\rightarrow \infty } \min \limits _{\underline{i}: i_0\not \in \underline{i} \subset \{1,\ldots ,m_n\}} D(f||f_{\underline{i}}^*) >0. \end{aligned}$$
(15)

Indeed, assumptions (A2) and (A5) imply as in Lemma 1 that there exists a constant \(C>0\) such that \(D(f||f_{\underline{i}}^*) \ge C \int _0^1 (\log (f/f_{\underline{i}}^*))^2\) and orthogonality of \((b_j)_{j=0}^\infty \) yields

$$\begin{aligned} \int \limits _0^1 (\log (f/f_{\underline{i}}^*))^2 = \sum _{j\in \underline{i}} (\theta _j-\theta ^*_j)^2 + \sum _{j\not \in \underline{i}} \theta _j^2 +(\psi (\theta )-\psi _{\underline{i}}(\theta _{\underline{i}}^*))^2\ge \theta ^2_{i_0}. \end{aligned}$$

(throughout, the integration is performed w.r.t. Lebesgue measure \(\lambda \) on [0,1]). Thus \(D(f||f_{\underline{i}}^*) > C \theta _{i_0}^2 > 0\) which proves (15).

On the other hand we have

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } D(f||f_{\underline{t}_{m_n}}^*) = 0. \end{aligned}$$
(16)

To see this note that since \(f_{\underline{t}_m}^*\) minimizes \(D(f||\cdot )\) on \(\mathcal{M }_{\underline{t}_m}\) then \(D(f||f_{\underline{t}_m}^*) \le D(f||f_{\theta ^{\underline{t}_{m}}})\), where \(\theta ^{\underline{t}_{m}}\) is defined in Sect. 2.2. Lemma 1 in Barron and Sheu (1991) implies

$$\begin{aligned} D(f||f_{\theta ^{\underline{t}_{m}}}) \le \frac{1}{2} e^{|| \log (f/f_{\theta ^{\underline{t}_m}}) ||_\infty }\int \limits _0^1 f(\log (f/f_{\theta ^{\underline{t}_{m}}}))^2. \end{aligned}$$

It is easy to see that assumption (i) implies \(\inf _x f_{\theta ^{\underline{t}_m}}(x)>\varepsilon \) for some \(\varepsilon >0\) and sufficiently large \(n\). Thus assumption (A5) yields \( D(f||f_{\theta ^{\underline{t}_{m}}}) \le C \int _0^1 (\log (f/f_{\theta ^{\underline{t}_{m}}}))^2 = C \left( \sum \nolimits _{i>m_n}\theta _i^2 + (\psi (\theta )-\psi _{\underline{t}_m}(\theta ^{\underline{t}_m}))^2\right) \) for some constant \(C>0\). Now (16) follows from the fact that \(\sum \nolimits _{i>m_n}\theta _i^2 \rightarrow 0\) and \(\psi (\theta )-\psi _{\underline{t}_{m_n}}(\theta ^{\underline{t}_{m_n}}) \rightarrow 0\) as \(n\rightarrow \infty \). The last convergence follows from the proof of Lemma 4 in Barron and Sheu (1991) which implies that \(|\psi (\theta )-\psi _{\underline{t}_{m_n}}(\theta ^{\underline{t}_{m_n}})|\le ||\sum _{i=m+1}^\infty \theta _ib_i||_\infty \rightarrow 0\).

Properties (15) and (16) imply (14). The rest of the proof is analogous to that of Theorem 2(a). \(\square \)

Remark 3

Observe that the above proof also yields the following more general fact. Assume that subsets \(M_n\subset 2^{\{1,\ldots ,m_n\}}\) are such that the following separability condition generalizing (14) holds

$$\begin{aligned} \max \limits _{\underline{i}\in M_n} \lambda _{\underline{i}} < \lambda _{\underline{t}_{m_n}} - \varepsilon \end{aligned}$$
(17)

for all \(n\in \mathbb{N }\) and some \(\varepsilon >0\), or equivalently \( \min _{\underline{i}\in M_n} D(f||f^*_{\underline{i}}) >D(f||f^*_{t_{m_n}})+\varepsilon . \) Then under conditions of Theorem 2 \(P(\hat{\underline{i}}_\mathrm{mPVC}\in M_n^c)\rightarrow 1\). If \(M_n:=\{\underline{i}\in 2^\mathrm{full}:\, i_0\not \in \underline{i}\}\) the conclusion of Theorem 3 is obtained.

Recall that \(\hat{f}_{\underline{i}}\) denotes the maximum likelihood estimator of density \(f\) in family \(\mathcal{M }_{\underline{i}}\) equal to \(f_{\hat{\theta }_\mathrm{{ML}}^{\underline{i}}}\). Let \(\hat{f}_\mathrm{mPVC}\) be the post-model-selection estimator of \(f\) based on mPVC method, i.e. \( \hat{f}_\mathrm{mPVC} = \hat{f}_{\hat{\underline{i}}_\mathrm{mPVC}}. \)

Theorem 4

Assume (A1)–(A6), \(|\underline{t}|<\infty , \lim \nolimits _{n\rightarrow \infty }m_n\ge \max \underline{t}\) and \(m_n \log m_n = o(\log n + a_n)\). Then \(D(f||\hat{f}_\mathrm{mPVC})=O_P(m_n/n)\).

Proof

Observe that we have for \(\hat{\underline{i}}=\hat{\underline{i}}_\mathrm{mPVC}\)

$$\begin{aligned} D(f||\hat{f}_\mathrm{mPVC})=D(f||f^*_{\hat{\underline{i}}}) + D(f^*_{\hat{\underline{i}}}||\hat{f}_\mathrm{mPVC}). \end{aligned}$$
(18)

The first term is 0 with probability tending to 1 in view of Theorem 2 (i). Using Lemma 7 analogously as in the proof of Lemma 4 yields \(D(f^*_{\underline{t}}||\hat{f}_{\underline{t}}) = O_P(m_n/n)\). This and convergence \(P(\hat{\underline{i}}=\underline{t})\rightarrow 1\) implied by Theorem 2 (i) completes the proof. \(\square \)

3.2 Maximal p-value criterion MPVC

Theorems 5 and 6 below are analogous to Theorems 1 and 2, respectively, for MPVC criterion.

Theorem 5

(MPVC consistency) If conditions (A1), (A5) and (A6) hold, \(a_n\rightarrow \infty \) and \(m_n=m\) is constant then \( \lim \nolimits _{n\rightarrow \infty }P(\hat{\underline{i}}_\mathrm{MPVC} ={\underline{t}_m^*})=1. \)

Proof

Let \(\underline{i} \subset \{ 1,\ldots ,m\}\) and assume that \(\underline{t}_m^* \subsetneq \underline{i}\) . Then \(|\underline{i}| > |\underline{t}_m^*|\) and we have

$$\begin{aligned}&P\left( p( \varLambda _{n,{\underline{t}_m^*},\mathrm{full}} \,|\, m-|{\underline{t}_m^*}| ) e^{-a_n| \underline{t}_m^*|}> \max _{\underline{i}: \, {\underline{t}_m^*} \subsetneq \underline{i} \subset \{1,\ldots ,m\}} \, p( \varLambda _{n,\underline{i},\mathrm{full}} \,|\, m-|\underline{i}| ) e^{-a_n|\underline{i}|} \right) \\&\quad \ge P\left( p( \varLambda _{n,{\underline{t}_m^*},\mathrm{full}} \,|\, m-|{\underline{t}_m^*}| ) e^{-a_n| \underline{t}_m^*|} > \max _{\underline{i}: \, \underline{t}_m^* \subsetneq \underline{i}\subset \{1,\ldots ,m\}} \, e^{-a_n|\underline{i}|} \right) \\&\quad \ge P\left( p( \varLambda _{n,{\underline{t}_m^*},\mathrm{full}} \,|\, m-|{\underline{t}_m^*}| ) > e^{-a_n} \right) \rightarrow 1. \end{aligned}$$

The last convergence follows from the assumption \(a_n\rightarrow \infty \) and the fact that \(\varLambda _{n,{\underline{t}_m^*},\mathrm{full}}=O_P(1)\) implied by Lemma 4.

Assume now that \(\underline{i} \subset \{ 1,\ldots ,m\}\) is such that \(\underline{t}_m^*\not \subset \underline{i}\). As \(\frac{1}{2n}\varLambda _{n,\underline{i},{\mathrm{full}}}\stackrel{\mathcal{P }}{\longrightarrow }D(f||f_{\underline{i}}^*) - D(f||f_\mathrm{full}^*) >0\) then analogously as in the proof of Theorem 1 we obtain using Lemma 3

$$\begin{aligned} P \left( \min _{\underline{i}: \, \underline{t}_m^*\not \subset \underline{i} \subset \{1,\ldots ,m\}} \, \frac{1}{2n}\varLambda _{n,{\underline{i}},\mathrm{full}} > \frac{1}{2n}\varLambda _{n,{\underline{t}_m^*},\mathrm{full}} +\varepsilon \right) \rightarrow 1 \end{aligned}$$
(19)

for some \(\varepsilon >0\). Moreover, Lemma 6 implies

$$\begin{aligned} p(\varLambda _{n,{\underline{t}_m^*},\mathrm{full}} \, | \, m-|\underline{t}_m^*|) \ge C(\varLambda _{n,{\underline{t}_m^*},\mathrm{full}}, m-|\underline{t}_m^*|) \end{aligned}$$

for \(\varLambda _{n,{\underline{t}_m^*},\mathrm{full}} > 0\) and \(m-|\underline{t}_m^*|>1\) and

$$\begin{aligned} p(\varLambda _{n,{\underline{i}},\mathrm{full}} \, | \, m-|\underline{i}|)&\le C(\varLambda _{n,{\underline{i}},\mathrm{full}}, m-|\underline{i}|)\left( 1+\frac{m-|\underline{i}|-2}{\varLambda _{n,{\underline{i}},\mathrm{full}}-m+|\underline{i}|+2} \right) \\&= C(\varLambda _{n,{\underline{i}},\mathrm{full}}, m-|\underline{i}|)(1+o_P(1)) \end{aligned}$$

for \(\varLambda _{n,{\underline{i}},\mathrm{full}} \rightarrow \infty \) and \(m-|\underline{i}|>1\). Analogous inequality holds for \(\underline{i}\) such that \(m-|\underline{i}|=1\). This together with (19) and assumption \(a_n/n\rightarrow 0\) imply that when \(m-|\underline{t}_m^*|>1\)

$$\begin{aligned} P \left( \max _{\underline{i}: \,\underline{t}_m^*\not \subset \underline{i}\subset \{1,\ldots ,m\}} \, p(\varLambda _{n,{\underline{i}},\mathrm{full}} \, | \, m\!-\!|\underline{i}|) e^{-a_n|\underline{i}|} < p(\varLambda _{n,{\underline{t}_m^*},\mathrm{full}} \, | \, m\!-\!|\underline{t}_m^*|) e^{-a_n|\underline{t}_m^*|} \right) \!\rightarrow \! 1. \end{aligned}$$

The proof in the cases \(1\ge m-|\underline{t}_m^*|\ge 0\) is analogous. \(\square \)

Theorem 6

(MPVC consistency) Assume (A1)–(A6), \(|\underline{t}|<\infty \) and \(\lim \nolimits _{n\rightarrow \infty }m_n\ge \max \underline{t}\). Then

  1. (a)

    \(\lim \nolimits _{n\rightarrow \infty }P(\underline{t} \subset \hat{\underline{i}}_\mathrm{MPVC} )=1\),

  2. (b)

    if \(m_n\log m_n=o(a_n)\) then \(\lim \nolimits _{n\rightarrow \infty }P(\hat{\underline{i}}_\mathrm{MPVC} =\underline{t})=1\).

Proof

We first consider the case when model \(\underline{i}\) is misspecified: \(\underline{t} \not \subset \underline{i}\) and \(\underline{t}\ne {\mathrm{full}}\). Observe that Lemma 3(i) implies that \(\max _{\underline{i}\subset \{1,\ldots ,m_n\}}|\varLambda _{n,\underline{i},{\mathrm{full}}}/(2n) -(\lambda _{\underline{t}}-\lambda _{\underline{i}})| \stackrel{\mathcal{P }}{\longrightarrow }0\) and thus it follows in view of Lemma 5 that \(\min _{\underline{i}\subset \{1,\ldots ,m_n\}: \,\underline{t}\not \subset \underline{i} } \varLambda _{n,\underline{i},{\mathrm{full}}}\rightarrow \infty \) in probability. Assume first that \(m_n-|\underline{i}|>1\). Whence using Lemma 6(ii) it is enough to show that with probability tending to \(1\) we have

$$\begin{aligned}&e^{-a_n|\underline{t}|} C(\varLambda _{n,\underline{t},{\mathrm{full}}}, m_n-|\underline{t}|)\nonumber \\&\quad >e^{-a_n|\underline{i}|} C(\varLambda _{n,\underline{i},\mathrm{full}}, m_n-|\underline{i}|)\left( 1+\displaystyle \frac{m_n-|\underline{i}|-2}{\varLambda _{n,{\underline{i}},\mathrm{full}}-m_n+|\underline{i}|+2} \right) \end{aligned}$$
(20)

for all \(\underline{i}\subset \{1,\ldots ,m_n\}: \, \underline{t}\not \subset \underline{i}\) and such that \(m_n-|\underline{i}|>1\). This easily follows as in the case of mPVC consistency from

$$\begin{aligned} P \left( \min _{\underline{i}: \, \underline{t}\not \subset \underline{i}\subset \{1,\ldots ,m_n\}} \frac{1}{2n}\varLambda _{n,\underline{i},{\mathrm{full}}} -\frac{1}{2n}\varLambda _{n,\underline{t},{\mathrm{full}}}>\varepsilon \right) \rightarrow 1 \end{aligned}$$
(21)

for some \(\varepsilon >0\). The proof for \(m_n-|\underline{i}|=1\) is analogous. The case \(\underline{t}=\mathrm{full}\) follows easily from \(a_n/n\rightarrow 0\) after noting that in this case the right hand side of (20) is \(O(e^{-\varepsilon n})\) for some \(\varepsilon >0\), whereas the left hand side equals \(e^{-a_n|\underline{t}|}\). This yields the proof of (a).

We now consider the case when model \(\underline{i}\) contains the minimal true model: \(\underline{t} \subsetneq \underline{i}\). As in the proof of Theorem 5 we obtain

$$\begin{aligned}&P\left( \max _{\underline{i}: \, \underline{t} \subset \underline{i}\subset \{1,\ldots ,m_n\}} \, p( \varLambda _{n,\underline{i},\mathrm{full}} \,|\, m_n-|\underline{i}| ) e^{-a_n|\underline{i}|} < p( \varLambda _{n,\underline{t},\mathrm{full}} \,|\, m_n-|\underline{t}| ) e^{-a_n|\underline{t}|} \right) \\&\quad \ge P\left( p( \varLambda _{n,\underline{t},\mathrm{full}} \,|\, m_n-|\underline{t}| ) > e^{-a_n} \right) . \end{aligned}$$

Observe that in view of Lemma 4 \({\varLambda }_{n,\underline{t},{\mathrm{full}}}=O_P(m_n)\). Thus it is enough to show that

$$\begin{aligned} e^{a_n} P( Z_{\chi _{m_n-|\underline{t}|}^2}>Cm_n)\rightarrow \infty \end{aligned}$$
(22)

for any fixed \(C>0\), where \(Z_{\chi _{m_n-|\underline{t}|}^2}\sim {\chi ^2_{m_n-|\underline{t}|}}\). This follows easily from Lemma 6 and the assumed condition on \(m_n\) as the above expression is bounded from below by

$$\begin{aligned} \exp \left\{ a_n-\frac{Cm_n}{2}+ \left( \frac{\bar{m}_n}{2}-1 \right) \log \left( \frac{Cm_n}{2} \right) - \log \left( \frac{\bar{m}_n}{2} \right) \frac{\bar{m}_n}{2} \right\} \rightarrow \infty , \end{aligned}$$

where \(\bar{m}_n=m_n- |\underline{t}|\). This yields the proof of (b). \(\square \)

Remark 4

Note that the assumption of Theorem 6 (b) implies that \(a_n\rightarrow \infty \) whereas Theorem 2 asserts that consistency of mPVC criterion holds also for constant \(a_n\) provided \(m_n=o(\log n)\).

From the proof of Theorem 6 (cf. (21)) it is easy to see that the analogue of Theorem 3 holds for MPVC criterion under the same conditions.

3.3 Greedy mPVC and MPVC criteria and their consistency

Optimization of a criterion function over all subsets of \(\{1,2,\ldots ,m_n\}\) involves a considerable computational cost for large \(m_n\). This is a drawback of all criterion based procedures. We discuss here a two-step modification of p-value criteria introduced in Pokarowski and Mielniczuk (2011) which involves only \(O(m_n)\) calculations of criterion instead of \(O(2^{m_n})\). The approach is motivated by Zheng and Loh (1997) who used such an approach for linear models.

Greedy mPVC In the first step for every \(j\in \{1,\ldots ,m_n\}\) we consider testing hypotheses

$$\begin{aligned} \begin{array}{l} H_0: f\in \mathcal{M }_0\\ H_1: f\in \mathcal{M }_{\bar{j}}\setminus \mathcal{M }_0, \end{array} \end{aligned}$$

where \(\bar{j}=\{1,\ldots ,m_n\}\setminus \{ j \}\). Then we order the variables with respect to the obtained p-values:

$$\begin{aligned} p(\varLambda _{n,0,\bar{j}_1} \,|\, m_n-1) \ge \cdots \ge p(\varLambda _{n,0,\bar{j}_m} \,|\, m_n-1) \end{aligned}$$

and apply mPVC method considering only nested list of \(m\) models indexed by the elements of \(M=\{\emptyset ,\{j_1\}, \{j_1,j_2\}, \ldots , \{j_1,\ldots ,j_m\}\}\). Thus the greedy minimal p-value criterion takes the form:

$$\begin{aligned} \hat{\underline{i}}_\mathrm{mPVC}^\mathrm{greedy} = \mathop {\arg \min }\limits _{\underline{i} \in M} p(\varLambda _{n,0,\underline{i}} \,|\, |\underline{i}|) e^{a_n|\underline{i}|}. \end{aligned}$$

Greedy MPVC In the first step for every \(j\in \{1,\ldots ,m_n\}\) we consider test of the form

$$\begin{aligned} \begin{array}{l} H_0: f\in \mathcal{M }_{\bar{j}}\\ H_1: f\in \mathcal{M }_{\mathrm{full}}{\setminus }\mathcal{M }_{\bar{j}}, \end{array} \end{aligned}$$

where \(\bar{j}=\{1,\ldots ,m_n\}\setminus \{ j \}\). Then we order the variables with respect to the obtained p-values:

$$\begin{aligned} p( \varLambda _{n,\bar{j}_1,\mathrm{full}} \,|\, 1 ) \le \cdots \le p( \varLambda _{n,\bar{j}_m,\mathrm{full}} \,|\, 1 ) \end{aligned}$$

and apply MPVC method considering only nested list of \(m_n\) models indexed by the elements of \(M=\{\emptyset ,\{j_1\}, \{j_1,j_2\}, \ldots , \{j_1,\ldots ,j_m\}\}\). Thus the greedy maximal p-value criterion takes the form:

$$\begin{aligned} \hat{\underline{i}}_\mathrm{MPVC}^\mathrm{greedy} = \mathop {\arg \max }\limits _{\underline{i} \in M} p( \varLambda _{n,\underline{i},\mathrm{full}} \,|\, m_n-|\underline{i}| ) e^{-a_n|\underline{i}|}. \end{aligned}$$

Observe that in both greedy methods all \(m\) likelihood ratio test statistics \(\mathrm {LRT}\) have under the null hypothesis the same asymptotic distribution, namely \(\chi _{m-1}^2\) in the case of Greedy mPVC and \(\chi _{1}^2\) in the case of Greedy MPVC. Hence in both cases ordering the p-values coincides with ordering the values of test statistics monotonically. Moreover, it follows that the sets \(M\) yielded by the both procedures are equal.

It is also of interest to note that selection methods based on truncation \( \hat{\underline{i}}=\{j: |\hat{\theta }^\mathrm{full}_{j}|>C_n\}\) can be also viewed as two-step procedures similar to these defined above. Namely, in the first step estimates of the parameters in the full model are ordered: \(|\hat{\theta }^\mathrm{full}_{R_1}|\ge |\hat{\theta }^\mathrm{full}_{R_2}|\cdots \ge |\hat{\theta }^\mathrm{full}_{R_m}|\). Then we choose a model \(\{R_1,R_2,\ldots ,R_{k_0}\}\) such that \(k_0=\mathrm{argmax}_k\{\sum _{i=1}^k (\hat{\theta }^\mathrm{full}_{R_i})^2-kC_n^2\}\). It is easy to see that \(\hat{\underline{i}}=\{R_1,R_2,\ldots ,R_{k_0}\}\). Observe that the criterion function in the second step is a penalized score statistic \(\sum _{i=1}^k (\hat{\theta }^\mathrm{full}_{R_i})^2\) for the model indexed by \(\{R_1,R_2,\ldots ,R_k\}\). We refer to Wojtyś (2011) for discussion of such rules.

Corollary 1

Under conditions of Theorem 2 (b) and Theorem 6 (b), respectively, greedy mPVC and MPVC methods are consistent.

Proof

For every \(j\notin \underline{t}\) we have \(\varLambda _{n,0,\underline{t}} \le \varLambda _{n,0,\bar{j}}\). Thus as for \(k\in \underline{t}\) we have \(\bar{k}\not \supset \underline{t}\) (13) implies that for every such \(k\)

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } P \left( \min _{j\notin \underline{t}} \, \frac{1}{2n}\varLambda _{n,0,\bar{j}} > \frac{1}{2n}\varLambda _{n,0,\bar{k}} \right) = 1. \end{aligned}$$

Thus with probability tending to 1 after the initial ordering all indices belonging to set \(\underline{t}\) will precede the remaining indices. Hence the consistency of both greedy methods follows from the consistency of their respective full search method applied to \(M\). \(\square \)

Remark 5

It can be shown using Lemma 3(i) that under its assumptions probability of incorrect ordering in the first step of the procedure is bounded by

$$\begin{aligned} P(\mathrm{min}_{i\not \in \underline{t}}\varLambda _{n,0,\bar{i}}< \mathrm{max}_{j \in \underline{t}}\varLambda _{n,0,\bar{j}})\le C\left( \frac{m^{1+2\omega }}{n}\right) (\lambda ^{-1} +\lambda ^{-2}), \end{aligned}$$

where \(\lambda =\mathrm{min}_{i\not \in \underline{t},j\in \underline{t}}(\lambda _{\bar{i}}-\lambda _{\bar{j}})\) and \(C\) is an absolute constant. Note that the bound becomes larger when the selection problem becomes more difficult, i.e. \(\lambda \) decreases.

4 Simulation study

We conducted numerical experiments to check how the considered selectors behave in practice for moderate sample sizes. The considered sample size was \(n=300\) with \(m_n=5\). Random samples were generated either form the uniform density or belonged to one of the following four families:

  1. (i)

    exponential family \(\mathcal{M }_1\) with \(\underline{t}=\{1\}\) and \(\theta _1=0.3,0.4,\ldots ,1\);

  2. (ii)

    exponential family \(\mathcal{M }_3\) with \(\underline{t}=\{3\}\) and \(\theta _3=0.3,0.4,\ldots ,1\);

  3. (iii)

    exponential family \(\mathcal{M }_5\) with \(\underline{t}=\{1,5\}, \theta _1=0.1\) and \(\theta _5=0.1,\ldots ,0.5\);

  4. (iv)

    beta densities with parameters \((a,b)=(1,1.2),(1.1,1.3),(1.5,1.5),(2,2)\).

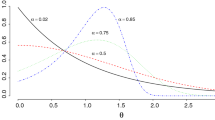
Recall that e.g. \(\underline{t}=\{1,5\}\) means that only the first and the fifth coefficient is allowed to be nonzero. In all cases we considered Legendre polynomials basis. The densities are plotted in Fig. 1. The values of the parameters were chosen to obtain typical shapes in the considered family. Number of Legendre polynomials appearing in the definitions of densities (i)–(iii) corresponds to shape complexity. Observe e.g. that typical density in example (ii) has two modes in (0,1) in contrast to four modes in the case (iii). Example (iv) corresponds to misspecification case, i.e. the situation when the underlying density does not belong to any model in the considered family.

Fig. 1
figure 1

Theoretical densities

Full size image

Six selection criteria were taken into account: BIC (Bayesian Information Criterion, Schwarz (1978)), mPVC, MPVC and their greedy counterparts. BIC is defined as

$$\begin{aligned} \mathrm{BIC}(\underline{i})= 2\varLambda _{n,0,\underline{i}} - |\underline{i}| \log n. \end{aligned}$$

Several values of scaling constants \(a_n\) for p-value based criteria were considered. We report the results for constants which performed the best on average: \(a_n=0\) for mPVC and \(a_n=\log n/2\) for MPVC, i.e. an unscaled \(p(\varLambda _{n,0,\underline{i}}||\underline{i}|)\) for mPVC and \(p(\varLambda _{n,\underline{i}, \mathrm{full}}|m-|\underline{i}|)\) scaled down by \(n^{-1/2}\) for MPVC.

For three main selectors ML estimators had to be calculated for any of \(2^m\) models or, after initial preordering, for \(m\) models in the case of their greedy counterparts. As ML estimators are calculated using iterative Newton-Raphson procedure some cases of non-convergence occur. In such a case corresponding model was excluded from the list and only the models for which ML estimators were obtained were considered for optimization. Number of cases when lack of convergence occurs increases with complexity of the model, however it does not exceed \(3\,\%\) of the number of the models considered.

Two main measures of performance were taken into account: fraction of correct model specifications averaged over \(10^4\) repetitions of the experiment and averaged empirical Integrated Squared Error ISE defined as

$$\begin{aligned} \mathrm{ISE}(\hat{f}) = \int \limits _{0}^1 (f(x)-\hat{f}(x))^2 dx, \end{aligned}$$

where \(f\) is the theoretical density of random sample and \(\hat{f}\) is its post-model-selection estimator. Mean of ISE is denoted as MISE in the plots. It turned out that (see Figs. 2, 3, 4, 5) these two measures are approximately concordant in the sense that a large probability of correct specification corresponds to a small ISE and the ranking of selectors with respect to both measures coincide in general. The only exception are the densities close to \(\mathcal{M }_0\) (e.g. members of \(\mathcal{M }_1\) with small \(\theta _1\)) for which a method may err by choosing the uniform density but still has a small MISE. For misspecification case the accuracy percent was replaced by averaged Kullback–Leibler distance \(D(f||\hat{f})\) from \(f\) to post-model-selection estimator. Both integrals, ISE and Kullback–Leibler distance, were calculated numerically using the Gaussian quadrature for Legendre polynomials. In order not to obscure the clarity of pictures in each example we plotted the best overally performing selector and depending on whether it was the main selector or one of the greedy modification we supplemented it by the two remaining selectors from the same group.

Fig. 2
figure 2

Percentage of correct model selections (left graph) and estimated MISE (right graph) for data pertaining to \(f_\theta (x) = c(\theta )\exp \{\theta _1 b_1(x)\}\), where \(\theta _1=0.3,0.2,\ldots ,1\)

Full size image
Fig. 3
figure 3

Percentage of correct model selections (left graph) and estimated MISE (right graph) for data pertaining to \(f_\theta (x) = c(\theta )\exp \{\theta _3 b_3(x)\}\), where \(\theta _3=0.3,0.4,\ldots ,1\)

Full size image
Fig. 4
figure 4

Percentage of correct model selections (left graph) and estimated MISE (right graph) for data pertaining to \(f_\theta (x) = c(\theta )\exp \{\theta _1 b_1(x)+\theta _5 b_5(x)\}\), where \(\theta _1=0.1, \theta _5=0.1,\ldots ,0.5\)

Full size image
Fig. 5
figure 5

Estimated Kullback–Leibler distance from theoretical density \(D(f||\hat{f})\) (left graph) and MISE (right graph) and for data pertaining to Beta distribution with parameters \(a\) and \(b\)

Full size image

We start with the comparison of methods for data pertaining to the uniform density presented in Table 1. In this case the best performance was achieved by greedy MPVC, which selected the correct model in more than \(99\,\%\) of Monte Carlo repetitions and yielded the smallest MISE. Also MPVC had comparably good properties as it attained nearly \(99\,\%\) accuracy of model selection and had MISE three times as large as the winner. BIC criterion achieved more than \(90\,\%\) of correct model selections, however the estimated MISE was 10 times larger than for greedy MPVC. The methods mPVC and greedy mPVC behaved considerably worse.

Table 1 Estimated MISE\((\hat{f})\) and probabilities of correct model selections for the data pertaining to the uniform distribution \(U(0,1)\)
Full size table

This may come as a surprise that the greedy method may actually perform the best even when optimization over all subsets is taken into account. It happens for the simplest densities considered (case (i), cf. Fig. 2) where greedy MPVC performs most favorably. For the other case with only one nonzero coefficient (example (ii), cf. Fig. 3) its non-greedy counterpart is the best. The similar situation occurs in the misspecification case (example (iv)). However, for the most complex shapes of densities (example (iii), cf. Fig. 4) minimal p-value criterion mPVC was a clear winner. This case is clearly the most difficult among cases considered as accuracy percent falls below 0.4 and it is here where the improvement is most desirable. Note that in this case the gain of the winner over its BIC competitor (greedy or non-greedy) was more pronounced in the terms identification of the correct model selection than for accuracy of estimator measured by MISE. This happened especially for the larger values of the considered parameters. Thus it seems that the main advantage of the introduced methods is in terms of increase of probability of model specification rather than increase of estimation accuracy of density estimator measured by MISE.

Figure 6 shows the probability of correct ordering in the fist step of greedy methods for model (i) as a function of \(m\). In this case in order to reduce computational cost of simulations the sample size was taken as \(n=100\). The plotted curves indicate that probability of correct ordering depends heavily on the size of the list of models, however, once the correct order is established it is relatively unlikely to commit errors in the second step using p-value based methods or BIC. This underlines the importance of choosing a small subfamily of models before optimizing the criterion.

Fig. 6
figure 6

Estimated probability of correct ordering of variables in the first step of greedy methods (dashed line) compared to percentages of correct model selections for these methods (solid lines) for data pertaining to \(f_\theta (x)=c(\theta )\exp \{\theta _1b_1(x)\}\) with \(\theta _1=0.5\)

Full size image

We also recorded the cases when a supermodel, that is a subset \(\underline{i}\supset \underline{t}\) instead of \(\underline{t}\), is selected. It turns out that greedy methods in general are more conservative than their full-search counterparts, i.e. much more prone to choosing supermodel. Moreover, mPVC is much more conservative than MPVC; for the first method in some cases fraction of supermodels chosen is around 30\(\,\%\), whereas in the case of MPVC it is always below 3\(\,\%\). This is possibly due to penalty \(a_n\) which equals 0 for mPVC.

Finally, note that in all the cases considered one of the proposed method performed better than its BIC-like competitor. The natural question being a topic of current research is whether some combined version of p-value based criteria would exhibit better performance overall.