Abstract
We study pillage games (Jordan in J Econ Theory 131(1):26–44, 2006), which model unstructured power contests. To enable empirical tests of pillage game theory, we relax a symmetry assumption that agents’ intrinsic contributions to a coalition’s power is identical. We characterise the core for all n. In the three-agent game: (i) only eight configurations are possible for the core, which contains at most six allocations; (ii) for each core configuration, the stable set is either unique or fails to exist; (iii) the linear power function creates a tension between a stable set’s existence and the interiority of its allocations, so that only special cases contain strictly interior allocations. Our analysis suggests that non-linear power functions may offer better empirical tests of pillage game theory.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We study allocation of resources in unstructured power contests. The underlying model is that of a pillage game (Jordan 2006) in which an aggregate wealth endowment is split among agents, who can form coalitions. A power function maps every coalition and its wealth to a real number. A more powerful coalition can non-consensually ‘pillage’ the resources of a less powerful coalition. As a pillage game’s power function completely encodes its dominance relation, this corresponds to the new allocation dominating the original one. The power function is assumed to be monotonic, so that coalitions become more powerful as they gain members, or gain resources.
A typical game-theoretic solution describes allocations of wealth (analogous to imputations in more general coalitional games) corresponding to the core (which may be empty), or a von Neumann-Morgenstern stable set (which may not exist). The core is appealing as the set of undominated allocations. As farsighted agents may recognise that a pillage operation that benefits them may allow another that does not (Harsanyi 1974), Jordan (2006) proved that, when agents shared common expectation functions over dominance paths, stable sets are equivalent to farsighted cores.Footnote 1
The existing literature on pillage games almost exclusively considers symmetric power functions, in which the identity of the agents in a coalition does not matter. We consider the simplest generalisation of this model: each agent has an intrinsic ‘strength’ that is added to its wealth endowment; the power of a coalition is the sum of the wealth and the intrinsic strengthes of its members. We term such games asymmetric majority pillage games (AMPG); they are parameterised by a number of players, and a vector of intrinsic strengths.
In the classic majority game (in characteristic function form), one allocation dominates another if and only if it is preferred by a strictly larger coalition. In the majority pillage game (Jordan and Obadia 2015), an allocation may also dominate another if the coalitions favouring and opposing it are the same size, as long as the former holds more resources. The AMPG studied here generalise the majority pillage game, both by allowing asymmetric intrinsic strength and by allowing the non-empty core case (in which resource holdings can dominate intrinsic strength).
As symmetry is the exception in practice, we relax it to aid both applications and tests of the theory. We are particularly interested in when stable sets exist, and when they allow interior allocations, so that no agent is left without resources.
We believe that pillage games are of interest for three reasons. First, we see unstructured interactions, without binding game forms, as pervasive: “procedures are not really all that relevant; that it is the possibilities for coalition forming, promising and threatening that are decisive, rather than whose turn it is to speak” (Aumann 1985). Second, we believe that resources often convey both utility and power. Third, we see the costless, predictable nature of pillage as consistent with sophisticated, well-informed agents, even in the presence of strong institutions: for example, by convention, losers of democratic elections publicly concede, signalling to their supporters not to engage in costly civil wars that they will lose.Footnote 2
Pillage games’ stable sets can yield sharp predictions: they are small (Jordan 2006; Kerber and Rowat 2011; Saxton 2011; Rowat and Kerber 2014; Beardon and Rowat 2013) and unicity seems to be the norm (Jordan 2006; Rowat and Kerber 2014).Footnote 3
Section 2 introduces pillage games. Theorem 1 establishes that only two types of allocations may belong to the core of AMPGs for any \(n \ge 3\), and the conditions under which they do. For the \( n=3 \) case, Corollary 1 identifies the corresponding strength vector for each of the eight possible cores.
The rest of the paper focuses on the three-agent AMPG. Thorough \(n=3\) analyses have typically been important steps towards developing more general analyses in the coalitional literature.Footnote 4 This is partly pragmatic:
Finding stable sets involves a new tour de force of mathematical reasoning for each game or class of games that is considered. ... there is no theory, no tools, certainly no algorithm. (Aumann 1985)
Of course, \(n=3\) is not just a useful stepping stone, but an appropriate model of some situations—from the geopolitical (e.g. the Chinese Three Kingdoms period of 220–280 AD) to the microeconomic (e.g. (Straffin 1993; McDonald 1977) on sharing communications satellites, or Hellman and Wasserman (2011) on splitting founders’ equity).
Section 3 analyses stable sets when the core is empty. Theorem 2 presents necessary and sufficient conditions for the existence of a unique stable set comprising three allocations, each splitting the resource equally between two of the agents. Perhaps surprisingly, this is identical to the stable set in the symmetric special case: power struggles over these 50/50 allocations pit one agent (without resources) against another agent (with half the resources); as long as the former’s intrinsic strength is not too much greater than the latter’s, the 50/50 split is defensible; otherwise, the stable set fails to exist. Thus, power asymmetries do not distort the stable set: they strain it to the point at which it breaks.
Section 4 analyses stable sets for non-empty cores. Although the geometry is more complicated, we may proceed algorithmically: first, if a stable set exists, the core must belong to it; second, allocations dominated by the core cannot; third, the remaining allocations—typically linear loci within which one agent is as powerful as the other two—can be analysed using techniques from the empty core case. Corollary 4 presents a general non-existence result; the remainder of the section presents results for stable sets under each of the eight possible cores. It finds a tension between a stable set’s existence and the possibility of interior allocations: as candidate interior allocations balance agents’ powers, they cannot dominate their neighbouring allocations; domination of the other allocations on the locus typically requires including an extremal allocation, which lies on the simplex’s edge; when agents have positive intrinsic strength, these extremal allocations are themselves dominated by core allocations, preventing existence.
Section 5 concludes the paper. Its overarching findings are: non-existence of stable sets is pervasive in \(n=3\) AMPG; strictly interior allocations only occur in special cases—including both new configurations and the symmetric case already known to the literature (Jordan 2006, Theorem 3.3); when stable sets do exist, they are unique. The link between the linear power function used here and the non-existence mechanism suggests that non-linear power functions may by better candidates for empirical work.
2 Pillage games
Let \(I \equiv \left\{ 1, \ldots , n \right\} \) be a finite set of agents, indexed by i. An allocation, \(\varvec{x}\), is a division of a unit resource among them, so that the feasible set of allocations is
Let \(\subset \) denote a proper set inclusion, and use \(\subseteq \) to allow the possibility of equality. Jordan (2006) defined a power function over subsets of agents and allocations, so that \(\pi : 2^I \times X \rightarrow {\mathbb {R}}\) satisfies:
-
(WC)
if \(C\subset C^{\prime }\subseteq I\), then \(\pi \left( C^{\prime },\varvec{x}\right) \ge \pi \left( C,\varvec{x}\right) ~\)for all\(~ \varvec{x}\in X\);
-
(WR)
if \(y_{i}\ge x_{i}\) for all \(i\in C\subseteq I\), then \(\pi \left( C,\varvec{y}\right) \ge \pi \left( C,\varvec{x}\right) \); and
-
(SR)
if \(\varnothing \ne C\subseteq I\) and \(y_{i}>x_{i}\) for all \(i\in C\), then \(\pi \left( C,\varvec{y}\right) >\pi \left( C,\varvec{x} \right) \).
Simply, the axioms imply that more is better: by axiom WC, adding agents makes a coalition more powerful; by axiom WR, weakly adding resources makes a coalition weakly more powerful; axiom SR is a strict version of axiom WR.
The class of power functions considered here is
where \(C\subseteq I\) is a non-empty coalition of agents, \(\varvec{x}\in X\) and \( v_{i}\in {\mathbb {R}}_{+}\) allows agents’ intrinsic strengths to differ. Power function (2) provides one of the simplest possible specifications of an asymmetric pillage game, introducing one parameter per agent. Jordan’s wealth-is-power function is a symmetric special case of this in which \(v_{i}=0\) for all i; the majority pillage game analysed in Jordan and Obadia (2015) sets \(v_{i}>1\) for all i.
We index agents in two different ways. First, to merely label them, we use the generic \(i,j,k,\ldots \) or \(1,2,3,\ldots \). Second, to order agents by their intrinsic contributions to their coalitions’ power, we use a, b and c such that
If we display an allocation’s constituent coordinates, we do so in the natural order implied by our choice of index, whether \(\varvec{x}=\left( x_{1},x_{2},x_{3}\right) \) or \(\varvec{x}=\left( x_{a},x_{b},x_{c}\right) \). This does not imply that, for example, \(x_{a}=x_{1}\).
An allocation \(\varvec{y}\) dominates an allocation \(\varvec{x}\), written  , iff
, iff
where \(W \equiv \left\{ i \left| y_i > x_i \right. \right\} \) and \(L \equiv \left\{ i \left| x_i > y_i \right. \right\} \) are called the win set and lose set, respectively. Thus, allocation \(\varvec{y}\) dominates allocation \(\varvec{x}\) if and only if the set of agents who benefit in a re-allocation from \(\varvec{x}\) to \(\varvec{y}\) are more powerful at the original allocation \(\varvec{x}\) than is the set of agents who lose from that re-allocation.Footnote 5
By the strict inequality, domination is irreflexive; by axiom SR, it is asymmetric; as in the general case (von Neumann and Morgenstern 1953), dominance is not generally transitive.
For \(Y \subset X\), let

be the dominion of Y, the set of allocations dominated by an allocation in Y.
This paper studies asymmetric majority pillage games:
Definition 1
An asymmetric majority pillage game (AMPG) is a profile \(\langle I, X, \left( v_i \right) _{i \in I},\pi \rangle \), where \(I = \left\{ 1, 2, \ldots , n \right\} \), X is defined by Eq. (1), \(\left( v_{i}\right) _{i\in I}\) are non-negative reals, and the power function \(\pi \) is defined by (2).
For tractability’s sake, we mainly consider the \(n=3\) case. Let 3-AMPG denote an AMPG with \(n=3\).
2.1 The core
The core is the set of undominated allocations, \(K \equiv X \backslash D \left( X \right) \). To characterise it, define two types of allocation:
Definition 2
(Jordan 2006) Let \(\varvec{t}^i \in X\) be a tyrannical allocation such that \(t^i_i = 1\) and \(t^i_j = 0\) for all \(j \ne i \in I\).
Let \(\varvec{b}^{ij}\in X\) be a bilaterally balanced allocation, so that \( \pi \left( \left\{ i\right\} ,\varvec{b}^{ij}\right) =\pi \left( \left\{ j\right\} ,\varvec{b}^{ij}\right) \) with \(b_{i}^{ij},b_{j}^{ij}>0\) for distinct i, j and \(b_{k}^{ij}=0\) for any other agents k.
Note that a tyrannical allocation may be a limit point of a sequence of bilaterally balanced allocations, but an allocation cannot be both tyrannical and bilaterally balanced.
Thus, given power function (2), we have:
Then:
Theorem 1
In the AMPG with \(n \ge 3\), the core can contain no allocations other than the tyrannical \(\varvec{t}^i\) and the bilaterally balanced \(\varvec{b}^{ij}\), for all distinct i and j:
-
1.
\(\varvec{t}^{i}\) belongs to the core iff \(v_{i}\ge \sum _{j\in I\backslash \left\{ i\right\} }v_{j}-1\); and
-
2.
\(\varvec{b}^{ij}\) belongs to the core iff \(v_k = 0\) for all k distinct from i, j, and \(v_i - v_j \in \left( - 1, 1 \right) \).
Proof
First, consider the allocations that assign the resource exclusively to a single agent. These are, by definition, the tyrannical \(\varvec{t}^i\). The theorem’s first condition is equivalent to the non-existence of \(\varvec{x} \in X \backslash \left\{ \varvec{t}^i \right\} \) such that  .
.
Now consider the allocations that split the resource between two agents, say i and j, so that \(x_k = 0\) for all other agents k. For these agents to defend their holdings against the other two, the following inequalities must be satisfied:
Combining these requires
As \(x_i, x_j, v_i\) and \(v_j\) are non-negative, this forces \(\sum _{k \in I \backslash \left\{ j, k \right\} } v_k = 0\), forcing all individual \(v_k = 0\). Thus, \(x_i + v_i = x_j + v_j\) which, with the unit endowment constraint, yields the \(\varvec{b}^{ij}\). Constraining \(b^{ij}_i\) and \(b^{ij}_j\) to lie in \(\left( 0, 1 \right) \) yields the interval condition for \(v_j\) in the statement of the theorem.
Finally consider allocations that split the resource between three agents, so that \(x_i, x_j, x_k > 0\). By the above reasoning, one of the necessary conditions is
This requires \(x_k = 0\), a contradiction. The possibility of core allocations with more than three agents holding resources is similarly ruled out. \(\square \)
As a \(\varvec{b}^{ij}\) can belong to the core only if both \(\varvec{t}^i\) and \(\varvec{t} ^j\) do, the following correspondences between cores and parameters holds for \(n = 3\):
Corollary 1
-
1.
\(K=\varnothing :\)
$$\begin{aligned} -v_{a}+v_{b}+v_{c}>1. \end{aligned}$$(6) -
2.
\(K=\left\{ \varvec{t}^{a}\right\} :\)
$$\begin{aligned} -v_{a}+v_{b}+v_{c}\le 1,-v_{a}+v_{b}-v_{c}<-1. \end{aligned}$$(7) -
3.
\(K=\left\{ \varvec{t}^{a},\varvec{t}^{b}\right\} :\)
$$\begin{aligned}&\left( -v_{a}+v_{b}-v_{c}\ge -1\right) ,\left( 0<v_{c}<v_{a}+v_{b}-1\right) ;\text { or} \end{aligned}$$(8)$$\begin{aligned}&v_{c}=0<v_{b}=v_{a}-1. \end{aligned}$$(9) -
4.
\(K=\left\{ \varvec{t}^{a},\varvec{t}^{b},\varvec{b}^{ab}\right\} :\)
$$\begin{aligned} v_{c}=0,v_{b}\ge v_{a}-1,v_{b}>1-v_{a}. \end{aligned}$$(10) -
5.
\(K=\left\{ \varvec{t}^{a},\varvec{t}^{b},\varvec{t}^{c}\right\} :\)
$$\begin{aligned} v_{c}&\ge v_{a}+v_{b}-1,v_{c}>0;or \end{aligned}$$(11)$$\begin{aligned} v_{a}&=1>v_{b}=v_{c}=0. \end{aligned}$$(12) -
6.
\(K=\left\{ \varvec{t}^{a},\varvec{t}^{b},\varvec{t}^{c},\varvec{b} ^{ab}\right\} :\)
$$\begin{aligned} v_{c}=0<v_{b}\le 1-v_{a}. \end{aligned}$$(13) -
7.
\(K=\left\{ \varvec{t}^{a},\varvec{t}^{b},\varvec{t}^{c},\varvec{b}^{ab}, \varvec{b}^{ac}\right\} :\)
$$\begin{aligned} 0=v_{c}=v_{b}<v_{a}<1. \end{aligned}$$(14) -
8.
\(K=\left\{ \varvec{t}^{a},\varvec{t}^{b},\varvec{t}^{c},\varvec{b}^{ab}, \varvec{b}^{ac},\varvec{b}^{bc}\right\} :\)
$$\begin{aligned} v_{c}=v_{b}=v_{a}=0. \end{aligned}$$(15)
The corollary follows from the theorem’s requirement that each agent holding resources must be at least as powerful as the other two combined: the cases instantiate the theorem’s conditions for the inclusion or exclusion of the \( \varvec{t}^i\) and \(\varvec{b}^{ij}\).
Empty core condition (6) thus generalises the symmetric condition in Jordan (2006, Proposition 4.2), which was restricted to \(v > 1\).
2.2 Stable sets
The stable set is the original von Neumann and Morgenstern (1953) solution concept, initially just called the ‘solution’. Unlike the core, which is defined pointwise, it is defined setwise, making it harder to compute. Intuitively, a set of allocations is stable if they satisfy internal stability (no allocation in a stable set dominates another) and external stability (every allocation outside a stable set is dominated by at least one allocation in a stable set).
A set of allocations, \(S \subseteq X\), is a stable set iff it satisfies internal stability,
and external stability,
The conditions combine to yield \(S \equiv X \backslash D \left( S \right) \).
While stable sets may not exist, or may be non-unique, the core necessarily belongs to any stable set; when the core also satisfies external stability, it is the unique stable set. Jordan (2006) proved that a pillage game’s stable set has the property of being the set of allocations that are undominated given a consistent set of expectations about what subsequent domination operation would be attempted following the initial one.
The rest of this paper analyses stable sets in the 3-AMPG, seeking to decide existence and—when they do exist—to derive them.
3 The empty core
The analysis in this section extends that in Jordan and Obadia (Jordan and Obadia (2015), §3) to the asymmetric case. The core is empty when inequality (6) holds.
The following lemma generalises Jordan and Obadia (2015, Lemma 3.4) beyond its symmetric case of \(v_1 = v_2 = v_3 > 1\):
Lemma 1
Suppose that S is internally stable in a 3-AMPG with an empty core. If \(\varvec{x}\) and \(\varvec{x}^{\prime }\) belong to S, then there exists an \(i\in I\) such that \(x_{i}=x_{i}^{\prime }\). Further, \( x_{k}+v_{k}\le x_{j}+v_{j}\) and \(x_{j}^{\prime }+v_{j}\le x_{k}^{\prime }+v_{k}\).
Proof
Assume, contrary to the lemma, that there exist \(\varvec{x}, \varvec{x}' \in S\) such that \(x_i \ne x_i'\) for all \(i \in I\). Then, without loss of generality, we generically have that \(x_i > x_i', x_j < x_j'\) and \(x_k < x_k'\). This yields a contradiction:
-
1.
the empty core property requires that \(x_i + v_i < 1 - x_i + v_j + v_k\) for all \(\varvec{x} \in X\) and distinct \(i,j,k \in I\);
-
2.
internal stability requires that
 , so that \(x_i + v_i \ge 1 - x_i + v_j + v_k\).
, so that \(x_i + v_i \ge 1 - x_i + v_j + v_k\).
Thus, for two internally stable allocations there must exist at least one agent for whom \(x_i = x_i'\). When these allocations are distinct, \(x_j - x_j' = - \left( x_k - x_k' \right) \ne 0\), so that \(W \equiv \left\{ i \in I \left| x_i > x_i' \right. \right\} \) and \(L \equiv \left\{ i \in I \left| x_i < x_i' \right. \right\} \) are singletons that exclude i. \(\square \)
Intuitively, the empty core ensures that the loci of allocations at which one agent is just as powerful as the other two lie outside the set of feasible allocations, X. In internally stable sets all pairs of allocations must lie on opposite sides of such balance of power loci. Thus, given an empty core, an internally stable set cannot contain two allocations that pit a given agent against the other two. Along the relevant balance of power loci, then, at least one agent must be indifferent.
Now extend Obadia’s Lemma 3.5 to the asymmetric case:
Lemma 2
Suppose that S is internally stable in a 3-AMPG with an empty core. Then S has no more than three elements.
The proof establishes that, under the lemma’s conditions, an internally stable set cannot contain four allocations, which also precludes it having more than four:
Proof
Consider three points, \(\varvec{x}, \varvec{y}\), \(\varvec{z}\), in an internally stable set S. By Lemma 1, the line running between any two of these must be parallel to the edge of the simplex X. Without loss of generality, there are two possible configurations:
-
1.
\(\varvec{x}, \varvec{y}\), and \(\varvec{z}\), are collinear, as depicted in Fig. 1, with (wlog) \(x_1 = y_1 = z_1\), \(x_2> y_2 > z_2\), and \(x_3< y_3 <z_3\).
In this case, as \(\pi \left( \left\{ 2 \right\} , \varvec{x} \right)> \pi \left( \left\{ 2 \right\} , \varvec{y} \right) > \pi \left( \left\{ 2 \right\} , \varvec{z} \right) \) and \(\pi \left( \left\{ 3 \right\} , \varvec{x} \right)< \pi \left( \left\{ 3 \right\} , \varvec{y} \right) < \pi \left( \left\{ 3 \right\} , \varvec{z} \right) \) hold, internal stability requires that \(\pi \left( \left\{ 2 \right\} , \varvec{y} \right) = \pi \left( \left\{ 3 \right\} , \varvec{y}\right) \). Assume, on the contrary, there is another distinct \(\varvec{w} \in S\). Then there are two cases to consider:
-
(a)
\(w_1 = x_1\). Then we have the following four possibilities, each leading to a contradiction: (i). \(w_2 > x_2\), so that
 holds by \(v_{2}+x_{2}>v_{3}+x_{3}\); (ii). \(x_2> w_2 > y_2\), so that
holds by \(v_{2}+x_{2}>v_{3}+x_{3}\); (ii). \(x_2> w_2 > y_2\), so that 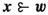 ; (iii). \(y_2> w_2 > z_2\), so that
; (iii). \(y_2> w_2 > z_2\), so that  ; and (iv). \(z_2 > w_2\), so that
; and (iv). \(z_2 > w_2\), so that  .
.Thus, the requirement that S is internally stable forces \(w_1 \ne x_1\) for \(\varvec{w} \in S\).
-
(b)
\(w_1 \ne x_1\). By Lemma 1, \(\varvec{w}\) and \(\varvec{x}\) share a coordinate other than \(i=1\), say \(w_{2}=x_{2}\), without loss of generality. Likewise, \(\varvec{w}\) and \(\varvec{y}\) share a coordinate other than \(i=1,2\), which implies \(w_{3}=y_{3}\). Then, to share a coordinate between \(\varvec{w}\) and \(\varvec{z}\), either \(w_{2}=z_{2} \) or \(w_{3}=z_{3}\) must hold, as \(w_{1}=z_{1}\) is impossible by \(x_{1}=z_{1}\). However, \(w_{2}=z_{2}\) implies \(x_{2}=z_{2}\), which together with \(x_{1}=z_{1}\) imply that \(\varvec{x}=\varvec{z}\), a contradiction. The same reasoning is applied for \(w_{3}=z_{3}\). Thus, there is no distinct \(\varvec{w}\) in S whenever \(\varvec{x}, \varvec{y}\), and \(\varvec{z}\), are collinear.
-
(a)
-
2.
\(\varvec{x}\), \(\varvec{y}\), and \(\varvec{z}\), are triangular, as depicted in Fig. 2, with \(x_{1}=y_{1}\), \(y_{2}=z_{2}\), and \(z_{3}=x_{3}\).
Again, assume that there is another distinct \(\varvec{w}\in S\). Then:
-
(a)
\(\varvec{w}\) cannot lie on any of the three lines passing through any two of \(\varvec{x}\), \(\varvec{y}\), and \(\varvec{z}\). Assume, wlog, that \(\varvec{w}\) was collinear with \(\varvec{y}\) and \(\varvec{z}\); this returns us to the collinear case, above, but with \(\varvec{x}\) as the fourth allocation that necessarily violates internal stability.
-
(b)
it remains only to consider (wlog) \(w_{2}=x_{2}\), the dotted line passing through \(\varvec{x}\) in Fig. 2. By Lemma 1, there must be an agent \(i\ne 2\) such that \(w_{i}=y_{i}\). It cannot be \(i=1\) as that would force, by \(x_1 = y_1\), \(\varvec{w}=\varvec{x}\). This leaves \(w_3 = y_3\), the dotted line through \(\varvec{y}\) in Fig. 2. Finally, Lemma 1 forces \(w_{1}=z_{1}\). The equalities imply
$$\begin{aligned} w_1 + w_2 = z_1 + x_2 = 1 - w_3 = 1 - y_3 = y_1 + y_2 = x_1 + z_2. \end{aligned}$$By the second and final terms in the above, we may define
$$\begin{aligned} k \equiv x_1 - x_2 = z_1 - z_2. \end{aligned}$$As \(\varvec{x}\) and \(\varvec{z}\) are feasible,
$$\begin{aligned} x_1 + x_2 + x_3 + k = z_{1}+z_{2}+z_{3} + k \Rightarrow 2x_{1}+x_{3}=2z_{1}+z_{3}. \end{aligned}$$Since \(z_3 = x_3\), the last equation implies that \(x_1 = z_1\), which further implies \(\varvec{x} = \varvec{z}\) holds, a contradiction.
-
(a)
Having eliminated the possibility of four internally stable allocations, we may conclude that more than four are also impossible, proving the result. \(\square \)
Definition 3
Let \(\varvec{s}^{ij}\) be the allocation that splits the resource equally between agents i and j, so that \(s^{ij}_i = s^{ij}_j = \tfrac{1}{2}\).
Thus, unlike the \(\varvec{b}^{ij}\) previously defined, the \(\varvec{s}^{ij}\) need not balance power.
Then:
Lemma 3
Suppose that S is stable in a 3-AMPG with an empty core. Then \(S=\left\{ \varvec{s}^{12},\varvec{s}^{13},\varvec{s}^{23}\right\} \).
Proof
The largest possible S contains, by Lemma 2, three elements, \(\left\{ \varvec{x},\varvec{y},\varvec{z}\right\} \). Consider that possibility first.
By Lemma 1, there are again two possible configurations of three internally stable allocations:
-
1.
linear: Without loss of generality, let \(\bar{x}\equiv x_{1}=y_{1}=z_{1}\), \(x_{2}>y_{2}>z_{2}\), and \(x_{3}<y_{3}<z_{3}\), as depicted in Fig. 1. We resolve this case in two steps:
-
(a)
\(\varvec{x}=\left( \bar{x}, 1-\bar{x}, 0 \right) \) and \(\varvec{z} = \left( \bar{x}, 0, 1-\bar{x} \right) \). We first show that \(\varvec{x} = \left( \bar{x}, 1-\bar{x}, 0 \right) \). Suppose, on the contrary, that \(x_{3}>0\). Then, there exists \(\varvec{x}'\) with \(x_2 > x_2'\), \(x_3' < x_3\), and \(x_1' = \bar{x}\). By external stability, this \(\varvec{x}'\) must be dominated by one of \(\varvec{x},\varvec{y},\varvec{z}\). All three possibilities require the same conditions:
$$\begin{aligned} \pi \left( \left\{ 3 \right\} , \varvec{x}' \right)> \pi \left( \left\{ 2 \right\} , \varvec{x}' \right) \Leftrightarrow x_3' + v_3 > x_2' + v_2. \end{aligned}$$However, by internal stability,
 , which implies \(\pi \left( \left\{ 3\right\} , \varvec{x}\right) \le \pi \left( \left\{ 2\right\} ,\varvec{x} \right) \Leftrightarrow x_{3}+v_{3}\le x_{2}+v_{2}\), contradicting
, which implies \(\pi \left( \left\{ 3\right\} , \varvec{x}\right) \le \pi \left( \left\{ 2\right\} ,\varvec{x} \right) \Leftrightarrow x_{3}+v_{3}\le x_{2}+v_{2}\), contradicting  . Thus, \(x_3 = 0\); identical reasoning obtains \(z_2 = 0\).
. Thus, \(x_3 = 0\); identical reasoning obtains \(z_2 = 0\). -
(b)
\(\left\{ \varvec{x}, \varvec{y}, \varvec{z} \right\} \) cannot satisfy external stability. Consider \(\varvec{x}'' \equiv \frac{1}{2} \left( \varvec{y} + \varvec{z} \right) + \left( \varepsilon , 0, - \varepsilon \right) \in X\) for sufficiently small \(\varepsilon > 0\). None of \(\varvec{x},\varvec{y},\varvec{z}\) dominate \(\varvec{x}''\): (i).
 : dominance would require \(\pi \left( \left\{ 3 \right\} , \varvec{x}'' \right) > \pi \left( \left\{ 1, 2 \right\} , \varvec{x}'' \right) \), but Theorem 1’s empty core property implies that \(1 + v_3 < v_1 + v_2\), a contradiction by axiom SR. (ii).
: dominance would require \(\pi \left( \left\{ 3 \right\} , \varvec{x}'' \right) > \pi \left( \left\{ 1, 2 \right\} , \varvec{x}'' \right) \), but Theorem 1’s empty core property implies that \(1 + v_3 < v_1 + v_2\), a contradiction by axiom SR. (ii).  and
and  : in either case, domination would require \(\pi \left( \left\{ 2 \right\} , \varvec{x}'' \right) > \pi \left( \left\{ 1, 3 \right\} , \varvec{x}'' \right) \). However, again, by Theorem 1’s empty core property with, \(1 + v_2 < v_1 + v_3\) holds, contradicting dominance.
: in either case, domination would require \(\pi \left( \left\{ 2 \right\} , \varvec{x}'' \right) > \pi \left( \left\{ 1, 3 \right\} , \varvec{x}'' \right) \). However, again, by Theorem 1’s empty core property with, \(1 + v_2 < v_1 + v_3\) holds, contradicting dominance.
-
(a)
-
2.
triangular: We resolve this case in three steps:
-
(a)
each of \(\varvec{x}, \varvec{y}\) and \(\varvec{z}\) must set one component to zero. Suppose not. Then \(\varvec{x} > \varvec{0}\) must hold with \(x_1 = y_1\), \(y_2 = z_2\), and \(z_3 = x_3\), as in Fig. 2. Then, consider \(\varvec{x}''' \equiv \varvec{x} + \left( \varepsilon , -2 \varepsilon , \varepsilon \right) \in X\) for sufficiently small \(\varepsilon > 0\). None of \(\varvec{x}, \varvec{y}, \varvec{z}\) can dominate \(\varvec{x}'''\): (i).
 : dominance would require \(\pi \left( \left\{ 2 \right\} , \varvec{x}''' \right) > \pi \left( \left\{ 1, 3 \right\} , \varvec{x}''' \right) \). Again, this contradicts Theorem 1’s empty core property, \(1 + v_2 < v_1 + v_3\). (ii).
: dominance would require \(\pi \left( \left\{ 2 \right\} , \varvec{x}''' \right) > \pi \left( \left\{ 1, 3 \right\} , \varvec{x}''' \right) \). Again, this contradicts Theorem 1’s empty core property, \(1 + v_2 < v_1 + v_3\). (ii).  and
and  : in either case, domination would require \(W=\left\{ 2 \right\} \) and \(L = \left\{ 1, 3 \right\} \) if \(x_2 < y_2 = z_2\). Thus, again by the empty core property with Theorem 1, neither \(\varvec{y}\) nor \(\varvec{z}\) can dominate \(\varvec{x}'''\) in this case. Now consider the remaining case, \(x_2 > y_2 = z_2\). It implies \(x_2''' > y_2 = z_2\) by choosing \(\varepsilon > 0\) sufficiently small. Then,
: in either case, domination would require \(W=\left\{ 2 \right\} \) and \(L = \left\{ 1, 3 \right\} \) if \(x_2 < y_2 = z_2\). Thus, again by the empty core property with Theorem 1, neither \(\varvec{y}\) nor \(\varvec{z}\) can dominate \(\varvec{x}'''\) in this case. Now consider the remaining case, \(x_2 > y_2 = z_2\). It implies \(x_2''' > y_2 = z_2\) by choosing \(\varepsilon > 0\) sufficiently small. Then,  is equivalent to \(\pi \left( \left\{ 3 \right\} , \varvec{x}''' \right) > \pi \left( \left\{ 1, 2 \right\} , \varvec{x}''' \right) \) with \(W = \left\{ 3 \right\} \) and \(L = \left\{ 1, 2 \right\} \), while
is equivalent to \(\pi \left( \left\{ 3 \right\} , \varvec{x}''' \right) > \pi \left( \left\{ 1, 2 \right\} , \varvec{x}''' \right) \) with \(W = \left\{ 3 \right\} \) and \(L = \left\{ 1, 2 \right\} \), while  is equivalent to \(\pi \left( \left\{ 1 \right\} , \varvec{x}''' \right) > \pi \left( \left\{ 2, 3 \right\} , \varvec{x}''' \right) \) with \(W = \left\{ 1 \right\} \) and \(L = \left\{ 2, 3 \right\} \). Either case is impossible by the empty core property with Theorem 1.
is equivalent to \(\pi \left( \left\{ 1 \right\} , \varvec{x}''' \right) > \pi \left( \left\{ 2, 3 \right\} , \varvec{x}''' \right) \) with \(W = \left\{ 1 \right\} \) and \(L = \left\{ 2, 3 \right\} \). Either case is impossible by the empty core property with Theorem 1.In summary, there exists \(\varvec{x}''' \in X\), undominated by any of \(\varvec{x}, \varvec{y}, \varvec{z}\), which contradicts the external stability of S.
-
(b)
\(S \subseteq \left\{ \varvec{s}^{12}, \varvec{s}^{13}, \varvec{s}^{23}\right\} \). By the previous step and Lemma 1, we only need to consider the following two possibilities:
-
(i).
\(\varvec{x} = \left( a, 0, 1-a \right) \), \(\varvec{y} = \left( a, 1-a, 0 \right) \), and \(\varvec{z} = \left( 0, a, 1-a \right) \).
-
(ii).
\(\varvec{x} = \varvec{t}^1\), \(\varvec{y} = \varvec{t}^2\), and \(\varvec{z} = \varvec{t}^3\).
The second case violates external stability: for any feasible \(\varvec{w} > \varvec{0}\) to be dominated by one of \(\varvec{t}^1, \varvec{t}^2\), and \(\varvec{t}^3\), it must be that \(\# W = 1\), \(\# L = 2\), and \(\pi \left( W, \varvec{w} \right) > \pi \left( L, \varvec{w} \right) \). However, by axiom SR, the last inequality is impossible by the empty core property.
For the first case, the resource constraint requires \(a = \tfrac{1}{2}\), so that \(\left\{ \varvec{x}, \varvec{y}, \varvec{z} \right\} = \left\{ \varvec{s}^{12}, \varvec{s}^{13}, \varvec{s}^{23} \right\} \).
-
(i).
-
(c)
\(S \supseteq \left\{ \varvec{s}^{12}, \varvec{s}^{13}, \varvec{s}^{23} \right\} \). Suppose, without loss of generality, \(\varvec{s}^{23} \notin S\). Then, consider \(\varvec{w} \equiv \tfrac{1}{2} \left( \varvec{s}^{12} + \varvec{s}^{13} \right) + \left( \varepsilon , 0, -\varepsilon \right) \in X\) for sufficiently small \(\varepsilon > 0\). By the reasoning developed in the external stability step of the linear case above, neither \(\varvec{s}^{12}\) nor \(\varvec{s}^{13}\) can dominate \(\varvec{w}\) due to Theorem 1’s empty core property.
-
(a)
\(\square \)
Intuitively, Lemma 1 allowed only linear or triangular three-element stable sets. Linear sets do not dominate some non-collinear allocations, violating external stability. In triangular sets, each allocation sets at least one term to zero: if not, they leave undominated more extremal allocations; the equal split configuration then also ensures that the allocations between stable elements are dominated.
The main result of this section generalises Jordan and Obadia (2015, Theorem 3.7) beyond the symmetric case:
Theorem 2
For a 3-AMPG with an empty core, \(v_{a}-v_{c}\le \tfrac{1 }{2}\) is necessary and sufficient for internal stability of \(S=\left\{ \varvec{s} ^{12},\varvec{s}^{13},\varvec{s}^{23}\right\} \). Empty core condition (6) suffices for the external stability of S, leaving it the unique stable set when it is internally stable.
Proof
By Lemma 3, the only candidate stable set is \(S = \left\{ \varvec{s}^{12}, \varvec{s}^{13}, \varvec{s}^{23} \right\} \).
Internal stability implies \(v_i \le \tfrac{1}{2} + v_j\) for all i and j. By inequality (3)’s ordering, this is equivalent to \(v_a \le \tfrac{1}{2} + v_c\), the lemma’s stated inequality. Now establish the other direction, that this inequality implies internal stability. By the resource monotonicity axioms, it must be that  : the agent with the greatest intrinsic strength (but no resources) cannot defeat that with the least intrinsic strength (but with half the resources); this is equivalent to the lemma’s inequality.
: the agent with the greatest intrinsic strength (but no resources) cannot defeat that with the least intrinsic strength (but with half the resources); this is equivalent to the lemma’s inequality.
By external stability, each \(\varvec{x} \in X \backslash S\) that is undominated by an \(\varvec{s} \in S\) implies that there are distinct j and k such that \(x_j, x_k < \tfrac{1}{2}\). By inequality (3), empty core inequality (6) implies that \(1 + v_i < v_j + v_k\) for agents j and k. As \(x_i \le 1\) and \(x_j, x_k \ge 0\), it follows that \(x_i + v_i < x_j + v_j + x_k + v_k\), so that  , establishing external stability. \(\square \)
, establishing external stability. \(\square \)
Perhaps surprisingly, the allocations in the stable set do not vary with \( v_i \) until the set ceases to exist. Intuitively, the empty core condition limits the relative strength of the intrinsically strongest agent. This prevents any single agent overpowering the other two for any allocation. As a result, the only power contests that must be considered are those between singleton coalitions. The theorem’s bound on relative power ensures that the intrinsically least powerful agent with half of the resource can defend itself against the most powerful with none of the resource. Thus, power need not be equally balanced at the \(\varvec{s}^{ij}\) allocations: while \(v_a\) increases relative to \(v_c\), there is no distortion in S until the asymmetry becomes too large, and internal stability fails completely.
4 The non-empty core
This section derives the stable sets (if any) corresponding to each of the possible non-empty cores identified in Corollary 1.
As the core must be included in any stable set, the proofs follow a similar pattern: the core seeds a candidate stable set; the allocations dominated by the core are excluded from consideration; over the remaining allocations (often just linear loci) it is as if the core is empty, allowing the use of techniques from the previous section. Of particular importance is the locus of allocations along which the most intrinsically powerful agent, a, is just as powerful as the other two, b, c; we prove that the existence of a stable set on X requires the existence of a stable set along that locus. When non-existence arises, it is for the same reason identified in the symmetric case in Rowat and Kerber (2014): allocations on these loci are only dominated by more extreme ones; thus, external stability requires including the most extreme allocations in a stable set; when these extreme allocations are themselves dominated by a core allocation, existence fails.
Define the balance of power locus for agent i to be:
The following lemma helps establish the result that existence of a stable set on X requires the existence of a stable set on non-empty balance of power loci:
Lemma 4
Consider a 3-AMPG with non-empty core. Then, for each \(i\in I \) such that \(B\left( i\right) \ne \varnothing \), \(\varvec{x}\in B\left( i\right) \Rightarrow \not \exists \varvec{y}\in X\backslash B\left( i\right) \) such that \(y_{i}<x_{i}\) and  .
.
Proof
As \(y_i < x_i\), agent i would oppose  . By definition, \(\varvec{x} \in B \left( i \right) \) implies that agent i on its own is as strong as agents j and k together. By axiom WC, this is the most powerful coalition that can oppose i, concluding the proof. \(\square \)
. By definition, \(\varvec{x} \in B \left( i \right) \) implies that agent i on its own is as strong as agents j and k together. By axiom WC, this is the most powerful coalition that can oppose i, concluding the proof. \(\square \)
This helps us decompose the search for stable sets: for all non-empty \(B \left( i \right) \), if a stable set exists, its intersection with \(B \left( i \right) \) must be a stable set on \(B \left( i \right) \):
Corollary 2
In a 3-AMPG with a non-empty core, if a stable set S exists in X, then \(S\cap B\left( i\right) \ne \varnothing \) and \(D\left( S\cap B\left( i\right) \right) \supseteq B\left( i\right) \backslash S\) hold for each \(i\in I\) with \(B\left( i\right) \ne \varnothing \).
Proof
For external stability to hold, each \(\varvec{x} \in B \left( i \right) \) must either belong to a stable set S or be dominated by an allocation in S. We will show that if the latter case applies, then that allocation in S also belongs to \(B \left( i \right) \).
If \(x_i = 1\) for \(\varvec{x} \in B \left( i \right) \), this implies \(\varvec{x} = \varvec{t}^i\). As \(\varvec{x} = \varvec{t}^i \in B \left( i \right) \), \(v_i + 1 = v_j + v_k\) holds, which implies by Theorem 1, \(\varvec{t}^i \in K\). Thus, \(\varvec{x} \in S\) holds.
If \(x_i \in \left[ 0, 1 \right) \) for \(\varvec{x} \in B \left( i \right) \), then consider the following three subcases:
-
1.
Let \(\varvec{z} \in X\) be such that \(z_i > x_i\). By \(\varvec{x} \in B \left( i \right) \) and axiom SR, \(\pi \left( \left\{ i \right\} , \varvec{z} \right) > \pi \left( \left\{ j, k \right\} , \varvec{z} \right) \), which implies that
 . Moreover, the last strict inequality implies that \(1 + v_i > v_j + v_k\), and thus \(\varvec{t}^i \in K \subseteq S\) by Theorem 1. Therefore, by the internal stability condition, \(\varvec{z}\notin S\) holds. Therefore, \(\varvec{z}\) cannot be used to show that \(\varvec{x} \notin S\).
. Moreover, the last strict inequality implies that \(1 + v_i > v_j + v_k\), and thus \(\varvec{t}^i \in K \subseteq S\) by Theorem 1. Therefore, by the internal stability condition, \(\varvec{z}\notin S\) holds. Therefore, \(\varvec{z}\) cannot be used to show that \(\varvec{x} \notin S\). -
2.
Let \(\varvec{y} \in X\) be such that \(y_{i}<x_{i}\). By Lemma 4,
 . Again, \(\varvec{y}\) cannot be used to show that \(\varvec{x}\notin S\).
. Again, \(\varvec{y}\) cannot be used to show that \(\varvec{x}\notin S\). -
3.
By the previous two subcases, if \(\varvec{x} \notin S\), then there must exist \(\varvec{x}' \in S\) such that both \(x_i' =x_i\) and
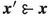 hold. By definition, \(\varvec{x}' \in B\left( i \right) \).
hold. By definition, \(\varvec{x}' \in B\left( i \right) \).
Thus, for each \(i \in I\) with \(B \left( i \right) \ne \varnothing \), \(S \cap B \left( i \right) \ne \varnothing \) and \(D \left( S \cap B \left( i \right) \right) \supseteq B \left( i \right) \backslash S\) hold. \(\square \)
Some elements in the \(B \left( i \right) \) play an important role in determining whether stable sets exist. First:
Define \(\bar{\varvec{\beta }}^i\) as the allocation on \(B \left( i \right) \) that balances the power of j and k, so that \(\bar{\beta }^i_j + v_j = \bar{ \beta }^i_k + v_k\):
where
Assuming \(v_j \ge v_k\) without loss of generality, it follows that
By definition,
Corollary 3
In a 3-AMPG with a non-empty core, let a stable set S exist in X. Then,
Moreover,
Before proving the Corollary, we provide some background for the non-existence mechanism (q.v. also Rowat and Kerber (2014)):
Definition 4
The dominance operator,  , is a strict total order on a set of allocations, A, iff, for any \(\varvec{x}, \varvec{y}, \varvec{z} \in A\) the following hold:
, is a strict total order on a set of allocations, A, iff, for any \(\varvec{x}, \varvec{y}, \varvec{z} \in A\) the following hold:
-
1.
trichotomy: exactly one of \(\varvec{x} = \varvec{y}\),
 and
and  holds; and
holds; and -
2.
transitivity:
 implies that
implies that  .
.
This is also called a complete ordering (von Neumann and Morgenstern 1953, §65.3.1). For concision’s sake, we adopt their terminology.
Before applying these concepts, first define:
Definition 5
Given \(B \left( i \right) \ne \varnothing \) with \(i, j, k \in I\) such that \( v_j \ge v_k\), let
Thus, whether or not \(\bar{\varvec{\beta }}^i\in X\), \(B\left( i \right) = \left[ \varvec{e}_j^i, \varvec{e}_k^i \right] \) holds whenever \(B \left( i \right) \ne \varnothing \).
Lemma 5
In a 3-AMPG, the dominance operator  completely orders the locus of allocations over the subsets of X specified below:
completely orders the locus of allocations over the subsets of X specified below:
-
1.
for \(B \left( a \right) \ne \varnothing \): \(\left[ \varvec{e}_b^a, \bar{ \varvec{\beta }}^a \right) \bigcup \left( \bar{\varvec{\beta }}^a, \varvec{e}_c^a \right] \) if \(\bar{\varvec{\beta }}^a \in X\), and \(\left[ \varvec{e}_b^a, \varvec{e}_c^a \right] \) otherwise;
-
2.
for \(B \left( b \right) \ne \varnothing \): \(\left[ \varvec{e}_a^b, \bar{ \varvec{\beta }}^b \right) \bigcup \left( \bar{\varvec{\beta }}^b, \varvec{e}_c^b \right] \) if \(\bar{\varvec{\beta }}^b \in X\), and \(\left[ \varvec{e}_a^b,\varvec{e}_c^b\right] \) otherwise;
-
3.
for \(B\left( c\right) \ne \varnothing \): \(\left[ \varvec{e}_a^c,\bar{ \varvec{\beta }}^c \right) \bigcup \left( \bar{\varvec{\beta }}^c, \varvec{e}_b^c\right] \) if \(\bar{\varvec{\beta }}^c\in X\), and \(\left[ \varvec{e}_a^c,\varvec{e}_b^c\right] \) otherwise.
Proof
Let \(B\left( a\right) \ne \varnothing \) and suppose that \(\bar{\varvec{\beta }}^a \in X\).
Consider \(\varvec{x},\varvec{y},\varvec{z}\in \left[ \varvec{e}_b^a, \bar{\varvec{\beta }}^a \right) \). Then, as \(\varvec{x},\varvec{y},\varvec{z}\in B\left( a\right) \), \(x_a = y_a = z_a = \beta _a^a\). Thus, if \(x_b=y_b\), then by the unit endowment, \(\varvec{x} = \varvec{y}\) holds. If \(x_b > y_b\), then since \(\bar{\beta }_b^a < x_b, y_b \le 1-\beta _a^a\) over \(\left[ \varvec{e}_b^a, \bar{\varvec{\beta }}^a \right) \), it follows that \(y_b+v_b>y_c+v_c\), so that  . This satisfies trichotomy over \(\left[ \varvec{e}_b^a, \bar{\varvec{\beta }}^a \right) \). As dominance on this locus is equivalent to \(x_b > y_b\), transitivity over \(\left[ \varvec{e}_b^a, \bar{\varvec{\beta }}^a \right) \) follows from that of strict inequality.
. This satisfies trichotomy over \(\left[ \varvec{e}_b^a, \bar{\varvec{\beta }}^a \right) \). As dominance on this locus is equivalent to \(x_b > y_b\), transitivity over \(\left[ \varvec{e}_b^a, \bar{\varvec{\beta }}^a \right) \) follows from that of strict inequality.
Now consider \(\varvec{x},\varvec{y},\varvec{z}\in \left( \bar{\varvec{\beta }}^a, \varvec{e}_c^a \right] \). As before, \(x_a = y_a = z_a= \beta _a^a\). Again, if \(x_b = y_b\), then \(\varvec{x} = \varvec{y}\). If \(x_b>y_b\), it implies \(x_c<y_c\). Then, since \(\bar{\beta }_c^a < x_c, y_c \le 1-\beta _a^a\) over \(\left( \bar{\varvec{\beta }}^a,\varvec{e}_c^a \right] \), it follows that \(x_c + v_c > x_b + v_b\), so that  . This satisfies trichotomy over \(\left( \bar{\varvec{\beta }}^a, \varvec{e}_c^a \right] \). As dominance on this locus is equivalent to \(y_c > x_c\), transitivity over \(\left( \bar{\varvec{\beta }}^a, \varvec{e}_c^a\right] \) follows from that of strict inequality.
. This satisfies trichotomy over \(\left( \bar{\varvec{\beta }}^a, \varvec{e}_c^a \right] \). As dominance on this locus is equivalent to \(y_c > x_c\), transitivity over \(\left( \bar{\varvec{\beta }}^a, \varvec{e}_c^a\right] \) follows from that of strict inequality.
Finally, suppose \(\bar{\varvec{\beta }}^a \notin X\). Consider \(\varvec{x}, \varvec{y}, \varvec{z} \in \left[ \varvec{e}_b^a, \varvec{e}_c^a \right] \). Note that \(\bar{\varvec{\beta }}^a \notin X\) while \(B \left( a \right) \ne \varnothing \) implies that \(\left( 1-\beta _a^a \right) < \left| v_c-v_b \right| \), which in turn implies \(\bar{\beta }_b^a < 0\). Thus, it implies \(v_b > \left( 1 - \beta _a^a \right) + v_c\). Hence, for any \(\varvec{w} \in \left[ \varvec{e}_b^a, \varvec{e}_c^a \right] \), \(w_b + v_b > w_c + v_c\) holds. Therefore, if \(x_b > y_b\), then \(y_b + v_b > y_c + v_c\), and thus  holds. This shows that
holds. This shows that  satisfies trichotomy and transitivity over \(\left[ \varvec{e}_b^a, \varvec{e}_c^a \right] \) in the same way as the above two cases.
satisfies trichotomy and transitivity over \(\left[ \varvec{e}_b^a, \varvec{e}_c^a \right] \) in the same way as the above two cases.
For \(B\left( b \right) \ne \varnothing \) and \(B \left( c \right) \ne \varnothing \), the same reasoning applies. \(\square \)
Proof of Corollary 3
Consider \(B\left( a\right) \ne \varnothing \) and \(\bar{\varvec{\beta }}^a \notin X\). As a stable set S exists, Corollary 2 implies that \(B\left( a\right) \cap S\ne \varnothing \). Suppose \(\varvec{e}_b^a\notin S\). Then there must exist \(\varvec{x}\in B\left( a\right) \cap S\) such that  . In a pillage from \(\varvec{e}_b^a \) to \(\varvec{x}\), \(W=\left\{ c\right\} \) and \(L=\left\{ b\right\} \) hold. However, \(B\left( a\right) =\left[ \varvec{e}_b^a, \varvec{e}_c^a\right] \) and Lemma 5 together imply both that the dominance operator
. In a pillage from \(\varvec{e}_b^a \) to \(\varvec{x}\), \(W=\left\{ c\right\} \) and \(L=\left\{ b\right\} \) hold. However, \(B\left( a\right) =\left[ \varvec{e}_b^a, \varvec{e}_c^a\right] \) and Lemma 5 together imply both that the dominance operator  completely orders over \(B\left( a\right) \), and that
completely orders over \(B\left( a\right) \), and that  holds for any \(\varvec{y},\varvec{z}\in \left[ \varvec{e}_b^a, \varvec{e}_c^a\right] \). Therefore,
holds for any \(\varvec{y},\varvec{z}\in \left[ \varvec{e}_b^a, \varvec{e}_c^a\right] \). Therefore,  , a contradiction. Therefore, \(\varvec{e}_b^a\in S\).
, a contradiction. Therefore, \(\varvec{e}_b^a\in S\).
Second, consider \(B\left( a\right) \ne \varnothing \) and \(\bar{\varvec{\beta }}^a\in X\). Then, via a symmetric argument to the previous case, it can be shown that \(\varvec{e}_b^a\in S\) by the proof of Corollary 2, \(\varvec{e}_b^a\in \left[ \varvec{e}_b^a,\bar{\varvec{\beta }}^a\right) \), and \(\left( 1-\beta _a^a\right) +v_b>v_c\). Likewise, \(\varvec{e}_c^a\in S\) by the proof of Corollary 2, \(\varvec{e}_c^a\in \left( \bar{ \varvec{\beta }}^a,\varvec{e}_c^a\right] \), and \(\left( 1-\beta _a^a\right) +v_c>v_b\).
Finally, suppose \(\bar{\varvec{\beta }}^a\notin S\). Then, there must exist \(\varvec{x}\in B\left( a\right) \cap S\) such that  . However, as \(v_b+ \bar{\beta }_b^a=v_c+\bar{\beta }_c^a\),
. However, as \(v_b+ \bar{\beta }_b^a=v_c+\bar{\beta }_c^a\),  holds, which is a contradiction. Therefore, \(\bar{\varvec{\beta }}^a\in S\).
holds, which is a contradiction. Therefore, \(\bar{\varvec{\beta }}^a\in S\).
For the cases of \(B\left( b\right) \ne \varnothing \) and \(B\left( c\right) \ne \varnothing \), the same arguments can be applied. \(\square \)
We may now present non-existence conditions directly on the parameters \(v_a, v_b\) and \(v_c\). In the following, the parameter conditions ensure that the maximal elements in the \(B \left( i \right) \) are dominated by a core element:
Corollary 4
In a 3-AMPG with a non-empty core, let \(v_{j}\ge v_{k}\), without loss of generality. Let \(-v_{i}+v_{j}+v_{k}\in \left[ -1,1\right) \) and one of the following two conditions be satisfied:
-
1.
\(v_k > 0\); or
-
2.
\(v_j > 0\) and \(1 + v_i -3 v_j + v_k > 0\).
Then, no stable set exists.
Proof
By \(-v_i + v_j + v_k \in \left[ -1, 1 \right) \), \( 0 \le \beta _i^i < 1\) holds, hence \(B\left( i\right) \ne \varnothing \). Assume, on the contrary, that a stable set S exists. Note also that \(-v_i + v_j + v_k < 1\) implies that \(\varvec{t}^i \in K\) by Theorem 1. Then, as \(S\ne \varnothing \) by assumption, \(\varvec{t}^i \in S\).
Consider the first inequality in the corollary’s statement. By Corollary 3, \(S \ne \varnothing \) and \(B\left( i \right) \ne \varnothing \) imply that \(\varvec{e}_j^i \in S\). However, \(v_i + \beta _i^i > v_j + \left( 1 - \beta _i^i \right) \) follows from \(v_k > 0\), which implies that  . This is a contradiction. Therefore, when the first inequality holds, no stable set exists.
. This is a contradiction. Therefore, when the first inequality holds, no stable set exists.
Now consider the second. Then, as \(1 + v_i -3 v_j + v_k > 0\) implies \(\left( 1 - \beta _i^i \right) > \left| v_k - v_j \right| \), and so \(\bar{\varvec{\beta }}^i \in X\) which is also an interior allocation in X. Then, by Corollary 3, \(S \ne \varnothing \) and \(B\left( i \right) \ne \varnothing \) imply that \(\varvec{e}_k^i \in S\). However, \(v_i + \beta _i^i > v_k + \left( 1 - \beta _i^i \right) \) follows from \(v_j > 0\). Then, by the same reasoning as in the first case, we derive a contradiction. Thus, in this case as well, no stable set exists. \(\square \)
The remainder of this section characterises stable sets for each of the non-empty core cases identified in Corollary 1 when \(n=3\). While the corollary worked directly with parameter values for \(\varvec{v}\), the theorems work with geometric objects in the simplex, X, to aid intuitions. Thus, following statement of the theorems, Table 1 provides a mapping between corollary’s parameter ranges the theorems’ geometric objects. Proofs are in the appendix.
Theorem 3
Consider a 3-AMPG with \(K=\left\{ \varvec{t}^{a}\right\} \). Then:
-
1.
if \(B\left( a\right) =\varnothing \), then there exists the unique stable set \(S=\left\{ \varvec{t}^a\right\} \).
-
2.
if \(B\left( a\right) =\left\{ \varvec{t}^a\right\} \), then no stable set exists.
-
3.
if \(\varvec{t}^a\notin B\left( a\right) \ne \varnothing \), then \(\varvec{e} _b^a \ne \varvec{b}^{ab}\) holds and no stable set exists.
Theorem 4
Consider a 3-AMPG with \(K=\left\{ \varvec{t}^{a},\varvec{t} ^{b}\right\} \). Then, \(B\left( a\right) \ne \varnothing \), and:
-
1.
there exists the unique stable set \(S=K=\left\{ \varvec{t}^a, \varvec{t} ^b\right\} \) if and only if \(\varvec{e}_b^a= \varvec{b}^{ab}\) and \(\bar{\varvec{\beta }} ^a\notin X\) hold.
-
2.
otherwise, no stable set exists.
When \(\varvec{e}_b^a=\varvec{b}^{ab}\), \(\varvec{e}_b^a=\varvec{b}^{ab}=\varvec{t}^b\) holds.
Theorem 5
Consider a 3-AMPG with \(K=\left\{ \varvec{t}^{a},\varvec{t} ^{b},\varvec{b}^{ab}\right\} \). Then, \(B\left( a\right) \ne \varnothing \), \( B\left( b\right) \ne \varnothing \), and \(\varvec{e}_{b}^{a}=\varvec{b}^{ab}=\varvec{e} _{a}^{b}\) hold, and:
-
1.
there exists the unique stable set \(S=\left\{ \varvec{t}^a, \varvec{t}^b,\varvec{b} ^{ab}\right\} \) if and only if \(\bar{\varvec{\beta }}^a \notin X\) holds.
-
2.
otherwise, no stable set exists.
Theorem 6
Consider a 3-AMPG with \(K=\left\{ \varvec{t}^{a},\varvec{t}^{b}, \varvec{t}^{c}\right\} \). Then, \(B\left( a\right) \ne \varnothing \), \(B\left( b\right) \ne \varnothing \), and \(B\left( c\right) \ne \varnothing \) hold. Moreover, the following statements hold:
-
1.
Let \(v_c=0\). Then, \(\varvec{e}_b^a=\varvec{b}^{ab} = \varvec{t}^b\) and \(\varvec{e}_c^a = \varvec{b}^{ac} = \varvec{t}^c\) hold, and there exists the unique stable set
$$\begin{aligned} S = \left\{ \varvec{t}^a,\varvec{t}^b,\varvec{t}^c, \varvec{b}^{bc}\right\} =\left\{ \varvec{t} ^a,\varvec{t}^b, \varvec{t}^c,\varvec{s}^{bc}\right\} =\left\{ \varvec{t}^a, \varvec{t}^b,\varvec{t} ^c,\bar{\varvec{\beta }}^a \right\} . \end{aligned}$$ -
2.
Let \(v_c>0\). Then, \(B\left( a\right) =\left\{ \varvec{t}^a\right\} \), \( B\left( b\right) =\left\{ \varvec{t}^b\right\} \), \(B \left( c \right) = \left\{ \varvec{t}^c \right\} \), and there exists the unique stable set
$$\begin{aligned} S=K\cup \left\{ \varvec{b}^{ab},\varvec{b}^{ac},\varvec{b}^{bc}\right\} =K\cup \left\{ \varvec{s}^{ab},\varvec{s}^{ac}, \varvec{s}^{bc}\right\} \end{aligned}$$if and only if \(v_a=v_b=v_c=1\) holds. Otherwise, no stable set exists.
Theorem 7
Consider a 3-AMPG with \(K=\left\{ \varvec{t}^{a},\varvec{t} ^{b},\varvec{t}^{c},\varvec{b}^{ab}\right\} \). Then, \(B\left( a\right) \ne \varnothing \), \(B\left( b\right) \ne \varnothing \), \(B\left( c\right) \ne \varnothing \), \(\varvec{e}_{b}^{a}=\varvec{b}^{ab}=\varvec{e}_{a}^{b}\) hold, and:
-
1.
there exists the unique stable set \(S=\left\{ \varvec{t}^a, \varvec{t}^b,\varvec{t} ^c,\varvec{b}^{ab}\right\} \) if and only if \(v_a=v_b=\frac{1}{2}\) holds.
-
2.
otherwise, no stable set exists.
Theorem 8
Consider a 3-AMPG with \(K=\left\{ \varvec{t}^{a},\varvec{t} ^{b},\varvec{t}^{c},\varvec{b}^{ab},\varvec{b}^{ac}\right\} \). Then, \(B\left( a\right) \ne \varnothing \), \(B\left( b\right) \ne \varnothing \), \(B\left( c\right) \ne \varnothing \), \(\varvec{e}_{b}^{a}=\varvec{b}^{ab}=\varvec{e}_{a}^{b}\), \(\varvec{e} _{c}^{a}=\varvec{b}^{ac}=\varvec{e}_{a}^{c}\), and \(v_{a}<1\) hold. Moreover:
-
1.
there exists the unique stable set \(S=K\cup \bar{\varvec{\beta }}^a\) if and only if \(v_a\ge \frac{1}{3}\) holds.
-
2.
otherwise, no stable set exists.
Finally, the case in which \(K = \left\{ \varvec{t}^a, \varvec{t}^b, \varvec{t}^c, \varvec{b} ^{ab}, \varvec{b}^{ac}, \varvec{b}^{bc} \right\} \), is the symmetric wealth-is-power case (Jordan 2006). In the present \(n=3\) case, the stable set—illustrated in Fig. 3—reduces to:
Theorem 9
Jordan (2006, Theorem 3.3) In the wealth-is-power pillage game with \(n=3\) and \(v_{i}=0\) for all \(i=1,2,3\), the unique stable set is
Table 1 maps between Corollary 1’s inequalities and the preceding theorems.
5 Discussion
This paper removes the symmetry assumption usually assumed in analysis of pillage games. It is motivated by a hope of identifying a tractable class of pillage games to allow empirical tests of this theory of unstructured power contests.
It finds, first, that stable sets are unique—when they exist—in \(n=3\) AMPG. MacKenzie et al. (2015) demonstrated that violating the symmetry axiom could lead to multiple stable sets in majority pillage games when the number of agents was at least four. This paper therefore establishes that as a lower bound for multiplicity in AMPG.
Second, it suggests a link between linear power functions and winner(s)-take-all contests: the only case in which the stable set contains interior allocations, \(\varvec{x} > \varvec{0}\), are the special cases of \(\varvec{v} = \varvec{0}\) and \(v_a \in \left[ \tfrac{1}{3}, 1 \right) , v_b = v_c = 0\). This reflects the tension between existence of a stable set and strictly interior allocations along balance of power loci: when there is an interior allocation at which the two contestants’ power is balanced, its extremal elements must also belong to a stable set; if, though, the relevant \(v_i > 0\), these elements may be dominated by a tyrannical allocation, preventing existence.
Third, it finds that non-existence is pervasive. Thus, the theory fails to deliver testable predictions for non-negligible sets of values of \(v_1, v_2\) and \(v_3\).
Tantalisingly, the theory yields predictions for almost the full range of the special cases noted above, for which \(v_b = v_c = 0\) and \(v_a > 0\)—so that agent a has some source of intrinsic strength that b and c do not. This power could arise from greater internal cohesion, a structural advantage (e.g. perhaps being located more centrally). Figure 4 illustrates, with \(v_a\) increasing from 0 in the leftmost diagram to \(v_a > 1\) in the rightmost. Filled dots represent allocations in a stable set.
When \(v_a = 0\), the fully symmetric case depicted in diagram 4a, a stable set exists with interior allocations, as per Theorem 3.3 of Jordan (2006). As \(v_a\) increases, \(D \left( \varvec{t}^a \right) \) reaches further into the simplex, as depicted in diagram 4b, so that \( \varvec{b}^{ab}\) no longer dominates the extremal \(\varvec{e}^b_c\); no stable set exists, as per the second case in Theorem 8. When \(v_a\) grows beyond \(\tfrac{1}{3}\) (q.v. diagram 4c), \(\varvec{b}^{ab}\) comes to dominate all allocations to the extremal \(\varvec{e}^b_c\); this allows the stable set in the first case of Theorem 8. When \(v_a = 1\), \(D \left( \varvec{t}^a \right) \) pushes further down, dominating the whole simplex except its bottom margin (as depicted in diagram 4d); now the stable set in the second case of Theorem 6 exists. Finally, when \(v_a > 1\), depicted in diagram 4e, \(\varvec{t}^a\) dominates the whole simplex, leaving it the singleton stable set, as per the first case of Theorem 3.
Thus, the cardinality of the unique stable set decreases in \(v_a\), with a gap at \(v_a \in \left( 0, \tfrac{1}{3} \right) \), for which no stable set exists.
We conclude by mentioning three possible ways forward for an empirically-testable theory of pillage games.
First, production could be considered, so that assigning an agent nothing inefficiently excludes its production function from society. In the terminology of Olson (1993), production provides an incentive for bandits to be stationary rather than roving. Production in pillage games was first considered by Jordan (2009), which gave each agent in a pillage game a production function for converting wealth into consumption goods. While production could be expected to favour interior allocations, it is less obvious that they would rescue existence.
Second, the tension between existence and interior allocations arises in part because the balance of power loci (e.g. Fig. 3’s dashed lines) are linear: interior allocations do not dominate their neighbours as the loci restrict power contests to those pitting one agent against another. However, a power function like
generates curved balance of power loci which allow the third agent (who would be indifferent along a linear balance of power locus) to benefit from moves towards the centre of the locus. Its involvement allows central allocations to dominate the extremes of the locus, rescuing existence and yielding strictly interior solutions. Figure 5 illustrates the symmetric special case in which \(v_i = 0\) for all agents. Its unique stable set contains strictly interior allocations:
For \(n > 3\), we conjecture that, in the empty core case, the results in the symmetric case studied by Jordan and Obadia (2015) can be extended to the asymmetric case with an additional condition ensuring that any larger coalition dominates any smaller coalition: for even n, no symmetric stable set should exist; for odd n, the unique symmetric stable set should be the set of allocations that split the allocation equally between a minimal majority of agents.
Third, solution concepts other than the stable set can be experimented with. For example, Jordan (2009) extended the stable set to the legitimate set in production pillage games. Chaturvedi (2016) has applied farsighted concepts from Chwe (1994) to pillage games. Duggan (2013) discussed other farsighted concepts, such as uncovered sets; in 3-AMPGs, the Gillies, Bordes and McKelvey uncovered sets are non-empty, and any stable set is a subset of the Gillies uncovered set.Footnote 6
Notes
Jackson and Morelli (2011) open their survey of the reasons for wars by asking why they, “occur and recur, especially in cases when the decisions involved are made by careful and rational actors?” Pillage games aid study of the cases short of war.
MacKenzie et al. (2015) constructed examples of pillage games with multiple stable sets. It is also the only paper to violate symmetry, which it did to construct counter-examples, rather than systematically.
For instance, von Neumann and Morgenstern (1953) for games in characteristic function form, and Thrall and Lucas (1963) for those in partition function form. These both establish results in the simplest non-trivial case, and build intuitions for further analyses. This partly reflects the computational complexity of the stable set as a solution concept: even in a special case, Deng and Papadimitriou (1994) found that “existence [of a stable set] may not even be decidable”
When referring to two allocations in the following, we may use W and L as a shorthand to indicate the agents benefiting and losing, respectively, from a move between them, even if we do not explicitly define them as such.
Proofs available on request. We are grateful to the AE for suggesting this.
References
Aumann RJ (1985) What is game theory trying to accomplish? In: Arrow K, Honkapohja S (eds) Frontiers of economics. Basil Blackwell, Oxford
Beardon AF, Rowat C (2013) Efficient sets are small. J Math Econ 49(5):367–374
Bloch F, van den Nouweland A (2020) Farsighted stability with heterogeneous expectations. Games Econ Behav 121:32–54
Chaturvedi R (2016) Stable property rights. mimeo
Chwe MS-Y (1994) Farsighted coalitional stability. J Econ Theory 63(2):299–325
Deng X, Papadimitriou CH (1994) On the complexity of cooperative solution concepts. Math Oper Res 19(2):257–266
Duggan J (2013) Uncovered sets. Soc Choice Welfare 41(3):489–535
Dutta B, Vohra R (2017) Rational expectations and farsighted stability. Theor Econ 12(3):1191–1227
Harsanyi JC (1974) An equilibrium-point interpretation of stable sets and an alternative definition. Manage Sci 20(11):1472–1495
Hellman TF, Wasserman N (2011) The first deal: the division of founder equity in new ventures. Working Paper 16922. NBER
Jackson MO, Morelli M (2011) The reasons for wars: an updated survey. In: Coyne CJ, Mathers RL (eds) Handbook on the political economy of war, Chap. 3. Edward Elgar, Northampton, pp 34–57
Jordan JS (2006) Pillage and property. J Econ Theory 131(1):26–44
Jordan JS (2009) Power and efficiency in production pillage games. Rev Econ Des 13(3):171–193
Jordan JS, Obadia D (2015) Stable sets in majority pillage games. Int J Game Theory 44(2):473–486
Kerber M, Rowat C (2011) A Ramsey bound on stable sets in Jordan pillage games. Int J Game Theory 40(3):461–466
MacKenzie S, Kerber M, Rowat C (2015) Pillage games with multiple stable sets. Int J Game Theory 44(4):993–1013. https://doi.org/10.1007/s00182-015-0462-1
McDonald J (1977) The game of business. Anchor Books, Garden City
Olson M (1993) Dictatorship, democracy, and development. Am Polit Sci Rev 87(3):567–576
Ray D, Vohra R (2015) The farsighted stable set. Econometrica 83(3):977–1011
Ray D, Vohra R (2019) Maximality in the farsighted stable set. Econometrica 87(5):1763–1779
Rowat C, Kerber M (2014) Sufficient conditions for unique stable sets in three agent pillage games. Math Soc Sci 69:69–80
Saxton D (2011) Strictly monotonic multidimensional sequences and stable sets in pillage games. J Comb Theory Ser A 118(2):510–524
Straffin PD (1993) Game theory and strategy, vol 36. Mathematical Association of America Textbooks, The Mathematical Association of America, Washington, D.C
Thrall RM, Lucas WF (1963) n-person games in partition function form. Nav Res Logist Q 10:281–298
von Neumann J, Morgenstern O (1953) Theory of games and economic behavior, 2nd edn. Princeton University Press, Princeton
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors are grateful to Sebastian Cea, Alex Kohlhas, Brian Tung, to audiences at SAET, Games and PET for useful conversations, and to an anonymous referee, an associate editor and co-editor for their improvements to the paper. Rowat is grateful to Birkbeck College, Hitotsubashi University, Kyoto University and the Rakuten Institute of Technology for their hospitality.
A Proofs
A Proofs
Proof of Theorem 3
-
1.
Together \(B \left( a \right) = \varnothing \) and \(K=\left\{ \varvec{t}^a\right\} \) imply that \(v_b+v_c+1<v_a\). Therefore, \(D\left( \varvec{t}^a\right) = X \backslash \left\{ \varvec{t}^a\right\} \) and \(S=\left\{ \varvec{t}^a\right\} \).
-
2.
Note that \(B \left( a\right) =\left\{ \varvec{t}^a\right\} \) implies \(v_a+1=v_b+v_c\) and \(\varvec{t}^a = \varvec{e}_b^a\). Moreover, \(B\left( i\right) =\left\{ \varvec{t}^i \right\} \) if \(v_i=v_a\), and \(B\left( i\right) =\varnothing \) otherwise, for \(i=b,c\). As \(\varvec{t}^i\notin K\) for \(i=b,c\), it follows that \(v_i+1<v_j+v_k\) for \(i=b,c\), thus \(B\left( i\right) = \varnothing \) for \(i=b,c\). Let \(\overset{\circ }{X}\equiv \left\{ \varvec{x}\in X\varvec{\mid x}>\varvec{0}\right\} \). Then, for any \(\varvec{x}\in \overset{\circ }{X}\),
 for \(i=b,c\). Moreover, for any \(\varvec{x}\in \overset{\circ }{X}\), it follows that \(v_i+x_i<v_j+v_k+\left( 1 - x_i \right) \) for any \(i,j,k\in I\), which implies that there exists \(\varvec{w}^{\varvec{x}}\in X\) such that \(w_i^{\varvec{x}}=0\) and \(w_j^{\varvec{x}} / w_k^{\varvec{x}} = x_j / x_k\). Then, it follows that
for \(i=b,c\). Moreover, for any \(\varvec{x}\in \overset{\circ }{X}\), it follows that \(v_i+x_i<v_j+v_k+\left( 1 - x_i \right) \) for any \(i,j,k\in I\), which implies that there exists \(\varvec{w}^{\varvec{x}}\in X\) such that \(w_i^{\varvec{x}}=0\) and \(w_j^{\varvec{x}} / w_k^{\varvec{x}} = x_j / x_k\). Then, it follows that  .
.Let \(\bar{X}_{jk}\equiv \left\{ \varvec{x}\in X\mid x_i=0\right\} \) for any \(i,j,k\in I\). If \(v_c+1<v_b\), then for any \(\varvec{w}\in \bar{X}_{bc}\backslash \left\{ \varvec{t}^b\right\} \),
 . If \(v_c+1\ge v_b\), then there exists \(\varvec{w}^{bc}\in \bar{X}_{bc}\) such that \(v_b+w_b^{bc}=v_c+w_c^{bc}\). Then, for any \(\varvec{w}\in \bar{X}_{bc}\),
. If \(v_c+1\ge v_b\), then there exists \(\varvec{w}^{bc}\in \bar{X}_{bc}\) such that \(v_b+w_b^{bc}=v_c+w_c^{bc}\). Then, for any \(\varvec{w}\in \bar{X}_{bc}\),  if and only if \(w_b > w_b^{bc}\);
if and only if \(w_b > w_b^{bc}\); 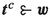 if and only if \(w_c > w_c^{bc}\); and there exists \(\varvec{x}^{\varvec{w}} \in \overset{\circ }{X}\) such that
if and only if \(w_c > w_c^{bc}\); and there exists \(\varvec{x}^{\varvec{w}} \in \overset{\circ }{X}\) such that  for \(\varvec{w}=\varvec{w}^{bc}\). In sum, cyclic relations of the dominance operator
for \(\varvec{w}=\varvec{w}^{bc}\). In sum, cyclic relations of the dominance operator  are observed over \(\overset{\circ }{X}\) and \(\bar{X}_{bc}\), which implies that none of allocations in \(\overset{\circ }{X}\cup \bar{X}_{bc}\) can constitute a stable set. Applying the same argument to \(\bar{X}_{ab}\backslash \left\{ \varvec{t}^a\right\} \) and \(\bar{X}_{ac}\backslash \left\{ \varvec{t}^a\right\} \) proves that no stable set intersects with \(X\backslash \left\{ \varvec{t}^a\right\} \).
are observed over \(\overset{\circ }{X}\) and \(\bar{X}_{bc}\), which implies that none of allocations in \(\overset{\circ }{X}\cup \bar{X}_{bc}\) can constitute a stable set. Applying the same argument to \(\bar{X}_{ab}\backslash \left\{ \varvec{t}^a\right\} \) and \(\bar{X}_{ac}\backslash \left\{ \varvec{t}^a\right\} \) proves that no stable set intersects with \(X\backslash \left\{ \varvec{t}^a\right\} \).Hence, if a stable set exists, it must be that \(S=\left\{ \varvec{t}^a\right\} \). However, \(D\left( \varvec{t}^a\right) \ne X\backslash \left\{ \varvec{t}^a \right\} \), as \(v_a+x_a<v_b+v_c+ \left( 1-x_a\right) \) for any \(\varvec{x}\in \overset{\circ }{X}\), which implies
 . Therefore, \(S \ne \left\{ \varvec{t}^a\right\} \), a contradiction. Hence, no stable set exists.
. Therefore, \(S \ne \left\{ \varvec{t}^a\right\} \), a contradiction. Hence, no stable set exists. -
3.
This implies that \(-1 \le -v_a + v_b + v_c < 1\), and so \(\varvec{e}_b^a \in X\). Suppose \(\varvec{e}_b^a = \varvec{b}^{ab}\). Then, \(v_c = 0\). Then, \(\varvec{t}^b\notin K\) implies \(v_b + 1 < v_a\) and \(v_b + v_c + 1 < v_a\), which contradicts \(-1 \le - v_a + v_b + v_c\). Thus, \(\varvec{e}_b^a \ne \varvec{b}^{ab}\), which implies \(v_c > 0\). Then, by Corollary 4, no stable set exists.
\(\square \)
Proof of Theorem 4
By \(K = \left\{ \varvec{t}^a, \varvec{t}^b \right\} \), Theorem 1 implies that \(v_a+1\ge v_b+v_c\) and \(v_b+1\ge v_a+v_c\), where the former implies \(\beta _a^a\le 1\). Moreover, the latter inequality implies \(v_b + v_c + 1 \ge v_a\), which implies \(\beta _a^a\ge 0\). Therefore, \(B\left( a\right) \ne \varnothing \).
Consider \(\varvec{e}_b^a = \varvec{t}^a\). Then, as \(v_b + 1 \ge v_a + v_c\) by \(\varvec{t}^b \in K\) and \(v_a + 1 = v_b + v_c\) by \(\varvec{e}_b^a=\varvec{t}^a\), it follows that \(v_a = v_b = v_c = 1\). Then, \(v_c + 1 = v_a + v_b\), which contradicts \(\varvec{t}^c \notin K\) by Theorem 1. Thus, \(\varvec{e}_b^a \ne \varvec{t}^a\) must hold, and \(\beta _a^a < 1\).
Consider \(\varvec{e}_b^a\ne \varvec{b}^{ab}\), which implies \(v_c > 0\): by Corollary 4, no stable set exists.
Consider \(\varvec{e}_b^a = \varvec{b}^{ab} \ne \varvec{t}^b\), which implies \(v_c=0\). Then, it follows from \(\varvec{e}_b^a = \varvec{b}^{ab}\ne \varvec{t}^b\) and \(v_c=0\) that \(\beta _a^a=\frac{1}{2}\left( 1+v_b-v_a\right) \in \left( 0, 1 \right) \), which implies \(\varvec{b}^{ab}\in K\) by Theorem 1. This contradicts \(K = \left\{ \varvec{t}^a, \varvec{t}^b \right\} \). Therefore, if \(\varvec{e}_b^a=\varvec{b}^{ab}\), then \(\varvec{e}_b^a=\varvec{b}^{ab}=\varvec{t}^b\).
Consider \(\varvec{e}_b^a = \varvec{b}^{ab} = \varvec{t}^b\). Then, as \(\beta _a^a = 0\) when \(v_c=0\), \(B\left( a \right) = \bar{X}_{bc} \equiv \left\{ \varvec{x}\in X\mid x_a=0\right\} \). Further, for any \(\varvec{x} \in X \backslash B\left( a\right) \), \(v_a + x_a > v_b + v_c + \left( 1-x_a\right) \) holds, which implies  .
.
As \(v_a = 1 + v_b\) by \(\varvec{e}_b^a = \varvec{b}^{ab} = \varvec{t}^b\), either \(v_a=1\) and \(v_b=0\), or \(v_a>1\). The first case also implies that \(v_a+v_b=1+v_c\), so that \(\varvec{t}^c\in K\) from Theorem 1; this contradicts \(K = \left\{ \varvec{t}^a, \varvec{t}^b \right\} \), which leaves only the second case, \(v_a > 1\). This further implies  . Then, by Corollary 3 and Lemma 5, we can conclude: \(S=\left\{ \varvec{t}^a, \varvec{t}^b \right\} \) if and only if \(\bar{\varvec{\beta }}^a \notin X\).
. Then, by Corollary 3 and Lemma 5, we can conclude: \(S=\left\{ \varvec{t}^a, \varvec{t}^b \right\} \) if and only if \(\bar{\varvec{\beta }}^a \notin X\).
Note that \(\bar{\varvec{\beta }}^a\in X\) if and only if \(v_b\le 1\), since \(\bar{\beta }_b^a=\frac{1-v_b}{2}\). Thus, \(\bar{\varvec{\beta }}^a\notin X\) if and only if \(v_b>1\) (or equivalently, \(v_a>2\)). When, \(\bar{\varvec{\beta }}^a\notin X\), Lemma 5 ensures that any allocation in \(B\left( a\right) \backslash \left\{ \varvec{t}^b\right\} \) is dominated by \(\varvec{e}_b^a = \varvec{t}^b\). Thus, \(D\left( \varvec{t}^a, \varvec{t}^b \right) = X\backslash \left\{ \varvec{t}^a, \varvec{t}^b\right\} \). Finally, \(\left\{ \varvec{t}^a, \varvec{t}^b\right\} = K\) satisfies internal stability, so that \(S=\left\{ \varvec{t}^a, \varvec{t}^b\right\} \). In contrast, when \(\bar{\varvec{\beta }}^a\in X\), then Corollary 3 implies that whenever S exists, \(\varvec{t}^c=\varvec{e}_c^a\in S\) holds. However, in this case, \(\varvec{t}^a\in S\) also holds by \(\varvec{t}^a\in K\), yielding a contradiction with  . Thus, S does not exist when \(\bar{\varvec{\beta }}^a\in X\). \(\square \)
. Thus, S does not exist when \(\bar{\varvec{\beta }}^a\in X\). \(\square \)
Proof of Theorem 5
By Theorem 1, \(K = \left\{ \varvec{t}^a, \varvec{t}^b, \varvec{b}^{ab}\right\} \) implies that \(v_c=0\), so that \(\varvec{b}^{ab} = \varvec{e}_b^a = \varvec{e}_a^b\). Therefore, \(B\left( a \right) \ne \varnothing \) and \(B\left( b\right) \ne \varnothing \), where \(B\left( a\right) =\left\{ \varvec{x}\in X\mid x_a = \bar{\beta }_a^a \right\} \) with \(\bar{\beta }_a^a=\frac{v_b-v_a+1}{2}\) and \(B\left( b\right) =\left\{ \varvec{x}\in X\mid x_b=\bar{\beta }_b^b \right\} \) with \(\bar{\beta }_b^b = \frac{v_a-v_b+1}{2}\). Then, for any \(\varvec{x}\in X\) with \(x_a>\bar{\beta }_a^a\), \(v_a+x_a>v_b+v_c+\left( 1 - x_a \right) \), which implies  . Likewise, for any \(\varvec{y}\in X\) with \(y_b > \bar{\beta }_b^b\) we have \(v_b+y_b>v_a+v_c+\left( 1-y_b\right) \), which implies
. Likewise, for any \(\varvec{y}\in X\) with \(y_b > \bar{\beta }_b^b\) we have \(v_b+y_b>v_a+v_c+\left( 1-y_b\right) \), which implies  . Consider \(\left\{ \varvec{x}\in X\mid x_a<\bar{\beta }_a^a, x_b<\bar{\beta }_b^b\right\} \). Then, for any \(\varvec{z}\in \left\{ \varvec{x} \in X \mid x_a< \bar{\beta }_a^a, x_b<\bar{\beta }_b^b\right\} \),
. Consider \(\left\{ \varvec{x}\in X\mid x_a<\bar{\beta }_a^a, x_b<\bar{\beta }_b^b\right\} \). Then, for any \(\varvec{z}\in \left\{ \varvec{x} \in X \mid x_a< \bar{\beta }_a^a, x_b<\bar{\beta }_b^b\right\} \),
follows from \(\varvec{t}^c\notin K\) with Theorem 1. Thus,  .
.
Let \(\bar{\varvec{\beta }}^a \in X\), so that \(1 + v_a - 3 v_b > 0\). In the case of \(v_b > 0\), no stable set exists (by Corollary 4). Otherwise, when \(v_b = 0\), \(\varvec{t}^b\in K\) implies that \(1\ge v_a\). However, \(\varvec{t}^c \notin K\) implies that \(1 < v_a\), a contradiction. Therefore, \(\bar{\varvec{\beta }}^a\in X\) with \(v_b = 0\) is impossible.
Let \(\bar{\varvec{\beta }}^a \notin X\). Then, \(1 + v_a - 3 v_b \le 0\), so that \(1 + v_b - 3 v_a \le 0\), and \(\bar{\varvec{\beta }}^b\notin X\). Then, by Lemma 5, for any \(\varvec{w} \in B\left( a\right) \),  holds. Likewise, for any \(\varvec{w}\in B\left( b \right) \),
holds. Likewise, for any \(\varvec{w}\in B\left( b \right) \),  holds. As \(\varvec{b}^{ab}=\varvec{e}_b^a=\varvec{e}_a^b\), \(B\left( a\right) \cup B \left( b\right) \subseteq D\left( \varvec{b}^{ab}\right) \) holds. In summary, \(D\left( K\right) =X\backslash K\) holds for \(K=\left\{ \varvec{t}^a,\varvec{t}^b,\varvec{b}^{ab}\right\} \). Thus, \(S=K=\left\{ \varvec{t}^a, \varvec{t}^b, \varvec{b}^{ab} \right\} \). \(\square \)
holds. As \(\varvec{b}^{ab}=\varvec{e}_b^a=\varvec{e}_a^b\), \(B\left( a\right) \cup B \left( b\right) \subseteq D\left( \varvec{b}^{ab}\right) \) holds. In summary, \(D\left( K\right) =X\backslash K\) holds for \(K=\left\{ \varvec{t}^a,\varvec{t}^b,\varvec{b}^{ab}\right\} \). Thus, \(S=K=\left\{ \varvec{t}^a, \varvec{t}^b, \varvec{b}^{ab} \right\} \). \(\square \)
Proof of Theorem 6
As \(K=\left\{ \varvec{t}^a,\varvec{t}^b,\varvec{t}^c\right\} \), Theorem 1 implies that \(1+v_a\ge v_b+v_c\), \(1+v_b\ge v_a+v_c\), and \(1+v_c\ge v_a+v_b\). Therefore, \(\beta _i^i \le 1\) holds for all \(i\in \left\{ a,b,c\right\} \). Moreover, \(1+v_c\ge v_a+v_b\) implies \(1+v_b+v_c\ge v_a\), and so \(\beta _i^i\ge 0\) holds for all \(i\in \left\{ a,b,c\right\} \). Thus, \(B \left( a \right) \ne \varnothing \), \(B\left( b\right) \ne \varnothing \), and \(B\left( c\right) \ne \varnothing \). Consider two cases:
-
1.
\(v_c=0\). Then, \(\varvec{t}^b\in K\) implies implies \(1\ge v_a-v_b\). As \(\varvec{b}^{ab} \notin K\), Theorem 1 implies that \(1=v_a-v_b\). Thus, \(1+v_b=v_a\) and \(1\ge v_a+v_b\) together imply that \(v_b=0\) and \(v_a=1\). Then, \(\varvec{e}_b^a = \varvec{b}^{ab} = \varvec{t}^b\) so that \(B\left( a \right) = \left\{ \varvec{x} \in X \mid x_a = 0 \right\} \). Moreover, \(\bar{\varvec{\beta }}^a=\left( 0,\frac{1}{2},\frac{1}{2}\right) = \varvec{b}^{bc} = \varvec{s}^{bc}\). Then, by Lemma 5, for any \(\varvec{w}\in B\left( a\right) \), if \(\varvec{w}\in \left( \varvec{t}^b,\bar{\varvec{\beta }}^a\right) \),
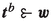 ; if \(\varvec{w}\in \left( \bar{\varvec{\beta }}^a,\varvec{t}^c\right) \),
; if \(\varvec{w}\in \left( \bar{\varvec{\beta }}^a,\varvec{t}^c\right) \),  holds, as \(\varvec{t}^c=\varvec{e}_c^a\). Finally, for any \(\varvec{x}\in X\backslash B\left( a\right) \),
holds, as \(\varvec{t}^c=\varvec{e}_c^a\). Finally, for any \(\varvec{x}\in X\backslash B\left( a\right) \),  holds. Thus, \(X\backslash \left( K \cup \left\{ \bar{\varvec{\beta }}^a\right\} \right) \subseteq D\left( K\right) \). Moreover, it can be seen that
holds. Thus, \(X\backslash \left( K \cup \left\{ \bar{\varvec{\beta }}^a\right\} \right) \subseteq D\left( K\right) \). Moreover, it can be seen that  and
and  for all \(i\in \left\{ a,b,c\right\} \). Thus, the stable set must be given by \(S=\left\{ \varvec{t}^a,\varvec{t}^b, \varvec{t}^c, \bar{\varvec{\beta }}^a\right\} \). As \(\bar{\varvec{\beta }}^a=\varvec{b}^{bc}=\varvec{s}^{bc}\), \(S=\left\{ \varvec{t}^a,\varvec{t}^b,\varvec{t}^c, \varvec{b}^{bc}\right\} =\left\{ \varvec{t}^a,\varvec{t}^b, \varvec{t}^c,\varvec{s}^{bc}\right\} \) holds.
for all \(i\in \left\{ a,b,c\right\} \). Thus, the stable set must be given by \(S=\left\{ \varvec{t}^a,\varvec{t}^b, \varvec{t}^c, \bar{\varvec{\beta }}^a\right\} \). As \(\bar{\varvec{\beta }}^a=\varvec{b}^{bc}=\varvec{s}^{bc}\), \(S=\left\{ \varvec{t}^a,\varvec{t}^b,\varvec{t}^c, \varvec{b}^{bc}\right\} =\left\{ \varvec{t}^a,\varvec{t}^b, \varvec{t}^c,\varvec{s}^{bc}\right\} \) holds. -
2.
\(v_c>0\). First consider \(v_c<v_a\). Then, \(1+v_a>v_b+v_c \) follows from \(1+v_c\ge v_a+v_b\). Then, by Corollary 4, no stable set exists. Now consider \(v_c = v_a\), the symmetric case. Satisfying \(1+v_a\ge v_b+v_c\), \(1 + v_b \ge v_a+v_c\), and \(1+v_c\ge v_a+v_b\) therefore forces \(v_a = v_b = v_c = 1\). Then, \(\varvec{e}_b^a = \varvec{t}^a\), \(\varvec{e}_a^b = \varvec{t}^b\), and \(\varvec{e}_a^c = \varvec{t}^c\), so that \(B\left( a\right) = \left\{ \varvec{t}^a \right\} \), \(B \left( b \right) = \left\{ \varvec{t}^b \right\} \), and \(B \left( c \right) = \left\{ \varvec{t}^c \right\} \). Then, for each interval \(\left[ \varvec{t}^i, \varvec{t}^j \right] \), any \(\varvec{w} \in \left( \varvec{t}^i, \varvec{s}^{ij} \right) \) implies
 , while any \(\varvec{w} \in \left( \varvec{s}^{ij}, \varvec{t}^j \right) \) implies
, while any \(\varvec{w} \in \left( \varvec{s}^{ij}, \varvec{t}^j \right) \) implies  , for any \(i,j \in \left\{ a, b, c \right\} \). Thus, \(\bar{X}_{jk}\backslash \left\{ \varvec{s}^{jk}\right\} \subseteq D\left( \varvec{t}^j,\varvec{t}^k\right) \) holds for any \(j,k\in \left\{ a,b,c\right\} \).
, for any \(i,j \in \left\{ a, b, c \right\} \). Thus, \(\bar{X}_{jk}\backslash \left\{ \varvec{s}^{jk}\right\} \subseteq D\left( \varvec{t}^j,\varvec{t}^k\right) \) holds for any \(j,k\in \left\{ a,b,c\right\} \).Moreover, we can show that \(\overset{\circ }{X}\subseteq D\left( \varvec{s}^{ab},\varvec{s}^{ac},\varvec{s}^{bc}\right) \). Let \(\varvec{x}\in \overset{\circ }{X}\) with \(x_i \ge \tfrac{1}{2}\), so that \(x_j, x_k < \tfrac{1}{2}\). Then, a pillage from \(\varvec{x}\) to \(\varvec{s}^{jk}\) implies that \(W=\left\{ j,k\right\} \) and \(L = \left\{ i \right\} \). Then, we have \(\frac{3}{2} \le v_i+x_i<2\) while \(v_j+x_j+v_k+x_k>2\), which implies \(v_j+x_j+v_k+x_k>v_i+x_i\). Thus,
 holds. Now let \(\varvec{x} \in \overset{\circ }{X}\) with \(x_i < \tfrac{1}{2}\), which implies there exists, say k such that \(x_k < \tfrac{1}{2}\). Then, a pillage from \(\varvec{x}\) to \(\varvec{s}^{ik}\) implies that \(W=\left\{ i,k\right\} \) and \(L=\left\{ j\right\} \). Again
holds. Now let \(\varvec{x} \in \overset{\circ }{X}\) with \(x_i < \tfrac{1}{2}\), which implies there exists, say k such that \(x_k < \tfrac{1}{2}\). Then, a pillage from \(\varvec{x}\) to \(\varvec{s}^{ik}\) implies that \(W=\left\{ i,k\right\} \) and \(L=\left\{ j\right\} \). Again  holds. This implies that \(\overset{\circ }{X}\subseteq D\left( \varvec{s}^{ab},\varvec{s}^{ac},\varvec{s}^{bc}\right) \).
holds. This implies that \(\overset{\circ }{X}\subseteq D\left( \varvec{s}^{ab},\varvec{s}^{ac},\varvec{s}^{bc}\right) \).In summary, \(X\backslash \left( K\cup \left\{ \varvec{s}^{ab}, \varvec{s}^{ac},\varvec{s}^{bc}\right\} \right) \subseteq D\left( K\cup \left\{ \varvec{s}^{ab}, \varvec{s}^{ac}, \varvec{s}^{bc} \right\} \right) \). Moreover, no allocation in \(K \cup \left\{ \varvec{s}^{ab},\varvec{s}^{ac},\varvec{s}^{bc}\right\} \) dominates another, satisfying internal stability. Therefore, \(S = K \cup \left\{ \varvec{b}^{ab},\varvec{b}^{ac},\varvec{b}^{bc}\right\} = K \cup \left\{ \varvec{s}^{ab}, \varvec{s}^{ac}, \varvec{s}^{bc} \right\} \).
\(\square \)
Proof of Theorem 7
By Theorem 1, \(K = \left\{ \varvec{t}^a, \varvec{t}^b, \varvec{t}^c, \varvec{b}^{ab} \right\} \) implies that \(v_c = 0\), \(1 + v_a > v_b\), \(1 + v_b > v_a\), and \(1 \ge v_a + v_b\). Then, \(\varvec{b}^{ab} = \varvec{e}_b^a = \varvec{e}_a^b\). Moreover, \(B \left( a \right) \ne \varnothing \), \(B\left( b \right) \ne \varnothing \) and \(B\left( c \right) \ne \varnothing \), where \(B\left( a \right) = \left\{ \varvec{x} \in X \mid x_a= \bar{\beta }_a^a \right\} \) with \(\bar{\beta }_a^a = \frac{v_b-v_a+1}{2} \in \left( 0, 1 \right) \), \(B\left( b \right) = \left\{ \varvec{x}\in X\mid x_b=\bar{\beta }_b^b\right\} \) with \(\bar{\beta }_b^b = \frac{v_a-v_b+1}{2} \in \left( 0, 1 \right) \), and \(B\left( c \right) = \left\{ \varvec{x} \in X \mid x_c = \bar{\beta }_c^c \right\} \) with \(\bar{\beta }_c^c = \frac{v_a+v_b+1}{2} \in \left( 0, 1 \right] \).
Let \(1 > v_a + v_b\). Then, by Corollary 4, no stable set exists whenever \(v_b > 0\). Assume \(v_b = 0\). Then, \(v_a < 1\), which implies that \(v_a - v_c < 1\), and so \(\varvec{b}^{ac}\in K\) by Theorem 1, a contradiction. Therefore, \(v_b > 0\) must hold.
Let \(1 = v_a + v_b\). If \(v_b = 0\), then \(1 = v_a + v_b\) implies \(1 = v_a\) while \(1 + v_b > v_a\) implies \(1 > v_a\), a contradiction. Thus, \(v_b > 0\). Thus, \(v_a < 1\). Assume \(v_a> \tfrac{1}{2} > v_b\). Then, \(1 + v_a > 3 v_b\) holds, so by Corollary 4(ii), no stable set exists.
Thus, let \(v_a = \tfrac{1}{2} = v_b\). Then, \(\bar{\beta }_a^a=\frac{1}{2}=\bar{\beta }_b^b\) and \(\bar{\beta }_c^c=1\). Thus, \(B \left( a \right) =\left\{ \varvec{x} \in X \mid x_a = \tfrac{1}{2} \right\} \), \(B \left( b \right) = \left\{ \varvec{x} \in X \mid x_b = \tfrac{1}{2} \right\} \), and \(B \left( c \right) = \left\{ \varvec{t}^c \right\} \). As usual, for any \(\varvec{x}\in X\) with \(x_a > \tfrac{1}{2}\), \(v_a + x_a > v_b + v_c + \left( 1 - x_a \right) \) holds, which implies  . Likewise, for any \(\varvec{y} \in X\) with \(y_b > \tfrac{1}{2}\), \(v_b+y_b>v_a+v_c+\left( 1 - y_b \right) \) holds, which implies
. Likewise, for any \(\varvec{y} \in X\) with \(y_b > \tfrac{1}{2}\), \(v_b+y_b>v_a+v_c+\left( 1 - y_b \right) \) holds, which implies  . Consider \(\left\{ \varvec{x}\in X\mid x_a< \tfrac{1}{2}, x_b< \tfrac{1}{2}, x_c < 1 \right\} \). Then, for any \(\varvec{z} \in \left\{ \varvec{x} \in X \mid x_a< \tfrac{1}{2}, x_b< \tfrac{1}{2}, x_c < 1 \right\} \),
. Consider \(\left\{ \varvec{x}\in X\mid x_a< \tfrac{1}{2}, x_b< \tfrac{1}{2}, x_c < 1 \right\} \). Then, for any \(\varvec{z} \in \left\{ \varvec{x} \in X \mid x_a< \tfrac{1}{2}, x_b< \tfrac{1}{2}, x_c < 1 \right\} \),
follows from \(B\left( c\right) =\left\{ \varvec{t}^c\right\} \). Thus,  . In summary, \(X \backslash K\subseteq D\left( \varvec{t}^a, \varvec{t}^b, \varvec{b}^{ab}\right) \), which implies \(S=\left\{ \varvec{t}^a, \varvec{t}^b, \varvec{t}^c, \varvec{b}^{ab}\right\} \). \(\square \)
. In summary, \(X \backslash K\subseteq D\left( \varvec{t}^a, \varvec{t}^b, \varvec{b}^{ab}\right) \), which implies \(S=\left\{ \varvec{t}^a, \varvec{t}^b, \varvec{t}^c, \varvec{b}^{ab}\right\} \). \(\square \)
Proof of Theorem 8
By Theorem 1, \(\varvec{b}^{ab}, \varvec{b}^{ac} \in K\) implies \(v_b = 0 = v_c\); \(\varvec{t}^a, \varvec{t}^b, \varvec{t}^c \in K\) then implies \(1 > v_a\). If \(v_a = 0\), then \(\varvec{b}^{bc} = \left( 0, \tfrac{1}{2}, \tfrac{1}{2} \right) \in K\) follows from Theorem 1, which is a contradiction. Therefore, \(v_a > 0\). Moreover, \(\varvec{b}^{ab} = \varvec{e}_b^a = \varvec{e}_a^b\), \(\varvec{e}_c^a = \varvec{b}^{ac} = \varvec{e}_a^c\), \(B \left( a \right) \ne \varnothing \), \(B\left( b \right) \ne \varnothing \) and \(B\left( c \right) \ne \varnothing \), where \(B\left( a\right) =\left\{ \varvec{x} \in X\mid x_a=\bar{\beta }_a^a\right\} \) with \(\bar{\beta }_a^a = \frac{-v_a+1}{2}\in \left( 0, 1 \right) \), \(B\left( b\right) = \left\{ \varvec{x}\in X\mid x_b=\bar{\beta }_b^b\right\} \) with \(\bar{\beta }_b^b=\frac{v_a+1}{2}\in \left( 0, 1 \right) \), and \(B\left( c\right) =\left\{ \varvec{x}\in X\mid x_c=\bar{\beta }_c^c\right\} \) with \(\bar{\beta }_c^c = \frac{v_a+1}{2} \in \left( 0,1\right) \).
Let \(v_a < \tfrac{1}{3}\). Then, by Corollary 4(ii), no stable set exists.
Let \(v_a \in \left[ \tfrac{1}{3}, 1 \right) \). Then, as usual, for any \(\varvec{x}\in X\) with \(x_a>\frac{-v_a+1}{2}\),  . Likewise, for any \(\varvec{y}\in X\) with \(y_b > \frac{v_a+1}{2}\),
. Likewise, for any \(\varvec{y}\in X\) with \(y_b > \frac{v_a+1}{2}\),  , and for any \(\varvec{z}\in X\) with \(z_c>\frac{v_a+1}{2}\),
, and for any \(\varvec{z}\in X\) with \(z_c>\frac{v_a+1}{2}\),  . Consider \(\left\{ \varvec{x}\in X\mid x_a< \frac{-v_a+1}{2}, x_b<\frac{v_a+1}{2}, x_c<\frac{v_a+1}{2} \right\} \). Then, for any \(\varvec{w}\in \left\{ \varvec{x}\in X\mid x_a<\frac{-v_a+1}{2}, x_b<\frac{v_a+1}{2}, x_c<\frac{v_a+1}{2}\right\} \),
. Consider \(\left\{ \varvec{x}\in X\mid x_a< \frac{-v_a+1}{2}, x_b<\frac{v_a+1}{2}, x_c<\frac{v_a+1}{2} \right\} \). Then, for any \(\varvec{w}\in \left\{ \varvec{x}\in X\mid x_a<\frac{-v_a+1}{2}, x_b<\frac{v_a+1}{2}, x_c<\frac{v_a+1}{2}\right\} \),
Thus,  .
.
Note that \(v_a \ge \tfrac{1}{3}\) implies that \(\bar{\varvec{\beta }}^i \in X\) if and only if \(v_a = \tfrac{1}{3}\) for \(i = b, c\). Moreover, in this case, \(\bar{\varvec{\beta }}^a = \left( \tfrac{1}{3}, \tfrac{1}{3}, \tfrac{1}{3} \right) \), \(\bar{\varvec{\beta }}^b = \left( 0, \tfrac{2}{3}, \tfrac{1}{3} \right) = \varvec{e}_c^b\), and \(\bar{\varvec{\beta }}^c = \left( 0, \tfrac{1}{3}, \tfrac{2}{3} \right) =\varvec{e}_b^c\) hold when \(v_a = \tfrac{1}{3}\).
Let \(v_a=\frac{1}{3}\). Then, for any \(\varvec{y}\in \left( \varvec{e}_a^b,\varvec{e}_c^b\right) \),  follows from Lemma 5. Likewise, for any \(\varvec{z} \in \left( \varvec{e}_a^c,\varvec{e}_b^c\right) \),
follows from Lemma 5. Likewise, for any \(\varvec{z} \in \left( \varvec{e}_a^c,\varvec{e}_b^c\right) \),  holds, as do
holds, as do  and
and  . In contrast, for any \(\varvec{x}\in \left( \varvec{e}_b^a, \bar{\varvec{\beta }}^a\right) \),
. In contrast, for any \(\varvec{x}\in \left( \varvec{e}_b^a, \bar{\varvec{\beta }}^a\right) \),  holds, while for any \(\varvec{x}\in \left( \bar{ \varvec{\beta }}^a,\varvec{e}_c^a\right) \),
holds, while for any \(\varvec{x}\in \left( \bar{ \varvec{\beta }}^a,\varvec{e}_c^a\right) \),  holds, by Lemma 5. Thus, we have \(X \backslash \left( K \cup \bar{\varvec{\beta }}^a \right) \subseteq D\left( K \right) \). As \(\bar{\varvec{\beta }}^a\) neither dominates nor is dominated by any allocation in K, \(K \cup \bar{\varvec{\beta }}^a\) satisfies internal stability. Therefore, \(S = K\cup \bar{\varvec{\beta }}^a\).
holds, by Lemma 5. Thus, we have \(X \backslash \left( K \cup \bar{\varvec{\beta }}^a \right) \subseteq D\left( K \right) \). As \(\bar{\varvec{\beta }}^a\) neither dominates nor is dominated by any allocation in K, \(K \cup \bar{\varvec{\beta }}^a\) satisfies internal stability. Therefore, \(S = K\cup \bar{\varvec{\beta }}^a\).
Let \(v_a \in \left( \tfrac{1}{3}, 1 \right) \). Then, for any \(\varvec{y}\in \left( \varvec{e}_a^b,\varvec{e}_c^b\right] \),  holds, while, for any \(\varvec{z}\in \left( \varvec{e}_a^c,\varvec{e}_b^c\right] \),
holds, while, for any \(\varvec{z}\in \left( \varvec{e}_a^c,\varvec{e}_b^c\right] \),  holds by Lemma 5. Moreover, for any \(\varvec{x}\in \left( \varvec{e}_b^a,\bar{\varvec{\beta }}^a \right) \),
holds by Lemma 5. Moreover, for any \(\varvec{x}\in \left( \varvec{e}_b^a,\bar{\varvec{\beta }}^a \right) \),  holds, while for any \(\varvec{x}\in \left( \bar{\varvec{\beta }}^a, \varvec{e}_c^a\right) \),
holds, while for any \(\varvec{x}\in \left( \bar{\varvec{\beta }}^a, \varvec{e}_c^a\right) \),  holds, by Lemma 5, where \(\bar{\varvec{\beta }}^a=\left( \frac{1-v_a}{2},\frac{1+v_a}{4},\frac{1+v_a}{4}\right) \).
holds, by Lemma 5, where \(\bar{\varvec{\beta }}^a=\left( \frac{1-v_a}{2},\frac{1+v_a}{4},\frac{1+v_a}{4}\right) \).
To conclude, \(X \backslash \left( K\cup \bar{\varvec{\beta }}^a\right) \subseteq D \left( K\right) \) holds. As \(\bar{\varvec{\beta }}^a\) neither dominates nor is dominated by any allocation in K, \(K \cup \bar{\varvec{\beta }}^a\) satisfies internal stability. Therefore, \(S = K \cup \bar{\varvec{\beta }}^a\). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kerber, M., Rowat, C. & Yoshihara, N. Asymmetric majority pillage games. Int J Game Theory 52, 1009–1035 (2023). https://doi.org/10.1007/s00182-023-00859-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-023-00859-y



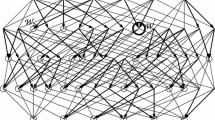

 , so that
, so that 
 holds by
holds by 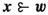 ; (iii).
; (iii).  ; and (iv).
; and (iv).  .
.
 , which implies
, which implies  . Thus,
. Thus,  : dominance would require
: dominance would require  and
and  : in either case, domination would require
: in either case, domination would require  : dominance would require
: dominance would require  and
and  : in either case, domination would require
: in either case, domination would require  is equivalent to
is equivalent to  is equivalent to
is equivalent to  . Moreover, the last strict inequality implies that
. Moreover, the last strict inequality implies that  . Again,
. Again, 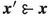 hold. By definition,
hold. By definition,  and
and  holds; and
holds; and implies that
implies that  .
.


 for
for  .
. . If
. If  if and only if
if and only if 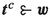 if and only if
if and only if  for
for  are observed over
are observed over  . Therefore,
. Therefore, 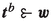 ; if
; if  holds, as
holds, as  holds. Thus,
holds. Thus,  and
and  for all
for all  , while any
, while any  , for any
, for any  holds. Now let
holds. Now let  holds. This implies that
holds. This implies that