Network disruption and the common-enemy effect

Abstract

We study the effect of a common enemy on the connections-model of network formation, where self-interested players can use links to build a network, knowing that they face a common enemy who can disrupt the links or nodes of the network. The goal of the common enemy is to minimize the sum of the benefits players obtain from the network. We find that for large linking costs, introducing such a common enemy can lead to the formation of pairwise stable and efficient networks which would not be pairwise stable without the threat of disruption. The reason is the large reduction in payoffs caused by disruption as soon as one player fails to maintain a link. However, we also find that for small linking costs, the empty network is pairwise stable under disruption, whereas it is not in the absence of disruption. The reason is that in the presence of disruption a link that is unilaterally formed is automatically targeted (or one of the players forming the link is automatically targeted). While the common enemy can thus have a positive effect on the incentives of the players to form an efficient network, it can also lead to the disintegration of the network.

1 Introduction

Networks are a key feature in many different parts of society. Companies depend crucially on transportation and distribution networks, whereas social relations often depend on communication or information networks. In these examples, being part of a network is beneficial for its members. The benefits of being part of the network depend on the structure of the network, where often it holds that players benefit more from their connections in the network the larger the number of players in it. However, before being able to benefit from a network, one first has to invest in building and maintaining costly connections within it to reach other players. Thus, from an economics standpoint one would like to know what network structures are efficient and whether individual players deciding on which links to form may actually achieve such efficient networks. A number of papers investigates networks from such an economics point of view (see, e.g., the seminal papers by Bala and Goyal (2000a) and Jackson and Wolinsky (1996) and the literature building on these papers).

Yet, networks often face external threats and the benefits of a network therefore do not only depend on its current structure, but on what remains of this structure after such threats have materialized. Thus, investing into being part of a network seems less beneficial if the network can be disrupted. Such disruption can arise from within the network as well as from outside the network and can be random as well as strategic. Random disruption is often modeled in epidemiology, climatology, and physics (see, e.g., Cerdeiro et al. 2017; Albert et al. 2000, and Bollobás and Riordan 2003). Strategic disruption is often modeled in the context of terrorist attacks (Arce et al. 2012) as well as in operations research (e.g., Lipsey 2006; Taylor et al. 2006), where the focus lies on survival analysis. Targets of such strategic disruption are often information, communication or financial networks (Haller 2016).

In general, disruption can be targeted at players within the network or at their connections and can, in both cases, have severe consequences on the functioning of the network as a whole. To ensure maximal functionality of networks after disruption, it is therefore important to analyze which network structures remain (largely) intact after disruption. For this, both types of network disruption - targeting the players within the network or the connections between them - need to be taken into account. In this paper, we are interested in the impact the threat of disruption has on a decentralized process of network formation. In such a decentralized process, which makes sense for instance in friendship or collaborative networks, the nodes in the network are players who decide themselves which connections to form. In particular, in this paper we develop a model in which a group of n players forms a network using costly connections (or: links) between them, knowing that afterwards the network will be attacked by a disruptor, who can either target the players (i.e., the nodes) or the links of the network. The players are assumed to be self-interested and therefore their aim is to maximize their own payoffs, whereas the disruptor’s aim is to cause as much damage as possible to the network.

Our model builds on the connections model of Jackson and Wolinsky (1996), where link formation is two-sided and where pairwise stability is employed as an equilibrium concept. In such a model, a link can only be formed if the players between which it is formed both consent to forming it (in which case both players incur linking costs), which seems an appropriate assumption for friendship or collaborative networks. Contrary to what is the case in the connections model, we abstract from information decay in order to isolate the effect of disruption (the effect of adding information decay is explored in the Conclusion, and in Appendix C).¹ We start off by analyzing the benchmark case without a disruptor and find that in this case the only pairwise stable networks are the minimally connected networks for small linking costs and the empty network for large linking costs. However, minimally connected networks are efficient both for small and large linking costs, so that for large linking costs minimally connected networks are efficient, but not pairwise stable (as only the empty network is pairwise stable).

We introduce a disruptor into this model who can either only remove links or only remove nodes (where initially we limit our analysis to the case where one link or one node can be removed). We describe two effects of the presence of a disruptor. First, the presence of a disruptor changes the structure of the networks that players form. When players are able to coordinate on forming a connected network, the network tends to be more tightly connected. At the same time, the presence of a disruptor means that it is always possible that the network-forming players coordinate on networks that are not connected, including on the empty network. Second, we find that the presence of a disruptor broadens the range of costs for which players are able to coordinate on a connected network. In detail, we find that for both link and node disruption, pairwise stable connected networks exist not only for the case of small linking costs, but also for the case of large linking costs. It follows that the presence of a disruptor makes it possible that the players efficiently form a network, which in the absence of a disruptor they were not able to do. We thereby find what can be termed as a common-enemy effect: individuals who face a common enemy are more likely to cooperate than if they do not face a common enemy. The intuition for such an effect is that the presence of the disruptor makes each player’s contribution to the network more critical, so that the individual player is less inclined to defect from joint network formation. In particular, for large linking costs, the circle is pairwise stable in the presence of a disruptor, because the removal of any link means that the disruptor will cut the network in two.

At the same time, as a consequence of the possibility that players are not able to coordinate on a connected network, we find that for small linking costs, there is an effect that is diametrically opposed to the (positive) common-enemy effect and which we term the negative common-enemy effect, where the presence of a common enemy decreases the probability of players cooperating. The intuition for the negative common-enemy effect in our results is that in the presence of a disruptor, no pair of players forms a link when no other pairs form links, as this one link is automatically targeted (or as one of the players forming the link is automatically targeted).

The paper is structured as follows. After a short literature review in Sects. 2, 3 presents the model of network formation and disruption. Section 4 analyzes the benchmark case without a disruptor, and Sects. 5 and 6 respectively analyze the case with a disruptor for unit disruption budgets, and for larger disruption budgets. Section 7 then concludes the paper.

2 Literature review

With this paper we add to two streams of literature - the literature on network disruption and the literature on the common-enemy effect. In the following, we discuss both streams concisely.

2.1 Literature on network disruption

Existing literature on strategic network disruption and defense mostly analyzes the defense by a centralized player against strategic disruption. In these models, disruption typically consists of the disruption of nodes in the networks and defense typically consists of investing in the protection of nodes, such as to reduce the effect of attacks on these nodes. Such defense is modeled as taking place on an existing network (Acemoglu et al. 2016; Kovenock and Roberson 2018). Alternatively, the centralized player also designs the network itself (Dziubiński and Goyal 2013; Goyal and Vigier 2014; Landwehr 2015; see Endres et al. (2019) for an experimental analysis of such models). Dziubiński and Goyal (2017) additionally consider the case where defense of the nodes takes place in a decentralized manner, but the network is exogenously given. In Cerdeiro et al. (2017), defense of the nodes is also decentralized, but the network is formed by a designer. Finally, Goyal et al. (2016) consider the case where both network formation and defense of the nodes takes place in a decentralized manner.

Bala and Goyal (2000b) analyze decentralized network formation when links independently fail with a positive probability, which can be seen as a model of non-strategic, random link disruption. Additionally, Jackson and Wolinsky (1995) shortly sketch an extension of their connections model to network reliability. In both papers, decentralized defense by network-forming players takes the form of these players adding extra links to minimally connected networks, as these create extra paths through which individual players can receive information. In Hoyer and De Jaegher (2016), defense also consists of adding links, but disruption is strategic, in that a strategic disruptor may either disrupt links or nodes. However, in this paper a centralized designer again designs the network.

Positioning our paper in the literature, contrary to Bala and Goyal (2000b), we focus on strategic disruption, and allow for node disruption (cf. literature reviewed in the first paragraph) as well as link disruption (cf. Hoyer and De Jaegher 2016). Contrary to the literature reviewed in the first paragraph, and in line with Bala and Goyal (2000b) and Hoyer and De Jaegher (2016), defense consists of adding extra links to the network. Also, we focus on decentralized defense. The paper most closely related to the present work is Haller and Hoyer (2019). These authors also analyze decentralized network formation in the presence of a strategic disruptor (who can only disrupt links), but focus on one-sided link formation and employ the Nash equilibrium as an equilibrium concept (cf. Bala and Goyal 2000a). In such a model, link formation decisions and costs are unilateral but benefits flow both ways. For a range of large linking costs, Haller and Hoyer find that the presence of a disruptor causes a negative common-enemy effect, which contrasts with our positive common-enemy effect for large linking costs. The reason is that with one-sided linking costs, in the absence of a disruptor, the periphery-sponsored star is a Nash network even for large linking costs. Yet, the presence of a disruptor decreases the benefit to a peripheral player to sponsor a link to the centre - hence the possibility of a negative common-enemy effect. Furthermore, for small linking costs, Haller and Hoyer do not find a negative common-enemy effect in our sense. The reason is that with one-sided link formation, one player can form several links at the same time and with small linking costs is inclined to do so whether or not a disruptor is present. In conclusion, the differences in results between the current paper and Haller and Hoyer (2019) are due to the different underlying network formation models. Whether link formation is one-sided or two-sided and which concept of stability is used determines the results. Different potential applications lead to these differences in modeling decisions. Whereas the model in Haller and Hoyer is more apt to model the formation of e.g. citation networks or networks of weblinks, our model more closely fits the formation of friendship networks or collaborative networks.

2.2 Literature on the common-enemy effect

The common-enemy effect can broadly be defined as saying that interaction with a common enemy fosters cooperation among individuals, an effect which has been discussed in a wide range of disciplines (for an overview, see De Jaegher 2021).² Typical rationales for the common-enemy effect are that the presence of a common enemy changes the information of the players, or changes their individual psychology or group psychology. Political scientists, for example, explain the effect that government repression against dissidents can backfire, by the fact that such repression informs dissidents about the violent character of the government (Pierskalla 2010). Alternatively, repression is argued to change the individual psychology of dissidents by making them angry and more eager to cooperate against the government (e.g. Siegel 2011). Other political scientists argue that common enemies change group psychology by creating a collective identity and/or increasing group solidarity (e.g. Koopmans 1997; Chang 2008).

Game-based laboratory experiments that test for such a change in psychology are designed such that the presence of a (perceived) common enemy has no effect on the incentives of the participants, so that a purely psychological common-enemy effect can be identified. For instance, Bornstein and Ben-Yossef (1994) find that participants playing a Prisoner’s Dilemma are more likely to cooperate when they perceive to be facing a competing group. Bornstein et al. (2002) and Riechmann and Weimann (2008) find a similar result for coordination in Stag-Hunt style games. In this paper, we instead model a purely rational common-enemy effect, where players cooperate more when facing a common enemy because the common enemy changes their incentives. This approach has also been taken in non-network models by De Jaegher and Hoyer (2016a, 2016b), where such a rational common-enemy effect arises in the context of public-good production. Yet, in these models, cooperation in the form of defense only has utility to the individual player when a common enemy is faced and the presence of a common enemy can never be beneficial to players (though a larger number of attacks can have a beneficial effect). By contrast, in the network model of the current paper, cooperating in the form of forming a link provides utility to the individual player even in the absence of a common enemy and the presence of a common enemy can make players better off.

Furthermore, a smaller number of papers formulates a hypothesis in line with a negative common-enemy effect (e.g. Carroll et al. 2005; McLauchlin and Pearlman 2012). At an intuitive level it is also plausible that the presence of a common enemy can create inner divisions and stop individuals from cooperating rather than encouraging them to cooperate (Stein 1976, p. 144). An additional contribution of our paper is to identify circumstances in which a rational positive common-enemy effect and a rational negative common-enemy effect should apply.

3 Model

Our model follows the connections model of Jackson and Wolinsky (1996) in a simplified version without information decay. We add to Jackson and Wolinsky’s model a disruptor who aims at causing maximal damage to the network and in order to do so either disrupts the network by removing a set of links or by removing a set of nodes from the network.³ This leads to two variants of a two-stage $(n+1)$-player game between a single disruptor and a set of network-forming players N with cardinality n, where $n\ge 4$.⁴ In the description of the model, for expositional reasons, we first look at the Stage-1 game of the network-forming players, who anticipate the Stage-2 best response of the disruptor. We then continue to define the disruptor’s benefits, which determine his Stage-2 best response. Finally, we also introduce some graph-theoretic concepts that we will use throughout the paper.

3.1 Stage-1 game of the network-forming players

Generic network-forming players (who are at the same time the nodes in the network) are referred to as i, j. In both variants of the game, at Stage 1, each pair of players $i,j \in N$ with $i\ne j$ either form a link to each other, denoted as $g^1_{ij}=1$ (alternatively, we also denote this as a link ij), or do not form a link to each other, in which case $g^1_{ij}=0$. Links are assumed to be undirected, so that it is always the case that $g^1_{ij}=g^1_{ji}$ (or put otherwise, there is no distinction between link ij and link ji). We assume that at most one link can be formed between two players $i \ne j$. The pre-disruption network $g^1$ formed by the players is the set of all links formed, i.e. the set of all pairs of players (i, j) such that $g^1_{ij}=1$. A subnetwork of a pre-disruption network $g^1$ consists of a subset $g^{1\prime } \subseteq g^1$.

The network-forming players anticipate that at Stage 2, the disruptor will observe $g^1$ and will disrupt this network (motivated by his benefits, as defined in Sect. 3.2). In the link-disruption variant of the game the disruptor chooses to delete links and in the node-disruption variant of the game he chooses to delete nodes in $g^1$ (where if node i is removed, any links of i with other players are also removed).⁵ An example of this are, e.g., authorities that ideally may be able to incarcerate a criminal who forms part of a criminal network (= node disruption), but when there is not enough evidence against this criminal may still be able to restrict the criminal’s communications or movements (= link disruption). In the variant of the game with link disruption, the disruptor chooses at Stage 2 a set $\mathfrak {D}_l$ of links to remove from $g^1$, where $|\mathfrak {D}_l|=D_l$ is the disruptor’s link-disruption budget and $D_l \ge 1$. In this case, the post-disruption network $g^2$ is a subnetwork of $g^1$ consisting of the set of all links in $g^1$ that were not removed by the disruptor; put otherwise, $g^2=g^1 {\setminus } \mathfrak {D}_l$. In the variant of the game with node disruption, the disruptor chooses at Stage 2 a set $\mathfrak {D}_v$ of nodes to remove from $g^1$, where $|\mathfrak {D}_v|=D_v$ is now the disruptor’s node-disruption budget and $D_v \ge 1$. In this case, the post-disruption network $g^2$ is a subnetwork of $g^1$ consisting of the subset of players that were not removed by the disruptor and of all the links in $g^1$ between these players; put otherwise, the post-disruption network $g^2$ is now the set of all pairs of players (i, j) such that $i,j \notin \mathfrak {D}_v$ and such that $g^1_{ij}=1$. Where appropriate, we use notation $g^2_{ij}=1$ with $i\ne j$ to denote that there is a link between players i and j in $g^2$, and $g^2_{ij}=0$ to denote that there is no such link.

In each variant, the disruptor at Stage 2 removes links or nodes according to a best-response correspondence $\gamma ^2(g^1)$, determining the post-disruption networks that the disruptor chooses as a function of the pre-disruption network $g^1$ he observed. Given the disruptor payoffs as will be defined in Sect. 3.2, it is possible that the disruptor is indifferent between several post-disruption networks. It follows that for any pre-disruption network $g^1$, the set $\gamma ^2(g^1)$ may contain more than one post-disruption network $g^2$, where we denote the cardinality of this set by $\Gamma$. When for a pre-disruption network $g^1$, $\gamma ^2(g^1)$ contains only one element ($\Gamma =1$), then we refer to $g^1$ as a non-stochastic pre-disruption network. When $\gamma ^2(g^1)$ contains more than one element ($\Gamma >1$), we refer to $g^1$ as a stochastic pre-disruption network, where $\gamma ^2(g^1)={g^2_1(g^1),g^2_2(g^1),...,g^2_\Gamma (g^1)}$. In this case, we assume that the network-forming players form common beliefs ${\mu [g^2_1(g^1)],\mu [g^2_2(g^1)],...,\mu [g^2_\Gamma (g^1)]}$, with $\sum _{x=1}^\Gamma \mu [g^2_x(g^1)]=1$, about the probability with which the disruptor chooses each post-disruption network in $\gamma ^2(g^1)$. While we state our results for generic beliefs where possible (referred to below as generic disruptor randomization),⁶ we assume in parts of our analysis that the network-forming players form uniform beliefs (referred to below as uniform disruptor randomization), where for every $g^2_x(g^x)$ in $\gamma ^2(g^1)$ it is the case that $\mu [g^2_x(g^x)]=\frac{1}{\Gamma }$. This assumption is in line with the Principle of Insufficient Reason (e.g. Bardsley and Ule 2017): as the disruptor obtains exactly the same payoff from each post-disruption network in $\gamma ^2(g^1)$, one can argue that the network-forming players have no reason to believe that the disruptor is more likely to choose one network than another. For node disruption, in case of a stochastic pre-disruption network, we further specify the set of post-disruption networks $\gamma ^2_{i}(g^1)$ in which player i is not removed from the network.

While each network-forming player forms his links at Stage 1 before the disruptor has disrupted links or nodes, he obtains his payoffs at the end of Stage 2, after the disruptor has disrupted links or nodes. As the individual network-forming player i anticipates the best response of the disruptor, when a pre-disruption network $g^1$ is formed at Stage 1, the expected payoff of player i can be expressed as a function of $g^1$. It takes the form $u_i(g^1)=b_i(g^1)-c_i(g^1)$, where $b_i(g^1)$ refers to player i’s expected benefit from network $g^1$ given his beliefs, and $c_i(g^1)$ denotes the costs that player i incurs in the network. The linking costs $c_i(g^1)$ are determined by the number of links of player i in the pre-disruption network. We assume that when $g^1_{ij}=1$, both players i and j incur a cost c. Given that each link bears a fixed cost c, this means that $c_i(g^1)=c\sum _{j=1}^{n}g^1_{ij}$, where $\sum _{j=1}^{n}g^1_{ij}$ is player i’s degree in $g^1$. The network benefits of a player i are determined by the number of players, including himself, to which he has access in $g^2$. A player i has access to the information of another player j if a path connects i and j in network $g^2$. We say that a path connects $i_1$ and $i_k$ in $g^2$ if $g^{2}_{i_1, i_2}= g^{2}_{i_2, i_3}=...=g^{2}_{i_{k-1},i_k}=1$, with $i_1, i_2, i_3,...,i_{k-1},i_k$ all distinct (note that any direct link $i_{1}i_{k}$ between $i_1$ and $i_k$ is also a path). We denote by $\mathcal {N}_i(g^2)$ the set of all nodes $j \ne i$ for which there is a path in the post-disruption network $g^2$ between i and j. We can now write the expected benefits of a network-forming player i as:

$$\begin{aligned} b_i(g^1)=\sum {_{x\in \gamma }\mu _x[g^2_x(g^1)][|\mathcal {N}_i(g^2_{x}(g^1))|+1]}. \end{aligned}$$

(1)

with $\gamma =\gamma ^2(g^1)$ for link disruption, and $\gamma =\gamma ^2_{i}(g^1)$ for node disruption. Note that with node disruption, the set $\gamma ^2_{i}(g^1)$ contains only the post-disruption networks in which player i is not disrupted, as player i’s payoff when being disrupted under node disruption is zero. Note as well that if under node disruption player i is always disrupted, the set over which summation is taken in (1) is empty, so that $b_i(g^1)=0$.

Finally, following Myerson (1977) and Jackson and Wolinsky (1996), we assume that the value of a network is the sum of all the individual expected payoffs of the players; since what we model is essentially a communications network and since information is non-rival, this assumption is reasonable. We therefore assume that the value of the network after disruption is given by $v(g^1)=\sum _{i \in N}u_i(g^1)$. We say that a network $g^1$ is efficient when for all $g^{1\prime }$ other than $g^1$, it is the case that $v(g^1)\ge v(g^{1\prime })$. We call a network $g^1$ more efficient than a network $g^{1\prime }$ when $v(g^1)>v(g^{1\prime })$.⁷ To further characterize the value of the network, define a subnetwork as being connected if there is at least one path between all the nodes in the subnetwork. Define the order of a subnetwork as the cardinality of its set of nodes.⁸ A component of a network is a connected subnetwork with maximal order. Note that a post-disruption network may consist of several components. As there is a path between all players in a component, it follows that all the players in a post-disruption component with order $n_1$ obtain benefit $n_1$. When a post-disruption network now consists of components $C_1,C_2,...,C_m$, then the benefit part of the value of this network equals $\sum _{i=1}^m|C_i|^2$. This follows Metcalfe’s law (Shapiro et al. 1998, p. 184), stating that the value of a communications network is proportional to the square of the number of nodes it connects.

Given that the network-forming players’ payoffs can be expressed solely as a function of the pre-disruption network (which in turn follows from the fact that the network-forming players anticipate the disruptor’s best response), the equilibrium achieved by these players can also be defined only in terms of the pre-disruption network. In particular, we assume that the network-forming players form a pairwise stable pre-disruption network. When $g_{ij}=0$ in g, $g+ij$ denotes that a link ij is added to g; when $g_{ij}=1$ in g, $g-ij$ denotes that a link ij in g is no longer maintained. We then define:

Given the disruptor’s best-response correspondence $\gamma ^2(g^1)$, and given common beliefs of the network-forming players ${\mu [g^2_1(g^1)],\mu [g^2_2(g^1)],...,\mu [g^2_\Gamma (g^1)]}$, with $\sum _{x=1}^\Gamma \mu [g^2_x(g^1)]=1$ corresponding to every stochastic predisruption network $g^1$, a pre-disruption network $g^{1*}$ is pairwise stable iff

• 1. for all $g^{1*}_{ij}=1$ in $g^{1*}$, $u_{i}(g^{1*})\ge u_{i}(g^{1*}-ij)$ and $u_{j}(g^{1*})\ge u_{j}(g^{1*}-ij)$, and

• 2. for all $g^{1*}_{ij}=0$ in $g^{1*}$, if $u_{i}(g^{1*}+ij)>u_{i}(g^{1*})$ then $u_{j}(g^{1*}+ij)<u_j(g^{1*})$.

With pairwise stability, while the decision to not maintain a link is unilateral, for link formation both players between whom the link is formed need to consent. Thus, a pre-disruption network is pairwise stable if and only if no player unilaterally wants to stop maintaining a link and no pair of players wants to add a link, always taking into account that the network will be disrupted and that this will influence the players’ respective expected payoffs. We limit our analysis to pairwise-stable pre-disruption networks that are either connected or are empty, and to the comparative efficiency of such networks. This is because our focus is on showing that for small linking costs, the presence of a disruptor can cause a decrease in efficiency (in that players may coordinate on an empty network), whereas for large linking costs, the presence of a disruptor can lead to an increase in efficiency (in that players may coordinate on a connected network).

3.2 Payoffs of the network disruptor and implied stage-2 best response

We finally look at the payoffs of the disruptor, which determine his best-response correspondence. We assume that the goal of the disruptor is to minimize total benefits from the post-disruption network. Given the quadratic structure of the total benefits from the network, this means that when comparing networks consisting of two components, the larger the largest of the two components is, the worse off the disruptor is. In part of our analysis of node disruption, to keep the analysis tractable, following Hoyer and De Jaegher (2016), we approximate a disruptor that minimizes total benefits from the network, by assuming that the disruptor has lexicographic preferences in the following sense.⁹ Comparing two post-disruption networks, the disruptor always prefers the network where the component with the largest order is smaller. If two networks have largest components of equal order, the disruptor always prefers the network of which the component with the second-largest order is smaller. If the second-largest components also have the same order, he prefers the network of which the component with the third-largest component is smaller, and so on. Formally, consider a post-disruption network $g^2$. This network can be characterized by ranking its components by their order. So the network is characterized by its components $C_1, C_2,...,C_k,...,C_m$, where it holds that $|C_1| \ge |C_2| \ge ... \ge |C_k| \ge ...\ge |C_m|$ and $|C_1|+|C_2|+...+|C_k|+...+|C_m|=n$. Given a pre-disruption network $g^1$ including n players, we can then compare two possible post-disruption networks $g^2_a$ and $g^2_b$. We assume that the disruptor has lexicographic preferences in the following way. Letting $\succ$ denote the preference relation, for the disruptor it holds that $g^2_a \succ g^2_b$ iff $|C^a_1|<|C^b_1|$ or $|C^a_k|= |C^b_k|$ and $|C^a_{k^*}| <| C^b_{k*}|$, where $k^*$ is the smallest rank for which a component in $g^2_a$ and a component in $g^2_b$ with identical rank have a different order.¹⁰$^{,}$¹¹ Under node disruption, with lexicographic preferences of the disruptor, any stochastic network can only be pairwise stable if the subnetworks that the disruptor can disconnect from the network all have the same order, which simplifies the analysis.

3.3 Graph-theoretic concepts

Before starting with the main analysis, we introduce some further graph-theoretic concepts and definitions that will be needed to describe our results. In the empty network, every node in N has zero links. A connected network is minimally connected if removal of any link means that it is no longer connected (note that every minimally connected network has exactly $(n-1)$ links). An end node (or end player) is a node that has only a single link; an end link is a link to an end node. An example of a minimally connected network is the star, where one central node has $(n-1)$ links to the $(n-1)$ end nodes. Another example is the line, where two nodes are end nodes, and all other nodes have two links.

For link disruption, we say that removing a set of links from a connected network disconnects this network if removing these links results in a network consisting of more than one component. Borrowing definitions from graph theory (e.g. Harary 1962; Halin 1969; Diestel 2010), we now define:

Definition 1

For $k\ge 2$, a connected network is k-link connected if it is impossible to disconnect the network by removing $k-1$ or fewer links. A network is minimally k-link connected if non-maintenance of any link in the network means that the network is no longer k-link connected.

When a network is k-link connected with $k\ge (D_l+1)$, we say that this network is robust against disruption with a disruption budget of $D_l$. Otherwise, we say that the network is non-robust.

For node disruption, we say that removing a set of nodes from a network disconnects this network if removing these nodes results in a post-disruption network of which the largest component has order strictly smaller than $n-D_v$. We now again borrow definitions from graph theory (e.g. Harary 1962; Halin 1969):

Definition 2

For $k\ge 2$, a connected network is k-node connected if it is impossible to disconnect the network by removing $k-1$ or fewer nodes. An network is minimally k-node connected if non-maintenance of any link in the network means that the network is no longer k-node connected.

When a network is k-node connected with $k\ge (D_v+1)$, we say that this network is robust against disruption with a disruption budget of $D_v$. Otherwise, we say that the network is non-robust.

Define a cycle as a path between nodes i and j in the network such that $i=j$ and which consists of at least three links. A circle network is a network consisting of a cycle containing of all players, and in which each node has exactly two links. Note now that the circle is an example of a minimally 2-link connected network and is robust against a link disruption budget of 1: disruption of any one link turns the network into a connected network in the form of a line. The circle at the same time is an example of a minimally 2-node connected network: disruption of any node results in a connected subnetwork linking $n-1$ nodes in a line.

4 Benchmark case

We begin our analysis by looking at the benchmark case in which there is no disruptor. This is the case analyzed by Jackson and Wolinsky (1996) in the symmetric connections model, with the difference that we abstract from decay.¹² While Jackson and Wolinsky do not treat the case without decay explicitly, it is straightforward to adjust their results to such a case. As without decay the distance between players in the network does not matter, for small linking costs (i.e. linking costs such that it is worth to be linked to one node for the benefit of that node alone) all minimally connected networks are pairwise stable. At the same time, minimally connected networks are efficient. This is because they link nodes with a minimal number of links and because of the increasing added benefits of connecting extra players: each extra player connected to the network creates benefits for all players that were already connected. For the case of large linking costs, the only pairwise stable network is the empty network. This is because no player is willing to link to an end player, so that minimally connected networks are not pairwise stable. At the same time, non-minimally connected network are not pairwise stable either, as they have redundant links. Yet, once redundant links are no longer formed, the network contains end players and because of the large linking costs the network will unravel. While the empty network is thus the only pairwise stable network, it is not efficient as long as linking costs are not too large (specifically, as long as $c<\frac{n}{2}$). For large linking costs, in the benchmark case there is thus a tension between stability and efficiency.¹³

Proposition 1

In the symmetric connections model without decay and without a threat of disruption, the following applies:

• for $c<1$, all minimally connected networks are pairwise stable and are also efficient;

• for $c>1$, only the empty network is pairwise stable, even though all minimally connected networks are efficient as long as $c<\frac{n}{2}$.

We thus obtain benchmark cases without disruption both for large linking costs and for small linking costs. For both these cases, Proposition 1 provides benchmark stability and efficiency results, which we will use throughout the paper as a point of comparison for the results with a disruptor.

5 Unit disruption budgets: pairwise stability and comparative efficiency of empty and connected networks

In this section, we provide our results for link disruption and node disruption when the disruption budget is 1. Our aim is two-fold. First, we want to know how the presence of a disruptor changes the structure of pairwise stable networks in comparison to the benchmark case. Our focus is on the empty network and on connected networks and we do not treat pairwise stable networks consisting of multiple components. This is because the fact that the empty network is pairwise stable already drives home the point that players can coordinate on inefficient networks; moreover, the structural characteristics of pairwise stable networks consisting of multiple components are similar to those of connected networks (for instance, when the circle networks are pairwise stable, then so are unconnected networks consisting of multiple circle components). Our analysis of pairwise stable connected networks considers both non-stochastic and stochastic networks.

Second, we want to know for what cost ranges the presence of a disruptor can improve network-forming players’ welfare by making it possible that they coordinate on a connected network (positive common-enemy effect) and for what cost ranges the presence of a disruptor can worsen the welfare of the network-forming players by making it possible that they coordinate on the empty network (negative common-enemy effect).

5.1 Link disruption with a unit disruption budget

For the case of link disruption, Proposition 2 provides general results for generic disruptor randomization and more detailed results for the case of uniform disruptor randomization. The empty network is always pairwise stable and non-robust networks (i.e. networks in which the disruptor can disconnect at least one player from the rest) can only be pairwise stable if they are stochastic (i.e., if the disruptor is indifferent between disrupting several links). Under uniform disruptor randomization, the only non-robust network that is pairwise stable is the star, and this for a small range of linking costs; for generic disruptor randomization, the star is part of a wider set of non-robust stochastic networks that can be pairwise stable, where each time the disruptor randomizes between disconnecting several end nodes from the rest of the network. Robust networks (i.e. networks for which the disruptor cannot disconnect any players from the rest) can only be pairwise stable if they are minimally 2-link connected (see Definition 1), and as the case of uniform disruptor randomization shows, such networks are pairwise stable for a wider range of parameters, with the circle the most efficient minimally 2-link connected network (i.e., the sum of network-forming players’ payoffs is highest). With uniform disruptor randomization, for a small range of intermediate linking costs, pairwise stable minimally 2-link connected networks exist, even though the empty network is more efficient. Finally, for sufficiently large linking costs, only the empty network is pairwise stable.

Proposition 2

In the symmetric connections model without decay and with link disruption ($D_l=1$), the following applies:

• With generic disruptor randomization:

  • the empty network is always pairwise stable;

  • any robust connected network that is pairwise stable is a minimally 2-link connected network;

  • the only non-robust connected networks that can be pairwise stable are stochastic networks where the subnetworks that the disruptor can disconnect from the network have order 1.

• With uniform disruptor randomization, the only non-robust connected networks that can be pairwise stable are the stars. In detail:

  • for $c<\frac{n-1}{2}$, the set of pairwise stable robust connected networks is non-empty and consists of a set of minimally 2-link connected networks, where additionally for $1-\frac{1}{n-1}<c<1$, the star is pairwise stable; among these networks, the circle is the most efficient;

  • for $\frac{n-1}{2}<c<\frac{n}{2}$, the set of pairwise stable robust connected networks is non-empty and contains the circle, but the empty network is more efficient than every network in this set;

  • for $c>\frac{n}{2}$, only the empty network is pairwise stable.

Intuitively, the empty network is always pairwise stable because if starting from the empty network, two players unilaterally form a link, then this link is automatically targeted by the disruptor, resulting in only extra costs for the two players and no extra benefits.

Looking at non-robust networks, it could be imagined that players coordinate on a non-stochastic network where the disruptor strictly prefers to disrupt one specific link connecting two subnetworks. To see why such a network cannot be pairwise stable, note first that the subnetwork with the weakly smallest order must be minimally connected, as the disruptor does not have any incentive to disrupt a link within this subnetwork. A player in such a smaller subnetwork with an end link only loses at most one unit of information when failing to maintain this end link, as this will still not lead the disruptor to disrupt a link in the mentioned subnetwork. At the same time, two players across the two subnetworks can gain several units of information by adding a link to each other. It follows that if linking costs are smalle enough for the mentioned end link to be maintained, then pairwise stability is not obtained because the two mentioned players want to form an extra link; if linking costs are large enough for the two mentioned players not to want to form an extra link, then pairwise stability is not obtained because the mentioned end link will not be maintained.

Other candidates for pairwise stable non-robust networks are stochastic networks where the disruptor is indifferent between disconnecting several subnetworks from the rest of the network. Such networks cannot be pairwise stable if the subnetworks have order larger than 1, because a player within such a subnetwork can then divert disruption towards another subnetwork by not maintaining a link. For stochastic networks with potentially disconnected subnetworks of order 1 to be pairwise stable, none of the end players in such subnetworks should prefer to form links to each other. With uniform disruptor randomization, end players are least inclined to do so in the star. In fact, with uniform disruptor randomization, the star is the only non-robust network that can be pairwise stable and even this network is only pairwise stable for a narrow range of linking costs. This is because linking costs must at the same time be low enough for the central player to want to form a link, and not so low that two end players want to form an extra link. As shown in Appendix A, allowing for generic disruptor randomization only slightly modifies the range of linking costs for which stars are pairwise stable. Moreover, with generic disruptor randomization, as illustrated in Appendix B core-periphery networks consisting of a central cycle with end nodes directly connected to the nodes in the cycle, are additionally pairwise stable for specific cost ranges and specific randomization strategies of the disruptor.

Looking at robust networks, by Definition 1, 2-link connected networks are robust, but cannot be pairwise stable unless they are minimally 2-link connected, as otherwise at least one link would not be maintained by the network-forming players. The circle (see Fig. 1a) was already given as an example of a minimally 2-link connected network, but is not the only such network. Figure 1b and c, referred to respectively as the spanning circle and the nested circle, represent two minimally 2-link connected networks that have more links than the circle. Each such minimally 2-link connected network is pairwise stable for an appropriate range of linking cost levels. With uniform disruptor randomization, the circle is the network that is pairwise stable for the largest range of cost levels (in the sense that if any non-circle 2-link connected network is pairwise stable, then so is the circle). This is because a player who fails to maintain a link in the circle has most to lose, as the disruptor is able to cut the network in two, disconnecting half of the other players from the player. For instance, the circle in Fig. 1a is pairwise stable for $c<4.5$, the spanning circle (Fig. 1(b)) is pairwise stable for $c<3$, and the nested circle (Fig. 1(c)) is pairwise stable for $c<1$. These conditions are only slightly changed with generic disruptor randomization. For instance, if n is odd, as in Fig. 1(a), the benefit of a player who fails to maintain a link in the circle with generic randomization can at most be reduced from 4.5 to 4, obtained when in the line the disruptor disrupts with probability 1 the link that is least favorable to this player. Also, as the driving force behind the pairwise stability of minimally 2-link connected networks is the disruption that takes place when a player removes a link, the results are also maintained in a variant of the model where the disruptor has a cost function over the number of disrupted links, instead of a disruption budget; if costs are sufficiently large, the disruptor then does not disrupt minimally 2-link connected networks.

Fig. 1

Minimally 2-link connected networks for $n=9$

Proposition 2 also considers efficiency by comparing the network value achieved for the pairwise stable networks (focusing on uniform disruptor randomization). Notably, for a narrow range of costs just below the largest cost levels (a range which vanishes as n becomes large), the circle and the empty network are both pairwise stable, even though the empty network is more efficient than the circle network. The presence of such an additional range of costs is a consequence of the assumption in the pairwise-stability concept that each player only considers removing a single link at a time. The individual player prefers to have no links rather than two links in the circle when $c>\frac{n-1}{2}$. The concept of a pairwise strong Nash equilibrium (Belleflamme and Bloch 2004), which is a variant of pairwise stability where the individual players can decide to stop maintaining any number of links, eliminates circles in the cost range $\frac{n-1}{2}<c<\frac{n}{2}$. Yet, except for this narrow range of costs, this alternative equilibrium concept does not change our results.¹⁴

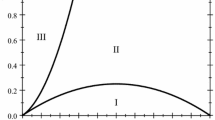
We are now ready to compare the benchmark case without disruption (Proposition 1), to the case of a unit linking budget (Proposition 2), where we focus on uniform disruptor randomization. This comparison is graphically represented in Fig. 2. We first look at the case of small linking costs ($0<c<1$). In this case, players are always able to coordinate on forming a connected network in the absence of a disruptor. When a disruptor is present who can disrupt links, players can still coordinate on forming a connected network. However, they can also coordinate on forming an empty network. As soon as the latter happens with positive probability, the presence of a common enemy in the form of a strategic disruptor thus has a negative effect on the welfare of the network-forming players, as they may no longer coordinate on forming a network. The reason for this negative common-enemy effect is the following. Starting from the empty network two players are always better off forming a link in the absence of disruption. In the presence of a strategic disruptor, however, this is not the case as a link formed by these two players is automatically disrupted. The presence of a strategic disruptor thus means that players may no longer be able to escape a situation where no player cooperates.

We next compare the benchmark case to the case of link disruption for large linking costs (i.e. the range $1<c<\frac{n-1}{2}$) (but not for the largest linking costs, where only the empty network is pairwise stable with or without a disruptor). As illustrated in Fig. 2, for n that is not small, this is a relatively large range compared to the range of small linking costs, $0<c<1$. In the absence of disruption, with large linking costs players are never able to coordinate on forming a connected network. This is because a necessary condition for networks to be pairwise stable is that they contain end players. For large costs, the cost of maintaining a link to an end player is larger than the benefit. For this reason, the only pairwise stable network is the empty network. Yet, with link disruption, while the empty network continues to be pairwise stable, connected networks are additionally pairwise stable. This is because deviating from joint cooperation by not maintaining a link can now lead to large losses for a player, if, for example, this leads to the network being cut in half by the disruptor. It follows that the benefits of forming links can still outweigh the large linking costs. For large linking costs, we therefore observe a positive common-enemy effect.

Fig. 2

For uniform disruptor randomization, overview of pairwise stability and relative efficiency of networks depending on disruption budget and linking costs c for $n \ge 5$

5.2 Node disruption with a unit disruption budget

Proposition 3 summarizes the results for node disruption, again looking first at generic disruptor randomization, and then at the more specific case of uniform disruptor randomization. Just as is the case for link disruption, with generic disruptor maximization, it is the case that the empty network is always pairwise stable, and that non-robust connected non-stochastic networks (i.e. networks where by disrupting a node the disruptor can disconnect at least one extra node from the rest of the network, and where the disruptor prefers to disrupt one specific node) are never pairwise stable. Specifically for lexicographic preferences of the disruptor (see Sect. 3.2), non-robust connected networks are never pairwise stable. With uniform disruptor randomization, for a range of small linking costs, robust networks (i.e. networks where by disrupting a node the disruptor cannot disconnect extra nodes from the rest of the network) that are pairwise stable exist in the form of minimally 2-node connected networks (see Definition 2). Among these networks, the circle is the most efficient (i.e., the sum of the network-forming players’ payoffs is largest). For larger linking costs, only the empty network is pairwise stable.

Proposition 3

In the symmetric connections model without decay and with node disruption ($D_v=1$), the following applies:

• With generic disruptor randomization:

  • the empty network is always pairwise stable;

  • non-robust connected non-stochastic networks are never pairwise stable;

  • specifically with lexicographic preferences of the disruptor, non-robust connected stochastic networks are never pairwise stable either.

• With uniform disruptor randomization:

  • for $c<\frac{(n-1)(n-2)}{2n}$, both empty and minimally 2-node connected networks are pairwise stable; among these networks, the circle network is the most efficient;

  • for $c>\frac{(n-1)(n-2)}{2n}$, only the empty network is pairwise stable.

Intuitively, under node disruption with uniform disruptor randomization, the empty network continues to be pairwise stable because when a pair of players deviates from the empty network and forms a link, they incur a cost but are disrupted with probability 0.5 rather than with probability 1/n. Considering generic disruptor randomization does not change this result, as a mixed disruption strategy that makes it more attractive for one player to deviate from the empty network and form a link, makes it less attractive for the other player. Also, non-robust connected non-stochastic networks are again never pairwise stable because a node that is always disrupted obtains payoff zero and can therefore only become better off by not maintaining the links that it has.

The analysis of non-robust connected stochastic networks is complicated by the fact that with node disruption, disrupting a single node may mean that the post-disruption consists of more than two components (e.g. by disrupting the central node in Fig. 3(b), the network is separated into three parts). In this case a disruptor who minimizes total benefits from the network can be indifferent between disrupting two nodes even if the order of the subnetworks that the disruptor can disconnect from the rest of the network is unequal.¹⁵ To avoid this complication, we focus this part of our analysis on a disruptor with lexicographic preferences, where the subnetworks that the disruptor can disconnect from the rest of the network necessarily have the same order (as the disruptor can otherwise not be indifferent). Non-robust connected stochastic networks with this characteristic are not pairwise stable because either a player that can be disconnected from the rest of the network prefers to remove a link to divert the disruptor’s attack to another part of the network, or prefers to add a link to another potentially disconnected player with the same purpose.

Considering pairwise stable robust networks, following Definition 2, analogously to what is the case for link disruption, 2-node connected networks are robust, but are only pairwise stable when they are minimally 2-node connected, as otherwise at least one link would not be maintained by the players. The circle (Fig. 1a) is again an example of a 2-node connected network, as is the nested circle (Fig. 1c). Yet, the spanning circle (Fig. 1b) is not 2-node connected, as can be seen by the effect of disrupting the node with four links. The set of minimally 2-node connected networks is therefore smaller than the set of minimally 2-link connected networks. Minimally 2-node connected networks are again pairwise stable for an appropriate range of linking costs, where with uniform disruptor randomization, as linking costs are raised, the circle network is the last to remain pairwise stable. For instance, it can be checked that the nested circle is pairwise stable for $c<\frac{1}{9}$, while the circle is pairwise stable for $c<3.11$. Proposition 3 does not consider the pairwise stability of robust networks for non-uniform disruptor randomization, which can considerably affect the results. For instance, if players believe that in the circle one specific player is disrupted with sufficiently high probability, then the circle is not pairwise stable, as this player will prefer not to maintain his links. However, when deviating from our simplifying assumption of a disruption budget and assuming instead that the disruptor faces disruption costs, the disruptor may find it too costly to disrupt a node in the circle, and may only disrupt in case several nodes can be disconnected such as in the line, in which case the circle continues to be pairwise stable even for generic disruptor randomization.

As far as efficiency is concerned, under uniform disruptor randomization, contrary to what is the case with link disruption, when robust networks exist that are pairwise stable, these networks always include a network that is more efficient than the empty network.

We finally compare the benchmark case to the case with node disruption for a unit disruption budget, focusing on uniform disruptor randomization. This comparison is again graphically represented in Fig. 2, which focuses on the case $n\ge 5$ (for $n=4$, it is the case that $1-\frac{1}{n}=\frac{(n-1)(n-2)}{2n}<1$ ). The results are similar to those for link disruption: the presence of a disruptor again means that there is a range of large linking costs for which connected pairwise stable networks exist, whereas no such networks existed in the absence of a disruptor (positive common-enemy effect). At the same time, for small linking costs, only connected networks are pairwise stable in the absence of a disruptor, but in the presence of a disruptor the empty network additionally becomes pairwise stable (negative common-enemy effect).¹⁶

6 Larger disruption budgets

Having analyzed the case of link disruption with disruption budget $D_l=1$ and of node disruption with disruption budget $D_v=1$, we now look at larger disruption budgets for both types of disruption, where we limit ourselves to uniform disruptor randomization. Our focus is on a particular class of robust networks and on the empty network. We start by defining some additional graph-theoretical concepts required for the description of the results. A k-regular network is a network where each node has precisely k links (i.e., has degree k). A particular class of regular networks are circulant networks, which are defined as follows.¹⁷

Definition 3

Label the nodes of a network as $0,1,2,..., n-1$. A circulant network $C_n(a_1, a_2,..., a_k)$, where $0<a_1<a_2...<a_k< \frac{n+1}{2}$, has node i linked to node $i\pm a_1, i \pm a_2,..., i \pm a_k$ (mod n). The sequence $(a_1, a_2,..., a_k)$ is called the jump sequence and $a_i$ (with $i=1,...,k$) is called a jump. For $a_k \ne \frac{n}{2}$, the network is 2k-regular, and for n even and $a_k=\frac{n}{2}$, it is $2k-1$-regular.

$D_{l}+1$-regular networks and $D_{v}+1$-regular networks seem good candidates for pairwise stability, as each individual node has precisely enough links not to be disconnected. Yet, as Fig. 3 illustrates for the case $n=16$ and $D_{l}=2$ or $D_{v}=2$, not all regular networks are pairwise stable. Figure 3a can be cut in half by removing two links or nodes. The network in Fig. 3b is also vulnerable, especially when it comes to node disruption. Figure 3c, however, represents the circulant $C_{16}(1,8)$, which can be checked to be pairwise stable for both link and node disruption.

Fig. 3

3-Regular networks for $n=16$

In Hoyer and De Jaegher (2016), applying graph-theoretic literature, it is shown that connected circulants that are regular of degree $D_{l}+1$ are minimally $D_{l}+1$ link-connected, and are therefore robust networks for link disruption with a disruption budget $D_l$. Moreover, it is shown that a specific class of circulants that are regular of degree $D_{v}+1$ are minimally $D_{v}+1$-node connected, and are therefore robust networks for node disruption with a disruption budget $D_v$. In detail, following the notation in Definition 3, this specific class of circulants has $a_{1}=1$ and has a convex jump sequence, meaning that $a_{i+1}-a_{i} \le a_{i+2}-a_{i+1}$ for $1<i<D_{v}+1$. In Propositions 4 and 5, we now derive the cost ranges for which the empty network on the one hand and specific classes of circulants on the other hand, are pairwise stable. When both circulants and the empty network are pairwise stable, we also determine which are more efficient.

Proposition 4

In the symmetric connections model without decay and with link disruption (where $1<D_{l}<n-2$), under uninform disruptor randomization, the following applies for the empty network and for the class of $D_{l}+1$-regular connected circulants (see Definition 3):

• for $c<\frac{n-1}{D_{l}+1}$, both the empty and the circulant networks are pairwise stable and the circulant networks are more efficient;

• for $\frac{n-1}{D_{l}+1}<c<\frac{n}{2}$, both the empty and the circulant networks are pairwise stable, but the empty network is more efficient;

• for $c>\frac{n}{2}$, only the empty network is pairwise stable.

It follows that with link disruption, the results for small disruption budgets (Proposition 2) and larger disruption budgets have a similar structure. We note that as the linking disruption budget is increased, the range of large linking costs decreases for which the presence of a disruptor can induce players to form a pairwise stable robust network that is more efficient than the empty network. We next look at the results for node disruption.

Proposition 5

In the symmetric connections model without decay and with node disruption ($1<D_{v}<\frac{n}{2}-1$), under uniform disruptor randomization, the following applies for the empty network and for the class of $D_{v}+1$-regular circulants (see Definition 3) with $a_{1}=1$ and with convex jump sequences:

• for $c<\frac{(n-D_v)(n-D_{v}-1)}{(D_{v}+1)n}$, both the empty and the circulant networks are pairwise stable and the circulant networks are more efficient;

• for $\frac{(n-D_v)(n-D_{v}-1)}{(D_{v}+1)n}<c<\frac{(n-D_v)(n-2D_{v})}{2n}$, both the empty and the circulant networks are pairwise stable, but the empty network is more efficient;

• for $c>\frac{(n-D_v)(n-2D_{v})}{2n}$, only the empty network is pairwise stable.

We note that with node disruption, we put additional restrictions on how large $D_v$ can be for the following reason. For the largest node disruption budgets, the presence of a disruptor makes network formation no longer pairwise stable, simply because of the fact that the individual player is so likely to be targeted that it makes forming links no longer worthwhile. Given the imposed restrictions, we can see that contrary to what is the case with a unit disruption budget, we now also obtain a case where the presence of a disruptor makes pairwise stable connected networks possible, even though these are less efficient than the empty network (just as is the case for link disruption). Again, larger disruption budgets reduce the range of large linking costs for which pairwise stable robust networks can be formed that are more efficient than the empty network.

We are now ready to compare the results for disruption in Propositions 4 and 5 to the benchmark results in Proposition 1. We note that, within the given restrictions on the size of the disruption budgets, all the critical cost levels in Propositions 4 and 5 are larger than 1. It follows that for both link and node disruption, there is a range of cost levels just above 1 such that forming a network is not pairwise stable but efficient without disruption. However, for the same cost range, with larger disruption budgets it is both pairwise stable and efficient to form a network. Therefore, a positive common-enemy effect is again obtained (just as is the case with a unit disruption budget). Yet, as the disruption budget is increased, this common-enemy effect applies for an increasingly narrow range of large linking costs. We conclude that the common-enemy effect has the most impact when the ability of the disruptor to disrupt is not too large; this make sense, as with a large ability to disrupt, it simply is not worthwhile to form a network. Furthermore, we obtain a range of cost levels (see second bullets in Propositions 4 and 5) such that disruption makes it pairwise stable to form a network, even though the empty network is more efficient. Again, when the concept of the pairwise strong Nash equilibrium (Belleflamme and Bloch 2004) is applied instead, only the empty network is obtained in equilibrium for this range of cost levels.¹⁸ Finally, just as was the case for a unit disruption budget, for small linking costs $c<1$ it is the case that the empty network is not pairwise stable without disruption, but is pairwise stable in the case of larger disruption budgets, leading to a negative common-enemy effect. It should be noted that with larger disruption budgets, such a negative common-enemy effect is not dependent on only pairs being able to form mutually beneficial links: even if larger sets of players are able to form mutually beneficial links (as is the case in the concept of ’strong’ stability (see Jackson and Van den Nouweland 2005)), for larger disruption budgets players will still not be able to escape the empty network.

We do not characterize all pairwise stable networks for larger disruption budgets, and in particular do not investigate the stability of non-robust networks except the empty network. Yet, as shown in Appendix D, with larger disruption budgets and link disruption, the star is never pairwise stable. Since, as argued in Sect. 5.1, the star network is the best candidate for a pairwise stable non-robust network, we conjecture that the empty network is the only non-robust pairwise stable network for larger disruption budgets.

7 Conclusion

Two conclusions can be drawn from our paper. The first conclusion concerns the network structures that players may form in a decentralized manner when facing strategic link or node disruption. These network structures always include the empty network, as two players who unilaterally deviate from the empty network by forming a link are automatically targeted. When players are able to coordinate on a non-empty network, two mechanisms may underlie network formation. First, players may form core-periphery networks, where peripheral players face the threat of disruption, but do not form extra links to protect themselves because the threat of disruption is spread across a large number of peripheral players. Second, players may form circular networks, in which a sufficient number of alternative paths connect the players, so that players remain connected even after disruption. We find only few instances of the former mechanism and this for a limited range of linking costs in the case of link disruption. The latter mechanism, however, operates across both link and node disruption, for both small and large disruption budgets. At the same time, the set of pairwise stable network networks under node disruption is smaller: intuitively, it is easier for the disruptor to do damage by disrupting nodes than by disrupting links.

The second conclusion concerns the impact of the presence of a strategic disruptor on the probability of network formation. Our analysis shows that when facing an outside force that aims to minimize total benefits from the network by either attacking the players’ links or the players themselves, a group of self-interested players may be able to efficiently build a network, whereas in the absence of this outside force they were not able to do this. This shows that a common-enemy effect may occur purely because of the effect of the presence of the common enemy on the players’ incentives; this contrasts with literature where the common enemy is assumed to change the psychology of the players, or the information they obtain (see Sect. 2.2). At the same time, our analysis shows that in particular for small linking costs, the common enemy can on the contrary have a negative effect on cooperation, where players fail to form a network even though they would have formed one in the absence of a common enemy. This is because in the presence of a common enemy, players can lock each other into not forming any network.

We end by exploring how robust these conclusions are to our modeling assumptions. First, we have focused on strategic network disruption, rather than on random network disruption where each link ((Bala and Goyal 2000b; Jackson and Wolinsky 1995) or node independently fails with a specific probability. One may then wonder whether such random network disruption leads to similar results as strategic network disruption. Adding the assumption that each link independently fails with probability $\epsilon$ to the benchmark connections model in Sect. 4, clearly the empty network is not pairwise stable as long as it is true for linking cost c that $c<(1-\epsilon )$. This shows that the pairwise stability of the empty network in our analysis is due to the strategic disruptor targeting any link added to the empty network. In connected networks, with the specified form of random network disruption, players equally have incentives to form additional paths between them, as this increases the probability that information is accessed. However, analyzing the pairwise stability of such networks requires comparing higher-degree polynomials, and is challenging beyond simple examples. An example in Appendix C for $n=4$ suggests that the positive common-enemy effect, where for high linking costs connected networks would become pairwise stable, is not maintained for random network disruption.

Second, our model abstracts from information decay (Jackson and Wolinsky 1996) and the question therefore additionally arises whether information decay can have similar results. Denoting the rate at which information decays as $\delta$, the empty network is not pairwise stable as long as it is the case for linking cost c that $c<(1-\delta )$. Contrary to what is the case in our results, information decay therefore does not result in the empty network always being pairwise stable. In connected networks, with information decay, intuitively players have an incentive to add links to minimally connected networks, not to create extra paths between nodes, but to bring nodes closer to one another. As is clear from the analysis of Jackson and Wolinsky (1996), a full characterization of pairwise stable networks cannot be provided, as this again requires comparing higher-degree polynomials. Still, as shown in Appendix C by reference to an example of Jackson and Wolinky, the introduction of information decay can cause networks to become pairwise stable, whereas in the absence of information decay they are not. Yet, such a result is obtained for only a small range of linking costs larger than 1, suggesting that the scope for an effect of information decay similar to our positive common-enemy effect is limited.

Third, as we employ pairwise stability as an equilibrium concept, the focus of our analysis lies purely on which networks are stable but not on how players can actually reach such networks. In the presence of a disruptor, the empty network is always pairwise stable in our results. The positive common-enemy effect we obtain for large linking costs thus relies on the assumption that the players are at least sometimes able to escape playing the empty network, and achieve one of the pairwise stable connected networks. Theoretical work on networks assuming farsightedness of players (see, e.g., the work by Morbitzer et al. (2011), Morbitzer et al. (2012) or Herings et al. (2009)) establishes the concept of (perfect) farsighted stability, which would allow our players to escape the empty network. Laboratory experiments (see, e.g., the work by Mantovani et al. (2011)) on the same topic show that players do tend to behave more farsightedly than myopically. At the same time, our negative common-enemy effect for small linking costs, where connected networks are pairwise stable with or without a disruptor, relies on the assumption that players are not always able to escape the empty network. In an experiment that builds on the theory of link disruption presented in this paper, Hoyer and Rosenkranz (2018) test whether a positive or a negative common enemy effect is observed more frequently, when players actually have to build a network. Using different starting networks, they show that when a disruptor is present, players are more often locked in the empty network than they manage to reach the circle network, even though the circle network is more efficient. A main factor influencing this result seems to be the risk aversion of players. Future research is still needed to look into this aspect of the common-enemy effect, as well as into an experimental analysis of node disruption, which so far is still missing.

Appendices

Appendix A. Lemmata and Proofs

Proof for Proposition 1

Any pairwise stable network must consist of minimally connected components, as otherwise at least one pair of players could save costs by deleting a link and would not lose any benefits. As any minimally connected component necessarily has end nodes, a player who forms a link to an end node rather than not forming it, gains 1 in benefits and loses c in costs. It follows that with $c>1$, no connected network is pairwise stable. For $c<1$, players who form a link to an end node are better off maintaining such a link. Furthermore, consider any network that consists of several components. Then two players in separate components incur an added cost c of adding a link and an added benefit of at least 1. It follows that for $c<1$ any pairwise stable network is connected. Looking at efficiency, note that the sum of the players’ benefits in a component increases convexly in the number of players in the component, whereas linking costs increase linearly. For this reason, if a minimally connected network has a higher value than the empty network, then any minimally connected network is also efficient. In particular, any minimally connected network is better than the empty network iff $n^2-2(n-1)c>n$ iff $c<\frac{n}{2}$. $\square$

The following lemmata are needed to prove Proposition 2.

Lemma 1

With a disruption budget of $D_l=1$, for a star network, denote by $p_I$ the weakly highest probability with which a link is targeted and by $p_{II}$ the weakly second-highest probability, with $p_I \ge p_{II}$. Then the star is pairwise stable for $p_{II}(n-2)<c<\min {(1,(1-p_I)(n-2))}$; specifically with uniform disruptor randomization, the star is pairwise stable when $1-\frac{1}{n-1}<c<1$.

Proof

For the star network $g^*$ to be pairwise stable, no pair of end players should each be better off when forming a link to each other and no individual end player should want to stop maintaining a link (point 1). Also, the central player should not be better off when stopping to maintain a link (point 2; note that a central player and a peripheral player cannot consider forming an extra link, as double links are assumed to be impossible).

• 1. The expected payoff to any end player i in a star network is $u_i(g^*)=p*1+(1-p)(n-1)-c$, where p denotes the probability that the link of the end player to the central player is disrupted, where the first part of the function denotes the payoff should node i be disconnected and the second part denotes the payoff should node i not be disconnected. Any end player i who fails to maintain his link to the central player k obtains payoff $u_i(g^*-g_{ik})=1$. The end player most inclined to stop maintaining his link is the one whose link to the central player is disrupted with the weakly highest probability, denoted $p_I$. This end player strictly prefers to maintain his link when $c<(1-p_I)(n-2)$. When two end players i and j add a link to each other, this ensures that they are not disconnected. The payoff of both i and j when adding a link to each other is thus $u_i(g^*+g_{ij})=u_j(g^*+g_{ij})=n-1-2c$ (note that as $n\ge 4$, the disruptor can still disconnect a node). For these players not to want to add a link, it suffices that the end player in the pair whose link to the central player is weakly less likely to be disrupted, strictly prefers not to add a link. In order for no pair of end players to want to add a link to each other, it follows that the end player whose link to the central player has the weakly second largest probability of being disrupted overall, denoted $p_{II}$, should not prefer to add a link. This is the case when $p_{II}(n - 2)<c$.

• 2. The payoff of the central player k is $u_k(g^*)=(n-1)-(n-1)c$. Should he stop maintaining a link to an end player i, his payoff is $u_k(g^*-g_{ki})=(n-2)-(n-2)c$. The central player k has no incentive to stop maintaining a link when $c<1$.

Merging the inequalities above, we find that the star is pairwise stable when $p_{II}(n-2)<c<\min {(1,(1-p_I)(n-2)})$. Two cases can be distinguished. First, for $\frac{1}{n-1}\le p_I \le \frac{n-3}{n-2}$, $\frac{1-p_I}{n-2}\le p_{II}<\frac{1}{n-2}$ and $p_{II} \le p_I$, the star is pairwise stable when $p_{II}(n-2)<c<1$. This includes the case where the links of all end players are disrupted with equal probability $\frac{1}{n-1}$ (uniform disruptor randomization), in which case the condition becomes $1-\frac{1}{n-1}<c<1$. Second, for $\frac{n-3}{n-2}<p_I<1$ and $\frac{1-p_I}{n-2}\le p_{II}<\frac{1}{n-2}$, the star is pairwise stable when $p_{II}(n-2)<c<(1-p_I)(n-2)$. $\square$

Lemma 2

For a disruption budget of $D_l=1$, with generic disruptor randomization, the only non-robust connected networks that can be pairwise stable are stochastic networks where the subnetworks that the disruptor can disconnect from the network have order 1. With uniform disruptor randomization, the only non-robust connected networks that can be pairwise stable are the stars.

Proof

The proof first considers non-robust connected stochastic networks and then non-robust connected non-stochastic networks. In part 1 of the proof we show that with generic disruptor randomization, a necessary condition for non-robust connected stochastic networks to be pairwise stable is that the subnetworks that the disruptor can disconnect from the network have order one; also, we show that with a uniform randomization strategy of the disruptor, non-robust connected stochastic networks can only be pairwise stable when they are stars. We then show in part 2 of the proof that non-robust connected non-stochastic networks can never be pairwise stable.

• 1. In non-robust connected stochastic networks there are $m \ge 2$ links that connect subnetworks with equal order y, where $y \in [1,\frac{n-1}{m}]$, to the rest of the network, such that disrupting any of these m links leaves the disruptor equally well off. (Note that if the m subnetworks would not have the same order, the disruptor would always prefer to disconnect the one with the largest order from the rest of the network, given that $(n-x)^2+x^2$ decreases in x for $x<\frac{n}{2}$.) Denote by v the number of links of any node k in any of the subnetworks.

  • (a) Suppose that contrary to our claim, pairwise stable non-robust connected networks exist with subnetworks of order larger than 1. We first show that a necessary condition for such networks to be pairwise stable, is that the subnetworks are minimally connected. When the disruptor disrupts one of the m links, total benefits from the network equal $(n-y)^2+y^2$. When a subnetwork is minimally connected, the disruptor is able to instead disrupt a link within this subnetwork and total benefits from the network become $(n-y')^2+y'^2$, with $y'<y$. Yet, given that $y<\frac{n}{2}$, disrupting in the subnetwork means higher total benefits from the network. It follows that the fact that the subnetworks are minimally connected, will not lead the disruptor to change his disruption strategy, meaning that players in subnetworks that are minimally connected do not have any incentive to add further links to each other.

  • (b) We next show that, whatever the mixed disruption strategy of the disruptor in response to a non-robust connected stochastic network, such networks cannot be pairwise stable when $y\ge 2$. Given that by (a) the potentially disconnected subnetworks of such a network must be minimally connected, each subnetwork contains at least one player i with an end link. When player i fails to maintain his end link, the disruptor will no longer disrupt the link that connects the subnetwork of i to the rest of the network, but any of the other $m-1$ potentially disrupted links. This follows from the fact that $1+(y-1)^2+(n-y)^2>1+y^2+(n-y-1)^2$ given that $y\le \frac{n-1}{2}$. The player in a subnetwork with an end link who is most inclined to remove this link, is the one whose subnetwork is weakly most likely to be disconnected from the rest of the network by the disruptor, which occurs with probability denoted $p_I$. Let this player form v links. Then this player does not prefer to remove a link to an end player when $p_Iy+(1-p_I)(n-y)-vc>n-y-1-(v-1)c$ iff $c<1-p_I(n-2y)$. This condition is less tight the smaller $p_I$ and the smaller n. $p_I$ equals at least $\frac{1}{m}$, n equals at least $1+my$ (which occurs when all potentially disrupted links are connected to a single central player). It follows that a necessary condition for no player i in a subnetwork wanting to stop maintaining an end link is that $c<1-\frac{1+my-2y}{m}=\frac{m-1-my+2y}{m}$. Now $m-1-my+2y>0$ when $y<\frac{m-1}{m-2}$. But $\frac{m-1}{m-2}\le 2$ for $m\ge 3$. It follows that a necessary condition for non-robust stochastic connected networks with $y\ge 2$ to be pairwise stable is that $m=2$.

    For non-robust connected stochastic networks with $y\ge 2$ and $m=2$ to be pairwise stable, it must additionally be the case that no two players across the two subnetworks that the disruptor can disconnect, prefer to form a link to each other. For pairwise stability, it suffices for this that a player k in the subnetwork that is weakly the least likely to be disconnected by the disruptor, does not prefer to form such a link. Denote by w the number of links of player k, and denote by z the order of the subnetwork that the disruptor can disconnect from the rest of the network after player k has formed an extra link, where $z<y$. Player k prefers not to add such a link when $(1-p_I)y+p_I(n-y)-wc\ge n-z-(w+1)c$ iff $c>y-z+(1-p_I)(n-2y)$. Overall, pairwise stability thus requires that $y-z+(1-p_I)(n-2y)\le c \le 1-p_I(n-2y)$. But given that $y>z$ and $n>2y$, this is not possible, so that we conclude that non-robust connected stochastic networks with $y\ge 2$ are not pairwise stable.

  • (c) We have so far shown that non-robust connected stochastic networks must have $y=1$ to be pairwise stable, so that each subnetwork that the disruptor can disconnect must consist of a single end player. We end the treatment of non-robust connected stochastic networks by showing that with uniform disruptor randomization, such networks can only be pairwise stable if they are stars. Considering all non-robust connected stochastic networks with $y=1$, we distinguish between those with $m\ge 3$, and those with $m=2$.

    When $m\ge 3$, the central player prefers to maintain each end link when $(n-1)-mc>(n-2)-(m-1)c$ iff $c<1$. No end player prefers to add a link to another player when $\frac{1}{m}+\frac{m-1}{m}(n-1)-c>(n-1)-2c$ iff $c>\frac{n-2}{m}$. Finally, no end player prefers to delete a link when $\frac{1}{m}+\frac{m-1}{m}(n-1)-c>1$ iff $c<\frac{m-1}{m}(n-2)$; the right-hand side is larger than 1 for $m>\frac{n-2}{n-3}$, which is always valid for $m>2$. Thus, pairwise stability of a non-robust connected stochastic network with $y=1$ and $m>2$ requires $\frac{n-2}{m}<c<1$, which is only possible when $m>(n-2)$. Yet, in any non-star non-robust connected stochastic network with $y=1$, it is the case that $m \le (n-3)$, as m is largest when the network consists of circle subnetwork of order 3, where the rest of the players are end players directly connected to this circle. As this is incompatible with $m>(n-2)$, it follows that non-star non-robust connected stochastic networks with $y=1$ and $m \ge 3$ cannot be pairwise stable.

    For $m=2$, no end player prefers to add a link to another player when $0.5+0.5(n-1)-c>n-2c$ iff $c>\frac{n}{2}$; yet, the condition for links to end players to be maintained continues to be $c<1$, which is incompatible with the condition $c>\frac{n}{2}$.

    Finally, the fact that cost levels exist such that the stars are pairwise stable follows from Lemma 1.

• 2. Consider a non-robust connected non-stochastic network such that the disruptor’s unique best response is to remove link ij. Given that the network is non-robust and connected, this means that the disruption of ij results in a post-disruption network consisting of two components $C_i$ and $C_j$, so that the predisruption network consists of two subnetworks $C_i$ and $C_j$ connected by link ij, where we denote by $y_i$ and $y_j=n-y_i$ the respective orders of these subnetworks.

  We first show that pairwise stability of such a network is only possible when at least one of the subnetworks $C_i$ and $C_j$ contains an end link. If subnetwork $C_i$ does not contain any end links, then $C_i$ must contain a link kl such that when this link is disrupted, $C_i$ is still connected. The only reason that players k and l can have to maintain link kl is that non-maintenance of this link leads the disruptor to disrupt a link in $C_i$, instead of disrupting ij, such that the payoff of players k and l is reduced. The disruptor in turn will only disrupt a link in $C_i$ instead of link ij when $y_i>y_j$. By the same reasoning, it is only possible that $C_j$ does not include any end links when $y_j>y_i$. As it is not possible that both $y_i>y_j$ and $y_j>y_i$, it follows that at least one of the subnetworks $C_i$ and $C_j$ must contain an end link.

  Having shown that pairwise stability of non-robust connected non-stochastic networks requires that at least one subnetwork contains an end link, we show that a necessary condition for such an end link to be maintained is that $c<1$. Consider a player k in subnetwork $C_i$ maintaining a link to an end player l. We show that when k fails to maintain this end link, the disruptor will either continue to disrupt link ij, or will disrupt a link in subnetwork $C_j$. Suppose that this is not the case, and that the disruptor is able to disrupt a link rs in $C_i$, and when link kl is not maintained prefers disconnecting the network by disrupting link rs to disrupting link ij. This requires that $1+(y_i^2-1)^2+y_j^2>1+(y_i-1-x)^2+(y_j+x)^2$ iff $(y_j+x)^2-y_j^2<(y_i-1)^2+(y_i-x-1)^2$, where $x\ge 1$. But if the disruptor is able to disconnect the network by disrupting link rs when players k and l do not maintain link kl, then the disruptor is also able to disconnect the network by disrupting link rs when players k and l do maintain link kl. In order for the specified non-robust connected non-stochastic network to be pairwise stable, the disruptor should then prefer to disrupt link ij rather than disrupt link rs. This requires $y_i^2+y_j^2<(y_i-x)^2+(y_j+x)^2$ iff $(y_i+x)^2-y_j^2>y_i^2-(y_i-x)^2$. We conclude that a necessary condition for the disruptor to prefer to disrupt link ij when link kl is maintained, and prefers to disrupt a link rs when kl is not maintained, is that $(y_i-1)^2-(y_i-1-x)^2>y_i^2-(y_i-x)^2$, which is not possible. It follows that when k no longer maintains link kl, the disruptor will either continue to disrupt ij, or will disrupt in $C_j$. But if the disruptor responds to non-maintenance of kl by disrupting in $C_j$, player k does not lose information when failing to maintain link kl, and therefore does not have any incentive to maintain it. It follows that when player k removes link kl, it must be that the disruptor continues to disrupt link ij, and that player k loses exactly one unit of information. Therefore, $c<1$ is a necessary condition for pairwise stability of a non-robust connected non-stochastic network.

  A further necessary condition for pairwise stability of the specified non-robust connected non-stochastic network is that a player k in $C_i$ with $k \ne i$, and a player l in $C_j$ with $l \ne j$, do not both prefer to add a link to each other. In the non-robust connected non-stochastic network, let k obtain $y_i-v_kc$ and let l obtain $y_j-v_lc$. When the two players add a link to each other, k obtains payoff $n-z-(v_k+1)c$, and l obtains $n-z-(v_l+1)c$, where z is the number of nodes the disruptor is able to disconnect from the rest of the network after player k and l have formed an extra link (where $z<y_i,y_j$). In order for the non-robust connected non-stochastic network to be pairwise stable, it should be the case that at least one of the players k and l does not prefer to add a link, for which it suffices that either $y_i-v_kc>y_i+y_j-z-(v_k+1)c$ iff $c>y_j-z$, or $y_j-v_lc>y_i+y_j-z-(v_k+1)c$ iff $c>y_i-z$. It follows that in order for player k and l not to want to add a link, it must be the case that $c>1$. But this is incompatible with the condition $c<1$ for a player to want to maintain an end link. It follows that non-robust connected non-stochastic networks cannot be pairwise stable.

$\square$

Lemma 3

For a disruption budget of $D_l=1$, with generic disruptor randomization, the empty network is pairwise stable for $c>0$.

Proof

In order for the empty network to be pairwise stable, no pair of players should want to form a link. In the empty network, each player obtains payoff 1. If two players deviate from the empty network by forming a link, the disruptor will disrupt this link. The expected payoff of each of these deviating players is therefore $1-c$. It follows that the empty network is pairwise stable when $1>1-c$ iff $c>0$. $\square$

Lemma 4

With $D_l=1$, given uniform disruptor randomization, any robust pairwise stable network is minimally 2-link connected and at least one robust pairwise stable network exists when $c<\frac{n}{2}$.

Proof

Any 2-link connected network is robust by Definition 1, as no nodes can be disconnected from the network. If two players i and j who do not have a direct link in a 2-link connected network add a link to each other, this does not change the benefits obtained from the network, but increases both players’ costs. It follows that no two players want to add a link in a 2-link connected network. At the same time, in any 2-link connected network that is not minimal, if the network continues to be 2-link connected after player i fails to maintain the link to player j, player i will prefer not to maintain this link, as he will obtain the same benefit from the network, but at lower linking costs. It follows that any pairwise stable robust network for $D_l=1$ must be minimally 2-link connected. Finally, in any minimally 2-link connected network, any player i obtains payoff $n-vc$, where v denotes the number of links of player i. When player i fails to maintain a link, the disruptor will be able to disconnect a number of players y from player i, who will now obtain payoff $n-y-(v-1)c$. Note now that the circle network is the minimally 2-link connected network that is pairwise stable for the highest linking cost ranges, as y is then equal to $\frac{n}{2}$ (where the latter is an expected value when n is odd; an example is found in Fig. 1a). It follows that at least one robust pairwise stable network exists when $c<\frac{n}{2}$. $\square$

Lemma 5

With $D_l=1$,

• for $c<\frac{n-1}{2}$, the circle is more efficient than either any other minimally 2-link connected network, the star or the empty network;

• for $c>\frac{n-1}{2}$, the empty network is more efficient than either any minimally 2-link connected network, or the star.

Proof

Among the minimally 2-link connected networks, the circle is the most efficient, as it achieves the same total benefits but has the least links. If any network that is not a minimally 2-link connected network is more efficient than the circle, then this network is also more efficient than any minimally 2-link connected network. The circle is more efficient than the star when $n^2-2nc>(n-1)^2+1-2(n-1)c$ iff $c<(n-1)$. The circle network is more efficient than the empty network when $n^2-2nc>n$ iff $c<\frac{n-1}{2}$. The star network is more efficient than the empty network when $(n-1)^2+1-2(n-1)c>n$ iff $c<\frac{n-2}{2}$. $\square$

Proof for Proposition 2

The proof follows directly from Lemmata 1, 2, 3, 4 and 5. $\square$

We next treat the lemmata that are needed for the proof of Proposition 3.

Lemma 6

In the connections model with node disruption ($D_v=1$), with generic randomization, the following applies: (i) non-robust connected non-stochastic networks are never pairwise stable; (ii) specifically with lexicographic preferences of the disruptor, non-robust connected stochastic networks are never pairwise stable either.

Proof

The proof first considers non-robust connected non-stochastic networks (first bullet), and then non-robust connected stochastic networks specifically for a disruptor with lexicographic preferences (second bullet).

• In any non-robust connected non-stochastic network, there is a single node i that will definitely be disrupted. The expected payoff to node i is then $u_i(g) = 0-vc$, where v stands for the number of links of node i. By deleting a link, player i will decrease his costs, and potentially will no longer be the target of disruption. Therefore, the payoff will at least be $u_i(g-g_{ij}) = 0- (v-1)c$, which is always better.

• With lexicographic preferences of the disruptor, for any non-robust connected stochastic network to be pairwise stable, we show that it must be that each of m potentially disrupted nodes connects to the rest of the network a minimally connected subnetwork (including the node itself) with the same order.

  These subnetworks must have the same order because if one subnetwork would have a strictly larger order than another, a disruptor with lexicographic preferences will always prefer to disconnect the larger subnetwork. To show that the subnetworks must be minimally connected, denote the order of the subnetworks that the potentially disrupted nodes connect to the rest of the network as y, where $y \ge 2$. Then n is at least 2y. As a disruptor with lexicographic preferences is always better off the smaller the largest component in the post-disruption network, the disruptor will never prefer to disrupt in one of the subnetworks, even if these are minimally connected.¹⁹ It follows that, with lexicographic disruptor preferences, a necessary condition for pairwise stability of a non-robust connected stochastic network, is that the mentioned subnetworks are minimally connected, and therefore include end nodes.

  Points 1 to 3 below now show further facts about non-robust connected stochastic networks when the disruptor has lexicographic preferences. We first show that non-robust connected stochastic networks cannot be pairwise stable if a potentially disrupted player has an end link (point 1). We next show that non-robust connected stochastic networks cannot be pairwise stable when $m>2$ (point 2). We finally show that non-robust connected stochastic networks with $m=2$ cannot be pairwise stable either (point 3).

  • 1. Let at least one potentially disrupted player k have an end link to l, and let k have v links. When player k fails to maintain the end link, given that the m subnetworks have the same order, the disruptor with lexicographic preferences prefers to disrupt one of the $(m-1)$ potentially disrupted nodes other than k. It follows that k does not want to remove link kl when $p \cdot 0+(1-p)(n-y)-vc>n-y-1-(v-1)c$ iff $c<1-p(n-y)$, with p the probability that k is disrupted, where we consider the player k who is weakly most likely to be disrupted. As p equals at least $\frac{1}{m}$ and n equals at least my, this condition can only be valid if $c<\frac{m-my+y}{m}$. The right-hand side is larger than zero when $m<\frac{y}{y-1}$. Given that y is at least 2, this is never valid. It follows that a non-robust connected stochastic network can never be pairwise stable if a potentially disrupted player has an end link.

  • 2. Given that the m subnetworks are minimally connected and that the m potentially disrupted nodes do not have end links (see 1.), it follows that in any pairwise stable non-robust connected stochastic network, each potentially disconnected subnetwork must contain a non-disrupted player i who has an end link; this in turn means that $y\ge 3$ (where we repeat that this includes the potentially disrupted player himself). Let player i’s subnetwork be disconnected with probability p, and let i form v links. Then i does not prefer to remove the end link when $p \cdot x+(1-p)(n-y)-vc>n-y-1-(v-1)c$ iff $c<1-p(n-y-x)$. x is the order of the component of which i is part when the player’s subnetwork is the one that is disconnected. Note that with lexicographic preferences of the disruptor, when player i fails to maintain the end link the disruptor necessarily prefers to remove one of the $(m-1)$ other potentially disrupted nodes, as this necessarily means that the order of the largest component in the post-disruption network will be smaller.

    Among all players of the same type as i, the player most inclined to stop maintaining an end link is the one facing the highest p, where the (weakly) highest p is at least $\frac{1}{m}$. n is at least my, and x is at most $(y-1)$. It follows that a necessary condition for the existence of a pairwise stable non-robust connected stochastic network is that $c<1-\frac{1}{m}[my-y-(y-1)]=\frac{-m(y-1)+2y-1}{m}$. Therefore, non-robust connected stochastic networks can only be pairwise stable when $m<\frac{2y-1}{y-1}$. For $y=3$ (which is the minimal y) the right-hand side equals 5/2, and furthermore the right-hand side decreases in y. It follows that a necessary condition for pairwise stability of a non-robust connected stochastic network is that $m=2$.

  • 3. For a non-robust connected stochastic network with $m=2$ to be pairwise stable, on top of the condition $c<1-p(n-y-x)$, we need that a pair of players (i, j) each in a different subnetwork which the disruptor can disconnect from the rest of the network, do not want to add a link ij to each other. This is the case when $(1-p)x+p(n-y)-vc>n-z-(v+1)c$ iff $c>n-z-x+p(n-y-x)$. It suffices to consider this condition for the player in the subnetwork that is least likely to be disconnected, as it suffices that this player does not want to add a link (given that p is the probability with which the disruptor disrupts the weakly most likely disrupted node, and given that $m=2$, the weakly least likely disrupted node is necessarily disrupted with probability $1-p$). z is the expected number of nodes that the disruptor can still disconnect after the mentioned pair of players have formed an extra link ij (note that $n-z$ can be an expected value, as is the case when players i and j are the end nodes in a line). Overall, taking into account point 2., for pairwise stability of a non-robust connected stochastic network with $m=2$, a necessary condition is that $n-z-x+p(n-y-x)<1-p(n-y-x)$. But n is at least 2y, and $z<y$, $x<y$, so that $n-z-x>1$, $n-y-x>0$, meaning that the condition cannot be valid.

$\square$

Lemma 7

For a disruption budget of $D_v=1$, with generic disruptor randomization, the empty network is pairwise stable for $c>0$.

Proof

In order for the empty network not to be pairwise stable, it should be that at least two players prefer to form a link to each other when the empty network is the starting point. Consider the two players i and j most inclined to form such a link. Let i be disrupted with probability $p_I$ in the empty network, and with probability $p_{II}$ when forming a link to player j. Then necessarily player j is disrupted with probability $(1-p_{II})$ when forming a link to player i. Denote by $p_{I}'$ the probability that player j is disrupted in the empty network. Then both players i and j prefer to form a link to each other when $c<p_1-p_{II}$ and $c<p_{I}'-(1-p_{II})$. This is only possible when $p_I>p_{II}$ and $p_{I}'>(1-p_{II})$. But $p_{I}'$ is at most equal to $1-p_{I}$, and $p_{I}>p_{II}$ is incompatible with $1-p_{I}>1-p_{II}$. $\square$

Lemma 8

When $D_v=1$, with uniform disruptor randomization, any pairwise stable robust network is minimally 2-node connected, and at least one pairwise stable robust network exists when $c<\frac{(n-1)(n-2)}{2n}$.

Proof

Any 2-node connected network is robust by Definition 2, as no additional node to the one disrupted can be disconnected. If two players i and j who do not have a direct link in a 2-node connected network add a link to each other, this does not change the benefits from the network, but increases both players’ costs. It follows that no two players want to add a link in a 2-node connected network. At the same time, in any 2-node connected network that is not minimal, if the network continues to be 2-node connected after player i fails to maintain his link to player j, player i will prefer not to maintain this link, as he will obtain the same benefit from the network, but at lower linking costs. It follows that any pairwise stable robust network for $D_v=1$ must be minimally 2-node connected. Finally, in any minimally 2-node connected network, as no additional node to the one targeted by the disruptor can be disconnected, with uniform disruptor randomization the disruptor targets each node with probability $\frac{1}{n}$. Any player i therefore obtains payoff $u_i(g)=\frac{(n-1)^2}{n}-vc$, where v denotes the number of links node i possesses. When player i fails to maintain a link, the disruptor will be able to disconnect a number of players y from player i, who will now obtain payoff $n-1-y-(v-1)c$. Note now that the circle network is the minimally 2-node connected network that is pairwise stable for the highest linking cost ranges, as y is then equal to $\frac{n-1}{2}$ (where the latter is an expected value when n is even). It follows that at least one robust pairwise stable network exists when $c<\frac{(n-1)(n-2)}{2n}$. $\square$

Lemma 9

When $D_v=1$,

• for $c<\frac{(n-1)(n-2)}{2n}$, the circle is more efficient than either any other minimally 2-node connected network, or the empty network;

• for $\frac{(n-1)(n-2)}{2n}<c$, the empty network is more efficient than any minimally 2-node connected network.

Proof

The circle leads to lower total costs than any other minimally 2-node connected network, but to the same total benefits, because it continues to be the case that the disrupted node does not disconnect extra nodes from the rest of the network. The circle is more efficient than the empty network when $(n-1)^2-2nc>(n-1)$ iff $c<\frac{(n-1)(n-2)}{2n}$ $\square$

Proof for Proposition 3

The proof follows directly from Lemmata 6, 7, 8 and 9. $\square$

Proof for Proposition 4

As the mentioned circulants are robust against link disruption with disruption budget $D_{l}$ (see Hoyer and De Jaegher (2016), Proposition 1), no player wants to add a link. Furthermore, as any considered circulant consists of a circle that includes all players, with additional links added according to the jump sequence procedure, to disconnect any subset of nodes from the rest of the network larger than 1, the disruptor would need to disrupt more than $D_l+1$ links. For this reason, when a link ij in the circulant is no longer maintained, the disruptor can only disconnect either i or j from the network. It follows that when link ij is not maintained, with uniform disruptor randomization, i and j are each disconnected from the rest of the network with probability $\frac{1}{2}$. The payoff a player i who fails to maintain a single link in a circulant equals $\frac{1}{2}+\frac{1}{2}(n-1)-D_{l}c$. Therefore, player i prefers to maintain the link when $n-(D_{l}+1)c>\frac{1}{2}+\frac{1}{2}(n-1)-D_{l}c$ iff $c<\frac{n}{2}$. A circulant where each player has exactly $D_{1}+1$ links is more efficient than the empty network when $n^{2}-n(D_{l}+1)c>n$ iff $c<\frac{n-1}{D_{l}+1}$. $\square$

Proof for Proposition 5

As the mentioned circulants are robust against node disruption with disruption budget $D_{v}$ (see Hoyer and De Jaegher (2016), Proposition 1), no player wants to add a link. Also, any considered circulant consists of a circle that includes all players, with additional links added according to a specific jump sequence procedure. Because of this fact, in order to disconnect a subset of nodes larger than 1 from the rest of the network, the disruptor would need to disrupt more than $D_v+1$ nodes. For this reason, when a link ij is not maintained, the disruptor can only disconnect i or j from the network (by disrupting $D_v$ nodes with links to i of j). With uniform disruptor randomization, the payoff of a player i who fails to maintain a single link ij in a circulant therefore equals $\frac{1}{2}+\frac{1}{2}(n-D_v-1)-D_{v}c$. When maintaining link ij, player i obtains payoff $(1-\frac{D_v}{n})(n-D_{v})-(D_{v}+1)c$. It follows that i wants to maintain link ij when $c<\frac{(n-D_v)(n-2D_{v})}{2n}$. A circulant of the described form is more efficient than the empty network when $(n-D_v)^{2}-(D_{v}+1)nc>n-D_v$ iff $c<\frac{(n-D_v)(n-D_{v}-1)}{(D_{v}+1)n}$. It can be checked that $\frac{(n-D_v)(n-D_{v}-1)}{(D_{v}+1)n}<\frac{(n-D_v)(n-2D_{v})}{2n}$ iff $1<D_{v}<\frac{n}{2}-1$. $\square$

Appendix B. Pairwise stability of core-periphery networks for a unit link disruption budget and non-uniform disruptor randomization

Consider a core-periphery network consisting of a minimally 2-link connected central subnetwork, with a number x of end nodes directly connected to it, where $x\ge 3$. Just as for the proof of Lemma 1, denote by $p_I$ the weakly highest probability with which an end link is targeted and by $p_{II}$ the second-highest probability, with $p_I \ge p_{II}$. Then the star is pairwise stable for $p_{II}(n-2)<c<\min {(1,(1-p_I)(n-2}))$. Two cases can now be distinguished:

• In Case 1, $p_I \le \frac{n-3}{n-2}$, in which case the condition on the linking costs becomes $p_{II}(n-2)<c<1$. This is only possible when $p_{II}<\frac{1}{n-2}$. At the same time, as $p_{II}$ is the second-highest probability, it must be the case that $p_{II}\ge \frac{1-p_I}{n-x-1}$, so that additionally it must be that $\frac{1-p_I}{n-x-1}\le p_{II}< \frac{1}{n-2}$. This in turn is only possible when $p_I>\frac{x-1}{n-2}$. We therefore obtain overall the conditions $\frac{1}{(n-2)(n-x-1)}\le p_{II}<\frac{1}{n-2}$, and $\frac{x-1}{n-2}<p_I\le \frac{n-3}{n-2}$.

• In Case 2, $p_I>\frac{n-3}{n-2}$, in which case the condition on the linking costs becomes $p_{II}(n-2)<c<(1-p_I)(n-2)$, which is only possible when $p_{II}<(1-p_I)$, meaning that at least a third end link must be targeted with positive probability. This conditions for this case are therefore $p_{II}<(1-p_I)$, $0<p_{II}<\frac{1}{n-2}$, $\frac{n-3}{n-2}<p_I<1$.

Appendix C. Comparison to link and node reliability, and information decay

In a related model to our model of link disruption, no disruptor is present but each link independently fails with probability $\epsilon$. As pointed out by Jackson and Wolinsky (1995), such a case is complex to analyze as establishing pairwise stability and efficiency requires the comparison of higher-degree polynomials. For $n=4$, the benefit of an individual player in the circle equals $\epsilon ^2 \cdot 1+2\epsilon (1-\epsilon )[\epsilon \cdot 2+(1-\epsilon )(\epsilon \cdot 3+(1-\epsilon \cdot 4)]+(1-\epsilon )^2[\epsilon ^2 \cdot 3+2\epsilon (1-\epsilon ) \cdot 4+(1-\epsilon )^2 \cdot 4]$. When this individual player does not maintain one of his links, his benefit equals $\epsilon \cdot 1+(1-\epsilon )[\epsilon \cdot 2+(1-\epsilon )(\epsilon \cdot 3+(1-\epsilon ) \cdot 4)]$. It can be checked that the difference between these two payoffs is never larger than 1, so that a necessary condition for the circle to be pairwise stable is that $c<1$. At the same time, networks that include end nodes can only be pairwise stable when $c<(1-\epsilon )$. This suggests that introducing link failure into the benchmark case does not mean that non-empty networks become pairwise stable, contrary to what is the case when introducing link disruption.

Similarly, in a related model to our model of node disruption, consider a model of node failure where each node independently fails with probability $\epsilon$. Again, we look at the example $n=4$. In the circle, the individual player now obtains benefit $\epsilon \cdot 0+(1-\epsilon )[\epsilon ^2 \cdot 1+2\epsilon (1-\epsilon )(\epsilon \cdot 2+(1-\epsilon ) \cdot 3)+(1-\epsilon )^2(\epsilon \cdot 3+(1-\epsilon ) \cdot 4)]$. When this individual player does not maintain one of his links, his benefit becomes $\epsilon \cdot 0+(1-\epsilon )[\epsilon \cdot 1+(1-\epsilon )(\epsilon \cdot 2+(1-\epsilon )(\epsilon \cdot 3+(1-\epsilon ) \cdot 4))]$. It can again be checked that the difference between these two benefits is smaller than one, so that a necessary condition for the circle to be pairwise stable is again that $c<1$. It continues to be the case that a network that involves end nodes can only be pairwise stable when $c<(1-\epsilon )$. Again, this suggests that, whereas introducing node disruption into the benchmark case makes non-empty pairwise stable networks possible for $c>1$, this is not the case when introducing node failure.

With information decay, the information obtained from nodes at distance of 1 in the network from oneself is discounted by a factor $\delta$ (with $0<\delta <1$), the information obtained from nodes at distance 2 by a factor $\delta ^2$, and so on. We compare the connections model of network formation without decay (see Sect. 4), to the connections model of network formation with decay (Jackson and Wolinsky 1996), as a function of critical levels of the linking costs. For linking cost levels such that $1<c<\delta +\frac{n-2}{2}\delta ^2$, the effect of introducing decay in the network rather than not having decay, can be that non-empty networks become pairwise stable. This is the case for Example 1 (tetrahedron network) in Jackson and Wolinsky (1996), when in their example c is slightly increased above 1. For this range of linking costs, both with and without decay, networks with end players are not pairwise stable, because end players want to stop maintaining end links then. Without decay, at the same time, non-minimally connected networks are not pairwise stable because players will never want to maintain redundant links. With information decay, however, there still is an incentive to maintain links that are redundant in the absence of decay. In this sense, for the specified cost levels, the introduction of decay into the model has a similar effect to the introduction of a common enemy. In the presence of a disruptor, failure to maintain link can lead to a large loss in benefits because the network can then be disconnected in separate components. In the presence of decay, failure to maintain a link can lead to a large loss in benefits because nodes that are relatively close become relatively remote from the individual player. As Jackson and Wolinsky (1996) do not provide a full characterization of pairwise stable networks for $c>\delta$, we cannot provide precise results for the similar effect of decay. Yet, the example of Jackson and Wolinsky suggests that this effect is only obtained for a limited range of costs. On the contrary, the common-enemy effect of the presence of a disruptor applies for a wide range of cost parameters, as e.g. with a linking budget of 1, in the circle the impact of failing to maintain one link is large.

Appendix D. Star not pairwise stable for larger linking disruption budget

We show that the star cannot be pairwise stable for a linking disruption budget $D_{l}>1$. For a general disruption budget $D_l$, in the star a peripheral player obtains payoff $\frac{n-D_{l}-1}{n-1}(n-D_l)+\frac{D_l}{n-1}-c$. A peripheral player who adds a link in a star obtains payoff $n-D_{l}-2c$; he therefore does not want to add a link when $c>\frac{(n-D_{l}-1)D_l}{n-1}$. A peripheral player who fails to maintain a link in a star obtains payoff 1; he therefore wants to keep his link when $c<\frac{(n-D_{l}-1)^2}{n-1}$. The central player in the star obtains payoff $n-D_{l}-(n-1)c$. When failing to maintain a single link, the central player instead obtains payoff $n-D_{l}-1-(n-2)c$; the central player therefore wants to keep all links when $c<1$. A peripheral player not wanting to add a link and the central player wanting to keep all links is compatible when $\frac{(n-D_{l}-1)D_l}{n-1}<1$ iff $n<\frac{D_{l}^2+D_{l}-1}{D_{l}-1}$. A peripheral player wanting to keep his link and not wanting to add a link is compatible when $\frac{(n-D_{l}-1)^2}{n-1}>\frac{(n-D_{l}-1)D_l}{n-1}$ iff $n>2D_{l}+1$. Thus, compatibility of all conditions for pairwise stability requires that $2D_{l}+1<\frac{D_{l}^2+D_{l}-1}{D_{l}-1}$ iff $D_{l}<2$. Yet, for larger disruption budgets $D_l$ equals instead at least 2.