1 Introduction

A “claims problem” (O’Neill 1982) models a situation where a group of individuals have claims on a resource but its endowment is not sufficient to honour all of the claims. Research on the problem attempts to shed light on basic questions of distributive justice. The seminal contributions studied the division of the liquidation value of a bankrupt firm among its creditors (O’Neill 1982; Aumann and Maschler 1985) and the distribution of a tax burden among citizens differing in their taxable incomes (Young 1987, 1988).

The literature on the claims problem evaluates the allocation mechanisms, or rules, examining their normative and practical properties.Footnote 1 In this paper, we consider the following stability property: when a problem can be separated into smaller problems by fractioning individual claims and the endowment across these, the allocations recommended for the smaller problems should add up to the allocation recommended for the original problem. This additivity property is appealing from an accounting perspective, since it enables the allocation of a grand budget to be decentralized into area-specific budgets.

When can a claims problem be separated? Upon closer inspection, separating arbitrary problems and then adding their solutions is unjustified. For instance, consider the distribution of a million euros among individuals A and B, each holding a claim of one million euros. Taken naively, additivity would allow us to separate this problem into two smaller problems. In the first problem, a million euros are to be distributed, A has a claim of a million euros, and B has a claim zero euros. In the second problem, zero euros are to be distributed, A has a claim of zero euros, and B has a claim of a million euros. The only overall solution to these problems involves A receiving one million euros. This particular separation is arbitrary, favouring A, and is, thus, incompatible with basic equity properties in the original problem. To overcome this pathological case, we only require additivity when the allocation recommended for each smaller problem is non-degenerate, assigning positive awards to each claimant.

We identify the family of all rules satisfying this modified version of additivity property as well as “consistency” and “endowment monotonicity”. The rest of the paper is organized as follows. Section 2 introduces the claims problem, notation, and defines the constrained equal losses rule and its asymmetric extensions. Section 3 discusses the axioms involved in our analysis and presents the main results. Section 4 contains the proofs. Section 5 concludes by discussing further corollaries of our results and a conjecture.

2 Model

An endowment of a divisible resource is to be distributed among a group of claimants drawn from a finite set A with \(|A| \ge 3\).Footnote 2 Let \({{\mathcal {N}}}\) denote the collection of all possible claimant groups drawn from A. For each \(N\in {\mathcal {N}}\), a claims problem is a pair consisting of a profile of claims and an endowment \((c,E)\in {\mathbb {R}}_+^N \times {\mathbb {R}}_+\), such that \(\sum _{N}c_i \ge E\). For each \(N\in {\mathcal {N}}\), let \({\mathcal {C}}^N\) denote the collection of claims problems involving the claimants in N. An allocation for \((c,E)\in {\mathcal {C}}^N\) is a profile \(z\in {\mathbb {R}}^N_+\) such that \(\sum _N z_i=E\) and, for each \(i\in N\), \(z_i\le c_i\). We refer to \(z_i\) as the award of claimant i and to \(c_i-z_i\) as her loss. Let Z(c, E) denote the collection of all allocations for (c, E). An adjudication rule is a function f recommending an allocation for each possible claims problem: for each \(N\in {\mathcal {N}}\) and each \((c,E)\in {\mathcal {C}}^N\), \(f(c,E)\in Z(c,E)\).

For each rule f, its dual (Aumann and Maschler 1985) is the rule g defined by setting for each \((c,E) \in {\mathcal {C}}^N\),

$$\begin{aligned} g(c,E)=c-f\left( c,\sum _{i \in N}c_i-E \right) . \end{aligned}$$

2.1 Rules

In this paper, we examine the relationship between additivity properties and two canonical rules attributed to medieval philosopher Maimonides (Aumann and Maschler 1985): the “constrained equal losses” and the “constrained equal awards” rules.

The constrained equal losses rule, denoted by CEL, equalizes the losses imposed on claimants subject to the constraint that no claimant receives a negative award: for each \((c,E)\in {\mathcal {C}}^N\) and each \(i\in N\),

$$\begin{aligned} CEL_i(c,E)=\max \{0, c_i- \uplambda \}, \end{aligned}$$

where \(\uplambda \in {\mathbb {R}}_+\) is chosen so as to satisfy \(\sum _{j \in N}\max \{0, c_j- \uplambda \}=E.\)

The constrained equal losses rule can be extended to allow for asymmetric treatment, by equalizing the weighted losses imposed on claimants (Moulin 2000).Footnote 3 The weighted constrained equal losses rule corresponding to a weights profile \(w\in {\mathbb {R}}_{++}^{A}\), denoted by \(CEL^w\), is such that for each \((c,E)\in {\mathcal {C}}^N\) and each \(i\in N\)

$$\begin{aligned} CEL_i^w(c,E)=\max \{0, c_i- w_i\uplambda \}, \end{aligned}$$

where \(\uplambda \in {\mathbb {R}}_+\) is chosen so as to satisfy \(\sum _{N}\max \{0, c_j- w_j\uplambda \}=E.\)

A weighted constrained equal losses rule can be further extended to include priority classes, whereby claimants in lower priority classes receive awards conditional on full compensation among those in higher classes (Moulin 2000). We refer to such a rule as priority-augmented weighted constrained equal losses rule, or PWCEL rule. Formally, a rule f is a PWCEL rule, if there is a partition of A into \(n\le |A|\) non-empty priority classes \(A_1, \dots , A_n\) and a weights profile \(w\in {\mathbb {R}}_{++}^{A}\) such that, for each \(N\in {\mathcal {N}}\) and each \((c,E)\in {\mathcal {C}}^N\), f(c, E) can be computed sequentially as follows:

$$\begin{aligned} \text {for each }i\in N\cap A_1,\quad&\begin{array}{c} f_i(c,E)=CEL^w(c_{N\cap A_1},E_1), \end{array}\\&\text { where} \begin{array}{c} E_1=\min \{\sum _{N\cap A_1}c_j, E\}; \end{array}\\&\vdots \\ \text {for each }i\in N\cap A_t,\quad&\begin{array}{c} f_i(c,E)=CEL^w(c_{N\cap A_t},E_t), \end{array}\\&\text { where} \begin{array}{c} E_t=\min \{\sum _{N\cap A_t}c_j, E-\sum _{N\cap [A_1 \cup \cdots \cup A_{t-1}]} f_j(c,E)\}; \end{array}\\&\vdots \end{aligned}$$

In the special case where each of the sets \(A_1, \dots , A_n\) is a singleton, we refer to the resulting rule as a priority rule.

The constrained equal awards rule, denoted by CEA, equalizes awards subject to the constraint that no claimant receives more than her claim: for each \((c,E)\in {\mathcal {C}}^N\) and each \(i\in N\),

$$\begin{aligned} CEA_i(c,E)=\min \{ c_i, \uplambda \}, \end{aligned}$$

where \(\uplambda \in {\mathbb {R}}_+\) is chosen so as to satisfy \(\sum _{j \in N}\min \{ c_j, \uplambda \}=E.\)

Like the constrained equal losses rule, this rule can also be generalized to allow for weights and priority classes (Moulin 2000).

3 Axioms, results, and duality

3.1 Axioms

We start recalling the two classical properties of adjudication rules, consistency and endowment monotonicity. Consistency is a basic property in the theory of distributive justice; it requires that if an allocation is considered desirable for a group of individuals, then it should remain so when restricted to each sub-group (Young 1987). More precisely, suppose that a rule is applied to settle a claims problem and a group of claimants is withdrawn along with their awards. If the situation is re-evaluated from the viewpoint of those who remain, in distributing the remaining endowment, a consistent rule assigns the same awards it did initially.

Consistency: For each pair \(N', N\in {\mathcal {N}}\) such that \(N'\subseteq N\), each \((c,E)\in {\mathcal {C}}^N\), if \(x=f(c,E)\), then, for each \(i\in N'\), \(x_i=f_i(c_{N'}, \sum _{N'} x_j)\).

Whereas consistency allows us to deduce that an allocation is desirable for each pair of individuals from its overall desirability, its converse allows us to deduce the desirability of an overall allocation from its desirability for each pair of individuals.

Converse consistency: For each \(N\in {\mathcal {N}}\), each \((c,E)\in {\mathcal {C}}^N\), and each \(x\in Z(c,E)\), if, for each pair \(\{i,j\}\subseteq N, f(c_{\{i,j\}},x_i+x_j)=x_{\{i,j\}}\), then \(f(c,E)=x\).

The following two properties are standard:

Endowment monotonicity: For each \((c,E)\in {\mathcal {C}}^N\) and each \(E'\in [0, E]\),

$$\begin{aligned} f(c,E')\le f(c,E). \end{aligned}$$

Endowment continuity: For each \(c\in {\mathbb {R}}^{N}_+\), \(f(c, \cdot )\) is continuous.

Endowment monotonicity implies endowment continuity. We say that a rule satisfies bilateral endowment monotonicity if it satisfies endowment monotonicity for the two-claimant case.Footnote 4

We now examine additivity in claims problems.Footnote 5 Additivity requires the overall allocation is invariant to whether two claims problems are solved independently or jointly, by aggregating each individual’s claims on the aggregate endowment.

Additivity: For each pair \((c,E),(c',E')\in {\mathcal {C}}^N\),

$$\begin{aligned} f(c,E)+f(c',E')=f(c+c',E+E' ). \end{aligned}$$

Despite appearing natural at first sight, the condition is demanding. Consider the example in the introduction stated formally:

Example 1

Let \(i,j\in A\) and \((c^*,E^*) \in {\mathcal {C}}^{\{i,j\}}\) be such that \(c_i^*=c_j^*=E^*=1\). Note that \((c^*,E^*)\) can be decomposed into \((c,E), (c',E') \in {\mathcal {C}}^{\{i,j\}}\) where \(c_i=E=1\), \(c_j=0\), \(c_i'=E'=0\), and \(c_j'=1\). Then, the definition of an allocation and additivity imply that, for each rule f, \(f_i(c^*,E^*)=1\) and \(f_j(c^*,E^*)=0\).

Bergantiños and Méndez-Naya (2001) and Bergantiños and Vidal-Puga (2004) use similar examples to show that, in fact, no rule satisfies additivity.Footnote 6 Another difficulty is that it requires ignoring an individual’s claim by transferring it into a subproblem with a null-endowment.

To rule out pathological cases featuring arbitrary transfers of claims and endowments across the subproblems, we consider a weaker property: additivity holds conditional on all individuals receiving positive awards in each of the smaller problems.

Positive-awards-conditional additivity: For each pair \((c,E), (c' ,E') \in {\mathcal {C}}^N\) such that \(f(c,E)>0\) and \(f(c',E') >0\), \(f(c,E)+f(c',E')=f(c+c',E+E' ).\)

For brevity, we refer to the above property as PAC additivity.

3.2 Results

The following lemma establishes that each PWCEL rule satisfies all of the properties that we will invoke. A proof can be found in the Appendix.

Lemma 1

The PWCEL rules satisfy consistency, endowment monotonicity, endowment continuity, PAC additivity, and converse consistency.

We can now state our result:

Theorem 1

A rule satisfies consistency, endowment continuity, and PAC additivity if and only if it is a PWCEL rule.

The axioms in Theorem 1 are logically independent (see Table 1 in the Appendix). Each PWCEL rule is not only endowment continuous, but continuous in both the claims and the endowment (a standard property used by Young 1987). Moreover, since each PWCEL rule is endowment monotonic, and hence endowment continuous, our main result is a corollary of Theorem 1:

Corollary 1

A rule satisfies consistency, endowment monotonicity, and PAC additivity if and only if it is a PWCEL rule.

The basic equity condition in claims problems specifies that claimants with equal claims receive equal awards:

Equal treatment of equals: For each \((c,E)\in {\mathcal {C}}^N\) and each pair \(i,j\in N\) such that \(c_i=c_j\), \(f_i(c,E)=f_j(c,E)\).

Since the only PWCEL rule satisfying equal treatment of equals is the constrained equal losses rule, the following is a corollary of Theorem 1 as well:

Corollary 2

A rule satisfies consistency, endowment continuity, PAC additivity, and equal treatment of equals if and only if it is the constrained equal losses rule.

The axioms in Corollaries 1 and 2 are also logically independent (see the Appendix).

3.3 Duality

The following axiom is linked through duality to PAC additivity and is used in the axiomatic derivation of the PWCEL rules.

Positive-losses-conditional additivity: For each pair \((c,E), (c' ,E') \in {\mathcal {C}}^N\) such that \(f(c,E)< c\) and \(f(c',E') < c'\), \(f(c,E)+f(c',E')=f(c+c',E+E')\).

For brevity, we refer to the above property as PLC additivity.

We say that two properties are dual if whenever a rule satisfies one of them, its dual satisfies the other (Thomson and Yeh 2008).

Lemma 2

PAC additivity and PLC additivity are dual.

Proof

Let f denote a rule satisfying PAC additivity and let g denote its dual rule. Let \((c,E), (c' ,E') \in {\mathcal {C}}^N\) be such that \(g(c,E)< c\) and \(g(c',E') < c'\). Thus, letting \(C=\sum _{i\in N} c_i\) and \(C'=\sum _{i\in N} c_i'\), \(f(c,C-E) > 0\) and \(f(c',C'-E') > 0\). Since f satisfies PAC additivity,

$$\begin{aligned} f(c,C-E) + f(c',C'-E')= f ( c+c', C+C'-E-E'). \end{aligned}$$
(1)

By definition, \(g(c,E) + g(c',E') = c-f(c,C-E) + c'-f(c',C'-E').\) Thus, by (1),

$$\begin{aligned} g(c,E) + g(c',E') = c+c'-f ( c+c', C+C'-E-E')= g(c+c', E+E'), \end{aligned}$$

as desired.

Conversely, if a rules satisfies PLC additivity, then its dual satisfies PAC additivity.

Let g denote a rule satisfying PLC additivity and let f denote its dual rule. Let \((c,E), (c' ,E') \in {\mathcal {C}}^N\) be such that \(f(c,E)> 0\) and \(f(c',E') > 0\). Thus, letting \(C=\sum _{i\in N} c_i\) and \(C'=\sum _{i\in N} c_i'\), \(g(c,C-E) < c\) and \(g(c',C'-E') < c'\). Since g satisfies PLC additivity,

$$\begin{aligned} g(c,C-E) + g(c',C'-E')= g ( c+c', C+C'-E-E'). \end{aligned}$$
(2)

By definition, \(f(c,E) + f(c',E') = c-g(c,C-E) + c'-g(c',C'-E').\) Thus, by (2),

$$\begin{aligned} f(c,E) + f(c',E') = c+c'-g ( c+c', C+C'-E-E')= f(c+c', E+E'), \end{aligned}$$

as desired. \(\square\)

The next lemma shows that PLC additivity implies that increasing the claims of a claimant does not change the outcome whenever no claimant achieved her claim.

Lemma 3

Let f denote a rule satisfying PLC additivity. Then, for each \((c,E) \in {\mathcal {C}}^N\) and each \(c'\in {\mathbb {R}}_+^N\) such that \(f(c,E)<c\le c'\), \(f(c',E)=f(c,E)\).

Proof

Let f denote a rule satisfying PLC additivity. Let \((c,E)\in {\mathcal {C}}^N\) be such that \(f(c,E)<c\) and \(c' \ge c\). By PLC additivity, \(f(c',E) = f(c+(c'-c),E + 0)= f(c,E)+f(c'-c,0)\). Since \(f(c'-c,0)=0\), \(f(c',E) = f(c,E)\), as desired. \(\square\)

A dual analysis of the results above concludes that (relying on Lemma 2), if we replace PAC additivity by PLC additivity, then we obtain the dual results of Theorem 1 and Corollaries 1 and 2.

Corollary 3

(Dual to Theorem 1). A rule is consistent, endowment continuous, and satisfies PLC additivity if and only if it is a PWCEA rule.

Analogously,

Corollary 4

(Dual to Corollary 1). A rule satisfies consistency, endowment monotonicity, and PLC additivity if and only if it is a PWCEA rule.

And,

Corollary 5

(Dual to Corollary 2). A rule satisfies consistency, endowment continuity, PLC additivity, and equal treatment of equals if and only if it is the constrained equal awards rule.

The axioms in Corollaries 3, 4, and 5 are logically independent. Their independence follows from the independence of the axioms in the original axiomatization.

4 Proofs

To prove Theorem 1, we proceed in two steps, corresponding to the following subsections. In the first step, we consider the implications of PAC-additivity and endowment continuity in two-claimant problems (Lemmata 4 and 5 below). Here we establish that, if a rule is endowment continuous and its dual satisfies PAC additivity, then it is either a weighted constrained equal awards or a priority rule (Lemma 6). The dual of a weighted constrained equal awards or a priority rule is a weighted constrained equal losses rule or a priority rule (Lemma 7).

The second step of the proof uses consistency to extend the two-claimant result to general claims problems. It relies on the fact that the PWCEL rules satisfy the property of “converse” consistency.

4.1 Two-claimant problems

The lemma below states that, for problems with two claimants, the additivity axioms jointly with endowment continuity imply endowment monotonicity.

Lemma 4

If a rule satisfies endowment continuity and either PAC or PLC additivity, then it is bilaterally endowment monotonic.

Proof

Let g denote a rule satisfying endowment continuity and PLC additivity. Let \(i,j\in A\) and \(c\in {\mathbb {R}}_{+}^{\{i,j\}}\). We first prove that, for each pair \(E,E'\in [0,c_i+c_j]\),

$$\begin{aligned} E<E', g(c,E)<c,\text { and }g(c,E')<c\text { imply }g(c,E)\le g(c,E'). \end{aligned}$$
(3)

Let E and \(E'\) be as specified in (3) and let \(c' \in {\mathbb {R}}_+^{\{i,j\}}\) be such that \(E'-E < \min \{c'_i,c_j'\}\). In \((c', E'-E)\), neither i nor j can feasibly be awarded their claim, \(0 \le g(c',E'-E)<c'\). By PLC additivity,

$$\begin{aligned} g(c+c',E') =g(c+c',E+E'-E) = g(c,E)+g(c', E'-E) \ge g(c,E). \end{aligned}$$

Since \(g(c,E')<c\), by Lemma 3, \(g(c+c',E')=g(c,E')\). Thus, \(g(c,E) \le g(c,E')\), establishing (3).

Let

$$\begin{aligned} \begin{aligned} E_i&\equiv \min \{E\in [0,c_i+c_j]:g_i(c,E)=c_i\},\\ E_j&\equiv \min \{E\in [0,c_i+c_j]:g_j(c,E)=c_j\}. \end{aligned} \end{aligned}$$

Since g is endowment continuous, \(E_i\) and \(E_j\) are well defined. Without loss of generality, suppose that \(E_j\le E_i\). We will prove that

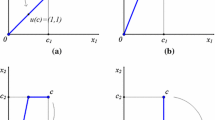
$$\begin{aligned} \text {for each }E\in [E_j,c_i+c_j], \quad g_j(c,E)=c_j. \end{aligned}$$
(4)

By way of contradiction, suppose that there is \(E^*\in [E_j,c_i+c_j]\) such that \(g_j(c,E^*)<c_j\). By endowment continuity, the set \(\{x\in {\mathbb {R}}_{+}^{\{i,j\}}:x=g(c,E), E\in [E_j,c_i+c_j] \}\) is a continuous path in \({\mathbb {R}}_{+}^{\{i,j\}}\) connecting \(g(c,E_j)\) and c, and containing \(g(c,E^*)\), as illustrated by the thick curve in Fig. 1. Thus, there are \(E_1, E_2\in [E_j, E^*]\) such that \(g(c,E_1)<c\), \(g(c,E_2)<c\), and \(E_1<E_2\) where it is not true that \(g(c,E_1)\le g(c,E_2)\), as illustrated in Fig. 1. This contradicts (3). This contradiction establishes (4).

Fig. 1
figure 1

Illustration of the proof of condition (4) in Lemma 4

Full size image

To conclude the proof, note that by (3), \(g_i(c,\cdot )\) and \(g_j(c,\cdot )\) are non-decreasing on \([0,E_j)\). By (4), for each \(E\in [E_j,c_i+c_j]\), \(g_i(c,E)=E-c_j\) and \(g_j(c,E)=c_j\). Thus, \(g_i(c,\cdot )\) and \(g_j(c,\cdot )\) are non-decreasing on \([E_j,c_i+c_j]\). Thus, \(g_i(c,\cdot )\) and \(g_j(c,\cdot )\) are non-decreasing on \([0,c_i+c_j]\). Recall that the claimants i, j and the claims profile c were chosen arbitrarily, and thus g is bilaterally endowment monotonic.

Let f denote a rule satisfying endowment continuity and PAC additivity. Then, immediately, the dual of f satisfies endowment continuity and PLC additivity. By the argument above, the dual of f is bilaterally endowment monotonic. This immediately implies that f is bilaterally endowment monotonic. \(\square\)

The next lemma shows that PLC additivity jointly with endowment monotonicity implies a linearity-type property (endowment linearity) whenever no claimant achieved her claim.

Lemma 5

Let g denote a rule satisfying bilateral endowment monotonicity and PLC additivity. Then, for each \(N\in {\mathcal {N}}\) such that \(|N|=2\), each \((c, E) \in {\mathcal {C}}^N\), each \(E'\in [ E, \sum c_i]\) such that \(g(c, E') < c\), and each \(\alpha \in [0,1]\),

$$\begin{aligned} g(c, \alpha E'+(1-\alpha ) E)=\alpha g(c, E')+(1-\alpha ) g(c, E). \end{aligned}$$

Proof

Let g denote a rule satisfying bilateral endowment monotonicity and PLC additivity. By PLC additivity, for each \(k \in {\mathbb {N}}\) and each \((c, E) \in {\mathcal {C}}^N\) such that \(g(c, E) < c\),

$$\begin{aligned} g(k c, k E)=k g(c, E). \end{aligned}$$
(5)

Let \((c, E) \in {\mathcal {C}}^N\) and \(E'\in [ E, \sum c_i]\) be such that \(g(c, E') < c\), and \(\alpha \in [0,1]\).

Case 1: \(\alpha =\frac{p}{q}\) where \(p, q \in {\mathbb {N}}\) and \(p \le q\). By bilateral endowment monotonicity, since \(E' \ge E\), \(c > g(c,E') \ge g\left( c,\frac{p}{q} E'+\frac{(q-p)}{q} E\right)\). By PLC additivity and (5), we have that,

$$\begin{aligned} q\cdot g\left( c,\frac{p}{q} E'+\frac{(q-p)}{q} E\right) = g( qc, p E'+ (q-p) E)= p g (c,E') + (q-p) g(c,E). \end{aligned}$$

It follows that,

$$\begin{aligned} g\left( c,\frac{p}{q} E'+\frac{(q-p)}{q} E\right) = \frac{pg(c, E')+(q-p) g(c, E)}{q}=\alpha g(c, E')+(1-\alpha ) g(c, E), \end{aligned}$$

as desired.

Case 2: \(\alpha \in [0,1] \setminus {\mathbb {Q}}\). Take an increasing sequence of rational numbers \(\{ \alpha _t \}\) and a decreasing sequence of rational numbers \(\{ \beta _t \}\), both converging to \(\alpha\). By bilateral endowment monotonicity, for each t,

$$\begin{aligned} g(c, \alpha _t E'+(1-\alpha _t) E) \le g(c, \alpha E'+(1-\alpha ) E) \le g(c, \beta _t E'+(1-\beta _t) E). \end{aligned}$$

By Case 1,

$$\begin{aligned} \alpha _t g(c, E')+(1-\alpha _t) g(c, E) \le g(c, \alpha E'+(1-\alpha ) E) \le \beta _t g( c, E')+(1-\beta _t) g(c, E) \end{aligned}$$

Letting \(t \rightarrow \infty\), \(g(c, \alpha E'+(1-\alpha ) E) = \alpha g(c, E')+(1-\alpha ) g(c, E),\) as desired. \(\square\)

The lemma below shows that if a rule satisfies bilateral endowment monotonicity and PLC additivity, then we obtain either a weighted CEA rule or a priority rule.

Lemma 6

Let g denote a rule satisfying bilateral endowment monotonicity and PLC additivity. Then, for each pair \(i,j\in A\), one and only one of the following statements is true:

  1. (i)

    There is \(\omega >0\) such that, for each \((c, E) \in {\mathcal {C}}^{\{i,j\}}\),

    $$\begin{aligned} \begin{aligned} g_i(c,E)&=\min \{c_i, \uplambda \},\\ g_j(c,E)&=\min \{c_j, \omega \uplambda \}, \\ \end{aligned} \end{aligned}$$

    where \(\uplambda \in {\mathbb {R}}_+\) is chosen so as to satisfy \(\min \{c_i, \uplambda \}+\min \{c_j,\omega \uplambda \}=E.\)

  2. (ii)

    There is \(k\in \{i,j\}\) such that, for each \((c, E) \in {\mathcal {C}}^{\{i,j\}}\), \(g_k(c,E)=\min \{c_k,E\}\).

Proof

Let g denote a rule satisfying bilateral endowment monotonicity and PLC additivity and let \(i,j\in A\). The proof consists of three claims.

Claim 1

Suppose that there is \((c,E) \in {\mathcal {C}}^{\{i,j\}}\) such that \(0< g(c,E) < c\). Then, there is \(\omega >0\) such that, for each \(E'\in [0,c_i+c_j]\),

$$\begin{aligned} \begin{aligned} g_i(c,E')&=\min \{c_i, \uplambda \},\\ g_j(c,E')&=\min \{c_j, \omega \uplambda \}, \\ \end{aligned} \end{aligned}$$

where \(\uplambda \in {\mathbb {R}}_+\) is chosen so as to satisfy \(\min \{c_i, \uplambda \}+\min \{c_j,\omega \uplambda \}=E'.\)

Fig. 2
figure 2

Illustration of the proof of Claim 1

Full size image

Let \((c,E) \in {\mathcal {C}}^{\{i,j\}}\) be such that \(0< g(c,E) < c\) and define \(\omega = \frac{g_j(c,E)}{g_i(c,E)}\). By Lemma 5, for each \(\alpha \in (0,1]\),

$$\begin{aligned} g(c, \alpha E) = g(c, \alpha E + (1- \alpha ) 0) = \alpha g (c,E) + (1- \alpha ) g (c, 0) = \alpha g (c,E)>0. \end{aligned}$$

Thus, \(\{x\in {\mathbb {R}}_+^{\{i,j\}}:x=g(c,e ), e \in [0, E]\}\) is a line with a constant slope of \(\omega\) connecting g(c, 0) to g(c, E), as illustrated in Fig. 2. Let

$$\begin{aligned} \begin{aligned} E_i&\equiv \min \{e\in [0,c_i+c_j]:g_i(c,e)=c_i\},\\ E_j&\equiv \min \{e\in [0,c_i+c_j]:g_j(c,e)=c_j\}. \end{aligned} \end{aligned}$$

Since g is bilaterally endowment monotonic, \(g(c,\cdot )\) is continuous and thus, \(E_i\) and \(E_j\) are well defined. Without loss of generality, suppose that \(E_j\le E_i\). By definition, for each \(E'<E_j\), \(g(c,E')<c\). Thus, by Lemma 5, for each \(\alpha \in (0,1)\),

$$\begin{aligned} g(c, \alpha E_j) = g(c, \alpha E_j + (1- \alpha ) 0) = \alpha g (c,E_j) + (1- \alpha ) g (c, 0) = \alpha g (c,E_j)>0. \end{aligned}$$

This implies that the set of points \(\{x\in {\mathbb {R}}_+^{\{i,j\}}:x=g(c,e ), e \in [0, E_j]\}\) is a line connecting g(c, 0) to \(g(c, E_j)\). Since there is \(\alpha \in (0,1)\) such that \(E=\alpha E_j\), the slope of this line is \(\omega\), as illustrated in Fig. 2. Thus, for each \(E' \in [0, E_j]\),

$$\begin{aligned}{} & {} g_i (c,E' ) = \min \{c_i, \uplambda \} \hbox {and} g_j (c,E' ) = \min \{ c_j, \omega \uplambda \}, \hbox {where} \uplambda \\{} & {} \quad \in {\mathbb {R}}_+ \hbox {is chosen so as to satisfy} \min \{c_i, \uplambda \}+\min \{c_j,\omega \uplambda \}=E'. \end{aligned}$$

By bilateral endowment monotonicity, the same is true for each \(E' \in [E_j, c_i+c_j]\).

Claim 2

Suppose there is no \((c,E) \in {\mathcal {C}}^{\{i,j\}}\) such that \(0< g(c,E) < c\). Then, for each \((c,E) \in {\mathcal {C}}^{\{i,j\}}\), either \(g_i(c, E)= \min \{c_i,E\}\) or \(g_j(c, E)= \min \{c_j,E\}\).

This follows immediately from the assumption that there is no \((c,E) \in {\mathcal {C}}^{\{i,j\}}\) such that \(0< g(c,E) < c\) and the fact that, since g is bilaterally endowment monotonic, \(g(c,\cdot )\) is continuous.

Claim 3

Let \((c,E)\in {\mathcal {C}}^{\{i,j\}}\). We have:

  1. (i)

    If there exist \(\uplambda \in {\mathbb {R}}_+\) and \(\omega >0\) such that \(g_i(c,E) = \min \{ \uplambda , c_i \}\) and \(g_j(c,E) = \min \{ \omega \uplambda , c_j \}\), then, for each \((c',E')\in {\mathcal {C}}^{\{i,j\}}\), \(g_i(c',E') = \min \{ \uplambda ' , c'_i \}\) and \(g_j(c',E') = \min \{ \omega \uplambda ', c'_j \}\) where \(\uplambda ' \in {\mathbb {R}}_+\) is chosen so as to satisfy

    $$\begin{aligned} \min \{ \uplambda ' , c'_i \} + \min \{ \omega \uplambda ', c'_j \} = E'. \end{aligned}$$
  2. (ii)

    If \(g_i(c, E)= \min \{c_i,E\}\), then, for each \((c',E')\in {\mathcal {C}}^{\{i,j\}}\), \(g_i(c', E')= \min \{c_i',E'\}\).

  3. (iii)

    If \(g_j(c, E)= \min \{c_j,E\}\) then, for each \((c',E')\in {\mathcal {C}}^{\{i,j\}}\), \(g_j(c',E')=\min \{c_j',E'\}\).

We prove statement (i); the proofs of (ii) and (iii) are analogous. Let \((c,E)\in {\mathcal {C}}^{\{i,j\}}\) and suppose that \(g_i(c,E) = \min \{ \uplambda , c_i \}\) and \(g_j(c,E) = \min \{ \omega \uplambda , c_j \}\) where

$$\begin{aligned} \min \{ \uplambda , c_i \} + \min \{ \omega \uplambda , c_j \} = E\text { and }\omega >0. \end{aligned}$$

Let \((c',E') \in {\mathcal {C}}^{\{i,j\}}\). Let \(c \wedge c'\) be the claims profile such that \((c \wedge c')_i=\min \{c_i,c_i'\}\) and \((c \wedge c')_j=\min \{c_j,c_j'\}\). Let \(E''>0\) denote an endowment strictly smaller than both \(c_{i} \wedge c'_{i}\) and \(c_{j} \wedge c'_{j}\). Then, \(g (c \wedge c', E'') < c \wedge c'\). By Lemma 3, \(c \wedge c' \le c\) implies \(g(c,E'')= g(c \wedge c', E'')\). By Claim 1,

$$\begin{aligned} \hbox {for each} \ E \in [0,(c_{i} \wedge c'_{i}) + (c_{j} \wedge c'_{j})], \quad g(c \wedge c', E)= g(c, E). \end{aligned}$$

Therefore, g recommends allocations for both claims profiles c and \(c\wedge c'\) following the same ray starting from the origin. Similarly, by Lemma 3, \(c \wedge c' \le c'\) implies \(g(c',E'')= (c \wedge c', E'')\). By Claim 1,

$$\begin{aligned} \hbox {for each} \ E \in [0,(c_{i} \wedge c'_{i}) + (c_{j} \wedge c'_{j})], \quad g(c \wedge c', E)= g(c', E). \end{aligned}$$

By Claim 1, \(g_i(c',E') = \min \{ \uplambda , c'_i \}\) and \(g_j(c',E') = \min \{ \omega \uplambda , c'_j \}\) where \(\uplambda \in {\mathbb {R}}_+\) is chosen so as to satisfy \(\min \{ \uplambda , c'_i \} + \min \{ \omega \uplambda , c'_j \} = E',\) Combining the above claims establishes the Lemma. \(\square\)

The lemma below shows that if a rule satisfies endowment continuity and PAC additivity, then we obtain either a weighted CEL rule or a priority rule.

Lemma 7

Let f denote a rule satisfying endowment continuity and PAC additivity. Then, for each pair \(i,j\in A\), one and only one of the following statements is true:

  1. (i)

    There is \(\omega >0\) such that, for each \((c, E) \in {\mathcal {C}}^{\{i,j\}}\),

    $$\begin{aligned} \begin{aligned} f_i(c,E)&=\max \{0,c_i- \uplambda \}\\ f_j(c,E)&=\max \{0,c_j- \omega \uplambda \},\\ \end{aligned} \end{aligned}$$

    where \(\uplambda \in {\mathbb {R}}_+\) is chosen so as to satisfy \(\max \{0,c_i- \uplambda \}+\max \{0,c_j- \omega \uplambda \}=E.\)

  2. (ii)

    There is \(k\in \{i,j\}\) such that, for each \((c, E) \in {\mathcal {C}}^{\{i,j\}}\), \(f_k(c,E)=\min \{c_k,E\}\).

A proof can be found in the Appendix.

4.2 Proof of Theorem 1

By Lemma 1, each PWCEL rule satisfies the axioms in Theorem 1. Conversely, let f denote a rule satisfying the axioms in Theorem 1. We will prove that f is a PWCEL rule.

For each pair \(i,j\in A\), define

  • \(i\sim j\) if and only if Statement (i) in Lemma 7 holds,

  • \(i\succ j\) if and only if Statement (ii) in Lemma 7 holds for \(k=i\),

  • \(j\succ i\) if and only if Statement (ii) in Lemma 7 holds for \(k=j\),

  • \(j\succsim i\) if either \(i\succ j\) or \(i\sim j\).

By Lemma 7, for each pair \(i,j\in A\),

$$\begin{aligned} \begin{aligned} i\sim j \quad \Leftrightarrow&\quad \text {there is }\omega >0\text { such that, for each }(c, E) \in {\mathcal {C}}^{\{i,j\}},\\&\quad f_i(c, E)=\max \{0,c_i- \uplambda \}\text { and } f_j(c, E)=\max \{0,c_j- \omega \uplambda \}, \hbox { where}\ \uplambda \in {\mathbb {R}}_+\\ {}&\quad \text {is chosen so as to satisfy} \max \{0,c_i- \uplambda \}+\max \{0,c_j-\omega \uplambda \}=E. \end{aligned} \end{aligned}$$
(6)

Throughout the rest of the proof, for each pair \(i,j\in A\) such that \(i\sim j\), we will use the notation \(\omega _{ij}\) for the corresponding parameter \(\omega\) in (6).

Completeness and transitivity of \(\succsim\): Completeness follows immediately from Lemma 7. To establish transitivity, let \(i,j,k\in A\) be such that \(i\succsim j\succsim k\). We need to show that \(i\succsim k\). By way of contradiction, suppose that this is not true, so that \(k\succ i\). Let \((c,E) \in {\mathcal {C}}^{\{i,j,k\}}\) be such that \(c_i=1/\omega _{ij}\) and \(c_j=c_k=E=1\). Let \(x=f(c,E)\). By consistency,

$$\begin{aligned} x_{\{i,j\}}=f(c_{\{i,j\}}, x_i+x_j), x_{\{i,k\}}=f(c_{\{i,k\}}, x_i+x_k), x_{\{j,k\}}=f(c_{\{j,k\}}, x_j+x_k). \end{aligned}$$
(7)

ThusFootnote 7Footnote 8

$$\begin{aligned} i\sim j \quad \text {and} \quad x_i+x_j>0 \quad \Rightarrow \quad x_i>0, \end{aligned}$$
(8)
$$\begin{aligned} j\sim k \quad \text {and} \quad x_j+x_k=1 \quad \Rightarrow \quad x_j>0, x_k>0, \end{aligned}$$
(9)

and, by the definition of \(\succ\),

$$\begin{aligned} k\succ i \quad \Rightarrow \quad x_i=0. \end{aligned}$$
(10)

We consider four cases:

  1. (a)

    \(i \succ j \succ k\). By the definition of \(\succ\) and (7), \(i \succ j\) implies \(x_j=0\) and \(j\succ k\) implies \(x_k=0\). Since \(x_i+x_j+x_k=1\), \(x_i=1\), contradicting (10). Thus, \(i \succ j \succ k\) is not possible.

  2. (b)

    \(i \sim j \sim k\). By the (9), \(x_i=0\). Thus, \(x_j+x_k=1\). By (9), \(x_j>0\). By (8), \(x_i>0\), a contradiction. Thus, \(i \sim j \sim k\) is not possible.

  3. (c)

    \(i\sim j \succ k\). By the definition of \(\succ\) and (7), \(j \succ k\) implies \(x_k=0\). Since \(x_i+x_j+x_k=1\), by (10), \(x_j=1\). By (8), \(x_i>0\), a contradiction. Thus, \(i \sim j \succ k\) is not possible.

  4. (d)

    \(i\succ j \sim k\). By the definition of \(\succ\) and (13), \(i \succ j\) implies \(x_j=0\). Since \(x_i+x_j+x_k=1\), by (10), \(x_k=1\). By (9), \(x_j>0\), a contradiction. Thus, \(i\succ j \sim k\) is not possible.

Thus, indeed, \(i\succsim k\), and \(\succsim\) is transitive.


Construction of the priority classes: Recursively define the subsets of A:

$$\begin{aligned} A_1&\equiv \{i\in A: \text {for each } j\in A, i\succsim j\},\\ A_2&\equiv \{i\in A \setminus A_1: \text {for each } j\in A\setminus A_1, i\succsim j\},\\ A_3&\equiv \{i\in A \setminus [A_1 \cup A_2]: \text {for each } j\in A\setminus [A_1 \cup A_2], i\succsim j\},\\&\ \ \vdots \end{aligned}$$

Since A is finite and \(\succsim\) is complete and transitive, there is \(n\le |A|\) such that A is partitioned by the sets \(A_1, \dots , A_n\).


Construction of the weights: Let \(m\in \{1,\dots , n\}\) and \((c,E)\in {\mathcal {C}}^{A_m}\) be such that, for each \(i\in A_m\), \(c_i=1\) and \(E=1\). Let \(r^m=c-f(c,E)\). Note that \(r^m\ge 0\). We next prove that

$$\begin{aligned} |A_m|\ge 2 \quad \text {implies that, for each }i\in A_m, \quad r_i^m>0. \end{aligned}$$
(11)

Suppose, instead, that there is \(i\in A_m\) such that \(r_i^m=0\) and let \(j\in A_m\setminus \{i\}\). Then, \(f_i(c,E)=1\) and \(f_j(c,E)=0\). By consistency, \(f_i(c_{\{i,j\}},1+0)=1\) and \(f_j(c_{\{i,j\}},1+0)=0\). Thus, (ii) in Lemma 7 holds, implying that \(i\succ j\). However, by definition, for each pair \(i,j\in A_m\), \(i\sim j\). This contradiction establishes (11).

By (11), we can define a weights profile \(w\in {\mathbb {R}}_{++}^A\) such that, for each \(m\in \{1,\dots , n\}\) and each \(i\in A_m\), \(w_i=r_i^m\).

We make an observation regarding the relationship between the coordinates of w corresponding to each agent. Suppose again that \(|A_m|\ge 2\) and let \(i,j\in A_m\). Thus, \(i\sim j\). Thus, by (6),

$$\begin{aligned} f_i(c,E)=1-\frac{1}{1+\omega _{ij}}, \quad f_j(c,E)=1-\frac{1}{1+\omega _{ij}}\omega _{ij}. \end{aligned}$$

Thus, \(w_i=r_i^m=\frac{1}{1+\omega _{ij}}\) and \(w_j=r_j^m=\frac{1}{1+\omega _{ij}}\omega _{ij}\). Thus,

$$\begin{aligned} \text {for each pair } i,j \in A_m, \quad \frac{w_j}{w_i}=\omega _{ij}. \end{aligned}$$
(12)

Concluding the proof: Let F denote the PWCEL rule specified by the partition \(A_1, \dots , A_n\) and weights profile w constructed above. We prove that \(f=F\).

Let \(N\in {\mathcal {N}}\), \((c,E)\in {\mathcal {C}}^N\), and \(x=f(c,E)\). By consistency,

$$\begin{aligned} \text {for each pair }i,j\in N,\quad f(c_{\{i,j\}},x_i+x_j)=x_{\{i,j\}}. \end{aligned}$$
(13)

Suppose that \(i,j\in N\) are such that \(i\sim j\). Then, by (6),

$$\begin{aligned} \begin{aligned}&x_i=\max \{0,c_i- \uplambda \}, \quad x_j=\max \{0,c_j- \omega _{ij}\uplambda \}, \text {where} \uplambda \in {\mathbb {R}}_+ \\&\text {is chosen so as to satisfy} \max \{0,c_i- \uplambda \}+\max \{0,c_j-\omega _{ij}\uplambda \}=x_i+x_j. \end{aligned} \end{aligned}$$

By the definition of F,

$$\begin{aligned} \begin{aligned}&F_i(c_{\{i,j\}},x_i+x_j)=\max \{0,c_i- w_i\uplambda '\}, \quad F_j(c_{\{i,j\}},x_i+x_j)=\max \{0,c_j- w_j\uplambda '\}, \text {where}\\&\uplambda ' \in {\mathbb {R}}_+ \ \text {is chosen so as to satisfy}\max \{0,c_i- w_i\uplambda '\}+\max \{0,c_j-w_j\uplambda '\}=x_i+x_j. \end{aligned} \end{aligned}$$

Thus, by (12),

$$\begin{aligned} \hbox {for each pair} \ i,j\in N \hbox {,} i\sim j \Rightarrow F_i(c_{\{i,j\}},x_i+x_j)=x_i, F_j(c_{\{i,j\}},x_i+x_j)=x_j. \end{aligned}$$
(14)

Suppose that \(i,j\in N\) are such that \(i\succ j\). Then, by (ii) in Lemma 7,

$$\begin{aligned} x_i=\min \{c_i,x_i+x_j\}. \end{aligned}$$

By the definition of F, \(F_i(c_{\{i,j\}},x_i+x_j)=\min \{c_i,x_i+x_j\}\) as well. Thus,

$$\begin{aligned} \hbox {for each pair} \ i,j\in N \hbox {,} i\succ j \Rightarrow F_i(c_{\{i,j\}},x_i+x_j)=x_i, F_j(c_{\{i,j\}},x_i+x_j)=x_j. \end{aligned}$$
(15)

By Lemma 1, F is conversely consistent. Thus, by (14) and (15) and since \(\succsim\) is complete, \(F(c,E)=x=f(c,E)\). Since \(N\in {\mathcal {N}}\) and \((c,E)\in {\mathcal {C}}^N\) were chosen arbitrarily, \(F=f\). \(\square\)

Note that, as established in the Appendix, the axioms in Theorem 1 are logically independent.

5 Concluding remarks

We discuss here some axiomatizations that are related to other results in the literature. For instance, Theorem 3* in Herrero and Villar (2001) states that the constrained equal losses rule is the only one satisfying equal treatment of equals, composition down, and minimal rights first. The result in our Corollary 2 adds consistency and replaces composition down and minimal rights first by endowment continuity and PAC additivity. Similarly, Flores-Szwagrzak (2015) says that a rule satisfies consistency, composition down, and minimal rights first if and only if is a PWCEL rule. Our main result in Theorem 1 replaces once again composition down and minimal rights first by endowment continuity and PAC additivity in order to axiomatize the PWCEL rules.

Regarding the constrained equal awards, we can invoke duality to conjecture similar conclusions. For instance, a rule satisfies equal treatment of equals, composition up (dual to composition down), and claims truncation invariance (dual to minimal rights first) if and only if is a constrained equal awards (Dagan 1996). Similarly, Flores-Szwagrzak (2015) states that a rule satisfies consistency, composition up, and claims truncation invariance if and only if is a PWCEA rule. The result dual to Theorem 1 replaces composition up and claims truncation invariance by endowment continuity and PLC additivity in order to axiomatize the PWCEA rules. Finally, if we replace endowment continuity by endowment monotonicity in all our results mentioned above, we obtain the very same conclusions.

Interestingly, Flores-Szwagrzak et al. (2020) study a version of additivity where a problem can be decomposed into two smaller problems whenever i) all individuals receive positive awards in each of the smaller problems, and ii) these smaller problems keep the same claims vector.

Restricted additivity: For each \(c \in {\mathbb {R}}_+^N\), and each pair \(E, E' \in [0, \sum _N c_i]\) such that \(f(c,E)>0\) and \(f(c,E') >0\),

$$\begin{aligned} f(c,E)+f(c,E')=f(c+c,E+E' ). \end{aligned}$$

In contrast, PAC additivity does not impose the restriction of keeping the same claim vectors in the decomposed problems. Note that if we replace PAC additivity by restricted additivity, the main result in Theorem 1 does not hold anymore since solutions like the priority-augmented proportional rules would also satisfy consistency, endowment continuity, and restricted additivity.

We finally discuss a conjecture suggested to us by Youngsub Chun, Hervé Moulin, and José Zarzuelo. Consider the following property: for each pair \((c,E), (c', E')\in {\mathcal {C}}^N\) such that \(0<f(c,E)<c\) and \(0<f(c',E')<c'\),

$$\begin{aligned} f(c,E)+f(c',E')=f(c+c',E+E'). \end{aligned}$$
(16)

Clearly, this property is implied by both PAC and PLC additivity. Is the family of consistent and endowment continuous rules satisfying this property the union of the PWCEA and the PWCEL rules? The answer is no. For a counterexample, see the subsection Counterexample 1 in the Appendix.