Abstract
This paper studies payoffs in subgame perfect equilibria of two-player discounted overlapping generations games with perfect monitoring. Assuming that mixed strategies are observable and a public randomization device is available, it is shown that sufficiently patient players can obtain any payoffs in the interior of the smallest rectangle containing the feasible and strictly individually rational payoffs of the stage game, when we first choose the rate of discount and then choose the players’ lifespan. Unlike repeated games without overlapping generations, obtaining payoffs outside the feasible set of the stage game does not require unequal discounting.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Overlapping generations (OLG) games have been widely studied to investigate economic settings whose members change over time. In OLG games, players in the same generation interact for a sufficiently long time, and are then sequentially replaced by successors in the next generation. Kandori (1992) first proved the folk theorem in general n-player OLG games, which stated that the players in each generation can obtain any payoffs in \(V^*\), the set of feasible and strictly individually rational one-shot payoffs. Following this study, Smith (1992) proved several versions of folk theorems with stronger results.
In the analyses of Kandori (1992), Smith (1992), and subsequent studies on OLG games, the characterization of the equilibrium set of payoffs is restrictive. They showed that players can obtain any payoffs in \(V^*\) without discounting, and that the result is robust against low discounting. However, this does not mean that players cannot attain payoffs outside \(V^*\); when they discount the future, they can transfer each other’s payoffs over time because young generations and old generations view current payoffs differently, which allows their equilibrium payoffs to go outside \(V^*\). Here, we do not require that the discount rate of future payoffs is different between players, without which, as Sorin (1986) showed, equilibrium payoffs never go outside \(V^*\) in the standard repeated games without overlapping generations.
We briefly illustrate how players improve their outcome in the following example of OLG chicken game with one-shot payoffs in Table 1. Here, each player with two periods of life has an action set of either \(A_1\) or \(A_2\) with \(A_1=A_2=\{ S,\ R\}\), and his opponent with the action set of different subscript is replaced one period after his entrance, as you can see in Table 2. When the young player plays R and the old player plays S, their actions form a one-shot Nash equilibrium in every period with a higher payoff to the young player. When players discount the future at a common \(\delta \) between zero and one, their average payoff is \(\frac{2}{1+\delta }\). If \(\delta <1\) holds, this value is strictly larger than one, that is, \((\frac{2}{1+\delta },\ \frac{2}{1+\delta })\) Pareto-dominates (1, 1), and is outside \(V^*\).
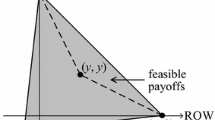
We generalize this result to any stage game with two players. Under the existence of a public randomization device and observability of mixed actions, we show that payoffs in the rectangular hull of \(V^*\), that is, payoffs in the smallest rectangle that contains \(V^*\), can be approximated in equilibria. In this chicken game, for example, it is \((0, 2)^2\), as shown by the gray area of the following Fig. 1.
In order to obtain this result, it is essential for players to discount future payoffs. In our study, the rate of discounting has two different roles, which can be seen as a trade-off. First, players must be so patient that do not deviate, the argument of which is seen everywhere in the literature on repeated games. The second role, which is novel to our paper, is that it must diminish the payoffs in players’ later days. If players do not discount the future, such intertemporal trade of payoffs in a Pareto improving way fails, as demonstrated by the example of the chicken game in Table 1; as \(\delta \) increases to one, the best symmetric payoff \(\frac{2}{1+\delta }\) goes to one, which is no better than the stage game.
It must also be noted that there is an order in the choice of parameters; we must fix the discount factor first, and then choose players’ lifespan depending on the discount factor. This is because, as \(\delta \) approaches one, we need a longer lifespan in order for players’ continuation payoffs after they become old to diminish sufficiently. This order is in contrast to that of the non-uniform OLG folk theorem in Smith (1992), where he first fixes players’ lifespan, allowing them to punish deviations strictly under no discount, and then chooses \(\delta <1\) with which the punishments are still incentive compatible.
It is important to relate our research on OLG games to those of infinitely repeated games without overlapping generations where players use unequal discount factors, which have accumulated since Lehrer and Pauzner (1999). Lehrer and Pauzner (1999) studied two-player infinitely repeated games with different discounting between players, and showed that players can obtain equilibrium payoffs outside \(V^*\). In their model, the player who evaluates future payoffs at a higher rate gives payoffs to his opponent with less patience first, and is rewarded later. This allows players to obtain higher payoffs outside \(V^*\). Chen and Takahashi (2012) generalized this analysis and showed that, as long as players have different discount factors, \(V^*\) is included in the set of equilibrium payoffs even when they have equivalent stage-game utilities. Sugaya (2015) considered the case of imperfect monitoring, and proved an unequal-discounting folk theorem for n-player games that includes perfect and imperfect public monitoring.
In models of repeated games with unequal discounting, however, there is an asymmetry of equilibrium payoffs between players; the maximum payoff of the impatient player increases relative to the stage game, but that of the more patient one remains the same. Concerning this issue, Lehrer and Pauzner (1999) pointed out that “The patient player is willing to forego early payoffs only if she can trust the impatient player to reciprocate later on. And this requires that the impatient player’s individually rational payoff level be low enough that he can be punished should he deviate. In other words, the benefits of intertemporal trade can be reaped only if the impatient player is vulnerable enough to be trusted” (Lehrer and Pauzner 1999, p. 394).
A typical example of this asymmetry in equilibrium payoffs is given by the repeated prisoner’s dilemma in Table 3 with unequal or asymmetric discounting, whose set of equilibrium payoffs is shown as the gray area in Fig. 2.Footnote 1 In our OLG model, on the other hand, every player’s payoff can be raised without diminishing his opponent’s payoff; any payoffs in the symmetric rectangle, \((0,\ 3)^2\), can be approximated in equilibria, as in Fig. 3.Footnote 2 This is because the two players are in different stages of their lives−when the younger player earns good payoffs, the other player earns low payoffs, but the latter’s overall payoff is not affected very much since he is in the later stage of his lifetime and these bad payoffs are more heavily discounted than the good ones he received when young.
The remainder of this paper is organized as follows. In Sect. 2, we define the model of OLG games and prove the main theorem. In Sect. 3, we discuss remaining important issues that could not be included in this paper.
2 Model and results
2.1 Stage games
Let \(G=(N,\ A,\ g)\) be a two-player stage game defined as follows. \(N=\{ 1,\ 2\}\) is the set of players in G. For \(i\in N\), \(A_i\) is i’s finite set of pure actions, and \(\triangle A_i\) is i’s set of mixed actions. We denote i’s payoff function as \(g_i:\ \triangle A_1\times \triangle A_2\rightarrow {\mathbb {R}}\). Let \(V=co\bigl ( g(A)\bigr )\) be the set of feasible payoffs, where \(A=A_1\times A_2\). The (mixed) minimaxing action of \(j\ne i\) against i, and i’s best response, are defined respectively, as follows:
The set of feasible and strictly individually rational payoffs is then defined as \(V^*=\bigl \{ v\in V:\ v_1>g_1(m^1),\ v_2>g_2(m^2)\bigr \}\), assuming that \(V^*\ne \emptyset \). We allow for the case of \(\dim V^*=1\). Without loss of generality, the infimum of i’s payoffs in \(V^*\) is normalized to zero, as follows:
This value determines the lower bound of players’ equilibrium payoffs.Footnote 3 We also denote the supremum of i’s payoffs in \(V^*\) as \(r_i\), defined as follows:
This value determines the upper bound of players’ equilibrium payoffs in our result. We then define the open rectangular hull of \(V^*\), say \(R(V^*)\), as follows:
Note that in many stage games, \(R(V^*){\setminus } V^*\ne \emptyset \) holds. In the prisoner’s dilemma in Table 3, for example, \(r_1=r_2=3\), and as shown by the gray area of Fig. 3, \(R(V^*)=(0,\ 3)^2\).
2.2 OLG games
Given a stage game G defined above, we construct the OLG game with perfect monitoring, \(OLG(G;\ \delta ,\ T)\) as follows (also see Table 4):
-
The game starts in period 1. In every period, G is played by two finitely-lived players, one with the action set \(A_1\) and the other with \(A_2\).
-
For \(i\in N\) and \(k\ge 1\), the player with \(A_i\) in generation k joins in the game at the beginning of period \(2(k-1)T+(i-1)T+1\), and lives for the following 2T periods, until he retires at the end of period \(2kT+(i-1)T\), where \(T\ge 1\) is fixed. The only exception is the player with \(A_2\) in generation 0, who participates in the game between periods 1 and T.
-
Each player’s per-period payoffs are discounted at a common \(\delta \in (0,\ 1]\).Footnote 4
We assume that in every period, players can observe each other’s mixed actions, and that a public randomization device (PRD) is available. When a sequence of actions \(\bigl (\alpha (t)\bigr ) _{t=1}^{2T}\in (\triangle A_1\times \triangle A_2)^{2T}\) is played throughout a player’s life with \(A_i\), his average payoff is as follows:Footnote 5
2.3 The Folk theorem
The following theorem holds.
Theorem 1
(A folk theorem in two-player discounted OLG games) Suppose that mixed actions are observable and a PRD is available in every period. Then, for every pair of payoffs \(v\in R(V^*)\), and for every \(\epsilon >0\), there exists \({\underline{\delta }}\in (0,\ 1)\) such that if \(\delta \in [{\underline{\delta }},\ 1)\), then for every sufficiently large \(T\in {\mathbb {N}}\), there exists a subgame perfect equilibrium in \(OLG(G;\ \delta ,\ T)\) where the pair of players in each generationFootnote 6 obtains average payoffs w that satisfies \(|w_i-v_i|<\epsilon \) for \(i\in N\).
Before the formal proof, we use the following Table 5 and briefly see how the players in each generation can obtain good equilibrium payoffs \((v^1 _1,\ v^2 _2)\in R(V^*)\), which are possibly outside \(V^*\).
As you can see in this table, each player with \(A_i\) obtains the target payoff \(v^i _i\) in his first \(T-S\) periods of life. Here, his opponent endures a relatively low payoff \(v^i _j\) so that players’ payoffs during these periods are feasible and strictly individually rational, i.e., \((v^i _i,\ v^i _j)\in V^*\). In the following S periods, he gives the maximum one-shot payoff \(g_j(b^j)\) to his opponent, where \(b^i\in \arg \max _{a\in A}g_i(a)\), in order to block the deviation by his opponent, who is going to retire. After his opponent is replaced by a new player, he helps the new opponent to obtain \(v^j _j\) for \(T-S\) periods, and then receives a terminal bonus \(g_i(b^i)\) in his final S periods. When he discounts the future and his lifespan is sufficiently long, his continuation payoff after he becomes old vanishes, and the average payoff throughout his life becomes almost equal to what he obtains early in his life, \(v^i _i\).
We investigate how such play becomes possible as an equilibrium path in more detail, using the prisoner’s dilemma in Table 3. Here, we show that the pair of players can obtain \((v^1 _1,\ v^2 _2)=(2.8,\ 2.8)\in R(V^*){\setminus } V^*\) within the error of \(\epsilon =0.1\) in an equilibrium, with \(S=1\), \(\delta =0.95\), and sufficiently large T. It is assumed that at the beginning of each period, the PRD draws one integer from 1 to 5 with equal probability 0.2, and that players commonly observe it.
Hereafter, we use the following notations without loss of generality:
-
(i)
In each period, we call the young player (i.e., the player in his earlier half of life) Young, and his opponent Old, respectively.
-
(ii)
The strategy profile is defined for any T-period block between \((k-1)T+1\) and kT for \(k\ge 1\), and period \((k-1)T+t\) is just called “period t” for \(t\in \{ 1,2,\ldots ,T\}\).
If there is no deviation, players play the following on-path strategy:
-
In period \(t\le T-1\): Old plays C. Young plays C after the PRD drew at most 3, and plays D otherwise. Here, the one-shot payoffs of \((Young,\ Old)\) are \((2.8,\ 0.4)\in V^*\).
-
In period \(t=T\): Old plays D and Young plays C.
If someone deviates, players play one of the following punishments:
-
Young’s deviation in period \(t\le T-3\): Players switch to play D until Old retires. After that, players switch to on-path.
-
Young’s deviation in period \(t\ge T-2\): Players switch to play D. After Old retires, players continue to play D for the following 16 periods, and then switch to on-path.
-
Old’s deviation: Players switch to play D until Old retires. After that, players switch to on-path.
We show that the above strategy profile forms an equilibrium. First, consider Young’s early deviation from C in period \(t=T-\ell \) for \(3\le \ell \le T-1\). Suppose that the PRD drew at most 3 at the beginning of period t. If he deviates, he gets 4 immediately, but his continuation payoff until the end of period T is reduced to 0. When he does not deviate, he receives \(2+2.8\sum _{s=1}^{\ell -1}\delta ^s-2\delta ^\ell \ge 2+2.8(\delta +\delta ^2)-2\delta ^3>4\) during these periods, which is better than the deviation.
Second, consider Young’s late deviation. Suppose that he deviates in period \(t=T-1\). If he deviates, he gets 4 immediately, but his continuation payoff during the following 17 periods is 0. When he does not deviate, his payoff during these periods is \(2-2\delta +0.4\sum _{s=1}^{16}\delta ^{s+1}>4\). By the analogous reason, he does not deviate in period \(t=T-2\), because he gets \(2+2.8\delta -2\delta ^2+0.4\sum _{s=1}^{16}\delta ^{s+2}>2+0.8\delta +4\delta >4\) on the path. Next, suppose that he deviates in period \(t=T\). If he deviates, he gets 0 not only immediately, but also during the following 16 periods. When he does not deviate, his payoff during these periods is \(\frac{1}{\delta }(-2\delta +0.4\sum _{s=1}^{16}\delta ^{s+1})>\frac{4-2}{\delta }>0\).
Now we consider Old’s deviation in period \(t=T-\ell \) for \(2\le \ell \le T-1\). When he does not deviate, his continuation payoff is \(0.4\sum _{s=1}^{\ell -1}\delta ^s+4\delta ^\ell \ge 0.4\delta +4\delta ^2=3.99\). Because \(g_i(D,\ C)-g_i(C,\ C)=g_i(D,\ D)-g_i(C,\ D)=2\) and the continuation payoff after the deviation is 0, the difference between the payoffs on the path and from the deviation is at least \(1.99>0\). By the analogous reason, he does not deviate in \(t=T-1\), because he gets \(4\delta >2\) in period T on the path.
Finally, each player’s average payoff is as follows:
When we choose \(T\ge 64\), this value is greater than 2.7, which is within the distance of 0.1 from the target.
We proceed to formally prove Theorem 1. In the above example, we did not have to consider the deviation from the punishment, because the punishment itself is a one-shot Nash equilibrium. In general, however, Nash equilibrium payoffs may not be able to provide a sufficient level of punishment. For this reason, we must generalize the structure of punishments against the three types of deviations described above: any player’s early deviation, Young’s late deviation, and Old’s late deviation.
Proof
Choose any \(v=(v^1 _1,\ v^2 _2)\in R(V^*)\) and \(\epsilon >0\). By the definition of \(R(V^*)\), there exists \(v^i _j\) for \(i\in N\) and \(j\ne i\) which satisfies \(v^i=(v^i _i,\ v^i _j)\in V^*\). Let \(a^i\) be (correlated) actions with one-shot payoffs \(v^i\). Because \(\dim R(V^*)=2\), there exist (correlated) actions \(c^i\) with one-shot payoffs \(g(c^i)\in V^*\) satisfying \(0<g_i(c^i)<v^j _i\). Players play \(c^i\) instead of \(a^j\) to punish the late deviation of Young with \(A_i\), after he becomes Old. We denote the mutual minimax profile and a one-shot Nash profile as \(m=(m^2 _1,\ m^1 _2)\) and e, respectively.
The game starts in period 1 with playing \(a^1\). The natural numbers Q, S, and P, which satisfy \(P+Q+S<T\), are determined later in this order so that the following strategy profile is subgame perfect. The profile consists of 5 steps. Here, Steps 3 and 5 need the observability of mixed actions in order to detect the deviation from minimaxing, either \(m^2 _1\) or \(m^1 _2\), which can be a mixed action. We also need the PRD for Steps 1 and 4 in order to let players play \(a^i\) and \(c^i\). Without loss of generality, we assume that the action set of Young (resp. Old) is \(A_i\) (resp. \(A_j\)).
When there is no deviation, players play the following on-path strategy.
-
Step 1. In period \(t\le T-S\), players play \(a^i\).
-
Step 2. In period \(t\ge T-S+1\), players play \(b^j\).
After someone unilaterally deviates, players play the following punishments. The punishments are also applied to the deviations from themselves. After each punishment, players return to on-path.
-
Step 3. When someone deviates in period \(t\le T-S-Q\), players play m for Q periods.
-
Step 4. When Young deviates in period \(t\ge T-S-Q+1\), players play e until Old retires. After that, players play \(c^i\) for P periods.
-
Step 5. When Old deviates in period \(t\ge T-S-Q+1\), players play \(m^j\) until Old retires.
According to this profile, \(a^i\) is played for \(T-S\) periods on the equilibrium path when each player with \(A_i\) is Young, and his average payoff is almost equal to \(v^i _i\) under the positive rate of discounting \(\delta <1\) and sufficiently long T relative to S, as you can see in Table 5.
In the remainder of this section, it is proved that the above strategy profile forms a subgame perfect equilibrium for \(\delta \) sufficiently close to 1 when we choose Q, S, and P appropriately. The methodology is to provide strictly positive penalties for any unilateral deviation from each step when \(\delta =1\). Then, by continuity of payoffs, there is some \({\underline{\delta }}\in (0,\ 1)\) for which all penalties are still positive for \(\delta \in [{\underline{\delta }},\ 1)\). In determining the parameters, we consider the “worst-case scenario,” where the incentive to deviate is greatest.
-
Deviations in period \(t\le T-S-Q\) when nobody is minimaxed: In this case, the player can get at least \({\underline{u}}=\min \bigl \{ v^1 _1,\ v^2 _2,\ g_1(c^1),\ g_2(c^1),\ g_1(c^2),\) \(g_2(c^2)\bigr \}>0\) in every period without deviation, until the end of period \(T-S\). When he deviates, he gets at most \(\beta =\max \bigl \{ g_1(b^1),\ g_2(b^2)\bigr \}\) immediately, but is minimaxed for the following Q periods, by Step 3. In order to block the deviation, we choose Q to satisfy the following inequality:
$$\begin{aligned} (1+Q){\underline{u}}>\beta . \end{aligned}$$(1) -
Deviations from minimaxing in period \(t\le T-S-Q\): In this case, Step 3 restarts and the deviator’s payoff from the current period to the next Q periods is at most 0. When he does not deviate, the players return to on-path within Q periods and he can get at least \({\underline{u}}>0\).
-
Deviations by Old in period \(t\ge T-S-Q+1\): Suppose that Old deviates in period \(t=T-S-Q+1\). He gets at most \(\beta \) immediately, but his continuation payoff until his retirement is at most 0 because of Step 5. When he does not deviate, his payoff during these \(Q+S\) periods is at least \(Q\omega +S{\underline{\beta }}\), where \(\omega =\min _{(i,a)\in N\times A}g_i(a)\) is players’ worst one-shot payoff, and \({\underline{\beta }}=\min \bigl \{ g_1(b^1),\ g_2(b^2)\bigr \}\). We can avoid the deviation when we choose S satisfying the following inequality:
$$\begin{aligned} Q\omega +S{\underline{\beta }}>\beta . \end{aligned}$$(2) -
Deviations by Young in period \(t\ge T-S-Q+1\): Suppose that Young deviates in period \(t=T-S-Q+1\). He gets at most \(\beta \) immediately. Then, because of Step 4, he gets at most \((Q+S-1)g_i(e)\) in the following \(Q+S-1\) periods. After Old’s retirement, his payoff in the following P periods is reduced to at most \(Pg_i(c^i)\), where \(g_i(c^i)<v^j _i\). When he does not deviate, he gets at least \((Q+S)\omega \) before Old’s retirement, and at least \(Pv^j _i\) after Old’s retirement. We can avoid the deviation when we choose P satisfying the following inequality for each \(i\in N\):
$$\begin{aligned} (Q+S)\omega +Pv^j _i>\beta +(Q+S-1)g_i(e)+Pg_i(c^i). \end{aligned}$$(3)Therefore, deviations from any steps strictly decrease deviators’ payoffs under no discount, which means that the above strategy profile forms a subgame perfect equilibrium also for some \({\underline{\delta }}\in (0,\ 1)\) and \(\delta \in [{\underline{\delta }},\ 1)\). Fix such \(\delta \). Note that the parameters Q, S, and P are independent of T. We then choose \({\underline{T}}\) which satisfies the following inequalities:
$$\begin{aligned}&{\underline{T}}> P+Q+S, \end{aligned}$$(4)$$\begin{aligned}&\frac{1}{1-\delta ^{2{\underline{T}}}}\bigl \{ (1-\delta ^{{\underline{T}}-S})v^i _i+(\delta ^{{\underline{T}}-S}-\delta ^{2{\underline{T}}})\omega \bigr \}> v^i _i-\epsilon ,\ and \end{aligned}$$(5)$$\begin{aligned}&\frac{1}{1-\delta ^{2{\underline{T}}}}\bigl \{ (1-\delta ^{{\underline{T}}-S})v^i _i+(\delta ^{{\underline{T}}-S}-\delta ^{2{\underline{T}}})\beta \bigr \}< v^i _i+\epsilon . \end{aligned}$$(6)Equations (5) and (6) must be satisfied for each \(i\in N\). The LHS of (5) (resp. (6)) determines the lower bound (resp. upper bound) of the average payoff of each player with \(A_i\) on the path, and as \({\underline{T}}\rightarrow \infty \), each converges to \(v^i _i\). Now, set \(T\ge {\underline{T}}\). Then in \(OLG(G;\ \delta ,\ T)\), the above strategy profile is well defined by (4), and it forms a subgame perfect equilibrium by (1), (2), and (3), where the average payoff of each player with \(A_i\) is within \(\epsilon \) of the target payoff \(v^i _i\), by (5) and (6).\(\square \)
3 Conclusions and discussions
In this study, we analyzed a model of two-player discounted OLG games. We have seen that players can obtain payoffs outside \(V^*\). Here, some readers may notice the following issues, which are the subject of the author’s ongoing research, including Morooka (2020). The first is to consider the possibility of obtaining better payoffs outside \(R(V^*)\). We are going to investigate whether the analogue of Sorin (1986) impossibility in the standard repeated games without overlapping generations applies to OLG games.
Second, the model of OLG games where a PRD is not available and players cannot observe mixed actions should be considered. In the standard repeated games, the minimax folk theorem proved by Fudenberg and Maskin (1986) using a PRD extends to the case where players cannot use a PRD. This is shown for equal discounting by Fudenberg and Maskin (1991) and for possibly unequal discounting by Dasgupta and Ghosh (2019). A similar refinement of equilibrium strategies will be required in order to get rid of these assumptions in OLG games.
The third is to investigate how the result changes when the stage game has three or more players. In two-player OLG games, the mutual minimaxing is available for the punishment. When more players play the stage game, such a useful construction is not available. In order to generalize our result to n-player OLG games, therefore, we will have to consider more complex strategies.
Finally, it will be convenient if we can compute the exact shape of the equilibrium payoff set of OLG games without a PRD for arbitrarily fixed \(\delta \) and T. For standard repeated games, Lehrer and Pauzner (1999) have an algorithm to find the shape of the frontier using a PRD as players become patient. Dasgupta and Ghosh (2019) provide a condition to identify all payoff profiles that can be obtained as subgame perfect equilibrium payoffs of some discount factor profile without using a PRD. When we apply these results to OLG games, however, recursive methods which can be used in the standard repeated games will be no longer available because, for example in Table 2, the continuation games beginning from odd periods are different from those beginning from even periods. We leave these issues to be resolved in future research.
Notes
In order to obtain this set with a smooth boundary, we require some notion of relative discounting fixed. Basically, we let the game be more and more frequently repeated while keeping the same rate of time discounting.
It should be noted that the region shown in Fig. 2 is the payoff set for one particular profile of relative discounting, while the region shown in Fig. 3 is obtained as we vary the discount factor and the generation span. The condition in Dasgupta and Ghosh (2019) tells us that if we allow all kinds of unequal discounting, the equilibrium payoffs will be \((0,\ 4)^2{\setminus } [3,\ 4)^2\), i.e., \(V^*\) plus any strictly individually rational point inside the rectangular hull of the feasible set that has at least one projection passing through the interior of \(V^*\) (see Fig. 2 on p. 10 of their paper for detail). Therefore, the region in Fig. 3 lies in between the non-OLG payoff sets for equal and all possible unequal discounting.
Sometimes this value is strictly greater than the player’s minimax value. To see this, consider the following example with actions \(A_1=\{ U,\ D\}\) and \(A_2=\{ L,\ R\}\), and payoffs \(g_i(a_1,\ L)=-0.5\) for \((i,\ a_1)\in N\times A_1\), \(g_1(U,\ R)=g_2(U,\ R)=g_1(D,\ R)=0.5\) and \(g_2(D,\ R)=0\). Here, we can verify that \(g_1(m^1)=-0.5\), but \(\inf _{v\in V^*}v_1=0\) holds, where \(V^*=co\Bigl (\bigl \{ (0,\ 0),\ (0.5,\ 0),\ (0.5,\ 0.5)\bigr \}\Bigr )\cap {\mathbb {R}}^2 _{++}\).
Although our result does not hold with \(\delta =1\), it is convenient to consider this case in order to construct the strict punishments under no discount that are still available with \(\delta <1\).
For the player with \(A_2\) in generation 0, replace 2T with T.
The player with \(A_1\) in generation 1 and the player with \(A_2\) in generation 0 are excluded from this result.
References
Chen B, Takahashi S (2012) A Folk theorem for repeated games with unequal discounting. Game Econ Behav 76:571–581. https://doi.org/10.1016/j.geb.2012.07.011
Dasgupta A, Ghosh S (2019) Repeated games without public randomization: a constructive approach. mimeo. http://www.bu.edu/econ/files/2019/02/PRD_AD_2019_v4.pdf. Accessed 31 Dec 2020
Fudenberg D, Maskin E (1986) The Folk theorem in repeated games with discounting or with incomplete information. Econometrica 54:533–554. https://doi.org/10.2307/1911307
Fudenberg D, Maskin E (1991) On the dispensability of public randomization in discounted repeated games. J Econ Theor 54:26–47. https://doi.org/10.1016/0022-0531(91)90163-X
Kandori M (1992) Repeated games played by overlapping generations of players. Rev Econ Stud 59:81–92. https://doi.org/10.2307/2297926
Lehrer E, Pauzner A (1999) Repeated games with differential time preferences. Econometrica 67:393–412. https://doi.org/10.1111/1468-0262.00024
Morooka C (2020) A New Folk Theorem in OLG Games. mimeo
Smith L (1992) Folk theorems in overlapping generations games. Game Econ Behav 4:426–449. https://doi.org/10.1016/0899-8256(92)90048-W
Sorin S (1986) On repeated games with complete information. Math Oper Res 11:147–160. https://doi.org/10.1287/moor.11.1.147
Sugaya T (2015) Characterizing the limit set of perfect and public equilibrium payoffs with unequal discounting. Theor Econ 10:691–717. https://doi.org/10.3982/TE1425
Acknowledgements
This is a revised version of Chapter 1 of my Ph.D. dissertation at the University of Tokyo. I would like to thank Michihiro Kandori, Akihiko Matsui, Hitoshi Matsushima, Daisuke Oyama, Tadashi Sekiguchi, and Zhonghao Shui for their helpful suggestions. I would also like to appreciate various useful comments from audiences at my presentation during the Japanese Economic Association 2019 autumn meeting at Kobe University. Two anonymous referees as well as the associate editor whose comments drastically helped with improving the content of this paper are gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that he has no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research did not receive any specific Grant from funding agencies in the public, commercial, or not-for-profit sectors.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Morooka, C. Equilibrium payoffs in two-player discounted OLG games. Int J Game Theory 50, 1021–1032 (2021). https://doi.org/10.1007/s00182-021-00779-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-021-00779-9