The (non-)robustness of influential cheap talk equilibria when the sender’s preferences are state independent

Abstract

Chakraborty and Harbaugh (Am Econ Rev 100(5):2361–2382, 2010) prove the existence of influential cheap talk equilibria in one sender one receiver games when the state is multidimensional and the preferences of the sender are state independent. We show that influential equilibria do not survive the introduction of any small degree of Harsanyi-uncertainty, i.e., uncertainty about the sender’s preferences in the spirit of Harsanyi (Int J Game Theory 2(1):1–23, 1973).

1 Introduction

This paper is concerned with the strategic information transmission (as first analyzed in Crawford and Sobel 1982) between one informed sender and one uninformed receiver. The sender can attempt to communicate her information to the receiver before the receiver takes an action. The receiver would, ideally, like to make his choice of action dependent on the state of the world, but in a way that differs from the sender’s ideal choice of action. Thus, there is a conflict of interest. Communication is costless (termed “cheap” in the literature). Messages the sender transmits to the receiver have no intrinsic meaning, or no intrinsic meaning that can be verified, and only possibly take on meaning (reveal information) in equilibrium.

One of the main findings of the cheap talk literature, started by Crawford and Sobel (1982), is that influential communication in one sender one receiver games is typically only possible if the conflict of interest is not too large.¹ This has been shown in the equilibrium characterization by Crawford and Sobel (1982) and expanded by Goltsman et al. (2009). If the conflict of interest is large, credible communication seemed only possible if messages are verifiable or costly (for a survey of this literature, see Sobel 2013).

Chakraborty and Harbaugh (2010) propose and analyze a one sender one receiver game with a multi-dimensional state space with an extreme form of conflict of interest. The receiver is essentially as modelled in Crawford and Sobel (1982), but the informed sender actually does not at all care about the state itself²: the sender’s preference is state independent.

Surprisingly, and by a beautiful argument—which eventually allows the use of the Borsuk–Ulam theorem (a fundamental fixed-point theorem)—Chakraborty and Harbaugh (2010) show that, in their model, influential cheap talk equilibria always exist.

To analyze games of incomplete information, such as those of the cheap talk literature, in addition to specifying players, strategies, and consequences (payoffs) to complete the model one has to make informational assumptions. The informational assumptions made in Chakraborty and Harbaugh (2010), as also in Crawford and Sobel (1982), are as follows. The utility functions of both sender and receiver are common knowledge, as is the receiver’s subjective belief about the state.

In fact Chakraborty and Harbaugh (2010) relax these informational assumptions in a robustness exercise in two different ways, and show, for each case, that the game so modified still exhibits influential equilibria. Both robustness exercises allow the sender to have possibly different utility functions. In both cases the sender knows her utility function and the receiver’s subjective belief about the sender’s utility function is common knowledge. In one specification this commonly known distribution has finite support with the number of positive probability utility functions less than the dimensionality of the state space. In the second specification this commonly known distribution places a sufficiently large atom on a single utility function.

As the state space is a compact subset of, at least, two-dimensional Euclidean space and as there are, in principle, an infinite number of possible utility functions the sender could have (even an infinite number of utility functions that are all very close to each other) we feel a different robustness check should also be undertaken. In this paper we assume that the receiver, while possibly having a good general idea about the sender’s preferences, does not believe that any particular utility function (out of the infinitely many possible ones) has positive probability. We call this the Chakraborty and Harbaugh (2010) model with Harsanyi-uncertainty, as the uncertainty is very much as it is in the purification argument of Harsanyi (1973). Completing this model by assuming that the receiver’s subjective belief about the sender’s utility function is common knowledge, we then find that this modified game has no influential equilibria. This result does not depend on the choice of the set of possible utility functions (as long as a belief without atom can be specified and a genericity assumption is satisfied) nor on the exact shape of the distribution of these beliefs.

One could possibly argue that the fact that Chakraborty and Harbaugh (2010) did not perform a robustness check with Harsanyi-uncertainty already indicates that no such robustness can be proven. Note however two things. First, the absence of such a robustness result could also simply mean that it is hard to prove that “there is a robust influential equilibrium in every game”. In Appendix A we show that in many cases there are in fact infinitely many other kinds of equilibria in the original Chakraborty and Harbaugh (2010) model, in addition to the hyperplane-based equilibria identified by Chakraborty and Harbaugh (2010), and it might be possible that one of these is robust. Second, the opposite statement to “there is a robust influential equilibrium in every game” is only that “there are some games in which there is no robust influential equilibrium”. We prove here that “no game has any robust influential equilibrium”, a much stronger statement.

The paper is organized as follows. We begin by stating the model of Chakraborty and Harbaugh (2010) and our modification to that model in Sect. 2. Section 3 demonstrates the main finding of Chakraborty and Harbaugh (2010), as well as the non-robustness to Harsanyi-uncertainty of all influential equilibria, by means of the simplest possible example. The main result of our paper is then stated and proven in Sect. 4 for the case of finite message spaces and in Sect. 5 for the case of infinite message spaces. Sect. 6 concludes.

2 The model

A sender (female) is privately informed about the realization of $\theta \in \Theta$, where $\Theta$ is a convex and compact subset of ${\mathbb {R}}^{N}$ with non-empty interior and $N\ge 2$. The sender can send a costless message m from a finite set of messages M to a receiver (male).³ The receiver observes the message and then takes an action in action space ${\mathcal {A}}=\Theta$. A sender strategy is thus a mapping from state space $\Theta$ to the set of messages M, while a receiver strategy is a mapping from message space M to action space $\Theta$. The utility function of the receiver is given by $-\Vert a-\theta \Vert ^{2}$, where $\Vert \cdot \Vert$ is the Euclidean distance. This implies that, in any equilibrium, the receiver, “knowing” the sender’s strategy, plays, as his best response, the (conditional) expectation of $\theta$. The prior of the receiver is described by the distribution function F with full support on $\Theta$. The utility of the sender is a function $u: {\mathcal {A}} \rightarrow {\mathbb {R}}$ that does not depend on the realization of the state variable $\theta$.

The equilibrium concept is Bayesian Nash. A Bayesian Nash equilibrium is termed influential if there are at least two messages (sent with positive probability according to F) that induce different actions.⁴$^,$⁵

Up to this point, the model we presented here is exactly the model introduced by Chakraborty and Harbaugh (2010). We now add uncertainty about the preferences of the sender in the following way to the model. There is a set of possible utility functions ${\mathcal {U}}$ for the sender. The sender is privately informed about her utility function $u\in {\mathcal {U}}$. The receiver has a prior belief given by distribution function $\phi$, a distribution over the set ${\mathcal {U}}$ which has no atoms.⁶ We call this extended model the Chakraborty and Harbaugh (2010) model with Harsanyi-uncertainty, as the way we introduce uncertainty is essentially as in Harsanyi (1973), the “purification” paper.

3 The main example

For our main example, also denoted as Example 1, suppose that $\Theta =[0,1]^{2}$ (i.e., $N=2$) and that the sender’s preferences are linear. That is, for any $a \in \Theta$, we have $u(a)=a_1+x a_2$. The “indifference slope” x is known to the sender, but not known to the receiver. The receiver has a non-atomic prior $\phi$ over x in the interval $[x_0-\epsilon ,x_0+\epsilon ]$ for some fixed and commonly known $x_0 \in {\mathbb {R}}$ and $\epsilon > 0$. In terms of our general model we have ${\mathcal {U}}=\{ u(a)= a_1+x a_2 | x \in [x_0-\epsilon ,x_0+\epsilon ]\}$. Suppose, further, that the set of messages M consists of exactly two elements $m_{+}$ and $m_{-}$.

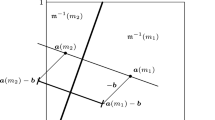
Consider first the case in which there is no uncertainty about the sender’s preference. For such a case Chakraborty and Harbaugh (2010) show that there is an equilibrium of the following kind, as illustrated in Fig. 1, which is essentially Fig. 1a in Chakraborty and Harbaugh (2010). There is a hyperplane h that divides the state space $\Theta$ into two regions. In region 1 (say, above the hyperplane) the sender sends message $m_{+}$, which induces action $a_{+}$, while in the other remaining region 2 the sender sends message $m_{-}$ inducing action $a_{-}$. The two actions are simply (and necessarily in equilibrium) the updated expected state given the sender’s strategy. If the sender is indifferent between actions $a_{+}$ and $a_{-}$, this is indeed an equilibrium. If the sender is not indifferent between these two actions, then the hyperplane can be rotated around any arbitrary state c on the hyperplane, to find a new hyperplane for which the sender is exactly indifferent between actions $a_{+}$ and $a_{-}$. That there must be such a hyperplane follows from the fact that if we flip the hyperplane by 180$^\circ$ we are back to where we started but with the old $a_{+}$ now $a_{-}$ and the old $a_{-}$ now $a_{+}$, i.e., with a reversal of the preference ranking of the two actions. As we are rotating the hyperplane continuously and as the sender utility function is continuous there must be an angle of rotation (between 0$^\circ$ and 180$^\circ$) where the sender is indifferent between the two actions. Therefore, an influential equilibrium exists.

Fig. 1

No uncertainty in the linear case. The lines parallel to the line through $a_{+}$ and $a_{-}$ are indifference curves

In Proposition 6 in their online appendix, Chakraborty and Harbaugh (2010) show that an influential equilibrium exists also when there is uncertainty about the sender preferences, as long as there is a sufficiently large atom on a single sender preference type. Chakraborty and Harbaugh (2010) show this, assuming a condition (S) that we utilize as well for our argument below, that implies that all other (small probability) sender types have a strict preference for one of the two actions. As long, however, as their is one high probability sender type, the proof of existence of an influential equilibrium is essentially the same as for the case of only one sender type. The hyperplane may have to be rotated a bit more in one or the other direction to account for the fact that the receiver will adjust his actions to the knowledge that the small probability sender types do not maker their message choice dependent on the state.

Suppose now, however, that there is Harsanyi-uncertainty about the slope of the indifference curve as modelled above. This case is illustrated in Fig. 2 with the uncertainty indicated by the range for indifference lines between the dotted and the dashed line. Now consider the following strategy. The state space is divided into two regions (by, for instance, but not necessarily, a hyperplane). As before, the sender sends message $m_{+}$ in region 1 and message $m_{-}$ in region 2. It is now possible that there is a preference-type of the sender who is indifferent between the two induced actions $a_{+}$ and $a_{-}$. Note, however, that this is true for only exactly a single one of these preference-types of senders. All other preference-types have a strict preference for one or the other action. This means all other preference-types (and they have cumulative probability 1 in this model) will want to deviate to a strategy that involves sending one and the same message irrespective of the state. Thus, there is no such influential equilibrium in the model with Harsanyi-uncertainty.

Fig. 2

Uncertainty in the linear case

4 The main result

We now state and prove the main theorem. In order to do so, we first define Condition (S), as stated in the online appendix of Chakraborty and Harbaugh (2010).

The set of possible utility functions ${\mathcal {U}}$ (that the sender might have, from the point of view of the receiver) satisfies Condition (S) if for any two distinct actions a and b, if $u^{'}(a)=u^{'}(b)$ for $u^{'}\in U$, then $u(a)\ne u(b)$ for all $u\in {\mathcal {U}}, u\ne u^{'}$. For example, the linear preference model in our main example (Sect. 3) satisfies this property. More generally, Condition (S) holds for preferences whose indifference curves satisfy a single crossing property.⁷ The following theorem is the main result of this paper.

Theorem 1

Consider a sender-receiver game as defined in Sect. 2. Suppose the set of possible utility functions for the sender, ${\mathcal {U}}$, satisfies Condition (S) and suppose that $\phi$, the receiver’s prior belief over ${\mathcal {U}}$, is non-atomic. Then there does not exist an influential equilibrium in this game.

Proof

The proof is by contradiction. Suppose there exists an influential equilibrium. Hence, there exist messages $m_{+}$ and $m_{-}$ that are sent with positive probability (under F and $\phi$) and induce different actions, $a_{+}=E(\theta |m_{+})\ne a_{-}=E(\theta |m_{-})$. For this to be possible there must be a positive mass of senders (under $\phi$) that send message $m_{+}$ in some states and $m_{-}$ in other states. Denote this set of senders by $V \subset {\mathcal {U}}$. Action $a_{\circ }$, for $\circ \in \{+,-\}$, is then the receiver’s unique (and pure) best response to receiving message $m_{\circ }$ (given the senders’ strategies).

The strategy profile given is thus such that the receiver behaves optimally. We now turn to the (various types of) senders in V. In order for a sender to use message $m_{+}$ in some states and message $m_{-}$ in other states (and given the sender has state-independent preferences) the sender must be exactly indifferent between both induced actions $a_{+}$ and $a_{-}$. We thus must, at a minimum, have that there is a sender-type $u' \in {\mathcal {U}}$ such that $u'(a_{+})=u'(a_{-})$. But then Condition (S) implies that for all $u\in {\mathcal {U}}, u\ne u^{'}$, we have $u(a_{+})\ne u(a_{-})$. Given that distribution $\phi$ is non-atomic, the “event” $u \ne u'$ has probability one under $\phi$. This means that a unit measure of senders has a strict preference to send only one of the two messages (over the other) irrespective of the state. This, in turn, implies that only a zero-measure (under $\phi$) of sender types in V make their choice of message dependent on the state. We thus arrive at a contradiction. $\square$

Fig. 3

Existence of influential equilibrium despite Harsanyi-uncertainty

Comments

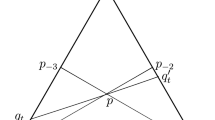
• 1. An example sketched in Fig. 3 explains why a condition like Condition (S) is needed for the non-existence of an influential equilibrium.

  Take an interior point c and a hyperplane h which splits the state space in two halves. The indifference curves of the different sender types are the dotted lines.⁸ Importantly all indifference curves intersect at two points (violating Condition (S)), which are exactly the best response actions $a_{+}$ and $a_{-}$ of the receiver to receiving message $m_{+}$ (state is above line h) and $m_{-}$ (state is below line h). Thus, there is an influential equilibrium. Condition (S) rules out such situations.

• 2. Nevertheless, it is straightforward to generalize Theorem 1 to a somewhat weaker condition than Condition (S): Say Condition ($\text {S}^{'}$) holds if for any two actions a and b, $P_{\phi }( u\in {\mathcal {U}}| u(a)\ne u(b))=1$. The proof is the same.

• 3. If all $u \in {\mathcal {U}}$ are $\epsilon$-close to some $u_0 \in {\mathcal {U}}$, then any influential equilibrium of the game with sender preference $u_0$ and without uncertainty about the sender’s preference remains an $\epsilon$-equilibrium of the sender-receiver game with Harsanyi-uncertainty.⁹

• 4. Suppose there is no Harsanyi-uncertainty about the preferences of the sender. Instead, there are possibly infinitely many different receiver types in terms of the receiver’s subjective belief F over the state space $\Theta$. That is, there is a set ${\mathcal {F}}$ of distributions over the state space. Each receiver privately knows his distribution F. The sender is not informed about the receiver’s prior, but holds her own prior $\psi$ over the set ${\mathcal {F}}$. This prior $\psi$ is commonly known and can be anything (e.g. discrete, continuous, with or without atom). The same argument as in the proof of the existence result of Chakraborty and Harbaugh (2010) can be used to prove also existence of an influential equilibrium in this context. The intuition for this result is that, as the receiver is not able to signal her preferences, the sender simply averages all optimal receiver reactions and the situation is essentially “as if” the receiver has one commonly known “average” preference.

• 5. Harsanyi-uncertainty, as modelled here, implies that there is no common knowledge between the sender and receiver as to what the sender’s preference over actions is. This is not necessary for the non-robustness result. Consider the situation (building on the previous comment), in which there is common knowledge of the sender’s preference, but the receiver does not know what the sender believes that the receiver’s subjective belief over the state-space is.¹⁰ To be specific, let $\theta \in \Theta$ be the state, privately known to the sender. Let $F \in {\mathcal {F}}$ be the subjective belief of the receiver about the state, privately known to the receiver. Let u be the sender’s utility function, commonly known to sender and receiver. Let $\psi \in \Psi$ be the subjective belief of the sender about the receiver’s subjective belief, privately known by the sender. Let, finally, $\mu$ be the belief of the receiver about the sender’s private belief $\psi$, commonly known to sender and receiver. Now suppose that there is an influential equilibrium with at least two used messages $m_{+}$ and $m_{-}$. Suppose each message $m_{\circ }$, for $\circ \in \{+,-\}$ induces optimal receiver actions $a_{\circ }^F$ (different for different receiver beliefs F). The sender evaluates the expected utility of these actions according to her private belief $\psi \in \Psi$ about the distribution over the receiver’s private belief F by ${\mathbb {E}}_{\psi } u(a_{\circ }^F)$. Suppose further that the commonly known belief of the receiver, $\mu$, over the private beliefs of the sender is non-atomic and the set $\Psi$ satisfies the following condition: if one sender-type $\psi$ is indifferent between the two messages, i.e., ${\mathbb {E}}_{\psi } u(a_{+}^F) = {\mathbb {E}}_{\psi } u(a_{-}^F)$, no other sender-type $\psi '$ is indifferent. That is, for all $\psi ' \in \Psi$ with $\psi ' \ne \psi$ we have that ${\mathbb {E}}_{\psi '} u(a_{+}^F) \ne {\mathbb {E}}_{\psi '} u(a_{-}^F)$. By the same argument as in the proof of Theorem 1 almost all sender-types will want to deviate from the proposed strategy. Thus, this game (with higher-order belief uncertainty as described here) has no influential equilibria.

• 6. As already mentioned in the Introduction, Chakraborty and Harbaugh (2010), in their online appendix, Sections A and B, show that a game with uncertainty over sender preferences has influential equilibria if there are not too many sender types or if one sender type has sufficiently high probability. In this comment we address the question whether there could be a discontinuity between a finite and an infinite number of sender types in terms of the informativeness in equilibrium. The answer is no. Suppose there is a finite number of K sender types, such that the set of their utility functions, satisfies Condition (S) (for all K) and put small weight, say $\frac{1}{K}$ on each sender type. What happens when we take K to infinity (i.e., have vanishing limiting probability on each type)? Fix k as the finite number of messages, which is fixed for all K.¹¹ Then the number of possible induced actions is also k. The number of individual sender types that are indifferent between at least two such induced actions is at most $k*(k-1)$ as there are k times $k-1$ pairs of induced actions and if one sender type is indifferent between one pair, by Condition (S) no other sender type is also indifferent between that pair. But then, in any influential equilibrium, at least a fraction of $\frac{K-k(k-1)}{K}$ sender types do not make their choice of action contingent on the state.¹² This fraction tends to 1 as K tends to infinity. Thus, any action is either induced with a vanishing probability, as K tends to infinity, or tends to the ex-ante average state. Thus, any such sequence of influential equilibria becomes non-influential in the limit.

• 7. Harsanyi (1973) uses, what we here call, Harsanyi-uncertainty to show that mixed equilibria, in which the players are indifferent between at least two pure strategies, can be thought of as pure strategy equilibria in the game played by, at least in the minds of the players, infinitely many possible “types”. As explained in Sect. 3, the influential equilibria in Chakraborty and Harbaugh (2010) also rely on indifference. One way to state our result is that the influential equilibria in Chakraborty and Harbaugh (2010), even though they are actually in pure strategies, cannot be purified in the sense of Harsanyi (1973). Alternatively, one could also say that the influential equilibria in Chakraborty and Harbaugh (2010) are not regular in the sense of Harsanyi (1973). This is reminiscent of the non-purifiability of many “belief-free” type equilibria in repeated games that are also based on indifference, see e.g., Bhaskar (1998, 2000), and Bhaskar et al. (2008, 2013). Bhaskar (2000) also proves a result, in the same spirit, on the difficulty of implementing direct mechanisms under Harsanyi-uncertainty.

5 Equilibria with infinitely many messages

In the previous sections, in particular also for Theorem 1, we assume, as in Chakraborty and Harbaugh (2010), that the message space is finite. In this section we investigate the possibility of the existence of an influential equilibrium with infinitely many messages.

Consider the following example, denoted Example 2, with a single-dimensional state space.¹³$^,$¹⁴ Let $\Theta ={\mathcal {A}}=[-1,1]$. Let F be uniform on $\Theta$. To make it as simple as possible let $x \in [\frac{1}{2},1)$ parameterize an infinite family of utility functions $u:{\mathcal {A}} \rightarrow {\mathbb {R}}$ as follows¹⁵:

$$\begin{aligned} u_x(a)=\left\{ \begin{array}{cc} 1 &{} \text{ if } a=-\frac{2}{9} \text{ or } a=x \\ \frac{1}{4}a+\frac{1}{4} &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

Let $\phi$, the distribution of sender utility functions, be the uniform distribution over $[\frac{1}{2},1)$. The message space is given by $M=\{0\} \cup [\frac{1}{2},1)$.¹⁶

This infinite set of utility functions ${\mathcal {U}}$ satisfies Condition (S). Consider the following strategy profile. For any $x \in [\frac{1}{2},1)$, the sender of utility type with parameter x sends message x if and only if the state $\theta \ge 2x-1$ and sends message 0 otherwise. If the receiver receives message x he knows that the sender is of type x (which he does not care about) and more importantly he knows that the state $\theta$ is uniformly distributed in the interval $[2x-1,1)$. Thus, the expected state, conditional on observing message x, is x. If the receiver receives message 0 all sender types are possible (not all equally likely, though) and he has to form a somewhat more complicated updated expectation of the state. It can be verified that the probability of the state being below some $\theta$ given message 0 is given by

$$\begin{aligned} G(\theta )=\left\{ \begin{array}{ll} \frac{2}{3} (\theta +1) &{} \text{ if } \theta < 0 \\ \frac{2}{3} + \frac{2}{3}\theta -\frac{1}{3} \theta ^2 &{} \text{ otherwise }. \end{array}\right. \end{aligned}$$

The density is then given by

$$\begin{aligned}g(\theta )=\left\{ \begin{array}{ll} \frac{2}{3} &{} \text{ if } \theta < 0 \\ \frac{2}{3} (1-\theta ) &{} \text{ otherwise, } \end{array}\right. \end{aligned}$$

and the conditional expected state is $-\frac{2}{9}$.

Thus, the receiver’s best response to the sender strategy is to play action $-\frac{2}{9}$ after observing message 0 and action x after observing message x. Then, each sender type x is exactly indifferent between sending message 0 and message x and prefers these two messages over all others. Thus, we have an equilibrium.

Recall that we call, following Chakraborty and Harbaugh (2010), a Bayesian Nash equilibrium influential if there are at least two messages (sent with positive probability according to F) which induce different actions. According to this definition the above equilibrium is not influential. The reason for this is that, while action $-\frac{2}{9}$ is induced by a message sent with positive probability, no other action message is sent with positive probability. The above equilibrium should, however, clearly also be called influential. Thus, when dealing with infinite message spaces, we need a weaker definition of what constitutes an influential equilibrium, one that reduces to our previous definition, i.e., the definition given in Chakraborty and Harbaugh (2010), for the case of finite message spaces.

In order to avoid confusion we shall denote this weaker notion of influential equilibrium by influential$^*$ equilibrium. Let $a^*:M \rightarrow {\mathcal {A}}$ denote the induced action function for a fixed given strategy profile. An equilibrium is termed influential$^*$ if there are two disjoint closed subsets of the set of all induced actions such that the overall probability of each of the two sets is positive.

Note that for the case M finite this definition is equivalent to the original definition. Note furthermore that the strategy profile described above (in which each payoff type sends two distinct messages) is influential$^*$.¹⁷ Thus, conditions ($\text {S}^{'}$) or (S) are not sufficient to rule out influential$^*$ equilibria.

We now provide a stronger condition than Condition ($\text {S}^{'}$) that suffices to rule out all influential$^*$ equilibria. The set of possible utility functions ${\mathcal {U}}$ (that the sender might have, from the point of view of the receiver) together with the atomless distribution $\phi$ over it, satisfies Condition ($\text {S}^{''}$) if for any two disjoint closed subsets $A,B \subset {\mathcal {A}}$ the probability that $\max _{a \in A} u(a) = \max _{b \in B} u(b)$ is zero under $\phi$. Note that this condition is, for instance, again satisfied for the linear preference model in our main example (Sect. 3) and also, more generally, for preferences whose indifference curves satisfy a single crossing property.

Condition ($\text {S}^{''}$) is strong enough to rule out the set of utility functions given in the example of this section. Consider the two disjoint sets of actions $A=\{-\frac{2}{9}\}$ and, e.g., $B=[\frac{1}{2},\frac{3}{4}]$. Then all types of senders with $x \in B$ are indifferent between their most preferred elements in A and B. The probability mass of all such senders is $\frac{1}{2}$ under $\phi$. Therefore, this set of sender utility functions, paired with distribution $\phi$, does not satisfy Condition ($\text {S}^{''}$).

We next show that Condition ($\text {S}^{''}$) is sufficient to preclude the existence of an influential$^*$ equilibrium.

Theorem 2

Consider a sender-receiver game as defined in Sect. 2. Suppose the set of possible utility functions for the sender, ${\mathcal {U}}$, is such that $\phi$, the receiver’s prior belief over ${\mathcal {U}}$, is non-atomic, and satisfies Condition ($\text {S}^{''}$). Then there does not exist an influential$^*$ equilibrium in this game.

Proof

For all $u \in {\mathcal {U}}$, let $\sigma _u: \Theta \rightarrow M$ denote the equilibrium strategy of the sender of type u. Let $\rho :M \rightarrow {\mathcal {A}}$ denote the receiver’s equilibrium strategy. Let ${\tilde{{\mathcal {A}}}}=\left\{ a \in {\mathcal {A}}\mid \rho (\sigma _u(\theta ))=a \text{ for } \text{ some } \theta \in \Theta \text{ for } \text{ some } u \in {\mathcal {U}}\right\}$ denote the set of induced actions in this equilibrium.

Given that the equilibrium is influential$^*$ there must be two closed subsets ${\tilde{{\mathcal {A}}}}_{+}$ and ${\tilde{{\mathcal {A}}}}_{-}$ of ${\tilde{{\mathcal {A}}}}$ with the property that ${\tilde{{\mathcal {A}}}}_{+} \cap {\tilde{{\mathcal {A}}}}_{-} = \emptyset$ and that $P_{F,\phi }\left( {\tilde{{\mathcal {A}}}}_{\circ }\right) > 0$ for both $\circ \in \{+,-\}$.

For this to be possible there must be a set $V \subset {\mathcal {U}}$ with positive mass under $\phi$ such that for all $u \in V$ and for both $\circ \in \{+,-\}$, $\rho (\sigma _u(\theta )) \in {\tilde{{\mathcal {A}}}}_{\circ }$ for some $\theta \in \Theta$. By condition ($\text {S}^{''}$) we have that $P_{\phi }\left( \{u \in {\mathcal {U}}\mid \max _{a \in {\tilde{{\mathcal {A}}}}_{+}} u(a) = \max _{b \in {\tilde{{\mathcal {A}}}}_{-}} u(b)\}\right) = 0$, which provides a contradiction. $\square$

6 Conclusion

We study sender-receiver games with a single sender and a single receiver. The sender is fully informed about a state that the receiver would like to know in order to make an informed decision by choosing an action as close as possible to the state. The sender has preferences about the receiver’s actions that are independent of the state.

Chakraborty and Harbaugh (2010) show that, provided the state space is multi-dimensional, such a game always has an influential equilibrium, where the sets of states, in which the sender sends any given message, are separated by hyperplanes. In the Chakraborty and Harbaugh (2010) model the receiver knows (at least with some sufficiently large probability) the preferences of the sender.

We show, that if the receiver is unsure about the sender’s preferences in such a way that she considers a continuum of possible sender utility functions (all close to each other) and has a belief about these that is a generic atomless distribution over these, then the game does not have influential equilibria.

This paper’s only goal was to investigate the robustness of influential equilibria to Harsanyi Uncertainty in sender receiver games in which the sender has state independent preferences. What would be an interesting alternative direction? There is a third and final robustness check in Chakraborty and Harbaugh (2010), in which they show that for every $\epsilon > 0$ when the sender preferences are state dependent but sufficiently close (as a function of $\epsilon$) to state independent and linear, then some influential equilibria of the limit game are $\epsilon$-equilibria of this nearby game. We are not pursuing this in this paper, but we feel that looking more generally at a model in which the sender has preferences that are close to but not completely state independent could provide interesting insights. Adding lying costs (this is an interpretation that Chakraborty and Harbaugh (2010) give $\epsilon$) such as in Kartik (2009) in more general situations may also be a worthwhile direction. Finally, the recent model of Lipnowski and Ravid (2020) nests the model of Chakraborty and Harbaugh (2010). As a consequence, equilibria in their model need not be robust to the introduction of a small degree of Harsanyi Uncertainty either.

Appendix: Multiplicity of equilibria in the original CH model

In this section we show that in the original Chakraborty and Harbaugh (2010) model (i.e., with common knowledge of the sender’s preferences), under a specific assumption, there are influential equilibria also in games with a single-dimensional state and action space. We then show how the argument used to prove this statement can be used to prove Theorem 1 of Chakraborty and Harbaugh (2010) that every sender receiver game considered by CH has a continuum of influential equilibria even with only two messages.¹⁸ Finally, we then show that many such games have a continuum of other types of continua of equilibria as well (even with only two messages).

A slightly different way to explain and prove the main result of Chakraborty and Harbaugh (2010) is as follows. Suppose $\Theta ={\mathcal {A}}=[0,1]$, i.e., the state and action space are both single-dimensional. Suppose the sender preference is state independent and is a continuous function $u:{\mathcal {A}}\rightarrow {\mathbb {R}}$ with the property that $u(0)=u(1)$. Suppose further that the receiver’s full support and atomless prior F over $\Theta$ is such that $u\left( {\mathbb {E}}[\theta ]\right) \ne u(0)$.

Any such game then has an influential equilibrium with two messages. To prove this suppose that the sender uses a message cutoff $x \in [0,1]$ such that she sends message $m_{-}$ if $\theta \le x$ and message $m_{+}$ if $\theta > x$. Let $u^*_{-}(x)=u\left( {\mathbb {E}}[\theta | \theta \le x]\right)$ and $u^*_{+}(x)=u\left( {\mathbb {E}}[\theta | \theta \ge x]\right)$. Finally, let $f(x)= u^*_{+}(x)-u^*_{-}(x)$. By assumption $f(0) \ne 0$ and $f(1)=-f(0)$. Then by the intermediate value theorem there is an $x^* \in (0,1)$ such that $f(x^*)=0$ and the cutoff strategy $x^*$ constitutes an influential equilibrium in this game.¹⁹

This can be used to prove the general theorem, Theorem 1 of Chakraborty and Harbaugh (2010), as follows. Let $\Theta ={\mathcal {A}}$ be again a compact subset of ${\mathbb {R}}^N$ with $N \ge 3$ with nonempty interior.²⁰ Take any point c in the interior of $\Theta$ and any hyperplane h going through c. Moreover, take any line l within the hyperplane h also going through c. Now rotate the hyperplane around l to obtain a new hyperplane h(x) that still contains point c and line l. Let $x \in [0,1]$ denote the normalized angle between hyperplane h(x) and h with $h(0)=h(1)=h$. For any h(x) the sender sends one message in all states “above” and another message in all states “below” the hyperplane.²¹ The sender, thus, induces distinct actions $a_{+}(x)$ and $a_{-}(x)$ with induced sender utility of $u^*_{+}(x)=u(a_{+}(x))$ and $u^*_{-}(x)=u(a_{-}(x))$. Suppose that $u^*_{+}(x)=u^*_{-}(x)$. Then the strategy constitutes an influential equilibrium. Suppose not. Then we can apply the previous proof to obtain, by the intermediate value theorem, an influential equilibrium for some $x\in (0,1)$.

This proof is, of course, very similar to the original proof in Chakraborty and Harbaugh (2010) in that the intermediate value theorem is very similar to the Borsuk Ulam theorem. One could probably call the Borsuk Ulam theorem a generalization of the intermediate value theorem. But note that this proof works for any interior point c and any line l through this point c.

By the same argument we can prove existence of another continuum of continua of influential equilibria with two messages, at least in some cases. Suppose that the sender has linear preferences, a case also considered in Chakraborty and Harbaugh (2010). This means that the sender’s indifference curves in ${\mathcal {A}}$ are hyperplanes. Let $c={\mathbb {E}}[\theta ]$ and let h be the sender’s indifference hyperplane that goes through c. Consider a point $y \in \Theta$, not on the hyperplane h and let $B(y) \subset \Theta$ be a small Euclidean ball around y that does not intersect the hyperplane h.²² Consider any $y' \in \Theta$ that lies on a circle that goes through y and has c as its center. Let $B(y')$ denote the Euclidean ball around $y'$ that is of the same size as B(y). For any $y'$ on this circle let $x \in [0,1]$ denote the normalized angle between the lines c, y and $c,y'$. The sender’s strategy for any x is then to choose one message in all states within $B(y')$ with $y'$ determined by x and another message in all other states. We need to assume that for any such $y'$ the set $B(y')$ includes an open set within $\Theta$. The original point y can always be chosen to guarantee this.

As B(y) does not intersect the hyperplane h and as the induced action given the message that indicates that the state is within B(y) must be in B(y) the sender is not indifferent between sending the two messages (for $x=0$). Similarly, for $x=1/2$, the corresponding $B(y')$ also does not intersect the hyperplane and the sender’s preferences over the two messages is reversed. Then the same argument applies as before and we get existence of an influential equilibrium of this kind for some x between 0 and 1/2 (and one for x between 1/2 and 1).