Linear evasion differential game of one evader and several pursuers with integral constraints

Abstract

An evasion differential game of one evader and many pursuers is studied. The dynamics of state variables $x_1,\ldots , x_m$ are described by linear differential equations. The control functions of players are subjected to integral constraints. If $x_i(t) \ne 0$ for all $i \in \{1,\ldots ,m\}$ and $t \ge 0$, then we say that evasion is possible. It is assumed that the total energy of pursuers doesn’t exceed the energy of evader. We construct an evasion strategy and prove that for any positive integer m evasion is possible.

1 Introduction

The field of differential games was pioneered by Isaacs (1965) in the 1960s and since then enormous amount of work has been devoted to its study (for example, see Friedman 1971; Hajek 1975; Pontryagin 1988; Krasovskii and Subbotin 1988; Petrosyan 1993; Başar and Olsder 1999; Buckdahn et al. 2011 and references therein). A substantial part of these works concern simple motion pursuit and evasion differential games of many players. Often, either geometric or integral constraints are imposed on the control parameters of players. In Croft (1964) Croft showed that in the n-dimensional Euclidean ball n lions can catch the man, while the man can escape from $n-1$ lions when the controls of the players are subject to geometric constraints. A similar game problem was studied by Ivanov (1980) on any convex compact set and an estimate from above was obtained for guaranteed pursuit time.

Interesting results were obtained in Alexander et al. (2009), Azamov (2008), Bakolas and Tsiotras (2011), Berkovitz (1986), Bhattacharya et al. (2016), Konstantinidis and Kehagias (2016) and Sun and Tsiotras (2014) for various games in unbounded regions as well as on graphs. Evasion problem on time interval $[t_0, \infty )$ was introduced and studied by Pontryagin and Mischenko (1971). In Mishchenko et al. (1977) Mishchenko et al. proposed a new manoeuvre for evasion in the game of many pursuers.

Chernous’ko (1976) studied an evasion game of one evader and several pursuers with a state constraint, i.e. the evader was supposed to remain in a neighborhood of a given ray for the duration of the game. He proved that if the evader is faster than the pursuers then evasion is possible. This result was extended by Chernous’ko and Zak (1985) and Zak (1978, 1981, 1982) to more general differential game problems. Related problems of evasion from a group of pursuers were studied in Borowko et al. (1988) and Chodun (1989).

In Pshenichnii (1976) Pshenichnii considered a simple motion differential game of many pursuers and one evader in ${\mathbb {R}}^n$, when all players have the same dynamic possibilities. He proved that if the initial state of the evader belongs to the interior of convex hull of pursuers’ initial states, then pursuit can be completed, otherwise evasion is possible. Based on this work, Pshenichnii et al. (1981) developed the method of resolving functions for solving linear pursuit problems with many pursuers. Later on, the results of paper (Pshenichnii 1976) were extended by many researchers to cover various cases. For example, when control sets of players are convex compact sets, Grigorenko (1990) obtained the necessary and sufficient conditions of evasion of one evader from several pursuers.

The papers Chikrii and Prokopovich (1992) and Kuang (1986) are also extensions of Pshenichnii (1976). In Kuchkarov et al. (2012) the game problem of many pursuers and one evader was studied on a cylinder. In the recent work of Kuchkarov et al. (2016), the results of Pshenichnii (1976) were extended to differential games on manifolds with Euclidean metric. In Blagodatskikh and Petrov (2009) Blagodatskikh and Petrov obtained necessary and sufficient condition of evasion in a simple motion differential game of a group of pursuers and a group of evaders in ${\mathbb {R}}^n$ where all evaders use the same control. By definition, pursuit is considered completed if the state of a pursuer coincides with the state of at least one evader. Also, the works (Bannikov and Petrov 2010; Vagin and Petrov 2001) related to such games. Recently in Scott and Leonard (2018) the authors consider a pursuit-evasion game involving one pursuer and multiple evaders motivated by the seminal “selfish herd” model of Hamilton (1971). The pursuer can freely move in any direction with bounded speed and evaders move with bounded speed and bounded turning speed. Using Isaacs’ heuristic argument they constructed an optimal strategy for the pursuer and concluded that the optimal strategy for the pursuer is to focus on a single evader that can be captured in minimum time. Moreover, “non-targeted” evaders are always able to escape. We refer to Kumkov et al. (2017) for a survey of results on differential games of many players with geometric constraints. In the case of integral constraints, simple motion evasion games of many players were solved in Alias et al. (2016), Ibragimov et al. (2012) and Ibragimov et al. (2018).

In the present paper, we study a linear evasion differential game of many pursuers and one evader. The controls of players are subjected to integral constraints. To the best of our knowledge no previous study has investigated the linear evasion game problem stated in the present paper. The main difficulties in solving the problem are the construction of evasion strategy and to prove the fact that the objects go around the origin on some specified time interval [0, T] maintaining some distances from the origin. Note that we employ non-anticipative strategies in the present game model (see, for example, Cardaliaguet et al. 2000).

Note that there is a similarity between the constructed evasion strategies and proofs of the main results of current and existing works (Ibragimov et al. 2012, 2018). They are (i) the definition of time intervals $[\tau _i, \tau '_i)$, (ii) the construction of a strategy for the evader which allows the evader to use a manoeuvre on $[\tau _i, \tau '_i)$ against the i-th pursuer, (iii) estimating the distances between the evader and pursuers, and establishing that evasion is possible. We believe that these steps will be common for the most of open evasion differential game problems of many players with integral constraints described by the linear system of equations as well. However, the main difficulties in solving the open problems will remain to overcome the steps (i)–(iii) listed above.

In the case of linear equations studied in the present paper, the strategies of existing papers do not work since, for the linear equation describing the game, we have to find its own $\tau _i$. Also, by contrast, we need bounded $\tau _i$, $\tau '_i$ and new techniques to estimate $x_p(t)$. Note that according to the strategy of the present paper, in contrast to previous works, each object, for any control functions of pursuers, moves with a positive speed in the direction of y-axis on the time interval [0, T]. Moreover, all the objects will become on the upper half plane by the time T, and then evasion is established. The fact that each time interval where the evader uses a manoeuver is contained in the interval [0, T] plays a key role in establishing a number of estimates in the proof of the main result.

This work is a milestone study to undertake a detailed analysis of linear evasion differential game problem of many pursuers and one evader with integral constraints. We are confident that the construction in the present paper will be a stepping stone to open problems and will open prospects for general multi person linear evasion differential games with integral constraints and this study makes a major contribution to research on general linear evasion differential games.

2 Statement of problem

Let $x_1, \dots , x_m$, $m\ge 1$, be the points moving in ${\mathbb {R}}^n$ whose dynamics are described by the equations

$$\begin{aligned} \dot{x}_i=-\lambda _i x_i+v-u_i, \quad x_i(0)=x_i^0, \quad i=1, 2, \dots , m, \end{aligned}$$

(1)

where $u_1, \dots , u_m$ are the control parameters of pursuers and v is that of evader, $\lambda _i>0$, $x_i, x_i^0, u_i,v\in {\mathbb {R}}^n$, $n\ge 2$, $x_i^0 \ne 0$, $i=1, \ldots , m$.

Definition 2.1

Measurable functions $u_i(t)$ and v(t), $t \ge 0$, that satisfy the following integral constraints

$$\begin{aligned} \int _0^\infty |u_i(t)|^2dt \le \rho _i^2, \ i=1, \dots m; \ \ \int _0^\infty |v(t)|^2dt\le \sigma ^2. \end{aligned}$$

(2)

are called controls of the ith pursuer and evader, respectively.

Definition 2.2

A function $(t, t_1, \ldots ,t_k, x_1, \ldots , x_m, u_1, \ldots , u_m) \mapsto V(t, t_1, \ldots ,t_k, x_1, \ldots , x_m, u_1, \ldots , u_m)$, $V:[0, \infty )^{k+1}\times {\mathbb {R}}^{2nm}\rightarrow {\mathbb {R}}^n$, where $t_1, \ldots ,t_k$, $0< t_1< \cdots< t_k < \infty$, are some positive numbers (unspecified) and k is a positive integer, is called strategy of evader if the following system of equations

$$\begin{aligned}&\dot{x}_i=-\lambda _i x_i+V(t, t_1, \ldots ,t_k, x_1, \dots , x_m, u_1, \dots , u_m) - u_i,\nonumber \\&\quad x_i(0)=x_i^0, \ i=1, \dots , m, \end{aligned}$$

(3)

has a unique solution $(x_1(t), \dots , x_m(t))$, $t\ge 0$, for any controls $(u_1(t), \dots , u_m(t))$, of pursuers and along this solution

$$\begin{aligned} \int _0^\infty |V(t, t_1, \ldots ,t_k, x_1(t), \dots x_m(t), u_1(t), \dots , u_m(t))|^2dt\le \sigma ^2. \end{aligned}$$

The strategy $V(t, t_1,\ldots ,t_k, x_1, \dots , x_m, u_1, \dots , u_m)$ is nonanticipatively defined with respect to the strictly increasing finite sequence of numbers $t_1,\ldots ,t_k$ as follows. Let the time $t_i$ ($t_0=0$), $i=0,1,\ldots ,k$, be occurred. The strategy of the evader is defined on the time interval $[t_i, t_{i+1})$, $i=0,1,\ldots ,k$, where $t_{k+1}=+\infty$, as a function $V=V^i(t,t_1,\ldots ,t_i, x_1, \dots , x_m, u_1, \dots , u_m)$. The trajectories of objects $x_1(t),\ldots ,x_m(t)$ i.e. the solution of (3) generated by this strategy and arbitrary controls of pursuers $u_1(t), \dots , u_m(t)$ are then defined as the solution of the initial value problem

$$\begin{aligned}&\dot{x}_j=-\lambda _j x_j+V^i(t, t_1,\ldots ,t_i, x_1, \dots , x_m, u_1, \dots , u_m) - u_j, \quad x_j(t)|_{t=t_i}\\&\quad =x_j(t_i), \ j=1, \dots , m, \end{aligned}$$

until the time $t_{i+1}$, $i=0,1,\ldots ,k$, occurs. The number $t_{i+1}$ is defined as the first time when the points $x_1(t),\ldots ,x_m(t)$ satisfy a certain condition. In this way, we define the solution of (3) on the intervals $[t_i, t_{i+1})$, $j=0,1,\ldots ,k$. It should be noted that the evader can predict neither the values of $t_1,\ldots ,t_k$ nor the length of the interval $[t_i, t_{i+1})$, $i=0,1,\ldots ,(k-1)$.

Definition 2.3

If there exists a strategy V of evader such that for any controls of pursuers $x_i(t)\ne 0$, $i=1, \dots , m$, $t\ge 0$, then we say that evasion is possible.

The problem is to find a condition for evasion to be possible.

Thus, the evader knows the values $x_1(t), \ldots , x_m(t)$, $u_1(t), \dots , u_m(t)$ of parameters $x_1, \ldots , x_m$, $u_1, \ldots , u_m$ at the current time t. Pursuers apply arbitrary controls $u_1(t), \ldots , u_m(t)$, $t\ge 0$, and try to realize the equation $x_i(t) = 0$ at least for one $i \in \{1,2,\ldots ,m\}$, whereas the evader tries to maintain the inequalities $x_i(t) \ne 0$ for all $i =1,\ldots , m$ and $t \ge 0$.

3 The main result

In this section we prove a theorem about evasion. To this end, we specify the conditions to define the numbers $t_i$ and construct an explicit nonanticipative strategy for the evader.The following is the main result of the current paper.

Theorem 3.1

If

$$\begin{aligned} \rho _1^2+\cdots +\rho _m^2\le \sigma ^2, \end{aligned}$$

(4)

then evasion is possible in game (1)–(2).

We prove the theorem in several subsections. The proof strategy is as follows. The solution of the initial value problem (1) is given by

$$\begin{aligned} x_i(t)=e^{-\lambda _it}y_i(t), \ \ y_i(t)=x_i^0+\int _0^te^{\lambda _is}(v(s)-u_i(s))ds. \end{aligned}$$

(5)

Since $x_i(t)=0$ if and only if $y_i(t)=0$, below we study the evolution of $y_i(t)$. We construct an evasion strategy such that the second coordinate of each point $y_i(t)$ strictly increases all the time. It remains to look at the situation with initial state $y_i(0)$ with $y_{i2}(0) < 0$ for some i.

Define an $a_i$-approach time $t=\tau _i$ as the first time for which $|y_i(t)| = a_i$ and $y_{i2}(t) < 0$. ($a_i$) is a strictly decreasing sequence so $\tau _i$ (if ever defined) is increasing. Time $\tau '_i > \tau _i$ is specified to ensure that $y_{i2}(\tau '_i) > 0$ if a “manoeuvre” is deployed on the time interval $[\tau _i, \tau '_i)$.

More essential for the proof of the theorem is that the sequence $\{\tau _i\}$ is bounded such that the set $I_1 = \bigcup _{i =1}^{m_0} [\tau _i, \tau '_i)$ is contained in [0, T] for some T. This is essentially implied by the fact that $y_{i2}(t)$ is strictly increasing for all i and at any time $t > 0$, and the definition for the $a_i$-approach time $\tau _i$ requires $y_{i2}(t) < 0$.

The “manoeuvre” is defined (see (16)) such that once some object $y_i(\tau _p)$ is close to the origin, i.e. $|y_i(\tau _p)| = a_p$ while $y_{i2}(\tau _p) < 0$ for some $\tau _p$, some energy is allocated on the first coordinate in order to increase $|y_{i1}(t)|$ (such that $|y_i(t)| \ge a_{p+1}$ on $[\tau _p, \tau '_p]$, (see (55)), avoiding the origin). Also, $y_{i2}(\tau _p)$ increases on $[\tau _p, \tau '_p]$ (such that $y_{i2}(t) \ge a_p$ on $[\tau '_p, \infty )$ (see (56))). The objective is that after the distance of point $y_i(t)$ from the origin is $a_p$ at $t=\tau _p$, it is not possible for it to be again at an $a_q$ distance at some $\tau _q$ with $q \ge p + 1$ (see (53)-(55))

The auxiliary trajectory $z_p(t)$ is the trajectory of $y_p(t)$ if the evader applies the “manoeuvre” against the p-pursuer on the whole interval $[\tau _p, \tau '_p)$. In the end, estimations of $|y_p(t)-z_p(t)|$ and $z_p(t)$ are needed to estimate $|y_p(t)|$.

3.1 Notations

It is sufficient to consider the case when $n=2$ and

$$\begin{aligned} \rho ^2:= \rho _1^2+\dots +\rho _m^2 < \sigma ^2 \end{aligned}$$

(6)

(see, for example, (Ibragimov et al. 2012, 2018).

Let $\alpha$ be any number satisfying the condition

$$\begin{aligned} 0< \alpha < \frac{(\sigma -\rho )^2}{2(\max _{1\le i\le m}|x_i^0|+1)}. \end{aligned}$$

(7)

We choose a number $a_1$ such that

$$\begin{aligned} 0< a_1 < \min \left\{ \frac{1}{2}, \frac{(\sigma -\rho )^2}{4\alpha }, \frac{\sigma ^2}{32\alpha }, \frac{\alpha }{2\Lambda }, \min _i|x_i^0|\right\} , \end{aligned}$$

(8)

where $\Lambda =\max _{1\le i\le m}\lambda _i$. Let

$$\begin{aligned} T_0=\frac{1}{\alpha }\max _{1\le i\le m}|x_i^0|, \ T=T_0 + \frac{2a_1}{\alpha }, \ \ \kappa =\min \left\{ \frac{1}{2}, \frac{\alpha }{16\sigma ^2e^{\Lambda T}}, \frac{\alpha ^3}{8\cdot 6^4\sigma ^{6}e^{4\Lambda T}}\right\} .\qquad \end{aligned}$$

(9)

Let a sequence $\{a_i\}_{i=1}^\infty$ be defined by the formula $a_{i+1}=\kappa \cdot a_i^4$. It is not difficult to see that this sequence has the following

Property 3.2

$\sum _{i=k}^\infty a_i\le 2a_{k}$ for any $k \ge 1$.

Let $y_i=(y_{i1}, y_{i2})$, $v=(v_1, v_2)$, and $u_i=(u_{i1}, u_{i2})$. Define $a_i$-approach time $\tau _i$ to be the first time such that

$$\begin{aligned} |y_j(\tau _i)|=a_i, \quad y_{j2}(\tau _i)<0, \quad i=1, \dots , m_0, \end{aligned}$$

(10)

for some $j\in \{1, \dots , m\}$, where $m_0$ is a positive integer. In Sect. 3.2 we’ll show that $\tau _i$ are defined for some points $y_i$, $i=1, \ldots ,m_0$, $m_0 \le m$. Note that $a_i$-approach times $\tau _i$ may not be defined as well ($m_0 = 0$).

First we define $\tau _1$ if relations (10) are satisfied at $i=1$ for some j. Then, we define $\tau _2$ and so on. Therefore, $\tau _1< \tau _2< \cdots < \tau _{m_0}$. Note that times $\tau _i$ are unspecified and depend on the evader’s strategy and the controls of the pursuers. It is important to note the fact that all the numbers $\tau _i$ will be in the interval [0, T], which will be established in Sect. 3.2.

Without loss of generality we relabel $y_j$ for which $|y_j(\tau _i)|=a_i$, $y_{j2}(\tau _i)<0$ by $y_i$. Note that the condition (10) can occur at the time $\tau _i$ for several j. If so, we label any one of them by $y_i$. Let

$$\begin{aligned} \tau _i'=\frac{1}{\lambda _i}\ln \left( e^{\lambda _i\tau _i}+\frac{2\lambda _ia_i}{\alpha }\right) , \quad i=1, \dots , m_0. \end{aligned}$$

Property 3.3

For any $i, k \in \{1, \dots , m_0\}$,

• (1) $\tau _i'-\tau _i\le \frac{2a_i}{\alpha }$.

• (2) $\sum _{i=k}^{m_0}(\tau _i'-\tau _i)\le \frac{4a_k}{\alpha }$.

Proof

To prove item (1), we have

$$\begin{aligned} \tau _i' - \tau _i = \frac{1}{\lambda _i}\ln \left( e^{\lambda _i\tau _i}+\frac{2\lambda _ia_i}{\alpha }\right) - \tau _i. \end{aligned}$$

(11)

Since for any $a \ge 1$ and $b \ge 0$ we have $\ln (a+b) \le \ln a + b$, therefore (11) implies that

$$\begin{aligned} \tau _i' - \tau _i \le \frac{1}{\lambda _i}\left( \lambda _i\tau _i + \frac{2\lambda _ia_i}{\alpha }\right) - \tau _i = \frac{2a_i}{\alpha }. \end{aligned}$$

(12)

The proof of item (2) follows from (12) as follows

$$\begin{aligned} \sum \limits _{i=k}^{m_0}(\tau _i' - \tau _i) \le \sum \limits _{i=k}^{\infty }\frac{2a_i}{\alpha } < \frac{4a_k}{\alpha } \end{aligned}$$

(13)

using Property 3.2. $\square$

Further, we define a function $r:[0, \infty )\rightarrow \{0, 1, \dots , m_0\}$ as follows: set $r(t)=i$, if $t\in [\tau _i, \tau _i'){\setminus } I_{i+1}$, $i=0, \dots , m_0$, where $\tau _0'=\infty$, $I_i=\cup _{j=i}^{m_0}[\tau _j, \tau _j')$, $I_{m_0+1}=\emptyset$. The function r has the following useful property:

Property 3.4

For $i=1, 2, \ldots , (m_0-1)$,

• (1) $r(t)=i$ for $\tau _i \le t < \tau _i'$ if $\tau _i' \le \tau _{i+1}$.

• (2) $r(t)=i$ for $\tau _i \le t < \tau _{i+1}$ if $\tau _{i+1} \le \tau _i'$.

Proof

Suppose that $\tau _{i}' \le \tau _{i+1}$. Then $[\tau _i, \tau _i'){\setminus } I_{i+1}=[\tau _i, \tau _i')$. Therefore, $r(t)=i$ for $t \in [\tau _i, \tau _i')$. This proves item (1).

To prove item (2), suppose that $\tau _{i+1}\le \tau _i'$. Since $\tau _i< \tau _{i+1}< \cdots < \tau _{m_0}$, we have $[\tau _{i}, \tau _{i+1}) \subset [\tau _{i}, \tau _i'){\setminus } I_{i+1}$. Therefore, $r(t)=i$ for $t\in [\tau _i, \tau _{i+1})$ by definition. $\square$

Example 3.5

If

$$\begin{aligned} 0 = \tau _0< \tau _1< \tau _2< \tau _1'< \tau _3< \tau _3'< \tau _2'< \tau _4< \tau _5< \tau _4' < \tau _5', \end{aligned}$$

then r(t) has the graph shown in Fig. 1.

Fig. 1

The graph of function r(x)

3.2 Strategy for the evader

Now we are ready to construct a strategy for the evader. Let $u_j(t)$, $j=1,\ldots ,m$, be arbitrary controls of pursuers. Set

$$\begin{aligned} v(t)= & {} V_0(t)=\left( 0, \alpha +\left( \sum _{j=1}^m|u_j(t)|^2\right) ^{1/2}\right) , \quad t\in [0, T]{\setminus } I_1, \end{aligned}$$

(14)

$$\begin{aligned} v(t)= & {} V_r(t)=(V_{r1}(t), U(t)), \ t\in [0, T]\cap I_1, \end{aligned}$$

(15)

where $r=r(t)$, $V_i(t)=(V_{i1}(t), U(t))$, $\tau _i \le t < \tau '_i$, $i=1, \dots , m_0$, is defined as follows

$$\begin{aligned} V_{i1}(t)= & {} {\left\{ \begin{array}{ll} \alpha +|u_{i1}(t)|, &{} y_{i1}(\tau _i)\ge 0,\\ -(\alpha +|u_{i1}(t)|),&{} y_{i1}(\tau _i)< 0, \end{array}\right. }\\ U(t)= & {} \alpha + \left( \sum _{j=1}^{m}u_{j2}^2(t)\right) ^{1/2}.\nonumber \end{aligned}$$

(16)

Note that U(t) doesn’t depend on i. Finally, let

$$\begin{aligned} v(t)=\left( 0, \left( \sum _{j=1}^m |u_j(t)|^2\right) ^{1/2} \right) , \quad t > T. \end{aligned}$$

(17)

Equation (15) shows that the function $r=r(t)$ assigns the control $V_r(t)$ for v(t).

For example, if there are 5 pursuers and the numbers $\tau _i, \tau '_i$, $i=1,\ldots ,5$, are arranged as in Example 3.5, then using the values of r(t) in Fig. 1 we obtain from (15) that

$$\begin{aligned} v(t)= {\left\{ \begin{array}{ll} V_1(t) &{}\quad \text {if} \quad t\in [\tau _1, \tau _2),\\ V_2(t) &{}\quad \text {if} \quad t\in [\tau _2, \tau _3)\cup [\tau _3', \tau _2')\\ V_3(t) &{}\quad \text {if} \quad t\in [\tau _3, \tau _3'),\\ V_4(t) &{} \quad \text {if} \quad t\in [\tau _4, \tau _5),\\ V_5(t) &{}\quad \text {if} \quad t\in [\tau _5, \tau _5'). \end{array}\right. } \end{aligned}$$

(18)

On the intervals $[0, \tau _1)$, $[\tau _2', \tau _4)$, and $[\tau _5', T]$, where $r(t)=0$ on [0, T], the evader’s strategy is defined by (14).

If $r(t)= i > 0$ on some time interval, then we say that evader is applying a manoeuvre $V_i(t)$ against the ith pursuer, or the evader is under the attack of the i-th pursuer on that interval. In Example 3.5, $r(t)=0$ on intervals $[0, \tau _1)$ and $[\tau _2', \tau _4)$ and so the evader is not under the attack of any pursuer on these intervals. Since $r(t)= 1$ on $[\tau _1, \tau _2)$, therefore the evader is under the attack of the first pursuer on this interval, and so evader applies the manoeuvre $V_1(t)$ against the first pursuer on this interval. Also, we can see other manoeuvres of evader in formula (18).

The evader chooses his maneuvers nonanticipatively stage by stage as the game progresses. For the Example 3.5, the numbers $t_1, t_2,\ldots , t_{k} \in [0, T]$ in Definition 2.2 are defined as follows: $t_0=0$, $t_1=\tau _1$, $t_2=\tau _2$, $t_3=\tau _3$, $t_4=\tau '_3$, $t_5=\tau '_2$, $t_6=\tau _4$, $t_7=\tau _5$, $t_8=\tau '_5$, $t_9=T$. As the time $t_i$, $i=1,2,\ldots ,8$ ($t_0=0$) occurs, the function r(t) assigns the strategy $V_{r_i}(t)$ for the evader defined by (14), (15), where $r_i=r(t_i)$. The evader uses this strategy until $t_{i+1}$ occurs, that is, on the interval $t_i \le t < t_{i+1}$. Note that $t_{i+1}$ is unspecified and defined as the first time when $r(t_i) \ne r(t_{i+1})$.

In general, the numbers $t_1, t_2,\ldots , t_{k} \in [0, T]$ are defined as follows. By (14) the evader uses strategy $v(t)=V_0(t)$, $\tau _0 \le t < \tau _1$. This means the evader applies $v(t)=V_0(t)$ until $\tau _1$ occurs. Set $t_1=\tau _1$, $t_k=T$. The numbers $t_2,\ldots , t_{k-1}$ are defined inductively. Let the time $t_i \in \{\tau _1, \tau '_1,\ldots , \tau _p, \tau '_p\}$, $i,p \ge 1$, occur and let $r_i=r(t_i)$. Then by (14) and (15) the evader applies the strategy $v(t)=V_{r_i}(t)$ starting from $t_i$ until the time $t_{i+1}$ occurs, for which $r(t_i) \ne r(t_{i+1})$ for the first time, where $t_{i+1} \in \{\tau _1, \tau '_1,\ldots , \tau _p, \tau '_p, \tau _{p+1}, \tau '_{p+1}\}$. As the time $t_{i+1}$ occurs the evader uses the strategy $v(t)=V_{r_{i+1}}(t)$ starting from the time $t_{i+1}$ where $r_{i+1}=r(t_{i+1})$ and so on. To determine the times $\tau _i$, $i=1,2,\ldots , m_0$, the evader uses the current values of states $y_i(t)$, $i=1,2,\ldots ,m$. To this end, it suffices for the evader to know the current time t and $x_i(t)$, $i=1,2,\ldots ,m$. Also, we can see from (14) and (15) that the strategy of evader has the form $v(t)=V_{r_i}(t)$ on the intervals $t_i \le t < t_{i+1}$, $i=0,1,\ldots ,k$.

We now show that the strategy defined by the equations (14)–(17) is admissible. Indeed, let

$$\begin{aligned}&f(t)={\left\{ \begin{array}{ll} (0, \alpha ),&{} t\in [0, T){\setminus } I_1 \\ (\alpha , \alpha ), &{} t\in I_1\\ (0, 0), &{} t> T \end{array}\right. }, \\&g(t)={\left\{ \begin{array}{ll} \left( 0, \left( \sum _{j=1}^{m}|u_{j}(t)|^2\right) ^{1/2} \right) , &{} t\in [0, T]{\setminus } I_1,\\ \left( |u_{r1}(t)|, \left( \sum _{j=1}^{m}u_{j2}^2(t)\right) ^{1/2}\right) , &{} t\in I_1, \\ \left( 0, \left( \sum _{j=1}^{m}|u_{j}(t)|^2\right) ^{1/2} \right) , &{} t > T. \end{array}\right. } \end{aligned}$$

Note that

$$\begin{aligned} \int _0^\infty |f(s)|^2ds \le 2\alpha ^2 T, \ \ |g(t)|^2 \le \sum _{j=1}^{m}|u_{j}(t)|^2. \end{aligned}$$

(19)

Clearly, for v(t) defined by (14)–(17) we have $v_1^2(t)+v_2^2(t)=|f(t)+g(t)|^2$. Therefore, using the Minkowskii inequality and (19) we obtain

$$\begin{aligned} \left( \int _0^\infty |v(s)|^2ds\right) ^{1/2}&=\left( \int _0^\infty |f(s)+g(s)|^2ds\right) ^{1/2}\\&\le \left( \int _0^\infty |f(s)|^2ds\right) ^{1/2}+\left( \int _0^\infty |g(s)|^2ds\right) ^{1/2}\\&\le (2\alpha ^2 T)^{1/2}+ \left( \int _0^\infty \sum _{j=1}^{m}|u_{j}(s)|^2ds\right) ^{1/2} \\&\le \alpha \sqrt{2T}+ \left( \sum _{j=1}^{m}\rho _i^2\right) ^{1/2} = \alpha \sqrt{2T}+\rho \le \sigma \end{aligned}$$

since by definition of $T, T_0$ and $\alpha$

$$\begin{aligned} \alpha \sqrt{2T}= & {} \alpha \sqrt{2\left( T_0+\frac{2a_1}{\alpha }\right) } = \sqrt{2\alpha \left( \max \limits _{i=1,...,m} |x_{i0}|+ 2a_1\right) }\\\le & {} \sqrt{2\alpha \left( \max \limits _{i=1,\ldots ,m} |x_{i0}|+ 1\right) } \le \sigma - \rho . \end{aligned}$$

Here, in the last inequality we used (7). Thus, the evasion strategy (14)–(17) is admissible.

Next, we prove the following statement.

Lemma 3.6

The following are true

• 1) For all $i=1, \dots , m$, we have (i) $y_{i2}(t) > 0$ for $t \ge T_0$ and (ii) $\tau _i' \le T$.

• 2)

  • (i) if $x^0_{j2} < 0$ for some $j \in \{1,\ldots ,m\}$, then $y_{j2}(\theta ) = 0$ at some unique $\theta$, $0< \theta < T_0$, and $y_{j2}(t) > 0$ for all $t > \theta$.

  • (ii) if $x^0_{j2} \ge 0$ for some $j \in \{1,\ldots ,m\}$, then $y_{j2}(t) > 0$ for all $t > 0$.

Proof

We first show that $y_{i2}(T_0) > 0$ for all $i=1, \dots , m$. Indeed, by (14)–(15) we have

$$\begin{aligned} v_2(t)\ge \alpha +|u_{i2}(t)|, \ 0 \le t \le T_0, \end{aligned}$$

(20)

and therefore,

$$\begin{aligned} \dot{y}_{i2}(t) = e^{\lambda _i t}(v_2(t) - u_{i2}(t)) \ge \alpha e^{\lambda _i t} > 0. \end{aligned}$$

(21)

Hence, $y_{i2}(t)$, $0 \le t \le T_0$, increases strictly. By (21) we have

$$\begin{aligned} y_{i2}(T_0)&= x_{i2}^0+\int _0^{T_0}e^{\lambda _is}(v_2(s)-u_{i2}(s))ds\\&\ge x_{i2}^0 + \alpha \int _0^{T_0}e^{\lambda _i s}ds\ge x_{i2}^0+\frac{\alpha }{\lambda _i}\left( e^{\lambda _iT_0}-1\right) \\&> x_{i2}^0 + \frac{\alpha }{\lambda _i}\lambda _i T_0 \ge -|x_i^0|+\max _{1\le j\le m}|x_j^0|\ge 0. \end{aligned}$$

Thus, $y_{i2}(T_0)>0$ for all $i=1, \dots , m$. Since $v_2(t) \ge |u_i(t)|\ge |u_{i2}(t)|$ for $t > T_0$, therefore for $t>T_0$ we have

$$\begin{aligned} y_{i2}(t)&=y_{i2}(T_0)+\int _{T_0}^te^{\lambda _is}(v_2(s)-u_{i2}(s))ds\\&\ge y_{i2}(T_0)+\int _{T_0}^te^{\lambda _is}(|u_{i2}(s)|-u_{i2}(s))ds \ge y_{i2}(T_0)>0. \end{aligned}$$

Thus, $y_{i2}(t)>0$, for all $t \ge T_0$ and $i=1, \dots , m$. In particular, we obtain that there is no $a_k$-approach time $\tau _k$ in the time interval $[T_0, \infty )$, since by definition (10) of an $a_k$-approach time $\tau _k$ one has to have $y_{k2}(\tau _k) < 0$. This is impossible for $\tau _k \ge T_0$ since by item 1) (i) $y_{k2}(t)>0$ for all $t \ge T_0$. Thus, $\tau _i \le T_0$ for all $i=1, \ldots ,m_0$.

Next, by item 1) (ii) of Property 3.3 we have

$$\begin{aligned} \tau _i' \le \tau _i + \frac{2a_i}{\alpha } \le T_0 + \frac{2a_1}{\alpha } = T, \end{aligned}$$

(22)

and the proof of item 1) of Lemma 3.6 follows. In particular, (22) implies that $I_1 \subset [0, T]$.

Remark 3.7

Due to the inclusion $I_1 \subset [0, T]$ the set $[0, T]\cap I_1$ in (15) is equal to $I_1$.

Next, we prove item 2) (i). Since by (21) $y_{j2}(t)$, $0 \le t \le T_0$, increases strictly and as shown above $y_{j2}(T_0)>0$, then we necessarily have that $y_{j2}(\theta ) = 0$ at some unique $\theta$, $0< \theta < T_0$. In view of (20) we then obtain for $t > \theta$ that

$$\begin{aligned} y_{j2}(t)&= y_{j2}(\theta ) + \int \limits _\theta ^t e^{\lambda _j s}(v_2(s) - u_{j2}(s))ds\\&\ge \int \limits _{[\theta ,t] \cap [\theta ,T_0]} e^{\lambda _j s}(\alpha + |u_{j2}(s)| - u_{j2}(s))ds > 0, \end{aligned}$$

which is the desired result. To show item 2) (ii), using $x^0_{j2} \ge 0$ we observe that for $t \ge 0$,

$$\begin{aligned} y_{j2}(t)&= x^0_{j2} + \int \limits _0^t e^{\lambda _j s}(v_2(s) - u_{j2}(s))ds\\&\ge \int \limits _{[0,t] \cap [0,T_0]} e^{\lambda _j s}(\alpha + |u_{j2}(s)| - u_{j2}(s))ds > 0. \end{aligned}$$

This completes the proof of Lemma 3.6. $\square$

Fig. 2

Initial states have negative y-coordinates

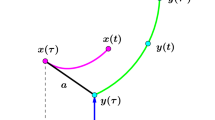
Item 1) (i) of Lemma 3.6 implies, in particular, that for the point $y_j$ with initial state $x_j^0$ for which $x_{j2}^0 < 0$, the inequality $y_{j2}(T_0) > 0$ is satisfied. Thus, we necessarily have either $|y_j(\tau _j)| = a_j$ and $y_{j2}(\tau _j) < 0$ at some $0< \tau _j < T_0$ (see the point $y_i$ in Fig. 2) or $y_{j2}(\theta ) = 0$ and $|y_{j1}(\theta )| \ge a_j$ at some $0< \theta < T_0$ (see the point $y_j$ in Fig. 2). The former case will be studied in the following subsections in detail. In the latter case, we ignore the point $y_{j}(t)$ starting from the time $\theta$ since by Lemma 3.6 2) (i) we have $y_{j2}(t) > 0$ and so $y_{j}(t) \ne 0$ for all $t > \theta$. That is why in definition of $a_i$-approach time $\tau _i$ (10) we required the inequality $y_{j2}(\tau _i) < 0$. The initial states $x_k^0$ with $x_{k2}^0 > 0$, and $x_l^0$ with $x_{l2}^0 = 0$, are shown in Fig. 3. We ignore the corresponding points $y_k(t)$ and $y_l(t)$ as well for $t \ge 0$ since by Lemma 3.6 2) (ii) $y_{k2}(t) > 0$ and $y_{l2}(t) > 0$ for all $t \ge 0$.

Fig. 3

Initial states have non negative y-coordinates

Property 3.8

For any $i \in \{1, \dots , m_0\}$ and $p \in \{1, \dots , m\}$,

$$\begin{aligned} \int \limits _{\tau _i}^{\tau _i'}e^{\lambda _p s}ds \le e^{\Lambda T}\cdot \frac{4a_i}{\alpha }. \end{aligned}$$

(23)

Proof

We use (12) and $\tau _i \le T_0 < T$ to obtain

$$\begin{aligned} \int \limits _{\tau _i}^{\tau _i'}e^{\lambda _p s}ds&= \frac{1}{\lambda _p} \left( e^{\lambda _p \tau _i'} - e^{\lambda _p \tau _i}\right) \nonumber \\&= \frac{e^{\lambda _p \tau _i}}{\lambda _p} \left( e^{\lambda _p (\tau _i' - \tau _i)} - 1 \right) \le \frac{1}{\lambda _p}e^{\Lambda T} \left( e^{\frac{2\lambda _p a_i}{\alpha }} - 1 \right) . \end{aligned}$$

(24)

Since by (8) $\frac{2\lambda _p a_i}{\alpha } \le \frac{2\Lambda a_1}{\alpha } \le 1$, then using the inequality $e^x - 1 \le 2x$, $0 \le x \le 1$, in (24) we obtain (23). This completes the proof of the property. $\square$

3.3 Auxiliary point $z_p$

Take any $p\in \{1, \dots , m_0\}$ and estimate $|y_p(t)|$ on $[\tau _p, \tau _p']$ assuming that $a_p$-approach was occurred at time $\tau _p$ with the point $y_p$. To this end we introduce an auxiliary point $z_p$ whose dynamics is described by the following equation

$$\begin{aligned} z_p(t)=y_p(\tau _p)+\int _{\tau _p}^te^{\lambda _ps}(V_p(s)-u_p(s))ds, \ \tau _p\le t \le \tau _p'. \end{aligned}$$

(25)

Note that the point $z_p(t)$ is defined only on the interval $[\tau _p, \tau _p']$. Since by (15) $v_2(t)=U(t)$, therefore

$$\begin{aligned} z_{p2}(t)= & {} z_{p2}(\tau _p)+\int _{\tau _p}^te^{\lambda _ps}(U(s)-u_{p2}(s))ds\nonumber \\= & {} y_{p2}(\tau _p)+\int _{\tau _p}^te^{\lambda _ps}(v_2(s)-u_{p2}(s))ds = y_{p2}(t), \ \tau _p \le t \le \tau _p'. \end{aligned}$$

(26)

Next, we show that

$$\begin{aligned} \int _{\tau _p}^{\tau _p'}|V_p(s)|^2 ds \le \sigma ^2. \end{aligned}$$

(27)

Indeed, denoting

$$\begin{aligned} f_1(t)=(\alpha , \alpha ), \ \ g_1(t)=\left( |u_{p1}(t)|, \left( \sum _{j=1}^{m}u_{j2}(t)^2\right) ^{1/2}\right) \end{aligned}$$

we obtain

$$\begin{aligned} |V_p(t)|^2=V^2_{p1}(t) + U^2(t)&= (\alpha +|u_{p1}(t)|)^2+\left( \alpha + \left( \sum _{j=1}^{m}u^2_{j2}(t)\right) ^{1/2}\right) ^2\\&=|f_1(t)+g_1(t)|^2. \end{aligned}$$

Therefore, using the Minkowskii inequality and then item (1) of Property 3.3 we obtain

$$\begin{aligned} \left( \int _{\tau _p}^{\tau _p'}|V_p(s)|^2 ds \right) ^{1/2}&=\left( \int _{\tau _p}^{\tau _p'}|f_1(s)+g_1(s)|^2ds \right) ^{1/2}\\&\le \left( \int _{\tau _p}^{\tau _p'}|f_1(s)|^2ds \right) ^{1/2}+ \left( \int _{\tau _p}^{\tau _p'}|g_1(s)|^2ds \right) ^{1/2}\\&\le (2\alpha ^2(\tau _p'-\tau _p))^{1/2}+ \left( \int _{\tau _p}^{\tau _p'}\sum _{j=1}^{m}|u_{j}(s)|^2ds\right) ^{1/2}\\&\le 2\sqrt{\alpha a_p}+\rho <\sigma , \end{aligned}$$

since by (8) $a_p\le a_1 <\frac{(\sigma -\rho )^2}{4\alpha }$, and hence (27) is true.

3.4 Estimation of $|z_p(t)|$

Let $\tau _p\le t<\tau _p'$ and for definiteness assume that $y_{p1}(\tau _p)\ge 0$. Then by (16) we have $V_{p1}(t)=\alpha +|u_{p1}(t)|$. Therefore,

$$\begin{aligned} |z_p(t)| \ge z_{p1}(t)&=y_{p1}(\tau _p) +\int _{\tau _p}^te^{\lambda _ps}(V_{p1}(t)-u_{p1}(t))ds \nonumber \\&\ge \int _{\tau _p}^te^{\lambda _ps}(\alpha +|u_{p1}(t)|-u_{p1}(t))ds\nonumber \\&\ge \alpha \int _{\tau _p}^te^{\lambda _ps}ds =\frac{\alpha }{\lambda _p}(e^{\lambda _pt}-e^{\lambda _p\tau _p}). \end{aligned}$$

(28)

On the other hand,

$$\begin{aligned} |z_p(t)|\ge |y_p(\tau _p)|-\int _{\tau _p}^te^{\lambda _ps}|V_p(s)-u_p(s)|ds. \end{aligned}$$

(29)

The integral in (29) can be estimated by using the Cauchy-Schwartz inequality as follows

$$\begin{aligned} \int _{\tau _p}^te^{\lambda _ps}|V_p(s)-u_p(s)|ds&\le \left( \int _{\tau _p}^te^{2\lambda _ps} ds\right) ^{1/2}\left( \int _{\tau _p}^t |V_p(s)-u_p(s)|^2ds \right) ^{1/2}\nonumber \\&\le \left( \int _{\tau _p}^te^{2\lambda _ps}ds \right) ^{1/2}\left( \int _{\tau _p}^t 2(|V_p(s)|^2+|u_p(s)|^2)ds \right) ^{1/2}. \end{aligned}$$

(30)

Since by (27) and the admissibility of control $u_p(s)$

$$\begin{aligned} \int _{\tau _p}^{t}|V_p(s)|^2 ds \le \sigma ^2, \ \ \int _{\tau _p}^{t}|u_p(s)|^2 ds \le \rho _p^2 \le \sigma ^2, \end{aligned}$$

then it follows from (30) that

$$\begin{aligned} \int _{\tau _p}^te^{\lambda _ps}|V_p(s)-u_p(s)|ds \le 2\sigma \left( \int _{\tau _p}^te^{2\lambda _ps} ds\right) ^{1/2}. \end{aligned}$$

(31)

Since by (22) $\tau _p \le t \le \tau '_p \le T$, therefore

$$\begin{aligned} \int _{\tau _p}^te^{2\lambda _ps} ds = \frac{1}{2\lambda _p}\left( e^{\lambda _p t} + e^{\lambda _p \tau _p}\right) \left( e^{\lambda _p t} - e^{\lambda _p \tau _p}\right) \le \frac{e^{\Lambda T}}{\lambda _p}\left( e^{\lambda _p t} - e^{\lambda _p \tau _p}\right) . \end{aligned}$$

Then by (31) we can see that

$$\begin{aligned} \int _{\tau _p}^te^{\lambda _ps}|V_p(s)-u_p(s)|ds \le 2\sigma \sqrt{\frac{e^{\Lambda T}}{\lambda _p}(e^{\lambda _pt}-e^{\lambda _p\tau _p})}. \end{aligned}$$

(32)

Combining (29) and (32), and using the equation $|y_p(\tau _p)|=a_p$ yields that

$$\begin{aligned} |z_p(t)|\ge a_p-2\sigma \sqrt{\frac{e^{\Lambda T}}{\lambda _p}(e^{\lambda _pt}-e^{\lambda _p\tau _p})}. \end{aligned}$$

(33)

It is easily seen from (28) and (33) that

$$\begin{aligned} |z_p(t)|\ge f(t)=\max \{f_1(t), f_2(t)\}, \ \ t \ge \tau _p, \end{aligned}$$

(34)

where

$$\begin{aligned} f_1(t)=\frac{\alpha }{\lambda _p}(e^{\lambda _pt}-e^{\lambda _p\tau _p}), \ \ f_2(t)=a_p-2\sigma \sqrt{\frac{e^{\Lambda T}}{\lambda _p}(e^{\lambda _pt}-e^{\lambda _p\tau _p})}. \end{aligned}$$

Note that $f_1(t)$, $t \ge \tau _p$, increases from 0 to $\infty$ and $f_2(t)$, $t \ge \tau _p$, decreases from $a_p$ to $-\infty$. It is not difficult to see that f(t), $t\ge \tau _p$, attains its minimum at the point $t=t_*$, where

$$\begin{aligned} f_1(t)=f_2(t), \quad t\ge \tau _p. \end{aligned}$$

(35)

Let $\left( e^{\lambda _pt}-e^{\lambda _p\tau _p}\right) ^{1/2} = z$. Then Eq. (35) takes the form

$$\begin{aligned} \frac{\alpha }{\lambda _p}z^2=a_p-2\sigma \sqrt{\frac{e^{\Lambda T}}{\lambda _p}}z, \end{aligned}$$

or $\alpha z^2 + 2\sigma \sqrt{e^{\Lambda T}\lambda _p}z-a_p\lambda _p=0$. This equation has the following positive root

$$\begin{aligned} z_*&=\frac{\sqrt{\lambda _p}}{\alpha }\left( -\sigma \sqrt{e^{\Lambda T}}+\sqrt{\sigma ^2e^{\Lambda T} + a_p\alpha }\right) \\&=\frac{a_p\sqrt{\lambda _p}}{\sigma \sqrt{e^{\Lambda T}}+\sqrt{\sigma ^2e^{\Lambda T}+a_p\alpha }}. \end{aligned}$$

Then

$$\begin{aligned} \min _{t\ge \tau _p}f(t)=f(t_*)=f_1(t_*)=\frac{\alpha }{\lambda _p}z^2_*= \frac{\alpha }{\lambda _p}\cdot \frac{a_p^2\lambda _p}{(\sigma \sqrt{e^{\Lambda T}}+\sqrt{\sigma ^2e^{\Lambda T}+a_p\alpha })^2}. \end{aligned}$$

(36)

By (8) we have $a_1<\frac{\sigma ^2}{32\alpha } < \frac{1}{\alpha }\sigma ^2e^{\Lambda T}$, and so $a_p\alpha \le a_1\alpha < \sigma ^2e^{\Lambda T}$, therefore (36) implies that

$$\begin{aligned} |z_p(t)|\ge \min _{t\ge \tau _p} f(t) >\frac{\alpha a_p^2}{6\sigma ^2 e^{\Lambda T}}. \end{aligned}$$

(37)

Next, since by definition

$$\begin{aligned} \tau _p'=\frac{1}{\lambda _p}\ln \left( e^{\lambda _p\tau _p} + \frac{2\lambda _pa_p}{\alpha }\right) , \end{aligned}$$

using the fact that $y_{p2}(\tau _p)\ge -|y_p(\tau _p)| = -a_p$ we obtain

$$\begin{aligned} \begin{aligned} z_{p2}(\tau _p')&=y_{p2}(\tau _p)+\int _{\tau _p}^{\tau _p'}e^{\lambda _ps}(U(s) -u_{p2}(s))ds\\&\ge -a_p+\int _{\tau _p}^{\tau _p'}e^{\lambda _ps}\left( \alpha + \left( \sum _{i=1}^mu_{i2}(s)^2\right) ^{1/2}-u_{p2}(s)\right) ds\\&\ge -a_p+\alpha \int _{\tau _p}^{\tau _p'}e^{\lambda _ps}ds=-a_p + \frac{\alpha }{\lambda _p}\left( e^{\lambda _p\tau _p'}-e^{\lambda _p\tau _p}\right) \\&=-a_p+\frac{\alpha }{\lambda _p}\left( e^{\lambda _p\tau _p}+\frac{2\lambda _pa_p}{\alpha }-e^{\lambda _p\tau _p}\right) =a_p. \end{aligned} \end{aligned}$$

(38)

Finally, let $t \ge \tau _p'$. By (26) $y_{p2}(\tau '_p) = z_{p2}(\tau '_p)$, and by (14), (15) and (17), $v_2(t) \ge |u_{p2}(t)|$. Then using (17), (38) we get

$$\begin{aligned} y_{p2}(t) = z_{p2}(\tau _p') + \int _{\tau '_p}^te^{\lambda _ps}(v_2(s)-u_{p2}(s))ds \ge z_{p2}(\tau _p')\ge a_p. \end{aligned}$$

Thus, we have the following inequalities

$$\begin{aligned}&|z_p(t)| > \frac{\alpha a_p^2}{6\sigma ^2e^{\Lambda T}}, \quad \tau _p\le t\le \tau _p', \end{aligned}$$

(39)

$$\begin{aligned}&y_{p2}(t) \ge a_p, \quad \qquad t \ge \tau _p'. \end{aligned}$$

(40)

3.5 Estimation of $|y_p(t)-z_p(t)|$

We have

$$\begin{aligned} |y_p(t)-z_p(t)|=\left| \int _{\tau _p}^t(v(s)-V_p(s))ds\right| , \ \ \tau _p\le t\le \tau _p'. \end{aligned}$$

(41)

By (15) and (26)

$$\begin{aligned} v(t)=(V_{r1}(t), U(t)), \ \ V_p(t)=(V_{p1}(t), U(t)), \ \ \tau _p \le t < \tau _p'. \end{aligned}$$

(42)

Consider two cases: (i) $\tau _p'\le \tau _{p+1}$ and (ii) $\tau _{p+1}\le \tau _p'$.

Case (i). Let $\tau _p'\le \tau _{p+1}$. Then by item (1) of Property 3.4$r=r(t)=p$ for $\tau _p \le t <\tau _p'$. Therefore by (42) we have $v(t)=V_p(t)$, $\tau _p \le t < \tau _p'$. Hence, by (41)

$$\begin{aligned} |y_p(t)-z_p(t)|=0. \end{aligned}$$

(43)

Case (ii). Assume now $\tau _{p+1} \le \tau _p'$. Then by item (2) of Property 3.4 we have $v(t)=(V_{p1}(t), U(t))$, $\tau _p \le t < \tau _{p+1}$. Therefore, (41) leads to

$$\begin{aligned}&|y_p(t)-z_p(t)|\nonumber \\&\quad =\left| \int _{\tau _{p+1}}^te^{\lambda _ps}(v(s)-V_p(s))ds\right| \le \int _{\tau _{p+1}}^te^{\lambda _ps}|v(s)-V_p(s)|ds\nonumber \\&\quad \le \int \limits _{[\tau _{p+1}, t){\setminus } I_{p+1}}e^{\lambda _ps}|v(s)-V_p(s)|ds + \int \limits _{[\tau _{p+1}, t)\cap I_{p+1}}e^{\lambda _ps}|v(s)-V_p(s)|ds. \end{aligned}$$

(44)

Since by definition $r(t)=p$, $t\in [\tau _p, \tau _p'){\setminus } I_{p+1}$ and $[\tau _{p+1}, t){\setminus } I_{p+1} \subset [\tau _p, \tau _p'){\setminus } I_{p+1}$, therefore we have $r=r(t)=p$, and hence, $v(t)=V_p(t)$ for $t \in [\tau _{p+1}, t){\setminus } I_{p+1}$. Consequently, the first integral in (44) is 0, and so (44) takes the form

$$\begin{aligned} |y_p(t)-z_p(t)|\le \int _{[\tau _{p+1}, t]\cap I_{p+1}}e^{\lambda _ps}|v(s)-V_p(s)|ds. \end{aligned}$$

(45)

By (16) and (42)

$$\begin{aligned} |v(s)-V_p(s)|=|V_{r1}(s)-V_{p1}(s)|\le 2\alpha +|u_{r1}(s)|+|u_{p1}(s)|, \end{aligned}$$

and therefore (45) implies that

$$\begin{aligned} |y_p(t)-z_p(t)|\le \int _{I_{p+1}}e^{\lambda _ps}(2\alpha +|u_{r1}(s)|+|u_{p1}(s)|)ds. \end{aligned}$$

(46)

To estimate the integral in (46), we need to estimate the integrals

$$\begin{aligned} \int _{I_{p+1}}e^{\lambda _ps}ds, \ \int _{I_{p+1}}e^{\lambda _ps}|u_{r1}(s)|ds, \text { and }\int _{I_{p+1}}e^{\lambda _ps}|u_{p1}(s)|ds. \end{aligned}$$

(47)

The first integral can be estimated using (23) and Property 3.2 as follows

$$\begin{aligned} \int _{I_{p+1}}e^{\lambda _ps}ds \le \sum _{i=p+1}^m\int _{\tau _i}^{\tau _i'}e^{\lambda _ps}ds \le \sum _{i=p+1}^m e^{\Lambda T} \frac{4a_i}{\alpha } \le e^{\Lambda T} \frac{8a_{p+1}}{\alpha }. \end{aligned}$$

(48)

Next, we estimate the second integral in (47). Using the Cauchy-Schwartz inequality we have

$$\begin{aligned} \int _{I_{p+1}}e^{\lambda _ps}|u_{p1}(s)|ds\le \left( \int _{I_{p+1}}e^{2\lambda _ps}ds\right) ^{1/2}\cdot \left( \int _{I_{p+1}}|u_{p1}(s)|^2ds\right) ^{1/2}. \end{aligned}$$

(49)

Since

$$\begin{aligned} \int _{I_{p+1}}|u_{p1}(s)|^2ds \le \sum _{i=1}^m\int _0^\infty |u_i(s)|^2ds \le \sigma ^2 \end{aligned}$$

and similar to (48) we get

$$\begin{aligned} \int _{I_{p+1}}e^{2\lambda _ps}ds \le \sum _{i=p+1}^{m}\int _{\tau _i}^{\tau _i'}e^{2\lambda _ps}ds \le e^{2\Lambda T}\frac{8a_{p+1}}{\alpha }. \end{aligned}$$

Then it follows from (49) that

$$\begin{aligned} \int _{I_{p+1}}e^{\lambda _ps}|u_{p1}(s)|ds\le \sigma e^{\Lambda T}\sqrt{\frac{8a_{p+1}}{\alpha }}. \end{aligned}$$

(50)

Similarly, for the third integral in (47), we have

$$\begin{aligned} \int _{I_{p+1}}e^{\lambda _ps}|u_{p1}(s)|ds\le \sigma e^{\Lambda T}\sqrt{\frac{8a_{p+1}}{\alpha }}. \end{aligned}$$

(51)

Combining (48), (50), and (51) we obtain from (46) that

$$\begin{aligned} |y_p(t)-z_p(t)|\le 2 \alpha \cdot \frac{8a_{p+1}}{\alpha }\cdot e^{\Lambda T} + 2\sigma e^{\Lambda T}\sqrt{\frac{8a_{p+1}}{\alpha }} \le 3\sigma e^{\Lambda T}\sqrt{\frac{8 a_{p+1}}{\alpha }} \end{aligned}$$

using the inequality

$$\begin{aligned} 16 a_{p+1} < \sigma \sqrt{\frac{8 a_{p+1}}{\alpha }} \end{aligned}$$

which follows from the inequalities $a_{p+1} \le a_1 < \frac{\sigma ^2}{32\alpha }$ (see (8)).

Thus,

$$\begin{aligned} |y_p(t)-z_p(t)|\le 3\sigma e^{\Lambda T}\sqrt{\frac{8a_{p+1}}{\alpha }}, \ \tau _p \le t\le \tau _p'. \end{aligned}$$

(52)

3.6 Estimation of $|y_p(t)|$

Using (39) and (52) we obtain

$$\begin{aligned} |y_p(t)|\ge |z_p(t)|-|y_p(t)-z_p(t)| \ge \frac{\alpha a_p^2}{6\sigma ^2e^{\Lambda T}} - 3\sigma e^{\Lambda T}\sqrt{\frac{8 a_{p+1}}{\alpha }} \ge \frac{\alpha a_p^2}{12\sigma ^2 e^{\Lambda T}},\nonumber \\ \end{aligned}$$

(53)

for $t\in [\tau _p, \tau _p']$ since by (9)

$$\begin{aligned} a_{p+1} \le \frac{\alpha ^3 }{8\cdot 6^4\sigma ^6e^{4\Lambda T}}a_p^4. \end{aligned}$$

Also, it follows from the definition of $\kappa$ and the inequality $a_p < 1$ that

$$\begin{aligned} a_{p+1}\le \frac{\alpha }{16 \sigma ^2 e^{\Lambda T}}a_p^4\le \frac{\alpha }{12 \sigma ^2e^{\Lambda T}}a_p^2. \end{aligned}$$

Therefore, (53) implies that $|y_p(t)| > a_{p+1}$. Also, by (40)

$$\begin{aligned} y_{p2}(t) \ge a_p, \quad t \ge \tau _p'. \end{aligned}$$

Thus,

$$\begin{aligned}&|y_p(t)| \ge a_p, \text { for } 0\le t\le \tau _p, \ \ \text {(by definition of } \tau _p\text {) } \end{aligned}$$

(54)

$$\begin{aligned}&|y_p(t)| \ge \frac{\alpha a_p^2}{12\sigma ^2 e^{\Lambda T}}>a_{p+1}, \text { for } \tau _p \le t \le \tau '_p, \ \ \text {(by }(53)\text {)} \end{aligned}$$

(55)

$$\begin{aligned}&y_{p2}(t) \ge a_p, \text { for } t\ge \tau _p', \ \ \text {(by }40\text {)} \end{aligned}$$

(56)

Thus we conclude:

If an $a_p$-approach time $\tau _p$ occurs with the point $y_p$ (see the point $y_i$ in Fig. 2), then $y_p(t)\ne 0$, for all $t\ge 0$ (see (54)–(56)). Moreover, for any $i\ge p+1$, there is no $a_i$-approach time $\tau _i$ for the point $y_p$

• (1) on the time interval $[\tau _p, \tau _p']$ since $|y_{p}(t)| > a_{p+1} \ge a_i$ for any $i \ge p+1$ (see (55)).

• (2) on the time interval $[\tau _p', \infty )$, since $|y_{p}(t)| \ge y_{p2}(t) \ge a_p > a_i$ for any $i\ge p+1$ (see (56)).

The proof of Theorem 3.1 is completed.

4 Conclusion

We have studied a linear evasion differential game of many pursuers and one evader. We have constructed a strategy for the evader and proved the possibility of evasion. The evader uses a manoeuvre on the set $I_1$ and on the set $[0, T]{\setminus } I_1$ evader uses the control $v(t) = \left( 0, \alpha +\left( \sum _{j=1}^m|u_j(t)|^2\right) ^{1/2}\right)$. The measure of the set $I_1$ can be made by choosing parameters $a_1$ and $\alpha$ as small as we wish. We have also shown that all the approach times $\tau _i$ can occur only before a specified time $T_0$, moreover $\tau _i' \le T$. The total number of approach times $\tau _i$ of all pursuers doesn’t exceed the number of pursuers m. For $t \ge T$, the evader uses the control $v(t) = \left( 0, \left( \sum _{j=1}^m|u_j(t)|^2\right) ^{1/2}\right)$ and there is no longer an approach time occurs. The main contributions of the paper are (i) the construction of evasion strategy, (ii) estimating the distances of objects from the origin, (iii) the possibility of evasion from many pursuers.