1 Introduction and main contribution

This paper addresses a problem where n players compete for a set of indivisible items \(j\in J\). Each item \(j\in J\) has a weight \(w_j\) which represents the item’s utility. The utility of an item is the same for all n players. In competing for these items, a player i is bound in her choice by a downward-closed set system \(\mathcal {S}_i\subseteq 2^J\), meaning that only the subsets \(S_i\in \mathcal {S}_i\) are feasible for her. Players aim to maximize their utility, which means maximizing the total weight of the chosen items \(w(S_i)=\sum _{j\in S_i} w_j\). Items are indivisible, hence a feasible solution consists of a profile of subsets \(S=(S_1,\dots ,S_n)\) such that \(S_i\in \mathcal {S}_i\) for all i and \(S_i\cap S_k=\emptyset \) for all \(i\ne k\). Our interest goes into the efficiency loss that occurs when the distribution of items is not controlled centrally, and hence we study the price of anarchy for three types of equilibria for this class of games. The motivation to address this problem is discussed in detail in Sect. 2.

Nash equilibria and sequential play A distinguishing feature of the game that we propose is that each item \(j\in J\) can only be selected by at most one of the players. In that situation, a pure strategy Nash equilibrium is a selection of subsets \(S_i\), one for every player \(i=1,\dots ,n\), so that \(S_i\cap S_k =\emptyset \) for any two players \(i\ne k\), and for each player i we have that \(w(S_i)\ge w(T_i)\) for all \(T_i\in \mathcal {S}_i\) with \(T_i\subseteq J{\setminus }(\cup _{k\ne i} S_k)\). In words, given the items \(S_k\) selected by players other than i, among the remaining items \(J{\setminus }\cup _{k\ne i} S_k\), player i selects a feasible subset of maximum weight. When interpreted as a single-shot strategic form game, to realize this disjointness restriction we can define the payoff of a strategy \(S_i\) equal \(-\infty \) whenever another player’s strategy is \(S_k\) with . While this seems a bit unnatural, our primary interest is to analyze the more natural variant of the game where players select their subsets sequentially. Then, the items selected by previous players are no longer available for subsequent players. We address both problem variants in this paper.

Equilibrium concepts and price of anarchy For the entire paper, we measure the quality of an (equilibrium) solution \(S=(S_1,\dots ,S_n)\) by the total value of all selected items, or equivalently, the sum of values of all selected items \(w(S):=\sum _{i=1}^n w(S_i)\). The question is by how much an equilibrium solution falls behind an optimal solution that could be computed by some central authority, in the worst case. For a maximization problem as the one considered here, the price of anarchy (Papadimitriou 2001; Koutsoupias and Papadimitriou 2009) denotes the ratio of the value of an optimal solution over the value of an equilibrium solution. We analyze the price of anarchy for three different equilibrium concepts, namely pure strategy Nash equilibria, subgame perfect equilibria (Selten 1965) of a sequential version of the game, and a third equilibrium concept that we refer to as k-collusion Nash equilibrium. The idea of the latter is that up to k players may collude and are allowed to use any profit sharing protocol among themselves, hence can be thought of as acting like a single player. This concept also appears in a paper by Hayrapetyan et al. (2006). In fact, k-collusion equilibria are a generalization of k-strong Nash equilibria as defined by Aumann (1959); see also Andelman et al. (2009).

An illustrating example

Example 1

Consider \(n=2\) players and two items \(J=\{1,2\}\), with weights \(w_1=w_2=1\), and the feasible subsets are \(\mathcal {S}_1=\{\emptyset ,\{1\},\{2\}\}\) and \(\mathcal {S}_2=\{\emptyset ,\{2\}\}\). \(\triangleleft \)

In an optimal solution, player 1 chooses the first and player 2 chooses the second item, that is, the strategy profile is \(S=(S_1,S_2)=(\{1\},\{2\})\) with payoffs (1, 1) and \(w(S)=2\). This allocation is a Nash equilibrium. There is another Nash equilibrium, namely \(S=(\{2\},\emptyset )\), because \(\{1\}\not \in \mathcal {S}_2\). As the payoffs are (1, 0) and \(w(S)=1\), this instance has a price of anarchy of 2. The strategic form of this game is depicted in Fig. 1.

Fig. 1
figure 1

Strategic form for Example 1 with Nash equilibria in bold

Full size image

Considering the sequential game where player 1 precedes player 2, this yields a game tree that is depicted in Fig. 2. A strategy for player 2 now specifies three actions, one for every possible choice of player 1. When the order is \(1\rightarrow 2\), all Nash equilibria of the strategic form game are also obtained as subgame perfect equilibria, namely \((\{1\},(\{2\},\emptyset ,\{2\}))\) and \((\{2\},(\{2\},\emptyset ,\{2\}))\), with outcomes \((S_1,S_2)=(\{1\},\{2\})\) and \((\{2\},\emptyset )\), and payoffs (1, 1) and (1, 0), respectively. The worst case subgame perfect equilibrium is indicated in bold in Fig. 2.

For the reverse order of the sequential game (player \(2\rightarrow \) player 1), the only subgame perfect equilibria are \((\{2\},(\{1\},\{1\}))\) and \((\{2\},(\{2\},\{1\}))\), with as unique outcome \((S_1,S_2)=(\{1\},\{2\})\) and corresponding payoff (1, 1). As the sequential price of anarchy takes the worst case over all possible sequential games, Example 1 has sequential price of anarchy of 2.

Fig. 2
figure 2

Game tree for sequential version (player \(1\rightarrow \) player 2) of Example 1. The worst-case subgame perfect equilibrium is marked bold

Full size image

Finally, assume that both players collude, then obviously, the only allocation that maximizes their joint payoff is \((S_1,S_2)=(\{1\},\{2\})\) and corresponding payoff (1, 1). Therefore, the 2-collusion price of anarchy equals 1.

Relation to set packing and maximum coverage problems The set packing problem is one of Karp’s 21 problems first proved to be \(\mathsf {NP}\)-complete (Karp 1972); it is listed as problem [SP3] in Garey and Johnson’s classic on computers and intractability (Garey and Johnson 1979). In set packing, the task is to select from a given collection \(\mathcal {S}\) of subsets of a set of items J, a collection of k disjoint subsets, for a given number k. In the weighted optimization version of the problem each subset \(S\in \mathcal {S}\) has a weight w(S), and the goal is to find disjoint subsets of maximum total weight. The general set packing problem with or without weights is NP-complete (Garey and Johnson 1979), and in general it is not even approximable to within any constant. We refer to Chandra and Halldórsson (2001) and Hazan et al. (2006) for more details. The problem that is considered in this paper corresponds to the much simpler variant of set packing where items \(j\in J\) have weights \(w_j\), and \(w(S):=\sum _{j\in S}w_j\). Due to our assumption that the set system is downward-closed, as an instance of maximum weight set packing this problem is trivial when there is no limit on the number of chosen subsets (e.g., take all singletons in \(\cup _{i=1}^n \mathcal {S}_i\)). However if only a given number of n subsets may be chosen -which is the problem that we consider- the downward closedness yields that the problem is equivalent with the the NP-hard maximum coverage problem. That problem can be approximated to within a factor \(1+ 1/(e-1)\) (Hochbaum 1997), and the same approximation guarantee is recovered in this paper as the sequential price of anarchy for symmetric set packing games.

Throughput scheduling A subclass of set packing games are throughput scheduling games. These games were the subject of an extended abstract underlying this paper (de Jong et al. 2013). Throughput scheduling has been studied from the algorithmic perspective e.g. by Bar-Noy et al. (2001) and Berman and DasGupta (2000). Here, the set of items J corresponds to a set of non-preemptive jobs, each with a release time \(r_j\), a due date \(d_j\), and a weight \(w_j\). There are \(m\ge 1\) machines to process these jobs. In the most general setting, the machines can be unrelated, meaning that the processing time of any job j may depend on the machine \(\ell \) it is processed on, and the \(\ell \times m\) matrix \((p_{\ell j})\) of processing times on machines can have rank \(>1\). A subset \(S_i\) of jobs is feasible for player i if there exists a schedule of the jobs in \(S_i\) on the set of machines of player i, so that each job can be processed in the time window \([r_j,d_j]\). The job sets \(\mathcal {S}_i\) that are feasible for player i is then a downward closed set system. Except one, all lower bounds on the price of anarchy for set packing games are presented as instances of throughput scheduling games.

Approximate equilibria We generally consider \(\alpha \)-approximate versions for all three equilibrium concepts, for any fixed \(\alpha \ge 1\). That means that a strategy profile is considered in \(\alpha \)-approximate equilibrium if the corresponding payoffs per player are maximal up to a multiplicative constant \(\alpha \), given the strategies of the other players. Indeed, the idea of considering approximate instead of exact equilibria is by now a widely accepted concept in algorithmic game theory, with different variations. Already Roughgarden and Tardos (2002) consider it for network routing games, and for example Skopalik and Vöcking (2008) discuss corresponding hardness results in the context of congestion games. Approximate equilibria can be generally motivated in at least two ways: The first is that players may be reluctant to changing strategies for small improvements, and the second is that players may be computationally bounded, and restricted to approximate equilibria by the computational hardness of computing a best response. We come back to this point later. It is important to note that our price of anarchy bounds are tight for all \(\alpha \)-approximate versions of the three equilibria that we consider.

Main contribution Our contribution is as follows. If all players play \(\alpha \)-approximate Nash equilibria, the price of anarchy for set packing games equals \(\alpha +1\). We also show that sequential play, that is the game where players select their sets subsequently, does not allow to improve on that bound in general. However, for the special case of symmetric set packing games (to be defined later), sequential play does yield improved results for the price of anarchy: We show that subgame perfect equilibria yield a price of anarchy of \({\root \alpha \of {e}}/({\root \alpha \of {e}-1})\), which is tight, too. Note that for \(\alpha =1\), this equals \(1+1/(e-1)\). Finally, we analyze k-collusion Nash equilibria, and show that when players are assumed to play \(\alpha \)-approximate k-collusion Nash equilibria, the price of anarchy interpolates between \(\alpha \) and \(\alpha +1\), as it is equal to \(\alpha +(n-k)/(n-1)\).

2 Related work and motivation

Throughput scheduling games have been the subject of the extended abstract (de Jong et al. 2013) underlying this full-length paper. We are not aware that set packing games as defined in this paper have been addressed in the literature. Generally spoken, much of the work in algorithmic game theory addresses auctions, network routing or congestion games, as well as scheduling and load balancing games. Refer e.g. to Section III of the textbook by Nisan et al. (2007) for several of such models.

Covering games There is a set of publications on so-called covering games that are very closely related to our work. When allowing that one item is chosen by more than only one player, the resulting game is a covering game as studied by Garing (2009). In this case, one needs to define a utility sharing function for the items that are chosen by several players. Gairing shows that there exist utility sharing functions such that worst case Nash equilibria are at most a factor \(1+1/(e-1)\) away from the optimum. Covering games can also be interpreted as a generalization of market sharing games as studied e.g. by Goemans et al. (2004). For covering games with uniform utility sharing, the price of anarchy equals \(2-1/n\) for n-player games (Garing 2009; Brethouwer 2018). That result can also be obtained by a smoothness argument, so it extends to more than Nash equilibria (Brethouwer 2018). In that context, note that the price of anarchy bound for set packing games as proved in this paper is 2, which is tight for any number of players \(n\ge 2\). In contrast to covering games, a distinguishing feature of set packing games is the property that items can only be chosen by one player, and as a consequence, rational players affect each other only through the availability of strategies from the strategy set \(\mathcal {S}_i\), but not each other’s payoffs. As a result, there are Nash equilibria of the non-sequential game that cannot be realized as subgame perfect equilibria of a sequential game, and this feature allows us to obtain improved price of anarchy results for subgame perfect equilibria. This is indeed no longer the case when items are uniformly shared: generalized market sharing games have a price of anarchy lower bound of \(2-1/n\) even for subgame perfect equilibria of a sequential game (Brethouwer 2018). Finally, we note that generalizations of covering games have also been addressed recently by Paccagnan and Marden (2018); Paccagnan et al. (2018).

Sequential price of anarchy The analysis of subgame perfect equilibria as opposed to Nash equilibria is one of the main contributions of this paper, and it is maybe also the most interesting result from an applications point of view. At the time of writing the conference publication underlying this full-length paper (de Jong et al. 2013), the idea of considering sequential versions of games, and Selten’s subgame perfect equilibria as an alternative to avoid the “curse of simultaneity” of Nash equilibria had just been brought up by Paes Leme et al. (2012). In contrast to the price of anarchy which relates the outcome of the worst possible Nash equilibrium to that of an optimal solution (Papadimitriou 2001; Koutsoupias and Papadimitriou 2009), the sequential price of anarchy Paes Leme et al. (2012) relates the outcome of the worst possible subgame perfect equilibrium of all sequential versions of the game where players act subsequently (and farsighted), to the outcome of an optimal solution. For set packing games, it is not hard to see that any outcome of a subgame perfect equilibrium of a sequential version of the game is also a Nash equilibrium in the non-sequential, strategic form of the game, but not necessarily vice versa; see also Theorem 6. It should be noted that subgame perfect equilibria of a sequential game are not generally Nash equilibria of the corresponding non-sequential game: Correa et al. (2015) give an instance of a network routing problem where the sequential price of anarchy is unbounded, while the price of anarchy is known to be 5/2 (Awerbuch et al. 2005; Christodoulou and Koutsoupias 2005). Indeed, subsequent to the work by Paes Leme et al. (2012), for a handful of problems it was shown that the sequential price of anarchy is lower than the price of anarchy (Paes Leme et al. 2012; de Jong et al. 2013; de Jong and Uetz 2014; Hassin and Yovel 2014), while for others this is exactly opposite (Angelucci et al. 2015; Bilò et al. 2015; Correa et al. 2015). To conclude, it should be noted that also earlier than (Paes Leme et al. 2012), sequential versions of (routing) games have been considered, however with different utility sharing functions. This includes Olver (2006), Harks et al. (2009), Harks and Vegh (2007), as well as Farzad et al. (2008).

Approximate equilibria and hardness of optimal play The necessity to also consider \(\alpha \)-approximate equilibrium concepts is best motivated by considering some concrete examples of throughput scheduling. For example, consider the special case where the feasibility system of a player i consists of all sets of jobs \(j\in J\) that can be feasibly scheduled on a single machine. In the 3-field notation of Graham et al. (1979), this problem reads \(1 |r_j|\sum w_jU_j\), where “1” stands for one single machine, \(r_j\) specifies that there are release dates, and the objective \(\sum w_jU_j\) is to maximize the total weight of jobs scheduled before their due date \(d_j\). In that case, the input of the problem would not be a list of all feasible sets \(\mathcal {S}_i\), but only the set of jobs \(j\in J\) with their time windows \([r_j,d_j]\), processing times \(p_j\) and values \(w_j\). It follows from Lenstra et al. (1977) that the problem to compute a subset of jobs maximizing the total weight is NP-hard, hence players cannot generally be assumed to be able to compute a strategy to optimize their payoff. More generally, if players control a set of several (unrelated) machines each, the problem to compute a best response reads \(R |r_j|\sum w_jU_j\) in scheduling notation, where “R” stands for unrelated machines. This problem is equivalent to the throughput scheduling problem as it has been addressed e.g. by Bar-Noy et al. (2001), and subsequently by Berman and DasGupta (2000). For this problem, only constant factor approximation algorithms are available, and this constant is essentially 2; see Berman and DasGupta (2000). Hence, assuming that players are equipped with such approximation algorithms, the outcome of such a game would be an \(\alpha \)-approximate equilibrium with \(\alpha =2\). On the other hand, there are relevant special cases of throughput scheduling where players can be assumed to be able to play optimally. One such case is when feasibility sets \(\mathcal {S}_i\) are the sets of jobs that can be feasibly scheduled on a single machine, and jobs have unit weights and zero release dates. This single-machine problem is solved in polynomial time by the Moore-Hodgson algorithm (Moore 1968). Another case is when the feasibility system \(\mathcal {S}_i\) is the set of jobs with unit processing times that can be scheduled on a set of identical, parallel machines. This problem can be solved as an assignment problem (Brucker 2004). In light of this discussion, recall that all our results are parametric in the parameter \(\alpha \).

Motivation On the one hand, we believe that the game theoretic version of a classical combinatorial problem such as set packing is interesting in its own right. On the other hand, the original driver of this research was to understand the potential loss of efficiency when the procurement of indivisible services is not controlled centrally. Here, think of the following service procurement setting: Each item corresponds to a service request –such as a computational task or a physical service—with a monetary value that pays off once the service is executed. Given a collection of such service requests, e.g. on an internet portal or within a larger corporation consisting of several profit centers, players are service providers who can choose a subset of services in order to generate revenue. Service providers, however, are bound by limited resources and can therefore only choose certain subsets of services. Specifically, when these services are specified by a release time, processing time, and a due date, this gives rise to a throughput scheduling problem.

Sketch of applications We give three instances of application domains that lead to instances of set packing games. (1) When operating microgrids for decentralized energy production, the goal is to consume locally produced energy as much as possible. Here, the items are the operation of appliances in households (e.g. loading a car battery) which come with a time window and a certain monetary value. Players, on the other side, are intermediaries or local energy producers that want to maximize the total value of items than can be accommodated within a given a profile of available energy; see, e.g. Bakker et al. (2010) or Molderink et al. (2010) for more context. (2) In cloud computing, service providers such as Google or Amazon provide an infrastructure service. Here, the items are computational tasks that need to be distributed over data- and computing centers. Indeed, the aim of a federated cloud computing environment, as discussed e.g. in Buyya et al. (2010), is to “coordinate load distribution among different cloud-based data centers in order to determine optimal location for hosting application services”. Understanding the cost of uncoordinated load distribution is the question that we ask. (3) A final application domain is distribution logistics in a B-to-B context, like reverse auctions. Specifically, consider private car sharing portals like e.g. http://www.snappcar.de (2017), where items correspond to car rental requests for a certain time period and a predefined price. Owners of cars or car farms are players that select subsets of such requests from the portal to rent out their car(s) in order to maximize the total revenue.

While it is true that each of these applications has additional features or practical constraints that are not taken care of in the set packing games that we address here, the paper aims to identify the combinatorial flavour that lies at the heart of such problems. The overall conclusion is that the loss of efficiency caused by the lack of central coordination is moderate.

3 Preliminaries

We here fix some notation and the basic definitions. There are n players, and a finite ground set J of items. Each item \(j\in J\) has a value \(w_j\). For \(S\subseteq J\), we let \(w(S):=\sum _{j\in S}w_j\). Each player i has a strategy set \(\mathcal {S}_i\subseteq 2^J\) which is downward closed, i.e., if \(S_i\in \mathcal {S}_i\), then \(T_i\in \mathcal {S}_i\) for all \(T_i\subseteq S_i\). Given a strategy profile \(S=(S_1,\dots ,S_n)\), as usual define \(S_{-i}:=(S_1,\dots ,S_{i-1},S_{i+1},\dots ,S_n)\) as the strategies of all players except i, and for any set of players \(K\subseteq \{1,\dots ,n\}\), define \(S_{-K}\) accordingly.

When \((S_1,\dots ,S_n)\) is a strategy profile with \(S_i\in \mathcal {S}_i\) for all \(i=1,\dots ,n\), the payoffs for player i are defined as

$$\begin{aligned} w_i(S_i,S_{-i})= {\left\{ \begin{array}{ll} w(S_i) &{} \text {if } S_i\cap S_k=\emptyset \text { for all } k\ne i\,,\\ -\infty &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

A strategy profile \((S_1,\dots ,S_n)\) is an \(\alpha \)-approximate Nash equilibrium (for \(\alpha \ge 1\)) if it is true that for all players \(i=1,\dots ,n\)

$$\begin{aligned} w_i(S_i,S_{-i})\ge \frac{1}{\alpha }w_i(T_i,S_{-i})\quad \text {for all}\quad T_i\in \mathcal {S}_i\,. \end{aligned}$$
(1)

Note that the existence of Nash equilibria with \(w_i(S_i,S_{-i})\ge 0\) for all players i is guaranteed by the fact that the feasibility systems \(\mathcal {S}_i\) are downward closed.

For a solution \(S=(S_1,\dots ,S_n)\), in a slight but convenient abuse of notationFootnote 1 let us write \(w(S):=\sum _{i=1}^nw(S_i)\) for the total value that it achieves. The price of anarchy PoA (Papadimitriou 2001; Koutsoupias and Papadimitriou 2009) for a class of games \(\mathcal {I}\) is then the ratio

$$\begin{aligned} (\alpha \text {-approximate) PoA}=\sup _{I\in \mathcal {I}}\sup _{S\in \textit{NE}(I)}{\frac{w(\textit{OPT}(I))}{w(S)}}, \end{aligned}$$
(2)

where \(\textit{NE}(I)\) denotes the set of all \(\alpha \)-approximate Nash equilibria of instance \(I\in \mathcal {I}\), and \(\textit{OPT}(I)\) is an optimal allocation for I. Note that for set packing games, \(\textit{OPT}(I)\) is a Nash equilibrium too, hence the price of stability as proposed by Anshelevich et al. (2004) equals 1.

Next, consider the extensive form game that is obtained when imposing some order, say \(1,\dots , n\) on the players. A strategy for player i is then more complex, as it must specify one action \(S_i\) for all possible combinations of actions of preceding players \(1,\dots ,i-1\), that is, one action \(S_i\) for each node of the game tree on level i. An \(\alpha \)-approximate subgame perfect equilibrium is then a strategy that guarantees at least a \(1/\alpha \)-fraction of the optimal action for each of the nodes of the game tree on level i. As we deal with a full information game, (\(\alpha \)-approximate) subgame perfect equilibria can be computed via backward inductionFootnote 2. A nice feature of set packing games is that the computation of (\(\alpha \)-approximate) subgame perfect equilibria is not suffering from the typical hardness results for sequential games that is due to farsighted behaviour of players: Indeed, computing outcomes of subgame perfect equilibria may be PSPACE-hard with n players (Paes Leme et al. 2012), and NP-hard even with two players only (Correa et al. 2015). For set packing games, an optimal action for the i-th player, upon observing the actions \(S_1\), ..., \(S_{i-1}\) of the preceding players, is computed by solving the optimization problem

$$\begin{aligned} \max _{T\subseteq J} w(T)\text { s.t. } T\subseteq J{\setminus }\cup _{k=1}^{i-1}S_k\text { and } T\in \mathcal {S}_i\,, \end{aligned}$$

This suffices, as by the specific payoff structure of set packing games, the value attained by player i is no longer affected by payers \(i+1\),..., n, as long as they are all rational. This problem is computationally hard only if the combinatorial structure encoded by \(\mathcal {S}_i\) is hard; see the discussion in Sect. 2.

The price of anarchy for \(\alpha \)-approximate subgame perfect equilibria, also called sequential PoA (Paes Leme et al. 2012), is then defined analogously to the price of anarchy in (2),

$$\begin{aligned} (\alpha \text {-approximate) sequential PoA}=\sup _{I\in \mathcal {I}}\sup _{S\in \textit{SPE}(I)}{\frac{w(\textit{OPT}(I))}{w(S)}}, \end{aligned}$$
(3)

where the first supremum \(\sup _{I\in \mathcal {I}}\) is also taken over all possible orders of players, and \(\textit{SPE}(I)\) denotes all outcomes that can be obtained as \(\alpha \)-approximate subgame perfect equilibria of instance I.

Finally, assume that up to k of the given n players may collude, and are allowed to use any profit-sharing rule among them. In other words, we can think of a group K of up to k players as maximizing their joint value \(w(\cup _{i\in K}S_i)\). Then, \(w_K(S_K,S_{-K}):=\sum _{i\in K}w_i(S_i,S_{-i})\) is the joint value achieved by players in K, and an \(\alpha \)-approximate k-collusion Nash equilibrium is a strategy profile \((S_1,\dots ,S_n)\) such that the following is true for all sets K of at most k players,

$$\begin{aligned} w_K(S_K,S_{-K})\ge \frac{1}{\alpha }w_K(T,S_{-K})\quad \text {for all}\quad T=\cup _{i\in K}T_i\text { and } T_i\in \mathcal {S}_i\,. \end{aligned}$$
(4)

Obviously, the price of anarchy for \(\alpha \)-approximate k-collusion Nash equilibria is then again defined analogously to the price of anarchy in (2) by

$$\begin{aligned} (\alpha \text {-approximate})\, k\text {-collusion PoA}=\sup _{I\in \mathcal {I}}\sup _{S\in \textit{CE}_k(I)}{\frac{w(\textit{OPT}(I))}{w(S)}}\,, \end{aligned}$$
(5)

where \(\textit{CE}_k(I)\) denotes the set of \(\alpha \)-approximate k-collusion Nash equilibria of instance I.

Symmetric set packing We call a set packing game symmetric whenever there is only one feasibility system \(\mathcal {S}\) that is the same for all players i, and a player i can select \(x_i\ge 1\) feasible sets from \(\mathcal {S}\), for some integer \(x_i\ge 1\). Note that when all \(x_i=1\), this exactly means that the strategic form game is symmetric in the sense that all players have exactly the same strategy set. However we here choose a slightly more general definition of symmetry, in that we allow players to select multiple feasible sets. In the throughput scheduling context, that also captures a setting where each player controls a subset of a set of identical machines. We define \(x:=\sum _{i=1}^nx_i\) to be the total number of feasible sets from \(\mathcal {S}\) that can be chosen by all players together, and note that \(x\ge n\).

4 The price of anarchy for nash equilibria

We begin by giving the simple proof for the upper bound on the price of anarchy for arbitrary set packing games, assuming that the outcome is an \(\alpha \)-approximate Nash equilibrium.

Theorem 1

The \(\alpha \)-approximate price of anarchy equals \(\alpha +1\) for set packing games.

Proof

We first give the proof for the upper bound. Take any instance with optimal solution OPT and Nash equilibrium S, and let \(S_i\) and \({\textit{OPT}}_i\), \(i=1,\dots ,n\), be the items selected by player i in S and OPT, respectively. For \(W\subseteq J\), let \(\overline{W}=J{\setminus }W\) be the complement of W in J.

Since all items in \(\overline{S}\) are available, and all items in \({\textit{OPT}}_i\) are feasible for player i, and all \(\mathcal {S}_i\) are downward closed, by the definition of \(\alpha \)-approximate Nash equilibrium we have for all players i that \(\alpha w(S_i)\ge w(\textit{OPT}_i\cap \overline{S})\). Now we get, by the fact that \(S_i\cap S_k=\emptyset \) and \(\textit{OPT}_i\cap \textit{OPT}_k=\emptyset \) for any \(i\ne k\),

$$\begin{aligned} (\alpha +1) w(S)\ge & {} \alpha w(S)+w(\textit{OPT}\cap S) \\= & {} \sum \nolimits _{i=1}^n \alpha w(S_i)+ w(\textit{OPT}\cap S)\\\ge & {} \sum \nolimits _{i=1}^n w(\textit{OPT}_i \cap \overline{S})+ w(\textit{OPT}\cap S)\\= & {} w(\textit{OPT})\,. \end{aligned}$$

For a matching lower bound, see the proof of the next theorem. \(\square \)

We next give a matching lower bound example, which is an instance for throughput scheduling (and an asymmetric set packing game).

Example 2

Assume that \(\alpha ={p}/{q}\), where \(p\ge q\). When \(\alpha \) is not rational, note that we can approximate \(\alpha \) arbitrarily well by appropriate p and q. Consider a game with \(q+1\) players. For each player i, there is one machine, which we also denote by i. The set J of items are jobs that are partitioned into two sets P and Q, with \(|P|=p,|Q|=q\). Each job \(j\in J\) has deadline \(d_j=1\), unit weight \(w_j=1\), and its processing time on machine 1 is \(p_{j1}=1/p\). Moreover, jobs \(j\in Q\) have processing time \(p_{ji}=1\) on any other machine \(i\ne 1\), while jobs \(j\in P\) have processing time \(p_{ji}=2\) on any other machine \(i\ne 1\). Note that any subset of jobs of size p can be feasibly allocated to player 1. Players \(2\dots n\) can be allocated only one job each, and only jobs from Q. See Fig. 3 for an illustration in the case where \(\alpha =3/2\). \(\triangleleft \)

Fig. 3
figure 3

Example 2 for \(p=3\) and \(q=2\). Numbers represent machines. Rectangles represent jobs. The left side of each job is its starting time, its width is its processing time on the machine on which it is allocated. The dashed line is the deadline, which is the same for all jobs in this example

Full size image

Theorem 2

The \(\alpha \)-approximate price of anarchy equals \(\alpha +1\) for throughput scheduling games.

Proof

\(PoA \le \alpha +1\) follows from Theorem 1, since throughput scheduling games give rise to downward closed feasibility sets per player. To see that \(PoA \ge \alpha +1\), consider the instance of Example 2. In the optimum solution \(\textit{OPT}\), all \(p+q\) jobs are feasibly allocated: All jobs in P are allocated to player 1, and each of the jobs in Q is allocated to one of the q other players \(2,\dots , q+1\). Now consider the \(\alpha \)-approximate Nash equilibrium S where only q jobs are allocated: All jobs from Q are allocated to player 1, and no jobs are allocated to players \(2, \dots , q+1\). This is indeed an \(\alpha \)-approximate Nash equilibrium, as player 1 achieves a total value of q, while maximally that player can be allocated \(p=\alpha q\) jobs. In other words, the \(\alpha \)-approximate Nash condition (1) holds for player 1. Moreover, given that all jobs from Q are allocated to player 1, players \(2, \dots , q+1\) cannot do better than a value 0, as none of the jobs from P are feasible for these players. We conclude that \(PoA \ge w(\textit{OPT})/w(S)= (p+q)/q=\alpha +1\).    \(\square \)

Note that the upper bound is universal in the sense that it is independent of how the (\(\alpha \)-approximate) Nash equilibrium is obtained. It is conceivable that specific algorithms can yield a better bound for the price of anarchy. However, the existence of more complicated counter-examples for specific algorithms is not unlikely either; see the next Section 5 for an example.

4.1 Symmetric set packing games

The price of anarchy of set packing games does not improve if the game is symmetric.

Theorem 3

The \(\alpha \)-approximate price of anarchy equals \(\alpha +1\) for symmetric set packing games.

The upper bound \(\alpha +1\) is a consequence of Theorem 1. The lower bound follows from the following theorem for throughput scheduling games, based on Example 3 below, which is an instance of a symmetric set packing game.

Example 3

Let \(\alpha =p/q\). There are n players i, each corresponding to one machine. The set J of \(p+(q+1)(n-1)\) jobs is again partitioned into two sets P, Q, \(|Q|=q(n-1)+p, |P|=(n-1)\). All jobs \(j\in J\) have deadline \(d_r=1\). Jobs \(j\in Q\) have processing times \(p_j=1/(q(n-1)+p)\) and weight \(w_j=1\), while jobs \(j\in P\) have processing times \(p_j=1\) and weight \(w_j=p\). See Fig. 4 for an illustration for the case where \(p=3,q=2\) and \(n=3\). \(\triangleleft \)

Fig. 4
figure 4

Example 3 for \(p=3,q=2,n=3\). Numbers represent machines. Rectangles represent jobs. The left side of each job is its starting time, its width is its processing time. The dashed line is the deadline, which is the same for all jobs in this example

Full size image

Theorem 4

The \(\alpha \)-approximate price of anarchy equals \(\alpha +1\) for symmetric throughput scheduling games.

Proof

We are only left to show \(PoA \ge \alpha +1\). Consider Example 3. In the optimum solution \(\textit{OPT}\), player 1 is allocated all jobs \(j\in Q\), and each remaining player is allocated exactly one job in P. Consider Nash equilibrium S where each player is allocated q jobs in Q. Note that S is indeed an \(\alpha \)-approximate Nash equilibrium: Any player i could choose at most one job from P or at most p jobs from Q, since other players are allocated \(q(n-1)\) jobs from Q in total. Neither of the feasible deviations increases player i’s utility by more than a factor \(\alpha \). For this example, \(w(\textit{OPT})/w(S)=\frac{pn+q(n-1)}{qn}=\frac{p+q}{q}-\frac{1}{n}\rightarrow 1+\alpha \) for \(n\rightarrow \infty \). \(\square \)

However this Nash equilibrium is generally not subgame perfect when considering the corresponding sequential game. This observation is exploited in the following.

5 The sequential price of anarchy

In this section we aim to show that substantial improvements for the price of anarchy are possible when considering sequential games and subgame perfect equilibria. This improvement is interesting, we believe, because in almost all applications that we can think of, it is the sequential version of the game which is practically relevant. To start with, however, we observe that in general, Example 2 also provides a lower bound for the quality of subgame perfect equilibria, and we get the following.

Theorem 5

The \(\alpha \)-approximate sequential price of anarchy equals \(\alpha +1\) for set packing games and throughput scheduling games.

Proof

Let us first argue that the sequential \(PoA \ge \alpha +1\). Recall Example 2, and assume that player 1 is the first to make a selection. Then if player 1 makes the same selection of job set Q as in the proof of Theorem 2, the obtained solution can indeed be obtained as an \(\alpha \)-approximate subgame perfect equilibrium, as player 1 cannot improve by more than a factor \(\alpha \) by selecting other jobs, and given that, all other players have nothing to choose. (We can specify any reasonable actions for those parts of the game tree that are not played in this equilibrium.) By the same argument as before, the lower bound on the price of anarchy follows. To see that the upper bound on the sequential PoA also holds, the next theorem shows that any subgame perfect equilibrium of the sequential game is a Nash equilibrium of the corresponding non-sequential game, hence Theorem 1 carries over. \(\square \)

Theorem 6

For set packing games and any \(\alpha \ge 1\), the actions played in an \(\alpha \)-approximate subgame perfect equilibrium of any sequential version of the set packing game, are an \(\alpha \)-approximate Nash equilibrium in the corresponding non-sequential strategic form game.

Proof

Consider the actions \(S=(S_1,\dots ,S_n)\) played in any subgame perfect equilibrium \(\textit{SPE}\) of any sequential version of the set packing game. Assume w.l.o.g. the order was \(1, \dots , n\). Consider any player i choosing \(S_i\). We need to show that the Nash condition holds, which is \(\alpha w(S_i) \ge w(T_i)\) for all \(T_i\in \mathcal {S}_i\) with \(T_i\subseteq J{\setminus }\cup _{k\ne i}S_k\). But as the choice \(S_i\) is part of a subgame perfect strategy, we even know that \(\alpha w(S_i) \ge w(T_i)\) for all \(T_i\in \mathcal {S}_i\) with \(T_i\subseteq J{\setminus }\cup _{k=1}^{i-1}S_k\). This inequality must be true because i’s choice is \(\alpha \)-approximately optimal, and since in a subgame perfect equilibrium, i’s payoff is not affected by rational subsequent players \(k>i\), for any\(T_i\) that player i might choose. Hence S a Nash equilibrium in the non-sequential game. \(\square \)

It is not generally true that subgame perfect equilibria of a sequential game are Nash equilibria of the corresponding non-sequential game. See, e.g., Correa et al. (2015) for an example.

5.1 Symmetric set packing games

When considering symmetric set packing games, sequential play and subgame perfection rule out worst-case Nash equilibria. Assuming the outcome of such a game is an \(\alpha \)-approximate subgame perfect equilibrium, the main result of this section is:

Theorem 7

The \(\alpha \)-approximate sequential price of anarchy equals \({\root \alpha \of {e}}/({\root \alpha \of {e}-1})\) for symmetric set packing games.

We prove the theorem in several steps. First we derive the lower bound, which is again obtained by considering a throughput scheduling instance.

Example 4

There are n players. Each player i corresponds to one machine. The set J of \(n^2\) jobs is partitioned into n sets \(J_1,\dots ,J_n\), \(|J_k|=n\) for all \(k\in [n]\). We refer to a job from \(J_k\) as a k-job. All k-jobs have deadline k. All jobs \(j\in J\) have processing time \(p_j=1\) and weight \(w_j=1\). See Figure 5 for an illustration for the case where \(n=5\) and \(\alpha =1\). \(\triangleleft \)

Lemma 1

The \(\alpha \)-approximate sequential \(\text {PoA }\ge {\root \alpha \of {e}}/({\root \alpha \of {e}-1})\) for symmetric set packing games.

Fig. 5
figure 5

Example 4 in case of 5 players and \(\alpha =1\). Numbers represent machines. Rectangles represent jobs. The left side of each job is its starting time, its width is its processing time. The number in each job is its deadline

Full size image

Proof

In the optimum solution \(\textit{OPT}\), every player is allocated exactly one k-job for all \(k=1,\dots ,n\). Therefore \(w(\textit{OPT})=n^2\).

We construct an \(\alpha \)-approximate subgame perfect outcome S, as follows: For every player \(i=1,\dots ,n\) in this order, we find the maximum number of jobs that can be feasibly allocated to this player, given jobs already assigned to players \(1,\dots ,i-1\), and when considering jobs with the largest deadlines first (which are the most flexible jobs). Denote this number of jobs \(m_i\). We allocate to player i exactly \(\lceil {m_i}/{\alpha }\rceil \) of these jobs, so that the allocation is still an \(\alpha \)-approximation. Let \(S_i\) be the jobs allocated to player i in this way.

We bound w(S) in the following way: Let \(r_k(i)=\frac{|S_i\cap J_{k}|}{|S_i|}\), i.e. \(r_k(i)\) is the fraction of k-jobs allocated to player i, relative to the total number of jobs allocated to player i. Let \(r_k=\sum _{i=1}^n r_k(i)\). Now,

$$\begin{aligned} \sum _{k=1}^n r_k=\sum _{k=1}^n \sum _{i=1}^n r_k(i)=\sum _{i=1}^n \sum _{k=1}^n \frac{|S_i\cap J_k|}{|S_i|}=\sum _{i=1}^n1=n\,. \end{aligned}$$
(6)

In S, any player i who gets allocated a k-job, is not allocated any job from \(J_{j},j\ge k+2\), hence she is allocated at most \(\lceil {(k+1)}/{\alpha }\rceil \le {(k+1+\alpha )}/{\alpha }\) jobs. Therefore, each k-job contributes at least \({\alpha }/{(k+1+\alpha )}\) to \(r_k\). For any k for which all of the \(n\, k\)-jobs are allocated in S, we obtain

$$\begin{aligned} r_k \ge {n\alpha }/{(k+1+\alpha )}\,. \end{aligned}$$
(7)

Now, for some \(k'\ge 0\), by construction of the allocation we have that for all \(k\ge n-k'\), all nk-jobs are allocated, as well as a subset of the \((n-(k'+1))\)-jobs. We obtain

$$\begin{aligned} n\ge \sum _{k=n-k'}^{n} r_k \ge \sum _{k=n-k'}^{n} \frac{n\alpha }{k+1+\alpha } \ge \int _{k=n-k'}^{n}\frac{n\alpha }{k+1+\alpha }dk\,\,, \end{aligned}$$
(8)

where the first inequality follows from (6), the second inequality follows from (7), and the last inequality follows from basic calculus.

Because the last term is upper bounded by n, we can derive an upper bound on \(k'\). In fact, basic calculus shows that

$$\begin{aligned} k'>\frac{(n+1+\alpha )(\root \alpha \of {e}-1)}{\root \alpha \of {e}}\ \Rightarrow \ \int _{k=n-k'}^{n}\frac{n\alpha }{k+1+\alpha }dk > n\,, \end{aligned}$$

which together with (8) yields that \(k'\le \frac{(n+1+\alpha )(\root \alpha \of {e}-1)}{\root \alpha \of {e}}\). Because only k-jobs with \(k\ge n-(k'+1)\) are allocated, we conclude that

$$\begin{aligned} w(S)\le (k' +1)n\le \frac{\left( n+1+\alpha +\frac{\root \alpha \of {e}}{\root \alpha \of {e}-1}\right) \left( \root \alpha \of {e}-1\right) }{\root \alpha \of {e}}\cdot n\,. \end{aligned}$$

We see that

$$\begin{aligned} \frac{w(\textit{OPT})}{w(S)} \ge \frac{n\root \alpha \of {e}}{\left( n+1+\alpha +\frac{\root \alpha \of {e}}{\root \alpha \of {e}-1}\right) \left( \root \alpha \of {e}-1\right) } \rightarrow \frac{\root \alpha \of {e}}{\root \alpha \of {e}-1}\quad \text {for }\ n\rightarrow \infty \,, \end{aligned}$$

and the claim follows. \(\square \)

Note that the lower bound construction assumes that players choose the most flexible jobs first, which is reasonable from a practical point of view. Also note that in the lower bound example, \(x_i=1\) for all players. Therefore, the lower bound holds even in the special case when the strategic form game is a symmetric game.

To derive a matching upper bound on the sequential price of anarchy for symmetric set packing games, we generalize some of the proof ideas from Bar-Noy et al. (2001) in their analysis of the k-GREEDY algorithm for throughput scheduling. We here generalize the proof to the case where players may control more than one machine, or in our case, more that one feasible set. Algorithmically, that means that in one iteration of the greedy algorithm not only one but several sets from the feasibility system get chosen. Stripping off the technical details, one of the core ingredients of the proof below is the fact that the next player may greedily choose her feasible subset(s), and this choice approximates the optimal solution for the set of currently available items. That optimal value is in turn at least as large as the optimal solution restricted to the set of currently available items. This is expressed in inequality (9) below. Indeed, this is a generic approach when analyzing greedy algorithms for subset selection problems, and the same idea also appears in the analysis of the greedy algorithm for maximum coverage problems; see (Hochbaum 1997, Lemma 3.13). We want to prove:

Lemma 2

The \(\alpha \)-approximate sequential \(\text {PoA }\le {\root \alpha \of {e}}/({\root \alpha \of {e}-1})\) for symmetric set packing games.

Denote by \(S_i\) the items selected by player i in an \(\alpha \)-approximate subgame perfect equilibrium, and recall that S denotes both the strategy vector and \(S=\cup _{i=1}^n S_i\), the total set of selected items. The following lemma lower bounds the total weight collected by player i.

Lemma 3

We have for all players i

$$\begin{aligned} w(S_i)\ge \frac{x_i}{x\alpha } w\left( \textit{OPT}\left( J{\setminus }\cup _{j<i}S_j\right) \right) \,. \end{aligned}$$

where \(\textit{OPT}(W)\) denotes an optimal solution for a fixed subset of items \(W\subseteq J\).

Proof

Let \(W:=J{\setminus }\cup _{j<i}S_j\). Let \(\textit{OPT}^i\) denote the maximum weight set of items that player i can achieve from W. Observe that \(w(\textit{OPT}^i)\ge (x_i/x) w(\textit{OPT}(W))\). This follows because player i could potentially select the \(x_i\) most valuable feasible sets from \(\textit{OPT}(W)\). Now, because we assume an \(\alpha \)-approximate subgame perfect equilibrium, \(w(S_i)\ge {w(\textit{OPT}^i)}/{\alpha }\ge {x_i w(\textit{OPT}(W))}/{(x\alpha )}\). \(\square \)

Proof of Lemma 2

Let \(\gamma :=x\alpha \), and recall that \(w(\textit{OPT})=w(\textit{OPT}(J))\) denotes the value of an optimal solution. We use Lemma 3, to get

$$\begin{aligned} w(S_i) \ge \frac{x_i}{\gamma }w\left( \textit{OPT}\left( J{\setminus }\cup _{j<i}S_j\right) \right) \ge \frac{x_i}{\gamma }\left( w(\textit{OPT}) - \sum \nolimits _{j<i}w(S_j)\right) \,. \end{aligned}$$
(9)

Here the last inequality is crucial and it holds because \(w(\textit{OPT}) - \sum \nolimits _{j<i}w(S_j)\) represents the value of some feasible solution for the items \(J{\setminus }\cup _{j<i}S_j\). Now add \(\sum _{j=1}^{i-1}w(S_j)\) to both sides to get

$$\begin{aligned} \sum _{j=1}^{i}w(S_j)\ge \frac{x_i w(\textit{OPT})}{\gamma }+\frac{\gamma -x_i}{\gamma }\sum _{j=1}^{i-1}w(S_j)\,. \end{aligned}$$
(10)

We now follow the proof of Theorem 3.3 in Bar-Noy et al. (2001), and aim to prove that

$$\begin{aligned} \sum _{j=1}^{i}w(S_j)\ge \frac{\gamma ^{x'_i}-(\gamma -1)^{x'_i}}{\gamma ^{x'_i}}w(\textit{OPT})\,, \end{aligned}$$
(11)

where \(x'_i=\sum _{j=1}^i x_j\). This part of the proof is done by mathematical induction on the player index i. In contrast to Bar-Noy et al. (2001), this is technically more involved here. The proof of inequality (11) is by double induction and given in Appendix A. Now we get for \(i=n\) (cp. to the proof of Thm. 3.3 in Bar-Noy et al. (2001))

$$\begin{aligned} w(S)=\sum _{j=1}^nw(S_j)\ge \frac{\gamma ^{x}-(\gamma -1)^{x}}{\gamma ^{x}}w(\textit{OPT})\,. \end{aligned}$$

We conclude that the

$$\begin{aligned} \text {sequential PoA} \le \frac{\gamma ^x}{\gamma ^x-(\gamma -1)^x} = \frac{(x\alpha )^x}{(x\alpha )^x-(x\alpha -1)^x}\le \frac{\root \alpha \of {e}}{\root \alpha \of {e}-1}\,, \end{aligned}$$

where the last inequality follows because the right hand side is exactly the limit for \(x\rightarrow \infty \), and the series \(b_x={(x\alpha )^x}/({(x\alpha )^x-(x\alpha -1)^x})\) is monotone in x, with \(b_1=\alpha \le {\root \alpha \of {e}}/({\root \alpha \of {e}-1})\). This ends the proof of Lemma 2. \(\square \)

Basic calculus shows that

$$\begin{aligned} \alpha +\frac{1}{2}\le \frac{\root \alpha \of {e}}{\root \alpha \of {e}-1} \le \alpha +\frac{1}{e-1} \end{aligned}$$

for \(\alpha \ge 1\). Hence the improvement over the (pure Nash equilibrium) price of anarchy of \(\alpha +1\) is substantial, but only for small values of \(\alpha \). We explicitly mention the special case where \(\alpha =1\).

Corollary 1

The sequential price of anarchy for symmetric set packing games equals \(1+{{1}}/({{e}-1})\approx 1.58\).

6 The k-collusion price of anarchy

While sequential play is a way to reduce the price of anarchy for symmetric set packing games, we now show that collusion of players helps to reduce the price of anarchy, too. This is true also for general, asymmetric set packing games. Recall that an \(\alpha \)-approximate k-collusion Nash equilibrium means that no coalition K of up to k players can improve their total value \(w(S_K)\) by more than a factor \(\alpha \). The following theorem generalizes Theorem 1 to the case where collusion is possible.

Theorem 8

The \(\alpha \)-approximate k-collusion price of anarchy equals \(\alpha +\frac{n-k}{n-1}\) for set packing games.

Note that for \(k=n\), we consider an \(\alpha \)-approximate (centralized) solution, and for \(\alpha =1\), this is an optimal solution. First we give a proof for the upper bound.

Lemma 4

The \(\alpha \)-approximate k-collusion \(PoA \le \alpha +\frac{n-k}{n-1}\) for set packing games.

Proof

The proof mimics our earlier proof of Theorem 1, only here we have to keep track of the values of more subsets of J. We fix an optimal solution \(\textit{OPT}\) and a k-collusion Nash equilibrium S, write \(N=\{1,\dots ,n\}\), and use the following shorthand notation:

$$\begin{aligned} x_{ij}={\left\{ \begin{array}{ll} \text { the total weight of items in }\textit{OPT}_i\cap S_j &{} \text {for }i,j\in N\,, \\ \text { the total weight of items in }S_j{\setminus }\textit{OPT}&{} \text {for }i=0,j\in N\,, \\ \text { the total weight of items in }\textit{OPT}_i{\setminus }S &{} \text {for }i\in N,j=0\,. \end{array}\right. } \end{aligned}$$

Our proof is based on the following observation: players from any coalition K collude and collectively deviate if and only if the total weight of items allocated to them increases by more than a factor \(\alpha \ge 1\), by choosing any set of items in \((\cup _{i\in K}S_i)\cup (J{\setminus }\cup _{i\not \in K}S_i)\). Therefore, in particular for all coalitions K of size k in any \(\alpha \)-approximate k-collusion Nash equilibrium, we have by (4) that

$$\begin{aligned} \alpha \left( \sum _{j\in K}\left( \sum _{i\in N} x_{ij}+ x_{0j}\right) \right) \ge \sum _{i\in K} \left( \sum _{j\in K}x_{ij} + x_{i0}\right) \,. \end{aligned}$$

Note that all items that contribute to the left-hand side are allocated to players in K in the equilibrium S. Also note that all items that contribute to the right-hand side can be feasibly allocated to players in K, since these items are allocated to players from K in \(\textit{OPT}\). Also, these items are available for coalition K, since they are either allocated to players in K in S, or not allocated. We rewrite this as

$$\begin{aligned} \alpha \left( \sum _{j\in K}\left( \sum _{i\in N} x_{ij}+ x_{0j}\right) \right) \ge \mathop {\sum _{i\in K}\sum _{j\in K}}_{i\ne j}x_{ij} + \sum _{i\in K}\left( x_{ii} + x_{i0}\right) \,. \end{aligned}$$
(12)

Now, any player i is in \({\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) }\) coalitions of size k, and any combination of two players i, j is in \(\left( {\begin{array}{c}n-2\\ k-2\end{array}}\right) \) coalitions of size k. Therefore, summing (12) over all coalitions K of size k yields

$$\begin{aligned}&\alpha \left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) \left( \sum _{j\in N}\left( \sum _{i\in N} x_{ij}+ x_{0j}\right) \right) \\&\quad \ge \left( {\begin{array}{c}n-2\\ k-2\end{array}}\right) \mathop {\sum _{i\in N}\sum _{j\in N}}_{i\ne j} x_{ij}+\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) \sum _{i\in N}(x_{ii}+ x_{i0})\,. \end{aligned}$$

Adding

$$\begin{aligned} \left( {\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) }-{\left( {\begin{array}{c}n-2\\ k-2\end{array}}\right) }\right) \mathop {\sum _{i\in N}\sum _{j\in N}}_{i\ne j} x_{ij}={\left( {\begin{array}{c}n-2\\ k-1\end{array}}\right) }\mathop {\sum _{i\in N}\sum _{j\in N}}_{i\ne j} x_{ij} \end{aligned}$$

to both sides yields

$$\begin{aligned}&\alpha \left( {\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) }+{\left( {\begin{array}{c}n-2\\ k-1\end{array}}\right) }\right) \mathop {\sum _{i\in N}\sum _{j\in N}}_{i\ne j} x_{ij}+ \left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) \left( \sum _{j\in N}(x_{jj}+ x_{0j})\right) \nonumber \\&\quad \ge \left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) \mathop {\sum _{i\in N}\sum _{j\in N}}_{i\ne j} x_{ij}+\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) \sum _{i\in N}(x_{ii}+ x_{i0})\,. \end{aligned}$$
(13)

Therefore,

$$\begin{aligned}&\alpha \left( \left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) +\left( {\begin{array}{c}n-2\\ k-1\end{array}}\right) \right) w(S)\\&\quad = \alpha \left( \left( \left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) +\left( {\begin{array}{c}n-2\\ k-1\end{array}}\right) \right) \sum _{i\in N}\sum _{j\in N} x_{ij}+\left( \left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) +\left( {\begin{array}{c}n-2\\ k-1\end{array}}\right) \right) \sum _{j\in N} x_{0j}\right) \\&\quad \ge \alpha \left( {\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) }+{\left( {\begin{array}{c}n-2\\ k-1\end{array}}\right) }\right) \mathop {\sum _{i\in N}\sum _{j\in N}}_{i\ne j} x_{ij}+ \left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) \left( \sum _{j\in N}(x_{jj}+ x_{0j})\right) \\&\quad \ge \left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) \mathop {\sum _{i\in N}\sum _{j\in N}}_{i\ne j} x_{ij}+\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) \sum _{i\in N}(x_{ii}+ x_{i0})\\&\quad = \left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) w(\textit{OPT})\,, \end{aligned}$$

where the last inequality follows from (13). This yields

$$\begin{aligned} k\text {-collusion } PoA \le \alpha \frac{{\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) }+{\left( {\begin{array}{c}n-2\\ k-1\end{array}}\right) }}{{\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) }}=\alpha +\frac{n-k}{n-1}\,. \end{aligned}$$

\(\square \)

In fact, this proof of the upper bound provides us with an easy way to create a tight lower bound example for any n.

Example 5

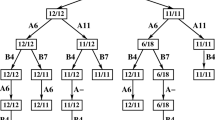
We make the upper bound analysis tight by setting \(x_{ii}=0\) and \(x_{0i}=0\) for all players \(i\in N\) . We normalize \(x_{ij}=1\) for all players \(i,j\in N\) for which \(i\ne j\), and finally we set \(x_{i0}=n-k+(n-1)(\alpha -1)\) for all players \(i\in N\). We construct the strategy spaces such that any player i can only choose subsets of either \(\textit{OPT}_i\) or \(S_i\), where \(S_i\) is the set chosen in the in the k-collusion Nash equilibrium. The resulting game for \(n=3, k=2\) is shown in Fig. 6.\(\triangleleft \)

Fig. 6
figure 6

The k-collusion Nash equilibrium from Example 5 for \(k=2\) and \(n=3\). Circled items are allocated to the same player. Each item is named after the value used in the upper bound proof

Full size image

Proof

(of the matching lower bound for \(\alpha \)-approximate k-collusion PoA.) To see that the above construction actually yields an \(\alpha \)-approximate k-collusion Nash equilibrium, consider any coalition K of k players. If players play strategy profile S, any player in K has utility \(n-1\). By switching to the strategy chosen in \(\textit{OPT}\), each player in K obtains utility \((k-1)1+1((n-1)(\alpha -1)+n-k)=\alpha (n-1)\), which is fine. If some players in K choose a subset of the items chosen in \(\textit{OPT}\), and other players in K choose a subset of the items chosen in S, then this yields a total value at most \(\alpha (n-1)\) for each player. We see that no coalition of k players can improve by deviating, from which the result follows. \(\square \)

For \(\alpha =1\), we obtain the following as a special case.

Corollary 2

The k-collusion price of anarchy equals \(1+\frac{n-k}{n-1}\) for set packing games.

Although the k-collusion price of anarchy is strictly lower than the price of anarchy for all \(k\ge 2\), note that this improvement becomes negligible for large n. Interestingly, as opposed to all other lower bound examples in this paper, we did not find a matching lower bound example for throughput scheduling games.

7 Concluding Remarks

As discussed earlier, when more than one player may select one and the same item, one needs a utility sharing protocol, and the game becomes a covering game for which several results have been obtained, e.g. by Garing (2009), and for more general settings also by Paccagnan and Marden (2018); Paccagnan et al. (2018). The price of anarchy for Nash equilibria is then \(2-1/n\), assuming that items are shared uniformly. Brethouwer (2018) has also studied the sequential version of that class of games, and observed that sequential play does not allow to improve this price of anarchy bound. To pin down the exact value of the sequential price of anarchy for that class of games is open.