Abstract
This paper provides a non-cooperative foundation for (asymmetric generalizations of) the continuous Raiffa solution. Specifically, we consider a continuous-time variation of the classic Ståhl–Rubinstein bargaining model, in which there is a finite deadline that ends the negotiations, and in which each player’s opportunity to make proposals is governed by a player-specific Poisson process, in that the rejecter of a proposal becomes proposer at the first next arrival of her process. Under the assumption that future payoffs are not discounted, it is shown that the expected payoffs players realize in subgame perfect equilibrium converge to the continuous Raiffa solution outcome as the deadline tends to infinity. The weights reflecting the asymmetries among the players correspond to the Poisson arrival rates of their respective proposal processes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
With two seminal articles published in the early fifties, Nash (1950, 1953) laid the foundation of the Nash program, a research agenda that bridges the gap between the cooperative and the non-cooperative side of game theory. Given a cooperative solution concept, the aim in this program is to construct reasonable non-cooperative games such that the payoffs realized in equilibrium yield, or somehow approximate the corresponding solution outcome. For any given cooperative solution concept, a successful Nash program result thus provides an understanding of what type of strategic interactions between rational, self-interested agents this concept subsumes.Footnote 1
This paper focuses on the Nash program for bargaining solutions. In particular, it provides an exact—i.e. approximation-free—support result for the continuous Raiffa solution (Raiffa 1953). A discrete version of the Raiffa solution is defined as the limit point of a sequence of intermediate agreements that is constructed by an iterative random dictator procedure: taking the disagreement point as the first intermediate agreement, the \(t+1\)-th agreement is obtained by first giving all players the utilities implied by the t-th agreement, and subsequently giving each player 1 / n-th of the maximal utility they could then still feasibly obtain. The continuous version of the Raiffa solution—the one considered in this paper—is in the same spirit, but assumes an infinitesimally small step size, i.e. rather than receiving 1 / n-th of their maximal claims (in excess of the previous intermediate agreement), the share players now receive is infinitesimally small.Footnote 2
Our support result for this solution is based on a non-cooperative bargaining game in the tradition of Ståhl (1972) and Rubinstein (1982). Players make proposals that are instantaneously and sequentially voted on by all players, including the proposer; if there is unanimous agreement, the proposal is implemented, otherwise it is rejected and the game continues. Apart from these common features, the game differs from the classic models in several important ways: bargaining occurs in continuous time and the game features a finite deadline that ends the negotiations with all players obtaining zero payoffs. Moreover, the timing of the proposals is stochastic in the sense that they are governed by player-specific Poisson processes: at the outset of the game, player 1’s process starts running until it produces an arrival, at which point she becomes the proposer; whenever a proposal is rejected, the game continues, and the rejecter is called to make the next proposal. While this game may have many subgame perfect equilibria (SPE), it turns out that in SPE, the payoff functions are unique. The main result of this paper is that the ex ante expectations of said payoffs converge to the continuous Raiffa solution outcome as the deadline tends to infinity. In addition, a simple extension of the game proposed by Trockel (2011) leads to an exact support result: whenever player 1’s process produces an arrival, she proposes the continuous Raiffa solution outcome, and this proposal is unanimously accepted.
The papers most closely related to the present work are Ambrus and Lu (2015) and Diskin et al. (2011). A detailed discussion of these papers is deferred to Sect. 4. We next discuss further related literature.
The Nash program: As previously mentioned, the origins of the Nash program lie in two seminal papers of Nash (1950, 1953). In the first, Nash defines and axiomatically characterizes the Nash solution, while in the second he provides the Nash solution’s first non-cooperative support result. In particular, he constructs a non-cooperative game in which two players simultaneously submit their respective utility demands while facing uncertainty about the size of the surplus to be divided, and in which incompatible demands lead to zero payoffs for both players; as the uncertainty vanishes, a particular Nash equilibrium outcome of this game converges to the Nash solution outcome.
A second support result for the Nash solution originates from the work of Rubinstein (1982), who constructs a dynamic non-cooperative bargaining game in which two players take turns to make proposals until one is accepted, and in which utilities are exponentially discounted. Rubinstein shows that this game has a unique subgame perfect equilibrium; Binmore et al. (1986) subsequently proved that the corresponding payoffs converge to the Nash solution outcome as the discount factor tends to one. There is a broad literature on n-player variations on these results, implementing the Nash solution or its asymmetric generalization (Harsanyi and Selten 1972; Kalai 1977).Footnote 3 Anbarci and Sun (2012) provide another implementation of the asymmetric Nash solution for two-person problems.
The Nash program for the Raiffa solution has primarily focused on its discrete version. Myerson (1991, pp. 393–394) describes a two-player non-cooperative bargaining game in the spirit of Rubinstein, but differing in three main respects: rather than taking turns to make proposals, it is assumed that at each round a proposer is randomly selected by a fair coin toss; there is a finite deadline T that ends negotiations; and there is no discounting of utilities. The unique SPE of this game implements the (discrete) Raiffa solution, as T goes to infinity. Sjöström (1991) proposes a similar game in which actions take place at T equidistant time points within a fixed time interval, and in which payoffs are exponentially discounted with discount factor \(r\ge 0\); as the partition of the bargaining interval becomes more refined (i.e., \(T\rightarrow \infty \)), the unique subgame perfect equilibrium of this game implements an outcome within distance r from the discrete Raiffa solution outcome. Tanimura and Thoron (2008) construct a game in which two risk averse players divide a perfectly divisible unit good by a particular procedure that generalizes the notion of final offer arbitration. The discrete Raiffa solution outcome is obtained in the unique subgame perfect equilibrium of this game.
The rejecter-proposes protocol: The dynamic bargaining games that implement the Nash and Raiffa solutions are set in discrete time, and typically adopt one of three bargaining protocols: either (i) players get to make proposals in a fixed rotating order (e.g. Rubinstein 1982; Haller 1986; Krishna and Serrano 1996); (ii) at each round a proposer is randomly selected in accordance with a given probability distribution (e.g. Myerson 1991; Sjöström 1991; Laruelle and Valenciano 2008; Britz et al. 2010); or (iii) one player makes the first proposal, and in the continuation of the game, the rejecter of each proposal gets to propose in the next round.
In this paper, we assume the last bargaining protocol. Selten (1981) was the first to study a bargaining game where proposers are selected in this way. While it is usually interpreted as an alternating offers game (and thus one with a fixed rotating order of proposers), in Rubinstein’s (1982) game too, the player who gets to propose at any time \(t+1\) is the one who rejected the time-t proposal. The games proposed by Chae and Yang (1994) and Suh and Wen (2006) are generalizations of Rubinstein’s game along these lines. The rejecter-proposes protocol has been most widely adopted in the context of coalition formation games; examples include Chatterjee et al. (1993), Bloch (1996), Ray and Vohra (1999), Imai and Salonen (2000), and Bloch and Diamantoudi (2011). Kawamori (2008) and Britz et al. (2014) study more general action-dependent bargaining protocols that include the rejecter-proposes protocol as a special case.
Bargaining with non-convex feasible sets: The Nash program with non-convex bargaining problems has received relatively little attention in the literature. Notable exceptions include Herrero (1989) and Conley and Wilkie (1994, 1996), who extend the definition of the Nash solution to the non-convex domain, and provide non-cooperative support for their respective solution concepts.
The rest of the paper is organized as follows. Section 2 details all relevant definitions and notations, Sect. 3 contains our main result, an exact non-cooperative support result for the continuous Raiffa solution, and Sect. 4, as indicated above, further discusses the related literature.
2 Preliminaries
2.1 The bargaining problem
A bargaining problem—in short, problem—is defined by a finite set of players \(N:=\{1,\ldots ,n\}\) with \(n\ge 2\), and a subset S of \({\mathbb {R}}^{n}\), that is closed and strictly comprehensive (i.e. \(y\in S\) and \(x\le y\) implies \(x\in S\); if in addition \(x\ne y\), then \(z > x\) for some \(z\in S\)),Footnote 4 that contains an outcome \(z>\bar{0}:=(0,\ldots ,0)\), and is such that \(S\cap {\mathbb {R}}^{n}_{+}\) is bounded. It is further assumed that S satisfies the following condition:Footnote 5
- (A1)::
-
There exists a finite \(K>0\) such that for all \(i,j \in N\), and for all \(x,y\in \partial (S)\cap {\mathbb {R}}^{n}_{+}\) with \(x_{-\{i,j\}}=y_{-\{i,j\}}: |x_{i}-y_{i}|\le K|x_{j}-y_{j}|\) (See Fig. 1).
Note that we do not insist on convexity of S. Fixing the set of players N, a bargaining problem is henceforth denoted by the set S. The class of all bargaining problems S is denoted by \({\mathcal {B}}\). A bargaining solution—in short, solution—is a map \(\varphi :{\mathcal {B}}\rightarrow {\mathbb {R}}^{n}\) that assigns to each problem \(S\in {\mathcal {B}}\) a unique outcome \(\varphi (S)\in S\).
The interpretation of the bargaining problem is as follows. An outcome \(x\in {\mathbb {R}}^{n}\) represents a utility allocation, in that each \(x_{i}\) represents the utility obtained by player i; S represents the set of all utility allocations players in N can jointly realize, and is thus also called the feasible set; players must find agreement on an outcome \(x\in S\), and failure to do so leads to the unfavorable outcome \(\bar{0}\); the latter is therefore also called the disagreement outcome. The outcome \(\varphi (S)\) is interpreted as the compromise reached by the players in N when faced with the problem S, and is thus also referred to as the solution outcome. Condition (A1) says that if a player i gives up any small amount \(\varepsilon >0\) of his utility, then there is an upper bound \(K\varepsilon \) on the associated compensation other players (i.e., \(j\in N{\setminus } i\)) can feasibly realize from this concession. This is a rather mild assumption: for instance, if the problem is a utility representation of an economic division problem, then (A1) already holds if the players’ utility functions are continuously differentiable.
2.2 A family of continuous Raiffa solutions
Given a problem \(S\in {\mathcal {B}}\) and an outcome \(x\in S\cap {\mathbb {R}}^{n}_{+}\), define \(m(x,S):=(m_{1}(x,S),\ldots ,m_{n}(x,S))\), where
for all \(i\in N\). Each \(m_{i}(x,S)\) is the maximal claim player i holds over the surplus that remains of S, given that an intermediate agreement has been reached on the outcome x. Note that \(m(\cdot ,S)\) is a well-defined vector function by compactness of \(S\cap {\mathbb {R}}^{n}_{+}\). When it is no cause for confusion, we will write m(x) rather than m(x, S).
Given a convex problem \(S\in {\mathcal {B}}\), the discrete Raiffa solution (Raiffa 1953) is defined as the limit of the sequence \(\{x^{t}\}_{t=0}^{\infty }\), where \(x^{0}:=\bar{0}\) and
for all \(t\in {\mathbb {N}}_{0}:={\mathbb {N}}\cup \{0\}\). It is based on the intuitive notion that agreement is found on the midpoint of all the maximal claims players hold over the surplus. If this midpoint is not efficient, then players again stake out maximal claims over the surplus that remains, and reach a next compromise on the midpoint of those claims. The solution outcome is reached by iteratively applying this reasoning, until the entire surplus is allocated.
The problem described by the difference Eq. (1), and as a consequence also the discrete Raiffa solution, discards much of the information that is contained in the bargaining problem. Therefore, Raiffa (1953) proposed the continuous Raiffa solution, which is obtained in similar fashion to its discrete version, but reduces the step size in problem (1) from 1 / n to 0. More precisely, problem (1) is turned into an initial value problem, so that its solution is no longer given by a series of intermediate agreements \(\{x^{t}\}_{t=0}^{k}\) with \(x^{0}=\bar{0}\), but by a continuous intermediate agreement curve x(t) with \(x(0)=\bar{0}\). The continuous Raiffa solution outcome then coincides with the limit point of this curve as t tends to infinity Fig. 2. For two-player convex problems, it has been axiomatically characterized by Livne (1989), Peters and van Damme (1991), and Peters (2010) among others; in these studies, the intermediate agreement curve is obtained as the solution of the initial value problem \(dx_{1}/dx_{2}=(m_{1}(x)-x_{1})/(m_{2}(x)-x_{2})\) with the initial condition \(x_{1}(0)=0\). In a multilateral setting, the intermediate agreement curve could similarly be obtained by parametrizing the utilities of players \(i\in N{\setminus } n\) in terms of the utility of player n. Diskin et al. (2011) explicitly use the continuous version of (1). The following generalizes their definition to a family of weighted continuous Raiffa solutions.
Definition. Let \(\Lambda \) be the set of all strictly positive vectors in the n-dimensional unit simplex, i.e., \(\Lambda :=\{\lambda \in \mathbb {R}^{n}_{++}\mid \sum _{i\in N}\lambda _{i}=1\}\). For \(\lambda \in \Lambda \), the \(\lambda \)-weighted continuous Raiffa solution \(R^{\lambda }:\mathcal {B}\rightarrow {\mathbb {R}}^{n}\) is defined as \(R^{\lambda }(S):=\lim _{t\rightarrow \infty }x(t)\), where \(x:[0,\infty )\rightarrow S\) is the unique solution of the Initial Value ProblemFootnote 6
The solution family \({\mathcal {R}}:=\{R^{\lambda }\mid \lambda \in \Lambda \}\) contains all such solutions.
If \(\lambda _{i}=1/n\) for all \(i\in N\), then \(R^{\lambda }\) is the unique symmetric solution in \({\mathcal {R}}\); this solution is also denoted R. Diskin et al. (2011) show that in the convex domain, \({\mathcal {R}}\) is a family of well-defined solutions. To extend their result to non-convex problems, we first prove the following useful lemma.
Lemma 2.1
For all \(S\in {\mathcal {B}}\) and \(\lambda \in \Lambda \), \(\lambda [m(x,S)-x]\) is Lipschitz continuous, with Lipschitz constant \(K+1\).
By this lemma and the Picard–Lindelöf theorem, it follows that for all \(S\in \mathcal {B}\) and \(\lambda \in \Lambda \), the corresponding problem (2) has a unique solution.
Proposition 2.2
For all \(S\in \mathcal {B}\) and \(\lambda \in \Lambda \), problem (2) has a unique solution \(x:[0,\infty )\rightarrow {\mathbb {R}}^{n}\), which has the property that \(x(t)\in \text {int}(S)\cap \mathbb {R}^{n}_{+}\) for all finite t. Furthermore, \(\lim _{t\rightarrow \infty }x(t)\) exists and is contained in \(\partial (S)\cap \mathbb {R}^{n}_{+}\).
Proof
See Theorem 5 of Diskin et al. (2011). \(\square \)
3 A non-cooperative support result
3.1 The non-cooperative bargaining game
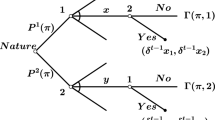
We consider a continuous-time bargaining game with stochastic timing of proposals and a finite deadline, similar to the game proposed by Ambrus and Lu (2015).Footnote 7 The underlying framework of this game is a bargaining problem \(S\in {\mathcal {B}}\), as defined in the previous section. Bargaining occurs in a continuous time interval [0, T], where the deadline T is finite and known to all players. For each player \(i\in N\), when she is called to make the next proposal, the opportunity to do so is produced by a Poisson process with the player-specific arrival rate \(\lambda _{i}>0\). We further assume \(\sum _{i\in N}\lambda _{i}=1\), so that \(\lambda \in \Lambda \); this is without loss of generality since the interval [0, T] can always be rescaled.
If at a time \(t'\in [0,T]\), a player i is called to be the next proposer, then i’s process, and i’s alone, starts running until it produces an arrival, say at time \(t\ge t'\). At this point i becomes the proposer, and thus puts an allocation \(x\in S\) on the table. All players, including i herself, subsequently make instantaneous and sequential accept/reject decisions on this offer. The order in which they do so is given by \([i, i+1\ (\text {mod} \ n),\ldots ,n,1,\ldots ,i-1]\).Footnote 8 If all players accept, then bargaining ends with the implementation of i’s proposal. If no unanimous agreement is obtained, then voting stops at the first rejection, and the above procedure is repeated from time t onward, now with the rejecter of i’s proposal in the role of designated next proposer. Without loss of generality, we assume that player 1 is the designated next proposer at time 0. If prior to the deadline T no agreement is reached, or infinitely many arrivals occur, then bargaining ends and all players realize their disagreement value 0.
A particular game of this form is described by \(\Gamma =\{S,\lambda , T\}\), where \(S\in {\mathcal {B}}\) is the underlying bargaining problem, \(\lambda \) the vector collecting the arrival rates of players’ processes, and T the deadline ending negotiations.
3.2 Histories, strategies, and equilibria
The payoffs players (expect to) realize at any point in the game, which proposals to make when proposing, and which offers to accept or reject when responding, may all depend on the history of play of the game. Fix a game \(\Gamma =\{S,\lambda ,T\}\), and consider a player \(i\in N\). If she is the proposer at some time \(t\in [0,T]\), then the relevant history—also called proposer history— specifies the times \(t_{1}\le \cdots \le t_{k}\le t\) of all previous offers (if any), and for each \(l, l=1,\ldots ,k\), the rejected proposal and the identity of the proposer.Footnote 9 If i is the designated next proposer, then the preceding history contains the same information as a proposer history. If i is a responder, then the responder history contains all information of a proposer history, but further includes the proposal to which she is responding.
Denote the set of all histories after which player i must make a proposal by \(H^{p}_{i}\), the set of all histories after which she is the designated next proposer by \(H_{i}^{d}\), and the set of all histories after which she is responding by \(H_{i}^{r}\). Player i’s strategy is described by a pair of functions \((f_{i},g_{i})\), where \(f_{i}:H^{p}_{i}\rightarrow S\) maps histories of \(H^{p}_{i}\) into feasible proposals \(x\in S\), and \(g_{i}:H^{r}_{i}\rightarrow \{\text{ accept },\text{ reject }\}\) maps histories of \(H^{r}_{i}\) into an accept/reject decision on the current offer. A strategy profile is a tuple \((f,g)\equiv (f_{i},g_{i})_{i\in N}\).
A Nash equilibrium is a strategy profile (f, g) from which no player has a unilateral profitable deviation: if all players \(j\in N{\setminus } i\) play \((f_{j},g_{j})\), then the optimal strategy of player i is to play \((f_{i},g_{i})\). A Subgame Perfect Equilibrium (SPE) is a strategy profile (f, g) that constitutes a Nash equilibrium at every node of the game. A weak SPE (WSPE) is a strategy profile that is a Nash equilibrium at every node of the game at which Nash equilibria exist.
3.3 Subgame perfect equilibria
Fix a game \(\Gamma =\{S,\lambda ,T\}\), let x(t) be the unique solution to the initial value problem (2) associated with S, and for \(t\in [0,T]\), define \(r(t):=x(T-t)\) and \(p(t):=m(r(t))\). It is demonstrated that in any SPE of this game, the payoff functions of a player i in the role of proposer and in the role of responder are respectively given by \(p_{i}(t)\) and \(r_{i}(t)\). First consider the following useful lemma.
Lemma 3.1
The system of equations
has a unique solution given by \(\theta (t)=r(t)\).
Proof
Problem (3) can be reformulated as an initial value problem. In the first place, \(\theta (T)=\bar{0}=x(T-T)\). Furthermore, for all \(i\in N\) and \(t\in [0,T]\),
Then by Proposition 2.2, \(\theta (t)=x(T-t)\) is the unique solution to (3). \(\square \)
Proposition 3.2
In any SPE, if a player i is the proposer at \(t\in [0,T]\), then she offers \(r_{j}(t)\) to all \(j\ne i\), claims \(p_{i}(t)\) for herself, and this proposal is unanimously accepted.
Proof
Let \({\mathcal {T}}\) be some time in (0, T], and assume that the proposition is true in the interval \([{\mathcal {T}},T]\)—i.e., for all SPE, if player i is the proposer at \(t\in [{\mathcal {T}},T]\), then she offers \(r_{j}(t)\) to all \(j\ne i\), claims \(p_{i}(t)\) for herself, and this proposal is unanimously accepted. The aim of the proof is to show that this then also holds true on a non-degenerate time interval that precedes \({\mathcal {T}}\), in particular, the interval \(I:=[{\mathcal {T}}-\tau ,{\mathcal {T}}]\) where \(\tau :=\min \left\{ {\mathcal {T}},-\ln \left( 1-\frac{1}{n(1+K)}\right) \right\} \). To this end, let \(\{(\underline{\theta }^{k}(t),\overline{\theta }^{k}(t))\}_{k\in {\mathbb {N}}_{0}}\) be two sequences of functions on I, defined as
and for all \(k\in {\mathbb {N}}_{0}\), for all \(t\in I\), and for all \(i\in N\),
The following two claims show that these functions describe paths in \(\text{ int }(S)\cap \mathbb {R}^{n}_{+}\). Henceforth, whenever the argument t is omitted, the claim is assumed to hold for all \(t\in I\).
Claim 3.3
\(\overline{\theta }^{0}\in \text {int}(S)\cap {\mathbb {R}}^{n}_{+}\).
Claim 3.4
For all \(k\in {\mathbb {N}}_{0}\), \(\overline{\theta }^{k}\ge \overline{\theta }^{k+1}\ge \underline{\theta }^{k+1}\ge \underline{\theta }^{k}\).
For all \(t\in [0,T]\) and for all \(i,j\in N\), let \({\overline{q}}_{i}^{j}(t)\) and \({\underline{q}}_{i}^{j}(t)\) respectively be the supremum and the infimum over all SPE and all histories in \(H^{d}_{j}\), of player i’s time-t expected payoff in the game. Furthermore, for all \(i\in N\), define \({\overline{r}}_{i}:={\overline{q}}_{i}^{i}\) and \({\underline{r}}_{i}:={\underline{q}}_{i}^{i}\).
Claim 3.5
\({\underline{r}}\ge \underline{\theta }^{0}\) and for all \(j\in N\), \(\overline{\theta }^{0}\ge {\overline{q}}^{j}\).
It follows that \(\overline{\theta }^{k}\ge {\overline{r}}\ge {\underline{r}}\ge \underline{\theta }^{k}\) for \(k=0\). We want to prove that these inequalities hold for all \(k\in {\mathbb {N}}_{0}\). To this end, assume that \(\overline{\theta }^{k}\ge {\overline{r}}\ge {\underline{r}}\ge \underline{\theta }^{k}\) for some \(k\in {\mathbb {N}}_{0}\). Furthermore, let \({\overline{p}}_{i}(t)\) and \({\underline{p}}_{i}(t)\) be the supremum and the infimum of i’s (expected) payoff at t, over all SPE and histories in \(H^{p}_{i}\).
Claim 3.6
\(m(\underline{\theta }^{k})\ge {\overline{p}}\ge {\underline{p}}\ge m(\overline{\theta }^{k})\).
Since \({\underline{p}}\ge m(\overline{\theta }^{k})\ge m(\overline{\theta }^{0})>\overline{\theta }^{0}\ge {\overline{q}}^{j}\) for all j, this claim implies that any SPE proposal in I is immediately accepted. It further implies that for all \(t\in I\),
That is, \(\overline{\theta }^{k+1}\ge {\overline{r}}\ge {\underline{r}}\ge \underline{\theta }^{k+1}\). This leads to the following result.
Claim 3.7
\(\overline{\theta }^{k}\ge {\overline{r}}\ge {\underline{r}}\ge \underline{\theta }^{k}\) for all \(k\in {\mathbb {N}}_{0}\).
By Claims 3.3 and 3.4, there are functions \(\overline{\theta }\) and \(\underline{\theta }\), defined on I and bounded within \(S\cap \mathbb {R}^{n}_{+}\), such that \(\lim _{k\rightarrow \infty }\overline{\theta }^{k}=\overline{\theta }\) and \(\lim _{k\rightarrow \infty }\underline{\theta }^{k}=\underline{\theta }\). By Claim 3.7, \(\overline{\theta }\ge {\overline{r}}\ge {\underline{r}}\ge \underline{\theta }\), and by continuity, \(m(\underline{\theta })\ge {\overline{p}}\ge {\underline{p}}\ge m(\overline{\theta })\).
Claim 3.8
\(\overline{\theta }=\underline{\theta }=r\) and \(m(\underline{\theta })=m(\overline{\theta })=p\).
Suppose that player i is the proposer at \(t\in I\). Since her proposal is accepted, all \(j\ne i\) must be offered at least \(r_{j}(t)\). However, since i’s payoff is given by \(p_{i}(t)\), all \(j\ne i\) are offered exactly \(r_{j}(t)\). In other words, player i offers \(r_{j}(t)\) to all \(j\ne i\), claims \(p_{i}(t)\) for herself, and this proposal is unanimously accepted.
Assume that \({\mathcal {T}}=T\), and note that the proposition holds on the degenerate interval [T, T]. By repeating the above argument, it may then be iteratively established on the intervals \([T-\tau ,T], [T-2\tau ,T]\), and so on. Since T is finite, and since \(\tau \) is strictly positive and independent from T, the entire interval [0, T] is covered in a finite number of iterations. \(\square \)
Corollary 3.9
In SPE, the game \(\Gamma \) is concluded when player 1’s process produces an arrival, say at time t; player 1 offers \(r_{j}(t)\) to all \(j\ne 1\), claims \(p_{1}(t)\) for herself, and this proposal is immediately accepted.
Remark 1
The assumption that the proposer is the first to respond to her own proposal is used in the proof of Claim 3.5 to determine an initial lower bound \(r_{i}({\mathcal {T}})\) on the expected payoff a player i realizes in SPE when she is the designated next proposer. In particular, in the interval I, i can unilaterally secure \(r_{i}({\mathcal {T}})\) by consistently rejecting her own proposals. If the response order were fixed, say at \([1,\ldots ,n]\), then for i to be the rejecter, these proposals would first have to be accepted by all of i’s predecessors. Since at that point in the argument nothing guarantees the existence of such proposals, it is necessary to assume that the proposer has no predecessors in the response order.
Proposition 3.2 implies that for each role in the game, the payoffs players realize are the same in all SPE. This regularity in the payoffs is helpful in establishing SPE existence. Consider the strategy profile \(({\hat{f}},{\hat{g}})\) defined as follows. For all \(i\in N\) and \(t\in [0,T]\):
-
If i is the proposer at time t, she offers \(r_{j}(t)\) to all \(j\ne i\), and claims \(p_{i}(t)\) for herself.
-
If i is responding to a proposal v at time t, she accepts if and only if two conditions are satisfied: (i) i has no successor in the response order who rejects; and (ii) \(v_{i}\ge r_{i}(t)\).
By the same reasoning as in Claim 3.5 in the proof of Proposition 3.2, \(q_{i}^{j}(t)\le r_{i}(t)\) for all \(i,j\in N\) and \(t\in [0,T]\). SPE existence is then easily established.
Proposition 3.10
The profile \(({\hat{f}},{\hat{g}})\) is an SPE.
There may be other SPE besides \(({\hat{f}},{\hat{g}})\). To see this, note that rejection in case of indifference is only excluded if the proposer makes the correct offer. Suppose for instance that at time t an outcome \(v\in S\) is proposed by player i, with \(v\ne (p_{i}(t),r_{-i}(t))\) and \(v_{j}=r_{j}(t)\) for some \(j\ne i\); if j gets to respond, and all of her successors accept, then also rejection is a best reply, and may thus be (the action implied by) an SPE strategy.
3.4 The limit behavior of expected SPE payoffs
Lemma 3.1 and Proposition 3.2 already hint at a connection between the Raiffa solution and the above-described game. The purpose of this section is to make this connection precise. To this end we consider players’ ex ante expected payoffs at time 0 as a function of the deadline T. Consider a game \(\Gamma =\{S,\lambda , T\}\), and note that by Corollary 3.9, expected payoffs are given by
We next show that these expected payoffs converge to the continuous Raiffa solution outcome as the deadline tends to infinity.
Theorem 3.11
For all \(S\in {\mathcal {B}}\) and \(\lambda \in \Lambda \), \(\lim _{T\rightarrow \infty }u(T; S,\lambda )=R^{\lambda }(S)\).
Proof
Fixing S and \(\lambda , u(T;S,\lambda )\) may be written as u(T), and \(m(\cdot ,S)\) as \(m(\cdot )\). Furthermore, let \(z:=R^{\lambda }(S)\). Applying the transformation \(\tau =T-s\) to the right hand sides of (4) and (5) yields
First consider the expected payoff of player 1, \(u_{1}(T)\). Differentiating on both sides w.r.t. T yields \(u_{1}'(T)=\lambda _{1}[m_{1}(x(T))-u_{1}(T)]\), and thus by Proposition 2.2, \(u_{1}'(T)=x_{1}'(T)+\lambda _{1}[x_{1}(T)-u_{1}(T)]\). Defining \(\phi (T):=u_{1}(T)-x_{1}(T)\), this yields \(\phi '(T)=-\lambda _{1}\phi (T)\). With the initial condition \(\phi (0)=0\), this solves to \(\phi (T)=0\) for all T. Then by continuity of \(\phi \), and by the definition of \(R^{\lambda }\),
Next consider \(j\in N{\setminus } \{1\}\) and let \(\epsilon >0\) be given. Since \(x_{j}(T)\) is strictly increasing in T and since \(\lim _{T\rightarrow \infty }x_{j}(T)=z_{j}\), \(z_{j}-x_{j}(T)\ge 0\) for all \(T\ge 0\). It further implies that there is a \(T_{0}\) such that \(z_{j}-x_{j}(T)\le \epsilon \) for all \(T\ge T_{0}\). Since for all \(a\in {\mathbb {R}}_{+}\), \(\lim _{T\rightarrow \infty }\int _{a}^{T}\lambda _{1}e^{-\lambda _{1}(T-\tau )}d\tau =1\),
Furthermore, since \(z_{j}-x_{j}(T)\ge 0\) for all T, the first equation above implies \(z_{j}-\lim _{T\rightarrow \infty }u_{j}(T)\ge 0\). Since \(0\le z_{j}-\lim _{T\rightarrow \infty }u_{j}(T)\le \epsilon \) for all \(\epsilon >0\), \(\lim _{T\rightarrow \infty }u_{j}(T)=z_{j}\). In conclusion, \(\lim _{T\rightarrow \infty }u(T)=z\), as desired. \(\square \)
There are three potential criticisms of Theorem 3.11. In the first place, since Proposition 3.2 only holds when the deadline is finite, the above result only provides approximate non-cooperative support for the Raiffa solution. Secondly, it remains silent on the payoffs players realize ex post; if the game is concluded close to the deadline, they will in fact deviate substantially from the Raiffa solution outcome. Finally, there is a strictly positive probability that bargaining ends before player 1 has the opportunity to make a proposal, in which case players realize zero payoffs without an action ever being played. Using the approach of Trockel (2011), these three criticisms may be tackled at once. In particular, consider an extension of the game \(\Gamma \) in which the deadline T is not exogenously specified, but rather, chosen by the rejecter of the first proposal. This provides exact support for the continuous Raiffa solution in WSPE—i.e., the game does not conclude before player 1 gets to make a proposal, she proposes exactly the (weighted) Raiffa solution, and this offer is immediately accepted by all players. For the specifics of this result, see Trockel (2011).
4 Related literature
4.1 Ambrus and Lu (2015)
Ambrus and Lu (2015) consider a bargaining game that is similar to the one presented in this paper.Footnote 10 However, rather than a pure bargaining problem, they assume that the underlying (cooperative) game is a monotonic TU game.Footnote 11 While their strategic game too is set in continuous time and takes place in a fixed time interval, they assume this interval to be \([-T,0]\) where \(-T\) represents the starting point, and 0 is the deadline ending negotiations. As in our version of the game, each player i’s opportunity to make proposals is governed by a Poisson process with player-specific arrival rate \(\lambda _{i}>0\), all processes are independent, and arrival rates sum up to a constant \({\hat{\lambda }}\) that can be normalized to one. While we assume that throughout the game only one process is active, Ambrus and Lu assume that all processes run concurrently at all times until the game is concluded, either because the deadline is attained or because a proposal has been accepted. When an arrival occurs and the corresponding player makes a proposal, then in a fixed order, all players except the proposer either accept or reject; in case of unanimous acceptance the game ends with the implementation of the proposal, in case of rejection all processes start up again until the first next arrival occurs. Payoffs are exponentially discounted with discount factor \(r\in (0,\infty )\); furthermore, as in our game, utilities have zero worth after the deadline.
For this game, Ambrus and Lu prove a number of results: they show that expected payoffs in Markov Perfect Equilibrium (MPE) are unique, that MPE are the only SPE that can be approximated by SPE in discrete versions of the game, and that as the deadline tends to infinity, the game implements, for each profile of arrival rates, a particular element of the core. However, closer to this paper, Ambrus and Lu also focus on a special case of their model in which only the grand coalition generates a positive value, so that the underlying cooperative game is a pure bargaining problem with transferable utility. Normalizing the worth of the grand coalition to one, they prove the following result.
Claim 3. (Ambrus and Lu 2015) In any SPE, the n-player group bargaining game ends at the first realization of the Poisson process for any player as follows: an offer is made to N and all players accept. SPE payoff functions are unique, with player i receiving \((\lambda _{i} + r)/({\hat{\lambda }} + r) + ({\hat{\lambda }}-\lambda _{i})/({\hat{\lambda }}+r)e^{({\hat{\lambda }}+r)t}\) when she is the proposer at time t, and \((\lambda _{i}/({\hat{\lambda }} + r))(1 - e^{({\hat{\lambda }}+r)t})\) when she is not.
This result is the analogue of Proposition 3.2. Both results imply that in SPE, if a player i makes an offer at time t, the realized payoffs are (the equivalents of) \(p_{i}(t)\) for i, and \(r_{j}(t)\) for \(j\ne i\). However, with the arrival process(es) running at time t, the expected payoffs in the two models differ: in the present paper, because only the process for one player—say, player i—is running, the time-t expected payoffs of players i and \(j\ne i\) are respectively \(p_{i}(t)\) and \(r_{j}(t)\), multiplied by the probability of an arrival before the deadline (that is, \(r_{i}(t)\) and \(q_{j}^{i}(t)\)); in the model of Ambrus and Lu, every player j’s expected payoff is \(r_{j}(t)\). In other words, in this paper, an arrival is good news for everyone, while in Ambrus and Lu’s model, it is good news only for the proposer.
The difference in bargaining protocol also means that the proofs of Proposition 3.2 and of Claim 3 follow different strategies. We follow the approach of Ma and Manove (1993), who through an iterative process find increasingly tight upper and lower bounds on players’ expected SPE payoffs in their game, and subsequently show that in the limit these bounds coincide. In contrast, Ambrus and Lu construct for each player two SPE—one yielding the supremum, the other the infimum of that player’s expected SPE payoff—and use this to set up 2n equations with supremum and infimum SPE expected payoffs as the 2n unknowns; solving these equations, they find that these suprema and infima coincide, and are as specified in the theorem. Since constructing SPE requires comparing the payoffs a player realizes when she is the rejecter with those she realizes when some other player rejects, this approach does not work under the rejecter-proposes protocol. Consider for instance an SPE in which a player i realizes the expected payoff \({\overline{r}}_{i}\). If she is offered less than \({\overline{r}}_{i}\), she should be rewarded for rejecting by having the game move to an SPE in which her expected payoff is \({\overline{r}}_{i}\); under the random-proposer protocol of Ambrus and Lu, \({\overline{r}}_{i}\) is at least as high as any payoff i realizes when another player j rejects, whereas under the rejecter-proposes protocol this cannot be asserted without further assumptions on i’s expected payoff in subgames where j is the designated next proposer.
We adopted the rejecter-proposes protocol because it avoids a particular technical issue that arises in Ambrus and Lu’s version of the game. In particular, Ambrus and Lu take for granted that the supremum payoff a player i obtains from an accepted SPE proposal is equal to \({\overline{r}}_{i}\), the supremum expected payoff she realizes in the continuation of the game. While at first glance this seems intuitive, it is in fact possible for an SPE proposal to be unanimously accepted, while giving i a payoff \(v_{i}\ge {\overline{r}}_{i}\). The reason is that the SPE strategy of a player \(j\ne i\) could be to reject any proposal that gives a player i less than \(v_{i}\); this is optimal for j as long as her rejection of such proposals moves the game to an SPE in which her expected payoff is \({\overline{r}}_{j}\). While Claim 3 remains true, using the correct bounds on expected payoffs does make its proof more involved, and more importantly, requires notation that is rather heavy in nature. We therefore chose to adopt the rejecter-proposes protocol. Since under this protocol, the supremum expected SPE payoff the designated next proposer realizes does not depend on the supremum payoff she can realize as a responder in the game, this simplifies the argument, and considerably declutters the notation.
The one loss of generality we have to accept when adopting the rejecter-proposes protocol, is that the proposer responds to her own proposal, and that she does so first. Suppose that on \([{\mathcal {T}},T]\), the expected SPE payoffs of designated next proposers are given by the function r(t); then one way in which a player who is designated next proposer at a time \(t<{\mathcal {T}}\) can secure her \(r({\mathcal {T}})\)-payoff, is to give her the option to remain the designated next proposer throughout the interval \([t,{\mathcal {T}}]\). As explained in Remark 1, this is achieved by assuming that the proposer responds to her own proposal first, and that the rejecter becomes designated next proposer. Under the random-proposer protocol of Ambrus and Lu, no assumptions on the response order are required: if expected payoffs in \([{\mathcal {T}},T]\) are uniquely given by r(t), then any player can at any time \(t<{\mathcal {T}}\) unilaterally secure her \(r({\mathcal {T}})\)-payoff by rejecting all proposals in the interval \([t,{\mathcal {T}}]\).
Other differences between Ambrus and Lu’s framework and the one in the present paper are immaterial. Ambrus and Lu assume that utilities are discounted, but this plays no role in the proof of Claim 3, other than the influence it has on SPE payoffs. They further assume that bargaining takes place in the interval \([-T,0]\) rather than [0, T], but this only serves the purpose of simplifying their notations. Finally, they assume that all players (except the proposer) vote on a made proposal, while we assume that voting stops at the first rejection. This difference is unimportant: with only minor modifications to our argument, Proposition 3.2 could be proven assuming all players respond to each proposal, and as easily, Claim 3 of Ambrus and Lu could be proven assuming that voting stops at the first rejection.
4.2 Diskin et al. (2011)
For convex n-person bargaining problems, Diskin et al. (2011) define and axiomatically characterize generalized Raiffa solutions, a family of solutions that bridge the gap between the discrete and the continuous Raiffa solution. Given \(p\in (0,1]\) and a convex problem \(S\in {\mathcal {B}}\), the corresponding generalized Raiffa solution is defined as \(\varphi ^{p}(S):=\lim _{t\rightarrow \infty }x^{t}\) where \(x^{0}:=\bar{0}\) and
for all \(t\in {\mathbb {N}}_{0}\). When \(p=1\), this solution corresponds to the discrete Raiffa solution, and as \(p\rightarrow 0\) it approaches the continuous Raiffa solution (see Theorem 6 of Diskin et al.). Like these two solutions, a generalized Raiffa solution is obtained as the limit point of a series (or path) generated by a particular difference (or differential) equation. As indicated in Sect. 2, Diskin et al. were the first to parametrize this series (or path) in terms of time, rather than the utility of a numeraire player. It is this innovation that makes the connection between the continuous Raiffa solution and our non-cooperative bargaining game intuitive.
Based on the game of Myerson (1991), Diskin et al. further provide non-cooperative support for their solutions. Let \(p\in (0,1]\), let S be a convex problem in \({\mathcal {B}}\), and let \(\{x^{t}\}_{t\in {\mathbb {N}}_{0}}\) be the series generated by (6). Then for each \(k\ge 0\), they define a game \(G^{k}\) with k rounds, as follows. In the game \(G^{0}\), no actions occur, and players realize zero payoffs. In the first round of the game \(G^{k}\) with \(k\ge 1\), the game moves to \(G^{0}\) with probability \(1-p\), and with probability p a random order is drawn. The first player in this order makes a proposal \(x\in S\), which all subsequent players in this order, one after the other, either accept or reject. In case of rejection, the game moves to \(G^{k-1}\). In case of unanimous acceptance, the proposal is implemented.
Theorem 4.1
(Diskin et al. 2011) For each \(k\ge 0\), there exists a unique SPE in \(G^{k}\). In this equilibrium, if i is selected as proposer in the first round she proposes \((m_{i}(x^{k},S),x_{-i}^{k})\) and all players accept it. The expected payoff in \(G^{k}\) is \(x^{k}\).Footnote 12
From this result it follows that as \(k\rightarrow \infty \), the unique expected SPE payoffs in \(G^{k}\) converge to the generalized Raiffa solution associated with the probability p. Then using the approach of Trockel (2011), this leads to exact support for the generalized Raiffa solutions. While the continuous Raiffa solution is approached by the generalized Raiffa solutions as \(p\rightarrow 0\), it is itself not a generalized Raiffa solution. Hence, Diskin et al. do not provide an exact support result. To the best of our knowledge, we are not aware of any exact support results for the continuous Raiffa solution.
Notes
See Serrano (2005) for a relatively recent survey on the Nash program.
If utilities are transferable, both the discrete and the continuous Raiffa solution divide the surplus equally among the agents. Hence, these solutions are only of interest when utilities are non-transferable.
For \(x,y\in {\mathbb {R}}^{n}\), \(x\ge y\) is taken to mean \(x_{i} \ge y_{i}\) for all \(i\in N\); the vector inequalities >, \(\le \) and < are similarly defined.
For a closed set \(S\in {\mathbb {R}}^{n}\), \(\partial (S):=S{\setminus } \text{ int }(S)\), where \(\text{ int }(S)\) denotes the interior of S.
For \(x,y\in {\mathbb {R}}^{n}\), we define \(xy:=(x_{1}y_{1},\ldots ,x_{n}y_{n})\).
While the subsequent response order is irrelevant, it is important that the proposer responds first to her own proposal. See Remark 1 below.
Note that the identities of the rejecters at all times \(t_{l}\), \(l=1,\ldots ,k-1\), can be inferred from the identity of the proposer at \(t_{l+1}\); the proposer is the rejecter of the time-\(t_{k}\) proposal.
The addendum to this paper provides a more elaborate discussion of Ambrus and Lu’s (2015) results than presented here, in particular, of their Claim 3. Specifically, we draw the distinction between this result and our Proposition 3.2, and motivate more carefully the different approach by which we prove our result.
A monotonic TU game is defined by a set of players \(N=\{1,\ldots ,n\}\) with \(n>1\), and a characteristic function \(V:2^{N}\rightarrow {\mathbb {R}}_{+}\), where V(C) denotes the worth of the coalition \(C\subseteq N\), and is such that for all \(C_{1}\subseteq C_{2}\subseteq N\), \(V(C_{1}) \le V(C_{2})\).
Note that this result is not entirely correct—i.e., there is a multiplicity of SPE. However, also here the expected SPE payoffs are unique, and as indicated, in \(G^{k}\) given by \(x^{k}\).
References
Ambrus A, Lu S-E (2015) A continuous-time model of multilateral bargaining. Am Econ J: Microecon 7:208–249
Anbarci N, Sun C-J (2012) Asymmetric Nash bargaining solutions: a simple Nash program. Econ Lett 120:211–214
Binmore K, Rubinstein A, Wolinsky A (1986) The Nash bargaining solution in economic modelling. RAND J Econ 17:176–188
Bloch F (1996) Sequential formation of coalitions in games with externalities and fixed payoff division. Game Econ Behav 14:90–123
Bloch F, Diamantoudi E (2011) Non-cooperative formation of coalitions in hedonic games. Int J Game Theory 40:263–280
Britz V, Herings PJJ, Predtetchinski A (2010) Non-cooperative support for the asymmetric Nash bargaining solution. J Econ Theory 145:1951–1967
Britz V, Herings PJJ, Predtetchinski A (2014) On the convergence to the Nash bargaining solution for action-dependent bargaining protocols. Game Econ Behav 86:178–183
Chae S, Yang J-A (1994) An \(N\)-person pure bargaining game. J Econ Theory 62:86–102
Chatterjee K, Dutta B, Ray D, Sengupta K (1993) A non-cooperative theory of coalitional bargaining. Rev Econ Stud 60:463–477
Conley JP, Wilkie S (1994) Implementing the Nash extension bargaining solution for non-convex problems. Rev Econ Des 1:205–216
Conley JP, Wilkie S (1996) An extension of the Nash bargaining solution to non-convex problems. Game Econ Behav 13:26–38
Diskin A, Koppel M, Samet D (2011) Generalized Raiffa solutions. Game Econ Behav 73:452–458
Haller H (1986) Non-cooperative bargaining of \(N\ge 3\) players. Econ Lett 22:11–13
Harsanyi J, Selten R (1972) A generalized Nash solution for two-person bargaining games with incomplete information. Manag Sci 18:80–106
Herrero M-J (1989) The Nash program: non-convex bargaining problems. J Econ Theory 49:266–277
Huang C-Y (2002) Multilateral bargaining: conditional and unconditional offers. Econ Theor 20:401–412
Imai H, Salonen H (2000) The representative Nash solution for two-sided bargaining solutions. Math Soc Sci 39:349–365
Kalai E (1977a) Nonsymmetric Nash solutions and replications of 2-person bargaining. Int J Game Theory 6:129–133
Kawamori T (2008) A note on selection of proposers in coalitional bargaining. Int J Game Theory 37:525–532
Krishna V, Serrano R (1996) Multilateral bargaining. Rev Econ Stud 63:61–80
Kultti K, Vartiainen H (2010) Multilateral non-cooperative bargaining in a general utility space. Int J Game Theory 39:677–689
Laruelle A, Valenciano F (2008) Noncooperative foundations of bargaining power in committees and the Shapley–Shubik index. Game Econ Behav 63:341–353
Livne Z (1989) Axiomatic characterizations of the Raiffa and the Kalai- Smorodinsky solutions to the bargaining problem. Oper Res 37:972–980
Ma AC, Manove M (1993) Bargaining with deadlines and imperfect player control. Econometrica 61:1313–1339
Miyakawa T (2008) Non-cooperative foundation of \(n\)-person asymmetric Nash bargaining solution. J Econ Kwansei Gakuin Univ 62:1–18
Myerson R (1991) Game theory: analysis of conflict. Harvard University Press, Cambridge, MA
Nash J (1950) The bargaining problem. Econometrica 18:155–162
Nash J (1953) Two-person cooperative games. Econometrica 21:128–140
Peters H (2010) Characterizations of bargaining solutions by properties of their status quo sets. In: van Deemen A, Rusinowska A (eds) Collective decision making. Springer, Berlin
Peters H, van Damme E (1991) Characterizing the Nash and Raiffa bargaining solutions by disagreement point axioms. Mathe Oper Res 16:447–461
Raiffa H (1953) Arbitration schemes for generalized two person games. In: Kuhn HW, Tucker AW (eds) Contributions to the theory of games II. Princeton University Press, Princeton, NJ
Ray D, Vohra R (1999) A theory of endogenous coalition structures. Game Econ Behav 26:286–336
Rubinstein A (1982) Perfect equilibrium in a bargaining model. Econometrica 50:97–109
Selten R (1981) A non-cooperative model of characteristic function bargaining. In: Böhm V, Nachtkamp HH (eds) Essays in game theory and mathematical economics in honor of Oskar Morgenstern. Bibliografisches Institut, Mannheim, pp 131–151
Serrano R (2005) Fifty years of the Nash program, 1953–2003. Invest Econ 29:219–258
Sjöström T (1991) Ståhl’s bargaining model. Econ Lett 36:153–157
Ståhl I (1972) Bargaining theory. Economics Research Institute, Stockholm School of Economics, Stockholm
Suh S-C, Wen Q (2006) Multi-agent bilateral bargaining and the Nash bargaining solution. J Math Econ 42:61–73
Tanimura E, Thoron S (2008) A mechanism for resolving bargaining impasses between risk averse parties. Working paper GREQAM, nr. 2008–31
Trockel W (2011) An exact non-cooperative support for the sequential Raiffa solution. J Math Econ 47:77–83
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Proofs
Proofs
1.1 Proof of Lemma 2.1
Consider \(S\in {\mathcal {B}}\), and let \(\Vert \cdot \Vert \) denote the taxicab metric—i.e., for \(x\in {\mathbb {R}}^{n}\), \(\Vert x\Vert :=\sum _{i=1}^{n}|x_{i}|\). Let \(v,w\in S\cap {\mathbb {R}}^{n}_{+}\) with \(v\ge w\) be given, and let \(\{z^{k}\}_{k=0}^{n}\) be a sequence in \({\mathbb {R}}^{n}_{+}\), iteratively defined by \(z^{0}:=v\) and \(z^{k}:=(w_{k},z^{k-1}_{-k})\) for each \(k=1,\ldots ,n\). In other words, \(z^{1}\) is obtained by decreasing the first entry of \(z^{0}=v\) from \(v_{1}\) to \(w_{1}\), \(z^{2}\) is obtained by decreasing the second entry of \(z^{1}\) from \(v_{2}\) to \(w_{2}\), and so on. Since \(w\ge \bar{0}\) and \(v\in S\) it follows by comprehensiveness of S that each \(z^{k}\) is an element of \(S\cap {\mathbb {R}}^{n}_{+}\). By construction, \(z^{k}\) and \(z^{k-1}\) only differ in the k-th coordinate, if at all. For \(k\in N\) and \(i\in N{\setminus } k\), \((m_{i}(z^{k}),z_{-i}^{k})\) and \((m_{i}(z^{k-1}),z_{-i}^{k-1})\) are in \(\partial S\cap {\mathbb {R}}^{n}_{+}\). Since \(S\in {\mathcal {B}}\), it then follows from condition (A1) that
Moreover, \(|m_{k}(z^{k})-m_{k}(z^{k-1})|=0\le K|w_{k}-v_{k}|\). Then for all \(i\in N\),
Therefore, \(\Vert \lambda m(w)-\lambda m(v)\Vert =\sum _{i=1}^{n}\lambda _{i}|m_{i}(w)-m_{i}(v)|\le K\Vert w-v\Vert \).
Now consider any \(v,w\in S\cap {\mathbb {R}}^{n}_{+}\), and let \(u\in {\mathbb {R}}^{n}\) with \(u_{i}:=\min \{v_{i},w_{i}\}\) for all \(i\in N\). Note that \(u\in S\cap {\mathbb {R}}^{n}_{+}\), and that for all \(i\in N\), \(|w_{i}-v_{i}|=|u_{i}-w_{i}|+|u_{i}-v_{i}|\). Then by the above,
Then since \(\lambda _{i}\le 1\) for all i, \(\Vert \lambda (m(w)-w)-\lambda (m(v)-v)\Vert \le (K+1)\Vert w-v\Vert \), as desired. \(\square \)
1.2 Proposition 3.2: Proofs of Claims
Proof of Claim 3.3
Let \(y:=r({\mathcal {T}})+\alpha ^{*}(p({\mathcal {T}})-r({\mathcal {T}}))\) where \(\alpha ^{*}:=\max \{\alpha \mid r({\mathcal {T}})+\alpha (p({\mathcal {T}})-r({\mathcal {T}}))\in S\}\). By the arguments in Lemma 2.1 and the fact that \(m(y)=y\),
Then since \(\Vert p({\mathcal {T}})-r({\mathcal {T}})\Vert >0\) and \(n>1\), \(\alpha ^{*}\ge 1/(1+nK)>1/n(1+K)\). By the choice of \(\tau \), \(\overline{\theta }^{0}\le r({\mathcal {T}})+(1-e^{-\tau })(p({\mathcal {T}})-r({\mathcal {T}}))<r({\mathcal {T}})+\alpha ^{*}(p({\mathcal {T}})-r({\mathcal {T}}))=y\). Since \(y\in S\), the claim follows by comprehensiveness of S. \(\square \)
Proof of Claim 3.4
Observe that
Furthermore, \(\lambda _{i}\le 1\) for all \(i\in N\). Then for all \(i\in N\) and \(t\in I\),
Assume that \(\overline{\theta }^{k}\ge \overline{\theta }^{k+1}\ge \underline{\theta }^{k+1}\ge \underline{\theta }^{k}\) for some \(k\in {\mathbb {N}}_{0}\). Then for all \(i\in N\) and \(t\in I\),
Hence, \(\overline{\theta }^{k}\ge \overline{\theta }^{k+1}\ge \underline{\theta }^{k+1}\ge \underline{\theta }^{k}\) for all \(k\in {\mathbb {N}}_{0}\). \(\square \)
Proof of Claim 3.5
Since in the interval I, any player i who is the designated next proposer can unilaterally secure \(r_{i}({\mathcal {T}})\) by rejecting all proposals she may get to make in I, \({\underline{r}}_{i}(t)\ge r_{i}({\mathcal {T}})\) for all \(t\in I\). Hence, \({\underline{r}}\ge r({\mathcal {T}})=\underline{\theta }^{0}\), establishing the first part of the claim.
Suppose that at time \(t\in [{\mathcal {T}},T]\), player j is the designated next proposer. By Lemma 3.1 and the initial assumption that the proposition holds on \([{\mathcal {T}},T]\), i’s expected payoff is then given by \(r_{i}(t)\) if \(j=i\), and by
otherwise. Since \(r_{i}\) is a strictly decreasing function, \(q_{i}^{j}(t)\le r_{i}(t)\) for all \(t\in [{\mathcal {T}},T]\). Suppose now that at \(t\in I\), player j is the designated next proposer. If j’s process does not produce an arrival in \([t,{\mathcal {T}}]\)—an event that occurs with probability \(e^{-\lambda _{j}({\mathcal {T}}-t)}\)—i’s expected payoff is at most \(r_{i}({\mathcal {T}})\), regardless whether \(j=i\) or \(j\ne i\). If j’s process does produce an arrival within \([t,{\mathcal {T}}]\), say at s, then i’s (expected) payoff at s is bounded from above by \(p_{i}({\mathcal {T}})\), again, regardless whether \(j=i\) or \(j\ne i\). To see this, note that any proposal in I that gives i strictly more than \(p_{i}({\mathcal {T}})\) gives some \(j'\ne i\) strictly less than \(r_{j'}({\mathcal {T}})\), and is thus rejected. Then since \(\lambda _{j}\le 1\),
for all \(t\in I\). Hence, \({\overline{q}}^{j}\le \overline{\theta }^{0}\) for all \(j\in N\). \(\square \)
Proof of Claim 3.6
Let a player i be the proposer at \(t\in I\). It is first shown that \({\underline{p}}_{i}(t)\ge m_{i}(\overline{\theta }^{k}(t))\). Suppose, contrary to what we want, that there is an SPE and a time-t history in \(H_{i}^{p}\), such that i’s (expected) payoff at time t—say \({\tilde{p}}_{i}\)—is strictly below \(m_{i}(\overline{\theta }^{k}(t))\). Then \((m_{i}(\overline{\theta }^{k}(t)),\overline{\theta }^{k}_{-i}(t))\in S\) and \(({\tilde{p}}_{i},\overline{\theta }^{k}_{-i}(t))\lneq (m_{i}(\overline{\theta }^{k}(t)),\overline{\theta }^{k}_{-i}(t))\). Hence, by strict comprehensiveness of S there exists a \(v\in S\) with \(v_{i}>{\tilde{p}}_{i}\) and \(v_{j}>\overline{\theta }_{j}^{k}(t)\) for all \(j\ne i\). It is next argued that i can profitably deviate by proposing v, which is in contradiction with SPE.
Thus suppose that i proposes v. If the last player in the response order, player \(i-1\), gets to respond, then she accepts, since by the induction hypothesis, rejecting yields at most \({\overline{r}}_{i-1}(t)\le \overline{\theta }_{i-1}^{k}(t)\), while accepting yields \(v_{i-1}>\overline{\theta }_{i-1}^{k}(t)\). Thus, if \(i-1\)’s predecessor in the response order, player \(i-2\), gets to respond, and she accepts, i’s proposal will be unanimously accepted. Then \(i-2\) realizes \(v_{i-2}\) by accepting, and at most \(\overline{\theta }^{k}_{i-2}(t)\) by rejecting, which by the induction hypothesis means that \(i-2\) accepts. In general, if a player j gets to respond, then by accepting she induces all of her successors in the response order to accept as well. Since unanimous acceptance gives her a payoff of \(v_{j}\), while rejection yields at most \(\overline{\theta }^{k}_{j}(t)\), j accepts.
To see that \({\overline{p}}_{i}(t)\le m_{i}(\underline{\theta }^{k}(t))\), assume that there is an SPE and a time-t history in \(H_{i}^{p}\), such that i’s (expected) payoff at time t—say \({\hat{p}}_{i}\)—is strictly higher than \(m_{i}(\underline{\theta }^{k}(t))\). By Claim 3.5, a rejection proposal would give player i at most \(\overline{\theta }^{0}_{i}(t)\); since
player i realizes \({\hat{p}}_{i}\) by means of an accepted proposal. But then there is a player \(j\ne i\) who is offered strictly less than \(\underline{\theta }_{j}^{k}(t)\), and accepts. This player could profitably deviate by rejecting, which contradicts SPE. \(\square \)
Proof of Claim 3.8
By the Lebesgue monotone convergence theorem and its reverse,
for all \(i\in N\) and \(t\in I\). Define the function \(h(t):=\Vert \overline{\theta }({\mathcal {T}}-t)-\underline{\theta }({\mathcal {T}}-t)\Vert \) on I, where \(\Vert \cdot \Vert \) is again the taxicab metric. Observe that
By Grönwall’s lemma, \(h(t)\le h(0)e^{(1+K)t}\) for all \(t\in I\). Since \(h(0)=0\) and \(h(t)\ge 0\) for all \(t\in I\), \(\underline{\theta }=\overline{\theta }\). By Lemma 3.1 and the observation that \(\overline{\theta }({\mathcal {T}})=\underline{\theta }({\mathcal {T}})=r({\mathcal {T}})\), it then follows that \(\overline{\theta }=\underline{\theta }=r\). That \(m(\underline{\theta })=m(\overline{\theta })=p\) then follows by continuity of m. \(\square \)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Driesen, B., Eccles, P. & Wegner, N. A non-cooperative foundation for the continuous Raiffa solution. Int J Game Theory 46, 1115–1135 (2017). https://doi.org/10.1007/s00182-017-0567-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-017-0567-9