Surplus efficiency of ex ante investments in matching markets with nontransferabilities

Abstract

Does a competitive equilibrium in a matching market provide adequate incentives for investments made before the market when utility is not perfectly transferable? In a one-sided market with a continuum of agents and finite types there is a constrained surplus efficient equilibrium, when a social planner can only affect investments but not payoffs nor matches, if an equal treatment property holds in equilibrium. Sufficient (but not full) utility transferability in a well defined sense implies this property. Ex post efficiency of payoffs (i.e., individual payoffs maximize the surplus in each match) alone is not sufficient to ensure that equilibrium investments maximize aggregate surplus.

1 Introduction

Do equilibrium allocations and payoffs in matching markets provide adequate incentives for investments in attributes that are relevant to matching partners and are made before the market? This is a relevant question, in particular for policy discussion concerning education acquisition and labor markets. For instance, there appear to be widespread concerns that—possibly because of asymmetric information (see Bénabou and Tirole (forthcoming))—salaries in the labor market may not adequately reflect the social marginal benefit of employees’ productivity or human capital, distorting incentives for education investment. Similarly, when admission to good schools and colleges, and thus access to high quality peers in the classroom, is based partly on parents’ income through user fees or house prices in the presence of borrowing constraints, rewards to prior effort in education acquisition or early childhood investments will be distorted.

The question has attracted considerable attention in the literature. Cole et al. (2001b) show that surplus efficient investments are in the equilibrium set when utility is perfectly transferable.¹ At the other extreme, for strictly nontransferable utility, such that surplus has to be split equally among partners, Peters and Siow (2002) establish Pareto (though not necessarily surplus) efficiency of investments in a two-sided matching market. Bhaskar and Hopkins (2014) point out the limits of this result, and Gall et al. (2006) provide an example of surplus inefficient investments in a one-sided market when utility is less than perfectly transferable and distorts the matching pattern. Gall et al. (2009) find investment distortions in form of simultaneous over-investment at the top and under-investment at the bottom, and analyze rematching policies. Mailath et al. (2013) examine the relation of the dimensionality of the price system and potential investment distortions in a two-sided market. This raises the question of the degree of utility transferability required to ensure that investments maximize aggregate surplus. Evaluating allocations in terms of surplus efficiency appears reasonable from a normative, ex ante perspective (in the sense of Harsanyi 1953), and from a positive point of view when surplus relates to output.

In essence, nontransferable utility may distort ex ante investments away from the surplus maximizing allocation through two possible channels. First, payoff distortions may cause the equilibrium assignment to differ from the first best. That is, given equilibrium investments and payoffs there may be another assignment that is not necessarily stable but generates higher aggregate surplus, which may affect incentives. Second, given an equilibrium assignment nontransferabilities may cause the equilibrium payoffs to not adequately reflect the externalities that an agent’s investment generates on potential matches. This paper shall be concerned with the second channel only; analyzing surplus efficiency of the matching pattern and possible remedies is done elsewhere (Gall et al. 2009).

One obvious way in which nontransferable utility may affect equilibrium payoffs is in that they may not maximize joint surplus in each match formed in equilibrium. That is, ex post efficiency of surplus may fail in that given an equilibrium assignment and investments, in some matches a different surplus division would increase joint surplus. This implies, of course, that also the associated equilibrium investment incentives are distorted away from a surplus efficient allocation that maximizes aggregate surplus by choosing investments and surplus distribution in matches.

As fully transferable utility ensures that payoffs are ex post efficient and an equilibrium allocation maximizes aggregate surplus (see Cole et al. 2001b among others), the first observation in this paper is perhaps a little surprising: ex post efficiency of equilibrium payoffs does not guarantee a surplus efficient allocation. The reason for this is that with nontransferabilities ex post efficiency leaves open the possibility that two agents with the same attribute receive strictly different equilibrium payoffs ex post. Hence, the expected remuneration of this attribute at the investment stage (a convex combination of different payoffs) generally will not coincide with the social marginal contribution of this attribute (which is precisely the extra surplus generated in the match that an extra agent with the attribute will be assigned to, when all other agents obtain their equilibrium payoffs).

If, however, in equilibrium all agents with the same attribute receive the same payoff ex post, ex post efficiency guarantees that each attribute is remunerated with the social marginal surplus generated by having one more agent with that attribute. That is, when an equal treatment of equal attributes property holds, ex post efficiency of equilibrium payoffs implies that an equilibrium allocation is surplus efficient conditional on the equilibrium assignment. Since the surplus efficient allocation is also an investment cum matching equilibrium allocation this means that some equilibrium allocation is surplus efficient, absent coordination failures. One example are matching models where surplus has to be shared equally among partners and joint surplus is a strictly monotone function of attributes: the unique matching equilibrium has only homogeneous matches. Splitting the surplus is ex post efficient and satisfies the equal treatment property, so that these matching markets will generally have an investment and matching equilibrium that is surplus efficient.²

When equilibrium payoffs are not ex post efficient, the equal treatment property will still ensure that each attribute is remunerated commensurate with its marginal contribution to social surplus, albeit in terms of the payoffs constrained by nontransferabilities. Hence, the equal treatment property implies that an investment cum matching equilibrium will be constrained surplus efficient, i.e., constrained to the payoffs achievable in equilibrium given the nontransferabilities. This means a social planner who can adjust investments, but not the sharing of surplus, could not increase aggregate surplus given the matching. This result is particularly interesting in light of policies of rematching individuals, such as affirmative action, suggesting the resulting equilibrium will induce constrained efficient investment incentives.

The equal treatment property of equilibrium payoffs, which is key to the welfare properties, can be tied to the primitives: a sufficient condition for equal treatment is marginally transferable utility (MTU): partners in any match can transfer utility to each other at a bounded, strictly positive rate in each possible match of attributes.

The results are derived in a model of ex ante investments, made before a one-sided matching market with a continuum of agents. Costly investment determines the probability distribution over possible attributes an agent may attain. After attributes have realized agents enter the market, match into pairs, and jointly generate surplus, which depends on attributes. A matching equilibrium is a stable match with side payments, and equilibrium investments are optimal anticipating the matching equilibrium payoffs. Side payments are subject to nontransferabilities, captured by the Pareto frontier in each match, which may take any form between fully transferable and strictly nontransferable utility. Surplus in a match may not be monotone and transferability may vary between different attribute pairs, allowing for substantial heterogeneity in preferences over possible matches.³ The results follow from deriving the graph structure of the payoff externalities of a change in investments and using the structural properties of an equilibrium match of attributes.

The paper is organized as follows. Section 2 lays out the model framework and provides an example. The main result is in Sect. 3, complemented by an application to matching markets yielding full segregation. Section 4 concludes and the appendix contains proofs and details omitted in the text.

2 A model of matching and investments

An economy is populated by a continuum of agents I endowed with measure one. Agents are characterized by a type $\theta \in \Theta$ where $\Theta$ denotes a finite set of types. Before the match agents spend effort $e_i$ at a cost $c(e_i,\theta )$. The cost function is strictly increasing, strictly convex, and differentiable in $e_i$ and satisfies the Inada conditions. An individual’s attribute $a \in A$ is stochastic and depends on effort: exerting effort $e_i$ yields probability $p(a,e_i)$ of attaining attribute a. Attribute draws are independent across individuals. Suppose the set of attributes is finite. Probabilities add up to one, i.e., $\sum _{a \in A} p(a, e_i) = 1$ and are differentiable in $e_i$. Suppose the attribute distribution has full support by assuming that $p(a, e_i) \in (0, 1)$ for all $a \in A$ and all $e_i$.⁴

Matching market

Once attributes have realized, agents match into pairs. Unmatched agents obtain zero payoff, and a matched pair of agents (i, j) jointly generates surplus, leaving each partner with a real valued payoff from the match of $u_i$ and $u_j$. Joint surplus may depend on its distribution among partners (for instance due to moral hazard problems in the match, limited liability, or behavioral concerns), so that individual payoffs $u_i$ and $u_j$ satisfy

$$\begin{aligned} u_i \le \phi (a_i, a_j, u_j) \text{ with } u_j + \phi (a_i, a_j, u_j) \le y(a_i, a_j), \end{aligned}$$

where $y(a_i, a_j)$ denotes the maximum surplus in match $(a_i, a_j)$, which is assumed to be finite. $\phi (a_i, a_j, u_j)$ is the Pareto or utility possibility frontier in a match (i, j), giving i’s maximum payoff when j receives $u_j$, given attributes $a_i$ and $a_j$ (the notation follows Legros and Newman 2007). Suppose $\phi (a_i, a_j, u_j)$ is continuous and weakly decreases in $u_j$ with $\phi (a_i, a_j, 0) > 0$ and $\phi (a_i, a_j, u) = 0$ implies $u > 0$ for all $a_i, a_j \in A$. Since transferability may depend on the match of attributes $(a,a^\prime )$ some combinations may allow for full transferability, while others may not. This may be a source of gains from trades, as more transferability with some partner than with another may compensate for lower maximal joint surplus.

To see that $\phi (.)$ captures the degree of payoff transferability in a match, note that full transferability of utility corresponds to

$$\begin{aligned} \phi (a, a^\prime , u) = y(a, a^\prime ) - u, \text{ for } 0 \le u \le y(a,a^\prime ), \end{aligned}$$

which ensures that for every distribution of surplus in the match $(u_i, u_j)$ the joint surplus is maximized, i.e., $u_i + u_j = y(a_i, a_j)$. At the other extreme is strictly nontransferable utility, e.g., if joint surplus has to be shared at a fixed ratio, say $\delta \in [1/2, 1]$ with $\phi (a, a^\prime , u_j) = \delta y(a,a^\prime )$ for $u_j \le (1-\delta ) y(a, a^\prime )$, and $\phi (a, a^\prime , u_j) = (1-\delta ) y(a,a^\prime )$ for $(1-\delta ) y(a, a^\prime ) < u_j \le \delta y(a,a^\prime )$. The ratio could depend on the match, of course.

In most relevant applications surplus will monotonically increase as own effort investment cost increases, assume therefore

Assumption 1

(Investment Technology). Suppose that

• (i) expected payoff is monotone in investment: for all $a \in A$

  $$\begin{aligned} \sum _{a^\prime \in A} y(a, a^\prime ) \frac{\partial p(a^\prime , e_i)}{\partial e_i} > 0. \end{aligned}$$

  (1)

• (ii) $p (a, e_i) \in (0, 1)$ is an affine, strictly monotone function of $e_i$ for all $a \in A$.

Part (i) means that for any given attribute a the expected maximal joint surplus in a match increases in effort, which imposes some order on the attribute space, though attributes may well be multidimensional. Part (ii) ensures that first order conditions will pin down investments given a matching assignment (see “Appendix” for a generalization).

Timing

Events unfold as follows.

• 1. Nature draws cost types $\theta$.

• 2. Agents spend effort $e_i$.

• 3. Attributes $a_i$ realize.

• 4. Agents match into pairs in a frictionless market, agreeing on feasible payoffs $u_i$ and $u_j$.

Equilibrium concept

Denote the measure of attribute realization a given investments $e = (e_i)_{i \in I}$ in the matching market by q(a, e). The matching in pairs results in measures $\rho (a,a^\prime )$ of matched pairs of unordered attributes $(a,a^\prime ) \in A \times A$. For all attributes a any match is preferable to the singleton payoff 0. Therefore all agents match into pairs and feasibility of the match requires

$$\begin{aligned} q(a,e) = 2 \rho (a,a) + \sum _{a^\prime \ne a \in A} \rho (a,a^\prime ) \text{ for } a \in A. \end{aligned}$$

(2)

An equilibrium match $\rho$ pins down the attribute assignment $\mu$ that maps A into its power set, defined by $\mu (a) = \{a^\prime \in A: \rho (a, a^\prime ) > 0\}$ for all $a \in A$.

The solution concept for the matching market based on attributes is a stable match with side payments subject to nontransferabilities captured by the utility possibility frontiers. This is best interpreted as a competitive market for attributes, yielding market prices for attributes. Market payoffs and the matching pattern will depend on attribute measures q(a, e). An equilibrium is defined as follows.

Definition 1

(Matching market equilibrium) A matching market equilibrium $(u^*, \rho )$ are payoffs $u^*: I \mapsto {\mathbb {R}}$ and a matching of agents into pairs, such that measures $\rho = (\rho (a,a^\prime ))_{a, a^\prime \in A \times A}$ satisfy feasibility (2), and for all matched agents $i, j \in I$ payoffs are feasible, i.e., $u_i \le \phi (a_i, a_j, u_j)$, and there are no agents i and j with attributes $a_i$ and $a_j$ and payoffs $u_i, u_j$ such that $u_i \le \phi (a_i, a_j, u_j)$ and both $u_i > u^*_i$ and $u_j > u^*_j$.

Existence of a stable match and thus of a matching market equilibrium follows from Kaneko and Wooders (1986), as feasibility implies measures are preserved, the set of attributes A is finite, and per capita surplus is finite by assumption.

Note that rationing may be required when two agents with the same attribute obtain different equilibrium payoffs. Assume that agents with attribute a are assigned randomly with probabilities implied by the relative frequencies of matches $(a,a^\prime )$ for all $a^\prime \in \mu (a)$: an agent with attribute a is assigned to an agent with attribute $a^\prime$ with probability $\rho (a,a^\prime )/q(a,e)$ if $a \ne a^\prime$ and $2 \rho (a,a^\prime )/q(a,e)$ otherwise. This uniform rationing implies that all agents of the same attribute a have the same expected payoff in a match $(a,a^\prime )$. Denote this expected payoff by $Eu^*_a(a, a^\prime )$. Defining an attribute’s expected payoff by

$$\begin{aligned} v(a) = Eu^*_a(a, a) + \sum _{a^\prime \ne a \in \mu (a)} \frac{\rho (a,a^\prime )}{q(a,e)} [Eu^*_{a}(a, a^\prime ) - Eu^*_{a}(a, a)], \end{aligned}$$

(3)

an agent’s expected payoff at the investment stage is

$$\begin{aligned} Eu_i = \sum _{a \in A} p(a, e_i) v(a) - c(e_i, \theta _i). \end{aligned}$$

Individual effort is chosen before the market to maximize expected payoff anticipating matching market equilibrium payoffs. An equilibrium of the investment and matching problem is thus a profile of effort investments and a matching market equilibrium, such that investments are individually optimal given equilibrium payoffs resulting from the attribute distribution generated by the investments.

Definition 2

(Investment cum matching equilibrium) An investment cum matching equilibrium are investments $e^* = (e^*_i)_{i \in I}$ and a matching market equilibrium $(u^*, \rho )$ given the measures of attributes $q(a,e^*)$ induced by $e^*$, such that no individual $i \in I$ can obtain strictly higher expected payoff given the matching equilibrium $(u^*, \rho )$ choosing investment $e_i^\prime \ne e_i^*$.

The investment stage is an anonymous game, for which equilibrium existence has been established, for instance, by Mas-Colell (1984). Note that the investment cum matching equilibria relies on rational expectations of the matching equilibrium payoffs given aggregate investments. Therefore there may be multiple investment cum matching equilibria. Whether a matching equilibrium maximizes total surplus given the realized attributes depends on the properties of $\phi (a, a^\prime )$, see e.g. Legros and Newman (2007).

Since all agents with the same type face the same optimization problem before the market, and thus choose the same effort level $e_\theta$, partitioning the agent space I into intervals $I(\theta )$ such that $\theta _i = \theta$ for all $i \in I(\theta )$ for all $\theta \in \Theta$, will ensure that all $i \in I(\theta )$ will face the same distribution $p(a, e_\theta )$. Then for each $I(\theta )$ the frequency of each a converges to the expected frequency given $p(a, e_\theta )$.⁵ Therefore the realized measure of an attribute $a \in A$ given the different investments $(e_\theta )_{\theta \in \Theta }$ is given by

$$\begin{aligned} q(a,e) = \int _{i \in I} p(a, e_{\theta _i}) di. \end{aligned}$$

2.1 Efficiency benchmarks

Two different benchmarks can be used to evaluate efficiency of a matching cum investment equilibrium depending on whether a social planner is able to choose effort investment levels and the payoff distribution within matches, or is constrained to set investments, unable to affect nontransferabilities.

Surplus optimal allocation

Suppose first a social planner can choose investment levels and the surplus sharing to ensure $u_i + u_j = y(a_i,a_j)$ in all matches (i, j), i.e., the surplus is ex post efficient within matches. That is, a surplus optimal allocation solves

$$\begin{aligned} \max _{(e_i)_{i \in I}} \sum _{a \in A} \left( \rho (a,a) y(a,a) + \frac{1}{2} \sum _{a^\prime \ne a \in A} \rho (a,a^\prime ) y(a,a^\prime ) \right) - \int _I c(e_i, \theta _i) di, \end{aligned}$$

(4)

such that $\rho$ results as a matching market equilibrium assignment given e. The optimization is over investments e of a continuum of individuals, but since the investment cost is strictly convex and all individuals i of the same type $\theta$ have the same expected profits, they will have the same investment $e_\theta$ in optimum. With a finite type space the optimization is really only over a finite vector of investments.

Constrained surplus optimal allocation

If one is interested in surplus maximizing investments constrained on taking joint surplus in each match as given by the equilibrium payoffs, it suffices to substitute maximal surplus $y(a,a^\prime )$ with equilibrium surplus $\hat{y}(a_i,a_j) = u_i^* + u_j^*$ for all $a_i \in \mu (a_j)$ in the optimization problem (4):

$$\begin{aligned} \max _{(e_i)_{i \in I}} \sum _{a \in A} \left( \rho (a,a) \hat{y}(a,a) + \frac{1}{2} \sum _{a^\prime \ne a \in A} \rho (a,a^\prime ) \hat{y}(a,a^\prime ) \right) - \int _I c(e_i, \theta _i) di, \end{aligned}$$

(5)

such that $\rho$ results as a matching market equilibrium assignment given e. This formulation takes into account the non-transferabilities present at the matching equilibrium allocation, since $u_i^* = \hat{y}(a_i,a_j) - \phi (a_i, a_j, u^*_j)$ for an equilibrium match $a_j \in \mu (a_i)$.

2.2 Example: heterogeneous matches

To illustrate the result in the simplest way possible consider the following example with a binary attribute space $A = \{a_0, a_1\}$. Agents are homogeneous and share the cost function $c(e_i, \theta _i) = e_i^2/2$. Let $e_i \in (0, 1)$ and $p(a_1, e_i) = e_i$ and $p(a_0, e_i) = 1 - e_i$. Suppose that maximal joint surplus is

$$\begin{aligned} y(a_0, a_0) = 0 < y(a_0, a_1) = 4/3 < y(a_1, a_1) = 2, \end{aligned}$$

implying condition (1). Nontransferabilities are severe in that payoff has to be split equally in homogeneous matches, so that $u_i = y(a, a)/2$ in a match (i, j) with $a_i = a_j = a$. In a heterogenous match surplus $y(a_0, a_1)$ can be split equally, or according to a sharing rule: $u_i = \delta _0 y(a_0, a_1)$ if $a_i = a_0$ and $u_i = \delta _1 y(a_0, a_1)$ if $a_i = a_1$. Suppose for now that $\delta _0 + \delta _1 = 1$. This means that payoffs are ex post efficient, i.e., $u_i + u_j = y(a_i, a_j)$ for all matches $(a_i, a_j)$.

Matching market outcome

Starting with the matching market equilibrium outcome, suppose that

$$\begin{aligned} y(a_0, a_0)/2 \le \delta _0 y(a_0, a_1) \text{ and } \delta _1 y(a_0, a_1) \ge y(a_1, a_1)/2. \end{aligned}$$

(GDD)

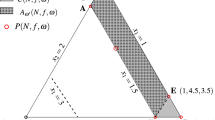
Condition (GDD) implies that a heterogeneous match $(a_0, a_1)$ is weakly preferred by both partners to their respective payoff in a homogeneous match. Hence, negative assortative matching will be an equilibrium (the only one when the inequalities are strict), exhausting all possible $(a_0, a_1)$ matches (i.e., $a_0 \in \mu (a_1)$ and $a_1 \in \mu (a_0)$) and matching the remaining agents in homogeneous matches. Figure 1 shows the possible assignments.

Fig. 1

Possible assignments in the example: attributes have the same measure (left), $a_1$ are scarce (middle), or $a_0$ are scarce (right)

Which regime will occur depends on parameters through the investment incentives. Recall that v(a) denotes the expected market equilibrium payoff for an attribute a. An agent i chooses effort $e_i$ to solve $\max _{e_i} p(a_1, e_i) [v(a_1) - v(a_0)] + v(a_0) - e_i^2/2$. The optimal effort choice $e^*_i$ satisfies

$$\begin{aligned} e^*_i = v(a_1) - v(a_0). \end{aligned}$$

(6)

Equilibrium payoffs v(a) depend on relative scarcity: if $q(a_1, e^*) > 1/2$ then both $(a_1, a_1)$ and $(a_0, a_1)$ matches will occur and

$$\begin{aligned} v(a_1) - v(a_0) = \frac{y(a_1, a_1)}{2} + \frac{q(a_0, e^*)}{q(a_1, e^*)} \left( \delta _1 y(a_0, a_1) - \frac{y(a_1, a_1)}{2} \right) - \delta _0 y(a_0, a_1). \end{aligned}$$

If, on the other hand, $q(a_1, e^*) < 1/2$, then

$$\begin{aligned} v(a_1) - v(a_0) = \delta _1 y(a_0, a_1) - \frac{q(a_1, e^*)}{q(a_0, e^*)} \left( \delta _0 y(a_0, a_1) - \frac{y(a_0, a_0)}{2} \right) - \frac{y(a_0, a_0)}{2}. \end{aligned}$$

Finally, $q(a_1, e^*) = 1/2$ iff $(\delta _1 - \delta _0) y(a_0, a_1) = 1/2$. That is, investment incentives $v(a_1) - v(a_0)$ strictly decrease in $q(a_1, e^*)$ and thus in investments. Hence, the matching cum investment equilibrium is unique.

To ease exposition focus on one case, say $q(a_1, e^*) > 1/2$, corresponding to the right graph in Fig. 1. Setting $\delta _1 = 4/5$ will ensure that $(\delta _1 - \delta _0) y(a_0, a_1) > 1/2$ and thus $q(a_1, e^*) > 1/2$. This yields equilibrium payoffs and effort: $v(a_0) = \delta _0 y(a_0, a_1) = 4/15$ and $e^* = (1+\sqrt{8/5})/3 \approx 3/4$.

Surplus optimal outcome

The parametrization ensures that

$$\begin{aligned} y(a_0, a_0) + y(a_1, a_1) < 2 y(a_0, a_1), \end{aligned}$$

(DD)

so that $\mu (a_0) = a_1$ and $\mu (a_1) = \{a_0; a_1\}$ maximize total surplus given attributes if $q(a_1, e) > q(a_0, e)$. Surplus optimal investments solving (4) satisfy

$$\begin{aligned} e_i = y(a_1, a_1) - y(a_0, a_1). \end{aligned}$$

(7)

That is, marginal cost equals the expected marginal benefit of investment, which is given by turning an $(a_0, a_1)$ match into an $(a_1, a_1)$ match. This implies $q(a_1, e) = 2/3 > 1/2$ in our setup, which is the unique optimum as $y(a_1, a_1) - y(a_0, a_1) < y(a_0, a_1) - y(a_0, a_0)$ by assumption.

Comparing equilibrium and surplus optimal investments yields

$$\begin{aligned} v(a_1) - v(a_0)&= \frac{y(a_1, a_1)}{2} + \frac{q(a_0, e^*)}{q(a_1, e^*)} \left( \delta _1 y(a_0, a_1) - \frac{y(a_1, a_1)}{2}\right) - \delta _0 y(a_0, a_1) \\&> \frac{y(a_1, a_1)}{2} - \left( y(a_0, a_1) - \frac{y(a_1, a_1)}{2}\right) . \end{aligned}$$

That is, there is overinvestment in the investment cum matching equilibrium compared to the surplus optimal outcome. Given the investment cum matching equilibrium outcome, decreasing investments (for instance through taxation) will increase total surplus in the economy. That is, investments in the matching cum investment equilibrium are not surplus efficient.

This occurs despite the fact that payoffs are ex post efficient, i.e., $u_i + u_j = y(a_i, a_j)$ in all matches. However, the market equilibrium remunerates attribute $a_1$ ”too well” in $(a_0, a_1)$ matches: its payoff is strictly greater than its opportunity cost $y(a_1,a_1)/2$.

Equal treatment

The inefficiency above stems from a failure of equal treatment of equal attributes: $a_1$’s equilibrium payoff is greater in $(a_0, a_1)$ than in $(a_1, a_1)$ matches: $\delta _1 y(a_0, a_1) > y(a_1,a_1)/2$. To see this suppose now:

$$\begin{aligned} \delta _1 y(a_0, a_1) = y(a_1, a_1)/2. \end{aligned}$$

(8)

Negative assortative matching remains an equilibrium as (GDD) still holds.⁶ Suppose that payoffs are still ex post efficient ($\delta _0 = 1 - \delta _1$), so that $v(a_1) = y(a_1, a_1)/2$ and $v(a_0) = y(a_0, a_1) - y(a_1, a_1)/2$, and

$$\begin{aligned} e^*_i = y(a_1, a_1) - y(a_0, a_1). \end{aligned}$$

(9)

Hence, when all agents with attribute $a_1$ obtain the same payoff for $q(a_1, e^*) \ge 1/2$ (which holds as argued above) investments are surplus efficient.

Suppose now that (8) still holds, but payoffs are not ex post efficient, i.e., $\delta _0 < 1 - \delta _1$, say $\delta _0 = 1/8$. If $q(a_1, e^*) \ge 1/2$, $v(a_1) = y(a_1, a_1)/2$ and $v(a_0) = \delta _0 y(a_0, a_1)$, yielding

$$\begin{aligned} e^*_i = y(a_1, a_1)/2 - \delta _0 y(a_0, a_1) > y(a_1, a_1) - y(a_0, a_1). \end{aligned}$$

(10)

In this parametrization indeed $q(a_1, e^*) = 5/6 \ge 1/2$. That is, investment incentives are not surplus optimal as equilibrium payoffs are not ex post efficient. Accessing the surplus optimal outcome would require to force $(a_0, a_1)$ matches to split the surplus, however, compromising stability of the match.

Ex post inefficient payoffs and constrained efficiency

Often the social planner is limited to adjusting investment and cannot affect the surplus sharing among matching partners. The constrained surplus optimal allocation accounts for this, and takes the joint surplus in the matching equilibrium as given, i.e., $\hat{y}(a_0, a_1) = (\delta _0 + \delta _1) y(a_0, a_1)$, and $\hat{y}(a,a) = y(a,a)$ for $a = a_0, a_1$. With $\delta _0 = 1/8$ and $\delta _1 = 3/4$, $\hat{y}(a_1, a_1) + \hat{y}(a_0, a_0) < 2 \hat{y}(a_0, a_1)$, so that negative assortative matching still maximizes total surplus. For $\mu (a_1) = \{a_0; a_1\}$, both equilibrium and surplus optimal investments satisfy

$$\begin{aligned} e_i = \hat{y}(a_1, a_1) - \hat{y}(a_1, a_0) = y(a_1, a_1) - \delta _1 y(a_0, a_1) - \delta _0 y(a_0, a_1) = e_i^*. \quad \end{aligned}$$

(11)

That is, with equal treatment the matching cum investment equilibrium outcome coincides with the constrained surplus optimal outcome.

These results extend to other parametrizations, which may give rise to the remaining assignments shown in Fig. 1. The marginal surplus from investing depends on the changes of the frequencies of different matches. If $q(a_0, e^*) > q(a_1, e^*)$, more investment transforms an $(a_0, a_0)$ into an $(a_0, a_1)$ match, so that investments are surplus optimal if

$$\begin{aligned} e_i = y(a_0, a_1) - y(a_0, a_0). \end{aligned}$$

If $q(a_0, e^*) = q(a_1, e^*)$ (on the left in Fig. 1) a change in investments will change the attribute assignment $\mu$, adding new attribute matches, namely $(a_1, a_1)$ if e increases, and $(a_0, a_0)$ if e decreases. Hence, if $q(a_0, e^*) = q(a_1, e^*)$ market equilibrium investments are surplus optimal if

$$\begin{aligned} e^*_i \in [y(a_1, a_1) - y(a_0, a_1), y(a_0, a_1) - y(a_0, a_0)], \end{aligned}$$

(12)

which is ensured if market payoffs are ex post efficient and satisfy equal treatment in all three allocations depicted in Fig. 1.

That is, conditions for optimality depend on the particular properties of the attribute assignment $\mu$, and in particular on whether the assignment will change discretely in response to a marginal change in investment. Interpreting the attribute assignment as a graph will be useful to establish a more general result in the next section. For now it is easily checked that the efficiency result above carries over to the cases other than $q(a_0, e^*) < q(a_1, e^*)$. This is summarized in the following proposition.

Proposition 1

(Simple example) Suppose that conditions (GDD) and (DD) hold. Then under equal treatment, i.e. condition (8), a matching cum investment equilibrium is constrained surplus optimal, and surplus optimal if equilibrium payoffs are ex post efficient.

That is, conditional on the match (under the assumption market equilibrium and surplus optimal match coincide), a social planner cannot change investments alone to increase aggregate surplus when equilibrium payoffs satisfy an equal treatment property. Equal treatment of attributes in all equilibrium matches ensures that each attribute is paid its marginal contribution to social surplus, possibly constrained by utility nontransferabilities. Otherwise, remuneration differs across matches and in some match an attribute is either under- or overpaid. If additionally equilibrium payoffs are ex post efficient then investments are surplus optimal.

3 General case

The result illustrated above generalizes beyond the simple example. Return therefore to the more general environment laid out in Sect. 2.

3.1 Equal treatment

The efficiency result above hinges on equal treatment of equal attributes. Define the equal treatment property accordingly as follows.

Definition 3

A matching market equilibrium satisfies the equal treatment property, if individual payoffs $u_i^*$ depend only on attributes, and for all $a \in A$, $u^*_a(a,a^\prime ) = u^*_a(a,a^{\prime \prime })$ for all $a^\prime , a^{\prime \prime } \in \mu (a)$, or, in terms of utility possibility frontiers:

$$\begin{aligned} v(a) = \phi (a,a^\prime , v(a^\prime )) \text{ for } \text{ all } a, a^\prime \in A \text{ with } \rho (a,a^\prime ) > 0. \end{aligned}$$

(ET)

This is precisely condition (8) above. It is rather undesirable to state an efficiency result relying on a property of equilibrium payoffs. The following proposition relates the equal treatment property to the primitives in form of the degree of utility transferability, details are in the “Appendix”.

Proposition 2

(Equal treatment property) The equal treatment property holds in a matching market equilibrium $(u^*, \rho )$ if $\phi (a, a^\prime , u)$ is differentiable in u and for all $a, a^\prime \in A$ for $u \in [0, \phi (a,a^\prime ,0)]$

$$\begin{aligned} 0 > \frac{\partial \phi (a,a^\prime , u)}{\partial u} > - \infty . \end{aligned}$$

(MTU)

Condition (MTU) states that for any match $(a,a^\prime )$ and given some feasible sharing of surplus, marginally increasing the payoff of one agent marginally decreases the payoff of the other one, independently of whether this decreases or increases joint surplus. This property holds if partners in a match can exchange utility at a bounded, positive rate for every feasible division of surplus. That is, if utility is marginally transferable for every feasible surplus sharing, a matching market equilibrium will have the equal treatment property.

3.2 Main result

Thus equipped it is possible to state the main result.

Theorem 1

(Surplus efficiency of ex ante investments) Let Condition (MTU) hold. Then there is an investment cum matching equilibrium such that equilibrium investments are constrained surplus efficient, so that a social planner cannot increase aggregate surplus by changing only investments.

To prove this result start by establishing that under equal treatment ex post efficiency of payoffs implies surplus efficiency. This then implies that an equilibrium is constrained surplus efficient, i.e., surplus efficient if payoffs are constrained by nontransferabilities to the payoffs reached in equilibrium. For (constrained) surplus efficiency note first that it is sufficient to show that the necessary conditions of the investment cum matching equilibrium coincide with the necessary conditions of a surplus efficient allocation. This is because any surplus efficient allocation that satisfies the necessary conditions of the investment cum matching equilibrium is in fact an investment cum matching equilibrium allocation.

Start by characterizing the matching cum investment equilibrium. An individual i of type $\theta _i$ chooses effort $e_i$ to solve $\max _{e_i} \sum _{a \in A} p(a,e_i) v(a) - c(e_i,\theta _i)$. The optimal effort choice $e^*_i$ satisfies

$$\begin{aligned} \sum _{a \in A} v(a) \frac{\partial p(a, e^*_i)}{\partial e_i} = \frac{\partial c(e^*_i, \theta _i)}{\partial e_i}. \end{aligned}$$

(13)

This pins down for each type $\theta$ a unique individually optimal investment $e^*_\theta (v(a))$ for equilibrium payoffs v(a) given by (3) and determined by the matching equilibrium given $e^*$. That is, an investment cum matching equilibrium need not be unique, explaining the qualifier in the theorem.

The next step is to show the necessary conditions (13) are consistent with the necessary conditions with respect to marginal deviations of investment in a (constrained) surplus efficient allocation. This is in fact sufficient to prove the theorem, because if the necessary conditions of the investment cum matching equilibrium allocation and the (constrained) surplus efficient allocation coincide, then the (constrained) surplus efficient allocation must be an investment cum matching equilibrium. This is because the necessary conditions (13) determine investments e given the equilibrium attribute assignment $\mu$ and, if they are satisfied in a (constrained) surplus efficient allocation, equilibrium investments e and the associated matching allocation with assignment $\mu$ will also be a (constrained) surplus efficient allocation. Hence, a (constrained) surplus efficient allocation that satisfies conditions (13) will be an investment cum matching equilibrium.

Therefore it is in order to focus on marginal deviations of effort investment, i.e., to examine deviations conditional on the match. Here another complication arises, as even a marginal change of investments may produce a discrete change of the associated equilibrium attribute assignment $\mu$. Hence, a marginal investment change may potentially yield a discrete change of marginal benefits. If $\mu$ remains unchanged on the other hand, measures $\rho (a,a^\prime )$ given in (2) are differentiable with respect to q(a, e) and thus with respect to $e_\theta$, and a first order condition approach can be used. This is guaranteed when the attribute assignment $\mu$ satisfies a property that is inspired by graph theory: the graph generated by $\mu$ has at least one cycle.

The matching market equilibrium as a graph

The set of attributes A and the assignment $\mu$ define an undirected graph G with a set of vertices A and a set of edges $E = \{(a,a^\prime ) : a^\prime \in \mu (a)\}$, denoting attribute matches. Let C denote the set of connected components in G. For instance, if all matches are homogeneous (i.e., $a_0$ only match with $a_0$ and $a_1$ with $a_1$) in equilibrium (full segregation), then $\rho (a, a^\prime ) > 0$ iff $a = a^\prime$, so that $\mu (a) = a$ for all $a \in A$. Hence, each vertex $a \in A$ has only one edge, (a, a) and is a connected component, so that the set of components is $C = A$.

What follows focuses on matching market equilibria such that each connected component $c \in C$ has at most as many edges as vertices. An equilibrium with this property always exists, and the surplus maximizing one for given attributes has this property. It necessarily holds if the equilibrium is unique. See “Appendix” for details on this and the next statements. Denote the sets of vertices and edges in c by $A^c$ and $E^c$ to state the following fact.

Fact 1

In a graph G associated to an equilibrium assignment $\mu$ such that $|E^c| \le |A^c|$ for each connected component c, in each connected component either

• (i) c contains exactly one cycle of length $n \ge 0$ of $n+1$ vertices $\{a_0; \ldots ; a_n\}$ and edges $(a_n, a_0)$ and $(a_i, a_{i+1})$ for $i=1,\ldots ,n-1$, or

• (ii) $a \notin \mu (a)$ for all $a \in A^c$ and $|A^c| > |E^c|$, then c does not contain a cycle.

That is, for each component either $|A^c| = |E^c|$ and c contains a cycle or an edge (a, a) (which is a cycle of length 0), or $|A^c| > |E^c|$ and c has at least two terminal vertices. For instance, the left assignment in Fig. 1 corresponds to case (ii), whereas the other two assignments have cycles (of length 0, linking an attribute to itself) and thus fall into case (i).

Whether an equilibrium assignment $\mu$ contains a cycle can be tied to whether it responds to a marginal change in investments e. Recall that measures $\rho (.)$ satisfy the system of equations (2). If $|A| > |E|$, then G has a component c with $|A^c| > |E^c|$. For this component the measures $\rho (.)$ solve

$$\begin{aligned}&q(a, e) = \sum _{a^\prime \in \mu (a)} \rho (a, a^\prime ) \text{ for } a \in A^c. \end{aligned}$$

Starting at some $a_0$ with $|\mu (a_0)| = 1$ this implies that

$$\begin{aligned} \sum _{i=0}^{n} (-1)^{i+1} \sum _{a \in A^c : \, d(a, a_0) = i} q(a,e) = 0, \end{aligned}$$

where $d(a, a_0)$ indicates the distance (minimal path length) between a and $a_0$, and $n = \max _{a \in A^c} d(a, a_0)$. Therefore a marginal change of a type $\theta$’s investments $e_\theta$, changing measures q(a, e), violates the condition, unless the changes of the measures exactly offset each other, that is:

$$\begin{aligned} \sum _{i=0}^{n} (-1)^{i+1} \sum _{a \in A^c : \, d(a, a_0) = i} \frac{\partial q(a,e)}{\partial e_\theta } = 0 \text{ for } \text{ all } c \in G \text{ with } |A^c| > |E^c|. \end{aligned}$$

(14)

That is, unless condition (14) holds, the assignment $\mu$ must change (adding new matches or removing old ones) in response to an investment change. If all components contain as many edges as vertices, they contain a cycle, corresponding to case (i) of Fact 1, so that any marginal change in measures $q(a,e(\theta ))$ is accommodated by adjusting measures of attribute pairs in the cycle, without needing to adjust the graph. This yields the following fact.

Fact 2

If, and only if, in the graph G associated to an equilibrium assignment $\mu$ the number of vertices strictly exceeds the number of edges, $|A| > |E|$, then a marginal change in investment e implies that $\mu$ is no longer an equilibrium assignment, unless condition (14) holds.

The following definition characterizes equilibrium assignments $\mu$ that do not change in response to a marginal change in investments.

Definition 4

(Static assignment) An equilibrium assignment $\mu$ is static if the number of edges in the graph G induced by $\mu$ at least equals the number of vertices.

Static case

Suppose first that $\mu (a)$ indeed satisfies Definition 4. In this case investments that solve (4) must satisfy for each $\theta \in \Theta$

$$\begin{aligned}&\sum _{a \in A} \left( \frac{\partial \rho (a,a)}{\partial e_\theta } y(a,a) + \sum _{a^\prime \ne a \in A} \frac{\partial \rho (a,a^\prime )}{\partial e_\theta } \frac{y(a,a^\prime )}{2} \right) = \int _{i \in I :\, \theta _i = \theta } \frac{\partial c(e_\theta , \theta )}{\partial e_\theta } di \quad \end{aligned}$$

(15)

Since the first derivative of expected surplus (1) decreases in investment $e_{(\theta )}$, as p(.) is concave and c(.) strictly convex in $e_\theta$, (15) is a sufficient and necessary condition for a solution of the social planner’s problem (4) conditional on $\mu$. The LHS of (15) can be decomposed into the set of disjoint connected components C, since by definition $\rho (a,a^\prime )=0$ for any $a \in A^c$ and $a^\prime \notin A^c$: for every type $\theta$

$$\begin{aligned} \sum _{c \in C} \sum _{a \in A^c} \left( \frac{\partial \rho (a, a)}{\partial e_\theta } y(a,a) + \sum _{a^\prime \ne a \in A^c} \frac{\partial \rho (a, a^\prime )}{\partial e_\theta } \frac{y(a,a^\prime )}{2} \right) \!=\! \int _{i \in I : \, \theta _i = \theta } \frac{\partial c(e_\theta , \theta )}{\partial e_\theta } di, \qquad \end{aligned}$$

(16)

That is, the marginal cost of investment must equal its expected marginal return. An increase in investment will increase the measure of some matches and decrease the one of others. The marginal return of investment is then given by the difference in joint surplus in the matches whose measures increase and those whose measures decrease. These marginal matches will depend on the entire graph defined by the attribute assignment. In the example above more investment simply transformed some $(a_0, a_1)$ into $(a_1, a_1)$ matches, but in general the change of measures needs to be traced through each component. Doing this for an assignment $\mu$ and comparing equilibrium investments to the social planner’s solution yields the following proposition, its proof can be found in the “Appendix”.

Proposition 3

Suppose an equilibrium assignment $\mu$ is static and the equal treatment property holds for equilibrium payoffs $u^*$. Then, given $\mu$, investments $e^*$ are surplus efficient for any $p(a, e_i)$ satisfying (1) if, and only if, equilibrium payoffs $u^*$ maximize joint surplus in each match.

This implies, of course, that investments $e^*$ are constrained surplus efficient, when the social planner is constrained to payoffs $\hat{y} (a,a^\prime ) = v(a) + v(a^\prime )$. That is, if equal treatment holds, then a social planner who cannot alter the sharing of surplus nor the match cannot increase aggregate surplus by changing investments, and investment are constrained surplus efficient.

Non-static case

Focus now on equilibrium assignments $\mu$ that are not static and contain a component c satisfying case (ii) of Fact 1. That is, a marginal change of investment triggers a change in the equilibrium assignment of attributes $\mu$, since there is no cycle in c to adjust to balance any excess or shortfall of attributes. This change in assignment may correspond to a jump in in the marginal benefits from investment, as they depend on the precise graph of $\mu$. Hence, for efficiency of a particular investment profile $e^*$ that is compatible with a non-static graph, the social marginal cost of investing needs to lie between the different social marginal returns resulting from a discrete change in assignment due to either increasing or decreasing investment, as in condition (12) in the simple example above.

Therefore, the necessary condition (15) for the static case need not hold. Instead investments are characterized by lower and upper bounds that depend on the change in assignment $\mu$ that is triggered by a change in investment of some type $\theta$. For each type $\theta$ denote by $\overline{\mu }_\theta$ ($\underline{\mu }_\theta$) the equilibrium assignment and measures $\overline{\rho }_\theta$ ($\underline{\rho }_\theta$) that arises if all agents of type $\theta$ increase (decrease) their investment $e_i$. The counterpart of the necessary condition in the static case (15) is now for all $\theta \in \Theta$

$$\begin{aligned}&\int _{i \in I : \, \theta _i = \theta } \frac{\partial c(e_\theta , \theta )}{\partial e_\theta } di \le \sum _{a \in A} \left( \frac{\partial \underline{\rho }_\theta (a,a)}{\partial e_\theta } y(a,a) + \sum _{a^\prime \ne a \in A} \frac{\partial \underline{\rho }_\theta (a,a^\prime )}{\partial e_\theta } \frac{y(a,a^\prime )}{2} \right) \text{ and } \\&\int _{i \in I : \, \theta _i = \theta } \frac{\partial c(e_\theta , \theta )}{\partial e_\theta } di \ge \sum _{a \in A} \left( \frac{\partial \overline{\rho }_\theta (a,a)}{\partial e_\theta } y(a,a) + \sum _{a^\prime \ne a \in A} \frac{\partial \overline{\rho }_\theta (a,a^\prime )}{\partial e_\theta } \frac{y(a,a^\prime )}{2} \right) . \end{aligned}$$

That is, the marginal cost of effort for all types needs to be between the return of marginally increasing and marginally decreasing investment for each type. The following proposition states that for surplus efficiency the upper and lower bounds have to reflect the true marginal returns, which under equal treatment is assured by ex post efficiency.

Proposition 4

Suppose an equilibrium assignment $\mu$ is not static. If the equal treatment property holds for payoffs for all equilibrium assignments $\underline{\mu }_\theta$ and $\overline{\mu }_\theta$, then equilibrium investments are surplus efficient if $u^*_i + u_j^* = y(a_i, a_j)$ for equilibrium payoffs associated to assignments $\mu$, $\underline{\mu }_\theta$ and $\overline{\mu }_\theta$ for $\theta \in \Theta$.

Hence, as long as equal treatment holds, conditional on the assignment $\mu$ (including the one that is surplus efficient) the only distortion of investments stems from ex post inefficiency of equilibrium payoffs. This in turn implies that there is an investment cum matching equilibrium such that a social planner who cannot alter the surplus sharing within matches cannot increase aggregate surplus by changing investments.

3.3 Application: full segregation

A particular class of static equilibrium assignments are those characterized by full segregation (only matches of the type (a, a)). Suppose that surplus $y(a, a^\prime )$ in each match has to be split equally. Imposing some order on A, $\min \{y(a,a); y(a^\prime , a^\prime )\} < y(a,a^\prime ) < \max \{y(a,a); y(a^\prime , a^\prime )\}$ for all $a, a^\prime \in A$, implies that equilibrium matching takes the form of full segregation: $\mu (a) = a$ for all $a \in A$ for any distribution of attributes, as all agents have the same preference ranking over attributes to match with and less attractive attributes cannot outbid more attractive attributes (see e.g. Legros and Newman 2010). Hence, the graph induced by the equilibrium is static with components $C = A$ for any investment e.

The investment cum matching equilibrium satisfies equal treatment, as $\phi (a, a, v(a)) = y(a,a)/2 = v(a)$ for all $a \in A$ by assumption (surplus has to be split equally). Since also $u_i^* + u_j^* = y(a_i, a_j)$ by definition, the Theorem above implies that the investment cum matching equilibrium is surplus efficient. For more general payoffs that imply an equilibrium assignment with full segregation the Theorem implies the following useful corollary.

Corollary 1

(Full segregation) Suppose that an investment cum matching equilibrium necessarily induces an assignment $\mu (a) = a$ for all $a \in A$. The investment cum matching equilibrium is surplus efficient if, and only if payoffs are ex post efficient, i.e., if $\phi (a, a, y(a,a)/2) = y(a,a)/2$ for all $a \in A$. The investment cum matching equilibrium is constrained surplus efficient if condition (MTU) holds.

Surplus efficiency follows from the assumption that equal division maximises joint surplus in each match as this implies both equal treatment and ex post efficiency of payoffs. The condition that equal division of the payoff is ex post efficient in a match of agents with equal attributes seems likely to be satisfied in most, if not all, relevant applications. A counterexample in the “Appendix” demonstrates that it may fail, although rather extreme assumptions are needed.

4 Discussion and conclusion

This paper has examined competition in large matching markets where participants have an opportunity to invest in their attributes relevant for matching payoffs before entering the matching market. The main result is positive: if payoffs satisfy a relatively mild property, namely that matching surplus is marginally transferable at any strictly positive rate between matching partners, an investment cum matching equilibrium allocation will be constrained efficient, in the sense that a social planner who cannot alter the payoff distribution within matches cannot increase aggregate surplus by altering investment alone. A limitation of the result is that there may be multiple equilibria due to rational expectation, meaning there is still scope for coordination failure (explored e.g. by Bhaskar and Hopkins 2014, in a two-sided framework).

The result is quite relevant from a policy perspective: not only does it suggest that taxing or subsidising investments will have limited effect on aggregate surplus, but also, and perhaps more importantly, the result has an interesting implication for the use of matching rules as a policy tool, for instance in form of affirmative action (as in Gall et al. 2009) or team formation. Given a modicum of transferability such policies will therefore yield constrained surplus efficient investments conditional on the matching that is imposed and given the payoffs in the matching stage.

Technically, transferability of matching surplus at a strictly positive rate implies that an equal treatment property holds in the matching equilibrium, which then ensures that ex post efficiency of payoffs ensures surplus efficiency, i.e., the only distortion of investment incentives stems from the nontransferabilities. This implies an interesting corollary when full segregation is necessarily the matching outcome: if equal sharing of surplus maximizes joint surplus in each match then an investment cum matching equilibrium resulting in full segregation is surplus efficient.

Appendix: Mathematical appendix

1.1 Relaxing assumption 1

Assumption (1) can be replaced by a more general investment technology. Suppose that every individual i chooses a portfolio of effort levels $e_{ai} \ge 0$ with $a \in A$. The probability $p_a(e_{ai})$ of attaining attribute a is differentiable, strictly concave and increases in $e_{ai}$. Let the cost $c(e_i, \theta _i)$ depend on an aggregate of portfolio investments $e_i = f(\sum _{a \in A} e_{ai})$, where f(.) is differentiable and strictly increases such that $\frac{\partial p_a (e_{ai})}{\partial e_{ai}} / \frac{\partial f(.)}{\partial e_{ai}}$ decreases, e.g., f(.) is the identity function.

In an investment cum matching equilibrium an individual chooses the optimal portfolio of effort, constrained by aggregate individual investment $e_i$. Since $\sum _{a \in A} p_a (e_{ai}) = 1$ there is $a_0$ with $p_{a_0} (e_{a_0i}) = 1 - \sum _{a \not a_0 \in A} p_a (e_{ai})$. Denote by $a_0$ the attribute that has least expected payoff $v(a_0)$. Then the optimal portfolio of effort solves $e_{a_0} = 0$ and

$$\begin{aligned} \max _{(e_{ai})_{a \ne a_0 \in A}} \sum _{a \in A} p_a(e_{ai}) [v(a) - v(a_0)] \text{ s.t. } f\left( \sum _{a \in A} e_{ai}\right) = e_i. \end{aligned}$$

Then $\frac{\partial p_a (e_{ai})}{\partial e_{ai}} [v(a) - v(a_0)] = \frac{\partial p_{a^\prime } (e_{a^\prime i})}{\partial e_{ai}} [v(a^\prime ) - v(a_0)]$ and the resource constraint determines the unique optimal effort portfolio $(e^*_{ai}(e_i))$. Note that all $e^*_{ai}(e_i)$, $a \ne a_0 \in A$, increase in $e_i$. This also defines the probabilities $p(a, e_i) = p_{ai}(e_{ai}^*(e_i))$ for all $a \in A$. Applying the envelope theorem, optimal aggregate individual investment $e_i$ is given by

$$\begin{aligned} \frac{ \frac{\partial p_a (e_{ai})}{\partial e_{ai}} [v(a) - v(a_0)] }{\frac{\partial f(\sum _{a \in A} e_{ai})}{\partial e_{ai}}} = \frac{\partial c(e_i, \theta _i)}{\partial e_i} \text{ for } \text{ any } a \ne a_0 \in A. \end{aligned}$$

Hence, the first order condition pins down a unique effort portfolio for each individual given the anticipated matching payoffs v(a).

An analogous argument holds for maximizing (constrained) total surplus. Surplus maximizing effort solves for every $\theta \in \Theta$

$$\begin{aligned} \max _{(e_{a\theta })_{a \in A}} \sum _{a \in A} \rho (a,a) y(a,a) + \sum _{a^\prime \ne a \in A} \rho (a, a^\prime ) \frac{y(a,a^\prime )}{2} \text{ s.t. } f\left( \sum _{a \in A} e_{a\theta }\right) = e_\theta . \end{aligned}$$

Again either $e_{a\theta } = 0$ or for $a, a^{\prime \prime } \in A$:

$$\begin{aligned}&\frac{\partial \rho (a,a)}{\partial e_{a\theta }} y(a,a) + \sum _{a^\prime \ne a \in A} \frac{\partial \rho (a, a^\prime )}{\partial e_{a\theta }} \frac{y(a, a^\prime )}{2} \\&\quad = \frac{\partial \rho (a^{\prime \prime } , a^{\prime \prime })}{\partial e_{a^{\prime \prime }\theta }} y(a^{\prime \prime } , a^{\prime \prime }) + \sum _{a^\prime \ne a \in A} \frac{\partial \rho (a^{\prime \prime } , a^\prime )}{\partial e_{a^{\prime \prime }\theta }} \frac{y(a^{\prime \prime }, a^\prime )}{2}. \end{aligned}$$

Again the envelope theorem ensures that optimal aggregate investment $e_\theta$ of individuals with type $\theta$ is given by

$$\begin{aligned} \frac{\frac{\partial \rho (a,a)}{\partial e_{a\theta }} y(a,a) + \sum _{a^\prime \ne a \in A} \frac{\partial \rho (a,a^\prime )}{\partial e_{a\theta }} y(a,a^\prime )}{\frac{\partial f(\sum _{a \in A} e_a)}{\partial e_{a\theta }}} = \int _{ i \in I : \, \theta _i = \theta } \frac{\partial c(e_\theta , \theta )}{\partial e_\theta }, \end{aligned}$$

for attributes with $e_{a\theta } > 0$. Since $\frac{\partial \rho (a,a^\prime )}{\partial e_{a \theta }}$ is zero or $\pm \frac{\partial p_a (e_{a \theta })}{\partial e_{a \theta }}$, concavity of $p_a(e_{a \theta })$ ensures a unique solution $e_\theta$.

To see that this technology nests affine functions $p(a,e_i)$, assume that, e.g., $p_a (e_{ai}) = \sqrt{e_{ai}}$, restrict the domain of $e_{ai}$ appropriately, and $f(.) = \sqrt{(.)}$. Then $p(a, e_i)$ is a linear function of $e_i$.

1.2 Edges and vertices

A necessary condition for a unique matching equilibrium $\mu (.)$ is that $|E^c| \le |A^c|$. Otherwise the system of equations

$$\begin{aligned} q(a,e) = \sum _{a^\prime \in \mu (a)} \rho (a,a^\prime ) + 2 \rho (a,a) \text{ for } a \in A^c \end{aligned}$$

(17)

has a solution $\rho _1$ such that $\rho _1(a,a^\prime ) = 0$ for some $a, a^\prime \in A^c$. Since all matches defined by $\mu$ cannot be blocked by other matches as $\mu$ is a matching equilibrium, the assignment defined by $\rho _1$ must also be a matching equilibrium, with $\mu _1 \ne \mu$. Hence, $|E^c| \le |A^c|$ is a necessary condition for uniqueness of $\mu$.

Suppose a matching equilibrium $\mu$ such that $|E^c| > |A^c|$. Then the maximal surplus satisfying (17) can be achieved by a choice of $\rho$ with $\rho (a,a^\prime ) = 0$ for some $a, a^\prime \in A^c$. Otherwise $\rho$ can still be changed such that surplus weakly increases, since if there is a change of $\rho$ that strictly decreases total surplus there must an opposite change that increases total surplus.

Finally, suppose that a matching equilibrium satisfies the equal treatment property and has $|E^c| > |A^c|$. Then choosing $\rho$ such that $\rho (a,a^\prime ) = 0$ for some $a, a^\prime \in A^c$ will not alter payoffs since by the equal treatment property all attributes are indifferent between all their matches.

1.3 Proof of fact 1

This fact re-states well-known results in graph theory. Let c be a connected component of G induced by an equilibrium assignment $\mu$.

(i) Suppose first c contains some a such that $a \in \mu (a)$. Suppose that c also contains a cycle. Then $|E^c| > |A^c|$, since a cycle has as many edges as vertices. The same argument can be applied to the case of c containing some $a^\prime \ne a$ with $a^\prime \in \mu (a^\prime )$. Suppose now that $a \notin \mu (a)$ for all $a \in A^c$ and $|E^c| = |A^c|$. If there is no cycle in c, then c must be a chain, since c is assumed to be a connected component, and the number of vertices must exceed the number of edges by one. This contradicts the assumption. Therefore c must contain a cycle. c cannot contain more than one cycle since this would imply that the number of edges exceed the number of vertices in a connected component.

(ii) Suppose that $|E^c| < |A^c|$, which implies $|E^c| = |A^c|-1$. Then a connected component c cannot contain a cycle of any length, as a cycle has as many edges as vertices, but $|E^c| < |A^c|$. Hence, c is a tree, possibly with many terminal nodes.

1.4 Proof of proposition 2

Suppose the condition in the proposition holds, but equal treatment in equilibrium does not. Then in equilibrium there is an attribute $a_i$ with $a_k, a_j \in \mu (a_i)$ such that $\phi (a_i,a_j,u^*_j) > \phi (a_i,a_k,u^*_k)$. But then an agent with attribute $a_i$ who is matched to an agent with an attribute $a_k$, and an agent with an attribute $a_j$ who is matched to an agent with attribute $a_i$, find it both strictly profitable to match together if there are payoffs $\phi (a_i,a_k,u^*_k) + \epsilon _i$ with $\epsilon _i > 0$ for the one with $a_i$ and $u^*_j + \epsilon _j$ with $\epsilon _j > 0$ for the one with $a_j$, such that

$$\begin{aligned} \phi (a_i,a_k,u^*_k) + \epsilon _i \le \phi (a_i,a_j,u^*_j + \epsilon _j). \end{aligned}$$

(18)

Since $\phi (a_i,a_j,u^*_j) > \phi (a_i,a_k,u^*_k)$ by assumption, condition (18) is ensured if the function $\phi (a_i, a_k, u)$ is continuous in u and strictly decreasing with a slope bounded away from $- \infty$. Noting that $\phi (a,a^\prime ,u)$ is non-increasing in u by definition, this is implied by the condition in the proposition.

1.5 Proof of proposition 3

It is useful to distinguish between static graphs that have a cycle of length 0 and those that have a cycle of greater length, requiring slightly more notation.

Cycle of length 0

Suppose a component c contains $a \in A^c$ with $a \in \mu (a)$; denote it by $a_0$. Define the distance $d(a,a^\prime )$ of two vertices $a, a^\prime \in c$ by the number of edges in the shortest path connecting them, e.g. $d(a,a^\prime ) = 1$ if $a^\prime \in \mu (a)$. Denote the maximum distance from vertex $a_0$ by $n = \max _{a \in A^c} d(a_0, a)$ and the set of vertices with common distance j from $a_0$ by $A^c_j = \{a \in A^c : d(a_0,a) = j\}$, see Fig. 2.

Fig. 2

Example for a component c with one vertex $a_0$ that links to itself

The necessary condition (16) can be written as $\sum _{c \in C} \sigma ^c = \nu (\theta ) \frac{\partial c(e_\theta , \theta )}{\partial e_i}$, where $\nu (\theta )$ denotes the measure of agents with type $\theta$ and

$$\begin{aligned} \sigma ^c =&\sum _{a \in A^c} \left( \frac{\partial \rho (a, a)}{\partial e_\theta } y(a,a) + \sum _{a^\prime \ne a \in A^c} \frac{\partial \rho (a, a^\prime )}{\partial e_\theta } \frac{y(a,a^\prime )}{2} \right) . \end{aligned}$$

denotes the effect of a change of investments for a type $\theta$ on attributes in component c. It can be derived by summing up the effects on each match $(a,a^\prime )$ in c ordered by their distance from $a_0$:

$$\begin{aligned} \sigma ^c =&y(a_0, a_0) \frac{\partial \rho (a_0,a_0)}{\partial e_\theta } + \sum _{j = 1}^n \left( \sum _{a_j \in A_j^c} \sum _{a_{j-1} \in A_{j-1}^c \cap \mu (a_j)} y(a_{j-1}, a_{j}) \frac{\partial \rho (a_{j-1}, a_j)}{\partial e_\theta } \right) . \end{aligned}$$

Let $a_j \in A_j^c$ and $a_{j-1} \in A_{j-1}^c$. Then $\rho (a_{j-1}, a_j) = q(a_j, e)$ if $a_j$ is a terminal vertex ($\mu (a_j) = a_{j-1}$). For $a_j$, $j \ge 1$, that are not terminal vertices:

$$\begin{aligned} \rho (a_{j-1}, a_j) = q(a_j, e) - \sum _{a_{j+1} \in \mu (a_j) \cap A_{j+1}^c} \rho (a_j, a_{j+1}). \end{aligned}$$

Finally, $\rho (a_0,a_0) = q(a_0, e)/2 - \sum _{a_1 \in A_1^c} \rho (a_0, a_1)/2$. Since there is a chain from any node to node $a_0$, the predecessor node of a node $a_j \in A_j$ can be defined recursively by

$$\begin{aligned} a^{-t} (a_j) = A_{j-t} \cap \mu (a^{-(t-1)}(a_j)),\, j \ge t > 0, \text{ and } a^{-0} (a_j) = a_j. \end{aligned}$$

For instance, $a^{-t} (a_j) = a_0$ for any $a_j \in A_t$. Denoting by $\nu (\theta )$ the measure of type $\theta$, $\sigma ^c$ can be expressed as

$$\begin{aligned} \frac{\sigma ^c}{\nu (\theta )} =&\frac{y(a_0, a_0)}{2} \frac{\partial p (a_0, e_\theta )}{\partial e_\theta } + \sum _{a_1 \in A_1^c} \left( y(a_0, a_1) - \frac{y(a_0,a_0)}{2} \right) \frac{\partial p(a_1, e_\theta )}{\partial e_\theta } \\&+ \sum _{a_2 \in A_2^c} \left( y(a^{-1}(a_2), a_2) - y(a^{-2}(a_2),a^{-1}(a_2)) + \frac{y(a_0,a_0)}{2} \right) \frac{\partial p (a_2, e_\theta )}{\partial e_\theta } + \cdots \\&+ \sum _{a_n \in A_n^c} \left( y(a^{-1}(a_n), a_n) - \cdots (-1)^n \frac{y(a_0,a_0)}{2} \right) \frac{\partial p(a_n,e_\theta )}{\partial e_\theta }. \end{aligned}$$

Define the “externality” that vertices closer to $a_0$ have on those further apart by

$$\begin{aligned} x(a_j) = y(a^{-1} (a_j), a_j) - x(a^{-1} (a_j)) \text{ for } j = 1,\ldots , n, \end{aligned}$$

(19)

and $x(a_0) = y(a_0,a_0)/2$. Then

$$\begin{aligned} \frac{\sigma ^c}{\nu (\theta )} = \frac{y(a_0, a_0)}{2} \frac{\partial p (a_0, e_\theta )}{\partial e_\theta } + \sum _{j = 1}^n \left( \sum _{a_j \in A_j^c} \left[ y(a^{-1} (a_{j}), a_{j}) - x(a^{-1}(a_{j}))\right] \frac{\partial p (a_j, e_\theta )}{\partial e_\theta } \right) . \end{aligned}$$

(20)

To verify whether surplus efficient investments coincide with equilibrium investments recall that the latter were determined by

$$\begin{aligned} \sum _{c \in C} \sum _{a \in A^c} v(a) \frac{\partial p(a, e_\theta ^*)}{\partial e_\theta } = \frac{\partial c(e_\theta ^*, \theta _i)}{\partial e_i}. \end{aligned}$$

Hence, for each component c the condition $\sigma ^c/\nu (\theta ) = \sum _{a \in A^c} v(a) \frac{\partial p(a, e_\theta ^*)}{\partial e_i}$ is equivalent to

$$\begin{aligned}&\sum _{j = 1}^n \left( \sum _{a_j \in A_j^c} \left( y(a^{-1} (a_j), a_{j}) - x(a^{-1} (a_{j})) - v(a_j)\right) \frac{\partial p(a_j, e_\theta ^*)}{\partial e_i} \right) \nonumber \\&\quad + \left( \frac{y(a_0, a_0)}{2} - v(a_0)\right) \frac{\partial p (a_0,e^*_\theta )}{\partial e_i} = 0. \end{aligned}$$

(21)

This is implied by $v(a_j) = y(a^{-1} (a_j), a_{j}) - x(a^{-1} (a_j))$ for all $a_j \in A_j^C$ for $j = 1,\ldots ,n$. Recall that $x(a_j) = y(a^{-j} (a_j), a_{j}) - x(a^{-1} (a_j))$, which means that

$$\begin{aligned} v(a_j) = y(a^{-1} (a_j), a_{j}) - v(a_{j-1}) \text{ for } j > 0, \text{ and } v(a_0) = y(a_0,a_0)/2, \end{aligned}$$

(22)

implies (21). Note that (22) characterizes the equilibrium payoffs supporting a stable match under fully transferable utility: each attribute $a_j$’s payoff is determined by its value added to its match $a^{-1}(a_j)$.

Arbitrary cycles

Allow now for cycles that have length greater than 0, repeating the argument above replacing cycles of length 0 with larger ones. Let now $d^c(a)$ denote the distance of a vertex $a \in A^c$ to the cycle, e.g. $d^c(a) = 0$ if, and only if, a is part of the cycle. Then $n = \max _{a \in A^c} d^c(a)$ is the maximum distance from the cycle. Again $A^c_j = \{a \in A^c : d^c(a) = j\}$ denotes the set of vertices with common distance j from the cycle. Figure 3 shows an example.

Fig. 3

Example for a component c with a cycle (vertices $a_0, a_0^\prime$, and $a_0^{\prime \prime }$)

Still each node $a_j \in A^c_j$ with $j > 0$ has exactly one predecessor, denoted by $a^{a-1} (a_j)$ as above. The effects of a change in investment on attributes in component c, $\sigma ^c$, can be derived by summing up the effects on each pair $(a,a^\prime )$ in c ordered by their distance from the cycle:

$$\begin{aligned} \sigma ^c =&\sum _{a_0 \in A_0^c} \sum _{a_0^\prime \in \mu (a_0) \cap A_0^c} \frac{y(a_0, a_0^\prime )}{2} \frac{\partial \rho (a_0,a_0^\prime )}{\partial e_\theta } \\&+ \sum _{j = 1}^n \left( \sum _{a_j \in A_j^c} y(a^{-1} (a_j), a_{j}) \frac{\partial \rho (a^{-1} (a_j), a_j)}{\partial e_\theta } \right) . \end{aligned}$$

As above, if $a_j \in A_j^c$ is a terminal vertex then $\rho (a^{-1} (a_j), a_j) = q(a_j, e)$. Otherwise, $\rho (a^{-1}(a_j), a_j) = q(a_j, e) - \sum _{a_{j+1} \in \mu (a_j) \cap A_{j+1}^c} \rho (a_j, a_{j+1})$. Since each vertex in the cycle has exactly two neighbors, $\rho (a_0, a_0^\prime ) + \rho (a_0,a_0^{\prime \prime }) = q(a_0, e) - \sum _{a_1 \in \mu (a_0) \cap A_1^c} \rho (a_0, a_1)$ for any $a_0 \in A_0^c$ and $a_0^\prime , a_0^{\prime \prime } \in \mu (a_0) \cap A^c_0$. Denote by $n^0 = \lceil (|A_0^c|-1)/2\rceil$ the maximum distance between any two vertices in the cycle. Then the “externality” in the cycle that vertices closer to $a_0$ have on those further away can be expressed as

$$\begin{aligned} x(a_0) = \frac{1}{2} \sum _{j = 0}^{n^0 - 1} (-1)^j \sum _{a \in A^c_0 : \, d(a,a_0) = j} \sum _{a^\prime \in \mu (a) \cap A^c_0 : d(a^\prime ,a_0) \ge j} y(a, a^\prime ), \end{aligned}$$

(23)

and, using the recursive definition of $x(a_j)$ in (19) above,

$$\begin{aligned} \frac{\sigma ^c}{\nu (\theta )} = \sum _{a_0 \in A^c_0} x(a_0) \frac{\partial p (a_0, e_\theta )}{\partial e_\theta } + \sum _{j = 1}^n \left( \sum _{a_j \in A_j^c} \left( y(a^{-1} (a_{j}), a_{j}) - x(a^{-1}(a_{j}) ) \right) \frac{\partial p (a_j, e_\theta )}{\partial e_\theta } \right) .\nonumber \\ \end{aligned}$$

(24)

This expression coincides with (20) if $A^c_0 = a_0$, i.e. the cycle has length 0.

Again for each component c the condition $\sigma ^c/\nu (\theta ) = \sum _{a \in A^c} v(a) \frac{\partial p(a, e_\theta ^*)}{\partial e_\theta }$ is equivalent to

$$\begin{aligned}&\sum _{j = 1}^n \left( \sum _{a_j \in A_j^c} \left( y(a^{-1} (a_j), a_{j}) - x(a^{-1} (a_j)) - v(a_j)\right) \frac{\partial p(a_j, e_\theta ^*)}{\partial e_\theta } \right) \nonumber \\&\quad + \sum _{a_0 \in A_0^c} (x(a_0) - v(a_0)) \frac{\partial p (a_0,e^*_\theta )}{\partial e_\theta } = 0. \end{aligned}$$

(25)

Note that (25) becomes (21) if the cycle has length 0. Here $v(a_0) = x(a_0)$ holds if payoffs $v(a_0)$ solve the system of equations

$$\begin{aligned} v(a_0) = y(a_0, a_0^\prime ) - v(a_0^\prime ) \text{ for } \text{ all } a_0, a_0^\prime \in A_0^c \text{ with } a_0 \in \mu (a_0^\prime ). \end{aligned}$$

Hence, if equilibrium payoffs do not coincide with the matching market equilibrium payoffs under fully transferable utility, the conditions $v(a_j) = y(a^{-1}(a_j), a_{j}) - x(a^{-1}(a_j))$ or $v(a_0) = x(a_0)$ must fail for some attributes. Unless distortions for some attribute $a_j$ with predecessor $a_k$ exactly compensate this, (25) must fail. Even if for some attributes $a_j$ and $a_k$ the respective distortions in payoff exactly offset each other, this is not robust to a small change of $\frac{\partial p(a, e_i)}{\partial e_i}$, i.e., a marginal perturbation of the investment technology.

These arguments are summarized in the following statement.

Fact 3

(Static Assignments). Suppose an equilibrium assignment $\mu$ is static. Then, given $\mu$, equilibrium investments coincide with the ones chosen by a surplus maximizing social planner if, and only if for all $i \in I$

$$\begin{aligned}&\sum _{c \in C} \sum _{j = 1}^n \left( \sum _{a_j \in A_j^c} \left( x(a_{j}) - \phi (a^{-1} (a_j), a_j, u^*_{a^{-1} (a_j)}) \right) \frac{\partial p(a_j, e_\theta ^*)}{\partial e_\theta } \right) \nonumber \\&\quad + \sum _{c \in C} \sum _{a_0 \in A_0^c} (x(a_0) - v(a_0)) \frac{\partial p (a_0,e^*_\theta )}{\partial e_\theta } = 0, \end{aligned}$$

where $x(a_i)$ is defined by (19) and (23).

This condition is satisfied if equilibrium payoffs $u^*$ coincide with equilibrium payoffs when utility is fully transferable ($\phi (a,a^\prime ,u) = y(a,a^\prime ) - u$).

Suppose now that equal treatment holds, i.e. $v(a_j) = \phi (a_j, a_k, u_k^*)$ for all $a_k \in \mu (a_j)$ for all $a_j \in A$. Denote the joint payoff in a match $(a, a^\prime )$ by

$$\begin{aligned} \hat{y}(a,a^\prime ) = v(a) + v(a^\prime ). \end{aligned}$$

Then $v(a_j) = \hat{y}(a_{j-1},a_j) - v(a_{j-1})$ for $a_j \in A_j^c$ and $a_{j-1} \in A_{j-1}^c \cap \mu (a_j)$ for distances $j = 1, \ldots , n$ in component c of the graph G. Moreover, $v(a_0)$ with $a_0 \in A_0^c$ solve

$$\begin{aligned} v(a_0) = \hat{y}(a_0, a_0^\prime ) - v(a_0^\prime ) \text{ for } \text{ all } a_0, a_0^\prime \in A_0^c \text{ with } a_0 \in \mu (a_0^\prime ). \end{aligned}$$

Then the condition in Fact 3 is satisfied if $y(a, a^\prime ) = \hat{y}(a, a^\prime )$ for all $a, a^\prime \in A$ such that $a^\prime \in \mu (a)$, i.e., $u_i^* + u_j^* = y(a_i, a_j)$ for all matches (i, j). This means that under equal treatment a matching cum investment equilibrium is surplus efficient if payoffs are ex post efficient, independent of the investment technology $p(a, e_i)$. If payoffs are not ex post efficient the condition in Fact 3 will not be satisfied when allowing for marginal perturbations of the investment technology.

1.6 Proof of proposition 4

Fix $\theta$ and denote by $\underline{G}$ and $\overline{G}$ the graphs associated to $\underline{\mu }_\theta$ and $\overline{\mu }_\theta$, and their set of connected components by $\underline{C}$ and $\overline{C}$. A marginal change in investment implies that $\underline{G}$ and $\overline{G}$ will both contain a cycle each in some component. The marginal surplus resulting from an increase (decrease) of investment is then given by $\sum _{c \in \overline{C}} \overline{\sigma }^c$ and $\sum _{c \in \underline{C}} \underline{\sigma }^c$, respectively, with $\underline{\sigma }^c$ and $\overline{\sigma }^c$ defined by (24). There is no marginal deviation from equilibrium investments $e^*$ that can increase aggregate surplus if, and only if, for each type $\theta \in \Theta$

$$\begin{aligned} \int _{i \in I : \, \theta _i = \theta } \frac{\partial c(e^*_\theta , \theta )}{\partial e_\theta } \in \left[ \sum _{c \in \overline{C}} \overline{\sigma }^c, \sum _{c \in \underline{C}} \underline{\sigma }^c \right] . \end{aligned}$$

(26)

Privately optimal investments in the investment cum matching equilibrium imply

$$\begin{aligned} \frac{\partial c(e^*_\theta , \theta )}{\partial e_\theta } = \sum _{c \in \underline{C}} \sum _{a \in c} v (a) \frac{\partial p(a, e_\theta ^*)}{\partial e_\theta }. \end{aligned}$$

Denote by $\underline{v} (a)$ and $\overline{v} (a)$ the equilibrium payoffs in assignments $\underline{\mu }_\theta$ and $\overline{\mu }_\theta$ as defined above. Since $\mu$ is a stable assignment, the payoffs v(a) have to satisfy $v(a) \ge \overline{v} (a)$ for all a such that $\frac{\partial p(a, e_\theta ^*)}{\partial e_\theta } > 0$ and $v(a) \le \overline{v} (a^\prime )$ for all $a^\prime$ such that $\frac{\partial p(a^\prime , e_\theta ^*)}{\partial e_\theta } < 0$. That is, attributes that are scarcer under $\mu$ than under $\overline{\mu }$ receive weakly higher payoffs whereas attributes that are more abundant receive weakly lower payoffs. Analogously, $v(a) \le \underline{v} (a)$ for all a such that $\frac{\partial p(a, e_\theta ^*)}{\partial e_\theta } > 0$ and $v(a) \ge \underline{v} (a^\prime )$ for all $a^\prime$ such that $\frac{\partial p(a^\prime , e_\theta ^*)}{\partial e_\theta } < 0$.

This implies in particular that in an investment cum matching equilibrium for all agents i of type $\theta$

$$\begin{aligned} \frac{\partial c(e^*_\theta , \theta )}{\partial e_\theta } \in \left[ \sum _{a \in A} \overline{v} (a) \frac{\partial p(a, e_\theta ^*)}{\partial e_\theta }, \sum _{a \in A} \underline{v} (a) \frac{\partial p(a, e_\theta ^*)}{\partial e_\theta } \right] , \end{aligned}$$

(27)

with $\sum _{a \in A} \underline{v} (a) \frac{\partial p(a, e_\theta ^*)}{\partial e_\theta } \ge \sum _{a \in A} \overline{v} (a) \frac{\partial p(a, e_\theta ^*)}{\partial e_\theta }$.

Hence, using the definitions from above, given a matching equilibrium that is not static, a marginal change of investment cannot increase surplus, i.e., condition (26) holds, if

$$\begin{aligned} \sum _{c \in \overline{C}} \frac{\overline{\sigma }^c}{\nu (\theta )} \le \sum _{a \in A} \overline{v} (a) \frac{\partial p(a, e_\theta ^*)}{\partial e_\theta } \text{ and } \sum _{a \in A} \underline{v} (a) \frac{\partial p(a, e_\theta ^*)}{\partial e_\theta } \le \sum _{c \in \underline{C}} \frac{\underline{\sigma }^c}{\nu (\theta )}. \end{aligned}$$

(28)

Note that by the arguments above lower and upper bounds coincide, if equilibrium payoffs coincide with those when utility is perfectly transferable. Otherwise the investment technology has to exactly offset any distortions. Proposition 3 implies that if the equal treatment property holds for equilibrium payoffs in matches $\underline{\mu }$ and $\overline{\mu }$ surplus efficiency of equilibrium payoffs implies that both conditions in (28) hold with equality.

Example: moral hazard in partnerships

To illustrate the type of non-transferabilities needed for a counterexample, consider an application: the partnership problem. Two partners i and j exert effort $x_i$ and $x_j$, which affect the probability $g(x_i,x_j)$ that the partnership succeeds. In case of success the partnership’s revenue is $R(a_i, a_j)$, depending on partners’ attributes, otherwise it is 0. The success probability is given by

$$\begin{aligned} g(x_i,x_j) = x_i^\alpha x_j^{1-\alpha }. \end{aligned}$$

Let $\alpha \ge 1/2$. Exerting effort $x_i$ an agent incurs utility cost $x_i^2/2$. Non-transferabilities arise as partners agree on the revenue share s that goes to i, but cannot use lump sum transfers, e.g. due to liquidity constraints. Hence,

$$\begin{aligned}&u_i = s x_i^\alpha x_j^{1-\alpha } R(a_i,a_j) - x_i^2/2 \text{ and } u_j = (1-s) x_i^\alpha x_j^{1-\alpha } R(a_i,a_j) - x_j^2/2. \end{aligned}$$

Individual optimal effort choice pins down effort levels depending on s:

$$\begin{aligned}&x_i (s) = (\alpha s)^{\frac{1+\alpha }{2}} ((1-\alpha )(1-s))^{\frac{1-\alpha }{2}} R(a_i, a_j) \text{ and } \\&x_j (s) = (\alpha s)^{\frac{\alpha }{2}} ((1-\alpha )(1-s))^{\frac{2-\alpha }{2}} R(a_i, a_j). \end{aligned}$$

Therefore individual payoffs depend also on s and are given by

$$\begin{aligned}&u_i (s) = s (\alpha s)^{\alpha } ((1-\alpha )(1-s))^{1-\alpha } (1 - \alpha /2) R(a_i, a_j)^2 \text{ and } \\&u_j (s) = (1-s) (\alpha s)^{\alpha } ((1-\alpha )(1-s))^{1-\alpha } (1 - (1-\alpha )/2) R(a_i, a_j)^2. \end{aligned}$$

That is, the sharing rule s determines a pair of $u_i$ and $u_j$ and thus joint surplus in match (i, j). This can be used to construct the Pareto frontier,

$$\begin{aligned} \phi (a_i, a_j, u) = \arg \max _s u_i(s) \text{ s.t. } u_j(s) \ge u. \end{aligned}$$

The sharing rule that maximizes joint surplus in a match (i, j), $s^*$ solves

$$\begin{aligned} \max _s (\alpha s)^{\alpha } ((1-\alpha )(1-s))^{1-\alpha } R(a_i, a_j)^2 [(1+\alpha )/2 + (1/2 - \alpha )s)]. \end{aligned}$$

The surplus maximizing sharing rule $s^*$ is a function of $\alpha$ but not of R(a, a), and $s^* = 1/2$ if and only if $\alpha = 1/2$. Maximal surplus in match (i, j), $y(a_i,a_j) = u_i(s^*) + u_j(s^*)$ is

$$\begin{aligned} y(a_i, a_j) = \left( \alpha s^*\right) ^{\alpha } ((1-\alpha ) (1-s^*))^{1-\alpha } [(1+\alpha )/2 + (1/2 - \alpha )s^*] R(a_i, a_j)^2. \end{aligned}$$

Denote the sharing rule that allows to share joint surplus equally, such that that $u_i(\hat{s}) = u_j(\hat{s})$, by $\hat{s}$. Setting $u_i(\hat{s}) = u_j(\hat{s})$ implies $\hat{s} = (1+\alpha )/3$. Indeed $\hat{s} = 1/2 = s^*$ for $\alpha =1/2$. Otherwise $s^* > \hat{s}$ since $u_i(s) + u_j(s)$ strictly increases in s at $s = \hat{s}$.

Fig. 4

Utility possibility frontiers

Figure 4 depicts $\phi (a_i, a_j, u)$ for three different matches (a, a), $(a, a^\prime )$, and $(a^\prime , a^\prime )$ with $a > a^\prime$. The $45^\circ$ line pins down payoffs for equal sharing and the dashed lines indicate the surplus maximizing payoff sharing.

Suppose that $\mu (a) = a$ in equilibrium (this is implied by, e.g., $R(a,a) - R(a,a^\prime )$ sufficiently high for all $a > a^\prime$, see below). To verify that payoffs are not ex post efficient, compute the difference in $y(a,a)/2 = (u_i(s^*) + u_j(s^*))/2$ and $u_i(\hat{s}) = u_j(\hat{s}) = \phi (a,a,u_a^*)$:

$$\begin{aligned} \frac{y(a,a)}{2} - \phi (a,a,u_a^*) =&\frac{y(a,a)}{2} \left( \frac{\hat{s}}{s^*} \right) ^{\alpha } \left( \frac{1-\hat{s}}{1-s^*} \right) ^{1-\alpha } \frac{1 + \alpha + (1-2\alpha ) \hat{s}}{1 + \alpha + (1 - 2 \alpha ) s^*}. \end{aligned}$$

Since neither $s^*$ nor $\hat{s}$ depend on R(a, a) the difference is a constant fraction of $R(a,a)^2$. Hence, there is a constant $\kappa (\alpha ) > 0$ depending only on $\alpha > 1/2$, such that for all $a \in A$

$$\begin{aligned} y(a,a)/2 - E[\phi (a,a,u_a^*)] = \kappa (\alpha ) R(a,a)^2. \end{aligned}$$

Therefore investments are not surplus efficient unless the investment technology ($\partial p(a, e_i)/\partial e_i$) exactly compensates the differences $\kappa (\alpha ) R(a,a)^2$.

Hence, a social planner who could enforce a different surplus distribution than equal sharing could increase aggregate surplus. For instance, set $s^p = \hat{s} + \epsilon$ for each match (i, j). If $R(a,a) - R(a,a^\prime )$ is high enough for all $a > a^\prime$ full segregation remains the equilibrium outcome and thus $u_i (s^p) + u_j (s^p) > u_i(\hat{s}) + u_j(\hat{s})$ for all matches (i, j). This decreases the difference $y(a,a)/2 - E[\phi (a,a,u_a^*)]$ and increases both aggregate surplus and investments.

A sufficient condition to ensure full segregation is that the maximum utility attribute a can obtain when matching with $a^\prime < a$ falls short of sharing the surplus in a (a, a) match, that is, if for all $a, a^\prime \in A$ with $a^\prime < a$

$$\begin{aligned} \left( \frac{\overline{s}}{\hat{s}}\right) ^{1 + \alpha } \left( \frac{1 - \overline{s}}{1 - \hat{s}}\right) ^{1 - \alpha } \frac{2 - \alpha \overline{s}}{2 - \alpha \hat{s}} < \left( \frac{R(a,a)}{R(a,a^\prime )}\right) ^2, \end{aligned}$$

(29)

where $\overline{s} = \arg \max _{s} u_i(s)$,

$$\begin{aligned} \overline{s} = \frac{4 + 2\alpha + \alpha ^2 - \sqrt{(2 - \alpha )(8 - 6\alpha ^2 - \alpha ^3)}}{6 \alpha }. \end{aligned}$$

Note that (29) holds whenever the additional revenue generated by having a high attribute partner, $R(a,a) - R(a,a^\prime )$, is sufficiently great for all attributes.