Educational choice, initial wage and wage growth

Abstract

We study the effects of expected initial wages, expected wage growth, and observed and unobserved heterogeneity in the choice of college major in a sample of American college graduates. We propose a three-stage empirical model that relates future earnings to individual choices. In the first stage, starting from revealed choices, observed wages, and life-cycle wage profiles, we estimate the expectation on initial wages and wage growth from the individual point of view, where the panel structure of the data allows us to produce estimates corrected for self-selection bias. We find substantial differences in expected real wages and expected real wage growth between majors and that both characteristics of life cycle earnings influence major choice. Our parametric models show a strong correlation between salary trends and major choice, whereas semiparametric models yield less reliable results. We interpret our results as being consistent with agents being rational and as a validation for our estimation strategy based on counterfactual imputation.

1 Introduction

The major that a college student chooses can have a significant impact on their future earnings. Altonji et al. (2012b) estimate that the salary difference between an electrical engineer and a general education graduate is almost as large as the difference in earnings between a high school graduate and a college graduate. As a result, choosing a college major is just as important as deciding to attend college. However, despite a large body of research on how expectations of future earnings affect educational investments (Willis and Rosen 1979; Keane and Wolpin 1997; Belzil and Hansen 2002; Kaufmann 2014), evidence on what determines the choice of type of education is still thin and is not yet resolved. Some argue for the primary importance of monetary considerations (Berger 1988; Arcidiacono et al. 2012; Altonji et al. 2016b), while others emphasize the role of taste for a particular field or other non-pecuniary factors (Montmarquette et al. 2002; Beffy et al. 2012; Wiswall and Zafar 2015).

Previous studies have used either initial wages or average wages to assess how financial considerations affects major choice. This is an innocent assumption if those measures correlate positively with differences in present value of earning streams, but the age profile of wages vary considerably between majors. For example, a recent study (Deming and Noray 2020) found that applied science majors earn 44% more than non-STEM majors at age 24, but only 14% more at age 35. However, entry-level salaries for pure science majors such as biology, chemistry, physics, and mathematics tend to be low, but increase over time. Furthermore, the long-term payoff for STEM majors may be smaller than short-term comparisons suggest. This observation indicates that to fully understand the significance of financial considerations in selecting a college major, it is necessary to analyze the entire pattern of earnings over the course of one’s life. This is exactly what we do in this paper.

In this paper, we study how earnings over the life cycle affect the choice of university major in a sample of American college graduates. In contrast to most previous studies that addressed the same question¹ (Montmarquette et al. 2002; Arcidiacono 2004; Beffy et al. 2012; Wiswall and Zafar 2015), we separate the effect of initial wages and wage growth rates on the choice of major and show that initial wages and wage profiles differ considerably between majors and that both characteristics of life cycle earnings influence major choice. This distinction has rarely been made in previous research. To our knowledge, only Berger (1988) and more recently Hampole (2023) and Leighton and Speer (2023) have adopted it.

Our findings strongly support the idea that both entry-level salaries and wage growth rates have a positive effect on major selection. Increasing both the average initial salary and the average wage growth rate by one standard deviation increases the probability of choosing a major in social sciences by 16% and by up to 36% for humanities majors.

To understand the impact of expected wages on the choice of majors in college, we use the National Longitudinal Survey of Youth 1979 (NLSY79) and estimate a structural model in two steps. In the first, we exploit the panel structure of the NLSY79 to account for any time-invariant unobserved heterogeneity that could affect both the choice of major and the personal earning profile over the life-cycle. This data feature enables us to obtain consistent estimates for both wage components and to create meaningful counterfactual scenarios without relying on exclusion restrictions.²

In the second step, we include the corrected wage expectations as an explanatory factor in the major choice equation and estimate this equation both parametrically and semiparametrically. The two parametric models, multinomial logit and probit, that we estimate are the workhorses for estimating multinomial choice models. But these models impose quite strict and unappealing assumptions on the error structure.³ For this reason, we resort to the semiparametric estimators of Manski (1975) and Li (2011) which require only minimal distributional assumptions on the error term. The practical application of semiparametric techniques for the estimation of unordered choice models has been very limited so far.⁴ In our application, the assumption on the error structure that we impose is the common assumption that is the basis for any panel data estimation: we divide the error term in a time-constant fixed effect different across individuals and a time- and individual-dependent idiosyncratic error.

We find large differences in life-cycle earnings profiles across majors even after controlling for selection and unobserved heterogeneity. Graduates in Health are those experiencing the steepest wage growth and graduates in Humanities the lowest. In the first 15 years of their working career, the wages of health graduates increase at an annual rate of 9.2% on average. For comparison, the growth in the humanities is only 2.6%.

Initial wages between different categories are not significantly different. Health has the highest initial wages, while education has the lowest, with a difference of approximately 16%. Interestingly, apart from health graduates, no other graduate selects the major with the highest expected initial wage. We also find large penalties for women’s life-cycle earning profiles. For example, wages for women Health graduates grow at less than half the rate of those of men. For initial wages, the picture is less clear, as we find statistically significant gaps only for graduates in Social Sciences, where women suffer a 9.4% penalty at labor market entry.

In the final stage, we add the projected initial wage and wage growth to the personal utility function and estimate the main parameters. Our parametric models show a strong correlation between salary trends and major choice, whereas semiparametric models yield imprecise results.

Our paper is related to the literature on the effects of expected wages on schooling choices. This effect is challenging to identify due to inherent missing data and self-selection. The econometrician can only observe the earnings of the chosen alternative, but the revealed choice needs to be compared to the possible outcomes for the other available options. To address this issue, the literature on schooling choices has resorted to two strategies: either to directly elicit students’ subjective expectations about future payoffs from surveys (Arcidiacono et al. 2012; Stinebrickner and Stinebrickner 2012; Zafar 2013; Kaufmann 2014; Wiswall and Zafar 2015) or to assume rational agents who are utility maximizers and whose preference can be inferred from the choice data (Berger 1988; Siow 1984; Arcidiacono 2004; Beffy et al. 2012). Both approaches impose assumptions and come with limitations.

A research design based on subjective expectations has two main drawbacks. First, studies based on such design usually collect information on expected wages only at one moment of the respondent’s career, therefore overlooking differences in the progression of wages.⁵ Second, the results of these types of studies are sensitive to the exact moment when data on expectations are collected, since asking about expectations after choices have been made might bias the results. Some studies interview students still in high school (Jensen 2010; Zafar 2013; Kaufmann 2014); others interview former college students after graduation (Webber 2014; Ruder and Van Noy 2017), and some others a combination of these two groups (Arcidiacono et al. 2012; Wiswall and Zafar 2015). But especially when collected after making the actual decision, subjective expectations can be endogenous (Bertrand and Mullainathan 2001; Bound et al. 2001; Benitez-Silva et al. 2004; Zafar 2013; Kaufmann 2014) as individuals might try to rationalize their past or future choices. If this is the case, these studies could be conflating students’ expectations and the rationalizations of a choice already made. This is the endogeneity that researchers should be careful about, as it is likely to introduce a serious measurement error leading to biased estimates.

Studies that adopt a more traditional revealed preference approach (Arcidiacono 2004; Beffy et al. 2012; Webber 2014), instead, try to determine the relevant factors of the choice process from the observed data. These models require assumptions on how students form their expectations—usually modelled as myopic or rational—both for the chosen and counterfactual options. The disadvantage of this methodology is clear: since the econometrician only observes the revealed choice, selection bias needs to be addressed because of the endogeneity of educational choices. Or, to put it differently, the counterfactuals are not observed and need to be created from the model, and that is only possible under relatively strong assumptions. However, given an appropriate dataset, a clear advantage of using revealed preference information is the availability of richer data. For example, if panel data are available, the econometrician can observe the full evolution of age-wage profiles throughout the working life for the revealed choice. This is the approach we take in this study.

This paper makes three contributions. First, we introduce new evidence on the importance of financial rewards in the choice of the field of study in college. We believe this to be important for at least two reasons. The first has to do with how economists think about, and model, individual decisions on human capital investments. The second has to do with the implications of results for policies to address the shortages of skills—usually scientific ones—in the labor market, which are often decried in the public debate. If students are insensitive to the monetary returns of college majors, financial incentives as a solution to shortages will be ineffective.

The second contribution is to disentangle the separate effect of initial wages and wage growth on college major selection. This is a useful relaxation of the standard assumptions, and it improves the understanding of the mechanics of educational choice formation. The distinction also has policy implications, as knowing what feature of future payoffs influences student choices can help policymakers design more effective policies.

The third contribution is to illustrate an application of semiparametric estimation methods for polychotomous choice models with panel data. Given the clear and well-understood limitations of standard parametric techniques, one would wish to see more applications of this class of estimators to unordered choice models. This has not been the case so far. We believe that one possible explanation for this lack of applications could reside in the heavy computational burden that these techniques entail. In our application, we find that the global optimum of the semiparametrically estimated polychotomous choice model is very difficult to find. Another explanation is the considerably reduced significance of the parameters compared to parametric estimation methods.

The remainder of the paper proceeds as follows. In Sect. 2 we present our structural model and how we identify its parameters. Section 3 describes our data. In Sect. 4 we present our results connecting them to the theoretical model. Section 5 concludes.

2 Major choice and wages

In this section, we outline our model of major choice. The model takes a standard Roy model approach as a starting point for multiple and unordered educational choices. Our focus is on students who have completed college education only. In our model, rational students are utility maximizers who choose a major during their college education. The utility generated by a major depends on the wages a specific major is expected to generate and several control variables. On top of that, we allow for an unobserved heterogeneity term in the utility function. This term is individual-specific and gathers all unobserved factors that influence major choice.

The expected wages for different majors are not directly observed. Instead, we only have data on wages for the chosen major. To address this issue, we adopt a two-step modeling approach for wages. First, we model the initial or entry wage, and then we model wage growth over time. Although this approach is not commonly used in the literature, it has been used in previous studies such as Mincer (1974), Willis and Rosen (1979), and Heckman et al. (2008). Both the initial wages and wage growth are influenced by the unobserved heterogeneity present in the major choice specification. This allows us to account for selectivity in the choice of major. The modeling of selectivity in this way is consistent with the approach used by Heckman (1979) as explained in detail by Olsen (1980). By estimating the equations for initial wages and wage growth, we can calculate the expected wages for both the chosen major and the majors that were not chosen. These counterfactual expected initial wages and expected wage growth capture the comparative advantages that individuals have in each of the majors.

The major choice is made once in an individual life during college education. Wages are observed multiple times for a specific major choice. The decision to choose a major is influenced by the expected earnings associated with each major and certain individual characteristics that remain constant over time. Expected wages per major are characterized by a time-constant expected initial wage and a time-constant expected wage growth.

Our primary focus in modeling major choice and wages is to reduce the number of assumptions made. In particular, we avoid incorporating any distributional assumptions, even in the major choice model. However, we will compare our results with those from standard parametric choice models. To capture the relationships between the unobserved random factors, such as error terms and unobserved heterogeneity, in the major choice, initial wage, and wage growth equations, we adopt the commonly used setup found in panel data analysis, which includes an individual-specific fixed effect,⁶ related to the unobserved heterogeneity term, is part of each of these equations.

Despite our intention to make as few assumptions as possible, some assumptions will have to be made. In many cases, our equations are linear functions of regressors. The initial wage is a linear function of relevant regressors, and although wage growth enters the model nonlinearly, its argument is linear.

2.1 Major choice

We distinguish five major categories⁷: Natural Sciences ($m_{i}=1$); Social Sciences ($m_{i}=2$); Humanities ($m_{i}=3$); Education ($m_{i}=4$) and Health ($m_{i}=5$), where the subscript i indicates a specific individual. After graduating from high school, students have to decide on the major they want to pursue in college. This is time $t=t_{<0}$. It happens before the individual starts working ($t=0$), but we leave the exact time unspecified. After graduating from college, people start working in the labor market and a stream of income is expected for T periods.

When choosing the favorite major, each individual compares the wages available in the five educational categories and opts for the one maximizing the utility. Utility is a function of the expected lifetime earnings perceived by the individual at $t=t_{<0}$, $h(E(Y_{mi0}),E(Y_{mi1}),..,$ $E(Y_{miT}))$, where $Y_{mit}$ is the income of the individual i at time t if major m is chosen. Also, we allow some time-constant observed personality traits that capture the non-pecuniary benefits of the choice made, as collected in the vector $Z_i$, to have an impact on utility.⁸ We will also include an unobserved heterogeneity term ($\nu _i$) in the utility function, and it will be part of the error term. $\nu _i$ collects all unobserved individual characteristics that do not vary over time. By adding an error term, $\xi ^{*}_{mi}(\nu _i)$ for each major $m=1,2,3,4,5$ and for each individual $i=1,..,N$, we can specify the following utility function⁹:

$$\begin{aligned} U_{mi}=h(E(Y{}_{mi0}),E(Y_{mi1}),..,E(Y_{miT});Z_i)+\xi ^{*}_{mi}(\nu _i), \end{aligned}$$

(1)

To individually assess expected wages, we need to rely on observed wages during working life. We are now faced with three problems:

• How do individual expectations relate to economic reality, that is, wage observations?

• All the wages that we observe are conditional on the optimal choice made at $t=t_{<0}$. This will result in a selectivity bias that requires appropriate corrections.

• We observe only the wage of the optimal choice and not the counterfactual wages, i.e. the expected entry wage and expected wage growth for each of the other majors not chosen by the individual.

In the following subsections, we discuss how we tackle each issue. At the end, we also summarize the main assumptions of our model and briefly discuss how to perform the statistical inference correctly.

2.2 The wage equation

After making the educational choice and after graduating, the individual starts working and wages are observed for several periods. Following Mincer (1974), Willis and Rosen (1979), and Heckman et al. (2008) we build wages from two parts: a wage at the entry of the labor market and wage growth. The combination of initial and wage growth determines the evolution of wages over time. The initial wage is the wage observed at labor market entry, and we model it as follows:

$$\begin{aligned} log(y_{mi0})=\beta _{m}'x_{i0}+\varepsilon _{mi0}=log({\tilde{y}}_{mi0})+\varepsilon _{mi0} \end{aligned}$$

(2)

where $x_{i0}$ indicates a vector of observable characteristics at time $t=0$. Note that in this specification there is no time dimension. Only $t=0$ is relevant here. All wages earned after the starting period contribute to forming the age-wage profile. We model the later period individual wages as follows:

$$\begin{aligned} y_{mit}=y_{mi0}e^{\rho _{mi}(t)}\quad \quad t>0 \end{aligned}$$

(3)

where $\rho _{mi}(t)$ is a time-varying growth rate of wages, specific to individual i and major m. This growth rate is approximated by a Kth order polynomial of time¹⁰:

$$\begin{aligned} \rho _{mi}(t)=\rho _{mi0}\left( \sum _{j=1}^{K}\alpha _{mj}t^{j}\right) +\varepsilon _{mit}^{*}\qquad t>0 \end{aligned}$$

(4)

This functional form of individual wage growth allows the empirical observation of a concave function of wages in time, initially increasing but at a diminishing rate and potentially decreasing for large t. In our specification, such a functional form is only possible when $K>1$. By using a Kth order polynomial a large number of functional forms can be approximated.¹¹ We will assume that $\rho _{mi0}>0$, indicating that the initial growth rate of wages ($t=0$) is positive for every individual and major choice. Substituting (4) into (3) we obtain the following.

$$\begin{aligned} y_{mit}=y_{mi0}e^{\rho _{mi0}\left( \sum _{j=1}^{K}\alpha _{mj}t^{j}\right) +\varepsilon _{mit}^{*}} ={\tilde{y}}_{mi0}e^{\rho _{mi0}\left( \sum _{j=1}^{K}\alpha _{mj}t^{j}\right) +\varepsilon _{mit}}\quad \quad t=1,2,...,T_{i}\nonumber \\ \end{aligned}$$

(5)

where $y_{mit}$ is the individual wage received at the moment t if the major choice m is made and $\varepsilon _{mit}=\varepsilon _{mit}^{*}+\varepsilon _{mi0}$, a zero mean error term. Taking logarithms, this can be written as:

$$\begin{aligned} log(y_{mit})=\beta _{m}'x_{i0}+\rho _{mi0}\left( \sum _{j=1}^{K}\alpha _{mj}t^{j}\right) +\varepsilon _{mit}. \end{aligned}$$

(6)

The wage equation (6) is different for each major, as reflected by the major-specific initial wage, growth rates, and error structure. In the panel data literature, it is common to specify the error structure as follows¹²:

$$\begin{aligned} \varepsilon _{mit}=\varepsilon _{mit}^{*}+\varepsilon _{mi0}=e_{mi}+\varsigma _{mit}+\varepsilon _{mi0}. \end{aligned}$$

(7)

This error structure consists of an individual fixed effect $e_{mi}$ and an idiosyncratic term $\varsigma _{mit}$. This idiosyncratic error term is uncorrelated with the other error terms in the model, and this is a standard assumption in the analysis of panel data. For the error term of (2) we make an equivalent assumption:

$$\begin{aligned} \varepsilon _{mi0}={\tilde{e}}_{mi}+\varsigma _{mi0}. \end{aligned}$$

(8)

Note that we distinguish two individual fixed effects: $e_{mi}$ and ${\tilde{e}}_{mi}$. The reason for this is that $\varepsilon _{mi0}$ contains $\varepsilon _{mit}^{*}$, and both have a different origin: $\varepsilon _{mi0}$ stems from the initial wage equation, while $\varepsilon _{mit}^{*}$ refers to the wage growth equation. Effectively, we allow the polynomial approximation of the growth rate to have an individual fixed effect of its own, although we will impose a direct relation later.

An important problem is that wages differ between majors and are only observed for the utility-maximizing major choice. As a result, the error term of the major choice equation ($\xi _{mi}^{*}(\nu _i)$) and the wage equation ($\varepsilon _{mit}$) are likely to be correlated due to self-selection and, as a result, estimating the wage equations in (6) with OLS will result in biased estimates.¹³ As in Chen (2008) and Mazza and van Ophem (2018), we will assume that there is no statistical relation between $\xi _{mi}^{*}(\nu _i)$ and $\varsigma {}_{mit}$, but we will allow for a potential correlation between $\xi _{mi}^{*}(\nu _i)$ and $e_{mi}$ and ${\tilde{e}}_{mi}$. The assumption that the correlation depends only on fixed effects $e_{mi}$, ${\tilde{e}}_{mi}$, and $\nu _i$ is restrictive, but it is commonly made in the extensive literature on panel data estimation techniques.

The expected value for major $m_{i}=m$, is given by the value of the initial wage $y_{mi0}$ and the life-cycle profile of wages:

$$\begin{aligned} \begin{aligned} E(log(y_{mi0})|m_{i}=m)&=\beta _{m}'x_{i0}+E({\tilde{e}}_{mi}|m_{i}=m)\\ E(log(y_{mit})|m_{i}=m)&=\beta _{m}'x_{i0}+\rho _{mi0}\left( \sum _{j=1}^{K}\alpha _{mj}t^{j}\right) +E(e_{mi}+{\tilde{e}}_{mi}|m_{i}=m)\\ \textrm{with} \quad t=1,...,T_{i}, \end{aligned} \end{aligned}$$

(9)

where $T_i$ reflects that individuals wages are observed for several periods but that the number of times differs across individuals. When forming expectations about future wages, students will use what they know about their abilities, inclinations, and tastes for each major m. This information is not available to the econometrician as it is not observed in the data; therefore, we refer to it as private. This private information is captured in the fixed effects $e_{mi}$ and ${\tilde{e}}_{mi}$. This private information is assumed to be constant in time.

When forming the counterfactual initial wages and wage growth for each major that was not chosen by the individual, an additional structure has to be imposed. This will be discussed in Sect. 2.5. At this point, we need to specify the relation between the two fixed effects. They are related, as they both come from the same private information. We state that:

$$\begin{aligned} {\tilde{e}}_{mi}=\tau _{m}e_{mi}. \end{aligned}$$

(10)

This allows the fixed effect to have a different impact on initial wages and wage growth due to the scaling factor $\tau _m$. Note that $E(e_{mi}+{\tilde{e}}_{mi}|m_{i}=m)=(1+\tau _m)E(e_{si}|m_i=m)$ in Eq. (9) under this assumption.

In the next three subsections, we discuss how we estimate the model as we have described thus far. We need to estimate relevant equations in the specific order described if we want to identify all parameters of the model. Section 2.6 discusses the most important assumptions made, and Sect. 2.7 discusses statistical inference.

2.3 The estimation and identification of the wage equations

We aim to estimate the major choice faced by college students. Students maximize utility, and this utility, as reflected in (1), depends on expected future wages and unobserved personal characteristics. As specified in the previous subsection, wages over time are characterized by an initial wage $(y_{mi0})$ and a growth rate $(\rho _{mit})$. The individual has to make expectations about these factors using the individual information available. Part of this information is observable, but another part is only known by the individual and this is part of the fixed effects $e_{mi}$ and ${\tilde{e}}_{mi}$. In this subsection, we show how the parameters of the model described previously can be estimated.

Wages are only observed given the educational choice made by the individual, and as a result we need to correct for this potential selectivity. Under our assumptions, the element in the wage equation (6) that introduces selectivity is the fixed effects $e_{mi}$ (and therefore in ${\tilde{e}}_{mi}$, see Eq. (10)). Focusing first on wage growth, the fixed effect $e_{mi}$, and consequently the selectivity problem, can be removed from the equation by taking difference across the mean in time, that is, the usual within transformation in panel data models.¹⁴ Alternatively, the first difference estimator can be used. Due to the dependence of the growth rate on time, it is more straightforward to use this estimator¹⁵:

$$\begin{aligned} \triangle log(y_{mit})= & {} log(y_{mit})-log(y_{mit_{-}})=\rho _{mi0}\sum _{j=1}^{K}\alpha _{mj}(t^{j}-t_{-}^{j}) +(\varsigma _{mit}-\varsigma _{mit_{-}})\nonumber \\{} & {} \quad t=2,...,T_{i} \end{aligned}$$

(11)

$t_{-}$ indicates the previous observation in time. As the time-invariant component of the error term, i.e. the fixed effect, in (7) cancels, the selectivity is removed. The baseline growth rate is specified as:

$$\begin{aligned} \rho _{mi0}=e^{\delta _{m0}+\delta _{m}'z_{i0}}, \end{aligned}$$

(12)

where $z_{i0}$ is a vector of individual characteristics observed at $t=0$ that also (potentially) includes a constant.¹⁶ Given this specification, we can rewrite (11) as follows:

$$\begin{aligned} \triangle log(y_{mit})&=\left( \alpha _{m1}e^{\delta _{m0}}\right) e^{\delta _{m}'z_{i0}}\left( (t-t_{-})+\sum _{j=2}^{K} \left( \frac{\alpha _{mj}}{\alpha _{m1}}\right) (t^{j}-t_{-}^{j})\right) +\zeta _{mit}-\zeta _{mit_{-}}\nonumber \\&\qquad t=2,...,T_{i} \end{aligned}$$

(13)

From this it is clear that $\alpha _{m1}$ and $\delta _{m0}$ are not identified separately, but that the sign of $\alpha _{m1}$ is identified. By applying NLS on the selected sub-sample having opted for major m, we find consistent estimates of the parameters of $\rho _{mi}(t)$, that is, $\alpha _{m1}e^{\delta _{m0}}$, $\delta _{m}$, and $\alpha _{mj}/\alpha _{m1}$ $\,(j=2,..,K)$. Since

$$\begin{aligned} log(y_{mit})-\rho _{mi0}\left( \sum _{j=1}^{K}\alpha _{mj}t^{j}\right)&=\beta _{m}'x_{i0}+e_{mi}+\varsigma _{mit}+\varepsilon _{mi0} \end{aligned}$$

(14)

$$\begin{aligned} log(y_{mi0})=\beta _{m}'x_{i0}+\varepsilon _{mi0} \end{aligned}$$

(15)

where the left-hand sides are observed or can be calculated given the estimates obtained thus far, the difference between Eqs. (14) and (15) for a given t ($t=1,...T$) equals:

$$\begin{aligned} log(y_{mit})-\widehat{\left[ \rho _{mi0}\left( \sum _{j=1}^{K}\alpha _{mj}t^{j}\right) \right] }-log(y_{mi0}) =e_{mi}+\varsigma _{mit} \end{aligned}$$

(16)

Since $E(\varsigma _{mit})=0$, we can obtain a consistent estimate of $e_{mi}$, indicated by ${\hat{e}}_{mi}$, by averaging the left-hand side over time for each individual. This is possible only for the observed major choice, though.

Given all the estimates retrieved thus far, we can obtain consistent estimates of $\beta _{m}$ for each major m, after having substituted ${\hat{e}}_{mi}$ and using assumption (10), employing OLS on:

$$\begin{aligned} log(y_{mit})-\widehat{\left[ \rho _{mi0}\left( \sum _{j=1}^{K}\alpha _{mj}t^{j}\right) \right] } - {\hat{e}}_{mi}&=\beta _{m}'x_{i0}+\tau _{m} {\hat{e}}_{mi} + \varsigma _{mit}+\varsigma _{mi0}\qquad \mathrm {for\;}\,t=2,..,T_i\nonumber \\ log(y_{mi0})&=\beta _{m}'x_{i0}+\tau _{m} {\hat{e}}_{mi} +\varsigma _{mi0}\qquad \textrm{for}\;\,t=0 \end{aligned}$$

(17)

we estimate $\tau _{m}$. Both equations in (17) represent initial wages. The first equation corrects the post-initial wages so that on the right-hand side the initial wage remains, although with additional random error ($\varsigma _{mit}$). The resulting serial correlation and heteroskedasticity will not introduce a bias, but we need to correct the standard errors.¹⁷ For this reason, we bootstrap all standard errors when estimating our parameters of interest.

2.4 The estimation and identification of the counterfactual initial wages and wage growth

Given the estimates obtained thus far, we can now retrieve the expected wages for each major other than the chosen one, or more precisely the major-specific counterfactual initial wage and wage growth. We first start with the observed major for each individual. The relevant expectations are:

$$\begin{aligned} E(log(y_{mi0})|e_{mi})&=\beta _{m}'x_{i0}+\tau _{m} e_{mi} \end{aligned}$$

(18)

$$\begin{aligned} E(\rho _{mi}(t)|e_{mi})=&\rho _{mi0}\sum _{j=1}^{K}\alpha _{mj}t^{j}+ e_{mi} \end{aligned}$$

(19)

To estimate the counterfactual expected initial wages and expected wage growth, we need to impose more structure on the fixed effects. We opt to assume:

$$\begin{aligned} e_{mi}&=\gamma _{m}\nu _{i}. \end{aligned}$$

(20)

The scalar $\nu _{i}$ is not observed. This unobserved heterogeneity term represents unobserved individual traits, represented by $\nu _i$, which can potentially influence both wages and the major choice. What we assume here is that the fixed effect $e_{mi}$ depends on the unobserved heterogeneity $\nu _i$ independent of the major m, and that the differences between majors are due to the major-specific scale factors $\gamma _m$. Given Eq. (10), we automatically also assume:

$$\begin{aligned} {\tilde{e}}_{mi}=\tau _{m}e_{mi}=\tau _{m}\gamma _{m}\nu _{i}. \end{aligned}$$

(21)

As a result, we allow unobserved abilities, interests, and motivation, as captured by $\nu _{i}$, to influence both initial wages and their growth and we allow the influence to be major specific, but in a specific manner. Later we will evaluate empirically how restrictive this assumption is (see Sect. 4.4.3).

Next, we need to estimate the expected initial wage and the wage growth for the counterfactuals, i.e. the alternative majors not chosen by the individual. We only observe earnings for the major the individual chooses. For the most part, we can calculate the expectations in Eqs. (18) and (19) since we already estimated $\beta _{m}$, $\tau _{m}$, $\rho _{mi0}$, $\alpha _{mj}$, $e_{mi}$ and $\tau _m$. The problem is that $\gamma _{m}$ and $\nu _{i}$ are not identified separately: we only have an estimate ${\hat{e}}_{mi} = \widehat{\left[ \gamma _{m}\nu _{i} \right] }$ for the major that is actually chosen. Note that this is only a scaling problem: the order of ${\gamma _{m}\nu _{i}}$, and therefore $\nu _{i}$, is fixed, and only the absolute level of $\nu _{i}$ is unknown. To put it differently, we want to estimate $\gamma _s \nu _i$ for the majors $s \ne m$. We know the ranking order, because it is the same as $\gamma _m \nu _i$, but not the relative scaling ($\gamma _s/\gamma _m$). We solve this identification problem in three steps:

• 1. We calculate the Mahalanobis distance of the observations using all the explanatory variables.

• 2. Given m, we match ${\hat{e}}_{mi} = \widehat{\left[ \gamma _{m}\nu _{i} \right] }$ using kernel matching for each alternative major s $(s=1,..,5, j \ne m)$. We do this for all majors s. This gives us $\widetilde{\left[ \gamma _{s}\nu _{i} \right] }$ for each major s and individual i.

• 3. To maintain the ordering, for each individual who opted for the major m and for each counterfactual major s, $s \ne m$, we regress the matched $\widetilde{\left[ \gamma _{s}\nu _{i} \right] }$ on the estimated $\widehat{\left[ \gamma _{m}\nu _{i} \right] }$ and use the predicted value from this regression as the counterfactual estimate of $\gamma _{s}\nu _{i}$.

The counterfactual fixed effects are based on the ordering of our estimate of $\widehat{\left[ \gamma _{m}\nu _{i} \right] }$ and this ordering given m is undisturbed. Only the unknown scaling component $\gamma _{s}$ for the majors that the individual did not choose is determined by kernel matching. Regression ensures that the estimated order is not violated. Note that we do not apply full-scale matching. We only need matching to make the scales of $\gamma _{s}$ comparable, and as a result, we can estimate the expected initial wage and the expected wage growth for each major using Eqs. (18) and (19) and using assumption (20).

2.5 The estimation and identification of the major choice equation

We characterize expected future wages by expected initial wages and growth rates. The procedure described in the previous subsection yields the expected initial wage and $T_{i}$ different expected growth rates for each individual and each major. To reduce the number of, quite likely highly correlated, explanatory variables in the major choice equation and to solve the problem of an unequal number of growth rates per individual, we will reduce the $T_{i}$ growth rates to dimension 1 by averaging over time. This average is denoted by ${\bar{\rho }}_{mi}$. Moreover, we will also introduce major-specific constants: $\kappa _{0m}$. The utility of choosing major m as perceived by the individual i is specified as¹⁸:

$$\begin{aligned} U_{mi}=\theta _{1}E(log(y_{mi0}))+\theta _{2}{\bar{\rho }}_{mi}+\kappa _{0m}+\zeta _{m} Z_i + \xi ^{*}_{mi}(\nu _i), \end{aligned}$$

(22)

where $Z_i$ is a vector of observed time-constant personality traits intended to capture the non-pecuniary benefits of a major. The error term $\xi ^{*}_{mi} (\nu _i)$ is a function of unobserved heterogeneity $\nu _{i}$. $\nu _i$ is related to the fixed effects $e_{mi}$ and ${\tilde{e}}_{mi}$, as specified in Eqs. (20) and (21), and therefore $E(log(y_{mi0}))$ and ${\bar{\rho }}_{mi}$ are also related to $\nu _i$. We make the relation between $\xi ^*_{mi}(\nu _i)$ and $\nu _i$ explicit by assuming¹⁹:

$$\begin{aligned} \xi ^{*}_{mi}(\nu _i)=\kappa _{1m}\gamma _{m}\nu _{i} + \xi _{mi}. \end{aligned}$$

(23)

Note that we do not have an estimate of $\nu _{i}$, but of $\gamma _{m}\nu _{i}$. This is what determines our choice of this error structure. It is not particularly restrictive since the inclusion of alternative constant regressors allows the inclusion of alternative specific coefficients and $\kappa _{1m}$ automatically corrects the scaling. Substituting in (22) yields:

$$\begin{aligned} U_{mi}=\theta _{1}E(log(y_{mi0}))+\theta _{2}{\bar{\rho }}_{mi}+\kappa _{0m}+\kappa _{1m}\gamma _{m}\nu _{i}+\zeta _{m} Z_i+\xi _{mi}, \end{aligned}$$

(24)

Two determinants are alternative and individual specific ($E(log(y_{mi0}))$ and ${\bar{\rho }}_{mi}$) and two individual-specific regressors ($\nu _{i}$ and $Z_i$) plus a constant ($\kappa _{0m}$).

In the empirical Sect. 4, we estimate the major choice semiparametrically by implementing the estimation method proposed by Manski (1975) and Li (2011), and parametrically by multinomial logit and probit. Our preferred methods are semiparametric, as they do not require any distributional assumptions on the error term $\xi _{mi}$. See “Appendix 3” for more details on the semiparametric estimation methods utilized in this investigation.

2.6 The main assumptions of the model

To identify the parameters of the model, we have to make several assumptions. The most important ones are:

• The error terms have the standard panel data structure consisting of an individual specific part, the fixed effect, and an independent individual- and time-dependent part.

• The fixed effects of the initial wage and wage growth errors are related as speficied in Eq. (10).

• The fixed effects in the initial wage and wage growth equation linearly depend on unobserved heterogeneity, as reflected in Eqs. (20) and (21).

• The unidentified scaling parameter $\gamma _i$ can be identified by matching on observables. However, note that matching only ensures that the order of $\nu _i$ between individuals is maintained but does not identify the relevant parameters.

2.7 Statistical inference

Our estimation process comprises multiple stages. The standard errors for the estimation of the wage growth equations in the first step of the process can be calculated using conventional methods. To obtain the correct standard errors in the next steps of the estimation procedure, i.e., the estimation of the initial wage equations and the major choice equation, we employ a non-parametric bootstrap with 200 replications,²⁰ As a result, we can evaluate the statistical significance of the estimated parameters in the usual way.

Note that our model is, in essence, fully structural, although we have tried to reduce the number of assumptions as much as possible.

3 Data

We study the effect of expected wages on major choices using the 1979 (NLSY79) waves of the National Longitudinal Survey of Youth. The NLSY79 is a widely used longitudinal survey representative of the US population. It started in 1979 surveying 12,686 individuals who were 14 to 22 years old at the time, and it is currently ongoing. We use all waves up to 2014. The respondents were interviewed annually until 1994 and twice a year thereafter. The maximum number of waves observed per individual is 23.

NLSY79 includes a wide variety of economic, sociological, and psychological measures. In particular, it includes information on the major selected in college for those individuals who proceed to tertiary education.

Since our analysis regards major choice in college, we restrict the sample to men and women who completed college and for whom the major choice is known. This reduces our sample to 5205 individuals.

Our model has two dependent variables: major choice for the selection probabilities and earnings for the wage equation. In the NLSY79 the major in college is recorded as a four-digit code distinguishing among the various fields of study (e.g.: Biological Sciences, Engineering, Business and Management, etc.) and subfields within the bigger field (e.g.: Microbiology, Chemical Engineering, Banking and Finance, etc.). We combine this information into five major categories: Natural Sciences, Social Sciences, Humanities, Education and Health.²¹ Earnings are expressed as the logarithm of hourly earnings in the period considered translated in 2010 constant dollars. The historical series for the Consumer Price Index (CPI) in the US for the period considered is taken from the Bureau of Labor Statistics.²² We are interested only in wages earned after graduation, and therefore our initial wage is the first wage earned thereafter. In the NLSY79 the first ‘graduate’ wage observed is in 1990 and 2013 is the final observation year.

The information contained in the NLSY allows us to control for sex, ethnic background, and geographical characteristics for the area of origin at age 17.²³ Following other studies (Neal and Johnson 1996; Altonji et al. 2012a; Deming and Noray 2020) we use respondents’ standardized scores on the Armed Forces Qualifying Test (AFQT) for the wage equations to proxy ability. These are a series of tests in mathematics, science, vocabulary, and automotive knowledge. The AFQT was administered in 1980 to all subjects regardless of their age and schooling level. For this reason, it can include age and schooling effects in the ability index that the test is meant to construct. To correct for these undesirable effects, we follow Kane and Rouse (1995) and Neal and Johnson (1996). First, we regress the original test score on age dummies and quarter of birth, then replace the original test score with the residuals obtained from this regression. Several scores of the Armed Service Vocational Aptitude Battery (ASVAB) scores are also available and are used in the major choice equation to represent personal traits and non-pecuniary benefits that affect major choice. We use four of these scores in the major choice equation to partially account for personality traits and non-pecuniary benefits. We distinguish ASVAB-A (measuring arithmetic reasoning), ASVAB-W (word knowledge), ASVAB-P (paragraph comprehension), and ASVAB-M (mathematic knowledge).

After having removed unknown and unrealistic hourly wages, (i.e. wages smaller than $e^{1}$ = $2.71), wages observed before college graduation and individuals with majors that could not be assigned to any of the five groups, we are left with 25,683 observations of 3257 individuals. We observe 7.9 wages per individual on average with a maximum of 23 wages. The number of observed wages is summarized in Table 1. For 838 individuals, we observe only one wage, whereas for 2419 individuals we observe more than one wage.

In the NLSY wages are recorded in each survey. Unemployment between two consecutive surveys is ignored by us. If an individual is unemployed at the time the survey took place, no wage is recorded, and hence the observation of this individual at that point of time is ignored. If the individual is observed to be employed at a later point in time, the wage of the individual is again used in our analysis.

Table 1 Count of the observed number of wages

We report both the initial wages and the mean wages observed throughout the survey period in Table 2. For both measures, education is the lowest-paying field, while health pays the highest wages at the start and throughout the career. The gap between the highest and lowest pay fields is around 14% for the initial wages and 34% for average wages. AFQT test scores are highest for Humanities graduates and lowest for Health graduates, and the spread is substantial. For the four ASVAB test scores, a more diverse picture emerges. Natural Science graduates score on average very well on arithmetic reasoning and mathematics knowledge, whereas Humanities graduates score best for word knowledge and paragraph comprehension. Education graduates on average score worst on three of the four ASVAB subtests. The score for paragraph comprehension is lowest for Social Science students.

As expected, education and health are fields dominated by women, and, in general, women are more numerous than men in our sample. About 22% of our sample are black, 13% Hispanic and 81% grew up in a city. In health, respondents start working at the late age of 30, whereas in natural sciences and humanities, the first working experience after college completion is at 28. We also observe that more than half of the sampled individuals graduated in a Social Science discipline, 1631 in Natural Science, and only 103 in one of the Humanities.

Table 2 Descriptive statistics

4 Estimation results

Before estimating the major choice equation (24), we first estimate the wage growth rates and the determinants of the initial wage. As discussed in Sect. 2.3, this estimation involves three steps: (i) the wage growth equation specified in (13) is estimated with non-linear least squares; (ii) the unobserved heterogeneity term $\gamma _m \nu _i$ is estimated using (16); (iii) the parameters of the determinants of the initial wage results from an ordinary least-squares estimation of Eq. (17). These estimation results are then combined to retrieve the expected initial wage and the expected annual growth rate as specified in Eqs. (18) and (19). Finally, these expected initial wage and growth rates are used to estimate the major choice equation (24).

4.1 Estimation of the wage growth rates

To start with, let us stress that we analyze real wages. The wage growth considered here is the real wage growth. We estimate wage growth rates separately for each major as described in Eq. (13) by non-linear least squares. Estimates are presented in Table 3.

Factors that influence wage growth are not clearly indicated by economic theory. We attempted to include commonly used variables in wage estimations, but it was difficult to find significant results. As a result, we decided to estimate a very simple model with only two personal characteristics: the AFQT test and a female dummy variable. We had to limit the number of explanatory variables to achieve reasonable significance. None of the explanatory variables that were deleted, as discussed in Sect. 3, had a significant effect. To demonstrate this issue, even the simple addition of black and Hispanic dummy variables significantly reduces the significance, as shown in Table 3, to the point where no significance remains. The time variables presented in the lower panel of the table do not experience any loss of significance. However, in the upper panel, there are 6 estimates that are significantly different from 0, but this reduces to only 1 significant effect when the dummy variables for black and Hispanic are included.

Equation (13) consists of two parts: a time pattern, involving the $\alpha$-parameters, and an individual scale factor, involving the $\delta$ parameters, which makes the observation of wage growth specific. The time pattern is generic, although different between majors. Individual variation is reflected in the scale factors.

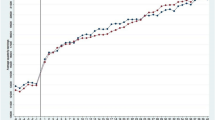
The order of the polynomial in the wage growth time pattern is chosen according to the AIC criterion.²⁴ The lowest AIC values were found for a third-order polynomial. Patterns are difficult to evaluate using only the estimates presented. To get a better intuition of our results, consider Fig. 1. In this plot, we show the estimated real wage growth rate for a male with an average AFQT-score of 70.528. All curves show the expected curvature: a stronger increase at the start of working life and a leveling off later in working life. The growth paths of natural and social sciences, education, and humanities are relatively similar, although the paths of the sciences are more similar than those of education and humanities. The only real exception is the growth curve for health graduates. After 15 years in the labor market, humanities graduates experience about 39% wage growth, corresponding to about 2.6% real wage growth per year. The growth is 49% (3.3% per year) in 15 years for graduates in education. For Natural and Social Science graduates, the real wage growth is 4.8% and 5.1% per year, respectively. With an estimated annual wage growth of 9.2%, health graduates are those who enjoy the strongest growth. The leveling of wage growth begins early for education majors. Already before 15 years of experience, wage growth stops. For the other majors, wages plateau just after 15 years of work experience.

Table 3 Estimates of the growth rate equation (13) across majors

Fig. 1

Estimated growth rates across majors

Regarding the scaling factor in the wage growth specification, that is, $\alpha _{m1} e^{\delta _{m0}} e^{\delta '{m}z_{i0}}$ in Eq. (13), we find a significant effect for all explanatory variables only for the Social Sciences. This is by far the category with the most observations. The scale factor appears to be lower for women than for men, indicating that women experience slower wage growth than men. The differences are quite substantial: in social sciences, women experience a 32% lower real wage growth, and in health it is even 113%. For Natural Sciences, Humanities, and Education the effects are not significant, and, if anything, in Humanities, females are estimated to experience a larger wage growth than men. The AFQT test score has a positive effect on wage growth, but it is only significant for Social Sciences and Health and only at the 10% level. A one-point increase in the test score, which ranges between 0 and 100, is associated with a 0.8% higher wage growth for social sciences and about 1.7% faster wage growth for health. Figure 4 in “Appendix 2” gives a visual representation of the scaling factors.

4.2 Estimation of initial wages

We present the results of the OLS estimation of Eq. (17) in Table 4.

Table 4 Estimated initial wage equations (17) across majors

Except for Health and Humanities, initial wages are strongly and positively affected by people’s AFQT-test score. A 1 point increase in the test score is associated with a 0.4–0.6% increase in wages. The effect of gender is statistically significant only for the social sciences, where the initial wages of women are 9.4% lower than those of comparable men. Our estimates of ethnic background are not statistically significant for most major groups, except for a negative and high penalty for black Health graduates of about 15%, and a positive premium for black education graduates of 10%. Living in an urban area in 1979 has a positive effect on wages, but it is only significant for the Social Sciences. Living in the northeast or west of the US at the age of 18 increases initial wages compared to living in the south. The effect of age at labor market entry is positive for four out of five majors. Starting 1 year later, the initial wage of around 3–4% for Natural and Social Sciences, Education, and Health. Finally, the effect of the fixed effect $e_{mi}$, that is, $(1+\tau _m)$, is positive and significant for all majors. The strong significance indicates that there is time-invariant unobserved heterogeneity. Regarding the estimated sign, remember that since the coefficient of the fixed effect $e_{mi}$ is $\tau _m$ in the initial wage equation and $(1+\tau _m)$ in the post-initial wage equations (see Eqs. (9) and (10)), the estimated sign of $\tau _m$ is negative, so the unobserved heterogeneity term posits a negative effect on initial wages and a positive impact on wages earned at a later date.

Table 5 and Fig. 2 report our estimated initial wages for the counterfactuals, i.e. the estimated entry major for each of the majors not chosen by the individual. The expected initial wages for the alternative majors are estimated using Eq. (18). From Table 5, we see that the observed wages correspond more or less to the calculated wages for the relevant major.²⁵ We find larger deviations for the counterfactuals. For example, if a Natural Science graduate had completed one of the Health studies instead, her initial wage would have been about 8.0% lower. For Humanities and Education, the counterfactual penalty would have been 12.2% and 5.4%, respectively. Choosing the Social Sciences, on the other hand, would have increased the wage by about 3%. The expected initial wages of either the Health or Natural Science majors are the highest regardless of the real choice, whereas the lowest wages are estimated for Humanities. The education major also offers relatively low initial wages. Figure 2 provides a kernel plot of the estimated counterfactual initial wages. The estimated wage is most concentrated for Education and Natural Sciences, whereas the largest spread is found for Social Sciences and Health.

Table 5 Mean and standard deviation of actual and expected initial wages across majors

Fig. 2

Kernel density plots of the expected initial log wages across majors

4.3 Estimation of major choice

After having estimated expected initial wages and wage growth profiles, in Tables 6 and 7 we present the major choice estimates with four different estimation methods. In column (1) we present the results of Manski’s semiparametric estimation method of a multinomial choice model (Manski 1975). Column (2) presents the results of the Li method (Li 2011), which is essentially a flexible parametric method with a semiparametric interpretation. Columns (3) and (4) present the results estimated with two parametric methods: multinomial probit and multinomial logit, respectively. In the probit specification, correlations between the errors of different majors are not restricted to 0, whereas that is the case in the multinomial logit specification.²⁶

In Table 6 we present our estimates for our two key parameters: the effect of initial wages and wage growth rates on the major choice. Recall that we have calculated major-specific initial wages and average wage growth rates; therefore, in the multinomial estimation, these two parameters are alternative-specific, implying that only one coefficient is estimated per major and variable. The estimated unobserved heterogeneity and ASVAB scores for the categories arithmetic reasoning (ASVAB-A), word knowledge (ASVAB-W), paragraph comprehension (ASVAB-P) and mathematical knowledge (ASVAB-M) are also added as regressors.²⁷ Still, these variables are individual-specific, so we obtain one estimate per major. We set the Social Sciences category as the reference group. Apart from these variables, we also include a major-specific constant. The estimation results of the four ASVAB scores are presented in Table 7. All standard errors are bootstrapped.

We calculate the average wage growth rates over only 2 years. Using 3 or 5 years hardly changes the estimation results, but when we use 10 years or more, we lose significance and we start seeing some unexpected negative signs. This might indicate that the wage growth rates for the more recent future are more reliable or that people only look at the wage growth for the near future. In our robustness analysis, cf. Sect. 4.4, we will provide more information on this.

Concentrating on the parameters of the initial wage and wage growth, we find no statistically significant effects of the effect of expected initial wages and expected wage growth for the semi-parametric estimation methods of Manski and Li, although the estimated coefficients are all positive, as theory predicts. For both parametric estimation methods, we find significant effects of the main explanatory variables. Both the effect of the expected initial wage and the expected wage growth are positive, indicating that individuals prefer higher initial wages and higher wage growth. The estimates of the probit specification are somewhat smaller, but the scaling of logit and probit models differ, so it makes more sense to compare ratios. In fact, these are more similar. The loss of precision of the estimated coefficients using more flexible, e.g. semiparametric, estimation methods is quite common in the empirical literature. Since the major choice models that we estimate are not nested, it is impossible to test whether the estimated parameters are different. As a result, we can only draw conclusion on the effect of expected initial wages and wage growth if we use the more restrictive parametric models. The semiparametric method do not offer precise enough results to conclude anything. This may be why semiparametric choice models are not used in major choice investigations as far as we can tell.

Table 6 Estimated major choice equation (24)

Table 7 Estimated major choice equation (24)

The overall significance of the other regressors is very limited, in particular for the estimates of the Manski-, Li- and multinomial probit-estimation methods. Even the constants per major, despite the quite different number of individuals in each group, are only all significant in the multinomial logit estimation. Fixed effects are usually estimated to be positive but only significant for 4 out of 16 estimates. The four ASVAB scores, which aim to identify non-monetary factors that impact the choice of major, are seldom significant. If they are significant, it is usually only in the multinomial logit model, except in one case. If anything, individuals scoring well on mathematical knowledge tend to choose either the Health or the Natural Sciences major. Paragraph comprehension is a positive factor in choosing Education. Arithmetic reasoning negatively affects the choice of majors in Health major, just as word knowledge negatively affects the choice of Natural Sciences.

To gain a sense of the impact of our two variables of interest on major choice, consider Table 8. In the top panel, the table shows the change in probabilities of choosing the major m estimated by multinomial logit, following a one standard deviation increase in our two variables of interest calculated at the average values for the two variables in each alternative.²⁸ The results indicate that the effect of the explanatory variables is considerable. If both the initial wage and the wage growth rate were to increase by one standard deviation for a specific major, the probability of choosing this major would increase by 30.6% (Social Sciences; 0.155/0.506), 64.2% (Natural Sciences), 78.2% (Health), 62.4% (Education) or 82.2% (humanities). In the middle and bottom panels, we show the effect of a 1 standard deviation increase in initial wage and wage growth, respectively. We see that the effect of increasing only one of the two wage attributes on major choice is very similar. We interpret this as an indication that the expected initial wage and expected wage growth are equally important factors in the major choice.

Table 8 Estimated probabilities and probability difference of major choice

In summary, our results point to the importance of financial factors in the choice of majors as long as we use parametric estimation methods. Both initial wages and wage growth positively influence the choice of major and the effect is stronger for initial wages. While the direction of the effect is consistent across estimation methods, the precision of the estimates is not, as the effects estimated by more flexible semiparametric methods are never statistically significant. We interpret our results as being consistent with agents being rational and as a validation for our estimation strategy based on counterfactual imputation.

Our estimation has also disclosed some interesting features of the methods used that a researcher interested in these applications might find useful. The estimation of the semiparametric (Manski (1975)) was quite erratic. We found numerous local optima, and finding the global one was difficult. To this end, we employ simulated annealing in combination with optimizing the objective function. On top of that, we also used many different starting values to find the global maximum. The model always converged readily.

In our application, the multinomial probit model is also rather unpractical. We applied simulated maximum likelihood, and convergence depended on the seed and the number of replications per simulated probability used.²⁹ While bootstrapping the standard errors, we found strongly fluctuating estimated variances and constants per major and variances and covariances. This is also the case for some of the estimated variances and their standard errors. For example, the estimated variance of the error term of the Humanities major is 1.997 with a standard error of 5.156. On the contrary, the estimated effects of initial wages and annual wage growth were more stable, as represented by the bootstrapped standard errors in Table 6.

4.4 Robustness checks

In this section, we check if our results are robust to the inclusion of additional covariates in the major choice equation and to different methods of imputation for initial wages and wage growth rates. As the four methods produce comparable results for the robustness checks, we concentrate on the multinomial logit specification only.

4.4.1 Specification checks

In Table 9, panel A, we present how our result changes when adding additional individual-specific variables as explanatory variables. Specification 1 is our benchmark in Table 6 and is added for comparison. This specification includes a constant, the unobserved heterogeneity terms ($\nu _i$) and the four ASVAB scores as individual-specific regressors in the major choice equation. Specification 2 adds gender, while specification 3 also adds ethnic background (Black and Hispanic). Specification 4 also adds the AFQT test score. In specification 5, we omit all individual specific but major constant regressors, so that we only use the expected log initial wage, the expected annual wage growth, and major-specific constants in the estimation.

Concentrating on the main parameters of expected log initial wage and expected annual wage growth, we see that the inclusion of alternative regressors reverts the sign for the expected log initial wage, which now becomes negative even though it is not significant. The effect of expected annual wage growth remains positive and significant, although estimates drop by approximately 50%. The change is mostly driven by the inclusion of a female dummy. Gender has a strong and significant effect, and this is true for three majors, except for the Humanities (Social Sciences is the reference category). Both ethnic background and test scores are rarely significant and, when significant, only at the 10% level. Specification 5 illustrates that the inclusion of the four ASVAB scores—intended to partially capture non-pecuniary preferences for majors—has only a marginal effect on our parameters of interest. Pecuniary motives appear to be relatively unaffected by these sets of controls.

In our analysis, we calculated the expected wage growth as the average wage growth over a time horizon of just 2 years. This is a rather short period. In Table 10, we show the estimated effects of the expected initial wage and expected wage growth for different time horizons. We find the expected positive effects of the expected initial wage only for time horizons up to 5–10 years. For longer periods, the significance is lost. Note that significance decreases as the period under consideration becomes longer. The impact of anticipated wage growth is more consistent and remains positive, although its significance diminishes with longer time horizons. The explanation for these results is attrition in the sample. The estimation of wage growth is based on the wage observed at specific points in time, and Table 1 shows that the number of observations drops rapidly over time. For example, Table 1 shows that about two-thirds of the sample is lost after 10 years. Expected wages are therefore more precisely estimated for smaller periods.

Table 9 Robustness checks using mulitnomial logit

Table 10 Different time horizons for the expected wage growth using multinomial logit

4.4.2 Alternative estimation methods

So far, we estimate the expected initial log wage and the expected annual wage growth using regression. In particular, we estimate Eqs. (13) and (17). In Table 9 Columns B1 to B3, we present simpler measures for the two key parameters. In specifications B1 and B2, we use averages across majors and sexes. Specifications B2 and B3 are based on regression, but in specification B2 we do not correct for self-selection, while in specification B3 we do not include the fixed-effects term and therefore ignore unobserved heterogeneity.

Specification B1 gives as expected positive, but very large, and significant estimated effects of initial wages on major choice. Omitting correcting for selectivity in Column B2 leaves the effect of initial wages unchanged, but reverts the effect of wage growth, which, in this specification, is estimated to be negative and significant, albeit only at 10%. Ignoring selectivity appears to be important. The effect of dropping unobserved heterogeneity, in Column B3, does not affect our main results significantly.

In conclusion, together with our main results, these robustness checks suggest that regression methods seem to provide support to theories of major choices based on rational expectations and the importance of monetary payoffs for these decisions. They also highlight the importance of correcting for selectivity in the estimations and suggest a minor role for unobserved taste components. More elaborate specifications do not change the conclusions, but there appear to be differences between the sexes. Separate estimation between men and women considerably reduces the significance of the estimation results, but the estimated effects of both initial wages and wage growth remain positive. Simplification of the estimation of expected initial log wages and expected annual wage growth is no problem, but selectivity needs to be taken into account. Although we corrected for gender to some extent in our estimations, our results indicate that the major choice behavior differs between sexes. We estimated separate models for men and women, but this substantially reduced the coefficients’ significance.

4.4.3 The determination of the counterfactuals

Knowledge of the returns to education varies by socioeconomic status (Dynarski et al. 2021). A good reliability test for our counterfactual imputation procedure is for it to be able to reproduce this feature of the data showing decreasing differences between the expected and the actual wages by parental education as students with a more favorable socioeconomic background should be able to foresee their future wages more accurately. Figure 3 shows the decreasing gaps between the two wages in socioeconomic background, as we expected. Looking at the figure, we see that—except for graduates in Education—graduates whose parents are both high-school dropouts make between 10 and 15% less than our counterfactual imputation procedure would estimate. At the other extreme, the gap for graduates whose parents are both at least college graduates themselves is less than 5%, except for graduates in the Social Sciences for whom this gap is around 7%. We interpret these results as a good indication that our counterfactual imputation procedure works as intended.

Fig. 3

Percentage difference in realized and predicted initial wages, by major and parental education

In our estimation, we create counterfactuals using the assumption specified in Eq. (20). Although the estimation of the initial wage and wage growth equations do not depend on this assumption, the determination of the counterfactuals in the major choice equation does. To create these counterfactuals, we have to impose more structure, and for this reason, we introduce the assumption in Eq. (20). This assumption assumes that the unobserved heterogeneity component is composed of a parameter that is specific to each major ($\gamma _m$) and another parameter that is specific to each individual ($\nu _i$). This structure allows us to avoid using full matching on the observables to generate the counterfactuals. We only apply matching to maintain the order of the unobserved heterogeneity as implied by the assumption in Eq. (20).

However, the assumption in Eq. (20) is equivalent to assuming a one-dimensional unobserved heterogeneity factor whose loading factors differ by major. This could be seen as too restrictive. Alternatively, we can abandon this assumption by directly determining the counterfactuals by full matching on the available observables, i.e. only carrying out steps 1 and 2 of the matching procedure described in Sect. 2.4 without resorting to Eq. (20).³⁰ Admittedly, this procedure introduces the strong assumption that major choice is governed only by the socio-economic characteristics, personality traits, and ability measures that we can observe in the dataset. Nevertheless, as this alternative procedure imposes a different assumption than the one that we exploit in our original estimation, we believe that by comparing our estimated coefficients under the two procedures we can gain some relevant insight into how much our estimated parameters are sensitive to the choice of a one-dimensional unobserved factor.

If we do this, we find very similar estimation results. Of course, the estimates of the wage equations do not change. The estimates of the choice equation, using multinomial logit, change only to a small extent. Estimates of the parameters of the main variables Expected initial log wages and Expected annual wage growth are 0.960 and 0.017 with bootstrapped standard errors of 0.318 and 0.005. As we have found before, both effects are positive and strongly significant. From this, we can infer that our assumption stated in Eq. (20) is not the main factor influencing our finding that both initial wages and wage growth impact the decision of selecting a college major.

5 Conclusion

In this paper, we study the determinants of major choice for a sample of American college graduates. In particular, we focus on the separate effect of short-run, i.e. the initial wage—and longer-run wage effects—i.e. wage growth.

We propose a three-stage empirical model that relates future earnings to individual choices. In the first stage, starting from revealed choices, observed wages, and life-cycle wage profiles, we estimate the expectation on initial wages and wage growth from the individual point of view, where the panel structure of the data allows us to produce estimates corrected for self-selection. In the second stage, we create counterfactual wages and wage growth for the alternative not chosen. In the third and last stage, we use the estimated expected wage profiles for the revealed choice and the counterfactuals to study how these affect major choice. We estimate this last step with four procedures, two semiparametric and two parametric. This is one of the rare empirical applications of semiparametric estimation methods for unordered choice settings that we are aware of.

Our findings indicate a significant positive impact of expected earnings on major selection, although the strength of this relationship is influenced by the chosen estimation method. We observe that a 1 standard deviation increase in both short- and long-term wages would nearly double the likelihood of choosing a major in the Humanities. The increase in probabilities for other majors is comparatively lower, ranging from one third to more than two-thirds. Our results on wage growth remain consistent when considering alternative specifications that incorporate individual-specific factors and alternative representations of wage growth. Furthermore, our estimates suggest that long-term wage development has a greater impact than short-term initial wages. Many previous empirical studies either overlook wage growth or only consider a limited representation of future wages.

Regarding our estimation procedures, we find that both the multinomial probit and the Manski semiparametric estimation do not guarantee to provide a global optimum. Multinomial probit often tends to produce unrealistically large variance and covariance estimates. Manski’s maximum-score estimator requires extensive computational time to find the global optimum even with few explanatory variables.

Our results indicate that the economic return on investments in a college major matters. Policies aimed at encouraging enrollment in specific majors through financial incentives can affect student choices.

Although we tried to minimize the number of assumptions in our investigation, we had to make some. As in most econometric analyses, we assume some linear relations. We also chose to impose a unidimensional form of unobserved heterogeneity; cf. Eq. (20). Although we would prefer to be less restrictive, this assumption is needed to identify the unobserved heterogeneity component in our analysis. Our key assumption though is that any unobserved differences between individuals that are relevant to our analysis remain constant over time and can be accounted for by an individual fixed term. The extent to which we can interpret our estimates causally depends on how much we are willing to assume that this assumption holds. We hope that future research will succeed in conjugating the demanding fixed-effects assumption that we work with to a multidimensional unobserved heterogeneity factor.

Appendices

Appendix 1: Major grouping

Assigned category	NLSY major
Natural Sciences	Mathematics
	Physics
	All Other Engineering
	Mechanical Engineering
	Electrical Engineering
	Chemistry
	Computer & Info Tech.
	Civil Engineering
	Chemical Engineering
	Engineering Tech.
	Earth and Other Physical Sci.
	Computer Programming
	Biological Sciences
	Multidisciplinary or General Sci.
	Agriculture and Agr. Science
Social Sciences	Economics
	Accounting
	Architecture
	Business Management and Admin.
	Family and Consumer Science
	Psychology
	Communications
	Other Social Science
	Area, Ethnic, and Civ. Studies
	Political Science
	History
	Art History and Fine Arts
	Public Administration and Law
	Social Work and Human Resources
	Journalism
Humanities	Foreign Language
	Music and Speech/Drama
	Letters: Lit, Writing, Other
	Philosophy and Religion
Education	Secondary Education
	Library Science and Education (Other)
Health	Misc. Business and Med. Support
	Other Med/Health Services
	Public Health (Physical and Mental)
	Nursing

Appendix 2: The growth rates for different majors

In Fig. 4, we have plotted the kernel density of the scale factor per major relative to the same reference as used in Fig. 1, that is, each of the curves shows the estimated distribution of $e^{\delta _{m}'(z_{i0}-z_{reference})}$ for a specific major. The relative scale factor starts at a minimum of about 0.2 in our sample. Values below 0.2 are artificial and due to the smoothing process used to plot kernel densities. The curves indicate that Fig. 1 exaggerates the true wage growth differences between majors. The major experiencing the highest wage growth, Health, tends to have a smaller relative scale factor, whereas, for Humanities, the wage growth appears to be small, but there is some compensation due to a higher scale factor. The other majors are between these extremes and the scale factors for Natural and Social Sciences look very similar.

Fig. 4

Kernel density plots of the estimated scale factors in the wage growth equation across majors

Appendix 3: Semiparametric estimation of major choice

The theoretical literature on semiparametric estimation of choice models has focused mainly on the binary case (Lee 1982; Cosslett 1983; Robinson 1988; Newey 2009). Semiparametric estimators for multiple and unordered choice models are harder to find. Two theoretical examples of this class of estimators are Manski (1975) and Lee (1995). However, in the empirical literature, very few applications of these methods can be found. In this paper, we present a practical application of these two methods that have rarely been used in the applied literature. We apply the maximum score estimator of Manski (1975) and use the smoothing idea of Horowitz (1992) to make the objective function continuous and differentiable. The idea is to maximize the number of correct major predictions, where the predicted major is the major with the highest probability. Due to the yes (correct prediction) or no (incorrect prediction) character of the objective function, it is hard to maximize it using standard techniques. Horowitz (1992) suggests smoothing the objective function by using a continuous function that closely approximates the 0–1 situation. This can be done, for example, by $\Phi ((V_{ij}-V_{ik})/h)$ where $V_{ij}$ is the deterministic part of utility, j indicates the chosen major and k represents the other majors, h is a bandwidth parameter that needs to be chosen. The smaller it is, the closer it resembles the 0–1 situation, and the harder it is to maximize the objective function. Although the resulting objective function is now continuous and differentiable, the global optimum is still hard to find because of the existence of many local optima. We first use simulated annealing (10 million iteration steps) to find good starting values and then optimize our routine. The optimum we find is the best result that we have encountered in a large number of attempts. The simplicity of the objective function makes the procedure tractable. Note that Manski (1975, 1985) is designed on a conditional logit model setting that only includes alternative specific explanatory variables, but this can be generalized to include individual-specific regressors, as discussed in Maddala (1983, p. 42, footnote 4).³¹

The second semiparametric estimator we consider is based on a different idea. The idea, in this case, is to use a multinomial logit model and thereby assume independent type I extreme value distributed error terms, but to estimate the systematic component semiparametrically. Such methods are discussed in, e.g., Briesch et al. (2002) and Li (2011). We follow the suggestion of Li (2011) and use splines to approximate the systematic part of the utility in (24).