Abstract
This study examines the state-dependent effects of crude oil price shocks on the US aggregate economy. Using a smooth transition vector autoregressive model, we assess the effects of normalized supply and demand shocks in the global oil market over the different phases of the business cycle. Our findings show that the link between oil prices and macroeconomic dynamics is nonlinear and that structural shocks in the oil market conditional on recessions have a greater and more persistent contractionary impact on macroeconomic variables including industrial production, employment, and consumer price inflation. Forecast error variance decomposition confirms that oil prices have much stronger stagflationary effects during recessions.






Similar content being viewed by others
Notes
This index is available at Baumeister’s website (https://sites.google.com/site/cjsbaumeister/research).
The RAC series is available monthly starting in January 1974 and going back one more year following (Barsky and Kilian 2002), which allows us to include the first oil shock during October 1973 through March 1974.
They use the US GDP as the output. However, due to the data unavailability at monthly frequency, we use employment and industrial production as plausible substitutes to GDP.
The main goal is to describe the transition between different phases of the business cycle as accurate as possible in our model. For this purpose, we use 12 month moving average terms. The transition indicator with 12 months reflects well our goal than other terms over the observed frequencies of the US NBER-recessions. Details for this issue are available upon request.
The smoothness parameter \(\gamma \) is calibrated as defined by the “NBER based Recession Indicators for the United States from Peak through Trough” (https://fred.stlouisfed.org/series/USRECM). In the full sample, there are 78 recession indicators over 552 observations (that is, 78/552 \( \cong \) 14%). Then, “recessions” are defined as periods in which \(F (z_{t}) \ge \) 0.86 so that the probability of being in a recession is sufficiently high, and \(\gamma \) is calibrated in order that Pr(\(F (z_{t})\) \( \ge \) 0.86) \( \cong \) 14%, implying \(\gamma =\) 2.0.
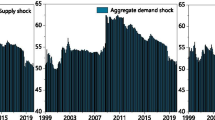
Figure 1 plots the transition by our logistic function \(F (z_{t})\). \(F (z_{t})\) is highly correlated with NBER-recession indicator, and shows that high realization of \(F (z_{t})\) easily takes over threshold value \(F (z_{t}) \ge 0.86\) which is over each of the six NBER-recession episodes. The Pearson correlation coefficient between two data sets is \(r =0.45\) with associated p value = 0.00.
We use 20,000 draws for our baseline and robustness estimates and drop the first 80% draws to maintain the adequate acceptance rates of candidate draws. For details, refer to Auerbach and Gorodnichenko (2012).
For details, see Appendix 7.1.
For robustness, we consider different orderings of the second block, \(X_{2 t}\), and confirm that variations on the orderings are reasonable and markedly robust. The results are available upon request.
We appreciate the anonymous referee to point out this issue. To identify the structural shocks for the US-variable block, we also estimate four-variable models that contain only one of the US variables at a time and confirm that an absence of interaction between US macroeconomic variables somewhat weakens the contractionary effects of oil price shocks during recessionary periods. However, it does not substantially change the results from the baseline estimates (See Fig. 6). Further, we also run variations on the different orderings of the second block, \(X_{2 t}\) (See Sect. 5.3).
According to Kilian (2009), this residual is related with a precautionary demand for oil with high uncertainty because the more uncertain the global crude oil market, the higher the amount of precautionary demand of oil.
Following Kilian (2009), we normalize three structural shocks to represent to raise the real price of oil, implying that two demand-driven shocks are positive, while a supply shock is negative.
Global demand shocks have direct and indirect effects on the US economy through raising the price of oil. As shown in Kilian (2009), both effects on the aggregate economy are of opposite signs and the adverse effect of higher oil prices makes the aggregate demand shock contractionary with a delay. This delay is explained by two dynamic responses: (1) as global activity rises, the aggregate demand shock stimulates the US economic activity, and (2) the real price of oil increases and then output growth declines over time.
References
Auerbach AJ, Gorodnichenko Y (2012) Measuring the output responses to fiscal policy. Am Econ J Econ Pol 4(2):1–27
Barsky RB, Kilian L (2002) Do we really know that oil caused the great stagflation? A monetary alternative. NBER Macroecon Annu 16:137–183
Baumeister C, Hamilton JD (2019) Structural interpretation of vector autoregressions with incomplete identification: Revisiting the role of oil supply and demand shocks. American Economic Review 109(5):1873–1910
Bernanke BS (1983) Irreversibility, uncertainty, and cyclical investment. Quart J Econ 98:85–106
Bloom N (2009) The impact of uncertainty shocks. Econometrica 77(3):623–685
Burbidge J, Harrison A (1984) Testing for the effects of oil-price rises using vector autoregressions. Int Econ Rev 25(2):459–484
Caggiano G, Castelnuovo E, Figueres JM (2017) Economic policy uncertainty and unemployment in the United States: A nonlinear approach. Econ Lett 151:31–34
Caggiano G, Castelnuovo E, Groshenny N (2014) Uncertainty shocks and unemployment dynamics in US recessions. J Monet Econ 67:78–92
Chernozhukov V, Hong H (2003) An MCMC approach to classical estimation. J Econom 115(2):293–346
Choi S, Furceri D, Loungani P, Mishra S, Poplawski-Ribeiro M (2018) Oil prices and inflation dynamics: evidence from advanced and developing economies. J Int Money Finance 82:71–96
Darby MR (1982) The price of oil and world inflation and recession. Am Econ Rev 72(4):738–751
Davis SJ, Haltiwanger J (2001) Sectoral job creation and destruction responses to oil price changes. J Monet Econ 48:465–512
Gao L, Kim H, Saba R (2014) How do oil price shocks affect consumer prices? Energy Econ 45:313–323
Granger CWJ, Teräsvirta T (1993) Modeling nonlinear economic relationships. Oxford University Press, Oxford
Hamilton JD (1983) Oil and the macroeconomy since world war II. J Polit Econ 91(2):228–248
Hamilton JD (1988) A neoclassical model of unemployment and the business cycle. J Polit Econ 96(3):593–617
Hamilton JD (2003) What is an oil shock? J Econom 113(2):363–398
Hamilton JD (2011) Nonlinearities and the macroeconomic effects of oil prices. Macroecon Dyn 15(S3):364–378
Hamilton JD (2021) Measuring global economic activity. J Appl Econom 36(3):293–303
Herrera AM, Lagalo LG, Wada T (2011) Oil price shocks and industrial production: Is the relationship linear? Macroecon Dyn 15(S3):472–497
Hooker MA (1996) What happened to the oil price-macroeconomy relationship? J Monet Econ 38(2):195–213
Hooker MA (2002) Are oil shocks inflationary? Asymmetric and nonlinear specifications versus changes in regime. J Money Credit Bank 34(2):540–561
Jurado K, Ludvigson SC, Ng S (2015) Measuring uncertainty. Am Econ Rev 105(3):1177–1216
Hwang I, Kim J (2021) Oil price shocks and the US stock market: a nonlinear approach. J Empir Finance 64:23–36
Kilian L (2009) Not all oil price shocks are alike: disentangling demand and supply shocks in the crude oil market. Am Econ Rev 99(3):1053–1069
Kilian L, Park C (2009) The impact of oil price shocks on the US stock market. Int Econ Rev 50(4):1267–1287
Kilian L, Vigfusson RJ (2011) Nonlinearities in the oil price-output relationship. Macroecon Dyn 15(S3):337–363
Kilian L, Vigfusson RJ (2017) The role of oil price shocks in causing U.S. recessions. J Money Credit Bank 49(8):1747–1777
Kilian L, Zhou X (2018) Modeling fluctuations in the global demand for commodities. J Int Money Financ 88:54–78
Koop G, Potter S (1999) Dynamic asymmetries in U.S. unemployment. J Bus Econ Stat 17(3):298–312
Lee K, Ni S (2002) On the dynamic effects of oil price shocks: a study using industry level data. J Monet Econ 49(4):823–852
Ludvigson SC, Ma S, Ng S (2021) Uncertainty and business cycles: Exogenous impulse or endogenous response? Am Econ J Macroecon 13(4):369–410
Mork KA (1989) Oil and the macroeconomy when prices go up and down: An extension of Hamilton’s results. J Polit Econ 97(3):740–744
Morley J, Piger J (2012) The asymmetric business cycle. Rev Econ Stat 94(1):208–221
Nodari G (2014) Financial regulation policy uncertainty and credit spreads in the US. J Macroecon 41:122–132
Pindyck RS (1991) Irreversibility, uncertainty, and investment. J Econ Literat 29(3):1110–1148
Rahman S, Serletis A (2010) The asymmetric effects of oil price and monetary policy shocks: a nonlinear VAR approach. Energy Econ 32:1460–1466
Teräsvirta T, Yang Y (2014) Linearity and misspecification tests for vector smooth transition regression models. CREATES Research Papers, 2014-04
Van Dijk D, Teräsvirta T, Franses PH (2002) Smooth transition autoregressive models–A survey of recent developments. Econom Rev 21(1):1–47
Zhu H, Su X, You W, Ren Y (2017) Asymmetric effects of oil price shocks on stock returns: evidence from a two-stage Markov regime-switching approach. Appl Econ 49(25):2491–2507
Acknowledgements
We are grateful to an anonymous referee, Robert M. Kunst (editor), and Lutz Kilian for his constructive comments and suggestions. We also have benefited from helpful comments from Lee Adkins, Wenyi Shen, David Carter and participants at the 2022 Asian Meeting of the Econometric Society in Tokyo, WEAI conference in Portland, SETA 2022 Econometric Theory and Applications Conference and the KEA International Conference in Korea for helpful comments and discussions. Our special thanks go to Efrem Castelnuovo for providing technical support.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised due to space adjustments in Figure 6’s caption and an updated Figure 7 citation in Section 7.2.
Appendix
Appendix
1.1 Linearity test at a multivariate level
Following Caggiano et al. (2014, 2017), to test nonlinearity at the multivariate level, we perform the Lagrange multiplier (LM) linearity test proposed by Terasvirta and Yang (2014). The p-dimensional 2-regime first-order Taylor approximation of a logistic STVAR with a single transition variable takes the following form:
where \(X_{t} =[\Delta p r o d_{t},r e a_{t},r p o_{t},\pi _{t}, \Delta e m p l_{t}, \Delta i p_{t}]^{ \prime }\) is the \((p \times 1)\) vector of endogenous variables, \(Y_{t} =[X_{t -1} \vert \ldots X_{t -k}\vert \alpha ]^{ \prime }\) is the \(((k \times p +q) \times 1)\) vector of exogenous variables, \(z_{t}\) is the transition indicator variable, and \(\Theta _{0}\) and \(\Theta _{1}\) are matrices of parameters. In this case, the number of endogenous variables is \(p =6\), the number of exogenous variables is \(q =1\), and the number of lags is \(k =1\) (via (Terasvirta and Yang 2014)). Under the null hypothesis of linearity, \(\Theta _{1} =0.\) This LM-type test is performed as follows:
-
1.
Estimate the restricted model (\(\Theta _{1} =0\)) by regressing \(X_{t}\) on \(Y_{t}\) and collect the residuals \({\tilde{E}}\) and the matrix residual sum of squares \(R S S_{0}\) = \({\tilde{E}}^{ \prime } {\tilde{E}}\).
-
2.
Run an auxiliary regression of \({\tilde{E}}\) on the unrestricted model (A1) and collect the residuals \({\tilde{\Xi }}\) and the matrix residual sum of squares \(R S S_{1} ={\tilde{\Xi }}^{ \prime } {\tilde{\Xi }}\).
-
3.
Compute the test statistic \(L M =T \times t r a c e (R S S_{0}^{ -1} (R S S_{0} -R S S_{1}))\), where T is the sample size. The test statistic is distributed as a \(\chi ^{2}\) with \(p \times (k p +q)\) degrees of freedom.
For this model, a value of the LM-test statistic is 104.6 (d.f. = 42) and its corresponding p value is 0.00. Thus, the p value rejects the null hypothesis of linearity, \(\Theta _{1} =0\) at any conventional confidence level.
1.2 Nonlinearity inherent in the global oil market
We examine how the effect of different structural oil price shocks on oil prices themselves varies over the different phases of the business cycle. The first block \(X_{1 t} =[\Delta p r o d_{t},r e a_{t},r p o_{t}]^{ \prime }\), which constitutes the structural global oil market model, is forced apart and re-estimated via the STVAR. Our finding indicates that the effect of aggregate demand shock on oil prices is business-cycle dependent, while the remaining two shocks have no considerable heterogeneous effects on variations in oil prices over the business cycle (see the Figure 7). The aggregate demand shock triggers the peak in the eighth month (0.45%), but it rises a little bit in the fourth month (0.24%) and then dies out quickly during recessionary periods. It states that a strong decline in US domestic industrial activity substantially attenuates a global boom that tends to lift the real price of oil. This implies that the expansionary effect of aggregate demand shock might be weakened during recessions, but the output response is likely to bounce back via the downward pressure of such shock on the price of oil.
Responses of the real price of oil to structural shocks in the global oil market: 1973–2018. Note Responses of the real price of oil to one standard-deviation supply and demand shocks in the global oil market. Three structural shocks are normalized to represent that each shock tends to raise the real price of oil following Kilian (2009). Our model features the vector of three endogenous variables: \(X_t = [\Delta prod_t; rea_t; rpo_t]^\prime \)
1.3 Extra tables for robustness
Table 3 presents the descriptive statistics and data sources for additional variables we used in robustness checks. Tables 4, 5 and 6 reports the 60-month ahead forecast error variance decomposition for robustness checks. Table 4 shows that US unemployment vs. employment qualitatively displays a very similar pattern across different phases of the business cycle. In Table 5, the contribution on headline inflation conditional on recession is fairly muted from 57.6% (our baseline) to 46.6% due to the fact that WTI spot price was under control of the US government partially in our sample. Finally, in Table 6, we confirm that the money-supply growth has much stronger effects on all the variables in recessions than in non-recessions. However, the variation by adding the monetary policy variable is milder for the total explaining power of oil price shocks.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Hwang, I., Kim, J. Oil price shocks and macroeconomic dynamics: How important is the role of nonlinearity?. Empir Econ 66, 1103–1123 (2024). https://doi.org/10.1007/s00181-023-02484-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00181-023-02484-w
Keywords
- Oil price shocks
- Industrial production
- Smooth transition vector autoregression
- State-dependent effects
- Asymmetric dynamics