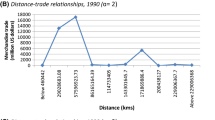
Abstract
This paper studies the impact of macroeconomic factors on co-movement in the foreign exchange rate markets. Data of foreign exchange rates from 24 merging markets is used to this end along with a dynamic spatial Durbin model as to examine spatial dependencies among markets. Our empirical findings show no evidence that cultural ties exert a role in spreading macroeconomic shocks in the exchange rate of a country to the exchange rates of other countries. Moreover, we show that economic closeness through foreign direct investment (FDI) and international bilateral trade is the most prominent channel in spreading macroeconomic shocks and spatial effects in emerging markets through the foreign exchange rates. In addition, geographical proximity reinforces the interdependence relationship of emerging markets. Our findings show that the co-movement of foreign exchange rate markets across the selected emerging markets is positively influenced by their gross domestic product (GDP) and interest rate differential and negatively affected by the terms of trade and remittance. In addition, we reveal that terms of trade, the inflation differential, and remittance are the most prominent fundamental factors affecting foreign exchange rate movements.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Examining the co-movement between exchange rates is of great importance for both investors and the central banks as it reveals discernible patterns of how local currency jointly appreciates or depreciates against a foreign currency. The central bank also benefits from knowing how the exchange rates co-move when drafting policy interventions. Moreover, large swings in the exchange rate affect the real economy, financial markets, international competitiveness, real income, and inflation, as exchange rate movement affects the price of imported goods and the competitiveness of export firms. Therefore, understanding the behaviour pattern of foreign exchange rate and how local currency jointly moves against foreign currency becomes crucial given its countless implications for economic policies and portfolio allocation since a negative shock from one market can be quickly transmitted to other markets in the network through contagion effect.
The issue of co-movement had received considerable thought in the impressive literature devoted to examining the behaviour of financial markets. An appropriate analysis of the co-movement of foreign exchange rates reduces the hedging costs of exposure to it. Although there is limited research on the co-movement analysis of foreign exchange rates focusing on emerging markets, assessing the co-movement pattern of foreign exchange rates in emerging markets has become an exciting topic as emerging markets are the largest market worldwide and characterised by high volatility and uncertainty. According to International Monetary Fund (IMF) data, Emerging markets (EMs) represent one of the largest economies around the world. Its total population represents 57% of the world population, with the GPD estimated at 25% of the global GDP, making these markets more attractive for investors seeking a risk-returns opportunity.
Studies addressing the co-movement between foreign exchange rates and emphasising cross-markets or cross-regional analysis have more attraction and interest in the emerging market context. Emerging markets represent more than 48% of the daily turnover of global financial markets, with China the largest EMs. It is, therefore, essential to understanding not only how a shock to one country is transmitted to other countries through cross-country linkages but also to estimate the degree of spatial autocorrelation between foreign exchange rates and macroeconomic factors that may influence the co-movement in emerging markets. Assessing the co-movement among currencies helps explore cross-border linkages, which transmit market-specific shocks to other markets while constructing international portfolio diversification and explaining how one market responds to currency fluctuations in other markets. Mensah and Adam (2020) argued that currency markets are not only influenced by idiosyncratic factors such as macroeconomic factors and monetary policy direction but also by other external drivers. These external drivers may be geographically related phenomena (Asgharian et al. 2013; Amidi and Majidi 2020; Shikimi and Yamada 2019), cross-market spatial effects, cross-market trade linkages (Frankel and Rose 1998; Jiang et al. 2022), cultural ties (Falck et al. 2012) and financial integration linkages. It is, therefore, imperative to assess the co-movement between foreign exchange rates through these external channels.
The dependence structure of foreign exchange rates, also known as the bilateral linkages between currency pairs, can be defined as the co-movement between the appreciation and depreciation of currency pairs. In contrast, spatial dependence refers to the degree of spatial autocorrelation between independently measured values observed in geographical spaces (Crawford 2009). Legendre and Legendre (1998) argue that spatial dependence is a property of a spatial stochastic process in which the outcomes at a different location may be different. Further to the spatial dependence definition that clearly emphasises the existence of spatial autocorrelation, Overmars et al. (2003) define then the spatial correlation as the property of random variables to take values over a distance that are more similar or less similar than expected for randomly associated pairs of observations, due to geographic proximity. In recent years, scholars and practitioners have begun to understand financial markets' dynamic relationship and co-movement. The extensive literature dealing with the issues of co-movement and dependencies of financial markets has been more directed into stock markets and commodities markets, while little attention has been placed on foreign exchange rate markets and, more precisely, in the emerging markets context. A considerable number of studies on the co-movement and dependencies have been devoted to examining the co-movement between foreign exchange rate and stock market or commodities markets (Carvalho and Gupta 2018; Embrechts et al.2002; Ghosh et al. 2021; Yeap et al. 2020) while few studies look only to foreign exchange rates co-movement in emerging markets. Many approaches and models have been proposed to study foreign exchange rates co-movement and interdependencies. These approaches range from linear correlation models such as vector autoregressive (VAR) model (Donkor et al. 2022; Sosa et al.2018; Casarin et al. 2018), Dynamic conditional correlation (Engle 2002; Carsamer 2016; Zaiane and Jrad 2020) Bayesian-generalised autoregressive conditional heteroskedasticity (GARCH) model (Yeap et al. 2020) contagion approach (Forbes and Rigobon 2002), cross-correlation (Reboredo 2012; Reboredo et al. 2014); cointegration analysis (Tang and Yao 2018); Copula approach (Wang et al. 2013 and Patton 2006;Wu et al. 2012);Wavelet decomposition approach (Kumar et al. 2017; Yang et al. 2016; Xu et al. 2021), while other studies explored the network approach in financial economics to analyse the co-movement among assets (see Mantegna 1999; Allen and Gale 2000; Gai and Kapadia 2010; Carvalho and Gupta 2018; Wang et al. 2014). The drawback of these proposed approaches is the inability of linear correlation to describe a nonlinear relationship between two heterogeneous variables and the failure of the copula to account for the non-stationarity of the co-movement of assets. In addition, such approaches use prior assumptions in the building block of the copula function and do not take into account the time-varying effect of the exchange rate, its stochastic property, and the spatial interconnectedness among markets.
In contrast, the network approach appears to be more suitable for assessing the spatial interconnectedness of financial markets. It remains unclear whether the geographical proximity, cultural ties, and other measures of closeness influence the transmission of foreign exchange rate movement from one country to another and the extent to which the macroeconomic variables affect the co-movement between foreign exchange rates. Moreover, the afford-mentioned approaches failed to investigate the co-movement of foreign exchange rate markets and their spatial dependence in emerging markets. The closest study is that of Fernández-Avilés et al. (2020) which examined the co-movement in commodity markets during distress periods. This is a study that focus on co-movement in commodity markets, but did not focus on exchange rate. It also did not use spatial econometric approach. To the best of our knowledge, no study has attempted to investigate the spatial dependence and co-movement of the foreign exchange rates in emerging markets and analyse how macroeconomic factors influence co-movement in the foreign exchange rate markets.
We explore applying the spatial econometric approach that has recently emerged as one of the best approaches to investigating the spatial dependence between variables to address this gap. Our econometric approach is motivated by Santi et al. (2021), who show that spatial dependence is modelled through spatial weight matrices, which departs from the standard Gauss-Markov assumption of no serial correlation and exogeneity of regressors. In other words, individual foreign exchange rate markets are assumed to be spatially correlated and be affected by macroeconomic factors. Although Fernández-Avilés et al. (2012) first applied the spatial model to financial assets to model the pairwise relationship in financial markets. They found that stock market co-movements are unrelated to geographical proximity, while foreign direct investment (FDI) proxy to financial linkages is responsible for financial market co-movement. The study fails to emphasise the presence of spatial dependence and explore the degree of influence of macroeconomic factors on foreign exchange rate co-movement. Following the same methodology, Asgharian et al. (2013) attempted to investigate the extent to which countries' economic and geographical relations affect the co-movements of their respective stock markets. Their findings revealed a strong effect of a unit shock to regionally dominant countries on other countries through the trade linkages. The studies mentioned above (see Fernández-Avilés et al. 2012; Asgharian et al. 2013) focused on stock markets, while foreign exchange markets are omitted in the literature. Previous studies that apply spatial techniques to model the co-movement of exchange rate concentrate effort on inter-country analysis and fail to consider cross-regional analysis, especially the emerging markets. Moreover, few studies (see Zhang et al. 2019; Hondroyiannis et al. 2009; Fernandez 2011) attempted to focus on the co-movement of the foreign exchange rate in emerging markets have considered only a single geospatial effect. These studies do not investigate spatial dependence channels such as colonial legacy's proximity, financial integration and international trade linkages, and geographical closeness. We also noticed that they did not investigate the role of fundamental macroeconomic variables in transmitting shocks into foreign exchange rates, which are vital for policy interventions in international trade and finance.
The innovation in this paper lies in the fact that we explore the role of cultural identity, geographical phenomena, financial integration, and trade linkages in spreading macroeconomic shocks in a country's exchange rate to other countries' exchange rates. We model the spatial effects on foreign exchange rate co-movement in emerging markets and perform a robust analysis to control spatial autocorrelation through the spatial weight matrices, which synthesise the spatial relation for all pairs of currencies in the emerging markets considered to control the cross-country linkages. We will address the misidentification of the degree of spatial interconnectedness in the selected emerging foreign exchange markets that affect the risk of exchange rate spillover. To address this shortcoming, we propose a methodology based on the dynamic spatial Durbin model (SDM) with fixed effects to analyse the spatial dependence among currencies, taking into account the space and time-varying of exchange rate movement spillover of the model's features that identify the most significant interconnectedness among currencies. The SDM assesses the cross-border linkages where negative shocks, such as depreciation or appreciation in one currency, may affect the entire network, especially when this currency is at the node's centre. Our findings show that terms of trade, inflation differential, and remittance are the most prominent fundamental factors affecting foreign exchange rate movements within the spatial network.
Moreover, we suggest that economic ties and financial integration reinforce the spatial interdependence relationship of emerging markets. Furthermore, we find that economic closeness through international trade linkages is the most prominent channel in spreading a spatial effect among emerging foreign exchange rate markets. We find no evidence that cultural ties play a role in spreading macroeconomic shock to foreign exchange rates in emerging markets.
The rest of this paper is structured as follows: Sect. 2 presents a brief literature review; Sect. 3 focuses on the methodology and data; Sect. 4 provides the empirical results and an interpretation thereof, and Sect. 5 presents our conclusions and policy recommendations.
2 Literature review
Understanding the co-movement across emerging financial markets is extremely important given its substantial implications in constructing international portfolio allocation and designing risk mitigation strategies. Due to market integration, liberalisation, and globalisation, global financial markets have become increasingly interdependent. That has compelled researchers to investigate the cross-market linkages in emerging foreign exchange rate markets because a shock in one market can affect returns and volatility in others, with severe implications for portfolio risk assessment. In this regard, exploring the transmission of exchange rate movement from one country to another may significantly contribute to investors' diversification strategy and thus mitigate the underlying risk attached to foreign exchange rate exposure. Therefore, it remains necessary to understand the co-movement among currencies; explore the cross-border linkages which transmit market-specific shocks to other markets and explain how one market responds to currency fluctuations in other markets. Doing so will help decision-makers design an efficient hedging technique against foreign exchange rate exposure and help investors build an efficient and optimal portfolio allocation. Kole et al. (2007) and Chollete et al. (2009) argued that failing to capture the co-movement or misidentification could lead investors to make costly decisions. However, the proper assessment of co-movement among currencies pair in emerging markets is only achieved by clearly defining the spatial weight matrix, which synthesises the spatial relation for all currency pairs in the emerging markets in order to capture not only the spatial effect (spatial autocorrelation and spatial heterogeneity) but also the nonlinear properties of the joint distribution of foreign exchange rates returns. This study aimed to investigate the co-movement between foreign exchange rates in emerging markets, focusing on spatial dependence and macroeconomic influence on the considered currency pairs.
Past studies have proposed several techniques to model the co-movement of financial markets. Approaches such as the capital asset pricing model and the arbitrage pricing theory mainly use the Pearson correlation coefficient to measure the co-movement between financial markets. Campbell et al. (1998) and Henry (1998) argued that correlation is central in financial theory. The Pearson correlation coefficient only captures the linear correlation, thus considering random variables uncorrelated when the dependence is nonlinear. However, the absence of autocorrelation between two random variables does not necessarily mean that there is no dependence among variables but instead assumes finite variances of the assets. In addition, Embrechts, et al. (2002) concluded that assuming finite variances of financial assets could be a problem when assessing the dependence structure of financial assets with heavy-tailed distributions. The copula has emerged as a powerful model for overcoming correlation's linearity assumption and capturing co-movement between assets. Patton (2006) applied a copula to capture the co-movement in the foreign exchange markets and found that foreign exchange markets are asymmetrically dependent. This result suggests that it is essential for central banks to develop asymmetric responses to exchange rate movements. It stated that the currency rate fluctuates more significantly when it depreciates than when it appreciates. Thus, examining the co-movement beyond the simple linear correlation is pivotal when making investment decisions.
To this end, Patton (2006) proposed a simple framework for modelling the co-movement of the exchange rate based on a conditional copula. This conditional copula model to foreign exchange rate data shows that currencies are more correlated during appreciation than depreciation and exhibit asymmetric dependence in the tails. Similar studies on co-movement using copula such as Reboredo et al. (2014); Longin and Solnik (2001) pointed out that asymmetric dependence is where financial returns exhibit superior correlation during the market downturn than market upturns. Several studies, such as those (Joe et al.2010; Smith et al. 2010), have argued that the copula allows for nonlinear and asymmetric cross-sectional and serial dependence. However, the dynamic conditional copula model developed by Patton (2006) is based on AR (p). T-GARCH (M) (autoregressive-generalised autoregressive heteroscedasticity model) failed to capture both cross-sectional and serial dependence, only capturing the latter. Therefore, finding models that enable risk managers to capture both cross-sectional and serial dependence of exchange rate risk remains a challenge in the finance literature.
Several studies (such as Longin and Solnik 2001; Garcia and Tsafack 2011) emphasised that asymmetric dependence is due to evidence of a nonlinear causality between international financial assets. Lien et al. (2013), Boero et al. (2011), and Wang et al. (2011) pointed out that foreign exchange markets exhibit asymmetric dependence. Henceforth, the most suitable methodology for modelling this asymmetric dependence shall account for spatial proximity, time-varying interconnectedness, economic proximity, cross-sectional dependence, and serial dependence. None of the reviewed literature discussed above clearly develops a methodology to examine the co-movement among foreign exchange rate markets while accounting for asymmetric dependence features of this asset. However, some studies have proposed methodology based on spatial econometrics, whereas others are based on the network approach.
Nevertheless, it is widely acknowledged that foreign exchange rate markets exhibit dynamic features such as heavy-tailed distribution, volatility cluster, volatility spillover, and asymmetric volatility. It is thus unsuitable to use the Pearson correlation coefficient to capture the co-movement among the foreign exchange rate markets. The drawbacks of the Pearson correlation coefficient have motivated scholars to seek an alternative statistical model to estimate the co-movement of financial markets. To overcome the constant conditional correlation problem observed in the GARCH model on other linear models, Engle (2002) proposed the dynamic conditional correlation (DCC) model with the flexibility of a univariate GARCH model coupled with parsimonious models for the correlation. After that, several studies on co-movement adopted the DCC approach. Among others, Carsamer (2016) empirically assesses the co-movement of foreign exchange rates in selected African countries using the DCC model to unearth the determinants of foreign exchange rates co-movement. The result shows evidence of external determinants of foreign exchange rate co-movement. It concludes that regional interest rate differential, trade intensity, competition and world interest rate decrease the degree of co-movement. Zaiane and Jrad (2020) employed the DCC and vector error correlation (VEC) model to examine the dynamic linkages between exchange rates and the stock markets of Tunisia. They found a unidirectional relationship between foreign exchange rates and stock markets. Mohd Amin and Janor (2016) also find unidirectional movement from foreign exchange rates to stock prices in emerging markets. These results are consistent with the flow-oriented theory (Dornbusch and Fischer 1980), stating that exchange rate fluctuations affect international competitiveness. Although the DCC is used to estimate the bilateral linkages, it is proven that shocks to one country are transmitted to other countries through cross-country linkages such as bilateral trade, export competition, capital account openness or bilateral investment flows.
In most cases, historical data, including these transmission channel data, are available in low-frequency dimensions (monthly, quarterly, and yearly frequencies), which does not provide relevant information to portfolio allocation as trading decisions require high-frequency information (hourly, daily or weekly). The DCC model fails to analyse the cross-linkages at high frequency, and hence model with the ability to decompose the series into high and low frequency is required to study co-movement conducted independently for the high and low frequency.
In this regard, the Wavelet analysis has emerged as a powerful tool to analyse the time–frequency co-movement of financial markets. Assessing the co-movement in daily returns of currency pairs, Kumar et al. (2017) employ the Wavelet cohesion approach and found that currency markets are nearly perfectly integrated in the long run scale (monthly, quarterly and biannual) while the cross-correlation analysis shows that British pound (GBP) act as potential leader/follower across the scale. Further to this, they found the presence of a dynamic pattern of co-movement among the major currency futures. Owusu Junior et al. (2018) found the existence of a mixed interplay of lead-lag relationship, while Amewu et al. (2022) found the low-medium term lead-lag connection between foreign exchange rates. Özmen and Yılmaz (2017) investigated the relationship between exchange rate change in some selected emerging markets and its foremost financial determinants. They found that the change in the exchange rate is correlated with interest differentials, risk premium, the Federal Reserve Bank (FED) monetary policy implementation and policy uncertainty, with the strongest co-movement of exchange rate change occurring with risk premium in all countries considered. Exploring the co-movement between foreign exchange rates and emerging stock markets using the wavelet analysis, He et al. (2023) found unidirectional causality runs from the emerging stock market to foreign exchange rates. Qureshi and Aftab (2020), investigating the interdependencies and contagion among exchange rates of Asian emerging markets, found regional market convergence in the long run with a substantial increase of co-movement among exchange rate pairs during the global financial crisis.
Contrary to the previous literature on wavelet analysis in emerging markets, Yang et al. (2016) addressed the co-movement problem of foreign exchange rates in developed markets (GBP/USD, EUR/USD and JPY/USD) using the wavelet analysis. This study found strong interdependence between Euro and Pound at all frequencies. Although the wavelet analysis can decompose the data into low and high frequency, allowing the researcher to study the shorter time period (daily, weekly) and more extended time period (monthly, quarterly, bi-annually or yearly) independently, it cannot cater to the spatial relation of the bilateral exchange rate.
Wang et al. (2014) analysed the foreign exchange market network using the network approach's minimum spanning tree (MST) model. The study found that the distribution of the cross-correlation coefficient in the foreign exchange market network is fat-tailed and negatively skewed. In other words, the study found asymmetric dependence between foreign exchange rate markets of the 42 major currencies. Chen et al. (2015) analysed the interaction effect among industries and stocks using a network approach and found a close relationship between stock centrality and stock returns. Wang et al. (2012) studied the topology of similarity networks in foreign exchange markets using the MST approach and found that the Singapore dollar became a new centre currency for the network after the United States sub-prime crisis. Huang et al. (2009) showed that a small-world network is sensitive to long-distance attacks. Thus, a topological change can help understand correlation patterns among foreign exchange rates, although it fails to tackle emerging markets' spatial effect issues.
A novel technique based on spatial econometric analysis was proposed to unearth the spatial dependence. Santi et al.(2021) argued that spatial dependence is modelled through a spatial weigh matrix which synthesises the spatial relation for all pairs of foreign exchange rates in the model, while Asgharian et al. (2013) argued that the spatial econometrics approach allows for the modelling dependence between countries' financial markets and investigates the linkages effect of shocks among countries.
The spatial econometric model is widely used in the context of emerging markets (Hondroyiannis et al. 2009; Miled et al.2022; Chen et al. 2020; Jiang et al. 2022) to investigate the contagion between financial markets. These studies found evidence of the existence of contagion among emerging markets.
Chen et al. (2020) focused their attention on China's stock markets. They investigated the interdependence of this market and attempted to understand the co-movement and its spatial pattern. The results show that the co-movement between provinces is positively influenced by their GDP and negatively affected by the economic structure. Although their study investigated co-movement and spatial dependence, it was conducted for a specific emerging market (China), focused on cross-provincial linkages rather than cross-country linkages, and directed to stock markets instead of foreign exchange rate markets.
Asgharian et al. (2013) investigate how geographical relation affects stock market co-movement in emerging and developed economies. The study indicated a strong effect of a unit shock to regionally dominant countries on other countries through trade linkages. That implies that bilateral trade outperforms the other linkages that are considered when capturing the dependencies between stock markets. There is no empirical evidence on whether their findings are relevant to the exchange rate markets. Additionally, the study omitted to assess the spatial dependence and other spatial linkages such as common language closeness and financial integration linkages. Previously to their work, Fernández-Avilés et al. (2012) studied the dependencies of the financial market using spatial econometric techniques. Their study showed that geographically clustered countries are more concerned about stock market co-movement. However, the study was limited to the stock market rather than the foreign exchange rate market. The study concluded that financial linkages are important in accounting for market co-movement. Prior to Fernández-Avilés et al. (2012), Asgharian et al. (2013) suggested that financial dependencies are more pronounced in the geographically proximate country. Similarly, Orlov (2009) argued that geographically proximate countries are more likely to have similar trade and investment patterns, thus transmitting shock to neighbouring countries through the dependent variables. The spatial techniques could thus help to assess the foreign exchange co-movement. Zhang et al. (2019) investigated the spatial returns spillover among G20 financial markets using the spatial autoregressive (SAR) model and found that the space weight matrix captures multidimensional spatial spillover effects among stock markets. Further, the study concludes that inflation and government debt and macroeconomic performance are significantly positively correlated with stock returns, while interest rate and stock market volatility have a negative effect on stock returns.
Flavin et al. (2002) argued that physical distance might be important in explaining cross-country stock market correlation. Similarly, Fazio (2007) found that contagion is more likely to occur between countries in the same geographical region, while Benos et al. (2015) showed that proximately located countries are likely to have stronger links that cause spillover. Thus, geographical proximity appears to be an important determinant of international capital flows and may affect co-movement among foreign exchange rates in emerging markets. Contrary to the previous literature, Fernández-Avilés et al. (2012) argued that physical distance does not play a critical role in stock market co-movement as has been previously thought. However, this study was limited to the stock market under volatility spillover and did not investigate the same for the foreign exchange rate market, where high volatility is experienced due to trade linkages.
Contrary to Fernández-Avilés et al. (2012), who argued that geographical distance does not influence stock market co-movement, Amidi and Majidi (2020) argued that geographical position and bilateral trade flow are key determinants of spatial dependence. It added that proximity is one way of creating a spillover. In other words, a shock in the home currency in the region will impact the neighbouring countries. In this regard, Anselin (1988) argued that ignoring spatial dependence in an econometric analysis while variables are spatially correlated would lead to bias in econometric estimation. It is, therefore, essential to assess the determinants of spatial dependence.
Moreover, previous studies using spatial techniques mainly consider the physical distance and omit the financial, economic, and cultural distance, which might be crucial as they reflect market interdependence. Falck et al. (2012), study the effect of cultural ties proxy by linguistic identity on the economic exchange using gravity analysis and show that highly time persistent cultural ties impact economic exchange across regions. Although Fernández-Avilés et al. (2012) first applied the spatial model to financial assets, our research is the first to use the spatial regression approach to examine co-movement among foreign exchange rates, investigate their spatial dependencies in emerging markets, and consider cultural proximity in the transmission link of foreign exchange rate co-movement. We focus on understanding the role of some selected macroeconomic variables in the transmission of foreign exchange rate movement to neighbouring markets while considering the cultural, geographical, economic, and financial closeness of the countries in the network to capture the effect of currency movements on a country's neighbours.
We revisited several modelling techniques used in the literature to assess co-movement, including the copula approach, spatial analysis, wavelet decomposition approach, correlation and network approaches and highlighted a shortcoming in the existing literature. The linear model ignores the nonlinearity between two heterogeneous financial assets. This nonlinearity can be captured by spatial econometric analysis newly applied in foreign exchange markets, especially the SDM approach, which emerges as a robust spatial econometric model. However, the latter accounts for the non-stationarity of co-movement in asset dynamic features such as asymmetric volatility spillover and can detect the spatial dependence effect of macroeconomic variables used to control foreign exchange rate co-movement.
This study looks to fill the gap in the literature by assessing the co-movement of foreign exchange rate markets, taking into account the importance of geographical and cultural distance, international trade, and financial integration while considering that foreign exchange movement will be transmitted to neighbouring countries.
3 Materials and methods
3.1 Econometric modelling
Numerous studies approach the problem of co-movement of foreign exchange rates with the view that fundamental macroeconomic variables are likely to influence the direction of foreign exchange rates (Djemo et al. 2021; Mulugetta et al. 2004), it remains controversial in the literature how the imported shocks spillover to other countries and affect theirs fundamental macroeconomic variables.
In this study, we based our analysis on the theory of an open economy, where markets become more dependent on one another. We investigate the co-movement by assessing how shock in one country may spread to neighbouring country providing that exchange rates movement depend on its own fundamentals. According to Held et al. (2000), we also consider the concept of globalisation that embodies a transformation in the spatial organisation of social relations, interregional flows, and network of activity. They argued that globalisation increases the magnitude of interconnectedness and flows of trade, culture, migration, investment, and finance. For this concept, we introduce the cultural identity with the assumptions that it is likely for international investors to trade with the trading partner which speak the same language; trade, geographical, and finance flows in our model to assess their influence on the spatial dependence of foreign exchange rates in emerging markets. Therefore, we reject the assumptions that countries are independent of each other. We use a spatial econometric approach to model spatial effects and investigate the co-movement among foreign exchange rates in emerging markets.
The spatial analysis proposed in this study will help us to examine the co-movement between foreign exchange rates across the selected emerging markets focusing on four transmission channels: cultural linkages, international trade linkages, financial linkages, geographical linkages, and understand how one currency's appreciation or depreciation (exchange rate change) is affected by shocks in another country while accounting for neighbouring effects.
3.1.1 Spatial model
Since our panel data contains both time series and cross-sectional data, we employ a spatial model for the regression analysis. We assume that foreign exchange rates are spatially correlated and can be affected by fundamental macroeconomic variables such as remittance, GDP, inflation differential, terms of trade, interest rate differential, and stock returns. To analyse the spatial dependence, we focus our study on four transmission channels: geographical linkages, economic linkages, cultural identity linkages, and financial integration linkages. Shikimi and Yamada (2019) and Haile and Pozo (2008) suggest that cross-country linkages are more likely to occur in geographically clustered countries through trade and financial channels, contrary to Fernández-Avilés et al. (2012) who find no evidence of geographical closeness to influence the cross-country linkages. Falck et al. (2012) show that cultural ties faster economic exchange across countries. We also investigate the role of fundamental macroeconomic variables (i.e., control variables) in the co-movement of foreign exchange rate markets (dependent variables). We thus focus on the interaction among a network of foreign exchange rate markets. LeSage (2008); Basile et al. (2014) defined spatial dependence in a regression model as a situation where the value of the dependent variable at one location depends on the value of the neighbouring observations at other locations. Thus, spatial dependence may be the consequence of spatial correlated omitted variables rather than being the result of spillover (Basile et al. 2014).
Several alternative spatial regression models have been proposed based on the source of spatial dependencies, ranging from the spatial error model (SEM) to the spatial Durbin model (SDM) and the spatial autoregressive (SAR) model.
3.1.1.1 Spatial autoregressive model
The SAR model, also known as the spatial lag model, assumes that the autoregressive process occurs only in the response variables, and this implies that spatial dependence ensues from the error term and control variables. It means that shocks to both error terms and explanatory variables at one location are transmitted to other locations within the spatial system. In contrast, the SEM model assumes that only shocks in the error term are transmitted to other locations.
where \({W}_{i,j}{F}_{ex}\) capture the co-movement between foreign exchange rate markets; \(\gamma \) is the spatial autoregressive parameter; \({W}_{i,j}\) is weight matrix that captures the cross-country correlation. \(X\) is a matrix that controls country-specific factors; β is a coefficient vector that measures changes in the country-specific variables on foreign exchange rate change in the respective country.
3.1.1.2 Spatial error model
The SEM model assumes that the autoregressive process is found only in the error term. In other words, spatial dependence affects only the error terms.
where \(\gamma \) is the spatial autoregression coefficient; \({W}_{i,j}\) is the spatial weight matrix that models how market \(i\) is affected by the shock from market \(j\); \(\beta \) is a vector representing the slope;\(X\) are the fundamental macroeconomic variables ( stock returns, interest rate differential, inflation differential, term of trade, remittance and GDP) of the countries being considered.
3.1.1.3 Spatial Durbin model
To estimate the spatial dependence in the selected emerging foreign exchange rate markets and account for different sources of spatial correlation, we employ the SDM with the fixed-effect model. Asgharian et al. 2013 argued that SDM has the capability to nest the SAR and SEM and produce unbiased coefficient estimates under the data generating process. The SEM looks to correct the inefficiency of estimates, whereas the SAR model appears suitable for model decomposition into direct and indirect effects. LeSage and Pace (2014) recommend using the SDM in general to overcome the shortcoming in the SAR and SEM models. Thus, our proposed model will help us capture spatial dependence through the spatial lag of the dependent variable and the spatial externalities in the idiosyncratic random shock through the spatial autoregressive error term.
The model is written as follows:
where \({Fex}_{it}\) is a vector of the dependent variables (foreign exchange rate changes of country i); \({X}_{it}\) is a matrix that controls for country-specific factors in period \(t,\) including stock returns, inflation differential, interest differential, term of trade, remittance and GDP per capita (explanatory variables) with an associated vector of coefficient β; \({\varepsilon }_{it}\) is a vector of the idiosyncratic error (error term); \({W}_{ij}\) is a spatial weight matrix which synthesises the spatial correlation and enables the spatial dependence to be modelled in various ways; \(\rho \) is a SAR parameter; φ is a spatial effects coefficient of the control variables; and \({\delta }_{i}\) and \({\gamma }_{i}\) represent specific effects in time and space, respectively. \({W}_{ij}{X}_{ij}\) captures the impact of foreign explanatory variables across country. \({W}_{ij}{Fex}_{jt}\) capture the co-movement between foreign exchange rate markets. The advantage of an SDM model is the simplicity of decomposing the foreign exchange movement into contagion, systematic, and idiosyncratic components. The linkages, denoted by \(\sum_{j=1}^{N}{W}_{ij}{X}_{it}\), \({Fex}_{it},\) explore how shock from one foreign exchange market is transmitted to other markets in the network.
3.1.2 Weighting matrix
The weight matrix determines the structure of the spatial dependence between foreign exchange rate markets and allows us to determine the connectivity structure between foreign exchange rate movement and the channel of cross-sectional linkages. We construct the weights from pair economies among n countries at time t using the cross-sectional data as follows:
where \({w}_{ij}\) denotes the weight, which corresponds to country pairs \(ij\).
3.1.3 Transmission channels
This study considers different spillover channels, including economic, financial, cultural, and geographical closeness, through which shocks in the explanatory variables propagate to other cross-sectional units. We expect these spillover channels to exert a role in spreading macroeconomic shocks in a country's exchange rate to the exchange rates of other countries, this type of shock transmission will be capture in our analysis as an indirect effect whereas the effect of local fundamental shock on its own foreign exchange will be capture as direct effect. The innovation in this study lies in the fact that we investigate the cross-market multidimensional spatial effects around emerging foreign exchange markets in contrast to existing studies on the spatial effect that focus on a single spatial effect. The transmission channels proposed in constructing the spatial weight matrix in this study are motivated by the existing empirical and theoretical underpinning arguments in the spatial analysis literature. Frankel and Rose (1998) and Jiang et al. (2022) show that trade linkages capture by bilateral trade and trade competition and capital account proxy of financial integration linkages are the main transmission channels of financial spillover. Amidi and Majidi (2020) and Shikimi and Yamada (2019) argued that geographic closeness and bilateral flows (FDI, trade) are the most prominent channels of regional spillover. Falck et al. (2012) argued that linguistic ties foster economic exchange across regions.
3.1.3.1 Geographical distance
We define geographical distance as the great circle distance between two countries' capital cities. In this paper, we use the Haversine distance which is a built in the Stata software to compute the physical distance by measuring the length of the shortest path between two capitals along the surface. Although it does not provide high accuracy that Vincenty offers, it remains more practical to compute the distance on sphere since it uses longitude and latitude. It is also simple to compute compared to the Vincenty procedure which requires intensive computation and sophisticated algorithm.
In fact, because of migration, investors with different level of gain appetite or risk appetite might migrate from one capital city or country to another. Thus, affecting the fundamentals macroeconomics of both the original and the destination country. Moreover, investor’s decision to relocate might be prompted by economic agent welfare such as labour markets conditions, conflict, political instability, and other socioeconomic factors.
Geographic proximity can be an important driver of foreign exchange rate spillover since geographically clustered countries with similar trade patterns tend to import the same goods from the same exporter country. Having a similar import pattern, a currency appreciation of their leading supplier will reduce their export from this country. As a result, the price of imported goods will increase, leading to inflation. The central bank policy intervention will affect the exchange rates. We use the Haversine formula to compute the physical distance from the latitude and longitude as follows:
where R is the earth radius; \({Lat}_{i}\) and \({Lon}_{i}\) are latitude and longitude of the capital city of country i, respectively, and vice versa for country j; \({Dist}_{ij}\) is the physical distance between country i and country j; Cos and Sin are cosinus and sinus, respectively. Geographical proximity tends to accentuate common information spillover among countries that are close to each other’s. For example, Amidi and Majidi (2020) argued that geographical position and bilateral trade flow are key determinants of spatial dependence. However, geographic proximity may not be the only transmission channel when investigating the spillover effect across foreign exchange rates markets.
3.1.3.2 Economic linkages
We measure the economic distance using bilateral trade (export) and bilateral net foreign direct investment (FDI) inflows to calculate the closeness between two countries. The theoretical motivation to choose these variables lies in the assumption that foreign exchange rates co-movement can be transmitted to neighbouring countries through trade competition and income. A country's loss of competitive position in the international trade market and the decrease in demand for goods from this country will negatively affect its major trading partners, and hence, this leads to the depreciation of its domestic currency. Moreover, foreign exchange rate in a domestic country with high inflation, low GDP, interest rate would likely to react to the changes in fundamentals of neighbouring countries with similar economic or financial characteristics. Fundamentals economics shock would affect foreign exchange rate within the country, creating volatility in the currency markets. This disturbance in currency markets will be transmitted to currency markets in foreign country through various transmission channels including economic integration, financial integration, cultural integration, and geographical proximity.
Illustratively, international importer tends to import goods from country with weak currency where the price of goods is cheaper than a competitor’s countries with strong currency. This phenomenon will lead to more demand of currency in this country. As a result, domestic currency demand will increase which lead to the appreciation of foreign exchange rate and it will be transmitted to importer country and vice versa. We calculate the inverse economic distance as follows:
where \({Dist}_{ij}\) is the distance between the capital city of country \(i\) and country \(j\) obtained from Eq. (5), \({EX}_{i}\) is export of country \(i\), and \({EX}_{j}\) is export of country \(j\).
where \({FDI}_{i}\) is a net FDI inflow of country \(i\) and \({FDI}_{j}\) is net FDI inflow of country \(j\). We calculate the economic and financial integration distances using the cross-sectional mean across time of economic and financial variables (FDI, export, net capital account, and external debt).
3.1.3.3 Financial integration linkages
The spatial correlation can be explained by financial integration, which may be associated with either country's assets or liability. Illustratively, a rise of interest rate in one country could lower the borrowing cost of most firms and their regional branch. In effect since most firms are more likely to have regional branches in other country, the change of share price in one country will encompasses their foreign representation. We use the bilateral portfolio investment to construct the capital weight and external debt for financial weight. We derive the capital weight and financial weight, respectively, as follows:
where \({Inv}_{i} and\) \({Inv}_{j}\) are the portfolio investment in country \(i and j\) respectively, \({Debt}_{i} and {Debt}_{j}\) represent external debt in country i and j respectively.
3.1.3.4 Cultural identity linkages
Colonial legacies between countries, such as common language and common colonial relationships between countries colonised by the same coloniser or between coloniser and their former colonies, affect bilateral trade and, therefore, may be a channel of financial contagion. In this regard, Sousa and Lochard (2012) investigated the role of colonisation in trade performance across developing countries and found that former British colonies trade more on average than their French counterparts. This finding is supported by the fact that British colonies favoured free trade policies in contrast to French colonies that enforced protectionist measures. A common language clustered countries may tend to have intensive trade patterns among them as they develop a comparative advantage to reduce the trade cost. Therefore, it is important to investigate the contribution of colonial legacies (common language) in transmitting the shock from one country to another. We built the colonial weight matrix using a binary weight by assigning one to countries with a common language and zero otherwise following with row normalization as follow:
where \(i\) and \(j\) denote country and it trading partner. Our study uses the weight based on the assumption that country that do not share the same language might exhibit spatial dependence based on their language barrier among traders.
3.2 Data and variable selection
This study uses yearly data of 24 emerging markets – 10 large emerging markets (Argentina, Brazil, China, India, Indonesia, Mexico, Poland, Turkey, and South Africa) and other emerging markets around the world (Chile, Columbia, Hungary, Thailand, Philippines, Nigeria, Egypt, Malaysia, Morocco, Russia, Singapore, Ukraine, the United Arab Emirates, Mauritius, and the Czech Republic) – covering the period of January 2001 to January 2021. Table 1 describes the data source and variables used in this study. We define the neighbourhood effect by the geographical distance, economic and financial integration, and cultural distance. We employ the capital account to calculate the capital weight, while the external debt is used as a proxy to compute the financial weight matrix. Both capital and financial account are measures of financial integration distance.
We consider a common language to capture cultural closeness since two countries with the same language will tend to have intensive trade and close migration patterns. The spatial weight matrix W measured by linguistic distance is given a value of one if both countries speak the same language and zero if otherwise. We normalise all the spatial weight matrices so that the sum of each row is equal to one.
We use a set of control variables that capture the state of each economy. The leading macroeconomic indicators reflecting the free capital mobility and financial integration are remittance and interest rate differential. We also include the gross domestic product (GDP) as a proxy of income, inflation differential, terms of trade, capital account as a proxy of financial linkage, and equity market returns.
4 Results
We compute the spatial weight matrix, which synthesises the spatial relation for all pair of currencies considered and enables us to model the spatial dependence. We derive a variety of spatial weight matrices to analyse the multidimensional spatial effects around emerging foreign exchange rate markets. The spatial weight matrix helps us analyse the spatial relationship among economic variables and the economic and financial closeness with the minimum of the spatial weight object. Table 2 display the summary statistic of the selected weights matrices.
Table 2 display the descriptive statistics of the model. From the standard deviation, we notice that GDP, inflation, remittance, TOT, Bfdi are mostly centred around the mean whether the remaining variables are dispersed. We find that external debt and portfolio investment are highly dispersed and exhibit the largest mean.
In this study, we chose to perform a robust analysis approach of our sample. We conduct the Hausman test, which compares random effect (RE) and fixed effect (FE) models before selecting the best-fitted model to analyse the spatial dependence of the foreign exchange rate co-movement. Table 3 exhibits the specification test result for the robustness check. “Appendix” display the SDM with random effects outputs across different spatial distance. Comparing the Akaike information criterion (AIC) value of Table 8 in the appendix with the AIC value of the SDM analysis displayed in Table 5, we find that SDM with random effect (Table 8) exhibits a greater AIC value. We conclude that SDM-RE is not robust enough for our study, and this result supports our choice of using the SDM fixed-effect (SDM-FE) to perform the analysis.
Table 3 reports that SDM-FE with time and individual effects are consistent across spatial distance types. We conclude that our model specification is robust enough to account for a time-varying spatial dependence structure and to detect the spatial spillover effect of independent variables in foreign exchange rate markets.
Table 4 reports the optimal spatial lag test to select the structure of the spatiotemporal model in the construction of the dynamic SDM-FE estimation. The result shows that the time-lagged dependent variable is included in the model for all the spatial distances and better accounts for temporal interdependence between individual economies than the other models.
Table 5 shows that the spatial Durbin model (SDM) has larger spillovers than the SAR models with a spatially lagged dependent variable. Panel (1) exhibit the SDM with FE estimations, while panel (2) displays the robust analysis with SAR regression. Comparing the AIC of both panels, we find that the SDM-FE is more suitable for the data generating process. This implies that the selected model is robust for this analysis. We observe that the coefficients related to the spatial lags in the explanatory variables are generally non-significant and negative except for cultural and capital distance. The SDM-FE regression results show that remittance and terms of trade are significant and negatively correlated with foreign exchange rates, and stock returns are non-significant and negatively correlated with foreign exchange rates. At the same time, GDP and interest differential are positively correlated with foreign exchange rates. Our findings align with the theory that economic growth and interest rates positively affect the exchange rate. The results show from the estimated coefficient of remittance and terms of trade that these two factors have a significantly negative influence on foreign exchange rate co-movement in the emerging markets overall, with a severe impact in countries with geographical and cultural closeness financial integration. We observe that remittance and terms of trade play an important role in the depreciation and appreciation of foreign exchange, and these two factors negatively impact foreign exchange rate movement in spatial networks. A high volume of remittance inflow in the country contributes to the local currency appreciation, as indicated by the negative sign of the estimated coefficient across the spatial distance. Although inflow remittance contributes to foreign exchange rate appreciation of the receiver country, it leads to depreciation of the sender country, thus contributing substantially to foreign exchange rate spillover. As expected, the coefficient of spatial autocorrelation factor (rho) is positive and significant across spatial weights matrices. In other words, it implies that our model has proven able to address the misidentification of the degree of interconnectedness in the foreign exchange network that affects the exchange rate risk transmission and captures the spatial dependence.
Moreover, our model empirically shows that not only macroeconomics variables are responsible for the foreign exchange rate movement, but remittance and external debt are also likely to play an important role in analysing a country's foreign exchange rate movement. A positive coefficient of the spatial parameter reveals that FDI, international trade, external debt, and remittance are strong channels for exchange rate risk transmission between emerging markets. We find evidence that geographically clustered countries and economic and financial integration linkages play a role in spreading foreign exchange rate co-movement in emerging markets.
Table 6 reports a short-term spatial and time lags SDM-FE marginal output based on six spatial weight matrices. It shows direct and indirect effects. The direct effect is when the exchange rate in a country is determined by its own fundamentals. The direct effect is when the exchange rate in one country is determined by the fundamentals of another country. The total effect is the summation of direct and indirect effects. The short-term decomposition result shows that a change in the stock, terms of trade, inflation differential, and remittance of the local country contribute to the appreciation of the overall foreign exchange rate in the network. At the same time, a change in interest differential and GDP contributes to the foreign exchange rate depreciation in the country. It is noteworthy that remittance, terms of trade, and inflation differential are more than 80% responsible for the overall country's local foreign exchange rate movement in the short term. In addition, the shock in foreign exchange rate movement is transmitted to the neighbouring countries through the inflation differential, remittance, and terms of trade. We observe that for foreign exchange rate movement change within the overall economy, more than 65% of the overall foreign exchange rate movement in the network results from a shock in the individual market. A foreign exchange rate movement change is attributed to spillovers in other markets. This result implies the presence of spillover effects and a feedback loop in emerging markets in the short run. A country with a massive volume of remittance and terms of trade can adversely influence the exchange rate policy in a stable country, and the instability of the foreign exchange rate in the initially stable country is directed back to the country where the shock originated.
Table 7 displays the model decomposition result in the long run. The spatial spillover effects are significantly negative concerning remittance and terms of trade and positive in relation to GDP. The latter implies that, in the long run, a country with good economic performance within the selected emerging markets helps stabilise the foreign exchange rate of its main trading partners. The direct and indirect effects of remittance and terms of trade are negative in the long and short run, while the coefficient of remittance is significantly negative. These results indicate that remittance and international trade have a negative effect on foreign exchange rate co-movement in emerging markets. We observe a negative coefficient for the direct and indirect effects of GDP in cultural clusters in emerging markets, which implies that foreign exchange rate movements in countries with the same language are likely to be negatively influenced by the GDP. We conclude that cultural relations influence the destination of economic migrants and favour their economic interaction. In these countries, the central bank should implement an exchange rate policy that will reduce remittance outflow and thus potential net economic gains from their activities will be reinvested in the economy and contribute to growth.
5 Conclusion
The rising volume of foreign exchange trade in emerging markets has drawn the attention of both policymakers and academics. Due to market integration and liberalisation, foreign exchange markets have become increasingly interdependent. That has impelled researchers to investigate the cross-market linkages, as a shock in one market can affect depreciation or appreciation and volatility in another, with severe implications for portfolio construction and monetary policy. In this regard, analysing the co-movement of foreign exchange rates from one country to another may significantly contribute to investors' diversification strategies and guide policymakers in designing policies that protect individual economies from financial crises. The question arises regarding the extent to which the fundamental macroeconomic variables affecting foreign exchange rate co-movement may affect the investor's portfolio. This study investigates factors that influence foreign exchange rate direction with specific attention to understanding the spatial dependencies among emerging foreign exchange rate markets. Our study was the first attempt to address the co-movements of foreign exchange rates in emerging markets, taking into account multidimensional spatial effects such as geographical, cultural, economic, and financial integration clustering. We applied spatial analysis and found that cultural proximity is important in accounting for foreign exchange rate co-movement.
Moreover, our results supported the evidence of economic integration as we observed a spillover effect through FDI, trade, and financial integration channels. We also found that remittance, terms of trade and interest rate differential are the most prominent factors affecting the co-movement of foreign exchange rates in emerging markets. This finding justifies the choice of economic migrants as they tend to migrate to a country that has a common language, and, in addition to defining "distance" in spatial analysis in terms of capital flow, gravity, international trade, and external debt, this paper highlights the importance of cultural links in economics. Our result revealed evidence of spatial dependence through the transmission channels under consideration in this study and spatial spillover of foreign exchange rates to the neighbouring country. We proposed a better strategy for managing foreign exchange rate co-movement and implementing a policy that controls remittance flow.
Further to this research, we suggest important implications for theory and practice of international portfolio diversification to investors and fund managers on the one hand, and on the other, a strong economic policy to policymakers. In order to benefit from international portfolio diversification, fund managers should account for the geographical proximity that impacts the trade patterns among countries, thus and impacts co-movement between foreign exchange rate markets through international trade and financial integration channels. Change in the direction of foreign exchange rate across space and time should be accounted for in quantifying foreign exchange rate risk. Future research could use spatiotemporal statistics to model foreign exchange rate risk spillover in emerging markets. The finding in this paper can help decision-makers design an efficient hedging technique against foreign exchange rate exposure and build an efficient and optimal portfolio allocation.
Data availability
The data that support the findings of this study are available from different sources: (a) the datasets Distance (longitude and latitude) KAGGLE World capitals GPS https://www.kaggle.com/nikitagrec/world-capitals-gps/code, Bilateral exchange rate from Thomson Reuters https://www.thomsonreuters.com/en.html. Weight matrices compute by the authors, we use software analysis Stata/SE 16.0. Data and Stata codes are available upon reasonable request to djemoraoul@gmail.com Please refer to suggested Data Availability Statements in section.
References
Allen F, Gale D (2000) Financial contagion. J Polit Econ 108(1):1–33
Amewu G, Junior PO, Amenyitor EA (2022) Co-movement between equity index and exchange rate: fresh evidence from Covid-19 era. Sci Afr 16:e01146
Amidi S, Majidi FA (2020) Geographic proximity, trade and economic growth: a spatial econometrics approach. Ann GIS 26(1):49–63
Anselin L (1988) Spatial econometrics: methods and models. Springer Science & Business Media. https://doi.org/10.1007/978-94-015-7799-1
Asgharian H, Hess W, Liu L (2013) A spatial analysis of international stock market linkages. J Bank Finance 37(12):4738–4754
Basile R, Durbán M, Mínguez R, Montero JM, Mur J (2014) Modeling regional economic dynamics: Spatial dependence, spatial heterogeneity and nonlinearities. J Econ Dyn Control 48:229–245
Benos N, Karagiannis S, Karkalakos S (2015) Proximity and growth spillovers in European regions: the role of geographical, economic and technological linkages. J Macroecon 43:124–139
Boero G, Silvapulle P, Tursunalieva A (2011) Modelling the bivariate dependence structure of exchange rates before and after the introduction of the euro: a semi-parametric approach. Int J Financ Econ 16(4):357–374
Campbell JY, Lo AW, MacKinlay AC, Whitelaw RF (1998) The econometrics of financial markets. Macroecon Dyn 2(4):559–562
Carsamer E (2016) The pattern of exchange rate co-movement in selected African countries. J Econ Stud 43(6):928–953
Carvalho PJC, Gupta A (2018) A network approach to unravel asset price co-movement using minimal dependence structure. J Bank Finance 91:119–132
Casarin R, Sartore D, Tronzano M (2018) A Bayesian Markov-switching correlation model for contagion analysis on exchange rate markets. J Bus Econ Stat 36(1):101–114
Chen K, Peng L, Bianxia S, Huaiqing W (2015) Which stocks are profitable? A network method to investigate the effects of network structure on stock returns. Physica A 436:224–235
Chen H, Zheng X, Zeng DD (2020) Analysing the co-movement and its spatial–temporal patterns in Chinese stock market. Physica A 555:124655
Chollete L, Heinen A, Valdesogo A (2009) Modeling international financial returns with a multivariate regime-switching copula. J Financ Econom 7(4):437–480
Crawford TW (2009) Analytical scale. International encyclopedia of human geography, 1st edn. Elsevier, Amsterdam, pp 29–33
De Sousa J, Lochard J (2012) Trade and colonial status. J Afr Econ 21(3):409–439
Djemo CRT, Eita JH, Mwamba JWM (2021) Predicting foreign exchange rate movements: an application of the ensemble method. Rev Dev Finance 11(2):58–70
Donkor RA, Mensah L, Sarpong-Kumankoma E (2022) Oil price volatility and US dollar exchange rate volatility of some oil-dependent economies. J Int Trade Econ Dev 31(4):581–587
Dornbusch R, Fischer S (1980) Exchange rates and the current account. Am Econ Rev 70(5):960–971
Embrechts P, McNeil A, Straumann D (2002) Correlation and dependence in risk management: properties and pitfalls. Risk Manag Value Risk beyond 1:176–223
Engle R (2002) Dynamic conditional correlation: a simple class of multivariate generalised autoregressive conditional heteroskedasticity models. J Bus Econ Stat 20(3):339–350
Falck O, Heblich S, Lameli A, Südekum J (2012) Dialects, cultural identity, and economic exchange. J Urban Econ 72(2–3):225–239
Fazio G (2007) Extreme interdependence and extreme contagion between emerging markets. J Int Money Financ 26(8):1261–1291
Fernandez V (2011) Spatial linkages in international financial markets. Quant Finance 11(2):237–245
Fernández-Avilés G, Montero JM, Orlov AG (2012) Spatial modeling of stock market comovements. Financ Res Lett 9(4):202–212
Fernández-Avilés G, Montero JM, Sanchis-Marco L (2020) Extreme downside risk co-movement in commodity markets during distress periods: a multidimensional scaling approach. Eur J Financ 26:1207–1237
Flavin TJ, Hurley MJ, Rousseau F (2002) Explaining stock market correlation: a gravity model approach. Manch Sch 70(S1):87–106
Forbes KJ, Rigobon R (2002) No contagion, only interdependence: measuring stock market co-movements. J Finance 57(5):2223–2261
Frankel JA, Rose AK (1998) The endogenity of the optimum currency area criteria. Econ J 108(449):1009–1025
Gai P, Kapadia S (2010) Contagion in financial networks. Proc R Soc A: Math Phys Eng Sci 466(2120):2401–2423
Garcia R, Tsafack G (2011) Dependence structure and extreme co-movements in international equity and bond markets. J Bank Finance 35(8):1954–1970
Ghosh I, Sanyal MK, Jana RK (2021) Co-movement and dynamic correlation of financial and energy markets: An integrated framework of nonlinear dynamics, wavelet analysis and DCC- GARCH. Comput Econ 57(2):503–527
Haile F, Pozo S (2008) Currency crisis contagion and the identification of transmission channels. Int Rev Econ Financ 17(4):572–588
He X, Gokmenoglu KK, Kirikkaleli D, Rizvi SKA (2023) Co-movement of foreign exchange rate returns and stock market returns in an emerging market: evidence from the wavelet coherence approach. Int J Financ Econ 28:1994–2005
Held D, McGrew A., Goldblatt D, Perraton J (2000) Global transformations: politics, economics and culture. In: Politics at the edge. Palgrave Macmillan, London, pp 14–28
Henry O (1998) Modelling the asymmetry of stock market volatility. Appl Financ Econ 8(2):145–153
Hondroyiannis G, Kelejian HH, Tavlas GS (2009) Spatial aspects of contagion among emerging economies. Spat Econ Anal 4(2):191–211
Huang JJ, Lee KJ, Liang H, Lin WF (2009) Estimating value at risk of portfolio by conditional copula- GARCH method. Insur Math Econ 45(3):315–324
Jiang H, Tang S, Li L, Xu F, Di Q (2022) Re-examining the contagion channels of global financial crises: evidence from the twelve years since the US subprime crisis. Res Int Bus Financ 60:101617
Joe H, Li H, Nikoloulopoulos AK (2010) Tail dependence functions and vine copulas. J Multivar Anal 101(1):252–270
Kole E, Koedijk K, Verbeek M (2007) Selecting copulas for risk management. J Bank Finance 31(8):2405–2423
Kumar S, Pathak R, Tiwari AK, Yoon SM (2017) Are exchange rates interdependent? Evidence using wavelet analysis. Appl Econ 49(33):3231–3245
Legendre P, Legendre L (1998) Numerical ecology. Elsevier, Amsterdam
LeSage JP (2008) An introduction to spatial econometrics. Rev D’econ Ind 123(3):19–44
LeSage JP, Pace RK (2014) Interpreting spatial econometric models. In: Fisher MM, Nijkamp (eds) Handbook of regional science. Springer, Berlin, pp 1535–1552
Lien D, Lim G, Yang L, Zhou C (2013) Dynamic dependence between liquidity and the S&P 500 Index futures-cash basis. J Futur Mark 33(4):327–342
Longin F, Solnik B (2001) Extreme correlation of international equity markets. J Finance 56(2):649–676
Mantegna RN (1999) Hierarchical structure in financial markets. Eur Phys J B-Condens Matter Complex Syst 11(1):193–197
Mensah PO, Adam AM (2020) Copula-based assessment of co-movement and tail dependence structure among major trading foreign currencies in Ghana. Risks 8(2):55
Miled W, Ftiti Z, Sahut JM (2022) Spatial contagion between financial markets: new evidence of asymmetric measures. Ann Oper Res 313:1183–1220
Mohd Amin SI, Janor H (2016) The co-movement between exchange rates and stock prices in an emerging Market. J Pengurusan 48:61–72
Mulugetta A, Mulugetta Y, Tessema A (2004) Building empirical models for exchange rates forecasting under the managed exchange rate system. Int J Finance 16(3):3115–3140
Orlov AG (2009) A cospectral analysis of exchange rate co-movements during Asian financial crisis. J Int Finan Markets Inst Money 19(5):742–758
Overmars KD, De Koning GHJ, Veldkamp A (2003) Spatial autocorrelation in multi-scale land use models. Ecol Model 164(2–3):257–270
Owusu Junior P, Kwaku Boafo B, Kwesi Awuye B, Bonsu K, Obeng-Tawiah H (2018) Co-movement of stock exchange indices and exchange rates in Ghana: a wavelet coherence analysis. Cogent Bus Manag 5(1):1481559
Özmen MU, Yılmaz E (2017) Co-movement of exchange rates with interest rate differential, risk premium and FED policy in “fragile economies.” Emerg Mark Rev 33:173–188
Patton AJ (2006) Modelling asymmetric exchange rate dependence. Int Econ Rev 47(2):527–556
Qureshi S, Aftab M (2020) Exchange rate interdependence in ASEAN markets: a wavelet analysis. Glob Bus Rev. https://doi.org/10.1177/0972150920919371
Reboredo JC (2012) Modelling oil price and exchange rate co-movements. J Policy Model 34(3):419–440
Reboredo JC, Rivera-Castro MA, Zebende GF (2014) Oil and US dollar exchange rate dependence: a detrended cross-correlation approach. Energy Econ 42:132–139
Santi F, Dickson MM, Espa G, Taufer E, Mazzitelli A (2021) Handling spatial dependence under unknown unit locations. Spat Econ Anal 16(2):194–216
Shikimi M, Yamada K (2019) Trade and financial channels as the transmission mechanism of the financial crisis. Int Rev Econ Financ 63:364–381
Smith M, Min A, Almeida C, Czado C (2010) Modeling longitudinal data using a pair-copula decomposition of serial dependence. J Am Stat Assoc 105(492):1467–1479
Sosa M, Ortiz E, Cabello A (2018) Dynamic linkages between stock market and exchange rate in MILA countries: a Markov Regime Switching Approach (2003–2016). Anál Econ 33(83):57–74
Tang X, Yao X (2018) Do financial structures affect exchange rate and stock price interaction? Evidence from emerging markets. Emerg Mark Rev 34:64–76
Wang GJ, Xie C (2015) Correlation structure and dynamics of international real estate securities markets: a network perspective. Physica A 424:176–193
Wang K, Chen YH, Huang SW (2011) The dynamic dependence between the Chinese market and other international stock markets: a time-varying copula approach. Int Rev Econ Financ 20(4):654–664
Wang GJ, Xie C, Han F, Sun B (2012) Similarity measure and topology evolution of foreign exchange markets using dynamic time warping method: evidence from minimal spanning tree. Physica A 391(16):4136–4146
Wang YC, Wu JL, Lai YH (2013) A revisit to the dependence structure between the stock and foreign exchange markets: A dependence-switching copula approach. J Bank Finance 37(5):1706–1719
Wang GJ, Xie C, Zhang P, Han F, Chen S (2014) Dynamics of foreign exchange networks: a time-varying copula approach. Discret Dyn Nat Soc 2014:1–11
Wu CC, Chung H, Chang YH (2012) The economic value of co-movement between oil price and exchange rate using copula-based GARCH models. Energy Econ 34(1):270–282
Xu L, Hamori S, Kinkyo T (2021) Continuous wavelet analysis of Chinese renminbi: co-movement and lead-lag relationship between onshore and offshore exchange rates. N Am J Econ Finance 56:101360
Yang L, Cai XJ, Zhang H, Hamori S (2016) Interdependence of foreign exchange markets: a wavelet coherence analysis. Econ Model 55:6–14
Yeap XW, Lean HH, Sampid MG, Mohamad Hasim H (2020) The dependence structure and portfolio risk of Malaysia’s foreign exchange rates: the Bayesian GARCH–EVT–copula model. Int J Emerg Mark 16(5):952–974
Zaiane S, Jrad R (2020) The dynamic linkages between stock market and foreign exchange market: evidence from an emerging market. Int J Econ Financ Issues 10(3):245–254
Zhang W, Zhuang X, Li Y (2019) Spatial spillover around G20 stock markets and impact on the return: a spatial econometrics approach. Appl Econ Lett 26(21):1811–1817
Acknowledgements
In this section, you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).
Funding
Open access funding provided by University of Johannesburg. This research received no external funding.
Author information
Authors and Affiliations
Contributions
Conceptualisation, JHE; Data curation, CRTD; Formal analysis, CRTD and HE; Methodology, CRTD; Supervision, JHE; Writing—original draft, CRTD; Writing—review & editing, JHE.
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Djemo, C.R.T., Eita, J.H. Modelling foreign exchange rate co-movement and its spatial dependence in emerging markets: a spatial econometrics approach. Empir Econ 66, 979–1011 (2024). https://doi.org/10.1007/s00181-023-02482-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00181-023-02482-y
Keywords
- Spatial dependence
- Emerging markets
- Spatial panel
- Foreign exchange rates
- Co-movement
- Macroeconomic fundamentals