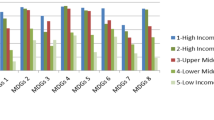
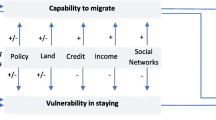
Abstract
Asian developing countries are frequently devastated by tropical cyclones. While the literature is replete with their impacts on economic growth, the impacts on critical sustainable development indicators, namely income inequality, health, and human capital accumulation, have seldom been explored. In this study, we measure the direct, indirect, and spillover impacts of tropical cyclones on the sustainable development of eight developing countries in Asia. This study uses the dynamic generalized method of moments model to estimate the impact of occurrences and casualties in these countries over 28 years. Our results indicate that recurrent tropical cyclones increase income inequality, reaching the threshold at 0.4 cyclone. The mortality rate tends to rise, which decreases after 2.5 cyclonic occurrences. Similarly, cyclones seem to initially reduce the expected years of schooling, which starts increasing after one cyclonic occurrence. These weakening impacts provide evidence of negative feedback loops. We also find evidence of domino effects and gender effects. The resilience factors are controlled for, as it helps the developing countries recover from the vicious cycles. The feedback loops can be broken by taking timely interventions, mitigation and adaptation.


(Source EM-DAT)

(Source EM-DAT)

(Source EM-DAT)

(Source SWIID)

(Source UNDP)

(Source UNDP)

(Source EM-DAT and World Bank)

(Source the authors)

(Source authors’ estimations)
Similar content being viewed by others
Notes
Henceforth, the notation \({\mathrm{TC}}_{n}\) is used to represent tropical cyclonic occurrences and TC_deaths is used for casualties from tropical cyclones, unless otherwise defined.
Specifications using higher-order cubic terms of tropical cyclonic occurrences were also tested, which were insignificant. This implies that the cubic specification does not yield any statistically meaningful explanatory power over the squared specification.
The ‘xtdpdgmm’ command of STATA 16 is used to estimate the dynamic panel data regression models (Kripfganz 2019).
We have taken the antilog of the estimated threshold and subtracted 1 from the estimated value. Accordingly, the formula becomes \(\left(-\frac{{\delta }_{1}+{\delta }_{2}}{{2\delta }_{3}}\right)=\mathrm{ln}(1+\widehat{{\mathrm{TC}}_{n}})\). Therefore, \(\widehat{{\mathrm{TC}}_{n}}=\mathrm{exp}\left(-\frac{{\delta }_{1}+{\delta }_{2}}{{2\delta }_{3}}\right)-1\). Note that \({\delta }_{1}\mathrm{ and }{\delta }_{2}\) are the coefficients of \({{\mathrm{TC}}_{n}}_{i,t} and {\mathrm{TC}}_{{n}_{i, t-1}}\), respectively. We have estimated the threshold values \(\widehat{{\mathrm{TC}}_{n}}\) considering both \({\delta }_{1}\mathrm{and }{\delta }_{2}\) or anyone based on their statistical sifgnificance.
Accordingly, the estimation of the threshold value of \({\mathrm{TC}}_{n}\) for income inequality \(\left(-\frac{0.7}{2*(-1.117)}\right)=\mathrm{ln}\left(1+\widehat{{\mathrm{TC}}_{n}}\right) \mathrm{gives} (1+\widehat{{\mathrm{TC}}_{n}})=1.4.\) Hence, the threshold of \({\mathrm{TC}}_{n}\) (\(\widehat{{\mathrm{TC}}_{n}}\)) for income inequality is 0.4 (\(=1.4-1\)).
The estimation of the threshold value of \({\mathrm{TC}}_{n}\) for mortality rate \(\left(-\frac{3.983}{2*(-1.609)}\right)=\mathrm{ln}\left(1+\widehat{{\mathrm{TC}}_{n}}\right) \mathrm{gives} (1+\widehat{{\mathrm{TC}}_{n}})=3.448\sim 3.5.\) Hence, the threshold of \({\mathrm{TC}}_{n}\) (\(\widehat{{\mathrm{TC}}_{n}}\)) for mortality rate is 2.5 (\(=3.5-1\)).
The estimation of the threshold value of \({\mathrm{TC}}_{n}\) for expected years of schooling \(\left(-\frac{(-4.002)}{2*(3.335)}\right)=\mathrm{ln}\left(1+\widehat{{\mathrm{TC}}_{n}}\right)\mathrm{gives} (1+\widehat{{\mathrm{TC}}_{n}})=1.83\sim 2.\) Hence, the threshold of \({\mathrm{TC}}_{n}\) (\(\widehat{{\mathrm{TC}}_{n}}\)) for expected years of schooling is 1 (\(=2-1\)).
References
Albala-Bertrand JM (1993) Natural disaster situations and growth: a macroeconomic model for sudden disaster impacts. World Dev 21(9):1417–1434. https://doi.org/10.1016/0305-750X(93)90122-P
Arellano M, Bover O (1995) Another look at the instrumental variable estimation of error-components models. J Econ 68(1):29–51. https://doi.org/10.1016/0304-4076(94)01642-D
Arrow KJ, Dasgupta P, Goulder LH, Mumford KJ, Oleson K (2012) Sustainability and the measurement of wealth. Environ Dev Econ 17(3):317–353. https://doi.org/10.1017/S1355770X12000137
Azam MS, Imai KS (2012) Measuring households’ vulnerability to idiosyncratic and covariate shocks—the case of Bangladesh. Discussion paper series. Research Institute for Economics and Business Administration, Kobe University, Tokyo
Baez JE, Caruso G, Niu C (2020) Extreme Weather and Poverty Risk: Evidence from Multiple Shocks in Mozambique. Econ Dis Cli Cha 4:103–127. https://doi.org/10.1007/s41885-019-00049-9
Banerjee R, Mishra V, Maruta AA (2021) Energy poverty, health and education outcomes: evidence from the developing world. Energy Econ 101:105447. https://doi.org/10.1016/j.eneco.2021.105447
Barrett CB, Carter MR (2000) Can’t get ahead for falling behind: new directions for development policy to escape relief and poverty traps. BASIS Brief 2:1–8
Barro RJ (2000) Inequality and growth in a panel of countries. J Econ Growth 5(1):5–32. https://doi.org/10.1023/A:1009850119329
Berg A, Ostry JD, Tsangarides CG, Yakhshilikov Y (2018) Redistribution, inequality, and growth: new evidence. J Econ Growth 23(3):259–305. https://doi.org/10.1007/s10887-017-9150-2
Besley T, Burgess R (2002) The political economy of government responsiveness: theory and evidence from India. Q J Econ 117(4):1415–1451. https://doi.org/10.1162/003355302320935061
Blundell, R., Bond, S. and Windmeijer, F. (2001). Estimation in dynamic panel data models: improving on the performance of the standard GMM estimator. In: Baltagi BH, Fomby TB, Carter Hill R (eds) Nonstationary panels, panel cointegration, and dynamic panels. Advances in econometrics, vol 15. Emerald Group Publishing Limited, Bingley, pp 53–91. https://doi.org/10.1016/S0731-9053(00)15003-0
Briguglio L, Cordina G, Farrugia N, Vella S (2009) Economic vulnerability and resilience: concepts and measurements. Oxf Dev Stud 37(3):229–247. https://doi.org/10.1080/13600810903089893
Butterworth P, Leach LS, Strazdins L, Olesen SC, Rodgers B, Broom DH (2011) The psychosocial quality of work determines whether employment has benefits for mental health: results from a longitudinal national household panel survey. Occup Environ Med 68(11):806–812. https://doi.org/10.1136/oem.2010.059030
Cannon T (1994) Vulnerability analysis and the explanation of ‘natural’ disasters. Disast Dev Environ 1:13–30
Cao Y, Liu J, Yu Y, Wei G (2020) Impact of environmental regulation on green growth in China’s manufacturing industry-based on the Malmquist–Luenberger index and the system GMM model. Environ Sci Pollut Res 27(33):41928–41945. https://doi.org/10.1007/s11356-020-10046-1
Cavallo EA, Noy I (2009) The economics of natural disasters: a survey. IDB Working Paper No. 35. https://doi.org/10.2139/ssrn.1817217
Checchi D, Garcı́a-Peñalosa C (2004) Risk and the distribution of human capital. Econ Lett 82(1):53–61. https://doi.org/10.1016/S0165-1765(03)00224-6
Chhotray V, Few R (2012) Post-disaster recovery and ongoing vulnerability: ten years after the super-cyclone of 1999 in Orissa, India. Glob Environ Change 22(3):695–702. https://doi.org/10.1016/j.gloenvcha.2012.05.001
Cuaresma JC (2010) Natural disasters and human capital accumulation. World Bank Econ Rev 24(2):280–302. https://doi.org/10.1093/wber/lhq008
Cuaresma JC, Hlouskova J, Obersteiner M (2008) Natural disasters as creative destruction? Evidence from developing countries. Econ Inq 46(2):214–226. https://doi.org/10.1111/j.1465-7295.2007.00063.x
Cyrek M, Fura B (2019) Employment for sustainable development: sectoral efficiencies in EU countries. Soc Indic Res 143(1):277–318. https://doi.org/10.1007/s11205-018-1970-8
Darvas Z (2019) Global interpersonal income inequality decline: the role of China and India. World Dev 121:16–32. https://doi.org/10.1016/j.worlddev.2019.04.011
Das S, Vincent JR (2009) Mangroves protected villages and reduced death toll during Indian super cyclone. Proc Natl Acad Sci 106(18):7357–7360. https://doi.org/10.1073/pnas.0810440106
De Alwis D (2020) Distributional impacts of disaster recovery: Sri Lankan households a decade after the 2004 Indian Ocean tsunami. Econ Disast Clim Change 4(1):195–222. https://doi.org/10.1007/s41885-020-00058-z
Deschenes O, Moretti E (2009) Extreme weather events, mortality, and migration. Rev Econ Stat 91(4):659–681. https://doi.org/10.1162/rest.91.4.659
EM-DAT: The emergency events database—Université catholique de Louvain (UCL)—CRED, D. Guha-Sapir—www.emdat.be, Brussels, Belgium
Esseghir A, Khouni LH (2014) Economic growth, energy consumption and sustainable development: the case of the Union for the Mediterranean countries. Energy 71:218–225. https://doi.org/10.1016/j.energy.2014.04.050
Feenstra RC, Inklaar R, Timmer MP (2015) The next generation of the Penn world table. Am Econ Rev 105(10):3150–3182. https://doi.org/10.1257/aer.20130954
Frankenberg E, Sumantri C, Thomas D (2020) Effects of a natural disaster on mortality risks over the longer term. Nat Sustain 3(8):614–619. https://doi.org/10.1038/s41893-020-0536-3
Ganda F (2019) The environmental impacts of financial development in OECD countries: a panel GMM approach. Environ Sci Pollut Res 26(7):6758–6772. https://doi.org/10.1007/s11356-019-04143-z
Güney T (2017) Governance and sustainable development: how effective is governance? J Int Trade Econ Dev 26(3):316–335. https://doi.org/10.1080/09638199.2016.1249391
Guptill SC (2001) Disease aftershocks—the health effects of natural disasters. Int Geol Rev 43(5):419–423. https://doi.org/10.1080/00206810109465023
Hallegatte S, Hourcade JC, Dumas P (2007) Why economic dynamics matter in assessing climate change damages: illustration on extreme events. Ecol Econ 62(2):330–340. https://doi.org/10.1016/j.ecolecon.2006.06.006
Haque U, Hashizume M, Kolivras KN, Overgaard HJ, Das B, Yamamoto T (2012) Reduced death rates from cyclones in Bangladesh: what more needs to be done? Bull World Health Organ 90:150–156. https://doi.org/10.2471/BLT.11.088302
Houweling TA, Kunst AE, Looman CW, Mackenbach JP (2005) Determinants of under-5 mortality among the poor and the rich: a cross-national analysis of 43 developing countries. Int J Epidemiol 34(6):1257–1265. https://doi.org/10.1093/ije/dyi190
Jones E (2003) The European miracle: environments, economies and geopolitics in the history of Europe and Asia. Cambridge University Press
Kahn ME (2005) The death toll from natural disasters: the role of income, geography, and institutions. Rev Econ Stat 87(2):271–284. https://doi.org/10.1162/0034653053970339
Kapsos, S. (2006). The employment intensity of growth: trends and macroeconomic determinants. In: Labor markets in asia. Palgrave Macmillan, London, pp 143–201
Kellenberg DK, Mobarak AM (2008) Does rising income increase or decrease damage risk from natural disasters? J Urban Econ 63(3):788–802. https://doi.org/10.1016/j.jue.2007.05.003
Khan HUR, Islam T, Yousaf SU, Zaman K, Shoukry AM, Sharkawy MA, Hishan SS (2019) The impact of financial development indicators on natural resource markets: evidence from two-step GMM estimator. Resour Policy 62:240–255. https://doi.org/10.1016/j.resourpol.2019.04.002
Kishore N, Marqués D, Mahmud A, Kiang MV, Rodriguez I, Fuller A, Buckee CO (2018) Mortality in Puerto Rico after hurricane maria. New Engl J Med 379(2):162–170. https://doi.org/10.1056/NEJMsa1803972
Kitamura Y, Phillips PC (1997) Fully modified IV, GIVE and GMM estimation with possibly non-stationary regressors and instruments. J Econ 80(1):85–123. https://doi.org/10.1016/S0304-4076(97)00004-3
Kripfganz S (2019) Generalized method of moments estimation of linear dynamic panel data models. In: London stata conference, vol 17
Loayza NV, Olaberria E, Rigolini J, Christiaensen L (2012) Natural disasters and growth: going beyond the averages. World Dev 40(7):1317–1336. https://doi.org/10.1016/j.worlddev.2012.03.002
Marshall MG, Gurr TR (2020) Polity 5: political regime characteristics and transitions, 1800–2018. Center for Systemic Peace. http://www.systemicpeace.org
Mendelsohn R, Emanuel K, Chonabayashi S, Bakkensen L (2012) The impact of climate change on global tropical cyclone damage. Nat Clim Change 2(3):205–209. https://doi.org/10.1038/nclimate1357
Nordhaus WD (2010) The economics of hurricanes and implications of global warming. Clim Change Econ 1(01):1–20. https://doi.org/10.1142/S2010007810000054
Noy I (2009) The macroeconomic consequences of disasters. J Dev Econ 88(2):221–231. https://doi.org/10.1016/j.jdeveco.2008.02.005
Noy I, Vu TB (2010) The economics of natural disasters in a developing country: the case of Vietnam. J Asian Econ 21(4):345–354. https://doi.org/10.1016/j.asieco.2010.03.002
O’Hara PA (2008) Principle of circular and cumulative causation: fusing Myrdalian and Kaldorian growth and development dynamics. J Econ Issues 42(2):375–387. https://doi.org/10.1080/00213624.2008.11507146
Padli J, Habibullah MS (2008) Natural disaster death and socio-economic factors in selected Asian countries: a panel data analysis. Munich Personal RePEc Archive. https://mpra.ub.uni-muenchen.de/id/eprint/11921
Palma JG (2019) Behind the seven veils of inequality. What if it’s all about the struggle within just one half of the population over just one half of the national income? Dev Change 50(5):1133–1213. https://doi.org/10.1111/dech.12505
Peduzzi P, Chatenoux B, Dao H, De Bono A, Herold C, Kossin J, Nordbeck O (2012) Global trends in tropical cyclone risk. Nat Clim Change 2(4):289–294. https://doi.org/10.1038/nclimate1410
Rajkumar AS, Swaroop V (2008) Public spending and outcomes: does governance matter? J Dev Econ 86(1):96–111. https://doi.org/10.1016/j.jdeveco.2007.08.003
Rao BB, Tamazian A, Kumar S (2010) Systems GMM estimates of the Feldstein–Horioka puzzle for the OECD countries and tests for structural breaks. Econ Model 27(5):1269–1273. https://doi.org/10.1016/j.econmod.2010.02.002
Raschky PA (2008) Institutions and the losses from natural disasters. Nat Hazard 8(4):627–634. https://doi.org/10.5194/nhess-8-627-2008
Ravallion M (2014) Income inequality in the developing world. Science 344(6186):851–855. https://doi.org/10.1126/science.1251875
Reichstein M, Riede F, Frank D (2021) More floods, fires and cyclones—plan for domino effects on sustainability goals. Nature 592:347–349. https://doi.org/10.1038/d41586-021-00927-x
Rodriguez E (2002) Marginal employment and health in Britain and Germany: does unstable employment predict health? Soc Sci Med 55(6):963–979. https://doi.org/10.1016/S0277-9536(01)00234-9
Rodriguez-Oreggia E, De La Fuente A, De La Torre R, Moreno HA (2013) Natural disasters, human development and poverty at the municipal level in Mexico. J Dev Stud 49(3):442–455. https://doi.org/10.1080/00220388.2012.700398
Ruiz ME, Vives A, Martínez-Solanas È, Julià M, Benach J (2017) How does informal employment impact population health? Lessons from the Chilean employment conditions survey. Saf Sci 100:57–65. https://doi.org/10.1016/j.ssci.2017.02.009
Sacerdote B (2012) When the saints go marching out: long-term outcomes for student evacuees from Hurricanes Katrina and Rita. Am Econ J Appl Econ 4(1):109–135. https://doi.org/10.1257/app.4.1.109
Sato Y, Söderbom M (2017) GMM estimation of panel data models with time-varying slope coefficients. Appl Econ Lett 24(21):1511–1518. https://doi.org/10.1080/13504851.2017.1302053
Sedova B, Kalkuhl M, Mendelsohn R (2020) Distributional impacts of weather and climate in rural India. Econ Disast Clim Change 4(1):5–44. https://doi.org/10.1007/s41885-019-00051-1
Sen A (1973) Poverty, inequality and unemployment: Some conceptual issues in measurement. Econ Polit Week 8:1457–1464
Sen AK (1992) Inequality reexamined. Oxford University Press
Sen A (1998) Mortality as an indicator of economic success and failure. Econ J 108(446):1–25. https://doi.org/10.1111/1468-0297.00270
Sen S, Nayak NC, Mohanty WK (2021) Long-term forecasting of tropical cyclones over Bay of Bengal using linear and non-linear statistical models. GeoJournal. https://doi.org/10.1007/s10708-021-10543-x
Seneviratne SI, Nicholls N, Easterling D, Goodess CM, Kanae S, Kossin J, Zhang X (2012) Changes in climate extremes and their impacts on the natural physical environment. In Field CB, Barros V, Stocker TF, Qin D, Dokken DJ, Ebi KL (eds) Managing the risks of extreme events and disasters to advance climate change adaptation. A special report of Working Groups I and II of the intergovernmental panel on climate change (IPCC). Cambridge University Press, pp 109–230
Siddiqui DA, Ahmed QM (2013) The effect of institutions on economic growth: a global analysis based on GMM dynamic panel estimation. Struct Change Econ Dyn 24:18–33. https://doi.org/10.1016/j.strueco.2012.12.001
Skidmore M, Toya H (2002) Do natural disasters promote long-run growth? Econ Inq 40(4):664–687. https://doi.org/10.1093/ei/40.4.664
Sodhi MS (2016) Natural disasters, the economy and population vulnerability as a vicious cycle with exogenous hazards. J Oper Manag 45:101–113. https://doi.org/10.1016/j.jom.2016.05.010
Solt F (2020) Measuring income inequality across countries and over time: the standardized world income inequality database. Soc Sci Q 101(3):1183–1199. https://doi.org/10.1111/ssqu.12795
Soriano B, Garrido A (2016) How important is economic growth for reducing undernourishment in developing countries? Food Policy 63:87–101. https://doi.org/10.1016/j.foodpol.2016.07.004
Stern DI, Common MS, Barbier EB (1996) Economic growth and environmental degradation: the environmental Kuznets curve and sustainable development. World Dev 24(7):1151–1160. https://doi.org/10.1016/0305-750X(96)00032-0
Strobl E (2012) The economic growth impact of natural disasters in developing countries: evidence from hurricane strikes in the Central American and Caribbean regions. J Dev Econ 97(1):130–141. https://doi.org/10.1016/j.jdeveco.2010.12.002
Sun F, Carson RT (2020) Coastal wetlands reduce property damage during tropical cyclones. Proc Natl Acad Sci 117(11):5719–5725. https://doi.org/10.1073/pnas.1915169117
SWIID, The Standardized World Income Inequality Database. Accessed in February 2020. https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/LM4OWF
Takasaki Y (2017) Do natural disasters decrease the gender gap in schooling? World Dev 94:75–89. https://doi.org/10.1016/j.worlddev.2016.12.041
Tol R, Leek F (1999) Economic analysis of natural disasters. In: Downing T, Olsthoorn A, Tol R (eds) Climate change and risk. Routledge, London, pp 308–327
Toya H, Skidmore M (2007) Economic development and the impacts of natural disasters. Econ Lett 94(1):20–25. https://doi.org/10.1016/j.econlet.2006.06.020
Ullah S, Akhtar P, Zaefarian G (2018) Dealing with endogeneity bias: the generalized method of moments (GMM) for panel data. https://doi.org/10.1016/0305-750X(96)00032-0
UNDP, United Nations Development Programme-Human Development Report. Accessed in January 2020. http://hdr.undp.org/en/data
World Bank, World Development Indicators. Accessed in January 2020. https://data.worldbank.org/indicator
Yamamura E (2015) The impact of natural disasters on income inequality: analysis using panel data during the period 1970 to 2004. Int Econ J 29(3):359–374. https://doi.org/10.1080/10168737.2015.1020323
Yitzhaki S (1982) Relative deprivation and economic welfare. Eur Econ Rev 17(1):99–113. https://doi.org/10.1016/0014-2921(82)90045-9
Zhou Z, Zhang L (2021) Destructive destruction or creative destruction? Unraveling the effects of tropical cyclones on economic growth. Econ Anal Policy 70:380–393. https://doi.org/10.1016/j.eap.2021.03.010
Acknowledgements
The authors are thankful to the editor and the anonymous reviewer for the valuable comments and careful review, which helped us immensely in preparing the final version of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
No potential conflict of interest was reported by the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Sen, S., Nayak, N.C. & Mohanty, W.K. Impact of tropical cyclones on sustainable development through loops and cycles: evidence from select developing countries of Asia. Empir Econ 65, 2467–2498 (2023). https://doi.org/10.1007/s00181-023-02431-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00181-023-02431-9
Keywords
- Developing countries
- Tropical cyclones
- Sustainable development indicators
- Feedback loops
- Resilience
- Asia