On the causality between household and government spending on education: evidence from a panel of 40 countries

Abstract

This paper sheds light on an important causality which is of primary interest for policy makers, at both country level and broad institutional level, though it is largely ignored in the literature. Using panel data from a diversified group of countries and after controlling for various factors and endogeneities within the context of multivariate models, we present evidence that an increase in the intensity of government spending on education leads to an overall increase in the intensity of household spending on education of a roughly equal magnitude, within a span of two years. Specifically, a 1% increase in the intensity of government spending on education induces a contemporaneous increase in the intensity of household spending on education of 3%, followed by a correction of 2% the subsequent year. We further find that the reverse causality does not hold. Our mediation analysis within our set of variables suggests that the causality is only direct, and that there is no statistically significant distinction between low- and high-income countries.

1 Introduction

Human capital accumulation via investment in education receives a lot of attention in the literature as it constitutes an engine of economic growth (e.g. Lucas 1988; Barro 2001; De La Fuente and Domenéch 2006) and is the foundation of understanding earnings and inequality (e.g. Castelló and Doménech 2002; Guvenen and Kuruscu 2010; Galor 2011).¹ This paper does not constitute another study that relates education and growth but one that focuses on an aspect of investment in education that is largely ignored in the literature. Specifically, we shed light on the causality between the intensities of government and household spending on education. This causality composes a major instrument of optimal policy and thus is of significant interest for policymakers. Do governments respond to changes in the intensity of household spending on education by revising their spending intensity or is it the other way around or both, and to what extent?

Although there is an extended theoretical literature that examines the role of investment in human capital in driving economic growth, the theoretical foundations of the interaction of different sources of investment in human capital, public versus private, are largely overlooked. Most theoretical macroeconomic models assume that investment in human capital originates from households that allocate part of their time-endowment (e.g. Lucas 1988, 2004; Barro 1997; Stokey 2015; Grossman et al. 2017) or income (e.g. Mankiw et al. 1992; Krebs 2003; Boldrin and Montes 2005) into education activities that augment human capital development. Theoretical work that is focused on governments being the source of investment in human capital is very limited. Blankenau and Simpson (2004) introduce an overlapping generations (OLG) model where human capital is funded by both the government and households. To channel funds towards education, the government uses taxation while households use the credit market. They show that the relationship between public education expenditures and growth can be non-monotonic and depends on various factors such as the size of government, the tax structure and production technology parameters. Kneller (2000) analyses the effects of government policy on growth by introducing a public input in the production function, defined as public capital which we may think of as education expenditures. The latter implies that human capital is funded solely by the government and that human capital is not dynamic in the sense that it does not accumulate over time. He then employs a Barro (1990)-type endogenous growth model relating the growth effects of this input to different levels of distortionary taxation.

In theory, the relationship between private and government investment in education can be distinguished by nature and timing. The nature of the relationship, if any, can be either substitutable or complementary. For instance, a government funded expansion of German language classes can substitute privately funded education of German language programs. An increase of government funded public lectures on computer applications could be complemented with increased household spending on auxiliary material such as textbooks, computers, and laptops. The question though is not only limited to the nature of the relationship but also whether one leads or lags the other, i.e. the timing of the relationship. For instance, an increase of government expenditures on school infrastructure, may motivate households to complement it gradually by increasing spending on learning materials.² Likewise, a scaling down of spending on agricultural education by the government may lead to a lagged increase of privately funded education in rural areas, as households gradually substitute publicly funded education with privately funded education. Finally, the source of funding of government investment in education differentiates it from household investment in education in terms of their implications on the wider economy. To raise funds for investment in education, the government may either borrow or raise taxes. Although the former is also used by households, the latter may create distortionary effects. As shown by Kneller (2000), government spending raises growth at a decreasing rate when the levels of distortionary taxation are low and decrease it when the levels of distortionary taxation are high.

In examining the relationship between education and growth, the literature measures education not only using expenditures but also outcomes such as the number of years at school, literacy rates and school enrolment rates. Since our aim is to examine the causality between government and household investment in education, a natural approach is to use expenditures which are directly comparable between households and governments. Furthermore, estimates of causalities using panel data could be very sensitive to the measurement differences in outcomes as well as the possible biases in the sampling of outcomes across countries, which are not always easy to address.³ For those reasons, we perceive measures of expenditures as relatively more standard measures of education within the context of a panel household-government comparison. Specifically, we use expenditures as a share of GDP for both households and governments, which we define as spending intensities on education. As noted by Kelly (1997), the pertinent need for efficient government expenditure on education can transform the economic landscape of the country. Optimal government spending on education does not only lead to routes out of poverty and towards long run economic development but also constitutes a tool of overcoming and mitigating economic downturns.⁴ Hence, the analysis of the relationship between government and household spending on education is critically important, primarily for policymakers. Understanding the causality, its magnitude, and the timing of the aggregate bilateral effect, facilitates design of assistance programs by institutions such as the IMF and the World Bank as well as the formulation of better fiscal policies.⁵

There are several empirical studies that attempt to evaluate the relationship between government expenditures on education and growth, contrary to the theoretical literature which is rather limited. While a few empirical studies report a positive contemporaneous effect of government’s education expenditures on growth (e.g. Evans and Karras 1994; Blankenau et al. 2014), others report a negative relationship (e.g. Vedder 2004; Mo 2007). Generally, these studies differ in terms of the sample, the nature of the data and the econometric model. Mo (2007) argues that the instantaneous negative effects must be viewed with care and provides further evidence which suggests that such effects are temporary as investment in education has a long run impact on growth. In other words, positive externalities induced by investment in education are missed if one considers only contemporaneous relationships. Vedder (2004) argues that the negative effect could be the result of inefficient allocation of public funds while Curs et al. (2011) find that the omission of the private higher education market potentially causes negative omitted variable bias on the effects of government expenditures on growth. Aghion et al. (2006) argue that the relationship between public expenditures on education and growth depends on the composition of expenditures in relation to the distance of the economy from the technological frontier. Their empirical work focuses solely on the US using a rich sample of cross-state data. It is unclear however as to whether the composition of expenditures would matter for the relationship between household and government spending on education at a broad cross-country level.

To estimate the causality between government and household intensities on education, we employ a diversified cross-country panel within the context of bivariate and multivariate models. In doing so, we allow for possible effects from a set of mediator variables. One of the mediator variables that we consider is a proxy for credit market constraints which differ significantly across countries. Hatcher and Pourpourides (2022) construct a cross-country indicator that measures the extent of credit provision which hints that countries with minimal credit market development tend to exhibit high intensities of household investment in education.⁶ Their findings regarding the significance of credit constraints in driving educational attainment are consistent with the findings of most studies in the literature (e.g. Belley and Lochner 2007; Bailey and Dynarski 2011; Lochner and Monge-Naranjo 2012; Johnson 2013; Hai and Heckman 2017).⁷

The theoretical literature that examines the effects of credit constraints on growth presents mixed results. On the one hand, Jappeli and Pagano (1994) and De La Croix and Michel (2002) use OLG models that show that borrowing constraints lead to increased savings which promote economic growth.⁸ On the other hand, De Gregorio (1996), highlights the significance of human capital within the context of an OLG model and shows that borrowing constraints may lower growth as they decrease the incentive to study for young individuals who choose to enter the work force early. Hatcher and Pourpourides (2022) allow within family transfers for education purposes and provide an interpretation that somehow compromises the conflicting findings for the impact of borrowing constraints on growth. Specifically, they show conditions which depend on the level of private financing of education where low credit market development implies a negative effect of private financing of education on growth whereas adequately developed credit markets imply a positive effect.⁹ Kitaura (2012) and Hatcher (2022) further argue that the effects of borrowing constraints on welfare differ across generations.

To control for possible direct and indirect effects of credit constraints and credit risk on the relationship between the intensities of government and household spending on education, we include the share of non-performing loans in total loans (NPL) into our analysis. The idea is that when banks are unable to collect interest payments from loans which are non-performing, they have less liquidity available to create new loans and thus new borrowers face fewer loan options. Credit restrictions induced by non-performing loans could be an important link connecting the intensities of household and government spending on education. For instance, intensified spending activity by households may increase credit risk which, in turn, may affect the accessibility of households to credit markers. Imperfect credit markets that reduce the accessibility of households to education loans may lead governments to increase their spending intensity to substitute the lack of private funding. The idea is that if households are credit constrained and thus unable to borrow to fund their education, the government may step in to subsidize education enabling more people to attain it. Therefore, there might be an indirect link embedded in the causality between household and government spending on education. Likewise, intensified spending activity by governments may reduce credit risk, increasing the accessibility of households to credit markers. Other possible mediator variables that we consider are consumer prices, as measured by the consumer price index, the state of the economy, as measured by the unemployment rate, and population density.

Our main findings from multivariate models are robust and indicate that the causal relationship between the intensities of government and household spending on education is dynamic and only direct. It runs from the former to the latter, exhibiting a significantly positive contemporaneous effect and a weaker negative lagged effect in the subsequent year. The correction in the household spending intensity following the change in the government spending intensity, is such that, overall, there is a one-to-one relationship between the two intensities. That is, when the spending intensity of the government increases by a percentage point, the spending intensity of households also increases by a percentage point within a span of two years. Although we find some evidence that the causality works the other way round for low-income countries under a bivariate model, this feature disappears in the multivariate model which controls for other factors, contemporaneous relationships, cross-country dependence, homoskedasticity and within countries autocorrelation. Likewise, the multivariate model further suggests that neither credit market restrictions as proxied by the share of non-performing loans nor any other of our variables impact the causality directly or indirectly.

The rest of this paper is organized as follows. Section 2 presents bivariate and multivariate causality tests, while Sect. 3 concludes.

2 Causality tests

In this section, we present causality tests between household and government spending on education using cross-country panel data. The ability of households to borrow is also considered because it may affect the causality both directly, as mediator, and indirectly, as control. In our cross-country analysis, we express both household and government spending on education as percentages of GDP, which we refer to as intensities. Our measure for household spending on education is initial household funding of secondary education which corresponds to total payments of households for educational institutions in secondary education, excluding any government transfers to households. The main reasons of using funding for secondary education rather than tertiary education or total funding are two. First, using funding for tertiary education instead of secondary education increases the number of missing observations for household education expenditures by 590%. Missing observations for household funding of secondary education constitute 10.5% of its total observations. Second, total expenditures in secondary education exceed total expenditures in tertiary education in most countries, and in most cases quite significantly. Thus, the use of expenditures on tertiary education may not capture well the overall relationship between household and government spending on education at the cross-country level. For those reasons, we consider the cost of using a series with a high number of missing observations higher than any benefit and thus we perceive the medium level of education as the most suitable measure of household spending on education for our cross-country analysis. Our measure for government spending on education corresponds to total government expenditures which includes expenditures for all levels of education. The source for household and government spending on education data is the World Bank.¹⁰ Specifically, $HEX_{it}$ and $GEX_{it}$, for $i = 1, 2, \ldots N$ and $t = 1, 2, \ldots T$, denote the logarithms of the ratios of household and government spending on education to GDP, respectively.

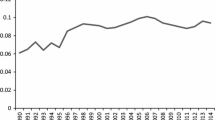
Measuring the difficulty for households in accessing credit markets, which translates to credit constraints, especially within the context of panel data analysis is a bit tricky. The literature employed various methods to proxy credit constraints.¹¹ In this paper, we measure the cost of bank financing for household using the logarithm of the ratio of non-performing loans to total gross loans, denoted by $NPL_{it}$. As shown by Huljak et al. (2020), an increase in the change in NPL ratios tends to depress bank lending volumes and widens bank lending spreads. Thus, we assert that the higher the current share of non-performing loans the more credit constrained the households are as banks become less willing to lend. The data on non-performing loans and total loans are obtained from the IMF’s International Financial Statistics database. The frequency of our data is annual, the sample period spans from 2004 to 2018 and our panel contains a mixture of 40 developed and developing countries. Missing observations for government spending on education and non-performing loans constitute 5% and 20% of their total observations, respectively.¹² The missing observations are interpolated using three year moving averages. Descriptive statistics of the variables are displayed in the appendix. To sketch out a preliminary sense of the overall-average behavior of HEX, GEX and NPL, Fig. 1 displays standardized cross-country averages of the three variables and Fig. 2, the standardized series for Austria, as an example of a country in the sample. As depicted in Figs. 1 and 2, the two aggregate intensities are positively correlated while the aggregate share of non-preforming loans displays a weaker connection to them. Among others, both figures display the characteristic sharp increase of the share of non-performing loans during the global financial crisis of 2008.

Fig. 1

Standardized cross-country averages: 2004–2018

Fig. 2

Standardized series for Austria: 2004–2018

2.1 Bivariate causality tests

First, we present bivariate causality tests. Since T is small, we follow the approach of Juodis et al. (2021) which accounts for the “Nickell” bias using the Half Panel Jackknife (HPJ) procedure of Dhaene and Jochmans (2015).¹³ Table 1 displays p-values from the HPJ-Wald test where the null hypothesis is that x does not Granger cause y. The table presents results for the whole sample, a subsample that contains only the low-income countries and a subsample that contains only the high-income countries.¹⁴ The only bivariate causality that holds robustly across all samples is the causality that runs from GEX to HEX.¹⁵ All other bivariate causalities either hold in one of the samples or at most in two of the samples. Specifically, the results for the whole sample indicate that there is a causal relationship that runs from GEX to HEX at the 1% significance level and causal relationships that run from HEX to NPL and from NPL to GEX at the 5% and 10% significance levels, respectively.

Table 1 Granger non-causality test—Juodis et al. (2021)

The causal relationship GEX to HEX is preserved in both the low-income and the high-income subsamples at the 5% significance level. However, the causal relationship NPL to GEX is preserved only in the high-income subsample at the 1% significance level, while the causal relationship HEX to NPL is preserved only in the low-income subsample at the 1% significance level. Moreover, the causal relationship from GEX to NPL is statistically significant only in the high-income sample at the 5% level and the causal relationship HEX to GEX is statistically significant only in the low-income sample at the 1% level. While the causality that runs from GEX to HEX is supported in all samples, the bivariate causality tests from the whole sample and the low-income subsample further suggest that the effect of GEX on HEX could be sourced, at least to some extent, by NPL that affects HEX via GEX.

2.2 Multivariate models

Although the bivariate causality approach of the previous subsection is useful as a preliminary diagnostic tool, it suffers of three shortcomings. First, the results for the effect of x on y are based solely on the impact of lagged values of x, ignoring any possible contemporaneous relationship between x and y. Second, the bivariate causality approach only considers the direct relationship between y and x, ignoring the presence of mediator variables and thus possible indirect relationship between y and x via, say, z. For instance, the results of the previous section suggest that GEX could be a mediator variable between NPL and HEX. If so, what is the direct effect of GEX on HEX? Third, the bivariate causality approach does not generally consider the impact of other control variables in estimating the causality between x and y. To address those issues in quantifying the causal relationships, we examine the following multivariate model:

$${\varvec{A}}_{i} {\varvec{Y}}_{i,t} = {\varvec{A}}_{i,0} + \mathop \sum \limits_{j = 1}^{K} {\varvec{A}}_{i,j} {\varvec{Y}}_{i,t - j} + {\varvec{\varepsilon}}_{i,t} ,$$

(1)

for country $i = 1, 2, \ldots N$ and year $t = 1, 2, \ldots T$, where ${\varvec{Y}}_{i,t}$ is an Mx1 vector of endogenous variables for country i, ${\varvec{A}}_{{\varvec{i}}}$ is an MxM matrix which captures the contemporaneous relationships between the variables in ${\varvec{Y}}_{i,t}$, ${\varvec{A}}_{i,0}$ is an Mx1 vector of intercepts and ${\varvec{\varepsilon}}_{i,t}$ is an Mx1 vector of iid error terms. Apart from $HEX_{i,t}$, $GEX_{i,t}$ and $NPL_{i,t}$, ${\varvec{Y}}_{i,t}$ consists of three additional auxiliary variables with potential direct and indirect effects on the relationship between $HEX_{i,t}$ and $GEX_{i,t}$. Specifically, the auxiliary variables aim to capture the effects of changes in the real and nominal sides of the economy as well as structural characteristics. To capture nominal effects, we use the logarithm of the consumer price index ($CPI_{i,t}$) which summarizes the impact of prices at the retail level. It is a measure that is commonly used to track changes in the cost of living for typical households and the basis to measure inflation. To capture effects in the real side of the economy we use the unemployment rate ($UNP_{i,t}$) which is commonly used as an indicator of the business cycle since it exhibits a high correlation with the cyclical component of real GDP. To capture the effects of structural characteristics, we use the logarithm of population density ($POP_{i,t}$) which is defined as the number of people per square mile of land area. Population density is argued to be a good indicator of agglomeration (see Boserup 1965), labor market conditions, commuting infrastructures (see Borgoni et al. 2002) and the state of development in general (e.g. Depetris-Chauvin and Weil 2018). Data for the three auxiliary variables are also obtained from World Bank’s database.

Equation (1) can be estimated as a structural VAR. The difficulty of doing so is that the estimation requires the identification of the elements in ${\varvec{A}}_{{\varvec{i}}}$ for $i = 1, 2, \ldots ,N$ or simply ${\varvec{A}}_{{\varvec{i}}} = {\varvec{A}}$ if we pool them together, which entails identifying restrictions that originate from theory. The problem is that there is no theory to guide us through regarding specific restrictions on the covariance matrix which would allow us to identify with relative confidence the coefficients in any ${\varvec{A}}_{{\varvec{i}}}$ or ${\varvec{A}}$. To address this problem, we estimate directly and separately each equation included in (1) using cross-country panel data. Before proceeding with estimation, we ensure that all variables in our panel including the controls are stationary. While CPI is found to be stationary using the Im et al. (2003) test, POP and UNP are stationary only in first differences and thus we include them as such. In the stationarity tests we excluded trends and statistical significance is concluded at the 5% level. The regressions are specified as follows:

$$y_{i,t} = \alpha^{y} + f_{i}^{y} + {\varvec{\beta}}^{y} \left( L \right){\varvec{Y}}_{i,t} + \varepsilon_{i,t}^{y}$$

(2)

where ${\varvec{Y}}_{i,t} \equiv \left[ {\begin{array}{*{20}c} {HEX_{i,t} } & {GEX_{i,t} } & {NPL_{i,t} } & {CPI_{i,t} } & {POP_{i,t} } & {UNP_{i,t} } \\ \end{array} } \right]^{\prime}$ and ${\varvec{\beta}}^{y} \left( L \right)$ is a 1 × 6 vector of polynomials in the lag operator, $L$, with elements $\beta_{s}^{y} \left( L \right) = \sum\nolimits_{j = 0}^{K} {\beta_{s,j}^{y} L^{j} }$ if $y \ne s$ and $\beta_{s}^{y} \left( L \right) = \sum\nolimits_{j = 0}^{K - 1} {\beta_{s,j + 1}^{y} L^{j + 1} }$ if $y = s$, for $y,s \equiv HEX, GEX, NPL, CPI, \Delta POP, \Delta UNP$. Parameter $\alpha^{y}$ is the country invariant intercept and $f_{i}^{y}$ is the time-invariant country specific intercept. Note that the use of logarithms allows us to interpret the coefficients in the regression as elasticities. Noticeably, there is an endogeneity problem as $y_{i,t}$ may also affect variables in ${\varvec{Y}}_{i,t}$; e.g. $HEX_{i.t}$ may affect $GEX_{i,t}$ and $GEX_{i,t}$ may affect $HEX_{i,t}$ as well. Therefore, the method of ordinary least squares is not an appropriate one to estimate the model. To deal with endogeneity, we estimate (2) by employing the two-step system Generalized Method of Moments (GMM), as suggested by Arellano and Bond (1991), Arellano and Bover (1995) and Blundell and Bond (1998).¹⁶ This estimation procedure also deals with fixed country effects, heteroskedasticity and autocorrelation within countries and it is designed for dynamic panels with small T and large N. The endogeneity is addressed using lagged values of the regressors as instruments. Specifically, the sets of regressors, $Y$, and instruments, $Z$, are both $NT \times \left( {5 + 6K} \right)$. Y is partitioned to $Y = \left[ {Y_{1} Y_{2} } \right]$, where $Y_{1}$ contains the five time-t endogenous variables, excluding the dependent variable, and $Y_{2}$ contains the lagged values of those variables at $t - 1, t - 2, \ldots , t - K$, including the lags of the dependent variable. $Z$ is partitioned into $Z = \left[ {Z_{1} Z_{2} } \right]$, where $Z_{1}$ contains the six time $t - K - 1$ variables and $Z_{2}$ contains the five time $t - 1$ variables, excluding the dependent variable and the lags of all six variables at $t - 2, \ldots ,t - K + 1, t - K$. Thus, $Z_{1}$ corresponds to the six excluded from the regression instruments while $Z_{2}$ contains the $5 + 6\left( {K - 1} \right)$ included in the regression instruments. This implies that the number of excluded instruments equals the number of endogenous variables. Since the number of regressors equals the number of instruments, the equation is exactly identified.

There are two major issues that need to be tested: cross-sectional dependence (CD) and the validity of the instruments. As Sarafidis and Robertson (2006) highlight, cross-sectional dependence in the errors of a panel regression implies that all estimation procedures that rely on instrumental variables and the GMM are inconsistent for large N relative to T. It may not only cause efficiency loss but also yield invalid test statistics. The Pesaran (2021) CD test, displayed in Table 2, shows that the p-values of the null hypothesis of cross-sectional independence are close to zero for all six regressions. Hence, clearly estimation of (2) suffers from strong cross-sectional dependence which causes doubts about the validity of the estimated coefficients. To control for cross-sectional dependence, we follow a common approach which replaces the dependent variable $y_{i,t}$ with $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y}_{i,t} = y_{i,t} - \overline{y}_{t}$, where $\overline{y}_{t} \equiv \left( {\sum\nolimits_{j = 1}^{N} {y_{j,t} } } \right)/N$. In other words, we proxy the common country component using the cross-country average for each t and then subtracting it from each observation of the dependent variable. The aim of subtracting the common component from the dependent variable is to eliminate or, at least, reduce cross-sectional dependence inhibited by the disturbances. Although results from the Pesaran CD test indicate that indeed, the null of cross-sectional independence cannot be rejected, the test in this case may suffer from lack of power in the sense that it may fail to reject the null while the correlation between the dependent variable $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y}_{i,t}$ and the error term of the regression is preserved.¹⁷ Therefore, rather than relying on the Pesaran CD test to evaluate the validity of the revised model, we draw conclusions based on the Sargan-Hansen test of overidentifying restrictions. According to Table 4, the Sargan-Hansen test indicates that the null hypothesis of valid moment conditions is not rejected which allows us to safely argue that our estimates are meaningful. The idea is that if time demeaning is sufficient for eliminating cross-sectional dependence, then the Sargan-Hansen test of overidentifying restrictions should fail to reject the null hypothesis. This is because cross-sectional dependence implies a violation of the moment conditions in standard GMM estimators. Table 3 displays the estimated coefficients of the six panel regressions where the dependent variables correspond to $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y}_{i,t}$ as defined previously. The estimates confirm the main result of the bivariate tests that GEX causes HEX. The causality is found to be only direct as there are no statistically significant mediators that would support an indirect relationship. Moreover, the estimates suggest that an increase of GEX by 1% affects HEX both in the current year as well as in the subsequent year, inducing an overall increase in HEX of a roughly equal percentage. Specifically, an increase in the intensity of government spending of education by 1% increases HEX on impact by about 3% and decreases it the following year by about 2%.

Table 2 Pesaran CD test on the errors of two-step system GMM

Table 3 Dynamic Panel Data Estimation: Two-step System GMM

To confirm the validity of the instruments, we perform further tests which are displayed in Table 4. Given that Table 3 displays no evidence for mediator variables that channel indirect relationships between GEX and HEX, we report results only for the first two main regressions. First, we check for serial correlation in the residuals of the system GMM by employing the Arellano-Bond test. The results for the main regressions are displayed in the first two columns. While the first-order measure is found to be statistically significant for both regressions with p-values 5.2% and 6.5%, respectively, the second-order measure is clearly statistically insignificant as the p-values are as high as 82% and 66%, respectively. The presence of first-order serial correlation is not surprising since residuals in first differences correlate by construction. On the other hand, the absence of second-order serial correlation implies that residuals are uncorrelated in levels which suggests that the instruments are strictly exogenous. As shown in Table 4, statistics from the Sargan and Hansen tests of overidentifying restrictions are in line with the Arellano and Bond test results. Specifically, the Sargan-Hansen result suggests that the instruments are jointly uncorrelated with the error term as the null hypothesis of overidentifying restrictions cannot be rejected.

Table 4 Two-step system GMM: test results

Our findings indicate that an increase in the intensity of government spending on education encourages households to increase the intensity of their own spending on education in the same year. Not only they do this, but the percentage increase is three times higher than the increase in the intensity of government spending. For instance, an increase in government investment in infrastructure, say via an investment in school premises and computer labs, induces households to increase their spending significantly more, say by enrolling to private classes and purchasing new equipment. The overreaction of households to the increase in the intensity of government spending on education is followed by a “correction” the year after. The “correction” in relative spending that occurs in the subsequent year, brings the overall percentage increase of the intensity of household spending to the same level as the initial percentage increase of the intensity of government spending. One may argue that the information that households possess over time plays a role to their initial reaction to the increase in the intensity of government spending on education and the correction of the following year. Although shocks in government spending tend to lead to an overreaction of households on impact, as soon as they realize the magnitude of the change, they “correct” their own in the subsequent year. We do not find any evidence that credit constraints, proxied by the share of non-performing loans, affect directly or indirectly the intensity of spending on education.

To examine whether there are differences in the causality across low and high-income countries, similarly to what the bivariate tests suggest, we extend (2) by introducing income-level dummies that enable us to capture possible differentiated effects. Nonetheless, the dummies are found to be statistically insignificant which indicates that, on average, income levels are irrelevant to the causality between the intensities of government and household spending on education.¹⁸ This finding refutes the differentiated responses across the two subsamples implied by Juodis et al. (2021) bivariate tests. The discrepancies between the results from multivariate and bivariate models could be attributed to the various aforementioned missing aspects of the bivariate test. Finally, to examine whether $GEX_{i,t}$ and $HEX_{i,t}$ respond to country invariant components of HEX and GEX, respectively, we replace regressors at time t with $\overline{HEX}_{t}$ and $\overline{GEX}_{t}$ and in all corresponding lags, and then re-estimate the models. We find that all regressors which involve the country invariant factors are highly statistically insignificant both contemporaneously and in lags. This result indicates that household spending intensities on education respond only to country specific changes in corresponding government intensities. To save on space, we do not report the full set of estimates which are available upon request. We report however the various tests for the two regressions in the last two columns of Table 4 to demonstrate that the models are well-specified.

3 Conclusion

In this paper, we examine the causality between the intensities of government and household spending on education. Using data from a cross-country panel, we show that appropriate bivariate causality tests indicate that the intensity of government spending on education causes the intensity of household spending on education, and that this result is robust across different samples. Although bivariate testing further suggests that the reversed causality holds for low-income countries, we demonstrate that this result as well as causalities with mediator variables disappear when we consider a multivariate model that controls for contemporaneous relationships, cross-country dependence, homoskedasticity and autocorrelation within countries as well as country fixed effects. This result is interesting and particularly useful for policy makers as it further shows that not only the causality clearly runs from the intensity of government spending on education to the corresponding household intensity, but the effect is only direct. Our findings suggest that households tend to overreact in the year that the government increases its spending intensity by increasing their own intensity three times more. The year that follows however, they correct their response by decreasing their spending intensity so that there is an overall one-to-one relationship between the two intensities. Within the context of a multivariate model, we find no evidence that credit market tightness as approximated by the percentage of non-performing loans affects either the intensity of household spending on education or the intensity of government spending on education.

Appendix: Data description and statistics

See the Table 5.

Table 5 Descriptive statistics