Modelling Okun’s law: Does non-Gaussianity matter?

Abstract

In this paper, we analyse Okun’s law—a relation between the change in the unemployment rate and GDP growth—using data from Australia, the euro area, the UK and the USA. More specifically, we assess the relevance of non-Gaussianity when modelling the relation. This is done in a Bayesian VAR framework with stochastic volatility where we allow the different models’ error distributions to have heavier-than-Gaussian tails and skewness. Our results indicate that accounting for heavy tails yields improvements over a Gaussian specification in some cases, whereas skewness appears less fruitful. In terms of dynamic effects, a shock to GDP growth has robustly negative effects on the change in the unemployment rate in all four economies.

1 Introduction

Okun’s law is a key macroeconomic relation which has become a popular tool for analysis and forecasting since its introduction almost 60 years ago (Okun 1962). Typically relating the change in the unemployment rate to GDP growth,¹ a fairly large literature has analysed various aspects of it, such as its stability over time, its forecasting properties or its validity in different countries; see, for example, Knotek (2007), IMF (2010), Meyer and Tasci (2012), Owyang and Sekhposyan (2012), Rülke (2012), Zanin and Marra (2012), Huang and Yeh (2013), Valadkhani (2015), Economou and Psarianos (2016), Ball et al. (2017), Grant (2018), An et al. (2019), Ball et al. (2019) and Karlsson and Österholm (2020) for some fairly recent contributions. Conclusions regarding the properties of the relation differ somewhat depending on the country and period studied, but Ball et al. (2017, p. 1439) nevertheless suggest that Okun’s law “… is strong and stable by the standards of macroeconomics”.

In this paper, we extend the literature on Okun’s law by investigating the importance of non-Gaussianity when modelling the relation between the change in the unemployment rate and GDP growth. We consider two aspects of non-Gaussianity. The first of these is heavy tails (or “fat tails”)—an issue that takes its starting point in the observation that many economic variables seem to experience large swings more frequently than what one would expect if the shocks hitting the economy are drawn from a Gaussian distribution; see, for example, Fagiolo et al. (2008), Ascari et al. (2015), Cross and Poon (2016), Liu (2019) and Kiss and Österholm (2020). The second aspect is that the unconditional distribution of many variables appears to be characterised by skewness. Particular interest has often been paid to GDP growth with respect to this issue; see, for example, Neftci (1984), Acemoglu and Scott (1997) and Bekaert and Popov (2019). The topic of non-Gaussianity appears to have gained interest over time. This is perhaps not surprising in the light of recent historical events; we have, for instance, seen both the Global Financial Crisis and the crisis associated with the corona pandemic in less than 15 years.

Heavy tails and/or skewness in the unconditional distribution of the variables (i.e. the distributions of the actual data) can potentially be caused by the conditional distribution of the error terms of the model having these properties.² Using data from Australia, the euro area, the UK and the USA, we assess the relevance of such non-Gaussianity. This is done by estimating bivariate Bayesian VAR models with stochastic volatility under three different assumptions regarding the error distributions: (i) Gaussian, (ii) Student’s t and (iii) generalised hyperbolic skew Student’s t, also known as “skew-t”. Our econometric setting—which has been recently developed by Karlsson et al. (2021)—allows us to conduct formal model comparison based on the marginal likelihoods of the estimated models. We can accordingly make statements regarding how well the different models fit the data based on a formal statistical criterion. By conducting this analysis, we contribute to the literature in two distinct ways. First, we make a general contribution concerning the importance of modelling the non-Gaussianity of the unconditional distribution of macroeconomic variables. Second, we provide international empirical evidence concerning Okun’s law in a state-of-the-art econometric setting.³

Our key results are the following: We find that the unconditional distributions of both variables for all four economies exhibit non-Gaussianity. Our main analysis is conducted using quarterly data up until 2019Q4, that is, we do not include data from the corona pandemic. The estimated models using these data suggest that allowing for error terms with heavy tails yields substantial improvements over a Gaussian specification for Australia and the euro area. Also for the USA is a t-distribution the preferred specification, but its benefits relative to a Gaussian distribution are minor judging by the marginal likelihoods of the estimated models. For the UK, the specification with Gaussian error terms is the preferred specification. In no case is the model with skew-t error terms supported by the data, and we conclude that modelling skewness appears less fruitful in this context.

In order to establish how robust our findings are, we also perform some additional analysis. This consists of two parts. We first conduct an out-of-sample forecast exercise. Using the log predictive score as an evaluation measure, we assess the forecasting properties of the different models. These results are somewhat more ambiguous but nevertheless indicate that in some cases—primarily for the euro area and the USA—there might be benefits to employing a t-distribution. Second, we also estimate our models with data up until 2021Q2 to see how the large swings associated with the corona crisis affect our results. Results from this exercise indicate—not surprisingly—that support for non-Gaussianity strengthens when these observations are added. Regarding the dynamic relationship between the variables, we find—regardless of which period we study—that Okun’s law prevails: A shock to GDP growth has robustly negative effects on the change in the unemployment rate in all four economies.

The rest of this paper is organised as follows: In Sect. 2, we describe the data we use in our analysis. The econometric framework is described in Sect. 3. We present our results—from both our main analysis and the robustness checks—in Sect. 4. Finally, Sect. 5 concludes.

2 Data

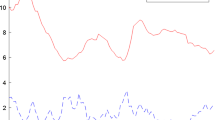
Data on GDP growth (g_t) and the change unemployment rate (Δu_t) are shown in Fig. 1; all data were sourced from Macrobond.⁴ The samples we use for the four economies vary with respect to their starting point due to availability of data, but all have the same end date. In our main analysis, the samples are 1978Q3–2019Q4 for Australia, 1995Q2–2019Q4 for the euro area, 1971Q3–2019Q4 for the UK and 1948Q2–2019Q4 for the USA. We do not include data from 2020 and later since the corona pandemic induced movements in the variables which were so large that they maybe should be considered outliers; this is clearly illustrated in Fig. 1. As can be seen, particularly the swings in GDP growth associated with the corona pandemic were of a magnitude which had never been seen before in the samples considered here. This was also the case for the change in the unemployment rate in the USA. However, for Australia, the euro area and the UK, the change in the unemployment rate was obviously large but not extreme by historical standards. We assess the importance of excluding the corona-related observations in the robustness analysis in Sect. 4.2.2.

Fig. 1

Source: Macrobond

Data. Note: Per cent on vertical axis for GDP growth. GDP growth is given as the percentage change in seasonally adjusted real GDP from the previous quarter. Percentage points on vertical axis for the change in the seasonally adjusted harmonised unemployment rate. Vertical green dashed line indicates the end of the sample for our main analysis.

In order to assess potential non-Gaussianity of the data, we present some key descriptive statistics in Table 1. We also show histograms which illustrate the unconditional distributions of the variables in Fig. 8 in Appendix. The unconditional distribution of the variables is in all cases associated with excess kurtosis. Regarding skewness, this seems fairly modest for GDP growth; it is negative in three out of four economies, but for both Australia and the USA, it is quite close to zero. Turning to the skewness of the change in the unemployment rate, this is found to be positive and more substantial in all four economies. The Jarque–Bera test strongly rejects normality in all cases. This provides an initial indication that a departure from a Gaussian distribution might prove useful when modelling the Okun’s law relation empirically.

Table 1 Descriptive statistics and Jarque–Bera test statistics

3 Econometric framework

We rely on bivariate Bayesian VAR models with stochastic volatility for our analysis of Okun’s law.⁵ In that sense, our analysis is closely related to Karlsson and Österholm’s (2020) analysis on US data. Unlike Karlsson and Österholm though, we do not allow for time variation in parameters and, importantly, we have flexible error term distributions that allow for heavy tails and skewness. Denoting ${\varvec{y}}_{t} = \left( {g_{t} ,\Delta u_{t} } \right)^{\prime }$ for $t = 1, \ldots ,T$, we have

$${\varvec{y}}_{t} = {\varvec{c}} + {\varvec{B}}_{1} {\varvec{y}}_{t - 1} + \cdots + {\varvec{B}}_{p} {\varvec{y}}_{t - p} + {\varvec{e}}_{t} ,$$

(1)

where c is a vector of intercepts and B₁ to B_p include the coefficients describing the dynamics of the VAR. We set lag length to p = 1 for Australia and the euro area and p = 2 for the UK and the USA.⁶ The stochastic representation of the error term e_t can be written in terms of a variance–mean mixture of normal distributions so that the marginal distribution of e_t follows a multivariate skew-t distribution (McNeil et al. 2015),

$${\varvec{e}}_{t} = \left( {{\varvec{w}}_{t} - \overline{\user2{w}}} \right){\varvec{\gamma}} + {\varvec{w}}_{t}^{1/2} {\varvec{A}}^{ - 1} {\varvec{H}}_{t}^{1/2} {\varvec{\varepsilon}}_{t} ,$$

(2)

where the lower triangular matrix A with unit diagonal contains the structural parameters of the VAR model and w_t is a scalar independent mixing variable drawn from an inverse-gamma distribution with identical scale and shape parameters equal to $\frac{\nu }{2}$, where ν is the degree of freedom and $\overline{\user2{w}} = \nu /\left( {\nu - 2} \right)$, γ is the vector of skewness parameters and ${\varvec{\varepsilon}}_{t} \sim N\left( {0,{\varvec{I}}} \right)$. The matrix ${\varvec{H}}_{t} = {\text{diag}}\left( {h_{1t} ,h_{2t} } \right)$ contains the stochastic volatilities of the variables, whose time-series evolution is described as

$$\log \left( {h_{it} } \right) = \log \left( {h_{it - 1} } \right) + \sigma_{i} \eta_{it} ,$$

(3)

for i = 1, 2 with σ_i > 0 and $\eta_{it} \sim N\left( {0,1} \right)$. Finally, when w_t, H_t and ε_t are mutually independent, the marginal distribution of e_t is a multivariate skew-t distribution with zero vector mean, scale matrix ${{\varvec{\Sigma}}}_{{\varvec{t}}} = {\varvec{A}}^{ - 1} {\varvec{H}}_{t} {\varvec{A}}^{{{\prime } - 1}}$, skewness vector γ, and degrees of freedom ν. The distribution in (2) allows for both leptokurtic and skewed distributions even after filtering out stochastic volatility. While the mixing variable w_t captures the high-frequency shock in mean and variance, the stochastic volatility accounts for the low-frequency shocks.

Our proposed specification nests several important models as special cases. Setting γ = 0, we get the Bayesian VAR model with stochastic volatility and Student’s t-distributed error terms proposed by Ni and Sun (2005), which has been a workhorse used in empirical modelling of heavy-tailed error terms in the Bayesian VAR context; see, for example, Cross and Poon (2016), Chiu et al. (2017), Chan (2020) and Carriero et al. (2021). The Gaussian distribution is also nested in this specification (${\varvec{\gamma}} = 0, \nu \to \infty$). We accordingly consider three Bayesian VAR models with stochastic volatility for each of the economies: the benchmark Gaussian, the Student’s t and the skew-t.

Bayesian estimation requires specifying prior distributions for the parameters. We use a diffuse normal prior (with zero mean and variance 10) for the free element of the lower triangular matrix A. We impose a Minnesota prior for the regression coefficients (c and B) with overall shrinkage l₁ = 0.2 and cross-variable shrinkage l₂ = 0.5 (Koop and Korobilis 2010).⁷ The priors for the rest of the parameters are given by $\nu \sim {\mathcal{G}}\left( {2,0.1} \right)$ for ν > 4, $\gamma_{i} \sim N\left( {0,1} \right)$ for i = 1, 2, and $\sigma_{i}^{2} \sim {\mathcal{G}}\left( {0.5,0.5} \right)$, where ${\mathcal{G}}\left( {a,b} \right)$ is a gamma distribution with shape and rate parameters a and b (Kastner and Frühwirth-Schnatter 2014).

As the error term is written in terms of a variance–mean mixture distribution, it is straightforward to make inference on the model parameters based on the Gibbs sampler of the VAR model with Gaussian stochastic volatility; see details in the online appendix of Karlsson et al. (2021). For example, in the VAR model with skew-t distribution and stochastic volatility, the conditional posterior distribution of parameters (c, B, γ) is a multivariate normal distribution (Clark 2011). The conditional posterior distribution of the parameter in the lower triangular matrix A is also a normal distribution (Cogley and Sargent 2005), and that of the parameters $\sigma_{i}^{2}$ is a generalised inverse Gaussian distribution (Hörmann and Leydold 2014). We sample the stochastic volatility following Kim et al. (1998) and Carter and Kohn (1994). We sample the mixing variable w_t based on the generalised inverse Gaussian distribution (Hörmann and Leydold 2014) and sample the degrees of freedom ν based on an adaptive random-walk Metropolis–Hastings algorithm (Roberts and Rosenthal 2009 and Karlsson et al. 2021).

In order to compare different specifications of the VAR model with stochastic volatility, we calculate the marginal likelihood based on the cross-entropy method of Chan and Eisenstat (2018). The marginal likelihood provides us with a measure of how well the model and the priors agree with the data, where the model with the highest marginal likelihood is the one preferred by the data. The marginal likelihood requires a high-dimensional integration over the fixed parameters θ = (c, B, γ, A, σ², ν) and the latent states φ = (h_1:T),

$$\begin{aligned} p\left( {{\varvec{y}}_{1:T} } \right) & = \smallint p{(}{\varvec{y}}_{1:T} {|} {\varvec{\theta}}) p\left( {\varvec{\theta}} \right)d{\varvec{\theta}} \approx \sum \frac{{p{(}{\varvec{y}}_{1:T} {|} {\varvec{\theta}}) p\left( {\varvec{\theta}} \right)}}{{f\left( {\varvec{\theta}} \right)}}, \\ p{(}{\varvec{y}}_{1:T} {|} {\varvec{\theta}}) & = \smallint p{(}{\varvec{y}}_{1:T} {|} \user2{\varphi }, {\varvec{\theta}}) p\left( {\user2{\varphi }|{\varvec{\theta}}} \right) d\user2{\varphi } \approx \sum \frac{{p{(}{\varvec{y}}_{1:T} {|} \user2{\varphi }, {\varvec{\theta}}) p\left( {\user2{\varphi }|{\varvec{\theta}}} \right)}}{g(\user2{\varphi })}. \\ \end{aligned}$$

Following Chan and Eisenstat (2018), we use two-stage importance sampling to calculate the marginal likelihood. In the first stage, we use the cross-entropy method to learn the proposal distribution of the fixed parameters f(θ) based on the posterior samples. Then, we obtain N = 20,000 proposal samples from f(θ) and calculate the integrated likelihood $p{(}{\varvec{y}}_{1:T} {|} {\varvec{\theta}})$ for each sample of θ based on an inner importance sampling loop. The proposal distribution of the latent states g(φ) is based on a sparse matrix representation. For further details concerning posterior inference and marginal likelihood calculations, see Karlsson et al. (2021).

4 Results

We initially present results based on our main sample, that is, where the last observation of each sample is 2019Q4. In Sect. 4.2, we present sensitivity analysis related to the highly volatile period associated with the corona pandemic.

4.1 Main results

Our main results are based on in-sample estimation of the Bayesian vector autoregressions proposed in Sect. 3. To keep the focus on the role of non-Gaussianity, Table 2 presents parameter estimates (posterior means) of the parameters governing non-Gaussianity in the distribution of the error term. In particular, the scalar degrees of freedom ν govern the heaviness of the tail of the distribution, where a lower value of ν indicates a heavier tail. The vector γ contains the variable-specific asymmetry parameters for the two variables. A positive asymmetry value means that the distribution of the error term has a positive skew. Furthermore, Table 2 shows the log marginal likelihoods of the estimated models. As described in the previous section, log marginal likelihoods can be considered as a summary measure, where a higher log marginal likelihood value suggests that the given model fits the data better.

Table 2 Log marginal likelihoods and estimated key parameters

Starting with the log marginal likelihoods, they suggest that it is beneficial to take heavy tails into account for Australia, the euro area and the USA. For Australia, the support for the Student’s t-distribution is “positive” against both other models when we use the scale of two times the difference in the log marginal likelihood and the terminology of Kass and Raftery (1995, p. 777). For the euro area, the support for the Student’s t-distribution is “positive” against the skew-t distribution and “very strong” against the Gaussian. For the USA, the support for the Student’s t-distribution is “not worth more than a bare mention” when compared with the Gaussian and “positive” against the skew-t. Turning to the UK, we find that the Gaussian model is preferred. The support for it is “not worth more than a bare mention” though when compared with the t-distribution but “very strong” relative to the skew-t.

These results are also reflected in the estimates of the parameters. For the models with a Student’s t-distribution, the estimated degrees of freedom are relatively low for Australia (14.34) and the euro area (11.01) signalling modestly heavy tails of the error terms. For the UK and the USA, the estimated degrees of freedom are substantially higher (27.93 and 24.53, respectively); with such high degrees of freedom, the distribution of the error terms is empirically indistinguishable from the Gaussian, which is also reflected in the log marginal likelihoods. For the skew-t models, the degrees of freedom parameters are higher for all four economies; hence, distributions become less heavy-tailed. It suggests that allowing for asymmetry helps capture some of the larger movements in the variables. Looking at the asymmetry parameter γ, we see a positive skewness in most variables; the only exceptions are the change in the unemployment rate for the UK and GDP growth for the USA, where the estimated skewness of the error terms is negative. While the sign of parameter γ pins down the direction of the asymmetry, the magnitude of the skewness of the error terms depends on both the asymmetry parameter—which is constant over time—and the stochastic volatility (see discussions in Karlsson et al. 2021). Figure 9 in Appendix shows the skewness of the error term for each variable over the sample periods. Looking at this figure, we can see that the absolute value of the skewness parameter is well below one in all cases for all periods. This is small in magnitude; see, for example, Mallery and George (2000). Hence, the evidence in favour of allowing for skewness is weak.

Fig. 2

Impulse-response functions. Response of change in the unemployment rate to a shock to GDP growth. Note: The impulse-response functions are based on the model with Student’s t-distributed errors. Percentage points on the vertical axis. Horizon is given in quarters on the horizontal axes. The size of the shock is one standard deviation

We conclude that it seems reasonable to rely on a Student’s t-distribution when modelling Australia and the euro area. For the UK and the USA, both the Gaussian and Student’s t-distribution seem like acceptable choices.

Having focused on the question of error distributions so far, we next attract our attention to a key aspect of Okun’s law in this framework, namely how the change in the unemployment rate responds to an unexpected increase in GDP growth; the size of the shock is one standard deviation (given as the square root of the estimate of h_1t). These impulse-response functions are presented in Fig. 2. For consistency—and comparability—we have used the model based on Student’s t-distributed errors for all four economies when conducting this analysis (even though it was not the best model for the UK).

As can be seen, the response is negative contemporaneously and remains negative (or zero) over the entire ten-quarter horizon, in all four economies. We note though that the effect of the shock appears somewhat longer lasting in the euro area and the UK. In the light of higher GDP growth than expected, we would accordingly revise our forecast of the unemployment rate downwards. This is in line with our expectations given previous research on Okun’s law.

Figure 2 does not give any indication regarding the uncertainty associated with the impulse-response functions. In order to illustrate this, we show the impulse-response functions for all economies at 2019Q4 together with the 90% credible interval in Fig. 3. At short horizons, the interval does in no case cover the zero line and we conclude that there is indeed a negative effect on the change in the unemployment rate from a shock to GDP growth.

Fig. 3

Impulse-response functions at 2019Q4. Response of change in the unemployment rate to a shock to GDP growth. Note: The impulse-response functions are based on the model with Student’s t-distributed errors. Percentage points on the vertical axis. Horizon is given in quarters on the horizontal axes. Coloured band gives 90% credible interval. The size of the shock is one standard deviation

Returning to Fig. 2, it is striking how the magnitude of the impulse response changes considerably over the sample period. Since the regression parameters of the model are constant, these changes are solely attributed to stochastic volatility. Since this is another important feature of the employed modelling framework, we present the posterior mean of the time-varying volatility of the shocks (i.e. the process h_it) to both variables in Fig. 4. In order to illustrate the difference between a Gaussian and a Student’s t-distribution, we provide the estimated stochastic volatilities under both assumptions.

Fig. 4

Stochastic volatility estimates from VAR models. Note: The red solid line gives the stochastic volatility under the assumption of a Student’s t-distribution with the coloured bands showing the 50% credible interval. The black dashed line gives the volatility under the assumption of a Gaussian distribution

Regarding the time-varying volatilities, the patterns obviously differ across economies and variables. However, some features tend to be common. For example, except for Australian GDP growth, there is an increase in volatility around the Global Financial Crisis in 2008. From a modelling perspective, we also note that there is substantial time variation in the estimates of the volatilities. This shows that it is relevant to use models which account for heteroskedasticity, such as the models employed here.

The volatility estimates based on a Gaussian and a Student’s t-distribution show overall similar patterns, but substantial differences can also be observed in some cases. For example, under the assumption of a Student’s t-distribution the volatility of the change in the unemployment rate in Australia is clearly smoother, and the overall level of the volatility is lower in the euro area. Further, the spikes in output growth volatility in crisis periods are more pronounced in the euro area if we use Gaussian error terms. This latter observation can be attributed to the fact that, in the absence of flexible error distributions, the effect of larger swings in the variables appears through increased volatility. However, in line with what we would expect based on the results presented in Table 2, we can also see that some differences are minor. For the UK and the USA—where the marginal likelihoods of the two models were quite similar and the estimated degrees of freedom of the Student’s t-distribution high for both variables—estimated volatilities are similar for both GDP growth and the change in the unemployment rate.

4.2 Robustness

In order to assess the robustness of the above findings, we next conduct some additional analysis. There are two aspects that we will look at more closely. The first of these is the forecasting properties of the different models; the second relates to the sample period employed.

4.2.1 Out-of-sample forecasts

Our analysis so far has been conducted in-sample. In this sub-section, we will instead investigate the out-of-sample forecasting performance of the different models using the log predictive score of the models. The purpose of this is twofold. First, it can be seen as a validation tool; if the in-sample and out-of-sample results point in the same direction, this implies that the evidence is stronger. Second, it gives us an opportunity to find out how the model evidence evolves over time, for which the cumulative Bayes factor based on log predictive scores (Geweke and Amisano 2010) is particularly suited.

The forecast exercise is conducted the following way for Australia, the UK and the USA: We first estimate the competing models using data from the beginning of the sample until T₀ = 1999Q4.⁸ Forecasts for horizons one, two, three, four and eight quarters are then generated, and the log predictive density for the forecasts of each model and horizon calculated. We then extend the sample one quarter, re-estimate the models, generate new forecasts and again calculate the log predictive density. This continues until the sample employed for estimation ends in T₁ = 2017Q4. Since the full sample for the euro area is substantially shorter than that for the other economies, we instead use the sample 1995Q2 to 2009Q4 for the first estimation; we then proceed in a similar fashion as for the other economies but get fewer forecasts that can be evaluated.⁹ Following Karlsson et al. (2021), the log predictive score (LPS) of the variable i at the horizon h is computed as the average of the log predictive density,

$${\text{LPS}}_{i,h} = \frac{1}{{T_{1} - T_{0} + 1}}\mathop \sum \limits_{{t = T_{0} }}^{{T_{1} }} \log p\left( {y_{i,t + h}^{o} |{\varvec{y}}_{1:t} } \right),$$

where $p\left( {y_{i,t + h}^{o} |{\varvec{y}}_{1:t} } \right)$ is the h-step ahead posterior predictive density function evaluated at the realisation of the variable i.

Our results are summarised in two ways. In Table 3, we present the LPS for all economies and forecast horizons. Figures 10, 11, 12, and 13 in Appendix present cumulative log Bayes factors based on the predictive score for the one-quarter-ahead forecast. The cumulative log Bayes factors show the effect of an individual observation to the evidence in favour of one model over another; see the discussion in Geweke and Amisano (2010). Note that the evidence is cumulated from time t = T₀ + 1 (whereas the full sample is used when calculating the log marginal likelihood). Figures 10 and 11 show comparisons between the Gaussian model and the model with a Student’s t-distribution, and Figs. 12 and 13 show comparisons between the model with a Student’s t-distribution and a skew-t distribution.

Table 3 Log predictive score and difference in log predictive score

Turning first to Table 3, we note that significant improvements in the log predictive score of GDP growth forecasts are obtained for the Student’s t distribution in the euro area and the USA, while improvements are modest to non-existent in Australia and the UK. We also see that the skew-t model performs worse than the Student’s t in all cases except for four quarters ahead in the USA. For the change in the unemployment rate, advantages of allowing for non-Gaussianity also concentrate on the euro area and the USA, with significant improvements only appearing for the latter. Interestingly, the change in the unemployment rate in the USA benefits from being modelled with skewness. These results overall confirm our in-sample finding that non-Gaussianity matters for modelling the Okun’s law relationship and point towards the importance of heavy tails, in particular for modelling GDP growth.

Next, we turn to the cumulative log Bayes factors based on the predictive score for the one-quarter-ahead forecast presented in Appendix. These provide information regarding how the model evidence evolves over time. Looking first at Figs. 10 and 11—which provide comparisons between the Gaussian model and the Student’s t specification—the panels for GDP growth suggest that improvements over Gaussianity are obtained for the euro area largely continuously for the evaluated period and for the USA after the Global Financial Crisis. Also for Australia does the Student’s t model perform better after the financial crisis but it can be noted that leading up to that point in time, the Gaussian model performed better; seen over the entire out-of-sample period, the Gaussian model performs better, as shown by the negative value for the cumulative log Bayes factor at the end of the sample. For the UK, the pattern is not very clear. Turning to the change in the unemployment rate, we find that the Student’s t model performs better in all four economies when looking at the full sample, though the differences are small in both the euro area and the USA. We also note that patterns over time are less easily spotted; an exception is the change in the US unemployment rate where the Gaussian model tended to perform better up until 2009 and the Student’s t model thereafter.

Looking at the cumulative log Bayes factors between the Student’s t and the skew-t model in Figs. 12 and 13, we can see that based on the full evaluation period, in most cases the skew-t model is worse than the one based on Student’s t; the only exception to this is the change in the unemployment rate for the USA, thereby confirming the log predictive score results in Table 3. The change in the US unemployment rate also provides the most stable pattern in terms of skew-t outperforming Student’s t most of the time (as shown by the relatively steady upward trend in the graph). Regarding patterns over time, we also find that for GDP growth, the Student’s t model tends to perform better in Australia and the UK after the Global Financial Crisis judging from the decreasing cumulative log Bayes factors during this period. However, leading up to the crisis the skew-t model performed somewhat better in both countries.

Summing up, we find that our results—while clearly not pointing unambiguously in one direction—indicate that in some cases, mainly for the euro area and the USA, there might be benefits to employing a t-distribution, while the usefulness of a skew-t distribution in an out-of-sample context continues to be limited and concentrates on the unemployment rate in the USA.

4.2.2 Including observations from the corona pandemic

Our results so far indicate that for some economies, there might be improvements to be made when it comes to modelling Okun’s law if error terms are assumed to be drawn from a Student’s t-distribution. However, our analysis has been based on a sample which excludes the corona pandemic and the economic crisis and the recovery which followed it. As pointed out in Sect. 2, the swings in the variables associated with this period were very large—so large that they perhaps should be considered outliers; see, for example, the discussion in Carriero et al. (2021). Issues associated with modelling the corona pandemic have recently been discussed in the literature; see, for example, Bobeica and Hartwig (2021), Carriero et al. (2021) and Hartwig (2021). Seeing that these data are something that empirical macroeconomists will have to handle in the future, we next assess the effects that they have in the context of the analysis in this paper.

We accordingly expand our sample so that it includes data up until 2021Q2 to see how the large swings associated with the corona crisis affect our results. In Table 4, we first provide descriptive statistics and results from the Jarque–Bera test for normality. The large movements in the variables around the corona pandemic affect higher-order moments of the unconditional distribution. The standard deviation of the variables increases somewhat compared with the baseline results in Table 1. A negative skewness of GDP growth and a positive skewness of the change in the unemployment rate also become salient features of the data in all economies. The most prominent difference compared with the baseline sample, which excludes the corona observations, is found in the excess kurtosis of the variables which shoots up by including observations from 2020 and 2021. The increase is most striking for GDP growth in all economies and the change in the unemployment rate in the USA, in which cases excess kurtosis becomes six to ten times larger.

Table 4 Descriptive statistics and Jarque–Bera test statistics—sample including corona pandemic

Estimation results are also impacted by the strong increase in excess kurtosis. In Table 5, we present the log marginal likelihoods and estimated key parameters from the models when relying on the sample including the observations during the corona pandemic, that is, up until 2021Q2. Considering the log marginal likelihoods first, it can be seen that the Student’s t-distribution is preferred in three cases, namely for Australia, the UK and the USA. The strength of the evidence varies though; compared with the Gaussian model, we find that it is “very strong” for Australia and the USA but “not worth more than a bare mention” for the UK. For the euro area, the skew-t model is now the preferred one and the support in favour of it is “very strong” and “strong” when compared with the models assuming a Gaussian and a Student’s t-distribution, respectively. As a general tendency, we see that the skew-t model is doing much better in this sample; while it is the preferred model only for the euro area, one should recall that for the sample excluding the corona pandemic, it is always the worst model (Table 2). Not surprisingly, we also see that the support for the Gaussian model declines when using the sample including the corona pandemic.

Table 5 Log marginal likelihoods and estimated key parameters—sample including corona pandemic

Turning to the estimated degrees of freedom and skewness parameters, we also see an effect of the pandemic observations. The degrees of freedom radically decrease for Australia and the USA if one considers the model with Student’s t-distribution. Interestingly, for the USA it remains low (signalling very heavy tails) even when allowing for skewness. In contrast, allowing for skewness in the case of Australia helps capturing large movements as the degrees of freedom parameter jumps up for the skew-t specification. For the other two economies, the change in the estimated degrees of freedom is less dramatic. The skewness parameters for each country also change somewhat (they tend to increase), but they retain the same sign as in the baseline sample. The only exception is the skewness of GDP growth in the euro area where the point estimate of the sign of the skewness parameter switches from positive to negative.

Another way of illustrating the influence of the observations associated with the corona pandemic is by looking at the posterior distribution of the estimated degrees of freedom for the model based on Student’s t-distributed error terms. This is shown in Fig. 5. First, we can note that the posterior distributions in the euro area and the UK change only in a fairly moderate manner. For the euro area, the sample including corona actually puts somewhat more weight on higher values of degrees of freedom, that is, the tails become less heavy. The changes are more drastic for Australia and the USA though, where the posterior distribution becomes heavily concentrated at low values (which is also reflected in the radically decreased point estimate which is taken to be the posterior mean).

Fig. 5

Posterior distributions of the estimated degrees of freedom—samples including and excluding the corona pandemic. Note: The blue density gives the degrees of freedom based on data which do not include the corona pandemic, that is, the samples end in 2019Q4. The yellow density gives the degrees of freedom based on data which do include the corona pandemic, that is, the samples end in 2021Q2. All densities are based on the model with Student’s t-distributed error terms

As established above, including the corona pandemic has implications for which model is preferred by the data. It also tends to affect the estimated volatilities of the models in a substantial manner, particularly near the end of the sample. Figure 6 shows the estimated log volatilities from the models. We see that in most cases there is a sharp jump in volatility, during 2020 and 2021, often reaching previously unprecedented levels. Note, however, that using our baseline sample ending in 2019, the volatility estimates were on a stable low level or slightly on the way down in most cases, signalling tranquil times. This drastically changes when the observations from 2020 and 2021 are included: Not only does the volatility spike during these latter years, but in order to match the high volatility during the crisis associated with the corona pandemic, volatility is also on the rise even a few years before that during the second half of the 2010s. Furthermore, for the USA—where the evidence on heavy tails is also the strongest in the longer sample—we also see that using the Student’s t-distribution allows the model to capture the large movements around the end of the sample. Using a non-Gaussian specification allows stochastic volatility for both the change in unemployment rate and GDP growth to remain at a modest level (in contrast to the large upward jump in the Gaussian case). A similar effect can be observed for Australia regarding the change in unemployment rate. The volatility estimates for the euro area and the UK are almost identical regardless of the distributional assumption, which is in line with the fact that the Student’s t-distribution is less useful for these economies.

Fig. 6

Log volatility estimates from VAR models—samples including and excluding the corona pandemic. Note: The red (blue) solid line gives the logarithm of the volatility of the variables using a model with Gaussian (Student’s t) error terms up to 2021Q2, that is, including the pandemic period. The orange (green) dashed line gives the logarithm of the volatility of the variables using a model with Gaussian (Student’s t) error terms up to 2019Q4, that is, excluding the pandemic period

Finally, we also look at the impulse-response functions of the change in the unemployment rate to a shock to GDP growth; for comparability with the main specification, we continue to use the model based on a Student’s t-distribution. We present the impulse-response functions at 2021Q2, that is, the end of the extended sample. These are given in Fig. 7. The shape of the impulse responses remains similar to the ones reported in Fig. 3. We still find that all the impulse responses start in the negative region and remain significantly negative for several quarters. It can be noted though that the magnitudes are quite different to those in Fig. 3. This is of course only to be expected given the much higher volatility in 2021Q2.

Fig. 7

Impulse-response functions at 2021Q2. Response of change in the unemployment rate to a shock to GDP growth—sample including corona pandemic. Note: The impulse-response functions are based on the model with Student’s t-distributed errors. Percentage points on the vertical axis. Horizon is given in quarters on the horizontal axes. Coloured band gives 90% credible interval. The size of the shock is one standard deviation

To sum up, we conclude that including the corona pandemic has non-negligible effects on the results. The large swings in the variables during this time generally result in stronger evidence against Gaussianity. This is supported by the radically decreasing degrees of freedom for the distribution of the error terms for Australia (for the model with Student’s t-distribution) and the USA (for both the Student’s t and skew-t models), and the fact that models with non-Gaussian error terms (either with Student’s t or skew-t distribution) become the preferred model based on log marginal likelihoods in all four economies. The cases of Australia and the USA also highlight that accounting for heavier tails in the error terms also helps avoiding large jumps in stochastic volatility.

5 Conclusion

In this paper, we have analysed the relevance of taking non-Gaussianity into account when empirically modelling Okun’s law in Australia, the euro area, the UK and the USA. Our results based on Bayesian VAR models with stochastic volatility suggest that heavier-than-Gaussian tails find support in some cases. Taking skewness into account is generally less beneficial, even if our robustness analysis suggests some benefits of a skewed distribution for the change in the unemployment rate in the USA. Our results confirm that it can be important to account for heavy tails in the distribution of macroeconomic variables, an argument put forward by Fagiolo et al. (2008) and Ascari et al. (2015) among others.

It should be noted though that our results to some extent depend on whether data from the corona pandemic are included or not. We believe that including them might be problematic since they should probably be treated as outliers. If they nevertheless are treated as regular observations, our analysis indicates that the evidence of non-Gaussianity strengthens. In addition, it can be noted that accounting for non-Gaussianity not only improves the model fit in several cases, but it also captures the large swings in the variables without causing large swings in the stochastic volatility.

Apart from the modelling perspective, our analysis has also provided updated international empirical evidence concerning Okun’s law. We find that the dynamic relationship between the variables in all four economies is such that a shock to GDP growth has robustly negative effects on the change in the unemployment rate. This finding is robust to whether we include the period associated with the corona pandemic or not. It confirms Ball et al. (2017) and Ball et al. (2019) who argue that Okun’s law continues to be a robust relationship in empirical macroeconomics. This should be highly relevant information to the central banks of the economies studied here, suggesting that Okun’s law—which has been an important empirical relationship when modelling the economy—continues to be useful regardless of modelling choices and time periods.

Appendix

See Table

Table 6 Log marginal likelihoods for different lag lengths of VAR models with Gaussian innovations

6 and Figs.

Fig. 8

Unconditional distributions of the data. Note: Histograms and smoothed kernel density estimates (red line) of the data series ending in 2019Q4. Frequency on vertical axis. Per cent on horizontal axis for GDP growth. Percentage points on horizontal axis for the change in the unemployment rate

8,

Fig. 9

The time-varying skewness of the conditional distribution of the error terms with their 50% credible interval in the VAR model with skew-t innovations

9,

Fig. 10

Cumulative log Bayes factors based on the predictive score for the one-quarter-ahead forecast between the VAR with Gaussian innovations and Student’s t innovations. Note: The positive values (red) mean the VAR with Student’s t innovations predicts better and negative values (blue) mean the VAR with Gaussian innovations predicts better; see Geweke and Amisano (2010) for details

10,

Fig. 11

Cumulative log Bayes factors based on the predictive score for the one-quarter-ahead forecast between the VAR with Gaussian innovations and Student’s t innovations. Note: The positive values (red) mean the VAR with Student’s t innovations predicts better and negative values (blue) mean the VAR with Gaussian innovations predicts better; see Geweke and Amisano (2010) for details

11,

Fig. 12

Cumulative log Bayes factors based on the predictive score for the one-quarter-ahead forecast between the VAR with Student’s t innovations and skew-t innovations. Note: The positive values (red) mean the VAR with skew-t innovations predicts better and negative values (blue) mean the VAR with Student’s t innovations predicts better; see Geweke and Amisano (2010) for details

12, and

Fig. 13

Cumulative log Bayes factors based on the predictive score for the one-quarter-ahead forecast between the VAR with Student’s t innovations and skew-t innovations. Note: The positive values (red) mean the VAR with skew-t innovations predicts better and negative values (blue) mean the VAR with Student’s t innovations predicts better; see Geweke and Amisano (2010) for details

13.