Baldwin versus Cecchini revisited: the growth impact of the European Single Market

Abstract

The European Single Market created a common market for millions of Europeans. However, 30 years after its introduction, it appears that the benefits of the common European project are occasionally being questioned at least by some parts of the population. Others, by contrast, strive for deeper integration. Against this background, we empirically gauge the growth effect that arose from the Single Market. Using the synthetic control method, we establish the growth premium for the Single Market overall and for its founding members. Broadly in line with the predictions made by Richard Baldwin at the onset of the Single Market project, we find significantly higher real GDP per capita for the overall Single Market area of around 12–22 %. In comparison, smaller EU Member States seem to have benefited somewhat more compared to larger countries. The estimated growth effects underline the case for further deepening and broadening the Single Market where possible.

1 Introduction

Thirty years after the ratification of the Single European Act, which created a common market for millions of European citizens, it appears that the benefits of the common European project are occasionally being questioned by some parts of the population. At the same time, others strive to further deepen European Union (EU) integration. Against this background, this paper reviews the growth effect of one of the most far-reaching steps of the European integration process, the creation of the European Single Market.

The paper revisits the growth impact of the European Single Market using the synthetic control method (SCM) developed by Abadie and Gardeazabal (2003), Abadie et al. (2010) and Abadie et al. (2015). To the knowledge of the authors, this is the first paper using the SCM to study the growth effect of the Single Market for the area as a whole and for a broad set of participating countries.

The creation of the European Single Market dates back to the early 1950s with the formation of the European Coal and Steel Community (ECSC) and the European Economic Community (EEC). The founding members of these organisations (Belgium, France, Italy, Luxembourg, Netherlands and West Germany) were seeking to increase the economic integration among participating countries. One of the core objectives of the EEC was the establishment of a common market offering the free movement of goods, services, people and capital within its borders. However, it proved difficult to reduce (intangible) barriers with mutual recognition of standards and common regulations, partially due to a lack of centralised decision-making. Thus, the failure to complete the European common market in the 1970s and 1980s limited further integration.

The process was re-initiated in 1985 with European Commission’s White Paper on Completing the Single Market with a list of requirements to achieve further integration. In an influential report, Cecchini et al. (1988) put forward a narrative of the economic necessities, channels and impact of creating a true Single Market. Following this, the Member States agreed on the Single European Act in 1986 which foresaw creating a common market by January 1993.

The Commission’s White Paper put forward around 300 harmonisation measures which were mostly focused on goods. However, further liberalisation directives in the area of services were added shortly after, most importantly related to facilitating competition in network industries (such as energy, telecommunication and transport services).

The countries forming the market from the beginning of 1993 were Belgium, Denmark, France, Germany, Greece, Ireland, Italy, Luxembourg, Netherlands, Portugal, Spain and the United Kingdom (UK). Later, the Single Market was extended through the accession of Austria, Finland, Liechtenstein and Sweden in 1995. Subsequently, all countries joining the EU have automatically become members of the Single Market. In addition, other countries, such as Switzerland and Turkey, have entered into special arrangements with the EU and participate in the Single Market, at least to some extent.

The assumed channels for higher growth were the elimination of trade barriers, the harmonisation of legislation and standards (also in the area of public procurement), and the effect of more forceful and consistent competition policies, and state aid rules. As Cecchini et al. (1988) note, those channels together provided the impetus for a large supply-side shock to the Community’s economy as a whole.

Those channels were assumed to be multiplied by the emerging economies of scale that firms could reap by tapping, not only the domestic, but also the other EU markets.

With the channels outlined above in mind, policymakers and academics also put the benefits of the European Single Market into concrete numbers. Under the chairmanship of Paolo Cecchini (Cecchini et al. 1988), the European Commission assessed the effect to be a one-off increase in income of Member States between 4.25 % and 6.50 %. By contrast, Baldwin (1989) calculated the growth impact to be at least double the size, more towards 13 %. In one of the scenarios, he stipulated the potential of a higher growth premium of up to 33 % if the innovation effect of a typical endogenous growth model would be realised to the full extent.

The large difference between the estimates mainly relates to the role of dynamic effects being explicitly accounted for in the latter and ignored in the former approach. The competitive pressure from market integration brought about by the European Single Market should be expected to have a positive impact on innovation and productivity of firms. Cecchini et al. (1988) do not, per se, reject the possibility of such dynamic effects, but they find them too difficult to measure. However, even irrespective of the dynamic impact, Baldwin (1989) suggests that Cecchini et al. (1988) have underestimated the static effect of the creation of the Single Market. This analysis gets some theoretical support from Khandelwal et al. (2013) who note that productivity gains from trade liberalisation are often far greater than models would predict as trade barriers are managed by inefficient institutions.

Our results suggest that the common market has created a significant growth impact for the group of members as a whole. On the country level, the results are heterogeneous and suggest that smaller Member States have benefited somewhat more from the creation of the Single Market. Of the larger countries, Spain stands out as having realised a significant growth premium, followed by the UK. By contrast, the three largest EU countries, Germany, France and Italy, did not benefit on a similar scale.

In addition to the estimates of the growth effect produced before the Single Market started, some papers have studied various aspects of the Single Market after its implementation. For example, Boltho and Eichengreen (2008) suggest that the EU GDP is about 5 per cent higher than it would be without the introduction on the Single Market programme, Ilzkovitz et al. (2007) simulate the total GDP effect of 1.96 to 2.18 % in EU25 countries, and in ‘t Veld (2019) estimates within a DSGE-framework an average of 8–9 % higher EU GDP in the long run.

There are some papers which are somewhat similar in scope, such as Campos et al. (2019) who use the SCM to measure the benefits of European integration and being part of the EU. Other methods have also been applied to study the impact of the Single Market. For example (Allen et al. 1998) and in ‘t Veld (2019) estimate the competition and trade effects in a DSGE-framework. Some studies specifically analyse the growth effect of the Single Market for individual member countries, such as Straathof et al. (2008) who find a 4–6 per cent higher income per capita for the Netherlands, or Dhingra et al. (2017) who looked at the possible welfare implications of an exit of the UK from the Single Market and find that incomes could drop by 6.4–9.4 %.

There are also several papers studying the impact of the Single Market on other economic variables that could impact growth. Allen et al. (1998) study the early effects of the Single Market and find significant reductions in price-cost margins. They conclude that the system had welfare increasing effects on all participating economies, although there is a large variance in the distributions across countries. Mayer et al. (2018) estimate an average trade growth effect of EU integration of 109 % in goods and 58 % for services, and in ‘t Veld (2019) estimates increases of 55 % for goods and 33 % for services. The positive welfare effect from trade liberalisation is also confirmed by Billmeier and Nannicini (2013), and Vermeulen (2021) notes a significant negative impact from remaining outside the Single Market for firms in border regions of Central and Eastern Europe.

The remainder of the paper is organised as follows: Sect. 2 introduces the synthetic control method and data underlying our analysis, Sect. 3 presents the main results for the Single Market as a whole while Sect. 4 reports on various robustness checks. Section 5 discusses the growth effect of the Single Market for individual countries. Section 6 concludes.

2 Methodology and data used

Measuring the realised effect of policy decisions is challenging as it requires the construction of a counterfactual. Without a counterfactual, it is difficult to disentangle the effect of the policy (i.e. the treatment) and other effects. An increasingly popular method of case study analysis is the synthetic control method (SCM) that calculates an explicit counterfactual which simulates how the unit of treatment would have developed in the absence of any treatment, or vice versa. We follow the SCM as originally proposed by Abadie and Gardeazabal (2003), Abadie et al. (2010) and Abadie et al. (2015) and suggested by Athey and Imbens (2017) to be “arguably the most important innovation in the policy evaluation literature in the last 15 years”.

The sample of $J+1$ countries includes the particular country of interest $j=1$ which will undergo a particular treatment in period $T_0$. The remaining set of countries $j=2,...,J+1$ are not impacted by the treatment and therefore are considered the control group. The notational focus on a single country being treated is without the loss of generality. Abadie et al. (2015) note that in cases where multiple units are affected by the event of interest, in our case the creation of the common European market, the method can be applied to each affected unit separately or to an aggregate of all affected units. Borrowed from the medical literature (Abadie et al. 2010) denote $j=1$ to be the “treated unit” while the remaining, non-treated countries provide the “donor pool”. For a proper identification, it is key that the donor countries are not driven by the same structural process and did not undergo a structural shock of the outcome variable in the post-treatment phase. For our analysis, we define the treatment units as the countries that formed the Single Market at the beginning of 1993.

The sample covers the time periods (in our case years 1964–2014) $t=1,...,T$, with a certain number of pre-treatment years (1964–1992), $T_0$, as well post-treatment periods (1993–2014), $T_1$, so that $T_0+T_1=T$. The treatment country 1, is exposed to the intervention during the years $T_0+1,...,T$. At the same time, the intervention did not have an impact on the pre-treatment years $1,...,T_0$. Given that most countries ratified the corresponding legal acts establishing the European Single Market by 1993, this leaves us with 30 pre-treatment years, a very long period by SCM standards (Abadie et al. 2015). The sample used in the study ends in 2014 which is two decades after the initial introduction of the Single Market.

The counterfactual non-treatment development is calculated with the help of the countries in the donor pool. We explain further below the selection of the donor countries. The synthetic control can be extracted from one or multiple countries in the donor pool. For the latter case, Abadie et al. (2015) define the synthetic control as a weighted average of the countries in the donor pool, mirrored by a $J\times 1$ vector of weights $W=(w_2,...,w_{J+1})'$ with $0\le w_j\le 1$ of $j=2,...,J+1$ and $w_2,...,w_{J+1}=1$. Following Mill (1848) and specifically the Method of Difference, Abadie et al. (2015) propose selecting the value of W such that the characteristics of the treated unit are best resembled by the characteristics of the synthetic control.

Accordingly, $X_1$ is a $(k \times 1)$ vector containing the values of the pre-treatment characteristics of the treated unit that we aim to match as closely as possible. At the same time, $X_0$ is the $k \times J$ matrix collecting the values of the same variables for the units in the donor pool. The pre-intervention characteristics in $X_1$ and $X_0$ may include pre-intervention values of the outcome variable. We select a synthetic control, $W^{*}$, that minimises the differences between the treated and synthetic control, i.e. minimising the vector $X_1-X_0W$.

For this, we need to identify appropriate covariates that match the pre-treatment characteristics of the treated unit as closely as possible. First, we borrow explanatory variables from growth accounting literature as well as from the seminal SCM-literature that also studied treatment effects on GDP per capita. Second, we use a validation technique, applying root mean squared prediction errors (RMSPE) that calculate the pre-treatment fit.

Overall, we follow Abadie et al. (2010), Abadie et al. (2015) and Adhikari et al. (2018) in selecting the right-hand-side variables. We use the capital stock, population and a measure of human capital to measure the capital and labour input, respectively. For the capital intensity, we also include the investment rate. To proxy for productivity, we use total factor productivity. Most of the variables are retrieved from the Penn World Tables (Feenstra et al. 2015). Given that we look at GDP per capita in log levels, the initial level is also essential for the match of donor to treatment countries. We therefore include real GDP per capita for the first year of our sample in the equation.

In the second step, factors outside the neoclassical growth model are included as they also have the potential to influence growth. We proxy those broader factors through indicators such as the institutional strength, regulation intensity, knowledge intensity or trade openness, as compiled by the Economic Complexity Indicator (Hidalgo et al. 2009) or the Fraser Economic Freedom Index.¹ We provide a list of all variables as well as their sources in Appendix A.

The conceptual approach outlined above can now be operationalised, defining for $m = 1,...,k$, $X_{1m}$ being the value of the m-th variable for the treated country and $X_{0m}$ the $1 \times J$ vector containing the values of the m-th variable for the countries in the donor pool. Abadie and Gardeazabal (2003) choose v and W to minimise

$$\begin{aligned} W^{*} = \sum _{m=1}^k\upsilon _m(X_{1m}-X_{0m}W)^2, \end{aligned}$$

(1)

with $\upsilon _m$ being the weight reflecting the importance that the model attributes to the m-th variable when establishing the difference between $X_1$ and $X_0W$.

Having calculated appropriate weights, the synthetic control estimator of the effect of the treatment is given by the difference of post-intervention outcomes in the treated country on the one hand and the outcome variables of the weighted donor pool of countries on the other, i.e.

$$\begin{aligned} Y_{1t}-\sum _{j=2}^{J+1}w_j^{*}Y_{jt}, \end{aligned}$$

(2)

with $Y_{jt}$ being the outcome variable of country j at time t and $Y_1$ being a $(T_1\times 1)$ vector collecting the post-intervention values of the outcome for the treated country. To study the growth effect of the Single Market for Europe, our variable Y is real GDP per capita. $Y_0$ would then be a $(T_1\times J)$ matrix, with columns j containing the post-intervention values of the outcome for country $j+1$.

Relating Eq. (1) and Eq. (2), it becomes clear that the matching variables in $X_0$ and $X_1$ are serving as the predictors of the post-intervention outcome. Factors unaccounted for in determining the outcome variables could, in theory, limit the validity of the results. Yet, Abadie et al. (2010) show that with a sufficiently large pre-treatment period, unobserved factors are controlled for in the matching of the pre-intervention counterpart $Y_0$ and $Y_1$. This follows from the intuition that countries that are similar in terms of observed and unobserved determinants of the outcome variables over a longer period of time, would only produce different trajectories if one of the two groups was affected by the studied intervention.

Abadie et al. (2015) also formally derive the close relation between SCM and standard regression techniques. Linear regressions, by contrast, do not restrict the weights of the linear combination to be between zero and one. Against this background, estimates of counterfactuals based on linear regressions may extrapolate beyond the support of comparison units to provide a perfect fit of the regression line with the data. While extrapolation beyond the support of the data is not necessary following the SCM, an interpolation bias could arise if the donor pool contains units with very different characteristics than the treated unit. This has been initially outlined by Abadie et al. (2010), and more recently formalised in Abadie and L‘Hour (2021) and Kellogg et al. (2020).

Against this background and given the above mentioned recommendation to apply a donor pool with roughly similar observed and unobserved determinants, it is advisable to limit the donor pool to countries with similar characteristics. This additionally controls for unobservable characteristics, for example, associated with the level of economic development and any other secular changes over time that might affect countries from different income groups differently (Adhikari et al. 2018).

Such precautionary measures help to ensure the validity of the results. This notwithstanding, Abadie et al. (2010) show that even if there is a synthetic control that provides a good fit for the treated units, interpolation biases could potentially still exist if the simple linear model above does not hold over the entire set of regions. Such nonlinearity between the outcome variables and the predictors could, for example, arise if the combination of two extreme donor units is used to construct a synthetic unit that has average value of the covariate. This provides a third argument to focus on donor countries with similar characteristics with the treated country.

Accordingly, we restrict the donor pool in the first step to OECD countries (that joined before 1994). This is to focus the set of potential donor countries to cases with similar income levels and thus reduce the likelihood of interpolation biases. In the second step, we remove countries which have undergone treatment, i.e. became members of the European Single Market in 1993 or at a later stage. Overall, this leaves Australia, Canada, Israel, Japan, New Zealand and the United States (USA) as potential donor countries. However, we show in Sect. 4 with a wide array of robustness checks, that even when we extend (or limit) the donor pool, our results remain qualitatively unchanged.

Abadie et al. (2015) elaborate in detail on the limitation for inference in comparative case studies, in particular given the small sample size, absence of randomisation and that probabilistic sampling is not employed to select sample units. However, inference can be undertaken through means of falsification exercises or so-called placebo experiments. Verifying the baseline model results through alternation of the intervention time, or attributing the intervention to countries in the donor pool offers two out of many ways to study whether the effects found are robust. For example, for the latter type of tests, each country of the donor pool would individually serve as a treated country. This creates a fan-chart type of distribution of placebo effects. In turn, the baseline results would be deemed robust in case the impact of the actually treated country falls outside or is squarely at the upper range of the placebo tests. We will conduct a two-level analysis, one for the aggregate and one for country-specific Single Market effects. For the former, we aggregate the country-specific variables by using population-weighted averages.

3 Results for the Single Market as a whole

In this section, we present the results of the growth impact for the Single Market as a whole. Before presenting the results we explain the weight and values of the variables as well as the countries chosen for the control group.

Table 1 Predictor balance

Table 2 Covariate selection for synthetic unit

Table 1 lists the mean values across indicator and time for the two groups of interest. The level of log real GDP per capita is very close, and the same holds for TFP, the share of investment in GDP, openness to trade and the Economic Freedom index. Differences across the mean value of the change in population, human capital, the Economic Complexity indicator and the capital stock between treated and synthetic group are somewhat higher.

The differing values are also reflected in the actual weight that the SCM allocates to the respective covariates (Table 2) in the benchmark model. The openness to trade and the Economic Freedom index (the latter summarising the similarity of economic structures and institutions) have the largest weight. TFP performance, the share of investment in total GDP and the real GDP per capita also contribute with significant weight. The human capital variable only plays a marginal role, while zero weight is attached to the capital stock, which is most likely because of its strong relation to the share in investment, and the Economic Complexity Indicator.

As discussed in Sect. 2, the set of control countries is limited to similarly developed countries as suggested by Adhikari et al. (2018) and Abadie et al. (2015), i.e. all countries that were members of the OECD at the time of the creation of the Single Market and were not part of the market (directly or per third-country agreement). This leaves Australia, Canada, Israel, Japan, New Zealand and the USA.

The SCM calculates the country weights to minimise GDP per capita of the treated country over the pre-treatment period using the root mean squared prediction error (RMSPE) as the criterion. Table 3 lists the weights chosen by the SCM for the benchmark model. The USA, Israel and Japan carry the highest weight, while Australia only adds a fraction to the aggregate time series of the group and New Zealand and Canada carry zero weight.

The choice of covariates and country weights for the generation of the synthetic control group is essential for the outcome of the counterfactual that, in turn, is the basis for the calculation of the effect of a respective policy choice. In the light of the crucial importance of covariates and countries chosen, the robustness of results needs to be proven by showing to which degree the results are sensitive to changes in both the set of variables and control countries. We will demonstrate extensive robustness checks in line with the standard approaches in the literature in this section and Sect. 5.

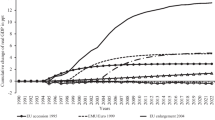
According to our baseline results, the European Single Market has created a significant growth-enhancing effect for its member countries. Figure 1 depicts the aggregate GDP per capita of the countries that joined the Single Market at its inception in 1993. The pre-treatment fit of the counterfactual to the treatment group in terms of GDP per capita from 1964 until 1992 is rather close (the pre-treatment RMSPE is very low with 0.0034), in particular taking into account that we use an exceptionally long pre-treatment period of about 30 years.

Table 3 Donor country weights

Fig. 1

The growth effect for the aggregate Single Market area

The vertical line in Fig. 1 denotes the entry into force of the large set of directives that formed the common market in January 1993. It becomes evident from this chart that a few years after the start of the Single Market, both curves deviate significantly. Given that the lines are denoted in log of real GDP per capita, the distance between the two lines can be taken as the accumulated or medium-term growth impact of the Single Market. At the end of our sample, in 2014, the growth impact has been 20.8 %. This is constructed by comparing the Single Market area’s GDP per capita and the synthetic control groups GDP per capita in 2014 and computing the growth differential.

However, it is important to review how long a reasonable post-treatment period is. In principle, there is no limit assuming that the structural process governing the two series remains the same. This means assuming that no major idiosyncratic event affecting only one of the two time series has taken place beyond the studied policy treatment. Of course, the more time elapses after the treatment, the more difficult it becomes to exclude that the structural processes started to differ, namely that either the treatment country or the donor group is affected by factors which the other group is not (or not very differently) impacted by. A prominent example of a common shock with vastly different impacts on countries has been the Global Financial Crisis and the ensuing euro area sovereign debt crisis. While the crisis impacted nearly all countries worldwide in 2008, the decline in output was very heterogeneous between different countries.

Against this background, it might be more prudent to stop the evaluation exercise in 2008, i.e. about 15 years after the implementation of the Single Market. This is in line with the length that Abadie et al. (2010) and Abadie et al. (2015) chose in their seminal papers. Focusing the effect of the Single Market on the time span from 1993 to 2008 yields an accumulated effect of around 22 %. While this is the result of the baseline model, we will conduct a number of robustness and sensitivity checks.

4 Robustness tests

Before studying the country level differences in terms of growth effects, we look at a battery of sensitivity checks that should allow an assessment to what extent the above mentioned growth effect measured in the baseline model is robust to chosen assumptions.

Alternative approaches, complementing the SCM, could also serve as useful cross-check. In an earlier version of the paper, Lehtimäki and Sondermann (2020), we conduct a sensitivity analysis employing difference-in-difference estimations, which show qualitatively similar results when compared to our SCM baseline estimations. In this paper, by contrast, we focus on a larger set of robustness checks within the model environment offered by the SCM.

The most critical assumptions are the choice of control countries, the covariates used and the timing of the policy treatment. The choices taken for the latter two are particularly important to cross-check in case of possible anticipation effects. Such anticipation effects have arguably been present given that the Single European Act had to be negotiated and included a multi-year implementation period.

Fig. 2

Start year of the Single Market

We start with robustness checks as regards the timing of the policy treatment. The Single Market formally went into force in 1993. This was the year from which onwards the largest set of directives were in place. However, as the common market evolved up to the agreed starting point in 1993, the actual project started much earlier, e.g. with the Single Market Act in 1986, and thus could already have had an effect prior to 1993. We aim to test to what extent the magnitude of the baseline effect depends on the specific year chosen as the treatment year. Figure 2 depicts the effect for different starting years. It suggests that the baseline results with the year 1993 are overall rather prudent. Choosing the year 1987, 1988 or 1989 would even result in somewhat higher growth effects whereas using 1990, 1991 or 1992 would result in similar or slightly lower growth impact.

The variation of starting years in the proximity of the treatment year, however, is not to be mistaken with the classical in-time placebo tests as presented in Abadie et al. (2015), who suggest to test the robustness of the main results by bringing forward the placebo treatment year into the pre-treatment period and end the placebo post-treatment period when the actual treatment took place. We also undertake such a proper in-time placebo test and show the results in Fig. 3. Assuming the treatment would have taken place in 1980 (instead of 1993) does not yield a positive growth dividend of the treated versus the non-treated countries, but instead sees rather similar behaviours of the lines.

The second type of robustness test relates to the covariates applied. Covariates should ideally be unaffected by anticipation effects and thus be exogenous to the event. While most policies do not substantially impact the drivers of economic growth and there were very few significant policies undertaken in the years preceding the official start of the Single Market in 1993, some of the covariates (in particular TFP and Economic Freedom Index) may be affected by the policies and reforms which took place between the negotiation of the Single European Act around 1986 and the final implementation towards the end of 1992.

Fig. 3

In-time placebo

Against this background, we test how sensitive the results are to changes in the set of covariates by removing critical variables such as TFP, Economic Freedom, or the capital stock. In Fig. 4, we check to what extent individual variables are significantly determining the final results by iteratively removing one variable from the set of covariates. This also allows the SCM to reallocate weights among the remaining variables, thus giving more space to variables which might have been dominated by others in the baseline model. Figure 4 suggests that altering the set of covariates only marginally affects the synthetic control line, i.e. the counterfactual, non-Single Market scenario. The line most distant from the baseline is the counterfactual without the Economic Freedom indicator. Here the cumulative growth impact in 2008 falls to 16 %. The only covariate that cannot be easily changed is the starting level of GDP per capita. Removing this covariate from the equation would cause the loss of an important anchor for finding a common starting position. The key importance of this is also underpinned by the literature selecting a priori countries with similar income levels to ensure an unbiased comparison (e.g. Abadie et al. 2010, Abadie and L‘Hour 2021 and Kellogg et al. 2020) as discussed in Sect. 2.

The third type of sensitivity check relates to the choice of countries in the donor pool. As noted in Sect. 2, the SCM is sensitive to interpolation biases, among others by defining countries to be similar although they are structurally not comparable. It is thus important to use countries with similar levels of GDP to reduce the likelihood of such biases. This notwithstanding, the set of donor countries should not be too small as it otherwise constrains the searching for optimal weights to construct the counterfactual. The selection of the 6 donor countries for the baseline model is well-motivated to avoid interpolation biases, mainly by selecting similarly developed countries with not too different GDP per capita starting positions (as done in Adhikari et al. (2018)).

However, we want to show that adding more countries to the donor group leaves the results qualitatively unchanged. We add a further four countries, namely Argentina, Brazil, Chile and Mexico. Those countries are considerably less developed (in terms of GDP per capita), yet still closer to the average GDP per capita than other countries that would remain available as potential control countries. Running the SCM with these additional countries gives the algorithm more degrees of freedom to choose other countries outside the ones picked in the baseline model. The initial selection of donor countries is supported as only Brazil would receive a small contribution in the creation of the donor group, while the other additional donor countries would not be considered relevant. Figure 5 displays the result with the larger set of donors with the overall picture unchanged and the overall growth dividend to arrive at a cumulative 17 % higher GDP per capita in 2008 compared to the counterfactual.

Fig. 4

Changing covariates

Fig. 5

Enlarging the set of donor countries

Fig. 6

Reducing the set of donor countries

Another way of showing the robustness of the results is by forcing a sub-set of the original donor countries (see Fig. 6). Klößner et al. (2018) argue that many robustness checks in studies done with the SCM are driven by the USA. In our study, the SCM applies the highest weight in the baseline model to the USA, Israel and Japan. Australia, Canada and New Zealand receive a weight close to or exactly zero. When iteratively removing one of the countries, the SCM reassigns the weights in the donor pool. In particular, removing the USA and Israel somewhat changes the counterfactual, bringing the cumulated growth impact down to 12 % and 15 %, respectively. In all robustness checks in Fig. 6 the counterfactual line remains clearly and significantly below the GDP per capita of that of the Single Market countries. Moreover, it should be noted that excluding potential donors or covariates could reduce the pre-treatment fit. Thus, while such sensitivity checks are plausible and informative, they tend to constrain the potential of the SCM to find the best fit to the treated unit.

Fig. 7

Placebo treatment

One additional common and crucial test of the validity of the method is the use of “in-space placebos”. As elaborated in Sect. 2, Abadie et al. (2015) suggest that inference can be undertaken through means of falsification exercises or placebo experiments. The idea is to randomly test whether the effect would be similar if a non-treated country from the donor pool would be considered to be the alleged treated country. The growth effect of the SCM using the actual treated country should be systematically higher than that of the placebo-treated countries. We apply the same logic to the Single Market case by iteratively using another country from the donor pool as the treated country. We use the extended donor pool from the robustness check above, i.e. the ten countries to allow for a greater number of control cases. Figure 7 displays the effects derived under the different models. The effect is the difference of log GDP per capita between the treated countries’ GDP and the counterfactual built from the remaining donor countries. The figure reveals that the Single Market effect stands out from the placebo effects, confirming the robustness of the baseline results. At first glance, it seems that two countries, Argentina and Chile have a higher growth dividend although they have not received the treatment. Yet, when looking at the pre-treatment fit, it becomes clear that both countries do considerably worse than most other control cases in matching the control group. As noted by Abadie et al. (2010), the pre-treatment fit is essential to ensure that the growth gap between the real and the synthetic unit has not been artificially created by lack of fit. Similarly, in this placebo test the better performance likely stems from an insufficient fit pre-treatment.

In evaluating the in-space placebo, Abadie et al. (2010) and Abadie et al. (2015) suggest the ratio between the post-treatment RMSPE to the pre-treatment RMSPE as an indicator for the degree of pre-treatment fit. Figure 8 displays the ratios for all placebos and the true treatment group. The true Single Market area stands out in comparison to the other countries, and thus confirms the robustness of the baseline results. An important caveat of in-space placebos is that it becomes more powerful when more placebo countries are added to the test. Yet, given the desire to avoid interpolation biases as explained earlier, we stop with ten control countries out of which the SCM can select. This is not an unusually small control group and is comparable to studies like Abadie and Gardeazabal (2003), Abadie et al. (2015) or Puzzello and Gomis-Porqueras (2018).

Fig. 8

Ratio of Post-treatment RMSPE to Pre-treatment RMSPE: Single Market area and Control Countries

Reviewing again the baseline effects shown in Fig. 1, it seems that the growth effect of the Single Market took some time to unfold. In particular in the initial years, perhaps up to the end of the century, the growth effect was rather small. As the growth effect gradually increased, another important event happened in Europe: the introduction of the euro as common currency for some of the countries that formed the Single Market. It is therefore important to exclude that the effect captured in Fig. 1 is formed by the introduction of the common currency instead of the Single Market.

Fig. 9

Euro effect

Luckily, it is straightforward to test this in our context as only a sub-set of the Single Market countries joined the euro area. This allows us to test within the SCM environment whether euro area Single Market countries saw a higher growth effect than non-euro area Single Market countries. The treated country group thus excludes the non-euro area countries which are moved into the donor pool of countries next to the other non-EU OECD countries that formed the pool so far.² Figure 9 depicts the effect the euro had on the aggregate set of Single Market countries that joined the common currency. The results indicate that there has been no clear growth effect from the introduction of the single currency for the overall group of countries when compared to the counterfactual. This finding is in line with the literature that aims to measure the growth effect of the euro introduction (Fernández and García Perea (2015) or Puzzello and Gomis-Porqueras (2018)). This confirms the baseline results likely identifying a growth effect caused by the creation of the Single Market rather than the common currency.

Outside the adoption of the euro, the growth dividend could also be driven by other steps of European integration which happened in proximity to the inception of the Single Market. The Maastricht treaty signed in 1993 foresaw that countries interested in joining the common currency needed to comply with quantitative benchmarks in relation to fiscal variables (deficit and debt), as well as inflation and exchange rate behaviour. The Maastricht treaty could therefore have boosted confidence and reduced risk perception in the signatory countries and contributed to growth in particular in countries with adjustment needs in the 1990s. Reduced macroeconomic volatility, e.g. lower inflation and interest rates, might have facilitated financing and investment conditions. We explicitly check for the relevant convergence criteria as additional covariates to see whether they reduce the Single Market implied growth dividend observed in our baseline results. We do so in two separate estimations. Figure 10 adds inflation and interest rates to the covariates. Estimated results are qualitatively similar compared to the baseline results, but the growth dividend is somewhat smaller at 18 % compared with the 22 % identified for the baseline results. Similarly, adding inflation and debt as covariates reduces the growth dividend to 17 %. While this is very close to our baseline results, the slightly lower growth dividend might suggest that some part of the growth captured by the Single Market baseline model could (also) be attributed to the confidence-enhancing and stabilisation promoting effect of the Maastricht convergence criteria.

Fig. 10

Baseline model with inflation and interest rates

Fig. 11

Baseline model with inflation and inflation and government debt

Another, and final, cross-check refers to countries’ fiscal policies before and after the treatment. Countries could potentially have shown rather similar growth patterns before the treatment, but an exogenous policy shock in one or multiple treatment countries might have resulted in significantly more accommodative fiscal policies than before the treatment and thus be the main determinant of the growth premium compared to the control group. We take a look at the government expenditure of countries in per cent of GDP before and after the treatment to verify this hypothesis. Figure 12 depicts two lines, government spending of the treated and the control group. While there is a level difference between the two groups, it is not meaningfully different between pre-treatment and post-treatment, in turn supporting the baseline results.

To summarise, reviewing the growth effect of the creation of the European Single Market seems to have significantly raised real GDP per capita for the area as a whole. The baseline suggests a long-term growth premium of up to 22 % in 2008. Even when manually constraining the SCM parameters, and therefore restricting the model’s choice to find the best fit to the treated unit, the lowest overall growth estimates do not fall below 12 %.

Fig. 12

Government expenditure paths before and after the treatment

5 Results for individual countries

The Single Market area covers a large set of countries. In the previous section, we have shown that the creation of the common market had a significant growth effect for the area as a whole. In this part of the paper, we want to go more granular and study the growth impact for the individual countries. We focus on the countries that joined the Single Market at the beginning for ease of comparison.

For each of the countries, we not only display the baseline results, but also a battery of robustness checks. Specifically, we let the model iteratively go through any possible combination of covariates and donor countries and produce one synthetic counterfactual for each scenario. This has been mainly done, as explained for the case of the aggregate, to test whether leaving out covariates that might be affected by anticipation effects would change the results. As explained in Sect. 4, variables like TFP growth might be affected by anticipation of measures in the realm of competition policies before the start of the Single Market. With the nine covariates listed in Table 2, we arrive at a possible set of 255 combinations. For the six donor countries, we can study 63 different combinations of control countries. In order to not overburden the reader with too many charts, we transform the set of 318 counterfactual time series into fan chart format. The fan chart will show the benchmark counterfactual, the 25th and 75th percentile as well as the 10th and 90th percentile of all the synthetic counterfactuals.

Looking across all figures showing country-specific results, in Figs. 13, 14, 15, 16, 17, 18, 19 and 20, it becomes evident that all countries experienced a positive growth impact through the creation of the Single Market up until 2008. This can be taken from the fact that all country-specific GDP per capita lines are above the full interval of counterfactuals at the brink of the financial crisis. However, there is stark heterogeneity among countries. Table 4 displays the growth impact from 1993 to 2008 across all countries.

Table 4 Single Market growth impact of individual countries

As described with regards to the baseline results for the aggregate Single Market area, the results in Table 4 are constructed by comparing the country’s GDP per capita to the GDP per capita of the synthetic control groups at the end of the sample and computing the growth differential. Given that the lines are denoted in log of real GDP per capita, the distance between the two lines can be taken as the accumulated or medium-term growth impact of the Single Market. The most significant gains are found for Ireland, Spain, Netherlands and Portugal, all with above 30 % increase in real GDP per capita up until 2008 compared to a hypothetical country that remained outside the Single Market.

Fig. 13

Single Market effect Ireland

Greece still realised a growth premium around 20 %, followed by the UK. By contrast, in particular Germany, France and Italy gained less with cumulated growth differentials of around 10 %.³

Fig. 14

Single Market effect Netherlands

Fig. 15

Single Market effect Portugal

Fig. 16

Single Market effect Spain

Fig. 17

Single Market effect UK

Fig. 18

Single Market effect Greece

Fig. 19

Single Market effect Belgium

Fig. 20

Single Market effect Denmark

Table 4 shows the cumulative growth effects for the entire period and broken down into two periods. The breakdown shows that most of the countries reaped most of the benefits of the common market in the second half of the sample. Aside from specific country factors, the general trend could be related to the slow de facto implementation of the Single Market as in the initial phase several countries lagged behind in terms of full transposition of measures into national legislation.⁴

In terms of main beneficiaries from the Single Market programme, looking at Table 4, it becomes clear that that smaller, more open countries have benefited more from establishing a common market. This is in line with the study, for example, by Scitovsky (1960), who argues that international trade can offset the disadvantages of small size. As such, trade liberalisation leading to reduced trade barriers helps firms in smaller countries as they are no longer disadvantaged by small home markets (Aiginer and Pfaffermayr 2004). By establishing one common market, small countries get access to production factors, such as capital and high-skilled labour, from other EU partner countries. Due to the expectation of higher marginal returns, incentives for investment and migration increase. The benefits are not restricted to producers, as consumers in small countries would also likely gain welfare through access to a larger variety of goods than was available before the integration process.

Figure 13 displays the effect for Ireland. The pick-up in real GDP per capita in Ireland since the inception of the Single Market stands out compared to other countries. It seems unlikely that such a high figure could be completely due to a higher trade and/or competition effect. For Ireland, a number of factors probably came together that are captured in the overall growth effect. Having been an already very open and flexible economy, Ireland was best prepared to benefit from the increased opportunities to export. Moreover, and probably most importantly, many multinational companies over the years used the low-regulation, low-tax environment on the island to shift parts of their production there. Other studies (e.g. Aiginer and Pfaffermayr (2004) or Campos et al. (2019)) have also found that Ireland (as well as Portugal) has experienced a particularly positive effect from integrating into the common European market.

Similarly, positive growth effects have also been found for Portugal and the Netherlands. Both countries are rather small open economies which depend on trade and for which the creation of the common European market established a much larger market to serve. Figures 13, 14 and 15 highlight that the fan chart, containing hundreds of counterfactuals, is clearly far below the real GDP per capita increase in Ireland, Portugal and the Netherlands.

For the larger countries, the growth effect of Spain stands out. Figure 16 suggests that the Single Market unfolded a positive growth effect in the first years and then extended it in the early 2000s. This is in line with Siotis (2003) who finds that economic integration led to a particular adjustment of margins and an increase in competitive pressure in Spain. He notes that in addition to the Single Market programme, Spain was in parallel embarking in major domestic reforms, basically being in a thorough political transition from the dictatorship that ended in the 1970s and with the previous economic system being progressively dismantled. Another factor that might be captured in the very positive growth effect is the contribution from structural and cohesion funds that Spain benefited from, in particular when entering the Community. It cannot be excluded that these “confounding treatments” might have impacted the growth dividend derived from the synthetic control method and that we primarily ascribe to the Single Market programme.

As shown in Fig. 17, the UK also seems to have built up a clear growth differential that can be linked to the Single Market. All different combinations of donor countries and covariates confirm this with a clear difference to the real GDP per capita series of the UK. Only towards the end of the sample, a few counterfactuals diminish the returns of the Single Market to some extent. Campos et al. (2019) also find a significant growth impact from European integration, although for a different time horizon.

Fig. 21

Single Market effect Germany

Fig. 22

Single Market effect France

Fig. 23

Single Market effect Italy

Similarly, looking at Fig. 18, Greece seems to have profited from the entry into the common market with a growth differential of around 19 % compared to the scenario in which the country would not have joined. For Belgium (Fig. 19) and Denmark (Fig. 20), the synthetic control estimator does not show any growth premium in the first years, but only from the mid-2000s.

The growth effects are even less clear for the larger countries, in particular for France, Germany and Italy. Figures 21, 22 and 23 document that the countries’ realised GDP per capita development exceeds that of the scenario without the Single Market only towards the very end of the sample. Even if the baseline counterfactual is comfortably below the real GDP per capita of the respective countries, the fan chart sometimes comes close to that line. This suggests increased model uncertainty with the estimated growth rates contained in Table 4 to be the ceiling while the floor is often closer to half of the estimates at best.

Fig. 24

The share of industry in total economy value added. Source: Eurostat

Another hypothesis that could explain different growth dividends across countries is the possible role of comparative advantages or sectoral specialisation before the treatment occurred. One could argue that countries with a dominant goods’ producing sector might have benefited more from the Single Market programme, which was predominantly focused on goods, while harmonisation of services did not play a similarly important role. Figure 24 displays the share of an economy’s industry value added in total value added in 1995.⁵ Some countries, like Ireland, are at the top of the ranking, lending support to this hypothesis. Yet, an even larger group of countries with rather small growth effects, as documented in this chapter, had industries of similar size on the year of interest, most notably Germany or Italy. While the share of the good-producing industries is not able to explain most of the differences in growth, it has likely paved the way for the smaller countries to reap the benefits in the years of opening markets.

On a different note, it is important to also look into specific country developments to carefully examine whether the SCM approach holds. A particular case is Germany. When describing the assumptions underlying the SCM in Sect. 2, we highlighted that the validity of the results hinges on the two series (the treated and the counterfactual) to follow the same structural process since the treatment. For example, any shock occurring to any of the two groups in the proximity of the treatment should also affect the other group to a similar extent. However, Germany has been substantially affected by another path-breaking event exactly in the years of the creation of the Single Market, namely the German unification.

One of the seminal papers on the synthetic control method specifically studied the economic impact of the German unification on West-Germany. Abadie et al. (2015) find that the German Unification led to around 8 % lower GDP per capita for West-Germany up until 2003 compared to a synthetic Germany without the reunification. It is thus likely that Fig. 21 captures both the positive effect of the Single Market as well as the negative effect that arose from the reunification.

Overall, many smaller countries seem to have been able to better reap the benefits of the common market compared to the larger EU countries. Our finding is in line with the hypotheses and results in the literature. Aiginer and Pfaffermayr (2004) argue that following the Single Market, a process of deconcentration dominated and this led to declining market shares of large producers and countries while smaller countries gained market shares. They specifically single out Ireland and Portugal as countries which benefited from the process and increased their market share. In addition, the authors find that this effect is not only confined to existing firms, but that also start-ups were promoted as firms were no longer disadvantaged by small home markets. Moreover, multinationals also played a role as they made use of the common market and predominantly channelled funds into smaller countries. Allen et al. (1998) and in ‘t Veld (2019) confirm this hypothesis in stating that the smaller economies in Europe experienced the most significant welfare gains. In addition, König (2015) establishes that smaller Member States should grow more quickly the further the common market integration progresses and that countries with lower initial income tend to grow faster. Mohler and Seitz (2012), in turn, estimate the welfare gains from increased product variety. While this is certainly not reflected in the GDP per capita figures we look at, it is noteworthy that they also come to the conclusion that the small and open economies benefited the most.

Overall, our results are in line with the existing literature. Campos et al. (2019) is the closest in terms of methodology as they also apply the SCM, but concentrate on the benefits of EU membership and use a different set of countries and time periods. In line with our results, they find a positive impact from EU membership, in particular for the smaller EU countries. However, in contrast to our results, they do not find a significantly positive impact for Greece. In addition, they do not analyse the effect on the largest three EU countries, Germany, Italy and France, and therefore a full comparison to our results is difficult. They conclude that in the absence of the economic and political integration process, per capita European incomes would have been, on average, 12 per cent lower.

Allen et al. (1998) and in ‘t Veld (2019) use DSGE models to study the question of the welfare effects of the European Single Market. The advantage of these papers is that they are able to explicitly model different channels through which the common market affected incomes in the EU. More specifically, they distinguish between trade and competition effects. in ‘t Veld (2019) estimates the economic benefits of the Single Market to be, on average, around 8–9 % of GDP for the EU. With this estimate, the author arrives above the original estimates of Cecchini et al. (1988) and comes close to the mid-point of the range estimated by Baldwin (1989). With 12–22 % growth impact, our benchmark results are somewhat higher for the aggregate.

6 Conclusions

The creation of the European Single Market has been a cornerstone of the European integration process. As the integration process has advanced, arguments and uncertainties about the advantages of EU membership arise on a regular basis with some questioning the benefits while others contemplate further integration. In this context, it seems worthwhile to empirically study the growth effects of the introduction of the common market.

We use the synthetic control method developed by Abadie and Gardeazabal (2003) and Abadie et al. (2010) as it is an ideal tool for undertaking comparative case studies and therefore also the creation of the common market.

We find that the Single Market has raised real GDP per capita by around 12-22%. This estimate describes the growth premium that the founding Single Market countries realised compared to a hypothetical counterfactual scenario in which the common market was not created. This is broadly in line with the results of Baldwin (1989), who estimated a growth effect of around 13 % in the baseline scenario, but sees the possibility of up to 33 % growth premium.

We demonstrate with a large battery of robustness checks that the results of the benchmark model hold. We turn all parameters of the SCM upside down by varying the set of donor countries and covariates. We implement in-space and in-time placebo estimates as well as check other hypotheses (e.g. the common currency effect or the Maastricht effect) and find that the results remain robust.

On the country level, our results suggest that smaller Member States have benefited somewhat more from the creation of the Single Market. In line with related studies, those countries likely realised the largest relative increase in market access and profited from the reduction of market power of larger producers in larger Member States. However, the effects are also heterogeneous among smaller Member States. Of the larger countries, Spain stands out as having realised a significant growth premium. The UK has also realised significant growth from having access to the common market. By contrast, the other three largest EU countries, Germany, France and Italy, did not seem to have benefited to a similar degree.

Going forward, the potential of the Single Market to increase the income of its members becomes all the more evident when acknowledging that the Single Market remains incomplete. Various studies (e.g. Monti 2010 or Mariniello et al. 2015) suggest that the Single Market has not yet been applied to the full extent. On one hand, this relates to the countries not having fully applied the EU directives. On the other, the Single Market has been predominantly focused on goods, while the Single Market for services has not yet achieved the same prominence.

The results of the paper, thus, make a case for a further integration through deepening and widening the Single Market where possible and desired by Member States.

Appendix: A description of the dataset

Table 5 Dataset