1 Introduction

The question of what moves asset prices has been at the forefront of the financial economics agenda for the past four decades. A strand of the literature has focused on investigating to what extent asset prices respond to the surprises contained in scheduled macroeconomic announcements. The rationale is that these news releases are likely to convey relevant information to investors about how the cyclical dynamics of the economy may affect the cash flows of listed companies, discount rates, and monetary policy reactions, and consequently they are expected to trigger immediate asset price responses that the econometrician tries to identify. Notwithstanding the large number of studies in this area, this line of research has enjoyed fluctuating fortunes. Studies of stock returns and exchange rates, in particular, have produced mixed results, and the consensus appears to be that very few types of announcement exert a significant influence on them.

The present paper adds to this growing corpus of knowledge by investigating the impact of UK macroeconomic surprises on the UK’s financial markets using data at a daily frequency. We make two main contributions to the literature. First, ours is the first study to jointly analyse the responses of the stock market, the foreign exchange market, the Treasury bond market, and the corporate bond market to scheduled macroeconomic announcements. With few exceptions, previous studies typically focused on a single market, which represents a serious limitation given that, as prior research has advocated, ‘only by considering jointly asset prices that should be differentially affected by updates in different state variables can our understanding of announcement effects be sharpened’ (Faust et al. 2007).Footnote 1 Second, we shed more light on the time-varying nature of market participants’ responses to macroeconomic surprises. While previous literature has shown that the response coefficients vary between states of the economy (e.g. McQueen and Roley 1993), we posit that their time-varying nature has not been fully explored yet. More specifically, based on a number of rational and behavioural arguments, we hypothesize that investors’ reactions to macroeconomic surprises are also moderated by the state of the stock market. For example, if investors believe that the central bank takes stock prices into account when setting its monetary policy (e.g. Rigobon and Sack 2003; Botzen and Marey 2010), they may assume that its reaction to a macroeconomic surprise depends on the state of the stock market, in turn leading to asset price responses that are contingent on the equity market regime. A second possible explanation borrows from the behavioural finance literature. Investor overconfidence and the so-called disposition effect are among the most widely investigated phenomena in this field, and both have been argued to cause market prices to underreact to public information (Frazzini 2006; Daniel et al. 1998). Since the intensity of these two behavioural biases varies between stock market regimes (Gervais and Odean 2001; Cheng et al. 2013), they provide another plausible mechanism for our hypothesis.

Our results are for the most part consistent with standard economic theory. A large number of announcements increase trading activity (number of shares traded, turnover, number of trades) in the stock market, which indicates that they do provide valuable information that leads market participants to revise their expectations and trade accordingly. Macroeconomic surprises concerning retail sales, claimant count rate, GDP, and industrial production have the most prevalent effects across the four markets that we examined. Our estimates reveal two general patterns: surprises suggesting a stronger-than-expected economy increase stock returns, lead to an appreciation of the domestic currency, make the yield curve steeper, and reduce the corporate credit quality spread; surprises indicating higher-than-anticipated inflation cause the home currency to appreciate and increase the slope of the yield curve. The first pattern is consistent with the interpretation that a stronger economy is expected to have a positive impact on companies’ net cash flows; both patterns are in line with the view that rising output and/or inflation are expected to trigger a monetary tightening reaction by an inflation targeting Bank of England. Our results also provide support for the hypothesis that the effects of some macroeconomic surprises vary not only between states of the economy but also between stock market regimes. More specifically, our estimates tend to be consistent with the interpretation that investors expect the central bank to react differently to a macroeconomic shock in a bull market than in a bear market. Lastly, we found only very weak evidence that macroeconomic announcements and surprises affect the volatility of asset prices.

The structure of the paper is as follows. Section 2 reviews the relevant literature. Section 3 gives an overview of the expected effects of macroeconomic news on asset prices. Section 4 develops the hypotheses under scrutiny. Section 5 describes the data set. Section 6 explains our methodology. Section 7 presents the empirical results, Sect. 8 discusses the results, and Sect. 9 concludes.

2 Literature review

Since the beginning of the 1980s, the question of whether and to which extent macroeconomic variables influence the dynamics of financial markets has been the subject of increasing interest and scrutiny. However, the majority of the investigations in this area has focused on the US market. With regard to the stock market, early studies typically found that asset prices are influenced by inflation and monetary surprises (Schwert 1981; Jain 1988; Pearce and Roley 1985; Flannery and Protopapadakis 2002), whereas support in favour of the role played by news concerning the real side of the economy has been weak (Hardouvelis 1987; Du et al. 2012). In an attempt to explain the mixed evidence on the subject, a stream of this literature has investigated whether the response of stock returns to macroeconomic news is conditional on the state of the economy. While some authors have uncovered evidence that the reaction of the stock market to surprises in inflation, monetary aggregates, and real activity is different during economic expansions than during contractions (McQueen and Roley 1993; Adams et al. 2004; Boyd et al. 2005), others have found none (Poitras 2004). With regard to the UK market, the question of the state dependence of stock price reactions to macroeconomic surprises has been largely ignored. Additionally, most of the studies employing monthly or daily data have focused on a subset of announcements related to money and prices, while real sector variables have been mostly overlooked. With a few exceptions (MacDonald and Torrance 1987; Joyce and Read 2002), these studies have generally detected a systematic relationship between inflation and money surprises and UK stock returns (Gultekin 1983; Goodhart and Smith 1985; Peel and Pope 1985, 1988; Bredin et al. 2007; Gregoriou et al. 2009). Though, more recently, some studies of the UK stock market have employed high-frequency data, they have mostly focused on the volatility of the returns on FTSE 100 futures contracts (Gwilym et al. 1998; Buckle et al. 1998; Jones et al. 2005) rather than on mean returns (Becker et al. 1995). Furthermore, they have predominantly analysed how volatility responds to macroeconomic announcements, per se, rather than to macroeconomic surprises, the typical finding being that volatility rises in response to macroeconomic announcements.

As for our second variable of interest, most of the literature that has examined the impact of scheduled macroeconomic announcements on the foreign exchange market has focused on a single bilateral exchange rate or on a small set of bilateral exchange rates, typically against the US dollar. Early studies employed data at daily frequency. The initial findings suggested that exchange rates react to money supply surprises (Hakkio and Pearce 1985; Ito and Roley 1987; Hardouvelis 1988), but subsequent studies also found evidence of a significant role played by real economic activity indicators such as retail sales and durable goods (Hardouvelis 1988), trade balance (Hogan et al. 1991; Aggarwal and Schirm 1992; Hogan and Melvin 1994; Edison 1997; Kim 1998), employment (Harris and Zabka 1995; Edison 1997; Kim 1998), and GDP growth (Kim 1998). More recently, Simpson et al. (2005) documented that surprises concerning consumer demand, inflation, and interest rates have a significant effect on a set of bilateral exchange rates against the US dollar, while Hayo and Neuenkirch (2012) found that both monetary and real activity (employment, industrial production, current account balance) surprises influence the CAD/USD exchange rate. During the past twenty years, the use of high-frequency data has produced further insights. Almeida et al. (1998) argued that the direction of the DEM/USD exchange rate responses is consistent with the view that investors try to anticipate the likely reactions of monetary authorities to macroeconomic surprises. Other authors have documented that the US dollar tends to appreciate against other major currencies in response to stronger-than-expected news about the US economy (Andersen et al. 2003; Faust et al. 2007; Pearce and Solakoglu 2007). A common finding has been that, besides affecting the conditional mean of exchange rate returns, surprises concerning several macroeconomic indicators also increase their volatility (Andersen and Bollerslev 1998; Laakkonen 2007); however, these effects are short-lived, as the adjustment process takes only a few minutes.

Likewise, the reactions of Treasury bond prices to macroeconomic surprises have attracted considerable attention from researchers. Owing to the fact that the latter affect the former only through their impact on discount rates, in this area there seems to be a fair amount of consensus in the literature, and at least with respect to the US market, ‘the stylized facts of how the yield curve reacts [to macroeconomic announcements] are well established’ (Hördahl et al. 2015). The earliest studies typically documented that Treasury bond prices are influenced by money supply announcements (Berkman 1978; Grossman 1981; Urich and Wachtel 1981; Roley 1983), but subsequent investigations have uncovered evidence that some additional indicators, such as CPI and PPI (Smirlock 1986; Hardouvelis 1988), the unemployment rate (Cook and Korn 1991; McQueen and Roley 1993), industrial production (Harvey and Huang 1993; Edison 1997), and retail sales and durable goods (Hardouvelis 1988), affect interest rates on government bonds. More recent studies relying on intraday data have confirmed that the entire yield curve systematically responds to the scheduled release of macroeconomic information (Fleming and Remolona 2001; Green 2004); however, intermediate-maturity Treasury bonds appear to be the most sensitive to macroeconomic surprises (Fleming and Remolona 2001; Balduzzi et al. 2001; Faust et al. 2007), which causes ‘a pronounced hump-shaped announcement reaction function’ (Hördahl et al. 2015).

Unlike stocks, exchange rates, and Treasury bonds, the reactions of corporate bonds to macroeconomic announcements have, to a large extent, been ignored by academic research. Only a handful of studies have been conducted in this area, and all of them have limited their attention to the US market. This is possibly due to the fact that, until recently, corporate bonds ‘lacked a centralized system of collecting and reporting secondary-market transaction information’, and consequently ‘their trading prices lack[ed] transparency’ (Chatrath et al. 2012). One of the first studies on this issue was conducted by Ramchander et al. (2005), who examined the yields on Moody’s Baa corporate bonds and found that higher-than-expected inflation reduces the credit quality spread, whereas positive news about the Treasury budget increases it. Using Merrill Lynch option-adjusted credit spread indices and two corporate bond indices from Standard & Poor’s, Kong and Huang (2008) found that favourable surprises in retail sales, nonfarm payroll, and consumer confidence significantly decrease the spreads between high-yield corporate bonds and Treasury bonds, while investment grade indices are essentially unaffected by macroeconomic news. Kosturov and Stock (2010) employed data from Salomon Brothers’ investment grade corporate bond indices and net asset values for Vanguard and Fidelity’s high-yield corporate bond funds; their analysis suggests that both investment grade and high-yield corporate bonds ‘earn positive announcement-day excess returns which increase monotonically with maturity’. Chatrath et al. (2012) found that the yield spreads between corporate bonds and Treasuries increase on announcement days, and better-than-expected economic news leads to a reduction in quality spreads, which is consistent with a ‘flight to risk’ explanation. Additionally, they claimed that high-yield corporate bonds are more sensitive to macroeconomic surprises.

It is open to question whether corporate bond markets outside the USA share similar reactions, and this is one of the areas on which we aim to shed light with the present study.

3 Relationships between macroeconomic surprises and asset prices

The efficient market theory affirms that asset prices incorporate all known information and change only in response to the arrival of unexpected news (Fama 1970). In this study, our focus is on unexpected news concerning macroeconomic indicators. From a theoretical point of view, the linkages between macroeconomic indicators and asset prices are extremely complex; to make the analysis tractable, but at the same time provide a frame of reference in relation to which the empirical results can be assessed, we follow an approach that was inspired by and extends Simpson et al.’s (2005) work on the impact of macroeconomic surprises on the foreign exchange market. More specifically, we posit that the 15 macroeconomic indicators in our data set affect one (or more) of five broad domestic macroeconomic factors, and in turn, we sketch the hypothesized effects that the latter exert on domestic stock returns, the effective exchange rate, the term premium, and the corporate credit quality spread. The five broad macroeconomic factors that we propose are consumer demand, economic growth, inflation, interest rates, and the central bank’s reaction function. Panel A of Table 1 summarizes how shocks to the macroeconomic indicators of interest are expected to influence these five factors. In Panel B, we indicate the impact that a positive surprise in one of the five broad macroeconomic factors is expected to have on each of the four dependent variables, all else constant. Throughout the paper, we strictly use the expression ‘positive (negative) surprise’ to refer to those instances where the actual value of an indicator turns out to be greater (less) than analysts’ median forecast.

Table 1 Hypothesized relationships among macroeconomic announcements, macroeconomic factors, and asset prices
Full size table

4 Hypotheses

As illustrated in the previous section, the unexpected components of scheduled macroeconomic releases provide information about consumer demand, economic growth, inflation, interest rates, and possible future reactions by the central bank. In turn, since economic theory predicts that these five factors influence stock returns, exchange rates, the yield curve’s slope, and the credit quality spread, our first testable hypothesis is that asset prices react to the unexpected components of macroeconomic announcements, which for all intent and purposes represent market ‘surprises’:

H1

Asset prices systematically respond to the surprises contained in scheduled macroeconomic announcements.

Besides this central hypothesis, we tested a set of ancillary hypotheses. The first one concerns the volatility of asset prices. Theory-wise, the arrival of new information may increase or decrease volatility. On the one hand, the release of public information may reduce uncertainty in the market, lessen informational asymmetries among investors, and diminish the amount of speculative trading; if the piece of news in question increases the degree of consensus among market participants about the value of an asset, then its volatility would be expected to fall. On the other hand, the anticipated arrival of macroeconomic news may encourage speculative trading or simply exacerbate the lack of consensus among traders about how monetary authorities will react, and therefore, about the values of the assets traded in secondary markets. Empirically, a number of studies have documented that scheduled macroeconomic announcements and surprises increase the volatility of returns in the stock, bond, and foreign exchange markets (e.g. Jones et al. 1998; Flannery and Protopapadakis 2002; Chang and Taylor 2003; Laakkonen 2007; Rangel 2011; Gospodinov and Jamali 2012). However, there is also some evidence in support of the opposite prediction (Kim 1998, 2003; Andritzky et al. 2007). Based on these insights, we tested the following hypothesis:

H2

Scheduled macroeconomic announcements and macroeconomic surprises affect the volatility of asset returns.

A further object that is worth of investigation in the present context, but that has received limited attention in the literature, is trading activity. A well-established tenet in financial theory is that ‘most trades in financial markets occur because of differing beliefs’, which implies that ‘[i]f market participants disagree about the effects of surprises in announcements, there should be increased trading activity in the market soon after the announcements’ (Jain 1988). Both Jain (1988) and Flannery and Protopapadakis (2002) examined this matter using US data; the former found no evidence that trading volume in the stock market is affected by macroeconomic releases, while the latter documented that some announcements (balance of trade, CPI, PPI, unemployment, housing starts, and money supply) and some surprises (CPI, PPI, and leading indicators) do raise trading volume. Due to data availability issues, we followed these authors, and we limited our attention to trading activity in the stock market, which nevertheless is a subject that previous studies about the UK’s financial markets have mostly neglected. The hypothesis that we set out to investigate is the following:

H3

Scheduled macroeconomic announcements and macroeconomic surprises affect trading activity in the stock market.

The last question that we examined is whether the effects of macroeconomic surprises vary over time. It has been argued that one of the reasons why little evidence has been found that macroeconomic news influences asset returns is that researchers typically employ econometric models that assume time-invariant response coefficients, whereas the effects of macroeconomic innovations are not constant (Flannery and Protopapadakis 2002). In this respect, some authors have put forward evidence suggesting that the effects of macroeconomic news on stock returns may vary over the business cycle (McQueen and Roley 1993; Adams et al. 2004; Boyd et al. 2005).

While we do believe that this is a valuable insight, and it is an important step towards our understanding of the phenomenon in question, we also suspect that assuming that the response of financial markets to macroeconomic surprises is conditional upon the state of the economy does not fully capture the time-varying nature of the response coefficients. In particular, we conjecture that the state of the stock market similarly plays a relevant role in moderating the reactions of market participants to macroeconomic surprises, and this is an area where we aim to make an original contribution to the literature.Footnote 2 There are both rational and behavioural arguments in support of our conjecture. From a rational perspective, some investors may harbour the belief that the central bank takes into account stock prices when setting its monetary policy and reacts asymmetrically to macroeconomic surprises depending on the state of the stock market. Indeed, economists have long been divided as to whether central banks should respond directly to asset prices, one faction being hostile to this approach (Bernanke and Gertler 2001), while the other openly embracing it (Cecchetti et al. 2000). Among monetary authorities, the pre-2008 crisis consensus seems to have been that monetary policy should react asymmetrically to asset price developments: it should ‘clean up’ after asset price busts, but it should not ‘lean against the wind’ (White 2009; Stark 2011; Issing 2011).

Empirically, considerable evidence has been produced that some central banks, including the Bank of England, the Fed, and the European Central Bank, do seem to respond to stock prices (Rigobon and Sack 2003; Chadha et al. 2004; Bjørnland and Leitemo 2009; Botzen and Marey 2010; Fiodendji 2011; Apergis 2017). The implication of these findings is not necessarily that central banks have been targeting stock prices directly; monetary authorities may systematically respond to them insofar as stock prices, being forward looking, contain relevant information about future aggregate output and inflation, which are the goal variables of central banks. In this regard, economic theory predicts that stock prices affect consumption through the wealth channel and investment through the credit channel and the Tobin Q effect, and consequently it should not be surprising that ‘stock market movements are likely to be an important determinant of monetary policy decisions’ (Rigobon and Sack 2003).

Behavioural finance offers some additional arguments in support of our conjecture, as investors’ attitudes and behaviours are likely to vary between stock market regimes.Footnote 3 One of the possible mechanisms at play here is the disposition effect, which refers to investors’ tendency to sell winning assets and hold onto to losing assets. Frazzini (2006) showed that, in the presence of limits to arbitrage, the disposition effect causes prices to underreact to new information. Since the strength of the disposition effect appears to vary between bear markets and bull markets (Cheng et al. 2013; Janssen et al. 2020), the responses of asset prices to macroeconomic news should be expected to vary between market regimes. A similar argument can be made with regard to the overconfidence bias, which refers to individuals’ tendency to overestimate their abilities. The model proposed by Daniel et al. (1998), according to which ‘investors view themselves as more able to value securities than they actually are’, shows that this bias implies that investors tend to ‘underreact to public information signals’. Since investor overconfidence is ‘likely to rise late in a bull market and to fall late in a bear market’ (Gervais and Odean 2001), one would expect market participants’ reactions to public macroeconomic information to vary between market regimes. Taking stock of these arguments, the last hypothesis that we set out to investigate is the following:

H4

The reaction of asset prices to macroeconomic surprises depends not only on the state of the economy but also on the state of the stock market (bull vs. bear).

5 Data

5.1 Macroeconomic announcements

We obtained data on macroeconomic announcements about the UK economy and on analyst forecasts from Bloomberg. The data set extends from 3 January 1997 through 30 June 2017. This sample period is particularly suitable for our purposes because, as Clare and Courtenay (2001) pointed out, after the Bank of England gained operational independence in May 1997, greater transparency in the conduct of monetary policy is expected to lead market participants to react less sharply to monetary policy announcements and more intensely to other macroeconomic announcements compared to the pre-independence period. Following the literature, we defined a macroeconomic surprise, Sit, concerning indicator i on day t as follows:

$$S_{it} = \frac{{A_{it} - F_{it} }}{{{\text{Std}}(A_{i} - F_{i} )}},$$

where Ait is the actual value announced for macroeconomic indicator i on day t and Fit is analysts’ prior median forecast of what that value would be. To make the regression coefficients directly comparable across indicators, we standardized the surprises by dividing them by the standard deviation of (Ai − Fi).

We selected a sample of announcements about 15 macroeconomic indicators, which are described in Table 2.Footnote 4 In the UK, most macroeconomic releases occur at 9:30 am, and consequently we assumed that asset prices absorb them on the same day of the announcement. A few releases in the data set occurred after 4:30 pm (the closing time for the London stock exchange), in which case we assumed they affected asset prices the next trading day; hence, we shifted these announcements to the next trading day in the sample. Since ours is one of the first studies about the reaction of the UK’s financial markets to macroeconomic surprises that employs analyst forecasts from Bloomberg, we find it useful to provide some summary statistics about the quality of these forecasts in Table 3.Footnote 5 Column 5 shows the mean surprise for each macroeconomic indicator, whereas column 6 reports the p-value for the hypothesis that the mean surprise is equal to zero. For almost half of the indicators, a two-sided t-test rejects the null hypothesis of unbiasedness at least at the 5% significance level. Column 7 reports the fraction of positive surprises, and column 8 shows the two-sided p-value for the hypothesis that this fraction is equal to 0.5. For four indicators, a binomial test rejects the null hypothesis that positive surprises are as likely as negative surprises at least at the 5% level. Analysts consistently tend to underestimate retail sales and overestimate visible trade balance, claimant count rate, and industrial production. These results are not unexpected, as similar violations of the unbiasedness hypothesis have been found in the literature (e.g. Flannery and Protopapadakis 2002). Overall, these tests suggest that the quality of the forecasts in our sample is comparable to that of similar studies on the US market.

Table 2 Macroeconomic indicator definitions
Full size table
Table 3 Descriptive statistics about the 15 macroeconomic indicators in the data set
Full size table

5.2 Asset prices

We chose to use daily rather than intraday data in our analysis because, as Hayo and Neuenkirch (2012) put it, what we want to investigate is whether macroeconomic surprises cause ‘economically important effects that persist over time’, while we are less interested in ‘short-term blips in the data’. Furthermore, as Brenner et al. (2009) pointed out, ‘higher-frequency data are afflicted by microstructure frictions […] that may bias inferences drawn upon them’. We downloaded from Datastream the daily times series of the FTSE 100’s total return index, dividend yield, and market value. From the London Stock Exchange’s website, we obtained daily data about trading activity (number of trades, turnover, number of shares traded) from October 20, 1997 through June 30, 2017.Footnote 6 And from Bloomberg, we obtained the daily time series of a total return index for the world stock market excluding the UK (code: FTAW03), which covers 98% of the world’s investable market capitalization.

To measure the British pound effective exchange rate, we obtained from the Bank of England’s website the daily time series of the Sterling Narrow Exchange Rate Index (code: XUDLBK67). This index tracks the trade-weighted value of the British pound and is calculated by combining data on bilateral exchange rates; more specifically, a country is included in this index if it accounts for more than 1% of the UK’s imports or exports (Lynch and Whitaker 2004).

To compute the term premium (i.e. the spread between the 10-year UK government bond yield and the 3-month UK Treasury bill yield), we downloaded the time series of the 10-year yield from Datastream (code: GBUK10Y) and the time series of the 3-month gilt repo rate from the Bank of England’s website (code: IUDGR3M).

Lastly, to construct a proxy for the corporate credit quality spread, we relied on the Markit iBoxx corporate bond indices available from Datastream. More precisely, our quality spread is the difference between the redemption yields on UK sterling BBB and AAA-rated non-financial corporate bonds (codes: IB£NBAL and IB£NDAL, respectively).Footnote 7 Since these data are available from July 2006, when analysing the quality spread we employed a shorter sample period than for the other asset classes.

Descriptive statistics for the four dependent variables are displayed in Table 4. The mean values are close to zero, and as expected for financial data of daily frequency, a considerable variation around this mean can be observed. The high skewness and substantial kurtosis in the distributions of term premium and quality spread are partly driven by two and one outliers, respectively, which we address in our modelling process in Sect. 7.1.

Table 4 Descriptive Statistics for the four dependent variables
Full size table

5.3 State of the economy and state of the equity market

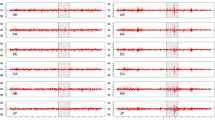
To identify the state of the economy, we obtained from the Office for National Statistics the beginning and ending dates of economic recessions in the UK, which are displayed in the top panel of Fig. 1.Footnote 8 Since there is no generally accepted definition of a bull (or bear) market, to identify stock market regimes we relied on two alternative algorithms developed by Pagan and Sossounov (2003) and Lunde and Timmermann (2004). For details, we refer the interested reader to the original articles in which these algorithms were proposed. The middle and bottom panels of Fig. 1 give a graphical depiction of bull and bear market phases according to these two algorithms and reveal that they are, to a large extent, consistent with each other.

Fig. 1
figure 1

Regime clustering. The top panel shows UK recessions (shaded areas) according to the Office for National Statistics. The middle panel shows bear market phases (shaded areas) according to Pagan and Sossounov’s (2003) algorithm, and the bottom panel shows bear market phases (shaded areas) according to Lunde and Timmermann’s (2004) algorithm. In all three graphs, the solid line represents the FTSE 100 index

Full size image

6 Baseline model specification and estimation procedure

In Sect. 4, we formulated four hypotheses. We discuss in what follows the methodology that we developed to test them. The baseline model specification relevant for hypothesis H1, which concerns the effects of macroeconomic surprises on our four dependent variables, is as follows:

$$\begin{aligned} {r}_{t} & = \upsilon +\sum\limits_{i=1}^{n}{\alpha }_{i}{S}_{it}+\sum\limits_{j=0}^{1}{\psi }_{j}{r}_{t-j}^{w}+\sum\limits_{k=1}^{m}{\phi }_{k}{X}_{k(t-1)}+\sum\limits_{l=1}^{h}{\omega }_{l}{Y}_{l(t-5)} \\ & \quad +\sum\limits_{q=1}^{g}{\beta }_{q}{Z}_{qt}+\sum\limits_{s=1}^{p}{\tau }_{s}{r}_{t-s}+{\varepsilon }_{t} \\ \end{aligned}$$

where

$$\varepsilon_{t} \sim WN\left( {0,\sigma_{t}^{2} } \right).$$
(1)

The dependent variable, \({r}_{t}\), which is, in turn, the log return to the FTSE 100 index from day t − 1 to day t, the effective exchange rate log return, the change in the term premium, or the change in the credit quality spread, is regressed on the surprise components of macroeconomic announcements, \({S}_{it}\), the return of a world-ex-UK stock market index, \({r}_{t}^{w}\), one-day-lagged control variables, \({X}_{k(t-1)}\), five-day-lagged control variables, \({Y}_{l(t-5)}\), day-of-the-week and pre- and post-holiday dummies, \({Z}_{qt}\), and a set of autoregressive terms.Footnote 9 The return to the world stock market index excluding the UK enters the model both contemporaneously as well as with a one-day lag; its role is to capture external economic and political shocks that may affect the UK financial markets and help us isolate more precisely the effects of interest. The one-day-lagged control variables, \({X}_{k(t-1)}\), consist of the three remaining asset price variables.Footnote 10 Following Flannery and Protopapadakis (2002), the FTSE 100 index’s dividend yield and log market value are included as controls with a five-day lag, \({Y}_{l(t-5)}\).Footnote 11

The error term, \({\varepsilon }_{t}\), in regression model (1) is heteroscedastic and non-normal. To take its time-varying volatility into account, following Andersen et al. (2003) and Ehrmann and Fratzscher (2005), we relied on an iterative weighted least squares (IWLS) approach.Footnote 12 In the first step, we ran regression model (1). In the second step, we regressed the log squared residuals from Eq. (1) on a set of independent variables, as follows:

$$ \begin{aligned} \ln \left( {\hat{\varepsilon }_{t}^{2} } \right) & = \omega + \sum\limits_{i = 1}^{n} {\gamma_{i} } \left| {S_{it} } \right| + \sum\limits_{j = 1}^{f} {\zeta_{j} A_{jt} } + \delta \ln \left( {\hat{\sigma }_{t}^{2^{w}} } \right) + \sum\limits_{q = 1}^{g} {\rho_{q} Z_{qt} } \\ &+ \sum\limits_{s = 1}^{{p_{2} }} {\theta_{s} } \ln \left( {\hat{\varepsilon }_{t - s}^{2} } \right) + \mu_{t} \end{aligned} $$
(2)

The right-hand side of Eq. (2) contains the absolute surprises, \(\left|{S}_{it}\right|\), a set of announcement dummies, \({A}_{jt}\), which take value of 1 when an announcement is made about indicator j and 0 otherwise, the log variance of the return to the world-ex-UK stock market index, \(\ln \left( {\hat{\sigma}_{t}^{{2}^{w}}} \right)\), which we estimated with a GARCH(1,1) model, day-of-the-week and pre- and post- holiday dummies, \({Z}_{qt}\), and lags of the left-hand side variable. In the third step, we used the estimated volatility from Eq. (2), \(\mathrm{exp}\left(\widehat{\mathrm{ln}\left({\widehat{\varepsilon }}_{t}^{2}\right)-{\mu }_{t}}\right)\), as a weight in a WLS estimation of Eq. (1). To determine the optimal number of autoregressive terms in the mean and variance equations, we relied on the Bayesian Information Criterion (BIC). We then iterated this procedure until the estimated coefficients converged.Footnote 13 We opted for this approach, instead of simply estimating Eq. (1) by OLS and relying on heteroscedasticity and serial correlation robust standard errors, because it allowed us to investigate directly the impact of macroeconomic announcements and surprises on the volatility of asset returns, which is the subject of hypothesis H2. Additionally, by taking the time-varying volatility of the error term into account, the IWLS estimator is asymptotically more efficient than OLS. Nevertheless, since a miss-specification of the variance equation might affect the validity of statistical inference, we followed Wooldridge’s (2015, pp. 262–263) advice, and after implementing the IWLS procedure, we computed standard errors that are robust to heteroscedasticity and autocorrelation to perform statistical inference on the coefficients in Eq. (1).Footnote 14 Unless otherwise stated, the same procedure described above applies to the remaining models in the paper.

7 Empirical analysis

As Table 3 reveals, not all surprise components of the macroeconomic indicators in our data set are available throughout the sample period. For about half (8 out of 15) of the indicators, the surprises are available from at least October 1998. Beginning from January 2005, the surprises are available for all indicators. For this reason, we conducted all our analyses on two overlapping sample periods: a longer one (10/1998–06/2017) and a more recent one (01/2005–06/2017). The only exception concerns the corporate credit quality spread, for which data availability issues limited our sample to the period 07/2006–06/2017.

7.1 Macroeconomic surprises and asset prices

We begin our discussion by examining hypothesis H1. Table 5 reports the estimates generated by fitting Eq. (1) by IWLS. Before delving into the details, we believe it useful to provide a bird’s eye view of the results. Two general patterns emerge: (1) a stronger-than-expected economy raises stock returns, causes the domestic currency to appreciate, increases the slope of the yield curve, and lowers the corporate credit quality spread; (2) higher-than-anticipated inflation leads to an appreciation of the home currency and makes the yield curve steeper. Both patterns can be reconciled with standard economic theory. The first pattern is consistent with the interpretation that a stronger economy is expected to improve firms’ net cash flows. Both patterns are consistent with the view that rising output and/or inflation are expected to trigger a monetary tightening reaction by an inflation targeting central bank.

Table 5 H1: Macroeconomic surprises and asset prices
Full size table

Getting down to the fine points, the data reveal that a handful of macroeconomic indicators have an economically and statistically significant effect on the returns to the FTSE 100 index (columns 1 and 2).Footnote 15 In the more recent sub-sample, positive surprises in retail sales, GDP, and the Bank of England’s policy rate tend to raise stock returns; however, with respect to the Bank of England’s policy rate, the sub-sample in question contains only 5 actual surprises, and consequently we believe that this estimate is not reliable. The direction of the other two effects is consistent with economic theory, and more specifically, with the interpretation that investors believe that positive shocks to consumer demand (retail sales) and economic growth (GDP) have a stronger impact on future dividends than on discount rates. From a practical perspective, the estimated effects are economically significant: the coefficient on GDP suggests that a one-standard-deviation surprise increase in economic growth raises stock returns by about 13 basis points, which is six times the size of the unconditional daily mean return. This result is different from the typical finding observed in studies based on US data; for example, Flannery and Protopapadakis (2002) found no evidence that GDP and retail sales surprises affect US stock returns.

Moving to the effective exchange rate (columns 3 and 4), there is considerable evidence that macroeconomic shocks do exert an influence on the foreign exchange market, and the sizes of the forces at play are relevant in economic terms. Retail sales and nationwide house prices are both statistically significant and suggest that stronger-than-expected consumer demand leads to an appreciation of the domestic currency. As for inflation, RPI is statistically significant in the whole sample, and so is CPI in the more recent sub-sample; the signs of their coefficients indicate that higher-than-expected domestic inflation causes the British pound to appreciate. The coefficient on claimant count rate is negative and statistically significant at conventional levels, which implies that a surprise increase in the number of people claiming unemployment benefits leads to a depreciation of the home currency. These three effects are consistent with the view that higher-than-anticipated inflation is expected to raise nominal interest rates as per the Fisher effect and is likely to trigger an interest rate hike by the central bank. They are also consistent with portfolio-balance theory, which predicts that higher interest rates cause the home currency to appreciate. As for the interest rates category, our estimates suggest that positive surprises in the Bank of England’s policy rate lead to an appreciation of the domestic currency, an effect that is directly consistent with portfolio-balance theory. Surprise increases in net lending secured on dwellings and (marginally) in mortgage approvals are accompanied by an appreciation of the home currency, which is consistent with the view that investors interpret them as signalling stronger demand in the market for loanable funds and rising interest rates. However, the coefficient on consumer credit, which too is statistically significant, features a negative sign. Given that consumer credit and net lending secured on dwellings are the two components of total lending to individuals, this is possibly the only result that is in direct conflict with the others and is not easily reconcilable with economic theory. With regard to economic growth, our estimates indicate that positive shocks to industrial production and GDP result in a stronger British pound. Stronger-than-expected economic growth, just like higher-than-anticipated consumer demand, may lead investors to expect an interest rate hike from an inflation targeting central bank, and consequently these patterns are in line with portfolio-balance theory. Overall, the coefficient on CPI features the largest point estimate in absolute value; a one-standard-deviation surprise increase in this indicator causes the British pound to appreciate by about 17 basis points. For comparison, Simpson et al. (2005) estimated that a one-standard-deviation surprise increase in the US CPI leads to an appreciation of the US dollar by 58 basis points against a set of major currencies.

The next dependent variable of interest is the term premium (columns 5 and 6).Footnote 16 The estimates are mostly consistent across the two sample periods. Five indicators have a statistically significant influence on the slope of the yield curve. Positive surprises in consumer demand (retail sales), inflation (RPI and CPI), and economic growth (GDP and industrial production) make the yield curve steeper. The effect of claimant count rate approaches statistical significance and indicates that surprise decreases in this variable are estimated to increase the term premium. These effects are of practical importance: for example, a one-standard-deviation surprise increase in retail sales leads to a 1.5 basis point increase in the term premium, which is more than ten times the size of the median daily change in this variable. From the perspective of economic theory, these estimates generate meaningful insights. They are consistent with the interpretation that investors take the above shocks as evidence of stronger-than-predicted economic activity, anticipate an interest rate hike by the Bank of England, and believe that its monetary policy operates with a high degree of inertia (Rudebusch and Wu 2008). They can also be reconciled with the argument that investors consider the surprises in retail sales, GDP, industrial production, RPI, CPI, and claimant count rate to be shocks to the short-run components of real activity or inflation (Doshi et al. 2018).

The last dependent variable in our analysis is the credit quality spread (column 7). The only three indicators that are statistically significant in this case are the Bank of England’s policy rate, claimant count rate, and industrial production. The first one can be safely ignored, given that only 5 actual surprises took place during the sample period. A one-standard-deviation surprise increase in claimant count rate increases the quality spread by 0.3 basis points. The impact of industrial production shocks is of similar magnitude, and as expected, it works in the opposite direction. Though, at first sight, these effects may appear negligible, one needs to consider that, in absolute value, almost 50% of the daily changes in the quality spread in the sample are actually smaller than 0.3 basis points. Secondly, the literature suggests that investment grade corporate bonds are less sensitive to macroeconomic news than high-yield ones (Kong and Huang 2008; Chatrath et al. 2012). Lastly, our use of daily rather than intraday data is likely to bias these estimators towards zero. Viewed from this perspective, and given that the difference in credit rating between AAA and BBB corporate bonds is modest, we believe that the size of the two effects in question is practically relevant. Additionally, their signs are in line with previous findings (Chatrath et al. 2012), and theory-wise, they are consistent with the interpretation that a stronger-than-expected economy increases the projected profitability of domestic firms. Since this causes a greater reduction in default probability and default severity for higher-default-risk issuers than for lower-default-risk ones, it compresses the credit quality spread.

As for the controls, positive shocks affecting the rest of the world have an effect on all four dependent variables that is highly statistically significant and economically relevant: a 1% increase in the world stock market index excluding the UK leads to an immediate increase of about 0.75% in the returns to the FTSE 100 index, has a negative effect on the value of the British pound, makes the UK yield curve steeper, and reduces the credit quality spread. There also appears to be a statistically significant relationship between the one-day-lagged world stock market index and the FTSE 100 index, but most likely this is simply an artefact caused by non-synchronous trading, as owing to time-zone differences, the American markets close later than the London stock exchange. Though not reported in Table 5, there is also some evidence of lagged spillover effects across asset classes; for instance, an appreciation of the British pound raises the returns on the FTSE 100 index and decreases the quality spread; a steeper yield curve, instead, lowers stock returns. The pre- and post-holiday dummies are mostly statistically insignificant, regardless of the dependent variable and sample period, as is the FTSE 100’s log market value. The FTSE 100’s dividend yield, instead, affects only stock returns and the quality spread.

7.2 Macroeconomic surprises and the volatility of asset returns

Table 6 reports the estimated coefficients for Eq. (2) and reveals two key results concerning hypothesis H2: there is barely any evidence that macro announcements influence the volatility of financial markets, and there is only minor evidence that their surprise components do so. More precisely, CPI/RPI announcements have a statistically significant effect on one of the dependent variables: scheduled releases of these indicators are estimated to reduce the variance of the credit quality spread. Surprises in CPI and nationwide house prices significantly increase the volatility of exchange rate returns; the former also have a (marginally significant) positive effect on the volatility of the credit quality spread. In the interest rates category, surprises in net lending lead to increased volatility in the stock market and (marginally) in the foreign exchange market, surprises in mortgage approvals raise the variance of the quality spread, and shocks to consumer credit actually reduce the variance of the term premium. In summary, to a large extent, our findings are consistent with previous studies according to which, in financial markets, ‘identifiable news events do not appear to drive much of the volatility of prices’ (Jones et al. 1998).

Table 6 H2: Macroeconomic surprises and the variance of asset prices
Full size table

7.3 Scheduled announcements, macro surprises, and trading activity in the stock market

The next hypothesis that we set out to test, H3, concerns the impact of scheduled macroeconomic announcements and surprises on trading activity in the stock market. To address this question, we fitted the following regression equation:

$$\begin{aligned} {DV}_{t} & =\upsilon +\sum\limits_{i=1}^{n}{\alpha }_{i}{|S}_{it}|+\sum\limits_{w=1}^{f}{\zeta }_{w}{A}_{wt}+\upkappa {|r}_{t}|+\sum\limits_{j=0}^{1}{\psi }_{j}|{r}_{t-j}^{w}| \\ & \quad +\sum\limits_{k=1}^{m}{\phi }_{k}{X}_{k(t-1)}+\sum\limits_{l=1}^{h}{\omega }_{l}{Y}_{l(t-5)}+\sum\limits_{q=1}^{g}{\beta }_{q}{Z}_{qt}+\sum\limits_{s=1}^{5}{\tau }_{s}{DV}_{t-s}+{\varepsilon }_{t} \\ \end{aligned}$$

where

$$\varepsilon_{t} \sim WN\left( {0,\sigma_{t}^{2} } \right).$$
(3)

The dependent variable, \({DV}_{t}\), was first detrended as follows:

$$DV_{t} = \ln ({\text{vol}}_{t} ) - \frac{1}{21}\mathop \sum \limits_{n = 1}^{21} \ln \left( {{\text{vol}}_{t - n} } \right)$$

where \({\mathrm{vol}}_{t}\) represents, in turn, the number of shares traded, turnover, or number of trades on day t. The remaining variables in Eq. (3) have the same meaning as in the previous sections. Equation (3) is the only equation in this study that we did not fit by IWLS. Given the nature of the dependent variable, we followed the literature and estimated the parameters of the model by OLS. To perform statistical inference, we computed Newey–West robust standard errors.

Table 7 shows the estimates generated by fitting model (3), where the dependent variable measures the approximate percentage change in the number of shares traded (turnover, number of trades) on a given day relative to the average of the previous month (i.e. 21 trading days). The first element that emerges from inspecting the table is that several macroeconomic announcements do have an economically and statistically significant impact on trading volume. Scheduled announcements concerning consumer demand (GfK consumer confidence), inflation (CPI, RPI, claimant count rate), interest rates (Bank of England’s policy rate, lending to individuals, public sector net borrowing), and economic growth (industrial production) are accompanied by an increase in the three trading activity proxies. For example, on days when the value of the GfK consumer confidence indicator is announced, the number of shares traded and turnover increase by about 14%, and the number of trades rises by about 7%. Industrial production and claimant count rate announcements raise the three proxies by about 3–4%. The only indicator whose effect appears to be counterintuitive is GDP, as in the whole sample, GDP announcements reduce the number of shares traded and (marginally) turnover.

Table 7 H3: Macroeconomic announcements, macroeconomic surprises, and trading activity in the stock market
Full size table

As for the surprise components of macroeconomic announcements, there is less evidence that they exert a substantial influence on trading activity. The only indicators whose surprises are statistically significant are consumer confidence, consumer credit, mortgage approvals, and public sector net borrowing. Somewhat counterintuitively, with the exception of consumer confidence, the signs of the corresponding coefficients indicate that larger surprises tend to reduce the amount of trading activity taking place.

Overall, these results are, to a large extent, consistent with the findings of Flannery and Protopapadakis (2002) about the US stock market; while the release of macroeconomic news definitely raises trading volume, the size of the surprises contained in such announcements does not seem to matter much.

7.4 Are the effects of macroeconomic surprises contingent on the state of the stock market?

To examine the last hypothesis, H4, we allowed the response coefficients to vary both between states of the economy (recession vs. expansion) and between stock market phases (bull vs. bear), as follows:

$$\begin{aligned} r_{t} & = \upsilon + \pi_{1} D_{t}^{\exp } + \pi_{2} D_{t}^{{{\text{bull}}}} \\ & \quad + \mathop \sum \limits_{i = 1}^{n} (\alpha_{i}^{{{\text{rec}}}} S_{it}^{{{\text{rec}}}} + \alpha_{i}^{\exp } S_{it}^{\exp } + \mu_{i} S_{it}^{{{\text{rec}}}} D_{t}^{{{\text{bull}}}} + \gamma_{i} S_{it}^{\exp } D_{t}^{{{\text{bull}}}} ) \\ & \quad + \mathop \sum \limits_{j = 0}^{1} \psi_{j} r_{t - j}^{w} + \mathop \sum \limits_{k = 1}^{m} \phi_{k} X_{{k\left( {t - 1} \right)}} + \mathop \sum \limits_{l = 1}^{h} \omega_{l} Y_{{l\left( {t - 5} \right)}} + \mathop \sum \limits_{q = 1}^{g} \beta_{q} Z_{qt} + \mathop \sum \limits_{s = 1}^{p} \tau_{s} r_{t - s} + \varepsilon_{t} \\ \end{aligned}$$

where

$$\varepsilon_{t} \sim WN\left( {0,\sigma_{t}^{2} } \right).$$
(4)

The variables \({S}_{it}^{\mathrm{rec}}\) and \({S}_{it}^{\mathrm{exp}}\) measure macroeconomic surprises during economic recessions and expansions, respectively, \({D}_{t}^{\mathrm{exp}}\) is a dummy that takes value of 1 during economic expansions, \({D}_{t}^{\mathrm{bull}}\) is a dummy that takes value of 1 during bull market phases, and the remaining variables are as previously defined. Similarly, the variance equation contains separate absolute surprises and announcement dummies for economic recessions (\(\left|{S}_{it}^{\mathrm{rec}}\right| \mathrm{and} {A}_{jt}^{\mathrm{rec}}\)) and expansions (\(\left|{S}_{it}^{\mathrm{exp}}\right| \mathrm{and} {A}_{jt}^{\mathrm{exp}}\)), the economic expansion dummy, \({D}_{t}^{\mathrm{exp}}\), and the bull market dummy, \({D}_{t}^{\mathrm{bull}}\), as follows:

$$ \begin{aligned} \ln \left( {\hat{\varepsilon }_{t}^{2} } \right) & = \omega + \pi_{1} D_{t}^{\exp } + \mathop \sum \limits_{i = 1}^{n} (\gamma_{i}^{{{\text{rec}}}} \left| {S_{it}^{{{\text{rec}}}} } \right| + \gamma_{i}^{\exp } \left| {S_{it}^{\exp } } \right|) + \mathop \sum \limits_{j = 1}^{f} (\zeta_{j}^{{{\text{rec}}}} A_{jt}^{{{\text{rec}}}} + \zeta_{j}^{\exp } A_{jt}^{\exp } ) \\ & \quad + \pi_{2} D_{t}^{{{\text{bull}}}} + \mathop \sum \limits_{i = 1}^{n} \left( {\upchi_{i} \left| {S_{it}^{{{\text{rec}}}} D_{t}^{{{\text{bull}}}} \left| { + \psi_{i} } \right|S_{it}^{\exp } D_{t}^{{{\text{bull}}}} } \right|} \right) \\ & \quad + \mathop \sum \limits_{j = 1}^{f} \left( {\xi_{j} A_{jt}^{{{\text{rec}}}} D_{t}^{{{\text{bull}}}} + \vartheta_{j} A_{jt}^{\exp } D_{t}^{{{\text{bull}}}} } \right) \\ & \quad + \delta \ln \left( {\hat{\sigma }_{t}^{2w} } \right) + \mathop \sum \limits_{q = 1}^{g} \rho_{q} Z_{qt} + \mathop \sum \limits_{s = 1}^{p2} \theta_{s} \ln \left( {\hat{\varepsilon }_{t - s}^{2} } \right) + \mu_{t} \\ \end{aligned} $$
(5)

Since the results based on Lunde and Timmermann’s (2004) algorithm are qualitatively very similar to the ones obtained using Pagan and Sossounov’s (2003) algorithm, Table 8 displays only the latter.Footnote 17 To set the stage for our discussion, it is worth focusing first on whether there is evidence that the response of financial markets to macroeconomic surprises is contingent upon the state of the economy. The last two rows of the table report the Wald statistics and the corresponding p-values for a test of the joint null hypothesis that αirec = αiexp and μi = γi for all i in Eq. (4). For all dependent variables and sample periods, the test clearly rejects the null hypothesis that the surprise response coefficients are constant between states of the economy, thus confirming previous findings (e.g. Boyd et al. 2005).

Table 8 H4: Do the effects of macroeconomic surprises depend both on the state of the stock market (bull vs. bear) and on the state of the economy (recession vs. expansion)?
Full size table

Having established that the response coefficients vary between states of the economy, we now turn to the question of whether they also vary between stock market regimes. The fourth from last row and the third from last row of the table report the Wald statistics and the corresponding p-values for a test of the joint null hypothesis that μi = γi = 0 for all i in Eq. (4). For all dependent variables and sample periods, the test strongly rejects the null hypothesis that market participants’ responses to macroeconomic surprises are constant between bull and bear markets. This evidence leads us to conclude that the surprise response coefficients vary not only between states of the economy but also between stock market regimes.

With regard to the effects of individual macro indicators, in what follows we restrict our attention to economic expansion phases because the recessionary phase in the sample period is fairly short, and consequently most macroeconomic surprises occurred during expansions, which renders the corresponding estimates more reliable. In the stock market (columns 1 and 2), surprises about economic growth appear to have a different impact on stock returns during a bull market than during a bear market, as the coefficients on the interaction terms gdpexp × Dbull and indpexp × Dbull are positive and statistically significant, whereas the coefficients on gdpexp and indpexp are negative (and statistically significant in the case of indpexp). Since the data show that negative surprises about GDP and industrial production are more common than positive ones in a bear market, the implication is that bad news about economic growth is estimated to increase stock returns in a bear market and good (bad) news increases (decreases) stock returns in a bull market. These results are consistent with the interpretation that investors believe that the Bank of England reacts asymmetrically: it will loosen its monetary policy aggressively (i.e. ‘clean up’) in response to negative news about economic growth in a bear market, while it will be less reactive in response to good and bad news about economic growth in a bull market.

With regard to the foreign exchange market, the coefficients on salesexp × Dbull and conscoexp × Dbull are negative and statistically significant, whereas the coefficients on salesexp and conscoexp are positive and statistically significant. This suggests that shocks to consumer demand (retail sales and GfK consumer confidence) have a stronger impact on the value of the domestic currency during bear markets. This, once again, is consistent with the interpretation that investors believe that the Bank of England reacts asymmetrically. It is expected to loosen its monetary policy vigorously in response to negative news about consumer demand in a bear market, causing a substantial depreciation of the domestic currency through the portfolio-balance effect, and it is less reactive in response to good and bad news about consumer demand in a bull market. With regard to the effects of interest rates, the coefficient on mortgexp × Dbull is positive and statistically significant, suggesting that stronger demand in the market for loanable funds has a larger impact on the value of the domestic currency in a bull market. However, the coefficient on conscredexp × Dbull is negative and statistically significant, which, just like in Sect. 7.1, makes the signs of these two effects difficult to reconcile with each other. Lastly, surprise increases in GDP are estimated to cause a depreciation (an appreciation) of the home currency in bear (bull) markets. Here, a possible interpretation is that, in a bear market, in line with the Keynesian model, an increase in real activity, and therefore, in aggregate income, increases import demand and leads to a depreciation of the domestic currency. In a bull market, instead, investors may expect a monetary tightening response to a positive surprise in real economic activity, and the portfolio-balance effect is likely to dominate, leading to an appreciation of the home currency.

In the Treasury bond market, surprises in visible trade balance and nationwide house prices are estimated to affect the term premium only in bear markets. The sign of the two effects is positive. Our interpretation is that investors presume that, in a bear market, the central bank will be willing to cut its policy rate briskly in response to weaker-than-expected net exports or house prices, which leads to a flatter yield curve in the presence of a high degree of monetary policy inertia (Rudebusch and Wu 2008) or if the surprise in question is believed to represent a shock to the short-run components of real economic activity (Doshi et al. 2018). On the other hand, surprises in retail sales affect the term premium only in bull markets. More specifically, the positive sign of the coefficient on salesexp × Dbull indicates that stronger-than-expected sales make the yield curve steeper in a bull market. As for the effects of inflation, in bear markets, surprise increases in PPI and RPI are estimated to make the yield curve steeper, whereas in bull markets inflation surprises do not appear to influence the term premium.

The last variable of interest is the corporate credit quality spread. In bear markets, stronger-than-expected economic growth (industrial production) and inflation (RPI) are estimated to reduce the quality spread. No such effects are present in bull markets. Lastly, while in bull markets a surprise increase in claimant count rate increases the quality spread, it has the opposite effect in bear markets. Our interpretation is that, in bear markets, investors anticipate that the central bank will cut its policy rate aggressively in response to bad news about employment, and it will be less likely to do so in a bull market.

8 Discussion

Overall, our analysis of UK data indicates that stock returns, the effective exchange rate, the slope of the yield curve, and the corporate credit quality spread do respond to the surprises contained in scheduled domestic macroeconomic announcements in a manner that is, to a very large extent, consistent with economic theory. The exchange rate and the yield curve, in particular, are affected by a considerably large number of indicators in an economically and statistically significant way. Should we be surprised that only a limited number of macroeconomic indicators exert a significant influence on stock returns and the corporate credit quality spread? We believe that the answer is no, and our view is motivated by several reasons: (1) in the case of stocks, and to a lesser extent, corporate bonds, which are a hybrid sharing both equity and bond features, economic shocks may affect both future cash flows and discount rates, and such effects may cancel each other out. (2) There is more to a macroeconomic surprise than the numbers can tell. Two 0.25% surprise increases in GDP do not necessarily have the same meaning; for example, the first one could be caused by a demand shock and the second one by a supply shock. In turn, their impact on stock returns should be different. Since the econometrician treats both observations in the same way, the resulting response coefficients tend to be biased towards zero. (3) Any broad index of the UK stock market ‘contain[s] a large number of multinational firms that are not overly exposed to the local economy’ (Brusa et al. 2015). (4) Lastly, some macroeconomic surprises may only affect some sectors of the economy or have opposite effects on the valuations of companies operating in different sectors, which makes it difficult for analyses based on broad stock market indices to detect any effect. Given all these caveats, we believe that the evidence suggesting that trading activity in the stock market is highly affected by macroeconomic announcements already provides a strong indication that investors in the stock market do respond to macroeconomic news.

9 Conclusion

We investigated the links between unexpected changes in macroeconomic fundamentals and the pricing of four major asset classes, i.e. stocks, exchange rates, Treasury bonds, and corporate bonds. The country under investigation (the United Kingdom) and the sample period (1998–2017) that we employed are particularly suitable for this purpose because economic theory suggests that, after the Bank of England gained operational independence in May 1997, investors would react more intensely to macroeconomic announcements. Our results highlight the importance of considering multiple markets at once when conducting this type of analysis, as changes in fundamentals are likely to affect different asset classes in dissimilar ways. One of our main contributions is that we shed more light on the time-varying nature of the asset price response coefficients; our study provides original evidence that not only the state of the economy but also the state of the stock market is (at least partly) responsible for their time-varying behaviour. Furthermore, our results are generally consistent with the interpretation that the mechanism underlying this time-varying behaviour is related to investors’ expectations about how the central bank will react to a surprise change in macroeconomic fundamentals.