Predicting recessions with a frontier measure of output gap: an application to Italian economy

Abstract

Despite the long and great history, developed institutions, and high level of physical and human capital, the Italian economy has been fairly stagnant during the last three decades. In this paper, we merge two streams of literature: nonparametric methods to estimate frontier efficiency of an economy, which allows us to develop a new measure of output gap, and nonparametric methods to estimate probability of an economic recession. To illustrate the new framework, we use quarterly data for Italy from 1995 to 2019 and find that our model, using either nonparametric or the linear probit model, is able to provide useful insights.

1 Introduction

How to predict economic recessions of a country? This is a very important and challenging question which is of interest to a fairly wide audience. Many papers in the empirical macroeconomic literature have proposed various methods to predict economic recessions, mainly focusing on the USA. Here we follow one of the paradigms, started by Estrella and Mishkin (1995, 1998) and further elaborated in various papers (e.g., see Duecker 1997; Kauppi and Saikkonen 2008, and references cited therein), and we try to elaborate further by adapting some newly advanced methods in nonparametric statistics and in productivity and efficiency analysis.

In this paper, we focus on Italian economy, one of the oldest in the World, with roots going back to at least the Roman Empire. Notwithstanding the long and great history, developed institutions, and high level of physical and human capital, Italian Economy has been stagnant during the last decades. Semiparametric and nonparametric methods are increasingly popular to analyze data in economics, business, and other fields (e.g., see Horowitz 2009; Henderson and Parmeter 2015). Specifically, we use a nonparametric version of the dynamic probit for time series (Park et al. 2017) to model the dependent variable (recession vs. non-recession). Meanwhile, for the explanatory variables, besides the standard predictor such as the spread, we try to develop a method to incorporate the estimates of the efficiency scores of a country. For this purpose, we use the method of frontier estimation in nonparametric location-scale models (Florens et al. 2014) and robust conditional frontier methods (Cazals et al. 2002; Daraio and Simar 2005; Daouia and Gijbels 2011; Mastromarco and Simar 2018, etc.). We illustrate our approach on the case of the Italian economy.

Our paper is also related to and in the spirit of the work of Wheelock and Wilson (1995), who pioneered the use of efficiency estimates among predictors in the parametric probability models, in their case for predicting bank failures. Besides the focus on macroeconomic recessions rather than banks, the major distinctive features of our paper relative to theirs include (i) the use of recent nonparametric estimation methods for the discrete choice model (rather than a parametric one), (ii) the use of time-series data, with a dynamic component modeled explicitly, and (iii) the use of more advanced methods for efficiency estimation that have become available very recently.

1.1 Predicting recessions

Among the variety of different approaches attempting to model and forecast economic recessions, we will focus on those that employed the parametric binary choice approach and find that a good model for the prediction of the US recessions is a parsimonious model with only one of a few predictors, the most important of which is the interest rate spread and one discrete variable, the lagged dependent variable. The roots of this approach go back to at least the seminal work of Estrella and Mishkin (1995, 1998), who thoroughly investigated various parametric models with many variables and concluded that the best forecasts resulted from a parsimonious probit model involving only one explanatory variable, the lagged spread. Duecker (1997) confirmed this result, yet also found that including the lagged dependent variable among regressors substantially improved the predicting power of the Estrella and Mishkin (1995, 1998) approach, especially for the recessions of the 1970s and 1990s that were missed by various other forecasting methods. Overall, the analyses in Estrella and Mishkin (1995, 1998) and Duecker (1997) suggest that their parsimonious model outperforms many alternative models that included many variables to gain a high in-sample fit, yet happened to be poorly forecasting the future. Also see Kauppi and Saikkonen (2008) for further refinements and more references and discussions.

This paper contributes to the empirical literature on predicting recessions by adding two novelties: (i) we apply a nonparametric dynamic time series discrete response model suggested by Park et al. (2017) and (ii) we use a new measure of output gap as one of the recession predictors. In particular, we employ a robust nonparametric frontier panel data model proposed by Mastromarco and Simar (2015) to estimate the time-dependent conditional efficiency of countries and use this as a measure of output gap.¹ In a macroeconomics context, where countries are producers of output (i.e., GDP), given inputs (e.g., capital, labor), and technology, inefficiency can be identified as the distance of the individual production from the frontier. This frontier can be estimated by the maximum output of the reference country regarded as the empirical counterpart of an optimal boundary of the production set. Hence, at least on intuitive grounds, we might interpret the inefficiency as a measure of output gap with respect to the potential output of the technological frontier.

1.2 Existing measures of output gap

Output gap is traditionally obtained as a deviation from a statistical measure of trend. One of the earliest and currently widely used statistical methods for measuring the output gap is based on measuring the output trend calculated by fitting a polynomial in time to the output, the residual being the estimated cycle. This method imposes a strong prior on the smoothness of the trend. Another popular statistical approach uses a filter, Hodrick and Prescott (1997), to identify the trend and the cycle. The trend measure in this case is smooth but not deterministic. The Baxter and King (1999) filter defines the cycle as having spectral power in pre-specified frequencies. However, Murray (2003) stresses that this filter extracts an estimate of the cycle which includes some trend shock. Other statistical approaches need a model to identify the stochastic trend component. These statistical methods do not require smoothness but impose the restriction of no correlation between the cycle and the trend, which may lack theoretical support. Beveridge and Nelson (1981) suggest a measure of trend as a long run forecast of an ARMA model. The unobserved components model extracts an estimate of the trend and cycle using the Kalman filter (Harvey 1985; Watson 1986; Clark 1987).

Differently from the statistical methods, the economic approaches estimate the output gap in the framework of the production function (for example Galí and Gertler 1999). Recently, various studies (Kuttner 1994; Gerlach and Smets 1999; Apel and Jansson 1999; Roberts 2001; Basistha and Nelson 2007; Basu and Fernald 2009) tried to combine the statistical approach with the economic approach by estimating the unobserved components of the multivariate model. These approaches do not impose smoothness or restrictive correlation structure, but estimate the output gap based on the empirical implications of the forward-looking Phillips curve.

1.3 Inefficiency as an alternative measure of output gap

Often, potential output is referred to as the production capacity of the economy. In our framework of the frontier model, potential output refers to the maximum level of output that can be produced for a given level of inputs, using full employment and capital utilization. The gap between the potential and actual outputs is interpreted as a measure of inefficiency which in our paper also captures the varying factor utilization over the cycle. The approach is closely linked to the production theory based approach in measuring the output gap. We cast our empirical model in frontier form, treating the gap as an unobserved variable—efficiency scores—estimated using nonparametric frontier methods. In pursuing an economic based approach, we avoid imposing strong priors on the smoothness of the trend or cycle, and the restrictive correlation structure between the trend and the cycle shocks.

Furthermore, parametric modeling may suffer from misspecification problems when the data generating process is unknown, as is usual in the applied studies. We propose a unified nonparametric framework for accommodating simultaneously the problem of model specification uncertainty and time dependence in the panel data frontier model. Specifically, we estimate the panel data frontier model using a flexible nonparametric two step approach to take into account the time dependence. Following recent developments in nonparametric conditional frontier literature (Florens et al. 2014; Mastromarco and Simar 2015, 2018), we adapt the nonparametric location-scale frontier model, where we link production inputs and output to time. In the first step we clean the dependence of inputs and outputs on time factors. These time factors capture the correlation among units. By eliminating the effect of these factors on the production process, we mitigate the problem of dependence across our time units and we are able to estimate a nonparametric frontier model from the panel data. (In the application we illustrate this approach for the data on 16 OECD countries.) In the second step, we estimate the frontier and the efficiency scores using inputs and outputs whitened from the influence of time.

1.4 The contribution in a nutshell and a roadmap

The main idea of this paper is to merge the interesting streams of literature described above: the novel nonparametric methods to estimate frontier efficiency of an economy as a new measure of output gap and the novel nonparametric method to estimate the probability of an economic recession. We do this by deploying a generalized nonparametric quasi-likelihood method in the context of dynamic discrete choice models for time series data (Park et al. 2017). To illustrate the new framework, we use data from 1995 to 2019 with quarterly frequency and find that our model using either nonparametric or the linear probit model, applied frequently in this context, is able to offer additional insights into the literature.

The paper is organized as followed. Section 2 presents the methodology. Specifically, Sect. 2.1. explains the nonparametric discrete choice models for time series to predict recessions. Section 2.2. introduces our proposed measure of output gap and explains time-dependent conditional efficiency scores and the nonparametric estimation. This section elucidates the location-scale models to eliminate the influence of common time factors and external variables. Section 3 illustrates an empirical application for the case of Italian economy. Section 4 gives concluding remarks.

2 Methodology

2.1 Forecasting model

In this section, we summarize the elements from Park et al. (2017) (hereafter PSZ) that are needed in our setup to forecast economic recessions. The model should provide the elements for analyzing the behavior of a discrete variable in a time series setup. The approach is nonparametric.

Suppose we observe $({{\varvec{X}}}^{t},{{\varvec{Z}}}^{t},Y^{t})$, $t=1,\ldots ,T$, where $\left\{ ({{\varvec{X}}}^{t},{{\varvec{Z}}}^{t},Y^{t})\right\} _{t=-\infty }^{\infty }$ is a stationary random process. We assume as in PSZ that the process satisfies strong mixing conditions that typically allows time dependence which disappears at a geometrical rate when the time lags are too large.²

The response variable is binary taking the values 0 and 1; in our set-up, $Y=1$ for a recession and $Y=0$ is otherwise. The vector of covariates ${{\varvec{X}}}^{t}$ is of dimension r and of continuous type, whereas ${{\varvec{Z}}}^{t}$ is a discrete vector of dimension k. The components of ${{\varvec{Z}}}^{t}$ may be lagged values of the response Y, e.g., $Y^{t-1},\ Y^{t-2}$. The idea is to estimate the mean function

$$\begin{aligned} m({{\varvec{x}}},{{\varvec{z}}})={{\mathbb {E}}}\left( Y|{{\varvec{X}}}={{\varvec{x}}},{{\varvec{Z}}}={{\varvec{z}}}\right) . \end{aligned}$$

(2.1)

Since Y is binary, we have

$$\begin{aligned} {{\mathbb {P}}}\left( Y=y|{{\varvec{X}}}={{\varvec{x}}},{{\varvec{Z}}}={{\varvec{z}}}\right) =m({{\varvec{x}}},{{\varvec{z}}})^{y}\left[ 1-m({{\varvec{x}}},{{\varvec{z}}})\right] ^{1-y},\hbox {for}\ y\in \{0,1\}. \end{aligned}$$

(2.2)

A key ingredient in these discrete choice models is the link function g, which is a strictly increasing function, defining the function f as

$$\begin{aligned} f({{\varvec{x}}},{{\varvec{z}}})=g(m({{\varvec{x}}},{{\varvec{z}}})). \end{aligned}$$

(2.3)

In parametric models, it is assumed that $f({{\varvec{x}}},{{\varvec{z}}})$ takes a parametric form, and then, $m({{\varvec{x}}},{{\varvec{z}}})=g^{-1}(f({{\varvec{x}}},{{\varvec{z}}}))$. Thus, a wrong choice may jeopardize the estimation of m. In nonparametric settings, $f({{\varvec{x}}},{{\varvec{z}}})$ will be locally approximated by some local polynomial around $({{\varvec{x}}},{{\varvec{z}}})$, so the choice of g is much less important. Approximating locally the functions $g_{1}(m({{\varvec{x}}},{{\varvec{z}}}))$ or $g_{2}(m({{\varvec{x}}},{{\varvec{z}}}))$ for two different link functions $g_{1}$ and $g_{2}$ does not make much difference. One may simply take the identity function, though since the range of the target m is [0, 1], we will choose a link that guarantees the correct range (like Probit or Logit). Now, given the link g and the sample $\left\{ ({{\varvec{X}}}^{t},{{\varvec{Z}}}^{t},Y^{t})\right\} _{t=1}^{T}$, we see from (2.2) that the log-likelihood of f is given by $\sum _{t=1}^{T}\ell \left( g^{-1}\left( f({{\varvec{X}}}^{t},{{\varvec{Z}}}^{t})\right) ,Y^{t}\right)$ where $\ell (\mu ,y)=y\log \left( \frac{\mu }{1-\mu }\right) +\log (1-\mu )$.

Let $({{\varvec{x}}},{{\varvec{z}}})$ be a fixed point of interest at which we want to estimate the value of the mean function m, or equivalently of its transformed function f. In a nonparametric approach, we will apply local smoothing techniques to the observations $({{\varvec{X}}}^{t},{{\varvec{Z}}}^{t})$, which are in the neighborhood of $({{\varvec{x}}},{{\varvec{z}}})$. As explained in PSZ, this leads to weighting the observation $({{\varvec{X}}}^{t},{{\varvec{Z}}}^{t})$ near $({{\varvec{x}}},{{\varvec{z}}})$ by some kernel. For the continuous variables (X), usual continuous kernels (Gaussian, Epanechnikov, etc.) can be used, while for the discrete variables (Z), some appropriate discrete kernels have to be used. Here we use the product kernel $w_{c}^{t}({{\varvec{x}}},{{\varvec{z}}})\times w_{d}^{t}({{\varvec{z}}})$ defined as

$$\begin{aligned} w_{c}^{t}({{\varvec{x}}},{{\varvec{z}}})= & {} \prod _{j=1}^{r}K_{h_{j}}(x_{j},X_{j}^{t},{{\varvec{z}}}). \end{aligned}$$

(2.4)

$$\begin{aligned} w_{d}^{t}({{\varvec{z}}})= & {} \prod _{l=1}^{k}\gamma _{l}^{\mathbb {1}(Z_{l}^{t}\ne z_{l})} \end{aligned}$$

(2.5)

where $\mathbb {1}(A)$ denotes the indicator function such that $\mathbb {1}(A)=1$ if A holds and zero otherwise and $\gamma _{l}\in [0,1]$ is the bandwidth for the $j{\mathrm{th}}$ discrete variable, while for the continuous kernels, we have

$$\begin{aligned} K_{h_{j}}(x_{j},X_{j}^{t},{{\varvec{z}}})&=\frac{1}{h_{j}(1)}K\left( \frac{X_{j}^{t}-x_{j}}{h_{j}(1)}\right) \times \mathbb {1}(Z^{t}=z(1)) \\&\quad +\frac{1}{h_{j}(2)}K\left( \frac{X_{j}^{t}-x_{j}}{h_{j}(2)}\right) \times \mathbb {1}(Z^{t}=z(2)) \end{aligned}$$

for a symmetric kernel function K and two bandwidth, $h_{j}(1)>0$ and $h_{j}(2)>0$, corresponding to the two groups denoted as z(1) and z(2), for each jth continuous variable. The discrete kernel is in the spirit of Aitchison and Aitken (1976), except that it is standardized to be between 0 and 1. The continuous kernel is a generalized kernel proposed by Li et.al. (2016), which allows different bandwidths for the continuous variables across various groups defined by the values of ${{\varvec{Z}}}$, thus allowing for more flexibility in terms of the fitted curvatures in the two groups. It is worth noting that when $\gamma _{l}=0$, one performs a separate estimation for each group identified by the values of $Z_{l}$. When $\gamma _{l}=1$, one considers that $Z_{l}$ is irrelevant and so all the groups are pooled together, although different bandwidths for continuous variables may still imply different curvatures in the two groups.

For approximating $f(\cdot ,\cdot )$ locally near the point $({{\varvec{x}}},{{\varvec{z}}})$, we will not make use of the link function, nor of the likelihood function. The local approximation is linear in the direction of the continuous variable and constant in the direction of the discrete variables. To be specific, we have

$$\begin{aligned} f({{\varvec{u}}},{{\varvec{v}}})\approx f({{\varvec{x}}},{{\varvec{z}}})+\sum _{j=1}^{r}f_{j}({{\varvec{x}}},{{\varvec{z}}})(u_{j}-x_{j}), \end{aligned}$$

(2.6)

where $f_{j}({{\varvec{x}}},{{\varvec{z}}})=\partial f({{\varvec{x}}},{{\varvec{z}}})/\partial x_{j}$. So the local approximation can be viewed as a first order Taylor’s expansion of f in ${{\varvec{x}}}$, near $({{\varvec{x}}},{{\varvec{z}}})$.

To estimate $f({{\varvec{x}}},{{\varvec{z}}})$ and its partial derivatives $f_{j}({{\varvec{x}}},{{\varvec{z}}})$, we thus maximize

$$\begin{aligned} T^{-1}\sum _{t=1}^{T}w_{c}^{t}({{\varvec{x}}},{{\varvec{z}}})w_{d}^{t}({{\varvec{z}}})\ell \left( g^{-1}\left( \beta _{0}+\sum _{j=1}^{r}\beta _{j}(X_{j}^{t}-x_{j})\right) ,Y^{t}\right) \end{aligned}$$

(2.7)

with respect to $\beta _{0}$ and $\beta _{j}$, $j=1,\ldots ,r$. The solutions ${\hat{\beta }}_{0}={\widehat{f}}({{\varvec{x}}},{{\varvec{z}}})$ and ${\hat{\beta }}_{j}={\widehat{f}}_{j}({{\varvec{x}}},{{\varvec{z}}})$ for $j=1,\ldots ,r$. Then, an estimator of the mean function $m({{\varvec{x}}},{{\varvec{z}}})$ is obtained by inverting the link function: ${\widehat{m}}({{\varvec{x}}},{{\varvec{z}}})=g^{-1}({\hat{\beta }}_{0})$.

The theory in PSZ shows that the asymptotic properties of the estimators do not much depend on the choice of the link function, as long it is smooth enough and strictly increasing, because the estimation is performed locally. We will choose below the probit link, i.e., $g(s)=\Phi ^{-1}(s)$, where $\Phi$ is the cumulative distribution function of the standard normal distribution. So we have to maximize in $(\beta _{0},\beta _{j})$, $j=1,\ldots ,r$

$$\begin{aligned}&T^{-1}\sum _{t=1}^{T}w_{c}^{t}({{\varvec{x}}},{{\varvec{z}}})w_{d}^{t}({{\varvec{z}}}) \left[ Y^{t}\log \left( \frac{\Phi \left( \beta _{0}+\sum _{j=1}^{r}\beta _{j}(X_{j}^{t}-x_{j})\right) }{1-\Phi \left( \beta _{0}+\sum _{j=1}^{r}\beta _{j}(X_{j}^{t}-x_{j})\right) }\right) \right. \nonumber \\&\quad \left. +\log \left( 1-\Phi \left( \beta _{0}+\sum _{j=1}^{r}\beta _{j}(X_{j}^{t}-x_{j})\right) \right) \right] . \end{aligned}$$

(2.8)

The properties of the resulting estimators follow from PSZ. In summary, under certain regularity assumptions and with the optimal order of the bandwidths, $h_{c,j}:=(h_{j}(1)+h_{j}(2))/2\propto T^{-1/(r+4)}$ and $\gamma _{l}\propto T^{-2/(k+4)}$, Theorem 3.1 in PSZ establishes

$$\begin{aligned} \sqrt{T{\bar{h}}_{c}}\left( {\widehat{f}}({{\varvec{x}}},{{\varvec{z}}})-f({{\varvec{x}}},{{\varvec{z}}})+\sum _{j=1}^{r}O\left( h_{c,j}^{2}\right) +\sum _{l=1}^{k}O\left( \gamma _{l}\right) \right) {\mathop {\longrightarrow }\limits ^{{{{{\mathcal {L}}}}}}}N(0,V({{\varvec{x}}},{{\varvec{z}}})),\nonumber \\ \end{aligned}$$

(2.9)

where ${\bar{h}}_{c}=\prod _{j=1}^{r}h_{c,j}$ and the variance V has a complicated expression which depends on the properties of the data generation process (DGP) (see PSZ for details). We see from (2.9) that the optimal bandwidths balance, as often the case, is between the square of the bias terms and the variance.

Remark 1

It is worth noting that if the bandwidths for continuous variables increase such that they cover all the observations on those variables, the nonparametric approach yields very similar estimates as the parametric approach that assumes (2.6) holds exactly. In this sense, the parametric approach can be viewed as a special case of the nonparametric approach, in the sense that the latter allows for much more flexibility and can be ‘reduced’ to the former by removing the flexibility through tuning the bandwidths to be large enough.

Remark 2

The nonparametric approach can also be viewed as a tool for validation of a suitable parametric approach. Indeed, when a parametric approach that assumes a particular (and perhaps very restrictive) functional form yields very similar results or conclusions as the nonparametric approach that allows for much more flexibility, this should give more confidence in the results or conclusions from the parametric approach, despite its restrictive assumptions. We will find this consideration very useful in our empirical application section for the particular data we use there.

2.2 Efficiency and estimation of the output gaps

We propose as an output gap our measure of inefficiency. The output gap is an economic measure of the difference between the actual output of an economy and its potential output. Potential output is the maximum amount of goods and services an economy can turn out when it is most efficient—that is, at full capacity. Often, potential output is referred to as the production capacity of the economy. In the context of this paper, we assume that a country is the producer of an output (i.e., GDP), given inputs (e.g., capital, labor), and available technology. The inefficiency is defined as the distance between the actual production and its maximum or frontier potential, given the inputs and technology.³

As explained above, we would like to use the level of inefficiency of the country for a particular year by considering the so-called conditional inefficiency (Cazals et al. 2002; Daraio and Simar 2005; Mastromarco and Simar 2015). Inputs here are Capital (K) and Labor (L), and the output is the GDP (Q), and we have quarterly data $t=1,\ldots ,T$ for 16 OECD countries. Evaluating the marginal efficiency measures by considering the so-called meta-frontier of the 3-dimensional cloud of T points $\{(K_{t},L_{t},Q_{t})\}_{t=1}^{T}$ would not make too much sense since the technology certainly varies over the years. We will rather consider the conditional efficiency measure where we condition on the time period. This enables us to take into account that production factors adjust to fluctuations of aggregate demand and supply with time delays due to market regulations and price stickiness.⁴

As suggested in Mastromarco and Simar (2015), to introduce the time dimension we consider indeed, with some abuse of notation, time as a conditioning variable W and we define the attainable production set at time t as the support of the conditional probability

$$\begin{aligned} H_{K,L,Q|W}(\xi ,\zeta ,\eta |W=t)={{\mathbb {P}}}\left( K\le \xi ,L\le \zeta ,Q\ge \eta \;|\;W=t\right) , \end{aligned}$$

(2.10)

which can be interpreted as the probability of observing, at time t, a production plan dominating a given point $(\xi ,\zeta ,\eta )$. So, the feasible technology $\Psi ^{t}$ can be defined as

$$\begin{aligned} \Psi ^{t}=\{(\xi ,\zeta ,\eta )\in {{\mathbb {R}}}_{+}^{3}|H_{K,L,Q|W}(\xi ,\zeta ,\eta \;|\;W=t)>0\}. \end{aligned}$$

(2.11)

Finally, this leads to consider for the output orientation the conditional efficiency score

$$\begin{aligned} \lambda (\xi ,\zeta ,\eta |t)=\sup \{\lambda |(\xi ,\zeta ,\lambda \eta )\in \Psi ^{t}\}\ge 1, \end{aligned}$$

(2.12)

which is known as the Farrell–Debreu output oriented efficiency measure (see, e.g., Kumar and Russell 2002, for its use in a related context but using a simpler estimator). Nonparametric estimators of these efficiency scores have been developed and their asymptotic properties are well known (see e.g. Jeong et al. 2010). Here, we will follow the approach suggested by Florens et al. (2014) which has some advantages described below.

In the first step, a flexible nonparametric model is used to whiten the inputs (K, L) and the output Q from the effect of time W. We have the following model

$$\begin{aligned} K_{it}&=\mu _{K}(t)+\sigma _{K}(t)\varepsilon _{K,t}\nonumber \\ L_{it}&=\mu _{L}(t)+\sigma _{L}(t)\varepsilon _{L,t}\nonumber \\ Q_{it}&=\mu _{Q}(t)+\sigma _{Q}(t)\varepsilon _{Q,t}, \end{aligned}$$

(2.13)

where we assume that $(\varepsilon _{K},\varepsilon _{L},\varepsilon _{Q})$ are ‘independent’ of time W, with ${{\mathbb {E}}}[\varepsilon _{\ell }]=0$ and ${{\mathbb {V}}}[\varepsilon _{\ell }]=1$ for $\ell =K,L,Q$. The estimation of the mean and variance functions is done by local polynomial smoothing as explained in detail in Florens et al. (2014). They suggest also a bootstrap test for testing the assumption of independence, but in our application below we will evaluate various correlations (Spearman, Pearson, and Kendall) to check if this assumption is reasonable.

In our application, we first use the local-linear methods to estimate the mean functions $\mu _{\ell }(t)$, $\ell =K,L,Q$. From the squared residuals, we estimate the variance functions $\sigma _{\ell }^{2}(t)$ by local constant methods (to avoid negative variances). Finally, Florens et al. (2014) define the estimated ‘pure’ inputs and the estimated ‘pure’ outputs as

$$\begin{aligned} {\widehat{\varepsilon }}_{K,it}&=\frac{K_{it}-{\widehat{\mu }}_{K}(t)}{{\widehat{\sigma }}_{K}(t)},\nonumber \\ {\widehat{\varepsilon }}_{L,it}&=\frac{L_{it}-{\widehat{\mu }}_{L}(t)}{{\widehat{\sigma }}_{L}(t)},\nonumber \\ {\widehat{\varepsilon }}_{Q,it}&=\frac{Q_{it}-{\widehat{\mu }}_{Q}(t)}{{\widehat{\sigma }}_{Q}(t)}, \end{aligned}$$

(2.14)

which are ‘pure’ in the sense of being filtered from time dependence. In this ‘pure units space,’ we can compute the output directional distance to the efficient frontier.⁵ Since the output here is univariate, the efficient frontier in pure units is the function

$$\begin{aligned} \varphi (e_{K},e_{L})=\sup \{e_{Q}|{{\mathbb {P}}}(\varepsilon _{K}\le e_{K},\varepsilon _{L}\le e_{L},\varepsilon _{Q}\ge e_{Q})>0\}, \end{aligned}$$

(2.15)

so that the directional distance of a point $(e_{K},e_{L},e_{Q})$ to the frontier is simply given by

$$\begin{aligned} \delta (e_{K},e_{L},e_{Q})=\varphi (e_{K},e_{L})-e_{Q}\ge 0, \end{aligned}$$

(2.16)

where the value zero indicates the point $(e_{K},e_{L},e_{Q})$ is on the efficient frontier. Under the location-scale assumptions, it can be proved that the conditional frontier in original units can be recovered as (see Florens et al. 2014, for details)

$$\begin{aligned} \tau (\xi ,\zeta |t)=\mu _{Q}(t)+\sigma _{Q}(t)\varphi \left( \frac{\xi -\mu _{K}(t)}{\sigma _{K}(t)},\frac{\zeta -\mu _{L}(t)}{\sigma _{L}(t)}\right) , \end{aligned}$$

(2.17)

so that the gap in the output to reach the frontier level is given by

$$\begin{aligned} G_{Q}(\xi ,\zeta ,\eta |t)=\sigma _{Q}(t)\delta (e_{K},e_{L},e_{Q}). \end{aligned}$$

(2.18)

The nonparametric estimators of these various elements are obtained by plugging the estimators of the mean and variance functions derived above. One of the main advantages of this location-scale approach is that for estimating the functions $(\mu _{\ell }(t),\sigma _{\ell }(t))$ we require only smoothing in the center of the data in a standard regression setup. As pointed out in Bădin et al. (2019), a direct estimation of $\lambda (\xi ,\zeta ,\eta |t)$ requires delicate problems of optimal bandwidths selection for estimating the support of the conditional $H_{K,L,Q|W}(\xi ,\zeta ,\eta \;|\;W=t)$.

So at the end of this step of efficiency estimations, we end up in practice with estimated efficiency scores in the pure units $\delta (e_{K_{t}},e_{L_{t}},e_{Q_{t}})$ and, if wanted, the measures of the gaps in original units of the DGP, i.e., $G_{Q}(K_{t},L_{t},Q_{t}|t)$ at each observation $t=1,\ldots ,T$. These values (eventually lagged) will be used to improve the prediction of a recession in our application below.

Real data samples contain in general some anomalous data, and the estimated frontier obtained by these nonparametric techniques can be fully determined by these outliers or extreme data points, jeopardizing the measurement of inefficiencies, potentially leading to unrealistic results. Cazals et al. (2002), Daouia and Simar (2007), in the frontier literature, propose an approach which aims to keep all the observations in the sample but replace the frontier of the empirical distribution by (conditional) quantiles or by the expectation of the minimum (or maximum) of a sub-sample of the data. This latter method defines the order-m frontier that we will use here.

In brief, the partial output frontier of order-m is defined for any integer m and for input values $e_{K_{t}},e_{L_{t}}$, as the expected value of the maximum of the output of m units drawn at random from the populations of units such that $\varepsilon _{K}\le e_{K},\varepsilon _{L}\le e_{L}$. Formally,

$$\begin{aligned} \tau _{m}(\xi ,\zeta |t)={{\mathbb {E}}}\left[ \max \left( \varepsilon _{Q,1t},\ldots ,\varepsilon _{Q,mt}\right) \right] , \end{aligned}$$

(2.19)

where the $\varepsilon _{Q,it}$ are drawn from the empirical conditional survival function ${\widehat{S}}_{\varepsilon _{Q}|\varepsilon _{x}}(e_{Q}|{{\varepsilon }}_{x,it}\le e_{x})$. This can be computed by Monte Carlo approximation or by solving a univariate numerical integral (for practical details see Simar and Vanhems 2012).

If m increases and converges to $\infty$ and $n\rightarrow \infty$, it has been shown (see Cazals et al. 2002) that the order-m frontier and its estimator converge to the full frontier, but for a finite m, the frontier will not envelop all the data points and so is much more robust than the Free Disposal Hull (FDH) to outliers and extreme data points (see, e.g., Daouia and Gijbels 2011, for the analysis of these estimators from a theory of robustness perspective). Another advantage of these estimators is that besides the fact that their limiting distribution is normal, they achieve the parametric rate of convergence ($\sqrt{n}$).

3 Empirical illustration: the case of modern Italy

3.1 Data in brief

There are different ways to measure the spread to be used in the models that we consider here. For the US economy, it is often (albeit not always) measured as the difference between the 10-year US Treasury bond rate and the 3-month US Treasury bill rate, though there are other variants (e.g., see Park et al. (2020) and references there in). For other countries, including those in the EU, there appears to be no ‘one-fit-all’ rule on how to best measure the spread, as it may depend largely on the country of interest or even the time period considered. Here we choose to measure it as the difference between the 10-year Italy Treasury bond rate and the 10-year Germany Treasury bond rate, in per cent per annum. The logic behind using this measure of spread is grounded in the belief that the 10-year yield on German bonds is typically considered as the benchmark for the Euro area since they are viewed by investors as a risk-free market asset, at least in relative terms.⁶ The data for this variable were sourced from OECD.stat Monthly Monetary and Financial Statistics (MEI).⁷ However, again, we acknowledge that other measures of the spread can be tried, and some of them potentially may work better for some countries, yet not others, or differ across different periods for the same country. In fact, finding such a measure of spread that would serve as the best predictor for a given country may be a research question in itself and we leave it for future research endeavors.

The variables on recessions are constructed as following. We use the Composite Leading Indicators from OECD Reference Turning Points and Component Series data, which is analogous to the information from the Business Cycle Dating Committee of NBER typically used for timing the recessions in the USA.⁸ In particular, note that the OECD identifies months of the so-called turning points (peaks and troughs) of the business cycle. The periods between a peak and a trough that follows it are then deemed as the recessionary periods ($Y_{t}=1$), while the periods between a trough and a peak that follows it are deemed as the expansionary periods ($Y_{t}=0$). To be more precise, since the turning points are announced for a particular month while we use quarterly data, to construct this time series we use the following rule: the recession begins on the quarter of the month of the peak and ends on the quarter of the month on the trough.⁹

To construct our measure of output gap, we need to go beyond the data on Italy and consider a few other countries that may be deemed as relevant peers for Italy, to estimate a relevant technological frontier. For this illustrative exercise, we choose the following OECD countries: Austria, Belgium, Denmark, Finland, France, Germany, Ireland, Israel, Italy, South Korea, Netherlands, New Zealand, Norway, Spain, Sweden and UK.¹⁰

The data for these countries were sourced from OECD.stat (OECD Quarterly National Accounts) and include 99 quarterly observations from (1995 : Q1) till (2019 : Q2), on capital, labor and output.¹¹ To be precise, the output Q is proxied by gross domestic product (GDP), and is measured in millions of US dollars, at 2015 constant price level. For the labor input L, we use the number of employed persons (in thousands) seasonally adjusted. Meanwhile, the capital K is also measured in millions of US dollars at 2015 constant price and constructed applying the perpetual inventory method (PIM) by using the real investment series (gross fixed capital formation).¹² As often suggested with macroeconomic data, all these variables are transformed in logarithms before the frontier estimation.

3.2 Brief economic background on Italy

The Italian economy is one of the oldest in the World, with roots going thousands years back to at least the Roman Empire. Through its long evolution on its way to the modern days, it has witnessed a myriad of ‘ups and downs’ of its economy—what is now usually referred to as Business Cycles. In a broad sense, even a book cannot give a full picture of this interesting country and its economy, yet a brief snapshot on the recent years might be useful here.¹³

Despite the long and great history, fairly developed institutions, and relatively high level of physical and human capital, the Italian economy has been fairly stagnant during the last three decades, the period we focus on in this study. For example, in Fig. 1 we depict the growth rate of Italian GDP during 1995–2019.¹⁴ Note that for the late 1900s, the figure exhibits negative growth in Q2 (2nd quarter) of 1996 and Q1 (1st quarter) of 1998. In the Q1 (1st quarter) of 2009, as the figure reveals, GDP growth registers the largest negative value, and by the Q3 (3rd quarter) of 2009 the economy began to re-grow slightly. In the Q3 (3rd quarter) of the year 2011, Italy’s growth was negative till Q1 (1st quarter) of 2013; then, Italy’s economy recovered with positive economic growth rates, but in Q1 of 2019 it starts to contract again. Here it is worth noting that, similarly as with the NBER data on recessions in the US, the OECD data on recessions in Italy (highlighted with gray shadow in Fig. 1) are not the same as the casual definition of a recession being two consecutive quarters of negative growth, but are based on the identification of the turning points of the business cycle, as described above.

Fig. 1

Growth rate of real GDP in Italy during 1995–2019

Fig. 2

Spread variable during 1995–2019, calculated as the difference between the 10-year Italy Treasury bond rate and 10-year Germany Treasury bond rate in per cent

Various reasons have been advocated in the literature as explanations for such poor economic performance of Italy. One of them is the lagging productivity growth relative to its peer countries. In particular, it was argued that insufficient productivity growth may be pivotal to Italy’s competitiveness problem, witnessed by the continual erosion of world export market shares and the limited ability to attract foreign direct investment (Faini et al. 2004). These problems appear to be particularly relevant in Italian manufacturing industries where productivity has been low and international competitiveness has worsened over the recent decades (Bassanetti et al. 2004; Aiello et al. 2011; Pellegrino and Zingales 2017). For example, Pellegrino and Zingales (2017) credit the inability of Italian firms to take full advantage of the information and communication technology revolution as one of the key reasons for the poor productivity or what they dubbed as ‘Italy’s productivity disease.’ In turn, and as for many other failures or successes of a country, the existence and persistence of this ‘disease’ appear to be due to specific institutional aspects; or, as Pellegrino and Zingales (2017) put it:

“While many institutional features can account for this failure, a prominent one is the lack of meritocracy in the selection and rewarding of managers. ...the prevalence of loyalty-based management in Italy is not simply the result of a failure to adjust, but an optimal response to the Italian institutional environment. Italy’s case suggests that familism and cronyism can be serious impediments to economic development even for a highly industrialized nation.”

Clearly, disentangling the true reasons for the recessions in Italy is well beyond the scope of this paper, if at all possible. What seems more feasible, however, is to compare or benchmark Italy to some of its peers—as we do via the proposed output gap measure explained above—in the hope that it may potentially help in providing some useful information for predicting upcoming recessions via the dynamic choice models.

Table 1 Correlation between $W=time$ and pure inputs $\varepsilon _{X1}$, $\varepsilon _{X2}$ and pure output $\varepsilon _{Y}$

Turning the attention to the spread dynamics, one can also note that Fig. 2 reveals the spread between the 10-year Italy Treasury bond rate and 10-year Germany Treasury bond rate increases during the period of low economic growth. This indicates a lack of confidence of investors in the Italian economy due to the deterioration of potential determinants of the spread, namely the current or expected macroeconomic fundamentals, such as fiscal policy, international risk, liquidity conditions, sovereign credit ratings, to mention a few. Again, note that while in some periods the dynamics of the spread to some extent matches the upcoming changes in the recession indicators (highlighted with gray shadow), the relationship appears to be not very strong, e.g., relative to what we found in the literature for the recessions in the USA (see Park et al. 2020 and references therein).

3.3 Filtering the inputs/output and efficiency estimates

Here, we first have to run three location-scale models for K, L, Q, respectively, to clean the effect of time W.¹⁵ This provides the ‘pure’ inputs and ‘pure’ output, $\{({\widehat{\varepsilon }}_{K_{t}},{\widehat{\varepsilon }}_{L_{t}},{\widehat{\varepsilon }}_{Q_{t}})\}_{t=1}^{T}$ as explained above. The correlations of these ‘pure’ inputs/output with time are given in Table 1 (where $X_{1}=K,X_{2}=L,Y=Q$ and $Z=W$). Clearly these correlations are very small so we can infer that the assumption of independence between $(\varepsilon _{K},\varepsilon _{L},\varepsilon _{Q})$ and W, which is part of our location-scale model, seems reasonable.

Robust measures of efficiency scores, providing the gaps in ‘pure’ units were computed with $m=1500$. This choice was done for letting less than 25% of points above the order-m frontier, as shown in Fig. 3. Note that from the values of $m=1500$ and m $\rightarrow$ $\infty$ (the full FDH frontier), all the results are quite similar.

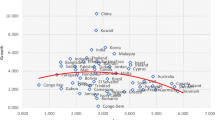
The resulting efficiency scores ${\widehat{\delta }}_{m,t}$ are shown in Fig. 4, which illustrates that most of the time, the time effect has indeed been cleaned from the production process. We see also that most of the values of ${\widehat{\delta }}_{m,t}$ are positive and some take very small (near zero) negative values. Figure 5 exhibits the time path of output gaps in original units (in logs and re-scaled by their mean). Figure 6 reports the values of the gap in original units for each country in our sample at the first period of observation (1995: Q1) and last period (2019: Q2).

Fig. 3

Percentage of points left above the order-m frontier, as a function of m. We selected $m=1500$ letting less than 25% of data points above the frontier

Fig. 4

Evolution of estimated inefficiency scores of Italy $({\widehat{\delta }}_{m,t})$ over time

Fig. 5

Evolution of GAP of Italy over time

Fig. 6

Boxplots of the estimated local $\beta$’s, with the full sample of $n=98$ data points

We give in “Appendix C” the full table of results for all the time periods. The table also indicates the gaps $G_{t}$ in original units of the DGP, as defined above (in log scale and re-scaled by their mean). Figure 9 in “Appendix C” reports the values of output gap in original units for all countries in our analysis for the first and last year of the observation period.

3.4 In-sample fit of the model

Our next step is to fit the prediction model described above by estimating the parametric linear probit model and the nonparametric model of PSZ to the data described above. In particular, we fit the following model:

$$\begin{aligned} {{\mathbb {E}}}\left( Y|{{\varvec{X}}}={{\varvec{x}}},{{\varvec{Z}}}={{\varvec{z}}}\right) =m({{\varvec{x}}},{{\varvec{z}}})=m(X_{1},X_{2},Z), \end{aligned}$$

(3.1)

where $X_{1,t}={Sp}_{t-r_{1}}$ is the spread lagged by $r_{1}$ periods, $X_{2,t}=\Delta _{G,t-r_{2}}$ is the first difference of the estimates of output gaps (production efficiency) lagged by $r_{2}$ periods. Finally, $Z_{t}=Y_{t-r_{3}}$, where we recall that $Y_{t}$ is the dichotomous dependent variable, defined as $Y_{t}=1$ if “Italian economy is in recession” in the quarter t and 0 otherwise and $r_{3}$ is its chosen lag. Finally, for smoothing $Z_{t}$ in the nonparametric approach we use the complete smoothing technique suggested by Li et.al. (2016), allowing different bandwidths for the continuous variables in the two groups determined by the values of Z, as described in Sect. 2.1.

Even though there are only three potential predictors in the general specification (3.1), many variations in it are possible that are based on different subsets of predictors and different choices of lags for each predictor. In the following sub-sections, using data on Italy we briefly show and discuss how a model selection can be done in such situations.¹⁶

3.4.1 Selection of lags

As is typical in empirical time-series studies, there is no theory on what lags should be chosen—it is largely an empirical issue. Here we will focus our discussion on the case when $r_{1}=r_{2}=2$ and $r_{3}=1$. Thus, intuitively, our model assumes that the first difference of our measure of output gap affects the probability of an economy to be in recession with some delays, e.g., due to market imperfections and frictions. In particular, in this model it is expected to act as an indicator of recession two periods in advance, similarly as the other indicator, the spread, often used to forecast the recession, which in our case is expected to indicate two periods before a recession.

We also considered other combinations of lags and none of them have dominated the one we focus on here in the main text of the paper (see “Appendix A” for the related results). In particular, as suggested in the literature for measuring the quality of the model fit, we used the values of the achieved Maximum Likelihood and the Estrella Pseudo-$R^{2}$ to compare the models, although alternative measures of goodness-of-fit can also be used.¹⁷

Table 2 Parametric and nonparametric estimates of the dynamic probit model of recessions in Italy, 1995–2019 (when lag of $X_1=$ 2, lag of $X_2=$ 2, lag of $Z=$ 1)

3.4.2 Selection of predictors

For each combination of lags, we tried several specifications to check the sensitivity of results with respect to dropping/adding of predictors of interest. The estimation results are shown in Table 2 for the case when $r_{1}=r_{2}=2$ and $r_{3}=1$, and analogous results for other choices of the lags are presented in “Appendix A”. Specifically, the first column indicates which coefficients of the index function were estimated: $\beta _{0}$ is the constant, $\beta _{1}$ is the coefficient for the spread, $\beta _{2}$ is the coefficient for the output gap and $\beta _{3}$ is the coefficient for lagged dependent variable. The second column reports the parametric estimates and the third column presents their standard errors, while the fourth and the fifth columns present the corresponding t statistics and p values for the two-sided tests (relying on the asymptotic normality), respectively. Since the nonparametric estimates of the coefficients vary across the observations, in this table we only present their averages (where available)—reported in the last column of the table and discussed in more detail further on.¹⁸

In principle, it is possible to automatize the model selection process, e.g., using currently popular statistical approaches in Machine Learning (e.g., forward step-wise selection, best subset selection, various LASSO approaches, etc.) to our modeling, to arrive at a final parsimonious model suggested by “the machines” based on some pre-specified statistical criteria. However, in the case of a small number of predictors like ours, it might be more valuable, at least for illustration/pedagogical purposes, to discuss how a model can be selected by practitioners, also in the spirit of forward step-wise and best subset selection methods, yet thoughtfully rather than automatically.

We start with the Specification 1 in Table 2, which considers the spread as the only predictor, i.e., it is the specification that Estrella and Mishkin (1997) used for the US economy and the originator of the paradigm we tried to adapt and extend here. One can see that the parametric estimate of $\beta _{1}$ is 0.364 and is statistically significant at 1%. Note, however, that the average of the nonparametric estimates is substantially smaller, around 0.184. Moreover, the Pseudo-$R^{2}$ of the parametric model is quite low, about 0.074, while for the nonparametric it is 0.15, i.e., about 2 times higher than for the parametric model, yet still relatively low from a perspective of predictive power, thus encouraging to try other or more predictors, as we do below.

The Specification 2 considers the output gap as the only predictor. One can see that the parametric estimate of $\beta _{2}$ is 1.444 and is also statistically significant at 1%. Notably, it is substantially larger in magnitude than the estimate of $\beta _{1}$ in the Specification 1 (note that the data on both variables were standardized). Interestingly, the average of the nonparametric estimates is 1.531, i.e., has the same sign of the relationship and is also similar in magnitude to the parametric estimate. Meanwhile, the Pseudo-$R^{2}$ of the parametric and nonparametric models are still fairly low, about 0.123 and 0.158, respectively, which is somewhat better than for Specification 1, especially for the parametric model.

The Specification 3 considers both the spread and the output gap as the two predictors. The parametric estimate of the coefficient of the spread ($\beta _{1}$) is now 0.470, which is a bit larger relative to what it was in Specification 1, and continues to be statistically significant at 1%. Note that the average of the nonparametric estimates for this coefficient is about two times smaller. Meanwhile, the parametric estimate of the output gap ($\beta _{2}$) is now 1.81, which is slightly larger than what it was in Specification 2 (and continues to be a statistically significant predictor at 1%), while the average of the nonparametric estimates of $\beta _{2}$ is higher, about 2.0, which is still fairly similar in magnitude to the parametric estimate. The Pseudo-$R^{2}$ of the parametric and nonparametric models is now 0.23 and 0.32, i.e., both improved substantially relative to Specifications 1 and 2, suggesting that both variables have something ‘valuable to tell us’ in terms of predictions of the recession for these data.

Specification 4 is analogous to Specifications 1 and 2, except that it takes the lagged value of the dependent variable as the only predictor. Since there is no continuous variable in this specification we only use a parametric approach here, which gives 2.406 as the estimate of $\beta _{3}$, with a high statistical significance (well under 1%). Moreover, the Pseudo-$R^{2}$ here is 0.6, which is the highest so far.

Specification 5 has the spread variable and the lagged recession indicator, i.e., this is the model analogous to Duecker (1997), Kauppi and Saikkonen (2008), Park et al. (2020) and many others. Specification 6 has the output gap variable and the lagged recession indicator, while Specification 7 has all three variables in the model. In all three cases, the estimate of $\beta _{3}$ remained similar (albeit slightly lower) relative to Specification 4, while the Pseudo-$R^{2}$ increased to some extent, with the highest one for Specification 7 (about 0.64 for the parametric and 0.71 for the nonparametric approaches). Meanwhile, relative to those from Specifications 1, 2 and 3, the magnitudes of the estimates of $\beta _{1}$ and $\beta _{2}$ decreased further (especially relative to Specification 3, which had both of them), while their standard errors increased further. In turn, this led to a substantial increase in p-values to around 0.137 and 0.235 for $\beta _{1}$ and $\beta _{2}$ in Specifications 5 and 6, respectively, and 0.076 and 0.145 in Specification 7, for the two-sided tests or half of those values for the one-sided tests.

Note that while we presented the two-sided test results, the one-sided tests might be indeed more relevant here: a priori we would expect that the increasing output gap of a country (i.e., its further lagging behind relative to peer countries) could serve as an early signal of the country entering a recession. Similarly with our definition of the spread: the increase in the difference between the Italian bonds and the German bonds is a cumulative signal of what investors sense about the Italian economy, which may reflect the true dynamics or contribute to the ‘self-fulfilling prophecies’ by forcing local businesses to pay higher local interest rates or reduce the local investments. Even more evident is the expected sign for the relationship between the recession indicator and its lagged value: the majority of the quarters are where $Y_{t}=0$ (i.e., no recession) and most of them are also followed by $Y_{t}=0$, until the switch to $Y_{t}=1$ (recession) that stays for a few quarters as $Y_{t}=0$ until it switches back to $Y_{t}=1$ and so on, i.e., implying a positive relationship between $Y_{t}$ and $Y_{t-1}$.

The phenomenon where a powerful predictor of the dependent variable is the lagged dependent variable, and possibly dominating all other predictors is, of course, very common in time series. However, while it appears as the most powerful predictor of the three variables that we considered here, it is important to note that the precise information on our lagged value of the recession indicator is often not available for the most recent periods in real time, which are also the periods that are the most important for the prediction of future periods. This is because the OECD decisions on the turning points of a business cycle (peak or trough) from which the variable is constructed usually come with some delay (similarly as for NBER data about USA), which may be as long as a few months to a few quarters. That is, while there is a lot of useful historical information in this variable, most of it is ‘too old’ for the actual prediction of the future. And, this is where the other two predictors might be useful, although their overall predictive power is partially taken over by the lagged dependent variable once it becomes available, making $\beta _{1}$ and $\beta _{2}$ significant only at 5% and 10%, respectively, in the one-sided tests. Overall, considering this phenomenon and the relatively small sample (96 observations), we deem these two continuous variables as useful predictors for the case of Italy and in what follows we will focus on Specification 7, which we will refer to as the ‘final specification.’¹⁹

3.4.3 Insights from the final specification

While focusing on the final specification, one can see that the nonparametric complete smoothing approach offers similar (and slightly better) results as the parametric probit on both the achieved maximum likelihood value and of the Pseudo-$R^{2}$. Indeed, the Pseudo-$R^{2}$ is around 64% for the parametric approach, while it is 71% for the nonparametric approach. This suggests that the linearity assumption in the parametric approach may be a reasonable approximation for both $X_{1}$ (the Spread, $S_{p,t-2}$) and $X_{2}$ (the output gap, $\Delta _{G,t-2}$) for these data. Although this simplification led to a slightly lower attained goodness of fit, its simplicity of estimation, especially due to the readily available inference procedures, may warrant it a status of the preferred approach for these data and specification. Meanwhile, the nonparametric approach can serve here as a robustness check tool and so a few words on this are in order.

Figure 6 exhibits the boxplots of the resulting local estimates of $\beta _{0},\beta _{1}$ and $\beta _{2}$ for the two states of the economy $Y_{t}=1$ (recessions) and $Y_{t}=0$ (expansions).²⁰ It is interesting to see some similarity as well as substantial difference in the local estimates of $\beta _{0},\beta _{1}$ and $\beta _{2}$ across the two groups of observations. In particular, note that only the medians of $\beta _{2}$ are somewhat similar, suggesting about some stability of the relationship between the predictors and the response variable regardless of the state of the economy. (The estimates are very different for $\beta _{0}$, which is expected since the estimate of $\beta _{0}$ determines the estimate of the probability of recession, via the link function.) Also note that the median of the nonparametric estimates for $\beta _{1}$ is nearly zero for $Y_{t}=1$ and positive (around 0.5) when $Y_{t}=0$. This suggests that in these data the spread variable ($X_{1,t}=S_{p,t-2}$) appears to be a more powerful predictor during expansionary periods relative to recessionary periods, which is somewhat intuitive and resembles the so-called liquidity-trap phenomenon in macroeconomics. One can also observe a greater range and the interquartile range, as well as more outliers in the recessionary periods for this variable, suggesting about greater possible estimation noise. It is also coherent with the fact that while all recessions are coded here as $Y_{t}=1$, many (if not all) of them have many unique features as well as those caused by possible different compositions of factors and triggers, which in turn make predicting recessions a very challenging task.

We see an even greater difference for the first difference of our measure of output gap ($X_{2,t}=\Delta _{G,t-2}$). In particular, note that while the median of estimates for $\beta _{2}$ are similar in the two states of the economy, the range is very different and is larger for the recessionary periods. In both cases, the median is around 1.5, suggesting that the positive growth in inefficiency, our measure of output gap, is associated with an increase in the probability to be in a recession. This positive association seems to be more pronounced in expansionary periods of the economy, as we see mostly a positive range there.²¹

Fig. 7

In-sample fit for recessions in Italy, 1995–2019, with $n=98$ data points

We now look at the in-sample fit for modeling the probability of recessions in Fig. 7. We can indeed observe that both the nonparametric and parametric approaches fit the data well (as seen with various measures described above). In particular, note that most of the recession periods, as established by the turning points of OECD.stat, are successfully captured by our model both using the parametric and the nonparametric approaches.

3.5 Out-of-sample forecasts

We now proceed with the out-of-sample forecasts, to see if we can have a reasonably good prediction of the recession periods (one-period and two-periods ahead), using the data from the beginning till 2016:Q1 from either the parametric or nonparametric approaches.²²

The forecasts of the recessions are displayed in Fig. 8. In most cases (and on average), we can observe a slightly better forecast value for the parametric approach, both for the case of the one-period ahead and for the two-periods ahead forecasts. In particular, note that, with the one-period ahead forecasts, both approaches correctly and somewhat similarly warn about the recession in Q1-2018–Q2-2019, with the parametric approach slightly outperforming. Both approaches with the one-period ahead forecasts correctly alert us to the non-recession (or expansions) in Q1-2016 through Q3-2017, though both miss on warning about the start of the recession in Q4-2017, while they manage to warn correctly about the subsequent quarters being in the recession.

Fig. 8

Forecast of the Recessions, starting after $T=Q1-2016$ periods

Finally, it is worth recalling here that the parametric approach can be viewed as a special case of the nonparametric approach, in the sense that the latter allows for much more flexibility and can be restricted further to obtain the former through reducing this flexibility. Interestingly, for this data set we see that despite assuming a naive (linear) and quite restrictive (e.g., constancy of the first derivative) functional form for the index function, the parametric approach still produced very similar conclusions and very similar or even slightly better forecasts than the nonparametric approach which allows for much more flexibility. This suggests that, for this sample and the specifications we considered, we can have more confidence in the results and conclusions from the parametric approach, even though it imposes fairly restrictive assumptions. Of course for other data (e.g., for other countries or even the same country but for different time periods or with different variables), this similarity of parametric and nonparametric approaches may or may not hold a priori and so needs to be verified and validated on a case-by-case basis. Indeed, it is very easy to construct an example when parametric and nonparametric approaches deliver very different results and conclusions, (e.g., see Monte Carlo examples in PSZ).

4 Concluding remarks

In this paper, we have attempted to merge two so far largely unrelated streams of literature. The first stream is about the non-parametric methods to estimate frontier efficiency of an economy, which we tailor to estimate the output gap of a country. The other stream is the literature on predicting economic recessions. We considered various methods among the myriad of approaches, selecting and tailoring one that currently appears to be the most suitable for a new measure of output gap to be used, inter alia, for estimating the probability of economic recessions. For the latter goal, we have chosen the paradigm started by Estrella and Mishkin (1995, 1998), further refined by Duecker (1997) and Kauppi and Saikkonen (2008) as well as their nonparametric version recently developed by Park et al. (2017, 2020). Naturally, endeavoring to merge the economic efficiency literature with other methods from the many paradigms for forecasting of economic recessions would be a natural direction for future research.

To illustrate our proposed framework that resulted from the merger of two different literatures, we apply it to the context and data on the Italian economy. In particular, we utilize the data from 1995 to 2019 and find that the proposed approach (using both the linear probit model and its non-parametric version) is capable of giving useful insights, although of course it is not a ‘crystal ball’ and more work is needed to refine and further improve this method and, possibly, synthesize it with other methods as well as try it on other data sets. In particular, it appears that our measure of output gap, based on efficiency measures in general and via the estimation approach we considered here, is sound conceptually and can be useful as a predictor (or a proxy) in the models for forecasting recessions and perhaps other macroeconomic models. We acknowledge that there, of course, could be many other good predictors or proxies for similar or different reasons and they could be fruitful avenues for future research. Also, development of the asymptotic theory for the statistical inference in the nonparametric approach (e.g., via bootstrap) would be an important direction for future theoretical research.

Appendices

Sensitivity analysis and model validation

Table 3 Parametric and nonparametric estimates of dynamic probit model of recessions in Italy, 1995–2019 (when lag of $X_1=$ 1, lag of $X_2=$ 2, lag of $Z=$ 1)

Table 4 Parametric and nonparametric estimates of dynamic probit model of recessions in Italy, 1995–2019 (when lag of $X_1=$ 3, lag of $X_2=$ 2, lag of $Z=$ 1)

Table 5 Parametric and nonparametric estimates of dynamic probit model of recessions in Italy, 1995–2019 (when lag of $X_1=$ 3, lag of $X_2=$ 3, lag of $Z=$ 1)

Table 6 Parametric and nonparametric estimates of dynamic probit model of recessions in Italy, 1995–2019 (when lag of $X_1=$ 2, lag of $X_2=$ 3, lag of $Z=$ 1)

Table 7 Parametric and nonparametric estimates of dynamic probit model of recessions in Italy, 1995–2019 (when lag of $X_1=$ 1, lag of $X_2=$ 3, lag of $Z=$ 1)

Table 8 Parametric and nonparametric estimates of dynamic probit model of recessions in Italy, 1995–2019 (when lag of $X_1=$ 2, lag of $X_2=$ 2, lag of $Z=$ 2)

Data description

Country		Y	K	L
Austria	Mean	3.35E+05	1.25E+06	3963.9
	SD	40359	1.13E+05	235.81
Belgium	Mean	4.11E+05	1.43E+06	4403.5
	SD	48008	2.16E+05	285.89
Denmark	Mean	2.34E+05	9.16E+05	2777.3
	SD	21562	2.10E+05	78.092
Finland	Mean	1.94E+05	7.41E+05	2405.5
	SD	25712	41161	156.8
France	Mean	2.24E+06	6.87E+06	26681
	SD	2.34E+05	2.15E+06	1356.2
Germany	Mean	3.14E+06	1.02E+07	40683
	SD	3.02E+05	6.55E+05	2052.3
Ireland	Mean	1.95E+05	2.48E+06	1854.3
	SD	63151	2.48E+06	250.37
Israel	Mean	2.01E+05	7.37E+05	3193.9
	SD	51294	1.37E+05	596.6
Italy	Mean	2.03E+06	5.78E+06	23710
	SD	92116	1.53E+06	1146
Korea	Mean	1.38E+06	6.84E+06	23429
	SD	3.92E+05	1.08E+06	2170.3
Netherlands	Mean	7.07E+05	2.31E+06	8412.5
	SD	84283	3.30E+05	485.19
New Zealand	Mean	1.27E+05	3.98E+05	2096.1
	SD	24578	1.06E+05	276.78
Norway	Mean	2.71E+05	8.50E+05	2498.4
	SD	34325	2.09E+05	221.85
Spain	Mean	1.36E+06	5.07E+06	18192
	SD	1.89E+05	9.93E+05	2143
Sweden	Mean	3.67E+05	1.24E+06	4480.6
	SD	59666	2.82E+05	336.44
UK	Mean	2.19E+06	5.69E+06	29036
	SD	2.93E+05	7.03E+05	1878.7

Measures of efficiencies

Table 9 Different measures of efficiency: efficiency $\delta$, Order-m Efficiency $\delta _m$, Time Conditional Efficiency $\lambda$, Order-m time conditional efficiency $\lambda _m$, pure time conditional efficiency GAP, Order-m pure time conditional Efficiency $GAP_m$

Fig. 9

Our estimates of output gap for a sample of 16 countries from for 1995 and 2019