Abstract
This paper proposes a practical and data-driven preference estimation method from reported lists in a deferred acceptance mechanism when there are incentives to report these lists strategically. Data on centralized college admissions from Turkey show many pieces of evidence that students construct their lists strategically according to their admission chances and previous years’ admission outcomes. We develop a preference estimation method to evaluate reported lists within the set of colleges that are considered accessible to each student. This method allows us to create personal choice sets and to estimate student preferences by making valid utility comparisons that are supported by data and theory. We show the robustness of our estimation method compared to the existing estimation methods. A counterfactual admission analysis based on our preference estimates suggests that students from low-SES households are better off under a student sorting rule only based on high school GPAs.




Similar content being viewed by others
Notes
Stability implies that students match with their favorite feasible college. A college is feasible in score-based centralized college admissions if the cutoff score of all of the admitted students is lower than the student’s score.
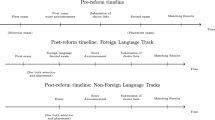
There are two versions of the DA algorithm. In the algorithm, one side of the two-sided matching proposes to become a pair to the other side. The recipients decide to hold the offer or not. The names of the matching algorithm and admission outcome change with the proposing side. There are also incentives for the recipient side to deviate from submitting a ROL truthfully. Balinski and Sönmez (1999) note that the matching outcome in Turkey corresponds to a college-proposing DA mechanism because of the ranking variations across education tracks. However, except for rare cases, students apply in the same education tracks, and Balinski and Sönmez (1999)’s note does not hold in practice. Moreover, the proposing side does not matter in a large admission model because there is a unique equilibrium in the limit.
The admission criterion is \(Totalscore_i= CEE_i + 0.8\times HS\;GPA_i\) if the choice is in the same track, \(Totalscore_i= CEE_i + 0.3\times HS\;GPA_i\) otherwise.
More detailed data for the college admissions and the college entrance examinations in 2005 can be found on https://www.osym.gov.tr/Eklenti/694,osysilgilipdf.pdf?0.
Students may not submit a ROL because they want to try again in the following years or have another outside option. According to Krishna et al. (2018), around two-thirds of all first-time applicants retake the college admission examination, and around 10 percent of students take it at least 4 times.
The high tuition cost for unfunded private college programs may create restrictions for students’ application behavior. While, in principle, the proposed estimation methodology easily incorporates these restrictions in the estimations compared to other estimation methods, we did not apply these restrictions in our empirical application because of the lack of sufficient wealth status data on students’ families.
To fix ideas of private college admissions with different funding programs, consider a private college A. College A accepts students to economics major with two programs: (i) funded economics and (ii) unfunded economics. While these two programs will serve the same education after admissions, the admissions are separate based on the funding structure. Since funded programs are more demanded, private college funding decisions become merit-based.
We rely on rational expectation assumption to include these programs in the consideration set approach.
A similar empirical analysis has been done by Larroucau and Rios (2018) using Chile data. The authors provide empirical evidence on strategic behavior in ROL construction.
This approach has been used to evaluate many different college admission policies (e.g., Azevedo and Leshno (2016)—school quality investment, Bodoh-Creed and Hickman (2017, (2018)—affirmative action, Olszewski and Siegel (2018)—performance disclosure), but it has not been frequently applied in preference estimation literature.
In our model, student priorities are strict, and we can express the outcomes of a matching with ex post cutoff scores.
The existence of a ROL that maximizes utility is a result of the bounded utilities. However, the uniqueness of the ROL requires more conditions that make the expected utility function smooth and concave.
We can generalize Lemma 1 with the knowledge of differences in the variance of cutoff scores. If there is common knowledge on the variance of cutoff scores, students’ limit score—where above the limit scores they believe that their admission chances are zero—becomes a function of support of the distribution of cutoff scores. Consideration sets can be easily constructed from the support of the distribution of cutoff scores.
A comparable result of Theorem 1 is presented by Calsamiglia et al. (2010). They show that submitting a ROL truthfully up to and including the “safe” colleges (i.e., a college to which student is very likely to be admitted) is a weakly dominant strategy. However, Theorem 1 does not impose any “safe” college condition. Moreover, recall that Fig. 2 shows the substantial number of students do not submit a ROL that includes a “safe” college.
Fack et al. (2019) include a notable exception. In addition to the asymptotic stability-based estimation, they provide an alternative estimation method with the partial orders of colleges in ROLs. Their method uses a moment inequalities approach. However, its generalization to bigger settings is impossible because of the number of inequalities.
Our empirical application is a classic example of score-based centralized college admissions from Turkey. Our procedure can be easily adapted by other mechanisms that use an admission criterion that generates strict sorting among the applicants. For example, usnews.com provides information regarding the competitiveness of college admission in the USA.
In all five specifications, we assume that students choose college programs conditional on their reported field-of-study choices. In other words, we only consider students’ college preferences, and the results do not incorporate field-of-study preferences.
Details of sample selection and summary statistics are in Appendix.
We selected ROLs with 9 and 10 choices because these are the most commonly submitted ROL lengths in Turkey.
We present estimation results with samples that have different numbers of colleges in ROLs in Table 12.
Bogazici is one of the most popular colleges among students who have the highest admission scores. Figure 5 presents the first choices of the top hundred students in all education tracks.
Note that we implemented Hausman specification test under the distributional assumptions, and these tests are more likely to favor less restrictive economic assumptions if the parametric model is incorrectly specified.
See Fig. 8 for the visual illustration.
There are some exceptions for specific cases. For example, a special training high school student may become advantaged for specific programs.
The details of this construction of true preference orders and counterfactual assignment principles are explained in Sect. 8.6.
Since counterfactual HS GPA-based admissions provide information about the admission outcomes from the CEE-based admissions as the approximate opposite case, we drop CEE-based admission results for the sake of brevity.
Note that the average chance of being assigned to a college program in only HS GPA-based admissions is lower than the current admission rule. This number shows that high school GPA scores and entrance examination scores are not perfectly correlated.
Note that in order to incorporate into our estimation sample two-year degree programs and students who included these programs, we have to make many simplifications of the admission rules for these programs.
References
Abdulkadiroglu A (2013) School Choice. In: Vulkan N, Roth AE, Neeman Z (eds) The handbook of market design. Oxford: Oxford University Press, Chapter 5, pp 138–169
Abdulkadiroglu A, Sönmez T (2003) School choice: a mechanism design approach. Am Econ Rev 93(3):729–747
Abdulkadiroğlu A, Agarwal N, Pathak PA (2017) The welfare effects of coordinated assignment: evidence from the New York City high school match. Am Econ Rev 107(12):3635–89
Agarwal N, Somaini P (2018) Demand analysis using strategic reports: an application to a school choice mechanism. Econometrica 86(2):391–444
Ajayi KF (2015) School Choice and Educational Mobility: Lessons from Secondary School Applications in Ghana, Technical report, Working paper
Akyol P, Krishna K (2017) Preferences, Selection, and value added: a structural approach. Eur Econ Rev 91:89–117
Alkan A, Carkoglu A, Filiztekin A, Inceoğlu F (2008) Value Added Production in Turkish Secondary Education Institutions: College Admission Contest (in Turkish), Technical report, Sabanci University, Available on: https://research.sabanciuniv.edu/11135/1/proje.pdf. Accessed 01 June 2018
Arslan HA (2019) An Empirical Analysis of College Admissions with Endogenous Entrance Exam Scores Available on: https://ssrn.com/abstract=3346459
Artemov G, Che Y-K, He Y (2017) Strategic ‘Mistakes’: Implications for Market Design Research, Technical report, Working paper
Attanasio OP, Meghir C, Santiago A (2011) Education choices in Mexico: using a structural model and a randomized experiment to evaluate progresa. Rev Econ Stud 79(1):37–66
Azevedo EM, Leshno JD (2016) A supply and demand framework for two-sided matching markets. J Polit Econ 124(5):1235–1268
Balinski M, Sönmez T (1999) A tale of two mechanisms: student placement. J Econ Theory 84(1):73–94
Bodoh-Creed AL, Hickman BR (2017) Pre-College Human Capital Investment and Affirmative Action: A Structural Policy Analysis of US College Admissions, Technical report, Working paper
Bodoh-Creed AL, Hickman BR (2018) College assignment as a Large Contest. J Econ Theory 175:88–126
Burgess S, Greaves E, Vignoles A, Wilson D (2015) What parents want: school preferences and school choice. Econ J 125(587):1262–1289
Calsamiglia C, Fu C, Güell M (2020) Structural estimation of a model of school choices: The Boston mechanism vs. its alternatives. J Polit Econ 128:642–680
Calsamiglia C, Haeringer G, Klijn F (2010) Constrained school choice: an experimental study. Am Econ Rev 100(4):1860–1874
Drewes T, Michael C (2006) How do Students Choose a University? An analysis of Applications to Universities in Ontario, Canada. Res Higher Educ 47(7):781–800
Fack G, Grenet J, He Y (2019) Beyond truth-telling: preference estimation with centralized school choice and college admissions. Am Econ Rev 109(4):1486–1529
Gale D, Shapley LS (1962) College admissions and the stability of marriage. Am Math Month 69(1):9–15
Haeringer G, Klijn F (2009) Constrained school choice. J Econ Theory 144(5):1921–1947
Hassidim A, Romm A, Shorrer RI (2016) Strategic Behavior in a Strategy-proof Environment. In: Proceedings of the 2016 ACM Conference on Economics and Computation, ACM, pp 763–764
He Y (2012) Gaming the Boston School Choice Mechanism in Beijing. Manuscript, Toulouse School of Economics
He Y, Magnac, T (2020) Application Costs and Congestion in Matching Markets. Available at SSRN 3661425
Hernández-Chanto A (2018) Centralized Assignment of Students to Majors: Evidence from the University of Costa Rica, Technical report, Working paper
Kapor A, Neilson CA, Zimmerman SD (2020) Heterogeneous beliefs and school choice mechanisms. Am Econ Rev 110(5):1274–1315
Kirkebøen LJ (2012) Preferences for Lifetime Earnings, Earnings Risk and Nonpecuniary Attributes in Choice of Higher Education. Discussion Papers, 725
Krishna K, Lychagin S, Frisancho V (2018) Retaking in high stakes exams: is less more? Int Econ Rev 59(2):449–477
Larroucau T, Rios I (2018) Do “Short-List” Students Report Truthfully? Strategic Behavior in the Chilean College Admissions Problem, Technical report, Working paper
Li C, Pereyra JS (2019) Self-selection in school choice. Games Econ Behav 117:59–71
Luflade M (2018) The value of information in centralized school choice systems, Technical report, Working paper
Olszewski W, Siegel R (2018) Pareto Improvements in the Contest for College Admissions, Technical report, Working paper
Pathak PA, Sönmez T (2008) Leveling the playing field: sincere and sophisticated players in the Boston mechanism. Am Econ Rev 98(4):1636–52
Song Y, Tomoeda K, Xia X (2019) Sophistication and Cautiousness in College Applications, Technical report, Working paper
Sönmez T, Ünver MU (2011) Matching, allocation, and exchange of discrete resources. Handbook Soc Econ 1(781–852):2
Wang T, Zhou C (2018) Purchasing seats for high school admission in China. Available on: https://ssrn.com/abstract=3579819
Zafar B (2011) How do College Students form Expectations? J Labor Econ 29(2):301–348
Acknowledgements
I thank Atila Abdulkadiroğlu, Ahmet Alkan, Inacio Bo, Eric Bond, Estelle Cantillon, Yeon-Koo Che, Andrew Dustan, Liran Einav, Yinghua He, Molly Helferty, Eun Jeong Heo, Ali Fırat Inceoğlu, Fuhito Kojima, Tong Li, Antonio Miralles, Inci Sariz, Keith Teltser, the participants of the Matching in Practice Workshop (Cologne, 2018), IIOC (Indianapolis, 2018), and RES (Warwick, 2019) for their constructive comments and questions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Survey
The survey study that is used in the analysis is conducted by Alkan et al. (2008). In this study, the sample of college applicants are selected from the senior high school students who took the college entrance examination in 2005. For this sample, high schools are selected randomly based on their locations and types. The survey study is given to all senior high school students in the selected high schools. The random selection of high schools takes the population of students in Turkey and performance of the high school types into account. To achieve a representative sample of the population, 33 cities are selected from 12 different geographical regions of Turkey and 448 high schools are selected based on the student populations in the selected cities.
Figure 7 presents the frequencies of the selected number of high schools by city on the map of Turkey. It is observed that students from Istanbul and Ankara are more represented in the sample. Participation rate of high schools is considerably high. Only 2 high schools rejected to participate in this study. Students within the selected high schools were interviewed within the school time in classrooms and absent students were interviewed additionally. In total, 13727 students participated in the survey study, and 898 participants were excluded from the analysis because the information of these students could not pass the internal validation analysis (Figs. 8 and 9).
1.2 Technical details on assumptions in Section 3.3
We restrict our attention to previous year’s admission outcomes as they are the most important information for generating a distribution of cutoffs and make the following assumption to incorporate this information into the subjective admission beliefs of students.
Assumption 2
The mean and support for subjective admission beliefs are as follows:
-
1.
\(\int {\varOmega }_{ij}({\tilde{p}}_{i}, \sigma ; T) dF(T | t^{-1}_{j^{\prime }}, \xi _i ) \le \int {\varOmega }_{ij^{\prime }} ({\tilde{p}}_{i}, \sigma ^{\prime }; T) dF(T | t^{-1}_j, \xi _i )\) if \(t^{-1}_j > t^{-1}_{j^{\prime }}\) for all \(i \in N\).
-
2.
the support of the distribution of cutoff scores follows the monotonicity w.r.t. previous year’s cutoffs, i.e., \({\overline{t}}_{j}(t_j^{-1})> {\overline{t}}_{j^{\prime }}(t_{j^{\prime }}^{-1}) \; and \; {\underline{t}}_{j}(t_j^{-1}) > {\underline{t}}_{j^{\prime }}(t_{j^{\prime }}^{-1})\) if \(t_{j}^{-1} > t_{j^{\prime }}^{-1}\), where \({\overline{t}}_{j}\) is the upper boundary of the cutoff domain for college j and \({\underline{t}}_{j}\) is the lower boundary of the cutoff domain for college j.
where \(t_j^{-1}\) denotes the cutoff score of college j in the previous year. Assumption 2.1 says that student i’s admission belief for a college j is lower or equal to admission belief for college \(j^{\prime }\) if college j has a higher cutoff score than college \(j^{\prime }\) in the previous admission period. Assumption 2.2. restricts the support of subjective admission beliefs. According to Assumption 2.2., subjective admission beliefs satisfy a monotonicity condition to previous year’s cutoff scores such that support of admission beliefs does not switch their orders between adjacent years. These two conditions follow from the fact that cutoff scores across years are highly correlated in many centralized admission systems. It is realistic to expect the same cutoff score orders of colleges across years and the students to generate their beliefs accordingly.
In the centralized admission mechanism, we also observe that students generally submit an incomplete ROL. We make Assumptions 3 and 4 to eliminate peculiarities as a result of incomplete ROLs in the data.
Assumption 3
For all \(i\in N\), \(0< \kappa < (u_{ij} Pr(t_j \le {\tilde{p}}_i | T^{-1}, \xi _i)\) if \(Pr(t_j \le {\tilde{p}}_i | T^{-1}, \xi _i)> 0\).
Assumption 3 says that application cost is not negligible. Students do not add any colleges to their list if they have zero admission beliefs for these colleges. This is a legitimate assumption because even most of the low-scoring students did not submit a complete ROL in 2005.
Assumption 4
\(F(T | T^{-1}, \xi _i)\) has continuous and strictly positive density \(f(T| T^{-1}, \xi _i)\);
-
1.
the support of distribution of cutoff scores is student-specific, i.e., \([{\underline{T}}_i, {\overline{T}}_i]\),
-
2.
the boundaries for cutoff support of each college are different, e.g., \({\overline{t}}_{ij} \ne {\overline{t}}_{ij^{\prime }}, {\underline{t}}_{ij} \ne {\underline{t}}_{ij^{\prime }}\) \(\forall j, j^{\prime } \in C, \; j\ne j^{\prime }\).
Assumption 4 imposes regularity conditions for the support of the distribution of cutoff scores. According to these conditions, each student has a personal distribution of cutoff score domain that makes her admission beliefs different from other students. A student’s admission beliefs are zero for the colleges whose cutoff scores do not belong to the student-specific cutoff score support. It also assumes that the distributions of cutoff scores do not overlap perfectly. This is a realistic assumption under the strict priority orders because there are no ties among cutoff scores under no ties in priorities.
1.3 Proof of Lemma 2
We want to show that for a given student i with score \(p_i\),
From Assumption 2, we know that subjective admission probabilities decrease with the previous year’s cutoff scores. Therefore, if \(E_i [{\varOmega }_{ik}(p_i, \sigma ) | t_k^{-1} ] = 0\) and \(t_j^{-1}> t_k^{-1}\) we know that \(\int {\varOmega }_{ij}({\tilde{p}}_{i}, \sigma ; T) dF(T (t_j^{-1}, \xi _i) ) \le \int {\varOmega }_{ik} ({\tilde{p}}_{i}, \sigma ; T) dF(T (t_{k}^{-1}, \xi _i)\). Moreover, \(E_i [{\varOmega }_{ij}(p_i, \sigma ) | t_j^{-1} ] \ge 0\) because it is probability measure and cannot be less than 0. Then,
\(\square \)
1.4 Proof of Theorem 1
According to Theorem 1, \(L_i^{*}\) is the ranking of the most preferred colleges within student i’s consideration set. Then, we need to show that
where \({\mathcal {R}}\) is all possible rank order lists in the consideration set of student i and \(Pr(L_i)\) indicates the probability of assignments of colleges in the list \(L_i\). According to the condition in Theorem 1, the number of reported colleges is strictly fewer than the limit number of colleges in the list, i.e., \(|L| < K\). There are two different ways of deviating from listing most preferred colleges in the \(L_i\) within student i’s consideration set:
-
1.
Adding a college \(j\not \in L_i^*\) into list \(L_i^*\)
-
2.
Changing the order of colleges in list \(L_i^*\)
To show that \(L_i\) consists of the most preferred colleges within the consideration set of student i, we need to show that all these deviations have to be worse off for student i.
Case 1: We know that from the condition in Theorem 1 students that have only \(|L_i| < K\) number of colleges from which they can attain positive utility in their consideration sets. There are two cases in which student i can add a college j in her lists: College j should be either one from which she derives non-positive utility because she has already added all colleges she prefers to go or it that does not belong to her consideration set. Therefore,
where \(u_{ij} \le 0\) if she does not prefer college j or she believes that \(Pr(c_j \in L_i)= 0\). Either case’s expected utility (\(V_{ij}\)) of college j in \(L_i\) is equal to zero. According to Assumption 3 there is a nonnegative cost of adding college in a list, and the total gain of adding a college j is negative.
Case 2: Assume that student i prefers college j over college \(j^{\prime }\). Colleges \(j, j^{\prime }\) are part of the student i’ consideration set, where \(u_{ij}, u_{ij^{\prime }} > 0\). For simplicity, we only cover changing order of two adjacent colleges in the list. If student i lists \(c_{j^{\prime }}\) before \(c_j\) in a new list \(L_i^{\prime }\)—keeping everything else the same—the expected utility of new list \(L_i^{\prime }\) should be higher than the expected utility of \(L_i^*\) so that this deviation makes student i better off.
where \(Pr(c_{j^{\prime }} | L_i^{\prime })\) indicates the probability of assignment of college \(j^{\prime }\) in the \(L_i^{\prime }\). According to DA algorithm, an agent is assigned to a college in her reported list if she is rejected by all colleges that are ranked before it in the list. We know that \(Pr(c_{j} | L_i^*) = Pr(t_j< p_i | L_i) > Pr(c_{j} | L_i^{\prime }) = (1- Pr(t_{j^{\prime }}< p_i | L_i) ) \times Pr(t_j < p_i | L_i) \). Also, \(Pr(c_{j^{\prime }} |L_i^{\prime }) = Pr(t_{j^{\prime }}< p_i | L_i) > Pr(c_{j^{\prime }} | L_i^{*}) = (1- Pr(t_{j}< p_i | L_i) ) \times Pr(t_{j^{\prime }} < p_i | L_i)\).
Then, we can rewrite Equation 6 as
which contradicts with \(u_{ij^{\prime }} < u_{ij} \). Hence, changing the order of colleges is not better off for student i. \(\square \)
1.5 Sample selection for the estimation
In our estimations, we select a sample to satisfy the identification requirements of 4 different estimation methods that we want to compare. Among 12829 students, 5495 students submitted ROLs and have a full set of variables. Among 5495 students, we restrict attention to the students who applied to only four-year degree programs. Students can apply to a two-year degree without entrance examination scores, and their assignments require additional conditions. Since admissions to two-year degree programs differ considerably, we exclude students who included two-year degree programs in order to estimate college preferences from our main specifications. This exclusion decreases the sizes of choice sets in the analysis and provides uniform priority rules among the students. Also, we drop unassigned students, students who submitted a complete ROL, and students who submitted a ROL with one college program. With these restrictions, we can satisfy a uniform estimation sample that meets estimation conditions of (i) outcome-based estimation method as in Fack et al. (2019), (ii) consideration set approach, (iii) using only ROL. In other words, we do not contaminate our comparison of estimation methods by differences in the sample.
Table 7 presents summary statistics from different selections of the survey sample. Panels 2-4 provide information to make comparisons with the estimation sample that is used in Sect. 5 in the main text in which summary statistics are in panel 1. The selected samples differ in being admitted to a program or not, the length of the submitted ROL, and submitting a ROL.
The sample in panel 2 includes, in addition to our estimation sample, students who submitted a one-college program ROL or a complete ROL. The entrance examination and high school GPA scores, as well as observable characteristics of these two samples, are quite similar. Exclusion of students who submitted a complete ROL is a required condition for the proposed estimation strategy, and therefore, observing balanced samples mitigates bias concerns related to differences in the estimation samples.
In Panel 3, entrance examination scores differ compared to panel 1. Since the sample in panel 3 includes students who were not admitted to a four-year degree program, it is expected to observe lower examination scores. Exclusion of unassigned students who had submitted a ROL shows the importance of the proposed consideration set approach. Since the outcome-based estimation approach cannot utilize the ROL information of these students, estimation results alter just because of the differences between the selected samples.
Panel 4 presents the summary statistics of students who did not submit a ROL. Some of these students cannot qualify to submit a ROL because they do not pass the score threshold. The other students prefer not to submit a ROL even though they are eligible to so. In our data, on average, the entrance examination and high school GPA scores of the students who did not submit a ROL are lower than the scores of other selected samples. Furthermore, these students come from families of lower income and lower parental education. College preferences of these students cannot be included in the analysis because we do not have their preference lists.
We perform a t-test to investigate the difference between the lengths of submitted ROLs by whether a student is admitted to a program or not. Among all students in the survey study who submitted a ROL, we do not find any statistically significant difference between the lengths of the submitted ROLs. The average length of ROLs among the assigned students is 13.15. The average length of ROLs among unassigned students is 13.12. The difference is 0.03 with a p-value of 0.91.
Finally, to compare the frequencies of the selected number of college programs among the students in the estimation sample with all survey participants, we prepared Fig. 10. This figure shows that the selected sample does not show a different pattern compared to all survey participants that have submitted a ROL.
1.5.1 Robustness checks
While the proposed consideration sets method identifies the true preferences parameters of students under required conditions, we present in Table 11 the estimation results with other samples to make comparisons. We applied \(Cons-Sets^2\) method, as in Table 5, (1) to all survey participants who submitted a ROL, (2) all admitted students, and (3) all students who submitted an incomplete ROL. Different from the estimation sample whose estimation results we presented in Table 5, two-year degree colleges and students who have applied to these programs are now in our estimation sample.Footnote 35
Since the samples of these estimations change, we need to be careful about interpreting and comparing the results. The magnitudes of the parameter estimates are changing across different samples, but the directions of the effects are the same. This result provides another point of robustness for at least for the directions of the estimates. Sample restrictions and/or choice set restrictions are requirements of the true preference estimation methods in the centralized school/college admission literature. However, Table 11 provides a positive result for the consideration sets method in terms of robustness in many different estimation samples.
Finally, we present estimation results for cases that use different subsamples. We estimate student preferences with students who submitted a ROL with fewer than 23 and 22 college programs and more than 2 and 3 college programs. We also exclude students whose ROLs’ including 10 college programs. These estimation results show that estimates for college preferences are stable across different subsamples, and provide additional evidence for the independence of student college preferences and submitted numbers of college programs in ROLs. Note that preference estimates are different from those in Table 5 Column 5 and Table 12 Column 1 (i.e., the original sample for the estimation) because of the differences in the empirical specifications. We omit college fixed effects from our regressions in order not to contaminate our results due to the changes in the sample sizes across estimation results in Table 12.
1.6 Welfare analysis details
The first step of performing a counterfactual admission analysis is to predict unrestricted true preference orders of students. Parameter estimates of the utility function in Equation 2 allow us to predict cardinal utilities for each student–college program pair and to create personal preference orders. When constructing the predicted true preference orders of college programs for each student, we follow the following principles to incorporate information in ROLs into our analysis:
-
If a student submits an incomplete ROL, we deduce that the last choice in her ROL indicates the student’s reservation utility, and we do not add any program that has a lower expected cutoff score and predicted cardinal utility in her predicted true preference order.
-
If a student submits an incomplete ROL, we include programs that have higher expected cutoff scores than the highest expected cutoff scores in her ROL, and these programs have higher predicted cardinal utilities than her selected choices in her predicted true preference order.
-
If a student submits a complete ROL, in addition to programs that have higher expected cutoff scores and higher predicted cardinal utilities, we include programs that have higher expected cutoff scores than the lowest expected cutoff score in her ROL and the programs that have higher predicted cardinal utilities than the student’s selected choices in her predicted true preference order.
After the construction of the predicted true preference orders, we perform counterfactual admission simulations with only entrance examination score-based priorities and only high school GPA score-based priorities. Since our data only include a small sample of students from a large college admission mechanism, we assume that the changes in students’ scores in our sample have negligible effects on college admission outcomes, and therefore, we can use the same cutoff scores to generate admissions with counterfactual scores. In the counterfactual admission, we also ignore:
-
Capacity constraints of college programs,
-
The limitation in the ROL’s length,
-
Changes in the ROL construction strategies.
In the counterfactual admissions, we adopt the following rule for student assignment: a student is assigned to her most preferred college program among the programs with lower cutoff scores than the student’s score.
1.6.1 Tables and figures
An illustration of consideration sets construction under different scenarios. Notes: In this figure, a blue box indicates the ROL of a candidate and a black box indicates the set of all college program options. The numerical orders and \(C_k\) indicate the ranking in the submitted ROL (in the blue box), which is observed by the econometrician. \(C^*\) is the assigned college in the admissions and is also observed by an econometrician. \({\tilde{p}}\) denotes the student’s score (i.e., priority). The cutoff score index line shows the college programs’ cutoff score orders in the program sets (i.e., black box). The curly brackets that are on the right side of the black boxes 1, 2, and 3 indicate consideration sets (P) for a student who has a score \({\tilde{p}}\) and has submitted a ROL indicated by the blue box. (Color figure online)
An illustration of differences among the preference estimation methods in Table 5. Notes: From left to right, each figure illustrates the choice sets of the corresponding estimation presented in Table 5. In this figure, a blue box indicates the ROL of a candidate and a black box indicates the set of all college program options. The numerical orders and \(C_k\) indicate the ranking in the submitted ROL (in the blue box), which is observed by the econometrician. \(C^*\) is the assigned college in the admissions and is also observed by an econometrician. \({\tilde{p}}\) denotes student’s score (i.e., priority). The cutoff score index line shows the college programs’ cutoff score orders in the program sets (i.e., black boxes). The curly bracket that is on the right side of the 3rd black box indicates the feasible college program set (F) for a student that has a \({\tilde{p}}\) score. The curly brackets that are on the right side of the 4th and 5th black boxes indicate consideration sets (P) for a student who has a score \({\tilde{p}}\) and has submitted a ROL indicated by the blue box. (Color figure online)
Rights and permissions
About this article
Cite this article
Arslan, H.A. Preference estimation in centralized college admissions from reported lists. Empir Econ 61, 2865–2911 (2021). https://doi.org/10.1007/s00181-020-01974-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00181-020-01974-5
Keywords
- Preference estimation
- Centralized admission mechanisms
- Deferred acceptance algorithm
- Admission criteria