Alternative estimation approaches for the factor augmented panel data model with small T

Abstract

In this paper, we compare alternative estimation approaches for factor augmented panel data models. Our focus lies on panel data sets where the number of panel groups (N) is large relative to the number of time periods (T). The principal component (PC) and common correlated effects (CCE) estimators were originally developed for panel data with large N and T, whereas the GMM approaches of Ahn et al. (J Econ 728 174:1–14, 2013) and Robertson and Sarafidis (J Econ 185(2):526–541, 2015) assume that T is small (that is T is fixed in the asymptotic analysis). Our comparison of existing methods addresses three different issues. First, we analyze the possibility of an inappropriate normalization of the factor space (the so-called normalization failure). In particular we propose a variant of the CCE estimator that avoids the normalization failure by adapting a weighting scheme inspired by the analysis of Mundlak (Econometrica 46(1):69–85, 1978). Second, we analyze the effects of estimating versus fixing the number of factors in advance. Third, we demonstrate how the design of the Monte Carlo simulations favors some estimators, which explains the conflicting findings from existing Monte Carlo experiments.

1 Introduction

The seminal work of Holtz-Eakin et al. (1988) has provided two important contributions to the statistical analysis of panel data. First, it proposes a GMM framework for estimating dynamic panel data models that were further developed and popularized by Arellano and Bond (1991). This approach has become standard in the dynamic analysis of panel data. The second contribution, the introduction of time varying individual effects, was less influential and went largely unnoticed for many years. For example, the excellent monograph of Baltagi (2005)—as all other textbooks on panel data analysis of the early 2000s—does not consider time varying individual effects or any other factor structure. Bai (2009) pointed out that time varying individual effects are just a special case of a factor structure and provided a general framework for estimating a panel data model with “interactive fixed effects”, which is also referred to as the factor-augmented panel data model.

With the work of Ahn et al. (2001, 2013), Pesaran (2006), and Bai (2009) the interest in models that account for time varying heterogeneity and cross-section correlation surged considerably and the 25th International Conference on Panel Data in Vilnius 2019 included a large number of papers dealing with factor-augmented panel data models. In empirical practice, the Common Correlated Effects (CCE) approach proposed by Pesaran (2006) has recently become very popular among empirical researchers. This is due to the fact that this estimator is easy to understand and implement, a STATA routine (xtmg) and a Gretl add-on (xtcsd) is available and it performs well in Monte Carlo studies. It is, however, not clear, whether the CCE approach is similarly attractive in empirical applications where the number of time periods T is small (say 5–15). Ahn et al. (2013) and Robertson and Sarafidis (2015) proposed a GMM approach that is shown to be consistent for finite T, whereas the CCE and the principal component (PC) estimator were developed for samples with large T and N. Su and Jin (2012) and Westerlund et al. (2019) showed that the CCE approach is consistent and asymptotically (mixed) normal if T is fixed and $N\rightarrow \infty$, whereas the consistency of the PC estimator requires quite restrictive assumptions (such as i.i.d. errors across time) in this case. It is, however, not clear how large T should be in order to ensure reliable estimation and inference.

An important assumption for the CCE estimator is that the (weighted) mean of the factor loadings is different from zero. This assumption is difficult to verify as the factors loadings are typically unknown. Furthermore, we show that the CCE estimator is already biased if the mean of the factor loadings is $O(N^{-1/2})$. To escape such a “normalization failure”, we suggest a data-dependent weighting scheme that is inspired by the Mundlak (1978) approach. In our Monte Carlo simulations we show that this simple weighting scheme performs well, whenever the original CCE estimator suffers from a normalization failure.

The rest of the paper is organized as follows. Section 2 compares the existing estimation methods and Sect. 3 reviews and complements the asymptotic results for fixed T and $N\rightarrow \infty$. Possible problems with the normalization of the estimators are analyzed in Sect. 4. An extension to multiple factors is considered in Sect. 5 and empirical approaches for selecting the number of common factors are examined in Sect. 6. We argue that popular selection rules for the number of factors are generally inconsistent if T is fixed. The small sample properties of alternative estimation procedures are investigated in Sect. 7. Specifically, we illustrate the detrimental effect of a normalization failure and demonstrate the robustness of the Mundlak-type CCE estimator. Furthermore, we investigate the effects of estimating the number of factors on the performance of the estimation procedures. Finally, we employ three general model setups from the literature in order to compare the competing methods in more challenging and realistic scenarios. Section 8 concludes.

2 Existing estimation approaches

Consider the factor augmented panel data model:¹

$$\begin{aligned} y_{it}&= \varvec{\beta }'\varvec{x}_{it} + e_{it} \end{aligned}$$

(1)

$$\begin{aligned} \text {with } \ e_{it}&= \lambda _i f_t + u_{it} \ , \end{aligned}$$

(2)

where $\varvec{x}_{it}$ and $\varvec{\beta }$ are $k\times 1$ vectors. For the ease of exposition, we first consider a single factor with $r=1$, that is, $f_t$ and $\lambda _i$ are scalars. The extension to multiple factors is considered in Sect. 5.

We adopt a “classical” panel data framework where the coefficient vector $\varvec{\beta }$ is the same for all cross-section units (homogeneous panel). Furthermore, we assume that T may be small relative to N, which is typical for many panel data applications. It should be noted that the asymptotic framework of Pesaran (2006) and Bai (2009) assumes that N and T tend to infinity, whereas Ahn et al. (2013) and Robertson and Sarafidis (2015) suppose that T is small and fixed. Furthermore, the latter approach treats $f_t$ as parameter and thereby avoids making any assumptions on these parameters, whereas Pesaran (2006) and Bai (2009) assume that the factors are weakly correlated random variables and the loadings are treated as parameters (or also as random variables). We make the assumption that $u_{it}$ is independent (strictly exogenous) of $\varvec{x}_{it}$, $f_t$ and $\lambda _i$. This rules out dynamic specifications.²

It is well known that in the two-way panel data model the individual and time specific effects (which result as special cases of the factor model with constant factor and loading, respectively) can be removed by a simple data transformation, where the variables are adjusted by the individual and time specific averages. It is not difficult to see that a similar transformation exists for the model with interactive fixed effects, which is given by

$$\begin{aligned} y_{it} - \lambda _i {\overline{y}}_{t}(\pmb {\lambda })&= \varvec{\beta }'\left[ \varvec{x}_{it}-\lambda _i \overline{\varvec{x}}_t(\varvec{\lambda })\right] + u_{it}-\lambda _i {\overline{u}}_t(\varvec{\lambda }) , \end{aligned}$$

(3)

where $\pmb {\lambda }=(\lambda _1,\ldots ,\lambda _N)'$ and

$$\begin{aligned} {\overline{y}}_{t}(\pmb {\lambda })&= \frac{1}{N\overline{\lambda ^2} } \sum _{i=1}^N \lambda _i y_{it} \end{aligned}$$

with $\overline{ \lambda ^2 } = N^{-1} \sum _{i=1}^N \lambda _i^2$. The weighted averages $\overline{\varvec{x}}_{t}(\varvec{\lambda })$ and ${\overline{u}}_t(\varvec{\lambda })$ are constructed in an analogous manner. Note that ${\overline{e}}_{t}(\pmb {\lambda })={\overline{y}}_{t}(\pmb {\lambda })- \varvec{\beta }'\overline{\varvec{x}}_t(\varvec{\lambda })=f_t + {\overline{u}}_t(\varvec{\lambda })$ serves as an estimate of $f_t$. Estimating the transformed regression (3) is equivalent to the least-squares estimator, treating $\varvec{\beta }$ and $f_1,\ldots ,f_T$ as parameters and $\varvec{x}_{it}$ and $\lambda _i$ as regressors. Accordingly, the resulting estimator is efficient if $u_{it} {\mathop {\sim }\limits ^{iid}} {{\mathcal {N}}}(0,\sigma ^2)$.

2.1 The PC estimator

For the PC approach suggested by Bai (2009), equation (3) is replaced by the feasible version

$$\begin{aligned} y_{it} - {\widehat{\lambda }}_i {\overline{y}}_{t}(\widehat{\pmb {\lambda }})&= \varvec{\beta }'\left[ \varvec{x}_{it}- {\widehat{\lambda }}_i \overline{\varvec{x}}_t(\widehat{\pmb {\lambda }})\right] + e_{it}-{\widehat{\lambda }}_i \overline{e}_t(\widehat{\pmb {\lambda }}), \end{aligned}$$

(4)

where $e_{it}=y_{it}-\varvec{\beta }'\varvec{x}_{it}=\lambda _i f_t +u_{it}$ and ${\widehat{\lambda }}_i$ denotes the PC estimator of the factor loading $\lambda _i$, which is equivalent to the element of the eigenvector associated with the largest eigenvalue of the sample covariance matrix $\varvec{\Omega }_{ee}({\varvec{\beta }}) = T^{-1} \sum _{t=1}^T \varvec{e}_t(\varvec{\beta }) \varvec{e}_t(\varvec{\beta })'$ with $\varvec{e}_t(\varvec{\beta }) = (y_{i1}-\varvec{\beta }'\varvec{x}_{i1},\ldots ,y_{iT}-\varvec{\beta }'\varvec{x}_{iT})'$. As shown by Moon and Weidner (2015) the sum of squared residuals can be obtained by minimizing the objective function

$$\begin{aligned} \widehat{\varvec{\beta }}&= \mathop {\mathrm{argmin}}\limits \left\{ \mu _{\mathrm{min}}\left[ \sum _{i=1}^N \left( \varvec{y}_i - \varvec{X}_i \varvec{\beta }\right) \left( \varvec{y}_i - \varvec{X}_i \varvec{\beta }\right) ' \right] \right\} \end{aligned}$$

(5)

where $\varvec{y}_i =(y_{i1},\ldots ,y_{iT})'$ and $\varvec{X}_i =(\varvec{x}_{i1},\ldots ,\varvec{x}_{iT})'$ and $\mu _{\mathrm{min}}\{\varvec{A}\}$ denotes the smallest eigenvalue of the matrix $\varvec{A}$. The minimum can be obtained by standard numerical methods, whereas Bai (2009) proposed to compute the (nonlinear) least-squares estimator of (4) sequentially by starting with the pooled OLS or within-group estimator of $\varvec{\beta }$ (that is by ignoring the factor structure in the errors). The first principal component of the residual $e_{it}(\widehat{\varvec{\beta }})$ yields a first estimator of the common factor and the associated loadings are used to obtain the estimated analog of the weighted averages in (4). The estimation procedure is iterated until the estimators converge to the least-squares estimators of $\varvec{\beta }$ and $\varvec{\lambda }$.

Moon and Weidner (2019) pointed out that the least-squares objective function may exhibit several local minima and therefore it is possible that the gradient-based minimization algorithm fails to find the global minimum. To cope with this problem, Moon and Weidner (2019) propose a nuclear norm penalty that results in a convex optimization problem. Another possibility is to initialize the minimization algorithm by a $\sqrt{NT}$-consistent initial estimator. In this case it is sufficient to assume convexity in the $1/\sqrt{NT}$ vicinity around the true value.

2.2 The CCE estimator

In contrast to the PC estimator, the CCE approach proposed by Pesaran (2006) does not adopt an (asymptotically) efficient weighting scheme, but employs instead pre-specified weights $\varvec{\lambda }_0$.³ In practice $\varvec{\lambda }_{0}=(1,\ldots ,1)'$ is the default option, but any other granular weighting scheme is possible. This gives rise to a modified transformation,

$$\begin{aligned} y_{it} - \lambda _i^* \, {\overline{y}}_{t}(\pmb {\lambda }_0)&= \varvec{\beta }'\left[ \varvec{x}_{it}-\lambda _i^* \, \overline{\varvec{x}}_t(\pmb {\lambda }_0)\right] + u_{it}-\lambda _i^* \, {\overline{u}}_t(\pmb {\lambda }_0), \end{aligned}$$

(6)

where

$$\begin{aligned} \lambda _i^*&= \lambda _i \, \frac{\sum _{i=1}^N \lambda _{0,i}^2 }{ \sum _{i=1}^N \lambda _{0,i} \lambda _i } \end{aligned}$$

is required to drop the factor from the model. Note that if $\lambda _{0,i}=\lambda _i$ for all i, then $\lambda _i^*=\lambda _i$ and the transformation is equivalent to (3). Furthermore, if $\lambda _{0,i}=1$ then $\lambda _i^* = \lambda _i/{\overline{\lambda }}$, where ${\overline{\lambda }}=N^{-1} \sum _{i=1}^N \lambda _i$. By reorganizing (6), we obtain the cross-section augmented regression equation,

$$\begin{aligned} y_{it}&= \varvec{\beta }' \varvec{x}_{it}+ \lambda _i^* {\overline{y}}_{t}(\pmb {\lambda }_0) + \varvec{\gamma }_i'\overline{\varvec{x}}_t(\pmb {\lambda }_0) + v_{it} \ , \end{aligned}$$

(7)

where $\varvec{\gamma }_i=-\lambda _i^* \varvec{\beta }$ and $v_{it}=u_{it}- \lambda _i^* {\overline{u}}_t(\pmb {\lambda }_0)$. In practice, the nonlinear restriction $\varvec{\gamma }_i=-\lambda _i^* \varvec{\beta }$ is ignored and, therefore, $\varvec{\gamma }_i$ is treated as an additional parameter.⁴

2.3 The HNR and ALS approach

While the CCE and PC approach replace the unobserved factor by (weighted) averages of $y_{1t},\ldots ,y_{Nt}$ and $\varvec{x}_{1t},\ldots ,\varvec{x}_{Nt}$, the approaches suggested by Holtz-Eakin et al. (1988) (HNR) and Ahn et al. (2013) (ALS) replace the unknown factor loadings by linear combinations of $y_{i1},\ldots ,y_{iT}$ and $\varvec{x}_{i1},\ldots ,\varvec{x}_{iT}$:

$$\begin{aligned} \text {HNR: }\quad&\frac{1}{f_{t-1}} (y_{i,t-1} - \varvec{\beta }'\varvec{x}_{i,t-1}) ~=~ \lambda _i + \frac{1}{f_{t-1}} u_{i,t-1} \end{aligned}$$

(8)

$$\begin{aligned} \text {ALS: }\quad&\frac{1}{f_{T}} (y_{iT} - \varvec{\beta }'\varvec{x}_{iT}) ~=~ \lambda _i + \frac{1}{f_{T}} u_{iT} \ . \end{aligned}$$

(9)

The main difference between these two approaches is that in (8) the linear combination is time dependent, whereas in (9) the linear combination is the same for all time series. As we do not see any advantage in using the variant HNR (and in our simulations the HNR estimator tends to perform worse than the ALS estimator), we focus on the ALS variant in the following analysis.

Inserting (9) in model (1) yields

$$\begin{aligned} \text {ALS:} \quad&y_{it} = \varvec{\beta }'\varvec{x}_{it} + \theta _t y_{iT} - \theta _t \varvec{\beta }'\varvec{x}_{iT} + \nu _{it} \quad \ \text { for } t=1,\ldots ,T-1, \end{aligned}$$

(10)

where $\theta _t = f_t/f_T$ and $\nu _{it}=u_{it} - \theta _t u_{iT}$. Note that this approach involves $T-1$ additional parameters $\theta _1,\ldots ,\theta _{T-1}$, whereas the CCE approach involves $N(k+1)$ additional parameters, which may be a much larger number of parameters, in particular if N is large relative to T.

Equation (10) can be estimated as a linear equation by ignoring the nonlinear relationship $\varvec{\delta }_t = \theta _t \varvec{\beta }$ and treating $\varvec{\delta }_t$ as additional parameters, cf. Hayakawa (2012). Furthermore, as the regressor $y_{iT}$ is correlated with the errors, an instrumental variable approach is required for estimating the coefficients efficiently. Since it is assumed that $\varvec{x}_{it}$ is strictly exogenous, we employ observations of all time periods to construct the $Tk \times 1$ instrumental variable vector $\varvec{z}_i=(\varvec{x}_{i1}',\varvec{x}_{i2}',\ldots ,\varvec{x}_{iT}')'$. The first stage regression yields ${\widehat{y}}_{iT} = \widehat{\varvec{\pi }}'\varvec{z}_i$, where $\widehat{\varvec{\pi }}'\varvec{z}_i$ is the fitted value from a regression of $y_{iT}$ on $\varvec{z}_i$. The second stage regression is

$$\begin{aligned} y_{it}&= \varvec{\beta }'\varvec{x}_{it} + \theta _t {\widehat{y}}_{iT} - \theta _t \varvec{\beta }'\varvec{x}_{iT} + \nu _{it}. \end{aligned}$$

Estimating the latter equation by OLS yields the two-stage least squares (2SLS) estimator. Since the error term $\nu _{it}$ is autocorrelated (due to the common component $\theta _t u_{iT}$), a GMM estimator based on the moment condition ${\mathbb {E}}(\varvec{\nu }_i \otimes \varvec{z}_i)=\varvec{0}$ with $\varvec{\nu }_i=(\nu _{i1},\ldots , \nu _{iT})'$ is more efficient, in general.

2.4 The RS estimator

The GMM estimator of Robertson and Sarafidis (2015) results from multiplying the original model by the vector of instruments $\varvec{z}_i$ (e.g. the instruments of the ALS estimator) such that

$$\begin{aligned} \varvec{z}_i y_{it}&= \left( \varvec{z}_i \varvec{x}_{it}' \right) \varvec{\beta } + \left( \varvec{z}_i \lambda _i \right) f_t + \varvec{z}_i u_{it} \ . \end{aligned}$$

The respective moment condition is given by

$$\begin{aligned} {\mathbb {E}}\left( \varvec{m}_{zy} - \varvec{M}_{zx}\varvec{\beta } - \varvec{f} \otimes \varvec{\gamma } \right)&= 0, \end{aligned}$$

where

$$\begin{aligned} \varvec{m}_{zy} ~=~ \begin{pmatrix} \frac{1}{N} \sum \limits _{i=1}^N \varvec{z}_i y_{i1} \\ \vdots \\ \frac{1}{N} \sum \limits _{i=1}^N \varvec{z}_i y_{iT} \end{pmatrix}&\ \quad \ \varvec{M}_{zx} ~=~ \begin{pmatrix} \frac{1}{N} \sum \limits _{i=1}^N \varvec{z}_i \varvec{x}_{i1}' \\ \vdots \\ \frac{1}{N} \sum \limits _{i=1}^N \varvec{z}_i \varvec{x}_{iT}' \end{pmatrix} \\ \varvec{\gamma } ~=~ \frac{1}{N} \sum _{i=1}^N \varvec{z}_i \lambda _i&\ \quad \ \mathbf {f} ~=~ \begin{pmatrix} f_1&\cdots&f_T \end{pmatrix}^\prime . \end{aligned}$$

Note that in this model the N factor loadings $\lambda _1,\ldots ,\lambda _N$ enter in form of the Tk dimensional vector $\varvec{\gamma }$, resulting in a considerable dimensionality reduction whenever N is much larger than T. The GMM estimator results from minimizing the criterion function

$$\begin{aligned} Q(\varvec{\beta }, \varvec{\gamma }, \varvec{f})&= \left( \varvec{m}_{zy} - \varvec{M}_{zx}\varvec{\beta } - \varvec{f} \otimes \varvec{\gamma } \right) ' \varvec{W}_N \left( \varvec{m}_{zy} - \varvec{M}_{zx}\varvec{\beta } - \varvec{f} \otimes \varvec{\gamma } \right) , \end{aligned}$$

(11)

where $\varvec{W}_N$ is a consistent estimator of the optimal weighting matrix

$$\begin{aligned} \varvec{W}&= \left[ {\mathbb {E}}\left( \frac{1}{N}\sum \limits _{i=1}^N \widetilde{\varvec{u}}_{i} \widetilde{\varvec{u}}_{i}' \right) \right] ^{-1} \end{aligned}$$

with $\widetilde{\varvec{u}}_{i}=\varvec{m}_{zy} - \varvec{M}_{zx}\varvec{\beta } - \varvec{f} \otimes \varvec{\gamma }$. Robertson and Sarafidis (2015) propose to minimize the function $Q(\cdot )$ by applying a sequential GMM estimator. Let $f_t^0$ denote some starting value. Replacing $f_t$ by $f_t^0$, the parameters $\varvec{\beta }$ and $\varvec{\gamma }$ are obtained by linear GMM. Replacing $\varvec{\gamma }$ by the respective GMM estimator, we obtain an updated estimator for $f_t$ by another linear GMM estimation step. This sequential GMM estimator eventually converges to the minimum of (11). An alternative estimator based on linear GMM is proposed by Juodis and Sarafidis (2020).

It is important to notice that the first-order condition of the GMM estimator is invariant to some scaling factor c, such as $\varvec{f}^* =c \varvec{f}$ and $\varvec{\gamma }^*=\varvec{\gamma }/c$. The PC estimator implies $c=1/\sqrt{ \sum _{t=1}^T f_t^2 }$ and the original ALS estimator imposes $c=1/f_T$. The objective function of the least-squares estimator does not impose any normalization of the factors. There exists a unique minimum for the product $\varvec{f}\otimes \varvec{\gamma }$, but the decomposition into $\varvec{\gamma }$ and $\varvec{f}$ is somewhat arbitrary and depends on the starting value of the iterative algorithm.

3 Asymptotic properties for fixed T

The asymptotic properties of the PC and CCE estimators are typically derived by adopting a joint limit theory, where T and N tend to infinity (e.g. Pesaran 2006; Bai 2009; Greenaway-McGrevy et al. 2012 and Westerlund and Urbain 2015). The asymptotic analysis revealed that the PC and CCE estimators are $\sqrt{NT}$-consistent whenever $\sqrt{T}/N\rightarrow 0$ and $\sqrt{N}/T\rightarrow 0$. This requirement is fulfilled if for some fixed constant, $0<a<\infty$, the paths of the sample sizes admit the inequality $a T^{0.5+\epsilon }< N < aT^{2-\epsilon }$ for some $\epsilon >0$. Statistical inference based on these estimators suffers from an asymptotic bias whenever $T/N\rightarrow \kappa >0$. This bias does not show up in the asymptotic analysis of Pesaran (2006), as he assumes that the coefficient vector $\varvec{\beta }_i=\varvec{\beta } + \varvec{v}_i$ is individual specific, where $\varvec{v}_i$ is a random error that prevents the estimator from achieving the usual $\sqrt{NT}$ convergence rate. In the literature cited above, bias-corrected estimators are suggested that remove the asymptotic bias from the limiting distribution.

For fixed T and $N\rightarrow \infty$ the CCE estimator of the factors is consistent as ${\overline{e}}_t(\varvec{\lambda }_0)$ converges in probability to $cf_t$, where c is some scale factor that is different from zero. Therefore, the errors-in-variable problem vanishes for $N\rightarrow \infty$ and fixed T (cf. Westerlund et al. 2019).

For the asymptotic analysis of the PC estimator, it is usually assumed that $\min (N,T)\rightarrow \infty$ (cf. Bai 2009) and, therefore, the PC estimator may be inconsistent if T is fixed and $N\rightarrow \infty$ (see Remark 1 of Bai 2009). Under more restrictive assumptions it is, however, possible to show that the PC estimator of the factors is consistent if T is fixed and $N\rightarrow \infty$. To focus on the main issues assume that $\varvec{\beta }$ is known. Furthermore, we assume that the vectors $\pmb {f}=(f_1,\ldots ,f_T)'$ and $\pmb {\lambda }=(\lambda _1,\ldots ,\lambda _N)'$ are parameter vectors to be estimated. The PC estimator solves the first-order conditions:

$$\begin{aligned} \frac{1}{N} \sum _{i=1}^N (\pmb {e}_{i} - \widehat{\pmb {f}}{\widehat{\lambda }}_i ){\widehat{\lambda }}_i&= \varvec{0} \ \text { where } \varvec{e}_i=(e_{i1},\ldots ,e_{iT})' \end{aligned}$$

(12)

$$\begin{aligned} \frac{1}{T} \sum _{t=1}^T (\pmb {e}_{t} - {\widehat{f}}_t\widehat{\pmb {\lambda }}) {\widehat{f}}_t&= \varvec{0} \ \text { where } \varvec{e}_t=(e_{1t},\ldots ,e_{Nt})' , \end{aligned}$$

(13)

subject to $T^{-1} \sum _{t=1}^T {\widehat{f}}_t^2 = T^{-1} \widehat{\pmb {f}}'\widehat{\pmb {f}}= 1$. Since ${\widehat{\lambda }}_i = T^{-1} \widehat{\pmb {f}}'\pmb {e}_i$, we obtain

$$\begin{aligned}&\frac{1}{N} \sum _{i=1}^N \left( \varvec{e}_{i} - \frac{1}{T} \widehat{\varvec{f}} \widehat{\varvec{f}}' \varvec{e}_i\right) \varvec{e}_i'\widehat{\varvec{f}} ~=~ \varvec{M}_{\widehat{\varvec{f}}} \left( \frac{1}{N} \sum _{i=1}^N \varvec{e}_i \varvec{e}_i' \right) \widehat{\varvec{f}} ~=~ \varvec{0}, \end{aligned}$$

(14)

where $\varvec{M}_{\widehat{\varvec{f}}}=\varvec{I}_T- T^{-1} \widehat{\varvec{f}} \widehat{\varvec{f}}'$ with $\varvec{M}_{\widehat{\varvec{f}}} \widehat{\varvec{f}}=\varvec{0}$. For $N\rightarrow \infty$ we have

$$\begin{aligned} \frac{1}{N} \sum _{i=1}^N \varvec{e}_i \varvec{e}_i' {\mathop {\rightarrow }\limits ^{p}} \sigma _\lambda ^2 \varvec{f} \varvec{f}' + \varvec{\Sigma }_u, \end{aligned}$$

where $\sigma _\lambda ^2 = \mathop {\mathrm{plim}}\limits _{N\rightarrow \infty } N^{-1} \sum _{i=1}^N \lambda _i^2$, $\varvec{\Sigma }_u = \mathop {\mathrm{plim}}\limits _{N\rightarrow \infty } N^{-1} \sum _{i=1}^N \varvec{u}_i \varvec{u}_i'$, and $\varvec{u}_i=(u_{i1},\ldots ,u_{iT})'$. Assume that $u_{it}$ is i.i.d. with $\varvec{\Sigma }_u= \sigma _u^2 \varvec{I}_T$. As $N\rightarrow \infty$ the moment condition is solved by letting $\widehat{\varvec{f}} = \varvec{f}$ and, therefore, the PC estimator for $\varvec{f}$ is consistent (up to a scaling factor). If $u_{it}$ is heteroskedastic or autocorrelated, then $\varvec{M}_{\varvec{f}}\pmb {\Sigma }_u \pmb {f}\ne 0$ in general and, therefore, the PC estimator is inconsistent as $N\rightarrow \infty$. On the other hand, if both N and T tend to infinity, the PC estimator is consistent no matter of a possible heteroskedasticity or (weak) autocorrelation (cf. Chamberlain and Rothschild 1983).

The asymptotic theory for the HNR and ALS estimators assumes that T is fixed and N tends to infinity. The GMM estimator is based on $kT(T-1)$ moment conditions with $k+T-1$ unknown parameters. Therefore, no problem arises if T is fixed and N tends to infinity. Accordingly, the estimators are asymptotically normally distributed and centered around zero. Of course the problem of instrument proliferation arises if T gets large and the asymptotic theory breaks down if $T^3/N \rightarrow \kappa >0$ (cf. Bekker 1994 and Lee et al. 2017).⁵

4 Identification

Since the factor space is not identified without some normalization of the factors and factor loadings, the estimation approaches impose some normalization that may be problematical in empirical practice. The CCE and ALS approaches require the following conditions:

$$\begin{aligned} \text {CCE:} \qquad&\frac{1}{N} \sum _{i=1}^N \lambda _{0,i} \lambda _i \ne 0, \end{aligned}$$

(15)

$$\begin{aligned} \text {ALS:} \qquad&f_T \ne 0 \ , \end{aligned}$$

(16)

whereas the requirement for the PC estimator $T^{-1} \sum _{t=1}^T f_t^2>0$ is unproblematic, as otherwise the factor does not exist. The violation of the restrictions (15) and (16) may result in poor distributional properties of the estimator. If, for example, $N^{-1} \sum \lambda _{0,i} \lambda _i=0$, then the cross-section mean ${\overline{e}}_t(\pmb {\lambda }_0)$ does not depend on the factor and, therefore, the CCE estimator is biased whenever $\varvec{x}_{it}$ and $\lambda _i f_t$ are correlated (cf. Westerlund and Urbain 2013). Similarly, if $f_T=0$, then $y_{iT}=\varvec{\beta }'\varvec{x}_{iT}+u_{iT}$ and the instruments are not able to identify the parameters $\theta _t$ and $\varvec{\delta }_t$.

One may argue that the chance that (15) or (16) is exactly zero is negligible, so that problems only occur in rare cases (if at all). Unfortunately, this is not true, as the problems already arise whenever $N^{-1} \sum \lambda _{0,i} \lambda _i = O_p(N^{-1/2})$. For illustration, let us assume $\lambda _{0,i}=1$, such that ${\overline{y}}_t(\pmb {\lambda }_0)={\overline{y}}_t$ and ${\overline{\lambda }} = O_p(N^{-1/2})$. Including the cross-section averages ${\overline{y}}_t$ and $\overline{\varvec{x}}_t$ is equivalent to augmenting with ${\overline{e}}_t$ and $\overline{\varvec{x}}_t$. Furthermore,

$$\begin{aligned} {\overline{e}}_t&= {\overline{\lambda }} f_t + {\overline{u}}_t \\&= {\overline{\lambda }} f_t^* \ , \end{aligned}$$

where $f_t^* = f_t + ({\overline{u}}_t/{\overline{\lambda }})$. Since in our case ${\overline{u}}_t/{\overline{\lambda }}=O_p(1)$, it follows that the factor $f_t^*$ is different from $f_t$. In this case, ${\overline{e}}_t$ does not represent the true factor and the CCE estimator of $\varvec{\beta }$ is inconsistent whenever the factor is correlated with the regressors.

To sidestep this difficulty, we follow the analysis of Mundlak (1978) and decompose the factor loadings into a systematic component related to the ordinary average $\overline{\varvec{x}}_i$ and the projection error $\xi _i$:

$$\begin{aligned} \lambda _i&= \gamma _0 + \varvec{\gamma }_1' \overline{\varvec{x}}_i + \xi _i, \end{aligned}$$

(17)

where $\overline{\varvec{x}}_i=T^{-1} \sum _{t=1}^T \varvec{x}_{it}$ and $\xi _i$ is uncorrelated with $\overline{\varvec{x}}_{i}$. In this specification $\varvec{\gamma }_1' \overline{\varvec{x}}_i$ represents a possible linear dependence of $\lambda _i$ on the regressors that gives rise to an endogeneity bias. Inserting (17) in (1) yields

$$\begin{aligned} y_{it}&= \varvec{\beta }' \varvec{x}_{it} + \lambda _i^* f_t + e_{it}^* \ , \end{aligned}$$

where $\lambda _i^*=\gamma _0 + \varvec{\gamma }_1' \overline{\varvec{x}}_i$, $e_{it}^*=\xi _i f_t + u_{it}$ and ${\mathbb {E}}(e^*_{it}|\varvec{x}_{it})=0$. This estimation equation is related to the projection approach of Hayakawa (2012), who considers a projection of $\lambda _i$ on the vector $\varvec{z}_i=vec(\varvec{X}_i)$, also known as Chamberlain projection. A second difference to the Hayakawa (2012) approach is that he employs the projection for GMM estimation of ALS, whereas we employ the Mundlak projection in the context of CCE estimation.

The weighting scheme for the CCE estimator results as

$$\begin{aligned} {\overline{y}}_t(\varvec{\lambda }^*)&= \frac{1}{N\overline{\lambda _*^2} } \sum _{i=1}^N \lambda _i^* y_{it} \\&= {\widetilde{\gamma }}_0 \left( \frac{1}{N} \sum _{i=1}^N y_{it} \right) + \widetilde{\varvec{\gamma }}_1' \left( \frac{1}{N} \sum _{i=1}^N \overline{\varvec{x}}_i y_{it} \right) \\ \text { where } {\widetilde{\gamma }}_0&= \gamma _0/ \overline{\lambda _*^2} \ \text { and } \ \widetilde{\varvec{\gamma }}_1 = \varvec{\gamma }_1/ \overline{\lambda _*^2} \end{aligned}$$

and $\overline{\lambda _*^2}= \frac{1}{N} \sum _{i=1}^N (\lambda _i^*)^2$. Since ${\widetilde{\gamma }}_0$ and $\widetilde{\varvec{\gamma }}_1$ are unknown, we augment the regression by the following $(k+1)^2$ cross-section averages:

$$\begin{aligned}&\frac{1}{N} \sum _{i=1}^N y_{it}\ , \qquad \frac{1}{N} \sum _{i=1}^N x_{1,it} \ , \quad \cdots , \ \frac{1}{N} \sum _{i=1}^N x_{k,it} \ , \\&\frac{1}{N} \sum _{i=1}^N {\overline{x}}_{1,i} y_{it} \ , \ \frac{1}{N} \sum _{i=1}^N {\overline{x}}_{1,i} x_{1,it} \ , \ \cdots , \ \frac{1}{N} \sum _{i=1}^N {\overline{x}}_{1,i} x_{k,it} \ , \\&\quad \vdots \vdots \vdots \\&\frac{1}{N} \sum _{i=1}^N {\overline{x}}_{k,i} y_{it} \ , \ \frac{1}{N} \sum _{i=1}^N {\overline{x}}_{k,i} x_{1,it} \ , \ \cdots , \ \frac{1}{N} \sum _{i=1}^N {\overline{x}}_{k,i} x_{k,it}\ . \end{aligned}$$

This estimator is referred to as CCE(M).⁶ It is important to note that this approach implies the inclusion of $(k+1)^2$ cross-section averages, attached with individual specific coefficients. It follows that T needs to be larger than $(k+1)^2$ which may be a severe restriction in empirical practice. Furthermore, the small sample properties of the CCE(M) estimator may suffer from a large number of auxiliary regressors.

Similar normalization problems arise for the HNR and ALS approaches, but these estimators apply a normalization to the factors. For example, if $f_T$ is zero, then the linear combination of $y_{iT}$ and $\varvec{x}_{iT}$ is not able to identify the factor and, therefore, the ALS approach is biased whenever $f_T=0$ and $\varvec{x}_{it}$ is correlated with $\lambda _i f_t$. If T is small, then one may try out all possible time periods for normalization and select the normalization that minimizes the GMM objective function. For a large number of time series this approach is rather time-consuming. In such cases the normalization may be selected by estimating the factor by the PC approach. Then, the normalization period with the largest factor (in absolute value) is selected as the normalization period.

In appendix of Ahn et al. (2013) a more flexible approach is proposed, which we refer to as ALS$^*$. Let $\varvec{H}$ denote the $T\times (T-1)$ orthogonal complement of $\varvec{f}=(f_1,\ldots ,f_T)'$ such that $\varvec{H}'\varvec{f}=\varvec{0}$. To obtain (10) we let

$$\begin{aligned} \varvec{H}_{ \text {ALS}}'&= \begin{pmatrix} 1 &{} 0 &{} 0 &{} \cdots &{} 0 &{} -\theta _1 \\ 0 &{} 1 &{} 0 &{} \cdots &{} 0 &{} -\theta _2 \\ \vdots &{} &{} \ddots &{} &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} 1 &{} -\theta _{T-1} \end{pmatrix} . \end{aligned}$$

To avoid normalizing $T-1$ elements to unity, we transform the equations for unit i by using a more general matrix with property $\varvec{H}'\varvec{f}=\varvec{0}$, such that $\varvec{H}'\varvec{e}_i= \varvec{H}'(\varvec{y}_i-\varvec{X}_i\varvec{\beta })$, where $\varvec{y}_i=(y_{i1},\ldots ,y_{iT})'$, $\varvec{X}_i = (\varvec{x}_{i1},\ldots ,\varvec{x}_{iT})'$, $\widetilde{\varvec{e}}_i=\varvec{H}'\varvec{e}_i$. Given $\varvec{\beta }$, the estimator of $\varvec{H}$ is based on the moment condition ${\mathbb {E}}(\varvec{H}'\varvec{e}_i \varvec{z}_i')=\varvec{0}$, where $\varvec{z}_i=vec(\varvec{X}_i)$. Accordingly, a GMM estimator for $\varvec{H}$ can be obtained as

$$\begin{aligned} \widehat{\varvec{H}}&= \mathop {\mathrm{argmin}}\limits _{\pmb {H}} \left\{ tr\left( \varvec{H}'\varvec{\Omega }_{ez}\varvec{\Omega }_{zz}^{-1} \varvec{\Omega }_{ez}'\varvec{H} \right) \right\} \quad \text { s.t. } \ \varvec{H}'\varvec{H}=\varvec{I}_{T-1} , \end{aligned}$$

where $\varvec{\Omega }_{ez}=N^{-1} \sum _{i=1}^N \varvec{e}_i \varvec{z}_i'$ and $\varvec{\Omega }_{zz}=N^{-1} \sum _{i=1}^N \varvec{z}_i \varvec{z}_i'$. Accordingly, the estimator $\widehat{\varvec{H}}$ is obtained as the matrix of eigenvectors corresponding to the smallest $T-1$ eigenvalues of the matrix $\varvec{\Omega }_{ez}\varvec{\Omega }_{zz}^{-1} \varvec{\Omega }_{ez}'$. Given $\widehat{\varvec{H}}$, the estimator for $\varvec{\beta }$ is obtained from the OLS regression

$$\begin{aligned} \widehat{\varvec{H}}'\varvec{y}_i&= \widehat{\varvec{H}}'\varvec{X}_i \varvec{\beta } + \widetilde{\varvec{e}}_i. \end{aligned}$$

This estimation step yields an updated estimator for $\varvec{\beta }$ that can be used to obtain a new estimator of $\varvec{H}$, until convergence. A drawback of this variant of the ALS estimator is that no standard errors for $\varvec{\beta }$ are readily available, as the respective estimation step is affected by the estimation error in $\widehat{\varvec{H}}$.

It is interesting to compare this approach to the PC estimator of Bai (2009), which can be obtained by solving the problem

$$\begin{aligned} \widetilde{\varvec{H}}&= \mathop {\mathrm{argmin}}\limits _{\pmb {H}} \left\{ tr\left( \varvec{H}'\varvec{\Omega }_{ee} \varvec{H} \right) \right\} \quad \text {s.t. } \ \varvec{H}'\varvec{H}=\varvec{I}_{T-1} , \end{aligned}$$

where $\varvec{\Omega }_{ee} = N^{-1} \sum _{i=1}^N \varvec{e}_i \varvec{e}_i'$. Accordingly, the difference between the PC and ALS/RS approaches is that the former extracts the factors from the residual vector $\varvec{e}_i$, whereas the ALS/RS approach first projects the residuals on the space spanned by the vector of instruments $\varvec{z}_i$. Accordingly, the latter approach assumes that the factors are correlated with the regressors, whereas the PC approach does not.

Robertson and Sarafidis (2015) show that their estimator considered in Sect. 2.4 is asymptotically equivalent to ALS$^*$ if the error $u_{it}$ is i.i.d. If $u_{it}$ is heteroskedastic and/or serially correlated, then the weighting matrix $\varvec{W}_n$ results in an asymptotic efficiency gain.

5 Multiple factors

So far we assumed that there is only a single factor. It is not difficult to see that for a panel data model with a vector of $r\ge 1$ factors $\pmb {f}_t$ and the conformable $r\times 1$ loading vector $\pmb {\lambda }_i$, the estimation equation (3) is given by

$$\begin{aligned} y_{it} - \pmb {\lambda }_i' \overline{\pmb {y}}_{t}^*(\pmb {\Lambda })&= \left[ \varvec{x}_{it}'-\varvec{\lambda }_i' \overline{\pmb {X}}_t^*(\varvec{\Lambda })\right] \varvec{\beta } + u_{it}-\pmb {\lambda }_i' \overline{\pmb {u}}_t(\pmb {\Lambda }), \end{aligned}$$

(18)

where $\pmb {\Lambda }=(\pmb {\lambda }_1,\ldots ,\pmb \lambda _N)'$ and

$$\begin{aligned} \overline{\pmb {y}}_{t}^*(\pmb {\Lambda })&= \left( \sum _{i=1}^N \pmb {\lambda }_i \pmb {\lambda }_i' \right) ^{-1} \sum _{i=1}^N \varvec{\lambda }_i y_{it} \\ \text { and } \ \overline{\pmb {X}}_{t}^*(\pmb {\Lambda })&= \left( \sum _{i=1}^N \varvec{\lambda }_i \varvec{\lambda }_i' \right) ^{-1} \sum _{i=1}^N \varvec{\lambda }_i \pmb {x}_{it}' \end{aligned}$$

and the $r\times 1$ vector $\overline{\pmb {u}}_t(\varvec{\Lambda })$ is constructed in a similar manner. This shows that efficient estimation requires r linear independent weighting schemes applied to $\pmb {y}_{t}=(x_{1t},\ldots ,y_{Nt})'$ and $\pmb {X}_{t}=(\varvec{x}_{1t}',\ldots ,\varvec{x}_{Nt}')'$.

To show consistency of the modified CCE estimator, CCE(M), a different reasoning is required. For the ease of exposition assume $k=2$ regressors and $r=2$ factors. We obtain 2 different weighting schemes:

$$\begin{aligned} {\overline{y}}_t^{(1)}&= \frac{1}{N} \sum _{i=1}^N {\overline{x}}_{1,i} y_{it} \qquad {\overline{x}}_{1,t}^{(1)} = \frac{1}{N} \sum _{i=1}^N {\overline{x}}_{1,i} x_{1,it} \qquad {\overline{x}}_{2,t}^{(1)} = \frac{1}{N} \sum _{i=1}^N {\overline{x}}_{1,i} x_{2,it} \\ {\overline{y}}_t^{(2)}&= \frac{1}{N} \sum _{i=1}^N {\overline{x}}_{2,i} y_{it} \qquad {\overline{x}}_{1,t}^{(2)} = \frac{1}{N} \sum _{i=1}^N {\overline{x}}_{2,i} x_{1,it} \qquad {\overline{x}}_{2,t}^{(2)} = \frac{1}{N} \sum _{i=1}^N {\overline{x}}_{2,i} x_{2,it} \end{aligned}$$

that are used to obtain the following relationships:

$$\begin{aligned} \begin{pmatrix} {\overline{y}}_{t}^{(1)} \\ {\overline{y}}_{t}^{(2)} \end{pmatrix} - \begin{pmatrix} {\overline{x}}_{1,t}^{(1)} &{}\quad {\overline{x}}_{2,t}^{(1)} \\ {\overline{x}}_{1,t}^{(2)} &{}\quad {\overline{x}}_{2,t}^{(2)} \end{pmatrix} \varvec{\beta }&= \begin{pmatrix} \xi _{1}^{(1)} &{}\quad \xi _{2}^{(1)} \\ \xi _1^{(2)} &{} \quad \xi _{2}^{(2)} \end{pmatrix} \begin{pmatrix} f_{1,t} \\ f_{2,t} \end{pmatrix} + O_p(N^{-1/2}) \end{aligned}$$

where $\xi _{k}^{(\ell )} = N^{-1} \sum _{i=1}^N {\overline{x}}_{\ell ,i} \lambda _{k,i}$. Accordingly, if the matrix

$$\begin{aligned} \varvec{\Xi }&= \begin{pmatrix} \xi _{1}^{(1)} &{}\quad \xi _{2}^{(1)} \\ \xi _1^{(2)} &{}\quad \xi _{2}^{(2)} \end{pmatrix} \end{aligned}$$

is invertible⁷, we can obtain the linear combinations that represent the factors as

$$\begin{aligned} \begin{pmatrix} f_{1,t} \\ f_{2,t} \end{pmatrix}&= \varvec{\Xi }^{-1} \begin{pmatrix} {\overline{y}}_{t}^{(1)} \\ {\overline{y}}_{t}^{(2)} \end{pmatrix} - \varvec{\Xi }^{-1} \begin{pmatrix} {\overline{x}}_{1,t}^{(1)} &{}\quad {\overline{x}}_{2,t}^{(1)} \\ {\overline{x}}_{1,t}^{(2)} &{}\quad {\overline{x}}_{2,t}^{(2)} \end{pmatrix} \varvec{\beta } + O_p(N^{-1/2}). \end{aligned}$$

Thus, asymptotically the space spanned by $(f_{1,t},f_{2,t})$ is contained in the space spanned by the corresponding 6 cross-sectional averages ${\overline{y}}_{t}^{(1)}$, ${\overline{y}}_{t}^{(2)}$, ${\overline{x}}_{1,t}^{(1)}$, ${\overline{x}}_{2,t}^{(1)}$, ${\overline{x}}_{1,t}^{(2)}$, and, ${\overline{x}}_{2,t}^{(2)}$.⁸

6 Determining the number of factors

As argued by Pesaran (2006), the CCE estimator is consistent if the actual number of factors r is not larger than $k+1$. This requires, however, that $r-1$ factors are correlated with the k regressors. This is due to the fact that one factor can be identified by the cross-section average ${\overline{e}}_t(\varvec{\lambda }_0) = {\overline{y}}_t(\varvec{\lambda }_0) - \varvec{\beta }'\overline{\varvec{x}}_t(\varvec{\lambda }_0)$, whereas the identification of the other factors requires some relationship to the cross-section averages of the regressors $\overline{\varvec{x}}_t$. Furthermore, the correlation pattern needs to be sufficiently informative for identifying the factors.

It is often argued that the CCE approach is attractive, as we do not need to select the number of factors, whereas for all other approaches, the number of factors needs to be known (or determined from the data). If the number of factors is smaller than $k+1$ and the normalization requirements are satisfied, then the CCE estimator is consistent, but the small sample properties may suffer from including many cross-section averages. This is comparable to applying the PC estimator with $r=k+1$ factors. As shown by Moon and Weidner (2015), under some additional assumptions,⁹ the PC estimator is robust against over-specifying the number of factors. A similar result is obtained by Westerlund et al. (2019) for the CCE estimator. Since under certain conditions the CCE estimator for $\varvec{\beta }$ is as efficient as the OLS estimator using the true factors, there is no gain in (asymptotic) efficiency by changing the weighting scheme or imposing nonlinear restrictions to the auxiliary parameters that are implied by knowing the number of factors. It is, however, not clear whether this result provides a good guidance for empirical applications in finite samples.

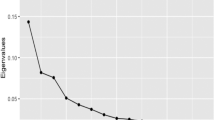
In practice, it may therefore be interesting to estimate the number of factors. To this end, we may invoke the criteria proposed by Bai and Ng (2002) and Ahn and Horenstein (2013). Both approaches are based on the eigenvalues of the residual covariance matrix. Denote by ${\widehat{\mu }}_1\ge \cdots \ge {\widehat{\mu }}_T$ the ordered eigenvalues of the $T\times T$ sample covariance matrix $\widehat{\varvec{\Omega }}_{ee}= N^{-1}\sum _{i=1}^N \widehat{\varvec{e}}_i \widehat{\varvec{e}}_i'$, where the residual vector $\widehat{\varvec{e}}_i$ is obtained by estimating the model with maximum number of factors $r^*$. Furthermore, let

$$\begin{aligned} {\widehat{\sigma }}_u^2(r)&= \frac{1}{NT} \sum _{i=1}^N \sum _{t=1}^T {\widehat{u}}_{it}^2 ~=~ \frac{1}{T} \sum _{j=r+1}^T {\widehat{\mu }}_j \end{aligned}$$

where ${\widehat{u}}_{it}$ denotes the residual from estimating the model with r factors. Bai and Ng’s (2002) criterion $IC_{p2}$ minimizes

$$\begin{aligned} \text {BN}(r)&= \log \bigl ( {\widehat{\sigma }}_u^2(r)\bigr ) + r \, \frac{N+T}{NT} \log (min[N,T]) , \end{aligned}$$

for $r\in \{0,1,\ldots ,r^*\}$, whereas the criterion proposed by Ahn and Horenstein (2013) maximizes the eigenvalue ratios

$$\begin{aligned} \text {AH}(r)&= {\widehat{\mu }}_j /{\widehat{\mu }}_{j+1} \quad \text { for } r\in \{1,2,\ldots ,r^*\} \end{aligned}$$

and the mock eigenvalue ${\widehat{\mu }}_0 = \left( \sum _{j=1}^T {\widehat{\mu }}_j\right) /\log (T)$. Let $r_0$ denote the true number of factors. If $\widehat{\varvec{\beta }}_*-\pmb {\beta } =O_p(1/\sqrt{NT})$, we have

$$\begin{aligned} \frac{1}{NT} \sum _{i=1}^N \sum _{t=1}^T (y_{it} - \widehat{\varvec{\beta }}_*'\varvec{x}_{it})^2&= \frac{1}{NT} \sum _{i=1}^N \sum _{t=1}^T e_{it}^2 - 2 \frac{1}{NT} \sum _{i=1}^N \sum _{t=1}^T e_{it}\varvec{x}_{it}'(\widehat{\pmb {\beta }}_*-\pmb {\beta } ) + O_p\left( \frac{1}{NT}\right) \\&= \frac{1}{NT} \sum _{i=1}^N \sum _{t=1}^T e_{it}^2 + O_p\left( \frac{1}{\sqrt{NT}}\right) . \end{aligned}$$

Accordingly, the BN and AH criteria include an additional term of order $O_p((NT)^{-1/2})$ that does not affect the asymptotic properties as N and T tend to infinity.

Let us consider the asymptotic properties of the respective estimators ${\widehat{r}}$ if T is fixed and $N\rightarrow \infty$. The condition $\lim _{N\rightarrow \infty } P({\widehat{r}}<r_0)=0$ implies (cf. Bai and Ng 2002)

$$\begin{aligned} c(N,T)&= \frac{N+T}{NT} \log (min[N,T]) \rightarrow 0. \end{aligned}$$

(19)

As condition (19) is not satisfied for fixed T, the BN criterion may select some ${\widehat{r}}<r_0$, even if $N\rightarrow \infty$. The requirement $\lim _{N\rightarrow \infty } P({\widehat{r}}>r_0)=0$ implies

$$\begin{aligned} \lim _{N\rightarrow \infty } \ P\left( (r-r_0) c(N,T) + \log \bigl ({\widehat{\sigma }}_u^2(r) \bigr ) - \log \bigl ({\widehat{\sigma }}_u^2(r_0) \bigr )>0 \right)&= 1 \quad \text { for all } r>r_0. \end{aligned}$$

(20)

Since $\log \bigl ({\widehat{\sigma }}_u^2(r_0) \bigr ) - \log \bigl ({\widehat{\sigma }}_u^2(r) \bigr ) = O_p(N^{-1}) + O_p(T^{-1})$ for $r>r_0$ (cf. Lemma 4 of Bai and Ng 2002), it may happen that for small T, condition (20) is violated as well. Hence, the BN criterion may not be consistent for fixed T. In practice it is nevertheless possible that the BN criterion selects the number of factors consistently, if the eigenvalues ${\widehat{\mu }}_1,\ldots ,{\widehat{\mu }}_{r_0-1}$ are sufficiently large and ${\widehat{\mu }}_{r_0+1},\ldots ,{\widehat{\mu }}_{r^*}$ are sufficiently small relative to ${\widehat{\mu }}_{r_0}$.

Since for fixed T, ${\widehat{\mu }}_{r}$ is $O_p(1)$ for all $r=1,\ldots ,T$, it follows that the eigenvalue ratio $\text {AH}(r)$ is $O_p(1)$ for fixed T and all $r\in \{1,\ldots ,r^*\}$. Therefore, the AH criterion cannot be shown to be a consistent selection rule for fixed T. It may nevertheless perform well, if the slope of the eigenvalue function is sufficiently steep at $r=r_0$.

A possibility to sidestep these problems is to adopt the BIC selection criteria of Ahn et al. (2013) and Robertson and Sarafidis (2015). These criteria are based on the Sargan–Hansen specification test for GMM estimators. If the number of factors is too small, then the remaining cross-correlation among the residuals results in a large value of the test statistic. The penalty function is constructed such that the sum of the test statistic and the penalty function obtains a minimum at the correct number of factors as N tends to infinity.

7 Monte Carlo simulations

In this section we assess the performance of alternative estimation methods in various settings and highlight some favorable and problematic aspects of alternative estimation methods. The simulation results in Sects. 7.1–7.2 are based on the following simple data-generating process

$$\begin{aligned} y_{it}&= \beta x_{it} + \lambda _i f_t + u_{it} \end{aligned}$$

(21)

$$\begin{aligned} x_{it}&= \mu + \lambda _i f_t + \lambda _i + f_t + \varepsilon _{it} \end{aligned}$$

(22)

with $\beta = 0.5$ and $r = 1$. Hence, the regressor is correlated with the loadings, the factor and the product of both. The regression error $u_{it}$ and the idiosyncratic component of the regressor, $\varepsilon _{it}$, are independent standard normal random variables. The constant $\mu$ is drawn from a U[0, 1] distribution. The DGPs in Sects. 7.1 to 7.2 differ with respect to the distributional assumptions on the factors and their loadings.

The (near) violation of the normalization restrictions for the CCE and ALS estimators is examined in Sect. 7.1. In Sect. 7.2, we compare the PC and CCE estimator with regard to their different weighting schemes. In Sect. 7.3 we address the estimation of the number of factors, r, for the PC, ALS* and RS approaches. There, we consider a similar DGP as in (21) and (22) for $r = 1$ and $r = 2$. The last Sect. 7.4 considers the relative performance of the CCE, PC, ALS* and RS estimation approaches in more general settings that are based on the DGPs considered by Bai (2009), Chudik et al. (2011) and Ahn et al. (2013).

7.1 Normalization failure

As argued in Sect. 4, the CCE and ALS/HRN approaches may suffer from a violation of their normalization conditions. The performance already deteriorates if the parameters approach the $\sqrt{N}$-vicinity of the problematic subspace. In a model with a single factor, the normalization of the equally weighted CCE estimator $(\lambda _{0,i}=1)$ requires that ${\overline{\lambda }} =N^{-1}\sum _{i=1}^N \lambda _i\ne 0$. We have argued that whenever ${\overline{\lambda }} = c/\sqrt{N}$, the factor cannot be represented by a linear combination of ${\overline{y}}_i$ and ${\overline{x}}_i$ as $N\rightarrow \infty$.

Sarafidis and Wansbeek (2012) and Westerlund and Urbain (2013) analyze the performance of the CCE estimator when the normalization condition is violated. In order to study the performance of the CCE estimator when $\overline{\lambda }$ is different but close to zero, we consider the model in (21) and (22), where we generate the factor loadings as

$$\begin{aligned} \text {DGP1:} \quad \lambda _i \sim \mathcal {N}(\mu _\lambda ,1) \ \text {for} \ \mu _\lambda \in [0,1] \ \text { and } \ f_t \sim \mathcal {N}(0,1). \end{aligned}$$

Hence, the loadings are normally distributed with expectation that ranges from 0 to 1.

Figure 1a–d presents the absolute bias for the original CCE, the Mundlak-type CCE(M) estimator suggested in Sect. 4, and the PC estimator for $N = 100$ and $N=500$ with a small ($T=10$) and moderate ($T = 50$) number of time periods. The PC estimator of Bai (2009) is obtained by a sequential estimation procedure using the pooled OLS estimator as starting value for $\beta$ (see Sect. 2.1). It turns out that the CCE estimator is severely biased even if the mean of $\lambda _i$ is substantially different from zero. This is due to the fact that a bias already occurs whenever $\mu _\lambda =O(N^{-1/2})$. This reasoning predicts that for fixed $\mu _\lambda$ the bias gets smaller if N increases. Indeed, this is what we observe when comparing panel (a) and (c) as well as (b) and (d). Note that $\sqrt{100}/\sqrt{500} \approx 0.44$ and, therefore, we expect that the bias reduces to a value less than one half which is a good approximation for $\mu _\lambda >0.1$. The other two estimators, PC and CCE(M), are virtually unbiased, which is expected as the estimators do not rely on the assumption $\mu _\lambda \ne 0$.

Fig. 1

Normalization failure for CCE (DGP1) and ALS (DGP2)

In a similar manner, the normalization of the ALS estimator may be problematic if the factors approach the problematic subspace. The ALS estimator requires $f_T \ne 0$. To examine the consequences of an (approximate) violation of this normalization condition, we consider the model in (21) and (22) where the factors are generated as

$$\begin{aligned} \text {DGP2:} \ f_t \sim \mathcal {N}(0,1) \ \text { for } t=1,...,T-1 \text { and } \ f_T \sim \mathcal {N}(\mu _{T},0.5) \ \text { for } \mu _{T} \in [0,1] \end{aligned}$$

and the factor loadings are standard normally distributed. As the final value of the factor is crucial, we generate it by a distribution with expectation ranging from 0 to 1.

Figure 1e–f presents the bias for the ALS estimator when $T = 5$ and $N = 100$ or $N=500$, respectively. As expected, the ALS estimator is severely biased whenever $\mu _{T}={\mathbb {E}}(f_T)$ is small. But even for moderate values of $\mu _{T}$ the bias remains substantial and decreases only gradually for larger values of $\mu _{T}$. It should be noted that if the regression includes an individual specific intercept, then the factors are demeaned and, therefore, assuming a nonzero mean appears inappropriate.

Figure 1e–f also presents the bias of two estimators that circumvent the problems with the normalization of the original ALS estimator. The estimator ALS$^*$ refers to the GMM estimator that estimates the matrix H that is used to remove the factors (see Sect. 4).¹⁰ Our simulation results suggest that this estimator performs quite well in terms of bias, as it is virtually unbiased for all values of $\mu _{T}$. Another approach to escape the normalization problem is the GMM$_{max}$ estimator, where in a first step the factor is estimated using the PC approach. In the second step, the time period for the normalization is chosen according to the maximum absolute value of the estimated factor and the original ALS estimator is adapted, where the time period with the largest factor is shifted to the end of the sample. Both estimators are able to reduce the bias dramatically.

The figures also include the RS estimator, which corresponds to the FIVU estimator of Robertson and Sarafidis (2015). This estimator does not require $f_T \ne 0$ for normalization (see Sect. 2.4) and thus the bias does not depend on the value of $\mu _{T}$. The RS estimator has a slight advantage in terms of bias when $N = 100$. With $N = 500$, the bias of the ALS$^*$, GMM$_{max}$ and RS estimators is nearly zero.

To summarize, our findings confirm earlier evidence that the normalization applied for the original CCE or ALS/HNR estimators may be problematical, whenever the factors or loadings approach a normalization failure. It is, however, easy to adjust the estimators such that they perform well for all values of the parameter space. Our Monte Carlo exercise indicates that the PC and CCE(M) estimators as well as ALS$^*$, GMM$_{max}$ and RS are very robust against a possible normalization failure.

7.2 Fixed versus data driven weights

From the reasoning of Sect. 2, it turns out that the CCE estimator is expected to outperform the PC estimator whenever the weighting scheme $\pmb {\lambda }_0$ comes close to the actual set of loadings $\pmb {\lambda }$, see also Westerlund and Urbain (2015). For equal weights with $\lambda _{0,i}=1$ for all i, the CCE estimator performs well, whenever (i) the absolute value of the mean of the loadings is large (to avoid the normalization failure) and (ii) the variance of the loadings is small. Our DGP3 represents such a scenario, whereas the DGP4 favors the PC estimator by generating factor loadings with large variance,

$$\begin{aligned} \text {DGP3:}&\ \lambda _i \sim \mathcal {N}(1,0.1), \ f_t \sim \mathcal {N}(0,1) \\ \text {DGP4:}&\ \lambda _i \sim \mathcal {N}(1,3), \ f_t \sim \mathcal {N}(0,1). \end{aligned}$$

The remaining details of the simulation setup are identical to the model in (21) and (22).

The results reported in Table 1 clearly confirm our assertion that the CCE estimator outperforms the PC estimator in DGP3, whereas the PC estimator performs better for DGP4. This finding suggests to find a weighting scheme that comes close to the actual distribution of the loadings. This is the notion behind the Mundlak-type CCE variant that employs the individual specific means ${\overline{y}}_i$ and ${\overline{x}}_i$, since a linear combination of these averages can be seen as (CCE type) estimates of the loadings $\lambda _i$. Therefore, we hope to improve the original CCE estimator by applying weights that are correlated with the loadings. Our results from the simple Monte Carlo experiment suggest that the CCE(M) approach of choosing a data driven weighting scheme performs similar to the best estimator in the respective situation. Furthermore, as shown in the previous subsection, the CCE(M) estimator sidesteps the risk of a normalization failure. Provided that this estimator is similarly easy to compute as the original CCE estimator, it appears as if this estimator is a robust variant of the original CCE estimator.

Table 1 Fixed versus data driven weights

7.3 Selecting the number of factors

In practice, it is necessary to select the number of factors for the PC and GMM estimation procedures. The choice is important, since misspecifying the number of factors can have severe consequences: Overspecifying the number of factors can have adverse effects on the sampling properties of the estimators, while an underspecification may lead to inconsistent estimates if the ignored factors are correlated with the regressors. One possibility for selecting the number of factors is simply to specify the number according to some ad hoc rule, for instance $r = k+1$, as usually advocated for the CCE approach. Another option is to use a consistent criterion for the number of factors, such as the ones proposed by Bai and Ng (2002) (hereafter: BN) and Ahn and Horenstein (2013) (AH). Note that these selection criteria were developed for the pure factor model without regressors. Furthermore, the asymptotic theory underlying these approaches requires $T\rightarrow \infty$ (see Sect. 6). It is therefore interesting to investigate the performance of these criteria that were not initially developed for a small number of time periods. For the GMM estimators, the number of factors can be estimated using model information criteria, such as the Schwarz Criterion (BIC) considered by Ahn et al. (2013) and Robertson and Sarafidis (2015).

In order to study the performance of these selection criteria, we consider a similar model as in (21) and (22) with $r = 1$ and $r = 2$. For the loadings and factors, we assume the following DGP,

$$\begin{aligned} \text {DGP5:} \ \lambda _{j,i} \sim \mathcal {N}(0,1), \ f_{j,t} \sim \mathcal {N}(0,1) \ \text { for } \ j=1,2. \end{aligned}$$

As reported in Table 2, the hit rates for a single factor, $r=1$, are nearly 100% for the BN and AH criteria whenever $T\ge 10$. For $T=5$ the BN criterium does not work and nearly always picks the maximum number of factors. On the other hand the AH criterion works remarkably well, even for a number of time periods as small as $T=5$.¹¹ The hit rates for the BIC criteria exceed 90% in all but one case. For $r=2$ the hit rates for the AH criterion are substantially lower, but the estimators are still quite accurate, even if $T=10$ and N is large. For the BIC criteria, the hit rates decrease by only a small amount and do not seem to be very sensitive to the number of factors, in particular if $N>100$.

Table 2 Hit rates for selection criteria

In Table 3, we report bias and RMSE for the PC, ALS$^*$ and RS estimators based on the true number of factors ($r=1$ and $r=2$) as a benchmark. In addition we assess the performance of the estimators, when the number of factors is estimated based on selection criteria.¹² As expected, using the AH method for $r=1$ in order to estimate the number of factors for the PC estimator produces bias and RMSE results that are of similar magnitude as the true number of factors. Applying the BIC criterion to estimate the number of factors for the GMM estimators produces very accurate estimates when $N>100$, accordingly.

Table 3 Selecting the number of factors

For $r=2$, the performance of the PC estimator using the AH criterion shows a considerable bias, in particular if T is as small as 5. In contrast, bias and RMSE of the GMM estimators applying the BIC criterion are similar to the estimators based on the true number of factors when $N>100$. When T increases to 10, there is still a substantial performance gap between the PC estimator using the AH method and the PC estimator based on the true number of factors, whereas the GMM estimators based on the BIC criterion perform much better. This is surprising as Table 2 suggests that the hit rates of the BIC criterion are only slightly better in these cases. The reason is that the AH criterion tends to underestimate the number of factors, whereas the BIC criterion overestimates the number of factors in case the correct number of factors is not found.

Consider, for instance, $T = 10$ and $N = 500$. The BIC estimator finds the correct number of factors $(r=2)$ in more than 95% of the cases and overestimates the number in the other $(< 5\%)$ cases. The AH estimator finds the correct value of $r = 2$ in 89.8% of the cases, however underestimates the number in all other cases. Since the estimator is biased if the number of factors is too small, the AH criterion tends to produce a large negative bias in some cases, whereas the BIC criterion tends to produce unbiased estimators with a slightly larger variance than estimating with the correct number of factors in some very rare cases.

7.4 Performance in more general setups

So far the DGPs considered in this paper were simplified versions of the ones considered in the literature and focus on the particular features of these models. In the following, we study the relative performance of the CCE, PC, ALS$^*$ and RS approaches in more sophisticated simulation setups, similar to the simulation experiments of Bai (2009), Chudik et al. (2011) and Ahn et al. (2013). The details of these data generating processes are presented in the online appendix to this paper. The Monte Carlo design of Bai (2009) employs two regressors that are correlated with two factors, their loadings and the product of both. The idiosyncratic error is i.i.d. across individuals and time periods. We refer to this model as DGP6. DGP7 refers to the factor model of Chudik et al. (2011) that includes two regressors and three factors. A special feature of this DGP is that the factor loadings of the regressors are independent of the loadings in the errors $e_{it}$ and, therefore, the regressors are not correlated with the errors. The factors are generated by independent AR(1) processes and the idiosyncratic component $u_{it}$ is heteroskedastic but mutually and serially uncorrelated. DGP8 corresponds to the Monte Carlo design of Ahn et al. (2013), which includes two regressors and two factors. The first regressor is correlated with the first factor and the second regressor is correlated with the second factor. The idiosyncratic error is autocorrelated, but the variances are identical across panel units and time periods.

The results in Table 4 indicate that the relative performance of the estimators depends quite sensitively on the DGP considered. The first panel of Table 4 presents the results for DGP6. The CCE estimator is not consistent in this setting, since the rank condition is violated and both factor and loading vectors are correlated with both regressors. The other three estimators are consistent in this setting, where the RS estimator is the least biased when $T = 5$ and the ALS$^*$ exhibits the lowest bias for $T \ge 10$. The latter performs best in terms of RMSE with only slight advantages over the PC estimator when $T \ge 10$.

Table 4 Performance in more general setups

The second panel of Table 4 reports the results for DGP7. The CCE estimator is the favored one in this setting. It has a very small bias and exhibits the lowest RMSE for nearly all considered (N, T) combinations, in particular if T is as small as 5. Comparing the PC and GMM estimators, the results slightly favor the PC estimator in terms of RMSE. The difference between the PC and the CCE estimator is negligible when $T = 15$ and $N = 500$. With regard to the GMM estimators, the RS estimator has a marginally lower RMSE when $T = 5$ and N is large, while the results indicate small advantages for the ALS$^*$ estimator when $T \ge 10$.

The third panel of Table 4 presents the results for DGP8. The GMM estimators are the least biased estimators in this setting. The ALS$^*$ estimator exhibits the smallest RMSE for all (N, T) combinations with only slight advantages over the RS estimator. For example, for $T = 10$ and $N = 500$, the RMSE of the ALS$^*$ estimator is about 40% lower than the RMSE of the PC estimator and more than 60% lower than the RMSE of the CCE estimator. The CCE estimator is problematic in this setting, since the expectation of the loadings is equal to zero. The PC estimator is problematic in this small T setting. However, the RMSE is lower for larger samples with $T = 15$ and $N = 500$.

8 Conclusion

In this paper we compare three existing approaches for estimating factor augmented panel data models. We argue that the PC estimator can be seen as an estimated analog of the optimal transformation for eliminating the common factors from the data. The CCE estimator applies a data transformation that has the important advantage that the weighting scheme is fixed and does not involve any sampling error. This ensures that the estimator is consistent even if T is fixed, whereas the PC estimator requires much more restrictive assumptions (such as i.i.d. errors) whenever T is fixed. The third estimation approach corresponds to the nonlinear GMM estimators of Ahn et al. (2013) and Robertson and Sarafidis (2015). In contrast to the PC and CCE estimators, the number of parameters does not depend on N, which makes these estimators particularly attractive for models with large N and small T.

In this paper we focus on the typical micro panel data setup where T is small compared to N. Since for an approximate factor model the consistency of the PC estimator requires $T\rightarrow \infty$, it is interesting to investigate how large T needs to be for ensuring the PC estimator to be approximately unbiased. Our Monte Carlo experiments indicate that for all data generating mechanisms considered in this paper $T=10$ is already sufficient to achieve reasonable small sample properties of the PC estimator.

Some versions of the estimators impose normalization conditions that may be problematical in practice. For the original CCE estimator, we propose a simple weighting scheme based on a decomposition similar to Mundlak (1978). The resulting CCE(M) estimator is able to escape the endogeneity bias that may occur in the $\sqrt{N}$ vicinity of the normalization failure at the cost of introducing a larger number of additional auxiliary parameters. The PC, ALS$^*$ and RS estimators sidestep the possibility of a normalization failure and perform well in all our Monte Carlo experiments. Sometimes the CCE and ALS$^*$ estimators perform slightly better than the PC estimator, but in other Monte Carlo setups the PC estimator tends to outperform all other competitors. Furthermore, we show that for small T the selection criteria for the number of factors proposed by Bai and Ng (2002) and Ahn and Horenstein (2013) may be inconsistent, whereas the BIC criteria of Ahn et al. (2013) and Robertson and Sarafidis (2015) perform well.