Nonparametric portfolio efficiency measurement with higher moments

Abstract

The paper considers a nonparametric approach to determine portfolio efficiency using specific directions toward the portfolio frontier function. This approach allows for a straightforward incorporation of higher moments of the returns distribution beyond mean and variance. The nonparametric approach is extended by the computation of optimal directions endogenously by maximizing the distance toward the portfolio frontier as a novel methodological feature. An empirical application to Fama–French portfolios demonstrates the applicability of the nonparametric approach. The results show that the optimal directions to the frontier depend on the portfolio considered as well as on the period for which the moments are estimated. Skewness in particular plays a role in determining the optimal direction, whereas kurtosis seems to be less crucial.

1 Introduction

Portfolio selection in the legacy of Markowitz (1952, (1959) is traditionally concerned with finding a compromise between a high return and low risk. This setting can be criticized, however, and in particular, it neglects the influence of higher moments of the returns distribution beyond mean and variance on the utility of an investor.¹ The consideration of those higher moments also has a long tradition in finance with Samuelson (1970) being one of the first contributions. There is a steady stream of articles following with a special focus on the third moment, skewness, but also considering the fourth moment, kurtosis (see, e.g., Kraus and Litzenberger 1976; Scott and Horvath 1980; Harvey and Siddique 2000; Jondeau and Rockinger 2006; Harvey et al. 2010 and the numerous references cited therein).

Assuming a specific utility function is restrictive and an approach which is workable without such an assumption would be valuable. One such approach applies methods originating from nonparametric productivity analysis, mostly based on variants of data envelopment analysis (DEA). DEA is usually applied to determine productive efficiency in general input–output relationships. In finance applications, the mean return is usually taken as the output variable, whereas measures of risk or transaction cost components are treated as inputs. This follows from the simple logic that the output should be maximized, whereas the inputs are to be minimized. There are numerous published articles reporting empirical analyses along these lines. See Murthi et al. (1997), Morey and Morey (1999) and Edirisinghe and Zhang (2007) as representative examples and Glawischnig and Sommersguter-Reichmann (2010) for a succinct summary.

Lamb and Tee (2012) point to various problems with applications of DEA for portfolio performance evaluation. One of these problems is the inability of most DEA analyses to take account of the effects of diversification. Better adapted to the task of portfolio performance evaluation is the nonparametric methodological approach put forward by Briec and Kerstens with their various co-authors based on the concept of the shortage function (Luenberger 1992, 1995) which is also known as the directional distance function (DDF) of Chambers et al. (1996). In contrast to DEA analyses which rely on linear programming solvers for their computation, the Briec–Kerstens approach leads to nonlinear constraints and requires the application of numerical methods for nonlinear optimization.

As mentioned above, higher moments of returns such as skewness and kurtosis also play a role for portfolio choice beyond mean and variance as additional sources of risk. Conventional parametric and Bayesian approaches to the analysis of portfolio selection under higher moments are explained in Jondeau and Rockinger (2006) and Harvey et al. (2010), respectively. The Briec–Kerstens approach also allows for a straightforward extension to incorporate higher moments (skewness, kurtosis) in addition to mean and variance into the nonparametric approach. This is developed by Briec et al. (2004) for the mean–variance analysis and extended by Briec et al. (2004) to a mean–variance–skewness analysis. Briec and Kerstens (2010) provide a generalization of the previous papers to moments of arbitrary order including partial moments. By this development, the mean–variance–skewness–kurtosis case is also covered. This case is also covered in the related analysis of Boudt et al. (2020a) who also apply shrinkage methods for the estimation of higher moments as we do subsequently.

In this paper, we follow the Briec–Kerstens approach to analyze portfolios constructed by Fama and French for various selected periods. The primary advantage of this approach is that there is no need to assume specific functional forms, neither for the frontier function nor for the distribution of the returns. We are able to determine appropriate benchmarks for evaluating the portfolios without having to rely on a specific theoretical model. In addition, the approach permits a straightforward incorporation of higher moments (of course at the expense of increasing computational complexity). We introduce the novel methodological feature of an endogenous determination of the direction toward the frontier function in the moment space for this type of methodological approach.

The results obtained with this approach show that the more efficient portfolios tend to be composed of small (rather than large) stocks, of high (rather than low) book-to-market value stocks, of stocks with high (rather than low) operating profitability and of stocks with low (rather than high) investment. There are major differences of the distance to the frontier and the optimal direction along which this distance is measured across the subperiods considered. In addition to the roles of mean and variance, skewness tends to play a larger role compared to kurtosis.

The paper proceeds with a discussion of the influence of higher moments on the utility derived from the final wealth of an investment in Sect. 2. This is followed by an outline of the nonparametric approach to compute portfolio efficiency with its extensions in Sect. 3. The results obtained with this approach for a selection of univariate sorts of portfolios and various subperiods are presented and discussed in Sect. 5. Beforehand, in Sect. 4 the data are explained in detail and statistical description is provided. The results are summarized, and conclusions are drawn in the final Sect. 6.

2 Higher moments and utility

This section relates the higher moments of the returns distribution to the utility of the investor holding a particular portfolio of assets (which may be stocks, bonds, funds or portfolios). The exposition is mainly linked to Jondeau and Rockinger (2006), but here, it is more strongly focused on the central utility motives of non-satiation, risk aversion, prudence and temperance corresponding to the first four moments of the returns distribution. For expositional convenience, we consider an investor holding a portfolio of n risky assets with returns collected in the vector ${\varvec{R}}=(R_{1},\ldots ,R_{n})'$. The returns are characterized by a joint distribution $F({\varvec{R}})$. At the end of a particular period, wealth is generated by $W=1+{\varvec{x}}'{\varvec{R}}$ where ${\varvec{x}}=(x_{1},\ldots ,x_{n})'$ denotes a vector of nonnegative portfolio weights summing to unity.

The utility derived from this wealth is given by the utility function u(W). By a Taylor approximation up to fourth order around the expected wealth E(W), we get

$$\begin{aligned} u(W)\approx & {} u(E(W))+(W-E(W))\cdot u'(E(W))+\dfrac{(W-E(W))^{2}}{2!}\cdot u''(E(W))\nonumber \\&+\dfrac{(W-E(W))^{3}}{3!}\cdot u'''(E(W))+\dfrac{(W-E(W))^{4}}{4!}\cdot u''''(E(W)) \end{aligned}$$

(1)

for the utility function. The appropriate order of the Taylor approximation is not clear, and adding more terms may even be harmful for the approximation quality under certain circumstances (see Hlawitschka 1994). Dittmar (2002) provides evidence in favor of a cubic pricing kernel which implies preferences over the first four moments of the returns distribution.

According to Arrow (1971), investors generally have utility functions with a positive marginal utility of wealth ($u'(\cdot )>0$, implying non-satiation) decreasing marginal utility of wealth ($u''(\cdot )<0$, representing risk aversion) and non-increasing absolute risk aversion. The latter property is associated with $u'''(\cdot )>0$ and implies prudence as a necessary condition. A prudent investor values precautionary savings as a protection against loss. A further characteristic of the utility function is so-called temperance associated with its fourth derivative $u''''(\cdot )<0$ (Gollier and Pratt 1996).

Taking expectations, we get

$$\begin{aligned}&E(u(W))\approx u(E(W))+\frac{1}{2}\mathrm {Var}(W)\cdot u''(E(W))+\frac{1}{6}\mathrm {Skew}(W)\cdot u'''(E(W))\nonumber \\&\quad +\frac{1}{24}\mathrm {Kurt}(W)\cdot u''''(E(W)) \end{aligned}$$

(2)

for expected utility. We see that expected utility is driven by the variance $\mathrm {Var}(W)=E((W-E(W))^{2})$ representing risk and reducing expected utility for a risk-averse investor. Skewness $\mathrm {Skew}(W)=E((W-E(W))^{3})$ is larger than zero if the probability of large positive returns is larger than the probability of negative returns of the same size (right-skewed distribution) and smaller than zero if the distribution of W is left-skewed with a higher probability of below-mean returns. Stock returns are frequently negatively skewed since very large losses are more likely than very large gains. The importance of skewness has already been discussed by Kraus and Litzenberger (1976). They point out that expected utility increases with skewness for an investor with non-increasing absolute risk aversion. Investors thus tend to have preference for positive skewness. A larger value for kurtosis $\mathrm {Kurt}(W)=E((W-E(W))^{4})$ indicates a higher probability for extreme market events associated with large gains or losses, therefore representing tail heaviness.² In the subsequent analysis, we will consider the three relevant cases with a second, third and fourth order separately.

3 Computing portfolio efficiency

Starting point of this nonparametric approach to portfolio analysis was Morey and Morey (1999) who were the first to integrate the optimization of the portfolio weights into a nonparametric efficiency analysis framework. Their quadratic optimization programs are specified either to maximize mean return for the actual variance of an asset or to minimize the variance for a given return. This mean–variance (MV) analysis has been extended to a simultaneous enhancement of mean return and reduction in variance by Briec et al. (2004). They use the device of the Luenberger (1992, (1995) shortage function, also used as directional distance function (DDF) by Chambers et al. (1996) for the formulation of the respective optimization problems. This framework has been extended by Briec et al. (2004) to a mean–variance–skewness (MVS) analysis and to a general moment space (including partial moments) by Briec and Kerstens (2010). This also covers the mean–variance–skewness–kurtosis (MVSK) analysis.³

3.1 Portfolio moments

The treatment of portfolio choice is based on a vector of returns for a cross section of n assets $R_{i}$, $i=1,\ldots ,n$, stacked to a vector ${\varvec{R}}=(R_{1},\ldots ,R_{n})'$ with expectation $\varvec{\mu }=E({\varvec{R}})$ and a covariance matrix ${\varvec{V}}=\mathrm {Var}({\varvec{R}})=E({\varvec{r}}{\varvec{r}}')$ with ${\varvec{r}}={\varvec{R}}-\varvec{\mu }$.⁴

In addition to these first two moments, skewness and kurtosis may also be relevant for portfolio selection, as explained above. For a scalar random variable Y, skewness is defined as $s=E((Y-\mu _{Y})^{3})$ with $\mu _{Y}=E(Y)$. Positive (negative) skewness $s>0$ ($s<0$) indicates a right-skewed (left-skewed) distribution with a higher probability of large positive (negative) returns. In the case of a symmetric (about the mean) distribution, we have $s=0$. Scalar skewness can be estimated by ${\hat{s}}=T^{-1}{\textstyle \Sigma _{t=1}^{T}}(y_{t}-{\bar{y}})^{3}$ for a time-series sample of observations $y_{t}$, $t=1,\ldots ,T$, and ${\bar{y}}=T^{-1}{\textstyle \Sigma _{t=1}^{T}}y_{t}$. Scalar kurtosis is likewise defined as $k=E((Y-\mu _{Y})^{4})$ and can be estimated by ${\hat{k}}=T^{-1}\Sigma _{t=1}^{T}(y_{t}-{\bar{y}})^{4}$. It measures the extent of fat tails of a distribution with $k>3\sigma ^{4}$ for fat-tailed distributions relative to the benchmark case of a normal distribution. Fat tails are associated with a larger probability of extreme returns.

To deal with portfolio skewness, we need the $n\times n^{2}$ co-skewness matrix ${\varvec{S}}=E({\varvec{r}}{\varvec{r}}'\otimes {\varvec{r}}')$ with elements of the type $E(r_{i}r_{j}r_{h})$.⁵ This comprises not only the skewness of asset i, i.e., $E(r_{i}^{3})$, but also co-skewness elements of the sort $E(r_{1}r_{3}^{2})$ or $E(r_{1}r_{2}r_{3})$, for example. Likewise, we define the $n\times n^{3}$ co-kurtosis matrix ${\varvec{K}}=E\left( {\varvec{r}}{\varvec{r}}'\otimes {\varvec{r}}'\otimes {\varvec{r}}'\right)$ with typical element $E(r_{i}r_{j}r_{h}r_{l})$. An example for the specific arrangement of the co-skewness and co-kurtosis terms in the matrices ${\varvec{S}}$ and ${\varvec{K}}$ can be found in Jondeau and Rockinger (2006, p. 36) and is defined by the form of indexing used in (3).

These moments can be estimated by using a data sample for a vector of returns ${\varvec{R}}_{t}=(R_{1t},\ldots ,R_{nt})'$, $t=1,\ldots ,T$. Defining ${\varvec{r}}_{t}=(r_{1t},\ldots ,r_{nt})'$ correspondingly with $r_{it}=R_{it}-{\hat{m}}_{i}$, $t=1,\ldots ,T$, we estimate the mean vector and the moment matrices (listed jointly with their typical elements) by

$$\begin{aligned} \hat{{\varvec{m}}}= & {} T^{-1}{\displaystyle \sum _{t=1}^{T}}{\varvec{R}}_{t} \quad \hbox {with} \quad {\hat{m}}_{i} = T^{-1}{\displaystyle \sum _{t=1}^{T}}R_{it}\nonumber \\ \hat{{\varvec{V}}}= & {} T^{-1}{\displaystyle \sum _{t=1}^{T}}{\varvec{r}}_{t}{\varvec{r}}_{t}' \quad \hbox {with} \quad {\hat{v}}_{i,j} = T^{-1}{\displaystyle \sum _{t=1}^{T}}r_{it}r_{jt}\nonumber \\ \hat{{\varvec{S}}}= & {} T^{-1}{\displaystyle \sum _{t=1}^{T}}{\varvec{r}}_{t}{\varvec{r}}_{t}'\otimes {\varvec{r}}_{t}' \quad \hbox {with} \quad {\hat{s}}_{i,n(j-1)+h} = T^{-1}{\displaystyle \sum _{t=1}^{T}}r_{it}r_{jt}r_{ht}\nonumber \\ \hat{{\varvec{K}}}= & {} T^{-1}{\displaystyle \sum _{t=1}^{T}}{\varvec{r}}_{t}{\varvec{r}}_{t}'\otimes {\varvec{r}}_{t}'\otimes {\varvec{r}}_{t}' \quad \hbox {with} \quad {\hat{k}}_{i,n^{2}(j-1)+n(h-1)+l} = T^{-1}{\displaystyle \sum _{t=1}^{T}}r_{it}r_{jt}r_{ht}r_{lt}, \nonumber \\ \end{aligned}$$

(3)

respectively. We find the scalar moments of asset i at ${\hat{m}}_{i}=\hat{{\varvec{m}}}_{i}$, ${\hat{v}}_{i}=\hat{{\varvec{V}}}_{ii}$, ${\hat{s}}_{i}=\hat{{\varvec{S}}}_{i,n(i-1)+i}$ and ${\hat{k}}_{i}=\hat{{\varvec{K}}}_{i,n(n+1)(i-1)+i}$.

There are many parameters to be estimated in higher moment matrices leading to noisy estimates, and their number is growing with dimensionality. Shrinkage estimation intends to improve estimation precision in terms of mean square error at the expense of some bias. We perform a shrinkage estimation of the covariance matrix and the higher moment matrices with shrinkage toward independence. Given independence the co-skewness and co-kurtosis matrices in particular would have many zeros and the estimator is shrunk towards this target. Shrinkage methods for covariance matrix estimation are outlined by Ledoit and Wolf (2003, (2004) as well as by Boudt et al. (2020a) and Martellini and Ziemann (2010) for higher moment matrices (co-skewness and co-kurtosis). Computations are performed using the R-package ‘PerformanceAnalytics’ (Peterson and Carl 2020).

For an investor holding a portfolio of assets with shares $0\le x_{i}\le 1$ (collected in a vector ${\varvec{x}}=(x_{1},\ldots ,x_{n})'$ with ${\textstyle \sum _{i=1}^{n}}x_{i}=1$), we have a portfolio return of $R({\varvec{x}})=\sum _{i=1}^{n}x_{i}R_{i}={\varvec{x}}'{\varvec{R}}$ with expectation $m_{p}({\varvec{x}})=E\left( R({\varvec{x}})\right) ={\varvec{x}}'\varvec{\mu }$ and variance $v_{p}({\varvec{x}})=\mathrm {Var}\left( R({\varvec{x}})\right) ={\varvec{x}}'{\varvec{V}}{\varvec{x}}$. Portfolio skewness is computed by $s_{p}({\varvec{x}})=\mathrm {Skew}\left( R({\varvec{x}})\right) ={\varvec{x}}'{\varvec{S}}({\varvec{x}}\otimes {\varvec{x}})$ and portfolio kurtosis by $k_{p}({\varvec{x}})=\mathrm {Kurt}\left( R({\varvec{x}})\right) ={\varvec{x}}'{\varvec{K}}({\varvec{x}}\otimes {\varvec{x}}\otimes {\varvec{x}})$.

For the portfolios defined by ${\varvec{x}}$, we estimate the portfolio moments by

$$\begin{aligned} {\hat{m}}_{p}({\varvec{x}})= & {} {\varvec{x}}'\hat{{\varvec{m}}} = {\displaystyle \sum _{i=1}^{n}}x_{i}{\hat{m}}_{i}\nonumber \\ {\hat{v}}_{p}({\varvec{x}})= & {} {\varvec{x}}'\hat{{\varvec{V}}}{\varvec{x}} = {\displaystyle \sum _{i=1}^{n}}{\displaystyle \sum _{j=1}^{n}}x_{i}x_{j}{\hat{v}}_{i,j}\nonumber \\ {\hat{s}}_{p}({\varvec{x}})= & {} {\varvec{x}}'\hat{{\varvec{S}}}({\varvec{x}}\otimes {\varvec{x}}) = {\displaystyle \sum _{i=1}^{n}}{\displaystyle \sum _{j=1}^{n}}{\displaystyle \sum _{h=1}^{n}}x_{i}x_{j}x_{h}{\hat{s}}_{i,n(j-1)+h}\nonumber \\ {\hat{k}}_{p}({\varvec{x}})= & {} {\varvec{x}}'\hat{{\varvec{K}}}({\varvec{x}}\otimes {\varvec{x}}\otimes {\varvec{x}}) = {\displaystyle \sum _{i=1}^{n}}{\displaystyle \sum _{j=1}^{n}}{\displaystyle \sum _{h=1}^{n}}{\displaystyle \sum _{l=1}^{n}}x_{i}x_{j}x_{h}x_{l}{\hat{k}}_{i,n^{2}(j-1)+n(h-1)+l} \end{aligned}$$

(4)

with the notation clarifying the dependence on ${\varvec{x}}$.

3.2 Directional distance functions

The cornerstone of the nonparametric approach to portfolio efficiency measurement is the so-called shortage function introduced by Luenberger (1992, (1995) in a production context. Chambers et al. (1996) propose the same concept as a directional distance function (DDF) for measuring the distance of an input–output point to the production frontier function along a particular direction. They have pointed out the interpretation of the distance measure as an efficiency measure.

The methodological extension pursued in this work is to treat the direction vector involved in computing the directional distances as a part of the optimization problem for calculating the optimal distances to the portfolio frontier function which is interpreted as portfolio efficiency. The following exposition directly turns to the MVSK case, while the MVS and MV cases can be easily obtained by deleting the respective constraints for skewness and kurtosis.

The formal definition of the DDF is based on the admissible set of all nonnegative vectors ${\varvec{x}}$ summing up to unity,

$$\begin{aligned} \mathfrak {{\mathcal {P}}}=\{{\varvec{x}}\in {\mathbb {R}}^{n}:{\varvec{x}}\ge {\varvec{0}},{\varvec{1}}'{\varvec{x}}=1\}, \end{aligned}$$

(5)

with ${\varvec{0}}$ and ${\varvec{1}}$ as conformable vectors of zeros and ones, respectively. Considering a vector of portfolio moments ${\varvec{z}}_{p}({\varvec{x}})$, e.g., ${\varvec{z}}_{p}({\varvec{x}})=(m_{p}({\varvec{x}}),-v_{p}({\varvec{x}}))'$ for the mean–variance case (where the negative sign of the variance indicates that this moment is to be minimized), the so-called disposal representation set is the admissible moment space

$$\begin{aligned} \mathbb {\mathtt {{\mathcal {D}}}}=\{{\varvec{z}}\in {\mathbb {R}}^{|{\varvec{z}}|}:{\varvec{x}}\in {\mathcal {P}},{\varvec{z}}\le {\varvec{z}}_{p}({\varvec{x}})\}, \end{aligned}$$

(6)

where $|{\varvec{z}}|$ denotes the length of the vector ${\varvec{z}}$ (i.e., 2 in the MV case, 3 in the MVS case and 4 in the MVSK case).

The shortage function or DDF as our measure of portfolio efficiency is defined as

$$\begin{aligned} S_{g}({\varvec{x}})=\sup \{\delta \ge 0:{\varvec{z}}_{p}({\varvec{x}})+\delta {\varvec{g}}\in {\mathcal {D}}\} \end{aligned}$$

(7)

with the vector ${\varvec{g}}$ controlling the direction in which moments are to be expanded or contracted. In the mean–variance case, we would specify $g_{1}>0$ and $g_{2}<0$ to get an expansion of the mean jointly with a contraction of the variance. The portfolio efficiency measure $\delta$ (which actually is a measure of inefficiency) is to be maximized simultaneously with ${\varvec{x}}$ to find a point on the portfolio frontier function along the direction ${\varvec{g}}$. In other words, the value of $\delta$ is chosen jointly with ${\varvec{x}}$ to maximize the moments along the direction ${\varvec{g}}$ so that the vector ${\varvec{z}}_{p}({\varvec{x}})+\delta {\varvec{g}}$ remains in ${\mathcal {D}}$ and therefore hits the frontier. For points on the frontier, we obtain $\delta =0$.

For computing the value of the shortage function, we use the basic DDF portfolio optimization problem which can be stated as

$$\begin{aligned} \begin{array}{cc} \underset{\delta ,{\varvec{x}}}{\max } &{} \delta \\ \mathrm {s.t.} &{} {\hat{m}}_{i} + \delta g_{m} \le {\hat{m}}_{p}({\varvec{x}})\\ &{}{\hat{v}}_{i} - \delta g_{v} \ge {\hat{v}}_{p}({\varvec{x}})\\ &{}{\hat{s}}_{i} + \delta g_{s} \le {\hat{s}}_{p}({\varvec{x}})\\ &{}{\hat{k}}_{i} - \delta g_{k} \ge {\hat{k}}_{p}({\varvec{x}})\\ &{}{\varvec{1}}'{\varvec{x}} = 1\\ &{}{\varvec{x}} \ge {\varvec{0}} \end{array} \end{aligned}$$

(8)

with the restriction ${\varvec{x}}\ge {\varvec{0}}$ excluding the possibility of short sales.⁶ In addition, the vector of portfolio weights is required to sum to unity ${\varvec{1}}'{\varvec{x}}=1$. If specific institutional restrictions on trading in a market exist, these could be introduced by additional restrictions of the general form ${\varvec{A}}{\varvec{x}}\le {\varvec{b}}$. Program (8) has to be computed for each asset $i\in \{1,\ldots ,n\}$ under consideration.⁷

The directions $g_{m}$, $g_{v}$, $g_{s}$, $g_{k}$ (now assuming all $\ge 0$) collected in the vector ${\varvec{g}}=(g_{m},g_{v},g_{s},g_{k})'$ are to be supplied by the analyst. A frequent choice in the literature is to base the directions on the moments of the asset i under evaluation, i.e., ${\varvec{g}}=(|{\hat{m}}_{i}|,{\hat{v}}_{i},|{\hat{s}}_{i}|,{\hat{k}}_{i})'$. In the subsequent empirical application, we compute (8) for the single fixed direction with maximizing only the mean (${\varvec{g}}=(|{\hat{m}}_{i}|,0,0,0)'$) minimizing only the variance (${\varvec{g}}=(0,{\hat{v}}_{i},0,0)'$) maximizing only the skewness (${\varvec{g}}=(0,0,|{\hat{s}}_{i}|,0)'$) or minimizing only the kurtosis (${\varvec{g}}=(0,0,0,{\hat{k}}_{i})'$) as derived from the effect of the moments on expected utility (2). All these choices share the particular advantage of making the efficiency measure $\delta$ invariant to units of measurement. This measure can then be interpreted as a percentage improvement of a single moment or of a mixture of all moments.⁸

We also treat a case named as fixed where the direction vector is specified as ${\varvec{g}}=(|{\hat{m}}_{i}|,{\hat{v}}_{i},|{\hat{s}}_{i}|,{\hat{k}}_{i})'$ and allows computing the distance to the portfolio frontier function in the direction of simultaneously increasing mean and skewness while reducing variance and kurtosis. The label ‘fix’ is here to be understood in the sense of being fixed for the specific values of the moments of asset i under evaluation but not in the sense of being fixed across the different assets in the sample. In particular, this direction vector is not the result of an optimal choice of the directions. This optimal choice is considered next.

3.3 Endogenous direction choice

The choice of the direction vector exerts an influence on the measured portfolio efficiency. In this respect, Kerstens et al. (2012) discuss several ways to choose the direction vector for mean–variance problems. They conclude that the choice of direction vector affects the relative ranking of the portfolios. However, they are not determining an optimal choice of the direction vector. In the following, we pursue this methodological extension. It is inspired by the work on direction choice for directional distance functions outside of portfolio efficiency analysis by Färe et al. (2013) and Hampf and Krüger (2015) in particular.

To endogenize the direction choice, we introduce weights $\varvec{\alpha }=(\alpha _{m},\alpha _{v},\alpha _{s},\alpha _{k})'$ for the directions into the optimization problem (8) and treat these weights as additional parameters to be optimized. This leads to the modified program

$$\begin{aligned} \begin{array}{cc} \underset{\delta ,\varvec{\alpha },{\varvec{x}}}{\max } &{} \delta \\ \mathrm {s.t.} &{} {\hat{m}}_{i} + \delta \alpha _{m}|{\hat{m}}_{i}| \le {\hat{m}}_{p}({\varvec{x}})\\ &{} {\hat{v}}_{i} - \delta \alpha _{v}{\hat{v}}_{i} \ge {\hat{v}}_{p}({\varvec{x}})\\ &{} {\hat{s}}_{i} + \delta \alpha _{s}|{\hat{s}}_{i}| \le {\hat{s}}_{p}({\varvec{x}})\\ &{} {\hat{k}}_{i} - \delta \alpha _{k}{\hat{k}}_{i} \ge {\hat{k}}_{p}({\varvec{x}})\\ &{} {\varvec{1}}'{\varvec{x}} = 1\\ &{}{\varvec{x}} \ge {\varvec{0}}\\ &{} {\varvec{1}}'\varvec{\alpha } = 1\\ &{} \varvec{\alpha } \ge {\varvec{0}} \end{array} \end{aligned}$$

(9)

where the direction weights $\varvec{\alpha }$ are restricted to be nonnegative and to sum to unity. This restriction is necessary to identify $\delta$.

Program (9) is a nonlinear program anyway because of the nonlinear dependence of the portfolio moments on ${\varvec{x}}$, see (4). In addition, the products of $\delta$ with the $\alpha$ weights can lead to instability of the numerical optimization procedure. Therefore, we actually solve an equivalent and presumably numerically more stable nonlinear program

$$\begin{aligned} \begin{array}{cc} \underset{\varvec{\gamma },{\varvec{x}}}{\max } &{} {\varvec{1}}'\varvec{\gamma }\\ \mathrm {s.t.} &{} {\hat{m}}_{i} + \gamma _{m}|{\hat{m}}_{i}| \le {\hat{m}}_{p}({\varvec{x}})\\ &{} {\hat{v}}_{i} - \gamma _{v}{\hat{v}}_{i} \ge {\hat{v}}_{p}({\varvec{x}})\\ &{} {\hat{s}}_{i} + \gamma _{s}|{\hat{s}}_{i}| \le {\hat{s}}_{p}({\varvec{x}})\\ &{} {\hat{k}}_{i} - \gamma _{k}{\hat{k}}_{i} \ge {\hat{k}}_{p}({\varvec{x}})\\ &{} {\varvec{1}}'{\varvec{x}} = 1\\ &{} {\varvec{x}} \ge {\varvec{0}}\\ &{} \varvec{\gamma } \ge {\varvec{0}} \end{array} \end{aligned}$$

(10)

with the endogenous direction weights now contained in the parameter vector $\varvec{\gamma }=(\gamma _{m},\gamma _{v},\gamma _{s},\gamma _{k})'$. Comparing (9) and (10), we immediately see the relation ${\varvec{1}}'\varvec{\gamma }=\delta \cdot {\varvec{1}}'\varvec{\alpha }=\delta$ (since ${\varvec{1}}'\varvec{\alpha }=1$ in (9)) which allows computing $\delta$ and retrieving $\alpha _{j}=\gamma _{j}/\delta$, $j\in \{m,v,s,k\}$.⁹ Hence, the target function value represents the same efficiency measure.

The computations are done using a sequential quadratic programming (SQP) algorithm for nonlinearly constrained gradient-based optimization by Kraft (1994). This algorithm solves a sequence of quadratic programming approximations and is able to deal with both equality and inequality constraints. For the procedure, we need the derivatives $\partial m_{p}/\partial {\varvec{x}}=\varvec{\mu }$, $\partial s_{p}/\partial {\varvec{x}}=2{\varvec{V}}{\varvec{x}}$, $\partial s_{p}/\partial {\varvec{x}}=3{\varvec{S}}({\varvec{x}}\otimes {\varvec{x}})$ and $\partial k_{p}/\partial {\varvec{x}}=4{\varvec{K}}({\varvec{x}}\otimes {\varvec{x}}\otimes {\varvec{x}})$. Details of the derivation can be found in the Appendix. We use the implementation in the R-package ‘nloptr.’¹⁰ The programs prove to be computationally very well behaved. Briec and Kerstens (2010) discuss conditions for the existence of a global optimum and the possibility of local optima. Starting several times from randomly drawn starting configurations leads only to minor changes of the solutions.

4 Fama–French portfolios

For the empirical application, we use the data which provide the basis for the influential work of Fama and French (e.g., 1993, 1995, 1996, 2015) on market efficiency. These data are generously provided by Kenneth French on his homepage, where the full details of the definitions can be found.¹¹ To keep the presentation of the results manageable, we stick to the univariate sorts of stocks into portfolios by their market equity, book-to-market ratio, operating profitability and investment. These portfolios are used to form the four factors in addition to market excess returns in the five-factor model of Fama and French (2015). We use the value-weighted returns for these sorts formed on quintiles and add the returns of the market portfolio as a further asset.

In particular, we use the following portfolios as assets (with their self-explanatory abbreviations):

• MKT: Returns of a broad value-weighted index as the market portfolio, formed on the universe of all CRSP firms incorporated in the USA and listed on the NYSE, AMEX or NASDAQ.

• ME1, ME2, ME3, ME4, ME5: Portfolios formed on size as measured by market equity quintiles at the end of June each year, including all NYSE, AMEX and NASDAQ stocks for which we have market equity data for June.¹²

• BM1, BM2, BM3, BM4, BM5: Portfolios formed on quintiles of the book-to-market equity ratio at the end of June each year.

• OP1, OP2, OP3, OP4, OP5: Portfolios formed on quintiles of operating profitability (annual revenues minus cost of goods sold, interest expense, and selling, general, and administrative expenses divided by book equity for the last fiscal year) at the end of June each year.

• INV1, INV2, INV3, INV4, INV5: Portfolios formed on quintiles of investment (defined as the change in total assets from the fiscal year ending in year $t-2$ to the fiscal year ending in $t-1$, divided by total assets in $t-2$) at the end of June each year.

Used are the monthly returns data over the period July 1963 until February 2020 for these 21 portfolios. Data from this archive is also used in other work on nonparametric portfolio efficiency analysis, e.g., Brandouy et al. (2010) and Branda (2015). Measurement errors and outliers may have detrimental effects on the estimation of the moments of the returns distribution. Chopra and Ziemba (1993) demonstrate the effects of measurement errors on the selection of optimal portfolios in a mean–variance framework. For dealing with this potential problem, we rely on the method of Boudt et al. (2008) who propose an algorithm using methods from robust statistics to mitigate the influence of outliers. This method is preferred to using so-called L-moments as in Kerstens et al. (2011b). In addition and as outlined above, shrinkage estimation is used as a further device to reduce the effects of estimation error on the moment estimates.

Table 1 reports descriptive statistics for the monthly returns series over the entire sample period which are used for the subsequent computations. Note that the Boudt et al. (2008) method for cleansing the data is used here for the entire time series, whereas it is applied to the observations of each of the subperiods in the subsequent analysis. Reported are the minimum, median, maximum, mean, standard deviation, skewness coefficient, kurtosis coefficient, Jarque–Bera normality test (Jarque and Bera 1980) first-order autocorrelation coefficient, and the ERS unit-root test outcome (Elliott et al. 1996) for each of the 21 portfolio returns.

Table 1 Descriptive statistics

We find positive mean and median returns for all portfolios, while the dispersion is quite large. Skewness is negative, and the kurtosis coefficient is larger than three throughout. Analogous descriptive statistics without cleansing (results not shown) reveal that means and standard deviations are about the same, but the returns are more negatively skewed, and kurtosis is larger for all portfolios (i.e., median kurtosis is about 5). Both skewness and kurtosis lead to strong rejections of normality for all portfolios by the Jarque–Bera test. Regarding temporal dependence, we recognize a rather low degree of first-order autocorrelation, except maybe for the portfolio ME1 where autocorrelation is nearly 0.2. This finding corresponds to the strong rejections of the unit-root hypothesis by the ERS test.

5 Results

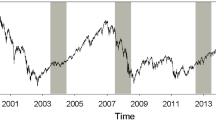
We consider the frontier functions for four subperiods. These subperiods are defined by relying on the stock market history of the USA as discussed in chapter 1 of Shiller (2015) and by Engle (2009, p. 94ff.). To support this discussion, Fig. 1 shows the time series of the Standard and Poors 500 performance index. The data at monthly frequency are retrieved from Yahoo Finance.¹³ The time-series length is restricted to the period since July 1963 when the portfolio data are also available.

Fig. 1

S&P 500 time series

The figure shows the index time series together with the NBER recession bars¹⁴ indicated by gray shades and major stock market events marked by vertical solid lines. These are (from left to right) the first oil price shock (January 1973), the Black Monday stock market crash (October 1987), the burst of the dot-com bubble (March 2000), the bankruptcy of Lehman Brothers (September 2008), the stock market selloff just before the Greece stock market crash (September 2015) and the global stock market downturn after September 2018.

The dashed vertical lines define the four periods for which we perform the nonparametric portfolio analysis and discuss the results subsequently. These periods are characterized as follows:

• Period 1 (1963:7–1982:7): This is the period before the start of the Millennium Boom phase, including the 1974/5 recession.

• Period 2 (1982:8–2000:8): This period is associated with a rapidly rising index disturbed by several crises such as the so-called Millennium Boom (or Bubble) including the October 1987 crash, the Tequila crisis of 1994, the Asian currency crisis of 1996/97, the October 1997 anniversary crash and the LTCM/Russian default crisis of 1998.

• Period 3 (2000:9–2009:2): This period is a period of stagnation and decline. It includes 9/11, the ownership society boom 2003-7 and the world financial crisis 2008/9 leading into the Great Recession.

• Period 4 (2009:3–2020:2): This is the boom period since March 2009, fueled by expansive monetary policy and low interest rates, only interrupted by two temporary downturns.

We see that the four periods are rather different regarding the specific events and the factors driving the stock market development. In particular, periods 2 and 4 are marked boom phases of stock market development.

Table 2 Moments in the subperiods

Table 2 reports the means, standard deviations, skewness and kurtosis coefficients for the returns across all portfolios (jointly with their standard deviations) for the four periods. The first period is characterized by a small mean, a comparably large standard deviation, skewness near zero and excess kurtosis. By contrast, the second period with the Millennium Boom is characterized by a much larger mean return, a slightly smaller standard deviation, more negative skewness and about the same degree of excess kurtosis. The third period is more similar to the first but has a negative mean return, the largest standard deviation, the smallest (in the sense of most negative) skewness and also some excess kurtosis. Finally, the fourth period after the decay of the Great Recession is a pronounced stock market boom phase with a large mean return, a standard deviation comparable to the second period, small skewness and mild excess kurtosis.

The presentation of the results of the portfolio efficiency analysis is structured in the following three subsections. First, we show the MV frontiers for the four periods. Then, we analyze the results for the nonparametric portfolio efficiency measures for the MV, MVS and MVSK cases with fixing single directions towards the frontier at either mean or variance or skewness or kurtosis. Finally, we turn to the results with the efficiency determined in all relevant directions, either fixed or endogenously chosen by optimization.

5.1 Mean–variance frontiers

Figure 2 shows the mean–variance frontier functions for the four periods defined above jointly in a single plot. The efficient portfolio frontiers are computed by quadratic programming using the Rmetrics suite [Würtz et al. (2009) in the R-package ‘fPortfolio’] and relying on the method of Goldfarb and Idnani (1983). The efficient part of the frontier is depicted as a solid line, whereas the inefficient part is plotted in dashes. The positions of the individual portfolios are indicated by dots and their abbreviations defined above. We find the four frontier functions to be separated with the best performance during periods 2 (red) and 4 (green) with the highest means and the lowest dispersion of variances. The worst performance is found in period 3 (blue) with very small and even negative returns and the largest dispersion of variances. Period 1 (black) is located between these extremes.

Fig. 2

Mean–variance frontier functions

We find quite large heterogeneity of the portfolio positions relative to the efficient frontier. Consistently on the frontier or close to the frontier during periods 1 and 3 are mainly the portfolios formed by stocks with small equity and high book-to-market ratios. During the boom periods 2 and 4, these portfolios are farther away from the frontier. Instead, the portfolios consisting of firms with lower investment and higher operating profitability are either on the frontier or close to the frontier.

Concerning the individual portfolios, we always find the market portfolio in between the others, although, admittedly, this is not always easy to spot visually. This is quite natural since the market portfolio is constructed from a value-weighted average of all returns, whereas the other portfolios are formed from systematically selected subsets.

The portfolios formed on size (i.e., market equity) ME1 to ME5 are quite dispersed with the lowest variances for the largest stocks (ME5) and the largest variances for the smallest stocks (ME1). We observe a weakly positive association of mean and variance for these portfolios in periods 1 and 3, while the association appears to be weakly negative in periods 2 and 4.

For the portfolios formed on book-to-market equity ratio, BM1 to BM5, we find BM1 among the portfolios with the lowest mean returns in periods 1 and 3, and in-between in the other periods. BM5, with the highest book-to-market ratio, is among the portfolios with the largest mean returns and a medium variance (with the most recent period being somewhat exceptional).

In the case of the portfolios formed on operating profitability, OP1 to OP5, we observe lower variances, with the separation of the low profitability stocks in OP1 in period 3. The association of mean and variance across these portfolios is clearly negative in periods 3 and 4. In contrast, the association is rather unclear in periods 1 and 2. The lowest profitability stocks in OP1 are consistently far away from the efficient frontier.

Finally, concerning the portfolios formed on investment, INV1 to INV5, the stocks in the fifth quintile with the highest investment (INV5) perform considerably worse in terms of their mean–variance relation compared to the stocks with smaller investment for all periods. This is different for the portfolios with lower investment, such as INV2 and INV3, which are quite close to the efficient frontier in all periods. An explanation may be that investments are frequently associated with adjustment costs caused by the reorganization within the firms and need time for becoming productive and leading to profits.

5.2 Single fixed directions

Figure 3 shows profile lines for the $\delta$-values resulting from the efficiency measurement in a single fixed direction. The directions are tuned to the pure cases of mean maximization only ($\delta _{\mathrm {m\,only}}$), variance minimization only ($\delta _{\mathrm {v\,only}}$), skewness maximization only ($\delta _{\mathrm {s\,only}}$) and kurtosis minimization only ($\delta _{\mathrm {k\,only}}$). The direction vectors for these four cases used in the computation of program (8) are specified as ${\varvec{g}}=(|{\hat{m}}_{i}|,0,0,0)'$, ${\varvec{g}}=(0,{\hat{v}}_{i},0,0)'$, ${\varvec{g}}=(0,0,|{\hat{s}}_{i}|,0)'$, ${\varvec{g}}=(0,0,0,{\hat{k}}_{i})'$ for portfolio i. The rows of the figure pertain to the four periods, and the columns pertain to the configuration of moments considered in the portfolio efficiency measurement (MV, MVS, MVSK). The abscissa lists the portfolios proceeding from the market portfolio to the portfolios sorted on market equity, book-to-market value, operating profitability and finally investment. On the ordinate, the respective $\delta$-values are connected by the profile lines.

Fig. 3

$\delta$-Values for single fixed directions

For the profile lines resulting from the MV analysis in the first column, we observe a larger portfolio inefficiency in the mean direction (solid line) during periods 1 and 3. These are the more stagnant phases of stock market development characterized by several crises leading to the Great Recession as seen from Fig. 1. The variance direction (dashed line) is more relevant during periods 2 and 4 which are the boom phases. Here, the portfolios tend to be farther away from the frontier in the variance direction, while they are closer to the frontier in the mean direction.

This corresponds to the configurations analyzed in Fig. 2, where we also observe relatively larger distances to the frontier in the vertical direction for periods 1 and 3 and relatively larger horizontal distances for periods 2 and 4. We also find zero or very low $\delta$-values more frequently occurring for particular portfolios, revealing that these portfolios are on or close to the frontier. These tend to be portfolios consisting of small stocks (e.g., ME1 or ME2) of stocks with high book-to-market ratios (e.g., BM4 or BM5) of stocks with high operating profitability (e.g., OP5) and low investment (e.g., INV1 or INV2).

When the skewness dimension is added to compute the distances toward the MVS frontier which are shown in the second column, some major changes are visible. The profile lines of the $\delta$-values in the skewness-only direction, shown by the dash-dotted lines, appear to be dominating in all except the third period where the distances are larger in the mean-only direction. During that particularly turbulent period, the large firm portfolios are much farther away from the frontier in the mean direction even when skewness is taken into account. The portfolios on or close to the frontier are similar to those of the MV case, i.e., the small rather than large stocks, high rather than low book to market, high rather than low profitability and low rather than high investment portfolios.

Introducing kurtosis to reach a full MVSK analysis for which the results reported in the third column does not lead to major changes of that pattern. The dotted profile line for the kurtosis-only variant either rests on a low level or does not exert a large impact on the other profile lines when compared to the MVS analysis. In the boom periods 2 and 4, the dotted lines are somewhere between the dashed and the dash-dotted lines for the variance-only and skewness-only cases, respectively. Hence, there is a certain distance to the frontier recognizable in the kurtosis direction, but this has only a minor effect on the distances in the other directions. This resembles the finding that adding skewness to a mean–variance analysis has a much larger impact on the analysis than adding kurtosis (see Briec and Kerstens 2010). From the findings here, one may conjecture that the addition of kurtosis does open a distinct dimension in which some portfolios are closer to the frontier than others but does not alter the space spanned by the other three moments substantially.

5.3 Multiple and optimized directions

We now turn from the consideration of directions pertaining to a single moment to the analysis with multiple directions combining increasing mean and skewness with decreasing variance and kurtosis toward the frontier function. The direction vector is either fixed at ${\varvec{g}}=(|{\hat{m}}_{i}|,{\hat{v}}_{i},|{\hat{s}}_{i}|,{\hat{k}}_{i})'$ for portfolio i in program (8) in the MVSK case or endogenously determined by the optimization in program (10). The direction vectors for the MV and MVS cases are ${\varvec{g}}=(|{\hat{m}}_{i}|,{\hat{v}}_{i})'$ and ${\varvec{g}}=(|{\hat{m}}_{i}|,{\hat{v}}_{i},|{\hat{s}}_{i}|)'$, respectively. These variants with fixed multiple and optimized directions lead to the efficiency measures indicated by $\delta _{\mathrm {fix}}$ and $\delta _{\mathrm {opt}}$, respectively.

In Fig. 4, these measures are plotted in the same way as previously with the four periods in the rows and the three moment configurations in the columns. We immediately see that the profile lines for the fixed directions lead to the smaller $\delta$-values as compared to the profile lines with the direction determined to maximize $\delta$ (with the exception of the efficient portfolios where the optimal direction vector is indeterminate).

Fig. 4

$\delta$-values for multiple and optimized directions

The profile lines are now overall closer to the zero line, and correspondingly, the portfolios are overall closer to being efficient in periods 2 and 4 compared to periods 1 and 3. The more efficient portfolios tend to be again those identified previously, i.e., the small, high book to market, high profitability and low investment portfolios. We again find larger changes of the profile lines when moving from MV to MVS compared to moving from MVS to MVSK. Thus, the impact of adding skewness is considerable, while the impact of adding kurtosis is minor. Overall, the level of the profile lines increases as more moments are considered.

Correspondingly, Fig. 5 depicts the optimal direction weights $\gamma$ from solving program (10). When compared to the solutions for the $\delta$-values from the single directions in Fig. 3, we find a close resemblance of the dominating profile lines.

Fig. 5

$\gamma$-values for optimized directions

In this respect, we find a larger distance in the direction of an increasing mean for period 1 in the MV case as well as in period 3 for all three configurations of moments. The distance is larger in the direction of reducing variance for most portfolios in the boom periods 2 and 4 in the MV case. Adding skewness shows that the distance to the frontier is considerable in the direction of increasing skewness in all periods except the third. Again, it appears that adding kurtosis seems to add a really distinct dimension. We observe considerable magnitudes of the direction weights in the kurtosis direction, while the weights for the other directions remain largely unaffected. This is particularly evident for the boom phases in the second and the fourth period.

Portfolio management can retrieve substantial information from the results. The $\delta$-value indicates the extent of the overall possible improvement of portfolio efficiency. It represents the distance of the MVSK position of the portfolio under consideration to an efficient point on the frontier function. The $\gamma$-values give a dissection of the overall portfolio efficiency in the directions of the moments under consideration. This can be analyzed for single directions (i.e., the distance to the frontier if just one moment is maximized or minimized) or in all directions with an optimally chosen mix. In addition, the x-weights show to which extent other portfolios or assets are used to construct the efficient point on the portfolio frontier function.

To illustrate this further, we look at the results for portfolio ME1 in the final period in greater detail. The actual moment estimates $({\hat{m}}_{i},{\hat{v}}_{i},{\hat{s}}_{i},{\hat{k}}_{i})$ for $i=\mathrm {ME1}$ are $(1.29,30.44,-33.64,2733.19)$. From the solution of the nonlinear program (10) with endogenous direction choice, we obtain an inefficiency measure of $\delta _{i}=2.389$ which is the sum of the $\gamma$-values (0.092, 0.575, 0.920, 0.802). These values show that ME1 is quite close to the frontier regarding the mean return, farther away regarding risk (variance) and even more distant regarding the higher moments. An improvement of the utility from an investment in these directions would be possible by increasing return slightly, reducing variance substantially as well as increasing skewness and reducing kurtosis by larger margins. The point on the frontier function reached by moving along the direction given by the $\gamma$-values has the coordinates $(1.41,12.93,-2.69,541.84)$ stated in the order of the moments. This point can be replicated by a convex combination of 6 portfolios ME5 (0.10) BM1 (0.20) BM2 (0.27) OP4 (0.18) OP5 (0.17) and INV3 (0.08), where the x-weights are stated in parentheses and all other weights are equal to zero.

6 Conclusion

In this work, we pursue a nonparametric approach adapted from the literature on the measurement of productive efficiency using directional distance functions to the problem of determining optimal distances to portfolio frontier functions in multiple dimensions. This approach permits the straightforward incorporation of higher moments beyond mean and variance. We find that this nonparametric approach leads to several interesting findings.

First, we find that the efficient (or close to efficient) portfolios are those composed of small stocks, those with a high book-to-market ratio, those with a high operating profitability as well as those with low investment. This pattern is quite consistent across all moment configurations. Second, in the mean–variance setting we find larger distances to the frontier in a dominating mean direction for the more stagnating periods. In contrast, the distances to the frontier are much larger in the variance direction for the booming periods. Third, adding the skewness dimension reveals a large role for skewness in the sense of many portfolios being far away from the frontier in this direction (except for one subperiod where the distances in the mean and variance directions remain considerable). Fourth, adding the kurtosis dimension appears not to be as important as adding skewness. The results not change much compared to the mean–variance–skewness setting.

One deficiency of the above analysis is that the portfolio optimization programs are purely deterministic and prone to be sensitive to outliers. Such outliers are surely present in the form of stock market crashes. In the analysis of this paper, the possible effect of those outliers is mitigated by cleansing the returns series before computing the moments as well as by using shrinkage estimators for the second, third and fourth moments. Future research could deal with this issue in another way by attempting to adapt stochastic methods for estimating directional distance functions as proposed by Simar and Vanhems (2012) and Simar et al. (2012) to the portfolio setting. Another promising line of research would be the exploration of the predictive content in the distances to the portfolio frontier, and the specific directions in which these distances are established. Those investigations could proceed along the lines of the research surveyed by Rapach and Zhou (2013).

Appendix

In this appendix, we provide the details of the calculation of the derivatives of portfolio mean, variance and in particular skewness and kurtosis with respect to the portfolio weights. In the literature, this is usually claimed to be straightforward [see, e.g., Jondeau and Rockinger (2006, p. 37)] and nowhere spelled out in detail. The present author only found this to be straightforward after recognizing the specific problem structure here. To beware others from spending much time on replicating these results, we spell out the calculations in full detail here.

For the portfolio mean $m_{p}={\varvec{x}}'\varvec{\mu }$, we immediately obtain $\partial m_{p}/\partial {\varvec{x}}=\varvec{\mu }$. Likewise for the portfolio variance $v_{p}={\varvec{x}}'{\varvec{V}}{\varvec{x}}$, we easily get $\partial v_{p}/\partial {\varvec{x}}=2{\varvec{V}}{\varvec{x}}$ since ${\varvec{V}}$ is a symmetric square matrix (see Harville (2008) or Magnus and Neudecker (1999)).

The derivative of the portfolio skewness $s_{p}={\varvec{x}}'{\varvec{S}}({\varvec{x}}\otimes {\varvec{x}})$ is less straightforward and requires paying attention to the specific structure of ${\varvec{S}}=E\left( {\varvec{r}}{\varvec{r}}'\otimes {\varvec{r}}'\right)$. Since

$$\begin{aligned} {\varvec{x}}'{\varvec{S}}({\varvec{x}}\otimes {\varvec{x}})=E\left( {\varvec{x}}'({\varvec{r}}{\varvec{r}}'\otimes {\varvec{r}}')({\varvec{x}}\otimes {\varvec{x}})\right) =E\left( {\varvec{x}}'{\varvec{r}}{\varvec{r}}'{\varvec{x}}\otimes {\varvec{r}}'{\varvec{x}}\right) =E\left( y\cdot y\cdot y\right) \end{aligned}$$

with $y={\varvec{r}}'{\varvec{x}}$ being scalar, we can apply the product rule of differentiation and the Kronecker product rules $({\varvec{A}}\otimes {\varvec{B}}\otimes {\varvec{C}})({\varvec{x}}\otimes {\varvec{x}}\otimes {\varvec{x}})={\varvec{A}}{\varvec{x}}\otimes ({\varvec{B}}\otimes {\varvec{C}})({\varvec{x}}\otimes {\varvec{x}})={\varvec{A}}{\varvec{x}}\otimes {\varvec{B}}{\varvec{x}}\otimes {\varvec{C}}{\varvec{x}}$ forwards and backwards [assuming conformable matrices ${\varvec{A}}$, ${\varvec{B}}$ and ${\varvec{C}}$, see Harville (2008, p. 341)]. Acknowledging the equivalence of ordinary multiplication and the Kronecker product for scalar factors we obtain

$$\begin{aligned} \dfrac{\partial s_{p}}{\partial {\varvec{x}}}= & {} E\left( \dfrac{\partial }{\partial {\varvec{x}}}y\cdot y\cdot y\right) \\= & {} E\left( \dfrac{\partial y}{\partial {\varvec{x}}}\cdot y\cdot y+y\cdot \dfrac{\partial y}{\partial {\varvec{x}}}\cdot y+y\cdot y\cdot \dfrac{\partial y}{\partial {\varvec{x}}}\right) \\= & {} 3E\left( \dfrac{\partial y}{\partial {\varvec{x}}}\cdot y\cdot y\right) \\= & {} 3E\left( {\varvec{r}}\cdot {\varvec{r}}'{\varvec{x}}\cdot {\varvec{r}}'{\varvec{x}}\right) \,\mathrm {using}\,\dfrac{\partial y}{\partial {\varvec{x}}}=\dfrac{\partial {\varvec{r}}'{\varvec{x}}}{\partial {\varvec{x}}}={\varvec{r}}\\= & {} 3E\left( {\varvec{r}}{\varvec{r}}'{\varvec{x}}\otimes {\varvec{r}}'{\varvec{x}}\right) \\= & {} 3E\left( ({\varvec{r}}{\varvec{r}}'\otimes {\varvec{r}}')({\varvec{x}}\otimes {\varvec{x}})\right) \\= & {} 3E\left( {\varvec{r}}{\varvec{r}}'\otimes {\varvec{r}}'\right) ({\varvec{x}}\otimes {\varvec{x}})\\= & {} 3{\varvec{S}}({\varvec{x}}\otimes {\varvec{x}}). \end{aligned}$$

The same reasoning can be applied to calculate the derivative for portfolio kurtosis $k_{p}={\varvec{x}}'{\varvec{K}}({\varvec{x}}\otimes {\varvec{x}}\otimes {\varvec{x}})$. Here, we have ${\varvec{K}}=E\left( {\varvec{r}}{\varvec{r}}'\otimes {\varvec{r}}'\otimes {\varvec{r}}'\right)$, and thus,

$$\begin{aligned} {\varvec{x}}'{\varvec{K}}({\varvec{x}}\otimes {\varvec{x}}\otimes {\varvec{x}})= & {} E\left( {\varvec{x}}'({\varvec{r}}{\varvec{r}}'\otimes {\varvec{r}}'\otimes {\varvec{r}}')({\varvec{x}}\otimes {\varvec{x}}\otimes {\varvec{x}})\right) \\= & {} E\left( {\varvec{x}}'{\varvec{r}}{\varvec{r}}'{\varvec{x}}\otimes {\varvec{r}}'{\varvec{x}}\otimes {\varvec{r}}'{\varvec{x}}\right) =E\left( y\cdot y\cdot y\cdot y\right) \end{aligned}$$

with $y={\varvec{r}}'{\varvec{x}}$ being scalar as above. Using the same approach as above for skewness, we get:

$$\begin{aligned} \dfrac{\partial k_{p}}{\partial {\varvec{x}}}= & {} E\left( \dfrac{\partial }{\partial {\varvec{x}}}y\cdot y\cdot y\cdot y\right) \\= & {} E\left( \dfrac{\partial y}{\partial {\varvec{x}}}\cdot y\cdot y\cdot y+y\cdot \dfrac{\partial y}{\partial {\varvec{x}}}\cdot y\cdot y+y\cdot y\cdot \dfrac{\partial y}{\partial {\varvec{x}}}\cdot y+y\cdot y\cdot y\cdot \dfrac{\partial y}{\partial {\varvec{x}}}\right) \\= & {} 4E\left( \dfrac{\partial y}{\partial {\varvec{x}}}\cdot y\cdot y\cdot y\right) \\= & {} 4E\left( {\varvec{r}}\cdot {\varvec{r}}'{\varvec{x}}\cdot {\varvec{r}}'{\varvec{x}}\cdot {\varvec{r}}'{\varvec{x}}\right) \,\mathrm {again\,using}\,\dfrac{\partial y}{\partial {\varvec{x}}}=\dfrac{\partial {\varvec{r}}'{\varvec{x}}}{\partial {\varvec{x}}}={\varvec{r}}\\= & {} 4E\left( {\varvec{r}}{\varvec{r}}'{\varvec{x}}\otimes {\varvec{r}}'{\varvec{x}}\otimes {\varvec{r}}'{\varvec{x}}\right) \\= & {} 4E\left( ({\varvec{r}}{\varvec{r}}'\otimes {\varvec{r}}'\otimes {\varvec{r}}')({\varvec{x}}\otimes {\varvec{x}}\otimes {\varvec{x}})\right) \\= & {} 4E\left( {\varvec{r}}{\varvec{r}}'\otimes {\varvec{r}}'\otimes {\varvec{r}}'\right) ({\varvec{x}}\otimes {\varvec{x}}\otimes {\varvec{x}})\\= & {} 4{\varvec{K}}({\varvec{x}}\otimes {\varvec{x}}\otimes {\varvec{x}}). \end{aligned}$$